Sway and disturbance rejection control for varying rope tower cranes suffering from friction and unknown payload mass

Abstract

Tower cranes are well-known underactuated systems, where the design of controllers for them with time-varying rope length was weak in the past because of their complex dynamic characteristic. The payload oscillation will become worse when the jib slew angle, the trolley position and the rope length are changed simultaneously. The proposed method is designed based on robust adaptive sliding mode control via tracking nonzero initial reference trajectories, in which frictions and lumped disturbances in the crane system are eliminated, and unknown payload mass is effectively estimated online. Lyapunov technique is combined with LaSalle’s invariance theorem to design controller and analyze stability. Various and strict simulations are applied, which validate the effectiveness and extreme robustness of the proposed method.

1 Introduction

Because of their combination of simple structure and complex dynamic characteristics, underactuated systems where the number of actuators is less than the DOF (degrees of freedom) have been paid more and more attention to the control technique improvement in recent years [1, 2]. Typical underactuated systems include underactuated manipulators [3], underactuated mobile robots [4], reaction wheel pendulums [5], and cranes [6], etc. Among them, cranes are common and utilized to transport payload over long distances in factories, ports, construction sites, and so on.

Tower crane is a kind of crane that transports goods in 3D (three-dimension) space. Its transportation process is often accompanied by the translation of the trolley and the rotation of the jib. These two driving mechanisms with different motion properties make the dynamic model and design corresponding control method more complicated. At the same time, with the lifting movement of the payload, the length of the rope will change, which will have a great impact on the dynamic characteristics of the tower crane, such as the natural frequency of the payload swing. In addition, at the actual control applications, it is inevitable that there will be friction effect, incomplete theoretical modeling, parameter uncertainties and external disturbances of full DOF. In these cases, it is a very challenging issue to realize the accurate positioning of the jib, trolley and payload lifting with quickly suppressing the swing of the payload.

The sliding mode control (SMC) can effectively cope with uncertainties and disturbances and is widely applied for nonlinear systems. Recently, Chereji et al. [7] have presented novel variant-designed LSMC and RSMC controllers handling uncertainties caused by unmodeled system dynamics and the simplified actuator model. The controllers improve the robust control performance and do not add complexity. Based on a finite-time extended state observer (FTESO) and a super-twisting SMC, Liu et al. [8] designed a finite-time decoupling control strategy, and its effectiveness and robustness demonstrated via simulations. Wang et al. [9] designed an USDE-based (unknown system dynamics estimator) SMC method for unknown dynamics servo mechanisms, and simulation and experiments showed the satisfying control performance. However, the above methods were aimed at full-actuated systems, which may not be effective for underactuated systems.

For underactuated systems control, some studies are existed. Based on the combination of Udwadia–Kalaba equations and underactuated equivalence principle, Pappalardo et al. [10] presented a control method for underactuated nonholonomic mechanical systems, and the effectiveness of the method is verified by a mobile robot dynamics model through many numerical experiments. A SMC method based on extended disturbance observer (SMCDO) was studied for a class of underactuated systems by Ding et al. [11], and simulation results showed the SMCDO has strong disturbance compensation ability and better control performance. Ashrafiuon et al. [12] designed a general SMC method for nonlinear underactuated multibody mechanical systems by full-state feedback.

In the past, many controllers aiming at cranes to realize payload transportation and swing suppression have been worked out, which include input-shaping [13], sliding mode control [14, 15], adaptive control [16,17,18,19,20], coupling based method [6, 21, 22], robust control [23,24,25], optimal control [26], intelligent control [27, 28] and adaptive neural network sliding mode control [29], which is control method combining intelligent algorithm and traditional controller.

However, to increase transportation efficiency, the rope is often hoisted and lowered in many actual conditions. Consequently, these above approaches that are all not mentioned the presence of the changed rope length are not certifiable the control performance and system stability.

To solve the control problems of time-varying rope length condition for cranes, Ramli et al. presented an efficient controller using NNUMZV-APIDLNN algorithm considering payload hoisting and disturbances for overhead cranes, where significant reduction effect in the swing angles was derived with experimental results [30].

Li et al. designed a coupling-based controller for underactuated overhead cranes to anti-swing and transferring payload [31]. Finite-time flatness-based regulation controllers [32] were designed for cranes with both constant and varying cable length, and anti-swing and high-speed positioning problems were cracked owing to Zhang et al. An adaptive coupling method subject to unknown model parameters was proposed by Sun et al. and verified by experiments, which could achieve precise trolley positioning and payload hoisting/lowering control as well as fast swing elimination [33]. Lu et al. [34] presented an enhanced-coupling adaptive controller for overhead cranes, which had improvement in the control performance and increased the robustness aiming at the unknown payload mass. But, this method just solves the unknown payload mass problem; other common influences such as friction or external disturbances are omitted. In another research to solve the payload hoisting effect problem, an improved UMZV shaper by using the PSO algorithm to select the optimal control parameters was utilized for underactuated 3D overhead cranes [35]. But, to solve the problems of dynamic modeling and trajectory optimization, Peng et al. [36] proposed a dynamic modeling and trajectory tracking control strategy. Yang et al. [37] designed a nonlinear actuator constraints controller combining state observer and online friction compensation, which achieved good results about jib/trolley positioning and payload sway suppression by experimental validation. Zhang et al. [38] reported an adaptive sway reduction controller for the tower crane, and the anti-sway effect is enhanced compared with PD controller.

After illustrating the recent existing researches, there are still some intractable problems that need to be solve:

• (1) Traditional underactuated crane positioning and anti-sway control is usually aimed at overhead crane systems [6, 15, 20]. Even if overhead cranes with multiple DOF move in 3D space, the driveable mechanism is still work in linear force, the dynamic characteristics are still simple, and the corresponding controllers design is relatively convenient. However, when different driving forces appear in the crane transportation task, such as in tower crane control, one direction is the translation force of the trolley, and the other direction is the jib torque. At this time, due to the participation of eccentric motion for payload, the system dynamics becomes very complicated. At the same time, when the payload is lifted and lowered, the natural frequency of the payload swing will change. Hence, the failure of the controller designed for the ordinary single-pendulum will inevitably occur.

• (2) For traditional controllers, on the one hand, only positioning can be achieved under normal circumstances [22, 31], but the swing suppression effect is not good, and the overall convergence speed is slow; on the other hand, most controllers use regulation control methods [38] for the target position, but in practical applications, the regulation control will produce a great initial output value of the controller, causing inevitable initial fluctuations, damaging the life of drivers and affecting the effect of anti-swing.

• (3) In real applications, many factors, such as the friction of input channel, unmodeled part effect, parameter uncertainties and full DOF external disturbances, inevitably appear in motion process, while many control strategies do not fully consider and restrain their adverse effects. Under these circumstances, it is a very challenging problem to achieve accurate positioning of the actuated mechanism while quickly suppressing the swing of the payload.

The above problems are clearly stated, and the main contributions of this paper are as follows:

• (1) Linearized model is not needed in the proposed controller, and a sliding mode surface vector with nonlinear variable gains and nonzero initial reference trajectories is designed. As long as there exists error in the system, the variable gains will continue to be changed adaptively, so that the stable convergence speed of the tower crane system is improved compared with traditional SMC methods.

• (2) Adaptive technology is used to suppress the influence of friction, unmodeled parts, parameter uncertainties and external disturbances, and specially, in order to solve the problem that the unknown payload mass has an impact on the rope lifting motion, the mass value is also self-adapted. Hence, the proposed controller presents both good control performance and extreme robustness in simulations.

Compared to the existing methods, the contributions are detailedly illustrated. Firstly, the sliding model surfaces in previous SMC controllers (e.g., [7,8,9]) are all changeless; however, the proposed controller RASMC has nonlinear variable gains for better convergence performance. And, many previous researches about adaptive control for cranes (e.g., [16, 18, 19]) only used adaptive technique to estimate frictional parameters or unknown model parameters, where not only the structure of the adaptive part is complicated, but also the external disturbances and the unmodeled nonlinearity factors are not considered in theory. In addition, although the new method reported in [38] addressed the unknown friction for the varying rope tower cranes, the disturbance and unknown m were not taken into account.

A robust adaptive sliding mode control (RASMC) method is proposed in this paper. Firstly, in Sect. 2, the control problems of time-varying underactuated systems considering friction, model parameters uncertainties, the unconsidered nonlinear factors and external disturbances are introduced. Then, the properties of nonzero initial reference trajectories are shown. In Sect. 3, a demonstrative example is presented. The model of a tower crane with time-varying rope length is shown, and specific model parameters is listed. In Sect. 4, to improve the convergence speed of traditional sliding mode control, a sliding mode surface with variable gains is designed, and the gains are changed by error adaptively. The friction, lumped disturbance and unknown payload mass are estimated by adaptive technique. The control system stability is proved by Lyapunov technique and LaSalle’s invariance principle strictly. In Sect. 5, many representative simulations are conducted to demonstrate its effectiveness on trajectory tracking, swing elimination, friction compensation, lumped disturbances suppression and payload mass estimation. And, Sect. 6 is conclusion of this paper.

2 Problem statement

This paper is aimed to solve the control problems of time-varying underactuated crane systems, where a typical underactuated system can be described as follows [39]:

$$\begin{aligned}&\varvec{M}( {\varvec{q}}){\ddot{\varvec{q}}} + {\varvec{C}}( {\varvec{q}}, {\dot{\varvec{q}}}){\dot{\varvec{q}}} + {\varvec{G}}( {\varvec{q}}) \nonumber \\&\quad = {\varvec{U}} - {{\varvec{F}}}_s({\dot{\varvec{q}}}) + {\varvec{D}}, \end{aligned}$$

(1)

where the dimensions of the actuated mechanism and DOF are m and n, respectively, ${\varvec{q}}=[q_1,...,q_n]^T \in {R^n}$ is the system generalized coordinates, $\varvec{M}( {\varvec{q}}) \in {R^{n \times n}}$ denotes the inertia matrix, ${\varvec{C}}( {\varvec{q}},\dot{ {\varvec{q}}}) \in {R^{n \times n}}$ represents the centripetal-Coriolis matrix, ${\varvec{G}}( {\varvec{q}}) \in {R^n}$ is the gravity-related vector, ${\varvec{U}}={[u_1,...,u_m,\;{\varvec{0}}_{(n-m) \times 1}]^T} \in {R^n}$ is the input vector, ${ { {{\varvec{F}}}_s(\dot{\varvec{q}})}} {=} {[F_{1f},...,F_{mf}, \; {\varvec{0}}_{(n{-}m) {\times } 1}]^T} \in {R^n}$ denotes the nonlinear friction-related vector, ${\varvec{D}}=[d_1,...,d_n]^T \in {R^n}$ represents the disturbance vector, including model parameters uncertainties, the unconsidered nonlinear factors and external disturbances, etc.

The following assumption needs to be declared for ease of analysis:

Assumption 1

The disturbance vector ${\varvec{D}}$ includes model parameters uncertainties, unconsidered nonlinear factors and external disturbances, etc., and ${\varvec{D}}$ is usually assumed to be limited, that is [15, 40],

$$\begin{aligned} |d_i| \le \nu _i,i=1,...,n, \end{aligned}$$

(2)

where $\nu _i$ denotes the upper limit of the aggregate uncertainties of each DOF. To quickly suppress the vibration of the underactuated mechanism and meanwhile drive actuated mechanism from the initial positions to the target values are the control objective, which can be presented mathematically as follows:

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } {\varvec{q}} = {{\varvec{q}}}_d, \end{aligned}$$

(3)

where ${{\varvec{q}}}_d= [ {{q _{1d}},...,{q _{\mathrm{md}}}\;{\varvec{0}}_{(n-m) \times 1} ]^T}$, with ${q _{id}}, i=1,...,m$ representing the target position.

To avoid problems, big initial actuators output values and unsmooth running process, the RASMC method tracks the reference trajectories to implement positioning, which have the following properties:

• (1) The final values for velocity and acceleration of the actuated part should be zero after $t_{d}$,

  $$\begin{aligned} r_i(t) {=} {q _{\mathrm{id}}},{{\dot{r} }_i}(t) {=} 0,{{\ddot{r} }_i}(t) {=} 0,t {\ge } {t_{ d}},i=1,...,m, \end{aligned}$$

  (4)

  where $r_i(t)$ means the reference trajectory.

• (2) For safety reasons and actual situations, the reference trajectories do not have infinite values state, that is,

  $$\begin{aligned} {r _i}(t),{\dot{r} _i}(t),{\ddot{r} _i}(t) \in L_{\infty }, i=1,...,m, \end{aligned}$$

  (5)

• (3) The definition of initial values for each target trajectories are as follows:

  $$\begin{aligned} {r _i}(0) = {q _{i0}},{{\dot{r} }_i}(0) = 0,{{\ddot{r} }_i}(0) = 0, i=1,...,m, \end{aligned}$$

  (6)

  where ${q _{i0}}$ denotes the initial position of the actuated part.

After the above analysis, the following reference trajectories that satisfy the requirements (4)–(6) are utilized:

$$\begin{aligned} {r_i} = \left\{ \begin{array}{l} \left( { { {q}}_{\mathrm{id}} - { {q}}_{i0}} \right) \left( {\frac{t}{{{t_d}}} - \frac{{\mathrm{sin}(\frac{{2\pi t}}{{{t_d}}})}}{{2\pi }}} \right) \\ \quad \quad \quad \quad \quad + { {q}}_{i0},t \in [0, {t_d} )\\ { {q}}_{\mathrm{id}},t \in [{t_d}, + \infty ] \end{array} \right. , i = 1,...,m, \end{aligned}$$

(7)

where it is found that the reference trajectories are a kind of cycloidal curve, and positioning time, initial position and target position can be adjusted freely.

Remark 1

According to some previous researches about crane anti-swing control, we know that trajectory planning method [41,42,43] is a kind of effective control scheme, which shows that reference trajectory has great effect on the swing-reduction performance. Thus, for closed-loop tracking control (e.g., the proposed method), choosing feasible reference trajectories is a certain necessity for improving control effect. Theoretically, any type of trajectory, such as step, cycloidal curve (e.g., the trajectory in (7)) and input shaped trajectory, can be applied to crane systems to evaluate the control performance of the designed method. However, because of the discontinuity of the step trajectory, it is not usually used in practical crane operation. As for the input shaped trajectory, when the natural frequency of the payload swinging system changes greatly, it has to be re-designed. However, the cycloidal curve trajectory not only meets the requirements of (4)–(6), but also has zero acceleration at both the starting point and the end point, which can smooth the start and stop. Therefore, the cycloidal curve like (7) has been widely used in industrial applications.

Remark 2

The initial values setting of all reference trajectories is essential in actual tower cranes operation circumstances. Firstly, the position of the trolley and the length of the rope cannot be zero considering tower cranes physical structure and safety. On the other hand, the values of the jib angle, the trolley position and the rope length are always changed in continuous positioning tasks; thus, to set reference trajectories initial values are more practical.

3 Demonstrative example

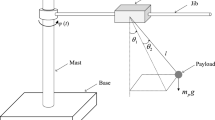
In this section, a demonstrative example is reported. The model diagram of tower cranes with time-varying rope length is presented as shown in Fig. 1, whose mathematical model is built by the Lagrange’s kinematics equations, and the relations are as follows [39]:

$$\begin{aligned}&\varvec{M}( {\varvec{q}})\ddot{ {\varvec{q}}} + {\varvec{C}}( {\varvec{q}}, \dot{ {\varvec{q}}})\dot{ {\varvec{q}}} + {\varvec{G}}( {\varvec{q}}) = {\varvec{U}} - {{\varvec{F}}}_s(\dot{ {\varvec{q}}}) + {\varvec{D}}, \end{aligned}$$

(8)

where the detailed internal terms of (8) are included in Appendix A. Noting that the system equation in (8) describes only the tower crane model in Fig. 1, but (1) describes typical underactuated systems, which is not the same. In (8), m and $M_t$ denote the payload mass and the trolley mass, respectively. $J_0$ is the rotational inertia of the jib, and g is the earth acceleration. $\alpha (t)$, x(t), l(t), $\theta _1(t)$ and $\theta _2(t)$ (i.e., $q_1,...,q_5$), respectively, represent the jib rotational angle, the trolley position, the rope length, the payload swing angle in the jib vertical plane and the payload swing angle out of that plane as shown in Fig. 1. Defining ${\varvec{q}} = [\alpha (t)\; x(t)\; l(t)\; \theta _1(t) \; \theta _2(t)]^T \in {R^5}$ is the tower crane system generalized coordinates, $\varvec{M}( {\varvec{q}}) \in {R^{5 \times 5}}$ denotes the inertia matrix, ${\varvec{C}}( {\varvec{q}},\dot{ {\varvec{q}}}) \in {R^{5 \times 5}}$ represents the centripetal-Coriolis matrix, ${\varvec{G}}( {\varvec{q}}) \in {R^5}$ is the gravity-related vector, ${\varvec{U}}={[T\;{F_x}\;{F_l}\;0\;0]^T} \in {R^5}$ is the input vector, ${{\varvec{F}}}_s(\dot{ {\varvec{q}}})={[{T_f}\;{F_{xf}}\;{F_{lf}}\;0\;0]^T} \in {R^5}$ denotes the nonlinear friction-related vector, ${\varvec{D}}=[d_1\;d_2\;d_3\;d_4\;d_5]^T \in {R^5}$ represents the disturbance vector, including model parameters uncertainties, the unconsidered nonlinear factors and external disturbances, etc. And, the model parameters of the tower crane are shown in Table 1. Besides, for ease of reading, we set $S_i=\sin \theta _i$ and $C_i=\cos \theta _i$ (i = 1, 2) in the full paper.

Fig. 1

Tower crane model

Table 1 Tower crane model parameters

In addition, ${T_f}$, ${F_{xf}}$ and ${F_{lf}}$ (i.e., ${F_{1f}}$, ${F_{2f}}$ and ${F_{3f}}$) are produced by the motion of the jib, trolley, and the rope hoisting/lowing, respectively. The following feed-forward friction compensation model is used [39]:

$$\begin{aligned} F_{if} = {f_{i1}}\tanh \left( \frac{ \dot{ { {q}}}_i}{\varepsilon }\right) + {f_{i2}}|{ \dot{ { {q}}}_i}|{ \dot{ { {q}}}_i},i = 1,2,3, \end{aligned}$$

(9)

where ${f_{i1}}$, ${f_{i2}}$, ${\varepsilon }$ denote the friction-related coefficients, noticing that the precise values of them are difficult to be chosen unless by cumbersome and unpractical repetition test.

4 Main results

4.1 Controller design

After simple mathematic operations, (8) changes its form to the following result:

$$\begin{aligned} \ddot{ {\varvec{q}}} = {\varvec{M}}{( {\varvec{q}})^{ - 1}}\Big ( { {\varvec{U}} - {{\varvec{F}}}_s(\dot{ {\varvec{q}}}) + {\varvec{D}} - {\varvec{C}}( {\varvec{q}},\dot{ {\varvec{q}}})\dot{ {\varvec{q}}} - {\varvec{G}}( {\varvec{q}})} \Big ), \end{aligned}$$

(10)

and (10) extracts $\ddot{ {\varvec{q}}}$ from dynamic equation (8). Then, the item of ${\varvec{D}}$ is separated, and we have

$$\begin{aligned} \ddot{ {\varvec{q}}}&= {\varvec{M}}{( {\varvec{q}})^{ - 1}}\Big ( {\varvec{U}} - {{\varvec{F}}}_s(\dot{ {\varvec{q}}})- {\varvec{C}}( {\varvec{q}},\dot{ {\varvec{q}}})\dot{ {\varvec{q}}}\nonumber \\&\quad - {\varvec{G}}'_c( {\varvec{q}}) - {\varvec{G}}'( {\varvec{q}})\Big ) + {\varvec{M}}{( {\varvec{q}})^{ - 1}} {\varvec{D}}, \end{aligned}$$

(11)

where ${{\varvec{G}}}'_c = {[0\;0\; - mgC_1C_2\;0\;0]^T} \in {R^5}$, ${\varvec{G}}'( {\varvec{q}})=[0\;0\; 0$ $mglC_2S_1\;mglC_1S_2]^T \in {R^5}$.

Taking out the driving force/torque and then composing a new input vector ${{\varvec{U}}}_a = {[T\;{F_x}\;{F_l}]^T} \in {R^3}$ to analysis, the following equation is derived:

$$\begin{aligned} \ddot{ {\varvec{q}}}&= {\varvec{\varGamma }} ( {\varvec{q}},\dot{ {\varvec{q}}}) + {\varvec{\varPhi }} ( {\varvec{q}})\Big ( { {{\varvec{U}}}_a - {{\varvec{F}}}_{\mathrm{sa}}(\dot{ {\varvec{q}}})} - {\varvec{G}}_c( {\varvec{q}})\Big ) \nonumber \\&\quad + {\varvec{M}}{( {\varvec{q}})^{ - 1}} {\varvec{D}}, \end{aligned}$$

(12)

where ${{\varvec{F}}}_{\mathrm{sa}}(\dot{ {\varvec{q}}}) = {[{T_f}\;{F_{xf}}\;{F_{lf}}]^T}\in {R^3}$, ${{\varvec{G}}}_c = [0\;0\; - mgC_1C_2]^T \in {R^3}$, besides, ${\varvec{\varGamma }} ( {\varvec{q}},\dot{ {\varvec{q}}}) \in {R^5}$ and ${\varvec{\varPhi }} ( {\varvec{q}}) \in {R^{5 \times 3}}$ are as follows:

$$\begin{aligned}&{\varvec{\varGamma }} ( {\varvec{q}},\dot{ {\varvec{q}}}) = {[{a_1}\;{a_2}\;{a_3}\;{a_4}\;{a_5}]^T}, \end{aligned}$$

(13)

$$\begin{aligned}&{\varvec{\varPhi }} ( {\varvec{q}}) = {\left[ \begin{array}{l} {b_{11}}\;{b_{21}}\;{b_{31}}\;{b_{41}}\;{b_{51}}\\ {b_{12}}\;{b_{22}}\;{b_{32}}\;{b_{42}}\;{b_{52}}\\ {b_{13}}\;{b_{23}}\;{b_{33}}\;{b_{43}}\;{b_{53}} \end{array} \right] ^T}, \end{aligned}$$

(14)

where the specific expressions in above (13) and (14) are included in Appendix B.

Recalling reference trajectories in (7), we redefine ${r_1} = {\alpha _r}(t)$, ${r_2} = {x_r}(t)$, ${r_3} = {l_r}(t)$, ${ {q}}_{1d} = {\alpha _d}$, ${ {q}}_{2d} = {x_d}$, ${ {q}}_{3d} = {l_d}$ $\le$ $l_u$, ${ {q}}_{10} = {\alpha _0}$, ${ {q}}_{20} = {x_0}$, ${ {q}}_{30} = {l_0}$ $\ge$ $l_l$, and $l_l \le l \le l_u$ for ease of understanding, in which $l_l$ is a positive value that represents the lower limiting value of the rope length, and $l_u$ denotes the upper limit value. In addition, we define ${\varvec{q}}_r(t)=[\alpha _r(t)\; x_r(t)\; l_r(t)\; 0\; 0]^T$.

To achieve smooth and fast convergence effect, the following adaptive sliding mode surface is constructed,

$$\begin{aligned}&{\varvec{S}} =\dot{ {\varvec{e}}} + {{\varvec{\varLambda }}} \hat{ {\varvec{\varDelta }}}(t) {\varvec{e}}, \end{aligned}$$

(15)

where ${\varvec{S}} \in {R^5}$, ${\varvec{e}} = [{e_\alpha }\;{e_x}\;{e_l}\;{\theta _1}\;{\theta _2}]^T= {\varvec{q}} - {{\varvec{q}}}_r(t) \in {R^5}$, ${\varvec{\varLambda }} = \mathrm{diag}\{ {k_1},...,{k_5}\} \in {R^{5 \times 5}}$ where its diagonal elements are all positive, $\hat{ {\varvec{\varDelta }}}(t) = \mathrm{diag}\{ {{\hat{\lambda }}_1}(t),...,{{{\hat{\lambda }} }_5}(t)\} \in {R^{5 \times 5}}$ is the adaptive diagonal matrix where its diagonal elements is time-varying by system condition. Note that the sliding surface ${\varvec{S}}$ has the following properties: (1) it is a vector in five dimensions; (2) it contains a constant gain and an adaptive gain diagonal matrix; (3) it contains reference trajectories. In a word, the sliding surface is adaptive and meets trajectory tracking demand of all DOF.

The following sliding mode reaching law is selected,

$$\begin{aligned} \dot{ {\varvec{S}}}&= - {\mathbf{I } } {\varvec{S}} - {{\mathbf{H } }}{\mathrm{sgn}} ( {\varvec{S}})\nonumber \\&= - \left[ {\begin{array}{*{20}{l}} {{\mu _1}({{\dot{ {e}}}_\alpha } + {k_1}{{{\hat{\lambda }} }_1}(t){e_\alpha })}\\ {{\mu _2}({{\dot{ {e}}}_x} + {k_2}{{{\hat{\lambda }} }_2}(t){e_x})}\\ {{\mu _3}({{\dot{ {e}}}_l} + {k_3}{{{\hat{\lambda }} }_3}(t){e_l})}\\ {{\mu _4}({{{\dot{\theta }} }_1} + {k_4}{{{\hat{\lambda }} }_4}(t){\theta _1})}\\ {{\mu _5}({{{\dot{\theta }} }_2} + {k_5}{{{\hat{\lambda }} }_5}(t){\theta _2})} \end{array}} \right] \nonumber \\&\quad -\left[ {\begin{array}{*{20}{l}} {{\gamma _1}{{\mathrm{sgn}}} ({{\dot{ {e}}}_\alpha } + {k_1}{{{\hat{\lambda }} }_1}(t){e_\alpha })}\\ {{\gamma _2}{{\mathrm{sgn}}} ({{\dot{ {e}}}_x} + {k_2}{{{\hat{\lambda }} }_2}(t){e_x})}\\ {{\gamma _3}{{\mathrm{sgn}}} ({{\dot{ {e}}}_l} + {k_3}{{{\hat{\lambda }} }_3}(t){e_l})}\\ {{\gamma _4}{{\mathrm{sgn}}} ({{{\dot{\theta }} }_1} + {k_4}{{{\hat{\lambda }} }_4}(t){\theta _1})}\\ {{\gamma _5}{{\mathrm{sgn}}} ({{{\dot{\theta }} }_2} + {k_5}{{\hat{\lambda }}_5}(t){\theta _2})} \end{array}} \right] , \end{aligned}$$

(16)

where ${{\mathbf{I } }} = \mathrm{diag}\{ {\mu _1},...,{\mu _5}\} \in {R^{5 \times 5}}$ in which its diagonal elements are all positive numbers to be designed, ${{\mathbf{H } }} = \mathrm{diag}\{ {\gamma _1},...,{\gamma _5}\} \in {R^{5 \times 5}}$ where its diagonal elements are also positive and to be determined. Therefore, the sliding mode converging condition is that

$$\begin{aligned} { {\varvec{S}}^T}\dot{ {\varvec{S}}}&= {\varvec{S}}^T\Big (- {{\mathbf{I } }} {\varvec{S}} - {{\mathbf{H } }}\mathrm{{sgn}} ( {\varvec{S}})\Big )\nonumber \\&=- {\varvec{S}}^T {{\mathbf{I } }} {\varvec{S}} - {\varvec{S}}^T {{\mathbf{H } }}\mathrm{{sgn}} ( {\varvec{S}}) \le 0. \end{aligned}$$

(17)

Taking the derivative of ${{\varvec{S}}}$ with respect to time, and substituting (12) into it, the result is that

$$\begin{aligned} \dot{ {\varvec{S}}}&= \ddot{ {\varvec{e}}} + {\varvec{\varLambda }} \dot{\hat{ {\varvec{\varDelta }}}}(t) {\varvec{e}} + {{\varvec{\varLambda }}} \hat{ {\varvec{\varDelta }}}(t)\dot{ {\varvec{e}}}\nonumber \\&= \ddot{ {\varvec{q}}} - \ddot{{{ {\varvec{q}}}}}_r(t) + {{\varvec{\varLambda }}} \dot{\hat{ {\varvec{\varDelta }}}}(t) {\varvec{e}} + {{\varvec{\varLambda }}} \hat{ {\varvec{\varDelta }}}(t)\dot{ {\varvec{e}}}\nonumber \\&= {\varvec{\varGamma }} ( {\varvec{q}},\dot{ {\varvec{q}}}) + {\varvec{\varPhi }} ( {\varvec{q}})\Big ( { {{\varvec{U}}}_a - {{\varvec{F}}}_{\mathrm{sa}}(\dot{ {\varvec{q}}})}- \varvec{G}_c( {\varvec{q}}) \Big )\nonumber \\&\quad + {\varvec{M}}{( {\varvec{q}})^{ - 1}} {\varvec{D}} - \ddot{{{ {\varvec{q}}}}}_r(t) + {{\varvec{\varLambda }}} \dot{\hat{ {\varvec{\varDelta }}}}(t) {\varvec{e}} + {{\varvec{\varLambda }}} \hat{ {\varvec{\varDelta }}}(t)\dot{ {\varvec{e}}}. \end{aligned}$$

(18)

The input vector $\varvec{U}_a$ is composed of two parts, and it is that

$$\begin{aligned} {{\varvec{U}}}_a&= {{\varvec{U}}}_{\mathrm{eq}} + {{\varvec{U}}}_{\mathrm{sw}}, \end{aligned}$$

(19)

$$\begin{aligned} {{\varvec{U}}}_{\mathrm{eq}}&= {({ {\varvec{\varPhi }}( {\varvec{q}}) ^T} {\varvec{\varPhi }} ( {\varvec{q}}) )^{ - 1}}{ {\varvec{\varPhi }} ( {\varvec{q}})^T}( - {\varvec{\varGamma }} ( {\varvec{q}},\dot{ {\varvec{q}}}) - { {\varvec{M}}^{ - 1}} {\varvec{D}}\nonumber \\&\quad + \ddot{{{ {\varvec{q}}}}}_r(t) - {{\varvec{\varLambda }}} \dot{\hat{ {\varvec{\varDelta }}}}(t) {\varvec{e}} - {{\varvec{\varLambda }}} \hat{ {\varvec{\varDelta }}}(t)\dot{ {\varvec{e}}}) + {{\varvec{F}}}_{sa}+ {\varvec{G}}_c( {\varvec{q}}), \end{aligned}$$

(20)

$$\begin{aligned} {{\varvec{U}}}_{\mathrm{sw}}&= {({ {\varvec{\varPhi }} ( {\varvec{q}})^T} {\varvec{\varPhi }} ( {\varvec{q}}))^{ - 1}}{ {\varvec{\varPhi }} ( {\varvec{q}})^T}\Big ( - {{\mathbf{I } }} {\varvec{S}} - {{\mathbf{H } }}\mathrm{{sgn}} ( {\varvec{S}})\Big ). \end{aligned}$$

(21)

Remark 3

It can be seen that the control law ${{\varvec{U}}}_a$ (19) includes two components. $\varvec{U}_{\mathrm{eq}}$ is designed to make the control system be more robust in external disturbances and parametric uncertainties. $\varvec{U}_{\mathrm{sw}}$ is used to make sure that in any case, the system state far from or close to the sliding mode surface, fast convergence is feasible.

However, the frictional parameters and aggregate disturbances are unmeasured, which means that the controller cannot contain these unknown parameters. Thus, we have to design adaptive terms to estimate them. Firstly, the estimated frictional model is presented as follows:

$$\begin{aligned} {\hat{F}}_{\mathrm{if}} = {{{\hat{f}}}_{i1}}\tanh \left( \frac{{\dot{ { {q}}}_i}}{\varepsilon }\right) + {{{\hat{f}}}_{i2}}|\dot{ { {q}}}_i|\dot{ { {q}}}_i,i=1,2,3, \end{aligned}$$

(22)

and to facilitate design, the following form is presented:

$$\begin{aligned}&\hat{{ {\varvec{F}}}}_{\mathrm{sa}} = {{\varvec{\upsilon }} }_1(\dot{{\varvec{q}}})\hat{{ {\varvec{{ {\varUpsilon }}}} }}_1 + {{\varvec{\upsilon }} }_2(\dot{{\varvec{q}}})\hat{{ {\varvec{{ {\varUpsilon }}}} }}_2,\nonumber \\&\quad \mathrm{{with}} \hat{{ {\varvec{{ {\varUpsilon }}}} }}_1 = {[{{{\hat{f}}}_{11}}\;{{{\hat{f}}}_{21}}\;{{{\hat{f}}}_{31}}]^T}, \hat{{ {\varvec{\varUpsilon }} }}_2 = {[{{{\hat{f}}}_{12}}\;{{{\hat{f}}}_{22}}\;{{{\hat{f}}}_{32}}]^T},\nonumber \\&{{{\hat{f}}}_{\mathrm{ij}}}(t_0)={{{\bar{f}}}_{\mathrm{ij}}}>0 \in R^+, i=1,2,3,j=1,2, \end{aligned}$$

(23)

where ${{\bar{f}}}_{\mathrm{ij}}$ is a positive constant representing the initial estimated value. ${{\varvec{\upsilon }} }_1(\dot{\varvec{q}})$ $=$ $\mathrm{diag}$ $\{ \tanh (\frac{{{\dot{\alpha }} }}{\varepsilon })$, $\tanh (\frac{{\dot{x}}}{\varepsilon }),$ $\tanh (\frac{{\dot{l}}}{\varepsilon })\}$, ${{\varvec{\upsilon }} }_2(\dot{\varvec{q}}) = \mathrm{diag}\{ |{\dot{\alpha }} |{\dot{\alpha }} ,|\dot{x}|\dot{x},|\dot{l}|\dot{l}\}$. It means the adaptive term ${{\hat{f}}}_{\mathrm{ij}}$ will update from a set positive value to some value, and ${{\bar{f}}}_{\mathrm{ij}}$ can be approximately chosen close to real friction parameters through experience.

Hence, $\varvec{U}_{\mathrm{eq}}$ and $\varvec{U}_{sw}$ are reconstructed as follows:

$$\begin{aligned} {{\varvec{U}}}_{\mathrm{eq}}&= {({ {\varvec{\varPhi }} ( {\varvec{q}}) ^T} {\varvec{\varPhi }} ( {\varvec{q}}) )^{ - 1}}{ {\varvec{\varPhi }} ( {\varvec{q}}) ^T}( - {\varvec{\varGamma }} ( {\varvec{q}},\dot{ {\varvec{q}}}) - { {\varvec{M}}^{ - 1}}\hat{ {\varvec{D}}}\nonumber \\&\quad + \ddot{ {\varvec{q}}}_r(t) - {{\varvec{\varLambda }}} \dot{\hat{ {\varvec{\varDelta }}}}(t) {\varvec{e}} - {{\varvec{\varLambda }}} \hat{ {\varvec{\varDelta }}}(t)\dot{ {\varvec{e}}}) \nonumber \\&\quad + {{\varvec{\upsilon }} }_1(\dot{\varvec{q}})\hat{{ {\varvec{\varUpsilon }} }}_1 + {{\varvec{\upsilon }} }_2(\dot{\varvec{q}})\hat{{ {\varvec{\varUpsilon }} }}_2+\hat{ {\varvec{G}}}_c( \varvec{q}), \end{aligned}$$

(24)

$$\begin{aligned} {{\varvec{U}}}_{\mathrm{sw}}&= {({ {\varvec{\varPhi }} ( {\varvec{q}})^T} {\varvec{\varPhi }} ( {\varvec{q}}))^{ - 1}}{ {\varvec{\varPhi }} ( {\varvec{q}})^T}\Big ( - {{\mathbf{I } }} {\varvec{S}} - {{\mathbf{H } }}\mathrm{{sgn}} ( {\varvec{S}})\Big ), \end{aligned}$$

(25)

where $\hat{ {\varvec{G}}}_c( {\varvec{q}})= {[0\;0\; - \hat{m}gC_1C_2]^T} \in {R^3}$, $\hat{m}$ represents the estimated value of payload mass with $\hat{m}(t_0)=\bar{m} >0 \in R^+$, $\bar{m}$ denotes the initial estimated value.

In (15), we present an adaptive variable gain matrix $\hat{ {\varvec{\varDelta }}}(t)$, and the change law of its diagonal elements are designed as follows:

$$\begin{aligned} {{\dot{{\hat{\lambda }}} }_i}(t) = \frac{{ { {e}}_i\Big ( {{{\ddot{r}}_i}(t) - {a_i} - {k_i}{{{{\hat{\lambda }}} }_i}(t)\dot{ { {e}}}_i} \Big )}}{{(| { {e}}_i{|^2} + \varepsilon )k_i}},i=1,..., 5, \end{aligned}$$

(26)

where $e_i, i=1,...,5$ denotes the element of ${\varvec{e}}$ and $\varepsilon$ is a pimping positive constant to avoid zeros in the denominator. This is an adaptive term related to ${\varvec{e}}$ in the sliding surface vector ${\varvec{S}}$. On one aspect, ${\hat{\lambda }} _i(t)$ is the gain of $e_i, i=1,...,5$, which affects the convergence time of error, on the other aspect, the adaptive law of ${{\hat{\lambda }}} _i(t)$ contains $e _i$ and ${\dot{ {e}}}_i$, which means its value is always adaptively changed until $e_i = 0$ and ${\dot{e}}_i = 0$. This characteristic reflects the adaptive gain ${{\hat{\lambda }}} _i(t)$ is sensitive to error and can improve error convergence effect to some extent.

Remark 4

The design of ${{\dot{{\hat{\lambda }}} }_i}(t)$ in (26) is based on (24). It is not hard to find some nonlinear terms in (24) are designed into (26), which is to guarantee eliminating the influence of these nonlinear terms for stability, and meanwhile make ${{ {{\hat{\lambda }}} }_i}(t)$ become an adaptive variable. ${{ {{\hat{\lambda }}} }_i}(t)$ meets the requirement of gain variation in the field of automatic control (i.e., “large error with small gain, small error with large gain” (as shown in Fig. 5)) for avoiding large overshoot and keeping steady-state performance [44]. The explanation is that ${{\ddot{r}}_i}(t)$ plays a lead role (i.e., ${{\dot{{\hat{\lambda }}} }_i}(t) \approx {e}_i {{\ddot{r}}_i}(t)/((| { {e}}_i{|^2} + \varepsilon )k_i)$) in the initial control time interval; therefore, ${{\hat{\lambda }}} _i(t)$ becomes smaller according to the relation ${e}_i {{\ddot{r}}_i}(t)<0$. Similarly, it can be inferred that the gain ${{\hat{\lambda }}} _i(t)$ will increase in the end time interval. Besides, the tunable constant gain $k_i$ in ${{\dot{{\hat{\lambda }}} }_i}(t)$ is related to (15), and it has two kinds of purposes. Firstly, as the gain of the update law, $k_i$ can adjust the change rate of ${{ {{\hat{\lambda }}} }_i}(t)$. The another aspect is that $k_i$ is a positive constant gain element of ${\varvec{\varLambda }}$ in (15) for the sliding mode surface ${\varvec{S}}$.

Reformatting the RASMC method in (24) and (25) and adding the gains adaptive update laws in (26), we have

$$\begin{aligned} {{\varvec{U}}}_a&= {({ {\varvec{\varPhi }} ( {\varvec{q}})^T} {\varvec{\varPhi }} ( {\varvec{q}}) )^{ - 1}}{ {\varvec{\varPhi }} ( {\varvec{q}})^T}\Big ( - {{\mathbf{I } }} {\varvec{S}} - {{\mathbf{H } }}\mathrm{{sgn}} ( {\varvec{S}})\nonumber \\&\quad - { {\varvec{M}}^{ - 1}}\hat{ {\varvec{D}}}\Big ) + {{\varvec{\upsilon }} }_1(\dot{\varvec{q}})\hat{{ {\varvec{\varUpsilon }} }}_1 + {{\varvec{\upsilon }} }_2(\dot{\varvec{q}})\hat{{ {\varvec{\varUpsilon }} }}_2 + \hat{ {\varvec{G}}}_c( {\varvec{q}}), \end{aligned}$$

(27)

To minimize the chattering effect of sliding mode control, the signum function is replaced by the hyperbolic tangent function, that is,

$$\begin{aligned} {{\varvec{U}}}_a&= {({ {\varvec{\varPhi }} ( {\varvec{q}})^T} {\varvec{\varPhi }} ( {\varvec{q}}))^{ - 1}}{ {\varvec{\varPhi }} ( {\varvec{q}})^T}\Big ( - {{\mathbf{I } }} {\varvec{S}} - {{\mathbf{H } }}\tanh ( {\varvec{S}})\nonumber \\&\quad - { {\varvec{M}}^{ - 1}}\hat{ {\varvec{D}}}\Big ) + {{\varvec{\upsilon }} }_1(\dot{\varvec{q}})\hat{{ {\varvec{\varUpsilon }} }}_1 + {{\varvec{\upsilon }} }_2(\dot{\varvec{q}})\hat{{ {\varvec{\varUpsilon }} }}_2 + {\hat{m}} {\varvec{G}}^*_c( {\varvec{q}}), \end{aligned}$$

(28)

where ${\varvec{G}}^*_c( {\varvec{q}})=[0 \;0 \;-C_1C_2g]^T$ and the update laws of adaptive terms are as follows:

$$\begin{aligned}&{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_1 = - {{\varvec{\varPi }} }_1^{ - 1} {{\varvec{\upsilon }} }_1(\dot{\varvec{q}})^T{ {\varvec{\varPhi }} ( {\varvec{q}})^T} {\varvec{S}}, \end{aligned}$$

(29)

$$\begin{aligned}&{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_2 =- {{\varvec{\varPi }} }_2^{ - 1} {{\varvec{\upsilon }} }_2(\dot{\varvec{q}})^T{ {\varvec{\varPhi }} ( {\varvec{q}})^T} {\varvec{S}},\end{aligned}$$

(30)

$$\begin{aligned}&\dot{\hat{ {\varvec{D}}}} = {{\varvec{\varPi }} }_d^{ - 1}{({ {\varvec{M}}({\varvec{q}})^{ - 1}})^T} {\varvec{S}},\end{aligned}$$

(31)

$$\begin{aligned}&\dot{{\hat{m}}}= -\frac{1}{{{\varphi _{m}} }} {\varvec{S}}^T {\varvec{\varPhi }} ( {\varvec{q}}) {\varvec{G}}^*_c( {\varvec{q}}), \end{aligned}$$

(32)

where ${{\varvec{\varPi }} }_d$ $=$ $\mathrm{diag}\{ {\varphi _{d1}},...,{\varphi _{d5}}\}$ $\in$ ${R^{5 \times 5}}$, ${{\varvec{\varPi }} }_1$ $=$ $\mathrm{diag}$ $\{ {\varphi _{11}},$ ${\varphi _{12}},{\varphi _{13}}\}$ $\in$ ${R^{3 \times 3}}$ and ${{\varvec{\varPi }} }_2$ $=$ $\mathrm{diag}\{ {\varphi _{21}},{\varphi _{22}},{\varphi _{23}}\}$ $\in$ ${R^{3 \times 3}}$ are all positive diagonal matrices, and, $\varphi _{m}$ is a positive gain.

Remark 5

Many previous researches about adaptive control for cranes (e.g., [16, 18, 19]) only used adaptive technique to estimate frictional parameters or unknown model parameters, where not only the structure of the adaptive part is complicated, but also the external disturbances and the unmodeled nonlinearity factors are not considered in theory.

4.2 Stability analysis

Theorem 1

The RASMC method is effective in the positioning of the actuated part (i.e., $\alpha$, x and l), and meanwhile capable of payload swing angles (i.e., $\theta _1$ and $\theta _2$) suppression. Thus, its mathematical expression is as follows:

$$\begin{aligned}&\mathop {\lim }\limits _{t \rightarrow \infty } {[\alpha \;x\;l\;{\theta _1}\;{\theta _2}\;{\dot{\alpha }} \;\dot{x}\;\dot{l}\;{{{\dot{\theta }} }_1}\;{{{\dot{\theta }} }_2}\;\ddot{\alpha }\;\ddot{x}\;\ddot{l}\;{{\ddot{\theta }}_1}\;{{\ddot{\theta }}_2}}]^T \nonumber \\&\quad = {[{\alpha _d}\;{x_d}\;{l_d}\;0\;0\;0\;0\;0\;0\;0\;0\;0\;0\;0\;0]^T\;}. \end{aligned}$$

(33)

Proof

The following positive definite function V is designed:

$$\begin{aligned} V&= \frac{1}{2}{{{{\varvec{S}}}}^T}{{{\varvec{S}}}} + \frac{1}{2}\sum \limits _{i = 1}^5 {{\varphi _{di}}{{\tilde{d}}}_i^2} + \frac{1}{2}\sum \limits _{i = 1}^3 {{\varphi _{i1}}{{\tilde{f}}}_{i1}^2} \nonumber \\&\quad + \frac{1}{2}\sum \limits _{i = 1}^3 {{\varphi _{i2}}\tilde{f}_{i2}^2}+ \frac{1}{2} {{\varphi _{m}}{{\tilde{m}}}^2}, \end{aligned}$$

(34)

where ${{\tilde{d}}}_i =d_i-{\hat{d}}_i$, ${{\tilde{f}}}_{i1} =f_{i1}-{\hat{f}}_{i1}$, ${{\tilde{f}}}_{i2} = f_{i2}-{\hat{f}}_{i2}$ and ${{\tilde{m}}} = m-{\hat{m}}$ denote the estimated error of unknown parameters.

Then, by taking the time derivative of (34) and considering (18), (23), (26) and (27), we have

$$\begin{aligned} \dot{V}&= {{{{\varvec{S}}}}^T}{{\dot{\varvec{S}}}} - \sum \limits _{i = 1}^3 {{\varphi _{i1}}{{\tilde{f}}}_{i1}^{}} \dot{{\hat{f}}}_{i1}^{} - \sum \limits _{i = 1}^3 {{\varphi _{i2}}{{\tilde{f}}}_{i2}^{}\dot{{\hat{f}}}_{i2}^{}} \nonumber \\&\quad - \sum \limits _{i = 1}^5 {{\varphi _{di}}{{\tilde{d}}}_i^{}\dot{{\hat{d}}}_i^{}}- {{\varphi _{m}}{{\tilde{m}}} \dot{{\hat{m}}}} \nonumber \\&= { {\varvec{S}}^T}\dot{ {\varvec{S}}} - {\tilde{ {\varvec{D}}}^T} {{\varvec{\varPi }} }_d\dot{\hat{ {\varvec{D}}}} - \tilde{{ {\varvec{\varUpsilon }} }}_1^T {{\varvec{\varPi }} }_1{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_1 \nonumber \\&\quad - \tilde{{ {\varvec{\varUpsilon }} }}_2^T {{\varvec{\varPi }} }_2{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_2- {{\varphi _{m}}{{\tilde{m}}} \dot{{\hat{m}}}} \nonumber \\&= { {\varvec{S}}^T}\Big ( {\varvec{\varGamma }} ( {\varvec{q}},\dot{ {\varvec{q}}}) + {\varvec{\varPhi }} ( {\varvec{q}})( {{\varvec{U}}}_a - {{\varvec{F}}}_{sa}- {\varvec{G}}_c( {\varvec{q}})) \nonumber \\&\quad + { {\varvec{M}}^{ - 1}} {\varvec{D}}- \ddot{ {\varvec{q}}}_r(t) + {{\varvec{\varLambda }}} {\dot{\hat{ {\varvec{\varDelta }}}}(t) } {\varvec{e}} + {{\varvec{\varLambda }}} \hat{ {{\varvec{\varDelta }}}}(t) \dot{ {\varvec{e}}} \Big )\nonumber \\&\quad - {\tilde{ {\varvec{D}}}^T} {{\varvec{\varPi }} }_d\dot{\hat{ {\varvec{D}}}} - \tilde{{ {\varvec{\varUpsilon }} }}_1^T {{\varvec{\varPi }} }_1{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_1 - \tilde{{ {\varvec{\varUpsilon }} }}_2^T {{\varvec{\varPi }} }_2{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_2 - {{\varphi _{m}}{{\tilde{m}}} \dot{{\hat{m}}}} \nonumber \\&= { {\varvec{S}}^T}\Big ( - {{\mathbf{I } }} {\varvec{S}} - {{\mathbf{H } }}\mathrm{{sgn}} ( {\varvec{S}}) - { {\varvec{M}}^{ - 1}} \hat{ {\varvec{D}}}\nonumber \\&\quad + {\varvec{\varPhi }} ( {\varvec{q}})( {{\varvec{\upsilon }} }_1(\dot{\varvec{q}})\hat{{ {\varvec{\varUpsilon }} }}_1 + {{\varvec{\upsilon }} }_2(\dot{\varvec{q}})\hat{{ {\varvec{\varUpsilon }} }}_2 - {{\varvec{F}}}_{sa}+{\hat{m}} {\varvec{G}}^*_c( {\varvec{q}})\nonumber \\&\quad - {\varvec{G}}_c( {\varvec{q}})) + { {\varvec{M}}^{ - 1}} {\varvec{D}} \Big )- {\tilde{ {\varvec{D}}}^T} {{\varvec{\varPi }} }_d\dot{\hat{ {\varvec{D}}}} \nonumber \\&\quad - \tilde{{ {\varvec{\varUpsilon }} }}_1^T {{\varvec{\varPi }} }_1{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_1 - \tilde{{ {\varvec{\varUpsilon }} }}_2^T {{\varvec{\varPi }} }_2{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_2 - {{\varphi _{m}}{{\tilde{m}}} \dot{{\hat{m}}}} , \end{aligned}$$

(35)

where $\tilde{ {\varvec{D}}} = {\varvec{D}} - \hat{ {\varvec{D}}}$, $\tilde{{ {\varvec{\varUpsilon }} }}_1 = {{\varvec{\varUpsilon }} }_1 - \hat{{{ {\varvec{\varUpsilon }}} }}_1$, $\tilde{{ {\varvec{\varUpsilon }} }}_2 = {{\varvec{\varUpsilon }} }_2 - \hat{{{ {\varvec{\varUpsilon }}} }}_2$, with $\hat{ {\varvec{D}}}=[{\hat{d}}_i] \in R^5,i=1,...,5$, $\hat{{{ {\varvec{\varUpsilon }}} }}_1=[{\hat{f}}_{j1}] \in R^3$, $\hat{{{ {\varvec{\varUpsilon }}} }}_2=[{\hat{f}}_{j2}] \in R^3$, $j=1,2,3$.

Arranging the form of $\dot{V}$, it is that

$$\begin{aligned} \dot{V}&= { {\varvec{S}}^T}\Big ( - {{\mathbf{I } }} {\varvec{S}} - {{\mathbf{H } }}\mathrm{{sgn}} ( {\varvec{S}}) - {\varvec{\varPhi }} ( {\varvec{q}})( {{\varvec{\upsilon }} }_1(\dot{\varvec{q}})\tilde{{ {\varvec{\varUpsilon }} }}_1\nonumber \\&\quad + {{\varvec{\upsilon }} }_2(\dot{\varvec{q}})\tilde{{ {\varvec{\varUpsilon }} }}_2 +{{\tilde{m}}} {\varvec{G}}^*_c( {\varvec{q}})) + { {\varvec{M}}^{ - 1}}\tilde{ {\varvec{D}}} \Big )\nonumber \\&\quad - {\tilde{ {\varvec{D}}}^T} {{\varvec{\varPi }} }_d\dot{\hat{ {\varvec{D}}}} - \tilde{{ {\varvec{\varUpsilon }} }}_1^T {{\varvec{\varPi }} }_1{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_1 - \tilde{{ {\varvec{\varUpsilon }} }}_2^T {{\varvec{\varPi }} }_2{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_2 - {{\varphi _{m}}{{\tilde{m}}} \dot{{\hat{m}}}} \nonumber \\&= { {\varvec{S}}^T}\Big ( - {{\mathbf{I } }} {\varvec{S}} - {{\mathbf{H } }}\mathrm{{sgn}} ( {\varvec{S}})\Big ) - \tilde{{ {\varvec{\varUpsilon }} }}_1^T{({ {\varvec{S}}^T} {\varvec{\varPhi }} ( {\varvec{q}}) {{\varvec{\upsilon }} }_1(\dot{\varvec{q}}))^T}\nonumber \\&\quad - \tilde{{ {\varvec{\varUpsilon }} }}_2^T{({ {\varvec{S}}^T} {\varvec{\varPhi }} ( {\varvec{q}}) {{\varvec{\upsilon }} }_2(\dot{\varvec{q}}))^T} -{{\tilde{m}}} {\varvec{S}}^T {\varvec{\varPhi }} ( {\varvec{q}}) {\varvec{G}}^*_c( {\varvec{q}}) \nonumber \\&\quad + {\tilde{ {\varvec{D}}}^T}{({ {\varvec{S}}^T}{ {\varvec{M}}^{ - 1}})^T}- {\tilde{ {\varvec{D}}}^T} {{\varvec{\varPi }} }_d\dot{\hat{ {\varvec{D}}}} \nonumber \\&\quad - \tilde{{ {\varvec{\varUpsilon }} }}_1^T {{\varvec{\varPi }} }_1{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_1 - \tilde{{ {\varvec{\varUpsilon }} }}_2^T {{\varvec{\varPi }} }_2{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_2 - {{\varphi _{m}}{{\tilde{m}}} \dot{{\hat{m}}}} \nonumber \\&= { {{\varvec{S}}}^T}\Big ( - {{\mathbf{I } }} {{\varvec{S}}} - {{\mathbf{H } }}\mathrm{{sgn}} ( {{\varvec{S}}})\Big ) \nonumber \\&\quad - \tilde{{ {\varvec{\varUpsilon }} }}_1^T\Big ( {{{({ {{\varvec{S}}}^T} {{\varvec{\varPhi }} ( {\varvec{q}})} {{\varvec{\upsilon }} }_1(\dot{\varvec{q}}))}^T} + {{\varvec{\varPi }} }_1{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_1} \Big )\nonumber \\&\quad - \tilde{{ {\varvec{\varUpsilon }} }}_2^T\Big ( {{{({ {{\varvec{S}}}^T} {{\varvec{\varPhi }} ( {\varvec{q}})} {{\varvec{\upsilon }} }_2(\dot{\varvec{q}}))}^T} + {{\varvec{\varPi }} }_2{ \dot{ \hat{ {\varvec{\varUpsilon }}} }}_2} \Big ) \nonumber \\&\quad + {\tilde{ {\varvec{D}}}^T}\Big ( {{{({ {{\varvec{S}}}^T}{ {\varvec{M}}^{ - 1}})}^T} - {{\varvec{\varPi }} }_d\dot{\hat{ {\varvec{D}}}}} \Big )\nonumber \\&\quad -{{\tilde{m}}} \Big ( {\varvec{S}}^T {\varvec{\varPhi }} ( {\varvec{q}}) {\varvec{G}}^*_c( {\varvec{q}})+{{\varphi _{m}} \dot{{\hat{m}}}}\Big ). \end{aligned}$$

(36)

Then, substituting (29)–(31) into the above equation, the result is as follows:

$$\begin{aligned} \dot{V} = - { {{\varvec{S}}}^T} {{\mathbf{I } }} {{\varvec{S}}} - { {{\varvec{S}}}^T} {{\mathbf{H } }}\mathrm{{sgn}} ( {{\varvec{S}}}) \le 0. \end{aligned}$$

(37)

From (37) and (34), it is implied that ${{{\varvec{S}}}} \in {L_\infty }$, and combining (16), yields, ${\dot{ {\varvec{S}}}} \in {L_\infty }$. To further prove it, the following invariant and compact set $\varXi$ with its largest invariant set $\varOmega$ is utilized:

$$\begin{aligned} \varXi = \{ ( {{\varvec{S}}}( {\varvec{q}},\dot{ {\varvec{q}}}, {\varvec{q}}_r, \dot{ {\varvec{q}}}_r),\dot{ {{\varvec{S}}}}( {\varvec{q}},\dot{ {\varvec{q}}}, {\varvec{q}}_r, \dot{ {\varvec{q}}}_r)|\dot{V} = 0\}. \end{aligned}$$

(38)

In $\varOmega$, the following relations ${{{\varvec{S}}}} = {{0}},{\dot{ {\varvec{S}}}} = {{0}}$ are derived. Thus, combining (15) and (18), the following equations are correct:

$$\begin{aligned}&\dot{ {{\varvec{e}}} }+ {\varvec{\varLambda }} \hat{ {\varvec{\varDelta }}}(t) { {\varvec{e}}} = 0, \end{aligned}$$

(39)

$$\begin{aligned}&\ddot{ {\varvec{e}}} + {\varvec{\varLambda }} \dot{\hat{ {\varvec{\varDelta }}}}(t) {\varvec{e}} + {\varvec{\varLambda }} \hat{ {\varvec{\varDelta }}}(t) \dot{ {\varvec{e}}} = 0. \end{aligned}$$

(40)

From (39), we have

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } {\varvec{e}} = 0,\mathop {\lim }\limits _{t \rightarrow \infty } \dot{ {\varvec{e}}} = 0, \end{aligned}$$

(41)

then, the conclusions in (40) and (41) produce $\mathop {\lim }\limits _{t \rightarrow \infty } \ddot{ {\varvec{e}}} = 0$.

Considering (4), the following relationship equations about reference trajectories are obvious,

$$\begin{aligned}&\mathop {\lim }\limits _{t \rightarrow \infty } \alpha = {\alpha _d},\mathop {\lim }\limits _{t \rightarrow \infty } x = {x_d},\mathop {\lim }\limits _{t \rightarrow \infty } l = {l_d}, \end{aligned}$$

(42)

$$\begin{aligned}&\mathop {\lim }\limits _{t \rightarrow \infty } {\dot{\alpha }} = 0,\mathop {\lim }\limits _{t \rightarrow \infty } \dot{x} = 0,\mathop {\lim }\limits _{t \rightarrow \infty } \dot{l} = 0,\end{aligned}$$

(43)

$$\begin{aligned}&\mathop {\lim }\limits _{t \rightarrow \infty } \ddot{\alpha }= 0,\mathop {\lim }\limits _{t \rightarrow \infty } \ddot{x} = 0,\mathop {\lim }\limits _{t \rightarrow \infty } \ddot{l} = 0. \end{aligned}$$

(44)

Besides, from (34) and (37), we can infer that $\mathop {\lim }\limits _{t \rightarrow \infty } {\tilde{f}}_{ij}=0,i=1,2,3,j=1,2$, $\mathop {\lim }\limits _{t \rightarrow \infty } {\tilde{d}}_{k}=0,k=1,...,5$, $\mathop {\lim }\limits _{t \rightarrow \infty } {\tilde{m}}=0$, which means the estimated parameters are consistent to the real values based on Lyapunov stability.

Therefore, through the above analysis, the system state at infinite time can be described as the following equation:

$$\begin{aligned}&\mathop {\lim }\limits _{t \rightarrow \infty } {[\alpha \;x\;l\;{\theta _1}\;{\theta _2}\;{\dot{\alpha }} \;\dot{x}\;\dot{l}\;{{{\dot{\theta }} }_1}\;{{{\dot{\theta }} }_2}\;\ddot{\alpha }\;\ddot{x}\;\ddot{l}\;{{\ddot{\theta }}_1}\;{{\ddot{\theta }}_2}}]^T\nonumber \\&\quad = {[{\alpha _d}\;{x_d}\;{l_d}\;0\;0\;0\;0\;0\;0\;0\;0\;0\;0\;0\;0]^T\;}, \end{aligned}$$

(45)

which distinctly means that $\varOmega$ only includes the desired equilibrium point of the tower cranes closed-loop control system. Hence, Theorem 1 is completely proved under Lyapunov technique and LaSalle’s invariance principle [45]. $\square$

5 Simulation results and discussion

In this section, MATLAB & Simulink was used, which verified the control effectiveness and strong robustness of the RASMC method. First of all, to compare with the RASMC method, an SMC, an LQR and an ASRC [38] method were applied to the tower crane control system. Then, the extremely strong robustness of the RASMC method was convincingly verified aiming at external disturbances of every DOF and model parameters uncertainties.

5.1 Simulation conditions

The model parameters of the tower crane given in Table 1 are used in simulations, and the controller parameters of the RASMC method were presented as follows:

$$\begin{aligned}&{k_1} = 0.19,{k_2} = 0.1,{k_3} = 5.5,{k_4} = 7.8,{k_5} = 7.8,\nonumber \\&{\mu _1} = {\mu _2} = {\mu _3} = {\mu _4} = {\mu _5} = 280,\nonumber \\&{\gamma _1} = {\gamma _2} = {\gamma _3} = {\gamma _4} = {\gamma _5} = 80,\nonumber \\&\varphi _{11} = 0.01,\varphi _{12} = 0.01,\varphi _{13} = 0.3,\nonumber \\&\varphi _{21} = 0.1,\varphi _{22} = 0.1,\varphi _{23} = 0.5,\nonumber \\&\varphi _{d1} = 0.5,\varphi _{d2} = 0.5,\varphi _{d3} = 0.5,\nonumber \\&\varphi _{d4} = 0.0005,\varphi _{d5} = 0.0005,\varepsilon = 0.5. \end{aligned}$$

(46)

Remark 6

The choice of controller gains in the RASMC method needs to satisfy the following rules: in the sliding mode surface vector ${\varvec{S}}$ of (15), the element $k_i$ in the diagonal matrix $\varvec{\varLambda }={\mathrm {diag}}\{k_1,..., k_5\}$ is positive, which determines the slope of the sliding surface ${\varvec{S}}$ and the update rate of ${{{{\hat{\lambda }}} }_i}(t)$; in the sliding mode reaching law of (16), elements $\mu _i$ and $\gamma _i$ in matrices (${{\mathbf{I } }} ={\mathrm {diag}}\{\mu _1,..., \mu _ 5\}$ and ${{\mathbf{H } }} = {\mathrm {diag}}\{\gamma _1,...,\gamma _5\}$) are both positive, where the principle of increasing convergence rate and reducing chattering should be followed; in the adaptive gain update law ${{\dot{{\hat{\lambda }}} }_i}(t)$ of (26), in order to prevent the meaningless in the denominator, there is $\varepsilon$, which is a small enough positive scalar adjusted freely in the practical application; in the frictional force adaptive compensation component (29) and (30), the elements of matrices ${\varvec{\varPi }}_1={\mathrm {diag}}\{\varphi _{11},\varphi _{12},\varphi _{13}\}$ and ${\varvec{\varPi }}_2={\mathrm {diag}}\{\varphi _{21},\varphi _{22},\varphi _{23}\}$ are both positive, and the smaller the value is, the faster the friction gain is updated (this rule also applies to the matrix ${\varvec{\varPi }}_d={\mathrm {diag}}\{\varphi _{d1},...,\varphi _{d5}\}$ in (31) and ${\varphi _{m}}$ in (32).

In addition, the reference trajectories parameters (i.e., $\alpha _d$, $x_d$, $l_d$, $t_ d$) were, respectively, set as 45.0[deg], 0.8[m], 1.0[m], 5[s], respectively.

5.2 Comparative simulations

In this section, an SMC, an LQR and an ASRC method were presented, which were compared with the RASMC method.

Compared controller 1: The SMC method was introduced as follows:

$$\begin{aligned} {{\varvec{U}}}_a&= {({ {{\varvec{\varPhi }} ( {\varvec{q}})}^T} {{\varvec{\varPhi }} ( {\varvec{q}})})^{ - 1}}{ {{\varvec{\varPhi }} ( {\varvec{q}})}^T}\Big ( - {\varvec{\varGamma }}( {\varvec{q}},\dot{ {\varvec{q}}}) + {{{\ddot{ {\varvec{q}}}}}}_r(t) \nonumber \\&\quad - {\varvec{\varTheta }} {\dot{ {{\varvec{e}}}}} - {{\mathbf{I } }} {{\varvec{S}}}- {{\mathbf{H } }}\tanh ( {{\varvec{S}}})\Big ), \end{aligned}$$

(47)

where ${{\varvec{S}}} = {\dot{ {\varvec{e}}}} + {\varvec{\varTheta }} {\varvec{e}}$, ${\varvec{\varTheta }}$ $=$ $\mathrm{diag}\{ {\varsigma _1}\;{\varsigma _2}\;{\varsigma _3}\;{\varsigma _4}\;{\varsigma _5}\}$ $\in$ ${R^{5 \times 5}}$, and ${\varsigma _1}=0.8$, ${\varsigma _2}=0.8$, ${\varsigma _3}=0.9$, ${\varsigma _4}=2.5$, ${\varsigma _5}=2.9$.

Compared controller 2: To design the LQR method, the tower crane system model was linearized in equilibrium point firstly, and it was designed as follows:

$$\begin{aligned}&{T} = - {k_{11}}{e_\alpha } - {k_{12}}{{{\dot{\varvec{e}}}}_\alpha } - {k_{13}}{\theta _2} - {k_{14}}{{{\dot{\theta }} }_2}, \end{aligned}$$

(48)

$$\begin{aligned}&{F_x} = - {k_{21}}{e_x} - {k_{22}}{{{\dot{\varvec{e}}}}_x} - {k_{23}}{\theta _1} - {k_{24}}{{{\dot{\theta }} }_1},\end{aligned}$$

(49)

$$\begin{aligned}&{F_l} = - {k_{31}}{e_l} - {k_{32}}{{{\dot{\varvec{e}}}}_l} , \end{aligned}$$

(50)

where ${[e_{\alpha }, \;\dot{e}_{\alpha },\;e_x,\;\dot{e}_x,\;e_l,\;\dot{e}_l,\; {\theta _1},\;{{\dot{\theta }} _1},\;{\theta _2},\;{{\dot{\theta }} _2}]^T}$ is state vector, and $Q=\mathrm{diag} \{1000, 1, 1000, 1, 500, 1, 5, 1, 5, 1 \}$, R=1. Thus, the controller gains $k_{11} = 31.62$, $k_{12} =24.89$, $k_{13} =-0.41$, $k_{14} =0.92$, $k_{21} = 31.62$, $k_{22} =16.83$, $k_{23} =1.33$, $k_{24} =2.00$, $k_{31} =22.36$, $k_{32} = 6.76$.

Compared controller 3: The form of ASRC method is as follows:

$$\begin{aligned}&F_{\alpha }=-k_{p \alpha } e_{\alpha d}-k_{d \alpha } \dot{\alpha }+\eta _{\alpha }^{T} \widehat{\omega }_{\alpha }-k_{\alpha }\left( \dot{\theta }_{1}^{2}+\dot{\theta }_{2}^{2}\right) \dot{\alpha }, \end{aligned}$$

(51)

$$\begin{aligned}&F_{x}=-k_{p x} e_{\mathrm{xd}}-k_{d x} {\dot{x}}+\eta _{x}^{T} \widehat{\omega }_{x}-k_{x}\left( \dot{\theta }_{1}^{2}+\dot{\theta }_{2}^{2}\right) {\dot{x}}, \end{aligned}$$

(52)

$$\begin{aligned}&F_{l}=-k_{p l} e_{ld}-k_{d l} {\dot{l}}-m_{p} g+\eta _{l} \widehat{\omega }_{l}-k_{l}\left( \dot{\theta }_{1}^{2}+\dot{\theta }_{2}^{2}\right) {\dot{l}}, \end{aligned}$$

(53)

where $e_{\alpha d} = \alpha -\alpha _d$, $e_{x d} = x-x_d$, $e_{l d} = l-l_d$, and other terms are as follows:

$$\begin{aligned}&{\eta _\alpha } = {\left[ {\tanh \left( {\frac{{{\dot{\alpha }} }}{{{\varepsilon _\alpha }}}} \right) \,\,\,|{\dot{\alpha }} |{\dot{\alpha }} } \right] ^T},\\&{\eta _x} = \left[ {\tanh \left( {\frac{{\dot{x}}}{{{\varepsilon _x}}}} \right) \,\,\,|\dot{x}|\dot{x}} \right] ^T,{\eta _l} = \dot{l},\\&{\dot{\hat{\omega }}_{\alpha }}=-\varGamma _{\alpha } \eta _{\alpha }^{T} \dot{\alpha },\dot{\hat{\omega }}_{x}=-\varGamma _{x} \eta _{x}^{T} {\dot{x}}, \dot{\hat{\omega }}_{l}=-\varGamma _l \eta _{l} {\dot{l}}, \end{aligned}$$

with $k_{p\alpha }=6$, $k_{d\alpha }=15$, $k_{px}=6$, $k_{dx}=15$, $k_{pl}=12$, $k_{dl}=18$, $k_{\alpha }=200$, $k_x=200$, $k_l=200$, $\varGamma _{\alpha } ={\mathrm {diag}}\{5,5\}$, $\varGamma _{x} ={\mathrm {diag}}\{2,2\}$, $\varGamma _{l} =1.5$.

Remark 7

Traditional methods are unable to cope with disturbances and model uncertainties, as shown in SMC (47) and LQR (48)–(50), where they all do not have the frictional compensation, gravity compensation and disturbance suppression terms. Especially, although the ASRC (51)–(53) copes with the unknown friction, disturbances and unknown m are not considered. Thus, the control system loses stability easily by using the compared methods.

Fig. 2

Comparative simulation results

Table 2 Quantified analysis data

In the comparative simulations, the disturbances were not considered, and the system only had friction condition. Figure 2 shows the comparative results, which contain the system state and controller outputs values. And meanwhile, the quantified control index data are presented in Table 2 for the sake of comparison of control effects directly. In Table 2, $t_{\alpha r}$ and $t_{\alpha c}$ represent the reaching time and computational time of the jib, respectively, and, the subscripts with x and l are for the trolley and the rope, respectively. $e_{\alpha s}$, $e_{x s}$ and $e_{l s}$ represent the steady-state error of the jib, the trolley and the rope, respectively. And, $\theta _{1m}$ and $\theta _{2m}$ denote the amplitude of $\theta _1$ and $\theta _2$ in the control process, respectively.

Fig. 3

Simulation results of estimation of friction

Fig. 4

Simulation results of estimation of m

Fig. 5

Simulation results of $\hat{\lambda }_{i}$

Firstly, the positioning effect aspect is discussed. On account of friction, the LQR method was hard to accomplish positioning tasks, and thus leaded to arrive target values after very long time. For rope length varying motion, because of gravity, the payload is left at a unexpected height by LQR, which is completely loss of control. However in the RASMC method, it estimated the frictional force as shown in Fig. 3; thus, the control speed was fast in achieving positioning. And for l, the value of m is estimated, where the result is in Fig. 4. Thus, the positioning subsystem of l is stable. For the SMC method, it is obvious that its sliding mode surface gains matrix ${\varvec{\varTheta }}$ was invariable, which would result in that the control-related gains were difficult to tune and the convergence speed was inflexible; however, in the RASMC, $\hat{\lambda }_i(t)$ was adaptive, as shown in Fig. 5. In Fig. 2, it can be found that the SMC method had evident overshoot in positioning and its outputs values were not close to zero until about 15 [s]. For the ASRC method, because of the unknown value of payload mass m, the payload lowering motion produced an obvious steady-state error. Also, because ASRC is a regulation control method, the movement of the actuated part was fast and then slow under large initial force, which came out poor initial state and long settling time. All in all, the RASMC method generated fast and steady positioning process benefited by the adaptive compensation component and adaptive gains.

Then, the swing angle suppression results of the SMC and LQR method were pale by comparison. In Table 2, it is shown that the maximum swing angles were smallest under the RASMC. In Fig. 2, the LQR controller was almost impossible to suppress the swing angles, where the oscillation phenomenon kept appearing. And, the convergence speed of the swing angles by using the SMC controller was slower than the RASMC method. Because of lacking of effective payload anti-sway component in controller, the ASRC also presents a underdamping response about swing suppression. And, due to regulation control mode of ASRC, the payload presents intense swing phenomenon earlier than other controllers.

Finally, the control advantages of the RASMC are analyzed quantitatively. In regard to the maximum of reaching time, the RASMC is 5.07 [s], which is 0.94 [s], 11.24 [s] and 0.91 [s] faster than the compared controllers, and approximately 15.64$\%$, 68.91$\%$ and 15.22$\%$ of positioning time is saved, respectively. Also, the computational time of RASMC is saved about 46.69$\%$, 62.15$\%$ and 31.49$\%$, respectively. The steady-state positioning error of RASMC is very small, one or even several orders of magnitude less than other controllers. Moreover, the positioning error can be limited to 0.006 [deg] or 0.002 [m] by RASMC, which is only 0.02$\%$ or 0.4$\%$ of the total slew/displacement. The amplitude suppression effect of swing angles is very effective by RASMC. For $\theta _{1m}$, there is 53.06$\%$, 67.14$\%$ and 74.25$\%$ reduction by using RASMC compared to other controllers, respectively. And for $\theta _{2m}$, the reduction is 51.47$\%$, 69.72$\%$ and 59.26$\%$, respectively.

5.3 Robust performance

In this section, the strong robustness of the RASMC method was verified in regard to disturbances of all DOF and model parameters uncertainties.

Fig. 6

Simulation results with external disturbances

The external disturbances were added, which were asynchronous, unordered, various and intense. Even though under such disturbances, the positioning and swing suppression aspect almost had none negative impacts, which were benefited by the adaptive compensation. For the RASMC, the compensation effect can be seen obviously in Fig. 6 where the controller outputs compensated the disturbance timely.

Fig. 7

Simulation results with model uncertainties

Different model parameters condition was considered, which is shown in Fig. 7. In this simulation, we changed the model parameters from that in Table 1 to $m=0.8$ [kg], $M_t=5.6$ [kg] and $J_0=4.8$ [$\mathrm {kg \cdot m^2}$] but still used the model parameters in Table 1 for the RASMC. It is found that the control effect did not have marked difference, and the adaptive part had work in compensating different m. Therefore, the RASMC is insensitive to unknown model parameters.

6 Conclusion

In this paper, we presented a robust adaptive sliding mode controller for the tower crane with time-varying rope length, which has nonlinear adaptive sliding surface and adaptive compensation for frictions, disturbances and unknown payload mass to effectively realize the positioning of the jib, trolley and rope and meanwhile achieve swing elimination. It is worth noting that the controller was designed and analyzed without a linearized model. And at the same time, the nonzero initial reference trajectories were used, leading to the controller is more practical and safer, and also do not have big initial output values even though in large control gains cases. Lyapunov technique and LaSalle’s invariance principle were detailed utilized to prove the control system stability theoretically. Sufficient simulations were applied, which showed that the tower crane control system is better and has strong robustness with respect to disturbances and model uncertainties under the RASMC.

Through this paper, the following conclusions are obtained: (1) compared with the existing SMC controllers, we find that if the gains in the sliding mode surface can change with the error, it is of great practical significance to improve the convergence performance of the sliding mode control; (2) when designing the controller, the operation without model linearization is more beneficial to the global stability of the control system; (3) the nonzero initial reference trajectories are more practical in actual; (4) in practice, frictions, model uncertainties and external disturbances are common cases; thus, solving these problems can promote the practical application of crane control methods; (5) the payload mass is always changeable; therefore, it is necessary to identify its value in real time to overcome the adverse effects.

In the future, the solution of the dynamic–static friction compensation and the finite-time stability control are two directions worth studying. It can be seen from this paper that although the friction model related to velocities has been used in many studies, it leads to the static friction cannot be compensated reasonably and effectively. In addition, the control scheme RASMC designed in this paper can only improve the convergence speed of the sliding mode surface, which is asymptotically stable, but the finite time stability can guarantee the efficiency of the control task theoretically, and the practical significance is greater.

Appendices

Appendix A

The detailed expressions of (8) are as follows:

$$\begin{aligned}&\varvec{M}( {\varvec{q}})\ddot{ {\varvec{q}}} + {\varvec{C}}( {\varvec{q}}, \dot{ {\varvec{q}}})\dot{ {\varvec{q}}} + {\varvec{G}}( {\varvec{q}}) = {\varvec{U}} - {{\varvec{F}}}_s(\dot{ {\varvec{q}}}) + {\varvec{D}}, \nonumber \\&\varvec{M}( {\varvec{q}}) = \left[ \begin{array}{l} {m_{11}}\;{m_{12}}\;{m_{13}}\;{m_{14}}\;{m_{15}}\\ {m_{21}}\;{m_{22}}\;{m_{23}}\;{m_{24}}\;{m_{25}}\\ {m_{31}}\;{m_{32}}\;{m_{33}}\;{m_{34}}\;{m_{35}}\\ {m_{41}}\;{m_{42}}\;{m_{43}}\;{m_{44}}\;{m_{45}}\\ {m_{51}}\;{m_{52}}\;{m_{53}}\;{m_{54}}\;{m_{55}} \end{array} \right] \; ,\nonumber \\&{m_{11}} = {J_0} + m{x^2} + {M_t}{x^2} + m{l^2} - m{l^2}{C_1}^2{C_2}^2\nonumber \\&+ 2mxl{C_2}{S_1},{m_{12}} = - ml{S_2},{m_{13}} = mx{S_2},\nonumber \\&{m_{14}} = - m{l^2}{C_1}{C_2}{S_2},{m_{15}} = m{l^2}{S_1} + mxl{C_2},\nonumber \\&{m_{21}} = - ml{S_2},{m_{22}} = {M_t} + m,{m_{23}} = m{C_2}{S_1},\nonumber \\&{m_{24}} = ml{C_1}{C_2},{m_{25}} = - ml{S_1}{S_2},{m_{31}} = mx{S_2},\nonumber \\&{m_{32}} = m{C_2}{S_1},{m_{33}} = m,{m_{34}} = {m_{35}} = 0,\nonumber \\&{m_{41}} = - m{l^2}{C_1}{C_2}{S_2},{m_{42}} = ml{C_1}{C_2},{m_{43}} = 0,\nonumber \\&{m_{44}} = m{l^2}{C_2}^2,{m_{45}} = 0,{m_{51}} = m{l^2}{S_1} + mxl{C_2},\nonumber \\&{m_{52}} = - ml{S_1}{S_2},{m_{53}} = {m_{54}} = 0,{m_{55}} = m{l^2},\nonumber \\&{\varvec{C}}( {\varvec{q}},\dot{ {\varvec{q}}}) = \left[ \begin{array}{l} {c_{11}}\;{c_{12}}\;{c_{13}}\;{c_{14}}\;{c_{15}}\\ {c_{21}}\;{c_{22}}\;{c_{23}}\;{c_{24}}\;{c_{25}}\\ {c_{31}}\;{c_{32}}\;{c_{33}}\;{c_{34}}\;{c_{35}}\\ {c_{41}}\;{c_{42}}\;{c_{43}}\;{c_{44}}\;{c_{45}}\\ {c_{51}}\;{c_{52}}\;{c_{53}}\;{c_{54}}\;{c_{55}} \end{array} \right] ,\nonumber \\&{c_{11}} = mx\dot{x} + {M_t}x\dot{x} + ml{C_2}{S_1}\dot{x} + ml\dot{l}\nonumber \\&- ml{C_1}^2{C_2}^2\dot{l} + mx{C_2}{S_1}\dot{l} + m{l^2}{C_1}{C_2}^2{S_1}{{{\dot{\theta }} }_1}\nonumber \\&+ mxl{C_1}{C_2}{{{\dot{\theta }} }_1} + m{l^2}{C_1}^2{C_2}{S_2}{{{\dot{\theta }} }_2} - mxl{S_1}{S_2}{{{\dot{\theta }} }_2},\nonumber \\&{c_{12}} = mx{\dot{\alpha }} + {M_t}x{\dot{\alpha }} + ml{C_2}{S_1}{\dot{\alpha }} ,{c_{13}} = ml{\dot{\alpha }} \nonumber \\&- ml{C_1}^2{C_2}^2{\dot{\alpha }} + mx{C_2}{S_1}{\dot{\alpha }} - ml{C_1}{C_2}{S_2}{{{\dot{\theta }} }_1}\nonumber \\&+ mx{C_2}{{{\dot{\theta }} }_2} + ml{S_1}{{{\dot{\theta }} }_2},{c_{14}} = m{l^2}{C_1}{C_2}^2{S_1}{\dot{\alpha }} \nonumber \\&+ mxl{C_1}{C_2}{\dot{\alpha }} - ml{C_1}{C_2}{S_2}\dot{l} + m{l^2}{C_2}{S_1}{S_2}{{{\dot{\theta }} }_1}\nonumber \\&+ m{l^2}{C_1}{{{\dot{\theta }} }_2} - m{l^2}{C_1}{C_2}^2{{{\dot{\theta }} }_2},\nonumber \\&{c_{15}} = m{l^2}{C_1}^2{C_2}{S_2}{\dot{\alpha }} - mxl{S_1}{S_2}{\dot{\alpha }} + mx{C_2}\dot{l}\nonumber \\&+ ml{S_1}\dot{l} + m{l^2}{C_1}{{{\dot{\theta }} }_1} - m{l^2}{C_1}{C^2}_2{{{\dot{\theta }} }_1}\nonumber \\&- mxl{S_2}{{{\dot{\theta }} }_2},{c_{21}} = - mx{\dot{\alpha }} - Mx{\dot{\alpha }} \nonumber \\&- ml{C_2}{S_1}{\dot{\alpha }} - m{S_2}\dot{l} - ml{C_2}{{{\dot{\theta }} }_2},{c_{22}} = 0,\nonumber \\&{c_{23}} = - m{S_2}{\dot{\alpha }} + m{C_1}{C_2}{{{\dot{\theta }} }_1} - m{S_1}{S_2}{{{\dot{\theta }} }_2},\nonumber \\&{c_{24}} = m{C_1}{C_2}\dot{l} - ml{C_2}{S_1}{{{\dot{\theta }} }_1} - ml{C_1}{S_2}{{{\dot{\theta }} }_2},\nonumber \\&{c_{25}} = - ml{C_2}{\dot{\alpha }} - m{S_1}{S_2}\dot{l} - ml{C_1}{S_2}{{{\dot{\theta }} }_1}\nonumber \\&- ml{C_2}{S_1}{{{\dot{\theta }} }_2},{c_{31}} = - ml{\dot{\alpha }} + ml{C_1}^2{C_2}^2{\dot{\alpha }} \nonumber \\&- mx{C_2}{S_1}{\dot{\alpha }} + m{S_2}\dot{x} + ml{C_1}{C_2}{S_2}{{{\dot{\theta }} }_1} - ml{S_1}{{{\dot{\theta }} }_2},\nonumber \\&{c_{32}} = m{S_2}{\dot{\alpha }} ,{c_{33}} = 0,{c_{34}} = ml{C_1}{C_2}{S_2}{\dot{\alpha }} \nonumber \\&- ml{C_2}^2{{{\dot{\theta }} }_1},{c_{35}} = - ml{S_1}{\dot{\alpha }} - ml{{{\dot{\theta }} }_2},\nonumber \\&{c_{41}} = - m{l^2}{C_1}{C_2}^2{S_1}{\dot{\alpha }} - mxl{C_1}{C_2}{\dot{\alpha }} \nonumber \\&- ml{C_1}{C_2}{S_2}\dot{l} - m{l^2}{C_1}{C_2}^2{{{\dot{\theta }} }_2},{c_{42}} = 0,\nonumber \\&{c_{43}} = - ml{C_1}{C_2}{S_2}{\dot{\alpha }} + ml{C_2}^2{{{\dot{\theta }} }_1},\nonumber \\&{c_{44}} = ml{C_2}^2\dot{l} - m{l^2}{C_2}{S_2}{{{\dot{\theta }} }_2},\nonumber \\&{c_{45}} = - m{l^2}{C_1}{C_2}^2{\dot{\alpha }} - m{l^2}{C_2}{S_2}{{{\dot{\theta }} }_1},\nonumber \\&{c_{51}} = - m{l^2}{C_1}^2{C_2}{S_2}{\dot{\alpha }} + mlx{S_1}{S_2}{\dot{\alpha }} + ml{C_2}\dot{x}\nonumber \\&+ ml{S_1}\dot{l} + m{l^2}{C_1}{C_2}^2{{{\dot{\theta }} }_1},{c_{52}} = ml{C_2}{\dot{\alpha }} ,\nonumber \\&{c_{53}} = ml{{{\dot{\theta }} }_2} + ml{S_1}{\dot{\alpha }} ,{c_{54}} = m{l^2}{C_1}{C_2}^2{\dot{\alpha }} \nonumber \\&+ m{l^2}{C_2}{S_2}{{{\dot{\theta }} }_1},{c_{55}} = ml\dot{l} ,\nonumber \\&{\varvec{G}}( {\varvec{q}}) = {[g_1\;g_2\; g_3\;g_4\;g_5]^T},\nonumber \\&g_1=0,g_2=0,g_3= - mg{C _1}{C _2},g_4=mgl{C _2}{S _1},\nonumber \\&g_5=mgl{C _1}{S _2}. \end{aligned}$$

(54)

Appendix B

The detailed terms in (13) and (14) are shown as follows:

$$\begin{aligned}&{\varvec{\varGamma }} ( {\varvec{q}},\dot{ {\varvec{q}}}) = {[{a_1}\;{a_2}\;{a_3}\;{a_4}\;{a_5}]^T},\nonumber \\&{a_1} = \frac{{ - 2{M_t}{\dot{\alpha }} \dot{x}x}}{{{M_t}{x^2} + {J_0}}},{a_2} = x{{{\dot{\alpha }} }^2},\nonumber \\&{a_3} =\frac{1}{{{{M_t}{x^2} + {J_0}}}} ({M_t}{{{\dot{\theta }} }_2}^2l{x^2} + {M_t}{{{\dot{\alpha }} }^2}l{x^2} + {J_0}{{{\dot{\theta }} }_2}^2lm\nonumber \\&+ {J_0}{{{\dot{\alpha }} }^2}l + {M_t}{{{\dot{\theta }} }_1}^2l{x^2}{C_2}^2 + {J_0}{{{\dot{\theta }} }_1}^2l{C_2}^2\nonumber \\&- 2{J_0}{\dot{\alpha }} \dot{x}{S_2} - 2{M_t}{{{\dot{\theta }} }_1}{\dot{\alpha }} l{x^2}{C_1}{C_2}{S_2}\nonumber \\&+ 2{M_t}{{{\dot{\theta }} }_2}{\dot{\alpha }} l{x^2}{S_1} + 2{J_0}{{{\dot{\theta }} }_2}{\dot{\alpha }} l{S_1}\nonumber \\&- {M_t}{{{\dot{\alpha }} }^2}l{x^2}{C_1}^2{C_2}^2 - {J_0}{{{\dot{\alpha }} }^2}l{C_1}^2{C_2}^2\nonumber \\&- 2{J_0}{{{\dot{\theta }} }_1}{\dot{\alpha }} l{C_1}{C_2}{S_2}),\nonumber \nonumber \\&{a_4} =\frac{1}{{{l{C_2}({M_t}{x^2} + {J_0})}}}( - {M_t}g{x^2}{S_1} - {J_0}g{S_1} \nonumber \\&- 2{M_t}{{{\dot{\theta }} }_1}\dot{l}{x^2}{C_2}- 2{J_0}{{{\dot{\theta }} }_1}\dot{l}{C_2} + 2{M_t}{\dot{\alpha }} \dot{l}{x^2}{C_1}{S_2}\nonumber \\&+ 2{J_0}{\dot{\alpha }} \dot{l}{C_1}{S_2} + 2{M_t}{{{\dot{\theta }} }_1}{{{\dot{\theta }} }_2}l{x^2}{S_2}\nonumber \\&+ 2{J_0}{{{\dot{\theta }} }_1}{{{\dot{\theta }} }_2}l{S_2} - 2{M_t}{\dot{\alpha }} \dot{x}lx{C_1}{S_2}\nonumber \\&+ {M_t}{{{\dot{\alpha }} }^2}l{x^2}{C_1}{C_2}{S_1} + {J_0}{{{\dot{\alpha }} }^2}l{C_1}{C_2}{S_1}\nonumber \\&+ 2{M_t}{{{\dot{\theta }} }_2}{\dot{\alpha }} l{x^2}{C_1}{C_2} + 2{J_0}{{{\dot{\theta }} }_2}{\dot{\alpha }} l{C_1}{C_2}),\nonumber \\&{a_5} =\frac{1}{ {{l({M_t}{x^2} + {J_0})}}} ( - 2{M_t}{{{\dot{\theta }} }_2}\dot{l}{x^2}- 2{J_0}{\dot{\alpha }} \dot{x}{C_2}\nonumber \\&- 2{M_t}{{{\dot{\theta }} }_1}{\dot{\alpha }} l{x^2}{C_1}{C_2}^2 - {M_t}{{{\dot{\theta }} }_1}^2l{x^2}{S_2}{C_2}\nonumber \\&- {J_0}{{{\dot{\theta }} }_1}^2l{S_2}{C_2} - 2{M_t}{\dot{\alpha }} \dot{l}{x^2}{S_1}\nonumber \\&- 2{J_0}{{{\dot{\theta }} }_1}{\dot{\alpha }} l{C_1}{C_2}^2\nonumber \\&- 2{J_0}{{{\dot{\theta }} }_2}\dot{l} + {M_t}{{{\dot{\alpha }} }^2}l{x^2}{C_1}^2{C_2}{S_2}\nonumber \\&- {M_t}g{x^2}{C_1}{S_2} + 2{M_t}{\dot{\alpha }} \dot{x}lx{S_1}\nonumber \\&- 2{J_0}{\dot{\alpha }} \dot{l}{S_1} + {J_0}{{{\dot{\alpha }} }^2}l{C_1}^2{C_2}{S_2}) , \end{aligned}$$

(55)

$$\begin{aligned}&{\varvec{\varPhi }} ( {\varvec{q}}) = {\left[ \begin{array}{l} {b_{11}}\;{b_{21}}\;{b_{31}}\;{b_{41}}\;{b_{51}}\\ {b_{12}}\;{b_{22}}\;{b_{32}}\;{b_{42}}\;{b_{52}}\\ {b_{13}}\;{b_{23}}\;{b_{33}}\;{b_{43}}\;{b_{53}} \end{array} \right] ^T},\nonumber \\&{b_{11}} = \frac{1}{{{M_t}{x^2} + {J_0}}},{b_{12}} = 0,{b_{13}} = \frac{{ - x{S_2}}}{{{M_t}{x^2} + {J_0}}},\nonumber \\&{b_{21}} = 0,{b_{22}} = \frac{1}{{{M_t}}},{b_{23}} = \frac{{ - {C_2}{S_1}}}{{{M_t}}},\nonumber \\&{b_{31}} = \frac{{ - x{S_2}}}{{{M_t}{x^2} + {J_0}}},{b_{32}} = \frac{{ - {S_1}{C_2}}}{{{M_t}}},\nonumber \\&{b_{33}} = \frac{1}{{{{M_t}m({M_t}{x^2} + {J_0})}}}( {M_t}^2{x^2} + {J_0}m{C_2}^2\nonumber \\&- {J_0}m{C_1}^2{C_2}^2 - {M_t}m{x^2}{C_1}^2{C_2}^2\nonumber \\&+ {J_0}{M_t} + {M_t}m{x^2}),\nonumber \\&{b_{41}} = \frac{{{C_1}{S_2}}}{{{C_2}({M_t}{x^2} + {J_0})}},{b_{42}} = \frac{{ - {C_1}}}{{{M_t}l{C_2}}},\nonumber \\&{b_{43}} = \frac{C_1}{{{{M_t}l{C_2}({M_t}{x^2} + {J_0})}}}( - {M_t}lx + {J_0}{C_2}{S_1}\nonumber \\&+ {M_t}lx{C_2}^2 + {M_t}{x^2}{C_2}{S_1})\nonumber \\&{b_{51}} = \frac{{ - x{C_2} - l{S_1}}}{{l({M_t}{x^2} + {J_0})}},{b_{52}} = \frac{{{S_1}{S_2}}}{{{M_t}l}},\nonumber \\&{b_{53}} = \frac{{S_2}}{{{{M_t}l({M_t}{x^2} + {J_0})}}}(- {J_0}{C_2} + {J_0}{C_1}^2{C_2}\nonumber \\&+ {M_t}{x^2}{C_1}^2{C_2} + {M_t}lx{S_1}). \end{aligned}$$

(56)