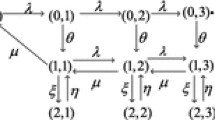Keywords

1 Introduction

During the last decades, the game-theoretic analysis of queueing systems with strategic customers has been paid considerable attention since the pioneer work by Naor (1969). In general, to reflect customers’ desire for service and their unwillingness to wait, some reward-cost structures are imposed on the system. Arriving customers can make decisions to decide whether to join or not, based on different levels of information of the system at their arrival, to maximize their utility. These customers take into account that the other customers have the same objective to maximize their benefit, so the situation can be regarded as a game among them. In these studies, the characterization and computation of individual and social optimal strategies is the fundamental problem.

Studies on customers decentralized behavior as well as socially optimal control of customers’ arrivals was pioneered by Naor (1969) with a single-server system in an observable framework, i.e., upon arrival, a customer is informed about the length of queue before his decision is made to join. Edelson and Hildebrand (1975) considered the unobservable case. There is more related work by Hassin and Haviv (2003) in their survey book. Burnetas and Economou (2007) assumed N = 1 and an exponential setup time when the server starts a new busy period. They considered the strategic behavior of customers under different levels of information. In particular, if only the queue length is known and the set-up time is of considerable length, the “Follow-The-Crowd” behavior of customers is observed.

The pioneering work on queues with N-policy can go back to Yadin and Naor (1963) for an M/M/1 queue with multiple vacations. The server is immediately turned on whenever N (N \( \ge \) 1) or more customers are present in the system and is switched off once there are no customers in the system. When the server shuts down, the server can not operate until N customers are present in the system. Guo and Hassin (2011) first considered customers’ strategic behavior and social optimization in a single Markovian queue with N-policy, in which the server is activated only if there are N customers in the system and turned off once there are no customers in the system. They concluded that a customer can induce positive externalities in the fully observable and the fully unobservable cases. Some recent papers that deal with the strategic behavior of customers in various queueing systems can be found in Economou and Kanta (2008a, b), Economou et al. (2011), Hassin (2007), Sun et al. (2010), Wang et al. (2017), Wang and Zhang (2011), Zhang et al. (2015), among others.

Evidently, frequent setups increase the operating cost, and it is crucial for the server to decide when to start service in practice. In principle, an appropriate value N can be determined by avoiding excessively frequent setups and the associated cost. For instance, to reduce the operating cost, in a Make-To-Order (MTO) system, the firm will set up the machines when the quantity of orders reaches a threshold. Another example is energy-saving issues arising from wireless sensor networks (WSNs), the N-policy is actually used in switching the sensor’s on-off states for prolonging the lifetime of the WSN system. Furthermore, the threshold-type control policy could be applied on optimizing elevator configuration, increasing the defense effectiveness of a missile defense system, and improving the connectivity of communications network.

The main objective of our work is to investigate the customers’ equilibrium balking strategies for both the partial observable single-server queues with N-policy and setup times which make our model more practical and valuable. In the present paper, we assume that customers are aware of the service policy, specifically the threshold N, and react to it in a strategic way. We also consider the social optimization problems. The model under consideration can be viewed as an M/M/1 queue in a Markovian environment. Also, customer equilibrium strategies are studied in each case, along with the system’s performance and the social welfare. Our model has potential in many practical applications.

2 Model Description

We consider a single server Markovian queue with infinite waiting room under the FCFS discipline, where customers arrive according to a Poisson process with rate \(\lambda \). We are interested in customers’ strategic behavior when they can decide whether to join or balk the system based on available information upon their arrival. The server works with service rate \(\mu \) and it shuts down once there is no customer upon completion of a service. After the server shuts down, the server can not work until N customers are presented in the queue and then a setup process begins, and we assume that the setup time is exponentially distributed with rate \(\theta \). We suppose that arrival times, service times, setup times are mutually independent. More specifically, every customer gets a reward of R units for completing service, however there exists a waiting cost of C per time unit when waiting in the queue or in service. Customers are risk neutral and they want to maximize their expected net benefit. We assume that \(R>\frac{C}{\mu }\), which enables that a customer joins in the queue when he finds the system empty, because the profit for service definitely surpasses the expected cost. Finally, the decisions are irrevocable, which means that retrials of balking customers and reneging of entering customers are not allowed.

The state of the system can be represented by a pair \(\left( {N\left( t \right) , I\left( t \right) } \right) \) at time t, where N(t) denotes the number of customers in the system, and I(t) stands for the state of the server. More specifically, the state (0, n), \(\mathrm{{0}} \le n \le N - 1\), implies that the system is down with n customers in the system; The state (1, n), \(n \ge N\), means the system is in a setup process with n customers in the system; And the state (2, n), \(n \ge 1\), implies that server is busy with n customers in the system. It is easy to see that the process \(\{ N(t), I(t), t \ge 0\}\) is a two-dimensional continuous time Markov chain with state space \(\mathbb {S}=\{ (n, i) | n=0, 1, 2, \ldots ; i=0, 1, 2 \}\) and non-zero transition rates are given by:

$$\begin{aligned} q_{(1,2)(0,0)}= & {} \mu ;\end{aligned}$$
(1)
$$\begin{aligned} q_{(N-1,0)(N,1)}= & {} \lambda ;\end{aligned}$$
(2)
$$\begin{aligned} q_{(n,i)(n+1,i)}= & {} \lambda ,~~~~n=1,2,...\ldots ,~~i=0,1,2;\end{aligned}$$
(3)
$$\begin{aligned} q_{(n+1,2)(n,2)}= & {} \mu ,~~~~n=1,2,...;\end{aligned}$$
(4)
$$\begin{aligned} q_{(n,1)(n,2)}= & {} \theta ,~~~~n=N,N+1..... \end{aligned}$$
(5)

In the next sections we will investigate the stationary probability distribution in the queueing system. In this paper, as mentioned above, we focus on two different levels of information that are available to customers before their decisions are made. We follow the notations in Burnetas and Economou (2007), i.e.

  1. (1)

    Almost observable case: Customers are informed only about the queue length N(t);

  2. (2)

    Almost unobservable case: Customers are informed only about the server state I(t).

For convenience, throughout this paper we denote \({S_{ao}}\) by the social benefit per time unit in almost observable case, and \({S_{au}}\) by the social benefit per time unit in almost unobservable case.

3 Almost Observable Case

In this section we proceed to the almost observable case where the arriving customers observe the number of the present customers in the system upon their arrival, but not the state of the server. The transition diagram is depicted in Fig. 1.

Fig. 1.
figure 1

Transition rate diagram for the \(n_e\) equilibrium threshold strategy in the almost observable model

Full size image

To this end, it is necessary to obtain the stationary distribution of the system when the customers follow a given pure threshold strategy. In general, the strategy of never joining is always an equilibrium when \(N > 1\), since if all customers adopt this strategy, the server is never active. We concentrate on the existence of other equilibrium strategies in which the server could be reactivated.

A threshold strategy with a threshold \(n_e\) is a strategy where customers join if and only if they find at most \(n_e\) customer in the system upon arrival. Thus the maximum number of customers in the system at any time is \(n_e+1\). We analyze the mean queue length and social welfare under this maximum number of customers. Firstly, we need to consider the condition for a server to be active in queues with setup time and N-policy which is different from the work of Guo and Hassin (2011). As mentioned, the server can only be active when the number of customers in the system reaches N. We know that, the longest expected waiting time for an arriving customer who arrives at state 0 is when there are n \((0<n<N)\) customers in the queue, thus the longest expected waiting time W can be reached when there are 0 or \(N-1\) customers in the queue, thus W is shown as follows:

$$\begin{aligned} W = \left\{ \begin{array}{ll} {{\frac{N -1}{\lambda }+\frac{1}{\mu }+\frac{1}{\theta }}} &{} \quad {n}= 0, \\ {{\frac{1}{\theta }+\frac{N }{\mu }}} &{} \quad {n}= {N} - 1.\\ \end{array} \right. \end{aligned}$$

By assumptions, an incoming customer always joins if his net benefit U is non-negative. The sufficient condition for a server to be active is given as follows.

$$\begin{aligned} R-CW=max\left\{ R-C(\frac{N-1}{\lambda }+\frac{1}{\mu }+\frac{1}{\theta }),R-C(\frac{1}{\theta }+\frac{N}{\mu })\right\} >0. \end{aligned}$$

Now we assume that the stability condition is satisfied. Obviously, a customer who arrives at state (n, 0) has a higher expected waiting time than one who arrives at state (n, 2). Thus, all arriving customers join the queue if there are no more than \(N > 1\) customers in the system. The equilibrium strategy is therefore characterized by a threshold value \(n_e> N\).

Lemma 1

In the almost observable M/M/1 queue with N policy and setup time where the customers enter the system according to a threshold strategy: While arriving at time t, observe N(t); enter if \(N(t)\le n_e\) and balk otherwise. The stationary distribution \((p_{ao}(n,i)\mathrm{{:}}(n,i) \in \{(0,0)\}\cup \{1,\ldots ,N-1\} \times \{0,2\}\cup \{ N, \ldots ,n_e+1 \} \times \{ 1,2\} )\) is given as follows:

$$\begin{aligned} p(n,0)= & {} p(0,0), \quad \quad \quad \quad n=1,...,N-1,\end{aligned}$$
(6)
$$\begin{aligned} p(N,1)= & {} \sigma p(0,0), \end{aligned}$$
(7)
$$\begin{aligned} p(n,1)= & {} \sigma ^{n-N+1}p(0,0),\quad \quad \quad \quad n=N+1,...,n_e, \end{aligned}$$
(8)
$$\begin{aligned} p(n_e +1,1)= & {} (1-\sigma )\sigma ^{n_e -N}p(0,0), \end{aligned}$$
(9)
$$\begin{aligned} p(1,2)= & {} \rho p(0,0), \end{aligned}$$
(10)
$$\begin{aligned} p(2,2)= & {} \frac{\rho }{1-\rho }(1-\rho ^2)p(0,0), \end{aligned}$$
(11)
$$\begin{aligned} p(n,2)= & {} \frac{\rho }{1-\rho }(1-\rho ^n)p(0,0),\quad \quad n=1,...,N-1, \end{aligned}$$
(12)
$$\begin{aligned} p(n,2)= & {} \left( \frac{{(1 - \sigma )\rho ^{n - N + 2} + (1 - \rho )\rho \sigma ^{n - N + 1} }}{{(1 - \sigma )(\sigma - \rho )}} - \frac{{\rho ^{n + 1} }}{{1 - \rho }}\right) p(0,0), n = N,...,n_e, \end{aligned}$$
(13)

where

$$\begin{aligned}&p(0,0)=((N-1)+\frac{\sigma ^2-\sigma ^{n_e -N+4}}{(1-\sigma )(\sigma -\rho )}+\frac{\rho ^{n_e+3}-N\rho ^2+(N-1)\rho }{(1-\rho )^2} \nonumber \\&\quad \quad \quad +\frac{(\sigma -1)(\rho ^2-\rho ^{n_e-N+4})}{(1-\rho )^2(\sigma -\rho )})^{-1}, \end{aligned}$$
(14)

and \(\rho =\frac{\lambda }{\mu }\), \(\sigma =\frac{\lambda }{\lambda +\theta }\).

Proof

The corresponding stationary distribution is obtained as the unique positive normalized solution of the following system of balance equations:

$$\begin{aligned} \lambda p(0,0)= & {} \mu p(1,2), \end{aligned}$$
(15)
$$\begin{aligned} \lambda p(n,0)= & {} \lambda p(n-1,0) \quad \quad n=1,2,...,N-1, \end{aligned}$$
(16)
$$\begin{aligned} (\lambda +\theta ) p(N,1)= & {} \lambda p(N-1,0), \end{aligned}$$
(17)
$$\begin{aligned} (\lambda +\theta ) p(n,1)= & {} \lambda p(n-1,1), \quad \quad n=N+1,...,n_e, \end{aligned}$$
(18)
$$\begin{aligned} \theta p(1,n_e+1)= & {} \lambda p(n_e,1), \end{aligned}$$
(19)
$$\begin{aligned} (\lambda +\mu ) p(1,2)= & {} \mu p(2,2), \end{aligned}$$
(20)
$$\begin{aligned} (\lambda +\mu ) p(n,2)= & {} \mu p(n+1,2)+\lambda p(n-1,2), \quad \quad n = 2,3...,N-1, \end{aligned}$$
(21)
$$\begin{aligned} (\lambda +\mu ) p(n,2)= & {} \mu p(n+1,2)+\lambda p(n-1,2) \quad \quad n=N+1,...,n_e. \end{aligned}$$
(22)

By iterating (16), we can get

$$\begin{aligned} p(n,0)=p(0,0). \end{aligned}$$

By (17) and iterating (18) we can get

$$\begin{aligned} p(1,n)=\sigma ^{n-N+1}p(0,0)\quad \quad n=N+1,...,n_e. \end{aligned}$$

By (19) we can get \(p({n_e} + 1,1)\) as follows

$$\begin{aligned} p(1,n_e +1)=(1-\sigma )\sigma ^{n_e -N}p(0,0). \end{aligned}$$

On the other hand, by (21), we can get

$$\begin{aligned} \mu p(n+1,2)- (\lambda +\mu )p(n,2)+\lambda p(n-1,2)=0,\quad \quad n = 2,3...,N-1. \end{aligned}$$
(23)

In the following, we use a rather standard method to solve this type of equation by solving a linear difference equation with constant coefficients as

$$\begin{aligned} \mu {x^2} - (\lambda + \mu )x + \lambda = 0. \end{aligned}$$
(24)

It is readily seen that the above equation has two roots 1 and \(\rho \) and the common root of the homogeneous transformation Eq. (21) is

$$\begin{aligned} \left\{ \begin{array}{ll} x_n^{\hom } = A{1^n} + B{\rho ^n}, &{} \rho \ne 1;\\ x_n^{\hom } = A{1^n} + Bn{1^n}, &{} \rho = 1. \end{array} \right. \end{aligned}$$
(25)

Since we assume \(\rho \ne 1\), thus the solution of Eq. (21) is

$$\begin{aligned} x_n = A+B\rho ^n \quad \quad n=1,2,3,...,N-1. \end{aligned}$$
(26)

Now, we need to know the values of A and B for the purpose of getting the expression of \(x_n(n=1,2,...,N-1)\).

Letting \(n=1\) and \(n=2\), we can get

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {A + B\rho = p(1,2)},\\ {A + B{\rho ^2} = p(2,2)}. \end{array}} \right. \ \end{aligned}$$
(27)

We get p(1, 1) and p(2, 1) from (15) and (20):

$$\begin{aligned} \left\{ \begin{array}{l} p(1,2) = \rho p(0,0),\\ p(2,2) = \frac{\rho }{1-\rho }(1-\rho ^2)p(0,0). \end{array} \right. \end{aligned}$$
(28)

Solving the Eq. (29), we can get A and B as follows

$$\begin{aligned} \left\{ \begin{array}{l} A = \frac{1-\rho }{\rho } p(0,0);\\ B = (-1)\frac{1-\rho }{\rho }p(0,0). \end{array} \right. \end{aligned}$$
(29)

Next, we consider \(p(n,2)(n= N,N+1,...,n_e+1)\). Similarly the general solution of Eq. (24) is \(x_n^{gen} = x_n^{\hom } + x_n^{spec}\), where \(x_n^{spec}\) is a special root of the Eq. (22).

We want to find a special root of Eq. (24) to replace \(x_n^{spec}\), and find the special root is like \(D{\sigma ^n}\) (when \(\sigma \ne 1\) and \(\sigma \ne \rho \)), or like \(Dn{\sigma ^n}\)(when \(\sigma = 1\) or \(\sigma = \rho \)), or like \(D{n^2}{\sigma ^n}\)(when \(\sigma = 1 = \rho \)). According to the discussion on the root solution given by Burnetas and Economou (2007), we need only consider the common situation. That is, find the special root is like \(D{\sigma ^n}\) for the regular case \(\sigma \ne 1{} \) and \(\sigma \ne \rho . \) Therefore, by simple computation, the solution of the Eq. (22) is given by:

$$\begin{aligned} x_n^{gen} = A{1^n} + B{\rho ^n} + D{\sigma ^n},{} \;{} n = 1,2,3, \ldots , {n_e} - 1. \end{aligned}$$
(30)

Letting \({x_n} = D{\sigma ^n}\) and take (24) into account, we can get the value of D as follows.

$$\begin{aligned} D=\frac{-\theta \sigma ^{2-N}}{(\mu \sigma ^2-(\lambda +\mu )\sigma +\lambda )}p(0,0) = \frac{\rho \sigma ^{1-N}}{(\sigma -\rho )}p(0,0). \end{aligned}$$

Now, we need to know the values of A and B for the purpose of getting the expression of \(x_n^{gen}\). Letting \(n=N\) and \(n=N+1\), using (33), we can get

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {A + B\rho ^N + D\sigma ^N = p(N,2)};\\ {A + B{\rho ^{N+1}} + D{\sigma ^{N+1}} = p(N+1,2)}. \end{array}} \right. \end{aligned}$$
(31)

So we can get the expression of p(N, 2), \(p(N+1,2)\) by taking (8) and (12) into (22):

$$\begin{aligned} \left\{ \begin{array}{l} p(N,2) = \frac{\rho }{1-\rho }(1-\rho ^N)p(0,0);\\ p(N+1,2) = (\frac{\rho }{1-\rho }(1-\rho ^{N+1})-\rho (1-\sigma ))p(0,0). \end{array} \right. \end{aligned}$$
(32)

Solving the Eq. (32), we can get A and B:

$$\begin{aligned} \left\{ \begin{array}{l} A =0;\\ B=\frac{\sigma -1-\rho ^{N-1}(\sigma -\rho )}{(1-\rho )(\sigma -\rho )}\rho ^{2-N}p(0,0). \end{array} \right. \end{aligned}$$
(33)

With the help of known values of A, B, D, we can obtain (13). Consequently, we can get the expression of \(p({n_e} + 1,2)\) by taking (13) into (22):

$$\begin{aligned} p(n_e+1,2)=\rho p(n_e,2)+\frac{1-\sigma }{\sigma }p(n_e+1,1). \end{aligned}$$
(34)

Based on the above results, we can conclude that all probabilities involved can be expressed via p(0, 0). Finally, we can get the expression of p(0, 0) by normalization equation:

$$\begin{aligned} \sum \limits _{n = 0}^{N-1}p(n,0) + \sum \limits _{n = N}^{{n_e} + 1} p(n,1)+\sum \limits _{n = 1}^{{n_e} + 1} p(n,2)=1, \end{aligned}$$
(35)

which reaches the result (14). This completes the proof of this lemma.    \(\square \)

Next, we will proceed to study the profit net of the almost observable case. In this case, the arriving customers can only observe the number of customers. \(T(n,i)(i=0,1,2)\) represents the sojourn time of an arriving customer when he finds n customers in front of him and the state of the sever \(I=i(i=0,1,2)\):

$$\begin{aligned}&T(n,2)=\frac{n+1}{\mu }, \nonumber \\&T(n,1)=\frac{1}{\theta }+\frac{n+1}{\mu },\nonumber \\&T(n,0)=\frac{1}{\theta }+\frac{n+1}{\mu }+\frac{N-(n+1)}{\lambda }. \end{aligned}$$
(36)

So for an arriving customer if he finds \(n(n>N-1)\) customers in front of him and decides to enter the system, the profit for this customer is given by

$$\begin{aligned} R- C(T(n,1)\Pr (I(t)=1|N(t)=n)+T(n,2) \Pr (I(t)=2|N(t)=n)), \end{aligned}$$
(37)

where \(\Pr (I(t)=1|N(t)=n)\) is the conditional probability that the server is on setup when the system have n customers waiting, and \(\Pr (I(t)=2|N(t)=n)\) is the conditional probability that the server is working when the system have n customers waiting.

To find the equilibrium strategies of threshold type, we should compute \(\Pr \left( {{I^ - } = i|{N^ - } = n} \right) (i=1,2)\) as follow.

$$\begin{aligned} \Pr ({I(t) }= & {} i\left| {{N(t)} = n} \right. ) = \frac{{\lambda {p_{ao}}\left( {n,i} \right) }}{{\lambda {p_{au}}\left( {n,1} \right) + \lambda {p_{au}}\left( {n,0} \right) I\left\{ {n \ge N} \right\} }}, \nonumber \\&n = N,N+1 \ldots ,{n_e} + 1, \end{aligned}$$
(38)

where

$$\begin{aligned} I\left\{ {n \ge N} \right\} = \left\{ {\begin{array}{*{20}{c}} {0, \;\;\;\;\;\;\;\;\;n <N; }\\ {1, \;\;\;\;\;\;\;\;\;n \ge N.} \end{array}} \right. \end{aligned}$$

Taking Eqs. (8), (13) and (36) into Eq. (38), we can get the profit of the customer as follows.

$$\begin{aligned} U=R - C\left\{ (\frac{1}{\theta }+\frac{n+1}{\mu })\Pr (I^{-} = 1|N^{ -} = n) + \frac{n+1}{\mu }\Pr (I^{-} = 2|N^{ - } = n) \right\} . \end{aligned}$$
(39)

Theorem 1

In the almost observable M/M/1 queue with N policy and setup time where the customers enter the system according to a threshold strategy ‘While arriving at time t, observe N(t); enter if \(N(t)\le n_e\) and balk otherwise’, we conclude that there exists unique equilibrium strategy of threshold \(n_e^*\) if \(\mu >\lambda +\theta \).

Proof

Take the expression of U into consideration and we can get:

$$\begin{aligned} U=R-C\left( \frac{n+1}{\mu }+ (\frac{\sigma ^{n-N+1}(1-\rho )(\sigma -\rho )}{(1-\rho )\sigma ^{n-N+1}+(\sigma -1)\rho ^{n-N+2} -(\sigma -\rho )\rho ^{n+1}})\frac{1}{\theta }\right) . \end{aligned}$$
(40)

More specifically, taking transformation of the formula

$$\begin{aligned}&\quad \frac{n+1}{\mu }+ \left( \frac{\sigma ^{n-N+1}(1-\rho )(\sigma -\rho )}{(1-\rho )\sigma ^{n-N+1}+(\sigma -1)\rho ^{n-N+2} -(\sigma -\rho )\rho ^{n+1}}\right) \frac{1}{\theta } \\&=\frac{n+1}{\mu }+\frac{1}{1+\frac{\rho }{\sigma -\rho }+(\frac{\sigma -1}{(1-\rho )(\sigma -\rho )(\frac{\rho }{\sigma })^{N-1}}-\frac{\rho }{1-\rho }\sigma ^{N-1})(\frac{\rho }{\sigma })^n}, \end{aligned}$$

which is strictly increasing when \(\rho <\sigma \), equally \(\mu >\lambda +\theta \), therefore U(n) is strictly decreasing. So, there exists a unique threshold, denoted by \(n_e^*\) = \(max\{n|U(n) \ge 0\}\).    \(\square \)

Lemma 2

In the observable M/M/1 queue with N policy and setup time where the arriving customers know the number of customers in the system, the social welfare per time unit \(SW_{ao}\) is given below:

$$\begin{aligned} SW_{ao}=R\lambda (1-p_{ao}(n_e,1)-p_{ao}(n_e,2))-CL_{ao}, \end{aligned}$$

Proof

The mean sojourn time of customer is \(E[W_{ao}]\) and the mean queue length is \(L_{ao}\).

$$\begin{aligned} E[W_{ao}]=L_{ao} \lambda (1-p_{ao}(n_e,1)-p_{ao}(n_e,2)), \end{aligned}$$

where \(p_{ao}(n_e,i)(i=1,2)\) is the steady state probability that the queue is at its maximum size, and \(\lambda (1-p_{ao}(n_e,1)-p_{ao}(n_e,2)\)) is the efficient arrival rate of customer.

The mean queue length is shown below:

$$\begin{aligned} L_{ao}= & {} \sum \limits _{n = 0}^{N-1}n(p(n,0)+p(n,2)) + \sum \limits _{n = N}^{{n_e} + 1}n( p(n,1)+p(n,2))\\= & {} \frac{1}{1-\rho }\left[ \frac{N(N-1)}{2}+\frac{\rho ^2-N\rho ^{N+1}+(N-1)\rho ^{N+1}}{(1-\rho )^2}\right] p(0,0)\\+ & {} \frac{N\rho ^2+(1-N)\rho ^3-(n_e+1)\rho ^{n_e-N+1}+n_e\rho ^{n_e-N+4}}{(\sigma -\rho )(1-\rho )^2}p(0,0)\\+ & {} \frac{\sigma (1-\rho )+\rho (\sigma -\rho )}{(1-\sigma )^3(\sigma -\rho )}(N\sigma +(1-N)\sigma ^2 -(n_e+1)\sigma ^{n_e-N}+n_e\sigma ^{n_e-N+3})p(0,0)\\- & {} \frac{N\rho ^{N+1}+(1-N)\rho ^{N+2}-(n_e+1)\rho ^{n_e+2}+n_e\rho ^{n_e+3}}{(1-\rho )^3}p(0,0)\\+ & {} (n_e+1)(1-\sigma )\sigma ^{n_e-N}p(0,0)+\frac{n_e+1}{\mu }\Bigg [\frac{\rho ^{n_e-N+1}(1-\sigma ) (\rho (\lambda +\mu )-\lambda )}{(1-\sigma )(\sigma -\rho )} \\&-\frac{\rho ^n_e(\rho (\lambda +\mu )-\lambda )}{1-\rho }\Bigg ]p(0,0). \end{aligned}$$

   \(\square \)

4 Almost Unobservable Case

We now turn our interest to the unobservable cases where the customers have no information on the queue length when they make their decision to join or balk. Two cases, almost unobservable case and fully unobservable case, will be studied separately regarding whether the customers can observe the state of the server or not at their arrival instants. We will prove that there exist equilibrium mixed strategies.

We begin with the almost unobservable case in which the customers are informed about the state of the server before their decision is made to join upon arrival. Now the optimal decision of a customer has to take into account the strategies of the other customers.

Fig. 2.
figure 2

Transition rate diagram for the (q(0), q(1), q(2)) mixed strategy in the almost unobservable model

Full size image

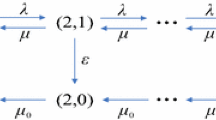
Since all customers are assumed indistinguishable, we can consider the situation as a symmetric game among them. In the present model, there are only two pure strategies, to join or to balk. And a mixed strategy is specified by the joining probability of an arriving customer that finds the server is on working vacation or not. Our goal is to identify the Nash equilibrium mixed balking strategies. Suppose that all customers follow a mixed strategy (q(0), q(1), q(2)), where q(i) is the probability of joining when the server is in state i. Then, the system behaves as the original, but with arrival rate \(\lambda _i=\lambda q(i)\) for states where the server is in state i instead of \(\lambda \). The transition diagram is shown in Fig. 2.

Lemma 1

In the almost unobservable queue with N policy and setup time in which all customers adopt a mixed balking strategy (q(0), q(1), q(2)), where q(i) is the probability of joining when the server is in state i, the stationary distribution is given as follows

$$\begin{aligned} p(n,0)= & {} p(0,0), \quad \quad \quad n=1,...,N-1, \end{aligned}$$
(41)
$$\begin{aligned} p(N,1)= & {} \frac{\lambda _0}{\lambda _1+\theta }p(0,0), \end{aligned}$$
(42)
$$\begin{aligned} p(n,1)= & {} \left( \frac{\lambda _0}{\lambda _1+\theta }\right) \sigma ^{n-N}p(0,0), \quad n=N+1,..., \end{aligned}$$
(43)
$$\begin{aligned} p(1,2)= & {} \frac{\lambda _0}{\mu }p(0,0), \end{aligned}$$
(44)
$$\begin{aligned} p(n,2)= & {} \frac{\lambda _0}{\mu }\frac{1-\rho ^n}{(1-\rho )}p(0,0), \quad \quad \quad n=2,3,...,N-1, \end{aligned}$$
(45)
$$\begin{aligned} p(n,2)= & {} \frac{\lambda _0}{\mu }\frac{\rho ^n(\sigma -\rho )+(1-\sigma )\rho ^{n-N+1}-(1-\rho )\sigma ^{n-N+1}}{(\rho -1)(\sigma -\rho )}, n=N,N+1,..., \end{aligned}$$
(46)

where

$$\begin{aligned} p(0,0)=\left( N+\frac{\lambda _0}{\lambda _1+\theta }\frac{1}{1-\sigma }+\frac{\lambda _0}{\mu }\frac{N(1-\sigma )+\sigma }{(1-\rho )(1-\sigma )}\right) ^{-1}, \end{aligned}$$
(47)

and \(\rho =\frac{\lambda _2}{\mu }\), \(\sigma =\frac{\lambda _1}{\lambda _1+\theta }\).

Proof

The corresponding stationary distribution is obtained as solution of the following system of balance equations:

$$\begin{aligned} \lambda _0 p(0,n)= & {} \mu p(n-1,0), \quad \quad \quad n=1,2,...N-1, \end{aligned}$$
(48)
$$\begin{aligned} (\lambda _1+\theta ) p(1,N)= & {} \lambda _1p(N-1,1), \quad \quad \quad n=N+1..., \end{aligned}$$
(49)
$$\begin{aligned} (\lambda _1+\theta ) p(1,n)= & {} \lambda _1p(n-1,1), \quad \quad \quad n=N+1..., \end{aligned}$$
(50)
$$\begin{aligned} \mu p(2,1)= & {} \lambda _0 p(0,0), \end{aligned}$$
(51)
$$\begin{aligned} (\lambda _2+\mu ) p(2,1)= & {} \mu p(2,2), \end{aligned}$$
(52)
$$\begin{aligned} (\lambda _2 +\mu ) p(2,n)= & {} \mu p(n+1,2)+\lambda _2 p(n-1,2), n=2,...,N-1, \end{aligned}$$
(53)
$$\begin{aligned} (\lambda _2 +\mu ) p(2,n)= & {} \mu p(2,n+1)+\lambda _2 p(n-1,2)+\theta p(n,1), n=N,N+1,.... \end{aligned}$$
(54)

By iterating (49) we can obtain

$$\begin{aligned} p(n,1)=(\frac{\lambda _0}{\lambda _1+\theta })\sigma ^{n-N}p(0,0), \quad n=N+1,.... \end{aligned}$$

From (53) and (54) it follows that p(n, 2) is a solution of the nonhomogeneous linear difference equation with constant coefficients, i.e.,

$$\begin{aligned} {\mu }{x_{n + 1}} - \left( {{\lambda _2} + {\mu }} \right) {x_n} + {\lambda _2}{x_{n - 1}} = -\theta (\frac{\lambda _0}{\lambda _1+\theta })\sigma ^{n-N}p(0,0). \end{aligned}$$

By using the same approach as used in the proof of Lemma 1, we can get (44). Solving equations with respect to p(n, 0) and substituting in

$$\begin{aligned} \sum \limits _{n=0}^{N-1}p(0,n)+\sum \limits _{n=N} ^{\infty }p(1,n)+\sum \limits _{n=1}^{\infty }p(2,n)=1, \end{aligned}$$
(55)

and we can obtain p(0, 0).    \(\square \)

Next, we consider an arriving customer who finds the server is at state \(i(i=0,1,2)\) and we will give the expected sojourn time of a customer that decides to enter given that the others follow the same mixed strategy \(\left( {q( 0 ),q( 1 ),q( 2 )} \right) \).

  • Case 1. When the server is at state 0, the expected sojourn time is

    $$\begin{aligned} {T_{au}}\left( 0 \right) = \frac{{E\left[ {N|0} \right] + 1}}{{{\mu }}}+\frac{1}{\theta }+\frac{N-(E\left[ {N|0} \right] +1)}{\lambda _0}. \end{aligned}$$
    (56)

  • Case 2. When the server is at state 1, the expected sojourn time is

    $$\begin{aligned} {T_{au}}\left( 1 \right) = \frac{{E\left[ {N|1} \right] + 1}}{{{\mu }}}+\frac{1}{\theta }. \end{aligned}$$
    (57)

  • Case 3. When the server is at state 2, the expected sojourn time is

    $$\begin{aligned} {T_{au}}\left( 2 \right) = \frac{{E\left[ {N|2} \right] + 1}}{{{\mu }}}. \end{aligned}$$
    (58)

    To get the \(T_{au}(i), (i=0,1,2)\), we first give the probability that the server in idle, setup, busy steady state as follows

    $$\begin{aligned} P(i=0)= & {} \sum \limits _{n=0}^{N-1}p(n,0)=Np(0,0), \nonumber \\ P(i=1)= & {} \sum \limits _{n=N}^{\infty }p(n,1)=(\frac{\lambda _0}{\lambda _1+\theta })(\frac{1}{1-\sigma })p(0,0), \\ P(i=2)= & {} \sum \limits _{n=1}^{\infty }p(n,2)=\sum \limits _{n=1}^{N-1}p(n,2)+\sum \limits _{n=N}^{\infty }p(n,2), \nonumber \\= & {} \frac{\lambda _0}{\mu }\frac{N(1-\sigma )+\sigma }{N(1-\rho )(1-\sigma )+\rho ^2(1-\sigma )+\sigma (1-\rho )}. \nonumber \end{aligned}$$
    (59)

Using Eq. (59) we can get:

$$\begin{aligned} P(n|0)= & {} \frac{p(n,0)}{P(i=0)}=\frac{1}{N}, \quad n=1,2,...,N-1; \nonumber \\ P(n|1)= & {} \frac{p(n,1)}{P(i=1)}=(1-\sigma )\sigma ^{n-N}, \quad n=N,N+1,...; \nonumber \\ P(n|2)= & {} \frac{p(n,2)}{P(i=2)} \\= & {} \left\{ \begin{array}{l} \frac{(1-\rho )(1-\rho ^n)(1-\sigma )}{N(1-\rho )(1-\sigma )+\rho ^2(1-\sigma )+\sigma (1-\rho )}, \quad \quad n=1,2...,N-1;\\ \\ \frac{(1-\sigma )(\rho -1)(\rho ^n(\sigma -\rho )+(1-\sigma )^{n-N+1})+(\rho -1)\sigma {n-N+1}}{(\sigma -\rho )(N(1-\rho )(1-\sigma )+\rho ^2(1-\sigma )+\sigma (1-\rho ))}, \quad \quad n=N,N+1, .... \end{array} \right. \nonumber \end{aligned}$$
(60)

With the help of Eqs. (59) and (60), we can compute \(E\left[ {N|i} \right] \) and get that

$$\begin{aligned}& E\left[ {N|0} \right] = \sum \limits _{n = 0}^{N-1} {nP(n|0)} = \frac{N-1}{2}, \end{aligned}$$
(61)
$$\begin{aligned}& E\left[ {N|1} \right] = \sum \limits _{n = N}^{\infty } {nP(n|1)} =N+\frac{\sigma }{1-\sigma }, \end{aligned}$$
(62)
$$\begin{aligned}& E\left[ {N|2} \right] = \sum \limits _{n = 1}^{N-1} {nP(n|2)} +\sum \limits _{n = N}^{\infty } {nP(n|2)} \nonumber \\= & {} \frac{1}{N+(1-N)\sigma }\Big (\frac{N(N-1)(1-\rho )(1-\sigma )}{2}\nonumber \\+ & {} \frac{(1-\sigma )((1-N)\rho ^{N+2}+(2N-1)\rho ^{N+1}-(N+1)\rho ^N+(2-\rho )(1-\rho )\rho ^2)}{(1-\rho )^2}\nonumber \\- & {} \frac{(1-\sigma )^2(N\rho +(1-N)\rho ^2)}{(1-\rho )^2(\sigma -\rho )}+\frac{(1-\rho )(N\rho +(1-N)\sigma ^2)}{\sigma -\rho }\Big ). \end{aligned}$$
(63)

Taking Eqs. (61), (62), and (63) into Eqs. (56), (57) and (58), we can derive the \({T_{au}}( 0 )\) and \({T_{au}}( 1 )\) and \({T_{au}}( 2 )\) as follows:

$$\begin{aligned}&{T_{au}}\left( 0 \right) = \frac{1}{\theta }+\frac{N-1}{2\lambda _0}+\frac{N+1}{2\mu },\\&{T_{au}}\left( 1 \right) = \frac{1}{\theta }+\frac{1}{\mu }(N+\frac{\sigma }{1-\sigma })=\frac{1}{\theta }+\frac{N+1}{\mu }+\frac{\lambda _1}{\mu \theta },\\&{T_{au}}\left( 2 \right) =\frac{E\left[ {N|2} \right] +1}{\mu }. \end{aligned}$$

Based on the reward-cost structure, the expected benefit for an arriving customer who is informed the server is at state i is given as follows.

$$\begin{aligned}&{S_{au}}\left( 0 \right) = R - C( \frac{1}{\theta }+\frac{N-1}{2\lambda _0}+\frac{N+1}{2\mu }),\\&{S_{au}}\left( 1 \right) = R - C(\frac{1}{\theta }+\frac{N+1}{\mu }+\frac{\lambda _1}{\mu \theta }),\\&{S_{au}}\left( 2\right) = R - C(\frac{E\left[ {N|2} \right] +1}{\mu }). \end{aligned}$$

According to the above assumptions, an incoming customer always joins when the state of sever I is 0 as long as his net benefit U is non-negative. The sufficient condition for the system stability is

$$\begin{aligned} \frac{1}{\theta }+\frac{N-1}{2\lambda _0}+\frac{N+1}{2\mu }<\frac{R}{C}, \end{aligned}$$
(64)

which means \({S_{au}}\left( 0 \right) >0\). We now assume that the stability condition is satisfied. Obviously, a customer who arrives at state (n, 0) suffers a higher expected waiting time than who arrives at state (N, 1). Thus, all arriving customers join the queue if there are less than N customers in the system and we can know \(q_e(0)=1\).

Next we consider \({q_e}( 1 )\). To this end, we tag an arriving customer when the server is at state 1. His expected benefit is given as follows:

$$\begin{aligned} {S_{au}}\left( 1 \right) = R - C(\frac{1}{\theta }+\frac{N+1}{\mu }+\frac{\lambda _1}{\mu \theta })=0. \end{aligned}$$

By solving the above equation, we can get \(q_e(1)=\frac{\mu \theta }{\lambda }(\frac{R}{C}-\frac{1}{\theta }-\frac{N+1}{\mu })\). We have the following lemma.

Lemma 2

In the almost observable M/M/1 queue with N policy and setup time where the arriving customers know the number of customers in the system, the social welfare per time unit \(SW_{au}\) is given below:

$$\begin{aligned} SW_{ao}=R\lambda (1-p_{ao}(n_e,1)-p_{ao}(n_e,2))-CL_{ao}, \end{aligned}$$

Proof

The mean sojourn time of customer is \(E[W_{au}]\) and the mean queue length is \(L_{au}\).

$$\begin{aligned} E[W_{au}]=L_{au} \lambda . \end{aligned}$$

The mean queue length is shown below:

$$\begin{aligned} L_{au}= & {} \sum \limits _{n = 0}^{N-1}n(p(n,0)+p(n,2)) + \sum \limits _{n = N}^{\infty }n( p(n,1)+p(n,2))\\= & {} \frac{N(N-1)}{2}\frac{\mu -\lambda _2+\lambda _0}{\mu -\lambda _2}p(0,0) +\frac{\lambda _0}{\mu }\frac{(N-1)\rho ^{N+1}-N\rho ^N+\rho }{(1-\rho )^3}p(0,0) \\&+\frac{\lambda _0(N+(1-N)\sigma )}{(\lambda _1+\theta )(1-\sigma )^2}p(0,0) +\frac{\lambda _0}{\mu }\Bigg (\frac{(N-1)\rho ^{N+1}-N\rho ^N}{(1-\rho )^3} \\&+\frac{(1-\sigma )(N-1)\rho ^2-N\rho }{(\sigma -\rho )(1-\rho )^3}+\frac{N\sigma +(1-N)\sigma ^2}{(\sigma -\rho )(1-\sigma )^2}\Bigg )p(0,0). \end{aligned}$$

This completes the proof.    \(\square \)

5 Conclusions

In this paper we analyzed the strategic behavior of the customers and social optimization in a single server queueing system with N-policy and setup time. Arriving customers decide whether to join or to balk the system. Specifically, two different cases with respect to the levels of information provided to arriving customers have been investigated extensively. The customers’ strategies have been analyzed and the expressions of the social welfare function of customers for two cases were derived. For future research, analyzing a model in which the setup time is generally distributed is worthy of further investigation.