1 Introduction

We consider a finite capacity observable M/M/1 queueing system, which provides non-customer-intensive service and follows a first-in-first-out (FIFO) queue discipline. In contrast to customer-intensive services where service value increases with service time, service value decreases with service time in non-customer-intensive services. The arriving customers are of two types—(1) impatient customers who are strategic and make balking decisions, (2) patient customers who are non-strategic, always join the queue, and do not make any decision at all. Nature first probabilistically selects the service rate (fast or slow). The impatient customers then update their beliefs on the service rate by observing the queue and then make balking decisions based on the net utility from the service.

A classic example of our setting is the queue in front of a ticket purchase counter in a railway station on the Mumbai suburban railway [22]. Consider the passengers waiting in a queue to purchase a ticket from a human server at the Churchgate station on the Western line. A passenger traveling from Churchgate to Dadar (approximately 11 km) is impatient, updates the belief on the human server’s rate of service based on the observed queue length, and balks in the case of a long queue at the ticket purchase counter as the cost of switching to another mode of transport is not high. On the other hand, a passenger traveling from Churchgate to Virar (approximately 86 km) is patient, does not make any strategic decision, and always joins the queue as the alternative modes of transport are expensive/tiresome.

McDonald’s is another example of a queueing system with a human server offering counter service. Two types of customers arrive at the facility to order food. A patient customer is fond of hamburgers and will consume a hamburger with certainty in this visit. An impatient customer, on the contrary, is not particular on a McDonald’s hamburger. Hence, an impatient customer updates the belief on the human server’s service rate based on the observed queue length. Further, the impatient customer joins the queue if it is valuable enough to consume the hamburger, given the waiting cost involved; otherwise, the impatient customer balks. In a certain sense, patient and impatient customers are similar to loyal and disloyal customers, respectively.

As evident from the motivating examples, the patient customers are non-strategic because such customers possess infinite valuation for the service of interest. They always join the queue as they derive higher utility from joining than balking. Thus, non-strategic customers are equivalent to strategic customers with infinite service valuation. In this article, we assume that the patient customers are non-strategic and always join the queue. Further, it is pertinent to note that the finite waiting area capacity always does not ensure a finite queue length in practice at a Mumbai suburban railway station and a McDonald’s outlet. Though the waiting area capacity is finite, queue length can sometimes explode, resulting in customers waiting outside the waiting area. While our primary focus is on analyzing the finite waiting area capacity model in this article, we also address the infinite waiting area capacity case in Sect. 7.

In this queueing environment, we develop a symmetric game amongst the impatient customers, where each impatient customer formulates the best response strategy in response to other impatient customers’ strategies. Though patient customers are non-strategic, we assert that their presence impacts the queue length distribution and, therefore, the impatient customers’ equilibrium strategies. Our results suggest that there always exists at least one pure threshold strategy equilibrium at which the impatient customers balk in the impatient customers’ game in the presence of the patient customers. We then analyze the effect of the proportion of impatient customers and the waiting area capacity on the likelihood ratio of a fast server to a slow server in an empty queue and the minimal pure threshold strategy equilibrium. As multiple pure threshold strategy equilibria can exist in some instances, we consider the minimal pure threshold strategy equilibrium, which is the minimum of the pure threshold strategy equilibria. We show that the likelihood ratio is monotonically decreasing in the proportion of impatient customers and monotonically increasing in the waiting area capacity. Further, we show that the minimal pure threshold strategy equilibrium is non-increasing in the proportion of impatient customers and non-decreasing in the waiting area capacity. We also observe that at least one pure threshold strategy equilibrium exists in an infinite capacity queue. We perform numerical analysis to analyze the effect of the proportion of impatient customers and the waiting area capacity on the expected throughput and the expected blocking rate.

In Sect. 2, we provide a review of the literature on queueing games and position our work in the context of the existing literature. We then describe the modeling environment in Sect. 3 and analyze the equilibrium structure in the impatient customers’ game in Sect. 4. In the subsequent section (Sect. 5), we perform sensitivity analysis and study the effect of the proportion of impatient customers and the waiting area capacity on the likelihood ratio and the minimal pure threshold strategy equilibrium. We then perform a numerical analysis of the system performance in Sect. 6. We discuss the case of infinite waiting area capacity in Sect. 7. Finally, we provide concluding remarks and suggest promising future research directions in Sect. 8.

2 Related work

The notion of strategic behavior in observable queues dates back to Naor [23]. Hassin and Haviv [10] and Hassin [11] present a detailed review of the literature on strategic behavior in queues. We draw our work from two different dimensions of literature on queueing games—(1) service type, and (2) customer’s strategic decision.

2.1 Service type

The extant literature on queueing games has considered various service types such as expert services where the service quality is not exactly known even after the service is provided [3], customer-intensive services where service value increases with service time [1], queues with catastrophes where a catastrophe forces the customers to abandon the system and makes the system inoperative for an exponential amount of time until the repair is done [2], and partial breakdowns where the rate of service comes down during a breakdown [19] among others. In recent times, there has been a surge in the literature on positive aspects of waiting. Debo et al. [4] developed a queueing game to signal service quality via queue lengths to uninformed customers in an environment consisting of both informed and uninformed customers. Meanwhile, Anand et al. [1] considered customer-intensive services such as medical, legal, and consultancy services where service time is positively correlated with service value, i.e., service value increases with service time.

Subsequently, Debo and Veeraraghavan [5] analyzed a queueing game amongst the customers in a customer-intensive environment when the service times are unknown, and the arriving customers update their beliefs on the service time based on observed queue length and then make queue-joining decisions. Recently, Liu and Shang [21] considered a queueing game amongst the customers when the service rates are unknown in a non-customer-intensive service environment where the service time is negatively correlated with service value. Our contribution to this strand of literature is similar to Liu and Shang [21] wherein the services are non-customer-intensive. However, the ensuing queueing game amongst the impatient customers in our case is not straightforward and perturbed by the presence of the patient customers. The proportion of patient customers influences the queue length distribution and, subsequently, the Bayesian updating in the utility functions of the strategic impatient customers. Therefore, it is of particular interest to understand the resultant equilibrium structure in this context.

2.2 Strategic customer decisions

Hassin [11] listed the various customer decisions in a queue such as balking, reneging, arrival time, jockeying, retrials, restart. Queueing games with strategic balking customers where the arriving customers decide whether to join the queue or balk in the current period have been studied thoroughly in different contexts [6, 8]. The other strategic customer decisions previously analyzed include arrival time, where the customers decide on the time to arrive at a queue [13, 15], and retrials, where the customer comes back after some time if the server is busy [7, 18] among others. There is also enough literature on loss systems wherein the arrivals are blocked in the presence of busy servers or finite waiting area capacity [11, 24].

Our focus is on a non-customer-intensive service environment with unknown service rates consisting of impatient customers who make strategic balking decisions and patient customers who always join the queue and do not make any decision. As mentioned earlier, impatient customers have been studied extensively in the literature. With respect to patient customers, there have been attempts at modeling customers’ patience in various environments different from ours. Iravani and Balciog̃lu [14] considered different classes of customers who exercise the reneging option when their waiting time exceeds the patience limit. Liu and Cooper [20] then studied a single product pricing problem consisting of impatient and patient customers. While a patient customer waits up to some time periods for the product price to fall below his/her valuation to make a purchasing decision, an impatient customer decides to purchase immediately or leaves without buying. Our work is closely related to Hassin and Roet-Green [12] who study the effect of inspection cost (the cost of acquiring queue length information) on revenue and social welfare in a single server queue consisting of urgent and non-urgent customers. While urgent customers always join the queue, non-urgent customers join the queue according to their equilibrium strategy. We can infer that impatient and patient customers in our model are similar to non-urgent and urgent customers in Hassin and Roet-Green [12]. However, we analyze the strategic impatient customers’ equilibrium balking decisions in the non-strategic patient customers’ presence in a non-customer-intensive service environment with unknown service rates.

2.3 Contribution to the queueing games literature

Our contribution to the literature on strategic queueing with unknown service rates is closely related, albeit different from Naor [23], Debo and Veeraraghavan [5] and Liu and Shang [21]. While impatient customers who make balking decisions have been studied in [5, 21, 23], we analyze the effect of patient customers who always join the queue (similar to urgent customers in Hassin and Roet-Green [12]) on the equilibrium strategies of impatient customers. In particular, we study the queueing game amongst the impatient customers when the service rates are unknown, similarly to Debo and Veeraraghavan [5] and Liu and Shang [21]. Further, we consider non-customer-intensive services similar to Liu and Shang [21] and unlike Debo and Veeraraghavan [5]. The comparison between our model, Naor [23], Debo and Veeraraghavan [5] and Liu and Shang [21] is presented in Table 1.

3 Model and notation

3.1 Notation

\(\Lambda \)

Arrival rate

\({\overline{\mu }}\)

Fast service rate

\({\underline{\mu }}\)

Slow service rate

p

Probability (prior) that the expected service rate is fast

q

Proportion of impatient customers

V

Service value

c

Waiting cost per unit time

\(\nu _{n}\)

Impatient customer’s posterior belief that the service rate is fast when the queue length is n

\(\psi _{n}\)

Impatient customer’s joining probability when the queue length is n

\(n_{b}\)

Highest balking threshold for an impatient customer

\({\overline{N}}\)

Capacity of the waiting area

\(\nu \)

Impatient customer’s posterior belief vector

\(\psi \)

Impatient customer’s joining strategy vector

\(U(n,\nu )\)

Impatient customer’s utility as a function of queue length and posterior belief

\(U(n,\psi ,q)\)

Impatient customer’s utility as a function of queue length, impatient customer’s joining probability and proportion of impatient customers

\(\pi _{n,\mu ,\psi ,q}\)

Stationary probability of n customers in the system as a function of service rate, impatient customer’s joining probability and proportion of impatient customers

b(k)

Best response of a focal impatient customer when the other customers join according to a pure threshold strategy k

3.2 Model description

Nature first chooses the mean service rate \(\mu \in \{{\underline{\mu }},{\overline{\mu }}\}\), where \({\underline{\mu }}<{\overline{\mu }}\). The expected service rate is the fast \({\overline{\mu }}\) with probability p and the slow \({\underline{\mu }}\) with probability \(1-p\), which is assumed to be common knowledge. Customers arrive at the service facility according to a Poisson process with parameter \(\Lambda \). The arriving customers are of two types. A proportion q of customers is impatient and make balk or join decisions, and the remaining \(1-q\) proportion of customers is patient and always joins the queue. The service times follow an exponential distribution. An impatient customer observes a queue of length n and updates the belief on the service rate. The posterior belief on service rate is described as follows: the impatient customer believes with probability \(\nu _{n}\) that the service rate is fast and probability \(1-\nu _{n}\) that the service rate is slow. The impatient customer obtains a service value V and incurs a waiting cost of \(\dfrac{n+1}{\mu }c\), where n is the observed queue length on arrival (including the customer in service), and c is the waiting cost per unit time. When the queue length is \(n^{*}\), we assume that the impatient customer obtains positive utility if the service rate is \({\overline{\mu }}\), \(V - \dfrac{(n^{*}+1)c}{{\overline{\mu }}} > 0\), and obtains negative utility if the service rate is \({\underline{\mu }}\), \(V - \dfrac{(n^{*}+1)c}{{\underline{\mu }}} < 0\).

Assumption 1

There exists \(n^{*} \ge 0\) such that \(V{\underline{\mu }}< (n^{*}+1)c < V{\overline{\mu }}\).

Therefore, the impatient customer’s utility function is defined as

$$\begin{aligned} U(n,\nu ) = \nu _{n}\left( V - \dfrac{n+1}{{\overline{\mu }}}c\right) + \left( 1-\nu _{n}\right) \left( V - \dfrac{n+1}{{\underline{\mu }}}c\right) . \end{aligned}$$
(1)
Table 1 Our model versus Naor [23] versus Debo and Veeraraghavan [5] versus Liu and Shang [21]
Full size table

We normalize the utility from balking to 0. Let \(n_{b} = \left\lfloor \dfrac{V{\overline{\mu }}}{c} \right\rfloor \), where \(n_{b}\) is the highest balking threshold for the impatient customer. To reflect the waiting area capacity in reality, we define \({\overline{N}} = w\), where \(w \in {\mathbb {N}}\). However, we will show that the existence of equilibrium is guaranteed even when the waiting area capacity is infinite in Sect. 7. At \({\overline{N}}\), the customers are blocked from entering the system. To avoid cases where the impatient customer is blocked from the system, we make the following assumption.

Assumption 2

We assume that \(n_{b} < {\overline{N}}\).

\(n_{b}\) is a result of impatient customer’s strategic decision making and can be computed by the service provider. The service provider can thus set the capacity greater than \(n_{b}\). There is abundant literature on queueing games with impatient customers who make balk or join decisions [11]. In such a setting, the notion of blocking does not arise because \(n_{b}\) is the highest balking threshold and \(n_{b} < {\overline{N}}\). On the other hand, patient customers always join the queue in a queueing system consisting of impatient and patient customers. Thus, queue lengths beyond \(n_{b}\) are attained with positive probability in the presence of patient customers. Subsequently, patient customers are blocked from entering the system at \({\overline{N}}\).

While the state space of observed queue lengths is \(n \in \{0,1,2,\ldots , {\overline{N}}\}\), the equilibrium analysis in the impatient customer’s game is restricted to \(n \in \{0,1,2,\ldots , n_{b}\}\). \(\psi _{n} \in [0,1]\) denotes the impatient customer’s joining probability after observing a queue of length n for all \(n \in \{0,1,2,\ldots , n_{b}\}\). We use the vectors \(\psi = (\psi _{0},\psi _{1},\ldots , \psi _{n_{b}})\) and \(\nu = (\nu _{0},\nu _{1},\ldots ,\nu _{n_{b}})\) to represent the impatient customer’s joining strategy and updated belief, respectively. We define \(\pi _{n,\mu ,\psi ,q}\) as the stationary probability of exactly n customers in the system when nature chooses service rate \(\mu \), proportion q of the customers are impatient and impatient customers play a strategy \(\psi \) for all \(n \in \{0,1,2,\ldots , n_{b}\}\).

Lemma 1

The stationary probability of n customers in the system \(\pi _{n,\mu ,\psi ,q}\) is given by

$$\begin{aligned}&\pi _{n,\mu ,\psi ,q} \nonumber \\&\quad ={\left\{ \begin{array}{ll} \pi _{0,\mu ,\psi ,q} \prod _{j=0}^{n-1} \left( [\psi _{j}q+(1-q)]\dfrac{\Lambda }{\mu }\right) , &{} n \in \{1,2,\ldots ,n_{b}\}, \\ \pi _{0,\mu ,\psi ,q} \left( \dfrac{(1-q)\Lambda }{\mu }\right) ^{n-n_{b}} \prod _{j=0}^{n_{b}-1} \left( [\psi _{j}q+(1-q)]\dfrac{\Lambda }{\mu }\right) , &{} n \in \{n_{b}+1,n_{b}+2,\ldots ,{\overline{N}}\}, \end{array}\right. }\nonumber \\ \end{aligned}$$
(2)

where \(\pi _{0,\mu ,\psi ,q}\) is the stationary probability of an empty system, which in turn is equal to

$$\begin{aligned} \pi _{0,\mu ,\psi ,q}= & {} \left[ 1 + \sum _{n=1}^{n_{b}} \prod _{j=0}^{n-1} \left( [\psi _{j}q+(1-q)]\dfrac{\Lambda }{\mu }\right) \right. \nonumber \\&\quad \left. + \prod _{j=0}^{n_{b}-1} \left( [\psi _{j}q+(1-q)]\dfrac{\Lambda }{\mu }\right) \sum _{n=n_{b}+1}^{{\overline{N}}} \left( \dfrac{(1-q)\Lambda }{\mu }\right) ^{n-n_{b}}\right] ^{-1}. \end{aligned}$$
(3)

The proofs of all lemmas are available in the appendix. We observe that the stationary probability of n customers depends on the impatient customer’s balking strategy and the proportion of impatient and patient customers. We use the PASTA property (Poisson Arrivals See Time Averages), which states that a randomly arriving customer in the limit observes a queue of length n with stationary probability \(\pi _{n,\mu ,\psi ,q}\) [25]. According to Bayes’ rule, the posterior probability that the service rate is fast is given by

$$\begin{aligned} \nu _{n} = \dfrac{p\pi _{n,{\overline{\mu }},\psi ,q}}{p\pi _{n,{\overline{\mu }},\psi ,q} + (1-p)\pi _{n,{\underline{\mu }},\psi ,q}}. \end{aligned}$$
(4)

4 Equilibrium analysis in the impatient customers’ game

We determine the equilibrium strategies \(\psi ^{*}\) and updated equilibrium beliefs \(\nu ^{*}\) of the impatient customer. In the following definition, we specify the equilibrium conditions in the customer’s game.

Definition 1

The impatient customers’ strategies \(\psi ^{*}\) and updated beliefs \(\nu ^{*}\) form an equilibrium under the following conditions:

  1. (i)

    The impatient customers are rational. For all \(n \in \{0,1,2,\ldots , n_{b}\}\),

    $$\begin{aligned} \psi ^{*}_{n} \in {{\,\mathrm{arg\,max}\,}}_{{\tilde{\psi }} \in [0,1]} {\tilde{\psi }} U(n,\psi ^{*},q). \end{aligned}$$
    (5)
  2. (ii)

    The beliefs of the impatient customers are consistent. Under the customer’s strategy \(\psi ^{*}\), the belief \(\nu _{n}^{*}\) satisfies Bayes’ rule for all queue lengths \(n \in \{0,1,2,\ldots , n_{b}\}\).

We can express the utility function \(U(n,\nu )\) as a function of strategies \(\psi \), and proportion of impatient customers q, by substituting \(\nu _{n}\) in \(U(n,\nu )\):

$$\begin{aligned} U(n,\psi ,q) = \dfrac{p\pi _{n,{\overline{\mu }},\psi ,q} \left( V - \dfrac{n+1}{{\overline{\mu }}}c\right) + (1-p)\pi _{n,{\underline{\mu }},\psi ,q} \left( V - \dfrac{n+1}{{\underline{\mu }}}c\right) }{p\pi _{n,{\overline{\mu }},\psi ,q} + (1-p)\pi _{n,{\underline{\mu }},\psi ,q}}. \end{aligned}$$
(6)

The equilibrium conditions for an impatient customer expressed in terms of \(\psi ^{*}\) are given by

$$\begin{aligned} \psi _{n}^{*} = 1 \iff U(n,\psi ^{*},q) > 0, \end{aligned}$$
(7)
$$\begin{aligned} \psi _{n}^{*} = 0 \iff U(n,\psi ^{*},q) < 0, \end{aligned}$$
(8)
$$\begin{aligned} \psi _{n}^{*} \in (0,1) \iff U(n,\psi ^{*},q) = 0. \end{aligned}$$
(9)

As the action space \([0,1]^{n_{b}}\) is compact and the best response function graph is closed, we conclude from the Kakutani fixed-point theorem that at least one equilibrium in mixed strategies exists [16]. Our equilibrium analysis is only applicable on queue lengths \(n \in \{0,1,\ldots ,n_{b}\}\).

The resulting equilibrium structure can be of threshold or non-threshold type. A threshold strategy is described by the threshold \(k = n + z\), where \(n \in {\mathbb {N}}\) and \(z \in [0,1)\). The customers join when the queue length is \(0 \le i \le n-1\); join with probability z and do not join with probability \(1-z\) when the queue length is n; do not join when \(i > n\). If \(z=0\) (k is an integer), it is a pure strategy; otherwise, it is mixed [10]. On the other hand, a non-threshold strategy describes the non-monotone joining behavior of customers and is not solely defined by the threshold. Some examples of non-threshold strategies include a sputtering strategy [5] and strategy with a hole [4]. In Debo and Veeraraghavan [5], a sputtering strategy is defined by two queue lengths \({\underline{k}}\) and \({\overline{k}}\) where the customers join when the queue length is \(0 \le i \le {\underline{k}} - 1\); join with probability \(\alpha _{{\underline{k}}}\) and do not join with probability \(1 - \alpha _{{\underline{k}}}\) at queue length \({\underline{k}}\); join again at queue lengths \({\underline{k}}+1 \le i < {\overline{k}}\); balk at queue length \({\overline{k}} > {\underline{k}} + 1\). Debo et al. [4] consider a non-threshold strategy with a hole for an uninformed customer in a population mix of informed and uninformed customers. At the hole \({\hat{n}}\), the uninformed customer does not join the queue; however, the uninformed customer follows the informed customer’s strategy at all queue lengths except \({\hat{n}}\). The informed customer joins at queue lengths \(i \ge {\hat{n}}\) for a high-quality firm. The uninformed customer’s strategy is of non-threshold type as the uninformed customer balks at \({\hat{n}}\) and joins at queue lengths greater than \({\hat{n}}\).

We perform the equilibrium analysis by adopting the framework of Debo and Veeraraghavan [5] to our context where the services are non-customer-intensive, and customers are of two types. Our focus is on threshold equilibrium structures for the queueing game where a pure or mixed strategy equilibrium exists. We first consider pure threshold strategies where the arriving impatient customers join at the first \(k-1\) queue lengths and balk at k. At queue lengths \(\{k,k+1,\ldots , {\overline{N}}-1\}\), only the patient customers join the queue. A threshold strategy k is an equilibrium if it satisfies the following conditions: \(U(n,k,q) \ge 0\) for all \(0 \le n \le k-1\) and \(U(n,k,q) \le 0\) for all \(k \le n \le n_{b}\). Let \(\omega (n) = \left( \dfrac{{\overline{\mu }}}{{\underline{\mu }}}\right) ^{n} \dfrac{\dfrac{n+1}{{\underline{\mu }}}c - V}{V - \dfrac{n+1}{{\overline{\mu }}}c}\) and \(\theta _{q}(k,{\overline{N}}) = \dfrac{1+ \sum _{j=1}^{k}\left( \dfrac{\Lambda }{{\underline{\mu }}}\right) ^{j} + \sum _{j=k+1}^{{\overline{N}}}(1-q)^{j-k}\left( \dfrac{\Lambda }{{\underline{\mu }}}\right) ^{j}}{1+\sum _{j=1}^{k}\left( \dfrac{\Lambda }{{\overline{\mu }}}\right) ^{j} + \sum _{j=k+1}^{{\overline{N}}}(1-q)^{j-k}\left( \dfrac{\Lambda }{{\overline{\mu }}}\right) ^{j}}\).

Lemma 2

The pure threshold strategy k is in equilibrium if and only if, \(\omega (n) \le \dfrac{p}{1-p} \theta _{q}(k,{\overline{N}})\) for \(n \in \{0,1,\ldots ,k-1\}\) and \(\omega (n) \ge \dfrac{p}{1-p} \theta _{q}(k,{\overline{N}})\) for \(n \in \{k,k+1,\ldots ,n_{b}\}\).

We now consider \(\omega (n)\) and \(\theta _{q}(k,{\overline{N}})\) as a function over the real numbers, and replace integer n by real \({\tilde{n}}\) and integer k by real \({\tilde{k}}\). Further, let \({\underline{n}} = \dfrac{V{\underline{\mu }}}{c} - 1\) and \({\overline{n}} = \dfrac{V{\overline{\mu }}}{c} - 1\). We also notice that \(\omega ({\tilde{n}})\) is non-negative for \({\tilde{n}} \in [{\underline{n}},{\overline{n}})\) and \(\omega ({\underline{n}}) = 0\) and \(\lim _{{\tilde{n}} \rightarrow {\overline{n}}} \omega ({\tilde{n}}) = +\infty \). In addition, \([{\underline{n}},{\overline{n}})\) is non-empty and the domain of \(\omega ({\tilde{n}})\) is \([{\underline{n}},{\overline{n}})\). As \(\theta _{q}({\tilde{k}},{\overline{N}})\) is non-negative for all \({\tilde{k}} \ge 0\), the domain of \(\theta _{q}({\tilde{k}},{\overline{N}})\) is \({\mathbb {R}}^{+}\). We then define \(N({\tilde{k}}) = min\left\{ {\tilde{n}} \in [{\underline{n}},{\overline{n}}):\omega ({\tilde{n}}) \ge \xi \theta _{q}({\tilde{k}},{\overline{N}})\right\} \) where \(\xi = \dfrac{p}{1-p}\). The domain of N(k) is not restricted to [0, k]. Then, \(b(k) = max\{0,\lceil N(k)\rceil \}\) is the best response of a focal customer when the other customers join based on a pure threshold strategy k. When the best response of a focal customer is equal to the strategy of other customers, i.e., \(b(k) = k\) or \(\omega (k-1)< \xi \theta _{q}(k,{\overline{N}}) < \omega (k)\), then the focal customer’s strategy b(k) is an equilibrium strategy.

Remark 1

At \(q=0\), \(\theta _{q}({\tilde{k}},{\overline{N}})\) is independent of \({\tilde{k}}\) and all customers are patient (non-strategic) and join the queue until \({\overline{N}}\) at which they are blocked.

Remark 2

At \(q=1\), the focal impatient customer’s best response depends on other customers’ threshold balking strategies and \(\theta _{q}({\tilde{k}},{\overline{N}})\) reduces to \(\dfrac{1+ \sum _{j=1}^{{\tilde{k}}}\left( \dfrac{\Lambda }{{\underline{\mu }}}\right) ^{j}}{1+\sum _{j=1}^{{\tilde{k}}}\left( \dfrac{\Lambda }{{\overline{\mu }}}\right) ^{j}}\), which is the inverse of \(\Phi ({\tilde{k}})\) in Debo and Veeraraghavan [5]. It follows that \(\theta _{q}({\tilde{k}},{\overline{N}})\) is monotonically increasing in \({\tilde{k}}\).

In our case, \(\theta _{q}(k,{\overline{N}})=\dfrac{\pi _{0,{\overline{\mu }},k,q}}{\pi _{0,{\underline{\mu }},k,q}}\) represents the likelihood ratio of a fast server to a slow server for an empty queue, which is the opposite of the likelihood ratio defined in Debo and Veeraraghavan [5]; however, \(1-q\) proportion of the customers are patient in our setting. On the other hand, we consider the likelihood ratio for a queue of length n as \(\dfrac{\pi _{n,{\overline{\mu }},k,q}}{\pi _{n,{\underline{\mu }},k,q}} = \left( {\underline{\mu }}/{\overline{\mu }}\right) ^{n} \theta _{q}(k,{\overline{N}})\). This holds under the assumption that customers join at queue lengths between 0 and \(n-1\). An arriving impatient customer is ambivalent between joining and not when \(\left( \dfrac{n+1}{{\underline{\mu }}}c - V\right) /\left( V - \dfrac{n+1}{{\overline{\mu }}}c\right) = \dfrac{p}{1-p} \left( {\underline{\mu }}/{\overline{\mu }}\right) ^{n} \omega (n)\). Similar to Debo and Veeraraghavan [5], we can interpret \(\omega (n)\) as the required likelihood ratio for an empty queue that makes the arriving customer ambivalent at queue length n.

Lemma 3

  1. (i)

    If \(q >0\), \(\theta _{q}({\tilde{k}},{\overline{N}})\) is monotonically increasing in \({\tilde{k}}\) for all \({\tilde{k}} \ge 0\).

  2. (ii)

    \(\omega ({\tilde{n}})\) is monotonically increasing in \({\tilde{n}}\) over \([{\underline{n}},{\overline{n}})\).

We show that the queue joining strategies of impatient customers are monotone in the queue length when there exists a negative correlation between service time and service value for all \(q > 0\). We observe the follow-the-crowd (FTC) behavior and then show that at least one pure threshold strategy equilibrium is guaranteed. Recently, Liu and Shang [21] proved the existence of at least one threshold equilibrium in a setting consisting of only impatient customers. However, we show that at least one pure threshold equilibrium strategy exists even in the presence of patient customers (Proposition 1). This result is also different from Naor’s model with negative externalities which exhibits neither the follow-the-crowd (FTC) nor the avoid-the-crowd (ATC) behavior where a customer’s decision is independent of the other customers’ decisions [11].

Proposition 1

If \(q > 0\), there exists at least one pure threshold strategy equilibrium in the impatient customer’s game.

Proof

Let \(k_{1} > k_{2}\). From Lemma 3, we observe that \(\theta _{q}(k_{1}) > \theta _{q}(k_{2})\) for all \(q > 0\). Also, \(\omega (n)\) is monotonically increasing in n. By the definition of b(k), it is clear that \(\theta _{q}(k_{1}) > \theta _{q}(k_{2}) \implies N(k_{1}) \ge N(k_{2})\). We then find that \(b(k_{1}) \ge b(k_{2})\) when \(k_{1} > k_{2}\) which demonstrates the FTC behavior. The higher the threshold adopted by other impatient customers, the higher is the focal impatient customer’s threshold to balk. We know that multiple fixed points exist and therefore, multiple symmetric equilibria of the threshold type in pure or mixed strategy space are possible in the presence of FTC behavior [10].

Further, if \(\omega (\lceil {\underline{n}} \rceil ) \ge \xi \theta _{q}(\lceil {\underline{n}} \rceil )\), \(\lceil {\underline{n}} \rceil \) is a pure threshold strategy equilibrium. Instead, if \(\omega (\lceil {\underline{n}} \rceil ) < \xi \theta _{q}(\lceil {\underline{n}} \rceil )\), we will show that there always exists a pure threshold strategy equilibrium at \(k > \lceil {\underline{n}} \rceil \). We know that \(\theta _{q}({\tilde{k}},{\overline{N}})\) is monotonically increasing in \({\tilde{k}}\) and \(\omega ({\tilde{n}})\) is monotonically increasing in \({\tilde{n}}\) (Lemma 3). However, \(\lim _{{\tilde{n}} \rightarrow {\overline{n}}} \omega ({\tilde{n}}) = +\infty \). Therefore, there always exists a \({\tilde{k}}'\) at which the functions \(\xi \theta _{q}({\tilde{k}}',{\overline{N}})\) and \(\omega ({\tilde{k}}')\) intersect. Let \(\lceil {\tilde{k}}' \rceil = k\). We then know that \(\omega (k-1) < \xi \theta _{q}(k-1,{\overline{N}})\) and \(\xi \theta _{q}(k,{\overline{N}}) < \omega (k)\). Moreover, as both \(\theta _{q}({\tilde{k}},{\overline{N}})\) and \(\omega ({\tilde{k}})\) are monotonically increasing in \({\tilde{k}}\) (Lemma 3), \(\omega (k-1) < \xi \theta _{q}(k,{\overline{N}})\). Hence, \(\omega (k-1)< \xi \theta _{q}(k,{\overline{N}}) < \omega (k)\) or \(b(k) = k\) and at least one pure threshold strategy equilibrium exists. \(\square \)

In the equilibrium analysis of priority queues, [9] illustrates the existence of a mixed threshold equilibrium strategy between two consecutive pure threshold equilibrium strategies. We also observe a similar phenomenon in our case when consecutive pure threshold strategy equilibria exist. Due to the FTC behavior in our queueing environment, multiple threshold equilibria are possible. When there are two consecutive pure threshold strategy equilibria (i.e., \(\xi \theta _{q}(k-1,{\overline{N}})< \omega (k-1)< \xi \theta _{q}(k,{\overline{N}}) < \omega (k)\)), we will show that there exist infinitely many mixed threshold strategy equilibria. The impatient customers join at queue length \(k-1\) with probability \(\psi _{k-1}\) and balk at k. The queue-joining probability \(\psi _{k-1}\) satisfies the condition \(\omega (k-2)< \dfrac{p}{1-p}{\hat{\theta }}_{q}(k-1,\psi _{k-1},k,{\overline{N}}) < \omega (k)\), where

$$\begin{aligned}&{\hat{\theta }}_{q}(k-1,\psi _{k-1},k,{\overline{N}}) \\&\quad = \dfrac{\sum _{j=0}^{k-1}\left( \dfrac{\Lambda }{{\underline{\mu }}}\right) ^{j} + (\psi _{k-1}q + 1-q) \left[ \left( \dfrac{\Lambda }{{\underline{\mu }}}\right) ^{k} + \sum _{j=k+1}^{{\overline{N}}} (1-q)^{j-k} \left( \dfrac{\Lambda }{{\underline{\mu }}}\right) ^{j}\right] }{\sum _{j=0}^{k-1}\left( \dfrac{\Lambda }{{\overline{\mu }}}\right) ^{j} + (\psi _{k-1}q + 1-q) \left[ \left( \dfrac{\Lambda }{{\overline{\mu }}}\right) ^{k} + \sum _{j=k+1}^{{\overline{N}}} (1-q)^{j-k} \left( \dfrac{\Lambda }{{\overline{\mu }}}\right) ^{j}\right] }. \end{aligned}$$
Fig. 1
figure 1

Two consecutive pure threshold strategy equilibria at \(b(k)=k=6\) and \(b(k)=k=7\), respectively

Full size image
Table 2 Focal impatient customer’s best response b(k) to the threshold strategy k
Full size table

Proposition 2

If there exist pure threshold strategy equilibria at consecutive queue lengths \(k-1\) and k, there are infinitely many mixed threshold strategy equilibria with randomization at \(k-1\).

Proof

The definition of pure threshold strategy equilibria at queue lengths \(k-1\) and k implies that the conditions \(\omega (k-2)< \xi \theta _{q}(k-1,{\overline{N}}) < \omega (k-1)\) and \(\omega (k-1)< \xi \theta _{q}(k,{\overline{N}}) < \omega (k)\) are satisfied, respectively. Further, we can infer that \(\xi \theta _{q}(k-1,{\overline{N}})< \omega (k-1) < \xi \theta _{q}(k,{\overline{N}})\). Using the definition of \({\hat{\theta }}_{q}(k-1,\psi _{k-1},k,{\overline{N}})\), it follows that \(\xi {\hat{\theta }}_{q}(k-1,0,k,{\overline{N}})< \omega (k-1) < \xi {\hat{\theta }}_{q}(k-1,1,k,{\overline{N}})\). As \({\hat{\theta }}_{q}(k-1,\psi _{k-1},k,{\overline{N}})\) is continuous in \(\psi _{k-1}\), there always exists infinitely many \(\psi _{k-1} \in [0,1]\) at which \(\omega (k-2)< {\hat{\theta }}_{q}(k-1,\psi _{k-1},k,{\overline{N}}) < \omega (k)\). Also, with monotonically increasing \(\omega (n)\) (Lemma 3), we know that \(\omega (n) < \omega (k-1)\) for all \(0 \le n < k-1\). This justifies the existence of infinitely many mixed threshold strategy equilibria with queue-joining probability \(\psi _{k-1}\) at \(k-1\) and balking at k. \(\square \)

We provide the intuition behind the existence of infinitely many equilibria with any randomization \(\psi _{k-1}\) at \(k-1\). A pure threshold strategy equilibrium at k implies that the impatient customers join at \(k-1\) with probability 1. Similarly, a pure strategy equilibrium at \(k-1\) implies that the impatient customers join at \(k-1\) with probability 0. As both joining and balking at \(k-1\) satisfy equilibrium conditions, any joining probability at \(k-1\) will satisfy the equilibrium conditions. Hence, there exist infinitely many mixed threshold strategy equilibria.

To illustrate the existence of infinitely many mixed threshold strategy equilibria between any two consecutive pure threshold strategy equilibria, we provide the following example. Let \(p=0.05, \Lambda = 15, {\overline{\mu }} = 12, {\underline{\mu }} = 6, q =0.5, {\overline{N}} = 15, V=2, c=2\). In Fig. 1, we illustrate the existence of consecutive pure threshold strategy equilibria at \(b(k)=k=6\) and \(b(k)=k=7\), respectively. We observe from Table 2 that \(\omega (5)< \xi \theta _{0.5}(6,15)< \omega (6)< \xi \theta _{0.5}(7,15)< \omega (7) \implies \omega (5)< \xi {\hat{\theta }}_{0.5}(6,0,7,15)< \omega (6)< \xi {\hat{\theta }}_{0.5}(6,1,7,15) < \omega (7)\). There exist infinitely many mixed threshold strategy equilibria at which \(\omega (5)< {\hat{\theta }}_{0.5}(6,\psi _{1},7,15) < \omega (7)\).

5 Sensitivity analysis

We perform sensitivity analysis by studying the impact of the proportion of impatient customers and the waiting area capacity on threshold equilibrium strategies. As multiple pure threshold strategy equilibria can possibly exist in certain cases, we particularly consider the effect of the proportion of impatient customers and the waiting area capacity on the minimal pure threshold strategy equilibrium. We first analyze the effect of the proportion of impatient customers on impatient customers’ equilibrium strategies. In this regard, we aim to understand how \(\theta _{q}(k,{\overline{N}})\) varies with the proportion of impatient customers (Lemma 4).

Lemma 4

\(\theta _{q}({\tilde{k}},{\overline{N}})\) is monotonically decreasing in q for all \({\tilde{k}} \ge 0\).

Proposition 3

The minimal pure threshold strategy equilibrium is non-increasing in the proportion of impatient customers.

Proof

From Lemma 4, we know that \(\theta _{q_{1}}(k,{\overline{N}}) < \theta _{q_{2}}(k,{\overline{N}})\) when \(q_{1} > q_{2}\). As \(\omega (n)\) is independent of q and monotonic, it follows that \(N_{q_{1}}(k) \le N_{q_{2}}(k) \implies b_{q_{1}}(k) \le b_{q_{2}}(k)\) for a given k. As a pure threshold strategy equilibrium is guaranteed to exist (Proposition 1), let the equilibrium for \(q_{2}\) occur at k, i.e., \(b_{q_{2}}(k) = k\). If multiple equilibria exist for \(q_{2}\), consider the smallest pure threshold strategy equilibrium. Now, as \(b_{q_{1}}(k) \le b_{q_{2}}(k)\), we can look at two cases:

Case 1. If \(b_{q_{1}}(k) = b_{q_{2}}(k)\), then the equilibrium for \(q_{1}\) also occurs at k.

Case 2. If \(b_{q_{1}}(k) < b_{q_{2}}(k)\), the equilibrium for \(q_{1}\) does not occur at k. From the FTC behavior, we know that \(b_{q_{1}}(k) \ge b_{q_{1}}(k-1)\). Now, if \(b_{q_{1}}(k-1) = k-1\), the pure threshold strategy equilibrium for \(q_{1}\) occurs at \(k-1\). Otherwise, there is no pure threshold strategy equilibrium at \(k-1\) for \(q_{1}\). Then, we can consider \(k-2, k-3,\ldots ,\lceil {\underline{n}} \rceil \). In general, \(b_{q_{1}}(k - \varphi )\) is bounded below by \(\lceil {\underline{n}} \rceil \) for all \(\varphi \in \{0,1,2,\ldots , k\}\). As \(b_{q_{1}}(k - \varphi + 1) \ge b_{q_{1}}(k - \varphi )\), we find that \(b_{q_{1}}(k - \varphi ) = \lceil {\underline{n}} \rceil \) if \(b_{q_{1}}(k - \varphi + 1) = \lceil {\underline{n}} \rceil \). Therefore, if there exists no pure threshold strategy equilibrium from \(k-1\) (i.e., \(b_{q_{1}}(k-1) \ne k-1\)) to \(\lceil {\underline{n}} \rceil + 1\) (i.e., \(b_{q_{1}}(\lceil {\underline{n}} \rceil + 1) \ne \lceil {\underline{n}} \rceil + 1\)), there will always exist a pure threshold strategy equilibrium for \(q_{1}\) at \(\lceil {\underline{n}} \rceil \) (i.e., \(b_{q_{1}}(\lceil {\underline{n}} \rceil ) = \lceil {\underline{n}} \rceil \)). \(\square \)

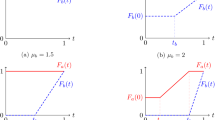
At this stage, it is essential to recall the physical interpretation of \(\theta _{q}(k,{\overline{N}})\), which is the likelihood ratio of a fast server to a slow server in an empty queue. We also know that an impatient customer prefers a fast server over a slow server when the queue length is 0. As the likelihood ratio is monotonically decreasing in the proportion of impatient customers, it follows that the minimal symmetric pure threshold strategy equilibrium is non-increasing in the proportion of impatient customers. From Proposition 3, we can also infer that the probability of attaining higher queue lengths is low when the proportion of impatient customers is high. Conversely, the probability of reaching higher queue lengths is high when the proportion of patient customers is high. The reason behind this behavior is that the minimal pure threshold strategy equilibrium and the joining rate are non-decreasing in the proportion of patient customers. We provide an example to show that the minimal pure threshold strategy equilibrium is non-increasing in the proportion of impatient customers where \(p=0.25,\Lambda =15, {\overline{\mu }} = 12, {\underline{\mu }} = 6, {\overline{N}} = 15, V =2, c = 2\) (refer to Fig. 2).

We next study how the pure threshold strategy equilibrium varies with the waiting area capacity.

Lemma 5

\(\theta _{q}({\tilde{k}},{\overline{N}})\) is monotonically increasing in \({\overline{N}}\) for all \({\tilde{k}} \ge 0\).

Proposition 4

The minimal pure threshold strategy equilibrium is non-decreasing in the capacity of the waiting area.

Proof

This proof is similar to the proof of Proposition 3 and is provided in the appendix. \(\square \)

As the likelihood ratio is monotonically increasing in the waiting area capacity, it follows that the minimal symmetric pure threshold strategy equilibrium is non-decreasing in the waiting area capacity. Proposition 4 is significant because the equilibrium in the impatient customers’ game occurs at potentially higher queue lengths when the waiting area capacity is high. We provide an example where \(p=0.25,\Lambda =15, {\overline{\mu }} = 12, {\underline{\mu }} = 6, q = 0.5, V =2, c = 2\) (refer to Figure 3) to illustrate that the minimal pure threshold strategy equilibrium is non-decreasing in the waiting area capacity.

Fig. 2
figure 2

Minimal pure threshold strategy equilibrium versus proportion of impatient customers

Full size image
Fig. 3
figure 3

Minimal pure threshold strategy equilibrium versus capacity of the waiting area

Full size image

6 Numerical analysis of the system performance

We perform numerical analysis to analyze how the proportion of impatient customers and the waiting area capacity influence the system performance. To understand the system performance, we first define throughput for a server of type \(\mu \) as \(TP_{\mu ,\psi ,q,{\overline{N}}} = \mu \left( 1-\pi _{0,\mu ,\psi ,q}\right) \), where \(\left( 1-\pi _{0,\mu ,\psi ,q}\right) \) denotes the probability that the server is busy [4, 5]. As a pure threshold strategy equilibrium k always exists, throughput becomes

$$\begin{aligned} TP_{\mu ,k,q,{\overline{N}}} = \mu \left( 1- \dfrac{1}{\sum _{j=0}^{k} \left( \dfrac{\Lambda }{\mu }\right) ^{j} + \left( \dfrac{\Lambda }{\mu }\right) ^{k} \sum _{j=k+1}^{{\overline{N}}} \left( \dfrac{(1-q)\Lambda }{\mu }\right) ^{j-k}}\right) . \end{aligned}$$
(10)

As the server can be fast or slow, we consider the expected throughput \(E\left[ TP\right] = p TP_{{\overline{\mu }},k,q,{\overline{N}}} + (1-p)TP_{{\underline{\mu }},k,q,{\overline{N}}}\) similar to Debo and Veeraraghavan [5].

As the waiting area capacity is finite, customers are blocked from entering the system at \({\overline{N}}\) [24]. From Assumption 2, it is apparent that only the patient customers are blocked from entering the system at \({\overline{N}}\) in our case. The blocking probability for a server of type \(\mu \) is then equal to

$$\begin{aligned} \pi _{{\overline{N}},\mu ,k,q} = \dfrac{\left( \dfrac{\Lambda }{\mu }\right) ^{k}\left( \dfrac{(1-q)\Lambda }{\mu }\right) ^{{\overline{N}}-k}}{\sum _{j=0}^{k} \left( \dfrac{\Lambda }{\mu }\right) ^{j} + \left( \dfrac{\Lambda }{\mu }\right) ^{k} \sum _{j=k+1}^{{\overline{N}}} \left( \dfrac{(1-q)\Lambda }{\mu }\right) ^{j-k} }. \end{aligned}$$
(11)

As only the patient customers are blocked from entering the system, we define the blocking rate as \(BR_{\mu ,k,q,{\overline{N}}} = \Lambda (1-q)\pi _{{\overline{N}},\mu ,k,q}\). We then consider the expected blocking rate \(E\left[ BR\right] = p BR_{{\overline{\mu }},k,q,{\overline{N}}} + (1-p)BR_{{\underline{\mu }},k,q,{\overline{N}}}\).

After setting \({\overline{\mu }}=12,{\underline{\mu }}=6,V=2,c=2\), we perform numerical analysis by considering different values of \(p = \{0.1, 0.9\},\Lambda = \{3, 9, 15\},q = \{0.1, 0.5, 0.9\}\) and \({\overline{N}} = \{15,20\}\). In particular, we analyze how the expected throughput varies with the proportion of impatient customers and the waiting area capacity. We also study how the expected blocking rate varies with the proportion of impatient customers and the waiting area capacity. When multiple pure threshold strategy equilibria exist, we consider the minimal pure threshold strategy equilibrium. The results are presented in Tables 3 and 4.

Table 3 Variation of the system performance with \(\Lambda , {\overline{N}}\) and q at \(p=0.1\)
Full size table
Table 4 Variation of the system performance with \(\Lambda , {\overline{N}}\) and q at \(p=0.9\)
Full size table

From the numerical analysis, we find that the expected throughput is monotonically non-increasing in the proportion of impatient customers. This follows from Proposition 3, which states that the minimal pure threshold strategy equilibrium is non-increasing in the proportion of impatient customers. Further, an increase in the proportion of impatient customers leads to a corresponding decrease in the proportion of patient customers who always join the queue. Since the joining rate is monotonically non-increasing in the proportion of impatient customers, the expected throughput is monotonically non-increasing in the proportion of impatient customers. On the other hand, the expected throughput is monotonically non-decreasing in the waiting area capacity since it follows from Proposition 4 that the minimal pure threshold strategy equilibrium is non-decreasing in the waiting area capacity.

We then find that the expected blocking rate is monotonically non-increasing in the proportion of impatient customers. This behavior follows from Proposition 3. Further, it is also due to the decrease in the proportion of patient customers who always join the queue. While the expected blocking rate is monotonically decreasing in the waiting area capacity in most cases, this is not always guaranteed. We provide an example to show that the expected blocking rate is not always monotonically decreasing in the waiting area capacity. Let \(p=0.05,\Lambda =22, {\overline{\mu }} = 20, {\underline{\mu }}=2,q=0.9,V=10,c=22\). At \({\overline{N}}=14\), multiple pure threshold strategy equilibria occur at 1 and 2. Then, at \({\overline{N}}=15\), multiple pure threshold strategy equilibria occur at 1, 2 and 3. Assume that the equilibrium occurs at \(b(k)=k=1\) when \({\overline{N}} = 14\) and at \(b(k)=k=3\) when \({\overline{N}}=15\). We then observe that the expected blocking rate is equal to 0.2571 at \({\overline{N}}=14\) and 0.2664 at \({\overline{N}}=15\).

Comparing Tables 3 and 4 , we find that the expected throughput is monotonically increasing in p. As the probability of the server being fast increases, it is intuitive that the expected throughput will increase. The expected blocking rate is monotonically decreasing in p because the customers are served fast with higher probability. It is also intuitive to observe that the expected throughput and the expected blocking rate are monotonically increasing in the arrival rate.

7 The case of infinite waiting area capacity

We now relax the assumption on finite waiting area capacity \({\overline{N}}\), and consider the case where the waiting area is of infinite capacity. We use the earlier notation with \(\infty \) in the superscript to reflect the infinite waiting area capacity. In this case, the stationary probability of n customers in the system is given by

$$\begin{aligned}&\pi _{n,\mu ,\psi ,q}^{\infty }\nonumber \\&\quad = {\left\{ \begin{array}{ll} \pi _{0,\mu ,\psi ,q}^{\infty } \prod _{j=0}^{n-1} \left( [\psi _{j}q+(1-q)]\dfrac{\Lambda }{\mu }\right) , &{} n \in \{1,2,\ldots ,n_{b}\}, \\ \pi _{0,\mu ,\psi ,q}^{\infty } \left( \dfrac{(1-q)\Lambda }{\mu }\right) ^{n-n_{b}} \prod _{j=0}^{n_{b}-1} \left( [\psi _{j}q+(1-q)]\dfrac{\Lambda }{\mu }\right) , &{} n \in \{n_{b}+1,n_{b}+2,\ldots , \infty \}, \end{array}\right. }\nonumber \\ \end{aligned}$$
(12)

where

$$\begin{aligned} \pi _{0,\mu ,\psi ,q}^{\infty }= & {} \left[ 1 + \sum _{n=1}^{n_{b}} \prod _{j=0}^{n-1} \left( [\psi _{j}q+(1-q)]\dfrac{\Lambda }{\mu }\right) \right. \nonumber \\&\quad \left. + \prod _{j=0}^{n_{b}-1} \left( [\psi _{j}q+(1-q)]\dfrac{\Lambda }{\mu }\right) \sum _{n=n_{b}+1}^{\infty } \left( \dfrac{(1-q)\Lambda }{\mu }\right) ^{n-n_{b}}\right] ^{-1}. \end{aligned}$$
(13)

With the additional stability condition \(\Lambda (1-q) < {\underline{\mu }}\), we can ensure that \(\sum _{n=n_{b}+1}^{\infty } \left( \dfrac{(1-q)\Lambda }{\mu }\right) ^{n-n_{b}}\) is finite. The necessary and sufficient condition for the pure threshold strategy k to be in equilibrium is \(\omega ^{\infty }(n) \le \dfrac{p}{1-p} \theta _{q}^{\infty }(k)\) for all \(0 \le n \le k-1\) and \(\omega ^{\infty }(n) \ge \dfrac{p}{1-p} \theta _{q}^{\infty }(k)\) for all \(k \le n \le n_{b}\), where \(\omega ^{\infty }(n) = \left( \dfrac{{\overline{\mu }}}{{\underline{\mu }}}\right) ^{n} \dfrac{\dfrac{n+1}{{\underline{\mu }}}c - V}{V - \dfrac{n+1}{{\overline{\mu }}}c}\) and \(\theta _{q}^{\infty }(k) = \dfrac{1+ \sum _{j=1}^{k}\left( \dfrac{\Lambda }{{\underline{\mu }}}\right) ^{j} + \sum _{j=k+1}^{\infty }(1-q)^{j-k}\left( \dfrac{\Lambda }{{\underline{\mu }}}\right) ^{j}}{1+\sum _{j=1}^{k}\left( \dfrac{\Lambda }{{\overline{\mu }}}\right) ^{j} + \sum _{j=k+1}^{\infty }(1-q)^{j-k}\left( \dfrac{\Lambda }{{\overline{\mu }}}\right) ^{j}}\). It follows that the existence of at least one pure threshold strategy equilibrium is guaranteed (Proposition 1). Propositions 2 and 3 also continue to hold.

8 Conclusion

In the analysis of an \(M/M/1/{\overline{N}}\) non-customer-intensive service queue with strategic impatient and non-strategic patient customers, we find that there exists at least one pure threshold strategy equilibrium in the impatient customers’ game. With the notion of FTC behavior, we also show the possibility of multiple threshold equilibria in pure or mixed space. Moreover, we understand the effect of the proportion of impatient customers and the waiting area capacity on the likelihood ratio of a fast server to a slow server in an empty queue and the minimal pure threshold strategy equilibrium. We show that the likelihood ratio is monotonically decreasing in the proportion of impatient customers and monotonically increasing in the waiting area capacity. Further, we show that the minimal pure threshold strategy equilibrium is non-increasing in the proportion of impatient customers and non-decreasing in the waiting area capacity. The pure threshold strategy equilibrium is also guaranteed to exist when the waiting area capacity is infinite. We then numerically analyze the effect of the proportion of impatient customers and the waiting area capacity on the expected throughput and the expected blocking rate.

Our equilibrium analysis comes with certain limitations. We did not analyze whether a non-threshold strategy equilibrium exists in this setting. Investigating the existence of non-threshold strategy equilibrium can generate further insights. Secondly, the non-strategic nature of patient customers is not exactly applicable in certain service environments. Instead, the patient customer could always join the queue and strategically decide whether to revisit the service facility or not. This is especially true for services that involve repeated visits by the customers. Studies have looked at revisit decisions in service systems, albeit on a limited scale [17, 26]. This notion of patient customers making a strategic revisit decision is a promising extension to the analysis of queueing games in services.