1 Introduction

Due to wide applications for management in service systems, there exists an emerging tendency to study customers’ behavior impact on the performance of queueing system. Customers in service systems act independently in order to maximize their welfare. However, each customer’s optimal behavior is affected by acts taken by the system managers and the other customers. This can be viewed as a game among the customers. Studies about the economic analysis of queueing systems can go back at least to the pioneering work of Naor (1969) who analyzed customers optimal strategies in an observable M/M/1 queue with a simple reward-cost structure. Edelson and Hildebrand (1975) reexamined the work of Naor and considered the unobservable case in which the customers make their decisions without being informed about the state of the queue. Naor’s model and results had already been extended by several authors(Chen and Frank 2004; Economou and Kanta 2011).The fundamental results on equilibrium behavior of customers and servers in queueing systems with extensive bibliographical references can be found in the comprehensive monograph of Hassin and Haviv (2003).

Queues with setup times have also been studied by many authors. In such models once the server is reactivated, a random time is required for setup before it can begin serving customers (Reddy et al. 1998; Bischof 2001; Choudhury 2000; Allahverdi et al. 2008). The research on the equilibrium customer behavior in queues with setup times was firstly presented by Burnetas and Economou (2007). Subsequently, Economou and Kanta (2008) considered a Markovian queue that alternates between on and off periods in observable cases.

Server failures which lead to service interruptions are quite common in many real life situations. It is well known that performance measures of unreliable queuing systems are heavily influenced by server failures (Wang et al. 2001; Boudali and Economou 2012; Zhang and Zhu 2013; Zhang et al. 2014).

This motivates us to analyze equilibrium strategies in the single server queue with setup times, breakdowns and repairs. Customers make decisions based on a natural reward-cost structure, which incorporates their desires for service as well as their unwillingness to wait. We consider separately the fully observable case where customers have informed not only about the state of the server but also about the exact number of customers in the system and the partially observable case where an arriving customer knows the state of the server but does not observe the number of customers waiting for service, as well as fully unobservable case where customers do not observe the state of the server and the exact number of customers in the system.

The paper is organized as follows. In Sect. 2, we describe the dynamics of the model and the reward-cost structure. In Sect. 3, we derive the equilibrium threshold strategies for the fully observable case and stationary probabilities of the system. In Sect. 4, we derive the stationary probabilities and equilibrium mixed strategies for the partially observable case. In Sect. 5, we study equilibrium threshold strategies for the fully unobservable case. In Sect. 6, some numerical results are given to illustrate the effect of the information levels and several parameters on the customers’ strategies. Finally, some conclusions are given in Sect. 7.

2 Model description

We consider a single-server queue with infinite waiting room in which customers arrive according to a Poisson process with rate \(\lambda \). The service times are assumed to be exponentially distributed with parameter \(\mu \). During the busy periods, the server may break down and once a breakdown occurs, the server will start to be repaired immediately. The lifetime of the server is assumed to be exponentially distributed with parameter \(\xi \), and the repair time is exponentially distributed with parameter \(\eta \). The server is deactivated and begins a vacation as soon as the queue becomes empty. When a new customer arrives at an empty system, a setup process starts for the server to be activated. The time required to setup is exponentially distributed with rate \(\theta \). In addition, we assume that once customers enter the system, they will not allowed to leave. The customers are not allowed to join the system during the repair time. We further assume that inter-arrival times, service times, setup times, lifetime of the server and repair times are mutually independent.

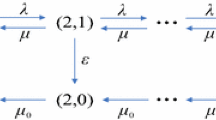
We denote the state of the system at time t by a random vector \((I(t),N(t))\), where t denotes the state of the server, and \(N(t)\) denotes the number of customers in the system. More specifically, (0, 0) implies that the system is deactivated; the vector \((0,n)\), \((1,n)\), \((2,n)\) corresponds to the server in setup, busy or broken periods with \(n\) customers in the system. It is clear that the process \(\{(I(t),N(t)):t\ge 0\}\) is a continuous time Markov chain with state space \(S=\{0,0\}\cup (\{0,1,2\}\times \{1,2,\ldots ,\})\) and the related transition rates are given by

$$\begin{aligned} q_{(0,n)(0,n+1)}= & \, \lambda ,n=0,1,2,\ldots ,\\ q_{(0,n)(1,n)}= & \, \theta ,n=1,2,\ldots ,\\ q_{(1,1)(0,0)}= & \, \mu ,\\ q_{(1,n)(1,n+1)}= & \, \lambda ,n=1,2,\ldots ,\\ q_{(1,n+1)(1,n)}= & \, \mu ,n=1,2,\ldots ,\\ q_{(1,n)(2,n)}= & \, \xi ,n=1,2,\ldots ,\\ q_{(2,n)(1,n)}= & \, \eta ,n=1,2,\ldots . \end{aligned}$$

The transition rate diagram is shown in Fig. 1.

Fig. 1
figure 1

Transition rate diagram of the original model

Full size image

In this paper, we assume that every customer receives a reward of R units for completing service. Besides, we assume that there exists a waiting cost of C units per time unit that is continuously accumulated from the time that the customer arrives at the system till the time he leaves the system after being served. From now on, we further assume that

$$\begin{aligned} R>C\left( \frac{\xi +\eta }{\mu \eta }+\frac{1}{\theta }\right) . \end{aligned}$$
(1)

Once a customer joins an empty system, his mean sojourn time equals the mean setup time plus the mean service time and the mean overall repair time due to failures during the service time, i.e. \(\frac{1}{\theta }+\frac{1}{\mu }+\xi \frac{1}{\mu }\frac{1}{\eta }\). The condition (1) ensures that the reward for service exceeds the expected cost for a customer who finds the system empty. Otherwise, after the system becomes empty for the first time, no customers will ever enter because of the negative net benefit.

We focus on studying the behavior of customers when they are allowed to decide whether to join or balk based on the available information upon their arrival, including the queue length and/or the state of the server. We consider separately three information cases in this paper, that is, (1) fully observable case: arriving customers get informed not only about the state of the server but also about the exact number of customers in the system; (2) partially observable case: arriving customers just observe the state of the server and don’t know how many customers in the system; (3)fully unobservable case: arriving customers do not observe the state of the system at all. We further assume that decisions are irrevocable: retrials of balking and reneging of entering customer are not allowed.

3 Equilibrium threshold strategies for the fully observable case

We now focus on the fully observable case, which assumes that customers observe not only the state of the server, but also the exact number of customers in the system. To study the general threshold strategy adopted by all customers in the fully observable case, we will first consider the mean overall sojourn time of a customer who faces different server state upon arrival.

Once the server is activated, the proportion of time that the server is operational is \(\frac{\eta }{\xi +\eta }\), thus, the effective service rate is \(\frac{\mu \eta }{\xi +\eta }.\) A customer who joins the system when he observes state \((i,n)\) has mean sojourn time \(T(i,n)\), which equals to

$$\begin{aligned} T(i,n)=\frac{\mu \eta (n+1)}{\xi +\eta }+\frac{1-i}{\theta },\quad i=0,1. \end{aligned}$$

His expected net benefit is \(B(i,n)=R-CT(i,n).\)

The customer prefers to join if \(B(i,n)>0\); he is indifferent between joining and balking if \(B(i,n)=0\) and prefers to balk if \(B(i,n)<0\). By solving inequality \(B(i,n)\ge 0\), we obtain the following results.

Theorem 1

In the fully observable M/M/1 queue with setup times, server breakdowns and repairs, there exists thresholds

$$\begin{aligned} (n_e (0),n_e (1))=\left( \left\lfloor {\frac{(R\theta -C)\mu \eta }{C\theta (\xi +\eta )}} \right\rfloor -1,\left\lfloor {\frac{R\mu \eta }{C(\xi +\eta )}} \right\rfloor -1\right) , \end{aligned}$$
(2)

such that the strategy ‘observe \((I(t),N(t))\), enter if \(N(t)\le n_e (I(t))\) and balk otherwise’ is a weakly dominant strategy.

We now turn our attention to the social profit problem. For the stationary analysis, note that if all customers follow the threshold strategy in (2), then the system follows a Markov chain \((I(t),N(t))\) with state space

$$\begin{aligned} S_{fo} =\left\{ (0,n)\left| {0\le n\le n_e (0)\text{+ }1} \right. \right\} \cup \{(i,n)\left| {1\le n\le n_e (1)\text{+ }1} \right. ,\quad i=1,2\}. \end{aligned}$$

The transition diagram is depicted in Fig. 2.

Fig. 2
figure 2

Transition rate diagram for the \((n_e (0),n_e (1))\) threshold strategy

Full size image

The corresponding stationary distribution \((p_{i,j} (i,j)\in S_{fo} )\) is given by the following proposition.

Proposition 1

Consider an \(M/M/1\) queue with setup times, server breakdowns and repairs, \(\sigma \ne 1, \rho \ne 1, \sigma \ne \rho \), in which the customers follow the threshold policy \((n_{e}(0),n_{e}(1))\). The stationary probabilities \((p_{fo}(i,j)\in S_{fo})\) are as follows:

$$\begin{aligned} p_{fo} (1,1)=\, & {} \eta (1-\rho )\rho ^{1+n_e(0)}(\rho -\sigma )(1-\sigma )\left\{ \rho ^{n_e (0)}\left[ (\eta +\xi \rho )(\rho -\sigma ) -(\eta +\xi )\rho ^{3+n_e(1)}\right. \right. \nonumber \\&\left. \left. \cdot (1-\sigma )\right] -(\eta +\xi )\rho \left[ \rho ^{n_e (0)}(\rho -\sigma )-\rho ^{1+n_e (1)}(1-\sigma )\right] \sigma ^{1+n_e (0)}\right\} ^{-1}, \end{aligned}$$
(3)
$$\begin{aligned} p_{fo} (0,n)= & {} \frac{\sigma ^np_{fo} (1,1)}{\rho },\quad n=0,1,\ldots ,n_e (0),\end{aligned}$$
(4)
$$\begin{aligned} p_{fo} (0,n_e (0)+1)= & {} \frac{\sigma ^{n_e (0)+1}p_{fo} (1,1)}{\rho (1-\sigma )},\end{aligned}$$
(5)
$$\begin{aligned} p_{fo} (1,n)= & {} \frac{(\sigma ^n-\rho ^n)p_{fo} (1,1)}{\sigma -\rho },\quad n=1,2,\ldots ,n_e (0)+1,\end{aligned}$$
(6)
$$\begin{aligned} p_{fo} (1,n)= & {} \frac{(\sigma ^{n_e (0)+1}-\rho ^{n_e (0)+1})\rho ^{n-n_e (0)-1}p_{fo} (1,1)}{\sigma -\rho },\quad n=n_e (0)+2,\ldots ,n_e (1)+1,\end{aligned}$$
(7)
$$\begin{aligned} p_{fo} (2,n)= & {} \frac{(\sigma ^n-\rho ^n)\xi p_{fo} (1,1)}{\eta (\sigma -\rho )},\quad n=1,2,\ldots ,n_e (0)+1,\end{aligned}$$
(8)
$$\begin{aligned} p_{fo} (2,n)= & {} \frac{\xi (\sigma ^{n_e (0)+1}-\rho ^{n_e (0)+1})\rho ^{n-n_e (0)-1}p_{fo} (1,1)}{\eta (\sigma -\rho )}, \quad n=n_e (0)+2,\cdots ,n_e (1)+1, \end{aligned}$$
(9)

where

$$\begin{aligned} \rho =\frac{\lambda }{\mu },\,\,\sigma =\frac{\lambda }{\lambda +\theta }. \end{aligned}$$
(10)

Proof

The stationary distribution is obtained from the following balance equations:

$$\begin{aligned} \lambda p(0,0)= & {} \mu p(1,1),\end{aligned}$$
(11)
$$\begin{aligned} (\lambda +\theta )p(0,n)=\, & {} \lambda p(0,n-1),\quad n=1,2,\ldots ,n_e (0),\end{aligned}$$
(12)
$$\begin{aligned} \lambda p(0,n_e (0))=\, & {} \theta p(0,n_e (0)+1),\;\end{aligned}$$
(13)
$$\begin{aligned} (\lambda +\mu +\xi )p(1,1)=\, & {} \theta p(0,1)+\mu p(1,2)+\eta p(2,1),\end{aligned}$$
(14)
$$\begin{aligned} (\lambda +\mu +\xi )p(1,n)=\, & {} \lambda p(1,n-1)+\theta p(0,n)+\mu p(1,n+1)+\eta p(2,n),\quad n=2,3,\ldots ,n_e (0),\end{aligned}$$
(15)
$$\begin{aligned} (\lambda +\mu +\xi )p(1,n)=\, & {} \lambda p(1,n-1)+\mu p(1,n+1)+\eta p(2,n),\quad n=n_e (0)+2,\ldots ,n_e (1),\end{aligned}$$
(16)
$$\begin{aligned} (\mu +\xi )p(1,n_e (1)+1)=\, & {} \lambda p(1,n_e (1))+\eta p(n_e (1)+1,2),\end{aligned}$$
(17)
$$\begin{aligned} \eta p(2,n)=\, & {} \xi p(1,n),\quad n=1,2,\ldots ,n_e (1)+1. \end{aligned}$$
(18)

By iterating (12) and (16), taking into account (11), (13), (17), (18) and (10), we can easily obtain expressions (4), (5), (6), (7) in Proposition 1, and the following equation:

$$\begin{aligned} p_{fo} (2,n)=\frac{\xi p_{fo} (1,n)}{\eta },\quad n=1,\ldots ,n_e (1)+1. \end{aligned}$$
(19)

From (14), (18) and (10), we get

$$\begin{aligned} p(1,2)=(\rho +\sigma )p(1,1). \end{aligned}$$
(20)

From (15), (18) and (4), we have

$$\begin{aligned} \mu p(1,n+1)-(\lambda +\mu )p(1,n)+\lambda p(1,n-1)=-\frac{\theta \sigma ^np_{fo} (1,1)}{\rho },\quad n=2,3,\ldots ,n_e (0). \end{aligned}$$
(21)

Combining (20) and the recursive formulas (21), we can obtain (6) by tedious calculations.Then, with the help of the normalizing equation

$$\begin{aligned} \sum \limits _{n=0}^{n_e (0)+1} {p_{fo} (0,n)} +\sum \limits _{n=1}^{n_e (1)+1} {p_{fo} (1,n)} +\sum \limits _{n=1}^{n_e (1)+1} {p_{fo} (2,n)} =1, \end{aligned}$$

we get the expression of \( p_{fo}(1,1).\) \(\square \)

Lemma 1

Proposition 1 holds for the stationary distribution corresponding to any threshold policy \((n_e (0),n_e (1))\) and not merely to the individually optimal policy specified by (2).

Because an arrival balks once he finds the system at state \((0,n_e (0)+1)\) or \((1,n_e (1)+1)\) or the server is broken, then the effective arrival rate of the system is given by

$$\begin{aligned} \lambda (n_e (0),n_e (1))=\lambda \left[ \sum \limits _{n=0}^{n_e (0)} {p_{fo} (0,n)} +\sum \limits _{n=1}^{n_e (1)} {p_{fo} (1,n)} \right] . \end{aligned}$$

Hence, the social benefit per time unit when all customers follow the threshold policy \((n_e (0),n_e (1))\) equals

$$\begin{aligned} S_{fo}= & \,\lambda R\left[ \sum \limits _{n=0}^{n_e (0)} {p_{fo} (0,n)} +\sum \limits _{n=1}^{n_e (1)} {p_{fo} (1,n)} \right] \\&-C\left[ \sum \limits _{n=0}^{n_e (0)+1} {np_{fo} (0,n)} +\sum \limits _{n=1}^{n_e (1)+1} {np_{fo} (1,n)} +\sum \limits _{n=1}^{n_e (1)+1} {np_{fo} (2,n)}\right] . \end{aligned}$$

4 Equilibrium mixed strategies for the partially observable case

In this section, we turn our attention to the partially observable case, where arrivals only observe the server state, and do not observe the number of customers in the system. We will prove that there exists equilibrium mixed strategies. A mixed strategy for a customer is specified by a vector \((q_0 ,q_1 ),\) where \(q_i =q(i)\) is the probability of joining when the server is in state i. If all customers follow the same mixed strategy \((q_0 ,q_1 ),\) then the system follows a Markov chain similar to that described in Fig. 1 except that the arrival rate equals to \(\lambda _i =\lambda q_i\). The state space \(S_{po} \) for the partially observable case is identical to the original state space S, and transition diagram is illustrated in Fig. 3.

Fig. 3
figure 3

Transition rate diagram for the \((q_0 ,q_1 )\) mixed strategy

Full size image

Proposition 2

Consider an M/M/1 queue with setup times, server breakdowns and \(\sigma _0 \ne \rho _1 ,\) in which the customers enter the system with probability \(q_i\) if observe the server in state \(i(i=0,1)\) upon arrival, and never enter the system whenever the server is broken. The system is stable if and only if \(\rho _1 <1\) and the stationary probabilities of the system are given by:

$$\begin{aligned} p_{po} (0,0)= & {} \frac{\eta (1-\rho _1 )(1-\sigma _0 )}{(\eta +\xi )\rho _0 +\eta (1-\rho _1 )},\end{aligned}$$
(22)
$$\begin{aligned} p_{po} (0,n)= & {} \frac{\eta (1-\rho _1 )(1-\sigma _0 )\sigma _0 ^n}{(\eta +\xi )\rho _0 +\eta (1-\rho _1 )},\quad n=0,1,2,\ldots ,\end{aligned}$$
(23)
$$\begin{aligned} p_{po} (1,n)= & {} \frac{\rho _0 \eta (1-\rho _1 )(1-\sigma _0 )(\sigma _0 ^n-\rho _1 ^n)}{(\sigma _0 -\rho _1) [\eta +(\eta +\xi )\rho _0 -\eta \rho _1 ]},\quad n=1,2,3,\ldots ,\end{aligned}$$
(24)
$$\begin{aligned} p_{po} (2,n)= & {} \frac{\rho _0 \xi (1-\rho _1 )(1-\sigma _0 )(\sigma _0 ^n-\rho _1 ^n)}{(\sigma _0 -\rho _1) [\eta +(\eta +\xi )\rho _0 -\eta \rho _1 ]},\quad n=1,2,3,\ldots , \end{aligned}$$
(25)

where

$$\begin{aligned} \rho _0 =\frac{\lambda _0 }{\mu },\rho _1 =\frac{\lambda _1 }{\mu },\sigma _0 =\frac{\lambda _0 }{\lambda _0 +\theta }. \end{aligned}$$
(26)

Proof

Let \((p_{po} (i,n):(i,n)\in S)\) be the stationary distribution of the corresponding system. The balance equations are presented below:

$$\begin{aligned} \lambda _0 p(0,0)=\, & {} \mu p(1,1),\end{aligned}$$
(27)
$$\begin{aligned} (\lambda _0 +\theta )p(0,n)=\, & {} \lambda _0 p(0,n-1),\quad n=1,2,3,\ldots ,\end{aligned}$$
(28)
$$\begin{aligned} (\lambda _1 +\mu +\xi )p(1,1)=\, & {} \theta p(0,1)+\mu p(1,2)+\eta p(2,1),\end{aligned}$$
(29)
$$\begin{aligned} (\lambda _1 +\mu +\xi )p(1,n)=\, & {} \lambda _1 p(1,n-1)+\theta p(0,n)+\mu p(1,n+1)+\eta p(2,n),\quad n=2,3,\ldots ,\end{aligned}$$
(30)
$$\begin{aligned} \eta p(n,1)=\, & {} \xi p(1,n),\quad n=1,2,3,\ldots . \end{aligned}$$
(31)

By iterating (28), we obtain

$$\begin{aligned} p_{po} (0,n)=\sigma _0 ^np_{po} (0,0),\quad n=0,1,2,\ldots . \end{aligned}$$
(32)

From (28)–(32), we can get

$$\begin{aligned}&p(1,1)=\rho _0 p(0,0),\end{aligned}$$
(33)
$$\begin{aligned}&p(1,2)=\rho _0 (\sigma _0 +\rho _1 )p(0,0),\end{aligned}$$
(34)
$$\begin{aligned}&\mu p(1,n+1)-(\lambda _1 +\mu )p(1,n)+\lambda _1 p(1,n-1)=-\theta \sigma _0 ^np(0,0),\quad n=2,3,\ldots . \end{aligned}$$
(35)

Combining (33)–(34)and the recursive formulas (35), we obtain the following equation by tedious calculations

$$\begin{aligned} p_{po} (1,n)=\frac{\rho _0 (\sigma _0 ^n-\rho _1 ^n)p(0,0)}{\sigma _0 -\rho _1},\quad n=1,2,3,\ldots . \end{aligned}$$
(36)

From (31), we get

$$\begin{aligned} p_{po} (2,n)=\frac{\xi p_{po} (1,n)}{\eta },\quad n=1,2,3,\ldots . \end{aligned}$$
(37)

Putting (33), (36) and (37) into the normalizing equation

$$\begin{aligned} p_{po} (0,1)+p_{po} (1,1)+p_{po} (2,1)=1, \end{aligned}$$

we obtain the expression of \(p_{p0} (0,0)\) in (22). From the expression \(p_{p0}(0,0)>0,\) we immediately get \(\rho _1 <1\). The conclusions (23)–(25) can be easily derived based on the above expressions (32), (36) and (37). \(\square \)

From Proposition 2, we can obtain the steady state probabilities of the server

$$\begin{aligned} p(i=0)=\sum \limits _{n=0}^{+\infty } {p_{po} (0,n)} =\frac{\eta (1-\rho _1 )}{\eta (1-\rho _1 )+(\eta +\xi )\rho _0 },\end{aligned}$$
(38)
$$\begin{aligned} p(i=1)=\sum \limits _{n=1}^{+\infty } {p_{po} (1,n)} =\frac{\eta \rho _0 }{\eta (1-\rho _1 )+(\eta +\xi )\rho _0 }. \end{aligned}$$
(39)

Let \(E(N^-\left| i \right. )\) be the expected number of customers in the system found by an arrival, given that the server is found at state \(i\), then we have

$$\begin{aligned} E(N^-\left| 0 \right. )= & {} \frac{\sum \nolimits _{n=0}^{+\infty } {np_{po} (0,n)} }{p(i=0)}=\frac{\sigma _0 }{1-\sigma _0 },\end{aligned}$$
(40)
$$\begin{aligned} E(N^-\left| 1 \right. )= & {} \frac{\sum \nolimits _{n=1}^{+\infty } {np_{po} (1,n)} }{p(i=1)}=\frac{1}{1-\sigma _0 }+\frac{\rho _1 }{1-\rho _1 }. \end{aligned}$$
(41)

Thus we can get a customer who finds the server at state \(i\) upon arrival, his mean sojourn time is

$$\begin{aligned} S(i)=\frac{(\xi +\eta )[E(N^-\left| i \right. )+1]}{\mu \eta }+\frac{1-i}{\theta }, \end{aligned}$$
(42)

the expected net benefit of such customer who decides to enter is

$$\begin{aligned} B(i)=R-C\cdot S(i)=R-C\left\{ \frac{(\xi +\eta )[E(N^-\left| i \right. )+1]}{\mu \eta }+\frac{1-i}{\theta }\right\} . \end{aligned}$$
(43)

Then the social benefit per time unit when all customers follow the mixed policy \((q_0 ,q_1 )\) can be eventually computed as:

$$\begin{aligned} S_{po}=\, & {} \lambda _0 \cdot p(i=0)\cdot B(0)+\lambda _1 \cdot p(i=1)\cdot B(1)\nonumber \\=\, & {} \lambda _0 \cdot \frac{\eta (1-\rho _1 )}{\eta (1-\rho _1 )+(\eta +\xi )\rho _0 }\cdot \left\{ R-\frac{C(\xi +\eta )[E(N^-\left| 0 \right. )+1]}{\mu \eta }-\frac{C}{\theta }\right\} \nonumber \\&+\lambda _1 \cdot \frac{\eta \rho _0 }{\eta (1-\rho _1 )+(\eta +\xi )\rho _0 }\cdot \left\{ R-\frac{C(\xi +\eta )[E(N^-\left| 1 \right. )+1]}{\mu \eta }\right\} \end{aligned}$$
(44)

Theorem 2

In the fully observable M/M/1 queue with setup times, server breakdowns and repairs, there exists a unique mixed equilibrium strategy \((q_e (0),q_e (1))\) ‘observe \(I(t)\) and enter with probability \(q_e (I(t))\)’ when condition \(\lambda <\mu \) holds, where the vector \((q_e (0),q_e(1))\) is given as follows.

Case I: \(_{ }\frac{1}{\theta }<\frac{\xi +\eta }{\mu \eta }_{,}\)

$$\begin{aligned} (q_e (0),q_e (1))=\left\{ {\begin{array}{l} \left( \frac{R\eta \theta \mu -C\left[ \eta (\theta +\mu )+\theta \xi \right] }{\lambda (\eta +\xi )C},0\right) \quad if\;R\in \left( \frac{C(\xi +\eta )}{\mu \eta }+\frac{C}{\theta },\frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\right) ; \\ (1,0) \; if\;R\in \left. \left[ \frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta },\frac{C(\xi +\eta )}{\mu \eta }\left( 1+\frac{\lambda +\theta }{\theta }\right)\right); \right. \\ \left(1,\frac{\mu \left[ R\mu \eta \theta -C(\lambda +2\theta )(\eta +\xi )\right] }{\lambda \left[ R\mu \eta \theta -C(\lambda +\theta )(\eta +\xi )\right] }\right); \\ \;if\;R\in \left. \left[ \frac{C(\xi +\eta )}{\mu \eta }(1+\frac{\lambda +\theta }{\theta }),\frac{C(\xi +\eta )}{\mu \eta }\left( \frac{\mu }{\mu -\lambda }+\frac{\lambda +\theta }{\theta }\right) \right); \right. \\ (1,1)\quad if\;R\in \left. \left[ \frac{C(\xi +\eta )}{\mu \eta }\left( \frac{\mu }{\mu -\lambda }+\frac{\lambda +\theta }{\theta }\right) ,+\infty \right).\right. \\ \end{array}} \right. \end{aligned}$$

Case II: \(_{ }\frac{\xi +\eta }{\mu \eta }\le \frac{1}{\theta }\le \frac{\xi +\eta }{(\mu -\lambda )\eta }_{,}\)

$$\begin{aligned} (q_e (0),q_e (1))=\left\{ {\begin{array}{l} \left( \frac{R\eta \theta \mu -C[\eta (\theta +\mu )+\theta \xi ]}{\lambda (\eta +\xi )C},\frac{\eta \mu -\theta (\xi +\eta )}{\lambda \eta }\right) \quad if\;R\in \left( \frac{C(\xi +\eta )}{\mu \eta }+\frac{C}{\theta },\frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\right) ; \\ \left( 1,\frac{\mu \left[ R\mu \eta \theta -C(\lambda +2\theta )(\eta +\xi )\right] }{\lambda \left[ R\mu \eta \theta -C(\lambda +\theta )(\eta +\xi )\right] }\right) \quad if\;R\in \left. \left[ \frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta },\frac{C(\xi +\eta )}{\mu \eta }\left( \frac{\mu }{\mu -\lambda }+\frac{\lambda +\theta }{\theta }\right) \right);\right. \\ (1,1) \; if\;R\in \left. \left[ \frac{C(\xi +\eta )}{\mu \eta }(\frac{\mu }{\mu -\lambda }+\frac{\lambda +\theta }{\theta }),+\infty \right).\right. \\ \end{array}} \right. \end{aligned}$$

Case III: \(_{ }\frac{1}{\theta }>\frac{\xi +\eta }{(\mu -\lambda )\eta }_{,}\)

$$(q_e (0),q_e (1))=\left\{ {\begin{array}{l} \left( \frac{R\eta \theta \mu -C\left[ \eta (\theta +\mu )+\theta \xi \right] }{\lambda (\eta +\xi )C},1\right) \quad if\;R\in \left( \frac{C(\xi +\eta )}{\mu \eta }+\frac{C}{\theta },\frac{C\left(\lambda +\theta \right)(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\right); \\ (1,1)\;if\;R\in \left. \left[ \frac{C\left(\lambda +\theta \right)(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta },+\infty \right).\right. \\ \end{array}}\right.$$

Proof

Consider a tagged customer who finds the server at state 0 upon arrival. From equations (40) and (43), if he decides to enter, his expected net benefit is

$$\begin{aligned} B(0)=R-\frac{C}{\mu \eta \theta }(\xi +\eta )(\lambda q(0)+\theta )-\frac{C}{\theta }, \end{aligned}$$

Then we discuss the values of \(B(0)\) in two cases below:

Case 1: \(B(0)\le 0,\,\,i.e.,\frac{C(\xi +\eta )}{\mu \eta }+\frac{C}{\theta }<R\le \frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }.\)

In this case, if all customers who find the system empty enter with probability \(q_e (0)=1,\) then the tagged customer suffers a negative expected benefit if he decides to enter. Hence \(q_e (0)=1\) does not lead to equilibrium. Similarly, if all customers use \(q_e (0)=0\), then the tagged customer receives a positive benefit from entering, thus \(q_e (0)=0\) also cannot be part of an equilibrium mixed strategy. Therefore, there exists a unique \(q_e (0)\) satisfying

$$\begin{aligned} R-\frac{C}{\mu \eta \theta }(\xi +\eta )(\lambda q(0)+\theta )-\frac{C}{\theta }=0, \end{aligned}$$

for which customers are indifferent between entering and balking. Solving the above linear equation with respect to \(q(0)\), we obtain

$$\begin{aligned} q_e (0)=\frac{R\eta \theta \mu -C[\eta (\theta +\mu )+\theta \xi ]}{\lambda (\eta +\xi )C}. \end{aligned}$$

Case 2: \(B(0)>0,i.e.R>\frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }.\)

In this case, for every strategy of the other customers, the tagged customer has a positive expected net benefit if he decides to enter, so the best response is \(q_e (0)=1\).

We next consider \(q_e (1)\) and tag a customer who finds the server at state 1 upon arrival. From (41) and (43), if he decides to enter his expected net benefit is equal to

$$\begin{aligned} B(1)=\, & {} R-\frac{C(\xi +\eta )}{\mu \eta }\left( \frac{1}{1-\sigma _0 }+\frac{\rho _1 }{1-\rho _1 }+1\right) =R-\frac{C(\xi +\eta )}{\mu \eta }\left( \frac{\lambda _0 +\theta }{\theta }+\frac{\mu }{\mu -\lambda _1 }\right) , \end{aligned}$$

so

$$\begin{aligned} B(1)= & {} \left\{ {\begin{array}{l} \frac{C}{\theta }-\frac{C(\xi +\eta )}{\eta (\mu -\lambda q(1))}\quad in\;Case\;1, \\ R-\frac{C(\xi +\eta )}{\mu \eta }\left( \frac{\lambda +\theta }{\theta }+\frac{\mu }{\mu -\lambda q(1)}\right) \quad in\;Case\;2. \\ \end{array}} \right. \end{aligned}$$

Therefore, to find \(q_e (1)\) in equilibrium, we must examine Cases 1 and 2 separately and consider the following subcases in each.

Case 1a: \(\frac{C(\xi +\eta )}{\mu \eta }+\frac{C}{\theta }<R\le \frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\) and \(\frac{C}{\theta }<\frac{C(\xi +\eta )}{\mu \eta }\), we have

$$\begin{aligned} (q_e (0),q_e (1))=\left( \frac{R\eta \theta \mu -C[\eta (\theta +\mu )+\theta \xi ]}{\lambda (\eta +\xi )C},0\right) . \end{aligned}$$

Case 1b: \(\frac{C(\xi +\eta )}{\mu \eta }+\frac{C}{\theta }<R\le \frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\) and \(\frac{C(\xi +\eta )}{\mu \eta }\le \frac{C}{\theta }\le \frac{C(\xi +\eta )}{(\mu -\lambda )\eta },\) we have

$$\begin{aligned} q_e (0),q_e (1))=\left( \frac{R\eta \theta \mu -C[\eta (\theta +\mu )+\theta \xi ]}{\lambda (\eta +\xi )C},\frac{\eta \mu -\theta (\xi +\eta )}{\lambda \eta }\right) . \end{aligned}$$

Case 1c: \(\frac{C(\xi +\eta )}{\mu \eta }+\frac{C}{\theta }<R\le \frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\) and \(\frac{C}{\theta }>\frac{C(\xi +\eta )}{(\mu -\lambda )\eta }\), we have

$$\begin{aligned} (q_e (0),q_e (1))=\left( \frac{R\eta \theta \mu -C[\eta (\theta +\mu )+\theta \xi ]}{\lambda (\eta +\xi )C},1\right) . \end{aligned}$$

Case 2a: \(R>\frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\) and \(R<\frac{C(\xi +\eta )}{\mu \eta }(1+\frac{\lambda +\theta }{\theta })\), we have \((q_e (0),q_e (1))=(1,0).\)

Case 2b: \(R>\frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\) and \(\frac{C(\xi +\eta )}{\mu \eta }(\frac{\lambda +\theta }{\theta }+1)\le R\le \frac{C(\xi +\eta )}{\mu \eta }(\frac{\lambda +\theta }{\theta }+\frac{\mu }{\mu -\lambda }),\) we have

$$\begin{aligned} (q_e (0),q_e (1))=\left( 1,\frac{\mu [R\mu \eta \theta -C(\lambda +2\theta )(\eta +\xi )]}{\lambda [R\mu \eta \theta -C(\lambda +\theta )(\eta +\xi )]}\right) \;. \end{aligned}$$

Case 2c: \(R>\frac{C(\lambda +\theta )(\xi +\eta )}{\mu \eta \theta }+\frac{C}{\theta }\) and \(R>\frac{C(\xi +\eta )}{\mu \eta }(\frac{\lambda +\theta }{\theta }+\frac{\mu }{\mu -\lambda })\), we have \( (q_e (0),q_e (1))=(1,1). \)

By rearranging Cases 1a–2c as \(R\) varies from \(\frac{C(\xi +\eta )}{\mu \eta }+\frac{C}{\theta }\) to infinity, keeping the operating parameters \(\lambda ,\mu ,\theta ,\xi ,\eta \) and the waiting cost rate \(C\) fixed, we obtain Cases I–III in the theorem statement. \(\square \)

Theorem 2 quantifies several expected situations about the behavior of the customers when they are informed about the server’s state upon arrival. The key factor in the theorem is the mean setup time \(\frac{1}{\theta }\) in comparison with the mean generalized service time (the mean service time plus the mean overall repair time due to failures during the service time \(\frac{\xi +\eta }{\mu \eta }\)) and \(\frac{\xi +\eta }{(\mu -\lambda ) \eta }\). As Theorem 2 shows: it is always true that \(q_e (0)\ge q_e(1)\) in case I, \(q_e (0)\le q_e (1)\) in case III and the situation varies in case II. If a tagged customer is given the information that the server is on setup and the mean setup time is small, it is optimal for the tagged customer to enter if few customers ahead of him, which belongs to case I. On the contrary, if a tagged customer is given the information that the server is on setup, the mean setup time is large and many customers ahead of him, this would mean that he may wait for a long time, then his optimal response is balking, which should be in accordance with case III. When the mean setup time is relatively moderate, the inequality relations of \(q_e(0)\) and \(q_e(1)\) is various, which should be in accordance with case II.

5 Equilibrium threshold strategies for the fully unobservable case

We finally study the fully unobservable case where the newly arriving customers are not admitted to join the system when the server is broken. Here a mixed strategy for a customer is specified by the probability \(q\) of entering, where \(q\) is the probability of joining the queue whenever the server is in a regular busy period or a setup period. The stationary distribution of the system state is given by Proposition 2 by taking \(q_0=q_1=q\). The equilibrium behavior of the customers is described in the following.

Proposition 3

In the fully unobservable M/M/1 queue with setup times,server breakdowns and repairs, where the newly arriving customers are not admitted to join the system when the server is broken. The expected mean sojourn time of a customer who decides to enter is given by

$$\begin{aligned} E(W)=\frac{\eta +\xi }{\eta (\mu -\lambda q)}+\frac{1}{\theta }+\frac{\lambda q \xi }{\eta \theta \mu }. \end{aligned}$$
(45)

Proof

By taking \(q_0=q_1=q\) in (23)–(25),then we have the mean number of customers in the system as follows:

$$\begin{aligned} E(N)&=\sum _{n=0}^{+\infty }n p(0,n)+\sum _{n=1}^{+\infty }n p(1,n)+\sum _{n=1}^{+\infty }n p(2,n) \\&=\lambda q \left( \frac{1}{\theta }-\frac{\mu (\eta +\xi )}{(\lambda q-\mu ) (\eta \mu +\lambda q \xi )}\right) , \end{aligned}$$

and the server is broken with probability

$$\begin{aligned} p(i=2)=\sum _{n=1}^{+\infty } p(2,n)=\frac{\lambda q \xi }{\eta \mu +\lambda q\xi }, \end{aligned}$$

since the newly arriving customers are not admitted to join the system when the server is broken, then the effective arrival rate is \(\lambda q \left( 1-p(i=2)\right) \). By using Little’s law, we have the expected mean sojourn time of a customer who decides to enter the system is

$$\begin{aligned} E(W)=\frac{E(N)}{\lambda q \left( 1-p(i=2)\right) }=\frac{\eta +\xi }{\eta (\mu -\lambda q)}+\frac{1}{\theta }+\frac{\lambda q \xi }{\eta \theta \mu }. \end{aligned}$$

\(\square \)

The social benefit per time when all allowed joining customers follow a mixed strategy q is given by

$$\begin{aligned} S_{un}&=\lambda q \left( 1-p(i=2)\right) (R-C E(W))\nonumber \\&=\frac{\lambda q \eta \mu }{\eta \mu +\lambda q \xi } (R-C E(W)). \end{aligned}$$
(46)

Theorem 3

In the fully unobservable M/M/1 queue with setup times,server breakdowns and repairs, where the newly arriving customers are not admitted to join the system when the server is under repair. there exists a mixed equilibrium strategy ‘enter with probability \(q_{e}\)’, where \(q_{e}\) is given by

$$\begin{aligned} q_e=\left\{ {\begin{array}{ll} q_e^*,&{}if\;R\in \left( C(\frac{\eta +\xi }{\eta \mu }+\frac{1}{\theta }), C \left( \frac{\lambda \xi }{\eta \theta \mu }+\frac{\eta +\xi }{\eta (\mu -\lambda )}+\frac{1}{\theta }\right) \right) ; \\ 1,&{} if\;R\in \left[ C \left( \frac{\lambda \xi }{\eta \theta \mu }+\frac{\eta +\xi }{\eta (\mu -\lambda )}+\frac{1}{\theta }\right) ,+\infty ).\right. \\ \end{array}} \right. \end{aligned}$$
(47)

where

$$\begin{aligned} q_e^*=\frac{U+C F \mu -\sqrt{4 C^2 F V+(U-C F \mu )^2}}{2 C F \lambda },\quad U=R-\frac{C}{\theta },\;V=\frac{\eta +\xi }{\eta },\;F=\frac{\xi }{\eta \theta \mu }. \end{aligned}$$

Proof

We consider a tagged customer at his arrival instant,if he is allowed to join the system and decides to enter with probability \(q\), his expected net benefit is

$$\begin{aligned} B(q)=R-C E(W)=R-C \left( \frac{\eta +\xi }{\eta (\mu -\lambda q)}+\frac{1}{\theta }+\frac{\lambda q \xi }{\eta \theta \mu }\right) , \end{aligned}$$
(48)

where \(q\in [0,1].\) It is easy to see that \(B(q)\) is strictly decreasing for \(q\in [0,1]\). We can get

$$\begin{aligned} B(0)=\,&R-C\left( \frac{\eta +\xi }{\eta \mu }+\frac{1}{\theta }\right) ,\\ B(1)=\,&R-C\left( \frac{\lambda \xi }{\eta \theta \mu }+\frac{\eta +\xi }{\eta (\mu -\lambda )}+\frac{1}{\theta }\right) . \end{aligned}$$

When \(R\in \left( C\left( \frac{\eta +\xi }{\eta \mu }+\frac{1}{\theta }\right) , C \left( \frac{\lambda \xi }{\eta \theta \mu }+\frac{\eta +\xi }{\eta (\mu -\lambda )}+\frac{1}{\theta }\right) \right) \),we find that (48) has a unique root in \((0,1)\), which is given by the first branch of (47). When \(R\ge C \left( \frac{\lambda \xi }{\eta \theta \mu }+\frac{\eta +\xi }{\eta (\mu -\lambda )}+\frac{1}{\theta }\right) \), \(B(q)\) is positive for every \(q\), then the unique equilibrium point is \(q_e=1\), which gives the second branch of (47). \(\square \)

6 Numerical results

In this section,we will present a set of numerical experiments that are based on the analytical results of this article. In particular, we concern about the values of the equilibrium thresholds for the fully observable case, the values of the equilibrium entrance probabilities for the partially observable and fully unobservable cases as well as the equilibrium social benefit per unit time when customers follow equilibrium strategies.

We first consider the fully observable case and explore the sensitivity of the equilibrium pure thresholds policies \((n_e (0),n_e (1))\) with respect to the service reward \(R\), setup rate \(\theta \),and the ratio of parameters \(\xi \) and \(\eta .\) The results are presented in Fig. 4a–c. We find that when adding parameter \(R\), the thresholds \((n_e (0),n_e (1))\) increase in a linear fashion, up to the integrality requirement; when the setup rate \(\theta \) varies, the threshold \(n_e (0)\) increases, while \(n_e (1)\) remains constant. Finally, when \(\xi /\eta \) increases, it means that the lifetime of the system becomes shorter, and the customers in the system need to wait longer for the server to restore, which leads to new customers leave the system and the thresholds decrease.

Fig. 4
figure 4

Equilibrium thresholds for observable system. a Sensitivity with respect to \(R\), for \(\mu =1, \theta =0.05, \xi =0.02,\eta =1,C=1\). b Sensitivity with respect to \(\theta \), for \(\mu =1, R=30,\xi =0.02,\eta =1,C=1\). c Sensitivity with respect to \(\xi /\eta \), for \(\mu =1,\theta =0.05,C=1,R=50\)

Full size image

We then turn to the partially observable and fully unobservable cases and investigate the sensitivity of the equilibrium entrance probabilities \(q_e (0),q_e (1)\) and \(q_e\). From the results of Fig. 5a–c, we find that the entrance probability \(q_e\) in the fully unobservable case is always inside the interval formed by \(q_e(0)\) and \(q_e(1)\) in the partial observable case. The entrance probabilities \(q_e (0),q_e (1)\) and \(q_e\) are expected to increase with respect to reward \(R\). The equilibrium entrance probabilities \(q_e (0),q_e (1)\) and \(q_e\) are nondecreasing with \(\theta \) for the most part, and there is a range of small values of \(\theta \) in \(q_e (1)\) is decreasing. The entrance probabilities \(q_e(0),q_e(1)\) and \(q_e\) are expected to decrease with respect to \(\xi /\eta \).

Fig. 5
figure 5

Equilibrium entrance probabilities \(q_e (0),q_e (1)\) and \(q_e\), a sensitivity with respect to \(R\), for \(\lambda =0.9,\mu =1, \theta =0.3,\xi =0.02,\eta =1, C=1\). b Sensitivity with respect to \(\theta \), for \(\lambda =0.9,\) \(\mu =1,\xi =0.1,\) \(\eta =1, C=1,R=15\). c Sensitivity with respect to \(\xi /\eta \), for \(\lambda =0.9,\mu =1,\theta =0.1, C=1,R=50\)

Full size image

The last three numerical experiments are concerned with the social benefit under the equilibrium strategy for fully observable, partially observable and fully unobservable cases. Generally speaking, the equilibrium social benefit is increasing with respect to the reward \(R\) in Fig. 6a. The two curves of fully observable and partial observable cases are getting closer with the increasing of \(R\). The equilibrium social benefit is decreasing with respect to the breakdown rate \(\xi \) in Fig. 6b and increasing with respect to the repair rate \(\eta \) in Fig. 6c. In our system, we find that the equilibrium social benefit in the partial observable case is always inside the equilibrium social benefit formed by fully observable case and fully unobservable case.

Fig. 6
figure 6

Equilibrium social benefit for three different cases, a sensitivity with respect to \(R\), for \(\lambda =0.9,\mu =1,\theta =0.3,\xi =0.02,\eta =1,C=1\). b Sensitivity with respect to \(\xi \), for \(\lambda =0.9,\mu =1,\theta =0.3,\eta =1,C=1,R=30\). c Sensitivity with respect to \(\eta \), for \(\lambda =0.9,\mu =1,\theta =0.3,\xi =0.02,C=1,R=20\)

Full size image

7 Conclusions

In this paper, we have considered customer’s equilibrium behavior in the \(M/M/1\) queue with setup times, breakdowns and repairs. We have analyzed the equilibrium thresholds in the fully observable case and the counterpart equilibrium entrance probabilities in the partially observable case and fully unobservable case. We also discussed the sensitivity with respect to various parameters in the three different cases.

We should pay attention to the effect of the server unreliability on the system performances. It is clear that customers’ equilibrium thresholds and optimal entrance probabilities decrease as \(\xi /\eta \) increases, which means that many customers unwillingness to join the system and the social welfare decreases at the same time. So, the analysis on the Nash equilibrium of the present model with server breakdowns is more important and practical than the model with a reliable server.