Keywords

1 Introduction

Recurrent neural networks are capable of producing high-dimensional complex dynamics due to feedback connections, which has often been utilized for information processing of sequential data [1]. The training methods for recurrent neural networks have been proposed, including the backpropagation through time algorithm, the real-time recurrent learning, and the extended Kalman filter method [2]. These algorithms try to adapt all the connection weights by minimizing the total error between the network output sequence and the desired output sequence. Since they have relatively high time complexity, their practical applications with large-scale networks are still not realized. Reservoir computing is one of the potent frameworks that can overcome the problem of the training cost in recurrent neural networks for energy efficient computing [3, 4]. The reservoir computing framework was established by combining the concepts from the echo state network (ESN) [5–7] and the liquid state machine [8].

The reservoir computing system consists of the reservoir part and the readout part. The reservoir part is used for mapping the input sequence to a high-dimensional spatiotemporal pattern. The readout part is used for adjusting the output connection weights so that the spatiotemporal pattern generated by the reservoir is appropriately mapped to the desired output sequence. Since not all the weights but only the output weights are adapted, the reservoir computing can save the learning time compared with the conventional recurrent neural networks. Moreover, the fixed reservoir can be implemented with nonlinear physical systems and devices, including optoelectronics [9], memristors [10], and wave phenomena [11, 12].

In the standard ESN [5], the reservoir is given as a randomly connected recurrent neural network. The performance of reservoir computing relies on the number of neurons and the weight matrix in the reservoir, which govern the length of the history of input sequence that can be embedded into its spatiotemporal dynamics. For constructing a good mapping from an input sequential data to an output one, the reservoir is required to satisfy the echo state property [5] which indicates the property that the influence of the input stream is gradually attenuated with time. This means that the mapping represented by the reservoir should be neither expanding nor highly contracting. Hence, the spectral radius of the weight matrix is often set to be less than and close to unity, corresponding to the edge of chaos [2]. However, the random reservoir topology is not mandatory. A deterministically designed reservoir with simple ring architecture is comparable to the standard random reservoir in their computational performance [13]. The simple cycle reservoir enables theoretical analyses of reservoir computing properties such as memory capacity. In addition, it is favorable for hardware implementation because only local connections and uniform weights are needed.

In this study, we incorporate variability into the neuron units in the simple cycle reservoir, motivated by two aspects. One is that the simple cycle reservoir with identical units seems to be too uniform to produce rich nonlinear dynamics. The unit variability is expected to diversify the dynamics of individual units. The other is that the variability of the reservoir units are inevitable when they are implemented with physical devices, particularly with nano/micro devices. We examine how heterogeneity of the reservoir units impacts on the reservoir dynamics and its computational capability. We show that the variability in the reservoir units can improve the performance of the simple cycle reservoir.

2 Methods

2.1 Model

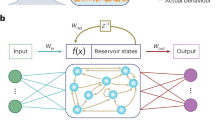
The reservoir in the standard ESN consists of neuron units which interact with each other through weighted random connections as illustrated in Fig. 1(a). The numbers of input units, internal units, and output units are denoted by L, N, M, respectively. Then, the states of the input, internal, and output units are represented by the column vectors \(\mathbf {u}(t)=(u_1(t),u_2(t),\ldots ,u_L(t))^T\), \(\mathbf {x}(t)=(x_1(t),x_2(t),\ldots ,x_N(t))^T\), and \(\mathbf {y}(t)=(y_1(t),y_2(t),\ldots ,y_M(t))^T\), respectively. The input connectivity, the reservoir connectivity, the feedback connectivity, and the output connectivity are represented by \(W^\mathrm{in} \in \mathbb {R}^{L \times N}\), \(W \in \mathbb {R}^{N\times N}\), an \(W^\mathrm{fb} \in \mathbb {R}^{M\times N}\), and \(W^\mathrm{out} \in \mathbb {R}^{N\times M}\), respectively.

The states of the ith internal unit (\(i=1,\ldots ,N\)) is updated as follows:

$$\begin{aligned} \mathbf {x}_i(t+1)= & {} f_i \left( (W_i^\mathrm{in})^T \cdot \mathbf {u}(t+1)+ (W_i)^T \cdot \mathbf {x}(t)+(W_i^\mathrm{fb})^T \cdot \mathbf {y}(t) \right) , \end{aligned}$$
(1)

where \(f_i\) stands for the activation function of the ith neuron in the reservoir and \(W_i^\mathrm{in}\), \(W_i\), and \(W_i^\mathrm{fb}\) are the ith row of the input, reservoir, and feedback weight matrices, respectively. The states of the jth output unit (\(j=1,\ldots ,M\)) is given by

$$\begin{aligned} \mathbf {y}_j(t)= & {} f^\mathrm{out} \left( (W_j^\mathrm{out})^T \mathbf {x}(t) \right) , \end{aligned}$$
(2)

where \(f^\mathrm{out}\) represents the activation function of the output neurons and \(W_j^\mathrm{out}\) is the jth row of the output weight matrix. Here we use \(f^\mathrm{out}(x)=\tanh (x)\).

Fig. 1.
figure 1

Structure of the reservoir. (a) Random topology. The standard architecture in the ESN [5]. (b) Ring topology called the simple cycle reservoir [13].

Full size image

When an input sequential data \(\mathbf {u}(t)\) is given, the output sequence is generated by Eqs. (1)–(2). The characteristic of the reservoir computing is that the weights in the input and reservoir connections are not adapted but only the output connection weights \(W^\mathrm{out}\) are determined by a learning rule. The output matrix \(W^\mathrm{out}\) is obtained to minimize the error between the network output sequence \(\mathbf {y}(t)\) and a desired output sequence \(\mathbf {d}(t)\), given by

$$\begin{aligned} E= & {} \langle ||\mathbf {y}(t)-\mathbf {d}(t)||^2 \rangle , \end{aligned}$$
(3)

where \(\langle \cdot \rangle \) denotes an average over a time period. The minimization of E can be achieved using regression methods. Here we employ the pseudoinverse computation [2].

2.2 Reservoir Structure

We use the simple cycle reservoir as shown in Fig. 1(b), where the connectivity of the reservoir nodes has ring topology and the connection weights are uniform [13]. It is represented as the weight matrix \(W=(w_{i,j})\) where \(w_{i+1,i}=r\), \(w_{1,N}=r\), and all the other entries are zero. For the standard reservoir, the necessary condition for the echo state property is given by \(\rho (W)<1\) where \(\rho (W)\) is the spectral radius of W and the sufficient condition is given by \(\bar{\sigma }(W)<1\) where \(\bar{\sigma }(W)\) is the largest singular value of W [5]. For the simple cycle reservoir [13], \(\rho (W)=\bar{\sigma }(W)=r\). The simple cycle reservoir is comparable to the standard reservoir in the performance of time series predictions and its memory capacity can be theoretically derived [13].

2.3 Heterogeneous Units

In most studies on reservoir computing, the units of the reservoir have been assumed to be identical. The hyperbolic tangent function is normally used as the nonlinear activation function of the units in ESNs. In the standard reservoir, the diversity of the dynamics of the reservoir units are brought about by the random weight matrix. However, in the simple cycle reservoir with identical units, the dynamics generated by the individual units become uniform. The total system can be essentially reduced to a lower-dimensional system. This is unbenefited for producing high-dimensional spatiotemporal dynamics. Thus, we introduce the variability in the activation function of the reservoir units, which are represented as follows:

$$\begin{aligned} f_i(x)= & {} \tanh (\beta _i x), \end{aligned}$$
(4)

where the parameter \(\beta _i\), corresponding to the slope of the function at the origin, controls the nonlinearity of the function. Although there are many ways to introduce variability in \(\beta _i\), for simplicity we assume that \(\beta _i\) is randomly generated from the uniform distribution in the range \([1-v,1]\), where v (\(0\le v \le 1\)) is the control parameter representing the degree of variability.

2.4 Simulation Setting

Initially, we give the internal state \(\mathbf {x}(0)\) and the output weight matrix \(W^\mathrm{out}\) randomly. The weights of input connections have the same absolute value p but the signs are randomly assigned. After a washout period with length \(T_\mathrm{init}\), the sample sequential data with length \(T_\mathrm{trn}\) are used for training the output weights and subsequently the sequential data with length \(T_\mathrm{test}\) are used for testing the generalization ability of the reservoir. The computational performance is evaluated using the normalized mean squared error (NMSE) defined as follows:

$$\begin{aligned} NMSE= & {} \frac{\langle || \mathbf {y}(t)-\mathbf {d}(t)||^2 \rangle }{\langle \mathbf {d}(t)^2 \rangle }. \end{aligned}$$
(5)

We use the following benchmark tasks on sequential data processing, which have been widely used to test the performance of reservoir computing.

  1. (1)

    Mackey-Glass equation [14]:

    $$\begin{aligned} \frac{dy(t)}{dt}= & {} \frac{ay(t-\tau )}{1+y(t-\tau )^{10}}-by(t), \end{aligned}$$
    (6)

    where \(a=0.2\), \(b=0.1\), and \(\tau =30\). The dataset was generated by numerically solving this equation with time step \(\varDelta t=1\) [15]. The task is to predict the value of \(y(t+1)\) from the past values up to time t.

  2. (2)

    Laser dataset: The Santa Fe Laser dataset is a crosscut through periodic to chaotic intensity pulsations of a real laser [16]. The task is the same as that in the previous one. The simple cycle reservoir has been applied to this task [13].

  3. (3)

    NARMA 10th-order system: The nonlinear auto-regressive moving average (NARMA) system of order 10 is described as follows:

    $$\begin{aligned} y(t+1) = 0.3y(t)+0.05y(t)\sum _{i=0}^9 y(t-i) + 1.5u(t-9)u(t)+0.1, \end{aligned}$$
    (7)

    where u(t) is the input sequence which is randomly sampled from the uniform distribution in the range [0, 0.5]. This task is widely used in the literature of recurrent neural networks and reservoir computing [7, 13].

  4. (4)

    NARMA 20th-order system: The NARMA system of order 20 is described as follows [13]:

    $$\begin{aligned} y(t+1) = \tanh \left( 0.3y(t)+0.05y(t)\sum _{i=0}^{19} y(t-i) + 1.5u(t-19)u(t)+0.01 \right) , \end{aligned}$$
    (8)

    where u(t) is generated as in the previous task. This task is more difficult compared with the NARMA 10th-order system due to the dependence of the current state on the longer history of inputs.

3 Results

In the following numerical experiments, the input and output data were scaled and shifted appropriately for each dataset. For the dataset generated by the Mackey-Glass equation, we set \(N=2\), \(T_\mathrm{init}=500\), \(T_\mathrm{trn}=1000\), \(T_\mathrm{test}=1000\), \(p=0.87\), and \(r=1\). The result of the test performance is shown in Fig. 2(a). The plot for the variability parameter \(v=0\) corresponds to the result for the simple cycle reservoir with the identical units [13]. As the variability parameter v is increased, the NMSE is gradually decreased. Namely, the variability of the units can improve the computational performance.

For the Laser dataset, we set \(N=100\), \(T_\mathrm{init}=500\), \(T_\mathrm{trn}=2000\), \(T_\mathrm{test}=3000\), \(p=0.87\), and \(r=0.7\). The result is shown in Fig. 2(b). As the variabililty increases, the prediction error decreases and reaches the bottom at around 0.7. The error slightly increases for further increase in v, but it is much lower than the case without variability.

Fig. 2.
figure 2

The performance of the simple cycle reservoir with heterogeneous neurons. The NMSE for the test set is plotted against the variability parameter v. The crosses represent the results of 10 trials for each parameter value. The open circle indicates the average of the 10 trials. (a) Mackey-Glass equation. (b) Santa Fe Laser dataset. (c) NARMA 10th-order system. (d) NARMA 20th-order system.

Full size image
Fig. 3.
figure 3

The parameter region for good prediction performance on the (r, v)-plane. The color bar indicates the NMSE for the test set. (a) The Mackey-Glass equation. (b) The Santa Fe Laser dataset. (c) The NARMA 10th-order system. (d) The NARMA 20th-order system.

Full size image

For the NARMA 10th-order system, we set \(N=100\), \(T_\mathrm{init}=200\), \(T_\mathrm{trn}=1000\), \(T_\mathrm{test}=1000\), \(p=0.87\), and \(r=0.86\). Figure 2(c) shows the result, where the variability can yield a better result if v is less than around 0.5 but for a larger value of v the result is worse than the case without variability.

For the NARMA 20th order system, we set \(N=100\), \(T_\mathrm{init}=500\), \(T_\mathrm{trn}=1000\), \(T_\mathrm{test}=1000\), \(p=0.87\), and \(r=0.95\). The result for the NARMA 20th-order system is similar to that for the NARMA 10-th order system as shown in Fig. 2(d). Although a large value of v significantly increases the prediction error, there exists a range of v in which the variability has a positive effect (the inset).

To clarify the conditions that the performance is improved by the unit variability, we indicated the parameter regions (black) for good computational performance in Fig. 3. The performance increases with the variability v for the range of r in Figs. 3(a), (b), whereas there is a optimal range of v in Figs. 3(c), (d). There is a correlation between the values of r and v, suggesting that the effective spectral radius is determined not only by r but by \(\beta _i\). It remains to explicitly give the formula for the spectral radius in the simple cycle reservoir with heterogeneous units.

4 Conclusions

We have proposed to exploit heterogeneity in the reservoir units for improving the computational performance in the reservoir computing with the simple cycle architecture. We have introduced variability in the slope parameter in the hyperbolic tangent activation functions of the reservoir units. Numerical experiments have shown that both the unit variability and the connection weight govern the performance on the benchmark tasks for sequential information processing.

Our result is beneficial for hardware implementation of reservoir computing because of the simple reservoir structure and the unavoidable unit variability when implemented with nano/micro devices. For verification of the effectiveness of our method, we need further numerical experiments using other datasets. It is significant to clarify the conditions under which the unit variability works well. The mathematical mechanism of the positive role of the unit variability still remains to be investigated.