Wave-Based Reservoir Computing by Synchronization of Coupled Oscillators

Abstract

We propose wave-based computing based on coupled oscillators to avoid the inter-connection bottleneck in large scale and densely integrated cognitive systems. In addition, we introduce the concept of reservoir computing to coupled oscillator systems for non-conventional physical implementation and reduction of the training cost of large and dense cognitive systems. We show that functional approximation and regression can be efficiently performed by synchronization of coupled oscillators and subsequent simple readouts.

1 Introduction

It never ceases to amaze us how biological systems perform complex cognitive tasks such as memorization, recognition and categorization. Cognitive computing is an approach for realizing such cognitive abilities artificially. However, software implementations at biologically realistic level have proved to be highly power-hungry and computer-intensive so far because of their serial operation and von-Neumann bottleneck of the current architecture. In this respect, hardware implementations are of great interest because of their parallel operation and distributed information representation.

On the other hand, current VLSI technologies also are facing several serious challenges. Complexity of placement and wiring in VLSI design increasingly becomes a major bottleneck of chip performance [5]. Since the flexible and diverse capabilities of brains come from massive synaptic inter-connections rather than the function of individual neurons, current hardware implementation is not necessarily efficient in terms of interconnections.

We need to consider other possibilities for implementation than conventional CMOS-based VLSI technology, such as nano-structures since it is quite unclear whether the integration by CMOS scaling continues in the future [3]. Our main question is that how we can realize interconnection-centric cognitive computing systems on such non-conventional physical systems beyond the bottleneck of hard wiring. To this end, we make use of physical waves as an alternative to hard wiring. The use of wave dynamics for computing is attracting much interest recently in the research pursuing post-CMOS technology. For example, wave-based multi-valued logic by superposition of spin waves was proposed as more power- and area-efficient computing framework than CMOS based digital computing [4]. From our perspective, waves have an attractive property that they can propagate in any direction and at any distance as long as there exists medium transmitting waves, which makes them a promising alternative for hard wiring. This lead us to explore computing systems where computing elements interacting through wave propagation. In this work, we use oscillators as computing elements and realize wave-based computing systems as coupled oscillators. We show the phase locking in a synchronized state of coupled oscillators can approximate a given function.

The cost of modifying inter-connections by learning will become another serious bottleneck if we are going to build cognitive systems on non-conventional physical systems. In this respect, it is useful to apply the framework of reservoir computing, where training is performed only in readout part outside computational part called reservoir [6]. The reservoirs do not need to be traditional neural networks but can be built on a variety of physical systems such as coupled oscillators. We realize the reservoirs as coupled oscillators and show that the phase dynamics of coupled oscillators can be viewed as a special case of reservoir computing in time domain. We also show function approximation problems can be robustly solved by wave-based reservoir computing using synchronization of coupled oscillators.

2 Wave-Based Reservoir Computing

The reservoir computing is an emerging computation framework for design of recurrent neural networks [6]. Generally, reservoir computing systems have two functional components. One is a fixed recurrent neural network, called reservoir, which is a (non-linear) mapping of input data to a high dimensional space and should be complex enough to generate rich dynamical behaviour. The other is adaptive read-out functions which extract desired results from the reservoir output.

In this work, we realize the interconnection in the reservoir as wave propagation to avoid interconnection bottleneck. In addition, we use oscillators as the computational elements because they can naturally interact through waves. Thus, we formulate the phase domain reservoir computing as phase dynamics of coupled oscillators. Even if the dynamics is restricted to phase domain, it can still exhibit very rich behaviour such as phase transition, clustering and synchronization, enough to potentially perform complex computational tasks [8]. For example, coupled oscillators has been applied to associative memory systems [2] and convolutional neural networks [7]. Since the wave-related phenomena and synchronization are abundant in the natural world, the wave-based computing is expected to be advantageous for physical implementation. Therefore, we use synchronization dynamics for stable computation in this work.

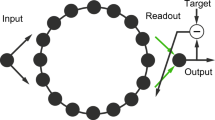
Figure 1 shows the overall architecture of the proposed wave-based reservoir computing. Multiple waves modulated by analog information are fed into the reservoir. The reservoir consists of coupled oscillators designed for specific computational tasks. Then, read-out functions are applied to obtain desired results after the reservoir dynamics reaches a final state. We can apply adaptive filters such as least mean square filters or simple perceptrons to read-out functions.

Fig. 1.

Proposed architecture of wave-based reservoir computing

3 Phase Dynamics of Coupled Oscillators

3.1 Phase Response Curves

Suppose that a stable limit cycle $X_0(\theta ),\theta \in [0,2\pi )\rightarrow \mathbb {R}^n$ is subject to a small impulse stimulus I. Since the limit cycle is neutrally stable along its orbit and stable in the directions orthogonal to its orbit, the small impulse stimulus I results in a small phase shift on the limit cycle. The phase shift caused by I can be described by the following phase response curve $g(\theta ; I) = \varDelta \theta = \theta (X_0(\theta ) + I)-\theta$, where $\theta (X):X\rightarrow [0,2\pi )$ is mapping from the point on the limit cycle X to its phase $\theta$. Since the strength of stimulus |I| is small, the phase response curve is well approximated by linear response as $g(\theta ; I) \cong Z(\theta )\cdot I$. Here, we introduce the linear response coefficient of phase response for small I as $Z(\theta ) = \nabla _X\theta (X)|_{X=X_0(\theta )}$. The linear response coefficient $Z(\theta )$ is the $2\pi$-periodic impulse response function for the phase shift and called phase sensitivity function. Though both I and $Z(\theta )$ are n dimensional vectors, we assume hereafter these two functions are scalar functions for simplicity.

Under some assumptions such as weakness of stimulus and linearity of response, the phase response can be understood from the viewpoint of linear system theory [1]. That is, the total phase response caused by input stimulus $I(\theta )$ during one cycle of oscillation is given by the circular linear convolution as

$$\begin{aligned} H(\theta ; I) = \int _0^{2\pi }Z(\theta _0) \cdot I(\theta -\theta _0)d\theta _0. \end{aligned}$$

(1)

The interactions through the phase response (1) is the counterpart of those in the reservoir of time domain. Since the interactions in the reservoirs of time domain are generally nonlinear, the linearity of response (1) means that the wave-based reservoir computing in phase domain is a special class of reservoir computing in time domain. However, we will show in Sect. 4 that wave-based reservoir can still perform complex tasks such as function approximations.

3.2 Phase Synchronization

Consider a N coupled stable limit cycle oscillators described by the following equation.

$$\begin{aligned} \frac{d X_i(t)}{dt} = F_i(X_i(t)) + \sum _{j\ne i}^N G_{ij}(X_j(t)), \quad i = 1,\ldots ,N. \end{aligned}$$

(2)

Here, $X_i= (x_i,y_i\ldots )^T\in \mathbb {R}^n$ is the state variables of the oscillator i, $F_i$ is a nonlinear function describing limit cycle oscillation. The function $G_{ij}$ means the interaction waveform from the oscillator j to the oscillator i determined by the physical interactions among the oscillators, for example, chemical materials, electric currents, surface acoustic waves on elastic bodies, spin waves on magnetic materials, etc. If the interaction is small enough, the Eq. (2) can be reduced to the following dynamical phase equations [9]

$$\begin{aligned} \frac{d\theta _i(t)}{dt} = \omega _i + \sum _{j\ne i}^N H_{ij}(\theta _i-\theta _j), \quad i = 1,\ldots ,N. \end{aligned}$$

(3)

Here, $\theta _i$ and $\omega _i$ are the phase and the natural frequency of oscillator i, respectively. The function $H_{ij}$ is called phase coupling function and computed as the phase response (1) with the input stimulus replaced with the interaction waveform between two oscillators:

$$\begin{aligned} H_{ij}(\theta _i-\theta _j) = \int _0^{2\pi } Z(\theta )\cdot G_{ij}(\theta _j-\theta _i+\theta )d\theta , G_{ij}(\theta ) = G_{ij}(X_j(\theta )). \end{aligned}$$

(4)

In a synchronized state, all the oscillators have a common frequency $\dot{\theta }_i = \bar{\omega }$ and their phase locked state are given by $\theta _i(t) = \bar{\omega } t + \phi _i$. Thus, the existence of a phase-locked synchronized state reduces to solving the following set of equations

$$\begin{aligned} \bar{\omega } = \omega _i + \sum _{j\ne i}^N H_{ij}(\phi _{ij}), \quad \phi _{ij} = \phi _i-\phi _j, \quad i = 1,\ldots ,N. \end{aligned}$$

(5)

4 Function Approximation and Regression by Wave-Based Reservoir Computing

4.1 Function Approximation by Two Coupled Oscillators

Consider a system of two symmetrically coupled oscillators given by

$$\begin{aligned} \frac{d\theta _1(t)}{dt} = \omega _1 + H(\theta _1-\theta _2),\quad \frac{d\theta _2(t)}{dt} = \omega _2 + H(\theta _2-\theta _1), \end{aligned}$$

(6)

where we assume the phase interaction function is an odd function $H(\theta _2-\theta _1) = - H(\theta _1-\theta _2)$. Then, in a synchronized state, it can be easily seen that the common frequency is given by $\bar{\omega }=(\omega _1+\omega _2)/2$ and the phase difference $\phi =\phi _1-\phi _2$ satisfies

$$\begin{aligned} \varDelta = - 2 H(\phi ), \quad \varDelta =\omega _1-\omega _2. \end{aligned}$$

(7)

The stability of the phase difference can be judged by two conditions. The first condition is that $-\varDelta /2$ is within the range $[\min H(\phi ), \max H(\phi )]$ so that Eq. (7) has at least one solution $\phi ^*$. The second condition is that the solution $\phi ^*$ satisfies $H^\prime (\phi ^*)<0$ so that the phase difference $\phi ^*$ is stable.

The basic idea for function approximation is that we design the phase coupling function H so that the phase difference after synchronization gives the inverse of the desired function of the difference of two frequencies $\omega _1$ and $\omega _2$. This is a kind of inverse problems where we need to find an interaction waveform which realize the given target function. Since the Eq. (4) is a linear convolution of two functions, we can find the appropriate interaction waveforms for the target phase interaction function by Fourier transforms [9]. Figure 2(a) shows the examples of interaction waveforms for the target function $H(\phi )=a\sqrt{\phi }$ and logit function (inverse of the sigmoid function) defined as $H(\phi )= a + \varepsilon \log (\phi /(2\pi -\phi ))$. Here, we extended the square root function as $H(\phi )=-\varepsilon \sqrt{-\phi },-\pi \le \phi \le 0$ and $H(\phi )=\varepsilon \sqrt{\phi },0\le \phi \le \pi$ so that $H(\phi )$ becomes a $2\pi$-periodic odd function. In addition, we assumed that the phase sensitivity function is $Z(\theta ) = \cos (\theta )-\sin (\theta )$ and applied numerical FFT and IFFT by digitizing H and Z with 100 sampling points equally spaced on $[0,2\pi )$.

We can realize arithmetic operations such as adder and multiplier based on this function approximation by two coupled oscillators. We can implement the adder $\omega _1\pm \omega _2$ by reading out $2\bar{\omega }$ of the synchronized oscillators in (6). Similarly, we can implement the square operation $\omega \mapsto \omega ^2$ by $\varDelta = -2H(\phi ) = - \sqrt{2\phi }$. Note that there is only one stable fixed point for $\varDelta <0$ since $-\sqrt{2\phi }$ is a monotonously decreasing function. Using these two operations and the identity $xy = ((x+y)^2-(x-y)^2)/4$, we can construct a multiplier $\omega _1\omega _2$ as is depicted in Fig. 2(b) under the restriction that input variables $\omega _1$ and $\omega _2$ satisfy $\omega _1\pm \omega _2 \in [\min H(\phi ), \max H(\phi )]$.

Fig. 2.

(a) Phase sensitivity function $Z(\theta ) = \sin \theta -\cos \theta$, interaction waveforms for square root function with $a=0.05$ and logit function with $a=0, \varepsilon = 0.01$. (b) Coupled oscillators computing the product $\omega _1\omega _2$.

4.2 Functional Regression by an Oscillator Reservoir

Though we can realize any target function as the phase interaction function by the method in Sect. 4.1, the problem is that we need to re-design the interactions depending on the target function. This is a disadvantage especially for non-conventional implementation such as nano structures. In this subsection, we show that one fixed oscillator reservoir can approximate different target functions. Let us consider the coupled oscillators connected in star-like topology as illustrated in Fig. 3. The phase dynamics is written as

$$\begin{aligned} \frac{d\theta _0(t)}{dt} = \omega + \sum _{j=1}^N H_{0n}(\theta _0-\theta _n), \quad \frac{d\theta _n(t)}{dt} = H_{n0}(\theta _n-\theta _0), n=1,\ldots ,N. \end{aligned}$$

(8)

We assume that the phase interaction functions are all odd $H_{0n}(-\phi ) = -H_{0n}(\phi )$, the interaction between oscillator 0 and n are symmetric $H_{0n}(\phi ) = H_{n0}(\phi )$ and all the oscillators have the same phase sensitivity function $Z(\theta )$. We initialize the coupled oscillators so that only the central one oscillates with frequency $\omega$ and the rest are all quiescent. After synchronization state is reached, the oscillators have common frequency $\bar{\omega }$ and relative phase difference $\phi _n-\phi _0$ which satisfies

$$\begin{aligned} \bar{\omega } = \omega + \sum _{n=1}^N H_{0n}(\phi _0-\phi _n), \quad \bar{\omega } = H_{n0}(\phi _n-\phi _0), n=1,\ldots ,N. \end{aligned}$$

(9)

It can be easily seen that the common frequency is $\bar{\omega } = \omega /(N+1)$. Assuming $\phi _0=0$ and replacing $\bar{\omega }$ with $\omega$, we calculate the n-th basis functions as $f_n(\omega ) = H_{n0}^{-1}(\omega )$ by the method in Sect. 4.1. Thus, we can view the reservoir of $N+1$ coupled oscillators as calculating N different basis functions in parallel. We employ sigmoid functions $f_n(\omega ) = \frac{1}{1+\exp (-(\omega -p_n)/\varepsilon )}$ as basis functions and set the parameters to $p_n=2\pi n/N$ and $\varepsilon =0.1$.

Fig. 3.

The oscillator reservoir for linear regression at training stage

Fig. 4.

Functional regression by oscillator reservoir.

Given a target function $f(\omega )$, we approximate $f(\omega )$ by the linear combination of basis functions $f_1,\ldots ,f_N$ as follows

$$\begin{aligned} \hat{f}(\omega ) = \sum _{n=1}^N a_n f_n(\omega ). \end{aligned}$$

(10)

The role of the readout function is to determine the coefficients ${{\varvec{a}}}=(a_1,\ldots ,a_N)$ by minimizing the mean square error

$$\begin{aligned} \min _{a_1,\ldots ,a_N} \int _0^{2\pi } (f(\omega )-\hat{f}(\omega ))^2 d \omega . \end{aligned}$$

(11)

at training stage and to output the estimated value $\hat{f}(\omega )$ by (10) at operation stage. The minimization of (11) can be achieved by solving the normal equation $C \mathbf{a} = {{\varvec{r}}}$, where $C =(c_{ij}), c_{ij}=\int _0^{2\pi } f_i(\omega )f_j(\omega )d \omega$ and ${{\varvec{r}}} = (r_1,\ldots ,r_N), r_i = \int _0^{2\pi } f(\omega )f_i(\omega )d \omega$. Figure 4(a) shows the regression for target function $\phi ^2$ by solving the normal equation. To perform the training online, we choose randomly $\omega _i$ from 100 sampling points equally spaced on $[0,2\pi )$ and inject wave with frequency $\omega _i$ to the central oscillator. After the oscillator reservoir reaches synchronization, the readout updates the coefficients by stochastic gradient descent method as ${{\varvec{a}}}\leftarrow {{\varvec{a}}} + \alpha e_i{\varvec{\phi }}_i, e_i=f(\omega _i) - \hat{f}(\omega _i), {\varvec{\phi }}_i=(f_1(\omega _i),\ldots ,f_N(\omega _i))$. We choose the step size parameter $\alpha =0.01$ and iterate this update $10^4$ times. Figure 4(b) shows that how root mean square error is improved by increasing the number of oscillators for $f(\omega )=\sqrt{\omega },\omega ^2,\sin \omega$.

5 Conclusion

We have proposed a framework for wave-based reservoir computing based on synchronization of coupled oscillators. We applied the proposed framework to function approximation and regression and showed that such problems can be solved efficiently due to the parallelism and stability of synchronized state. In summary, wave-based reservoir computing is promising for large scale and densely integrated cognitive computing systems.