Keywords

16.1 Introduction

Heuristic search methods represent powerful and effective means in solving combinatorial optimization problems since they do not require any additional information compared with the classical optimization methods and they accelerate the search towards objective or convergence through their parallel performed exploration and exploitation of the search space.

One well known combinatorial optimization task solved using such heuristic approaches is the Redundancy Allocation Problem (RAP) also referred to as Redundancy Optimization Problem (ROP) which consists of determining best series-parallel system designs in terms of redundancy depth on different subsystems level corresponding to minimal investment costs and that satisfies at the same time the predefined constraints and system design requirement specifications like availability, weight, volume and etc.

The Redundancy Allocation Problem (RAP) or Redundancy Optimization Problem (ROP) [1] is a single objective optimization and can often be encountered in many applications areas of the safety engineering world like electrical power systems and in the consumer electronic industry where system designs are mostly assembled using standard certified component types with different characteristics, e.g., reliability, availability, nominal performance, cost, etc. This matter has been intensively studied over last two decades and has been classified as a complex nonlinear integer programming combinatorial problem, where deterministic or conventional mathematical optimization approaches become ineffective by means of computational effort and quality of solution [1].

Using heuristic and metaheuristic search methods, e.g. Genetic Algorithms (GAs), Tabu Search (TS), Simulated Annealing, etc., in solving such kind of combinatorial optimization problems aims to determine an optimal or near optimal, also called pseudo-optimal solution, to the proposed RAP, i.e. to find the best or at least one acceptable solution that satisfies the constraint(s). However, these approaches have shown instead how powerful and effective they are in finding high qualitative solutions for the addressed kind of problems, especially when the search space corresponding to the problem becomes too large and where conventional classical optimization methods become ineffective and useless. This kind of problems was first introduced by Ushakov [1] and has been further analyzed by Levitin and Lisnianski et al. [2–4], Ouzineb [5–7] and many others.

This paper deals with the cost optimization of heterogeneous structured series assembled systems, where mixing of components or usage of non-identical components within the same subsystem is allowed. This feature, compared with the homogeneous case, includes more complexity to the task because the corresponding search or solution space becomes larger, since every component available on the market has to be taken into account. It represents a single objective optimization (cost function) subject to one constraint which is the availability of the system.

The remainder of the paper is organized as follows. Section 16.2 gives a short introduction into heterogeneous series-parallel multi-states configurations and a brief overview on the advantages obtained through mixing of components in addition to a short comparison with homogeneous systems. Section 16.3 shortly discusses genetic algorithms and its different operators while chromosomal encoding and random generating of solution candidates are implemented in Sect. 16.4. In Sect. 16.5 a detailed formulation of the optimization problem, which is solved using heuristic traditional GA genetic techniques, is presented. Section 16.6 deals with the Universal Moment Generating Function (UMGF), also called the Ushakov-transform, which represents the function used for the determination and evaluation of the availability of the different redundant structures. Section 16.7 reports different numerical and experimental results, evaluations and graphical representations obtained by the implemented GA algorithm for different analyzed models which will be compared with previously published evaluations in terms of efficiency, solution quality and accuracy in addition to algorithm computation speed and convergence time. Finally concluding remarks are resumed in Sect. 16.8.

16.2 Homogeneous vs. Heterogeneous Series-Parallel Configurations

In order to improve or to increase the system’s reliability and provide longer operation time, safety system designers may introduce different parallel technologies into a system also called redundancy [8]. Including homogeneous components redundancy is a great and effective technique to achieve a desired level of reliability in binary state systems or to increase the availability of multi-state systems. Reliability analysis have shown that the availability of homogeneous redundant structures or systems is extremely affected by common cause failure (CCF) that cannot be ignored since the CCF is the simultaneous failure of all components of the same type due to a common cause (CC), which leads in homogeneous redundant structures definitely to the failure of complete subsystems consisting of identical components causing herewith a total system failure. Common cause events may arise from environmental loads (humidity, temperature, vibration, shock, etc.), errors in maintenance and system design flaws [9]. In order to partly overcome this kind of facing problems and avoid total system failure subject to CCF heterogeneous redundancy is used.

The main concept of heterogeneous or non-homogeneous structures consists of the mixture of non-identical components within the same subsystem. That means that all non-identical components with the same functionality available on the market and which can be deployed in a redundant manner within the same subsystem have to be taken into account in this case, the fact that would definitely enlarge the size of the search space of feasible solutions and increase the exploration and hence the convergence time towards acceptable solutions.

The main advantages and benefits of components mixing lie in the improvement of the availability of the whole system and reducing the effect of common cause failure in addition of introducing flexibility and diversification into redundant system design through the allowed multiple component choice.

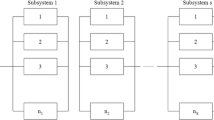
Figure 16.1 represents a heterogeneous series-parallel multi-state system consisting of s subsystems, which are connected serially.

Fig. 16.1
figure 1

Heterogeneous series-parallel configuration consisting of s-nodes or subsystems

Full size image

In Fig. 16.1 r ij represents the reliability of a component of version j within the subsystem i. In the case of a homogeneous configuration the reliabilities of all components within the same subsystem are the same since subsystems consists of identical components, i.e. all r ij ’s are equal for the same i, which must not be the case in heterogeneous systems since they mostly deal with non-identical components on the same stage.

For a brief explanation, in addition to a short mathematical computation that shows why series-parallel configurations are more suitable and studied than parallel-series configurations, the reader should refer to [1, 10]. This is due to the fact that the overall reliability or availability of a system in a series-parallel configuration is better than the corresponding parallel-series configuration using the same set of components.

16.3 Genetic Algorithms

Genetic algorithms (GAs) are biologically inspired metaheuristic search and optimization routines that mimic the act of self-evolution concept of natural species that has been first laid by Charles Darwin. Nowadays, they are frequently used in many engineering and mathematical fields like optimization, self-adaptiveness, artificial intelligence, machine learning, etc. As computational efforts and speeds have been increasingly improved over the last decade, GAs have been expanded to cover a wide variety of applications including numerical and combinatorial optimization tasks in engineering like the one discussed in the recent work. For further fundamentals and detailed information on genetic algorithms, the reader should refer to [11, 12].

GAs represent iterative self-adaptive stochastic techniques based on the concept of randomness. They mimic the process of the natural evolution of species. GAs have become very popular and widely used over the last decade and are very well suited as universal or common techniques for solving combinatorial optimization problems, e.g. multimodal functions (many peaks and local optima), the very well-known TSP (Travelling Salesman Problem) and redundancy allocation problems like the one discussed in this paper and many other matters [13].

GAs differ from normal optimization and search methods in four fundamental different ways [12]:

  • The first difference is that GAs require an encoding of the parameter set in so called solution candidates, also called chromosomes according to the biological genetic terminology.

  • Another difference is that GA starts the search from a start (initial) population and not from a single point like classical deterministic algorithms.

  • GAs use information provided directly by the objective function and do not require any additional information or auxiliary knowledge like derivatives, gradients, etc.

  • GAs apply probabilistic transition rules or operators (crossover, mutation) and not deterministic ones.

As mentioned before the search procedure starts from a random generated population of chromosomes that are encoded according to the addressed problem (binary, integer, decimal, etc.) conducting herewith a simultaneous search in many areas of the feasible solution space at once. The encoding of solutions constitutes the most difficult and challenging task of GAs and the evolving procedure from one population to the next is referred to as generation.

After each generation the new generated solutions are decoded and evaluated in terms of fitness with the help of the objective function. The fitness value of a chromosome represents a measure for its quality (fitness) and represents the decision maker of the selection operator since the probability of selection of chromosomes is proportional to its corresponding fitness value. A general overview of the genetic cycle is given in Fig. 16.2.

Fig. 16.2
figure 2

General overview of the genetic process

Full size image

The genetic run process terminates when at least one of its predefined termination criterions is met, e.g., when the predefined maximum number of generations or repetitions N rep or a specific number of successive runs without any solution’s improvement is reached, or for example when the current solution satisfies the predefined requirement specifications or constraints.

Three main operators, also called genetic operators, will be executed during one genetic cycle, hence the selection, crossover or recombination and the mutation operator. These operators are shortly discussed in the following subsections.

16.3.1 Selection or Reproduction: Operator

Outgoing from a start or an initial population of different solution candidates the selection operator is used to randomly select or choose individuals or chromosomes which will reproduce and help building the next population during the genetic cycle. This operator represents an artificial version of natural selection, the Darwinian principle of the survival of the fittest, which drives the evolution towards optimization. Since the selection probability is proportional to relative fitness, chromosomes with higher fitness have better chance or higher probability to survive into next population, while chromosomes with bad or lower fitness will die off. This phenomenon will improve the population’s average fitness from one population to the next.

There are many selection methods, some of them are listed in the following [14]

  • Roulette Wheel selection,

  • Tournament selection,

  • Rank selection,

  • etc.

16.3.2 Recombination or Crossover: Operator

Whereas the selection operator determines which chromosomes of the recent population are going to reproduce, the crossover operator performs jumps between the different solution subspaces enabling the exploration of new areas of the solution space and avoiding herewith premature convergence in addition to the exchange of some basic characteristics or genetic materials and inheriting these properties to the offsprings which will join next populations. The crossover occurs with a predefined crossover rate or probability of crossover p c . There are many crossover techniques used in genetic algorithms [1, 14, 15] like the one-point crossover, two-point crossover, uniform and half uniform crossover and many other crossover techniques.

In the following the one-point crossover operator is shortly discussed. For this purpose two parent chromosomes Parent1 and Parent2 are selected. Afterwards a pseudorandom real number is generated in [0; 1]. If and only if the generated number is less or equal p c both parents will undergo crossover; otherwise they will have to be recopied in the population and wait to undergo the next operator, hence the mutation operator.

In case 2 chromosomes undergo crossover, a crossover point or position depending on the length of the chromosome is randomly selected on both selected parent chromosomes. This step is done by a pseudorandom integer number generator that generates numbers in the interval [1;l c  − 1], where l c is the length of the vector representing the chromosome. All data beyond that point in either chromosome will be swapped between the two parent organisms which will result in two new individuals called offsprings or children chromosomes. The one-point crossover technique is depicted in Fig. 16.3.

Fig. 16.3
figure 3

One-point crossover technique

Full size image

Figure 16.4 shows a pseudo code which resumes the crossover procedure.

Fig. 16.4
figure 4

Pseudocode—one-point crossover

Full size image

16.3.3 Mutation Operator

After crossovering parent chromosomes the resulting offsprings or children undergo mutation with a low mutation rate or probability p m . The mutation operator introduces diversity into the GA algorithm and inserts small disturbance into the properties (genes) of the proposed solutions avoiding herewith premature convergence into local maxima. Mutation also helps recovering loss that might have been caused by crossover. After the mutation process has been accomplished, the new resulting mutated chromosomes constitute the new next population. The mutation of a binary encoded chromosome consists of inverting the randomly selected bit or position like depicted in Fig. 16.5, while a pseudo code which represents the mutation routine is shown in Fig. 16.6.

Fig. 16.5
figure 5

Mutation of a binary encoded chromosome

Full size image
Fig. 16.6
figure 6

Pseudocode—mutation operator

Full size image

16.4 Chromosomal Encoding and Random Generating of Solution Candidates

Genetic algorithms are population based combinatorial optimization approaches where populations consist of a predefined number of solution candidates, also called chromosomes or individuals. These candidates represent vectors of encoded information, referred to as genetic materials, which will be decoded using the fitness or objective function in order to find the optimal (minimum or maximum) or near optimal solution of the addressed problem, whereas the recent approaches for solving the RAP problem are based on the Universal Moment Generating Function (UMGF) for estimating the availability of multi-state systems [2, 5–7, 16]. The encoding of chromosomes represents one of the major challenges faced in the context of genetic computing.

With regard to such problems that are dealt with in this paper, i.e., in the case of heterogeneous redundant structures the chromosome length corresponding to a system is definitely longer than chromosome corresponding to the homogeneous case since each component version or type available on the market that may be deployed in a subsystem has to be taken into account, whereas in homogeneous systems, the chromosome length is equal to twice the number of subsystems, since only one component type or version is allowed on each stage. The chromosomes are integer encoded and each element x ij of the chromosome vector corresponds to the number of components of version j used in subsystem i. The chromosome dimension or length l c is given therefore through:

$$ {l}_c={\displaystyle \sum_{i=1}^s{J}_i}. $$
(16.1)

where s is the total number of subsystems or stages and J i the total number of component versions available on the market that can be used on stage or in subsystem i. For more clarification and to gain a deeper insight it is important to mention at this point that two components of different versions or non-identical components connected in parallel are supposed to perform the same task or function. The difference lies in the technical data (reliability/availability, nominal performance and etc.) in addition to purchasing costs.

For example let us consider a system consisting totally of four subsystems with the following version vector m = [4 6 8 5] representing the number of components available on the market for each subsystem. The chromosome length results in this case as the sum of all elements of the version vector and would give according to Eq. (16.1) a total chromosome length of 4 + 6 + 8 + 5 = 23 and the chromosome encoding or vector X will look like in the following:

$$ X=\left(\left[{x}_{11}\dots {x}_{14}\right],\left[{x}_{21}\dots {x}_{26}\right],\left[{x}_{31}\dots {x}_{38}\right],\left[{x}_{41}\dots {x}_{45}\right]\right). $$
(16.2)

where x ij denotes as mentioned previously the number of components of type j used in subsystem i.

For generating chromosomes or solution candidates according to the addressed optimization problem, discussed in this paper, a pseudo random number generator is used. Since events should happen at random but some events or numbers within the chromosomal encoding should have a higher probability of occurrence or happening than others, e.g. zeros which means that no components of this kind are used, a weighted pseudo random number generator is used.

As mentioned above, the step of generating numbers with predefined probabilities of occurrence in addition to the limitation of the maximum number of totally used components within each subsystem would reduce the search hypervolume. This would increase the computation speed drastically towards convergence and make the algorithm more efficient and time consuming.

16.5 Cost Optimization and Redundancy Allocation: Task Formulation

The cost optimization problem of heterogeneous series-parallel redundant systems discussed in this work deals with the determination of optimal redundant designs and the level of redundancy (redundancy allocation) to use in each subsystem that corresponds to the minimal total purchasing costs of the system and which satisfies at the same time the predefined availability constraints. This kind of optimization gives a rise to safety vs. economics conflicts resumed in the following two points [17]:

Choice of components: choosing high reliable components guarantees high system availability but may be largely non-economic due to high purchase prices; whereas choosing less reliable components for lower costs on one hand may decrease the availability of the system and increase drastically the accident costs on the other hand.

Choice of redundancy configuration: choosing highly redundant configurations increases definitely the reliability and availability of the system and is accompanied at the same time with higher purchase costs caused by additional equipment units required to improve individual subsystems reliabilities.

The previously described aspects of safety system design call for compromise choices which optimize system operation in view of recommended safety and longer operation time or budget constraint. As mentioned before this paper deals with customizing a GA for budgetary optimization and redundancy determination of multi state systems under a given availability constraint. This problem is considered as a single objective optimization and can be mathematically formulated as to minimize the cost function C sys (X) (objective function) of the whole system given by [1, 5–7, 16]:

$$ {C}_{sys}(X)={\displaystyle \sum_{i=1}^s{\displaystyle \sum_{j=1}^{m_i}{c}_{ij}{x}_{ij}}}. $$
(16.3)

where c ij being the cost of component of type j in subsystem i and x ij the number of components of type j used in subsystem i. m i is the number of component choices available on the market which may be deployed in subsystem i. The (cost) objective function represented in Eq. (16.3) results over the sum of the purchasing costs of all components used in system that should meet at the same time the system specified availability constraint, which implies that the total availability of the system A sys (X) must satisfy a minimum level of availability required A 0 (inequality or availability constraints)

$$ {A}_{sys}(X)\ge {A}_0. $$
(16.4)

Based on the UMGF or the Ushakov-transform, the total availability of the system A sys (X) is estimated as a function of system structure, performance and availability characteristics of its constituting components.

For a detailed overview of the UMGF in computing the availability of series-parallel systems the reader should refer to [2, 3, 5–7, 10, 17, 18].

16.6 Universal Moment Generating Function

The UMGF, also referred to as Ushakov-transform according to I. Ushakov (mid 1980s) or u-function, is a polynomial representation of the different states corresponding to a component or a system. For a great understanding of the mathematical fundamentals of the UMGF the reader should refer to [17]. For example, the u-transform u j (z) of a component or a random variable j having M different discrete states is given by

$$ {u}_j(z)={\displaystyle \sum_{m=1}^M{p}_m{z}^{W_m}}. $$
(16.5)

In Eq. (16.5) p m is the probability that the nominal performance of the component or value of the discrete random variable j at state m equal to W m .

Since in the recent study it is assumed that the used components are binary state, i.e., have two particular states (perfect working or complete failing), the Ushakov-polynomial representation of a binary state component j is given by

$$ {u}_j(z)={\displaystyle \sum_{m=1}^2{p}_m{z}^{W_m}}=\left(1-{A}_j\right){z}^0+{A}_j{z}^{W_j}=\left(1-{A}_j\right)+{A}_j{z}^{W_j}. $$
(16.6)

In Eq. (16.6) A j represents the probability that the component is available (perfect functioning) and delivers a nominal performance of W j (Pr[W m  = W j ] = A j ) while (1 − A j ) represents the probability of unavailability or failing (system not available, i.e., Pr[W m  = 0] = 1 − A j ). The 0 power factor in the failing state results from the absence of delivered performance in this state.

In order to determine the u-function of an entire series-parallel system for availability computation purposes, two different basic operators will be respectively applied [5, 6, 10, 17, 18]. These two operators also called composition operators applied respectively [17] will be implemented separately in the following subsections.

16.6.1 Γ-Operator: Ushakov Transform of Parallel Configurations

The Γ-composition operator is used to determine the u-function of parallel systems. Suppose a system consisting of x i parallel connected components, the corresponding u-function is given by the following equation

$$ {u}_{parallel}(z)=\varGamma \left({u}_1(z),{u}_2(z),\dots, {u}_{x_i}(z)\right). $$
(16.7)

where the total performance or the structure function f(W 1 ,W 2 ,…,W xi ) is given by the sum of the performances or capacities of the individual components or elements as described in the following equation

$$ f\left({W}_1,{W}_2,\dots, {W}_{x_i}\right)={\displaystyle \sum_{i=1}^{xi}{W}_i}. $$
(16.8)

For a pair of parallel connected components with the corresponding u-functions u 1 (z) and u 2 (z) given according to Eq. (16.5) the resulting u-function u parallel (z) of the entire parallel system is given by

$$ \begin{array}{c}{u}_{parallel}(z)=\Gamma \left({U}_1(z),{U}_2(z)\right)\\ {}={\displaystyle \sum_{i=1}^n{P}_{1i}{z}^{W_{1i}}{\displaystyle \sum_{j=1}^m{P}_{2j}{z}^{W_{2j}}}}\\ {}={\displaystyle \sum_{i=1}^n{\displaystyle \sum_{j=1}^m{P}_{1i}{P}_{2j}{z}^{W_{1i}+{W}_{2j}}}}.\end{array} $$
(16.9)

In Eq. (16.9), n and m represent the number of states of the components 1 and 2. W 1i and W 2j are respectively the nominal performances of the components 1 and 2 at states i and j, which occur with the respective probabilities P 1i and P 2j (i = 1…n and j = 1…m). All this means that the Γ-operator is nothing else than the polynomial product of the individual u-functions corresponding to all parallel connected components and therefore Eq. (16.9) can be represented as

$$ {u}_{parallel}(z)={\displaystyle \prod_{e=1}^{x_i}{u}_e(z)}. $$
(16.10)

For a subsystem i within a series-parallel configuration consisting of x i different parallel connected binary state components, whose UMGF representation is given by Eq. (16.6), the u-function according to Eq. (16.10) is written in the form

$$ {u}_{parallel}(z)={\displaystyle \prod_{e=1}^{x_i}\left[\left(1-{A}_{ij}\right)+{A}_{ij}{z}^{W_{ij}}\right]}. $$
(16.11)

j represents the index corresponding to the version of the component used in case of non-homogeneity. Suppose that all parallel connected components are identical, Eq. (16.11) is rewritten as

$$ {u}_{parallel}(z)={\left[\left(1-{A}_{ij}\right)+{A}_{ij}{z}^{W_{ij}}\right]}^{x_i}. $$
(16.12)

Using the binomial theorem the power representation of Eq. (16.12) can be expanded in a sum of the form

$$ \begin{array}{c}{u}_{parallel}(z)={\displaystyle \sum_{k=0}^{x_i}\left(\begin{array}{c}\hfill {x}_i\hfill \\ {}\hfill k\hfill \end{array}\right)}{\left({A}_{ij}{z}^{W_{ij}}\right)}^k{\left(1-{A}_{ij}\right)}^{x_i-k}\\ {}={\displaystyle \sum_{k=0}^{x_i}\left(\begin{array}{c}\hfill {x}_i\hfill \\ {}\hfill k\hfill \end{array}\right)}{A}_{ij}^k{\left(1-{A}_{ij}\right)}^{x_i-k}{z}^{k{W}_{ij}}\\ {}={\displaystyle \sum_{k=0}^{x_i}{\alpha}_{ik}}{z}^{k{W}_{ij}}\end{array} $$
(16.13)

with

$$ {\alpha}_{ik}= binm\left(k,{A}_{ij},{x}_i\right)=\left(\begin{array}{c}\hfill {x}_i\hfill \\ {}\hfill k\hfill \end{array}\right){A}_{ij}^k{\left(1-{A}_{ij}\right)}^{x_i-k} $$
(16.14)

and where the binomial coefficients are given by

$$ \left(\begin{array}{c}\hfill {x}_i\hfill \\ {}\hfill k\hfill \end{array}\right)=\frac{x_i!}{k!\left({x}_i-k\right)!}. $$
(16.15)

That means that the u-function or the polynomial z-representation of each parallel subsystem consisting of x i non-identical components (heterogeneous case) can be computed according to Eq. (16.11). If all x i or a specific number x n of components are identical, some simplification can be made using the binomial theorem according to Eq. (16.13).

16.6.2 η-Operator: Ushakov Transform of Series Configurations

In order to determine the u-function of a system consisting of s elements or components connected in series, the η-operator is applied according to

$$ {u}_{series}(z)=\eta \left({u}_1(z),{u}_2(z),\dots, {u}_s(z)\right). $$
(16.16)

In the case of series connected components, the element with the minimal or least performance becomes the bottleneck of the system. This system is the decision maker about the total system performance or productivity. Therefore the structure or the performance function f is given by

$$ f\left({W}_1,{W}_2,\dots, {W}_s\right)= \min \left({W}_1,{W}_2,\dots, {W}_s\right). $$
(16.17)

For a pair of components u 1 (z) and u 2 (z) connected in series and according to Eq. (16.17) the resulting u-function of the system u series (z) is given by

$$ \begin{array}{c}{u}_{series}(z)=\eta \left({u}_1(z),{u}_2(z)\right)\\ {}=\eta \left({\displaystyle \sum_{i=1}^n{P}_{1i}{z}^{W_{1i}}},{\displaystyle \sum_{j=1}^m{P}_{2j}{z}^{W_{2j}}}\right)\\ {}={\displaystyle \sum_{i=1}^n{\displaystyle \sum_{j=1}^m{P}_{1i}{P}_{2j}{z}^{f\left({W}_{1i},{W}_{2j}\right)}}.}\end{array} $$
(16.18)

Replacing the structure function according through Eq. (16.17), the u-function of two series connected components will be given by

$$ {u}_{series}(z)={\displaystyle \sum_{i=1}^n{\displaystyle \sum_{j=1}^m{P}_{1i}{P}_{2j}{z}^{\min \left({W}_{1i},{W}_{2j}\right)}}}. $$
(16.19)

16.6.3 Ushakov Transform of Series-Parallel Systems: (Γ, η)

As mentioned previously, in order to determine the u-function of the entire series-parallel MSS both composition operators Γ and η have to be performed respectively like depicted in Fig. 16.7.

Fig. 16.7
figure 7

Determination of the u(z)-function for the entire series-parallel system

Full size image

In Fig. 16.7 the individual s parallel systems consisting of non-identical binary state components will be replaced by single elements having multi-states u-functions (u 1 (z) … u s (z)) determined by the Γ-composition operator according to Eq. (16.11). Afterwards the η-composition operator will be applied on the resulting system consisting of the s-multi-states components connected in series which leads to the u-function u sys (z) of the entire system that would be computed with the help of Eq. (16.16) like in the following

$$ \begin{array}{c}{u}_{sys}(z)=\eta \left({u}_1(z),{u}_2(z),\dots, {u}_s(z)\right)\\ {}=\eta \left({\displaystyle \sum_{k=0}^{x_1}{\alpha}_{1k}{z}^{k{W}_{1j}}},{\displaystyle \sum_{k=0}^{x_2}{\alpha}_{2k}{z}^{k{W}_{2j}}},\dots, {\displaystyle \sum_{k=0}^{x_s}{\alpha}_{sk}{z}^{k{W}_{sj}}}\right)\\ {}={\displaystyle \sum_{m=0}^M{\delta}_m}{z}^{W_m}.\end{array} $$
(16.20)

δ m and W m are real numbers determined according to Eq. (16.19). The evaluation of the probability that the entire system satisfies a specific level of performance W 0 is given by the sum over all coefficients δ m that correspond to a nominal performance W m greater or equal W 0 . The resulting sum represents the availability A sys (X) corresponding to the series-parallel system, whose design is represented by X and is given by

$$ {A}_{sys}\left({W}_0\right)= \Pr \left({W}_m\ge {W}_0\right)={\displaystyle \sum_{W_m\ge {W}_0}{\delta}_m}. $$
(16.21)

Given K different demand levels represented by W k 0 where k = 1…K, which should be satisfied over different operation intervals T k the total availability A sys (X) of the system is obtained by the sum of the instantaneous availabilities corresponding to the different demand levels divided by the total operation or mission time and is given by

$$ \begin{array}{c}{A}_{sys}(X)=\frac{1}{T}{\displaystyle \sum_{k=1}^K{\displaystyle \sum_{W_m\ge {W}_0^k}{\delta}_m{T}_k}}\\ {}=\frac{1}{{\displaystyle \sum_{k=1}^K{T}_k}}{\displaystyle \sum_{k=1}^K{\displaystyle \sum_{W_m\ge {W}_0^k}{\delta}_m{T}_k}}.\end{array} $$
(16.22)

16.7 Tuning Parameters and Experimental Results: Validation

The simple genetic algorithm with some modifications in the context of its operators was used in this work. The algorithm has been implemented in Matlab which provides uniform pseudorandom number generators and powerful matrix and vector operations and allows great visualization and graphical representation. The three different models, which have been analyzed in the homogeneous case in a previous publication [10, 18], have been treated again in the heterogeneous case in order to show the effect of mixing of components on investment cost reduction and hence getting safer systems subject to CCFs for lower cost than the homogeneous case and for same given constraint factors. The used components are assumed to be binary state (perfect working or totally failing). The models and data, as mentioned previously, have been taken from [5–7], are listed below:

  • Lev4_4_6_3

  • Lev5_5_9_4

  • Ouz6_4_11_4

For a brief understanding of the decoding of the denotation of the individual models it is referred to Ouzineb in [5–7]. The purchasing price, reliability and nominal performance capacity for the components corresponding to the upper listed systems are supposed to be known and can be retrieved from a list with technical data (excel sheets).

The algorithm starts by retrieving the data of the analyzed problem from the appropriate sheet and by random generating a so called initial population of size Pop size that has been set to 100 chromosomes. The integer encoded chromosomes constituting the initial population have been generated in such a way that generated solutions that do not satisfy the given availability constraint are rejected and replaced by new acceptable ones in order to get a high qualitative start population. The constituting individuals or chromosomes have been created using a weighted pseudo random number generator which generates numbers between zero and the total number of components allowed in each subsystem, which have been set to ten. The probability of occurrence of 0 has been varied between 0.7 and 0.9 during the random chromosome generation process depending on the length of the chromosome corresponding to the analyzed problem. This limitation to the number of components allowed within a subsystem in addition to the rejection of non-feasible solutions. Furthermore a weighted generation of chromosome would limit the area that will be explored within the search space and should accelerate the search procedure towards convergence.

After evaluating and ranking populations (cost and availability estimation) chromosomes are selected to mate, recombine and finally mutate in order to build new offsprings that complete the next population of size Pop size . This genetic procedure repeats until the predefined maximal number of generations N rep is reached (Termination criterion). After completing each population through crossover and mutation the population will be checked for multiplicity before evaluation by term of fitness function and new chromosomes would be generated to replace the chromosomes that appear more than once and have therefore been removed. This procedure of inserting new chromosomes to the population is compared to the act of inserting new genetic materials and may lead to new search areas that have not been explored or searched before and may accelerate the convergence speed. Figures 16.8 and 16.9 show the results of one run of the GA over the Lev4-(4/6)-3 model (heterogeneous case) data by predefined availability constraints of A0 = 0.900 and A 0  = 0.960, and Fig. 16.10 shows the run of the GA over the Ouz6_(4/11)_4 by an availability constraint of A 0  = 0.99. The different plots show the evolution progress outgoing from the random initial population up to the predefined maximum number of generations. The best result (Cost—upper plots and Availability—lower plots), received after each genetic cycle, is depicted.

Fig. 16.8
figure 8

Results of the genetic algorithm run of the heterogeneous case (Levitin—model containing four subsystems, availability constraint A 0  = 0.900 and 300 generations). The cost-generation and availability-generation curves dependencies are depicted on the left-hand side. The cost-time and availability-time dependencies are depicted on the right-hand side

Full size image
Fig. 16.9
figure 9

Results of the genetic algorithm run of the heterogeneous case (Levitin—model containing four subsystems, availability constraint A 0  = 0.960 and 300 generations). The cost-generation and availability-generation curves dependencies are depicted on the left-hand side. The cost-time and availability-time dependencies are depicted on the right-hand side

Full size image
Fig. 16.10
figure 10

Results of the genetic algorithm run of the heterogeneous case (Ouzineb—model containing six subsystems, availability constraint A 0  = 0.990 and 300 generations). The cost-generation and availability-generation curves dependencies are depicted on the left-hand side. The cost-time and availability-time dependencies are depicted on the right-hand side

Full size image

The time needed to find the best solution (convergence time) depends on the quality of the start population and on how the selected fittest chromosomes evolve throughout crossover and mutation.

On the left-hand side of Figs. 16.8, 16.9 and 16.10 (heterogeneous case) the best solution found (Top: cost value, bottom: availability value for found cost) during each generation is plotted against generation number whereas the same plots are represented on the right hand side against algorithm processing time. On the head of each plot the best chromosome or system design corresponding to the optimal (minimal) found cost subject to the given availability constraint is represented. In the context of the plots the generation number and convergence time are reported for which the best result has been identified.

Figures 16.11, 16.12 and 16.13 represent the homogeneous case of the heterogeneous problems analyzed successively in Figs. 16.8, 16.9, and 16.10. These figures have been included in order to show that through mixing of components lower or better system costs (Lev4-(4/6)-3—Model) can be reached in comparison to the homogeneous case subject to the same availability constraint. In the analyzed Ouz6_(4/11)_4 model no better cost results have been achieved but at least the same results as in the homogeneous case have been reached. One additional reason is to show that with the GA approach analyzed in this paper it was also possible to get the same results got with the hybridized GA + TS algorithm implemented in [5, 7]. This fact shows the effectiveness and accuracy of the GA approach discussed in this work since with the GA implemented in [6, 7] different results have been achieved.

Fig. 16.11
figure 11

Results of the genetic algorithm run of the homogeneous case for the same upper system (Levitin—model containing four subsystems) and subject to the same availability constraint A 0  = 0.900. As one can see in the heterogeneous case a better cost factor can be reached (5.423) than the homogeneous case (5.986) due to the fact that components have been mixed

Full size image
Fig. 16.12
figure 12

Results of the genetic algorithm run of the homogeneous case for the same upper system (Levitin—model containing four subsystems) and subject to the same availability constraint A0 = 0.960. As one can see in the heterogeneous case a better cost factor can be reached (7.009) than the homogeneous case (7.303) due to the fact that components have been mixed

Full size image
Fig. 16.13
figure 13

Results of the genetic algorithm run of the homogeneous case for the same upper system (Ouzineb—model containing six subsystems) and subject to the same availability constraint A0 = 0.990. As one can see in both cases the same cost factor has been reached (12.764) but definitely for less computation time in the homogeneous case

Full size image

The best test results got within 15 successive runs of the genetic algorithm over the different models mentioned previously are shown in Table 16.1. Computing and convergence time for best achieved results are also included in the same table and serve to show how well the genetic algorithm customized for the heterogeneous case is performing in term of convergence speed, which can also be seen in the results depicted in Figs. 16.8, 16.9 and 16.10.

Table 16.1 Computation results of the homogeneous and the heterogeneous case using the GA
Full size table

16.8 Conclusion and Future Works

Based on the facts and experimental results shown in the previous section and resumed in Table 16.1 for the different analyzed models, it can be recognized and concluded that the GA algorithm for heterogeneous series-parallel multi-states systems implemented in this work was performing in a great and efficient manner in term of convergence speed towards optimal results being expected and represented by Ouzineb in [5–7] and obtained by the hybrid GA + TS metaheuristic approach, in addition to the high accuracy in determining or finding the optimal solution (minimal system cost). And since genetic searching seems like searching for a small fish in a big ocean one small disadvantage or drawback is the standard one known in (heuristic) genetic approaches and that is resumed in the fact that the best optimal solution is not guaranteed or ensured in each run due to the limitation of the maximum number of iterations that may result, that some regions of the search or solution space that may include the optimal solution remains unexplored or out of reach.

The genetic approach implemented in this paper represents a very effective means in solving single objective constrained redundancy design problems like the complex heterogeneous one discussed in this work.

One of our future intentions is to tune genetic algorithms with local search algorithms targeting to increase the level of search accuracy. This kind of tuning is referred to in the literature as hybridization of genetic global searching algorithms.