Active Redundancy Allocation in Complex Systems by Using Different Optimization Methods

Abstract

This paper addresses the issue of optimal allocation of spare modules in complex series-parallel redundant systems in order to obtain a required reliability under cost constraints. To solve this optimization problem, an analytical method based on the Lagrange multipliers technique is first applied. Then the results are improved by using other optimization methods such as an evolutionary algorithm and an original fine tuning algorithm based on the idea of hill climbing. The numerical results highlight the advantage of combining analytical approaches with fine tuning algorithms in case of very large systems. By using such a combined technique, better solutions are obtained than those given by classic heuristic search algorithms.

1 Introduction

The reliability design of a complex system is one of the most studied topics in the literature. The problems mainly refer to the kind of solution (reliability allocation and/or redundancy allocation), the kind of redundancy (active, standby, etc.), the type of the system (binary or multi-state), the levels of the redundancy (multi-level system or multiple component choice) etc. All these issues have practical applications and provide a good sphere for further research. An excellent overview of all these problems can be found in [1,2,3,4].

According to the decision variables [3, 4], a reliability optimization problem may belong to the following types: (a) reliability allocation, when the decision variables are component reliabilities, (b) redundancy allocation, when the variable is the number of component units, and (c) reliability-redundancy allocation, when the decision variables include both the component reliabilities and the redundancies.

In this paper we address the problem of redundancy allocation in which the number of redundant units in a series-parallel reliability model is the only decision variable. Unfortunately, as presented in [5], this is a problem that falls into the NP-hard category.

We have limited ourselves to the binary systems in which each component is either operational or failed and, regarding the kind of redundancy, we focus only on the active spares.

To solve this optimization problem of redundancy allocation, more methods or techniques can be applied, such as intuitive engineering methods [6], heuristic search algorithms [7,8,9,10], analytical methods based on Lagrange multipliers [11,12,13], or dynamic programming [14]. Other metaheuristic methods based on genetic algorithms are also appropriate [15,16,17,18].

2 Notations and Preliminary Considerations

Reliability is the probability that a component or a system works successfully within a given period of time. A series-parallel model is a reliability model corresponding to a redundant system consisting of basic components and other active spare components.

The following notations are used throughout the paper: n is number of components in the non-redundant system or number of subsystems in the redundant system, as the case; $r_{{{\kern 1pt} i}}$ is the reliability of a component of type i, i ∈ {1, 2, …, n}, for a given period of time; $c_{{{\kern 1pt} i}}$ is the cost of a component of type i; $R_{ns}$ is the reliability of the non-redundant system (system with series reliability model); $k_{{{\kern 1pt} i}}$ is the number of components that compose the redundant subsystem i, i ∈ {1, 2, …, n}; $R_{{{\kern 1pt} i}}$ is the reliability of subsystem i (subsystem with parallel reliability model); $C_{{{\kern 1pt} i}}$ is the cost of subsystem i; $R_{rs}$ is the reliability of the redundant system (system with series-parallel reliability model); $C_{rs}$ is the cost of the redundant system; R^* is the required reliability level for the system; C^* is the maximum accepted cost for the system.

It is assumed that: each component in the system is either operational or failed, i.e. a binary system, a spare is identical with the basic component, and the events of failure that affect the components of the system are stochastically independent.

3 Problem Description

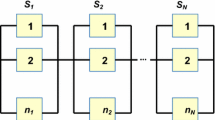
Let us consider a non-redundant system composed of n basic components for which the reliability model is a series one as presented in Fig. 1. For complex systems with a large number of components, the reliability of the system without redundancy is often quite low. To reach a required reliability, spare components are added so that the reliability model for this redundant system is a series-parallel one as presented in Fig. 2.

Fig. 1.

Series reliability model for a non-redundant system

Fig. 2.

Series-parallel reliability model for a redundant system with spare components

Typically, in this allocation process the criterion is reliability, cost, weight or volume. One or more criteria can be considered in an objective function, while the others may be considered as constraints [3, 4, 19]. From a mathematical point of view, one must solved an optimization problem of an objective function with constraints.

In this work, we address the issue of maximizing system reliability within the cost constraint. Thus, one must maximize the reliability function $R_{rs} = \prod\limits_{i = 1}^{n} {R_{i} ,}$ with the restriction of cost $\sum\limits_{i = 1}^{n} {C_{i} \le C^{ * } .}$

In case of large systems, to master the complexity of the problem, we choose to first apply an analytical method based on Lagrange multipliers in order to quickly obtain an approximate solution, and then, this approximate solution is improved by using other optimization methods such as an evolutionary algorithm and an original fine tuning algorithm. To check the results, we have also implemented some heuristic algorithms, as presented in the following section.

4 Heuristic Search Algorithms

For the reliability model presented in Fig. 2, the following equation is valid: $R_{rs} \left( t \right) = \prod\limits_{i = 1}^{n} {R_{i} \left( t \right) \le \mathop { \hbox{min} }\limits_{i} \left\{ {R_{i} \left( t \right)} \right\}.}$ Starting from this observation, the following two heuristic methods are applied to solve this optimal allocation problem.

Algorithm 1:

This is a greedy algorithm given by Misra [7] that tries to make an optimal choice at each step. Thus, starting with the minimum system design presented in Fig. 1 ($k_{{{\kern 1pt} i}} ,i \in \left\{ { 1,{ 2}, \, \ldots ,n} \right\}$), the system reliability is increased by adding one component to the subsystem with the lowest reliability. This process is repeated as long as the cost constraint is met.

Algorithm 2:

This algorithm given by Rajendra Prasad, Nair, and Aneja [9] ensures an acceleration of the allocation process. The basic idea is that the subsystem with the highest reliability will have the smallest number of components, and the least reliable subsystem, the greatest number of components. Thus, starting with the system in a non-redundant form, the reliability is increased by adding one component to each subsystem (a row allocation) as long as the cost constraint is met. For the most reliable subsystem, this is the final allocation. The process of allocation continues in the same manner with the other subsystems, until no allocation is possible any longer.

As presented in Sect. 8, these heuristic algorithms are useful in many cases, but sometimes they do not give good solutions. Therefore, we choose to apply first an analytical method based on Lagrange multipliers as presented in the following section.

5 Analytical Approach

As the spares are identical with the basic component, for the series-parallel reliability model presented in Fig. 2, the reliability function can be expressed by the equation:

$$ R_{rs} = \mathop \prod \limits_{i = 1}^{n} \left( {1 - (1 - r_{i} )^{{k_{i} }} } \right) . $$

(1)

We have to determine the values $k_{{{\kern 1pt} i}}$ that maximize the function $R_{rs}$ with the cost constraint:

$$ \mathop \sum \limits_{i = 1}^{n} c_{i} k_{i} \le C^{ * } . $$

(2)

Based on (1) and (2), the following Lagrangian function results:

$$ L\left( {k_{1} ,k_{2} , \ldots ,k_{n} ,\lambda } \right) = \mathop \prod \limits_{i = 1}^{n} \left( {1 - (1 - r_{i} )^{{k_{i} }} } \right) +\uplambda\left( {\mathop \sum \limits_{i = 1}^{n} c_{i} k_{i} - C^{ * } } \right), $$

(3)

where λ is the Lagrange multiplier.

Thus, instead of maximizing the function $R_{rs}$ given by (1) within the cost restriction (2), we have to maximize the Lagrange function given by (3) without constraints. For this propose, a system with partial derivatives must be solved, where $\partial L/\partial k_{i} = 0,\,\;i \in \{ 1,\,2,\, \ldots ,\,n\}$, and $\partial L/\partial \lambda = 0$. But the resulting system of algebraic equations is very difficult to solve because of the products that appear. For this reason, we use another way of expressing the reliability of the system, as presented as follows.

The reliability of a system can be expressed by the reliability function (R) or the non-reliability function (F = 1 − R), that means, by a point within the unit segment [0, 1]. As presented in Fig. 3, this value can be uniquely identified by a point on the diagonal of a square with the side length equal to the unit (denoted by P).

Fig. 3.

Another way of expressing the reliability

The point P in Fig. 3 is uniquely identified by the angle θ, and thus by $x = \tan (\theta )$. Related to the two reliability indicators, R and x, the following equations are valid: $x = (1 - R)/R = 1/R - 1$, and R = 1/(x + 1). Notice that, if R →1 then x → 0, and if R → 0 then x → ∞.

Let us now consider a system with a series reliability model, composed of n modules of reliability given by $x_{{{\kern 1pt} i}}$. The system reliability, denoted by $x_{S(n)}$, can be expressed by the following equation:

$$ x_{{{\text{S}}\left( n \right)}} = \frac{1}{{R_{S\left( n \right)} }} - 1 = \frac{1}{{\prod\limits_{i = 1}^{n} {\frac{1}{{x_{i} + 1}}} }} - 1 = \prod\limits_{i = 1}^{n} {\left( {x_{i} + 1} \right)} - 1. $$

(4)

This relationship is rather complicated, but for the values $x_{i} \ll 1,\;i \in \{ 1,\;2,\; \ldots ,\;n\} ,$ the products that are formed can be neglected and the reliability of the system can be approximated with good accuracy by the equation $x_{S\left( n \right)} \approx \sum\limits_{i = 1}^{n} {x_{i} .}$ In the same manner, one show that for a parallel reliability model with n components, when $x_{i} \ll 1,\;i \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$ the reliability of the redundant system denoted by $x_{P(n)}$ can be approximated with good accuracy by $x_{P(n)} \approx \prod\limits_{i = 1}^{n} {x_{i} }$.

In this form of representation for the system reliability, the optimization problem assumes the maximization of the reliability function $x_{rs} = \mathop \sum \limits_{i = 1}^{n} x_{i}^{{k_{i} }}$ with the cost constraint (2). In this case, the Lagrangian function is:

$$ L\left( {k_{1} ,k_{2} , \ldots k_{n} ,\lambda } \right) = \mathop \sum \limits_{i = 1}^{n} x_{i}^{{k_{i} }} +\uplambda\left( {\mathop \sum \limits_{i = 1}^{n} c_{i} k_{i} - C^{ * } } \right) . $$

(5)

By applying the partial derivatives, and using the notations $\alpha_{i} = 1/\ln \,x_{i}$ and $\beta_{i} = \alpha_{i} \left( {\ln c_{i} + { \ln }\,( - \alpha_{i} )} \right)$, $i \in \{ 1,\;2,\; \ldots ,\;n\}$, the system solution of algebraic equations is:

$$ \lambda = e^{\,\gamma } ,{\text{ where }}\gamma = {{\left( {C^{*} - \sum\limits_{i = 1}^{n} {c_{i} {\kern 1pt} \beta_{i} {\kern 1pt} } } \right)} \mathord{\left/ {\vphantom {{\left( {C^{*} - \sum\limits_{i = 1}^{n} {c_{i} {\kern 1pt} \beta_{i} {\kern 1pt} } } \right)} {\sum\limits_{i = 1}^{n} {c_{i} {\kern 1pt} \alpha_{i} {\kern 1pt} } }}} \right. \kern-0pt} {\sum\limits_{i = 1}^{n} {c_{i} {\kern 1pt} \alpha_{i} {\kern 1pt} } }},{\text{ and}}\,k_{i} = \alpha_{i} \ln \lambda + \beta_{i} ,\,i = 1,\;2,\; \ldots ,\;n $$

(6)

Note that, this analytical result is valid only if $\alpha_{i} < 0$ (i.e. $r_{i} > 0.5$).

The only impediment for solving the problem remains that the values k_i obtained by applying (6) are real values, and the allocation is, by its nature, a discrete problem. Therefore, it is necessary to determine the optimal allocation in integer numbers starting from the actual solution.

An approximate solution results by adopting the integers closest to the real values. But, in this case, it is possible that the new solutions for k_i, $i \in \{ 1,\;2,\; \ldots ,\;n\}$, not longer satisfy the cost constraint. Starting from the value of the Lagrange multiplier λ given by (6), a searching process is carried out in a neighborhood of this value in order to obtain a better approximate solution for k_i, $i \in \{ 1,\;2,\; \ldots ,\;n\}$, while satisfying the cost constraint. Unfortunately, this approximate solution is not accurate enough. Consequently, this approximate solution is further improved by applying other methods of refining the search process, as shown in the following sections.

As mentioned in Sect. 1, regarding the kind of redundancy, in this work we have limited ourselves to the active spares, because for the case of passive spares the Lagrangian function is more complicated and the system of partial derivatives is very difficult to solve. But the following optimization methods may be tailored to cover this case as well, or better, to cover the most general case in which some subsystems may have active spares and the others, passive spares.

6 Evolutionary Algorithm

Evolutionary algorithms are optimization methods inspired by natural selection. The search is made in parallel, with a population of potential solutions, also known as individuals or chromosomes, which are randomly initialized. Each chromosome is associated with a value determined by the fitness function that describes the problem to be solved. The evolution of the population is based on the successive application of genetic operators such as selection, which gives the better individuals more changes to reproduce, crossover, which combines the genetic information of two parents and creates offspring, and mutation, which may slightly change a newly generated child in order to introduce new genetic information into the population. The search progresses until a stopping criterion is met.

In our case, the encoding of the problem is real-valued, and each chromosome has n real genes, corresponding to k_i. The domain of the genes [1, k_max] depends on the problem. k_max is the maximum estimated value for any k_i.

The fitness function is the expression in (1). Since the genes are real-values and k_i are integer numbers, the gene values are rounded in order to convert them into integers.

Since we have a constraint, one method of handling it is to add a penalty to the fitness function of the chromosomes that do not satisfy the constraint. However, this can have a very negative impact on the quality of the solution, because, especially in the beginning, very few or no individuals may satisfy the cost constraint. This can likely lead to very poor local optima, or may cause the algorithm to fail altogether in finding any solution.

The method adopted in the present work was to repair the chromosomes that violate the cost constraint, i.e. randomly removing one redundant component at a time, until the remaining components satisfy the constraint. Each subsystem must have at least one component, so only redundant components may be removed.

The selection method is tournament selection with two individuals. We use arithmetic crossover and mutation by gene resetting. As a stopping criterion, both fitness convergence and a fixed number of generation were tried. It was found that after a small number of generation, the values of all the fitness functions become very close, but these small differences actually make a big difference for the quality of the final result. Thus, a fixed number of generations was chosen as a stopping criterion.

Several variants of genetic evolution were evaluated:

• the typical method that generates offspring from parents, creates a complete new generation and then the new generation replaces the old one;

• elitism, where the best individual of a generation is directly copied into the next one, and that guarantees that the best solution at one time is never lost;

• steady state evolution, where from the current population of size s a new population of size s is generated by regular selection, crossover and mutation, but the new population does not directly replace the old one; instead, the two populations are merged, and from the resulting population of size 2s, the best s individuals are selected to form the next generation;

• optimized offspring generation, where after a child has been created by regular selection, crossover and mutation, it is not directly inserted into the next generation; instead the individual with the best fitness out of the mother, the father and the child is inserted into the next generation.

From the experiments conducted for large problem instances, it was found that the optimized offspring generation combined with elitism provided the best results.

7 Pairwise Hill Climbing

An evolutionary algorithm has a good chance of find the global optimum, but it often finds a solution within the neighborhood of the optimum. On the other hand, the analytical method presented in Sect. 5 provides an approximate solution because of the conversion of the real solution into an integer one. In both situations, it is important to fine tune the initial approximation, it order to find a better solution, closer or equal to the actual optimum.

The typical hill climbing procedure starts from an initial solution and generates its neighbors in the problem space. The best neighbor is identified and if the value of its objective function is better than the one of the initial solution, the neighbor becomes the current solution and the same process is repeated until no neighbor is better that the current (and final) solution.

However, for the problems we study, the above algorithm cannot be applied because of the existence of the constraint. The approximate solvers usually find good, but sub-optimal solutions, which all have a cost very close or equal to C*. Therefore, the classic hill climbing procedure cannot increase reliability further by adding, for example, an additional component, because the cost constraint would be violated.

In order to increase reliability at fairly the same total cost, a few, e.g. usually 1–2, components need to be removed from one or a few redundant subsystems, while simultaneously a few components need to be added to other few redundant subsystems.

Therefore, beside the addition of a component, a swap operation must also be considered when generating the neighbors of an allocation.

In some situations, the initial solution may not be in a direct neighborhood of the optimum, and thus solely relying on the addition of new components, which is the only way to increase reliability, in not sufficient.

Consequently, we propose an original fine tuning algorithm, Pairwise Hill Climbing, presented in Pseudocode 1, based on the main idea of hill climbing, but with several heuristics that make it more appropriate for our class of problems.

As the pseudocode shows, the successive allocations, starting from n + 2 initial points, are added to a priority queue, which helps to first expand the most promising solution. However, if the corresponding subtree yields a suboptimal solution, other parts of the tree can be used to find a better one. From the practical point of view, the search may be limited to a maximum number of levels in the tree l_max and to a maximum number of solutions taken from the queue s_max.

8 Experimental Results

In this section, we present the results of the previously described methods for three problems, designed in such a way as to make the optimization more difficult. Thus, for some components, we have chosen values so that, for a very similar reliability, the cost is very different. For example, in Problem 3, as highlighted by bold face in Table 1, the components with order number 4 and 43 have quite similar reliabilities (0.74 and 0.75, respectively), but very different cost values (49 and 4, respectively). The same remark holds for components with order number 39 and 44. The parameters of the components are presented in Table 1. For all three problems, n = 50.

Table 1. The optimization problems considered in the experimental study

The obtained results are presented in Table 2.

Table 2. The results obtained (R_rs, Ef, C_rs) with different optimization methods

Methods 1 and 2 are the heuristic methods presented in Sect. 4.

Method 3 is the analytical method from Sect. 5 where the real-valued coefficients are converted into integers by rounding them down, i.e. $k_{i} = \left\lfloor {k_{i}^{r} } \right\rfloor$. This method obviously provides suboptimal results, but it can be a good starting point for solution improvement, because its solution has a good chance of being in the neighborhood of the optimal one.

Method 4 involves an additional heuristic search starting from the initial estimates of the analytical method.

Method 5 uses the same estimates given by the analytical method, but employs the Pairwise Hill Climbing (PHC) search presented in Sect. 7. For PHC, the parameters used are l_max = 20 and s_max = 1000.

Method 6 only uses the Evolutionary Algorithm (EA) described in Sect. 6 with a large number of generations, i.e. 10000. In all cases, the other parameters of the EA are the following: the population size is 100, the crossover rate is 0.9, the mutation rate is 0.1. The search range for this method is 1–15 for each gene, i.e. k_i. Since the EA is nondeterministic, 10 runs for each configuration were performed and the best result was reported.

Method 7 uses the EA with a smaller number of generations, i.e. 1000, and its solution is used as the initial point for the PHC search.

Finally, method 8 uses the solution of the analytical method to define the search range for the EA genes. The range of a gene is the suboptimal k_i ± 2, but ensuring that the lower limit remains at least 1.

Beside the actual reliability value of the redundant system R_rs, we included an additional, more intuitive measure of the results, namely the redundancy efficiency defined as: Ef = (1 − R_ns)/(1 − R_rs). The efficiency shows how many times the risk of a failure decreases for the redundant system, compared to the baseline, non-redundant one. For example, at the first glance, it may not seem to be a big difference between two reliability values of 0.88 and 0.98, e.g. for Problem 2. However, the efficiency shows us that the risk of a failure decreases almost 6 times.

As one can notice, the first two heuristic methods give very different results for all the three problems. This highlights the difficulty of the optimization problems we considered.

The first observation is that in all three cases, the best results are obtained by the hybrid Method 5. The results of the analytical method are a very good starting point for the PHC, because the component allocation is likely less than the optimal one and a procedure based on the hill climbing idea can easily add new components and thus improve the objective function.

Conversely, it is more difficult for the PHC to improve more extensively the EA solution, because that is already near the maximum cost, and therefore some components need to be removed in order to add others, while keeping the solution in the feasibility region, i.e. satisfying the cost constraint. As it was seen, such refining does not only address simple component swaps, but sometime, more components should be removed from or added to a subsystem, and the changes to be made involve not only two subsystems, but often more.

It is somewhat surprising that the EA does not seem capable of finding the optimum, even with a very large number of generations and even starting from an estimated neighborhood of the optimal solution. This is because the problem has many local optima with the maximum cost, and the genetic search procedure is also affected by the fact that infeasible solutions are repaired, i.e. modified outside the influence of the genetic operators, by randomly removing components until the cost constraint is met. This repairing procedure is however critical to the convergence of the EA; if one uses penalties for constraint violation, usually the EA does not find a solution at all, or finds a very poor one. Thus, a different repairing procedure may be needed, where components are not removed at random, but some problem specific information is used in order to find the most appropriate change that can help the optimization process.

It is also important to discuss the execution times of these methods. The first four techniques are very fast, because they are based on the application of formulas or a linear search in a very limited range, comparable with n. The average execution times for ten runs for each problem using a computer with a 4-core 2 GHz Intel processor and 8 GB of RAM are given as follows: Method 5 – 1061.98 ms, Method 6 – 45,603.83 ms, Method 7 – 6,877.77 ms, Method 8 – 4252.38 ms.

Therefore, Method 5, which gives the best results, is also the fastest.

In Table 3, the best solutions are presented for each of the three problems under study.

Table 3. The best solutions found, i.e. the k_i values and total cost for the best R_rs

9 Conclusions

In this paper several optimization methods where presented for the problem of maximizing the reliability of a redundant system, with a series-parallel reliability model, in the presence of cost-related constraints. Beside domain-specific heuristics and an analytical solution based on Lagrange multipliers, other general techniques were applied: an evolutionary algorithm with chromosome repairs meant to satisfy the constraint and an optimized offspring generation, and also a original algorithm based on the hill-climbing idea, but using swaps and a priority queue in addition to the incremental greedy improvements, in order to fine tune the approximate solutions found by other methods.

Our study shows that the hybrid methods provided the best results, especially the combination of the analytical method with the original Pairwise Hill Climbing algorithm, which is also the fastest.

As future directions of investigation, other optimization methods will be tried, and other variants of the problem will be addressed, for example, the issue of passive redundancy allocation and the converse problem of minimizing the cost while having a minimum imposed reliability, as a means to further verify the optimality of the solutions.