Keywords

1 Introduction

High-level approaches to big data analytics such as Hadoop MapReduce [26] or Apache Spark [1] are often inspired by bulk synchronous parallelism (BSP) [25] a model of scalable parallel computing. In this context, scalable means that the number of processors of the parallel machines running BSP programs could range from a few to several thousand cores or more. Bulk Synchronous Parallel ML (BSML) [19] is a pure functional library for the multi-paradigm language OCamlFootnote 1. BSML embodies the principles of the BSP model, at a higher level than libraries such as the BSPlib library [14] and can easily express patterns [13, 17] (or algorithmic skeletons [4]) of frameworks such as MapReduce or Spark.

Why3  [2, 3] is a framework for the deductive verification of programs. It provides a specification and programming language named WhyML which can be used directly or as an intermediate language for other tools to verify C [15], Java [9], Ada or Rust [7] programs. The framework itself also provides mini-C and mini-Python front-ends. Why3 generates verification conditions to be verified by external provers. A strong point of Why3 is that it targets a large variety of provers including Alt-Ergo [5], Z3 [21] and CVC5. Correct-by-construction OCaml code can be extracted from WhyML.

Our contributions are the formalization of BSML and its standard library in WhyML and its use in the specification and verification of a scalable parallel function for the maximum prefix sum problem, using map and reduce skeletons.

The remainder of the paper is organized as follows. In Sect. 2, we give an overview of Why3 and WhyML, including its limitations when dealing with higher-order functions. We introduce functional bulk synchronous parallel programming with BSML in Sect. 3. Section 4 is devoted to the formalization of the primitives of BSML and its application to the specification and verification of the BSML standard library. We consider the specification, development and verification of a small application: a parallel function that solves the maximum prefix sum problem in Sect. 5. We discuss related work in Sect. 6 and conclude in Sect. 7.

The set of Why3 modules is called WhyBSML and is available at:

https://doi.org/10.5281/zenodo.8166092.

2 An Overview of Why3

2.1 Specifying and Verifying Functional Programs with Why3

Why3 is often use in the verification of imperative programs. As BSML is purely functional and BSML applications mostly used the functional features of OCaml, we focus here on the verification of functional programs. This focus is also a necessity as we will explain in the next subsection.

In addition to its core features, Why3 provides a standard library with data structures such as lists and arrays, as well as basic arithmetic logic with integers and reals. We illustrate this short introduction with the example of Fig. 1. Note that this figure presents a pretty-printed version of the actual code, for example \(\mathtt {/\backslash }\) is rendered as \(\wedge \), \(\texttt {->}\) as \(\rightarrow \), ’a as \(\alpha \), etc.

WhyML developments are organized in modules. The example defines two modules: Max (lines 1–8) and MaxList (lines 10-32). Defined modules can be used in other modules with the keyword. We use some modules of the Why3 standard library: about integer arithmetic (lines 2 and 11) and , , for basic definitions and facts about lists (lines 12–14).

The module Max is devoted to the specification and definition of a function max which returns the larger of two integers. This function does not have any pre-condition but its post-conditions are introduced by the keyword .

Assuming the file maximum.mlw contains only the module , verifying that satisfies its preconditions using the prover Alt-Ergo can be done with the following command:

figure i

and the tool answers indeed satisfies its contract:

figure k

In our example, most of the functions to verify are recursive and often manipulate lists. Lines 19–31 are an example of a recursive function that takes a list of integers and returns the highest value the list contains.

Fig. 1.
figure 1

A WhyML Example

Full size image

To write the contract of function maximum, we use the notation l[i] to access the \(i^\text {th}\) element of list l. This notation is defined as a binary function in line 17 and is actually an alias for the nth function of the standard library. Note that this definition is introduced by the keyword instead of the keyword (as in line 4). The purpose of ([]) is to be used only in specifications while max is code that is meant to be executed. Pure functions may be used in both roles if they are defined using both keywords. In this example, max cannot be used in assertions while the bracket notation cannot be used in programs.

For maximum, we have a larger contract with new clause types. We add a pre-condition (following the keyword ) to this contract, due to the fact that our function is not defined on empty lists. To ensure termination, we define a , which must be decreasing with each recursive call. The recursive call in line 30 is indeed call on the tail of the input list, thus this call is made on a strictly smaller argument than l. The variant can be a term of any type as long as this type comes with a well-founded order relation. It can even be a sequence of terms: in this case, lexicographic ordering is used.

We need quantifiers to express our post-conditions. The maximum value must be contained in the list (line 22 using ), and must be greater than or equal to all the values in the list (line 21 using ).

The definition of the function follows in lines 24–30. It proceeds by pattern matching on the input list. The case of the empty list (constructor Nil) is as the pre-condition specifies the input list should not be empty (expressed as a fact on its length in line 20). If the list is a singleton (case (Cons h Nil)), the result is of course the only element of the list. Otherwise — and let us ignore lines 28–29 for the moment — the result is the maximum of the head and the recursive call on the tail (line 30). Without lines 28–29, the execution of the tool now answers:

figure s

Using Z3 or CVC5, or increasing the timeout, or changing the proof strategy does not change the outcome. It is possible to apply transformations to the goals. Using the Why3 IDE, just splitting the verification condition for maximum gives five verification conditions: one for verifying the empty case is indeed absurd, one to check that the recursive call is indeed decreasing, one to check the pre-condition of the recursive call and one for each post-conditions. All these sub-goals are valid except for the one corresponding to the post-condition in line 22 remain unknown. To help the provers, we added lines 28–29 which relate elements of l with elements of its tail via nth. This assertion is easily verified and then eases the verification of the post-condition. The answer of the tool changes to:

figure t
Fig. 2.
figure 2

Limitations with Higher-Order Functions

Full size image

2.2 Limitations with Higher-Order Functions

To show the limitations of Why3 in handling higher-order functions, let us consider the example of Fig. 2. Intuitively, extends the type with a value None and all the other values are encapsulated in the constructor Some.

In lines 1–10, we define a module Concrete containing the definition of a function remove_option that extracts the value encapsulated in an optional value assuming this value is not None. In the module Failure, we apply this function but through a higher-order function apply that just applies a function to a value. The tool fails to verify the function test_KO which intuitively does exactly the same as remove_option. Note that if remove_option was performing side effects or was partial because it may raise exceptions, Why3 would reject the program with an error. Here the problem is less visible. Indeed, the arguments of a higher-order function must be purely functional and total functions. In our case remove_option is not total as its pre-condition excludes None. The manifestation of the problem can be seen in a sub-verification condition generated by Why3: , which is impossible to prove.

Still, as most BSML primitives are higher-order functions, and we need to use functions such as remove_option, a work-around was needed. Our solution is shown in module Abstract (lines 19–24). Instead of writing a concrete implementation of remove_option, we declare a function remove_option without defining it, and we only give its semantics (with an ) when the pre-condition is met. It looks like a total function but if its application does not satisfy the precondition then it is impossible to reason about the result of the application. If the overall verification of a client code works despite an incorrect application of remove_option, it means the result of the incorrect application was not used. In module Success, the same client code as module Failure uses module Abstract instead of module Concrete and the verification succeeds.

3 Functional Bulk Synchronous Parallelism

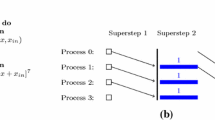
The OCaml language is a versatile programming language that combines functional, imperative and object-oriented paradigms. BSML [19] (Bulk Synchronous Parallel ML) is an OCaml-based library that embodies the principles of the BSP [25] (Bulk Synchronous Parallel) model. It provides a range of constants and functions to facilitate BSP programming. The BSP machine, viewed as a homogeneous distributed memory system with a point-to-point communication network and a global synchronization unit, serves as the underlying architecture for BSML. BSP programs, composed of consecutive super-steps, run on this kind of machine. The execution of each super-step follows a distinct pattern, starting with the computation phase where each processor-memory pair performs local computations using data available locally. This phase is followed by the communication phase, during which processors can request and exchange data with other processors. Finally, the synchronization phase concludes the super-step, synchronizing all processors globally.

With its collection of four expressive functions and constants like representing the number of processors in the BSP machine, BSML empowers developers to create BSP algorithms. While OCaml supports imperative programming and BSML can exploit it [16], in this paper we only consider the pure functional aspects of OCaml and BSML. Indeed, the four BSML functions are higher-order functions but Why3 does not handle non-pure function arguments. This deliberate focus differentiates it from the imperative counterparts provided by libraries such BSPlib for C [14]. The types and informal semantics of BSML primitives are listed in Fig. 3.

Fig. 3.
figure 3

BSML primitives

Full size image

Let us consider a function f that maps integers to values of type (denoted as in OCaml). The BSML primitive produces a parallel vector of type when applied to function f. Within this parallel vector, each processor, identified by the index value i within the range \(0\le i<\)  ,stores the computed value of . For instance, employing the expression yields a parallel vector denoted as \(\langle 0,~\ldots ,~\mathtt {bsp\_p}-1\rangle \) of type . Throughout subsequent discussions, we shall refer to this parallel vector as this. Additionally, the function replicate possesses the type and can be defined as follows: . By employing the expression replicate x, the value x becomes uniformly available across all processors within the parallel vector. Parallel vectors always have size .

To apply a parallel vector of functions (which is not a function) to a parallel vector of values, one has to use the primitive . Both and are executed within the pure computation phase of a super-step. For communications and an implicit synchronization barrier, the last two primitives and should be applied. is essentially an inverse of but the resulting function is partial and only defined on the domain . As the first constant constructor of any inductively defined type is considered as the empty message, allows to program any communication pattern of a BSP super-step. In the input vector of , each function encodes the message to be sent to other processors by the processor holding it. In the result vector, each function represents the message received from other processors by the processor holding the function.

Figure 4 presents a small BSML example using its primitives and which is part of its standard library. and are part of the OCaml standard library and are sequential map and reduce functions.

At lines 4–5, we define a function which converts a parallel vector into a list. This function requires a full super-step for its execution because it needs data exchanges. Also part of the BSML standard library, has type and is the list .

At lines 7–8, we define an algorithmic skeleton: a parallel map that operates on a distributed list (represented here as a value of type ). This function also requires the computation phase of a super-step and does not need any data exchange or synchronization.

From line 10 to 13, we define the algorithmic skeleton, using a binary associative operation and a neutral element e, it “sums” a distributed list into a single value. It proceeds in two steps. First, each processor compute a partial “sum” of the list it holds locally. Second, this vector of partial sums is transformed into a list which is finally summed up. As we call , a full super-step is required.

Finally, in lines 15–18, we implement a parallel function to solve the maximum prefix sum problem. The goal is to compute the maximum value among the sums of the prefixes of a list. Computing at the same time the maximum prefix sum and the sum of a list (in a pair) can be implemented using and . For example, on a machine with at least 4 processors, the value of is 6. Indeed, the argument of is a distributed version (on 4 processors) of the list and its prefix with the largest sum is the list without its last element. We specify and prove the correctness of in Sect. 5.

Fig. 4.
figure 4

A BSML Example

Full size image

4 Formalization of BSML Core and Standard Library

To be able to specify and write BSML programs, we need BSML primitives in WhyML. BSML primitives are implemented in parallel on top of MPI [23] called through OCaml’s Foreign Function Interface (FFI). Therefore, we cannot provide BSML in WhyML as an implementation. We need to give a BSML theory: a set of constant, axioms and function declarations. The axiomatization of BSML primitives can be found in Fig. 5. The semantics of functions and are expressed in their contract (lines 12–24) while the strict positivity condition on is given as an axiom on line 4. The type of parallel vector is abstract. Still we need to be able to observe parallel vectors. That is the role of logic function which is a function: it can only be used in specifications. A parallel vector is fully defined by the values all the processors hold as expressed by the axiom in lines 9-10. The axiomatization is very close to the informal semantics of Fig. 3. Instead of considering the parallel vectors globally with the notation \(\langle v_0,~\dots ,~v_{p-1}\rangle \), we consider each value \(v_i\) denoted by .

Fig. 5.
figure 5

BSML Theory in WhyML

Full size image

It is possible to realize this theory by a sequential implementation, for example implementing parallel vectors with sequential lists or arrays. This ensures the consistency of this theory.

To illustrate the use of this theory, we now specify, implement and verify several of the functions provided in the BSML standard library. The first one is :

figure bt

This verified function has only one post-condition: the result of replication is parallel vector which contains the same value everywhere.

In Sect. 3, we mentioned the function without defining it. Its implementation and specification follows, as well as the definition of function :

figure bw

It shows how to use the primitive. There is also a function omitted here.

Next, we use the communication primitive . As we wrote in Sect. 3, is essentially the inverse of . This function allows us to obtain the value of a vector at a given processor . However, it should not be used for such individual vector access, otherwise the performances would be extremely poor. Indeed, a call to requires a communication phase that is a total exchange and a global synchronization barrier. The use of should thus be thought as a collective operation. Note that and have the same semantics. However, the intent is very different: is written only in specifications, can be thought as an indexed array access, and is used for local reasoning, while is used only in programs and requires a full super-step to execute. should rather be thought as a global (i.e. concerning and involving all the processors) conversion of a parallel vector into a function.

To illustrate , we define . As we mentioned before this function requires a complete super-step to run. Again it should be seen as a global conversion from parallel vectors to lists:

figure cn

As in the BSML/OCaml version we call – which needs to be a function for Why3 to accept the code. returns the list of all processor identifiers. The definition of relies on a function itself implemented using a function. Our contribution does also contain a library of sequential functions, mostly on lists, as well as verified lemmas stating their properties. These functions can in most cases be used both in programs and in specifications.

Finally, the primitive is illustrated to implement a broadcast function. This data exchange (and implicit global synchronization) function is more precise than , in the sense that with each processor sends the same value to all processors, while with each processor can send a different value to each destination processor. Also, as some values are considered as empty messages, this makes possible to reduce exchange costs. We remind the reader that after a , for all processors and , the result function at destination processor d, applied to the identifier of source processor s returns the value of the input function at source processor s applied to destination processor d.

The definition of the function of the standard library follows. This function is used to broadcast a value from a processor to all other processors. To do so, first, we prepare a function vector for the processors to make the messages to send to each other (local definitions and ). It is clear that only the processor will send data. The other processors’ message is which is interpreted by the BSML/OCaml implementation as an empty message. Second, the local definition proceeds with the data exchange and ends the super-step. is a parallel vector of functions. What we are interested in is the value sent by processor . That is why the local definition then applies this parallel vector of functions to the replicated value . Of course, the obtained message is encapsulated in a constructor. Therefore, all the processors finally apply to yield the final result. The broadcast is meaningless if is not a valid processor identifier. In this case, the exception is raised:

figure dp

Our BSML theory allows us to write BSML programs and their specifications and is expressive enough for the Why3 framework to verify that they indeed satisfy their specifications.

We only presented a sub-set of the functions of the BSML standard library we implemented, and we refer to the companion artifact for the complete set of functions. For example, we also provide the , and communication functions, which offer a different communication pattern than : Each data item is shifted by a certain number of processors.

Fig. 6.
figure 6

Verified Algorithmic Skeletons in WhyML

Full size image
Fig. 7.
figure 7

Algebra Concepts

Full size image

5 Verified Scalable Maximum Prefix Sum

To exercise the formalization presented in the previous section, we specify and verify an implementation of the maximum prefix sum informally presented in Sect. 3. As in the BSML implementation, the implementation with WhyML relies on algorithmic skeletons. The skeleton is defined in lines 1–6 of Fig. 6. The only difference with its BSML/OCaml counterpart is the post-conditions including one expressed as a correspondence with the sequential . Given a distributed list (of type ), one obtains the same result by either applying then transforming the obtained distributed list into a list with , or applying the sequential to the sequentialization of the distributed list. Line 5 is just a hint for the provers: an application of lemma that basically commutes and .

The implementation (lines 8-20) of the parallel reduction is also very close to its BSML/OCaml counterpart of Fig. 4. As expected, the post-condition on line 16 is expressed with respect to the sequential reduction here implemented with the usual function. As the result is already a sequential value there is no need to sequentialize it. However, this correspondence is true only if is associative and is its neutral element which are two pre-conditions stated lines 10–11. There are two additional pre-conditions and a argument, i.e. an argument only used in the contract (and possible annotations) of the function. The reason is again to deal with a form of partial functions. is a total function, but it may not have the desired properties (associativity, neutral element) on all the values of its input type. Indeed, the OCaml version of for that we will also use in the WhyML version of , is not associative if we consider all pairs of integers. In the maximum prefix sum problem, the first component of such a pair represents the maximum prefix sum, it is therefore positive, and the second component the sum of the list, thus it is lower or equal to the first component. The ghost argument expresses such properties on the values manipulated during the reduction. This is an invariant: should preserve the property (line 12) and the input values and should satisfy this property (line 13). The predicates and are defined in Fig. 7. Such definitions work also well when there is no need for an invariant: in this case we simply use the constant boolean function always returning .

With these skeletons, it is possible to implement a parallel function to compute the maximum prefix sum of a distributed list as we did in Sect. 3. First, we define a specification as an inefficient function but direct translation of the informal specification: the function on lines 1–2 of Fig. 8. We also define (lines 7–8) and (line 10) which are the arguments to and as in the BSML/OCaml example of Fig. 4. This time they are not local definitions because we need to state and verify some lemmas about them and because we have two versions of : and . The invariant explained above is defined lines 12–13. We need an auxiliary function to verify the correctness of our functions with respect to the specification: (line 4–5) is the tupling of and . The rest of the code in Fig. 8 is the definitions of the sequential and parallel versions of the maximum prefix sum computation. Both of them are expressed as a composition of map and reduce.

Fig. 8.
figure 8

Verified Maximum Prefix Sum in WhyML

Full size image

The proof that indeed implements the specification proceeds by using the first homomorphism theorem. This theorem states that a homomorphic function can be implemented as a composition of map and reduce. A function is homomorphic when there exists a binary operation \(\odot \) such that: where denotes list concatenation. is not homomorphic but is. Two lines of annotations are necessary to guide the provers in the sequential case (lines 17–18). The parallel case does need any annotation: basically the contracts of and state their correspondence with their sequential counterpart thus the correspondence of the parallel with the sequential , and satisfies .

The full development is about 600 lines of WhyML with about 45% of specifications and 55% of code. It generates 74 goals, 100% of which are proved. Their verification produces 37 sub-goals. The strategy Auto level 2 is used: it tries the provers CVC4, Alt-Ergo, CVC5 and Z3 with a short timeout (1 s). If the goal is not proved then it splits the goal and tries on the sub-goals with the same timeout and finally if necessary tries with a larger timeout (10 s). Alt-Ergo version 2.4.3 proved 11 goals taking between 0.02 s and 0.56 s (when successful) and CVC4 version 1.6 proved 91 goals taking between 0.04 s and 2.45 s. Several sub-goals can contribute to a goal to be proved. For example the verification condition of is split in 3 sub-goals. In the number of the goals proved by CVC4 and Alt-Ergo the root goals verified because their sub-goals are proved are not counted. In our case, only 9 goals needed to be split to achieve their proofs.

All the parts of the WhyML development that need to use BSML functions include . When we extract the code however, the module cannot be extracted: there is no implementation for this module. For compiling the OCaml code obtained by extraction of the other modules of our WhyML development, we simply use the handwritten implementation of BSML in OCaml (which uses OCaml’s FFI to call MPI C functions). This is done via a very simple Why3 custom extraction driver: each BSML type or value is written using the OCaml qualified identifier notation. For example, if the WhyML development contains then the extracted code will contain where is the module containing the handwritten BSML parallel library.

6 Related Work

BSP-WHY [10, 11] also uses (a previous version of) Why to verify bulk synchronous parallel programs. However, the two approaches are very different. BSP-WHY considers BSP programs written in an imperative style close to BSPlib [14]. The verification proceeds by transforming well-formed programs — a sub-class of what has been formally defined later by Dabrowski as textually aligned programs [6] — into sequential simulating programs that are then verified using Why. The BSP-WHY code cannot be run on parallel machines.

The work closest to ours is the specification, verification and extraction of BSML programs using the Coq proof assistant. Early contributions started with the work of Gava [12]. A formalization of BSML primitives in a style very close to the Why3 formalization presented in this paper was proposed by Tesson and Loulergue [24] and used in a framework, named SyDPaCC, for the verification of BSP functional programs [8, 20]. The two main differences with our work is that: (1) proofs are much less automated in Coq than in Why3 but (2) the framework leverages the type-class resolution mechanism of Coq to automatically parallelize programs. For example in this framework, the user does not need to write the code for and , but only needs to write and to prove that its tupling with is leftwards and rightwards (i.e. can be written as calls to and ) and exhibits a weak right inverse. The framework would then use transformation theorems to automatically obtain and then verified correspondences as expressed in the post-conditions of and to automatically produce  [18].

Ono et al. [22] employed Coq to verify Hadoop MapReduce programs and extract Haskell code for Hadoop Streaming or directly write Java programs annotated with JML, utilizing Krakatoa [9] to generate Coq lemmas. The first part of their work is functional and therefore closest to our work. However, it is limited to MapReduce which is more general than the and skeletons but is less expressive than BSML. The second part of their work is more imperative.

7 Conclusion and Future Work

We were able to formalize the primitives of the parallel programming library BSML with WhyML and leverage Why3 for verifying a large part of the BSML standard library as well as an application written in BSML. We plan to experiment the extracted code more thoroughly and on larger parallel machines with a few thousand cores.

WhyML offers exceptions and references, thus allows to write imperative programs. However, such programs cannot be passed as arguments to higher-order functions. It therefore limits the usage of imperative features with BSML as all primitives are higher-order functions. The code outside BSML primitives can be imperative thus the sequencing of BSP super-steps could be imperative. It is also possible to use imperative features to implement pure functions passed as arguments to BSML primitives. Also, it is possible to deal with partial functions as we did with . We plan to explore all these possibilities in the future.