Abstract
We present solutions to the three challenges of the VerifyThis competition held at the 18th FM symposium in August 2012. These solutions use the Why3 environment for deductive program verification.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Why3 environment for deductive program verification is built around a kernel that implements a formal specification language, based on typed first-order logic. Logical goals can be proved using a large set of automated and interactive external theorem provers, such as Alt-Ergo [4], CVC3 [2], CVC4 [1], Z3 [8], E [17], SPASS [19], Vampire [16], Coq [3], or PVS [15]. When a goal is sent to a prover that does not support some features of the language, Why3 applies a series of encoding transformations, for example, to eliminate pattern matching or polymorphic types [7].
On top of this kernel, Why3 features a programming language WhyML, where functions can be formally specified using contracts. A VC generator produces proof obligations that need to be discharged to prove that a program respects its specification [9].
In this paper, we illustrate the use of Why3 by providing solutions to the three challenges that were given at the VerifyThis competition, held at the 18th FM symposium in August 2012. The description of the challenges can be found at http://fm2012.verifythis.org/challenges/. Reference Java implementations were given for the first two problems, and an algorithm in pseudocode was given for the third one.
We entered the competition with two teams, each with two members, both using Why3. By the end of the competition, our teams had partial solutions for the proposed challenges. After the competition, we merged our teams. For each challenge, we took the better approach of two as a basis upon which we built a complete solution. We estimate that we spent approximately 30 person-hour in that process. Our solutions use Why3 version 0.82 [6].
2 Why3 in a nutshell
In this section, we briefly describe Why3: the pure logic language of specifications, the programming language WhyML, and some peculiarities of program verification in Why3.
2.1 Specification language
Why3 is based on first-order logic with ML-style polymorphic types and several extensions: recursive definitions, algebraic data types, and inductive predicates. The specification language of Why3 does not depend on any features of its programming language, and can serve as a rich common format of theorem proving problems, readily suitable (via Why3) for multiple external provers.
Types. Built-in types in Why3 include integers ( ), real numbers (
), real numbers ( ), and tuples. A user-defined type can be non-interpreted or be a synonym for a type expression:
), and tuples. A user-defined type can be non-interpreted or be a synonym for a type expression:

Otherwise, it is an algebraic data type or a record. For instance, polymorphic lists and binary trees are defined in the standard library of Why3 as follows:

Record types are a special case of algebraic types with a single unnamed constructor and named fields. Here is a definition of a banker’s queue:

All types must be inhabited and Why3 checks that every algebraic type declaration admits at least one value. For example, the above definition of the list type would be rejected without constructor  .
.
Function and predicate symbols. Every function or predicate symbol in Why3 has a polymorphic type signature. For example, an abstract function that applies a mapping to an element of the domain can be declared as follows:

Both functions and predicates can be given definitions, possibly mutually recursive. As examples, we can specify that an  -to-
-to- mapping is strictly increasing:
mapping is strictly increasing:

or calculate the height of a tree:

Why3 automatically verifies that recursive definitions are terminating. To do so, it looks for an appropriate lexicographic order of arguments that guarantees a structural descent. Currently, we only support recursion over algebraic types. Other kinds of recursive functions have to be axiomatized or defined as programs, where termination is proved using variants (see Sect. 2.2).
Another extension to the first-order language adopted in Why3 is inductive predicates. Such a predicate is the least relation satisfying a set of clauses. For instance, the subsequence relation over lists is inductively defined as follows:

Standard positivity restrictions apply to ensure the existence of the least fixed point.
Terms and formulas. First-order language is extended, both in terms and formulas, with pattern matching,  -expressions, and conditional expressions. We stay faithful to the usual distinction between terms and formulas that is made in first-order logic. Thus we make a difference between a predicate symbol and a function symbol which returns a
-expressions, and conditional expressions. We stay faithful to the usual distinction between terms and formulas that is made in first-order logic. Thus we make a difference between a predicate symbol and a function symbol which returns a  -typed value,
-typed value,  being defined with
being defined with  . However, to facilitate writing, conditional expressions are allowed in terms, as in the following definition of absolute value:
. However, to facilitate writing, conditional expressions are allowed in terms, as in the following definition of absolute value:

Such a construct is directly accepted by provers not making a distinction between terms and formulas. To translate  constructs to traditional first-order language, Why3 lifts them to the level of formulas and rewrites them as conjunctions of two implications.
constructs to traditional first-order language, Why3 lifts them to the level of formulas and rewrites them as conjunctions of two implications.
Theories. Pure logical definitions, axioms, and lemmas are organized in collections, called theories. The standard library of Why3 contains numerous theories describing integer and real arithmetic, lists, binary trees, mappings, abstract algebraic notions, etc. To provide a fine-grained control of the premise set, we favor small theories which build on each other and introduce one or two concepts, such as Euclidean division, list membership, or injective maps. Instruction  imports a theory into the current context:
imports a theory into the current context:

2.2 Programming language
WhyML can be seen as a dialect of ML with extensive support for specification annotations. Program functions are provided with pre- and postconditions for normal and exceptional termination, and loop statements are annotated with invariants. To ensure termination, recursive functions and  -loops can be given variants, i.e., terms that decrease at each recursive call or iteration with respect to some well-founded ordering. Statically checked assertions can be inserted at arbitrary points in a program.
-loops can be given variants, i.e., terms that decrease at each recursive call or iteration with respect to some well-founded ordering. Statically checked assertions can be inserted at arbitrary points in a program.
Verification conditions are generated using a standard weakest-precondition procedure. To produce first-order proof obligations, WhyML is restricted to the first order, too: Nested function definitions are allowed but higher order functions are not. Furthermore, to keep proof obligations more tractable for provers and more readable (hence debuggable) for users, the type system of WhyML requires all aliases to be known statically, at the time of verification condition generation. This allows us to apply the Hoare-style rule for assignment, without resorting to a heap memory model. One consequence of this discipline is that recursive data types cannot have mutable components. As we demonstrate below, these restrictions do not preclude us from writing and verifying complex algorithms and data structures.
Types. WhyML extends the pure types of the specification language in several ways. First and foremost, the mutable state of a computation is exclusively embodied in mutable fields of record data types:

A program type can be provided with an invariant, i.e., a logical property imposed on any value of the type:

Type invariants in WhyML are verified at the function call boundaries. Since WhyML type system tracks aliases and side effects statically, it is easy to detect whenever a type invariant must be re-established. Keyword  in place of the equal sign means that, inside WhyML programs, type
in place of the equal sign means that, inside WhyML programs, type  is not a record, but an abstract data type. Thus, an attempt to access the
is not a record, but an abstract data type. Thus, an attempt to access the  field in a program would be rejected. However, inside specifications,
field in a program would be rejected. However, inside specifications,  is a record and its fields may be accessed.
is a record and its fields may be accessed.
Finally, a record field (or, more generally, an argument of a constructor in an algebraic type) can be declared ghost. Ghost data and ghost computations serve strictly for verification purposes. In particular, a typical use case for ghost fields is to equip a data structure with a pure logical “view”. For example, some intricate implementation of sparse matrices may carry a ghost fieldFootnote 1:

Formal arguments of program functions, as well as locally defined variables, can also be declared ghost.
To guarantee that ghost data and computations do not interfere with the program and cannot affect its final result, WhyML type system imposes a number of restrictions on their use. Ghost data cannot be used in a non-ghost computation. Ghost computations cannot modify a non-ghost mutable value or raise exceptions that escape into non-ghost code. However, ghost computations can read non-ghost values and ghost data can be used in program specifications.
Function prototypes. Unlike other ML variants, WhyML does not separate interface and implementation. One can freely mix in the same WhyML module fully implemented program functions with abstract function prototypes carrying only a type and a specification. For “model” types like  , whose structure is inaccessible from programs, function prototypes is the only way to provide a usable interface. Here is how lookup and update are specified for arrays:
, whose structure is inaccessible from programs, function prototypes is the only way to provide a usable interface. Here is how lookup and update are specified for arrays:

The names  and
and  define mixfix operators
define mixfix operators  and
and  . Clauses
. Clauses  and
and  specify the side effects in function prototypes; for example,
specify the side effects in function prototypes; for example,  modifies the mutable field of
modifies the mutable field of  , namely
, namely  . The term
. The term  in the postcondition of the second prototype refers to the pre-call value of the field
in the postcondition of the second prototype refers to the pre-call value of the field  , before it is modified by
, before it is modified by  .
.
Programs. The syntax of WhyML programs should give no surprise to anyone familiar with ML. As examples, let us show several functions to handle mutable references:

Contrary to function prototypes, we do not indicate  and
and  effects, since Why3 can extract this information from the code. Notice that the same prefix symbol
effects, since Why3 can extract this information from the code. Notice that the same prefix symbol  is used as the name for both a pure access function and a program function. Since program symbols cannot appear in specifications,
is used as the name for both a pure access function and a program function. Since program symbols cannot appear in specifications,  in pre- and postconditions can only refer to the pure function. In the program code,
in pre- and postconditions can only refer to the pure function. In the program code,  will refer to the WhyML function.
will refer to the WhyML function.
The last definition shows that pure types, functions, and predicates are accepted in WhyML programs. For instance, the type of integers and basic arithmetic operations are shared between specifications and programs. The only exception is made for logic functions and predicates specified directly on program types: such symbols can only be used in specifications. One reason for this restriction is that these functions and predicates have uncontrolled access to ghost components of program types. Had we not reused the  operator, WhyML would reject the last definition reporting that pure function
operator, WhyML would reject the last definition reporting that pure function  cannot appear in a program.
cannot appear in a program.
Modules. Akin to pure logical theories, WhyML declarations and definitions are grouped into modules. A module may import logical theories or contain pure declarations. The standard library modules introduce mutable references, arrays, hash tables, stacks, and queues.
2.3 Verifying programs with Why3
Simple Why3 formalizations can be verified directly from the command line: The why3 tool can run a designated automated prover on each proof obligation generated from a WhyML file and report eventual proof failures. For more complex developments, Why3 provides an interactive graphical environment whose main window is shown in Fig. 1. The big tree on the left shows the current state of the session. The root of the tree is the WhyML file in works, the first-level nodes are theories and modules, and the second-level nodes are primary proof obligations: logical lemmas and verification conditions for top-level WhyML functions.
Proof obligations, also called proof tasks, can be sent to automated provers or handled using interactive proof assistants (see the stack of buttons to the left of the session view). Why3 also puts at user’s disposal a number of so-called transformations which can be used to simplify a proof obligation under consideration or to split it into a number of sub-tasks.Footnote 2 These sub-tasks appear at the lower levels of the session tree.
In the session shown in the figure, the file being checked is verifythis_fm2012_LRS.mlw. The first module in this file contains a WhyML function named  (whose source code is shown in the bottom-right frame), and the verification condition for this function is decomposed into seven sub-tasks: two preconditions ensuring safety of array access in the loop condition, loop invariant initialization and preservation, and three postconditions covering each branch of the negated loop condition. The cursor is positioned on the first postcondition, where the first two parts of the loop condition are true and the third one is false. The proof obligation itself is shown in the top-right frame. Four automated provers were able to discharge this proof task successfully.
(whose source code is shown in the bottom-right frame), and the verification condition for this function is decomposed into seven sub-tasks: two preconditions ensuring safety of array access in the loop condition, loop invariant initialization and preservation, and three postconditions covering each branch of the negated loop condition. The cursor is positioned on the first postcondition, where the first two parts of the loop condition are true and the third one is false. The proof obligation itself is shown in the top-right frame. Four automated provers were able to discharge this proof task successfully.
Due to differences in prover technology (which are especially deep between SMT solvers and resolution-based provers), there is no single best prover for the purposes of program verification. Quite often, a proof obligation is only discharged by one or two provers out of half a dozen we use regularly. Being able to target diverse back-end provers is an important feature of Why3 which allows us to prove automatically more goals than we would be able to using just one dedicated prover.
Proof sessions are saved between runs of Why3, which facilitates development and debugging of verified programs. Special algorithms were devised for reconstruction of session trees after modification of the program code or specification [5]. Along with the session, Why3 stores proof scripts for interactive proof assistants (at this moment, Coq and PVS are supported) that handle proof obligations falling beyond the reach of automated provers. One characteristic case where one has to resort to interactive proof is proof tasks requiring reasoning by induction.
Another important functionality of Why3 is code extraction: a verified WhyML program can be translated to a compilable correct-by-construction OCaml program (a mechanism similar to that of Coq). Recently, work has started on a native WhyML evaluator which would allow for quick testing of programs and assertions, speeding up the development process.
3 Challenge 1: longest repeated substring
This challenge aims at computing the longest repeated substring in a given string. The two occurrences of that substring are allowed to overlap. For example, the longest repeated substring in ABCDBBCDA and ABCDBCDB are, respectively, BCD and BCDB, with an overlap in the second case.
A naive algorithm that checks all possible occurrences of each substring would be of cubic complexity. This challenge proposes a more efficient algorithm, that amounts to computing the array of suffixes of the given string. It is an array of integers that lists the positions of the suffixes of the input string, in increasing lexicographic order. For example the sorted array of suffixes of ABCDBCDB is [0; 1; 4; 7; 2; 5;3; 6], corresponding to suffixes ABCDBCDB, BCDBCDB, BCDB, B, CDBCDB, CDB, DBCDB, DB in that order. The longest repeated substring is then the longest common prefix of two consecutive strings in this array.
A preliminary step of this challenge is thus to compute the longest common prefix of two given substrings of the input; this part was expected to be solved during the competition.
We provide a complete solution to the challenge. The Why3 code follows the Java reference implementation as closely as possible. A noticeable difference is that the function for sorting does not apply to a  object: because the Java reference calls the
object: because the Java reference calls the  method inside a constructorFootnote 3 which is not possible in Why3. Our solution is made of four Why3 modules:
method inside a constructorFootnote 3 which is not possible in Why3. Our solution is made of four Why3 modules:
-
 : computation of longest common prefix of substrings.
: computation of longest common prefix of substrings. -
 : helper functions for sorting suffixes, roughly corresponding to the private part of the
: helper functions for sorting suffixes, roughly corresponding to the private part of the  class of the Java code.
class of the Java code. -
 : the suffixArray data type, roughly corresponding to the public part of the
: the suffixArray data type, roughly corresponding to the public part of the  class of the Java code.
class of the Java code. -
 : computation of longest repeated substring, corresponding to the
: computation of longest repeated substring, corresponding to the  class of the Java code.
class of the Java code.
In the following, we detail each module in turn, presenting first its specifications, and then the implementation and proofs. The full solution, including the complete Why3 input and the proof results, is available on the Toccata gallery of verified programs at http://toccata.lri.fr/gallery/verifythis_fm2012_LRS.en.html.
3.1 Longest common prefix
Our first module  implements the first part of the challenge: a function that computes the longest common prefix at two given indexes.
implements the first part of the challenge: a function that computes the longest common prefix at two given indexes.
Specification. The specifications are given in Fig. 2. We import arrays from the Why3 standard library. The predicate  is true when the prefixes of length
is true when the prefixes of length  at respective positions
at respective positions  and
and  in array
in array  are identical, i.e., when
are identical, i.e., when  and
and  are equal. The predicate
are equal. The predicate  is true when
is true when  is the maximal length of common prefixes at positions
is the maximal length of common prefixes at positions  and
and  in array
in array  . The postcondition of the
. The postcondition of the  function is the natural way of specifying that this function computes the longest common prefix.
function is the natural way of specifying that this function computes the longest common prefix.
Implementation and proofs. The Why3 code for the function that computes the longest common prefix is given in Fig. 3. It is a direct translation of the Java reference implementation. Since we need a mutable variable  for this code, we use a reference (
for this code, we use a reference ( is a function of the standard library that increments an integer reference, see Sect. 2.2). The loop invariant is natural, since the algorithm amounts to incrementing
is a function of the standard library that increments an integer reference, see Sect. 2.2). The loop invariant is natural, since the algorithm amounts to incrementing  until the characters at
until the characters at  and
and  differ.
differ.
To prove this function, we first state and prove two lemmas (Fig. 3). These lemmas are not strictly necessary for the proof, though they help some automated provers, but we need them later anyway. The first lemma states that if characters at positions  and
and  are different, then there is no common prefix of length
are different, then there is no common prefix of length  . The second lemma states that, for the longest common prefix to be of length
. The second lemma states that, for the longest common prefix to be of length  , it suffices to have a common prefix of length
, it suffices to have a common prefix of length  but not
but not  . The two lemmas and the verification conditions for the
. The two lemmas and the verification conditions for the  function are proved automatically, using SMT solvers. (Detailed statistics on proofs are summarized in Sect. 3.5.)
function are proved automatically, using SMT solvers. (Detailed statistics on proofs are summarized in Sect. 3.5.)
3.2 Sorting suffixes
Our next module deals with lexicographic order on suffixes and sorting.
Specification. In the specifications of this module (Fig. 4) we define the lexicographic order as a predicate  : the suffix at position
: the suffix at position  is smaller than the suffix at position
is smaller than the suffix at position  if there is some length
if there is some length  such that prefixes of length
such that prefixes of length  are the same, and the next character in
are the same, and the next character in  , if any, is smaller than the next character in
, if any, is smaller than the next character in  . The comparison function is then specified with postconditions that tell, depending on the sign of the result, whether suffixes at positions
. The comparison function is then specified with postconditions that tell, depending on the sign of the result, whether suffixes at positions  and
and  are equal, smaller or greater, respectively.
are equal, smaller or greater, respectively.
To specify the sorting algorithm, we need several ingredients (Fig. 4). First we define the “less or equal” predicate  , which is the ordering relation used for sorting. As usual with sorting algorithms, the postcondition is twofold: first, it says that the resulting array is sorted; second, that it contains a permutation of its initial contents. This sorting function is peculiar since it does not take only one array as usual, but takes two arrays,
, which is the ordering relation used for sorting. As usual with sorting algorithms, the postcondition is twofold: first, it says that the resulting array is sorted; second, that it contains a permutation of its initial contents. This sorting function is peculiar since it does not take only one array as usual, but takes two arrays,  and
and  as arguments, and sorts
as arguments, and sorts  using an order relation that depends on
using an order relation that depends on  . Because of this peculiarity, we cannot reuse the
. Because of this peculiarity, we cannot reuse the  predicate from the Why3 standard library to specify the
predicate from the Why3 standard library to specify the  function: the definition of this predicate is parametrized by only one array (see Appendix for details). We thus had to write our own version (Fig. 4) by making a copy of the relevant part of the Why3 standard library and adding an extra argument
function: the definition of this predicate is parametrized by only one array (see Appendix for details). We thus had to write our own version (Fig. 4) by making a copy of the relevant part of the Why3 standard library and adding an extra argument  .
.
On the other hand, we can reuse the  predicate from the standard library (see Fig. 24 in the Appendix for details). Finally, additional requirements are that the input arrays have the same length \(l\), and that the values in array
predicate from the standard library (see Fig. 24 in the Appendix for details). Finally, additional requirements are that the input arrays have the same length \(l\), and that the values in array  range in \(0\ldots l-1\), for which we can reuse the corresponding
range in \(0\ldots l-1\), for which we can reuse the corresponding  predicate from the standard library, where
predicate from the standard library, where  means that
means that  maps the domain \([0,\ldots ,n-1]\) into \([0,\ldots ,n-1]\) (See Fig. 25 in the Appendix).
maps the domain \([0,\ldots ,n-1]\) into \([0,\ldots ,n-1]\) (See Fig. 25 in the Appendix).
Implementation and proofs. The implementation is given in Fig. 5. The code of the  function is close to the Java reference implementation. Notice the use of the
function is close to the Java reference implementation. Notice the use of the  keyword to say that the last case is unreachable. All VCs for these functions are proved automatically.
keyword to say that the last case is unreachable. All VCs for these functions are proved automatically.
To prove the sorting algorithm, we first have to show that  is transitive (lemma
is transitive (lemma  ). To prove this lemma automatically, we pose an auxiliary lemma
). To prove this lemma automatically, we pose an auxiliary lemma  to handle the equality case. The loop invariants needed are no different from the ones needed for a generic insertion sort algorithm (see for instance http://toccata.lri.fr/gallery/sorting.en.html). We just add the fact that values in array
to handle the equality case. The loop invariants needed are no different from the ones needed for a generic insertion sort algorithm (see for instance http://toccata.lri.fr/gallery/sorting.en.html). We just add the fact that values in array  remain within \(0\ldots l-1\). The two assertions in the code are intended to help automated provers.
remain within \(0\ldots l-1\). The two assertions in the code are intended to help automated provers.
3.3 The suffixArray data structure
This module corresponds to the public part of the SuffixArray class in the Java reference implementation.
Specification. We first declare a type  (Fig. 6) corresponding to the
(Fig. 6) corresponding to the  class in the Java code. We equip this type with an invariant that specifies that the two arrays have the same length \(l\), that the suffix array is a permutation of \(0,\ldots ,l-1\), and that it is sorted in increasing order. The three functions correspond to the methods of the same name in the Java code, and their postconditions are natural.
class in the Java code. We equip this type with an invariant that specifies that the two arrays have the same length \(l\), that the suffix array is a permutation of \(0,\ldots ,l-1\), and that it is sorted in increasing order. The three functions correspond to the methods of the same name in the Java code, and their postconditions are natural.
Implementation and proofs. The implementation (Fig. 7) of  and
and  is simple and easy to prove. The
is simple and easy to prove. The  function acts as a constructor, and the difficulty is to establish the invariant. For this, we pose a lemma
function acts as a constructor, and the difficulty is to establish the invariant. For this, we pose a lemma  : when one is permuting elements of an array that represents a permutation, the result is still a permutation. Such a lemma cannot be proved automatically, because it requires induction (the
: when one is permuting elements of an array that represents a permutation, the result is still a permutation. Such a lemma cannot be proved automatically, because it requires induction (the  predicate is defined inductively). We perform this proof in Coq, which requires a few lines of tactics. The notion of permutation of an interval \(0 \ldots l-1\) and this lemma are good candidates for addition in the Why3 standard library.
predicate is defined inductively). We perform this proof in Coq, which requires a few lines of tactics. The notion of permutation of an interval \(0 \ldots l-1\) and this lemma are good candidates for addition in the Why3 standard library.
3.4 Longest repeated substring
Specification. This module contains only the main function for computing the longest repeated substring, specified in Fig. 8. As in the Java code, there are two global variables  and
and  that hold the results of the computation. To specify this function, we add an extra global ghost variable
that hold the results of the computation. To specify this function, we add an extra global ghost variable  that holds the index of the second occurrence of the repeated substring. The postconditions thus say that the two indexes
that holds the index of the second occurrence of the repeated substring. The postconditions thus say that the two indexes  and
and  are distinct, that
are distinct, that  is the length of their longest common prefix, and that for any other pair of two indexes, the longest common prefix is not longer than
is the length of their longest common prefix, and that for any other pair of two indexes, the longest common prefix is not longer than  .
.
Implementation and proofs.
The implementation of  follows the Java code, and is given in Fig. 9. The first three loop invariants are naturally derived from the first three postconditions. The most difficult part is to establish the last postcondition, for which we add a fourth loop invariant and two assertions after the loop.
follows the Java code, and is given in Fig. 9. The first three loop invariants are naturally derived from the first three postconditions. The most difficult part is to establish the last postcondition, for which we add a fourth loop invariant and two assertions after the loop.
The fourth loop invariant states that we already have computed the longest repeated substring for all suffixes in  ,...,
,..., . To show that it is preserved by a loop iteration, where only suffixes
. To show that it is preserved by a loop iteration, where only suffixes  and
and  are considered, it is necessary to show that for any \(j\) between \(0\) and \(i-1\), the longest common prefix of
are considered, it is necessary to show that for any \(j\) between \(0\) and \(i-1\), the longest common prefix of  and
and  is smaller that those of
is smaller that those of  and
and  . This property is true only because suffixes are sorted lexicographically. To complete the proof with automated provers, we pose the lemma
. This property is true only because suffixes are sorted lexicographically. To complete the proof with automated provers, we pose the lemma  given on Fig. 10. To prove it, we also pose the auxiliary lemma
given on Fig. 10. To prove it, we also pose the auxiliary lemma  . Both lemmas are proved automatically.
. Both lemmas are proved automatically.
The last part of the proof is to show the fourth postcondition, knowing that the fourth loop invariant is true at loop exit. To achieve this, we need to add two assertions. The first assertion is just to make the final loop invariant symmetric in \(j\) and \(k\), and needs the lemma  of Fig. 10. The second assertion states that the array of suffixes is surjective, that is we are sure that all indexes have been considered when the loop is finished. Since second assertion could not be proved automatically, we needed to perform the proof in Coq. The main reason is that it uses existential quantification, which is typically hard to handle automatically. Another difficulty is that this surjectivity property follows from the classical but non-trivial mathematical result that an injective function that maps a finite set (namely, \(0,\ldots ,l-1\)) to itself is also surjective. Fortunately, such a result is already proved in the Why3 standard library, so that we can reuse it in our Coq proof, which, in the end, is just a dozen lines long.
of Fig. 10. The second assertion states that the array of suffixes is surjective, that is we are sure that all indexes have been considered when the loop is finished. Since second assertion could not be proved automatically, we needed to perform the proof in Coq. The main reason is that it uses existential quantification, which is typically hard to handle automatically. Another difficulty is that this surjectivity property follows from the classical but non-trivial mathematical result that an injective function that maps a finite set (namely, \(0,\ldots ,l-1\)) to itself is also surjective. Fortunately, such a result is already proved in the Why3 standard library, so that we can reuse it in our Coq proof, which, in the end, is just a dozen lines long.
Finally, proving the postcondition from the second assertion must be done in Coq, it seems that the automated provers are not able to exploit the existential quantifications successfully (3 lines of tactics only).
3.5 Proof statistics
The detailed proof results are available at URL http://toccata.lri.fr/gallery/verifythis_fm2012_LRS.en.html. The table below summarizes these results. The time limit given to automated provers is 10 s.
Module | Number of VCs | Automatically proved |
|---|---|---|
LCP | 10 | 10 (100 %) |
Suffixsort | 62 | 62 (100 %) |
Suffixarray | 22 | 21 (95 %) |
LRS | 30 | 28 (93 %) |
Total | 124 | 121 (97 %) |
The table below shows the results per prover, among the 121 VCs proved automatically.
Prover | Number of VCs proved |
|---|---|
Alt-Ergo 0.95.2 | 116 |
CVC3 2.4.1 | 106 |
CVC4 1.3 | 105 |
Eprover 1.6 | 77 |
Vampire 0.6 | 75 |
Z3 3.2 | 85 |
Z3 4.3.1 | 82 |
3 VCs are proved only by Alt-Ergo. The three interactive proofs done using Coq amount to a total of 49 lines of script added manually, most of them being for proving the lemma  .
.
3.6 Lessons learned
The first part of the challenge, namely our  module, was easy and was indeed solved almost in the same way within the 45 min slot. On the other hand, achieving the other parts required significantly more work, that we estimate to a dozen of hours. It should be noticed that although the final specifications are, to our opinion, relatively short and natural, it was not easy to obtain them at first: a significant amount of time is needed to find adequate specifications that make the proofs almost fully automated.
module, was easy and was indeed solved almost in the same way within the 45 min slot. On the other hand, achieving the other parts required significantly more work, that we estimate to a dozen of hours. It should be noticed that although the final specifications are, to our opinion, relatively short and natural, it was not easy to obtain them at first: a significant amount of time is needed to find adequate specifications that make the proofs almost fully automated.
Our proofs were not done fully automatically, as we had to invoke Coq and write manually a few lines of proof script. In the case of the  lemma, this was necessary because an inductive reasoning was needed, on the definition of the permutation predicate. For the other VCs, this was needed to manually give witnesses of some existential quantifications, which could not be found by automated provers at our disposal. Notice that when we go to Coq to discharge a goal, we typically use a few lines of Coq tactics, e.g. to perform an induction. For the resulting subgoals, we can still use automated provers via the
lemma, this was necessary because an inductive reasoning was needed, on the definition of the permutation predicate. For the other VCs, this was needed to manually give witnesses of some existential quantifications, which could not be found by automated provers at our disposal. Notice that when we go to Coq to discharge a goal, we typically use a few lines of Coq tactics, e.g. to perform an induction. For the resulting subgoals, we can still use automated provers via the  Coq tactic, which amounts to send back a Coq goal to Why3 and call a given automated prover. It is an interesting question whether an interactive proof assistant is mandatory for such purposes, we will come back to this in the concluding section.
Coq tactic, which amounts to send back a Coq goal to Why3 and call a given automated prover. It is an interesting question whether an interactive proof assistant is mandatory for such purposes, we will come back to this in the concluding section.
Another point is that we were able to reuse a significant amount of theories from the standard library. This is good news since good library support is certainly an important point for the efficient use of a verification environment. However we also realized that some parts were not sufficiently generic, namely the  predicate for which the ordering relation cannot depend on another extra argument. A simple solution would be to add an extra parameter in the
predicate for which the ordering relation cannot depend on another extra argument. A simple solution would be to add an extra parameter in the  predicate in the library. Another direction would be to allow some form of partial application in the logic of Why3, that would be a first step towards higher order logic.
predicate in the library. Another direction would be to allow some form of partial application in the logic of Why3, that would be a first step towards higher order logic.
4 Challenge 2: sums of prefixes
This challenge proposes to compute the sums of the prefixes of an array. More precisely, given an array  , it amounts to computing each partial sum \(\sum _{0\le k < i}\mathtt {a}[k]\) and storing it back into \(\mathtt {a}[i]\). The array is thus modified in place. The proposed algorithm requires the length of
, it amounts to computing each partial sum \(\sum _{0\le k < i}\mathtt {a}[k]\) and storing it back into \(\mathtt {a}[i]\). The array is thus modified in place. The proposed algorithm requires the length of  to be a power of 2, and does not use any extra storage.
to be a power of 2, and does not use any extra storage.
The Why3 specification of the algorithm is given in Fig. 11. We import the function  from the theory
from the theory  of the Why3 standard library, where
of the Why3 standard library, where  denotes the sum \(\sum _{\mathtt {i}\le k < \mathtt {j}}\mathtt {a}[k]\).
denotes the sum \(\sum _{\mathtt {i}\le k < \mathtt {j}}\mathtt {a}[k]\).
The challenge is to verify a sequential version of a parallelizable algorithm. The idea is to identify the array with a binary tree. The algorithm traverses this tree by gathering information firstly from the leaves to the root (the upsweep phase) and secondly from the root to the leaves (the downsweep phase). First, we specify the state of array  during the upsweep and downsweep phases. Then we explain each phase separately.
during the upsweep and downsweep phases. Then we explain each phase separately.
The full solution is available on the Toccata gallery of verified programs at http://toccata.lri.fr/gallery/verifythis_PrefixSumRec.en.html.
4.1 Modeling the binary tree
The main difficulty in this challenge is to capture the operations performed by the upsweep phase. The array is identified with a complete binary tree and this operation updates nodes with sums of subtrees in an intricate way. The simplest ideaFootnote 4 is to use an inductive predicate  (see Fig. 12) that mimics the recursive structure of the algorithm. It takes as arguments two indices
(see Fig. 12) that mimics the recursive structure of the algorithm. It takes as arguments two indices  and
and  to identify a subtree, and two arrays
to identify a subtree, and two arrays  and
and  . Array
. Array  stands for the initial contents of the array, and array
stands for the initial contents of the array, and array  for its current state with partial sums.
for its current state with partial sums.
A subtree is represented by a pair of indices ( ,
,  ), with
), with  being a power of two. The elements of this subtree span from
being a power of two. The elements of this subtree span from  to
to  , included. We introduce two functions
, included. We introduce two functions  and
and  to descend into the left and right subtrees:
to descend into the left and right subtrees:

The left subtree is ( ,
,  ) and the right subtree is (
) and the right subtree is ( ,
,  ). A schematic representation of the algorithm and of the tree view of the array is in Fig. 13.
). A schematic representation of the algorithm and of the tree view of the array is in Fig. 13.
The main idea in predicate  is to describe the value in
is to describe the value in  but not the value in
but not the value in  . The main reason is that the root of a left subtree is not modified anymore once the left subtree has been processed. Since
. The main reason is that the root of a left subtree is not modified anymore once the left subtree has been processed. Since  is inductively defined, it describes the values at indices from
is inductively defined, it describes the values at indices from  to
to  , since they are all roots of left subtrees. For instance,
, since they are all roots of left subtrees. For instance,  defines the values stored at indices from 0 to 6. On the contrary, the value
defines the values stored at indices from 0 to 6. On the contrary, the value  is not specified in
is not specified in  . Indeed, functions
. Indeed, functions  and
and  have different specifications for
have different specifications for  .
.
Challenge 2: schematic view of the algorithm. The left column shows the upsweep phase, the right column the downsweep phase. The indices (\(_i\),\(_i\)) correspond to the subtrees and to the parameters ( ,
, ) of the recursive calls. The initial array is at the bottom left, the array after the upsweep phase is at the top left, the array before the downsweep phase is at the top right, the resulting array is at the bottom right. A plain arrow stands for a sum and an assignment performed in the first and second phase. A dashed arrow stands for an assignment \( \leftarrow \) performed in the second phase
) of the recursive calls. The initial array is at the bottom left, the array after the upsweep phase is at the top left, the array before the downsweep phase is at the top right, the resulting array is at the bottom right. A plain arrow stands for a sum and an assignment performed in the first and second phase. A dashed arrow stands for an assignment \( \leftarrow \) performed in the second phase
4.2 The “upsweep” phase
The implementation and the complete specification of  are presented in Fig. 14. This function on (
are presented in Fig. 14. This function on ( ,
,  ) sets
) sets  to the sum of the elements of the subtree. So when the left subtree has been processed,
to the sum of the elements of the subtree. So when the left subtree has been processed,  contains the sum of the elements of the left subtree. It is indeed the property which is described in
contains the sum of the elements of the left subtree. It is indeed the property which is described in  . Moreover the array
. Moreover the array  is modified by the recursive calls, so we need to specify the extent of these modifications. This is the purpose of the last two formulas in the postcondition. The conditions of preservation of
is modified by the recursive calls, so we need to specify the extent of these modifications. This is the purpose of the last two formulas in the postcondition. The conditions of preservation of  are described in the two-frame lemmas given in Fig. 15. These two lemmas are proved by induction over
are described in the two-frame lemmas given in Fig. 15. These two lemmas are proved by induction over  , using the Coq proof assistant.
, using the Coq proof assistant.
4.3 The “downsweep” phase
The implementation of the  function is presented in Fig. 16. We need the ghost argument
function is presented in Fig. 16. We need the ghost argument  that contains the initial array. Indeed
that contains the initial array. Indeed  cannot be used because it represents the intermediate state between the upsweep and downsweep phase. The traversal is the same as in the first phase so the inductive predicate
cannot be used because it represents the intermediate state between the upsweep and downsweep phase. The traversal is the same as in the first phase so the inductive predicate  is used directly for the proof. During the second phase the value
is used directly for the proof. During the second phase the value  is used again in a special way. Before the call to
is used again in a special way. Before the call to  , it contains the prefix sum of the value of the initial array
, it contains the prefix sum of the value of the initial array  before the subtree (
before the subtree ( ,
,  ):
):

Finally, the function  ensures that all the values of the subtree (
ensures that all the values of the subtree ( ,
,  ) are the prefix sums of the array
) are the prefix sums of the array  . As for the function
. As for the function  , we need to specify the extent of the modification of
, we need to specify the extent of the modification of  but we do not have to write and prove the frame lemmas for
but we do not have to write and prove the frame lemmas for  because they can be derived without induction from the frame lemmas of
because they can be derived without induction from the frame lemmas of  defined in the Why3 standard library. The frame lemma
defined in the Why3 standard library. The frame lemma  is also used for the frame of the first recursive call.
is also used for the frame of the first recursive call.
4.4 The main procedure
The main procedure  , in Fig. 17, calls the two phases sequentially and initializes
, in Fig. 17, calls the two phases sequentially and initializes  to the prefix sum of the index
to the prefix sum of the index  , which is
, which is  . The harness test proposed in the challenge is also proved (we do not give the code in this paper).
. The harness test proposed in the challenge is also proved (we do not give the code in this paper).
4.5 Proof statistics
The detailed proof results are available at http://toccata.lri.fr/gallery/verifythis_PrefixSumRec.en.html. The table below summarizes these results. The time limit given to automated provers is 10 s.
Function | Number of VCs | Automatically proved |
|---|---|---|
| 4 | 2 (50 %) |
| 24 | 24 (100 %) |
| 29 | 29 (100 %) |
| 12 | 12 (100 %) |
| 20 | 20 (100 %) |
Total | 89 | 87 (98 %) |
The table below shows the results per prover, among the 87 VCs proved automatically.
Prover | Number of VCs proved |
|---|---|
Alt-Ergo 0.95.2 | 100 |
CVC3 2.4.1 | 85 |
CVC4 1.2 | 96 |
Z3 3.2 | 64 |
Z3 4.3.1 | 70 |
The two lemmas  and
and  are proved using Coq by 4 lines of tactics: one induction on the inductive predicate
are proved using Coq by 4 lines of tactics: one induction on the inductive predicate  and then the subgoals are discharged using the
and then the subgoals are discharged using the  tactic, as in challenge 1. All remaining proof obligations are discharged by at least two automated provers.
tactic, as in challenge 1. All remaining proof obligations are discharged by at least two automated provers.
4.6 Lessons learned
As for challenge 1, we had to use the interactive proof assistant Coq to discharge some VCs. See the general conclusion for a discussion on such a use of Coq.
The hardest part of this challenge is the specification of the state between the two phases. During the competition, when we came up with the idea of using an inductive predicate, we got the indexes wrong several times. When the automated provers failed to prove a proof obligation, we added assertions that should have helped to find particular facts that could not be proved. We also tried to prove them in Coq to find the hole in the proof. After the competition, when the indexes in the specification were corrected, we removed the useless assertions and Coq proofs. This raises the general question on how we can debug the specifications. For such a purpose, we are currently implementing a step-by-step evaluator of WhyML functions. The user will thus be able to easily compare the behavior of the program to its specification.
5 Challenge 3: deletion in a binary search tree
The third challenge is to verify a procedure that removes the node with the minimal key from a binary search tree. The pseudocode given at the competition descends along the leftmost branch of the tree using a while loop. When it reaches a node with no left child, it makes its right child the new left child of its parent. The tree is mutated in place. Our solution respects the reference implementation. The full solution is available on the Toccata gallery of verified programs at http://toccata.lri.fr/gallery/verifythis_fm2012_treedel.en.html.
5.1 Preliminaries
Why3 has no native support for mutable trees. Hence we build a minimal memory model, given in Fig. 18. It introduces some uninterpreted type  to denote memory locations, with a particular value
to denote memory locations, with a particular value  . Then the heap is modeled as a global reference
. Then the heap is modeled as a global reference  holding a purely applicative map from memory locations to nodes. A node is a record with two fields
holding a purely applicative map from memory locations to nodes. A node is a record with two fields  and
and  of type
of type  and a third field
and a third field  of type
of type  .
.
To account for possible  -dereference, we do not access these three fields directly, but we use instead functions
-dereference, we do not access these three fields directly, but we use instead functions  ,
,  , and
, and  with suitable preconditions:
with suitable preconditions:

(and similarly for  and
and  ). In this model, we assume that any pointer that is not
). In this model, we assume that any pointer that is not  can be safely dereferenced, which is the case in languages that do not permit explicit deallocation, e.g. Java.
can be safely dereferenced, which is the case in languages that do not permit explicit deallocation, e.g. Java.
5.2 Specification
We import polymorphic immutable lists and trees from the Why3 standard library (see Sect. 2.1 for definitions). We also import a function  that lists the elements of a tree according to inorder traversal and a predicate
that lists the elements of a tree according to inorder traversal and a predicate  that expresses that all elements of a given list are distinct. Types
that expresses that all elements of a given list are distinct. Types  and
and  will only appear in specifications.
will only appear in specifications.
Our specification for problem 3 is given in Fig. 19. The central component is the inductively defined predicate  . Such an inductive definition should be read as a set of inference rules:
. Such an inductive definition should be read as a set of inference rules:

Given a memory state \(m\), a loc \(p\), and a tree of memory locations \(t\) (of type
 ), the predicate
), the predicate  means that memory \(m\) contains a well-formed tree rooted at \(p\), whose shape is exactly \(t\). The inductive nature of predicate
means that memory \(m\) contains a well-formed tree rooted at \(p\), whose shape is exactly \(t\). The inductive nature of predicate  ensures that such a tree is both finite and acyclic. But nothing prevents the heap-allocated tree to be a DAG; we will take care of that later.
ensures that such a tree is both finite and acyclic. But nothing prevents the heap-allocated tree to be a DAG; we will take care of that later.
The tree deletion operation  takes a non-null loc
takes a non-null loc  as argument. It is required to be the root of a tree, that is
as argument. It is required to be the root of a tree, that is
 , where
, where  is a tree of locations passed as an additional ghost parameter. To account for the absence of sharing in
is a tree of locations passed as an additional ghost parameter. To account for the absence of sharing in  , we also require that all locations in
, we also require that all locations in  are distinct, which is conveniently written as
are distinct, which is conveniently written as  . Let
. Let  be the pair returned by the function. The postcondition makes use of a second ghost parameter
be the pair returned by the function. The postcondition makes use of a second ghost parameter  to describe the shape of
to describe the shape of  . It simply says that
. It simply says that  , for some location
, for some location
 , with
, with  being the
being the
 field at
field at  . We avoid the use of an existential quantifier over
. We avoid the use of an existential quantifier over
 by performing pattern-matching over
by performing pattern-matching over  instead.
instead.
It is worth pointing out that our postcondition simply says that we deleted the first element from  , that is the leftmost innermost element in the tree rooted at
, that is the leftmost innermost element in the tree rooted at  . There is no need for the notion of binary search tree to show up. It would be an orthogonal (and easy) lemma to show that the minimal element in a binary search tree is located at the leftmost innermost node, and that after removal the remaining tree is still a binary search tree.
. There is no need for the notion of binary search tree to show up. It would be an orthogonal (and easy) lemma to show that the minimal element in a binary search tree is located at the leftmost innermost node, and that after removal the remaining tree is still a binary search tree.
5.3 Proof
The code itself is straightforward. First, it handles the particular case where there is no left subtree. Otherwise, it descends along the leftmost branch of the tree, using three variables  ,
,  , and
, and  to hold three consecutive nodes on this branch. This can be depicted as follows:
to hold three consecutive nodes on this branch. This can be depicted as follows:

We are done with the descent when  becomes
becomes  . Then we simply remove node
. Then we simply remove node  by turning the right subtree of
by turning the right subtree of  into the left subtree of
into the left subtree of  .
.
Proving the code, however, is not straightforward. The whole code annotated with assertions and equipped with ghost statements is given in Fig. 20. The loop performs some local computation, focusing on the subtree rooted at  , but the postcondition we wish to establish is related to the whole tree rooted at
, but the postcondition we wish to establish is related to the whole tree rooted at  . Thus we have to account for the “tree with a hole” depicted in gray in the picture above. Fortunately, there is a convenient way to define such a notion: Huet’s zipper [11]. The idea is to define a subtree placeholder as the path from the root of the subtree to the root of the whole tree. In the general case, this path should indicate whether we took the left or right subtree during the descent. In our case, however, we are always moving to the left subtree, so the zipper degenerates into a mere list, that is
. Thus we have to account for the “tree with a hole” depicted in gray in the picture above. Fortunately, there is a convenient way to define such a notion: Huet’s zipper [11]. The idea is to define a subtree placeholder as the path from the root of the subtree to the root of the whole tree. In the general case, this path should indicate whether we took the left or right subtree during the descent. In our case, however, we are always moving to the left subtree, so the zipper degenerates into a mere list, that is

The zipper \((\mathtt Left ~z~x~t)\) denotes a hole in place of the left subtree of a node with value \(x\), with right subtree \(t\), and with some upper context \(z\). The zipper Top denotes a hole at the root of the tree. For instance, the “tree with hole” \((\mathtt Node ~(\mathtt Node ~\Box ~x_2~t_2)~x_1~t_1)\) is denoted by the zipper \((\mathtt Left ~(\mathtt Left ~\mathtt Top ~x_1~t_1)~x_2~t_2)\).
From a zipper  and a subtree
and a subtree  , we can recover the whole tree with the following recursive function that rebuilds the nodes along the path:
, we can recover the whole tree with the following recursive function that rebuilds the nodes along the path:

The idea behind our proof is to maintain the zipper for the subtree rooted at  in a ghost variable
in a ghost variable  , as well as its left and right subtrees in two additional ghost variables
, as well as its left and right subtrees in two additional ghost variables  and
and  . This can be depicted as follows:
. This can be depicted as follows:

These three ghost variables are updated along the descent. Thus we have the following loop invariant:

Since the memory is not mutated within the loop, showing the preservation of this loop invariant is straightforward.
The difficult part of the proof lies in the final statement, once we have exited the loop and mutated the memory. The new tree is built from the zipper using

We have to show that the inorder traversal of that tree is the tail of the inorder traversal of the initial tree. But this only holds thanks to the lack of sharing in the tree, which is provided by the precondition  . Otherwise, more than one element could have disappeared from the list. We move that key property into the following lemma:
. Otherwise, more than one element could have disappeared from the list. We move that key property into the following lemma:

It is proved interactively using the Coq proof assistant. The proof introduces 8 sub-lemmas and requires 114 lines of Coq tactics, including the use of the  tactic to call external SMT solvers, as already mentioned for the two first challenges. The main reason for this proof to be that long is the lack of separation logic in Why3 (no notion of footprints, few lemmas about
tactic to call external SMT solvers, as already mentioned for the two first challenges. The main reason for this proof to be that long is the lack of separation logic in Why3 (no notion of footprints, few lemmas about  etc.).
etc.).
It is worth pointing out that the use of zippers is only an artifact of our proof. Zippers do not appear at all in our specification.
5.4 Proof statistics
Detailed proof results are given in Fig. 21 on page 15. (This does not include five auxiliary functions, for which proof details are available at URL http://toccata.lri.fr/gallery/verifythis_fm2012_treedel.en.html). The table below summarizes these results. The time limit given to automated provers is 5 s (apart from one goal, for which it is 60 s).
Function | # VCs | Automatically proved |
|---|---|---|
Auxiliary functions | 5 | 5 (100 %) |
Lemmas | 3 | 2 (67 %) |
| 30 | 29 (97 %) |
Total | 38 | 36 (95 %) |
Two VCs are discharged using Coq (128 lines of tactics).
The table below shows the results per prover, among the 36 VCs that are proved automatically.
Prover | Number of VCs proved |
|---|---|
Alt-Ergo 0.95.2 | 35 |
CVC3 2.4.1 | 34 |
CVC4 1.3 | 38 |
Z3 3.2 | 34 |
Z3 4.2 | 34 |
Since 36 VCs are discharged automatically, it is clear from this table that the cooperative use of several ATPs is a true asset.
5.5 Lessons learned
It is slightly unsatisfactory that we cannot handle this challenge in a direct way: Since WhyML does not allow arbitrary mutable data structures, we have to use an explicit encoding of a memory heap. Although we are able to handle this challenge successfully, it is clear that Why3 is not the language of choice to specify and prove pointer-heavy programs. It would be more natural to use verification tools dedicated to Java or C code, in particular since there exist such tools that are built upon Why3, using WhyML as an intermediate language: Krakatoa [13] for Java and Frama-C [10] and its Jessie plug-in [14] for C. Yet we think that doing the verification with Why3 has real benefits: it is easier to write and debug the specification and proof when VCs are not clobbered with a complex encoding of the memory heap. Once the specification with Why3 is completed and verified, one can adapt it to a Java or C implementation. In particular, we think that our idea of using a zipper in the proof can be readily reused.
6 Conclusions
We found the Why3 environment adequate for the given challenges. The specification language provides advanced tools that proved to be useful: algebraic data types, inductive predicates, and a rich standard library.
To perform the proofs, we needed several back-end provers; in particular, the more complex lemmas had to be proved interactively, using Coq. Even when considering only the VCs that were proved automatically, there is no prover among Alt-Ergo, CVC3, CVC4, and Z3 that was able to discharge all of them. Though the ability to use several provers is a clear advantage, it also makes the maintenance of proof sessions a difficult task. Why3 provides a mechanism for storing proof sessions that records which transformations and provers were used to prove each VC, so that a complete verification project can be replayed if needed [5]. Moreover, it is possible to dump such a session, e.g., Fig. 21 is automatically generated from the proof session of challenge 3. Similar tables for problems 1 and 2 are available online, in Why3’s gallery.
On the use of Coq. For each of the three challenges, we had to use Coq to discharge a few VCs that were not proved by automated provers. Writing a proof script for such VCs may seem to be a complex task that requires a fair knowledge of Coq. However, the  tactic helped us to keep such tasks reasonable: a proof starts with some powerful tactic that generates a few subgoals, and after a very little number of tactics, the
tactic helped us to keep such tasks reasonable: a proof starts with some powerful tactic that generates a few subgoals, and after a very little number of tactics, the  tactic is able to complete the proof. A typical example is a proof that requires induction. Another typical case is when explicit witnesses have to be provided for existential quantifiers, as in challenge 1. Although this process is reasonably quick and painless, it is necessary to know a little bit of Coq to use it. It is thus desirable to propose alternatives. Two recent features added to Why3 may help: first, a transformation that is able to perform induction on algebraic data types; second, a mechanism of “lemma functions”, similar to that of VeriFast and Dafny, that allows the user to write a recursive program to simulate an induction scheme of his choice. Lemma functions can also be used to generate witnesses for existentially quantified assertions. Still, the ability to perform an induction over an inductive predicate, as we did in challenges 1 and 2, remains to be studied. Last but not least, we are now planning to extend Why3 with a dedicated lightweight interactive prover that would simplify proofs even further.
tactic is able to complete the proof. A typical example is a proof that requires induction. Another typical case is when explicit witnesses have to be provided for existential quantifiers, as in challenge 1. Although this process is reasonably quick and painless, it is necessary to know a little bit of Coq to use it. It is thus desirable to propose alternatives. Two recent features added to Why3 may help: first, a transformation that is able to perform induction on algebraic data types; second, a mechanism of “lemma functions”, similar to that of VeriFast and Dafny, that allows the user to write a recursive program to simulate an induction scheme of his choice. Lemma functions can also be used to generate witnesses for existentially quantified assertions. Still, the ability to perform an induction over an inductive predicate, as we did in challenges 1 and 2, remains to be studied. Last but not least, we are now planning to extend Why3 with a dedicated lightweight interactive prover that would simplify proofs even further.
On the possible use of Frama-C/Jessie or Krakatoa. Why3 is indeed an intermediate verification language which is used by the front-ends Frama-C/Jessie (for C) and Krakatoa (for Java). Thus one might ask why we chose Why3 for the competition: after all, Java implementations were given for the first two challenges, and a language with pointers was mandatory for the third challenge. The first reason is that we decided, prior to the competition, that we were going to use Why3, because it is the tool we are developing. An important improvement that we developed in Why3 relies in the expressiveness of the specification language, that allows us to structure logical models into theories [7], and thus to design a well-structured, reusable standard library. This feature showed itself important during the competition. In the Jessie and Krakatoa front ends, there is no such a large standard library of specifications yet. Thus, another lesson we learned is that we should now improve the specification languages of the front ends. A non-trivial issue is how to reuse the same generic standard library for both Why3 and the front ends. Another point is that the modeling of the heap memory used by the front-ends results in VCs that are sometimes obscure. Finally, we believe that, when one wants to verify a given program, the first step is the design of adequate specifications and adequate proof elements such as loop invariants, auxiliary lemmas, assertions in the code, etc. This work is easier to carry out on a simple language such as WhyML. On a language such as C or Java, one immediately faces the extra burden of showing the absence of runtime errors such as integer overflow and invalid pointer dereferencing.
Notes
Notice that the non-ghost fields of
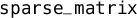 can still be used in regular, non-ghost code, which would not be the case were
can still be used in regular, non-ghost code, which would not be the case were  declared as a
declared as a  type.
type.Another purpose of transformations is to eliminate and encode various high-level features of Why3 language, such as pattern matching or type polymorphism, to make proof obligations acceptable for a range of external provers. These transformations are invoked by a driver for a particular prover and do not need to be applied explicitly by the user.
Calling a method on an object before it is fully constructed is indeed not recommended [18].
That came to our mind during the competition.
References
Barrett, C., Conway, C.L., Deters, M., Hadarean, L., Jovanović, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: Proceedings of the 23rd international conference on Computer aided verification, CAV’11, pp. 171–177. Heidelberg, Berlin (2011)
Barrett, C., Tinelli, C.: CVC3. In: Damm, W., Hermanns, H. (eds.) 19th International Conference on Computer Aided Verification, vol 4590 of Lecture Notes in Computer Science, pp. 298–302. Springer, Berlin (2007)
Bertot, Y., Castéran, P.: Interactive Theorem Proving and Program Development. Springer-Verlag, Berlin (2004)
Bobot, F., Conchon, S., Contejean, E., Iguernelala, M., Lescuyer, S., Mebsout, A.: The Alt-Ergo automated theorem prover. (2008) http://alt-ergo.lri.fr/
Bobot, F., Filliâtre, J.-C., Marché, C., Melquiond, G., Paskevich, A.: Preserving user proofs across specification changes. In: Cohen, E., Rybalchenko, A. (eds.) Verified software: theories, tools, experiments (5th International Conference VSTTE), vol 8164 of Lecture Notes in Computer Science, pp. 191–201. Springer, Atherton (2013)
Bobot, F., Filliâtre, J.-C., Marché, C., Melquiond, G., Paskevich, A.: The Why3 platform, version 0.82. LRI, CNRS & Univ. Paris-Sud & INRIA Saclay, version 0.82 edition. (2013) http://why3.lri.fr/download/manual-0.82.pdf
Bobot, F., Filliâtre, J.-C., Marché, C., Paskevich, A.: Why3: Shepherd your herd of provers. In: Boogie (ed.) First International Workshop on Intermediate Verification Languages, pp. 53–64. Wrocław, Poland (2011)
de Moura, L., Bjørner, N.: Z3, an efficient SMT solver. In: TACAS, vol 4963 of Lecture Notes in Computer Science, pp. 337–340. Springer, Berlin (2008)
Filliâtre, J.-C., Paskevich, A.: Why3—where programs meet provers. In: Felleisen, M., Gardner, P. (eds.) Proceedings of the 22nd European Symposium on Programming, vol 7792 of Lecture Notes in Computer Science, pp. 125–128. Springer, Berlin (2013)
The Frama-C platform for static analysis of C programs. (2008) http://www.frama-c.cea.fr/
Huet, G.: The Zipper. J. Fun. Progr. 7(5), 549–554 (1997)
Leino, K.R.M., Moskal, M.: VACID-0: Verification of ample correctness of invariants of data-structures. In: Proceedings of Tools and Experiments Workshop at VSTTE (2010)
Marché, C.: The Krakatoa tool for deductive verification of Java programs. Winter school on object-oriented verification, Viinistu, Estonia. (2009) http://krakatoa.lri.fr/ws/
Moy, Y., Marché, C.: The Jessie plugin for deduction verification in Frama-C – tutorial and reference manual. INRIA & LRI. (2011) http://krakatoa.lri.fr/
Owre, S., Rushby, J.M., Shankar, N.: PVS: A prototype verification system. In: Kapur, D. (ed). 11th International Conference on Automated Deduction, vol 607 of Lecture Notes in Computer Science, pp. 748–752. Springer, Saratoga Springs (1992)
Riazanov, A., Voronkov, A.: Vampire. In: Ganzinger, H. (ed.) 16th International Conference on Automated Deduction, vol 1632 of Lecture Notes in Artificial Intelligence, pp. 292–296. Springer, Trento (1999)
Schulz, S.: System description: E 0.81. In: Basin, D.A., Rusinowitch, M. (eds) Second International Joint Conference on Automated Reasoning, vol 3097 of Lecture Notes in Computer Science, pp. 223–228. Springer, Berlin (2004)
Summers, A.J., Mueller, P.: Freedom before commitment: a lightweight type system for object initialisation. In: Proceedings of the 2011 ACM international conference on Object oriented programming systems languages and applications, OOPSLA ’11, pp. 1013–1032. ACM, New York (2011)
Weidenbach, C., Dimova, D., Fietzke, A., Kumar, R., Suda, M., Wischnewski, P.: SPASS version 3.5. In: Schmidt, R.A. (ed.) 22nd International Conference on Automated Deduction, vol 5663 of Lecture Notes in Computer Science, pp 140–145. Springer, Berlin (2009)
Acknowledgments
We gratefully thank the editors and the anonymous referees for providing us very valuable comments and suggestions to improve the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Work partly supported by the Bware project of the French national research organization (ANR-12-INSE-0010, http://bware.lri.fr/).
Appendix: Relevant theories from the Why3 standard library
Appendix: Relevant theories from the Why3 standard library
In this Appendix, we provide details on relevant parts of the Why3 standard library, notably those used in the first challenge. The full contents of that library is available online at http://why3.lri.fr/stdlib-0.81/.
1.1 A.1 Library map
In Why3, arrays are modeled as references to purely applicative maps. Such maps are specified in the theory  presented in Fig. 22. These maps are parametric in both the type of their indexes and of their values, so the Why3 type for such maps is a polymorphic type
presented in Fig. 22. These maps are parametric in both the type of their indexes and of their values, so the Why3 type for such maps is a polymorphic type  . The main functions operating on maps are
. The main functions operating on maps are  and
and  , that, respectively, modify a map at a given index (purely applicatively, that is by returning a new map) and read a map at a given index. Both functions are axiomatized by
, that, respectively, modify a map at a given index (purely applicatively, that is by returning a new map) and read a map at a given index. Both functions are axiomatized by  and
and  . This is the classical theory of arrays in the context of satisfiability modulo theories. The additional operation
. This is the classical theory of arrays in the context of satisfiability modulo theories. The additional operation  returns a constant map.
returns a constant map.
Theory  (Fig. 23) specifies what it means for a map to be sorted in increasing order. This notion is restricted to maps indexed by integers. The theory is written with a type parameter
(Fig. 23) specifies what it means for a map to be sorted in increasing order. This notion is restricted to maps indexed by integers. The theory is written with a type parameter  and a predicate parameter
and a predicate parameter  , so that it can be reused, by cloning it, for an arbitrary order relation.
, so that it can be reused, by cloning it, for an arbitrary order relation.
Theory  (Fig. 24) specifies what it means for two maps to be permutations of each other, that is, to contain the same elements with the same number of occurrences. This is restricted to maps indexed by integers. Predicate (
(Fig. 24) specifies what it means for two maps to be permutations of each other, that is, to contain the same elements with the same number of occurrences. This is restricted to maps indexed by integers. Predicate ( \(m_1\, m_2\, l\, u\)) holds when map segments \(m_1[l\ldots u-1]\) and \(m_2[l\ldots u-1]\) are permutations of each other. This is defined as the smallest equivalence relation containing transpositions of elements.
\(m_1\, m_2\, l\, u\)) holds when map segments \(m_1[l\ldots u-1]\) and \(m_2[l\ldots u-1]\) are permutations of each other. This is defined as the smallest equivalence relation containing transpositions of elements.
Theory  (Fig. 25) defines several notions for maps on the domain \(0\ldots n-1\) for some integer \(n\): being injective, being a surjection into \(0\ldots n-1\), and ranging into \(0\ldots n-1\). Lemma
(Fig. 25) defines several notions for maps on the domain \(0\ldots n-1\) for some integer \(n\): being injective, being a surjection into \(0\ldots n-1\), and ranging into \(0\ldots n-1\). Lemma  is the classical mathematical result, more or less equivalent to the pigeon-hole principle, saying that any injection that ranges into \(0\ldots n-1\) is also surjective. This result is used to prove the first challenge. This is not the first time we had to use such a result to prove a program: we already used it to prove the challenge Sparse Arrays from the VACID-0 benchmarks [12].
is the classical mathematical result, more or less equivalent to the pigeon-hole principle, saying that any injection that ranges into \(0\ldots n-1\) is also surjective. This result is used to prove the first challenge. This is not the first time we had to use such a result to prove a program: we already used it to prove the challenge Sparse Arrays from the VACID-0 benchmarks [12].
1.2 A.2 Module Array
Figure 26 contains an excerpt of the Why3 module that defines arrays. This module is discussed in Sect. 2.2. The full contents of that library is available online at http://why3.lri.fr/stdlib-0.81/array.mlw.html.
Rights and permissions
About this article
Cite this article
Bobot, F., Filliâtre, JC., Marché, C. et al. Let’s verify this with Why3. Int J Softw Tools Technol Transfer 17, 709–727 (2015). https://doi.org/10.1007/s10009-014-0314-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10009-014-0314-5






 : computation of longest common prefix of substrings.
: computation of longest common prefix of substrings. : helper functions for sorting suffixes, roughly corresponding to the private part of the
: helper functions for sorting suffixes, roughly corresponding to the private part of the  class of the Java code.
class of the Java code. : the suffixArray data type, roughly corresponding to the public part of the
: the suffixArray data type, roughly corresponding to the public part of the  class of the Java code.
class of the Java code. : computation of longest repeated substring, corresponding to the
: computation of longest repeated substring, corresponding to the  class of the Java code.
class of the Java code.

 function
function
























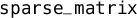 can still be used in regular, non-ghost code, which would not be the case were
can still be used in regular, non-ghost code, which would not be the case were  declared as a
declared as a  type.
type.




 (excerpt)
(excerpt)