An Axiomatization for BSP Algorithms

Abstract

The gurevich’s thesis stipulates that sequential abstract state machines (asms) capture the essence of sequential algorithms. On another hand, the bulk-synchronous parallel (bsp) bridging model is a well known model for hpc algorithm design. It provides a conceptual bridge between the physical implementation of the machine and the abstraction available to a programmer of that machine. The assumptions of the bsp model are thus provide portable and scalable performance predictions on most hpc systems. We follow gurevich’s thesis and extend the sequential postulates in order to intuitively and realistically capture bsp algorithms.

1 Introduction

1.1 Context of the Work

Nowadays, hpc (high performance computing) is the norm in many areas but it remains more difficult to have well defined paradigms and a common vocabulary as it is the case in the traditional sequential world. The problem arises from the difficulty to get a taxonomy of computer architectures and frameworks: there is a zoo of definitions of systems, languages, paradigms and programming models. Indeed, in the hpc community, several terms could be used to designate the same thing, so that misunderstandings are easy. We can cite parallel patterns [5] versus algorithmic skeletons [8]; shared memory (pram) versus thread concurrency and direct remote access (drma); asynchronous send/receive routines (mpi, http://mpi-forum.org/) versus communicating processes ($\pi$-calculus).

In the sequential world, it is easier to classify programming languages within their paradigm (functional, object oriented, etc.) or by using some properties of the compilers (statically or dynamically typed, abstract machine or native code execution). This is mainly due to the fact that there is an overall consensus on what sequential computing is. For them, formal semantics have been often studied and there are now many tools for testing, debugging, cost analyzing, software engineering, etc. In this way, programmers can implement sequential algorithms using these languages, which characterize properly the sequential algorithms.

This consensus is only fair because everyone informally agrees to what constitutes a sequential algorithm. And now, half a century later, there is a growing interest in defining formally the notion of algorithms [10]. Gurevich introduced an axiomatic presentation (largely machine independent) of the sequential algorithms in [10]. The main idea is that there is no language that truly represents all sequential algorithms. In fact, every algorithmic book presents algorithms in its own way and programming languages give too much detail. An axiomatic definition [10] of the algorithms has been mapped to the notion of abstract state machine (asm, a kind of Turing machine with the appropriate level of abstraction): Every sequential algorithm can be captured by an asm. This allows a common vocabulary about sequential algorithms. This has been studied by the asm community for several years.

A parallel computer, or a multi-processor system, is a computer composed of more than one processor (or unit of computation). It is common to classify parallel computers (flynn’s taxonomy) by distinguishing them by the way they access the system memory (shared or distributed). Indeed, the memory access scheme influences heavily the programming method of a given system. Distributed memory systems are needed for computations using a large amount of data which does not fit in the memory of a single machine.

The three postulates for sequential algorithms are mainly consensual. Nevertheless, to our knowledge, there is not such a work for hpc frameworks. First, due to the zoo of (informal) definitions and second, due to a lack of realistic cost models of common hpc architectures. In hpc, the cost measurement is not based on the complexity of an algorithm but is rather on the execution time, measured using empirical benchmarks. Programmers are benchmarking load balancing, communication (size of data), etc. Using such techniques, it is very difficult to explain why one code is faster than another and which one is more suitable for one architecture or another. This is regrettable because the community is failing to obtain some rigorous characterization of sub-classes of hpc algorithms. There is also a lack of studying algorithmic completeness of hpc languages. This is the basis from which to specify what can or cannot be effectively programmed. Finally, taking into account all the features of all hpc paradigms is a daunting task that is unlikely to be achieved [9]. Instead, a bottom up strategy (from the simplest models to the most complex) may be a solution that could serve as a basis for more general hpc models.

1.2 Content of the Work

Using a bridging model [20] is a first step to this solution because it simplifies the task of algorithm design, programming and simplifies the reasoning of cost and ensures a better portability from one system to another. A bridging model is an abstract model of a computer which provides a conceptual bridge between the physical implementation of the machine and the abstraction available to a programmer of that machine. We conscientiously limit our work to the bulk-synchronous parallel (bsp) bridging model [1, 18] because it has the advantage of being endowed with a simple model of execution. We leave more complex models to future work. Moreover, there are many different libraries and languages for programming bsp algorithms, for example, the bsplib for c [11] or java [17], bsml [?], pregel [12] for big-data, etc.

Concurrent asms [3] try to capture the more general definition of asynchronous and distributed computations. We promote a rather different “bottom-up” approach consisting of restricting the model under consideration, so as to better highlight the algorithm execution time (which is often too difficult to assess for general models) and more generally to formalize our algorithms of a bridging model at their natural level of abstraction, instead of using a more general model then restrict it with an arbitrary hypothesis.

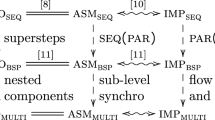
As a basis to this work, we first give an axiomatic definition of bsp algorithms ($\textsc {algo}_\textsc {BSP}$) with only 4 postulates. Then we extend the asm model [10] of computation ($\textsc {asm}_\textsc {BSP}$) for bsp. Our goal is to define a convincing set of parallel algorithms running in a predictable time and construct a model that computes these algorithms only. This can be summarized by $\textsc {algo}_\textsc {BSP}$ $=$ $\textsc {asm}_\textsc {BSP}$. An interesting and novel point of this work is that the bsp cost model is preserved.

1.3 Outline

Many definitions used here are well known to the asm community. Recalling all of them would be too long but they are available in the online technical report [22].

The remainder of this paper is structured as follows: In Sect. 2 we first recall the bsp model and define its postulates; Secondly, in Sect. 3, we give the operational semantics of $\textsc {asm}_\textsc {BSP}$ and finally, we give the main result. Section 4 concludes, gives some related work and a brief outlook on future work.

2 Characterizing BSP Algorithms

2.1 The BSP Bridging Model of Computation

As the ram model provides a unifying approach that can bridge the worlds of sequential hardware and software, so valiant sought [20] for a unifying model that could provide an effective (and universal) bridge between parallel hardware and software. A bridging model [20] allows to reduce the gap between an abstract execution (programming an algorithm) and concrete parallel systems (using a compiler and designing/optimizing a physical architecture).

The direct mode bsp model [1, 18] is a bridging model that simplifies the programming of various parallel architectures using a certain level of abstraction. The assumptions of the bsp model are to provide portable and scalable performance predictions on hpc systems. Without dealing with low-level details of hpc architectures, the programmer can thus focus on algorithm design only. The bsp bridging model describes a parallel architecture, an execution model for the algorithms, and a cost model which allows to predict their performances on a given bsp architecture.

A bsp computer can be specified by $\mathbf {p}$ uniform computing units (processors), each capable of performing one elementary operation or accessing a local memory in one time unit. Processors communicate by sending a data to every other processor in $\mathbf {g}$ time units (gap which reflects network bandwidth inefficiency), and a barrier mechanism is able to synchronise all the processors in $\mathbf {L}$ time units (“latency” and the ability of the network to deliver messages under a continuous load). Such values, along with the processor’s speed (e.g. Mflops) can be empirically determined by executing benchmarks.

Fig. 1.

A bsp super-step.

The time $\mathbf {g}$ is thus for collectively delivering a 1-relation which is a collective exchange where every processor receives/sends at most one word. The network can deliver an h-relation in time $\mathbf {g} \times h$. A bsp computation is organized as a sequence of supersteps (see Fig. 1). During a superstep, the processors may perform computations on local data or send messages to other processors. Messages are available for processing at their destinations by the next superstep, and each superstep is ended with the barrier synchronisation of the processors.

The execution time (cost) of a super-step s is the sum of the maximal of the local processing, the data delivery and the global synchronisation times. It is expressed by the following formula: $\text {Cost}(s)\!=\!w^{s} + h^s \times \mathbf {g} + \mathbf {L}$ where $w^{s}\!=\!\max _{0\le i< \mathbf {p}}(w_{i}^{s})$ (where $w_i^s$ is the local processing time on processor i during superstep s), and $h^s\!=\!\max _{0\le i< \mathbf {p}}(h_{i}^{s})$ (where $h_{i}^{s}$ is the maximal number of words transmitted or received by the processor i). Some papers rather use the sum of words for $h_{i}^{s}$ but modern networks are capable of sending while receiving data. The total cost (execution time) of a bsp algorithm is the sum of its super-step costs.

2.2 Axiomatic Characterization of BSP Algorithms

Postulate 1 (Sequential Time)

A bsp algorithm A is given by:

• 1. A set of states S(A);

• 2. A set of initial states $I(A) \subseteq S(A)$;

• 3. A transition function $\tau _A: S(A) \rightarrow S(A)$.

We follow [10] in which states, as first-order structures, are full instantaneous descriptions of an algorithm.

Definition 1 (Structure)

A (first-order) structure X is given by:

• 1. A (potentially infinite) set $\mathcal {U}(X)$ called the universe (or domain) of X

• 2. A finite set of function symbols $\mathcal {L}(X)$ called the signature (language) of X

• 3. For every symbol $s \in \mathcal {L}(X)$ an interpretation $\overline{s}^{X}$ such that:

  • (a) If c has arity 0 then $\overline{c}^{X}$ is an element of $\mathcal {U}(X)$

  • (b) If f has an arity $\alpha >0$ then $\overline{f}^{X}$ is an application: $\mathcal {U}(X)^\alpha \rightarrow \mathcal {U}(X)$

In order to have a uniform presentation [10], we considered constant symbols in $\mathcal {L}(X)$ as 0-ary function symbols, and relation symbols R as their indicator function $\chi _R$. Therefore, every symbol in $\mathcal {L}(X)$ is a function. Moreover, partial functions can be implemented with a special symbol $\mathbf {undef}$, and we assume in this paper that every $\mathcal {L}(X)$ contains the boolean type ($\lnot$, $\wedge$) and the equality. We also distinguish dynamic symbols whose interpretation may change from one state to another, and static symbols which are the elementary operations.

Definition 2 (Term)

A term of $\mathcal {L}(X)$ is defined by induction:

• 1. If c has arity 0, then c is a term

• 2. If f has an arity $\alpha >0$ and $\theta _1, \dots , \theta _\alpha$ are terms, then $f\left( \theta _1, \dots , \theta _\alpha \right)$ is a term

The interpretation $\overline{\theta }^{X}$ of a term $\theta$ in a structure X is defined by induction on $\theta$:

• 1. If $\theta =c$ is a constant symbol, then $\overline{\theta }^{X} \ {\mathop {=}\limits ^{\mathrm {def}}}\ \overline{c}^{X}$

• 2. If $\theta = f \left( \theta _1, \dots , \theta _\alpha \right)$ where f is a symbol of the language $\mathcal {L}(X)$ with arity $\alpha >0$ and $\theta _1,\dots ,\theta _\alpha$ are terms, then $\overline{\theta }^{X} \ {\mathop {=}\limits ^{\mathrm {def}}}\ \overline{f}^{X}(\overline{\theta _1}^{X},\dots ,\overline{\theta _\alpha }^{X})$

A formula F is a term with the particular form $\mathbf {true}| \mathbf {false}| R\left( \theta _1, \dots , \theta _\alpha \right) | \lnot F$ $| (F_1 \wedge F_2)$ where R is a relation symbol (ie a function with output $\overline{\mathbf {true}}^{X}$ or $\overline{\mathbf {false}}^{X}$) and $\theta _1, \dots , \theta _\alpha$ are terms. We say that a formula is true (resp. false) in X if $\overline{F}^{X} = \overline{\mathbf {true}}^{X}$ (resp. $\overline{\mathbf {false}}^{X}$).

A bsp algorithm works on independent and uniform computing units. Therefore, a state $S_t$ of the algorithm A must be a tuple $\left( X_t^1,\dots ,X_t^p\right)$. To simplify, we annotate tuples from 1 to p and not from 0 to $p\!-\!1$. Notice that $p$ is not fixed for the algorithm, so A can have states using different size of “p-tuples” (informally p, the number of processors). In this paper, we will simply consider that this number is preserved during a particular execution. In other words: the size of the p-tuples is fixed for an execution by the initial state of A for such an execution.

If $\left( X^1,\dots ,X^ p \right)$ is a state of the algorithm A, then the structures $X^1,\dots ,X^ p$ will be called processors or local memories. The set of the independent local memories of A will be denoted by M(A). We now define the bsp algorithms as the objects verifying the four presented postulates. The computation for every processor is done in parallel and step by step.

An execution of A is a sequence of states $S_0, S_1, S_2, \dots$ such that $S_0$ is an initial state and for every $t \in \mathbb {N}$, $S_{t+1} = \tau _{A}(S_t)$. Instead of defining a set of final states for the algorithms, we will say that a state $S_t$ of an execution is final if $\tau _A(S_t) = S_t$, that is the execution is: $S_0, S_1, \dots , S_{t-1}, S_t, S_t, \dots$ We say that an execution is terminal if it contains a final state.

We are interested in the algorithm and not a particular implementation (eg, the variables’ names), therefore in the postulate we will consider the states up to multi-isomorphism.

Definition 3 (Multi-isomorphism)

$\overrightarrow{\zeta }$ is a multi-isomorphism between two states $\left( X^1,\dots ,X^p\right)$ and $\left( Y^1,\dots ,Y^q\right)$ if $p = q$ and $\overrightarrow{\zeta }$ is a p-tuple of applications $\zeta _1$, ..., $\zeta _p$ such that for every $1 \le i \le p$, $\zeta _i$ is an isomorphism between $X^i$ and $Y^i$.

Postulate 2 (Abstract States)

For every bsp algorithm A:

• 1. The states of A are p-tuples of structures with the same finite signature $\mathcal {L}(A)$;

• 2. S(A) and I(A) are closed by multi-isomorphism;

• 3. The transition function $\tau _A$ preserves p, the universes and commutes with multi-isomorphisms.

For a bsp algorithm A, let X be a local memory of A, $f \in \mathcal {L}(A)$ be a dynamic $\alpha$-ary function symbol, and $a_1$, ..., $a_\alpha$, b be elements of the universe $\mathcal {U}(X)$. We say that $(f,a_1,\dots , a_\alpha )$ is a location of X, and that $(f,a_1,\dots , a_\alpha ,b)$ is an update on X at the location $(f,a_1,\dots , a_\alpha )$. For example, if x is a variable then (x, 42) is an update at the location x. But symbols with arity $\alpha > 0$ can be updated too. For example, if f is a one-dimensional array, then (f, 0, 42) is an update at the location (f, 0). If u is an update then $X\oplus u$ is a new structure of signature $\mathcal {L}(A)$ and universe $\mathcal {U}(X)$ such that the interpretation of a function symbol $f \in \mathcal {L}(A)$ is:

$$ \overline{f}^{X\oplus u}(\overrightarrow{a}) \ {\mathop {=}\limits ^{\mathrm {def}}}\ \left\{ \begin{array}{ll} b &{}\,\text {if }~ u = (f,\overrightarrow{a},b) \\ \overline{f}^{X}(\overrightarrow{a}) &{}\,\text {otherwise} \\ \end{array} \right. $$

where we noted $\overrightarrow{a}=a_1,\dots , a_\alpha$. For example, in $X\oplus (f,0,42)$, every symbol has the same interpretation than in X, except maybe for f because $\overline{f}^{X \oplus (f,0,42)}(0) = 42$ and $\overline{f}^{X \oplus (f,0,42)}(a) = \overline{f}^{X}(a)$ otherwise. We precised “maybe” because it may be possible that $\overline{f}^{X}(0)$ is already 42.

If $\overline{f}^{X}(\overrightarrow{a}) = b$ then the update $(f,\overrightarrow{a},b)$ is said trivial in X, because nothing has changed. Indeed, if $(f,\overrightarrow{a},b)$ is trivial in X then $X\oplus (f,\overrightarrow{a},b) = X$.

If $\varDelta$ is a set of updates then $\varDelta$ is consistent if it does not contain two distinct updates with the same location. Notice that if $\varDelta$ is inconsistent, then there exists $(f,\overrightarrow{a},b), (f,\overrightarrow{a},b') \in \varDelta$ with $b \not = b'$ and, in that case, the entire set of updates clashes:

$$ \overline{f}^{X\oplus \varDelta }(\overrightarrow{a}) \ {\mathop {=}\limits ^{\mathrm {def}}}\ \left\{ \begin{array}{ll} b &{} \text {if }~(f,\overrightarrow{a},b) \in \varDelta ~\text { and }~\varDelta \text { is consistent} \\ \overline{f}^{X}(\overrightarrow{a}) &{} \text {otherwise} \\ \end{array} \right. $$

If X and Y are two local memories of the same algorithm A then there exists a unique consistent set $\varDelta = \{(f,\overrightarrow{a},b)\ |\ \overline{f}^{Y}(\overrightarrow{a}) = b\text { and }\overline{f}^{X}(\overrightarrow{a}) \not = b\}$ of non trivial updates such that $Y = X \oplus \varDelta$. This $\varDelta$ is called the difference between the two local memories, and is denoted by $Y \ominus X$.

Let $\overrightarrow{X} = \left( X^1, \dots , X^ p \right)$ be a state of A. According to the transition function $\tau _A$, the next state is $\tau _A(\overrightarrow{X})$, which will be denoted by $(\tau _A(\overrightarrow{X})^1, \dots , \tau _A(\overrightarrow{X})^ p )$. We denote by $\varDelta ^{i}(A,\overrightarrow{X}) \ {\mathop {=}\limits ^{\mathrm {def}}}\ \tau _A(\overrightarrow{X})^i \ominus X^i$ the set of updates done by the i-th processor of A on the state $\overrightarrow{X}$, and by $\overrightarrow{\varDelta }(A,\overrightarrow{X}) \ {\mathop {=}\limits ^{\mathrm {def}}}\ (\varDelta ^{1}(A,\overrightarrow{X}), \dots , \varDelta ^{ p }(A,\overrightarrow{X}))$ the “multiset” of updates done by A on the state $\overrightarrow{X}$. In particular, if a state $\overrightarrow{X}$ is final, then $\tau _A(\overrightarrow{X}) = \overrightarrow{X}$, so $\overrightarrow{\varDelta }(A,\overrightarrow{X}) = \overrightarrow{\emptyset }$.

Let A be a bsp algorithm and T be a set of terms of $\mathcal {L}(A)$. We say that two states $\left( X^1,\dots ,X^p\right)$ and $\left( Y^1,\dots ,Y^q\right)$ of A coincide over T if $p = q$ and for every $1 \le i \le p$ and for every $t \in T$ we have $\overline{t}^{X^i} {=\,} \overline{t}^{Y^i}$.

Postulate 3 (Bounded Exploration for Processors)

For every bsp algorithm A there exists a finite set T(A) of terms such that for every state $\overrightarrow{X}$ and $\overrightarrow{Y}$, if they coincide over T(A) then $\overrightarrow{\varDelta }(A,\overrightarrow{X}) = \overrightarrow{\varDelta }(A,\overrightarrow{Y})$, i.e. for every $1 \le i \le p$, we have $\varDelta ^{i}(A,\overrightarrow{X}) = \varDelta ^{i}(A,\overrightarrow{Y})$.

T(A) is called the exploration witness [10] of A. If a set of terms T is finite then its closure by subterms is finite too. We assume that T(A) is closed by subterms and the symbol “$\mathbf {true}$” should always be in the exploration witness [10]. The interpretations of the terms in T(A) are called the critical elements and we prove in [22] that every value in an update is a critical element:

Lemma 1 (Critical Elements)

For every state $\left( X^1,\dots ,X^p\right)$ of A, $\forall i \ 1\!\le \!i\!\le \!p$, if $(f,\overrightarrow{a},b)\!\in \!\varDelta ^{i}(A,\overrightarrow{X})$ then $\overrightarrow{a},b$ are interpretations in $X^i$ of terms in T(A).

That implies that for every step of the computation, for a given processor, only a bounded number of terms are read or written (amount of work).

Lemma 2 (Bounded Set of Updates)

For every state $\left( X^1,\dots ,X^p\right)$ of the algorithm A, for every $1\!\le \!i\!\le \!p$, $|\varDelta ^{i}(A,\overrightarrow{X})|$ is bounded.

Notice that for the moment we make no assumption on the communication between processors. Moreover, these three postulates are a “natural” extension of the ones of [10]. And by “natural”, we mean that if we assume that $p =1$ then our postulates are exactly the same:

Lemma 3 (A Single Processor is Sequential)

A bsp algorithm with a unique processor ($p=1$) is a sequential algorithm. Therefore $\textsc {algo}_\textsc {seq} \subseteq$ $\textsc {algo}_\textsc {BSP}$. We now organize the sequence of states into supersteps. The communication between local memories occurs only during a communication phase. In order to do so, a bsp algorithm A will use two functions $\text {comp}_{A}$ and $\text {comm}_{A}$ indicating if A runs computations or if it runs communications.

Postulate 4 (Supersteps phases)

For every bsp algorithm A there exists two applications $\text {comp}_{A}: M(A) \rightarrow M(A)$ commuting with isomorphisms, and $\text {comm}_{A}: S(A) \rightarrow S(A)$, such that for every state $\left( X^1,\dots ,X^ p \right)$:

$$\tau _A\left( X^1,\dots ,X^p\right) = \left\{ \begin{array}{l@{}l} \left( \text {comp}_{A}(X^1),\dots ,\text {comp}_{A}(X^p)\right) {}&{}\text {if} ~\exists 1 \le i \le p \\ {}&{} \text {such that}~ \text {comp}_{A}(X^i) \not = X^i \\ \text {comm}_{A}\left( X^1,\dots ,X^ p \right) {}&{}\text {otherwise} \\ \end{array} \right. $$

A BSP algorithm is an object verifying these four postulates, and we denote by $\textsc {algo}_\textsc {BSP}$ the set of the bsp algorithms. A state $\left( X^1,\dots ,X^ p \right)$ will be said in a computation phase if there exists $1 \le i \le p$ such that $\text {comp}_{A}(X^i) \not = X^i$. Otherwise, the state will be said in a communication phase.

This requires some remarks. First, at every computation step, every processor which has not terminated performs its local computations. Second, we do not specified the function $\text {comm}_{A}$ in order to be generic about which bsp library is used. We discuss in Sect. 3.3 the difference between $\text {comm}_{A}$ and the usual communication routines in the bsp community.

Remember that a state $\overrightarrow{X}$ is said to be final if $\tau _A(\overrightarrow{X}) = \overrightarrow{X}$. Therefore, according to the fourth postulate, $\overrightarrow{X}$ must be in a communication phase which is like a final phase that would terminate the whole execution as found in mpi.

We prove that the bsp algorithms satisfy, during a computation phase, that every processor computes independently of the state of the other processors:

Lemma 4 (No Communication during Computation Phases)

For every states $\left( X^1,\dots ,X^p\right)$ and $\left( Y^1,\dots ,Y^q\right)$ in a computing phase, if $X^i$ and $Y^j$ have the same critical elements then $\varDelta ^{i}(A,\overrightarrow{X}) = \varDelta ^{j}(A,\overrightarrow{Y})$.

2.3 Questions and Answers

Why not using a bsp -Turing machine to define an algorithm?

It is known that standard Turing machines could simulate every algorithm. But we are here interested in the step-by-step behavior of the algorithms, and not the input-output relation of the functions. In this way, there is not a literal identity between the axiomatic point of view (postulates) of algorithms and the operational point of view of Turing machines. Moreover, simulating algorithms by using a Turing-machine is a low-level approach which does not describe the algorithm at its natural level of abstraction. Every algorithm assumes elementary operations which are not refined down to the assembly language by the algorithm itself. These operations are seen as oracular, which means that they produce the desired output in one step of computation.

But I think there is too much abstractions: When using bsplib , messages received at the past superstep are dropped. Your function ${\textit{comm}}_{ A}$ does not show this fact.

We want to be as general as possible. Perhaps a future library would allow reading data received n supersteps ago as the BSP+ model of [19]. Moreover, the communication function may realize some computations and is thus not a pure transmission of data. But the exploration witness forbids doing whatever: only a finite set of symbols can be updated. And we provide a realistic example of such a function which mainly correspond to the bsplib ’s primitives [22].

And why is it not just a permutation of values to be exchanged?

The communications can be used to model synchronous interactions with the environment (input/output or error messages, etc.) and therefore make appear or disappear values.

And when using bsplib and other bsp libraries, I can switch between sequential computations and bsp ones. Why not model this kind of feature?

The sequential parts can be modeled as purely asynchronous computations replicated and performed by all the processors. Or, one processor (typically the first one) is performing these computations while other processors are “waiting” with an empty computation phase.

In [2, 3, 15, 16], the authors give more general postulates about concurrent and/or distributed algorithms? Why not using their works by adding some restrictions to take into account the bsp model of execution?

It is another solution. But we think that the restrictions on “more complex” postulates is not a natural characterization of the bsp algorithms. It is better for a model to be expressed at its natural level of abstraction in order to highlight its own properties. For example, there is the problematic of the cost model which is inherent to a bridging model like bsp: It is not clear how such restrictions could highlight the cost model.

Fine. But are you sure about your postulates? I mean, are they completely (and not more) defined bsp algorithms?

It is impossible to be sure because we are formalizing a concept that is currently only intuitive. But as they are general and simple, we believe that they correctly capture this intuitive idea. We prove in the next section that a natural operational model for bsp characterizes exactly those postulates.

Would not that be too abstract? The bsp model is supposed to be a bridging model.

We treat algorithms at their natural level of abstraction, and not as something to refine to machines: We explicitly assume that our primitives may not be elementary for a typical modern architecture (but could be so in the future) and that they can achieve a potentially complex operation in one step. This makes it possible to get away from a considered hardware model and makes it possible to calculate the costs in time (and in space) in a given framework which can be variable according to what is considered elementary. For example, in an Euclidean algorithm, it is either the Euclidean division that is elementary or the subtraction. If your bsp algorithm uses elementary operations which can not be realized on the bsp machine considered, then you are just not at the right level abstraction. Our work is still valid for any level of abstraction.

3 BSP-ASM Captures the BSP Algorithms

The four previous postulates define the bsp algorithms from an axiomatic viewpoint but that does not mean that they have a model, or in, other words, that they are defined from an operational point of view. In the same way that the model of computation asm captures the set of the sequential algorithms [10], we prove in this section that the $\textsc {asm}_\textsc {BSP}$ model captures the bsp algorithms.

3.1 Definition and Operational Semantics of ASM-BSP

Definition 4

(ASM Program [10])

$$\begin{array}{rl} \varPi \ {\mathop {=}\limits ^{\mathrm {def}}}\ &{}f \left( t_1, \dots , t_\alpha \right) := t_0 \\ | &{}\mathtt {if}\ F\ \mathtt {then}\ \varPi _1\ \mathtt {else}\ \varPi _2\ \mathtt {endif} \\ | &{}\mathtt {par}\ \varPi _1 \Vert \dots \Vert \varPi _n\ \mathtt {endpar} \\ \end{array}$$

where f has arity $\alpha$; F is a formula; $\theta _1$, ..., $\theta _\alpha$, $\theta _0$ are terms of $\mathcal {L}(X)$. Notice that if $n=0$ then $\mathtt {par}\ \varPi _1 \Vert \dots \Vert \varPi _n\ \mathtt {endpar}$ is the empty program. If in $\mathtt {if}\ F\ \mathtt {then}\ \varPi _1\ \mathtt {else}\ \varPi _2\ \mathtt {endif}$ the program $\varPi _2$ is empty we will write simply $\mathtt {if}\ F\ \mathtt {then}\ \varPi _1\ \mathtt {endif}$. An asm machine [10] is thus a kind of Turing machine using not a tape but an abstract structure X.

Definition 5 (ASM Operational Semantics)

$$\begin{array}{rl} \varDelta (f \left( \theta _1, \dots , \theta _\alpha \right) := \theta _0,X) &{}\ {\mathop {=}\limits ^{\mathrm {def}}}\ \left\{ (f, \overline{\theta _1}^{X}, \dots , \overline{\theta _\alpha }^{X}, \overline{\theta _0}^{X})\right\} \\ \varDelta (\mathtt {if}\ F\ \mathtt {then}\ \varPi _1\ \mathtt {else}\ \varPi _2\ \mathtt {endif},X) &{}\ {\mathop {=}\limits ^{\mathrm {def}}}\ \varDelta (\varPi _i,X) \\ &{}\text {where} \left\{ \begin{array}{ll} i=1 &{} \text {if}~ F~ \text {is true on}~ X \\ i=2 &{} \text {otherwise} \\ \end{array} \right. \\ \varDelta (\mathtt {par}\ \varPi _1 \Vert \dots \Vert \varPi _n\ \mathtt {endpar},X) &{}\ {\mathop {=}\limits ^{\mathrm {def}}}\ \varDelta (\varPi _1,X) \cup \dots \cup \varDelta (\varPi _n,X) \\ \end{array}$$

Notice that the semantics of the $\mathtt {par}$ is a set of updates done simultaneously, which differs from an usual imperative framework. A state of a $\textsc {asm}_\textsc {BSP}$ machine is a $p$-tuple of memories $(X^1,\dots ,X^ p )$. We assume that the $\textsc {asm}_\textsc {BSP}$ programs are spmd (single program multiple data) which means that at each step of computation, the $\textsc {asm}_\textsc {BSP}$ program $\varPi$ is executed individually on each processor. Therefore $\varPi$ induces a multiset of updates $\overrightarrow{\varDelta }$ and a transition function $\tau _\varPi$:

$$\begin{array}{r@{}l} \overrightarrow{\varDelta }(\varPi ,\left( X^1, \dots , X^ p \right) ) &{}{}\ {\mathop {=}\limits ^{\mathrm {def}}}\ \left( \varDelta (\varPi , X^1), \dots , \varDelta (\varPi , X^ p )\right) \\ \tau _\varPi \left( X^1, \dots , X^ p \right) &{}{}\ {\mathop {=}\limits ^{\mathrm {def}}}\ \left( X^1 \oplus \varDelta (\varPi , X^1), \dots , X^ p \oplus \varDelta (\varPi , X^ p )\right) \\ \end{array}$$

If $\tau _\varPi (\overrightarrow{X}) = \overrightarrow{X}$, then every processor has finished its computation steps. In that case we assume that there exists a communication function to ensure the communication between processors.

Definition 6

An $\textsc {asm}_\textsc {BSP}$ machine M is a triplet (S(M), I(M), $\tau _M)$ such that:

• 1. S(M) is a set of tuples of structures with the same finite signature $\mathcal {L}(M)$; S(M) and $I(M) \subseteq S(M)$ are closed by multi-isomorphism;

• 2. $\tau _M : S(M) \mapsto S(M)$ verifies that there exists a program $\varPi$ and an application $\text {comm}_{M} : S(M) \mapsto S(M)$ such that:

  $$\tau _M(\overrightarrow{X}) = \left\{ \begin{array}{rl} \tau _\varPi (\overrightarrow{X}) &{}\text {if }~ \tau _\varPi (\overrightarrow{X}) \not = \overrightarrow{X} \\ \text {comm}_{M}(\overrightarrow{X}) &{}\text {otherwise} \\ \end{array} \right. $$

• 3. $\text {comm}_{M}$ verifies that:

  • (1) For every state $\overrightarrow{X}$ such that $\tau _\varPi (\overrightarrow{X}) = \overrightarrow{X}$, $\text {comm}_{M}$ preserves the universes and the number of processors, and commutes with multi-isomorphisms

  • (2) There exists a finite set of terms $T(\text {comm}_{M})$ such that for every state $\overrightarrow{X}$ and $\overrightarrow{Y}$ with $\tau _\varPi (\overrightarrow{X}) = \overrightarrow{X}$ and $\tau _\varPi (\overrightarrow{Y}) = \overrightarrow{Y}$, if they coincide over $T(\text {comm}_{M})$ then $\overrightarrow{\varDelta }(M,\overrightarrow{X}) = \overrightarrow{\varDelta }(M,\overrightarrow{Y})$.

We denote by $\textsc {asm}_\textsc {BSP}$ the set of such machines. As before, a state $\overrightarrow{X}$ is said final if $\tau _M(\overrightarrow{X}) = \overrightarrow{X}$. So if $\overrightarrow{X}$ is final then $\tau _\varPi (\overrightarrow{X}) = \overrightarrow{X}$ and $\text {comm}_{M}(\overrightarrow{X}) = \overrightarrow{X}$.

The last conditions about the communication function may seem arbitrary, but they are required to ensure that the communication function is not a kind of magic device. For example, without these conditions, we could imagine that $\text {comm}_{M}$ may compute the output of the algorithm in one step, or solve the halting problem. Moreover, we construct an example of $\text {comm}_{M}$ in [22] (Section D).

3.2 The BSP-ASM Thesis

We prove that $\textsc {asm}_\textsc {BSP}$ captures the computation phases of the bsp algorithms in three steps. First, we prove that during an execution, each set of updates is the interpretation of an asm program (Lemma 8 p.16 [22]). Then, we prove an equivalence between these potentially infinite number of programs (Lemma 9 p.17). Finally, by using the third postulate, we prove in Lemma 10 p.18 that there is only a bounded number of relevant programs, which can be merged into a single one.

Proposition 1 (BSP-ASMs capture Computations of BSP Algorithms)

For every bsp algorithm A, there exists an asm program $\varPi _A$ such that for every state $\overrightarrow{X}$ in a computation phase: $\overrightarrow{\varDelta }(\varPi _A,\overrightarrow{X}) = \overrightarrow{\varDelta }(A,\overrightarrow{X})$.

Theorem 1

$\textsc {algo}_\textsc {BSP}$ $=\!\!$ $\textsc {asm}_\textsc {BSP}$ (The proof is available in [22], Section C p.20).

3.3 Cost Model Property and the Function of Communication

There is two more steps in order to claim that $\textsc {asm}_\textsc {BSP}$ objects are the bsp bridging model algorithms: (1) To ensure that the duration corresponds to the standard cost model and; (2) To solve issues about the communication function.

Cost Model. If the execution begins with a communication, we assume that no computation is done for the first superstep. We remind that a state $\overrightarrow{X_t}$ is in a computation phase if there exists $1 \le i \le p$ such that $\text {comp}_{A}(X^i_t) \not = X^i_t$. The computation for every processor is done in parallel, step by step. So, the cost in time of the computation phase is $w\ {\mathop {=}\limits ^{\mathrm {def}}}\ \max _{1 \le i \le p}\left( w_i\right)$, where $w_i$ is the number of steps done by the processor i (on processor $X^i$) during the superstep.

Then the state is in a communication phase, when the messages between the processors are sent and received. Notice that $\text {comm}_{A}$ may require several steps in order to communicate the messages, which contrasts with the usual approach in bsp where the communication actions of a superstep are considered as one unit. But this approach would violate the third postulate, so we had to consider a step-by-step communication approach, then consider these actions as one communication phase. $\textsc {asm}_\textsc {BSP}$ exchanges terms and we show in [22] how formally define the size of terms. But we can imagine a machine that must further decompose the terms in order to transmit them (in bits for example). We just assume that the data are communicable in time $\mathbf {g}$ for a 1-relation.

So, during the superstep, the communication phase requires $h\times \mathbf {g}$ steps. It remains to add the cost of the synchronization of the processors, which is assumed in the usual bsp model to be a parameter $\mathbf {L}$. Therefore, we obtained a cost property which is sound with the standard bsp cost model.

A Realization of the Communication. An example of a communication function for the standard bsplib ’s primitives , , is presented in [22] (Section D).

Proposition 2 (Communication)

A function of communication, with routines for distant readings/writings and point-to-point sendings, performing an h-relation and requiring at most $h$ exchanges can be designed using asm.

One may argue that the last postulate allows the communication function to do computations. To avoid it, we assume that the terms in the exploration witness T(M) can be separated between $T(\varPi )$ and $T(\text {comm}_{M})$ such that $T(\varPi )$ is for the states in a computation phase, and that for every update $(f,\overrightarrow{a},b)$ of a processor $X^i$ in a communication phase, either there exists a term $t \in T(\text {comm}_{M})$ such that $b = \overline{t}^{X^i}$, or there exists a variable $v \in T(\varPi )$ and a processor $X^j$ such that $b = \overline{t_{\overline{v}^{X^j}}}^{X^i}$ (representation presented in Section D p.24). To do a computation, a term like $x+1$ is required, so the restriction to a variable prevents the computations of the terms in $T(\varPi )$. Or course, the last communication step should be able to write in $T(\varPi )$, and the final result should be read in $T(\varPi )$.

4 Conclusion and Future Work

4.1 Summary of the Contribution

A bridging model provides a common level of understanding between hardware and software engineers. It provides software developers with an attractive escape route from the world of architecture-dependent parallel software [20]. The bsp bridging model allows the design of “immortal” (efficient and portable) parallel algorithms using a realistic cost model (and without any overspecification requiring the use of a large number of parameters) that can fit most distributed architectures. It has been used with success in many domains [1].

We have given an axiomatic definition of bsp algorithms by adding only one postulate to the sequential ones for sequential algorithms [10] which has been widely accepted by the scientific community. Mainly this postulate is the call of a function of communication. We abstract how communication is performed, not be restricting to a specific bsp library. We finally answer previous criticisms by defining a convincing set of parallel algorithms running in a predictable time.

Our work is relevant because it allows universality (immortal stands for bsp computing): all future bsp algorithms, whatever their specificities, will be captured by our definitions. So, our $\textsc {asm}_\textsc {BSP}$ is not just another model, it is a class model, which contains all bsp algorithms.

This small addition allows a greater confidence in this formal definition compared to previous work: Postulates of concurrent asms do not provide the same level of intuitive clarity as the postulates for sequential algorithms. But our work is limited to bsp algorithms even if it is still sufficient for many hpc and big-data applications. We have thus revisited the problem of the “parallel ASM thesis” i.e., to provide a machine-independent definition of bsp algorithms and a proof that these algorithms are faithfully captured by $\textsc {asm}_\textsc {BSP}$. We also prove that the cost model is preserved which is the main novelty and specificity of this work compared to the traditional work about distributed or concurrent asms.

4.2 Questions and Answers About this Work

Why do you use a new model of computation $\textsc {asm}_\textsc {BSP}$ instead of asms only? Indeed, each processor can be seen as a sequential asm. So, in order to simulate one step of a bsp algorithm using several processors, we could use pids to compute sequentially the next step for each processor by using an asm.

Even if such a simulation exists between these two models, what you mean, a “sequentialization” (each processor, one after the other) of the bsp model of execution, cannot be exactly the function of transition of the postulates. Moreover, in order to stay bounded, having p exploration witness (one for each sequential asm) induces p to be a constant for the algorithm. In our work, p is only fixed of each execution, making the approach more general when modeling algorithms.

Is another model possible to characterize the bsp algorithms?

Sure. This can be more useful for proving some properties. But that would be the same set, just another way to describe it.

So, reading the work of [3], a distributed machine is defined as a set of pairs $(a,\varPi _a)$ where a is the name of the machine and $\varPi _a$ a sequential asm . Reading your definition, I see only one $\varPi$ and not “p” processors as in the bsp model. I thus not imagine a bsp computer as it is.

You are absolutely right but we do not model a bsp computer, our work is about bsp algorithms. The $\textsc {asm}_\textsc {BSP}$ program contains the algorithm which is used on each “processor” (a first-order structure as explain before). These are the postulates (axiomatic point of view) that characterize the class of bsp algorithms rather than a set of abstract machines (operational point of view). That is closer to the original approach [10]. We also want to point out that, unlike [3], we are not limited to a finite (fixed) set of machines: In our model, an algorithm is defined for $p=1,2,1000,$ etc. And we are not limited to point-to-point communications.

Ok, but with only a single code, you cannot have all the parallel algorithms...

We follow [4] about the difference between a PARallel composition of SEQuential actions (PAR of SEQ) and a SEQuential composition of PARallel actions (SEQ of PAR). Our $\textsc {asm}_\textsc {BSP}$ is SEQ(PAR). This leads to a macroscopic point of view¹ which is close to a specification. Being a SEQ(PAR) model allows a high level description of the bsp algorithms.

So, why are you limited to spmd computations?

Different codes can be run by the processors using conditionals on the “id” of the processors. For example “if pid=0 then code1 else code2” for running “code1” (e.g. master part) only on processor 0. Again, we are not limited to spmd computations. The asm program $\varPi$ fully contains the bsp algorithm, that is all the“actions” that can be performed by any processors, not necessarily the same instructions: Each processor picks the needed instruction to execute but there could be completely different. Only the size of $\varPi$ is finite due to the exploration witness. For example, it is impossible to have a number of conditionals in $\varPi$ that depends of p. Indeed, according to Lemma 4, during a computation phase, if two processors coincide over the exploration witness, then they will use the same code. And according to Postulate 3, the exploration witness is bounded. So, there exists only a bounded number c of possible subroutines during the computation phase, even if $p{\gg }c$.

Notice that processors may not know their own ids and there is no order in p-tuples; We never use such a property: Processors are organized like a set and we use tuples only for convenience of notation. We are using p-tuples just to add the bsp execution model in the original postulates of [10].

Ok, but I cannot get the interleavings of the computations as in [3]? Your model seems very synchronous!

The bsp model makes the hypothesis that the processors are uniform. So if one processor can perform one step of the algorithm, there is no reason to lock it just to highlight an interleaving. And if there is nothing to do, it does nothing until the phase of communication. Our execution model is thus largely “asynchronous” during the computation phases.

Speaking about communication, why apply several times the function of communication? When designing a bsp algorithm, I use once a collective operation!

An asm is like a Turing machine. It is not possible to perform all the communications in a single step: The exploration witness forbids doing this. Our function of communication performs some exchanges until there are no more.

What happens in case of runtime errors during communications?

Typically, when one processor has a bigger number of super-steps than other processors, or when there is an out-of-bound sending or reading, it leads to a runtime error. The bsp function of communication can return a $\bot$ value. That causes a stop of the operational semantics of the $\textsc {asm}_\textsc {BSP}$.

4.3 Related Work

As far as we know, some work exists to model distributed programs using asms [15] but none to convincingly characterize bsp algorithms. In [6], authors model the p3l set of skeletons. That allows the analyze of p3l programs using standard asm tools but not a formal characterization of what p3l is and is not.

The first work to extend asms for concurrent, distributed, agent-mobile algorithms is [2]. Too many postulates are used making the comprehension hard to follow or worse (loss of confidence). A first attempt to simplify this work has been done in [16] and again simplified in [7] by the use of multiset comprehension terms to maintain a kind of bounded exploration. Then, the authors prove that asms captures these postulates. Moreover, we are interested in distributed (hpc) computations more than parallel (threading) asms.

We want to clarify one thing. The asm thesis comes from the fact that sequential algorithms work in small steps, that is steps of bounded complexity. But the number of processors (or computing units) is unbounded for parallel algorithms, which motivated the work of [2] to define parallel algorithms with wide steps, that is steps of unbounded complexity. Hence the technicality of the presentation, and the unconvincing attempts to capture parallel algorithms [3].

Extending the asms for distributed computing is not new [3]. We believe that these postulates are more general than ours but we think that our extension still remains simple and natural for bsp algorithms. The authors are also not concerned about the problem of axiomatizing classes of algorithms using a cost model which is the heart of our work and the main advantage of the bsp model.

4.4 Future Work

This work leads to many possible work. First, how to adapt our work to a hierarchical extension of bsp [21] which is closer to modern hpc architectures?

Second, bsp is a bridging model between hardwares and softwares. It could be interesting to study such a link more formally. For example, can we prove that the primitives of a bsp language can truly “be bsp ” on a typical cluster architecture?

Thirdly, we are currently working on extending the work of [13] in order to give the bsp algorithmic completeness of a bsp imperative programming language. There are some concrete applications: There are many languages having a bsp-like model of execution, for example pregel [12] for writing large-graph algorithms. An interesting application is proving which are bsp algorithmically complete and are not. bsplib programs are intuitively bsp. mapreduce is a good candidate to be not [14]. Similarly, one can imagine proving which languages are too expressive for bsp. mpi is intuitively one of them. Last, the first author is working on postulates for more general distributed algorithm à la mpi .

In any case, studying the bsp-ram (such as the communication-oblivious of [19]) or mapreduce, would led to define subclasses of bsp algorithms.