Dynamic Buckling of Functionally Graded Plates and Shells Subjected to Thermal Shock

Abstract

In this work, the nonlinear dynamic response of suddenly heated functionally graded shells is studied through nonlinear transient analysis. To this end, a triangular shell finite element with 15 degrees of freedom is developed using the invariant-based approach and the concept of the surface of mass. Equations of motion of the shell finite-element model are integrated numerically by the Newmark method combined with iterative refinement of the solution using the Newton–Raphson procedure. For each time increment, the transient temperature field across the shell thickness is determined by iteratively solving the unsteady heat-conduction equation taking into account temperature-dependent properties of the material. The predicted temperature profile is used to compute the nodal thermal loads and temperature-dependent stiffness characteristics of the shell element. The proposed finite-element element formulation is validated against the available solutions of dynamic problems of plates and shells. A number of examples are given to demonstrate nonlinear capabilities of the proposed formulation and to estimate the effect of dynamic thermal loading on buckling instability of FGM plates and shells.

19.1 Introduction

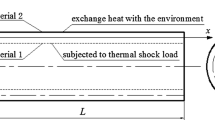
In various fields of engineering, structural members have to operate in thermal environment characterized by elevated temperatures and high thermal gradients. Aerospace technology and nuclear engineering are modern areas of engineering where structures may be subjected to rapid surface heating, which leads to unsteady heat conduction and high thermal stresses referred to as thermal shock. Thin-walled members subjected to thermal shock may experience large-amplitude motion and even exhibit unstable behavior that affects the performance of the structure.

Boley (1956) was the first to provide theoretical analysis of thermally induced vibrations of a thin beam subjected to step heating. Based on the linear beam bending theory, he obtained the exact analytical solution governing forced lateral vibrations caused by thermal moment that occurs due to transient non-uniform temperature distribution through the beam cross-section. Jones (1966), Seibert and Rice (1973) refined the solution of the problem by taking into account transverse shear effects and rotary inertia. One of the earliest finite-element formulations for dynamic analysis of beams and plates under unsteady heat conduction was proposed by Mason (1968). Stroud and Mayers (1971) studied the effect of temperature-dependent material properties on the dynamic response of a rapidly heated plate. It was shown that neglect or even incomplete consideration of the temperature dependence can lead to dangerously unconservative results. Das (1983) reported on vibrations of thin polygonal plates subjected to thermal shock through the complex variable theory. Irie and Yamada (1978) obtained analytical solution governing thermally induced axisymmetric vibrations of circular and annular plates subjected to a sinusoidally varying heat flux. Based on coupled equations of thermoelasticity, Al-Huniti et al. (2003) studied small transient deflections of a thin simply supported rectangular plate subjected to suddenly applied laser pulse of short duration. Nakajo and Hayashi (1988) studied dynamic axisymmetric response of circular plates under thermal impact by analytical and finite-element methods. They emphasized the significance of geometric nonlinearity in the analysis of plates with immovable edge. The studies mentioned above deal with homogeneous isotropic plates.

Tauchert (1989) investigated thermally induced vibrations of homogeneous orthotropic rectangular plates having two parallel simply supported edges. Chang et al. (1992) developed a finite element for linear analysis of thermally-induced vibrations of shear deformable laminated plates under thermal impact. Based on the finite-element results, they discussed the effect of boundary conditions and stacking sequence of laminates on the magnitude of vibrations. Adams and Bert (1999) studied the effect of orthotropic mechanical and thermal properties of the material on small-amplitude vibrations of a thin symmetrically laminated rectangular plate subjected to a step heat flux. The transient stresses and displacements in a thin orthotropic cylindrical shell subjected to instantaneous thermal shock were discussed by Huan and Wo (1980). Using the Donnel shell theory, Birman (1990) presented the analysis of dynamic response of linear and geometrically nonlinear reinforced cylindrical shells manufactured from composite materials. For various reinforcements, he evaluated the critical temperature at which the shells exhibit dynamic buckling behavior.

There has been a renewed interest in the analysis of thermally induced vibrations after the advent of functionally gradient materials (FGM) representing new class of advanced composite materials. Owing to high thermal resistance, FGMs are used in the design of structures operating under ultrahigh temperatures and large thermal gradients. There exists a large body of literature on stresses, vibrations, and buckling of mechanically and thermally loaded structural elements fabricated of FGMs. In what follows, we confine our review to those contributions that deal with thermally induced vibrations of rapidly heated thin-walled structures.

Ma and Lee (2011) reported on small-amplitude lateral vibrations of a shear-deformable FG beam about thermally bent configuration caused by uniform temperature distribution. Based on the numerical solution of the governing equations, they studied the effect of thermal load on the beam frequencies taking into account temperature-dependent material properties. A more accurate approach based on nonlinear transient analysis of FG beams was proposed by Ghiasian et al. (2014). Nonlinear equations of motion were solved by the multi-term p-Ritz method combined with the Newmark integration scheme in the time domain. The issue of dynamic buckling of beams subjected to uniform rapid heating was briefly discussed by Ghiasian et al. (2015) based on the Budiansky-Roth criterion. Using a finite-element formulation, Malik and Kadoli (2017, 2018) studied thermally induced vibrations of FG beams taking into account geometrical nonlinearity and temperature-dependent properties of the material. Javani et al. (2019a) presented nonlinear dynamic analysis of suddenly heated shallow circular arches. The governing differential equations based on the first-order shear deformation theory and strain–displacement relations of the von Karman type were discretized and solved by the hybrid generalized differential quadrature method combined with the Newmark time integration scheme. A similar approach was used to investigate large-amplitude thermally induced vibrations of annular sector plates (Javani et al. 2021) and circular plates (Kiani and Eslami 2014; Javani et al. 2019b). Axisymmetric dynamic response of suddenly heated shallow cylindrical and conical shells was studied in Esmaeili et al. (2019); Javani et al. (2019c), respectively. Javani et al. (2020) and Taleb et al. (2022) addressed the dynamic snap-through instability of shallow spherical caps.

Prakash et al. (2007) employed a finite-element procedure to investigate nonlinear dynamic buckling of shear-flexible FG spherical caps subjected to step heating. Zhang et al. (2019) dealt with axisymmetric dynamic thermal buckling of annular plates with small initial geometric imperfections. The governing equations based on the classical plate theory were solved by expanding the deflections in power series and integrating numerically in the time domain. Zhang et al. (2015) examined the effect of grading material properties on axisymmetric transient displacements of rapidly heated thin cylindrical shells by the differential quadrature method. Dynamic thermal buckling of geometrically perfect cylindrical shells was studied by Zhang et al. (2020) using the symplectic method. Pandey and Pradyumna (2018) proposed a finite-element formulation for transient stress analysis of FGM plates and panels based on the higher-order layerwise theory. Using a 20-node solid finite element, Czechowski (2015) studied dynamic buckling of a clamped rectangular plate FGM plate subjected to thermal heat flux loading of short duration.

The dynamic response of rapidly heated thin-walled structures made of FGMs represents a relatively new area of investigation. As can be seen from the existing literature, only a limited number of works have so far been reported on thermally induced nonlinear vibrations and dynamic buckling of suddenly heated plates and shells. The available results are confined to circular plates and shallow shells of revolution undergoing axisymmetric deformations. The effect of initial geometric imperfections, which play an important role in the dynamic buckling behavior, has been discussed only briefly.

It is of interest to examine the dynamic stability of suddenly heated FGM shells through nonlinear transient analysis, which appears to be the most realistic approach to the problem. Transient analysis of nonlinear shells can be efficiently carried out using time marching schemes combined with iterative determination of deformed configuration at each time increment. Among available numerical approaches, the finite element method is one of the most successful and powerful tools. Typically, a finite-element model of a shell of relatively simple geometry involves thousands and even more solution variables to be operated on. Hence, much computer memory and time is required to repeatedly solve large system of equations governing dynamic response of the model. In most cases, the computational process is very time-consuming even for the current state-of-the-art computers. It is therefore of importance to develop effective numerical techniques that would allow one to reduce computational effort while providing reasonable accuracy in the calculations.

Our goal in this work is to develop a computationally-effective finite-element formulation for geometrically nonlinear analysis of thermally induced motion of functionally graded shells. To this end, we revisit the formulation reported in Levyakov and Kuznetsov (2011, 2014) to take into account inertia forces, thermal loads due to unsteady heat conduction, and temperature-dependent material properties.

19.2 Material Properties

We consider a shell made of a functionally graded material consisting of metal and ceramic constituents. The material properties are assumed to be graded in the thickness direction according to the power law (Shen 2009)

$$P(z,T) = P_{m} (T) + [P_{c} (T) - P_{m} (T)](0.5 + z/h)^{n}$$

$$( - h/2 \le z \le h/2)$$

(19.1)

where $P$ denotes mechanical or thermal property of the material (Young's modulus, Poisson's ratio, coefficient of linear thermal expansion, etc.), $T$ is the current temperature, $h$ is the shell thickness, $z$ is the distance measured from the shell middle surface, subscripts m and c refer to metal and ceramic phases, respectively, and n is a positive constant referred to as the grading index.

Dependence of material properties on temperature is commonly described by the power law

$$P_{i} = P_{0} (P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} ), (i = c,m)$$

(19.2)

where $P_{ - 1} ,P_{0} , \ldots ,P_{3}$ are coefficients determined for each constituent material.

19.3 Temperature Distribution

We consider non-steady one-dimensional problem of heat transfer through the thickness of a shell with temperature dependent material properties, assuming that heat transfer does not depend on a deformed configuration of the shell. The one-dimensional Fourier-Biot heat conduction equation to be solved for the temperature field $T=T(z,t)$ is given by

$$(\kappa T^{\prime})^{\prime} - \rho c_{p} \dot{T} = 0$$

$$0 \le t,\quad - h/2 \le z \le h/2$$

(19.3.1)

where $\kappa = \kappa (z,T)$ is the thermal conductivity, $\rho = \rho (z)$ is the density of the material, $c_{p} = c_{p} (z,T)$ is the specific heat capacity, and prime and superposed dot denote partial derivatives with respect to the transverse coordinate $z$ and time $t$, respectively. Since the temperature profile varies with time, the material properties mentioned above are functions of $z$ and $t$.

The initial condition is assumed to be

$$T(z,0) = T_{ref}$$

(19.3.2)

where $T_{ref}$ is the reference temperature at which the shell is stress free. We confine our attention to the following three types of thermal boundary conditions:

$$T( - h/2,t) = f(t)$$

$$T(h/2,t) = f(t)$$

(19.3.3)

$$T( - h/2,\,t) = T_{ref}$$

$$T(h/2,t) = f(t)$$

(19.3.4)

$$T^{\prime}( - h/2,t) = 0$$

$$T(h/2,t) = f(t)$$

(19.3.5)

in which $f(t)$ is a prescribed boundary temperature.

The two common representations of the thermal shock are given by

$$f(t) = \Delta T \cdot H(t)$$

(19.3.6)

$$f(t) = \Delta T(1 - e^{ - \sigma t} ),\;\;\sigma > 0$$

(19.3.7)

where $H(t)$ is the Heaviside unit step function and $\sigma$ is the loading parameter.

Because of inhomogeneous structure of the material and temperature-dependent properties, the solution of the heat-conduction problem (19.3.1)–(19.3.5) by analytical methods encounters serious mathematical difficulties. To solve the problem, we employ the finite-element method with step-by-step computations in the time domain. Equation (19.3.1) is multiplied by a test function and then integrated to obtain the variational form of the problem. We divide the shell thickness into elements of equal length $\Delta z$ and assume that the material properties $\kappa$, $\rho$, and $c_{p}$ are constant within each element.

Following the standard approximation procedure (see, e.g. (Zienkiewicz and Morgan 1983) and (Reddy 2004)), we use piecewise linear test functions and integrate over $z$. As a result, we arrive at a system of nonlinear ordinary differential equations, which can be converted to matrix form

$${\mathbf{K}}(T){\mathbf{T}} + {\mathbf{R}}(T){\dot{\mathbf{T}}} = {\mathbf{0}}$$

(19.3.8)

where ${\mathbf{T}}$ is the vector representing nodal temperatures, ${\mathbf{K}}$ and ${\mathbf{R}}$ are tridiagonal symmetric matrices depending on the nodal temperatures.

Let the time domain be represented by a sequence of finite elements of length $\Delta t$. Within the $n$-th time element, the temperature field can be approximated by the linear shape functions

$${\mathbf{T}} = {\mathbf{T}}^{n} N_{1} + {\mathbf{T}}^{n + 1} N_{2}$$

$$N_{1} = 1 - (t - t^{n} )/\Delta t$$

$$N_{2} = (t - t^{n} )/\Delta t$$

(19.3.9)

where $t^{n} < t < t^{n + 1}$.

Using the weighted residual method to solve Eqs. (19.3.8), we require that the equations be satisfied at collocation points $t = t^{n} + \tau \Delta t$ ($0 < \tau < 1$). After integration of the equations, we obtain

$$(\tau \Delta t{\mathbf{K}}^{n + \tau } + {\mathbf{R}}^{n + \tau } ){\mathbf{T}}^{n + 1} + ((1 - \tau )\Delta t{\mathbf{K}}^{n + \tau } - {\mathbf{R}}^{n + \tau } ){\mathbf{T}}^{n} = {\mathbf{0}}$$

(19.3.10)

where ${\mathbf{K}}^{n + \tau } = {\mathbf{K}}({\mathbf{T}}^{n + \tau } )$, ${\mathbf{R}}^{n + \tau } = {\mathbf{R}}({\mathbf{T}}^{n + \tau } )$, and ${\mathbf{T}}^{n + \tau } = (1 - \tau ){\mathbf{T}}^{n} + \tau {\mathbf{T}}^{n + 1}$.

The matrices ${\mathbf{K}}^{n + \tau }$ and ${\mathbf{R}}^{n + \tau }$ are assembled from the elemental matrices

$${\mathbf{K}}_{e}^{n + \tau } = \frac{1}{\Delta z}\kappa^{\tau + n} \left( {\begin{array}{*{20}c} 1 & { - 1} \\ { - 1} & 1 \\ \end{array} } \right)$$

$${\mathbf{R}}_{e}^{n + \tau } = \frac{1}{6\Delta z}\rho c_{p}^{n + \tau } \left( {\begin{array}{*{20}c} 2 & 1 \\ 1 & 2 \\ \end{array} } \right)$$

(19.3.11)

where the material properties are calculated at the point $z_{\eta } = (1 - \eta )z_{e} + \eta z_{e + 1}$ $\left( {0 < \eta < 1} \right)$ within the element at instant $t = t^{n} + \tau \Delta t$.

Temperature at which the material properties are evaluated is given by

$$T_{\eta }^{n + \tau } = (1 - \tau )(1 - \eta )T_{e}^{n} + (1 - \tau )\eta T_{e + 1}^{n} + \tau (1 - \eta )T_{e}^{n + 1} + \tau \eta T_{e + 1}^{n + 1}$$

(19.3.12)

In the computations, we set $\tau = \eta = 1/2$, which gives errors of $O(\Delta t^{2} )$ and $O(\Delta z^{2} )$ in determining the temperature profile. To solve Eqs. (19.3.10), we use the iterative Newton–Raphson procedure assuming the Hessian to be constant at each time step. The computation scheme is given by

$$(\tau \Delta t{\mathbf{K}}_{(i)}^{n + \tau } + {\mathbf{R}}_{(i)}^{n + \tau } )\delta {\mathbf{T}}_{(i)}^{n + 1} + (\tau \Delta t{\mathbf{K}}_{(i)}^{n + \tau } + {\mathbf{R}}_{(i)}^{n + \tau } ){\mathbf{T}}_{(i)}^{n + 1} +$$

$$\quad \quad \quad \quad \quad \quad \quad \quad + ((1 - \tau )\Delta t{\mathbf{K}}_{(i)}^{n + \tau } - {\mathbf{R}}_{(i)}^{n + \tau } ){\mathbf{T}}^{n} = {\mathbf{0}}$$

(19.3.13)

$${\mathbf{T}}_{(i + 1)}^{n + 1} = {\mathbf{T}}_{(i)}^{n + 1} + \delta {\mathbf{T}}_{(i)}^{n + 1}$$

where $\delta {\mathbf{T}}$ is the increment in the nodal temperatures and subscript $i$ enumerates iterations in the time domain.

19.4 Shell Finite Element Formulation

We develop a shell finite element formulation for nonlinear dynamic analysis of FGM shells using the invariant-based approach proposed in Levyakov and Kuznetsov (2011); Levyakov and Kuznetsov 2014). We recall some basic statements of the approach.

19.4.1 Invariant Representations

Given two tensors $u_{mn}$ and $v_{mn}$ ($m,n = 1,2$) referred to Cartesian system of reference $\xi_{1} O\xi_{2}$, the combined invariant is defined as

$$I_{uv} = \frac{1}{2}e_{mp} e_{nq} u_{mn} v_{pq}$$

(19.4.1)

where $e_{mp}$ is the permutation tensor with the components $e_{11} = e_{22} = 0$,$\: e_{12} = - e_{21} = 1$ and summation is performed over dummy indices unless otherwise specified.

It is worth noting that Eq. (19.4.1) implies the well-known results. Namely, setting $v_{mn} = 2\delta_{mn}$ ($\delta_{mn}$ being the Kronecker delta) and $v_{mn} = u_{mn}$, from Eq. (19.4.1) we, respectively, obtain the first and second invariants of the tensor $u_{mn}$

$$I_{u} = u_{11} + u_{22}$$

$$I_{uu} = u_{11} u_{22} - u_{12}^{2}$$

(19.4.2)

When dealing with a triangular domain, it is reasonable to introduce three natural coordinates $\gamma_{i} \;\;(i = 1,2,3)$ defined by three directions along the triangle's edges (see Fig. 19.1). Then the tensor $u_{mn}$ can be represented by three natural components $u_{i} \;(i = 1,2,3)$ determined in the three directions (no summation over $i$).

$$u_{i} = \alpha_{mni} u_{mn}$$

(19.4.3)

Fig. 19.1

Natural coordinates of a triangular element

$\alpha_{mni} = \lambda_{mi} \lambda_{ni}$, $\lambda_{mi} = \frac{1}{{l_{i} }}(\xi_{mk} - \xi_{mj} )$, $(m,n = 1,2;\;\;i,j,k = 1,2,3)$,

where $\xi_{mk}$ is the $m$-th coordinate of the $k$-th vertex, $l_{i}$ is the length of the side opposite to the $i$-th vertex, and the subscripts $i$, $j$, and $k$ obey the rule of cyclic permutation.

Using matrix notation, the invariants (19.4.1) and (19.4.2) can be written in terms of the natural components as

$$I_{u} = \mathbf{u}^{T} \varvec{\uptau} ,I_{uu} = \mathbf{u}^{T} \left( {\mathbf{aa}^{T} - \varvec{\uprho} } \right)\mathbf{u},I_{uv} = \mathbf{u}^{T} \left( {\mathbf{aa}^{T} -\varvec{\uprho} } \right)\mathbf{v}$$

(19.4.4)

${\mathbf{u}} = \left\{ {\begin{array}{*{20}c} {\,u_{1} ,} & {u_{2} ,} & {u_{3} } \\ \end{array} } \right\}^{T}$, ${\varvec{v}} = \left\{ {\begin{array}{*{20}c} {\,v_{1} ,} & {v_{2} ,} & {v_{3} } \\ \end{array} } \right\}^{T}$, ${\mathbf{a}} = \left\{ {\begin{array}{*{20}c} {\,a_{1} ,} & {a_{2} ,} & {a_{3} } \\ \end{array} } \right\}^{T}$, ${{\varvec{\uptau}}} = 2\left\{ {\begin{array}{*{20}c} {\,a_{1} (a - 2a_{1} ),} & {a_{2} (a - 2a_{2} ),} & {a_{3} (a - 2a_{3} )} \\ \end{array} } \right\}^{T}$, ${{\varvec{\uprho}}} = diag(2a_{1}^{2} ,\;2a_{2}^{2} ,\;2a_{3}^{2} )$,

$\Delta = (l_{p} l_{p} )^{2} - 2l_{p}^{2} l_{p}^{2}$, $a_{p} = \frac{{(l_{p} )^{2} }}{\sqrt \Delta }$ (no summation over p),

$a = \frac{{l_{q} l_{q} }}{\sqrt \Delta }$ ${(}p,q{ = 1,2,3)}$,

where superscript T is a transpose of the matrix.

19.5 Reference Surface

To formulate kinematic relations of the finite element, we use the surface of mass as a reference surface whose position is given by

$$z_{R} = \int\limits_{ - h/2}^{h/2} {\rho zdz} \left( {\int\limits_{ - h/2}^{h/2} {\rho dz} } \right)^{ - 1}$$

(19.4.5)

where $\rho = \rho (z)$ is the density of the material.

The concept of the surface of mass is adopted here to decouple translations and rotations in the expression for the kinetic energy of FGM shell with non-uniform distribution of material properties across the thickness.

Under the assumptions of the first-order shear deformation theory, the position vectors of a material particle of the shell in the initial and deformed configurations are, respectively, written as

$${\mathbf{r}}^{z} = {\mathbf{r}} + (z - z_{R} ){\mathbf{d}}, \: {\mathbf{r}}^{*z} = {\mathbf{r}}^* + (z - z_{R} ){\mathbf{d}}^*$$

(19.4.6)

where ${\mathbf{r}}$ is the position vector of the surface of mass, ${\mathbf{d}}$ is the unit vector (director) normal to the undeformed middle surface, and the asterisk denotes variables that refer to a deformed state of the shell.

19.5.1 Kinematics of the Shell Element

A three-node triangular finite element proposed in Levyakov and Kuznetsov (2011); Levyakov and Kuznetsov 2014) is modified in the present work to incorporate inertia effects. The element geometry is determined by three nodal position vectors ${\mathbf{r}}_{i}$, ${\mathbf{r}}_{j}$, and ${\mathbf{r}}_{k}$ and three nodal directors ${\mathbf{d}}_{i}$, ${\mathbf{d}}_{j}$, and ${\mathbf{d}}_{k}$ normal to the reference surface in the undeformed state (see Fig. 19.2). We note that the three nodes and adjoined directors constitute a kinematic group which plays an important role in the formulation of the shell element.

Fig. 19.2

Shell element and nodal degrees of freedom

In accordance with the first-order shear deformation theory of plates and shells, the directors are not necessarily normal to the surface but do not change in length. The element possesses 5 degrees of freedom (DOF) per node: three translations in the coordinate directions and two rotations of the nodal director. A total number of DOFs is equal to 15, which represent 9 straining modes and 6 rigid-body modes of motion.

Possible changes in the position and configuration of the element are characterized by the vector of generalized coordinates

$$\delta {\mathbf{q}}_{e} = \left[ {\;\delta {\mathbf{q}}_{1}^{T} ,\;\delta {\mathbf{q}}_{2}^{T} ,\;\delta {\mathbf{q}}_{3}^{T} } \right]\;^{T} ,\;\delta {\mathbf{q}}_{n}^{T} = \left[ {\;\delta x_{1n}^{*} ,\;\delta x_{2n}^{*} ,\;\delta x_{3n}^{*} ,\;\delta \omega_{1n} ,\;\delta \omega_{2n} } \right]\;\;\left( {n = 1,2,3} \right)$$

(19.4.7)

where $x_{mn}^{*}$ are the components of the nodal position vector ${\mathbf{r}}_{n}^{*}$ in a deformed state and $\;\omega_{mn}$ are the components of the rotation vector of the nodal director ${\mathbf{d}}_{n}^{*}$.

19.5.2 Strain Energy

Using the assumptions of the first-order shear deformation theory, we write the strains of the heated shell as

$$S_{mn} = \varepsilon_{mn} + (z - z_{R} )\kappa_{mn} - \alpha (T - T_{ref} )$$

$$S_{m3} = \gamma_{m3} \quad (m,n = 1,2)$$

(19.4.8)

where $\varepsilon_{mn}$ and $\kappa_{mn}$ are the membrane strains and curvature changes of the reference surface $z = z_{R}$, respectively, $\alpha = \alpha (z,T)$ is the coefficient of linear thermal expansion, and $\gamma_{13}$ and $\gamma_{23}$ are the transverse shear strains.

The strain energy density of the shell can be expressed in terms of invariants as

$$\Pi_{V} = \frac{1}{2}\frac{E}{{1 - \nu^{2} }}\left( {I_{S}^{2} - 2(1 - \nu )I_{SS} + \frac{1 - \nu }{2}I_{\Gamma } } \right)$$

(19.4.9)

where $I_{S}$ and $I_{SS}$ are the first and second invariants of the strain tensor $S_{mn}$, respectively, $I_{\Gamma }$ is the first invariant of the tensor $\Gamma_{mn} = S_{m3} S_{n3}$, $E = E(z,T)$ is Young's modulus, and $\nu = \nu (z,T)$ is Poisson's ratio of the material. The invariants appearing in Eq. (19.4.8) are determined using the template Eqs. (19.4.2) or (19.4.3).

Substituting Eqs. (19.4.7) into Eq. (19.4.8) and integrating over the shell thickness, we obtain the strain energy

$$\begin{gathered} \Pi = \tfrac{1}{2}\iint\limits_{A} {(B_{1} I_{\varepsilon }^{2} - 2B_{2} I_{\varepsilon \varepsilon } + D_{1} I_{\kappa }^{2} - 2D_{2} I_{\kappa \kappa } + }\, \hfill \\ \quad \quad \quad \quad 2G_{1} I_{\varepsilon } I_{\kappa } - 4G_{2} I_{\varepsilon \kappa } + \,C_{\Gamma } I_{\Gamma } - 2N_{T} I_{\varepsilon } - 2M_{T} I_{\kappa } + 2\alpha_{0} )dA \hfill \\ \end{gathered}$$

(19.4.10)

where

$$(B_{1} ,G_{1} ,D_{1} ) = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left( {1,\;z - z_{R} ,\;(z - z_{R} )^{2} } \right)\frac{E}{{1 - \nu^{2} }}} dz$$

(19.4.11)

$$(B_{2} ,G_{2} ,D_{2} ) = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left( {1,\;z - z_{R} ,\;(z - z_{R} )^{2} } \right)\frac{E}{1 + \nu }} dz$$

(19.4.12)

$$(N_{T} ,\;M_{T} ) = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {(1,\;z - z_{R} )\frac{E}{1 - \nu }\alpha (T - T_{ref} )} dz$$

(19.4.13)

$$C_{\Gamma } = k\int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {Gdz}$$

$$\alpha_{0} = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\frac{E}{1 - \nu }\alpha^{2} (T - T_{ref} )^{2} } dz$$

(19.4.14)

Here $A$ is the area of the shell middle surface, $G = 0.5E/(1 + \nu )$ is the shear modulus, $k$ is the shear correction factor introduced to account for non-uniform distribution of transverse shear stresses in the thickness direction.

Since the material properties are functions of the coordinate $z$ and time $t$, the integrals in Eqs. (19.4.11)–(19.4.14) can be evaluated by numerical methods only. We employ the trapezoidal rule for this purpose.

Using Eqs. (19.4.3), we express the strain energy (19.4.9) of the triangular element in terms of the natural components of the strain tensors

$$\Pi_{e} = \tfrac{1}{2}\iint\limits_{{A_{e} }} {\{ {{\varvec{\upvarepsilon}}}^{T} [B_{1} {\varvec{\uptau \uptau }}^{T} - 2B_{2} ({\mathbf{aa}}^{T} - {{\varvec{\uprho}}})]{{\varvec{\upvarepsilon}}} + {{\varvec{\upkappa}}}^{T} [D_{1} {\varvec{\uptau \uptau }}^{T} - 2D_{2} ({\mathbf{aa}}^{T} - {{\varvec{\uprho}}})]{{\varvec{\upkappa}}} + }$$

$$2{{\varvec{\upvarepsilon}}}^{T} [G_{1} {\varvec{\tau \tau }}^{T} - 2G_{2} ({\mathbf{aa}}^{T} - {{\varvec{\uprho}}})]{{\varvec{\upkappa}}} + C_{\Gamma } {{\varvec{\uptau}}}^{T} {{\varvec{\Gamma}}} - 2{{\varvec{\uptau}}}^{T} (N_{T} {{\varvec{\upvarepsilon}}} + M_{T} {{\varvec{\upkappa}}}) + 2\alpha_{0} \} dA_{e}$$

(19.4.15)

where ${{\varvec{\upvarepsilon}}}^{T} = \left\{ {\begin{array}{*{20}c} {\,\varepsilon_{1} ,} & {\varepsilon_{2} ,} & {\varepsilon_{3} } \\ \end{array} } \right\}^{T}$, ${{\varvec{\upkappa}}}^{T} = \left\{ {\begin{array}{*{20}c} {\,\kappa_{1} ,} & {\kappa_{2} ,} & {\kappa_{3} } \\ \end{array} } \right\}^{T}$, ${{\varvec{\Gamma}}}^{T} = \left\{ {\begin{array}{*{20}c} {\,\Gamma_{1} ,} & {\Gamma_{2} ,} & {\Gamma_{3} } \\ \end{array} } \right\}^{T}$ are vectors of the natural strains, and $A_{e}$ is the element area computed by the formula $A_{e} = \tfrac{1}{4}\sqrt \Delta$, in which $\Delta$ is computed using Eqs. (19.4.4).

Using approximations of the natural strains considered in Levyakov and Kuznetsov (2011), after integration over the element area in Eq. (19.4.14), we obtain the strain energy of the element.

$$\Pi_{e} = \frac{1}{2}{\mathbf{u}}_{{}}^{T} {\mathbf{Ku}}_{{}} - {\mathbf{u}}_{{}}^{T} {\mathbf{P}} + \alpha_{0} A_{e}$$

(19.4.16)

where ${\mathbf{u}}_{{}}^{{}}$ is the 9 × 1 vector of the generalized elastic strains, ${\mathbf{K}}$ is the 9 × 9 stiffness matrix, ${\mathbf{P}}$ is the 9 × 1 vector of thermal loads (for detailed derivation, the reader is referred to Levyakov and Kuznetsov (2011)).

To formulate algorithm for determining the deformed configuration of the shell, it is necessary to find the first and second variations of the strain energy.

$$\delta \Pi_{e} = {\mathbf{g}}_{e}^{T} \delta {\mathbf{q}}_{e}$$

$$\delta^{2} \Pi_{e} = \delta {\mathbf{q}}_{e}^{T} {\mathbf{H}}_{e} \delta {\mathbf{q}}_{e}$$

(19.4.17)

where is ${\mathbf{g}}_{e}^{{}}$ and ${\mathbf{H}}_{e}$ the gradient and the Hessian of the element, respectively, and $\delta {\mathbf{q}}_{e}$ is given by Eq. (19.4.7).

19.5.3 Kinetic Energy

Using Eq. (19.4.6) and taking into account Eq. (19.4.5), we write the kinetic energy of the shell element

$$T_{e} = \frac{1}{2}\iint\limits_{A} {(I_{0}^{{}} {\dot{\mathbf{r}}}^{ * 2} + I_{2} {\dot{\mathbf{d}}}^{ * 2} )dA_{e} }$$

$$\left( {I_{0} ,\;I_{2} } \right) = \int\limits_{ - h/2}^{h/2} {(1,\;(z - z_{R} )^{2} )\rho } dz$$

(19.4.18)

We determine the mass matrix of the triangular finite element using the direct mass lumping. Assuming that nodal contribution of the mass distribution over the element is proportional to the angle at the node, we obtain the 15 × 15 diagonal mass matrix

$$\mathbf{M_{e}} = diag({{\varvec{\upmu}}}_{1}^{T} ,\;{{\varvec{\upmu}}}_{2}^{T} ,\;{{\varvec{\upmu}}}_{3}^{T} )$$

$${{\varvec{\upmu}}}_{i}^{T} = A_{e} (\alpha_{i} /\pi )\{ I_{0} ,\;I_{0} ,\;I_{0} ,\;I_{2} ,\;I_{2} \}$$

(19.4.19)

where $\alpha_{i}$ is the angle at the $i$-th vertex of the element. In what follows, we ignore the terms $I_{2}$ representing rotary inertia.

Assuming that rotary inertia $I_{2}$ is of minor significance compared to translational inertia $I_{0}$, we set $I_{2} = 0$.

19.6 Finite-Element Equations of Motion and Solution Method

The equations of motion of the shell finite-element model can be obtained using Hamilton’s principle

$$\delta \int\limits_{{t_{1} }}^{{t_{2} }} {\sum\limits_{e} {\left( {T_{e} - \Pi_{e} } \right)} \;dt} = 0$$

(19.5.1)

where $t_{1}$ and $t_{2}$ are instants of time and summation is performed over the finite elements.

Substituting expressions for the strain energy (19.4.15) and the kinetic energy (19.4.16) of the element into Eq. (19.5.1) and integrating by parts, we obtain nonlinear equations of motion

$${\mathbf{M} {\ddot{\mathbf{q}}}} + {\mathbf{C} {\dot{\mathbf{q}}}} + {\mathbf{g}} = {\mathbf{0}}$$

(19.5.2)

in which ${\mathbf{M}}$, ${\mathbf{C}}$, ${\mathbf{g}}$, and ${\mathbf{q}}$ are the mass matrix, the damping matrix, the gradient, and the vector of the generalized coordinates of the strain energy of the finite-element assemblage, respectively.

To integrate Eqs. (19.5.2) in the time domain, we employ Newmark’s implicit scheme. At each moment $t + \Delta t$, where $\Delta t$ is the time increment, solution of the dynamic equations is found iteratively using the Newton–Raphson procedure:

$$\left( {{\mathbf{H}}_{(p)}^{t + \Delta t} + a_{1} {\mathbf{M}} + a_{4} {\mathbf{C}}} \right)\delta {\mathbf{q}}_{(p + 1)}^{t + \Delta t} = - {\mathbf{g}}_{(p)}^{t + \Delta t} - (a_{1} {\mathbf{M}} + a_{4} {\mathbf{C}})\left( {{\mathbf{q}}_{(p)}^{t + \Delta t} - {\mathbf{q}}_{{}}^{t} } \right) +$$

(19.5.3)

$+ (a_{2} {\mathbf{M}} - a_{5} {\mathbf{C}}){\dot{\mathbf{q}}}_{{}}^{t} + (a_{3} {\mathbf{M}} - a_{6} {\mathbf{C}}){{\ddot{\mathbf{q}} }}_{{}}^{t}$,

$a_{1} = \frac{1}{{\alpha \Delta t^{2} }}$, $a_{2} = \frac{1}{\alpha \Delta t}$, $a_{3} = \frac{1 - 2\alpha }{{2\alpha }}$, $a_{4} = \frac{\beta }{\alpha \Delta t}$, $a_{5} = 1 - \frac{\alpha }{\beta }$, $a_{6} = \left( {1 - \frac{\beta }{2\alpha }} \right)\Delta t$,

where ${\mathbf{H}}$ is the Hessian of the finite-element model of the shell, $\delta {\mathbf{q}}$ is the increment in the vector of generalized coordinates, the subscript $p$ enumerates iterations, and $\alpha$ and $\beta$ are the parameters taken to be equal to 1/4 and 1/2, respectively (Bathe and Wilson 1976). The procedure for computing the gradient and Hessian of the shell element can be found in Levyakov and Kuznetsov (2011).

After the increment $\delta {\mathbf{q}}_{(p)}^{t + \Delta t}$ has been found from Eqs. (5.3), we update the nodal vectors using the formulas

$${\mathbf{r}}_{s}^{*(p + 1)} = {\mathbf{r}}_{s}^{*(p)} + \delta {\mathbf{r}}_{s}^{*(p)}$$

(19.5.4)

$${\mathbf{d}}_{s}^{*(p + 1)} = c_{1}^{(p)} {\mathbf{d}}_{s}^{*(p)} + c_{2}^{(p)} \left( {\,{\mathbf{t}}_{1s}^{*(p)} \delta \omega_{1s}^{(p)} + {\mathbf{t}}_{2s}^{*(p)} \delta \omega_{2s}^{(p)} } \right)$$

$${\mathbf{t}}_{ms}^{*(p + 1)} = {\mathbf{t}}_{ms}^{*(p)} - \delta \omega_{ms}^{(p)} \left[ {\,c_{2}^{(p)} {\mathbf{d}}_{s}^{*(p)} + c_{3}^{(p)} \left( {{\mathbf{t}}_{1s}^{*(p)} \delta \omega_{1s}^{(p)} + {\mathbf{t}}_{2s}^{*(p)} \delta \omega_{2s}^{(p)} } \right)} \right]$$

$$\delta \omega_{s}^{(p)} = \left( {\delta \omega_{1s}^{(p)2} + \delta \omega_{2s}^{(p)2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

$$c_{1}^{(p)} = \cos \delta \omega_{s}^{(p)}, c_{2}^{(p)} = \frac{{\sin \delta \omega_{s}^{(p)} }}{{\delta \omega_{s}^{(p)} }}, c_{3}^{(p)} = \frac{{1 - \cos \delta \omega_{s}^{(p)} }}{{\delta \omega_{s}^{(p)2} }}$$

where ${\mathbf{t}}_{1s}^{*}$ and ${\mathbf{t}}_{2s}^{*}$ are two auxiliary unit vectors normal to the director ${\mathbf{d}}_{s}^*$.

After the solution of Eqs. (19.5.2) has been found with a required accuracy, the nodal velocities and accelerations at each time step are computed using formulas (Bathe and Wilson 1976)

$${{\ddot{\mathbf{q}}}}^{t + \Delta t} = a_{1} {\mathbf{q}}^{t + \Delta t} - a_{1} {\mathbf{q}}^{t} - a_{2} {\dot{\mathbf{q}}}^{t} - a_{3} \ddot{\mathbf{{q}}}$$

(19.5.5)

$${\dot{\mathbf{q}}}^{t + \Delta t} = a_{4} {\mathbf{q}}^{t + \Delta t} - a_{4} {\mathbf{q}}^{t} + a_{5} {\dot{\mathbf{q}}}^{t} + a_{6} \ddot{\mathbf{{q}}}^{t}$$

19.7 Evaluation of Dynamic Buckling

After thermal shock of magnitude $\Delta T$ is applied to a surface of a shell, the stress resultants $N_{T}$ and $M_{T}$ (see Eqs. (19.4.12)) increase monotonically with time due to heat transfer through the wall thickness. The rate at which the thermal loads increase depends on the (1) magnitude of thermal shock, (2) material properties, (3) wall thickness, and (4) thermal boundary conditions. If the shell is restrained against thermal expansion, thermally induced compressive stresses can result in buckling. As the stresses reach the critical level, the shell jumps to oscillations about new equilibrium configuration. Volmir (1967) proposed the following simple criterion for dynamic buckling of plates and shells: given the time history of deflection at a certain characteristic point of the shell, the critical time is defined as a moment of the highest buckling rate, which corresponds to the inflection point on the time-deflection curve. In the general case, however, this approach is difficult to implement, since the location of the characteristic point is not known in advance. For this reason, to investigate dynamic buckling, we use the time history of the kinetic energy rather than deflection at a single point.

It is well known that initial geometric imperfections unavoidable in real structures play an important role in the stability of thin plates and shells. In the nonlinear analysis of imperfection-sensitive thin-walled structure, the dynamic buckling instability is interpreted as rapid development of the initial deflections under the time-dependent loads. Since the amplitude and pattern of deviation from ideal geometric shape are random, it is common practice to assume that the initial imperfection is similar in shape to eigenmodes obtained from the static buckling analysis.

19.8 Numerical Results and Discussion

The sample problems considered below deal with FGM plates and shells composed of silicon nitride Si₃N₄ (ceramic phase) and SUS304 stainless steel (metal phase) unless otherwise specified. Mechanical and physical properties of the phases are listed in Tables 19.1 and 19.2 (see, e.g. (Shen 2009)). Temperature-dependent properties are taken into account unless otherwise specified.

Table 19.1 Temperature-dependent properties of Si₃N₄

Table 19.2 Temperature-dependent properties of SUS304

In all the problems, transient analysis of the structures is performed under zero initial conditions. To determine temperature distribution across the wall thickness, we use a uniform mesh of 200 elements of equal size.

19.8.1 Comparison Studies

In this section, the present finite-element formulation formulation is validated by considering free vibration and transient problems for which analytical or numerical solutions are available in the literature.

19.8.1.1 Free Vibration of FGM Shells

The first example is free small-amplitude vibrations of a circular cylindrical panel of square plan form. The outer surface of the panel is ceramic rich and the inner surface is metal rich. The properties of the material are determined at the reference temperature $T_{ref} = 300\;K$. The grading index in Eq. (19.2.1) is set equal to $n = 2$. The geometric parameters are: wall thickness $h = 0.01$ m, side length $a = 10h$, radius of the middle surface $R = 10a$, and subtended angle $\theta = 0.05$.

The aim is to verify the mass matrix of the proposed shell element. We determine free-vibration frequencies $\omega$ of the shells with fully clamped and simply supported immovable boundary contour. Table 19.3 lists the nondimensional frequency parameter $\lambda = (\omega a^{2} /h)\sqrt {12(1 - \nu_{m}^{2} )\rho_{m} /E_{m} }$ computed for the first three vibration modes using uniform union-jack meshes. The computation results agree well with the numerical solution obtained by the element-free kp-Ritz method (Zhao et al. 2009) and with the finite-element solution obtained by the ANSYS software where the grading properties of the material were modeled using the Shell181 multilayered element.

Table 19.3 Frequency parameter λ of the FGM cylindrical panel for n = 2

19.8.1.2 Dynamic Response of an Isotropic Beam to Thermal Shock

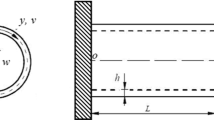
The second example deals with thermally-induced vibrations of a simply supported isotropic beam made of the Si₃N₄ material, which corresponds to $n = 0$ in Eq. (19.2.1). The length, thickness, and width of the beam are $l = 1$ m, $h = 0.01$ m, and $b = 0.1$ m, respectively. The upper surface of the beam is exposed to step temperature rise $\Delta T = 100\;\;{\text{K}}$, whereas the lower surface is kept at a reference temperature of 300 K (see Eqs. (19.3.4) and (19.3.6)).

For small-amplitude vibrations, the dynamic response of the beam with temperature-independent properties can be predicted using the analytical solution.

$$w = \sum\limits_{m = 1,3,5...}^{\infty } {\alpha_{m} (t)\sin \frac{m\pi x}{l} - \frac{{M_{T} }}{2D}} (x^{2} - lx)$$

(19.7.1)

$$\alpha_{m} (t) = \frac{{8l^{2} bE\alpha h^{2} \Delta T}}{{D\pi^{5} m^{3} }}\sum\limits_{k = 2,4,6...}^{\infty } {\frac{1}{{k^{2} }}\frac{{e^{{ - \gamma_{k} t}} - (\omega_{m} /\gamma_{k} )\sin \omega_{m} t - \cos \omega_{m} t}}{{1 + (\omega_{m} /\gamma_{k} )^{2} }}}$$

$$M_{T} = bE\alpha h^{2} \Delta T\left( {\frac{1}{12} - \frac{2}{{\pi^{2} }}\sum\limits_{k = 2,4,6...}^{\infty } {\frac{1}{{k^{2} }}e^{{ - \gamma_{k} t}} } } \right)$$

$$\gamma_{k} = \frac{\kappa }{{c_{p} \rho }}\left( {\frac{k\pi }{h}} \right)^{2}, \omega_{m} = \left( {m\pi /l} \right)^{2} \sqrt {D/I}, D = \frac{{Ebh^{3} }}{12}, I = \rho bh$$

where $w$ is the lateral deflection and $x$ is the axial coordinate.

The finite-element solution predicting dynamic response of the beam was obtained using the following data: a 4 × 40 uniform union-jack mesh with 320 elements, and the time increment in the Newmark integration scheme $\Delta t = 10^{ - 4}$ s.

The midspan deflection $w_{c}$ versus time is shown in Fig. 19.2. The finite-element results agree favorably with the linear analytical solution (19.7.1) in the case where the end supports are allowed to move in the axial direction. For axially immovable supports, the linear solution fails to predict the beam response adequately because of geometrically nonlinear effects. It is seen from Fig. 19.2 that the frequency of vibrations increases due to the additional constraints at the beam ends.

19.8.1.3 Dynamic Response of a Circular Plate to Thermal Shock

The third example is the thermally induced vibrations of a simply supported FGM circular plate with immovable edge. The upper surface of the plate is exposed to step temperature rise $\Delta T = 10\;K$, whereas the lower surface is kept at a reference temperature of 300 K (see Eqs. (19.3.4) and (19.3.6)). The radius and thickness of the plate are $a = 0.080$ m and $h = 0.001$ m, respectively.

To determine the dynamic axisymmetric deflections of the plate, we consider a quarter of the plate using the following data: number of elements $N$ = 16 and the time increment in the Newmark integration scheme $\Delta t = 0.5 \times 10^{ - 4}$ s.

The predicted central deflection $w_{c}$ versus time is shown in Fig. 19.3 for the grading index $n = 5$. The finite-element results are very close to the solution of Kiani and Eslami (2014) obtained by the Ritz method with simple polynomial functions.

Fig. 19.3

Time history of the midspan deflection for the simply supported isotropic beam

Fig. 19.4

Time history of the central deflection of the simply supported circular FGM plate

19.8.1.4 Snap-Through of a Shallow Spherical Cap

The next example deals with the snap-through instability of a suddenly heated isotropic spherical cap with immovable simply supported edge. This problem has recently been considered by Javani et al. (Javani et al. 2020). Given the wall thickness $h$, the geometry of the cap is determined by two nondimensional parameters

$$\lambda = \sqrt {12} \frac{{R\theta^{2} }}{h} , \, \mu = 2\sqrt {12} \frac{R\theta }{h}$$

where $R$ is the radius of curvature and $\theta$ is the half opening angle.

The cap is made of the SUS304 steel with temperature-independent properties. The inner surface of the cap is suddenly heated, whereas the outer surface is kept at the reference temperature (see Eqs. (19.3.4) and (19.3.6)). Under these loading conditions, the cap can jump to inverted position. Assuming that axisymmetric deformation occurs, we consider a quarter of the cap and impose symmetry conditions along two radial directions. In Fig. 19.5, we plot time histories of the normalized central deflection $w/f$ for $h = 1$ mm, $\lambda = 1.7$ and $\mu = 150$, where $f = R\theta^{2} /2$ is the rise of the cap. Using the model consisting of 400 elements, we found that snap-through instability occurs if $68.6K < \Delta T < 68.65K$. The same range was obtained using a finer mesh consisting of 1 600 elements. The present results agree well with the calculation results of Javani et al. (Javani et al. 2020) who found that the critical temperature rise lies in the range 68.25 K $< \Delta T <$ 68.5 K.

Fig. 19.5

Time history of the central deflection of the simply supported spherical cap

19.8.1.5 Large Thermal Displacements of an FGM Plate

Now we verify nonlinear capabilities of the proposed finite-element model in the dynamic analysis of large displacements and rotations. To this end, we consider thermal finite bending of a cantilevered thin narrow plate of length $L = 1$ m, width $b = L/80$, and thickness $h = L/200$. The grading index of the FGM is $n = 1$. The plate is heated according to Eqs. (3.4) and (3.7), where $\Delta T = 1{\kern 1pt} \,880\;$ K. Due to the increasing thermal bending moment $M_{T}$, the plate is rolled up into a circular cylindrical shape. The computation results are shown in Fig. 19.6 for two heating rates determined by parameters $\sigma = 1\;{\text{s}}^{ - 1}$ (slow heating) and $\sigma = 10\;{\text{s}}^{ - 1}$ (rapid heating) that enter Eq. (3.7). It is seen that, for slow heating, the plate is bent nearly statically performing small-amplitude oscillations about the deformed configuration. With time, the plate tends to assume closed circular shape (see Fig. 19.7), where the tip displacements approach their limiting values, i.e. $u/L \to 1$ and $w/L \to 0$. As a reference solution, we take the analytical solution based on the beam model and steady-state temperature distribution over the plate (Levyakov and Kuznetsov 2014). Using this solution, one finds that the temperature rise required to roll the plate into a closed circle is $\Delta T = 1\,\;814$ K, which is 3.5% lower than the above-mentioned magnitude. A slightly stiffer response of the present finite-element model compared to the beam model can be attributed to the fact that under non-uniform heating the plate is deformed into a doubly curved surface rather than into a cylindrical surface. The effect of Poisson's ratio on the dynamic thermal deflections was found to be of little significance. It is seen from Fig. 19.6 that under rapid heating, the pure thermal bending is accompanied by finite-amplitude oscillations. The solution obtained for 20 × 2 mesh agrees with that obtained for finer 80 × 2 mesh, the difference becomes noticeable after approximately 1 s. Deformed configurations of the rapidly heated plate are shown in Fig. 19.7. The effect of the time increment on accuracy of the solution is demonstrated by Table 19.4.

Fig. 19.6

Time histories of the tip displacements of the cantilevered FGM plate

Fig. 19.7

Equilibrium configurations of the cantilevered plate under rapid heating (80 × 2 mesh)

Table 19.4 Convergence study of the thermal bending of a rapidly heated cantilevered plate

19.8.2 Dynamic Thermal Buckling of a Clamped Rectangular Plate

We consider a fully clamped rectangular FGM plate of length $a = 0.3$ m, width $b = 0.15$ m, and thickness $h = 0.001$ m. It is assumed that initial geometrical imperfection is of the form.

$$w_{0} = \sum\limits_{m,k} {A_{mk} \varphi_{m} (x/a)\varphi_{k} (y/b)}$$

(19.7.2)

where $\varphi_{m} (x)$ is the m-th eigenfunction governing the vibration mode of the clamped–clamped beam and $A_{mk}$ represents amplitude of the imperfection mode. The eigenfunctions are normalized to unity.

We study nonlinear dynamic instability of the plate under thermal shock using the following discretization parameters: a uniform 32 × 16 union-jack mesh with 1 024 elements and the time increment $\Delta t = 0.5 \times 10^{ - 4}$ s. In thermal boundary conditions (19.3.3), (19.3.4), and (19.3.5), the loading function $f(t)$ is given by Eq. (19.3.6).

At the initial stage of heat transfer, the plate remains undisturbed. If the magnitude of thermal shock $\Delta T$ is high enough, the compressive stresses rapidly develop and reach the critical level. At this moment, the plate jumps to oscillations about new configuration. Figure 19.8 shows time histories of the deflection at point $A(a/2;\;b/4)$ for three types of thermal boundary conditions and for different magnitudes of thermal shock $\Delta T$. The curves were obtained for $n = 1$ and nonzero coefficients $A_{11} = A_{12} = 10^{ - 2} h$ in Eq. (19.7.2).

Fig. 19.8

Time histories of the deflection of the clamped rectangular FGM plate: a response under thermal boundary conditions (19.3.3); b response under thermal boundary conditions (19.3.4); c response under thermal boundary conditions (19.3.5).

Decreasing the magnitude of thermal shock $\Delta T$ leads to slower thermal loading. As a result, the critical time necessary for the plate to buckle increases and the amplitude of postbuckling vibrations becomes less and less pronounced. This result suggests that in the limit as $t \to \infty ,$ where steady-state temperature distribution is reached, the plate exhibits static buckling. It follows that the critical temperature rise $\Delta T_{cr}$ can be determined from the static buckling problem under steady-state temperature distribution.

In Fig. 19.8, the dark circles mark the critical moments where the kinetic energy of the plate reaches the first pronounced maximum. Given a magnitude of thermal shock $\Delta T > \Delta T_{cr}$, the shortest critical time occurs if the top and bottom surfaces are heated simultaneously (see Eqs. (19.3.3)). Comparing Figs. 8b and c, we infer that the curves obtained under thermal boundary conditions (3.4) and (3.5) differ only slightly.

In Fig. 19.9, we show normalized deflections of the plate subjected to thermal boundary conditions (19.3.4) for $\Delta T = 100$ K. The effect of the antisymmetric mode of imperfection $A_{12}$ shows up only at the onset of buckling. After the critical moment $t > 0.005$ s, its effect vanishes and the plate oscillates about a doubly symmetric bent configuration.

Fig. 19.9

Contour plots of the normalized deflections $w/h$ of the rectangular plate

It is of interest to estimate the effect of the rate of thermal loading on the dynamic buckling instability. Confining our attention thermal boundary conditions (19.3.4), we compute the dynamic load factor (DLF) using formula

$$DLF = \frac{{N_{T,cr}^{dyn} }}{{N_{T,cr}^{stat} }}$$

(19.7.3)

where $N_{T,cr}^{dyn}$ is the stress resultant at the critical moment and $N_{T,cr}^{stat}$ is the critical stress resultant obtained from the solution of the corresponding static buckling problem under steady-state temperature distribution. The computation results are summarized in Table 19.5. It is seen that the dynamic buckling resistance of the plate increases as the grading index $n$ and the magnitude of thermal shock $\Delta T$ increase. This effect can be attributed to inertia forces.

Table 19.5 Effect of thermal loading on the dynamic buckling of the clamped rectangular plate

19.8.3 Dynamic Buckling of a Shallow Cylindrical Panel

We consider a shallow cylindrical panel whose boundary contour is simply supported and immovable. Dimensions of the panel are: radius of curvature $R = 1$ m, wall thickness $h$, half opening angle $\theta = 0.1$, and length $l = 0.2$ m (see Fig. 19.10).

Fig. 19.10

Geometry of a shallow cylindrical panel

The initial imperfection is assumed to be of the form

$$w_{0} = \sum\limits_{m,k} {A_{mk} \sin \frac{m\pi x}{a}\sin \frac{k\pi y}{l}}$$

(19.7.4)

where $m$ and $k$ are the half-wave numbers in the coordinate directions. We consider two panels whose thicknesses are 0.5 mm and 1 mm. For $h = 0.5$ mm, the only nonzero coefficients in Eq. (7.3) are $A_{2,2} = - A_{3,2} = h/100$. For $h = 1$ mm, we set $A_{2,1} = - A_{2,3} = - h/100$, the remaining coefficients being zero. The imperfection shapes are roughly similar to the buckling mode shapes obtained by solving the corresponding static buckling problem under the steady-state temperature distribution across the thickness.

Using a uniform 32 × 32 mesh and setting $\Delta t = 3 \times 10^{ - 5} \;{\text{s}}$, we study dynamics of the cylindrical panel under thermal boundary condition (3.4), in which the loading function $f(t)$ is given by Eq. (3.7) and $\sigma = 10^{2} \;{\text{s}}^{ - 1}$.

Figure 19.11 shows time histories of the normalized central deflection $w_{C} /h$ and kinetic energy of thin cylindrical panel with $h = 0.5$ mm and $n = 1$. Contour plots of the normalized deflections are shown in Fig. 19.12. The first maximum of the kinetic energy occurs at $t = 0.01695$ s, where deformation of the panel changes from symmetric to asymmetric mode. The second, more pronounced maximum occurs at $t = 0.0269$ s, which is the evidence of the buckling mode switching. We note that, in contrast to plates, dynamic buckling of the panels occurs deeply in the region of large deflections. The results presented in Fig. 19.12 agree with the results obtained by static nonlinear analysis of the panel under static thermal loading (Levyakov and Kuznetsov 2014).

Fig. 19.11

Time histories of deflection and kinetic energy of thin cylindrical panel of thickness $h = 0.5$ mm under $\Delta T$ = 250 K

Fig. 19.12

Contour plots of the normalized deflections $w/h$ of thin cylindrical panel

To estimate the effect of dynamic thermal loading on the buckling instability of the panel, we compute the dynamic load factor defined by Eq. (19.7.3). The calculation results obtained under thermal boundary conditions (3.4) are summarized in Table 19.6. It is seen from the results that the buckling resistance of the panel slightly increases with the magnitude of thermal shock $\Delta T$ and index $n$. This effect can be attributed to lateral inertia.

Table 19.6 Effect of dynamic thermal loading on buckling resistance of the simply supported cylindrical panel

19.8.4 Buckling of Simply Supported Cylindrical Shells

Finally, we consider a closed cylindrical shell of radius $R = 0.4$ m, length $L = \sqrt 3/5$m, and wall thickness $h = 0.001$ m. The outer surface of the shell is ceramic rich and the inner surface is metal rich. The edges are simply supported and immovable. The shell is meshed into 5 120 elements obtained by dividing the cylindrical surface into 160 segments in the circumferential direction and into 16 segments in the axial direction.

We assume that initial imperfection is of the form

$$w_{0} = A_{0} (w_{01} + w_{02} + w_{03} )$$

(19.6.6)

where $A_{0} /h = 10^{ - 2}$ and $w_{01}$, $w_{02}$, and $w_{03}$ are the first three buckling modes obtained from the nonlinear static analysis of the shell subjected to uniform temperature rise. Fourier series approximations of the buckling modes are given by

$$w_{01} = \sin 17\phi \sum\limits_{k = 1,3,...}^{9} {a_{k} \sin \frac{k\pi z}{L}}$$

$$w_{02} = \sin 18\phi \sum\limits_{k = 1,3,...}^{9} {b_{k} \sin \frac{k\pi z}{L}}$$

(19.6.7)

$w_{03} = \sin 16\phi \sum\limits_{k = 2,4,...}^{10} {c_{k} \sin \frac{k\pi z}{L}}$,

where $a_{1} = 0.270$, $a_{3} = 1.0$, $a_{5} = 0.061$, $a_{7} = - 0.315$, $a_{9} = - 0.136$, $b_{1} = 0.188$, $b_{3} = 1.0$, $b_{5} = 0.071$, $b_{7} = - 0.372$, $b_{9} = - 0.171$, $c_{2} = 1.0$, $c_{4} = 0.398$, $c_{6} = - 0.165$, $c_{8} = - 0.270$, $c_{10} = - 0.047$.

The nonlinear transient simulation was performed under thermal shock governed by Eqs. (19.3.4) and (19.3.7), in which $\sigma = 10^{3} {\text{s}}^{ - 1}$. Figure 19.13 shows time histories of the axial reaction force $F$ and kinetic energy $T$ for the shell with grading index $n = 1$. It is seen that, due to unsteady heat conduction, the reaction force increases from zero and, after reaching a maximum, drops by approximately 45%. As the critical time, we take the moment at which the reaction force reaches a maximum.

Fig. 19.13

Axial reaction force versus time for the simply supported cylindrical FGM shell with grading index $n = 1$

Figure 19.14 shows deformed configurations of the shell computed for the moments marked by circles in Fig. 19.13. In the prebuckling state, the shell swells axisymmetrically near the immovable edges. In the postbuckling regime, the deflection pattern rapidly changes exhibiting no symmetry.

Fig. 19.14

Deformed configurations of the cylindrical FGM shell for states marked in Fig. 19.13 (deflection is magnified by a factor of 10)

Table 19.7 lists the dynamic load factor computed for various values of the grading index $n$. In contrast to the plates and shallow shells considered above, the dynamic load factor is less than unity. This can be attributed to high sensitivity of closed cylindrical shell to (1) initial imperfections introduced in the dynamic analysis and (2) time history of the stresses that develop under unsteady heat transfer through the shell thickness.

Table 19.7 Effect of dynamic thermal loading on buckling resistance of the simply supported cylindrical shell

The critical time and buckling resistance increase with the grading index of the material since higher content of the ceramic phase results in higher stiffness of the FGM shell and lower rate of heat transfer through the shell thickness.

19.9 Concluding Remarks

A finite-element formulation has been proposed for nonlinear dynamic analysis of functionally graded plates and shells subjected to thermal shock. A triangular element with 15 degrees of freedom has been developed using the invariant-based approach and the concept of the surface of mass. Among the computational advantages of the shell finite element are (1) small number of degrees of freedom, (2) exact representation of six rigid body modes, and (3) compact and closed-form formulas for computing the gradient and Hessian, which are used to formulate the equations of motion. Performance of the element has been tested in several problems and good agreement has been reported between the calculation results and solutions available in the open literature.

A nonlinear analysis of transient response of suddenly heated plates and shells fabricated of functionally graded materials has been performed. Based on the numerical results, the following conclusions can be drawn:

• (1) sudden heating of thin plates and shells leads to nonlinear vibrations and, under certain conditions, to dynamic buckling instability;

• (2) plates and shells with restrained edges exhibit dynamic buckling provided the magnitude of thermal shock is higher than the critical temperature rise obtained from the corresponding static buckling analysis under steady-state temperature distribution;

• (3) the critical buckling time at which dynamic buckling occurs decreases with an increase in the magnitude of thermal shock;

• (4) the dynamic load factor increases with the magnitude of thermal shock;

• (5) higher content of ceramic phase of the material tends to increase buckling resistance of FGM plates and shells.