Mathematical Modelling of Nonlinear Heat Conduction with Relaxing Boundary Conditions

Abstract

This paper considers one dimensional unsteady heat condition in a media with temperature dependent thermal conductivity. When the thermal conductivity depends on the temperature, the corresponding heat equation is nonlinear. At one or both boundaries, a relaxing boundary condition is applied. It is a time dependent condition that approaches continuously, as time increases, a certain time independent condition. Such behavior at the boundaries arises naturally in some physical systems. As an example, we propose a simple model system that can give rise to either Dirichlet or convective relaxing boundary condition. Due to the dependence of the thermal conductivity on the temperature, the convective condition is nonlinear. For the solution of the problem, we propose a new numerical approach that first discretizes the heat equation in time, whereby a sequence of two-point boundary value problems (TPBVPs) is obtained. We use implicit time discretization, which provides for unconditional stability of the method. If the initial condition is given, we can solve consecutively the TPBVPs and get approximations of the temperature at the different time levels. For the solution of the TPBVPs, we apply the finite difference method. The arising nonlinear systems are solved by Newton’s method. A number of example problems are solved demonstrating the efficiency of the proposed approach.

S. M. Filipov and A. Avdzhieva were supported by the Sofia University Research Fund under Contract No. 80-10-156/23.05.2022. I. Faragó was supported by the Hungarian Scientific Research Fund OTKA SNN125119 and also OTKA K137699.

1 Introduction

This work considers unsteady one dimensional heat conduction in a solid body with temperature dependent thermal conductivity. The body occupies a finite space region. The exchange of energy within the body and at the boundaries is assumed to be due to heat transfer only. It is assumed that no energy is exchanged through radiation and that there are no internal heat sources. Since we consider the one dimensional case, the temperature u within the body is a function of one space variable only. This variable is denoted by x. The temperature at any position x may depend on the time t, hence $u=u(x,t)$. Heat transfer processes for which the temperature changes with time are called unsteady. If we are given some initial distribution of the temperature within the body, i.e. a function u(x, 0), and certain appropriate boundary conditions, we should be able, in principle, to predict how the temperature distribution evolves with time, i.e. to find the function u(x, t).

From the energy balance in a differentially small element of the body, we can derive a partial differential equation (PDE) for the temperature u(x, t). This equation is called a heat equation and must hold at any point x within the considered space interval and any time $t>0$. Solving this equation, subject to the given initial and boundary conditions, would yield the sought function u(x, t) When the thermal conductivity of the media is constant, this equation is a linear parabolic equation. This PDE has been studies extensively over the years and many analytical and numerical methods for its solution have been developed [1]–[6]. However, when the thermal conductivity of the media depends on the temperature, which is the considered case, the heat equation is nonlinear. This nonlinear equation is quite significant in science and engineering but is much more difficult to solve. Because of that various methods for particular cases and approximate techniques have been developed [7]–[14]. An important numerical method for solving the equation is the method of lines (MOL). The method was originally introduced in 1965 by Liskovetz [15]–[17] for partial differential equations of elliptic, parabolic, and hyperbolic type. The method first discretizes the equation in space, whereby, adding the boundary conditions, a system of first order ordinary differential equations (ODEs) is obtained. The system, together with the initial condition, constitutes an initial value problem (Cauchy problem). It can be solved using various numerical approaches. However, when explicit time-discretization schemes are applied, the method is only conditionally sable.

To overcome this and other drawbacks of the MOL, the authors have recently proposed a method [18] that first discretizes the heat equation in time using implicit discretization scheme. The discretized PDE is a sequence of second order ODEs which, together with the boundary conditions, forms a sequence of two-point boundary value problems (TPBVPs). Using the initial condition, we can solve the first TPBVP from the sequence and get an approximation of the temperature u(x, t) at the first time level $t=t_1$. Then, using the obtained solution, we can solve the second TPBVP, and so on, getting approximations of the temperature at each time level $t=t_1,t_2,\dots$ For the solution of the TPBVPs, we employ the finite difference method (FDM) with Newton iteration. An important feature of the proposed method is that it is unconditionally stable. The technique was applied successfully for solving nonlinear heat and mass transfer problems [18]–[19]. Originally, the method was developed for Dirichlet boundary conditions. These boundary conditions are linear and time-independent. However, many important physical situations require the application of time-dependent or even nonlinear time-dependent boundary conditions. This paper extends the proposed method to incorporate such boundary conditions. To motivate their use, we propose a simple physical model that naturally gives rise to the so called relaxing boundary conditions. They have been introduced first for certain diffusion processes [20] but, as shown in this work, can be applied successfully in certain heat transfer problems. Roughly speaking, a relaxing boundary condition is a time-dependent condition that approaches continuously, as time increases, a certain time-independent condition. The relaxing boundary condition can be a Dirichlet type, which is linear, but also a Neumann or a Robin type, which, given the nonlinear nature of the considered process, lead to nonlinear time-dependent conditions at the boundary.

Fig. 1.

Physical system

2 Physical System and Mathematical Model

This section presents a continuous mathematical model of a simple physical system that gives rise to one dimensional nonlinear heat transfer with relaxing boundary condition. A silicon rod is situated along the x-axis between $x=a$ and $x=b$ (Fig. 1). The temperature in the silicon is denoted by u(x, t). Because of the symmetry of the problem, the temperature in the rod is a function of one spatial variable only. We have chosen the substance silicon because its thermal conductivity depends on the temperature. The silicon rod is laterally insulated so that no energy, in any form, can be transferred through the lateral surface. At the point $x=a$ the silicon rod is in thermal contact with a tank filled with liquid. Heat can flow freely through the contact surface in both directions. Apart from the thermal contact with the silicon, the tank is well insulated. The temperature in the tank is denoted by T(t). It is homogenous inside the tank. A possible exception could be a thin layer close to the silicon contact surface, where the temperature may not be equal to T(t). There are two pipes connected to the tank. Through one of them liquid at temperature $T_r$ is being pumped into the tank at a constant volume flow rate. Through the other pipe liquid at temperature T(t) is going out of the tank at the same volume flow rate. We assume that the liquid in the tank is well stirred throughout the process so that the incoming liquid is mixed with the liquid inside the tank fast enough. We also assume that the density and heat capacity do not depend on the temperature. How to find the function T(t) and how to use it to set the boundary condition at $x=a$ will be shown in the next section. In this section we will derive the heat equation for the silicon rod and set the other necessary conditions.

To derive the heat equation we consider a differentially small volume element in the silicon rod, e.g. the element shown with dashed line in Fig. 1. Energy can enter or leave the volume element only via heat transfer through the two vertical surfaces. Let the left surface be at position x and the right at position $x+\varDelta x$. Let $\kappa =\kappa (u)$ be the thermal conductivity of the silicon. The energy flux through the left surface is $-\kappa (u)\frac{\partial u}{\partial x}|_{x}$. It tells us how much energy per unit time per unit area enters the volume element. Note that, by definition, a positive value of the flux means that the energy flows in the positive direction of the axis, i.e. from left to right in Fig. 1. The sign minus in the flux expression ensures that the energy moves from regions with high temperature to regions with low temperature. The energy flux through the right surface is $-\kappa (u)\frac{\partial u}{\partial x}|_{x+ \varDelta x}$. It tells us how much energy per unit time per unit area leaves the volume element. Let A be the area of the cross section of the silicon rod. Then, the energy that enters the element per unit time minus the energy that leaves the element per unit time divided by the volume of the element is

$$\begin{aligned} \frac{A(-\kappa (u)\frac{\partial u}{\partial x}|_{x})-A(-\kappa (u)\frac{\partial u}{\partial x}|_{x+ \varDelta x})}{A \varDelta x}. \end{aligned}$$

(1)

Since there are no internal heat sources within the silicon rod, we can equate the limit of (1) as $\varDelta x \rightarrow 0$ to the rate of change of the energy density (energy per unit volume) at point x:

$$\begin{aligned} \rho c_p \frac{\partial u}{\partial t}=-\frac{\partial }{\partial x}\Big (-\kappa (u)\frac{\partial u}{\partial x}\Big ). \end{aligned}$$

(2)

In this equation $\rho$ is the density of the silicon, and $c_p$ is its heat capacity at constant pressure. In our model they are assumed to be constant. The left hand side of the equation represents the rate of change of the energy density. The quantity in the brackets on the right hand side is the energy flux, while the right hand side itself can be viewed as the negative divergence of the energy flux. Equation (2) is the heat equation for the silicon rod. It is a PDE for the unknown function u(x, t) and must hold for any $x\in (a,b)$ and any $t>0$. If $\kappa$ were a constant, the equation would be a linear parabolic PDE. However, since $\kappa =\kappa (u)$, the equation is a nonlinear PDE.

To define the particular process that is taking place, however, in addition to (2), we need to provide the initial condition and the boundary conditions at $x=a$ and $x=b$. Let the temperature distribution in the silicon rod at time $t=0$ be $u_0 (x)$. Then, the initial condition is

$$\begin{aligned} u(x,0)=u_0(x), x\in [a,b]. \end{aligned}$$

(3)

At the boundary $x=b$, we consider a simple Dirichlet boundary condition, namely

$$\begin{aligned} u(b,t)=\beta , t>0. \end{aligned}$$

(4)

Other boundary conditions can also be applied.

In the next section, we discuss possible approaches to define the boundary condition at $x=a$ and show that the considered physical system leads naturally to the so called relaxing boundary condition.

3 Relaxing Boundary Condition

Let the temperature in the tank at some initial time $t=0$ be $T_0$. Obviously, if the temperature $T_r$ of the incoming liquid is different from $T_0$, the temperature in the tank T(t) will be changing. Now we proceed to find the temperature in the tank T(t). Let Q be the volume flow rate of the incoming liquid (bottom pipe in Fig. 1). The rate at which energy is entering the tank with the incoming liquid is $\rho _l c_{p,l} T_r Q$, where $\rho _l$ is the density of the liquid and $c_{p,l}$ is its heat capacity at constant pressure. The volume flow rate of the outgoing liquid (top pipe in Fig. 1) is also Q. Therefore, the rate at which energy is leaving the tank with the outgoing liquid is $\rho _l c_{p,l} T(t)Q$. Note that the mechanism of energy transfer through the pipes is convective, i.e. liquid with some energy density moves in and replaces (pushes out) liquid with different energy density. As a result the total energy contained in the tank is changing. Since in our model we assume that the tank is well insulated and no heat transfer between the tank and its surroundings occur, conservation of energy tells us that

$$\begin{aligned} \rho _l c_{p,l} \frac{dT(t)}{dt} V=\rho _l c_{p,l} T_r Q-\rho _l c_{p,l} T(t)Q, \end{aligned}$$

(5)

where V is the volume of the tank. The left hand side of the equation is the rate of change of the tank energy. Note that we have neglected the heat transfer through the contact surface separating the liquid from the silicon rod. This is justifiable as long as the contact surface area A is small enough. In fact, since (1) is independent of A, as long as A is not zero, we can choose it to be as small as necessary without causing a change in the heat equation (2). Simplifying (5), we get

$$\begin{aligned} \frac{dT(t)}{dt}=-\frac{Q}{V}( T(t)-T_r). \end{aligned}$$

(6)

Equation (6) is a first order linear ordinary differential equation for the unknown function T(t). Solving the equation and taking into account the initial condition $T(0)=T_0$, we get

$$\begin{aligned} T(t)=T_r + (T_0-T_r)e^{-\frac{Q}{V}t}. \end{aligned}$$

(7)

Hence, the temperature in the tank T(t) is an exponentially relaxing function. As t approaches infinity, the temperature approaches the finite value $T_r$. For $T_r>T_0$, the function T(t) is monotonically increasing and looks like the one shown with blue in Fig. 2.

Fig. 2.

The temperature at $x=a$ as a function of time for the Dirichlet relaxing boundary condition (solid blue line) and the traditional Dirichlet boundary condition (dashed line).

Now we are ready to set the boundary condition at $x=a$. The first approach is to equate the temperature of the silicon at $x=a$ to the temperature in the tank

$$\begin{aligned} u(a,t)=T(t), t>0. \end{aligned}$$

(8)

This boundary condition is called Dirichlet relaxing boundary condition [20]. The main feature of this condition is that the temperature value at the boundary increases (or decreases) gradually with time and approaches some finite value. In the traditional Dririchlet boundary condition, the temperature at the boundary changes abruptly at $t=0$ and stays constant for all $t>0$, i.e. it is a Heaviside function of time (the dashed line in Fig. 2).

The second approach to set the boundary condition at $x=a$ is to apply the so called convective boundary condition (= convection boundary condition) wherein we equate the energy flux at $x=a$ expressed through the thermal conductivity and the temperature gradient in the silicon to the same energy flux expressed through the transport properties and the state of the liquid system:

$$\begin{aligned} -\kappa (u(a,t)) \frac{\partial u(x,t)}{\partial x}|_{x=a}=c(T(t)-u(a,t)), t>0, \end{aligned}$$

(9)

where c is the mean convection heat transfer coefficient. Condition (9) holds, to a good approximation, for solid-liquid contact surfaces where the heat transport mechanism is mainly due to convection in the liquid system. For this type of boundary condition, unlike in (8), the temperature at the surface u(a, t) is deemed essentially different from the temperature T(t) in the interior of the tank. In Fig. 3 you can see a typical temperature profile for the Dirichlet and the convective boundary condition when $T_0=0, T_r>T_0$, and $u_0 (x)=0$. Note that, in the case of convective boundary condition, the temperature inside the tank is T(t) but close to the silicon contact surface it differs from T(t). Since the thermal conductivity $\kappa$ of the silicon depends on the temperature, condition (9) is nonlinear. The numerical method proposed for solving the heat equation (2) was originally developed for linear boundary conditions. In this paper, we show how the method can be changed to incorporate the nonlinear condition (9). Condition (9), besides being nonlinear, is time dependent. As time increases, the function T(t) approaches the constant value $T_r$, hence the condition approaches a certain time independent steady state condition. Thus, the unsteady state is transient and will approach a steady state. Any time dependent boundary condition that approaches continuously some time independent condition can be considered a relaxing boundary condition. Hence, condition (9) will be called convective relaxing boundary condition.

Fig. 3.

The temperature profile in the tank ($x<a$) and along the silicon rod ($x \ge a$) at time t for (i) Dirichlet boundary condition and (ii) convective boundary condition (convection).

4 Numerical Method

In this section we briefly introduce the numerical method proposed in [18] and then we show how it can altered in order to incorporate the nonlinear condition (9). Discretizing Eq. (2) on the time mesh $t_n=n\tau , n=1, 2,\dots$, we get

$$\begin{aligned} \rho c_p\frac{u_n-u_{n-1}}{\tau }=\partial _u\kappa (u_n)\Big (\frac{du_n}{dx}\Big )^2+\kappa (u_n)\frac{d^2u_n}{dx^2}, \end{aligned}$$

(10)

where $u_n=u_n (x)$ approximates the unknown function u(x, t) at time $t=t_n$. Equation (10) is a second order ODE for the unknown function $u_n (x)$. In a more compact form (10) can be written as

$$\begin{aligned} \frac{d^2u_n}{dx^2}=f(u_n,v_n;u_{n-1}), \end{aligned}$$

(11)

where $f(u_n,v_n;u_{n-1} )=\phi _n/\kappa (u_n ),\phi _n=\rho c_p (u_n-u_{n-1} )/\tau -\partial _u \kappa (u_n ) v_n^2,v_n=du_n/dx$. Equation (11), together with the given boundary conditions, is a TPBVP [21]. If $u_{n-1} (x)$ is given, we can solve the problem and obtain $u_n (x)$. Therefore, starting from the initial condition $u_0 (x)$, we can solve consecutively the TPBVP for $n=1,2,\dots$ and get $u_1 (x), u_2 (x), \dots$ To solve the problem, the finite difference method (FDM) is used [21]–[23]. We introduce a uniform mesh on $x \in [a,b]: x_i=a+(i-1)h, i=1,2,\dots ,N, h=(b-a)/(N-1)$. The ODE (11) is discretized, using the central difference approximation

$$\begin{aligned} \frac{u_{n,i+1}-2u_{n,i}+u_{n,i-1}}{h^2}=f(u_{n,i},v_{n.i};u_{n-1,i}), \; i=2, 3, \dots , N-1, \end{aligned}$$

(12)

where $u_{n,i}$ is an approximation of $u_n (x_i )$ and $v_{n,i}=(u_{n,i+1}-u_{n,i-1})/(2h)$. Equations (12), together with the two equations for the boundary conditions, form a nonlinear system of N equations for the N unknowns $u_{n,i},i=1,2,\dots ,N$. To solve the system, we apply the Newton method. To implement the method, we need the partial derivatives of the function f with respect to $u_n$ and $v_n$. Let $f_n=f(u_n,v_n;u_{n-1} )$, then:

$$\begin{aligned} q_n=\frac{\partial f_n}{\partial u_n}=\frac{1}{\kappa (u_n) }\Big ( -f_n \partial _u \kappa (u_n)+\frac{\partial \phi _n}{\partial u_n}\Big ), p_n=\frac{\partial f_n}{\partial v_n}=\frac{1}{\kappa (u_n)} \frac{\partial \phi _n}{\partial v_n}, \end{aligned}$$

(13)

where $\partial \phi _n/\partial u_n=\rho c_p/\tau -\partial _{uu}^2 \kappa (u_n ) v_n^2, \partial \phi _n/\partial v_n=-2\partial _u \kappa (u_n ) v_n$. Now we can implement the Newton method. First, we introduce the vector

$$\textbf{G}_n=[G_{n,1},G_{n,2},\dots G_{n,N} ]^T$$

where

$$\begin{aligned} G_{n,i}=u_{n,i+1}-2u_{n,i}+ u_{n,i-1}-h^2 f_{n,i}, i=2, 3, \dots , N-1. \end{aligned}$$

(14)

The components $G_{n,1}$ and $G_{n,N}$ come from the boundary condition. They are given later on in the section. The nonlinear system can be written as $\textbf{G}_n (\textbf{u}_n )=0$, where $\textbf{u}_n=[u_{n,1},u_{n,2},\dots , u_{n,N} ]^T$. Using $\textbf{u}_{n-1}$ as initial guess $\textbf{u}_n^{(0)}$, we apply Newton iteration for $k=0,1,\dots$

$$\begin{aligned} \textbf{u}_n^{(k+1)}=\textbf{u}_n^{(k)}-(\textbf{L}_n^{(k)})^{(-1)} \textbf{G}_n (\textbf{u}_n^{(k)}), \textbf{L}_n^{(k)}=\frac{\partial \textbf{G}_n}{\partial \textbf{u}_n } (\textbf{u}_n^{(k)}). \end{aligned}$$

(15)

The nonzero elements of the Jacobian $\textbf{L}_n^{(k)}$ for rows $i=2, 3,\dots ,N-1$ are

$$\begin{aligned} L_{n (i,i-1)}^{(k)}=1+\frac{1}{2}hp_{n,i}^{(k)}, L_{n (i,i)}^{(k)}=-2-h^2 q_{n,i}^{(k)}, L_{n (i,i+1)}^{(k)}=1-\frac{1}{2}hp_{n,i}^{(k)}. \end{aligned}$$

(16)

The elements of the first row are determined from the first boundary condition, and the elements of row N from the second boundary condition.

First, we show how to apply the Dirichlet relaxing boundary condition (8). The boundary condition at time level n is $u(a,t_n )-T(t_n)=0$. Replacing $u(a,t_n )$ by $u_n (a)$ and then $u_n (a)$ by $u_{n,1}$ as required by the FDM, we get $u_{n,1}-T(t_n)=0$. Let

$$\begin{aligned} G_{n,1}=u_{n,1}-T(t_n ). \end{aligned}$$

(17)

Then, the only nonzero element of the first row of the Jacobian is

$$\begin{aligned} L_{n (1,1)}^{(k)}=\frac{\partial G_{n,1}}{\partial u_{n,1} }|_{\textbf{u}_n=\textbf{u}_n^{(k)}}=1. \end{aligned}$$

(18)

Analogously, the convective relaxing boundary condition (9) yields

$$\begin{aligned} G_{n,1}=\kappa (u_{n,1})(u_{n,2}-u_{n,1} )+hcT(t_n )-hcu_{n,1}, \end{aligned}$$

(19)

where we have used the forward finite difference to approximate $\partial u/\partial x$. The two nonzero elements of the first row of the Jacobian are

$$\begin{aligned} L_{ n (1,1)}^{(k)}=\frac{\partial G_{n,1}}{\partial u_{n,1}}|_{\textbf{u}_n=\textbf{u}_n^{(k)}}=\partial _u \kappa (u_{n,1}^{(k)} )(u_{n,2}^{(k)}-u_{n,1}^{(k)})-\kappa (u_{n,1}^{(k)})-hc, \end{aligned}$$

(20)

$$\begin{aligned} L_{ n (1,2)}^{(k)}=\frac{\partial G_{n,1}}{\partial u_{n,2}}|_{\textbf{u}_n=\textbf{u}_n^{(k)}}= \kappa (u_{n,1}^{(k)}). \end{aligned}$$

(21)

For the silicon rod, where $\kappa =\kappa _0 e^{\chi u}$ [24], formula (19) becomes

$$\begin{aligned} G_{n,1}=\kappa _0 e^{\chi u_{n,1}} (u_{n,2}-u_{n,1})+hcT(t_n )-hcu_{n,1}, \end{aligned}$$

(22)

and formulas (20)–(21) become

$$\begin{aligned} L_{ n (1,1)}^{(k)}=\frac{\partial G_{n,1}}{\partial u_{n,1}}|_{\textbf{u}_n=\textbf{u}_n^{(k)}}=\chi \kappa _0 e^{\chi u_{n,1}^{(k)}} (u_{n,2}^{(k)}-u_{n,1}^{(k)})- \kappa _0 e^{\chi u_{n,1}^{(k)}}-hc, \end{aligned}$$

(23)

$$\begin{aligned} L_{ n (1,2)}^{(k)}=\frac{\partial G_{n,1}}{\partial u_{n,2}}|_{\textbf{u}_n=\textbf{u}_n^{(k)}}= \kappa _0 e^{\chi u_{n,1}^{(k)}}. \end{aligned}$$

(24)

Finally, we apply the right boundary condition (4). At time level n the condition is $u(b,t_n )-\beta =0$. Replacing $u(b,t_n )$ by $u_n (b)$ and then $u_n (b)$ by $u_{n,N}$, we get $u_{n,N}-\beta =0$. Let

$$\begin{aligned} G_{n,N}=u_{n,N}-\beta . \end{aligned}$$

(25)

Then, the only nonzero element of the last row of the Jacobian is

$$\begin{aligned} L_{ n (N,N)}^{(k)}=\frac{\partial G_{n,N}}{\partial u_{n,N}}|_{\textbf{u}_n=\textbf{u}_n^{(k)}}=1. \end{aligned}$$

(26)

Of course, at $x=b$, instead of the simple condition (4), we can apply Dirichlet relaxing boundary condition or convective relaxing boundary condition. The approach is analogous to the one described for $x=a$. In the next section we show examples with Dirichlet relaxing condition at the left or right boundary, and also at both boundaries.

5 Computer Experiments

In this section the proposed numerical approach is applied for the solution of several nonlinear heat transfer problems with relaxing boundary condition. Example 1 compares the Dirichlet with the convective relaxing boundary condition. In Example 2 and Example 3, Dirichlet relaxing boundary conditions are applied at one or both boundaries. In all examples thermal conductivity $\kappa =0.1e^{0.5u}$ is considered. This dependence is similar to the one exhibited by silicon but the numerical values are different [24]. The density and the heat capacity are chosen to be $\rho =1$ and $c_p=1$. The solid rod is placed between $x=1$ and $x=3$. The heat equation is

$$\begin{aligned} \frac{\partial u}{\partial t}=\frac{\partial }{\partial x}\Big (0.1e^{0.5u}\frac{\partial u}{\partial x}\Big ), x \in [1,3]. \end{aligned}$$

(27)

The initial condition is $u(x,0)=1, x \in [1,3]$.

Example 1

We choose the following parameters for the liquid containing tank system: $T_r=2, T_0=1, Q=1, V=1$, hence $T(t)=2-e^{-t}$. At the right boundary the temperature is kept fixed at 1, i.e. $u(3,t)=1$. At the left boundary, we first apply the Dririchlet relaxing boundary condition (8):

$$\begin{aligned} u(1,t)=2-e^{-t}, t > 0. \end{aligned}$$

(28)

Then, we apply the convective relaxing boundary condition (9) with $c=0.1$:

$$\begin{aligned} -e^{0.5u(1,t)}\frac{\partial u(x,t)}{\partial x}|_{x=1}=2-e^{-t}-u(1,t), t>0. \end{aligned}$$

(29)

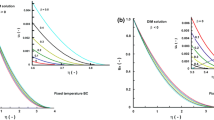
Results are shown in Fig. 4.

Fig. 4.

Example 1 - solution of (27) for the Dirichlet relaxing BC (28) (left) and the convective relaxing BC (29) (right).

Example 2

Equation (27) is solved with the same initial condition and a Dirichlet relaxing boundary condition at the left, right, and both boundaries. First we apply $T(t)=2-e^{-t}$ (Fig. 5 - top line) and then $T(t)=e^{-t}$ (Fig. 5 - bottom line).

Example 3

Equation (27) is solved with the same initial condition and Dirichlet relaxing boundary conditions $u(1,t)=2-e^{-t}, u(3,t)=e^{-t}$. Then, the problem is solved with $u(1,t)=e^{-t}, u(3,t)=2-e^{-t}$. Results are shown in Fig. 6.

Fig. 5.

Example 2 - solution of (27) with Dirichlet relaxing BC at the left, right, and both boundaries for $T(t)=2-e^{-t}$ (top) and $T(t)=e^{-t}$ (bottom).

Fig. 6.

Example 3 - solution of (27) with $u(1,t)=2-e^{-t}, u(3,t)=e^{-t}$ (left) and vice versa (right).

6 Conclusion

This paper considered unsteady nonlinear heat transfer in a thin silicon rod in thermal contact with liquid media that is being heated or cooled convectively. The mathematical model describing the system consists of nonlinear heat equation with initial condition and a Dirichlet relaxing or convective relaxing boundary condition. The convective condition is nonlinear. To solve the problem a new numerical approach was proposed that first discretizes the heat equation in time. The discretization scheme is implicit, which results in unconditional stability of the method. The resulting TPBVPs were solved by FDM with Newton method. Computer experiments were performed demonstrating the suitability of the approach for solving the nonlinear heat equation with variety of time-dependent and nonlinear conditions at the boundaries.