On the integral-balance approach to the transient heat conduction with linearly temperature-dependent thermal diffusivity

Abstract

Closed form approximate solutions to nonlinear transient heat conduction with linearly temperature-dependent thermal diffusivity have been developed by the integral-balance integral method under transient conditions. The solutions uses improved direct approaches of the integral method and avoid the commonly used linearization by the Kirchhoff transformation. The main steps in the new solutions are improvements in the integration technique of the double-integration technique and the optimization of the exponent of the approximate parabolic profile with unspecified exponent. Solutions to Dirichlet and Neumann boundary condition problems have been developed as examples by the classical Heat-balance integral method (HBIM) and the Double-integration method (DIM). Additional examples with HBIM and DIM solutions to cases when the Kirchhoff transform is initially applied have been developed.

1 Introduction

Most diffusion models concerning transport of heat (or mass) occur nonlinearly. Except some limited number of problems, there are no exact analytical solutions and, in general, numerical approaches have to be applied. However, in some cases approximate analytical solutions are possible. The present work reports new solutions of a non-linear transient heat conduction by Heat-balance integral method (HBIM) [1] and the Double-integration method (DIM) [2, 3].

1.1 Problem formulation

The communication considers a transient heat condition problem in a semi-infinite medium with temperature-dependent thermal diffusivity modelled by the equation.

$$\rho C_{p} \frac{\partial T}{\partial t} = \frac{\partial }{\partial x}\;\left( {k\left( T \right)\frac{\partial T}{\partial x}} \right)$$

(1a)

$$\frac{\partial T}{\partial t} = \frac{\partial }{\partial x}\;\left( {a\left( T \right)\frac{\partial T}{\partial x}} \right)$$

(1b)

$$a\left( T \right) = a_{0} \;\left( {1 + \beta T} \right)$$

(1c)

Equation (1b) and the relationship (1c) are related mainly to the temperature-dependent thermal conductivity $k = k_{0} \;\left( {1 + \beta T} \right)$ assuming the product $\rho C_{p}^{{}}$ temperature-independent [4–7].

The difficulties inherent in obtaining solutions for this class of equations have motivated a variety of solution methods, both exact and approximate ones. There exist several approaches to solve Eq. (1a), among them: orthogonal collocation method [6], Green function method [9], perturbation method [8, 10, 11], variational iteration method [8], homotopy-perturbation method [8], direct variational method [12], the least squares method [13], Networks models [14], iterative solutions with the solution of the linear problem as initial approximation [15], Finite difference solutions [5], Lattice Boltzmann method [16], numerical solutions [17], etc.

The Kirchhoff transformation [18] is the common approach to transform Eq. (1c) into a linear diffusion equation by applying (2a), namely

$$w = \int\limits_{0}^{T} {a_{0} \;\left( {1 + \beta T} \right)\;dT} = a_{0} T + \frac{{\beta T^{2} }}{2} \Rightarrow \frac{\partial w}{\partial t} = a_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$

(2a, b, c)

Then, the solution of (2c) has been performed by, series expansion [4], separation of variables [19, 20], homotopy-perturbation method [22], etc. The final solution in term of T may be developed either analytically [4] by the series reversion method [21] or by numerical methods [22].

The HBIM is among the approximate analytical methods allowing to develop closed-form solutions of the problem (1c), but its simple form known as Heat-balance integral method [1] has been used accidentally [1, 23] for solutions of the problem (1b) with thermal diffusivity expressed by (1c). The main approach in these solutions is the initial non-linear transform ${\text{v}} = \int_{0}^{T} {\rho C_{p} \;dT}$ to linearize Eq. (1b) and then applying HBIM with assumed cubic polynomial profiles. It is worth noting, that in these solutions [1, 23] the non-linear transform is mainly applied to the surface temperature (at x = 0). These solutions are not popular due to the inherent property of HBIM to predetermine the accuracy of approximation when a fixed order of the assumed profiles is used [1, 3] as well as due to the difficulties emerging in the reversion of the solution in the terms of T, when the order of the polynomial approximation is high [4].

The recent applications of the simple HBIM [24] and the double-integral balance method (DIM) [25] to Eq. (1b), when the thermal diffusivity is a of a power-law functional dependence of the temperature $a = a_{0} T^{m}$, demonstrate a new solution strategy were the non-linear Kirchhoff transformation can be avoided. The present article reports new solutions to Eq. (1b) with the additive functional relationship (1c) about the temperature-dependent diffusivity, using the technique of HBIM and DIM and the solution strategies developed in [25].

1.2 Aim and paper organization

The general task of the present study is the development of approximate integral-balance solutions of the model (1a, b) in avoiding the Kirchhoff linearization transformation of the thermal diffusivity (1c). The solutions developed refer to the cases with Dirichlet and Neumann boundary conditions. The approximate solutions are developed by HBIM and DIM applying an assumed parabolic profile with unspecified exponent [26–29]. In all cases numerical solutions (performed by the finite difference method and the 4th order Runge–Kutta method, and by the help of Maple (see “Appendix 1” for details) are used as benchmark examples allowing evaluating the accuracy of the developed integral-balance solutions.

The paper is organized as follows: (1) Sect. 2 presents the basic of the integral balance techniques, i.e. HBIM and DIM and the principles of application of the methods to non-linear heat conduction problems with temperature-dependent diffusivity. (2) Section 3 develops the solution strategies and general relationships of HBIM and DIM involving a parabolic profile with unspecified exponent and a linearly temperature-dependent thermal diffusivity. (3) Section 4 presents integral balance solutions for the problem (1b) with a fixed temperature as a boundary condition. (4) Section 5 demonstrates solutions of problem with fixed temperature and fixed flux boundary conditions. Section 5.1 especially stresses the attention on problems emerging when HBIM and the DIM are directly applied. Section 5.2 shows two alternative approaches to solve the problem by changing of variables and a preliminary rescaling of the conductivity-temperature relationship (1c), respectively, allowing to converted (1b) into a degenerate diffusion equation with a power-law diffusivity. Section 5.5 demonstrates numerical solutions and benchmarking examples of the developed approximate solutions. Section 6 refers to the classical Kirchhoff transform and presents comparative solutions and demonstrates that applying it to (1c) the techniques of HBIM and DIM can be straightforwardly applied.

2 Background of the integral-balance solution

The integral-balance method is based on the concept that the diffusant (heat or mass) penetrates the undisturbed medium at a final depth $\delta$. Therefore, the common boundary conditions at infinity

$$T\;\left( \infty \right) = 0\quad{\text{and}}\quad\frac{\partial T}{\partial x}\;\left( \infty \right) = 0$$

(3)

can be replaced by

$$T\;\left( \delta \right) = 0\quad{\text{and}}\quad\frac{\partial T}{\partial x}\;\left( \delta \right) = 0$$

(4a, b)

The conditions (4a, b) define a sharp-front movement $\delta \left( t \right)$ of the boundary between disturbed and undisturbed medium when an appropriate boundary condition at $x = 0$ is applied. The position $\delta \;\left( t \right)$ is unknown and should be determined trough the solution. When the thermal diffusivity is temperature-independent (i.e. $a = a_{0} = const.$), the integration of Eq. (1b) over a finite penetration depth $\delta$ yields (5a)

$$\int\limits_{0}^{\delta } {\frac{{\partial T\;\left( {x,t} \right)}}{\partial t}dx} = \int\limits_{0}^{\delta } {a_{0} \frac{{\partial^{2} T}}{{\partial x^{2} }}} dx\;{\text{or}}\;\frac{d}{dt}\int\limits_{0}^{\delta } {T\;\left( {x,t} \right)dx} = - a_{0} \frac{\partial T}{\partial x}\;\left( {0,t} \right)$$

(5a, b)

Applying the Leibniz rule to left-side of (5a) we get (5b). Alternatively, for the sake of the clarity of the further explanations of the method, Eq. (5a) can be expressed in an equivalent form (5c)

$$\int\limits_{0}^{x} {\frac{{\partial T\;\left( {x,t} \right)}}{\partial t}dx} + \int\limits_{x}^{\delta } {\frac{{\partial T\;\left( {x,t} \right)}}{\partial t}dx} = - a_{0} \frac{\partial T}{\partial x}\;\left( {0,t} \right)$$

(5c)

Physically, Eq. (5b), as well as (5c) imply that the total thermal energy accumulated into the finite layer (from x = 0 to $x = \delta$) is balanced by the heat flux at the interface x = 0. The left sides of (5a) and (5b) are the zero-order moments of the temperature distribution over the penetration depth $\delta$.

Equation (5b) is the principle relationship of the simplest version of the integral-balance method known as Heat-balance Integral Method (HBIM) [1]. After this first step, replacing T by an assumed profile $T_{a}$ (expressed as a function of the relative space co-ordinate ${x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta }$) the integration in (5b) results in an ordinary differential equation about $\delta \left( t \right)$ [1, 3, 24]. The principle problem emerging in application of (5a, b) is that the right-side depends on the gradient expressed through the type of the assumed profile.

An improvement, avoiding the principle problem of HBIM is the double integration approach (DIM) [2] recently renewed by T.G.Myers as Refined integral Method (RIM) [27, 29].

The first step of DIM is integration of (1b) from 0 to x, namely

$$\int\limits_{0}^{x} {\frac{{\partial T\;\left( {x,t} \right)}}{\partial t}dx} = a_{0} \frac{{\partial T\;\left( {x,t} \right)}}{\partial x} - a_{0} \frac{{\partial T\;\left( {0,t} \right)}}{\partial x},\quad a_{0} = const.$$

(6a)

Equation (6a) has the same physical meaning as Eq. (5b) but now the volume where the thermal energy is accumulated in bounded by 0 and x, and it is balanced by the differences of the heat fluxes at the interfaces x = 0 and x. Equivalently, (6a) is the zero-order moment of the temperature distribution over the penetration depth from 0 to x. Then, Eq. (6a) integrated again from 0 to $\delta$ results in the principle equation of DIM, following Myers [27, 29]

$$\frac{d}{dt}\int\limits_{0}^{\delta } {xT\;\left( {x,t} \right)dx} = a_{0} T\;\left( {0,t} \right)$$

(6b)

Equation (6b) is the first moment of the temperature distribution over the penetration depth and the right side is independent of the assumed temperature distribution (profile) since it is defined by the boundary condition.

An alternative expression of the DIM principle relationship can be easily derived, too. Representing the integral in the left-side of (5a) as $\int_{0}^{\delta } {f\left( \cdot \right)dx} = \int_{0}^{x} {f\left( \cdot \right)dx} + \int_{x}^{\delta } {f\left( \cdot \right)dx}$ we get Eq. (5c). Subtracting (6a) from (5c) one obtain

$$\int\limits_{x}^{\delta } {\frac{{\partial T\;\left( {x,t} \right)}}{\partial t}dx} = a_{0} \frac{{\partial T\;\left( {x,t} \right)}}{\partial x}$$

(7)

Equation (7) has the same physical meaning as Eq. (5a), but now the heat accumulated between x and $\delta$ is at issue. The left side of (7) is the zero-order moment of the temperature distribution over the section of the penetration depth bounded by the points x and the front ($x = \delta$). The integration of (7) from 0 to $\delta$ results in

$$\int\limits_{0}^{\delta } {\left( {\int\limits_{x}^{\delta } {\frac{\partial T}{\partial t}dx} } \right)\,dx} = a_{0} T\left( {0,t} \right)$$

(8)

The expression (8) is more general than (6b) since it allows to work with either integer-order time-derivatives (as in the present case) or with time-fractional derivatives [30, 31] where the Leibniz rule is inapplicable (see Refs. [25, 26] for more details).

If the thermal diffusivity is non-linear and expressed as a power-law $a = a_{p} T^{m}$ (m > 0), corresponding to degenerate diffusion problems) then Eqs. (6b) and (8) take the forms [25]

$$\frac{d}{dt}\int\limits_{0}^{\delta } {xT} \left( {x,t} \right) = \frac{{a_{p} }}{m + 1}\left[ {T\left( {0,t} \right)} \right]^{m + 1}$$

(9)

$$\int\limits_{0}^{\delta } {\left( {\int\limits_{x}^{\delta } {\frac{\partial T}{\partial t}} dx} \right)\,} dx = \frac{{a_{p} }}{m + 1}\left[ {T\left( {0,t} \right)} \right]^{m + 1}$$

(10)

The integral relations presented by (9) and (10) will be used further in this work in the development of the problems at issue. The application of both HBIM and DIM to the case with $a\left( T \right) = a_{0} \;\left( {1 + \beta T} \right)$ is demonstrated in the next section (see Sects. 3.3, 3.4). It is worthy that this approach does no use averaging procedure of the Kirchhoff transform such as that expressed by Eqs. (2a, b, c). For the sake of clarity and avoiding any doubts additional examples with mean thermal diffusivity $a_{m}$ are developed with both the HBIM and DIM integration techniques.

3 Solution strategies

The solution strategy used in this research is based on the results (5a), (9) and (10) applied to the linear form of the thermal diffusivity (1c) and an assumed parabolic profile with unspecified exponents.

3.1 Assumed profile

The solutions use an assumed parabolic profile with unspecified exponent [25–29]

$$T_{a} = T_{s} \left( {1 - \frac{x}{\delta }} \right)^{n}$$

(11)

The profile (11) satisfies the Goodman’s boundary conditions (4a, b), namely

$$T\left( {0,t} \right) = T_{s} \quad{\text{or}}\quad k\left( {\frac{\partial T}{\partial x}} \right)_{x = 0} = q_{0}$$

(12a, b)

$$T\left( {\delta ,t} \right) = T_{0} = 0\quad {\text{or}}\quad k\left( {\frac{\partial T}{\partial x}} \right)_{x = \delta } = 0$$

(13a, b)

3.2 Scaling and governing equations

The scaled thermal diffusivity is commonly expressed as $a = f\;\left[ {\left( {{T \mathord{\left/ {\vphantom {T {T_{ref} }}} \right. \kern-0pt} {T_{ref} }}} \right)^{m} } \right]$ where $T_{ref}$ is a reference temperature which differs from the initial medium temperature $T_{0}$. The functional relationship can be expressed as a simple power-law $a = a_{0} T^{m}$ [14, 24, 25] or as a linear relationship $a = a_{0} \left[ {1 + \beta \left( {{T \mathord{\left/ {\vphantom {T {T_{ref} }}} \right. \kern-0pt} {T_{ref} }}} \right)^{m} } \right],$ where m and β are dimensionless constants. In this context, when $T_{ref} \ne T_{0} \ne 0$ the power-law can be rescaled as $a_{eff} u^{m} = a_{0} k_{T} \left( {{T \mathord{\left/ {\vphantom {T {T_{0} }}} \right. \kern-0pt} {T_{0} }}} \right)^{m}$ where $u = \left( {{T \mathord{\left/ {\vphantom {T {T_{0} }}} \right. \kern-0pt} {T_{0} }}} \right),\;k_{T} = \left( {{{T_{0} } \mathord{\left/ {\vphantom {{T_{0} } {T_{ref} }}} \right. \kern-0pt} {T_{ref} }}} \right)^{m} = const.$ and $a_{eff} = a_{0} k_{T}$. Therefore the linear relationship for m = 1 can be presented as $a = a_{0} \left[ {1 + \beta k_{T} \left( {{T \mathord{\left/ {\vphantom {T {T_{ref} }}} \right. \kern-0pt} {T_{ref} }}} \right)} \right]$. When $T_{ref} = T_{0} \ne 0$, we get $k_{T} = 1$.

In order to be correct in the solutions performed next and for the sake of clarity of the expressions, we have to mention that the common literature data about the heat conductivity of the materials are presented in dimensional form $k = k_{0} \left[ {1 + \beta T} \right]$. It is easy, to transform this linear relationship into $a = a_{0} \left[ {1 + \beta k_{T} \left( {{T \mathord{\left/ {\vphantom {T {T_{ref} }}} \right. \kern-0pt} {T_{ref} }}} \right)} \right]$ by a simple rescaling procedure which affects only the pre-factor $\beta k_{T}$. An alternative scaling procedure by a translation transform allowing converting the linear relationship into a power-law is applied in Sect. 5.

In the case of the Dirichlet problems using the dimensionless variable $u = {{\left( {T - T_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{0} } \right)} {\left( {T_{s} - T_{0} } \right)}}} \right. \kern-0pt} {\left( {T_{s} - T_{0} } \right)}}$ or $u = {T \mathord{\left/ {\vphantom {T {T_{s} }}} \right. \kern-0pt} {T_{s} }}$ the dimensionless assumed is

$$u_{a} = \left( {1 - {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta }} \right)^{n} ,\quad u_{a} = {{T_{a} } \mathord{\left/ {\vphantom {{T_{a} } {T_{s} }}} \right. \kern-0pt} {T_{s} }},\quad u_{a} \left( {0,1} \right) = 1,\quad u\left( {\delta ,t} \right) = 0,\quad k\left( {\frac{\partial u}{\partial x}} \right)_{x = \delta } = 0$$

(14)

The governing equation in a dimensionless form using $u = {T \mathord{\left/ {\vphantom {T {T_{s} }}} \right. \kern-0pt} {T_{s} }}$ is

$$\frac{\partial u}{\partial t} = \frac{\partial }{\partial x}\left[ {a_{0} \left( {1 + \beta u} \right)\frac{\partial u}{\partial x}} \right]$$

(15)

The dimensionless form (15) requires the linear relationship $k = k_{0} \left[ {1 + \beta T} \right]$ to be initially rescaled as

$$k = k_{0} \left[ {1 + \beta \left( {\frac{{T - T_{0} }}{{T_{s} - T_{0} }}} \right)} \right]\quad {\text{or}}\quad {\text{as}}\quad k = k_{0} \left[ {1 + \beta \left( {{T \mathord{\left/ {\vphantom {T {T_{s} }}} \right. \kern-0pt} {T_{s} }}} \right)} \right] = k_{0} \left[ {1 + \beta u} \right]$$

(16a, b)

The procedure described by (16) addresses the preliminary treatment of the data related to a particular material and requires the numerical data to be presented in the form $k = k_{0} \left[ {1 + \beta \left( {{T \mathord{\left/ {\vphantom {T {T_{s} }}} \right. \kern-0pt} {T_{s} }}} \right)} \right] = k_{0} \left[ {1 + \beta k_{s} u} \right],\;k_{s} = \left( {{{T_{s} } \mathord{\left/ {\vphantom {{T_{s} } {T_{ref} }}} \right. \kern-0pt} {T_{ref} }}} \right)$. For the sake of simplicity we use $k_{s} = 1$ and this leads to Eq. (15).

3.3 Simple integration: heat-balance integral method (HBIM)

The classical HBIM considers integration over the penetration depth $\delta \left( t \right)$ as it is described by Eq. (5a, b), namely

$$\int\limits_{0}^{\delta } {\frac{\partial u}{\partial t}} dx = \int\limits_{0}^{\delta } {\frac{\partial }{\partial x}\left( {a_{0} \left( {1 + \beta u} \right)\frac{\partial u}{\partial x}} \right)} \,dx$$

(17a)

$$\frac{d}{dt}\int\limits_{0}^{\delta } u dx = - a_{0} \left( {\frac{\partial u}{\partial x}} \right)_{x = 0} - \beta \left( {u\frac{\partial u}{\partial x}} \right)_{x = 0}$$

(17b)

However, we may present the temperature gradient in (17a) as (18a)

$$a_{0} \left( {1 + \beta u} \right)\frac{\partial u}{\partial x} \Rightarrow a_{0} \left( {\frac{\partial u}{\partial x} + \frac{\beta }{2}\frac{{\partial u^{2} }}{\partial x}} \right)$$

(18a)

Then, the relation (17b) can be represented as (18b)

$$\frac{d}{dt}\int\limits_{0}^{\delta } u dx = - a_{0} \left( {\frac{\partial u}{\partial x} + \frac{\beta }{2}\frac{{\partial u^{2} }}{\partial x}} \right)_{x = 0}^{{}}$$

(18b)

With the assumed profile (11) the right side of (18b) is

$$- a_{0} \left( {\frac{\partial u}{\partial x} + \frac{\beta }{2}\frac{{\partial u^{2} }}{\partial x}} \right)_{x = 0}^{{}} = a_{0} \left( {\frac{n}{\delta } - \frac{\beta }{2}\frac{{n\left( {n - 1} \right)}}{{\delta^{2} }}} \right)$$

(18c)

This modification of HBIM, conceived here, allows solving non-linear heat conduction equations. It will be tested in the examples developed next, even though the inherent problem with the determination of the gradient at the boundary still remains.

Now, the reasonable question is: What happens if the mean thermal diffusivity (19a) is used in the governing equation?

$$a_{m} = \frac{1}{{u\left( {0,t} \right)}}\int\limits_{0}^{{u\left( {0,t} \right)}} {a_{0} \left( {1 + \beta u} \right)du} = a_{0} + \beta \frac{{u\left( {0,t} \right)}}{2} ,$$

(19a)

For the Dirichlet problem, for instance, we have $u\left( {0,t} \right) = 1$ (see the Example 1 further in this work) and therefore $a_{m} = a_{0} \;\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0pt} 2}} \right)$. Then, with $a_{m}$ the single integration procedure of HBIM provides

$$\frac{d}{dt}\int\limits_{0}^{\delta } {u\left( {x,t} \right)} dx = - a_{0} \left( {1 + \frac{\beta }{2}} \right)\left( {\frac{\partial u}{\partial x}} \right)_{x = 0}$$

(19b)

The results (18b) and (19b) are not equivalent. As a supporting example, with the assumed profile (11) and $u\left( {0,t} \right) = 1$, the right side of (19b) is

$$- a_{0} \left( {1 + \frac{\beta }{2}} \right)\left( {\frac{\partial u}{\partial x}} \right)_{x = 0} = a_{0} \left( {1 + \frac{\beta }{2}} \right)\left( {\frac{n}{\delta }} \right)$$

(19c)

The results (18c) and (19c) are not equivalent.

As a final point, the integration procedure of HBIM and the alternative one with the mean thermal diffusivity $a_{m}$ do not lead to equivalent results.

3.4 Double-integration method

The first step of the double integration approach is the integration of the governing equation from 0 to x. With the form (19b) this integration yields

$$\int\limits_{0}^{x} {\frac{\partial u}{\partial t}} dx = \int\limits_{0}^{x} {\frac{\partial }{\partial x}\left[ {a_{0} \left( {u + \frac{\beta }{2}\frac{{\partial u^{2} }}{\partial x}} \right)} \right]} \,dx \Rightarrow a_{0} \left( {u + \frac{\beta }{2}\frac{{\partial u^{2} }}{\partial x}} \right) - a_{0} \left[ {u\left( {0,t} \right) + \frac{\beta }{2}\frac{{\partial u^{2} \left( {0,t} \right)}}{\partial x}} \right]$$

(20a, b)

The second step of DIM is integration of (20b) from 0 to $\delta$, namely

$$\begin{aligned} \int\limits_{0}^{\delta } {\left( {\int\limits_{0}^{x} {\frac{\partial u}{\partial t}} dx} \right)\;dx} & = a_{0} \int\limits_{0}^{\delta } {u\left( {x,t} \right)dx} + \frac{{a_{0} \beta }}{2}\int\limits_{0}^{\delta } {\left( {\frac{{\partial u\left( {x,t} \right)}}{\partial x}} \right)} dx \\ & \quad - a_{0} \left[ {u\left( {0,t} \right) + \frac{\beta }{2}\frac{{\partial u\left( {0,t} \right)}}{\partial x}} \right]\delta \\ \end{aligned}$$

(21)

The last term in (20b) is a constant with respect to x and consequently the last term in (21) is a constant (with respect to x) multiplied by $\delta$. Further, taking into account that that right-hand side of (20b) and the last term of (21) are equal, as well integrating by parts the double integral of (21) we have

$$\frac{d}{dt}\int\limits_{0}^{\delta } {xu\,} dx = a_{0} u\left( {0,t} \right) + \frac{{a_{0} \beta }}{2}\left[ {u\left( {0,t} \right)} \right]^{2}$$

(22a)

Equation (22a) is the principle equation of DIM with a linear temperature-dependent thermal diffusivity. Its left-hand side is expressed in the form known from RIM [3, 27–29]. Alternatively, if the technique described by Eqs. (7) and (8) (as well as with Eqs. 9, 10) is applied it can be presented as

$$\frac{d}{dt}\int\limits_{0}^{\delta } {\int\limits_{x}^{\delta } u \,} dx = a_{0} u\left( {0,t} \right) + \frac{{a_{0} \beta }}{2}\left[ {u\left( {0,t} \right)} \right]^{2}$$

(22b)

Again, if the mean thermal diffusivity $a_{m}$ is applied, then the results of the double-integration are

$$\frac{d}{dt}\int\limits_{0}^{\delta } {xu\,} dx = a_{0} \left( {1 + \frac{\beta }{2}} \right)\left[ {u\left( {0,t} \right)} \right]^{2}$$

(23a)

$$\frac{d}{dt}\int\limits_{0}^{\delta } {\int\limits_{x}^{\delta } u \,} dx = a_{0} \left( {1 + \frac{\beta }{2}} \right)\left[ {u\left( {0,t} \right)} \right]^{2}$$

(23b)

The results obtained by the direct integration (22a, b) and the ones developed with the mean thermal diffusivity (23a, b) are equivalent only if $u\left( {0,t} \right) = 1$. Therefore, the approach with the mean thermal diffusivity $a_{m}$ works correctly with DIM in the case of the fixed temperature boundary condition only.

The solutions developed next (Examples 1 and 2) do not use the mean thermal diffusivity $a_{m}$ because the averaging procedure is a non-natural step which does not follow directly from the integration techniques of HBIM and DIM.

4 Solution Example 1: fixed temperature as a boundary condition at x = 0

In this section we develop approximate solutions by HBIM and DIM solutions without a preliminary treatment of the linear relationship (1c) of the temperature-dependent diffusivity, in contrast to the case of a fixed flux problem (see Sect. 5).

4.1 HBIM solution

The application of the assumed profile (14) and integration defined by (19) yields

$$\frac{d}{dt}\int\limits_{0}^{\delta } {\left( {1 - \frac{x}{\delta }} \right)}^{n} dx = \frac{{a_{0} }}{\delta }n\left( {1 + \beta } \right)$$

(24a)

The result of (24a) with the initial condition $\delta \left( {t = 0} \right) = 0$ is

$$\delta^{2} = \left( {a_{0} t} \right)2n\left( {n + 1} \right)\left( {1 + \beta } \right) \Rightarrow \delta_{{\left( {HBIM} \right)}}^{T} = \sqrt {a_{0} t} \sqrt {2n\left( {n + 1} \right)} \sqrt {\left( {1 + \beta } \right)}$$

(24b, c)

For β = 0, Eq. (24b) reduces to the linear problem with $\delta_{{0\left( {HBIM} \right)}}^{T} = \sqrt {a_{0} t} \sqrt {2n\left( {n + 1} \right)}$ [3, 26]. However, we have to bear in mind that the governing Eq. (1b) with $\beta = 0$ is purely parabolic, while for $\beta \ne 0$, even for very small values, the Eq. (1b) demonstrates behaviours of a degenerate diffusion due the term $a_{0} \beta T\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)$.

4.2 DIM solution

Applying Eq. (22a) with $u\left( {0,t} \right) = u^{m + 1} \left( {0,t} \right) = 1$ we get

$$\frac{d}{dt}\int\limits_{0}^{\delta } {x\left( {1 - \frac{x}{\delta }} \right)\,} dx = a_{0} + \frac{{a_{0} \beta }}{2} \Rightarrow \frac{1}{{\left( {n + 1} \right)\left( {n + 2} \right)}}\frac{{d\delta^{2} }}{dt} = a_{0} \left( {1 + \frac{\beta }{2}} \right)$$

(25a, b)

Then, the penetration depth is

$$\delta_{{\left( {DIM} \right)}}^{T} = \sqrt {a_{0} t} \sqrt {\left( {n + 1} \right)\left( {n + 2} \right)} \sqrt {\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0pt} 2}} \right)}$$

(26)

For β = 0, Eq. (26) reduces to the linear problem with $\delta_{{0\left( {DIM} \right)}}^{T} = \sqrt {a_{0} t} \sqrt {\left( {n + 1} \right)\left( {n + 2} \right)}$ [3, 26] but taking into account the comments done in the previous section.

4.3 Approximate profile and similarity variable

Therefore, the approximate profiles can be expressed as:

HBIM

$$\begin{aligned} u_{{a\left( {HBIM} \right)}} & = \left( {1 - \frac{x}{\delta }} \right)^{n} = \left( {1 - \frac{x}{{\sqrt {a_{0} t} \sqrt {2n\left( {n + 1} \right)} \sqrt {\left( {1 + \beta } \right)} }}} \right)^{n} \\ & = \left( {1 - \frac{\eta }{{F_{HBIM}^{T} \left( {n,\beta } \right)}}} \right)^{n} \\ \end{aligned}$$

(27a, b, c)

DIM

$$\begin{aligned} u_{{a\left( {DIM} \right)}} & = \left( {1 - \frac{x}{\delta }} \right)^{n} = \left( {1 - \frac{x}{{\sqrt {a_{0} t} \sqrt {\left( {n + 1} \right)\left( {n + 2} \right)} \sqrt {\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0pt} 2}} \right)} }}} \right)^{n} \\ & = \left( {1 - \frac{\eta }{{F_{DIM}^{T} \left( {n,\beta } \right)}}} \right)^{n} \\ \end{aligned}$$

(28a, b, c)

$$\begin{aligned} F_{HBIM}^{T} \left( {n,\beta } \right) & = \sqrt {2n\left( {n + 1} \right)} \sqrt {\left( {1 + \beta } \right)} ,\\ \;F_{DIM}^{T} \left( {n,\beta } \right) & = \sqrt {\left( {n + 1} \right)\left( {n + 2} \right)} \sqrt {\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0pt} 2}} \right)} \end{aligned}$$

(29a, b)

The parabolic profile directly defines the similarity variable $\eta = {x \mathord{\left/ {\vphantom {x {\sqrt {a_{0} t} }}} \right. \kern-0pt} {\sqrt {a_{0} t} }}$. The numerical factors $F_{HBIM}^{T} \;\left( {n,\beta } \right)$ and $F_{DIM}^{T} \left( {n,\beta } \right)$ define the penetration depths because for $\eta = F_{DIM}^{T} \left( {n,\beta } \right)$ we have $u_{a} = 0$, for example. It is also possible to define effective similarity variables $\eta_{{\beta \left( {HBIM} \right)}} = {x \mathord{\left/ {\vphantom {x {\sqrt {a_{0} t\left( {1 + \beta } \right)} }}} \right. \kern-0pt} {\sqrt {a_{0} t\left( {1 + \beta } \right)} }}$ or $\eta_{{\beta \left( {DIM} \right)}} = {x \mathord{\left/ {\vphantom {x {\sqrt {a_{0} t\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0pt} 2}} \right)} }}} \right. \kern-0pt} {\sqrt {a_{0} t\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0pt} 2}} \right)} }}$ thus allowing the numerical factors $F_{HBIM}^{T}$ and $F_{DIM}^{T}$ to be independent of β and equal to the ones of the linear problem [26]. However, with such an approach we loss the physical significance of integral balance solution and the fact that the penetration depth is affected by β. Moreover, as it was commented in Sect. 3.3, the mean thermal diffusivity $a_{m} = a_{0} \;\left( {1 + {\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0pt} 2}} \right)$ works correctly only if the DIM solution is applied. In this case we may use for comparative purposes the exact solution $1 - erf\;\left( {{{\eta_{\beta (DIM)} } \mathord{\left/ {\vphantom {{\eta_{\beta (DIM)} } 2}} \right. \kern-0pt} 2}} \right)$ but with caution because the averaging procedure applied to develop $a_{m}$ suppresses the degenerative behaviour of the model (1b, c) due to the term $a_{0} \beta T\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)$.

In order the compare the integral-balance solutions with numeral ones and it is more convenient to express the profiles through the dimensionless variable $X = {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta }$ as $u_{a} = \left( {1 - X} \right)^{n}$. With this independent variable, the solutions are normalized in the square [0, 1] (see “Appendix 1”).

4.4 Optimal exponents of the approximate profile

In the general moment method [32, 33] a desired accuracy in approximation can be attained be increasing the number of terms in the series $u_{a} = \sum\nolimits_{j = 1}^{N} {a_{j} \left( {1 - {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta }} \right)^{{n_{j} }} }$ (see Ref. [25] for comments), i.e. by increase in the order of the moments involved in the solution. Since both HBIM and DIM are restricted to the zeroth moment they use only the first term of the series. Therefore, the accuracy of approximation depends on the values of the exponent n because the coefficient $a_{1} = u_{s}$ depends on the boundary condition x = 0. The classical applications [1, 26] are with $n = 2$ and $n = 3$. However, when the exponent n is stipulated the approximation error is predetermined. Now, we focus the attention on the optimization of the exponent n in order to obtain solutions with minimal approximation errors bearing in mind that the approximate profile satisfies the integral-balance relations (19b) and (22b) but not the original heat conduction Eq. (1b).

4.4.1 Error measure and restrictions on the exponent n

The residual function $\varphi \;\left( {u_{a} \left( {x,t} \right)} \right)$ is defined from the requirement the approximate solution to satisfy the governing Eq. (1b)

$$\varphi \;\left( {u_{a} \left( {x,t} \right)} \right) = \frac{{\partial u_{a} }}{\partial t} - \frac{\partial }{\partial x}\left( {a_{0} \left( {1 + \beta u_{a}^{{}} } \right)\frac{{\partial u_{a} }}{\partial x}} \right)$$

(30)

If $u_{a}$ matches the exact solution then $\varphi \;\left( {u_{a} \left( {x,t} \right)} \right) = 0$, otherwise it should attain a minimum for a certain value of the exponent n (the only unspecified parameter of the approximate profile).

With $u_{a} = \left( {1 - {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta }} \right)^{n}$, we have

$$\frac{{\partial u_{a} }}{\partial t} = \frac{nx}{{\delta^{2} }}\frac{d\delta }{dt}\left( {1 - \frac{x}{\delta }} \right)^{n - 1}$$

(31a)

$$\begin{aligned} & \frac{\partial }{dx}\left( {a_{0} \left( {1 + \beta u_{a}^{{}} } \right)\frac{{\partial u_{a} }}{\partial x}} \right) \\ & \quad = a_{0} \left[ {\frac{{n\left( {n - 1} \right)}}{{\delta^{2} }}\left( {1 - \frac{x}{\delta }} \right)^{n - 2} + \beta \frac{{n\left( {2n - 1} \right)}}{{\delta^{2} }}\left( {1 - \frac{x}{\delta }} \right)^{2n - 2} } \right] \\ \end{aligned}$$

(31b)

For example, at x = 0 the residual function is decaying in time (since $\delta^{2} \equiv t$) but has to be minimized with respect to n

$$\varphi_{T} \left( {0,t} \right) = - \frac{{a_{0} }}{{\delta^{2} }}\left[ {n\left( {n - 1} \right) + \beta n\left( {2n - 1} \right)} \right]$$

(32)

Thus, searching for positive values of n, the heat equation is satisfied for $n = {{\left( {1 + \beta } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \beta } \right)} {\left( {1 + 2\beta } \right)}}} \right. \kern-0pt} {\left( {1 + 2\beta } \right)}}$, that is the exponent should be <1. However, in order to satisfy the Goodman boundary conditions $u_{a} \left( {\delta ,t} \right) = {{\partial u_{a} \left( {\delta ,t} \right)} \mathord{\left/ {\vphantom {{\partial u_{a} \left( {\delta ,t} \right)} {\partial x}}} \right. \kern-0pt} {\partial x}} = 0$, it is required that

$$\begin{aligned} & \lim_{x \to \delta } \varphi_{T} \left( {\delta ,t} \right) \\ & \quad = - \left[ {\frac{{n\left( {n - 1} \right)}}{{\delta^{2} }}\lim_{x \to \delta } \left( {1 - \frac{x}{\delta }} \right)^{n - 2} +\, \beta \frac{{n\left( {2n - 1} \right)}}{{\delta^{2} }}\lim_{x \to \delta } \left( {1 - \frac{x}{\delta }} \right)^{2n - 2} } \right] \\ \end{aligned}$$

(33)

Therefore, two conditions should be obeyed simultaneously: n – 2 > 0, and 2n – 2 > 0. This leads to the common condition n > 2.

4.4.2 Optimal exponents: minimization with the Langford criterion

Therefore, the function $\varphi \left( {u_{a} \left( {x,t} \right)} \right)$ should approach a minimum as $u_{a} \to u$, over the entire penetration depth $\delta$, that is $\int_{0}^{\delta } {\varphi \left( {u_{a} \left( {x,t} \right)} \right){\kern 1pt} dx} \to \hbox{min}$. More precisely, we may require, $\int_{0}^{\delta } {\left[ {\varphi \left( {u_{a} \left( {x,t} \right)} \right){\kern 1pt} } \right]^{2} dx} \to \hbox{min}$, that is, the Langford criterion [34]

$$E_{L} (n,m,t) = \int\limits_{0}^{\delta } {\left[ {\frac{{\partial u_{a} }}{\partial t} - \frac{\partial }{\partial x}\left( {a_{0} u_{a}^{m} \frac{{\partial u_{a} }}{\partial x}} \right)} \right]}^{2} dx \to \hbox{min}$$

(34)

With the profile (14) and the expressions (31a, b), after developing $\varphi_{T}^{2} \left( {x,t} \right)$, and the integration from 0 to $\delta$ we have

$$E_{LT} (n,\beta ,t) = \int\limits_{0}^{\delta } {\varphi_{T}^{2} \left( {x,t} \right)} dx = \frac{1}{{\delta^{4} }}e_{LT} \left( {n,\beta ,\delta } \right)$$

(35)

Hence, at a glance, $E_{LT} \left( {n,m,t} \right)$ vanishes in time with a speed proportional to $\delta^{4} \equiv t^{2}$. Therefore, the function $e_{LT} \left( {n,\beta ,\delta } \right)$ is time-independent and should be minimized with respect to n, for given values of β. In the proper evaluation of the minima of $e_{LT} \left( {n,\beta ,\delta } \right)$ the fact that product $\delta \;\left( {{{d\delta } \mathord{\left/ {\vphantom {{d\delta } {dt}}} \right. \kern-0pt} {dt}}} \right)$ is time-independent is used [25]. The minimization procedure is well described in [24, 25] and we will avoid cumbersome expressions here. The optimal exponents for both the HBIM and DIM solutions, for various β are summarized in Tables 1, 2, 3 and 4. The initial restriction of all minimization procedures is n > 2.

Table 1 Optimal exponents of the approximate profile: HBIM solutions with fixed temperature boundary condition

Table 2 Optimal exponents of the approximate profile: HBIM solutions with fixed temperature boundary condition

Table 3 Optimal exponents of the approximate profile: DIM solutions with fixed temperature boundary condition

Table 4 Optimal exponents of the approximate profile: DIM solutions with fixed temperature boundary condition

4.5 Benchmarking of the approximate solutions with optimal exponents

This section demonstrates numerical examples of the developed approximate HBIM and DIM solutions and benchmarking examples related to their accuracy. At the beginning, numerical simulations were performed for values of β larger than those corresponding to some real materials (see Table 5). This was especially done to demonstrate the features of the approximate solution and getting plots with disguisable curves. Moreover, the range [−0.5, 0.5] has been also used for numerical simulation by Sucec and Hedge [5] and Mehta [15], thus this approach is not an exception in solutions applicable to the problem.

Table 5 Real values of the terminal coefficient β for various materials

First, in order to demonstrate the effect of the factor β on the heat penetration into the medium, approximate solutions are presented in Fig. 1a, b. As an expected result, when β > 0 the increased heat conductivity is manifested by increased penetration depth $\delta$ (see the inst in Fig. 1a). In contrast, when β < 0 the penetration depth decreases with increase in the absolute value of β. Numerical experiments and related plots of pointwise (absolute) errors are shown in Figs. 2 and 3, respectively. As a general outcome of these numerical experiments it may be stated that when β < 0, that is the case of most native materials as pure metals [35] the accuracy of the integral-balance solutions is better than when β > 0 (the case of alloys, composites, wood, etc. see Table 5).

Fig. 1

Approximate temperature profiles with a fixed temperature as boundary condition and DIM solutions: insets zoomed section close to the fronts of the penetration layer. a Cases of positive β. b Cases of negative β

Fig. 2

Temperature profiles of approximate temperature HBIM solutions with a fixed temperature as boundary condition and numerical solutions (finite differences). a Cases of β = 0.1 and β = −0.1. b Cases of β = 0.2 and β = −0.2. c Cases of β = 0.3 and β = −0.3. d Cases of β = 0.4 and β = −0.4

Fig. 3

Comparison of approximate profiles (HBIM solutions) with numerical solutions (finite differences) (see also the plots in Fig. 2a–d). a Cases of β = 0.1, β = −0.1, β = 0.3 and β = −0.3. b Cases of β = 0.2, β = −0.1, β = 0.3 and β = −0.4

In addition, as an expected result, the accuracy of DIM (see Figs. 4, 5) is better that that exhibited by HBIM (see Fig. 3). The pointwise errors (see Fig. 6) and the plots in Fig. 3, (as well as in Figs. 4, 5) confirm the comments that the accuracy of the integral-balance solutions (both HBIM and DIM) is better when β < 0. The range of variations of the pointwise errors is typical for the integral-balance solutions [1], i.e. <0.03. In general, the increase in the absolute value of β leads to increased errors of approximations. It is important to note that the separation of β in positive and negative values is mechanistic. Generally, the conductivity-temperature relationship can be written as $a = a_{0} \;\left( {1 \pm \beta T} \right)$ where the positive sign means that the thermal diffusivity increases with the temperature, while the negative sign corresponds to the opposite tendency.

Fig. 4

Temperature profiles of approximate temperature DIM solutions with a fixed temperature as boundary condition and numerical solutions (finite differences and Runge–kutta-4th order) for positive β. a Case of β = 0.1. b Case of β = 0.3. c Case of β = 0.5

Fig. 5

Temperature profiles of approximate temperature DIM solutions with a fixed temperature as boundary condition and numerical solutions (finite differences and Runge–kutta-4th order) for negative β. a Case of β = −0.1. b Case of β = −0.3. c Case of β = −0.5

Fig. 6

Comparison of approximate profiles (DIM solutions) with numerical solutions (finite differences and Runge–Kutta-4th order) (see also the plots in Figs. 4, 5). a Cases of β = 0.1 and β = −0.1. b Cases of β = 0.3 and β = −0.3. c Cases of β = 0.5 and β = −0.5

Second, numeral experiments with approximate solutions using real values of β, both positive and negative, were performed (with data summarized in Table 1). The plots of the temperature profiles (see Fig. 7). and the pointwise errors (see Fig. 8) confirm the statements about the accuracy of approximation based on the pure numerical experiments (Figs. 3, 6).

Fig. 7

Approximate temperature profiles (DIM solutions) for real materials and a fixed temperature as boundary condition and numerical solutions (finite differences and Runge–Kutta-4th order). See Table 5 for details. a Case of aluminum with β < 0. b Case of wood with β > 0. c Case of iron with β < 0

Fig. 8

Comparison of approximate profiles (DIM solutions) for real materials with numerical solutions (finite differences and Runge–Kutta-4th order) (see also the plots in Fig. 7). a Case of aluminum with β < 0. b Case of wood with β > 0. c Case of iron with β < 0

5 Solution Example 2: fixed flux as a boundary condition at x = 0

This section presents three different strategies to develop integral-balance solutions when the boundary condition is defined as

$$- k\left( T \right)\left( {\frac{\partial T}{\partial x}} \right)_{x = 0} = q_{0}$$

(36)

• Direct application of HBIM and DIM

• Change of variables

• Preliminary rescaling of the conductivity-temperature relationship.

5.1 Direct application of HBIM and DIM

When the additive heat conductivity relationship (1c) $k = k_{0} \left( {1 + \beta T} \right)$ is not scaled as $k = k_{0} \;\left( {1 + \beta {T \mathord{\left/ {\vphantom {T {T_{ref} }}} \right. \kern-0pt} {T_{ref} }}} \right)$ (see the comments in Sect. 3.2), we have from the boundary condition that

$$- \left[ {k_{0} \left( {1 + \beta T} \right)\frac{\partial T}{\partial x}} \right]_{x = 0} = q_{0} \quad {\text{or}}\quad - k_{0} \left[ {\frac{\partial T}{\partial x} + \frac{\beta }{2}\frac{{\partial T^{2} }}{\partial x}} \right]_{x = 0} = q_{0}$$

(37a, b)

5.1.1 HBIM solution

The application of the HBIM Eq. (5b) with the assumed profile expressed by (11) yields

$$\frac{d}{dt}\int\limits_{0}^{\delta } {T_{s} \left( {1 - \frac{x}{\delta }} \right)}^{n} dx = - a_{0} \left[ {\left( {1 + \beta T} \right)\frac{\partial T}{\partial x}} \right]_{x = 0}$$

(38)

From (31b, 37b) we have that $- \left[ {\left( {1 + \beta T} \right)\frac{\partial T}{\partial x}} \right]_{x = 0} = {{q_{0} } \mathord{\left/ {\vphantom {{q_{0} } {k_{0} }}} \right. \kern-0pt} {k_{0} }}$ and therefore the right side of (38) can be replaced by ${{a_{0} q_{0} } \mathord{\left/ {\vphantom {{a_{0} q_{0} } {k_{0} }}} \right. \kern-0pt} {k_{0} }}$. This operation yields

$$\frac{d}{dt}\int\limits_{0}^{\delta } {T_{s} \left( {1 - \frac{x}{\delta }} \right)}^{n} dx = a_{0} \frac{{q_{0} }}{{k_{0} }} \Rightarrow \frac{1}{n + 1}\frac{d}{dt}\left( {T_{s} \delta } \right) = a_{0} \frac{{q_{0} }}{{k_{0} }}$$

(39a, b)

In (39a) we take unto account that the surface temperature $T_{s} \left( t \right)$ is time-dependent.

The integration of (39b) with the initial condition $\left( {T_{s} \delta } \right)_{t = 0} = 0$ results in

$$T_{s} \delta = \left( {a_{0} t} \right)\frac{{q_{0} }}{{k_{0} }}\left( {n + 1} \right) \Rightarrow T_{s} = \left( {a_{0} t} \right)\frac{{q_{0} }}{{k_{0} }}\frac{1}{\delta }\left( {n + 1} \right)$$

(40a, b)

Now, the next task is to determine $\delta \left( t \right)$. The boundary condition (37a, b) expressed through the assumed profile (see the form of Eq. 37b) is

$$- k_{0} \left[ {T_{s} \left( { - \frac{n}{\delta }} \right) + \beta T_{s}^{2} \left( { - \frac{n}{\delta }} \right)} \right] = q_{0} \Rightarrow T_{s} + \beta T_{s}^{2} = \frac{{q_{0} }}{{k_{0} }}\frac{\delta }{n}$$

(41a, b)

Now, inserting $T_{s}$ from (40b) into (41b) we get

$$\delta^{3} - \delta \left( {a_{0} t} \right)n\left( {n + 1} \right) - \beta \frac{{q_{0} }}{{k_{0} }}\left( {a_{0} t} \right)^{2} n\left( {n + 1} \right)^{2} = 0$$

(42)

For β = 0, Eq. (42) reduces to $\delta_{{0\left( {HBIM} \right)}}^{q} = \delta_{0}^{{}} = \sqrt {\left( {a_{0} t} \right)n\left( {n + 1} \right)}$ which is the classical HBIM solution [3, 26], but this means that the governing model (1b, c) is reduced to diffusion equation with $a = a_{0} = const.$ Eq. (42) allows to establish an approximate expression about $\delta$ (for details see “Appendix 2”) namely

$$\delta \left( t \right) \approx \left( {a_{0} t} \right)^{{\frac{2}{3}}} \left[ {n^{{\frac{1}{3}}} \left( {n + 1} \right)^{{\frac{2}{3}}} } \right]\left( {\frac{\beta }{4}\frac{{q_{0} }}{{k_{0} }}} \right)^{{\frac{1}{3}}}$$

(43)

With the result (43) the surface temperature $T_{s}$ (40b) can be expressed as

$$T_{s} \approx \left( {a_{0} t} \right)^{{\frac{1}{3}}} \left( {\frac{{q_{0} }}{{k_{0} }}} \right)^{{\frac{2}{3}}} \left( {\frac{n + 1}{n}} \right)^{{\frac{1}{3}}} \left( {\frac{4}{\beta }} \right)^{{\frac{1}{3}}}$$

(44)

5.1.2 DIM solution

With the principle equation of DIM we have

$$\frac{d}{dt}\int\limits_{0}^{\delta } {\int\limits_{x}^{\delta } {T_{a} \left( {x,\delta ,t} \right)} } dx = a_{0} T_{a} \left( {0,t} \right) + \frac{{a_{0} \beta }}{2}\left[ {T_{a} \left( {0,t} \right)} \right]^{2}$$

(45a)

Further with the assumed profile expressed by (11) we get from (45a) that

$$\frac{1}{{\left( {n + 1} \right)\left( {n + 2} \right)}}\frac{d}{dt}\left( {T_{s} \delta^{2} } \right) = a_{0} \left( {T_{s} + \frac{\beta }{2}T_{s}^{2} } \right)$$

(45b)

The boundary condition (see 41b) provides the relationship $T_{s} + \beta T_{s}^{2} = \frac{{q_{0} }}{{k_{0} }}\frac{\delta }{n}$ and therefore, the differential equation about the product $T_{s} \delta^{2}$ is

$$\frac{d}{dt}\left( {T_{s} \delta^{2} } \right) = a_{0} \frac{{q_{0} }}{{k_{0} }}\left( {n + 1} \right)\left( {n + 2} \right)\frac{\delta }{n} - a_{0} \frac{\beta }{2}T_{s}^{2}$$

(46)

In terms of $T_{s}$ the boundary condition (41b) is a quadratic equation with a positive root

$$T_{s} = \frac{1}{2\beta }\left( {\sqrt {1 + 4\beta \frac{{q_{0} }}{{k_{0} }}\frac{\delta }{n}} - 1} \right) \Rightarrow T_{s}^{2} = \frac{1}{{2\beta^{2} }}\left( {1 + 2\beta \frac{{q_{0} }}{{k_{0} }}\frac{\delta }{n} - \sqrt {1 + 4\beta \frac{{q_{0} }}{{k_{0} }}\frac{\delta }{n}} } \right)$$

(47a, b)

Next, the Eq. (46) can be transformed as one with a single dependent variable $\delta$ by using (47a, b). Obviously, this does not allow to obtain straightforwardly an explicit solution about $\delta \left( t \right)$. At this point we stop the development of the DIM solution and will comment some basic problems about the direct application of HBIM and DIM.

5.1.3 HBIM or DIM when the flux is defined at the boundary?

With the results (46) and (47) we may formulate the question: Is it reasonable to apply the double integration approach to the case when the flux is defined at the boundary and the thermal diffusivity is in the form (1c)? The answer can be found in the origin of DIM. Actually, the double integration approach was conceived [2] for solutions of hydrodynamic problems concerning a boundary layer velocity profile where the velocity at the rigid wall (x = 0) is defined [36]. This corresponds to the fixed temperature problem solved in this study. Since the simple approach (i.e. HBIM) needs the gradient ${{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0pt} {\partial x}}$ to be defined at x = 0 through the assumed profile, then the double integration fix the problem and makes the right-had side of the integral-balance relation independent of the assumed profile.

Therefore, when the flux is prescribed at the boundary, the use of DIM requires the surface temperature T _s in the right-had side of the integral-balance relation to be defined. This can be done through the boundary condition, but in this case T _s depends on the type of the assumed profile (see 41a, b). Therefore, we get a new problem for determination of the surface temperature from a strongly non-linear relationship and there are no benefits when DIM is applied directly to solve the problem with a thermal diffusivity expressed as the additive function (1c). In contrast, the simple approach (i.e. HBIM) allows the flux to be incorporated easily in the right-had side of the integral-balance relation, as it was demonstrated in Sect. 5.1.1.

In the context of the above comments, the reasonable question directly arising is: Does the additive function (1c) is the suitable form to correlate experimental data when the nonlinear thermal diffusivity should be incorporated in the energy equation (1b)? The answer is negative. The possible strategies to fix the emerged problem and obtain approximate solutions are developed next.

5.2 Solutions by a change of the variable

Let us denote $U = 1 + \beta T$. Therefore with ${{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial t}}} \right. \kern-0pt} {\partial t}} = \beta \;\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial t}}} \right. \kern-0pt} {\partial t}}} \right)$ and ${{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial x}}} \right. \kern-0pt} {\partial x}} = \beta \;\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)$ we may transform the governing equation and the boundary condition as

$$\frac{\partial U}{\partial t} = \frac{\partial }{\partial x}\left( {a_{0} U\frac{\partial U}{\partial x}} \right)$$

(48)

$$- \left[ {U\frac{1}{\beta }\frac{\partial U}{\partial x}} \right]_{x = 0} = \frac{{q_{0} }}{{k_{0} }}$$

(49)

The new equation (48) is a degenerate diffusion equation [2, 37–39] with a solution propagating with a sharp front. It is a special case of the diffusion equation with a power-law diffusivity $a = a_{0} U^{m}$ (for m = 1) solved by HBIM and DIM in (see Ref. [25] and references therein).

If we apply the transform $U = 1 + \beta T$ to the assumed profile (11), i.e. $\bar{U}_{a} = 1 + \beta T_{a} = 1 + \beta T_{s} \left( {1 - {x \mathord{\left/ {\vphantom {x {\delta \left( n \right)}}} \right. \kern-0pt} {\delta \left( n \right)}}} \right)^{n}$ we get

$$\partial {{\bar{U}_{a} \left( {\delta_{U} } \right)} \mathord{\left/ {\vphantom {{\bar{U}_{a} \left( {\delta_{U} } \right)} {\partial x}}} \right. \kern-0pt} {\partial x}} = \beta {{\partial T_{a} \left( \delta \right)} \mathord{\left/ {\vphantom {{\partial T_{a} \left( \delta \right)} {\partial x}}} \right. \kern-0pt} {\partial x}} = 0$$

(50a)

and

$$\bar{U}_{a} \left( {0,t} \right) = \bar{U}_{s} = 1 + \beta T_{a} \left( {0,t} \right) = 1 + \beta T_{s}$$

(50b)

However $\bar{U}_{a} \left( \delta \right) = 1$ and therefore the Goodman conditions are not completely satisfied.

Hence, we have to re-design the assumed profile as

$$U_{a} = \left( {1 + \beta T_{s} } \right)\left( {1 - \frac{x}{{\delta_{U} }}} \right)^{p} = U_{s} \left( {1 - \frac{x}{{\delta_{U} }}} \right)^{p}$$

(51a)

Then, for $x = 0,\;U_{a} \left( {0,t} \right) = U_{s} = 1 + \beta T_{s}$. Thus, the transform used to obtain (48) is satisfied. Moreover, the Goodman conditions are completely obeyed by U _a , namely:

$$\partial {{U_{a} \left( {\delta_{U} } \right)} \mathord{\left/ {\vphantom {{U_{a} \left( {\delta_{U} } \right)} {\partial x}}} \right. \kern-0pt} {\partial x}} = U_{a} \left( {\delta_{U} } \right) = 0\quad {\text{and}}\quad U_{a} \left( {\delta_{U} } \right) = 0$$

(51b)

The boundary condition (49) defines U _s as

$$U_{s} = \left( {\beta \frac{{q_{0} }}{{k_{0} }}\frac{{\delta_{U} }}{p}} \right)^{{\frac{1}{2}}} = Q_{0}^{{\frac{1}{2}}} \beta^{{\frac{1}{2}}} \left( {\frac{{\delta_{U} }}{p}} \right)^{{\frac{1}{2}}} ,\;Q_{0} = \left( {\frac{{q_{0} }}{{k_{0} }}} \right)^{{\frac{1}{2}}}$$

(52a, b, c)

The condition requires $U_{s} = 1 + \beta T_{s} > 0$ that implies β > 0 in (52b).

The Eq. (48) can be rescaled in terms of the variable $S = {U \mathord{\left/ {\vphantom {U {\left( {Q_{0} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \right. \kern-0pt} {\left( {Q_{0} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}$ as

$$\frac{\partial S}{\partial t} = \frac{\partial }{\partial x}\left( {A_{s} S\frac{\partial S}{\partial x}} \right),\;A_{s} = a_{0} \beta^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

(53a, b)

Next, with $S_{a} = {{U_{a} } \mathord{\left/ {\vphantom {{U_{a} } {\left( {Q_{0} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \right. \kern-0pt} {\left( {Q_{0} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}$ the assumed profile can be simply expressed as:

$$S_{a} = \left( {\beta \frac{{\delta_{U} }}{p}} \right)^{{\frac{1}{2}}} \left( {1 - \frac{x}{{\delta_{U} }}} \right)^{p}$$

(54)

The HBIM applied to (53a) with the profile (54) yields

$$\delta_{{U\left( {HBIM} \right)}}^{q} = \left( {A_{s} t} \right)^{{\frac{2}{3}}} p^{{\frac{1}{3}}} \left( {p + 1} \right)^{{\frac{2}{3}}} = \left( {a_{0} t} \right)^{{\frac{2}{3}}} \left( \beta \right)^{{\frac{1}{3}}} F_{{p\left( {HBIM} \right)}}$$

(55a, b)

$$F_{{p\left( {HBIM} \right)}} = p^{{\frac{1}{3}}} \left( {p + 1} \right)^{{\frac{2}{3}}}$$

(55c)

Equation (55a) is a special case of the HBIM solution of (53a) [25], namely:

$$\delta_{{HBIM\left( {power - law} \right)}} = \left( {A_{s} t} \right)^{{\frac{m + 1}{m + 2}}} p^{{\frac{1}{m + 2}}} \left( {p + 1} \right)^{{\frac{m + 1}{m + 2}}} \quad {\text{for}}\;m = 1$$

(55d)

The optimal exponent in this case is $p_{{opt\left( {HBIM} \right)}}^{q} \approx 0.799$. Recall, in this case $p_{{opt\left( {HBIM} \right)}}^{q} < 1$ as it was demonstrated in [25].

Further, the DIM solution of (53a) with the profile (54) developed in [25] is

$$\delta_{U(DIM)}^{q} = \left( {A_{s} t} \right)^{{\frac{2}{3}}} \left[ {p\left( {p + 1} \right)\left( {p + 2} \right)\left( {\frac{3}{10}} \right)} \right]^{{\frac{2}{3}}} = \left( {a_{0} t} \right)^{{\frac{2}{3}}} \left( \beta \right)^{{\frac{1}{3}}} F_{{p\left( {DIM} \right)}}$$

(56a, b)

$$F_{{p\left( {DIM} \right)}} = \left[ {p\left( {p + 1} \right)\left( {p + 2} \right)\left( {\frac{3}{10}} \right)} \right]^{{\frac{2}{3}}}$$

(56c)

Equation (56a) is a special case of the DIM solution of (53a) [25], namely

$$\begin{aligned} & \delta_{{DIM\left( {power - law} \right)}}^{q} \\ & \quad = \left( {A_{s} t} \right)^{{\frac{m + 1}{m + 2}}} \left[ {p^{m} \left( {p + 1} \right)\left( {p + 2} \right)\left( {\frac{m + 2}{{\left( {m + 1} \right)\left( {2m + 3} \right)}}} \right)} \right]^{{\frac{m + 1}{m + 2}}} \quad {\text{for}}\;m = 1 \\ \end{aligned}$$

(57)

The optimal exponent in this case is $p_{{opt\left( {HBIM} \right)}}^{q} \approx 0.870$ [25].

Equations (55b) and (56b) clearly indicate that the new penetration depth is $\delta_{U} = \beta^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} F_{p}$, where $F_{p}$ matches the expressions developed for the linear case when β = 1. Thus, there is a factor $\beta^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}$ while the new similarity variable is $\eta_{q} = {x \mathord{\left/ {\vphantom {x {\left( {a_{0} t} \right)}}} \right. \kern-0pt} {\left( {a_{0} t} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}$. For $\eta_{q} = F_{p}$ the assumed profile in terms of U _a is zero and $T = T_{ref}$, because at this point we have $x = \delta_{U}$. Besides, the ratio ${{\eta_{q} } \mathord{\left/ {\vphantom {{\eta_{q} } {F_{p} }}} \right. \kern-0pt} {F_{p} }} = {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta } = X_{q}$ is a dimensionless variable $\left( {0 \le X_{q} \le 1} \right)$ as it was mentioned in the case of the fixed temperature problem.

Now, in terms of U _a we have

$$U_{a} = \left( {\beta Q_{0} } \right)^{{\frac{1}{2}}} S_{a} = \left( {\beta Q_{0} } \right)^{{\frac{1}{2}}} \left( {\frac{{\delta_{U} }}{p}} \right)^{{\frac{1}{2}}} \left( {1 - \frac{x}{{\delta_{U} }}} \right)^{p} ,\;U_{s} = \left( {\beta Q_{0} } \right)^{{\frac{1}{2}}} \left( {\frac{{\delta_{U} }}{p}} \right)^{{\frac{1}{2}}}$$

(58a, b)

The reverse transform $T = {{\left( {U - 1} \right)} \mathord{\left/ {\vphantom {{\left( {U - 1} \right)} \beta }} \right. \kern-0pt} \beta }$ leads to

$$T_{a} = \frac{{U_{a} - 1}}{\beta } = \frac{1}{\beta }\left[ {\left( {\beta Q_{0} } \right)^{{\frac{1}{2}}} \left( {\frac{{\delta_{U} }}{p}} \right)^{{\frac{1}{2}}} \left( {1 - \frac{x}{{\delta_{U} }}} \right)^{p} - 1} \right]$$

(59)

From (58b) through the reverse transform (or with (59) for x = 0) the surface temperature is

$$T_{s} = \frac{1}{\beta }\left[ {\left( {\beta Q_{0} } \right)^{{\frac{1}{2}}} \left( {\frac{{\delta_{U} }}{p}} \right)^{{\frac{1}{2}}} - 1} \right]$$

(60a)

From (60a) at t = 0 we have $\delta_{U} \left( {t = 0} \right) = 0$ and $T_{s} = - {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }$. Is this result correct? The answer is yes, because at t = 0 we have $k\left( {t = 0} \right) = k_{0}$ and the surface temperature is equal to the reference temperature $T_{s} = T_{ref}$. Consequently, from the (1c) we have $k_{0} = k_{0} \left( {1 + \beta T_{ref} } \right)$ which leads to $T_{ref} = - {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }$ and this completes the answer. Therefore, Eq. (60a) can be presented in a more physically adequate form

$$T_{s} = T_{ref} + \left( {\frac{{Q_{0} }}{\beta }} \right)^{{\frac{1}{2}}} \left( {\frac{{\delta_{U} }}{p}} \right)^{{\frac{1}{2}}}$$

(60b)

Taking into account the expressions for $\delta_{U}$ (Eqs. 55b, 56b) we may derive from (60b) a scaling relationship with respect to the excess surface temperature $T - T_{ref}$, namely

$$T_{s} - T_{ref} = A_{qp} \beta^{{ - \frac{1}{6}}} \left( {a_{0} t} \right)^{{\frac{1}{3}}} ,\quad A_{qp} = Q_{0}^{{\frac{2}{3}}} \left( {{{F_{p} } \mathord{\left/ {\vphantom {{F_{p} } p}} \right. \kern-0pt} p}} \right)^{{\frac{1}{2}}}$$

(60c, d)

The result (60c) is physically adequate and it is easy to see that β affects the slopes of the curves $T_{s} - T_{ref} = f\left( t \right)$. The factor $\sqrt {F_{p} }$ is independent of β and depends of the type of integration method applied (HBIM or DIM). In addition, with increase in β, the heated body conducts the heat from the surface into the bulk more rapidly than a medium with lower β, because T _s is inversely proportional to $\beta^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0pt} 6}}}$. As a consequence, a medium with low β will be more “hot” at the surface than one with higher β, when equal heat flux is applied at x = 0. This is illustrated by the numerical experiments in Sect. 5.5.

5.3 Solution by a preliminary rescaling of the conductivity-temperature relationship

5.3.1 Preliminary rescaling of the heat conductivity relationship and change of variables

The general nonlinearity of the model at issue is due to the additive formulation of the temperature effect on the thermal conductivity (diffusivity)

$$k = k_{0} + \gamma T \Rightarrow k_{0} \left( {1 + \varepsilon T} \right),\quad \varepsilon = {\gamma \mathord{\left/ {\vphantom {\gamma {k_{0} }}} \right. \kern-0pt} {k_{0} }}$$

(61a)

$$a = a_{0} + \frac{\gamma }{{\rho C_{p} }}T \Rightarrow a_{0} \left( {1 + \beta T} \right),\;\beta = \varepsilon = \frac{\gamma }{{a_{0} \rho C_{p} }} = \frac{\gamma }{{k_{0} }}$$

(61b)

The dimension of γ is [Wm⁻¹ K⁻²], while β has a dimension [K⁻¹]. The relationship (61a) presents a common data correlation of experimental results, where γ is the slope (either positive or negative [5, 32, 40, 41]). Since, the value of k ₀ corresponds to a certain reference temperature $T_{ref}$, the coordinate frame $k - T$ can be shifted in order that its origin will be at the point k ₀. This can be done by a simple translation transform, namely

$$k_{shift} = \left( {k - k_{0} } \right) = \gamma \left( {T - T_{ref} } \right)\quad {\text{or}}\quad \alpha = \left( {a - a_{0} } \right) = a_{o} \beta \left( {T - T_{ref} } \right),\quad \alpha = a - a_{0}$$

(62a, b)

The relationships (62) are the same as (61) because the translation transform preserves the slope $\gamma = k_{0} \beta$. In (62b) α is a shifted thermal diffusivity.

5.3.2 Change of variables

With a new variable $\theta = \left( {T - T_{ref} } \right)$, i.e. the excess temperature, the relationship (62b) can be presented as $\alpha \left( \theta \right) = a_{o} \beta \theta$ which is a special case of the power-law temperature-dependent diffusivity $\alpha \left( \theta \right) = a_{0} \beta \theta^{m}$ for m = 1. It is worth to note that the transformation of the relationship $a\left( T \right)$ (or k (T)) is independent of the derivation of the basic model presented by Eqs. (1a, b). The only effect of this transform is that the energy equation shifts in the temperature scale, i.e. $\theta = T - T_{ref}$, which is the excess temperature. With the new variable θ the heat conduction Eq. (1b) can be presented as

$$\frac{\partial \theta }{\partial t} = \frac{\partial }{\partial x}\left[ {\alpha \left( \theta \right)\frac{\partial \theta }{\partial x}} \right] \Rightarrow \frac{\partial \theta }{\partial t} = \frac{\partial }{\partial x}\left[ {a_{0} \beta \theta \frac{\partial \theta }{\partial x}} \right]$$

(63a, b)

In the form (63b) there is no loss of generality since the reference temperate $T_{ref}$ is a constant, as well as it could be equal to the initial temperature of the medium T ₀. It is worth to note that we do not change the length scale. The model (63) is a degenerate diffusion equation [25, 36–39] as the previously derived Eq. (48) since the diffusivity goes to zero when $\theta = 0$. The solution propagates with a finite speed as a well defined front between the disturbed and the virgin medium, in contrast to the form (15a) which is a truly parabolic equation. In fact, the model (63) (6.3) is the Boussinesq equation [25, 37, 39].

5.3.3 Solutions

The integral-balance solutions of (63) developed in [25] and the HBIM and DIM relationships are given by (6) and (10a, b), respectively. For m = 1 we have

$${\mathbf{HBIM}}\;\;\frac{d}{dt}\int\limits_{0}^{\delta } \theta \left( {x,t} \right) = - a_{0} \beta \theta \frac{{\partial \theta \left( {0,t} \right)}}{\partial x}$$

(64)

$${\mathbf{DIM}}\;\;\frac{d}{dt}\int\limits_{0}^{\delta } {x\theta } \left( {x,t} \right) = \frac{{a_{0} \beta }}{2}\left[ {\theta \left( {0,t} \right)} \right]^{2} \;{\text{or}}\;\int\limits_{0}^{\delta } {\left( {\int\limits_{x}^{\delta } {\frac{\partial \theta }{\partial t}} dx} \right)\,} dx = \frac{{a_{0} \beta }}{2}\left[ {\theta \left( {0,t} \right)} \right]^{2}$$

(65)

Within the shifted frame $\left[ {k_{shift} = \left( {k - k_{0} } \right),\theta } \right]$ the flux boundary condition can be expressed as

$$- k_{shift} \left[ {\left( {T - T_{ref} } \right)\frac{{\partial \left( {T - T_{ref} } \right)}}{\partial x}} \right] = q_{0} \Rightarrow - \left[ {\beta \theta \frac{\partial \theta }{\partial x}} \right]_{x = 0} = \frac{{q_{0} }}{{k_{0} }}$$

(66)

The assumed profile satisfying the boundary conditions of the penetration layer can be expressed as $\theta_{a} = \theta_{s} \left( {1 - {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta }_{s} } \right)^{s}$. Then, the surface temperature $\theta_{s} = \theta \left( {0,t} \right)$ can be determined from (66) as

$$- \left( {\frac{\beta }{2}\frac{{\partial \theta_{a}^{2} }}{\partial x}} \right)_{x = 0} = \frac{{q_{0} }}{{k_{0} }} \Rightarrow \theta_{s} = \left( {\frac{1}{\beta }\frac{{q_{0} }}{{k_{0} }}\frac{\delta }{s}} \right)^{{\frac{1}{2}}}$$

(67)

Consequently, we obtained the result (52) which is reasonable because the variable $U = 1 + \beta T$ with $\beta = - {1 \mathord{\left/ {\vphantom {1 {T{}_{ref}}}} \right. \kern-0pt} {T{}_{ref}}}$ [recall Eq. (60a) and the related comments] can be expressed as: $U = 1 - {T \mathord{\left/ {\vphantom {T {T_{ref} }}} \right. \kern-0pt} {T_{ref} }} = - {{\left( {T - T_{ref} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{ref} } \right)} {T_{ref} }}} \right. \kern-0pt} {T_{ref} }} = \beta \left( {T - T_{ref} } \right)$. Therefore, the solution in terms in U is, in fact, a solution in term of the scaled excess temperature $\beta \theta$ (see 62b), eventhough the starting points for the two solutions were different. In addition, Eq. (48) does not change if the variable is $U - \beta T$, that is easy to check

Further, denoting $\Theta _{a} = \theta_{a}/\sqrt{(q_0/k_0)/\beta}$ (similar to the variable $S_{a}$) we may present the assumed profile as

$$\Theta _{a} = \left( {\frac{\delta }{s}} \right)^{{\frac{1}{2}}} \left( {1 - \frac{x}{{\delta_{s} }}} \right)^{s} ,\quad \Theta _{s} = \left( {\frac{\delta }{s}} \right)^{{\frac{1}{2}}}$$

(68a, b)

Further, from (66) and (68b) we have the DIM relationship (see Eq. 9)

$$\int\limits_{0}^{\delta } x \left( {\frac{\delta }{s}} \right)^{{\frac{1}{2}}} \left( {1 - \frac{x}{{\delta_{s} }}} \right)^{s} dx = a_{0} \left( {\frac{1}{s}} \right)\left( {\frac{{q_{0} }}{{k_{0} }}\beta } \right)^{{\frac{1}{2}}} \delta$$

(69)

The solution of (69) developed in [25] is

$$\delta_{s(DIM)}^{q} = \left( {a_{0} t} \right)^{{\frac{2}{3}}} \beta^{{\frac{1}{3}}} \left[ {s\left( {s + 1} \right)\left( {s + 2} \right)} \right]^{{\frac{2}{3}}} \left( {\frac{3}{10}} \right)^{{\frac{2}{3}}}$$

(70)

Hence, the classical square root behaviour of $\delta \left( t \right)$ is lost due to the nonlinearity at the boundary x = 0. The solution (70) confirms the results (43) and (56b), precisely that the front propagates with a speed proportional to $t^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}$. Further, with the integral-balance relation (6), it is easy to check that the HBIM solution of the penetration depth is in the form of (43) taking into account that the shifted thermal diffusivity is $\alpha \left( \theta \right) = a_{0} \beta \theta$. For the “shifted” model (63b), the HBIM and DIM solutions have optimal exponents $n_{{opt\left( {HBIM)} \right)}}^{q} \approx 0.799$ and $n_{{opt\left( {DIM)} \right)}}^{q} \approx 0.870$, correspondingly [25].

In the end, obtaining identical solutions with the variables U and θ, a reasonable question could be formulated: What approach is physically correct? To use U or θ? The physically adequate answer is: the solution in terms of U, because in this case thermal diffusivity in the transformed equation remains as a ₀. The shifted thermal diffusivity has no a physical meaning and this approach is only a mathematical technique. Moreover, it is easy to check that if in Eq. (63b) the coefficient β is not “incorporated” in the “shifted” thermal diffusivity $\alpha \left( \theta \right) = a_{0} \beta \theta$, then $\alpha \left( \theta \right) = a_{0} U$ because simply $U = \beta \theta$.

Therefore, to recapitulate, after changing the variables we get degenerate diffusion equations with power-law diffusivities whose integral-balance solutions are known and easily comparable with known exact numerical and approximate solutions. Then, by a reverse change of the variables the approximate solutions relevant to equations with the linearly temperature-dependent thermal diffusivities can be obtained. However, we have to remember that with the reversed approximate solutions the minimization of residual functions defined by the original Eq. (1b) identify new optimal exponents. This problem is discussed and resolved next.

5.4 The exponents of the approximate profile

In this end, it seems we solved the problem since the optimal exponent of the of the integral-balance solutions with respect to the transformed Eq. (48) in terms of U is known. However, this is not the exact value and an additional optimization procedure is required. The reason for that is the fact that the obtained profile with $\delta_{U}$ given by (55) and (56) was optimized to satisfy Eq. (48) (to minimize the residual function). Further, the initial Eq. (1b) with the (1c) can be expressed as

$$\frac{\partial T}{\partial t} = a_{0} \frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left( {a_{0} \beta T\frac{\partial T}{\partial x}} \right)$$

(71)

That is, in the transformation procedure we lost the term $a_{0} \left( {{{\partial^{2} T} \mathord{\left/ {\vphantom {{\partial^{2} T} {\partial x^{2} }}} \right. \kern-0pt} {\partial x^{2} }}} \right)$.

It was established that for the HBIM and DIM solutions of the heat conduction equation with a power-law diffusivity $a_{0} T^{m}$ (i.e. Eqs. 48 or 63b), the exponent m affects only the numerical prefactor of the time-dependent term of the penetration depth [25]: in the present study this is demonstrated by Eqs. (55d) and (57). Moreover, the product $\delta^{{{1 \mathord{\left/ {\vphantom {1 {\left( {m + 1} \right)}}} \right. \kern-0pt} {\left( {m + 1} \right)}}}} \left( {{{d\delta } \mathord{\left/ {\vphantom {{d\delta } {dt}}} \right. \kern-0pt} {dt}}} \right) = a_{0} F_{n} \left( {n,m} \right)$ is time-independent. In terms of the variables U and θ, and with m = 1 this means: $\delta_{U}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {{{d\delta_{U} } \mathord{\left/ {\vphantom {{d\delta_{U} } {dt}}} \right. \kern-0pt} {dt}}} \right) = a_{0} F_{p} = const.$ and $\delta_{S}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {{{d\delta_{S} } \mathord{\left/ {\vphantom {{d\delta_{S} } {dt}}} \right. \kern-0pt} {dt}}} \right) = A_{s} F_{s} = const.$ However, with this minimization procedure we lost the effect of β which is “absorbed” by the effective diffusivity $A_{s}$, for example. In the expressions about $\delta_{U}$ there is a factor $\beta^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}$ which cannot be ignored. Consequently, the determination of the approximate solutions of Eq. (71) with a profile

$$T_{a} = T_{s} \left( {1 - \frac{x}{{\delta_{U} \left( {\beta ,p} \right)}}} \right)^{p}$$

(72)

means determination of optimal exponents p which should take into account the effect of β. Moreover, it should be different from the optimal exponents corresponding to the approximate solutions of the transformed Eqs. (48) and (63b). With known constructions of the functions $F_{{p\left( {HBIM} \right)}}$ and $F_{{p\left( {DIM} \right)}}$ defined by (55c) and (56c), as well as with T _s defined by Eq. (60a) the task is: minimization of the squared error function $\int_{0}^{\delta } {\left[ {\varphi_{q} \left( {T_{a} \left( {x,t} \right)} \right)} \right]^{2} } dx$. The procedure is explained in [25] but involves cumbersome expressions which will be skipped here. However, we may establish the constraint on the exponent p at x = 0 with a procedure similar to the case of the Example 1.

With the Zener’s coordinate [25, 42] $\xi = {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta },\;0 < \xi < 1$, the normalized approximation profile $\phi_{a} = {{T_{a} } \mathord{\left/ {\vphantom {{T_{a} } {\beta^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \right. \kern-0pt} {\beta^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} = \left( {{\delta \mathord{\left/ {\vphantom {\delta p}} \right. \kern-0pt} p}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {1 - {x \mathord{\left/ {\vphantom {x {\delta_{U} }}} \right. \kern-0pt} {\delta_{U} }}} \right)^{p}$ can be represented as $\phi_{a} = \delta_{U}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} Y\left( {\xi ,t} \right)$ where $Y\left( {\xi ,t} \right) = \left( {{1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-0pt} p}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {1 - \xi } \right)^{n}$. From the diffusion Eq. (1b) (and 71, too) we may define the residual function $\Phi _{q} \left( {\xi ,t} \right)$ in the $\xi$-space, namely

$$\begin{aligned} \Phi _{q} \left( {\xi ,t} \right) & = \left[ {\frac{1}{2}\delta_{U}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \frac{{d\delta_{U} }}{dt}Y - \delta_{U}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \frac{{d\delta_{U} }}{dt}\xi \frac{\partial Y}{\partial \xi }} \right]\frac{1}{{\delta_{U} }} \\ & \quad - a_{0} \frac{1}{{\delta_{U} }}\frac{{\partial^{2} Y}}{{\partial \xi^{2} }} - a_{0} \beta \left[ {\frac{1}{{\delta_{U} }}Y^{{ - \frac{1}{2}}} \left( {\frac{\partial Y}{\partial \xi }} \right)^{2} } \right] \end{aligned}$$

(73)

From the condition $\varPhi_{q} \left( {0,t} \right) \ge 0$ it follows that

$$\left[ {p\left( {1 + 2\beta } \right) - \left( {1 + \beta } \right)} \right] \le 0 \Rightarrow p \le \frac{1 + \beta }{1 + 2\beta } = \frac{1}{1 + \varepsilon },\quad \varepsilon = \frac{\beta }{1 + \beta }$$

(74a, b, c)

The limits of p are $\lim \mathop p\limits_{\beta \to 0} = {{\left( {1 + \beta } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \beta } \right)} {\left( {1 + 2\beta } \right)}}} \right. \kern-0pt} {\left( {1 + 2\beta } \right)}} = 1$ and for large β: $\lim \mathop p\nolimits_{\beta \to \infty } = {{\left( {1 + \beta } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \beta } \right)} {\left( {1 + 2\beta } \right)}}} \right. \kern-0pt} {\left( {1 + 2\beta } \right)}} \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}$. With β = 0.5, for instance we have p ≤ 0.75 while with β = 0.1, we get p ≤ 0.911.

In general, the squared error function $E_{Mq} = \int_{0}^{1} {\left[ {\varPhi_{q} \left( {\xi ,t} \right)} \right]^{2} } d\xi$ can be expressed (with the DIM solution) as

$$\begin{aligned} & E_{{Mq\left( {DIM} \right)}} \\ & \quad = \frac{1}{{\delta^{4} }}\int\limits_{0}^{1} {\left\{ {\begin{array}{*{20}c} {p\left( {p + 1} \right)\left( {p + 2} \right)\left[ {(1 - \xi )^{p} + \xi (1 - \xi )^{p - 1} } \right]\frac{3}{10} } \\ { - \beta p\left( {2p - 1} \right)\left( {1 - \xi } \right)^{2p - 2} - p(p - 1)\left( {1 - \xi } \right)^{p - 2} } \\ \end{array} } \right\}^{2} d\xi } \end{aligned}$$

(75)

This results in $E_{{Mq\left( {DIM} \right)}} = {{e_{Lq} \left( {p,\beta } \right)} \mathord{\left/ {\vphantom {{e_{Lq} \left( {p,\beta } \right)} {\delta_{U}^{4} }}} \right. \kern-0pt} {\delta_{U}^{4} }}$. The rational function $e_{Lq} \left( {p,\beta } \right)$ has to be minimized with respect to p for given values of β. The denominator of function $e_{Lq} \left( {p,\beta } \right)$ defines multiple vertical asymptotes in the upper quadrant and one slant asymptote for p < 0. The behaviour of $e_{Lq} \left( {p,\beta } \right)$ with numerical values of β used in this study is shown in Fig. 9. We have two well-defined zones of positive p, namely: 0.5 < p < 0.65 and p > 0.75. Only in the range 0.5 < p < 0.65 both limits imposed on the exponents for $0.1 \le \beta \le 0.5$ by the constraint (74b) are obeyed. However, it is hard to see well defined minima of $e_{Lq} \left( {p,\beta } \right)$ when 0.5 < p < 0.65. By varying p (solvitur ambulando approach) within this zone and evaluating $e_{Lq} \left( {p,\beta } \right)$ we may define the optimal exponent $p_{opt}$. The only criterion for accept a given p is the value of the pointwise error when comparing the approximate profiles with the numerical solutions (see Sect. 5.5). This approach yielded an average $p_{opt} \approx 0.595$ for all solutions, irrespective of β. Numerical experiments with p = 0.870 defined by the solution of the transformed Eq. (48) and $p_{opt} \approx 0.595$ are presented in the next section.

Fig. 9

Behaviour of the squared error function $e\left( {p,\beta } \right)$ which has to be minimized with respect to p. DIM solutions and fixed flux as a boundary condition for different β > 0

5.5 Benchmarking against numerical solutions

Accepting an average $p_{opt} \approx 0.595$ for all solutions, irrespective of β, we get satisfactory accuracy of the approximate solutions (see Fig. 10a, b) since all pointwise errors (see Fig. 11a) are less than 0.05 (in the extreme section of the curves near the front $x \to \delta$ (i.e. $X_{q} = {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta } \to 1$), when compared with the numerical solution. In contrast with p = 0.870, the errors may attain unacceptable values up to 0.18 (see Fig. 11b). The special case with β = 0 is shown in Fig. 10c (see the comments in the next section).

Fig. 10

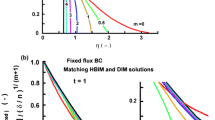
Fixed flux as a boundary condition. Normalized temperature profiles $T_{aN} = {{T_{s} } \mathord{\left/ {\vphantom {{T_{s} } {\left[ {\left( {{{Q_{0} } \mathord{\left/ {\vphantom {{Q_{0} } \beta }} \right. \kern-0pt} \beta }} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {{{\delta_{U} } \mathord{\left/ {\vphantom {{\delta_{U} } p}} \right. \kern-0pt} p}} \right)} \right]}}} \right. \kern-0pt} {\left[ {\left( {{{Q_{0} } \mathord{\left/ {\vphantom {{Q_{0} } \beta }} \right. \kern-0pt} \beta }} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {{{\delta_{U} } \mathord{\left/ {\vphantom {{\delta_{U} } p}} \right. \kern-0pt} p}} \right)} \right]}}$ of DIM solutions and numerical solutions (finite differences) for t = 1 and optimal exponent $p_{opt} = 0.595$. a Cases of β = 0.1, β = 0.2 and β = 0.3. b Cases of β = 0.4 and β = 0.5. c Case of β = 0. Comparison of the exact and DIM solutions. Inset: pointwise error. The DIM solutions ends at 4.13η

Fig. 11

Fixed flux as a boundary condition. Pointwise errors of approximation. Comparison of the normalized approximate profiles (DIM solutions T _aN with numerical solutions T _num (finite differences) for t = 1. a Cases of β > 0 and p _opt  = 0.595. b Cases of β > 0 and two exponents of the profile p _opt  = 0.595 and p = 0.870

The plots in Fig. 10a, b clearly demonstrate how the factor (thermal coefficient) β affects the solutions and determines the penetration depths. Precisely, with increase in β (β > 0) the penetration depth increases, i.e. easier propagation of the thermal wave in the medium due to increased thermal diffusivity, and vice versa. As a direct consequence of the effect of β on the temperature rise, with help of Eq. (63) it easier to demonstrate it by the time evolution of the normalized surface temperature $T_{s}$ (see Fig. 12).

Fig. 12

Fixed flux boundary condition problem. Time evolution of the normalized surface temperature ${{\left( {T - T_{ref} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{ref} } \right)} {A_{qp} }}} \right. \kern-0pt} {A_{qp} }} = \beta^{{ - \frac{1}{6}}} t^{{\frac{2}{3}}}$ (see Eq. 60). p _opt  = 0.595

As a final point, the approximate solutions were tested with real values of β > 0 for tree wood samples (see Table 5) and the profiles in Fig. 13a demonstrated adequate behaviour of the DIM solutions. The pointwise errors (Fig. 13b) confirm the behaviour of the integral balance solutions established for large β (i.e. $- 0.5 \le \beta \le 0.5)$ with errors less that 0.06 (in the extreme zone close to the front δ), which are inherent for this solution method. The rise of the surface temperature of the three wood samples is simulated in Fig. 13c.

Fig. 13

Fixed flux boundary condition problem. Solutions with real data pertinent to wood samples with β > 0 (see Table 5). a (DIM) and numerical solutions (finite differences) for wood samples. b Pointwise errors between DIM solutions and numerical ones (finite differences). c Time evolution of the normalized surface temperature ${{\left( {T - T_{ref} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{ref} } \right)} {A_{qp} }}} \right. \kern-0pt} {A_{qp} }} = \beta^{{ - \frac{1}{6}}} t^{{\frac{2}{3}}}$ of the wood samples (see Eq. (60) for the values of β). p _opt  = 0.595

5.6 Case with β = 0 against the problem with $\beta \ne 0$

Beyond comments in the preceding section, it is worthy to compare these cases with the approximate solution solutions for the extreme case with β = 0, both exact and approximate (by DIM, for example). Really, this point of the article was provoked by the comments of the reviewers and tries to encompass some problems that might lead to wrong step in the solution of the problem at issue. For β = 0 the DIM solution [3] and the exact one are

$$U_{{DIM\left( {\beta = 0} \right)}} = \frac{{\delta_{{DIM\left( {\beta = 0} \right)}} }}{{n_{0} }}\left( {1 - \frac{x}{{\delta_{{DIM\left( {\beta = 0} \right)}} }}} \right)^{{N_{0} }} ,\;\delta_{{DIM\left( {\beta = 0} \right)}} = \sqrt {\frac{{2\left( {n_{0} + 1} \right)\left( {n_{0} + 2} \right)}}{3}} ,\quad n_{0} = 3.822$$

(76a)

$$U_{{ex\left( {\beta = 0} \right)}} = 2\sqrt {\frac{t}{\pi }} \exp \left( { - \frac{{x^{2} }}{{4a_{0} t}}} \right) - xerfc\left( {\frac{x}{{2\sqrt {a_{0} t} }}} \right)$$

(76b)

The plots in Fig. 10c are concave profiles clearly demonstrating the difference in the behaviour with respect to the case when $\beta \ne 0$. The different behaviour is attributed to the fact that for $\beta \ne 0$ and β = 0 we have two different types of diffusion equations. Precisely, for β = 0 the diffusion equation is completely parabolic and the solutions are concave profiles as it is shown in Fig. 10c. Contrary, for $\beta \ne 0$ the equation remains parabolic but with dominating degenerate properties due the term $a_{0} \beta T\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)$ and consequently its profiles become convex and steeper as the value of β increases (see Fig. 10a, b). It is worthy that the optimal exponents for the integral-balance solutions (both HBIM and DIM) of the degenerate diffusion equation resulting in convex profiles are less that 1 as it was demonstrated in [25]. Contrary, HBIM and DIM applied to the pure diffusion equation with β = 0 have optimal exponents $n_{{HBIM\left( {\beta = 0} \right)}} = 3.584$ and $n_{{DIM\left( {\beta = 0} \right)}} = 3.822$, correspondingly [3]. In general, the HBIM and DIM solutions with exponents n > 1, precisely with n > 2 [3] have concave profiles.

For the sake of clarity and correctness of the developed results, as wells to complete this discussion we refer to an idea that might lead to imaginary results. In particular, we may formulate the question: Is it possible to use the exact solution (for β = 0) when the values of β are very small? Recall, the non-linearity of the diffusion coefficients in the case of the fixed flux problem appears simultaneously in both the governing equation and the boundary condition.

The assumption $a_{0} \left( {1 + \beta T} \right) \approx a_{0} = const.$ would result in a linearized boundary condition, but the principle problem emerging from this idea is that we have to define the circumstances under which this approximation is valid. Moreover, we need additional conditions allowing the term $a_{0} \beta {{\partial \left( {T{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)} \mathord{\left/ {\vphantom {{\partial \left( {T{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)} {\partial x}}} \right. \kern-0pt} {\partial x}}$ in the governing equation has to be neglected. Alternatively, if the governing equation is linearized by ad hoc assumption that the term $\beta T$ is negligible, but the non-linearity remains in the boundary condition, we get a problem with a time-dependent surface temperature as it is defined by Eq. (43) (HBIM solution) and Eq. (45). This problem cannot be modelled by the exact solution (76b). In general, a small values of β is not a serious reason to reduce both the governing equation and the boundary condition and apply the exact solution (76b).

6 Integral-balance solutions through the Kirchhoff transform

Even though, the emphasis of the present study is application of the integral balance method avoiding the initial linearization through the Kirchhoff transform, we will demonstrate briefly how HBIM and DIM work is this case. As mentioned in the beginning the common approach to solve such non-linear problem is to apply the Kirchhoff transform (2a, b). Then, the equation becomes with respect to the new variable w becomes homogeneous. Equation (2c) is a truly parabolic equation with infinite speed of the flux. Therefore, the finite penetration depth is a reasonable concept; even though the exact solution through the error function is well-known. With the new variable w the Goodman boundary conditions (4a, b) are satisfied because

$$w\left( \delta \right) = a_{a} T\left( \delta \right) + \frac{\beta }{2}T^{2} \left( \delta \right) = 0\;{\text{and}}\;\frac{\partial w}{\partial x}\left( \delta \right) = a_{a} \frac{\partial T\left( \delta \right)}{\partial x} + \beta T\left( \delta \right)\frac{\partial T\left( \delta \right)}{\partial x} = 0$$

(77)

Therefore, we may apply the well known solutions of the Eq. (2c) by HBIM and DIM [3, 26–29], as it demonstrated next.

6.1 Fixed temperature boundary condition

With prescribed $T\left( {0,t} \right) = T_{s}$ the Kirchhoff transform provides $w\left( {0,t} \right) = W_{s} = a_{0} T_{s} + {{\beta T_{s}^{2} } \mathord{\left/ {\vphantom {{\beta T_{s}^{2} } 2}} \right. \kern-0pt} 2}$. Further, the assumed profile can be $W_{a} = W_{s} \left( {1 - {x \mathord{\left/ {\vphantom {x {\delta_{w} }}} \right. \kern-0pt} {\delta_{w} }}} \right)^{p} \;{\text{or}}\;\phi_{w} = {{W_{a} } \mathord{\left/ {\vphantom {{W_{a} } {W_{s} }}} \right. \kern-0pt} {W_{s} }} = \left( {1 - {x \mathord{\left/ {\vphantom {x {\delta_{w} }}} \right. \kern-0pt} {\delta_{w} }}} \right)^{p}$. Then, applying the HBIM and DIM solutions to Eq. (2c) we get expressions about the penetration depth [3]

$$\delta_{{w\left( {HBIM} \right)}}^{T} = \sqrt {a_{0} t} \sqrt {2p\left( {p + 1} \right)}$$

(78a)

$$\delta_{{w\left( {DIM} \right)}}^{T} = \sqrt {a_{0} t} \sqrt {\left( {p + 1} \right)\left( {p + 2} \right)}$$

(78b)

The definition of the optimal p is a problem already solved [3], that is: $p_{{opt\left( {HBIM} \right)}}^{T} \approx 2.233$ and $p_{{opt\left( {DIM} \right)}}^{T} \approx 2.219$. Now, the question is: How to go back to a solution in term of the original dependent variable T? The answer is straightforward. This can be done directly from the Kirchhoff transform by using $W_{a}$, that is

$$W_{a} = a_{0} T_{a} + \frac{\beta }{2}T_{a}^{2} \Rightarrow \frac{\beta }{2}T_{a}^{2} + a_{0} T_{a} - W_{a} = 0$$

(79a, b)

The solution of (79b) should provide a positive root T _a which after rearrangement can be expressed as

$$T_{a} = \frac{{a_{0} }}{\beta }\left( {\sqrt {1 + 2\frac{{\beta^{{}} }}{{a_{0}^{2} }}W_{a} } - 1} \right) \Rightarrow T_{a} = \frac{{a_{0} }}{\beta }\left( {\sqrt {1 + 2\frac{{\beta^{{}} }}{{a_{0}^{2} }}W_{s} \left( {1 - \frac{x}{{\delta_{w} }}} \right)^{p} } - 1} \right)$$

(80a, b)

Because $W_{a} \ge 0$, the solution (80a) gives real T _a when

$$\beta \ge 0\quad{\text{and}}\quad \frac{{a_{0} }}{{2W_{a} }} \le \beta \le 0$$

(80c, d)

These are the conditions for β matching the results of Cobble [4].

From Eq. (80b) it follows that for $x = \delta$ we get $T_{a} \left( \delta \right) = 0$ and ${{\partial T_{a} \left( \delta \right)} \mathord{\left/ {\vphantom {{\partial T_{a} \left( \delta \right)} {\partial x}}} \right. \kern-0pt} {\partial x}} = 0$. Since the Kirchhoff transform can be expressed as $T_{a}^{2} = - 2\frac{{a_{0} }}{\beta }T_{a} + W_{a} \frac{2}{\beta }$ for x = 0 with $W_{a} \left( {0,t} \right) = W_{s} = \frac{\beta }{2}T_{s}^{2} + a_{0} T_{s}$ and Eq. (80) we get $T_{a} \left( {x = 0} \right) = T_{s}$, This completes the test that the solution (77b) satisfies the boundary condition at $x = 0$. The solution (80a) has the same form as the result of Cobble [4] where the exact solution  $W_{e} = erfc\left( {{\eta \mathord{\left/ {\vphantom {\eta 2}} \right. \kern-0pt} 2}} \right)$ is used instead W _a .

The comparative numerical experiments (see Figs. 14a, b, 15) indicate that better results with DIM solution used in (79b) can be obtained for β < 0 (Fig. 16a) rather then when β > 0 (see Fig. 16b), except the case of β = −0.5. In general, the pointwise error decreases as the absolute value of β decreases, as it was observed with the fixed temperature problem.

Fig. 14

Comparative plots of solutions developed through preliminary Kirchhoff transforms: of DIM approximate profiles (Eq. 79) and solution developed through the exact solutions of (2c). $p_{{opt\left( {DIM} \right)}}^{T} \approx 2.219$. a Cases of positive β. b Cases of negative β

Fig. 15

Relative pointwise errors in case of solutions with preliminary Kirchhoff transforms: DIM approximate profiles compared to solution developed through the exact solutions of (2c). a Cases of negative β. b Cases of positive β

Fig. 16

Benchmarking of DIM approximate profiles developed through preliminary Kirchhoff transforms against numerical solution (Runge–Kutta). Cases of β = 0.2 and β = 0.5. Inset zoomed section demonstrating the effect of β on the penetration depth

The benchmarking against the Runge–Kutta solution (see Fig. 16a) clearly shows the effect of β on the penetration depth (the inset of Fig. 15a) and acceptable approximation errors (Fig. 15b). Further, the benchmarking against the numerical solutions (Runge–Kutta and finite difference) reveals that the approximation error decreases as the absolute value of β decrease (see Fig. 17a–c). Moreover, with equal absolute values of β, the lower pointwise errors are exhibited by the case with negative β (see Fig. 17a, b for example).

Fig. 17

Pointwise errors when the DIM solutions developed through preliminary Kirchhoff transforms are compared with numerical solutions (finite differences). a Case of β = 1 and β = −1. b Case of β = 3 and β = −3. c Case of β = 5 and β = −5

In this end, this section of the article clearly demonstrates that the approximate solutions (HBIM and DIM) of the equations developed by the Kirchhoff transform can be successfully used for the determination of the solutions in terms of original variables without additional optimization of the exponent of the profile. To our point of view, this was a good attempt to apply HBIM and DIM after Kirchhoff transform because with the fixed temperature problem the nonlinearity exists only in the governing equation, but not at the boundary.

6.2 Fixed flux boundary condition

With the Kirchhoff transform the fixed flux boundary condition is

$$- k_{0} \left[ {\frac{\partial T}{\partial x} + \frac{\beta }{2}\frac{{\partial T^{2} }}{\partial x}} \right]_{x = 0} \Rightarrow - k_{0} \frac{\partial }{\partial x}W\left( {0,t} \right) = q_{0}$$

(81a, b)

Since the profile is assumed as $\phi_{w} = {{W_{a} } \mathord{\left/ {\vphantom {{W_{a} } {W_{s} }}} \right. \kern-0pt} {W_{s} }} = \left( {1 - {x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0pt} \delta }} \right)^{p}$, the (80b) can be presented as

$$- k_{0} \left( { - \frac{p}{\delta }} \right)W_{s} = q_{0} \Rightarrow W_{s} = \frac{{q_{0} }}{{k_{0} }}\frac{\delta }{p}$$

(81c)

as in the linear case and the transformed profile is

$$W_{a} = \frac{{q_{0} }}{{k_{0} }}\frac{\delta }{p}\left( {1 - \frac{x}{\delta }} \right)^{p}$$

(82)

The profile (82) satisfies the Goodman boundary conditions. The HBIM and DIM solutions about the penetration depths are [3]

$$\delta_{{w\left( {HBIM} \right)}}^{q} = \sqrt {a_{0} t} \sqrt {p\left( {p + 1} \right)}$$

(83a)

$$\delta_{{w\left( {DIM} \right)}}^{q} = \sqrt {a_{0} t} \sqrt {\frac{{2\left( {p + 1} \right)\left( {p + 2} \right)}}{3}}$$

(83b)

With optimal exponents: $p_{{op\left( {HBIM} \right)}}^{q} \approx 3.584$ and $p_{{op\left( {DIM} \right)}}^{q} \approx 3.822$ established by Myers [3]. Then, the approximate profiles in term of T can be obtained from $W_{a} = a_{0} T_{a} + \frac{\beta }{2}T_{a}^{2}$ in a way similar to that used for the problem with the fixed temperature boundary condition but will stop here the solution which is beyond the scope of the present article. Probably this will be developed in our future studies.

7 Conclusions

The solutions developed demonstrate how the integral balance approach in its two modifications (HBIM and DIM) can be applied to nonlinear transient heat conduction with a nonlinear thermal diffusivity represented as the additive functional relationship $a = a_{0} \left( {1 \pm \beta T} \right)$.

The main steps and contribution of the developed solutions may be outlined as:

• 1. The main step avoiding the initial linearization of the model equation is the use of the derivative of order (m + 1)in the right-side of the HBIM and DIM integrations procedures.

• 2. The application of the simple heat-balance integral technique (HBIM) to non-linear heat conduction equation is effective when the Dirichlet problem is at issue, while the direct application of HBIM and DIM to the fixed flux problem is unsuccessful.

• 3. The optimal exponents in the case of fixed temperature problem can be straightforwardly determined by minimization of the squared-error of approximation of the governing equation (criterion of Langford for the integral-balance solutions) and the method of Mitchell and Myers [27, 29].

• 4. The fixed flux problem can be solved with HBIM and DIM by either a change of variable as $U = 1 + \beta T$ or a preliminary treatment (rescaling) of the conductivity relationship $a = a_{0} \left( {1 + \beta T} \right)$ which transforms the initial model into an equation with a power-law thermal diffusivity $a_{0} T^{m}$, especially for m = 1. The transformed equations have known closed form approximate solutions which can be used in evaluation of the optimal exponents when they are used in the minimization of the residual function of the original equation.

• 5. Two comparative examples developed with application of the Kirchhoff transform clearly demonstrated the applicability of both HBIM and DIM with acceptable errors of approximation.

• 6. Irrespective of the techniques used the approximate solution with β < 0 are more successful rather then the ones when β > 0 and this judgment is based on the pointwise errors when comparing to the numerical results.

Appendices

Appendix 1: Fixed temperature problem: the numerical solutions used

• Finite difference solution

In order to validate the approximate integral-balance solutions, two numerical solutions were developed for the benchmarking procedures. The first numerical solution is found thanks to the method of finite difference, where an explicit scheme, due to its numerical stability and good convergence, was used. In additions, with a time step $\Delta t = 1/100$ and a space step $\Delta x = 1/50$ we got a good accuracy. In this contexts, in the approximation of Eq. (15) (with initial and boundary conditions $u\left( {x,0} \right) = 0$ and $u\left( {0,t} \right) = 1$ q $u\left( {\delta ,t} \right) = 0$) the error due to the numerical approximation is relatively high when for x is close to 0 but decreased rapidly when x increases. This high error close to 0 is due to the impossibility to calculate the derivative of u at 0.

• Runge–Kutta solution

With the Boltzmann transform $\eta = {x \mathord{\left/ {\vphantom {x {\sqrt {a_{0} t} }}} \right. \kern-0pt} {\sqrt {a_{0} t} }}$ and $X = x/\delta = \eta /f(n)$ we may express Eq. (15) in the forms

$$X\frac{{f(n)^{2} }}{2}\frac{\partial u(X)}{\partial X} + \frac{\beta }{1 + \beta u(X)}\left( {\frac{\partial u(X)}{\partial X}} \right)^{2} + \frac{{\partial^{2} u(X)}}{{\partial X^{2} }} = 0,\quad f\left( n \right) \ne 1$$

(84)

$$\begin{aligned} &\frac{1}{2}\frac{\partial u(\eta )}{\partial \eta } + \frac{\beta }{1 + \beta u(\eta )}\left( {\frac{\partial u(\eta )}{\partial \eta }} \right)^{2} + \frac{{\partial^{2} u(\eta )}}{{\partial \eta^{2} }} = 0,\\&\quad f\left( n \right) = 1\;{\text{and}}\;\eta = X \end{aligned}$$

(85)

The normalizing function $f(n)$ is introduced for consistency with the concept of the finite penetration depth $\delta$ which is missing in the classical solution of the linear equation expressed by the Gaussian error function. In fact, with $f\left( n \right) \ne 1$ the initial problem is transformed to a boundary value problem with $u(X = 0) = 1$ and $u(X = 1) = 0$ allowing to compare the integral-balance solutions with the numerical ones in the domain $0 \le X \le 1$. The solutions were developed by Maple 13 where Runge–Kutta solutions of 4th order are possible with absolute error less than $10^{ - 6}$. The normalizing function $f(n)$ for each β is expressed through the optimal n developed by minimization of the residual function (see Tables 2, 3) and it is equal either to $F_{HBIM}^{T} \left( {n,\beta } \right)$ or $F_{DIM}^{T} \left( {n,\beta } \right)$ (see Eqs. 27, 28), depending on the integration method applied.

Appendix 2: Fixed flux problem: the derivations of the approximations (43) and (44) HBIM solution

The equation about the penetration depth is developed by HBIM solution is (42), namely

$$\delta^{3} - \delta \left( {a_{0} t} \right)n\left( {n + 1} \right) - \beta \frac{{q_{0} }}{{k_{0} }}\left( {a_{0} t} \right)^{2} n\left( {n + 1} \right)^{2} = 0$$

(42)

For β = 0, it reduces to $\delta_{{0\left( {HBIM} \right)}}^{q} = \delta_{0}^{{}} = \sqrt {\left( {a_{0} t} \right)n\left( {n + 1} \right)}$ which is the classical HBIM solution [3, 26]. Denoting $\delta_{0}^{2} = \left( {a_{0} t} \right)n\left( {n + 1} \right) = \alpha_{1} > 0$ and $\beta \frac{{q_{0} }}{{k_{0} }}\left( {a_{0} t} \right)^{2} n\left( {n + 1} \right)^{2} = \alpha_{2} > 0$ we get a depressed cubic equation about $\delta \left( t \right)$, namely

$$\delta^{3} - \alpha_{1} \delta - \alpha_{2} = 0$$

(86)

The coefficients of (84) are related as $\alpha_{2} = \alpha_{1}^{2} \beta \left( {{{q_{0} } \mathord{\left/ {\vphantom {{q_{0} } {k_{0} n}}} \right. \kern-0pt} {k_{0} n}}} \right)$.

Now, let us suggest that the penetration depth for $\beta \ne 0$ is related to the $\delta_{0}^{2} = \left( {a_{0} t} \right)n\left( {n + 1} \right)$ by a correctional functional $f_{3} \left( {n,t} \right)$ that is $\delta^{2} = \delta_{0}^{2} f_{3}^{2}$. Now, we may rearrange (86) as

$$\delta_{0}^{3} f_{3}^{3} - \delta_{0}^{3} f_{3} - \delta_{0}^{4} \beta \frac{{q_{0} }}{{k_{0} }}\frac{1}{n} = 0 \Rightarrow f_{3}^{3} - f_{3} - \delta_{0}^{{}} \beta \frac{{q_{0} }}{{k_{0} }}\frac{1}{n} = 0$$

(87a, b)

For β = 0 it follows directly that $f_{3} = 1$ is a solution of Eq. (87a, b). The solution of the cubic equation $f_{3}^{3} = Af_{3} + B$ depends upon the sign of the determinant $D = \frac{{A^{3} }}{27} + \frac{{B^{2} }}{4}$. For D > 0 the equation has one real root and two imaginary roots. Since we need a unique real solution of the penetration depth, then D > 0 is the case. With A = 1 and $B = \delta_{0}^{{}} \beta \frac{{q_{0} }}{{k_{0} }}\frac{1}{n}$ we get

$$D = \frac{{A^{3} }}{27} + \frac{{B^{2} }}{4} = \delta_{0}^{2} \left( {\beta \frac{{q_{0} }}{{k_{0} }}\frac{1}{n}} \right)^{2} \left[ {1 - \frac{1}{27}\frac{1}{{\delta_{0}^{2} }}\left( {\frac{2}{\beta }\frac{{k_{0} }}{{q_{0} }}n} \right)^{2} } \right]$$

(88)

Therefore, the Cardano formula is $f_{3} = M + N$, where

$$M = \left( { - \frac{B}{2} + \sqrt D } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} = \left( {\delta_{0}^{{}} \beta \frac{{q_{0} }}{{k_{0} }}\frac{1}{n}} \right)^{{\frac{1}{3}}} \left[ {\frac{1}{2} + \sqrt {1 - \frac{1}{27}\frac{1}{{\delta_{0}^{2} }}\left( {\frac{1}{\beta }\frac{{k_{0} }}{{q_{0} }}n} \right)^{2} } } \right]^{{\frac{1}{3}}}$$

(89a)

$$N = \left( { - \frac{B}{2} - \sqrt D } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} = \left( {\delta_{0}^{{}} \beta \frac{{q_{0} }}{{k_{0} }}\frac{1}{n}} \right)^{{\frac{1}{3}}} \left[ {\frac{1}{2} - \sqrt {1 - \frac{1}{27}\frac{1}{{\delta_{0}^{2} }}\left( {\frac{1}{\beta }\frac{{k_{0} }}{{q_{0} }}n} \right)^{2} } } \right]^{{\frac{1}{3}}}$$

(89b)

$$\begin{aligned} f_{3} & = \left( {\delta_{0}^{{}} \beta \frac{{q_{0} }}{{k_{0} }}\frac{1}{n}} \right)^{{\frac{1}{3}}} \\ & \quad \times \left\{ {\left[ {\frac{1}{2} + \sqrt {1 - \frac{1}{27}\frac{1}{{\delta_{0}^{2} }}\left( {\frac{1}{\beta }\frac{{k_{0} }}{{q_{0} }}n} \right)^{2} } } \right]^{{\frac{1}{3}}} + \left[ {\frac{1}{2} - \sqrt {1 - \frac{1}{27}\frac{1}{{\delta_{0}^{2} }}\left( {\frac{1}{\beta }\frac{{k_{0} }}{{q_{0} }}n} \right)^{2} } } \right]^{{\frac{1}{3}}} } \right\} \\ \end{aligned}$$

(90a)

In (90a) the denominators of the second terms under the radicals grow in time rapidly because $\delta_{0}^{2} \equiv a_{0} t$. From this point of view, we may suggest that they could be neglected as smaller than 1 and this step allows to approximate f ₃ as

$$f_{3} \approx \left( {\delta_{0}^{{}} \beta \frac{{q_{0} }}{{k_{0} }}\frac{1}{n}} \right)^{{\frac{1}{3}}} \left[ {\left( {\frac{1}{2}} \right)^{{\frac{1}{3}}} + \left( {\frac{1}{2}} \right)^{{\frac{1}{3}}} } \right] \approx \left( {\delta_{0}^{{}} \frac{\beta }{4}\frac{{q_{0} }}{{k_{0} }}\frac{1}{n}} \right)^{{\frac{1}{3}}}$$

(90b)

Then the penetration depth $\delta \left( t \right)$ can be expressed as

$$\delta \left( t \right) = \delta_{0} f_{3} \approx \delta_{0} \left( {\delta_{0}^{{}} \frac{\beta }{4}\frac{{q_{0} }}{{k_{0} }}\frac{1}{n}} \right)^{{\frac{1}{3}}} \approx \delta_{0}^{{\frac{4}{3}}} \left( {\frac{\beta }{4}\frac{{q_{0} }}{{k_{0} }}\frac{1}{n}} \right)^{{\frac{1}{3}}}$$

(91a, b)

With the square-root expression of $\delta_{0} \left( t \right)$ inserted in (91b) we get (92) (that is the approximation (Eq. 43 in the main text)

$$\delta \left( t \right) \approx \left( {a_{0} t} \right)^{{\frac{2}{3}}} \left[ {n^{{\frac{1}{3}}} \left( {n + 1} \right)^{{\frac{2}{3}}} } \right]\left( {\frac{\beta }{4}\frac{{q_{0} }}{{k_{0} }}} \right)^{{\frac{1}{3}}}.$$

(92)