1 Introduction

Transient heat-transfer problems arise frequently in complex engineering applications and in general physical phenomena. For instance, the dynamic character of a temperature field enables defect sizing analysis through transient thermography [1, 2] with the help of infrared cameras. This technique is based on the scattering of the temperature field, initiated by a short-duration pulse of a heat flux to a free surface of a specimen, by virtue of the presence of various defects in a solid. Another example refers to the cooling of a hot solid by means of a fluid. The temperature difference may cause vaporisation of the liquid. Further cooling of the solid results in a steady-state process with an established boundary between parts of the solid covered by liquid and vapour, forming the so-called “quench front”. This problem is known as the “quench front propagation problem” [3, 4], and it plays an important role in the nuclear, metallurgical, chemical and cryogenic industries [5, 6]. One more interesting application concerns the hot-film technique, which is based on the dynamic heat exchange between a viscous fluid in a channel and a hot-film attached to its wall. It is possible to establish the dependence between the heat flux across the film and the local shear rate, which is important for the analysis of fluid behaviour [7] and can be determined through the knowledge of the heat flux. The movement of the fluid introduces some complications in the mathematical treatment of the problem although it is possible to determine analytical results by adopting some simplifications [8, 9]. Ignoring the temporal dependence of temperature allows one to obtain exact solutions [10, 11]; however, the problem reduces to one with mixed boundary conditions for which the derivation of final solutions is not straightforward and requires special treatment. Therefore, the development of mathematical models for transient heat propagation makes it possible to address a number of practical issues.

The difficulties in obtaining purely analytical results involve the presence of the dynamic terms in the heat equation and, what is more important, the mixed type of boundary conditions. The Wiener–Hopf technique [12] appears to be a powerful tool in handling the latter difficulty. This method allows one to obtain the solution of the problem in terms of the Fourier and Laplace transforms, which can be inverted either analytically (for some special cases) or numerically. The application of this technique is preferred to specific numerical modelling of the problem, e.g. by means of the finite element method (FEM), as it avoids problems associated with the changes in boundary conditions, and it also reduces computation times for the analysis of physical problems.

The aim of this work is to obtain the solution of a transient heat problem with the anisotropic thermal conductivity in the half-space with mixed boundary conditions of the Dirichlet and the Robin (convective) type by means of the Wiener–Hopf technique. This problem is of essential significance for numerous engineering applications and in this manuscript we demonstrate it on two practical examples. The mathematical challenge in obtaining the solution is related to the Wiener–Hopf method requiring the function factorisation which, to the best of our knowledge, is not available in an analytical form in the literature. Furthermore, the consideration of dynamic effects introduce additional difficulties for obtaining the factorisation. For these reasons, we perform the factorisation by using a robust algorithm developed for the considered transient problem and which can be adapted for more complicated problems as well. In such a case, the suitable reduction of singularities of the function can be achieved for better performance of the subsequent computations and improved accuracy of the results in comparison with the purely numerical methods. Moreover, we focus on the solution behaviour close to the location of the change in boundary condition where the computational difficulties usually appear. We estimate the asymptotic behaviour of functions in this region which shows that the associated accuracy of results is complicated to achieve with FEM unless significant mesh refinement is accomplished.

The paper is organised as follows. The formulation of the mathematical problem and associated notation are introduced in Sect. 2. Section 3 presents the reduction of the problem to one that is suitable for treatment by the Wiener–Hopf method and solutions are derived together with their asymptotic form close to the change in boundary condition. The numerical procedures that have been employed in the present study are described in Sect. 4, followed by the presentation of results for some particular cases in Sect. 5. We discuss particular application areas in Sect. 6. Conclusions are drawn and future work discussed in Sect. 7. The efficiency of the proposed numerical algorithm for the function factorisation is shown in Appendix A. For reference, the weak formulation for the FEM is provided in Appendix B.

Fig. 1
figure 1

Domain \(\varOmega \) of the problem under consideration with marked boundaries \(\partial \varOmega ^+\) and \(\partial \varOmega ^-,\) where the Dirichlet and Robin conditions are stated, respectively

Full size image

2 Governing equations and integral transforms

With reference to Fig. 1, we are interested in a transient heat problem in two spatial dimensions. The physical domain of interest occupies the half-space \(\varOmega =\{(x,y):0\le x<\infty ,-\infty<y<\infty \}.\) The governing equation for the temperature field T(x, y, t) in a medium with transversely isotropic thermal conductivity is given by

$$\begin{aligned} \begin{aligned} \frac{\kappa }{\rho c_\mathrm{V}}\left( \frac{\partial ^2 T}{\partial x^2}+\ell \frac{\partial ^2 T}{\partial y^2}\right) =\frac{\partial T}{\partial t}, \quad 0<x<\infty ,\quad -\infty<y<\infty ,\quad t>0, \end{aligned} \end{aligned}$$
(1)

where \(\kappa \) and \(\kappa \ell \) are the thermal conductivities in the x and y directions, respectively, where \(\ell >0\) is a non-dimensional constant, \(c_\mathrm{V}\) is the specific heat at constant volume, \(\rho \) is the mass density of the medium, and t is the time. Thanks to the specific type of the material anisotropy (a transverse anisotropy), one may perform a simple non-dimensionalisation, which also scales out the anisotropy coefficient \(\ell \) by introducing the following non-dimensional variables:

$$\begin{aligned} x^*=x,\quad y^*=\frac{y}{\sqrt{\ell }},\quad t^*=\rho c_\mathrm{V}\frac{t}{\kappa },\quad T^*=\frac{T-T_\mathrm{r}}{T_\mathrm{r}}, \end{aligned}$$
(2)

noting that we have introduced the reference temperature \(T_\mathrm{r}.\) Upon dropping asterisks the non-dimensional heat equation can then be written

$$\begin{aligned} \nabla ^2T=\frac{\partial T}{\partial t}, \end{aligned}$$
(3)

where the two-dimensional Laplacian differential operator is defined as \(\nabla ^2=\partial ^2/\partial x^2+\partial ^2/\partial y^2.\) We introduce the homogeneous initial condition

$$\begin{aligned} T(x,y,0)=0, \end{aligned}$$
(4)

and mixed boundary conditions are imposed in the form

$$\begin{aligned} \begin{aligned}&T|_{\partial \varOmega ^+}=T(x=0,y>0,t>0)=T_0f(t),\\&\varTheta |_{\partial \varOmega ^-}=\varTheta (x=0,y<0,t>0)=\varTheta _\mathrm{i}F(t), \end{aligned} \end{aligned}$$
(5)

where we have introduced the notation

$$\begin{aligned} \varTheta (x,y,t)=T(x,y,t)-h\frac{\partial T}{\partial x}(x,y,t), \end{aligned}$$
(6)

which is convenient for the convective boundary condition imposed. In the above \(T_0,\)\(\varTheta _\mathrm{i}\) and h are constants. Functions f(t) and F(t) are piecewise continuous and describe the time evolution of prescribed values of boundary conditions. The temperature \(T_0\) defines the magnitude of the applied temperature on \(\partial \varOmega ^+\) and the parameter \(\varTheta _\mathrm{i}\) is the specified internal temperature. Finally h is a positive quantity, determined experimentally, and depending on the type of “insulation” placed on \(x=0.\)

In the present case, we assume that there is no radiation source located at the remote point \(x\rightarrow \infty .\) Therefore, we search for the solution with the following condition:

$$\begin{aligned} T(x,y,t)\rightarrow 0,\quad \frac{\partial T}{\partial x}(x,y,t)\rightarrow 0,\quad \frac{\partial T}{\partial y}(x,y,t)\rightarrow 0\quad \text {as } x\rightarrow \infty . \end{aligned}$$
(7)

The first boundary condition in (5) is referred to as the Dirichlet boundary condition while the second of (5) is the Robin (convective) boundary condition. Due to the change in boundary condition type imposed along \(x=0,\) the solution of the problem is not straightforward and requires the utilisation of the Wiener–Hopf technique [12]. The closely related transient heat problem with Dirichlet and Neumann boundary conditions has been studied in [13] where it was shown that, via the Cagniard–de Hoop technique [14], it is possible to transform the final form of the solution into a single integral that is extremely fast to compute since its contour of integration is a path of steepest descent in the complex plane. The Cagniard–de Hoop method can also be successfully used in other transient diffusion problems and exact results can be obtained for specific settings. For example, this is the case for electromagnetic diffusion between two contacting media [15]. However, due to the specific type of boundary condition imposed in the present study, such a simplification is not possible, as we will illustrate. On the other hand, the convective type of boundary condition considered here produces different results for the temperature distribution and can be used in more realistic modelling of physical thermal processes. Potential applications are discussed in Sect. 6.

We proceed to determine the solution of the problem by means of integral transforms. In this regard, it is convenient to define notation for the Laplace transform in t and Fourier transform in y to an arbitrary function \(\phi =\phi (x,y,t).\) Throughout the current study we write

$$\begin{aligned} \tilde{\phi }(x,y,s)=\int _{0}^{\infty }\phi (x,y,t)\exp {(-st)}\,\text {d}t \end{aligned}$$
(8)

for the Laplace transform in t and

$$\begin{aligned} \hat{\phi }(x,p,s)=\int _{0}^{\infty }\left( \int _{-\infty }^{\infty }\phi (x,y,t)\exp {(\text {i}py)}\,\text {d}y\right) \exp {(-st)}\,\text {d}t \end{aligned}$$
(9)

for the combined Fourier transform in y and the Laplace transform in t,  where \(\text {i}^2=-1.\) Original function \(\phi (x,y,t)\) can be recovered through the inversion of both transforms

$$\begin{aligned} \phi (x,y,t)=\frac{1}{(2\pi )^2\text {i}}\int _{a-\text {i}\infty }^{a+\text {i}\infty } \left( \int _{-\infty }^{\infty }\hat{\phi }(x,p,s)\exp {(-\text {i}py)}\,\text {d}p\right) \exp {(st)}\,\text {d}s, \end{aligned}$$
(10)

where a is a real number so that the contour path of integration is in the region of convergence of \(\tilde{\phi }(x,y,s).\)

The application of the Laplace (in t) and Fourier (in y) transforms to both sides of Eq. (3) reduces the problem to an ordinary differential equation, i.e.

$$\begin{aligned} \left[ \frac{\text {d}^2}{\text {d}x^2}-(p^2+s)\right] \hat{T}(x,p,s)=0. \end{aligned}$$
(11)

Applying the transforms to the boundary conditions (5), they become

$$\begin{aligned} \begin{aligned} \hat{T}^+(0,p,s)=\frac{\text {i}T_0}{(p+\text {i}\epsilon )}\tilde{f}(s),\quad \hat{\varTheta }^-(0,p,s)=-\frac{\text {i}\varTheta _\mathrm{i}}{(p-\text {i}\epsilon )}\tilde{F}(s). \end{aligned} \end{aligned}$$
(12)

The transforms \(\hat{T}^+(0,p,s)\) and \(\hat{\varTheta }^-(0,p,s)\) result from the half-range Fourier transforms along \(y>0\) and \(y<0,\) respectively. Note that we have added the small imaginary part \(\epsilon >0\) to p in order to ensure convergence of the integrals at infinity, i.e. the convergence of the Fourier transforms of the Heaviside functions arising from the step-wise change in boundary conditions. It is in fact possible to justify this step rigorously and we refer the reader to [13] for a detailed explanation. In this analysis, superscripts “\(+\)” and “−” indicate functions that are analytic in domains of the complex variable p where its imaginary parts \(\mathfrak {I}(p)>-\epsilon \) and \(\mathfrak {I}(p)<\epsilon ,\) respectively. The solution of the original problem is recovered by taking the limit \(\epsilon \rightarrow 0.\)

Appealing to the physics, we seek the solution that decays at infinity. Thus, the solution of (11) that admits this condition can be written as

$$\begin{aligned} \hat{T}(x,p,s)=A(p,s)\exp {\left( -x\sqrt{p^2+s}\right) }, \end{aligned}$$
(13)

where the value of the complex square root is chosen in such a way that the real part of the square root \(\mathfrak {R}(\sqrt{p^2+s})\ge 0,\) so that the solution vanishes as \(x\rightarrow \infty .\) Imposing the transformed boundary conditions (12) then permits the determination of the coefficient A(p, s) and thus the final form of the solution as we will illustrate in the next section.

3 Boundary conditions and a Wiener–Hopf equation

Let us introduce \(\varPhi ^-(p,s)\) and \(\varPsi ^+(p,s)\) as follows:

$$\begin{aligned} \varPhi ^-(p,s)=\hat{T}^-(0,p,s),\quad \varPsi ^+(p,s)=\hat{\varTheta }^+(0,p,s). \end{aligned}$$
(14)

From the boundary conditions (12), together with the form of the solution of the problem in (13) and the functions introduced in (14), the following system of equations is obtained:

$$\begin{aligned} \hat{T}^+(0,p,s)+\varPhi ^-(p,s)=A(p,s),\quad \hat{\varTheta }^-(0,p,s)+\varPsi ^+(p,s)=A(p,s)K(p,s), \end{aligned}$$
(15)

where we have introduced the kernel function of the problem

$$\begin{aligned} K(p,s)=1+h\sqrt{p^2+s}. \end{aligned}$$
(16)

Once the functions \(\varPhi ^-(p,s)\) and \(\varPsi ^+(p,s)\) are determined, the desired factor A(p, s) is thus known.

To proceed, eliminate the function A(p, s) from the system (15) to arrive at the Wiener–Hopf equation

$$\begin{aligned} \hat{\varTheta }^-(0,p,s)+\varPsi ^+(p,s)=K(p,s)(\hat{T}^+(0,p,s)+\varPhi ^-(p,s)). \end{aligned}$$
(17)

Further application of the Wiener–Hopf technique requires the multiplicative factorisation of the kernel function in the form

$$\begin{aligned} K(p,s)=K^+(p,s)K^-(p,s). \end{aligned}$$
(18)

Note that \(K(p,s)=hp+O(p^{-1})\) as \(p\rightarrow \infty \) and \(K(p,s)=1+h\sqrt{s}+O(p^2)\) in the neighbourhood of \(p=0.\) Thus, we write the function K(p, s) in the form

$$\begin{aligned} K(p,s)=k(p,s)K_0(p,s),\quad k(p,s)=\sqrt{(hp)^2+(1+h\sqrt{s})^2}. \end{aligned}$$
(19)

It is important to note that \(K_0(p,s)\rightarrow 1\) as \(p\rightarrow \infty \) and \(K_0(0,s)=1.\) These properties and the fact that \(K_0(p,s)\) has zero index (winding number) permits its multiplicative factorisation by employing the Cauchy integral [12, Sect. 1.3]. The final factorisation of K(p, s) therefore becomes

$$\begin{aligned} \begin{aligned}&K^{\pm }(p,s)=k^{\pm }(p,s)K_0^{\pm }(p,s),\\&k^{\pm }=\sqrt{hp\pm \text {i}(1+h\sqrt{s})},\quad K_0^{\pm }(p,s)=\exp \left( \pm \frac{1}{2\pi \text {i}}\int _{-\infty }^{\infty }\frac{\text {Log}\,K_0(\xi ,s)}{(\xi -p)}\,\text {d}\xi \right) , \end{aligned} \end{aligned}$$
(20)

where \(\text {Log}\,\phi (p)=\log {|\phi (p)|}+\text {i}\arg \phi (p)\) is the complex logarithm of a complex function \(\phi (p).\) Also \(\log {|\phi (p)|}\) is the real-valued logarithm and \(\arg \phi (p)\) is the principal value of the argument. Among all the possible values of the argument of \(\phi (p),\) we choose its principal value defined as \(\arg \phi (p).\) One may recall the Plemelj formulæ [12, Sect. 1] which is applicable for the last integral

$$\begin{aligned} K_0^{\pm }(p,s)=\sqrt{K_0(p,s)}\exp \left( \pm \frac{1}{2\pi \mathrm{i}} P.V. \int _{-\infty }^{\infty }\frac{\text {Log}\,K_0(\xi ,s)}{(\xi -p)}\,\mathrm{d}\xi \right) ,\quad \mathfrak {I}{(p)}\rightarrow 0. \end{aligned}$$
(21)

In this expression, the notation \( P.V. \) refers to the Cauchy principal value integral. This expression is important for the inversion of the Fourier transform if the integration path passes along \(\mathfrak {I}{(p)}=0.\) With the determined factorisation of the kernel function, we arrive at the equation

$$\begin{aligned} \frac{1}{K^+(p,s)}\left( \hat{\varTheta }^-(0,p,s)+\varPsi ^+(p,s)\right) =K^-(p,s)(\hat{T}^+(0,p,s)+\varPhi ^-(p,s)). \end{aligned}$$
(22)

What remains is to sum split the known functions in (22) according to the form of the boundary conditions in (12). This leads to the following form for the known function: \(S(p,s)=S^+(p,s)+S^-(p,s),\) where

$$\begin{aligned} \begin{aligned} S^+(p,s)&=\hat{\varTheta }^-(0,p,s)\left( \frac{1}{K^+(p,s)}-\frac{1}{K^+(\text {i}\epsilon ,s)}\right) -\hat{T}^+(0,p,s)K^-(-\text {i}\epsilon ,s),\\ S^-(p,s)&=\hat{T}^+(0,p,s)\left( K^-(p,s)-K^-(-\text {i}\epsilon ,s)\right) -\hat{\varTheta }^-(0,p,s)\frac{1}{K^+(\text {i}\epsilon ,s)}. \end{aligned} \end{aligned}$$
(23)

These functions are obtained by the pole removal technique, and the components defining \(S^\pm (p,s)\) come from the imposed boundary conditions and factorised kernel function. The final form of the problem is then

$$\begin{aligned} \frac{\varPsi ^+(p,s)}{K^+(p,s)}+S^+(p,s)=K^-(p,s)\varPhi ^-(p,s)+S^-(p,s). \end{aligned}$$
(24)

The functions \(\varPsi ^+(p,s)\) and \(\varPhi ^-(p,s)\) should behave in such a way that the temperature field T(x, y, t) is continuous at the point \(y=0\) for any \(x\ge 0.\) With the help of the Abelian and Tauberian theorems, see, e.g. [12, Sect. 1.6] or [16, Appendix], this continuity condition can be reformulated in terms of the Fourier transforms. To be more precise, \(\varPsi ^+(p,s)\) and \(\varPhi ^-(p,s)\) should decay when \(p\rightarrow \infty .\) Hence, both left- and right-hand sides should vanish as \(|p|\rightarrow \infty .\) With the application of Liouville’s theorem [12, Sect. 1.2], we conclude that

$$\begin{aligned} \varPsi ^+(p,s)=-S^+(p,s)K^+(p,s),\quad \varPhi ^-(p,s)=-\frac{S^-(p,s)}{K^-(p,s)}. \end{aligned}$$
(25)

The last result completes the formal derivation of the solution in the transformed space. After taking the limit \(\epsilon \rightarrow 0\) for the calculation of \(K^\pm (\pm \text {i}\epsilon ,s)\) (equal to \(\sqrt{\pm \text {i}(1+h\sqrt{s})},\) respectively), the factor A(p, s) can be calculated from either of two formulæ,

$$\begin{aligned} \begin{aligned}&A=\left( \frac{\hat{\varTheta }^-(0,p,s)}{1+h\sqrt{s}}+\hat{T}^+(0,p,s)\right) \frac{\sqrt{-\text {i}(1+h\sqrt{s})}}{K^-(p,s)}, \quad \text {or} \quad \\&A=\left( \frac{\hat{\varTheta }^-(0,p,s)}{1+h\sqrt{s}}+\hat{T}^+(0,p,s)\right) \sqrt{-\text {i}(1+h\sqrt{s})}\frac{K^+(p,s)}{K(p,s)}. \end{aligned} \end{aligned}$$
(26)

Equations (13) and (26) lead to the final expressions for the temperature field in the transformed space. The evaluation of T(x, y, t) can be performed through numerical inversion of the Laplace and Fourier transforms of the function in (13). The utilised numerical methods are described in Sect. 4. The complementary computations by means of FEMs have been carried out by FreeFEM++ [17].

Before we proceed to the numerical calculation of the integrals in the next section, let us first make some comments on the asymptotic form of solutions close to the change in boundary condition. It is possible to estimate the asymptotic behaviour of the temperature field close to the origin if one recalls the Abelian and Tauberian theorems which establish relations between the asymptotics of functions and their transforms. From (13) and (15), the behaviour of the transform of the temperature at \(x=0\) is

$$\begin{aligned} \begin{aligned} \hat{T}(0,p,s)&=\frac{\text {i} T_0\tilde{f}(s)}{p}+\left( \left[ \frac{\varTheta _\mathrm{i}\tilde{F}(s)}{1+h\sqrt{s}} -T_0\tilde{f}(s)\right] \frac{\exp \left( {-\text {i}\frac{3\pi }{4}}\right) \sqrt{1+h\sqrt{s}}}{\sqrt{h}}\frac{1}{p^{3/2}}\frac{\mathrm{i}T_0\tilde{f}(s)}{p}\right) +O\left( \frac{1}{p^{5/2}}\right) ,\quad |p|\rightarrow \infty . \end{aligned} \end{aligned}$$
(27)

In order to obtain this expression, one should express \(\hat{T}(0,p,s)\) as a sum of “\(+\)” and “−” functions. Given this, the first term in the last expression corresponds to expansion of the “\(+\)” function, whereas the remaining term corresponds to the “−” function when \(|p|\rightarrow \infty .\) The behaviour of the Laplace transform of the temperature field when \(y\rightarrow 0\) is

$$\begin{aligned} \begin{aligned} \tilde{T}(0,y,s)&=T_0\tilde{f}(s)H(y)+\left[ \frac{2}{\sqrt{h\pi }}\left( \frac{\varTheta _\mathrm{i}\tilde{F}(s)}{\sqrt{1+h\sqrt{s}}}-T_0\tilde{f}(s)\sqrt{1+h\sqrt{s}}\right) \sqrt{-y}\right. \\&\quad +\left. T_0\tilde{f}(s)+O\left( (-y)^{3/2}\right) \right] H(-y), \end{aligned} \end{aligned}$$
(28)

where H(y) is the Heaviside step function. One can see that even though the behaviour of the solution close to \(x=0\) and \(y=0\) is continuous, its derivative, i.e. the heat flux, is not. The following section is devoted to an explanation of the numerical evaluation of the integral transforms.

4 Numerical evaluation of the integral transforms

In this section, we define the strategy for calculation of the integral transforms in order to recover the solution in the physical domain. We are interested in computing the following integrals (10). In the implementation of numerical algorithms, the parameter s of the Laplace transform should take complex values which improve the convergence, while p can be chosen to be real valued.

We should mention that we solve the problem for a particular type of kernel function for which the inversion of transforms is applied. The integration can be significantly accelerated if the following properties of the following functions (for real values of p) are taken into account:

$$\begin{aligned} \begin{aligned}&k(p,s)=k(-p,s),\quad K_0(p,s)=K_0(-p,s),\quad K(p,s)=K(-p,s),\\&k^+(-p,s)=\text {i} k^-(p,s),\quad K_0^+(-p,s)=K_0^-(p,s),\quad K^+(-p,s)=\text {i} K^-(p,s),\\&\hat{T}^+(0,p,s)=-\hat{T}^+(0,-p,s),\quad \hat{\varTheta }^-(p,s)=-\hat{\varTheta }^-(-p,s),\quad \epsilon \rightarrow 0. \end{aligned} \end{aligned}$$
(29)

We conclude that

$$\begin{aligned} A(-p,s)=-\text {i} A(p,s)\frac{K^-(p,s)}{K^+(p,s)}. \end{aligned}$$
(30)

Given these properties, it is possible to decrease the number of function evaluations at points p,  i.e. it is enough to evaluate functions for positive p only and then utilise these properties to construct values for negative p. In addition, one may notice that there is a singularity at \(p=0\) of the function A(p, s) which causes problems in the calculation of the integral transform since the function values become unbounded in the close neighbourhood of this point. To overcome this, (13) can be written as

$$\begin{aligned} \begin{aligned} \hat{T}(p,s)&=\left[ A(p,s)\exp {\left( -x\sqrt{p^2+s}\right) }-\left( \frac{\hat{\varTheta }^-(0,p,s)}{1+h\sqrt{s}}+\hat{T}^+(0,p,s)\right) \right. \\&\quad \left. \times \exp {\left( -(|p|+\sqrt{s})x\right) }\right] +\left( \frac{\hat{\varTheta }^-(0,p,s)}{1+h\sqrt{s}}+\hat{T}^+(0,p,s)\right) \exp {\left( -(|p|+\sqrt{s})x\right) }, \end{aligned} \end{aligned}$$
(31)

where we subtract and add the same term, the second and the third in the last expression, to the original expression. In this case, the inverse integral of the last term can be calculated analytically, whereas the function composed of the first two terms does not possess singularity at \(p=0\) any more. We include the factor \(\exp (-|p|x)\) which preserves the fast decay of the function when \(x>0\) and, at the same time, it does not affect the subtracted singularity at \(p=0.\) Hence, the expression in the first square parenthesis does not have any singularities along the real axis of p, while the second expression can be calculated analytically and added to the final result. For that purpose, we employ convolutions, noting the following integrals:

$$\begin{aligned} \begin{aligned}&\frac{1}{2\pi }\int _{-\infty }^{\infty }\exp {\left( -|p|x-\text {i}py\right) }\,\text {d}p=\frac{x}{\pi }\frac{1}{(x^2+y^2)},\\&H(y)\,*\,\left( \frac{x}{\pi }\frac{1}{(x^2+y^2)}\right) =\frac{1}{\pi }\text {atan}\left( \frac{y}{x}\right) +\frac{1}{2},\\&H(-y)\,*\,\left( \frac{x}{\pi }\frac{1}{(x^2+y^2)}\right) =\frac{1}{2}-\frac{1}{\pi }\text {atan}\left( \frac{y}{x}\right) , \end{aligned} \end{aligned}$$
(32)

where symbol “\(*\)” stands for the convolution of the functions in y and \(\text {atan}(x)\) is the inverse tangent function. The inverse Fourier transform of the term on the second line of (31) can thus be evaluated analytically, and it takes the form

$$\begin{aligned} \begin{aligned}&\frac{1}{(2\pi )^2\text {i}}\int _{a-\text {i}\infty }^{a+\text {i}\infty } \int _{-\infty }^{\infty }\left( \frac{\hat{\varTheta }^-(0,p,s)}{1+h\sqrt{s}}+\hat{T}^+(0,p,s)\right) \exp {\left( -(|p|+\sqrt{s})x-\text {i}py+st\right) }\,\text {d}p\,\text {d}s\\&\quad = \frac{1}{2\pi \text {i}} \int _{a-\text {i}\infty }^{a+\text {i}\infty }\left( \frac{\varTheta _\mathrm{i}\tilde{F}(s)}{1+h\sqrt{s}}\left[ \frac{1}{2}- \frac{1}{\pi }\text {atan}\left( \frac{y}{x}\right) \right] H(-y)\right. \\&\qquad \left. +\,T_0\tilde{f}(s)\left[ \frac{1}{\pi }\text {atan}\left( \frac{y}{x}\right) +\frac{1}{2}\right] H(y)\right) \exp {\left( -\sqrt{s}x+st\right) }\,\text {d}s. \end{aligned} \end{aligned}$$
(33)

It therefore remains to perform the following inverse Laplace transform in (33), which can be done through convolution formulae numerically or analytically, depending on the form of the functions F(t) and f(t) that appear on the right hand side of the boundary conditions (5).

What remains is the evaluation of the term in the first line of (31). Inversion of Laplace transform depends on the form of the functions \(\tilde{F}(s)\) and \(\tilde{f}(s).\) Below, we describe numerical schemes that have been used for calculations of final results.

  1. (1)

    Inversion of the Fourier transform For inversion of the Fourier transform, the fast Fourier transform (FFT) can be used. This procedure is implemented in many codes and can be applied straightforwardly. In the present study, MATLAB software has been used to present all the numerical results.

  2. (2)

    Inversion of the Laplace transform The Laplace transform was evaluated through the convolution quadrature method which was implemented in MATLAB; the method is described in [18]. In summary, this method evaluates the convolution of two arbitrary functions \(\phi (t)\) and \(\psi (t)\)

    $$\begin{aligned} Q(t)=\int _0^{t}\phi (t-\tau )\psi (\tau )\,\text {d}\tau . \end{aligned}$$
    (34)

    Firstly, the time step \(\Delta t\) is chosen and the value of the integral at the point \(n\Delta t\) is computed as

    $$\begin{aligned} Q(n\Delta t)=\sum _{m=0}^{n}\omega _{n-m}(\Delta t)\psi (m\Delta t),\quad n=0,1,\ldots ,N. \end{aligned}$$
    (35)

    Coefficients \(\omega _n\) are computed through the values of the Laplace transform \(\tilde{\phi }(s)\) of the function \(\phi (t)\)

    $$\begin{aligned} \begin{aligned}&\omega _n(\Delta t)=\frac{R^{-N}}{N}\sum _{k=0}^{N-1}\tilde{\phi }\left( \frac{\gamma \left( R\exp {\left( \text {i}k\frac{2\pi }{N}\right) }\right) }{\Delta t}\right) \exp {\left( -\text {i}nk\frac{2\pi }{N}\right) },\\&\gamma (z)=\frac{3}{2}-2z+\frac{1}{2}z^2. \end{aligned} \end{aligned}$$
    (36)

    Due to the presence of the exponential factor in the definition of \(\omega _n,\) the FFT can be applied, thus rendering computational efficiency in time. If the values \(\tilde{\phi }(s)\) are calculated with an error bounded by \(\varepsilon ,\) then the choice \(R^{-N}=\sqrt{\varepsilon }\) yields an error in \(\omega _n\) of \(O(\sqrt{\varepsilon }).\) Additionally, this formula allows the calculation of \(\tilde{\phi }(s)\) regardless of the value of t. This is advantageous if the computation of the function itself is time consuming.

  3. (3)

    Numerical factorisation of\(K_0\)in (20) The integral in (20) is known as the Hilbert transform. The detailed procedure of its computational treatment is described in [19, Appendix A.1] where the time change is not taken into account. Here, we mention the strategy that we followed for its evaluation and specifically extended the algorithm for the transient problem of interest. First, note that for the integral in (20), s can be considered fixed, i.e. \(s=s_k.\) Moreover, for any value \(s_k,\) the function \(K_0(p,s_k)\) is an even function of p,  when p is real. Thus, we can reduce the integration to a semi-infinite line

    $$\begin{aligned} \int _{-\infty }^{\infty }\frac{\text {Log}K_0(\xi ,s_k)}{(\xi -p)}\,\text {d}\xi = 2p\int _{0}^{\infty }\frac{\log |K_0(\xi ,s_k)|+\text {i}\arg (K_0(\xi ,s_k))}{(\xi ^2-p^2)}\,\text {d}\xi . \end{aligned}$$
    (37)

    In the last formula, we used the fact that the functions \(\log |K_0(\xi ,s_k)|\) and \(\arg (K_0(\xi ,s_k))\) are even functions of p for the problem under consideration. Therefore, we need to calculate the last integral only along the semi-infinite line, which saves computational time. The principal problem with this integral is that it possesses a singularity at \(\xi =p\) apart from the singularities that the kernel function may contain in some cases. We estimate the asymptotic behaviour of the functions \(\log |K_0(\xi ,s_k)|\) and \(\arg (K_0(\xi ,s_k)).\) Then we divide the integration interval into two: one along the interval \([0,A_0],\) and the other along \((A_0,\infty ).\) For the tail of the integral, we substitute functions with their asymptotics and integrate the last analytically. Then we divide the finite interval \([0,A_0]\) into subintervals, and on each subinterval, we approximate \(\log |K_0(\xi ,s_k)|\) and \(\arg (K_0(\xi ,s_k))\) with splines, and then perform the integration analytically. All the intermediate results are summed, and the final result is thus achieved. The point \(A_0\) is chosen by checking the relative error between the approximated asymptotic expressions and the values of functions. It has been validated that the change in relative error \(10^{-1}\) was sufficient in order to obtain an appropriate accuracy of the computed values of \(K_0^{\pm }(p,s)\) and in order to keep the computational time low.

All the implemented codes have been tested on simpler cases before application to the problem under consideration. The demonstration of the efficiency of the factorisation algorithm is discussed in Appendix A. We present some examples of solutions to the present problem in the next section.

Fig. 2
figure 2

Comparison of analytical results with results from FEM simulations with \(T_0=\varTheta _\mathrm{i}=1\) and \(h=1\): a dependence of temperature T on y at point \(t=0.1\) and different points x,  and b time dependence of temperature T at different points

Full size image

5 Results

The developed quasi-analytical solution can be evaluated and visualised if one chooses particular values of the physical parameters and functions F(t) and f(t) involved in the problem. It is interesting to consider a case of suddenly applied temperature and heat exchange to a free surface. In other words, we take \(F(t)=f(t)=H(t),\) and their Laplace transforms are \(\tilde{F}(s)=\tilde{f}(s)=1/s.\) Firstly, we may estimate the asymptotics of the temperature field at the point \(x=0\) close to \(y=0\) using (28). Referring to the Tauberian theorem [20, Sect. XIII.5] we conclude that \(T(0,y,t)=O(t^{-1/4})\) when t tends zero and y approaches zero from the left. Hence, it possesses a weak singularity at the beginning of the heating process which influences the accuracy of the FEM solution. Such behaviour is a direct consequence of the high-rate loading type in the boundary conditions.

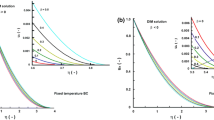
For this problem, in Fig. 2a, we have plotted the temperature as a function of y for two values of x,  at \(t=0.1,\) and we have illustrated the temporal dependence in Fig. 2b for specified spatial locations. We notice the rapid change of temperature profile close to a free surface, see Fig. 2a at the point \(x=0.05.\) On the other hand, the temperature T(x, y, t) possesses smaller gradients further away from the boundary. The rate of change of temperature with respect to time is much higher in the region where \(y<0\) which is, of course, dictated by the choice of the boundary conditions.

In the figures, we also determine the solution for this set-up and configuration with the FEM, the weak form of which is set out in Appendix B. This was implemented in FreeFEM++. As it is described in Appendix B we chose a rectangular domain for the FEM simulations with the sides \(a=5\) and \(b=10\) in order to avoid edge effects. We used regular grids in x and y directions with step sizes of \(\Delta x=0.01\) and \(\Delta y=0.02,\) respectively, and time step of \(\Delta t=0.01.\) The same steps are used for the evaluation of the integral transforms, and the number of interpolation points in y was chosen to be \(N=2500\) in order to have the same number of points as in the FEM simulations. The overall computation time required for the semi-analytical approach of the current work is 82 s. On the other hand, the FEM computations took 2171 s. The ratio between the two methods is close to 27 which is significant when the evaluation is repeated a large number of times.

Unfortunately, there is no analytical solution for the problem of interest for estimation of errors of the presented approaches. We would like to stress that the presented semi-analytical approach allows one to obtain the solution in a way alternative to the FEM method. The solution to model problems similar to the considered one in (semi-)infinite domains can be obtained more efficiently with the Wiener–Hopf method, although it does require intermediate steps.

Fig. 3
figure 3

Colour maps of the temperature field, computed from the analytical expressions for \(T_0=\varTheta _\mathrm{i}=1\) and \(h=1\): a at \(t=0.01,\) and b at \(t=0.5.\) The colour bars present the normalised temperature values \(T(x,y,t)/T_0\). (Color figure online)

Full size image

We present heat maps of the temperature field in Fig. 3 at two different moments of time. Figure 3a shows the early stage of heat propagation whereas Fig. 3b depicts a time when the heat has already advanced inside the medium. We present normalised heat maps. One can notice the contour lines become smoother when they advance inside the solid.

Other forms of F(t) and f(t) lead to expressions that can be evaluated analogously.

6 Potential applications of the model

The considered transient problem and its analogues together with the quasi-analytical solution form can play an important role in the analysis of various thermal phenomena. In particular, it can be exceptionally useful in applications where edge effects influence convection processes. We shall now present two examples of potential applications of this theory and describe the manner in which the theory can be adapted in order to tackle these problems.

6.1 Electrochemical measurements by ultramicroelectrodes

A common task performed by electrochemists is the prediction of the time-dependence of the concentration of an electroactive species at an electrode during some electrochemical experiment in which transport is dominated by diffusion. Decreasing the size of the electrodes, for which the name ultramicroelectrodes has been coined, brings advantages for studying electrode reactions at small spatial and temporal scales. It is possible to perform dynamic measurements in some poorly conductive media and obtain results that were not available before. Microelectrodes allow one to carry out much more straightforward measurements of rapid homogeneous and heterogeneous reactions with electrodes. A review paper [21] presents basic principles and results on this topic. The process can be stated as follows. When an electrode is introduced into an electroactive substance, the electron transfer between them is initiated. At the same time the concentrations at the electrode surface starts to change which causes the mass transfer to and from the electrode.

Fig. 4
figure 4

a Diffusive mass process in electrochemical cells and b typical geometries of ultramicroelectrodes

Full size image

The configuration that defines the problem is presented on Fig. 4a. There are numerous geometries of the electrodes and the commonly used options are illustrated in Fig. 4b. The measurements of interest are greatly influenced by the edge effects where a change in charge exchange conditions takes place and, hence, the results of the present work can be of significant interest in this application. Here, we focus mainly on the mathematical aspects of this problem. The electron-transfer reaction can be formulated by a diffusion equation [21, 22], a non-dimensional form of which is written as

$$\begin{aligned} \begin{aligned}&\frac{\partial c}{\partial t}=\nabla ^2c,\quad (z,y)\in \mathbb {R}^2,\,x>0,\\&c=0,\quad t=0,\\&\frac{\partial c}{\partial x}\Big |_{\mathbb {R}^2\setminus \varOmega }=0,\quad \left( c-h\frac{\partial c}{\partial x}\right) \Big |_{\varOmega }=1,\quad x=0. \end{aligned} \end{aligned}$$
(38)

In the last equation, the function \(c=c(x,y,z,t)\) defines a diffusion field, and the reference frame (x, y, z) is shown in Fig. 4. The operator \(\nabla ^2\) should be taken in a three-dimensional space. The domain \(\varOmega ,\) marked in grey in Fig. 4, is occupied by the cross-section of an electrode and its extent depends on its geometry. Although the physical process is essentially different, the mathematical formulation remains the same as considered in the present study. The model analysed in the current study refers to the analysis of the effects that arise in the vicinity of the boundary \(\partial \varOmega \) and can be employed as a good approximation to the results in this area at early stages of the convection process during an electrode reaction. The problem as is formulated for the function c(x, y, z, t) possesses mixed boundary conditions that are different from the ones considered in the main part of this work. On the other hand, however, the developed formulae can be adjusted to suit to this electrochemical problem. In this regard, the kernel function becomes

$$\begin{aligned} K(p,s)=\frac{1+h\sqrt{p^2+s}}{\sqrt{p^2+s}}, \end{aligned}$$
(39)

for which the following preliminary factorisation can be expressed as

$$\begin{aligned} K(p,s)=k(p,s)K_0(p,s),\quad k(p,s)=\frac{\sqrt{(hp)^2+(1+h\sqrt{s})^2}}{\sqrt{p^2+s}}. \end{aligned}$$
(40)

The function k(p, s) can be easily factorised analytically, and the function \(K_0(p,s)\) is exactly the same as shown in our study above. To complete the model, the initial conditions should be taken into account. The derivation of the final solution remains almost unchanged.

Fig. 5
figure 5

Diffusion process for electrode reaction with \(h=1\): a concentration of electroactive substance at two points close to the boundary and b concentration field at \(t=0.5\)

Full size image

To adapt the results presented previously, we suppose that the diffusion process is independent of z coordinate and \(\varOmega =\{(x,y):0\le x<\infty ,-\infty<y<\infty \}.\) The zero flux condition is imposed for \(y>0,\,x=0,\) whereas the Robin condition is set for \(y<0,\,x=0.\) The results for this particular problem are shown in Fig. 5 with \(h=1.\) One can see that diffusion of this process happens slower than the heat propagation in studied in Fig. 5. The reason for this comes directly from the different types of boundary conditions. Nonetheless, the mixed boundary conditions at \(x=0\) still reveal high gradients of diffusion field at point \(y=0\) of the boundary. Thus, this region should be carefully taken into account when electrode reactions are analysed.

6.2 Green roofs as a cooling system

A second application refers to the area of civil engineering and the associated design of cooling systems. During warm seasons and in specific regions with hot weather, there are a variety of mechanisms to ensure that the temperatures inside buildings remain cool. A common technique is to utilise electrical cooling systems, which are very efficient when the exterior temperature is very high. However, in areas with a lack of access to electricity, alternative solutions are required. Amongst them, natural cooling techniques can be employed, and in particular green roofs, which are able to provide a desirable protection from heating [23, 24]. Soil with growing vegetation protects a roof from the direct solar radiation and evaporation process and therefore enhances the cooling of a building. In addition, this method is also eco-friendly and, thus, is highly preferable to electrical cooling systems.

Green roofs therefore provide a potentially exceptional solution for cooling systems. Nevertheless, the investigation of the capacity for such techniques is still in question. For this reason, many studies are aimed at solving heat-transfer problems associated with buildings with roofs covered by layers of vegetation [23, 24]. It should be mentioned that these layers bring extra load on roofs. Thus, it can be more advantageous to cover roofs only partially as shown in Fig. 6, which will not impose extra load on the roof and at the same time the building will remain cool inside. In this case, the model presented in the study above can be directly applied to study the temperature distribution if all model parameters are known, together with the time-dependent functions f(t) and F(t) and initial conditions.

Fig. 6
figure 6

A simplified model of a cooling system for a building partially covered with a green roof

Full size image

For illustrative purposes, we suppose that f(t) and F(t) are slowly varying functions of time which increase from 0 and approach to 1 at infinite times. This case corresponds to the slow increase of outside temperature from zero to its final steady-state value. One may set \(f(t)=F(t)=\tan ^{-1}(t),\) the inverse tangent function, as it corresponds to the desired behaviour. One can see in Fig. 7 that temperature slowly grows inside the building. However, the vegetation level prevents its rapid growth and provides the required cooling effect.

Fig. 7
figure 7

Temperature propagation inside the building for \(h=1\): a temperature at two points close to the boundary and b temperature field at \(t=0.5\)

Full size image

This problem can be extended if the temperature field of a vegetation layer is considered as time dependent. Indeed, due to chemical reactions and the evaporation process, the temperature of the green roof may change. In this case, the mathematical treatment becomes more complicated but, on the other hand, it can be possible to achieve a more precise description of the convection process.

7 Conclusion and future work

The present work demonstrates the significant features of solutions of transient heat problems in a two-dimensional half-space when the boundary condition type is discontinuous. Heat propagation is initiated by an applied temperature on one half of the free boundary whilst a convective boundary condition is imposed on the remaining part of the boundary. This type of problem requires special mathematical techniques for its solution. Specifically, the Wiener–Hopf method has been used and the final expressions for the solutions were derived in integral form. It transpires that for this problem it is impossible to obtain the explicit analytical expression for the solution. In this regard, we selected numerical procedures suitable for the evaluation of the solution and successfully implemented them into computer codes. The algorithms can be applied and adopted for different problems involving the Wiener–Hopf technique. The results were demonstrated for the case of step-change boundary conditions. We also performed complementary FEM analysis of the problem for comparison and verification of the quasi-analytical results. We subsequently described some practical problems, to which aspects of this analysis apply.

The considered problem supplements the results of [13] where more specific inhomogeneous Dirichlet or Neumann boundary conditions were chosen. Future plans involve the consideration of dynamic problems in thermoelasticity. In this problem, the coupling between thermal and elastic fields is often weak, and therefore the problem decouples into solving a decoupled heat equation and the problem of elasticity with external forces induced by the temperature field that arises from the solution to the heat equation. The transient temperature field induces thermal stresses [25] and the evaluation of the solution with mixed boundary conditions can be helpful in the subsequent stress analysis. In this case, the solution for the values of the temperature field are provided by results of the present work and can then be used for the solution of the equations of motion for the solid. Note that there is a similarity between the equations of thermoelasticity and poroelasticity [26]. For the latter problem, coupling becomes essential, and the two physical problems should be treated simultaneously. Hence, the problem becomes even more complicated from a mathematical point of view and can be reduced to a matrix Wiener–Hopf problem. The factorisation procedure for a matrix problem turns out to be sophisticated and may require different approach to solve. However, the algorithms employed in the present study can be adapted for the factorisation of matrix components and thus can, eventually, allow a study of the effects of interplay between different physical processes.