Integral solutions to transient nonlinear heat (mass) diffusion with a power-law diffusivity: a semi-infinite medium with fixed boundary conditions

Abstract

Closed form approximate solutions to nonlinear heat (mass) diffusion equation with power-law nonlinearity of the thermal (mass) diffusivity have been developed by the integral-balance method avoiding the commonly used linearization by the Kirchhoff transformation. The main improvement of the solution is based on the double-integration technique and a new approach to the space derivative. Solutions to Dirichlet and Neumann boundary condition problems have been developed and benchmarked against exact numerical and approximate analytical solutions available in the literature.

1 Introduction

The present analysis focuses the attention on problems with temperature (concentration)-dependent thermal (mass) diffusivities modelled by the diffusion equation

$$\rho C_{p} \frac{\partial T}{\partial t} = \frac{\partial }{\partial x}\left( {k\left( T \right)\frac{\partial T}{\partial x}} \right)$$

(1a)

$$\frac{\partial T}{\partial t} = \frac{\partial }{\partial x}\left( {a\left( T \right)\frac{\partial T}{\partial x}} \right)$$

(1b)

The temperature (concentration)-dependent diffusivity can be expressed by a scaled power-law relationship a = a ₀(T/T _ref )^m, m > 0, which is related to temperature-dependent thermal conductivity k = k ₀(T/T _ref )^m assuming the product ρC _p temperature-independent when heat conduction is modelled.

Problems of heat conduction (mass diffusion) in media with constant properties m = 0 expiring sudden changes of the temperature (concentration) or the flux at the boundaries have been widely analyzed in the literature. They will not be analyzed in this work, but only those of them relevant to method of solutions will be commented as sources of reference results.

This model (1a, 1b), in contrast to the linear diffusion equation (m = 0), is uniformly parabolic in any region where T is not zero, but degenerates in the vicinity of any point where T = 0 [2]. The main performance of this degeneracy is that any disturbances propagate at finite speed giving rise to a front or interface in the solution. Therefore, due to the non-linearity of thermal-diffusivity there exist solutions with well-defined front separating the disturbed (T ≠ 0) and the undisturbed medium [3, 4].

It is worthy to note that despite the fact that the problem (1) at issue is defined as a transient heat conduction there are many physical process described by model (1a). Power-law diffusivities and leading to sharp front solutions of (1a) are commonly observed in creeping flows [5, 6], non-linear heat conductivity [7, 8], diffusion with a concentration-dependent diffusivity coefficient (with m varying from 1 to 10) [2, 9], etc. In this context, the second-order equations with m = 2 is known as the porous media equation modelling of gas-filtration in porous media [10–12]. For m = 3 the model is relevant to the process of isolation oxidation of silicon [13] and the lubrication theory approximation [5]. With m = 1 we have the Boussinesq equation [14] or a nonlinear reaction–diffusion equation [15]. Many problems defined with various positive integer values of mare analyzed in [3, 6, 16] and the references therein.

1.1 Solution approaches

The difficulties inherent in obtaining solutions for this class of equations have motivated a variety of solution methods, both exact and approximate ones. There exist several approaches to solve Eq. (1a), among them:

• Waiting-time solutions [6, 14, 17] describing evolution of u(x) behind a front at a fixed position during a finite waiting time t _w .

• Asymptotic methods [11, 13].

• Similarity solutions [1, 4, 13, 18, 19] using the Boltzmann similarity variable.

• Analytic methods, based on the moment approach, about solution close the front [2].

• The Kirchhoff transformation [20] $w = \int\limits_{0}^{T} {T^{m} } dT$ is the common approach to transform Eq. (1) into

  $$\frac{\partial w}{\partial t} = a_{0} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$

  (2)

The final solution may be developed either analytically or by numerical methods [8, 13, 21–25].

However, when the diffusion process is non-linear at the boundary, such the flux boundary condition problem (see further the boundary condition 4b) no exact analytical solutions exist and numerical or approximate analytical methods should be applied. The heat-balance integral method is among these approaches and it will be at issue in the further development of approximate closed form solutions reported in this work.

• Heat-balance integral approach. For accuracy of the literature background, Heat-balance integral approach (HBIM) to heat conduction with temperature-dependent diffusivity has been applied by Goodman [26] by a quasi-Kirchhoff transformation involving only the thermal properties at the surface x = 0.

All these problems has been solved for fixed boundary conditions (temperature or flux)

• HBIM has been recently applied to (1a) by initial transformations of the variables λ = T ^m and τ = t/m which allow Eq. (1a) to be expressed as [12]

  $$\frac{\partial \lambda }{\partial \tau } = a_{0} \left[ {\left( {\frac{\partial \lambda }{\partial x}} \right)^{2} + m\lambda \frac{{\partial^{2} \lambda }}{{\partial x^{2} }}} \right]$$

  (3)

The structure of Eq. (3) reveals that the time evolution of λ is a result of superposition of non-linear wave propagation (the first term in RHS) and a diffusion (the second term in RHS) [12]. The application of HBIM to (3) avoids the application of the Kirchhoff transformation, dominating as a solution approach in the literature. The solution of the case with Dirichlet boundary condition is available elsewhere [27] and some of it will be commented further in this article.

1.2 Background of the integral-balance solution

The heat-balance integral method (HBIM) of Goodman [26] suggests integration of Eq. (1) with respect to the space co-ordinate over a finite penetration depth δ with a prescribed approximate profile T _a . The integration, in accordance with HBIM yields

$$\frac{d}{dt}\int\limits_{0}^{\delta } {T\left( {x,t} \right)dx - T\left( {\delta ,t} \right)\frac{d\delta }{dt}} = \int\limits_{0}^{\delta } {a\frac{{\partial^{2} T}}{{\partial x^{2} }}} dx$$

(4a)

In case of a semi infinite medium the value of T(x, t) far away from the boundary x = 0 is assumed T(∞, t) = 0. The HBIM replaces this condition with two, namely

$$T\left( \delta \right) = 0\quad {\text{and}}\quad \frac{\partial T}{\partial x}\left( \delta \right) = 0$$

(4b, c)

The conditions (4b, c) define a sharp-front movement of the heat (or mass) penetrating by diffusion the undisturbed medium when an appropriate boundary condition at x = 0 is applied. The position of this front δ(t) is unknown and it should be determined as a part of the solution. After these assumption and imposed conditions, the integration of Eq. (1) yields

$$\frac{d}{dt}\int\limits_{0}^{\delta } {T\left( {x,t} \right)dx} = - a\frac{\partial T}{\partial x}\left( {0,t} \right)$$

(4d)

Then, replacing T by an assumed profile T _a , as parabolic one used in this work or a polynomial [26] an ordinary differential equation describing the time-evolution of δ(t) can be derived. The principle problem emerging in application of HBIM is the approximation of the gradient of right-side of (6) because it should be defined through the approximate profile. Improvement of the integral-balance method, avoiding this problem led to a double integration approach (DIM) [30] recently renewed by T. G. Myers as refined integral method (RIM) [31, 32].

The above mentioned problems and the relevant solutions have been developed to cases with constant diffusivities. The present article reports solutions for cases with power-law temperature (concentration)-dependent diffusivities developed by the HBIM and DIM avoiding the Kirchhoff transformation, commonly used in solutions of such problems.

1.3 Aim

The present article reports integral-balance solutions of the model (1a, 1b) in two cases: Dirichlet boundary condition and Neumann boundary condition avoiding the Kirchhoff linearization transformation. The solutions are based on HBIM and DIM. To the author’s knowledge, no research articles are available in the literature employing direct solutions of such non-linear problems by the integral-balance method.

2 Integral-balance method: solution strategies

2.1 Approximate profile and dimensionless equations

The solutions envisage applications of the heat-balance integral method (HBIM) [26] and its double-integration technique [30–32] by the following assumed parabolic profile with unspecified exponent [30–34]

$$T_{a} = T_{s} \left( {1 - x/\delta } \right)^{n}$$

(5)

The profile (5) satisfies the Goodman’s boundary conditions [26]

$$T\left( {0, t} \right) = T_{s} \quad or\quad k\left( {\frac{\partial T}{\partial x}} \right)_{x = 0} = q_{0}$$

(6a, b)

$$T\left( {\delta , t} \right) = T_{0} = 0 \, \quad or\quad k\left( {\frac{\partial T}{\partial x}} \right)_{x = \delta } = 0$$

(6c, d)

The scaled diffusivity in case of heat conduction is commonly expressed as a = a ₀(T/T _ref )^m where T _ref  = T ₀ is the initial medium temperature. Otherwise, when a mass diffusion is modelled, the diffusivity should be scaled to the surface concentration C _s , i.e. D = D ₀(C/C _s )^m, since the initial concentration C ₀ in the medium is zero. In this context, the case of thermal diffusivity with T _ref  = T ₀ ≠ 0 can be rescaled as a _eff u ^m = a ₀ k _T (T/T _s )^m where k _T  = (T _s /T ₀)^m = const. and a _eff  = a ₀ k _T .

Therefore, introducing the dimensionless variable u = (T − T ₀)/(T _s  − T ₀) which reduces to u = T/T _s when T ₀ = 0, we get the following approximate profile

$$u_{a} = u_{s} \left( {1 - x/\delta } \right)^{n}$$

(7)

Hereafter, for seek of simplicity and clarity in the problem development we will use the dimensionless formulation (6a) of the governing Eq. (1), namely

$$\frac{\partial u}{\partial t} = \frac{\partial }{\partial x}\left( {a_{0} u^{m} \frac{\partial u}{\partial x}} \right)$$

(8a)

Further, for fixed temperature (concentration) boundary condition

$$u\left( {0,t} \right) = u_{s} = 1$$

(8b)

For fixed flux boundary condition

$$- k\left( u \right)\left( {\frac{\partial u}{\partial x}} \right)_{x = 0} = q_{0}$$

(8c)

The Goodman’s’ boundary conditions read

$$u\left( {\delta , t} \right) = u_{0} = 0\quad {\text{or}}\quad k\left( {\frac{\partial u}{\partial x}} \right)_{x = \delta } = 0$$

(9a, b)

2.2 Integration techniques: steps and refinements relevant to the non-linear problem

2.2.1 Heat-balance integral method (HBIM)

The classical HBIM considers integration over the penetration depth δ(t) as it is described by Eq. (4a)

$$\int\limits_{0}^{\delta } {\frac{\partial u}{\partial t}} dx = \int\limits_{0}^{\delta } {\frac{\partial }{\partial x}\left( {a_{0} u^{m} \frac{\partial u}{\partial x}} \right)} \,dx$$

(10a)

$$\int\limits_{0}^{\delta } {\frac{\partial u}{\partial t}} dx = - \left( {a_{0} u^{m} \frac{\partial u}{\partial x}} \right)_{x = 0}^{{}}$$

(10b)

Equation (10b) is the principle equation of HBIM for either constant or nonlinear diffusivity. The main problem emerging in its application is that the product of the surface temperature and the gradient at x = 0 should be evaluated through the approximate profile. However, we may present the temperature gradient in (10a) as u ^m[∂u(x,t)/∂x] = [∂u ^m+1(x,t)/∂x]/(m + 1). Then, the integration in (10b) yields

$$\int\limits_{0}^{\delta } {\frac{\partial u}{\partial t}} dx = - \left( {\frac{{a_{0} }}{m + 1}\frac{{\partial u^{m + 1} }}{\partial x}} \right)_{x = 0}^{{}}$$

(11)

This modification of the method, conceived here, allows solving non-linear heat conduction equations and it will be tested in the examples developed next, even though the problem with the determination of the gradient at the boundary still remains.

2.2.2 Double-integration method

The first step of the double integration approach is integration of (8a) from 0 to x, namely

$$\int\limits_{0}^{x} {\frac{\partial u}{\partial t}} dx = \int\limits_{0}^{x} {\frac{\partial }{\partial x}\left( {a_{0} u^{m} \frac{\partial u}{\partial x}} \right)} \,dx \Rightarrow \int\limits_{0}^{x} {\frac{\partial u}{\partial t}} dx = a_{0} u^{m} \frac{\partial u}{\partial x} - a_{0} u^{m} \left( {0,t} \right)\frac{{\partial u\left( {0,t} \right)}}{\partial x}$$

(12a, b)

The second integration step is from 0 to δ of (12b), namely

$$\int\limits_{0}^{\delta } {\left( {\int\limits_{0}^{x} {\frac{\partial u}{\partial t}} dx} \right)\,} dx = a_{0} \int\limits_{0}^{\delta } {u^{m} \frac{{\partial u\left( {x,t} \right)}}{\partial x}} dx - \left[ {a_{0} u^{m} \left( {0,t} \right)\frac{{\partial u\left( {0,t} \right)}}{\partial x}} \right]\delta$$

(13)

The last term in (12b) is a constant with respect to x. Then, last term in (13) is a constant (with respect to x) multiplied by δ. Further, taking into account that that right-hand side of (10b) and the last term of (13) are equal, as well integrating by parts the double integral of (13) we have

$$\frac{d}{dt}\int\limits_{0}^{\delta } {xu\,} dx = - a_{0} \int\limits_{0}^{\delta } {u^{m} \frac{{\partial u\left( {x,t} \right)}}{\partial x}} dx$$

(14)

When the thermal diffusivity is constant, we have $\frac{d}{dt}\int\limits_{0}^{\delta } {xu\,} dx = a_{0} u\left( {0,t} \right)$ [31, 32].

To overcome the integration problem, emerging when the thermal diffusivity depends on the temperature we may apply the transformation resulting in Eq. (11). Then, the right-hand side of (14) reads as: $- a_{0} \int\limits_{0}^{\delta } {u^{m} \frac{{\partial u\left( {x,t} \right)}}{\partial x}} dx = \frac{{a_{0} }}{m + 1}u^{m + 1} \left( {0,t} \right)$. With this step, Eq. (14) reads

$$\frac{d}{dt}\int\limits_{0}^{\delta } {xu\,} dx = \frac{{a_{0} }}{m + 1}u^{m + 1} \left( {0,t} \right)$$

(15)

Equation (15) is the principle equation of the double integration approach when the diffusivity is temperature (concentration)-dependent (power-law). Hence, we have to mention, that the transformation u ^m[∂u(x, t)/∂x] = [∂u ^m+1(x, t)/∂x]/(m + 1) is the principle procedure step in the integration technique allowing applying the result (10b) known from a = a ₀ = const. to the case (14) inasmuch as the general idea of DIM predicted: to use the surface temperature at the right-side of the integral relation instead of the temperature gradient which depends on the structure of the assumed profile.

3 Results: solution examples

3.1 Example 1: fixed temperature as a boundary condition at x = 0

3.1.1 HBIM solution

The integration of (8a) with the boundary condition (8b) over the penetration depth and applying the assumed profile (7) with u(0, t) = u ^m+1(0, t) = 1 yields

$$\left( {\frac{{a_{0} }}{m + 1}\partial u^{m + 1} /\partial x} \right)_{x = 0} = a_{0} \left( {n/\delta } \right)$$

(16a)

$$\frac{d}{dt}\int\limits_{0}^{\delta } {u_{a} } dx = - a_{0} \frac{n}{\delta }$$

(16b)

Then, by the assumed profile (7) in left side of (16b) we get

$$\delta_{{T\left( {HBIM} \right)}} = \sqrt {a_{0} t} \sqrt {2n\left( {n + 1} \right)}$$

(17)

Therefore, with a fixed temperature problem and the transformation leading to (11) there is no refinement of the method, with respect to the classical HBIM, since the gradient is determined through the assumed profile again. Moreover, the non-linearity appearing in the equations through the exponent m disappears. Hence, the single-integration approach of HBIM is inapplicable to this type of non-linear problems when the model equation is (1a). To apply HBIM to the Dirichlet problem of the model (1), a transformation described by (3) should be done [27].

DIM solution

Applying Eq. (15) with u(0, t) = u ^m+1(0, t) = 1 we have

$$\frac{d}{dt}\int\limits_{0}^{\delta } {x\left( {1 - \frac{x}{\delta }} \right)\,} dx = \frac{{a_{0} }}{m + 1} \Rightarrow \frac{1}{{\left( {n + 1} \right)\left( {n + 2} \right)}}\frac{{d\delta^{2} }}{dt} = \frac{{a_{0} }}{m + 1}$$

(18a,b)

Then the penetration depth is

$$\delta_{{T\left( {DIM} \right)}} = \sqrt {a_{0} t} \sqrt {\frac{{\left( {n + 1} \right)\left( {n + 2} \right)}}{m + 1}} \quad {\text{or}}\quad \delta_{{T\left( {DIM} \right)}} = \sqrt {a_{0} t} F_{n,m} \,,\,\quad F_{n,m} = \sqrt {\frac{{\left( {n + 1} \right)\left( {n + 2} \right)}}{m + 1}}$$

(19a, b, c)

For m = 0 we have the linear case a = a ₀ and the result (19a) reduces to the solution developed by Myers [31, 32]. i.e., $\delta_{{T\left( {DIM} \right)\left( {m = 0} \right)}} = \sqrt {a_{0} t} \sqrt {\left( {n + 1} \right)\left( {n + 2} \right)}$.

Because m > 0, then from (19a) and (19b) we have δ _T(DIM) < δ _T(DIM)(m=0) as a direct manifestation of the front retardation with increase in the value of m. In this context, we have to refer to [35] where the diffusion processes with power-law diffusivity are classified as: slow diffusion with m > 0 and fast diffusion with m < 0.

3.1.2 Example2: fixed flux as a boundary condition at x = 0

The prescribed flux boundary condition is

$$- k\left( T \right)\left( {\frac{\partial T}{\partial x}} \right)_{x = 0} = q_{0}$$

(20a)

Applying the Goodman’s boundary conditions (9a, b) we have

$$T_{a} = T_{s} \left( {1 - \frac{x}{\delta }} \right)^{n}$$

(20b)

With the scaled heat conductivity k(T) = k ₀(T/T _ref )^m the boundary condition (18a) reads as

$$- \left( {k_{0} T^{m} \frac{\partial T}{\partial x}} \right)_{x = 0} = q_{0} T_{ref}^{m} = Q_{0}$$

(21a)

or

$$- \frac{{k_{0} }}{m + 1}\frac{\partial }{\partial x}T_{{}}^{m + 1} \left( {0,t} \right) = Q_{0} \Rightarrow \frac{\partial }{\partial x}T_{{}}^{m + 1} \left( {0,t} \right) = - \frac{{Q_{0} }}{{k_{0} }}\left( {m + 1} \right)$$

(21b, c)

From the assumed profile (20b) we have

$$\left( {T_{a} } \right)^{m + 1} = T_{s}^{m + 1} \left( {1 - \frac{x}{\delta }} \right)^{{n\left( {m + 1} \right)}} \Rightarrow \frac{\partial }{\partial x}T_{{}}^{m + 1} \left( {0,t} \right) = - T_{{}}^{m + 1} \left( {0,t} \right)\frac{{n\left( {m + 1} \right)}}{\delta }$$

(21a, b)

Therefore, combining (21c) and (21b) the surface temperature reads

$$T_{a}^{m + 1} \left( {0,t} \right) = \frac{{Q_{0} }}{{k_{0} }}\frac{\delta }{n} \Rightarrow T_{a} \left( {0,t} \right) = \left( {\frac{{Q_{0} }}{{k_{0} }}\frac{\delta }{n}} \right)^{{\frac{1}{m + 1}}}$$

(22)

With θ _a  = T _a /(Q ₀/k ₀)^1/(m+1) (we use the symbol θ to distinguish the solution form that of Example 1) the profile (18b) reads

$$\theta_{a} = \left( {\frac{\delta }{n}} \right)^{{\frac{1}{m + 1}}} \left( {1 - \frac{x}{\delta }} \right)^{n}$$

(23)

HBIM solution

The application of the HBIM Eq. (11) with the profile (23) reads

$$\frac{d}{dt}\int\limits_{0}^{\delta } {\left( {\frac{\delta }{n}} \right)^{{\frac{1}{m + 1}}} \left( {1 - \frac{x}{\delta }} \right)^{n} } dx = a_{0}$$

(24a)

Then the penetration depth is

$$\delta_{{q\left( {HBIM} \right)\left( {m > 0} \right)}} = \left( {a_{0} t} \right)^{{\frac{m + 1}{m + 2}}} n^{{\frac{1}{m + 2}}} \left( {n + 1} \right)^{{\frac{m + 1}{m + 2}}}$$

(24b)

For m = 0 we have the classical HBIM solution

$$\delta_{{q\left( {HBIM} \right)\left( {m = 0} \right)}} = \sqrt {a_{0} t} \sqrt {n\left( {n + 1} \right)}$$

(24c)

Obviously, in the case of a prescribed flux at x = 0 and m > 0 the classical square-root behavior of the penetration depth δ(t) was lost.

DIM solution

With the principle equation of DIM modified to the case of m > 0 and the profile (23) we have

$$\frac{d}{dt}\int\limits_{0}^{\delta } {x{\kern 1pt} \left( {\frac{\delta }{n}} \right)^{{\frac{1}{m + 1}}} \left( {1 - \frac{x}{\delta }} \right)\,} dx = \frac{{a_{0} }}{m + 1}\frac{\delta }{n}$$

(25a)

$$\frac{d}{dt}\delta^{{\frac{2m + 3}{m + 1}}} = a_{0} \left[ {\frac{{\left( {n + 1} \right)\left( {(n + 2} \right)}}{{\left( {m + 1} \right)}}n^{m} } \right]\delta$$

(25b)

Denoting (2m + 3)/(m + 1) = p (also $p = 2 + \frac{1}{m + 1}$ and for m = 0, p = 3) we have,

$$\frac{d}{dt}\delta^{p} = b\delta ,\quad b = a_{0} \frac{{\left( {n + 1} \right)\left( {(n + 2} \right)}}{{\left( {m + 1} \right)}}n^{m}$$

(26a)

The solution is

$$\delta \left( t \right) = \left[ {\left( {bt} \right)\left( {\frac{p - 1}{p}} \right)} \right]^{{\frac{1}{p - 1}}}$$

(26b)

Expressing p by m and n we get

$$\delta_{{qDIM\left( {m > 0} \right)}} = \left( {a_{0} {\kern 1pt} t} \right)^{{\frac{m + 1}{m + 2}}} \left[ {n^{m} \left( {n + 1} \right)\left( {(n + 2} \right)\left( {\frac{m + 2}{{\left( {m + 1} \right)\left( {2m + 3} \right)}}} \right)} \right]^{{\frac{m + 1}{m + 2}}}$$

(27)

For the linear case with m = 0 we have a = a ₀ and from (27) the penetration depth is

$$\delta_{{qDIM\left( {m = 0} \right)}} = \sqrt {a_{0} t} \sqrt {\frac{{2\left( {n + 1} \right)\left( {(n + 2} \right)}}{3}}$$

(28)

Equation (28) is the solution developed by Myers [31, 32].

At the end of this section, it is worthy to mention that in the solution derived by HBIM and DIM, the square-root behavior of behavior of the penetration depth δ(t) was lost due the non-linearity imposed by the thermal diffusivity affecting the flux boundary condition. In this context, it follows that in the power-law relationship (1c) the coefficient a ₀ has a dimension [m²/s K^m] which reduces to [m²/s] for m = 0. Therefore, the term (a ₀ t)^1/(p−1) has a fractional dimension $\left[ {\left( {{\text{m}}^{2} /{\text{s}}\,{\text{K}}^{\rm m} } \right){\text{s}}} \right]^{1/(p - 1)}$; for m = 0, for example, p = 3 ⇒ [m²]^1/2 = [m]. These results, therefore, are in agreement with the analytical results of similarity solutions of point source problems [9, 18] where the font propagate at a finite velocity rate ∼t ^1/(m+2). Example confirming these results are also available in [16], where the cases of m = 1 and m = 2 are considered, and the spreading of the pulse solution is at rates t ^1/3 and t ^1/4, respectively in accordance with the rule ∼t ^1/(m+2).

4 Optimal exponents of the profile and errors of approximation

Since both HBIM and DIM are moment methods, the accuracy of approximation depends on the values of the exponent n. The classical applications [26] are with n = 2 and n = 3. The undefined exponent of the profile has been analyzed in [33] and the problem has been further developed in two directions: (1) a fixed exponent minimizing the mean-squared error of approximation [31, 33, 36], and (2) a variable exponent [37].

The present analysis focuses the attention on minimizing the error of approximation over the entire penetration depth with the concept of a fixed (no-time varying) exponent. Two approaches are explored

• Matching between HBIM and DIM

• Global minimization in accordance with the modified method of Mitchell and Myers [32, 38].

4.1 Matching HBIM and DIM penetration depths

At this point we like to find a straightforward estimation, even approximate, what should be the behavior of the exponent n when one more parameter (comparing the linear problems [26, 28–34] solved by the integral balance method) controls the approximate profile. We will use the so-called Combined Integral Method (CIM) [36, 38]. In accordance with the idea of CIM the penetration depths developed by HBIM and DIM should match. Therefore, from (17) and (19), for the case of fixed temperature at the boundary we have

$$\delta_{{T\left( {HBIM} \right)}} = \delta_{{T\left( {DIM} \right)}} \Rightarrow \sqrt {2n\left( {n + 1} \right)} = \sqrt {\frac{{\left( {n + 1} \right)\left( {n + 2} \right)}}{m + 1}} \Rightarrow n_{m}^{T} = \frac{2}{2m + 1}$$

(29a, b)

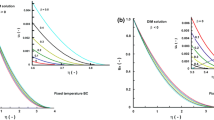
For m = 0 we get the Goodman’s exponent $n_{m = 0} = 2$. However, increasing the non-linearity through the values of mwe obtain that the exponents $n_{m}^{T} < 1$, when m > 0. These data are summarized in Table 1 and the qualitative plots are shown in Fig. 1a. In general, the behaviour of the temperature profiles in Fig. 1 confirms qualitatively exact analytical solutions [2, 9, 14, 16, 18, 19, 21, 23], that is with increase in m the profile becomes steeper and cuts shorter penetration depths from the abscissa. Since, the parabolic profile satisfies the Goodman’s conditions and the heat-balance integrals (HBIM and DIM) for every positive n, these results do not contradict any previous studies (see for example [31, 33, 38, 47]). Restrictions may be imposed by conditions requiring the approximate profile to satisfy the heat conduction Eq. (1a or 6a), as it will be discussed further in accordance with the Langford criterion [39] and the Mitchell-Myers method of optimization [38].

Table 1 Exponents defined by matching the penetration depths determined by HBIM and DIM penetration depths

Fig. 1

Dimensionless temperature profiles with exponents of the parabolic profile established by matching the penetration depths of HBIM and DIM solutions. a For the fixed temperature boundary condition for the fixed flux boundary condition at t = 1. b For the fixed flux boundary condition at t = 1

Similarly to (29), for the fixed flux boundary problem, matching (24b) and (27) we get

$$n^{{\left( {\frac{{m^{2} + m - 1}}{m + 1}} \right)}} \left( {n + 2} \right) = \frac{{\left( {m + 1} \right)\left( {2m + 3} \right)}}{m + 2}$$

(30)

For m = 0 we have $(n + 2)/n = 3/2 \Rightarrow n_{0}^{q} = 4$, i.e. the solution obtained in [38]. For any m > 0 we have to solve Eq. (30), for example: for m = 1 we get $\sqrt n \left( {n + 2} \right) = 10/3$ and $n_{1}^{q} = 1.1324$; for m = 2 we get n ^5/3(n + 2) = 21/4 and n ^q₂  = 1.3171, etc. The values of the exponent $n_{m}^{q}$ [the Eq. (30) was solved numerically by Maple] are summarized in Table 1. Profiles with some of these exponents are presented in Fig. 1b.

As a summary, the procedure of matching of the penetration depths provides results which to this moment are still qualitative showing only what the effect of the parameter m is. However, the approximate profiles in Fig. 1a,b are not optimal because the established values of the exponents do not assure minimal errors of approximation. Optimal exponents are at issue in the next sections.

4.2 Global minimization approach

4.2.1 Restrictions on the exponent n

First of all, we stress the attention on the fact that the approximate profile satisfies the heat-balance integral but not the original heat conduction equation. Therefore, the function φ(u _a (x, t))

$$\varphi \left( {u_{a} \left( {x,t} \right)} \right) = \frac{{\partial u_{a} }}{\partial t} - \frac{\partial }{\partial x}\left( {a_{0} u_{a}^{m} \frac{{\partial u_{a} }}{\partial x}} \right)$$

(31)

should be zero if u _a matches the exact solution, otherwise it should attain a minimum for a certain value of the exponent n (the only unspecified parameter of the approximate profile).

We will use the definition (31) to find some constraints which the exponent n should obey.

• Fixed temperature boundary condition

With u _a  = (1 − x/δ)ⁿ and x = 0 we have

$$\varphi_{T} \left( {0,t} \right) = - \frac{{n\left[ {n\left( {m + 1} \right) - 1} \right]}}{{\delta^{2} }} \Rightarrow n = \frac{1}{m + 1}$$

(32)

Thus, searching for positive values of n, the heat equation is satisfied for n = 1/(m + 1). However, in order to satisfy the Goodman’s boundary conditions $u_{a} (\delta ,t) = \partial u_{a} (\delta ,t)/\partial x = 0$, it is required that n(m + 1) > 1, that is n > 1/(m + 1). Hence, because the estimation established by matching HBIM and DIM [see (29a, b)] states that n = 1/(m + 1/2) we see that the requirement is obeyed.Further, for x → δ we have

$$\varphi_{T} \left( {\delta ,t} \right) = \lim_{x \to \delta } \varphi_{T} \left( {\delta ,t} \right) = - \frac{{n\left[ {n\left( {m + 1} \right) - 1} \right]}}{{\delta^{2} }}\lim_{x \to \delta } \left( {1 - \frac{x}{\delta }} \right)^{{n\left( {m + 1} \right) - 2}}$$

(33)

With the previous constraint, n > 1/(m + 1), it follows from (33) that the diffusion equation is satisfied at x = δ when n > 2/(m + 1). This second restriction matches the estimation (27b) imposed by δ _T(HBIM) = δ _T(DIM). For m = 0, we have n > 2 as it was established in [32].

• Fixed flux boundary condition

With $\theta_{a} = (\delta /n)^{1/(m + 1)} (1 - x/\delta )^{n}$ and x = 0 we have $\phi_{q} (0,t) = - [n(m + 1) - 1]/\delta$ resulting in the condition n > 1/(m + 1). This constraint is the same as that established for fixed temperature boundary condition. Further, for x → δ we get

$$\lim_{x \to \delta } \varphi_{T} \left( {\delta ,t} \right) = \frac{{n\left( {m + 1} \right) - 1}}{\delta }\lim_{x \to \delta } \left( {1 - \frac{x}{\delta }} \right)^{{n\left( {m + 1} \right) - 2}} \Rightarrow n > \frac{2}{m + 1}$$

(34a, b)

The condition (34b) is stronger, that is 2/(m + 1) > 1/(m + 1/2). In this case, the exponents determined by the matching procedure (Table 1) satisfy this constraint. However, they are not the exact values. Only the optimization procedures may clarify which of these two constraints is obeyed by the final optimal exponents of the approximate profiles.

4.2.2 Minimization in accordance with the method of Mitchell and Myers

Therefore, the function φ(u _a (x, t)) (see Eq. 31) should approach a minimum as u _a  → u, over the entire penetration depth δ, that is $\int\limits_{0}^{\delta } {\varphi \left( {u_{a} \left( {x,t} \right)} \right){\kern 1pt} } dx \to \hbox{min}$. More precisely, we may require,$\int\limits_{0}^{\delta } {\left[ {\varphi \left( {u_{a} \left( {x,t} \right)} \right){\kern 1pt} } \right]}^{2} dx \to \hbox{min}$, that is, the Langford criterion [39] for the integral-balance method

$$E_{L} \left({n,m,t} \right) = \int\limits_{0}^{\delta} {\left[{\frac{{\partial u_{a}}}{\partial t} - \frac{\partial}{\partial x}\left({a_{0} u_{a}^{m} \frac{{\partial u_{a}}}{\partial x}} \right)} \right]}^{2} dx \to \hbox{min}$$

(35)

4.2.2.1 Fixed temperature boundary condition

The approach of Mitchell and Myers [32, 38] represents the approximation profile u = (1 – x/δ)ⁿ in the Zener’s coordinate [40] ξ = x/δ, 0 < ξ < 1, that is V(ξ, t) = (1 − ξ)ⁿ. The diffusion Eq. (1a) in ξ-space becomes

$$- \frac{d\delta }{dt}\frac{\xi }{\delta }\frac{\partial V}{\partial \xi } = a_{0} \left[ {\frac{m}{{\delta^{2} }}{V^{m - 1}}\left( {\frac{\partial V}{\partial \xi }} \right)^{2}} \right]$$

(36)

Then, with ${{\partial V}/{\partial \xi }} = - n(1-\xi)^{n-1}$ the approximation of the function φ(x, t), is

$${\boldsymbol{\Phi}}_{T} \left( {\xi ,t} \right) = \delta \frac{d\delta }{dt}\xi n {(1-\xi)^{n-1}} - a_{0} \frac{m}{\delta^{2}}n^{2}(1-\xi)^{n(m+1)-2}$$

(37)

Then, the optimal value of the exponent n can be obtained by minimization of the least-square error

$$ E_{MT} = \int\limits_{0}^{1} {{\boldsymbol{\Phi}}_{T}^{2} \left( {\xi ,t} \right)} d\xi \rightarrow {\text {min}}$$

(38)

The method developed in [32] uses the fact that for m = 0 the product δ(dδ/dt) is time-independent and the function E _MT depends only on n. The fact that dδ ²/dt is time-independent was used by Hamill and Bankoff [41, 42] to develop similarity solutions for melting problems with a Dirichlet condition at x = 0. For the fixed temperature problem, analyzed in the present work, this specific feature can be expressed as δ(dδ/dt) _T  ≡ (F _T(DIM))². For the fixed flux boundary condition, with both HBIM and DIM, we have δ(dδ/dt) _q  = ∼t ^m/(m+2) and only for m = 0 we have δ(dδ/dt) _q  = const. However, we can demonstrate further in this article that the philosophy of this method can be successfully applied to the fixed flux boundary problem, too.

Integrating (38) and using the DIM solution, for the fixed temperature boundary condition, we have E _MT(DIM) = e _MT(DIM)(n, m)δ(dδ/dt), where

$$\begin{aligned} e_{{MT\left( {DIM} \right)}} \left( {n,m} \right) & = \left[ {\frac{{2n^{2} }}{{\left( {2n + 1} \right)\left( {2n + 2} \right)\left( {2n + 3} \right)}} - \frac{2}{{n\left( {m + 1} \right)}} - \frac{2}{{\left( {2n + nm - 2} \right)\left( {2n + nm - 1} \right)}}} \right] \\ & \quad + \frac{{m^{2} }}{4n - 3} + \frac{1}{2mn + 4n - 3} + \frac{2m}{2n - 1} = 0 \\ \end{aligned}$$

(39)

Since the squared error of minimization is $E_{MT} = e_{MT(DIM)} /\delta^{4} \equiv e_{MT(DIM)} /t^{2}$ and it decays rapidly in time, therefore, the focus of the minimization procedure is to minimize e _MT(DIM) with respect to n. To be clear, the assumed profile (7) generates convex profiles for n < 1 and concave profiles for n > 1, thus the result is strongly determined by the approach in the exponent determination. Here we have two approaches discussed next.

4.2.3 Two approaches to determine the optimal exponent n

• Approach 1 assumes a numerical solution of E _MT(HBI)(n, m) = 0 thus finding approximate roots and then determining for which of them E _MT obtains a minimal value. With this approach we formally envisage exact solutions, although, in fact, we find approximate ones due the numerical solutions. Performing numerical solutions of E _MT(HBI)(n, m) = 0 we really determine approximately points where E _MT gets minima, because practically exact solutions do not exist. Then, by evaluation of E _MT for these roots we may establish the optimal exponents of the profile.

• Approach 2 considers a minimization of E _MT(HBIM)(n, m) with respect to n at given m in the zone for n > 1 where the curve E _MT(HBIM) is decaying smoothly, thus defining optimal exponents. From the constraints imposed on the exponent n it follows that all of then will be satisfied when n > 1. This approach seems reasonable because E _MT is a scaled function and it is in agreement with the solutions developed for the linear problem with m = 0 [31, 32, 36, 37].

Now, the principle question in the optimization procedure is: What the correct approach defining the exponents is? To answer this principle question refer to the recent results [27] where the transformed model (3) has been solved by HBIM. The exponents determined by both approaches are summarized in Table 2 and examples of the approximate solutions are shown in Fig. 2a, b. The plots in Fig. 2a reveal strong change in the profile shape from concave to convex when the optimal exponent changes from the zone with n > 1 towards the zone n < 1. To find the correct answer to the principle question we will compare the developed approximate solutions (Example 1) to the series solution of Heaslet and Alksne [43] as it was done in other studies (see Ref. [2], for instance). The comparative plots shown Fig. 3a, c definitely indicate that the concave profiles developed for on the basis of optimal n > 1 (see Fig. 3c) are by far away from the series solutions, while the convex profiles developed with n < 1 (Fig. 3a) are too close to them. The profiles in Fig. 3a reveal that the HBIM solutions are more adequate (close to the series solutions) with increase in the value of m. Further, the pointwise errors between the HBIM approximate profiles and the series solutions support this standpoint, that is, the profiles generated on the basis of n < 1 demonstrate pointwise errors less than 4 % in contrast to 25–30 % when the optimal exponents are determined on the basis of n > 1.

Table 2 Two approaches in determination of the optimal exponents of the parabolic profile developed by the method of Mitchell and Myers

Fig. 2

Dimensionless temperature profiles with various degrees of nonlinearity (the parameter m). From [27]. By courtesy of Thermal Science. a Approximate solutions with n _opt determined by numerical solution of E _MT(HBI) = 0 and n < 1. b Approximate solutions with n _opt determined by minimization of E _MT(HBI)in the range n > 1

Fig. 3

Dimensionless temperature profiles determined on the basis of n in two ranges n < 1. a For n < 1. Comparison to the series solution of Heaslet and Alksne [43] (4 terms solutions). b For n < 1. Pointwise error between the approximate HBIM solutions and the series solutions [43]. c For n > 1. Comparison to the series solution of Heaslet and Alksne [43] (4 terms solutions); d Pointwise error between the approximate HBIM solutions and the series solutions [32]

Further, the plots in Figs. 2 and 3 are presented in the form u(X, t) = (1 − X)ⁿ, where 0 < X = η/F _n,m  < 1 and F _n,m is the function defined by the penetration depth (depending on the method of integration) in the form $\delta_{T} \left( t \right) = \sqrt {a_{0} t} F_{n,m}$, Therefore, all curves cross the abscissa at X = 1. In the solution of Heaslet and Alksne [43] the function F _n,m is denoted as η _F and calculated through the solution, as in the case of the integral-balance method. When the profiles are expressed against the similarity variable $\eta = x/\sqrt {a_{0} t}$ only, then the curves cross the abscissa at different positions because the condition u = 0 means η = F _n,m which depends on both the values of m and n _opt as it is shown in Figs. 1a and 4 (next section). The increase in m reduces the penetration depth and this effect is visible when the similarity variable η is used as independent variable, but becomes indistinguishable when the profiles are presented against X = η/F _n,m as independent variable.

Fig. 4

Dimensionless profiles with the optimal exponents for various values of m for the fixed temperature boundary condition problem and DIM solution

Therefore, we answered the question which method in defining the optimal exponent should be applied. The real profiles corresponding to the model (1) are convex in shape and their approximate solutions appear through the assumed profile (7) when n < 1.

4.2.4 Optimal exponent for the DIM solution

Now, we will briefly comment some results of Approach 1 with the DIM solution. Therefore, setting different values of m in (39) we may solve e _MT(DIM) = 0 with respect ton. The solutions of (37) provide multiple roots, but only positive values of n satisfying the condition n > 1/(m + 1) are acceptable. For m = 1, for instance, we get 2 positive roots of (39): n ₁ = 0.383 and n ₂ = 0.815, however, only the second one satisfies the condition n > 1/(m + 1) = 0.5. Further, the stronger condition (29b) yields n > 1/(m + 0.5) = 0.666 which allows selecting n ₂ = 0.815 as optimal exponent. Similarly, for m = 2 we have 1 positive root of e _MT(DIM)(n, 2) = 0, i.e. n = 0.537 which satisfies the condition n > 1/(m + 1) = 0.333 and leads to minimization of E _MT . Further, for m = 3, from 5 roots of e _MT(DIM)(n, 3) = 0 but only n ≈ 0.305 satisfy the condition n > 1/(m + 0.5) = 0.285 and minimize E _MT . With Approach 1 for m = 5 the approximate numerical solution provides n ≈ 0.216 but a careful analysis of the behaviour of E _MT around this point evaluated n ≈ 0.185 as that giving a minimum of the squared-error function. We will compare these two optimal exponents in the next section. In the same way, it was established that for m = 0.5 the optimal exponent is n ≈ 1.333. The numerical results from Approach 1 resulted in optimal exponents summarized in Table 3. Approximate profiles generated by optimal exponents defined by Approach 1 are shown in Fig. 4.

Table 3 Optimal exponents of the approximate profile: DIM solution and fixed temperature boundary condition

It is worth noting that the optimal exponents determined by approach 1 are close, but greater than the values obtained by matching the penetration depths. As a practical rule, established in this study, the optimal exponent are just greater of that determined by matching method. The values of E _MT for the exponents determined by the matching approach are summarized in Table 1. Comparing the values of E _MT in Tables 1 and 3, it is clears that they are of one and the same order of magnitude and too close in the range 1 < m < 5 .

4.2.5 Fixed flux boundary condition

Now, we will briefly demonstrate the optimization procedure for the case of Example 2. With the Zener’s coordinate $\xi = x/\delta ,\quad 0 < \xi < 1$, the approximation profile $\theta_{a} = (\delta /n)^{1/m + 1} (1 - x/\delta )^{n}$ can be represented as $\theta_{a} = \delta^{1/(m + 1)} U(\xi ,t)$ where $U(\xi ,t) = (1/n)^{1/m + 1} (1 - \xi )^{n}$. For m = 0 we have the case studied in [32] (see some examples and comments further in the text). From the diffusion Eq. (1a) we may define the error function Φ _q (ξ, t) in the ξ-space, namely

$${\boldsymbol{\Phi}}_{q} \left( {\xi ,t} \right) =\left[\frac{1}{m+1} \delta^{{\frac{1}{m + 1}}} \frac{d\delta }{dt}U - \delta^{{\frac{1}{m + 1}}} \frac{d\delta }{dt}\xi \frac{\partial U}{\partial \xi } \right]\frac{1}{\delta}- {a_{0}} \left[{\frac{m}{\delta}}{U^{m-1}}\left( {\frac{\partial U}{\partial \xi }} \right)^{2}\right]$$

(40)

In this case the product $\delta^{1/(m + 1)} d\delta /dt$ is time-independent because taking into account the expressions (24b) and (27) we have

HBIM

$$\delta_{q}^{{\frac{1}{m + 1}}} \frac{{d\delta_{q} }}{dt} = a_{0} \left( {\frac{m + 1}{m + 2}} \right)n^{{\frac{1}{{\left( {m + 1} \right)}}}} \left( {n + 1} \right)$$

(41)

For m = 0 we have $\delta^{1/(m + 1)} d\delta /dt = [a_{0} n(n + 1)]/2$ as it was used in [32].

DIM

$$\delta_{q}^{{\frac{1}{m + 1}}} \frac{{d\delta_{q} }}{dt} = a_{0} n^{m} \left( {n + 1} \right)\left( {n + 2} \right)\frac{{\left( {m + 2} \right)}}{{\left( {m + 1} \right)(2m + 3)}}$$

(42)

For m = 0 we have, $\delta^{1/(m + 1)} d\delta /dt = [2a_{0} (n + 1)(n + 2)]/3$ as it was used in [32].

Therefore, the squared-error function is $E_{Mq} = \int\limits_{0}^{1} {\varPhi_{q}^{2} } (\xi ,t)d\xi$, namely

$$E_{{Mq\left( {HBIM} \right)}} = \int\limits_{0}^{1} {\left\{ {\frac{{(m + 1)n^{{\frac{1}{m + 1}}} \left( {n + 1} \right)\left[ {(1 - \xi )^{n} + \xi (1 - \xi )^{n - 1} } \right]}}{(m + 2)} - mn^{2} \left( {1 - \xi } \right)^{2n - 2} - n(n - 1)\left( {1 - \xi } \right)^{n - 2} } \right\}}^{2} d\xi$$

(43)

and

$$E_{{Mq\left( {DIM} \right)}} = \int\limits_{0}^{1} {\left\{ {\frac{{n^{m} \left( {n + 1} \right)\left( {n + 2} \right)\left( {m + 2} \right)\left[ {(1 - \xi )^{n} + \xi (1 - \xi )^{n - 1} } \right]}}{{(m + 1)\left( {2m + 3} \right)}} - mn^{2} \left( {1 - \xi } \right)^{2n - 2} - n(n - 1)\left( {1 - \xi } \right)^{n - 2} } \right\}}^{2} d\xi$$

(44)

Setting different values of m > 0 in (43) and (44) and applying the both approaches discussed in the previous point we can define the optimal exponents (see Table 4). Plots of surface temperature evolution and temperature profiles generated with these optimal exponents are shown in Figs. 5 and 6. The normalized temperature profiles in Fig. 6b, c clearly show the retardation effect of the nonlinearity with increase of the parameter m. The HBIM solutions are practically insensitive to the variation of m even though there is retardation in the profiles as m increases: see Fig. 6a with profiles generated by Eq. (23) and Fig. 6b with normalized profiles: the ratio $[\theta_{a} /(\delta /n)^{1/m + 1} ] = [T_{a} /(q_{0} /k_{0} )(\delta /n)^{1/m + 1} ]$ (see Eq. 22) is dimensionless. Recall the dimension of δ is [m]. For better understanding this remarks, recall that for m = 0 we have $[T_{a} /(q_{0} /k_{0} )(\delta /n)]$ is dimensionless: The expression for $\theta_{a} = T_{a} /(q_{0} /k_{0} )$ has a dimension as that of δ. The temperature profiles (normalized) with optimal exponents established by DIM are shown in Fig. 6c. It is evident the effect of retardation due to the non-linearity as the value of m increases.

Table 4 Optimal exponents of the approximate profile: HBIM and DIM solutions and fixed flux boundary condition

Fig. 5

Fixed flux boundary condition problem- Surface temperature evolution in time. a HBIM solutions with optimal exponent established by the method of Mitchell and Myers. b DIM solutions with optimal exponent established by the method of Mitchell and Myers

Fig. 6

Fixed flux boundary condition problem: Solutions by HBIM and DIM. a Dimensional temperature profiles established by the HBIM solution at t = 1. b Dimensionless (normalized) temperature profiles established by the HBIM solution at t = 1. c Dimensionless (normalized) temperature profiles established by the DIM solution at t = 1

5 Benchmarking the integral-balance solutions

In order to verify the validity of the developed approximate solutions we are obliged to compare them to those available in the literature. No closed form solution to the model (1) is available [44, 45] and the first solution provided by Philip [46] is hybrid in nature by an analytical step and numerical solutions (see details in [44] [Crank]). Although is easy to prove that for the center of mass is valid the relationship [45] (Dirichlet BC)

$$\int\limits_{0}^{\infty } {xudx} = \frac{{D_{0} }}{m + 1}u^{m + 1} \left( {0,t} \right)$$

(45)

In the context of the present study and the finite penetration depth concept, by replacement of the upper terminal of the integral in (43) by δ and the assumed profile (5) we immediately get

$$\int\limits_{0}^{\infty } {xudx} \approx \int\limits_{0}^{\delta } {xudx} = \frac{{\delta^{2} }}{{\left( {n + 1} \right)\left( {n + 2} \right)}}$$

(46)

Hence, we got the principle relationship defining the penetration depth in accordance to DIM. This, therefore, clearly defines DIM as a first-moment method, while HBIM is a zero-moment.

Now, we will compare the approximate closed form solution developed in this study to other solutions available in the literature.

5.1 Fixed temperature BC

Most of these solutions [43–50] use initially the Boltzmann transformation $\eta = x/t_{*}^{1/2}$, where $t_{ * }$ denotes a horizontal co-ordinates, i.e. in the terms of present study this is $t_{ * } = D_{0} t$. This is a very convenient step for comparison the results of the present study because the integral-balance solution also defines the similarity variable η in a straightforward manner.

5.1.1 Benchmarking against the Philip’s solution

Weisberg and Blanc [47] have performed experimental study of zinc diffusion into GaAs and solved the model (1) by the method of Philip [46]. The numerical data of Weisberg and Blanc are compared to the DIM solutions in Fig. 7a with a good agreement. The pointwise errors are in the range 0–0.02 (see Fig. 7b). The sharp increase in the curve corresponding to m = 2 (Fig. 7b) corresponds to the section close to edge of the penetration front. In this case the DIM solution predicts larger penetration depth then the numerical solution. In addition data provided by the same method and published in [50] are presented in Fig. 7c demonstrating a good agreement with the DIM solutions. In general, with increase in m the pointwise differences between the DIM solutions and numerical ones decrease and we can see that this tendency will be exhibited in the other comparative studies developed next.

Fig. 7

Comparison of the DIM solution to the numerical results of Weisberg and Blanc. The numerical data are taken from Table 01 in [47]. a Plots of profiles for m = 1, m = 2 and m = 3. b Pointwise errors corresponding to the plots in a

5.1.2 Benchmarking against the series solution of Heaslet and Alksne [43]

This is a benchmark procedure to the series solution of Heaslet and Alksne [43] for testing the new solutions of the model (1) as it was done in other studies [48–50]. In the context of the analysis of the present study, this series solution also uses the concept of a finite depth denoted in the original study as $\eta_{F}$. Then the series is with respect to the normalized variable $X = \eta /\eta_{F}$, where in the case of integral-balance solutions η _F corresponds to the function F _n,m . The plots comparing the DIM solution and the series solutions are presented in Fig. 8a, c. The pointwise errors (Fig. 8b, d) reveal acceptable errors of approximations which becomes, as a rule, higher at the vicinity of the sharp front of the profile. Figure 8e shows the pointwise errors in case of the two exponents for m = 5 and confirms that n = 0.185 provides better results. The case for m = 0.5 is presented in Fig. 9.

Fig. 8

Comparison of the DIM solutions with optimal exponents to the series solution of Heaslet and Alksne [43] (4 terms solutions): a solutions for m = 2, m = 3 and m = 5. b Pointwise errors corresponding to m = 2, m = 3 and m = 5. c Solutions for m = 1, m = 3 and m = 4. d Pointwise errors corresponding m = 1, m = 3 and m = 4

Fig. 9

Comparison of the DIM solution for m = 0.5 to the series solution of Heaslet and Alksne [43] (3 terms solutions). aTemperature profiles. b Pointwise errors

5.1.3 Comparison to the series solution of Brutsaert and Weisman [1970]

With the Boltzmann transformation $\eta = x/t_{ * }^{1/2}$ the governing Eq. (1a) reduces to an ordinary differential equation [50]

$$\frac{{d^{2} }}{{d\eta^{2} }}\left[ {\frac{{S^{m + 1} }}{m + 1}} \right] + \frac{\eta }{2}\frac{dS}{d\eta } = 0$$

(47)

with transformed boundary conditions: S = 0 for η → ∞ and S = 1 for η = 0. We use the symbol S to distinguish the solution of (47) from this of the present article, where the same variable is denoted as u.

Brutsaert and Weisman [48, 49] have analyzed the approximation errors between the Philip’s numerical results [46], the series solution of Heaslet and Alksne [43] and their solution. The first approximation developed in the neighborhood of S = 1 (i.e. when η → 0) is [48]

$$S_{1} = \left\{ {1 - \eta \left[ {\frac{{\left( {m + 1} \right)^{2} }}{{2\left( {m + 2} \right)}}} \right]^{\frac{1}{2}} } \right\}^{{\frac{1}{m + 1}}}$$

(48)

The second approximation was derived at the vicinity of the penetration depth η → η _B  = δ that is for S = 0 which reduces to (47)

$$\frac{{d^{2} }}{{d\eta^{2} }}\left[ {\frac{{S^{m + 1} }}{m + 1}} \right] + \frac{{\eta_{F} }}{2}\frac{dS}{d\eta } = 0,\quad {\text{with}}\quad S = S^{m} \frac{dS}{d\eta } = 0,\quad {\text{for}}\quad \eta > \eta_{B}$$

(49a, b)

The condition (49b) is equivalent to the Goodman’s condition. In this case, the critical point (penetration depth) is η _B  = (2/m)^1/2 and the approximate solution is

$$S_{0} = \left(1 - \eta \sqrt{ \frac{m}{2}}\right)^{\frac{1}{m}}$$

(50)

This solution matches the first term of the series solution of Heaslet and Alksne [43].

Figure 10a presents the DIM solution and the S ₁ approximation of Brutsaert and Weisman [50] for various values of the parameter m and points provided by the method of Philip [46]. The plot of the pointwise errors (Fig. 10b) reveals that acceptable errors are possible in the range 0 < η < 0.5 corresponding to 0.6 < u < 1. The S ₀ solution generates distributions which qualitatively are as those obtained by the DIM solution (Fig. 11a). However, the plots (Fig. 11a, b) reveal that discrepancies between both solutions may reach 0.05 from η = 0 up to η ≈ 0.5: a range corresponding to 0.75 < u < 1. In general, the differences between the DIM solution and S ₀ (and S ₁) decreases with increase in m (see Figs. 9b, 10b). This confirms the results of Brutsaert and Weisman [48] where their solutions were compared to that of Philip [46]. In the error charts different levels of pointwise differences are marked by dashed lines, so it is easy to determine the range of application of the DIM solution when a desired accuracy is predetermined.

Fig. 10

Comparison of the DIM solution to the S ₁ approximate solution of Brutsaert and Weisman [48]. The data points are for m = 5, calculated by the numerical method of Philip [46] and taken from Table 1 of [48]. a DIM solution and S ₁ approximation. b DIM solution and S ₀ approximation

Fig. 11

Comparison of the DIM solution to theS ₁ and S ₀approximate solutions of Brutsaert and Weisman [48]. a Pointwise differences between DIM and and S ₁ approximation. b Pointwise differences between DIM and and S ₀ approximation

5.1.4 Comparison to the Tuck’s approximate solution

Tuck [51] have developed approximate solutions in case of m = 2 by approximating the diffusion profile in two zones, denoted as T1 and T2, namely:

$$T1{:}\quad \eta = \frac{x}{{\sqrt {D_{0} T} }} = \frac{{\left( {e^{2} - e^{2u} } \right)}}{{\sqrt {30.99} }},\quad 0.4 < u < 1$$

(51)

$$T2{:}\quad \eta = \frac{x}{{\sqrt {D_{0} T} }} = 1 - u^{2} ,\quad 0 < u < 0.4$$

(52)

The plots in Fig. 12a, presents these approximate solutions together with the result of the DIM approach for m = 2. The absolute error (Fig. 12b) between T1 and the DIM solution is less that 0.03 in the range 0.4 < u < 1, corresponding to 0 < η < 0.923. With the second approximation (T2), the absolute pointwise difference may reach about 0.05 in the range 0 < η < 0.5. Beyond these ranges the pointwise differences raise drastically. As a summary, the DIM solution for m = 2 exhibits acceptable pointwise difference, less that 0.03, with respect to the solution T1, in the range 0 < η < 0.923.

Fig. 12

Comparison of the DIM solution for m = 2 to the Tuck’s solution [51]. a Approximate profiles. b Pointwise errors

5.2 Fixed flux BC

5.2.1 Benchmarking

The solutions developed by HBIM and DIM are benchmarked in Fig. 13a against the exact numerical solutions derived by Parlange et al. [52] using the integration method of Shampine [53], in which the profiles are plotted over a normalized range. For large m both HBIM and DIM solutions converge to the reference solutions. For the case m = 10 its was established that optimal exponents are: n _HBIM (10) ≈ 0.180 and n _DIM (10) ≈ 0.115. The error curves presented in Fig. 13b reveal that only for m = 5 the difference between the DIM solution and the numerical one raises strongly at the end of the normalized interval, while, in general, the other plots indicate acceptable errors of approximation, close to errors commented in the case of the fixed temperature problem. In general, the increase of the error close to the edge of the penetration layer is an inherent feature of the integral-balance methods [26, 31–34, 37] as well as of the other approximate methods commented in the previous Sect. 5.2.

Fig. 13

Fixed flux boundary condition problem. Benchmarking of the DIM solution to the exact (numerical) solutions of Parlange et al. [52]. The points are data taken from Table 3 of [52]. a Approximate profiles for three different values of the parameter m. b Pointwise errors

5.2.2 Comparison to the moment solution of Prasad and Salomon

Prasad and Solomon [2] have developed a moment solution using the classical approach [56] expressed as

$$\theta = \delta^{\alpha } \left( {1 - X} \right)^{\alpha } \sum\limits_{k = 0}^{K} {A_{k} \delta^{k} \left( {1 - X} \right)^{k} } = \delta^{{\frac{1}{m + 1}}} \sum\limits_{k = 0}^{K} {a_{k} \delta^{k} \left( {1 - X} \right)^{k + \alpha } } ,\quad \alpha = \frac{1}{m}$$

(53a, b, c)

where the penetration depth is

$$\delta = \left[ {\left( {\frac{m + 2}{m + 1}} \right)\left( \frac{1}{m} \right)a_{0}^{m} } \right]^{{\frac{m + 1}{m + 2}}} t^{{\frac{m + 1}{m + 2}}} ,\quad a_{0} = 1.20263$$

(53b)

It is worthnoting that in the case of a flux boundary condition both the expression (53a) and the DIM solution (see Eqs. 24b, 27) define the similarity variable $\eta_{q} = x/(a_{0} t)^{{\left( {\frac{m + 1}{m + 2}} \right)}}$ Then the normalized abscissa following the DIM solution is X _q  = η _q /F _q(n,m), where the function F _q(n,m) is defined by Eq. (27). The integral-balance solutions developed by DIM and the profiles of Prasad and Salomon [2] are presented in Fig. 14a. For large m the behaviour is the same as that exhibited in Fig. 13a but the pointwise errors presented in Fig. 14b indicate unacceptable differences between the DIM solutions and the moment method, even though both methods are approximate and belong to family of the weighted residuals method [56]. Moreover, the quantitative error of approximation of the moment method with respect to exact solution of Parlange et al. [52] is not discussed in [2], but the simulation was performed by varying the number of the terms in the series (53). With respect to the DIM solution, it is important that the maximum error of approximation with respect the exact solution (see Fig. 13b) does not exceed 3–4 % 3.

Fig. 14

Fixed flux boundary condition problem. Comparison of the DIM solution to the moment method solution (3 terms) of Prasad and Salomon (P&S) [2]. a Approximate profiles generated by both approximate solutions for three different values of the parameter m like in Fig. 13a. b Pointwise errors between the DIM solutions and the moment method of Prasad and Salomon [2]

The solution of Prasad and Salomon [2] uses the zero-moment method and the accuracy can be increased by increasing the number of terms of the series (53). In contrast, DIM is a first-moment method and provides one-term closed form solution [see the comments about Eq. (46)]. Moreover, the series solution (53) is imposed only to the condition of the integral relation like that expressed by Eq. (4a) while the DIM solution should satisfy, in addition, the governing equation (Eqs. 1a or 8a, for example) through the optimization procedure with respect to the unknown exponent n. This additional requirement allows to develop approximate one-term closed form solution by DIM which has the same accuracy as that of the one expressed by a series (53).

5.3 The law of the optimized exponents

Now, we like briefly to comment the values of the optimized exponents developed in this study and leading to good approximate profiles demonstrating acceptable errors when considered against benchmark solutions. The pure analytically studies [43, 50, 54, 55] demonstrate that solution can be approximated as one term profile (1 − x/δ)ⁿ with n = 1/m. In the present article this is illustrated by the S ₀ approximation of Brutsaert and Weisman [48]—see Eq. (50) and the moment solution of Prasad and Salomon [2] (see Eq. 53c). Besides, the constraints that should be obeyed by the exponent at the boundaries give n ∼ 1/(m + 1). Thus, the question is: Do the optimized exponents exhibit similar behaviour? The exponents determined in this work are compared in Fig. 15a, b to the theoretical n = 1/m and the additional condition n = 1/(m + 1)imposed at the x = 0. Both plots confirm the theoretical prediction n = 1/m with exception about the values related to the fixed flux problem and determined by the matching method (see Table 1). In general, for the fixed temperature problem, with increase in m the optimized exponents converge to the theoretical profile n = 1/m but for m < 3 they are close to the behaviour n = 1/(m + 1). For the case of the fixed flux problem, however, the exponents strongly converge to the line n = 1/m. Moreover, for both problems, with increase in m the exponents vary in very close ranges as it is seen from Tables 3 and 4, as well as from the almost flat tail of the function n = 1/m for large m.

Fig. 15

The law of the exponents of the optimized approximate profiles. a Fixed temperature boundary condition problem. b Fixed flux boundary condition problem

Therefore, the optimal exponents determined by application the Langford criterion [39] and the method of Mitchell and Myers [32, 38] follows the theoretical prediction n = 1/m with some deviations for m < 3 (Dirichlet problem).

6 Conclusions

The solutions developed demonstrate how the integral balance approach in its two modifications (HBIM and DIM) can be applied to nonlinear transient heat conduction without initial linearization, commonly applied by the Kirchhoff transform. The main steps and contribution of the developed solutions may be outlined as:

• 1. The main step avoiding the initial linearization of the model equation is the use of the derivative of order (m + 1)in the right-side of the HBIM and DIM integrations procedures.

• 2. The application of the simple heat-balance integral technique (HBIM) to non-linear heat conduction equation is effective when the Neumann problem is at issue, while the HBIM solution to the Dirichlet problem is insensitive to the non-linearity.

• 3. The double integration method (DIM) allows the non-linearity to be accounted adequately in the final closed-form approximate solutions when it exists in the transport coefficient (thermal diffusivity) only (Dirichlet problems) as well as in the complicated case with the Neumann problem.

• 4. The solutions developed by both HBIM and DIM reduces to the classical ones available in the literature when m = 0.

• 5. The optimization procedures of the approximate profiles towards minimal global error of approximations prove the applicability of the method of Mitchell and Myers [32, 38] to non-linear problems.

• 6. The optimal exponents determined by minimization of the squared-error of approximation of the governing equation (criterion of Langford for the integral-balance solutions) and the method of Mitchell and Myers [32, 38] obey the law n = 1/m for large values of m when the Dirichlet problem is at issue, while for m < 3 they are close to the line n = 1/(m + 1). In the case of the Newman problem, the lawn = 1/m is strongly followed by the optimal exponents over the entire range of variations of m studied.