Adaptive fuzzy backstepping hierarchical sliding mode control for six degrees of freedom overhead crane

Abstract

Most overhead crane control studies attempt to position the payload accurately and minimize its horizontal swing without considering axial oscillation. The axial vibration caused by the lifting rope’s elasticity significantly affects the actuators’ reliability and the system’s overall performance over time. In this paper, a novel overhead crane model is developed to describe an actual crane’s behavior more closely by further considering the effect of axial payload oscillation. Furthermore, an adaptive fuzzy backstepping hierarchical sliding mode controller is designed to guarantee precise movements and reduce vibrations of payload in both horizontal and vertical directions under complex conditions, such as unknown external disturbances and cable elasticity. Three inputs consisting of the trolley-moving force, the bridge-pulling force, and the payload-hoisting torque stabilize six outputs simultaneously, including trolley motion, bridge travel, hoisting drum rotation, two payload swings, and axial payload oscillation. The controller is first designed using the backstepping hierarchical sliding mode control strategy. This controller’s parameters are then adjusted online using a fuzzy logic system, ensuring system states’ stability on the sliding surface. The system’s stability is analyzed and proved mathematically by LaSalle’s principle. Several simulations on MATLAB/Simulink have been conducted with constant or trapezoidal reference signals, with and without external disturbances. These simulation results show the proposed method’s effectiveness, such as motion precision, minor load swings, and minimal axial oscillation.

1 Introduction

An overhead crane, commonly called a bridge crane, is the essential equipment used in factories, construction sites, or harbors to lift and transport heavy and dangerous cargoes. Increasing productivity often requires overhead cranes to operate at incredibly high speeds, leading to increased cargo swings and, thus, increased dangers for the people and goods around them [1]. Also, wind disturbances often affect overhead cranes in outdoor environments, causing cargo swing to increase significantly. Thus, developing a suitable control strategy is essential for reducing cargo swing and increasing motion accuracy, regardless of the crane’s speed or wind disturbances.

Many methods of overhead crane control have been published since the 1990s. All these methods can be classified into two categories: open-loop and closed-loop schemes [2]. Generally, the open-loop, or feedforward control, method is primarily used to reduce load vibrations without adding extra sensors. Among the open-loop methods, input shaping is one of the most popular ones [3, 4]. This approach can suppress the system’s vibration by convolving the command input signal with a sequence of impulses to match the system’s natural frequencies and damping ratios. Like other open-loop control techniques, its main drawback is sensitivity towards external disturbances, parameter variations, and the frequency of the oscillations [2].

Meanwhile, the closed-loop method, also known as feedback control, requires several sensors to measure the position and swing angles for adjusting the actuators based on the desired output [5]. As a result, this method seems less sensitive to external disturbances or parameter changes. Although this method has drawbacks regarding feedback loop input delay and possible sensor measurement errors, it is still the most efficient method for crane control [2]. Numerous feedback control approaches have been published in the literature, ranging from simple linear methods, such as proportional-integral-derivative (PID) control [6,7,8], linear quadratic regulator (LQR) [9, 10], and partial linearization feedback control [11,12,13,14] to complex nonlinear methods, such as model predictive control (MPC) [15,16,17], sliding mode control (SMC) [18,19,20,21], and backstepping control [22,23,24]. Besides, these methods are combined with a neural network [25,26,27,28] or a fuzzy logic system (FLS) [10, 29,30,31,32] to increase the adaptability and robustness of the controller under real-world conditions. The neural network-based methods are excellent solutions to the problem of mathematical modeling. Not only that, but neural networks also possess strong nonlinear processing capabilities due to their inherent parallelism [33]. Our previous works [26, 27, 34] introduced the adaptive hierarchical SMC (HSMC) schemes using radial basis function network (RBFN) for the 2D and 3D overhead cranes. Our approach enables the crane control system to be robust under uncertain conditions when determining some unknown and uncertain parameters are quite challenging.

Likewise, fuzzy-based methods are also intelligent approaches with robust adaptability to system uncertainties and external disturbances [35]. Moreover, this approach does not require an exact model of the overhead crane. A fuzzy model replaces the mathematical model based on if-then rules [29]. Therefore, it is well suited for practical crane control, where it is difficult to obtain an accurate mathematical model. For instance, Aguiar et al. [36] presented a compact state-space fuzzy-rule-based model of overhead cranes and then developed a fuzzy controller based on a linear matrix inequality (LMI) problem. Simulation results reveal the remarkable effectiveness of the fuzzy LMI crane controller in handling disturbances and minimizing load swing angle compared to the quadratic optimal controller. However, this paper only uses a simple 2D overhead crane model for the fuzzy system design process. This model limits the crane’s range of motion in the working area with only 2 degrees of freedom: the cart position and load swing angle.

Besides, there are also some other recent approaches to controlling the crane system. For example, the paper [37] introduced a passivity-based adaptive overhead crane control method, whose results showed that in a closed-loop system, input-output is stable, and this ensures that the payload tracking error converges to zero vertically and remains bound horizontally. The paper [38] proposed an observer-based motion control scheme for an overhead crane system to prevent swaying and ensure the precise positioning of loads. More specifically, they proposed an adaptive unscented Kalman filter with condition-based selective scaling (AUKF-CSS) to solve the simultaneous estimation problem under a control mechanism. Simulation results have shown that the proposed method can achieve excellent motion control for different initial load angles without additional sensors, even with unknown inputs. However, [37] and [38] have used 2D crane models, with three degrees of freedom. Since 2D overhead cranes can only operate in the plane, they are less flexible in practical applications than 3D cranes.

The above works attempted to accurately drive overhead cranes’ motions while rapidly reducing undesirable payload swings under high-speed operating conditions. Several results have been relatively successful in controlling overhead crane systems in both simulation and experiments. Nevertheless, these studies treated the lifting cable as a rigid (inelastic) rope to eliminate payload swings in the horizontal plane and ignored its oscillation along the hoisting cable. Due to the elasticity of the lifting cable, the axial vibrations are significantly increased during high-speed operation. Consequently, this reduces system quality, shortens actuator life, reduces response time, and increases energy consumption. In a recent study, Xing and Liu [39] developed a new overhead crane model that incorporates the elastic deformation of lifting cables. Furthermore, they designed a controller based on the backstepping technique to reduce the 3D vibration of a variable-length cable. However, this study investigated the scenario of a crane system with only a trolley’s movement.

Motivated by the discussion mentioned above, this paper proposes a new model for a 3D overhead crane with six degrees of freedom, named the 3D-6DOF overhead crane, which considers the elasticity of the hoisting rope. Consequently, the overhead crane is analyzed as a multiple-input multiple-output (MIMO) system, comprising three inputs and six outputs. In addition, the system’s dynamic behavior is analyzed under complex operating conditions, where both the bridge and trolley are moved while the payload is hoisted simultaneously. The six system outputs are required to control the bridge travel, the trolley movement, the hoisting drum rotation, two payload swings, and axial payload oscillation. However, only three actuators composed of trolley-pulling, bridge-pushing, and payload-hoisting motors are equipped. The overhead cranes are robust under-actuated mechanical systems with sophisticated nonlinear dynamic behavior, complex geometric and kinematic constraints, and complicated motion interactions. Such systems are much more challenging to control than those with full actuators.

Among the wide variety of control techniques for underactuated nonlinear systems, we found two notable ones: backstepping and SMC. The backstepping technique is a design technique that stabilizes system states through a step-by-step recursive process [40]. More importantly, this technique can handle both matched and unmatched uncertainties in a nonlinear system with a strict feedback form [41]. However, the classical backstepping design mainly supposes that the uncertainties and the disturbance are constant or slowly altering. As a variable structure controller, SMC has some unique features such as robustness against parametric uncertainties and external disturbances, fast convergence, and the desired signal tracking accuracy [42]. In this method, the controller is designed to switch between two different structures to drive the system’s states toward a predesigned sliding surface [43]. Despite the mentioned advantages, SMC experiences a high-frequency phenomenon called “chattering”[44].

Considering the above control benefits, we propose an adaptive fuzzy backstepping hierarchical sliding mode control (AFBHSMC) strategy for the 3D-6DOF overhead crane, combining three techniques: backstepping, HSMC, and FLS. In our design, a BHSMC is built as the central controller to stabilize the system states on the sliding surface. Then, FLSs are applied to tune the BHSMC controller parameters to increase robustness against system model uncertainty and the influence of unknown external disturbance (wind) and internal disturbance (the elasticity of the cable). By incorporating FLS into BHSMC, the sliding surfaces are adjusted automatically to limit the chattering phenomenon as the system state approaches equilibrium. As a result, the proposed controller (AFBHSMC) has high quality in reference tracking control and eliminates payload swings and axial load oscillation. Although, methods based on a combination of FLS, SMC, and backstepping have effectively been used to control various uncertain nonlinear systems [45,46,47,48,49]. However, this approach does not seem to be applied in overhead crane control.

Briefly speaking, the main contributions in this study are as follows:

1) A novel dynamic model for overhead cranes is developed that incorporates axial load oscillations. This new crane system, named 3D-6DOF overhead crane, is built by considering all three movements of the trolley, bridge, and lifting drum to drive three actuated states to their desired position while eliminating the three undesirable underactuated states.

2) The AFBHSMC method is proposed for the 3D-6DOF overhead crane, which combines three techniques: backstepping, HSMC, and fuzzy logic. In addition, the system’s stability is also analyzed and proved mathematically as well as through simulations.

The rest of this paper is organized as follows. Section 2 presents the dynamic model of the 3D-6DOF overhead crane. A backstepping hierarchical sliding mode control strategy and its stability analysis are presented in Sect. 3, while a fuzzy logic-based controller parameter tuning algorithm is described in Sect. 4. Simulation results are provided in Sect.  5. Finally, Sect. 6 presents the concluding remarks.

2 Dynamic model

This section presents a crane model in 3D space with six degrees of freedom (6DOF) corresponding to six generalized coordinates, named 3D-6DOF overhead crane. Before developing a crane motion equation, the generalized coordinates of the load are determined in a fixed 3D coordinate system.

2.1 Definition of generalized coordinates

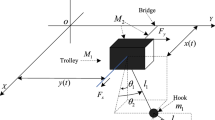
A 3D overhead crane system is shown in Fig. 1, including three movements: a bridge moves on the bridge track, a trolley travels on the bridge, and a hoisting drum rotates around its axis.

Fig. 1

Overhead crane system in 3D space. It includes a bridge moves on the bridge track, a trolley travels on the bridge, and a hoisting drum rotates around its axis

In the fixed coordinate system XYZ, x is the trolley displacement in the x-direction, y is the bridge displacement in the y-direction, and $\psi$ is the rotation angle of the hoisting drum. We denote $\vartheta _x$ is the angle between the cable axis and its projection on the YZ plane, $\vartheta _y$ is the angle between the projection of the cable axis on the YZ plane and Z-axis, and $\delta$ is the payload oscillation along the hoisting cable. Hence, six degrees of freedom of overhead crane corresponding to six generalized coordinates, characterized by a status vector as follows:

$$\begin{aligned} {\chi }=(x \quad y \quad \psi \quad \vartheta _x \quad \vartheta _y \quad \delta )^T \end{aligned}$$

where $x, y, \psi$ are the actuated states, and $\vartheta _x, \vartheta _y, \delta$ are the underactuated states or unexpected states in the system.

The designing of the controller is how the actuated states track their reference values, and the underactuated states are stable at the origin, that is

$$\begin{aligned} \begin{matrix} \lim \limits _{t \rightarrow \infty }{\chi }=(x_d &{} y_d &{} \psi _d &{} 0 &{} 0 &{} 0)^T={\chi }_{d} \\ \end{matrix} \end{aligned}$$

(1)

where ${\chi }_{d}$ is the desired state vector of the system.

The position of the cargo in the XYZ coordinate system is determined as follows

$$\begin{aligned} {x_c}&= x + l\sin \left( {{\vartheta _x}} \right) + r\cos \left( {{\vartheta _x}} \right) \end{aligned}$$

(2)

$$\begin{aligned} {y_c}&= y + l\sin \left( {{\vartheta _y}} \right) \cos \left( {{\vartheta _x}} \right) \end{aligned}$$

(3)

$$\begin{aligned} {z_c}&= l\cos \left( {{\vartheta _y}} \right) \cos \left( {{\vartheta _x}} \right) - r\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \end{aligned}$$

(4)

where $l=\delta + \Delta \delta + r(\vartheta _x+\psi )$ is the hoisting cable length, $\Delta \delta$ is the original stretch of the hoisting cable (constant), and r is the radius of the spindle lifting the load (constant).

2.2 Motion equation

In this study, the size and motion range of the cargo is assumed to be small compared to the size and motion range of the entire system. The dynamic equation of the system is obtained from Euler–Lagrange [50] with some assumptions: the payload is considered a point mass, and its motion in the y-direction is caused only by the bridge’s movement; the pulley’s ratio is one; the elastic coefficient of the cable is constant; the mechanical system is rigid and is only subjected to ideal holonomic internal kinematic constraints.

Let $m_b, m_c$, and $m_t$ denote the bridge, cargo, and trolley mass, respectively. The damping coefficients $\eta _m, \eta _b, \eta _t$ and $\eta _r$ represent the effects of friction on the motion of the hoisting drum, the bridge, trolley, and inside the hoisting cable, respectively. g is the gravitational acceleration. $u_t, u_b$ (N) are forces acting on the trolley and the bridge, respectively; and $u_d$ (N.m) is the drum motor’s torque lifting the load.

The system’s potential energy (E) includes the potential energy of the load and the potential energy due to the cable’s elasticity:

$$\begin{aligned} E&= {m_c}g\left( {\delta + \Delta \delta + r\left( {\psi + {\vartheta _x}} \right) } \right) \cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \nonumber \\&-{m_c}gr\cos \left( {{\vartheta _y}} \right) \sin \left( {{\vartheta _x}} \right) + \frac{1}{2}\rho {\delta ^2} \end{aligned}$$

(5)

The system’s kinetic energy (T) consists of the kinetic energy of the trolley, the kinetic energy of the bridge, the kinetic energy of the hoisting drum and the kinetic energy of the load.

$$\begin{aligned} T&= \frac{J}{2}{\dot{\psi }} ^2 + \;\frac{{{m_c}}}{2}\left( {{\dot{x}}_{c}^{2}} + {{\dot{y}}_{c}^{2}} + {{{\dot{z}}_{c}}^{2}} \right) \; + \frac{{{m_t}}}{2}\left( {\dot{x}^{2}} + {{\dot{y}}^{2}} \right) \nonumber \\&+\frac{{{m_b}}}{2}{{\dot{y}}^{2}} \end{aligned}$$

(6)

In addition, the energy wasted by the friction and the damping coefficients is as follows:

$$\begin{aligned} \Phi&= \frac{1}{2}{\eta _m}{{\dot{\psi }} ^2} + \frac{1}{2}{\eta _r}{{\dot{\delta }}^2} + \frac{1}{2}{\eta _t}{{\dot{x}}^2} + \frac{1}{2}{\eta _b}{{\dot{y}}^2} \end{aligned}$$

(7)

The crane system’s motion equation is built using Euler–Lagrange equation [50] as follows:

$$\begin{aligned} \frac{d}{{dt}}{\left[ {\left( {\frac{{\partial L}}{{\partial {\dot{\chi } } }}} \right) } \right] ^T} - {\left[ {\frac{{\partial L}}{{\partial {\chi } }}} \right] ^T} = {u} - {\left[ {\frac{{\partial \Phi }}{{\partial {\dot{\chi }} }}} \right] ^T} \end{aligned}$$

(8)

where

$L{=}T - E$ is the Lagrange function, ${\dot{\chi }}{=}\begin{matrix} ({\dot{x}}&{\dot{y}}&{\dot{\psi }}&{\dot{\vartheta }}_{x}&{\dot{\vartheta }}_{y}&{\dot{\delta }} )\end{matrix}^T$ is the first-order time derivative vector of the crane’s states, and ${u}=\begin{matrix} (u_t&u_b&u_d&0&0&0)\end{matrix}^T$ is the control input vector.

Substituting Eqs. (2)–(7) into (8), the dynamic model of the system can be obtained in the following matrix form:

$$\begin{aligned} M{\ddot{\chi }}+(C+D_n){\dot{\chi }}+G ={u} \end{aligned}$$

(9)

where M is a positive-definite symmetric mass matrix, C denotes a Coriolis force matrix, G indicates a gravitational vector, and $D_n$ is the loss coefficient matrix.

$M = M({\chi },t) ={\left[ {{m_{ij}}} \right] ^{6 \times 6}}= {M^T} > 0$

$C = C({\chi },{\dot{\chi }},t) ={\left[ {{c_{ij}}} \right] ^{6 \times 6}}$ $G = G({\chi },t) ={\left[ {{g_{ij}}} \right] ^{6 \times 1}}$

${D_n} = diag\left( {\begin{matrix} {{\eta _t}}&{{\eta _b}}&{{\eta _m}}&0&0&{{\eta _r}} \end{matrix}} \right)$

The elements $m_{ij}, c_{ij}$ and $g_{ij}$ are detailed in Appendix A.

3 Backstepping hierarchical sliding mode control

This section describes a backstepping hierarchical sliding mode control (BHSMC) strategy using backstepping and HSMC techniques. A controller is designed to stabilize the overhead crane under complex operating conditions, including lifting payload while simultaneously moving the trolley and bridge. The controllers simultaneously perform six functions: tracking the trolley to its destination, driving the bridge to its position, lifting/lowering the payload to a desired angle of the hoisting drum, suppressing payload swing, and the axial payload oscillation caused by cable elasticity.

3.1 Definition and lemma

Before designing the controller, some definitions and lemmas should be mentioned.

Definition 1

A real function ${f}({x})\in {\mathbb {R}}$ with ${x} \in {\mathbb {R}}, {x} \geqslant {0}$ is called to be of class K if it is monotonically increasing and ${f}({0}) = {0}$. If there is an additional $\lim \limits _{{x} \rightarrow \infty } {f}({x}) = \infty$, then it is said to be of class ${K_\infty }$.

Definition 2

A multi-variable function ${f}({x},t) \in {\mathbb {R}}$ with vector ${x} \in {\mathbb {R}^m}$, time $t \geqslant 0$ is called proper if there exist two functions ${f_1}(.), {f_2}(.) \in K$ such that ${f_1}(\left\| x \right\| )\leqslant {f}({x},t) \leqslant {f_2}(\left\| x \right\| )$.

Lemma 1

(LaSalle’s) [51]: Considering a non-excited and balanced nonlinear system at the origin as ${{{\dot{x}}}} = {{f}({x},t)}$ with vector ${x} \in {\mathbb {R}^m}, {f}({0},t)={0}$ for $\forall t \geqslant 0$. Notation V(x, t) is a smooth function satisfying

$$\begin{aligned}&{f_1}(\left\| x \right\| )\leqslant V({x},t) \leqslant {f_2}(\left\| x \right\| ) ; {f_1(.)}, {f_2(.)}\in K \\&\frac{{dV({x},t)}}{{dt}} = \frac{{\partial V({x},t)}}{{\partial t}} + \frac{{\partial V({x},t)}}{{\partial {x}}}{{f}({x},t)} \leqslant - \kappa ({x},t) \end{aligned}$$

If there exists a function $y(.)\in K$ and $T_0>0$ such that $\kappa ({x},t)\geqslant y(\left\| x \right\| )$ for $\forall {x} \in \partial \left( O \right) ,\forall t \geqslant T_0$, then the system will be asymptotically stable at $T_0$, where the stable domain $\partial (O)$ is an open neighborhood containing the origin.

Lemma 2

The inequality of the quadratic form is stated as follows: ${\lambda _{q\mathrm{max}}}{\Vert {x}\Vert ^2} \geqslant {x} ^T Q {x} \geqslant {\lambda _{q\mathrm{min}}}{\Vert {x}\Vert ^2}$ for $\forall {x} \in {\mathbb {R}^m}, {x} \ne {0}$, where $\lambda _{q\mathrm{min}}, \lambda _{q\mathrm{max}}$ are the smallest and largest eigenvalues of a square matrix $Q\in {\mathbb {R}^{m \times m}}$.

3.2 Control strategy

From the above definitions and lemmas, the controller design steps are as follows:

Step 1: Let us denote ${\chi _e}={\chi }-{\chi _d}$. Differentiating the 1st and 2nd order with respect to time yields:

$$\begin{aligned} \left\{ \begin{aligned} {\dot{\chi }_e}&= {\dot{\chi }}-{\dot{\chi }_d}, \\ {{\ddot{\chi }}_e}&= {{\ddot{\chi }}}-{{\ddot{\chi }}_d} \end{aligned} \right. \end{aligned}$$

Substituting ${\chi _e}, {\dot{\chi }_e}$ and ${{\ddot{\chi }}_e}$ into (9), we obtain:

$$\begin{aligned} M{{\ddot{\chi }}_e}+C_n{\dot{\chi }_e}+G ={u}- M{{\ddot{\chi }}_d}-C_n{\dot{\chi }_d} \end{aligned}$$

(10)

where $C_n= C+D_n \in {\mathbb {R}^{6 \times 6}}$

Let us denote

${\chi _{1d}} = {\left[ {\begin{matrix} {{x_d}}&{{y_d}}&{{\psi _d}} \end{matrix}} \right] ^{{\text { }}T}}$, $M = \left[ {\begin{matrix} {{M_{11}}}&{}{{M_{12}}} \\ {{M_{21}}}&{}{{M_{22}}} \end{matrix}} \right]$,

$C_n = \left[ {\begin{matrix} {{C_{11}}}&{}{{C_{12}}} \\ {{C_{21}}}&{}{{C_{22}}} \end{matrix}} \right]$

${u_e}={u}- M{{\ddot{\chi }}_d}-C_n{\dot{\chi }_d}={\left[ {\begin{matrix} {{u_1}}&{{u_2}} \end{matrix}} \right] ^{{\text { }}T}}$

where ${u_1},{u_2} \in {\mathbb {R}^{3 \times 1}}$ are submatrices of ${u_e}$; ${M_{{\text {ij}}}},{C_{{\text {ij}}}} \in {\mathbb {R}^{3 \times 3}}$ are submatrices of M and C, respectively.

$\Rightarrow {u_2}=-M_{21}{{\ddot{\chi }}_{1d}}-C_{21}{\dot{\chi }_{1d}}$

(10) is rewritten as follows:

$$\begin{aligned} {{\ddot{\chi }}_e}=M^{-1}({u_e}-G-C_n{\dot{\chi }_e}) \end{aligned}$$

(11)

Step 2: Defining new tracking error vectors

${Z_1}={\chi _e}={\left[ {\begin{matrix} {x - {x_d}}&{y - {y_d}}&{\psi - {\psi _d}}&{\begin{matrix} {{\vartheta _x}}&{{\vartheta _y}}&\delta \end{matrix}} \end{matrix}} \right] ^{\text {T}}}$

${Z_2} = {\dot{Z}_1} \in {\mathbb {R}^{6 \times 1}}$.

For backstepping to be applied, one must rewrite (11) using a strict feedback form as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{\dot{Z}}_1} = {Z_2} \\&{{\dot{Z}}_2} = {M^{ - 1}}\left( {{u_e} - G - C_n {\mathrm{Z}_2}} \right) \\ \end{aligned} \right. \end{aligned}$$

(12)

Step 3: Considering the first subsystem in (12): ${\dot{Z}_1} = {Z_2}$.

A positive-definite Lyapunov function is defined as:

$$\begin{aligned} {V_1} = \frac{1}{2}{Z_1}^T\Upsilon _1^{ - 1}{Z_1} + \frac{1}{2}{\left( {\int _0^t {{Z_1}d\tau } } \right) ^T}{\Gamma _1} {\int _0^t {{Z_1}d\tau } } \end{aligned}$$

(13)

where ${\Upsilon _1},{\Gamma _1} \in {\mathbb {R}^{6 \times 6}}$ are arbitrary positive diagonal matrices.

Differentiating $V_1$ with respect to time yields:

$$\begin{aligned} {{\dot{V}}_1}&= {Z_1}^T \Upsilon _1^{ - 1}{\dot{Z}_1} + {\left( {\int _0^t {\frac{{\partial {Z_1}}}{{\partial \tau }}d\tau } } \right) ^T}{\Gamma _1} {\int _0^t {{Z_1}d\tau } } \nonumber \\&= {Z_1}^T \left( {\Upsilon _1^{ - 1}{Z_2} + {\Gamma _1} {\int _0^t {{Z_1}d\tau } } } \right) \end{aligned}$$

(14)

$$\begin{aligned} {{\dot{V}}_1}&= {Z_1}^T \left( {\Upsilon _1^{ - 1}{Z_2} + {\Gamma _1} {{\small \int _0^t} {{Z_1}d\tau } } }+\Gamma _2 {Z_1}-\Gamma _2 {Z_1} \right) \end{aligned}$$

(15)

where ${\Gamma _2} \in {\mathbb {R}^{6 \times 6}}$ is arbitrary positive diagonal matrix.

Let us denote

$$\begin{aligned} {Z_{2d}}&= - {\Upsilon _1}{\Gamma _1} {\int _0^t {{Z_1}d\tau } } - {\Upsilon _1}{\Gamma _2}{Z_1} \nonumber \\&\Leftrightarrow \Upsilon _1^{ - 1}{Z_{2d}} + {\Gamma _1}\left( {\int _0^t {{Z_1}d\tau } } \right) + {\Gamma _2}{Z_1} = 0 \end{aligned}$$

(16)

It can be seen from (15) that if $\mathop {\lim }\limits _{t \rightarrow \infty } {Z_2} = {Z_{2d}}$, then ${{\dot{V}}_1} = - {Z_1}^T{\Gamma _2}{Z_1} \leqslant 0$.

Thus, the first subsystem in (12) is stable at the origin if the control signal vector ${u_e}$ is found such that:

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow T} {Z_2} = {Z_{2d}},{\text { }}t \in \left[ {0,T} \right] \end{aligned}$$

(17)

where T is a finite-time and ${Z_{2d}}$ denotes the reference state.

Step 4: Considering the second subsystem in (12):

$$\begin{aligned} {\dot{Z}_2}=M^{-1}({u_e}-G-C_n{\dot{\chi }_e}) \end{aligned}$$

(18)

Definition of error vector as follows:

$$\begin{aligned} {\xi }&={Z_2} - {Z_{2d}} = {Z_2} + {\Upsilon _1}{\Gamma _2}{Z_1} + {\Upsilon _1}{\Gamma _1} {\int _0^t {Z_1}d\tau } \nonumber \\&= \left[ {\begin{matrix} {{\xi _1}} \\ {{\xi _2}} \end{matrix}} \right] \end{aligned}$$

(19)

where ${\xi _1}, {\xi _2} \in {\mathbb {R}^{3 \times 1}}$ are submatrices of ${\xi }$.

The first subsystem in (12) is rewritten as:

$$\begin{aligned} {\dot{Z}_1} = {\xi } - {\Upsilon _1}{\Gamma _2} {Z_1} - {\Upsilon _1}{\Gamma _1} {\int _0^t {{Z_1}d\tau }} \end{aligned}$$

(20)

Represent the matrices in the following form:

${M^{- 1}} = K = \left[ {\begin{matrix} {{K_{11}}}&{}{{K_{12}}} \\ {{K_{21}}}&{}{{K_{22}}} \end{matrix}} \right] = \left[ {\begin{matrix} {{K_1}} \\ {{K_2}} \end{matrix}} \right]$,

${K_1} = \left[ {\begin{matrix} {{K_{11}}}&{{K_{12}}} \end{matrix}} \right]$, ${K_2} = \left[ {\begin{matrix} {{K_{21}}}&{{K_{22}}} \end{matrix}} \right]$

${Z_1} = \left[ {\begin{matrix} {{Z_{11}}} \\ {{Z_{12}}} \end{matrix}} \right]$, ${\Upsilon _1} = \left[ {\begin{matrix} {{\Upsilon _{11}}}&{}\Theta \\ \Theta &{}{{\Upsilon _{12}}} \end{matrix}} \right]$,

${\Gamma _1} = \left[ {\begin{matrix} {{\Gamma _{11}}}&{}\Theta \\ \Theta &{}{{\Gamma _{12}}} \end{matrix}} \right]$, ${\Gamma _2} = \left[ {\begin{matrix} {{\Gamma _{21}}}&{}\Theta \\ \Theta &{}{{\Gamma _{22}}} \end{matrix}} \right]$

where ${K_{{\text {ij}}}},{\Gamma _{{\text {ij}}}} \in {\mathbb {R}^{3 \times 3}}$,${\Upsilon _{11}},{\Upsilon _{12}} \in {\mathbb {R}^{3 \times 3}}, \Theta = {\left[ 0 \right] ^{3 \times 3}}$ and ${Z_{11}}, {Z_{12}} \in {\mathbb {R}^{3 \times 1}}$.

Taking the time derivative of (20), it gives:

$$\begin{aligned} \left[ {\begin{matrix} {{\dot{\xi }}_1} \\ {{\dot{\xi }}_2} \end{matrix}} \right]&= \left[ {\begin{matrix} {{K_{11}}} \\ {{K_{21}}} \end{matrix}} \right] {u_1} + \left[ {\begin{matrix} {{K_{12}}} \\ {{K_{22}}} \end{matrix}} \right] {u_2} - \left[ {\begin{matrix} {{K_1}\left( { {C_n}{Z_2} + G} \right) } \\ {{K_2}\left( { {C_n} {Z_2} + G} \right) } \end{matrix}} \right] \nonumber \\&\quad + \left[ {\begin{matrix} {{\Upsilon _{11}}{\Gamma _{11}}{Z_{11}}} \\ {{\Upsilon _{12}}{\Gamma _{12}}{Z_{12}}} \end{matrix}} \right] + \left[ {\begin{matrix} {{\Upsilon _{11}}{\Gamma _{21}}{\xi _1}} \\ {{\Upsilon _{12}}{\Gamma _{22}}{\xi _2}} \end{matrix}} \right] \nonumber \\&\quad - \left[ {\begin{matrix} {{\Upsilon ^2}_{11}{\Gamma ^2}_{21}{Z_{11}}} \\ {{\Upsilon ^2}_{12}{\Gamma ^2}_{22}{Z_{12}}} \end{matrix}} \right] \nonumber \\&\quad - \left[ {\begin{matrix} {{\Upsilon _{11}}{\Gamma _{21}}{\Upsilon _{11}}{\Gamma _{11}}\int _0^t {{Z_{11}}d\tau } } \\ {{\Upsilon _{12}}{\Gamma _{22}}{\Upsilon _{11}}{\Gamma _{12}}\int _0^t {{Z_{12}}d\tau } } \end{matrix}} \right] \end{aligned}$$

(21)

Next, let us define:

$$\begin{aligned} {f_1}&= {K_{12}}{u_2} - {K_1}\left( { {C_n} {Z_2} + G} \right) + {\Upsilon _{11}}{\Gamma _{11}}{Z_{11}} \nonumber \\&\quad + {\Upsilon _{11}}{\Gamma _{21}}{\xi _1}- {\Upsilon ^2}_{11}{\Gamma ^2}_{21}{Z_{11}} \nonumber \\&\quad - {\Upsilon _{11}}{\Gamma _{21}}{\Upsilon _{11}}{\Gamma _{11}}\int _0^t {{Z_{11}}d\tau } \end{aligned}$$

(22)

$$\begin{aligned} {f_2}&= {K_{22}}{u_2} - {K_2}\left( {{C_n}{Z_2} + G} \right) + {\Upsilon _{12}}{\Gamma _{12}}{Z_{12}} \nonumber \\&\quad + {\Upsilon _{12}}{\Gamma _{22}}{\xi _2}- {\Upsilon ^2}_{12}{\Gamma ^2}_{22}{Z_{12}} \nonumber \\&\quad - {\Upsilon _{12}}{\Gamma _{22}}{\Upsilon _{11}}{\Gamma _{12}}\int _0^t {{Z_{12}}d\tau } \end{aligned}$$

(23)

where ${u_2}=-M_{21}{{\ddot{\chi }}_{1d}}-C_{21}{\dot{\chi }_{1d}}$

Then, (21) becomes

$$\begin{aligned} \left\{ \begin{aligned} {{{\dot{\xi }} }_1} = {f_1} + {K_{11}}{u_1} \\ {{{\dot{\xi }} }_2} = {f_2} + {K_{21}}{u_1} \\ \end{aligned} \right. \end{aligned}$$

(24)

Step 5: As can be seen in (21), ${Z_2}$ and ${Z_{2d}}$ are related by nonlinear (24).

For (17) to be satisfied, then

$$\begin{aligned} \left\{ \begin{aligned} \mathop {\lim }\limits _{t \rightarrow T} {\xi _1}={0}, \\ \mathop {\lim }\limits _{t \rightarrow T} {\xi _2}={0} \end{aligned} \right. \end{aligned}$$

For this purpose, the hierarchical sliding mode control (HSMC) method [18] is applied.

The first-layer sliding surfaces for subsystems (24) is defined as follows:

$$\begin{aligned} \left\{ \begin{aligned} {s _1}&= {\xi _1}, \\ {s _2}&= {\xi _2} \end{aligned} \right. \end{aligned}$$

(25)

First, consider the first subsystem in (24):

$$\begin{aligned} {{\dot{\xi }} _1} = {f_1}+K_{11}{u_{11}} \end{aligned}$$

(26)

where ${u_{11}}$ is the first subsystem’s control signal.

Using a positive-definite Lyapunov function as follows:

$$\begin{aligned} V_{1\xi }&= \frac{1}{2}{\left( {1 - {\gamma _1}} \right) ^p}{\left( {\int _0^t {{\xi _1}d\tau } } \right) ^T}{\Xi _2} {\int _0^t {{\xi _1}d\tau } } \nonumber \\&\quad +\frac{1}{2}{\xi _1}^T\Upsilon _2^{ - 1}{\xi _1} \end{aligned}$$

(27)

where ${\Upsilon _2},{\Xi _2} \in {\mathbb {R}^{3 \times 3}}$ are arbitrary positive diagonal matrices, $p > 0$ and ${\gamma _1} \in \left[ {0,1} \right]$.

Let ${\lambda _{\Upsilon \min }},{\lambda _{\Upsilon \max }}$ be the minimum and maximum eigenvalues of $\Upsilon _2^{ - 1}$, respectively. Also, ${\lambda _{{\Xi _2}\min }},{\lambda _{{\Xi _2}\max }}$ denote the minimum and largest eigenvalues of ${\Xi _2}$, respectively.

The quadratic form inequality is applied to (27), we have:

$$\begin{aligned} \left\{ {\begin{matrix} {{\lambda _{\Upsilon \min }}{{\left\| {{\xi _1}} \right\| }^2} + {{\left( {1 - {\gamma _1}} \right) }^p}{\lambda _{{\Xi _2}\min }}{{\left\| {\int \limits _0^t {{\xi _1}d\tau } } \right\| }^2} \leqslant {V_{1\xi }}} \\ {{\lambda _{\Upsilon \max }}{{\left\| {{\xi _1}} \right\| }^2} + {{\left( {1 - {\gamma _1}} \right) }^p}{\lambda _{{\Xi _2}\max }}{{\left\| {\int \limits _0^t {{\xi _1}d\tau } } \right\| }^2} \geqslant {V_{1\xi }}} \end{matrix}} \right. \end{aligned}$$

(28)

Since $0 \leqslant {\gamma _1} \leqslant 1$, ${\lambda _{{\Xi _2}\min }},{\lambda _{{\Xi _2}\max }} > {0}$ (the eigenvalues of a positive definite matrix are always positive), it leads to

$$\begin{aligned} \left\{ {\begin{array}{l} {{\lambda _{\Upsilon \min }}{{\left\| {{\xi _1}} \right\| }^2} \leqslant {V_{1\xi }}} \\ {{\lambda _{\Upsilon \max }}{{\left\| {{\xi _1}} \right\| }^2} + {\lambda _{{\Xi _2}\max }}{{\left\| {\int \limits _0^t {{\xi _1}d\tau } } \right\| }^2} \geqslant {V_{1\xi }}} \end{array}} \right. \end{aligned}$$

(29)

It can be seen that if ${\lambda _{{\Xi _2}\max }}$ is sufficiently small, $V_{1\xi }$ can be considered as a proper function (see definition 2).

Taking the time derivative on both sides of (27) and pay attention to (26), it gives:

$$\begin{aligned} {{\dot{V}}_{1\xi }} = {\xi _1}^T\left( \begin{aligned} \Upsilon _2^{ - 1}{f_1} + \Upsilon _2^{ - 1}{K_{11}}{u_{11}} + \\ {\left( {1 - {\gamma _1}} \right) ^p}{\Xi _2}{\int _0^t {{\xi _1}d\tau } } \\ \end{aligned} \right) \end{aligned}$$

(30)

The first subsystem’s control signal $u_{11}$ includes two components $u_{11\mathrm{eq}}$ and $u_{11\mathrm{sw}}$, where $u_{11\mathrm{eq}}$ (equivalent control law) maintains the system state on the sliding surface while $u_{11\mathrm{sw}}$(switching control law) pulls system state back to the sliding surface if it is pushed away.

Hence, (30) can be rewritten as follows:

$$\begin{aligned} {{\dot{V}}_{1\xi }} = {\xi _1}^T\left( \begin{aligned}&\Upsilon _2^{ - 1}{f_1} + \Upsilon _2^{ - 1}{K_{11}}\left( {{u_{11\mathrm{eq}}} + {u_{11\mathrm{sw}}}} \right) + \\&{\left( {1 - {\gamma _1}} \right) ^p}{\Xi _2}{\int _0^t {{\xi _1}d\tau } } \end{aligned} \right) \end{aligned}$$

(31)

The control signals are defined as follows:

$$\begin{aligned} \left\{ \begin{aligned}{l} {u_{11\mathrm{eq}}} =&- {\left( {\Upsilon _2^{ - 1}{K_{11}}} \right) ^{ - 1}}\left( \begin{aligned} {\left( {1 - {\gamma _1}} \right) ^p}{\Xi _2}\int _0^t {{\xi _1}d\tau + } \\ \Upsilon _2^{ - 1}{f_1} \\ \end{aligned} \right) \\ {u_{11\mathrm{sw}}} =&- {\left( {\Upsilon _2^{ - 1}{K_{11}}} \right) ^{ - 1}}\left( {{c_1}{\xi _1} + {c_2}\mathrm{sign}\left( {{\xi _1}} \right) } \right) \\ \end{aligned} \right. \end{aligned}$$

(32)

with ${c_1},{c_2} \in {\mathbb {R}^{3 \times 3}}$ are any positive diagonal matrices.

Then, (31) becomes:

${{\dot{V}}_{1\xi }} = - \xi _1^T{c_1}{\xi _1} - \xi _1^T{c_2}\mathrm{sign}\left( {{\xi _1}} \right)$

$\Rightarrow {{\dot{V}}_{1\xi }} \leqslant - \lambda _{{\text {min}}}^{{c_1}}\xi _1^T{\xi _1} - \lambda _{{\text {min}}}^{{c_2}}\xi _1^T\mathrm{sign}\left( {{\xi _1}} \right) = -\kappa _1 \left( {\left\| {{\xi _1}} \right\| } \right)$, where $\lambda _{{\text {min}}}^{{c_1}}, \lambda _{{\text {min}}}^{{c_2}}$ are the smallest eigenvalues of matrices $c_1$ and $c_2$, respectively.

This indicates that the first subsystem in (24) is asymptotically stable, according to Lemma 1.

The second subsystem’s control signal is denoted $u_{12}$, including two components: $u_{12eq}$ (equivalent control law) and $u_{12sw}$ (switching control law).

In the same manner as above, the control equivalent law for the second subsystem in (24) is determined as follows:

$$\begin{aligned} {u_{12eq}} = - {\left( {\Upsilon _3^{ - 1}{K_{21}}} \right) ^{ -1}}\left( \begin{aligned} {\left( {1 - {\gamma _2}} \right) ^p}{\Xi _3}\int _0^t {{\xi _2}d\tau + } \\ \Upsilon _3^{ - 1}{f_2} \\ \end{aligned} \right) \end{aligned}$$

(33)

Here, $\Upsilon _3^{ - 1}, \Xi _3 \in {\mathbb {R}^{3 \times 3}}$ are arbitrary positive diagonal matrices, and ${\gamma _2} \in \left[ {0,1} \right]$.

Next, define the second-layer sliding surface as:

$$\begin{aligned} S = {\alpha _1}{s_1} + {\alpha _2}{s_2} \end{aligned}$$

(34)

where ${\alpha _1},{\alpha _2} \in {\mathbb {R}^{3 \times 3}}$ are diagonal matrices.

Using the Lyapunov candidate function as follows:

$$\begin{aligned} {V_S} = \frac{1}{2}{S^T}\Upsilon S + \frac{1}{2}{\left( {\int _0^t {Sd\tau } } \right) ^T}\Upsilon {\left( {1 - \gamma } \right) ^p}\Xi \int _0^t {Sd\tau } \end{aligned}$$

(35)

where $\Upsilon ,\Xi \in {\mathbb {R}^{3 \times 3}}$ are arbitrary positive diagonal matrices, $p > 0$.

Let $\lambda _{\min }^\Upsilon ,\lambda _{\max }^\Upsilon$ be the minimum and maximum eigenvalues of $\Upsilon$, respectively. Also, let $\lambda _{\min }^\Xi ,{\text { }}\lambda _{\max }^\Xi$ be the minimum and largest eigenvalues of $\Upsilon \Xi$, respectively.

Similar to (29), applying the quadratic form inequality into (35), it yields:

$$\begin{aligned} \lambda _{\min }^\Upsilon {\left\| S \right\| ^2} \leqslant {V_S} \leqslant \lambda _{\max }^\Upsilon {\left\| S \right\| ^2} + \lambda _{\max }^\Xi {\left\| {\int _0^t {Sd\tau } } \right\| ^2} \end{aligned}$$

(36)

It can be seen that if $\lambda _{\max }^\Xi$ is sufficiently small, ${V_S}$ can be considered as a proper function (see definition 2).

Taking the time derivative on both sides of (35) and paying attention to (34), it yields:

$$\begin{aligned} {{\dot{V}}_S}&= {S^T}\Upsilon {\left( {1 - \gamma } \right) ^p}\Xi \int _0^t {\left( {{\alpha _1}{s_1} + {\alpha _2}{s_2}} \right) d\tau } \nonumber \\&\quad +{S^T}\Upsilon \left( {{\alpha _1}{{\dot{s}}_1}+{\alpha _2}{{\dot{s}}_2}} \right) \end{aligned}$$

(37)

In (24), the control signal for the entire system is designed as follows:

$$\begin{aligned} {u_1} = {u_{11\mathrm{eq}}} + {u_{11\mathrm{sw}}} + {u_{12\mathrm{sw}}} + {u_{12\mathrm{eq}}} \end{aligned}$$

(38)

Determine matrices ${\Xi _2}$ and ${\Xi _3}$ such that:

$$\begin{aligned} {\left( {1 - {\gamma _1}} \right) ^p}{\Upsilon _2}{\Xi _2} = {\left( {1 - {\gamma _2}} \right) ^p}{\Upsilon _3}{\Xi _3} = {\left( {1 - \gamma } \right) ^p}\Xi \end{aligned}$$

(39)

Substituting (24), (25) and (38) into (37), we obtain:

$$\begin{aligned} {{\dot{V}}_S} = {S^T}\Upsilon \left( \begin{aligned} {\alpha _1}{\Upsilon _2}\left( \begin{aligned} \Upsilon _2^{ - 1}{f_1} + \Upsilon _2^{ - 1}{K_{11}}{u_{11\mathrm{eq}}} + \\ {\left( {1 - {\gamma _1}} \right) ^p}{\Xi _2}\int _0^t {{s_1}d\tau } \\ \end{aligned} \right) + \\ {\alpha _2}{\Upsilon _3}\left( \begin{aligned} \Upsilon _3^{ - 1}{f_2} + \Upsilon _3^{ - 1}{K_{21}}{u_{12\mathrm{eq}}} + \\ {\left( {1 - {\gamma _2}} \right) ^p}{\Xi _3}\int _0^t {{s_2}d\tau } \\ \end{aligned} \right) + \\ {\alpha _1}{K_{11}}\left( {{u_{11\mathrm{sw}}} + {u_{12\mathrm{sw}}} + {u_{12\mathrm{eq}}}} \right) + \\ {\alpha _2}{K_{21}}\left( {{u_{11\mathrm{eq}}} + {u_{11\mathrm{sw}}} + {u_{12\mathrm{sw}}}} \right) \\ \end{aligned} \right) \end{aligned}$$

(40)

Substituting (32) and (33) into (40) yields:

$$\begin{aligned} {{\dot{V}}_S} ={S^T}\Upsilon \left( \begin{aligned}&\left( {{\alpha _2}{K_{21}} + {\alpha _1}{K_{11}}} \right) \left( {{u_{11\mathrm{sw}}} + {u_{12\mathrm{sw}}}} \right) +\\&{\alpha _1}{K_{11}}{u_{12eq}} + {\alpha _2}{K_{21}}{u_{11eq}} \\ \end{aligned} \right) \end{aligned}$$

(41)

The control signals are designed to satisfy:

$$\begin{aligned} \begin{aligned} \left( {{\alpha _2}{K_{21}} + {\alpha _1}{K_{11}}} \right) \left( {{u_{11\mathrm{sw}}} + {u_{12\mathrm{sw}}}} \right) + {\alpha _1}{K_{11}}{u_{12\mathrm{eq}}} + \\ {\alpha _2}{K_{21}}{u_{11\mathrm{eq}}} = - {\lambda _1}S - {\lambda _2}\mathrm{sign}\left( S \right) \end{aligned} \end{aligned}$$

(42)

where ${\lambda _1},{\lambda _2} \in {\mathbb {R}^{3 \times 3}}$ are positive diagonal matrices.

It means that

$$\begin{aligned} {u_{11\mathrm{sw}}} + {u_{12\mathrm{sw}}} = - {\left( \begin{aligned}{\alpha _2}{K_{21}} + \\ {\alpha _1}{K_{11}} \end{aligned}\right) ^{ - 1}}\left( \begin{aligned} {\alpha _1}{K_{11}}{u_{12\mathrm{eq}}} + \\ {\alpha _2}{K_{21}}{u_{11\mathrm{eq}}} + \\ {\lambda _1}S + \\ {\lambda _2}\mathrm{sign}\left( S \right) \\ \end{aligned} \right) \end{aligned}$$

(43)

Substituting (42) into (41) yields:

$$\begin{aligned} {{\dot{V}}_S} = - {S^T}\Upsilon {\lambda _1}S - {S^T}\Upsilon {\lambda _2}\mathrm{sign}\left( S \right) \leqslant 0 \end{aligned}$$

(44)

$\Rightarrow {{\dot{V}}_{S }} \leqslant - \lambda _{{\text {min}}}^{\Upsilon {\lambda _1}}S^TS - \lambda _{{\text {min}}}^{\Upsilon {\lambda _2}}S^T\mathrm{sign}\left( {S} \right) = -\kappa \left( {\left\| S \right\| } \right)$. Here, $\lambda _{{\text {min}}}^{\Upsilon {\lambda _1}}$ and $\lambda _{{\text {min}}}^{\Upsilon {\lambda _2}}$ are the smallest eigenvalues of matrices $\Upsilon {\lambda _1}$ and $\Upsilon {\lambda _2}$, respectively.

Thus, the second-layer sliding surface (S) is asymptotically stable by the LaSalle’s principle (see Lemma 1).

As a result of the steps described above, we can derive the following theorem.

Theorem 1

If the control law is defined as in (38) and the sliding surfaces are defined as in (25), (34), then, the subsystems and the entire system in (24) will stabilize asymptotically at the origin, i.e.,

1) $\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _1} = {0} ,{\text { }}\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _2} = {0}$

2) $\mathop {\lim }\limits _{t \rightarrow \infty } S = {0}$

$where \,\,u_{11\mathrm{eq}}$ and $u_{12\mathrm{eq}}$ are defined as in (32) and (33), respectively; $u_{11\mathrm{sw}}$ and $u_{12\mathrm{sw}}$ are determined to satisfy (43).

A detailed proof of this theorem based on the concept of asymptotic stability can be found in Appendix B.

In addition, to minimize the chattering phenomenon, the function $\mathrm{sat}(S)$ is proposed to replace the function $\mathrm{sign}(S)$ in (43), which is defined as follows:

$$\begin{aligned} \mathrm{sat}\left( S \right) = \left\{ \begin{aligned}&S,{\text { }}\left\| S \right\| \leqslant 1 \\&\mathrm{sign}\left( S \right) ,{\text { }}\left\| S \right\| > 1 \\ \end{aligned} \right. \end{aligned}$$

(45)

4 Proposed adaptive fuzzy backstepping hierarchical sliding mode control

4.1 System control structure diagram

We know that crane control aims to track the desired value and minimize load vibration even during high-speed operations. Given the position and velocity errors as inputs, the BHSMC controller can achieve the desired control quality if the dynamic parameters are precisely defined and the assumptions mentioned in Sect. 2 are satisfied. However, this scenario does not occur in actuality. Furthermore, the overhead crane is also susceptible to unknown external disturbances like wind and rain when operating outside. In order to increase BHSMC’s robustness in real-life overhead crane control, we integrated an FLS that adjusts the controller parameters accordingly to uncertainty and external disturbances. The proposed control structure diagram for the overhead crane is shown in Fig.  2.

Fig. 2

The proposed control structure diagram. It includes a BHSMC controller (central controller) and a fuzzy logic system to adjust parameters ${\alpha _1},{\alpha _2},{\lambda _1},{\lambda _2}$ of BHSMC

Fig. 3

Membership functions for input and output variables used to tune the parameter a of ${\lambda _1}$

Table 1 Fuzzy tuning rules for the parameter a

Fig. 4

Membership functions for input and output variables used to tune the parameter b of ${\lambda _1}$

As can be seen in (43) and (44), the parameters ${\alpha _1},{\alpha _2},{\lambda _1}$, and ${\lambda _2}$ directly affect the sliding surface and stability. This section introduces a fuzzy system-based approach for adjusting those parameters to change the sliding surface. To reduce computation and design efforts, ${\lambda _1}$ will be adjusted by FLS, and the remaining parameter matrices ${\alpha _1},{\alpha _2}$, and ${\lambda _2}$, will be represented linearly by ${\lambda _1}$, as follows:

$$\begin{aligned}&{\lambda _1} = \mathrm{diag}\left\{ {a,b,c} \right\} , \nonumber \\&{\alpha _1} = {A_2}.{\lambda _1}, {\alpha _2} = {A_3}.{\lambda _1},{\lambda _2} = {A_4}.{\lambda _1} \end{aligned}$$

(46)

with ${A_2},{A_3},{A_4} \in {\mathbb {R}^{3 \times 3}}$ are fixed positive diagonal matrices

4.2 Fuzzy algorithm design

Using FLS for ${\lambda _1}$, the parameter a is tuned via the inputs ${e_x} = x - {x_d}$ and its derivative with respect to time ${{\dot{e}}_x}$, b is tuned via the inputs ${e_y} = y - {y_d}$ and its derivative with respect to time ${{\dot{e}}_y}$, and c is tuned via the inputs ${e_\psi } = \psi - {\psi _d}$ and its derivative with respect to time ${{\dot{e}}_\psi }$.

A two-input and one-output FLS is designed to tune parameter a, including fuzzification, fuzzy rule base, and defuzzification. The first linguistic input variable for this FLS is trolley position error: ${e_x} = x - {x_d}$. Five fuzzy sets cover this variable’s range: Negative Big (NB), Negative Small (NS), Zero (Z), Positive Small (PS), and Positive Big (PB). The Gaussian membership functions are used to describe this linguistic variable, as shown in Fig.  3a. The second linguistic input variable is trolley velocity error ${{\dot{e}}_x}$ which is described similarly, as shown in Fig. 3b. The linguistic output variable a is covered by three fuzzy sets: Zero (Z), Small (S) and Big (B). The Gaussian membership functions are used to describe this linguistic variable, as shown in Fig. 3c.

Thus, these fuzzy tuning rules for the parameter a are given in Table 1, which can be expressed as

$$\begin{aligned}&R_i : \text {IF } {e_x} \text {is } A_i^1 \text {and } {{\dot{e}}_x} \text {is } A_i^2 \text {THEN } a \text {~is } \\&\qquad \qquad \qquad (i=1,2...N) \end{aligned}$$

where $R_i$ is the $i^{th}$ rule of the N rules; $A_i^1,A_i^2,{B_i}$ are fuzzy sets characterized by Gaussian membership functions ${\mu _{A_i^1}}\left( {{e_x}} \right) ,{\mu _{A_i^2}}\left( {{{{\dot{e}}}_x}} \right)$ and ${\mu _{{B_i}}}\left( a \right)$, respectively.

Lastly, the 25 rules in Table 1 were combined using the product inference engine, the singleton fuzzifier, and the center average defuzzifier [52], the output of the FLS can be expressed by:

$$\begin{aligned} a = \frac{{\sum \nolimits _{i = 1}^N {{{\bar{a}}_i}\left( {{\mu _{A_i^1}}\left( {{e_x}} \right) \times {\mu _{A_i^2}}\left( {{{{\dot{e}}}_x}} \right) } \right) } }}{{\sum \nolimits _{i = 1}^N {\left( {{\mu _{A_i^1}}\left( {{e_x}} \right) \times {\mu _{A_i^2}}\left( {{{{\dot{e}}}_x}} \right) } \right) } }} \end{aligned}$$

(47)

where ${\bar{a}_i}$ is the center of the fuzzy set ${B_i}$ at which ${\mu _{{B_i}}}$ achieves its maximum value.

Table 2 Fuzzy tuning rules for the parameter b

Fig. 5

Membership functions for input and output variables used to tune the parameter c of ${\lambda _1}$

Repeat the process with variables b and c. The fuzzy sets and rules for tuning parameter b are depicted in Fig. 4 and Table 2. The fuzzy sets and rules for tuning parameter c are depicted in Fig. 5 and Table 3. By adjusting each parameters a, b and c, the FLS controller adjusts ${\lambda _1}$, and thus also adjust other parameter matrices ${\alpha _1},{\alpha _2}$, and ${\lambda _2}$ according to (46).

5 Simulation results

This section presents the results of simulations performed to validate the effectiveness of the proposed method for 3D overhead crane control. As BHSMC serves as the primary controller in our design, we performed simulations and compared the system response results between BHSMC and AFBHSMC. In the simulation results below, solid blue lines indicate the results from AFBHSMC, while red dashed lines represent the results from BHSMC.

Simulations are performed assuming that system parameters are known. The controller parameters are also selected based on experience (i.e., trial and error) to achieve the best quality possible through simulation.

The system parameters are as follows:

${m_b} = 2316(\text {Kg}),{m_c} = 5000(\text {Kg})$

${m_t} = 372(\text {Kg}),J = 180\left( {{\text {Kg}}{\text {.}}{{\text {m}}^{\text {2}}}} \right)$

$r = 0.31\left( {\text {m}} \right) , g = 9.81\left( {{\text {m/}}{{\text {s}}^{\text {2}}}} \right)$

$\Delta \delta = 0.01\left( {\text {m}} \right) , \rho = 300000\left( {{\text {N/m}}} \right)$

${\eta _b} = 350\left( {{\text {N.m/s}}} \right) , {\eta _t} = 310\left( {{\text {N.m/s}}} \right)$

${\eta _r} = 260\left( {{\text {N.m/s}}} \right) ,{\eta _m} = 170\left( {{\text {N.m/s}}} \right)$

The controller parameters are selected as

${\Upsilon _1} = \mathrm{diag}\left( {1,1,1,1,1,1} \right)$

$\Upsilon = {\Upsilon _2} = {\Upsilon _3} = \Xi = {\Xi _2} = {\Xi _3} = \mathrm{diag}\left( {1,1,1} \right)$

${\Gamma _1} = \mathrm{diag}\left( {250,1,2,5000,0.5,1} \right)$

${\Gamma _2} = \mathrm{diag}\left( {150,15,70,80,20,10} \right)$

$\gamma = {\gamma _1} = {\gamma _2} = 0.9,{\text { }}p = 3$

${\alpha _1} = \mathrm{diag}\left( {1000,1000,10} \right)$

${\alpha _2} = \mathrm{diag}\left( { - 50, - 50,30} \right)$

${\lambda _1} = \mathrm{diag}\left( {0.05,0.06,0.01} \right) ,{\text { }}{\lambda _2} = \left( {0.5,1,1} \right)$

Table 3 Fuzzy tuning rules for the parameter c

We conducted three experiments in Matlab’s simulation environment to verify the system responses in cases where the reference values are constants or trapezoidal signals with/without the influence of unknown external disturbances.

5.1 Preset value tracking control

First, we consider the movement of the overhead crane system from the initial state ${\chi _0} = {\left( {\begin{matrix}0&0&0&0&0&0.01 \end{matrix}} \right) ^T}$ to the desired state ${\chi _d} = {\left( {\begin{matrix}10&10&15&0&0&0 \end{matrix}} \right) ^T}$, where these six extended coordinates correspond to the 6 DOF to be controlled: trolley displacement (m), bridge displacement (m), rotation angle of the hoisting drum (rad), two payload swing angles (rad), and the axial payload oscillation (cm).

Fig. 6

Preset value tracking control results

Fig. 7

Simulated force signals acting on a 3D overhead crane

As shown in Fig. 6, the system’s actuated states include trolley motion, bridge travel, and hoisting drum rotation, reaching their steady-state value for BHSMC and AFBHSMC controllers. In addition, the underactuated states, including the two payload swing angles and the axial payload oscillation, are also suppressed and eliminated. The payload does not swing or oscillate axially as soon as the trolley reaches its destination. AFBHSMC has a significantly better control quality than BHSMC, as shown in Fig. 6a, d, and e. The results show that AFBHSMC-based system state converges to steady values faster than BHSMC-based system state. In Fig. 6c, the state $\psi$ has an overshoot, but only by about 6% of the reference value, and it rapidly settles to the desired value of 15 (rad) within six seconds. In Fig. 6d, the payload initially oscillates along the lifting cable by up to 2 (cm), but it is quickly eliminated within six seconds. Meanwhile, there are still small axial payload oscillations with BHSMC. As a result of the FLS integration into AFBHSMC, the chattering phenomena in the output have almost completely eliminated, as seen in Fig. 6f.

Figure 7 shows the system’s control signals: the trolley force ($u_t$), the bridge force ($u_b$), and the torque of the rotating drum ($u_d$). It can be seen that AFBHSMC’s control signals have a much smaller overshoot and more quickly reach a steady-state than those of BHSMC. Compared to BHSMC, the superior control quality of AFBHSMC derives from its ability to self-adjust the sliding surface through an FLS to actively “catch” the system state that is not on the sliding surface (red dashed line in Fig.  8). This means that the control signals of AFBHSMC pull the system state back to the sliding surface (Fig. 8) when it is pushed away. Thus, the overshoot and the undershoot are significantly reduced, as seen in Figs. 6 and 7.

Fig. 8

The system’s state changes on the sliding surface for BHSMC and AFBHSMC

Fig. 9

Manhattan norm of the sliding surfaces for first- and second-layer sliding surface

Fig. 10

Trajectory tracking control results without external disturbances

Figure 9 shows the trend of the sliding surfaces within the first ten seconds using AFBHSMC and BHSMC controllers. It can be seen that the Manhattan norm of the sliding surfaces rapidly approaches zero after about six seconds. In addition, the sliding surfaces for AFHSMC are smoother and approaching zero faster than those for BHSMC.

5.2 Trajectory tracking control without external disturbances

The crane system has a high degree of inertia during operation (the preset values cannot be changed suddenly), and it is assumed as a trapezoidal signal for simplicity. Figure 10 shows the trajectory tracking control responses for both BHSMC and AFBHSMC. It can be seen that AFBHSMC forces the trolley, bridge, and hoisting drum to follow its reference trajectory excellently. Additionally, unexpected payload swings are kept small during each reference value change and eliminated ten seconds later. Notably, the axial payload oscillation caused by the elasticity of the cable is also quickly entirely excluded by the proposed controller.

As shown in Fig. 10b, and c, the response curves of both AFBHSMC and BHSMC almost coincide with the reference trajectories. As a result, both controllers respond very well to bridge motion requests or payload lifting/lowering. For the remaining cases, as shown in Fig. 10a, d, e, and f, the AFBHSMC-based system responses have much smaller overshoots and settling times than those based on BHSMC. Furthermore, the “chattering” phenomenon in output responses, which appeared with BHSMC, was eliminated using AFBHSMC.

Fig. 11

The system’s state changes on the sliding surface for BHSMC (a) and AFBHSMC (b)

Fig. 12

External disturbances affect the trolley movement (a), bridge travel (b) and hoisting drum rotation (c)

As shown in Fig. 11, integrating FLS into AFBHSMC to adjust controller parameters and automatically adjust the sliding surface (green dashed line) as the setpoint changes enables the control signals that pull the system state back to the sliding surface (red dashed line) to be significantly reduced. In this way, the quality of AFBHSMC is superior to that of BHSMC.

Fig. 13

Trajectory tracking control results with external disturbances

5.3 Trajectory tracking control with external disturbances

Next, we examine the trajectory tracking control performance of the proposed controller against uncertain external disturbances. As shown in Fig. 12, the external disturbances on the trolley, bridge, and drum are square pulses acting on the system randomly.

As shown in 13, using the same reference signals as in the previous case (Fig. 10), these disturbances have almost no effect on the system’s moving states, except for the moving state of the trolley and the bridge (Fig. 13a and b). Even so, these states quickly reach their destination without oscillation. The results show that the proposed controller is highly adaptable to preset value changes and the influence of unknown external disturbances.

Figure 14 shows the variation of first- and second-layer sliding surfaces over time. It can be seen that whenever the reference value changes, for example, at 20 seconds, 40 seconds and 60 seconds, the sliding surfaces are knocked out of the equilibrium position, and then it quickly returns to equilibrium at the origin within 10 seconds. Thus, the proposed controller has a high level of stability once the system states are stabilized on the sliding surface.

Fig. 14

Manhattan norm of the sliding surfaces for first- and second-layer sliding surfaces

6 Conclusion

This paper has developed a novel dynamic model for 3D overhead cranes with six degrees of freedom. The sixth degree of freedom is that the axial load oscillation component caused by the elasticity of the lifting rope has been neglected in previous studies. This new crane model is built based on the Euler–Lagrange equation by considering all three movements of the trolley, bridge, and lifting drum to drive three actuated states (trolley motion, bridge travel, hoisting drum rotation) to their desired position while eliminating the three undesirable underactuated states (two payload swings and axial payload oscillation). In addition, an efficient adaptive control strategy (AFBHSMC) has been proposed using the backstepping, the HSMC techniques, and the FLS. The proposed control system’s stability has also been analyzed and proved mathematically as well as through simulations. Simulation results show that the proposed controller stabilizes the overhead crane system under constant reference signals or trapezoidal reference signals, with/without external disturbances. All system responses asymptotically approach the desired values within a short time. The bridge and trolley were controlled to move them to the desired position, and the cargo was lifted with a desired angle of the hoisting drum precisely. Additionally, the payload swings during the transfer process were minimized and eliminated at the destination. In particular, the payload oscillation along the lifting cable is suppressed and eliminated quickly.

Future work will verify the proposed controller’s effectiveness for the actual overhead crane system. In addition, we also extend this research direction by considering 3D cable elastic deformations and develop adaptive control schemes using deep neural networks.

Appendices

The coefficients of matrices

1. The coefficients of matrix M.

$$\begin{aligned}&l = \delta + \Delta \delta + r{\vartheta _x} + r\psi \\ {m_{11}}&= {m_c} + {m_t}\\ {m_{12}}&= {m_{21}} = {m_{51}} = {m_{15}} = 0\\ {m_{13}}&= {m_{31}} = {m_c}r\sin \left( {{\vartheta _x}} \right) \\ {m_{14}}&= {m_{41}} = {m_c}l\cos \left( {{\vartheta _x}} \right) \\ {m_{16}}&= {m_{61}} = {m_c}\sin \left( {{\vartheta _x}} \right) \\ {m_{22}}&= {m_c} + {m_b} + {m_t}\\ {m_{23}}&= {m_{32}} = {m_c}r\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ {m_{24}}&= {m_{42}} = \\&={m_c}\left( {r\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - l\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) } \right) \\ {m_{25}}&= {m_{52}} = {m_c}l\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \\ {m_{26}}&= {m_{62}} = {m_c}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ {m_{33}}&= J + {m_c}{r^2}\\ {m_{34}}&= {m_{43}} = {m_c}{r^2}{\text {co}}{{\text {s}}^2}\left( {{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ {m_{35}}&= {m_{53}} = \frac{1}{4}{m_c}{r^2}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ {m_{36}}&= {m_{63}} = {m_c}r\\ {m_{44}}&= {m_c}\left( \begin{aligned} {l^2} + {r^2}{\sin ^2}\left( {{\vartheta _y}} \right) {\text {co}}{{\text {s}}^2}\left( {{\vartheta _x}} \right) - \\ r\delta {\sin ^2}\left( {{\vartheta _y}} \right) \sin \left( {2{\vartheta _x}} \right) \\ \end{aligned} \right) \\ {m_{45}}&= {m_{54}} = \frac{1}{2}{m_c}rl\sin \left( {2{\vartheta _y}} \right) {\text {cos}}\left( {2{\vartheta _x}} \right) \\ {m_{46}}&= {m_{64}} = {m_c}r{\sin ^2}\left( {{\vartheta _y}} \right) {\cos ^2}\left( {{\vartheta _x}} \right) \\ {m_{55}}&= {m_c}\left( \begin{aligned} {l^2}{\cos ^2}\left( {{\vartheta _x}} \right) + {r^2}{\sin ^2}\left( {{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) - \\ rl\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {m_{56}}&= {m_{65}} = \frac{1}{4}{m_c}r\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ {m_{66}}&= {m_c} \end{aligned}$$

2. The coefficients of matrix C

$$\begin{aligned} {c_{11}}&= {c_{21}} = {c_{31}} = {c_{33}} = {c_{41}} = {c_{51}} = {c_{15}} = {c_{61}} = 0\\ {c_{12}}&= {c_{22}} = {c_{32}} = {c_{42}} = {c_{52}} = 0\\ {c_{62}}&= {c_{36}} = {c_{63}} = {c_{66}} = 0\\ {c_{13}}&= 2{m_c}r{{\dot{\vartheta }} _x}\cos \left( {{\vartheta _x}} \right) \\ {c_{14}}&= {m_c}\left( {r{{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) - l{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) } \right) \\ {c_{16}}&= 2{m_c}{{\dot{\vartheta }} _x}\cos \left( {{\vartheta _x}} \right) \\ {c_{23}}&= 2{m_c}r\left( \begin{aligned} {{\dot{\vartheta }} }_y\cos \left( {\vartheta _x} \right) \cos \left( {\vartheta _y} \right) - \\ {{\dot{\vartheta }} }_x\sin \left( {\vartheta _x} \right) \sin \left( {\vartheta _y} \right) \\ \end{aligned} \right) \\ {c_{24}}&= {m_c}\left( \begin{aligned} 2r{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ 2r{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ l{{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{25}}&= - {m_c}l\left( \begin{aligned} 2{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) + \\ {{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{26}}&= 2{m_c}\left( {{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - {{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) } \right) \\ {c_{34}}&= {m_c}r\left( \begin{aligned} - l{{{\dot{\vartheta }} }_x} + r{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) + \\ \frac{l}{2}{{{\dot{\vartheta }} }_y}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) + \\ r{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _x}} \right) - \\ \frac{r}{2}{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) \left( {1 + {{\sin }^2}\left( {{\vartheta _x}} \right) } \right) \\ \end{aligned} \right) \\ {c_{35}}&= {m_c}r\left( \begin{aligned} \frac{r}{2}{{{\dot{\vartheta }} }_y}\sin \left( {2{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) -\\ l{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) - \\ \frac{l}{2}{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{43}}&= {m_c}r\left( \begin{aligned} 2l{{{\dot{\vartheta }} }_x} + r{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) - \\ r{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{44}}&= {m_c}\left( \begin{aligned} - \left( \begin{aligned} l\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ r\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \times \\ \left( \begin{aligned} 2r{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ 2r{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ l {{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) + \\ lr{{{\dot{\vartheta }} }_x}{\cos ^2}\left( {{\vartheta _x}} \right) - {l^2}{{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _x}} \right) - \\ {l^2}{{{\dot{\vartheta }} }_y}{\sin ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ + \frac{{{l^2}}}{2}{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) + \\ lr{{{\dot{\vartheta }} }_x}{\sin ^2}\left( {{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{45}}&= {m_c}\left( \begin{aligned} \left( \begin{aligned} {l^2}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ rl\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \times \\ \left( \begin{aligned} 2{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) + \\ {{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) + \\ {l^2}{{{\dot{\vartheta }} }_y}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) - \\ rl{{{\dot{\vartheta }} }_y}{\sin ^2}\left( {{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{46}}&= {m_c}\left( \begin{aligned} 2l{{{\dot{\vartheta }} }_x} + r{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) - \\ r{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{53}}&= 2{m_c}r\left( \begin{aligned} l{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) - \\ r{{{\dot{\vartheta }} }_x}{\sin ^2}\left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \sin \left( {{\vartheta _y}} \right) - \\ r{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{54}}&= {m_c}\left( \begin{aligned} l\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \times \\ \left( \begin{aligned} 2r\left( \begin{aligned} {{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ {{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) - \\ l {{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ \left( {r\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - l\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) } \right) \times \\ \left( \begin{aligned} l\left( \begin{aligned} {{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ 2{{{\dot{\vartheta }} }_y}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) + \\ r{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ \end{aligned} \right) \\ {c_{55}}&= {m_c}\left( \begin{aligned} \left( \begin{aligned} r{{{\dot{\vartheta }} }_y}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ l{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \times \\ \left( \begin{aligned} r\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ l\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) - \\ {l^2}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \times \\ \left( \begin{aligned} 2{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) + \\ {{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ \end{aligned} \right) \\ {c_{56}}&= {m_c}\left( \begin{aligned} 2l{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) - r{{{\dot{\vartheta }} }_x}{\sin ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) - \\ r{{{\dot{\vartheta }} }_y}\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{64}}&= {m_c}\left( \begin{aligned} - l{{{\dot{\vartheta }} }_x} - \frac{1}{2}r{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) + \\ \frac{1}{2}l{{{\dot{\vartheta }} }_y}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) + \\ r{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{65}}&= {m_c}\left( \begin{aligned} - l{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) + r{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \times \\ \sin \left( {{\vartheta _y}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) - \\ \frac{l}{2}{{{\dot{\vartheta }}}_{x}}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ \end{aligned} \right) \end{aligned}$$

3. The coefficients of vector G.

$$\begin{aligned} {g_1}&= {m_c}gr\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \\ {g_2}&= - {m_c}gl\sin \left( {{\vartheta _x}} \right) {\text {cos}}\left( {{\vartheta _y}} \right) \\ {g_3}&= - {m_c}g\left( {l\sin \left( {{\vartheta _y}} \right) {\text {cos}}\left( {{\vartheta _x}} \right) - r\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) } \right) \\ {g_4}&= {m_c}g\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) + \rho \Delta \delta \end{aligned}$$

Proof of system stability

Let’s begin with following assumption.

Assumption 1

The backstepping control errors ${\xi _1},{\text { }}{\xi _2}$ in (19) and its time derivative are bounded, i.e., there exists a large enough number $A \in {\mathbb {R}}$ such that ${\left\| {{\xi _1}} \right\| }, {\left\| {{\xi _2}} \right\| }, {\left\| {{{{\dot{\xi }} }_1}} \right\| },{\left\| {{{{\dot{\xi }} }_2}} \right\| } \leqslant A < + \infty$

This assumption is suitable for most natural systems, as states have a certain allowable limit.

Theorem 2

If the control law is defined as in (38) and the sliding surfaces are defined as in (25), (34), then, the subsystems and the entire system in (24) will stabilize asymptotically at the origin, i.e.,

1) $\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _1} = {0} ,{\text { }}\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _2} = {0}$

2) $\mathop {\lim }\limits _{t \rightarrow \infty } S = {0}$

where $u_{11\mathrm{eq}}$ and $u_{12\mathrm{eq}}$ are defined as in (32) and (33), respectively; $u_{11\mathrm{sw}}$ and $u_{12\mathrm{sw}}$ are determined to satisfy (43).

Proof

Applying the inequality of the quadratic form to (44), it yields:

$$\begin{aligned} {\dot{V}}_S&= - {S^T}\Upsilon {\lambda _1}S - {S^T}\Upsilon {\lambda _2}\mathrm{sign}\left( S \right) \nonumber \\&\leqslant - \lambda _{\min }^{\Upsilon {\lambda _1}}{\left\| S \right\| ^2} - \eta {S^T}\mathrm{sign}(S) \leqslant 0 \end{aligned}$$

(B1)

where $\lambda _{\min }^{\Upsilon {\lambda _1}}$ is the smallest eigenvalue of the coefficient matrix $\Upsilon {\lambda _1}$, and $\eta$ is any eigenvalue of the matrix $\Upsilon {\lambda _2}$.

Integrating both sides of (B1) with time, one obtains:

$$\begin{aligned} \int _0^t {{{\dot{V}}_S}d\tau }&\leqslant - \lambda _{\min }^{\Upsilon {\lambda _1}}\int _0^t {{\left\| S \right\| }^2}d\tau \nonumber \\ {}&- \eta \int _0^t {S^T}\mathrm{sign}(S) d\tau \nonumber \\ {V_S}\left( t \right)&\leqslant {V_S}\left( 0 \right) - \lambda _{\min }^{\Upsilon {\lambda _1}}\int _0^t {{\left\| S \right\| }^2}d\tau \nonumber \\ - \eta \int _0^t {S^T}\mathrm{sign}(S) d\tau&\leqslant {V_S}\left( 0 \right) \end{aligned}$$

(B2)

$\square$

From (35) and (36), it can be deduced that:

$$\begin{aligned} \lambda _{\min }^\Upsilon {\left\| S \right\| ^2}&\leqslant \frac{1}{2}{\left( {\int _0^t {Sd\tau } } \right) ^T}\Upsilon {\left( {1 - \gamma } \right) ^p}\Xi \int _0^t {Sd\tau } \nonumber \\&+\frac{1}{2}{S^T}\Upsilon S \leqslant {V_S}\left( 0 \right) \end{aligned}$$

(B3)

Inequality in (B3) shows that the energy inside the system is constantly decreasing. It can be seen that if $\left\| S \right\| \rightarrow 0$ as $t \rightarrow \infty$, the system state gradually approaches and stabilizes at its reference state.

In addition, given Assumption, it can be clearly seen that:

$$\begin{aligned} \left\| S \right\| = \left\| {{\alpha _1}{\xi _1} + {\alpha _2}{\xi _2}} \right\| \leqslant \left\| {{\alpha _1}{\xi _1}} \right\| + \left\| {{\alpha _2}{\xi _2}} \right\| < +\infty \end{aligned}$$

(B4)

Considering the following expressions:

$$\begin{aligned} \left\{ {\begin{matrix} {{\Phi _1} = {c_1}{\xi _1} + {\xi _2}} \\ {{\Phi _2} = {c_2}{\xi _1} + {\xi _2}} \end{matrix}} \right. \end{aligned}$$

(B5)

where ${c_1},{c_2} \in {\mathbb {R}^{3 \times 3}}$ are any positive diagonal matrices, and ${c_1} \ne {c_2}$.

Without loss of generality, it may be assumed that $\left\| {{c_1}} \right\| > \left\| {{c_2}} \right\|$.

Based on the inequality of the quadratic form, it can be deduced that:

$$\begin{aligned}&\begin{aligned} 0 \leqslant {\left( {\int _0^{ + \infty } {{\Phi _1}d\tau } } \right) ^T}\int _0^{ + \infty } {{\Phi _1}d\tau } \leqslant \int _0^{ + \infty } {\Phi _1^T{\Phi _1}d\tau } \\ = \int _0^{ + \infty } {\left( {\xi _1^Tc_1^T{c_1}{\xi _1} + \xi _2^T{\xi _2}} \right) } d\tau + 2\int _0^{ + \infty } {\xi _1^Tc_1^T{\xi _2}d\tau } \\ \end{aligned} \\&\begin{aligned} 0 \leqslant {\left( {\int _0^{ + \infty } {{\Phi _2}d\tau } } \right) ^T}\int _0^{ + \infty } {{\Phi _2}d\tau } \leqslant \int _0^{ + \infty } {\Phi _2^T{\Phi _2}d\tau } \\ = \int _0^{ + \infty } {\left( {\xi _1^Tc_2^T{c_2}{\xi _1} + \xi _2^T{\xi _2}} \right) } d\tau + 2\int _0^{ + \infty } {\xi _1^Tc_2^T{\xi _2}} d\tau \\ \end{aligned} \end{aligned}$$

On the other hand,

$$\begin{aligned}&\int _0^{ + \infty } {\left( {\Phi _1^T{\Phi _1} - \Phi _2^T{\Phi _2}} \right) d\tau } \nonumber \\&=\int _0^{ + \infty } {\xi _1^T\left( {c_1^T{c_1} - c_2^T{c_2}} \right) {\xi _1}d\tau }+ \nonumber \\&\quad + 2\int _0^{ + \infty } {\xi _1^T\left( {c_1^T - c_2^T} \right) } {\xi _2}d\tau \end{aligned}$$

(B6)

Substituting ${\xi _2} = {\Phi _1} - {c_1}{\xi _1}$ into (B6), and note that $c_2^T{c_1} = c_1^T{c_2}$, simplifying yields:

$$\begin{aligned}&\int _0^{ + \infty } {\left( {\Phi _1^T{\Phi _1} - \Phi _2^T{\Phi _2}} \right) d\tau } \nonumber \\&=2\int _0^{ + \infty } {{{\xi }}{{_1^T}}\left( {c_1^T - c_2^T} \right) {\Phi _1}d\tau }+ \nonumber \\&+\quad \int _0^{ + \infty } {{{\xi }}_1^T{{\left( {{c_1} - {c_2}} \right) }^T}\left( {{c_1} - {c_2}} \right) {{{\xi }}_1}d\tau } \end{aligned}$$

(B7)

Because $\left\| {{c_1}} \right\| > \left\| {{c_2}} \right\|$, so we have

$$\begin{aligned} \int _0^{ + \infty } {\left( {\Phi _1^T{\Phi _1} - \Phi _2^T{\Phi _2}} \right) d\tau > 0} \end{aligned}$$

(B8)

Let $\Delta {c^T} = c_1^T - c_2^T$ be a positive diagonal matrix. Then

$$\begin{aligned} \int _0^{ + \infty } {\xi _1^T\Delta {c^T}\Delta c{\xi _1}d\tau }&\leqslant 2\int _0^{ + \infty } {\xi _1^T\Delta {c^T}{\Phi _1}d\tau } \nonumber \\&\leqslant 2\int _0^{ + \infty } {\sup \left( {\xi _1^T\Delta {c^T}{\Phi _1}} \right) d\tau } \end{aligned}$$

(B9)

Inequality of quadratic form leads to

$$\begin{aligned} \xi _1^T\Delta {c^T}{c_1}{\xi _1} \leqslant \lambda _{\max }^{\Delta {c^T}{c_1}}{\left\| {{\xi _1}} \right\| ^2} \end{aligned}$$

where $\lambda _{\max }^{\Delta {c^T}{c_1}}$ is the largest eigenvalue of the matrix $\Delta {c^T}{c_1}$.

It can be deduced from (B8) that:

$$\begin{aligned} \int _0^{ + \infty } {\xi _1^T\Delta {c^T}\Delta c{\xi _1}d\tau } \leqslant 2\int _0^{ + \infty } {\sup \left( {\xi {{_1^T}}\Delta {c^T}{\Phi _1}} \right) d\tau } \nonumber \\ \leqslant {\left\| {2\lambda _{\max }^{\Delta {c^T}{c_1}}{{\left\| {{\xi _1}} \right\| }^2}} \right\| _1} + \left\| {\xi _1^T\Delta {c^T}{\xi _2}} \right\| _1 < + \infty \end{aligned}$$

(B10)

Note that $\Delta {c^T} = c_1^T - c_2^T$ is a constant. Thus, there exists a constant ${\partial _1} > 0$ such that:

$$\begin{aligned} \int _0^{ + \infty } {\xi _1^T{\xi _1}d\tau } \leqslant {\partial _1} < + \infty \end{aligned}$$

(B11)

A completely similar proof, one can infer that there exists a positive constant ${\partial _2}$ such that:

$$\begin{aligned} \int _0^{ + \infty } {\xi _2^T{\xi _2}d\tau } \leqslant {\partial _2} < + \infty \end{aligned}$$

(B12)

According to the convergence theory of the Barbalat integral, one can deduce that: $\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _1} = {0} ,{\text { }}\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _2} = {0}$.

On the other hand, ${\alpha _1}$ and ${\alpha _2}$ are preselected coefficients (finite). Hence, from (34) it can be easily deduced that $\mathop {\lim }\limits _{t \rightarrow \infty } {S} = {0}.$

Theorem 1 has been proved.