Abstract
When transverse or torsional vibration amplitudes in a rotor dynamic system is high, energy is often drawn from the drive to sustain those motions. Therefore, the part of the drive energy available for spinning the rotor reduces in that condition. This can lead to perpetual or transient capture of the rotor speed in the regime where large amplitude vibrations occur. A critical amount of additional drive power is often needed to escape the capture of the rotor speed and such an escape is often associated with a sudden jump to a higher rotor speed and reduction in the vibration amplitudes, which is formally recognised as the Sommerfeld effect. Till now, Sommerfeld effect and resonance capture has been studied for rotor dynamic systems with unbalanced rotor disc under synchronous whirl condition. In this chapter, it will be shown that two more kinds of Sommerfeld effects can exist even if the rotor shaft and disc are perfectly balanced. One of those is related to high amplitude transverse asynchronous whirl of the non-circular rotor shaft due to parametric instability. The other is related to resonance capture in torsional vibrations of the transmission shaft in a universal joint driveline. In this chapter, three simple academic examples have been considered for each of these kinds of Sommerfeld effect.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
Rotating equipment often operate at a speed which is above one or more of its critical speeds. This is desired for good vibration isolation behaviour. However, in a rotor system, a small unbalance may exist due to manufacturing defects, installation error, faults in the rotor blades or bearings, asymmetric loading, or due to natural wear and tear process. Sometimes, the unbalance may be intentionally added to create vibrations, such as in vibrating screens, mixers, and drying cycle of washing machines. A rotor system has large vibration amplitude at its critical speeds and sustained operation at any of these critical speeds can cause failure of the entire system [1]. In the region of resonance, most of the power supply to the rotating system from the drive of the rotor, such as an engine or motor, goes to increase the structural vibration rather than increasing the rotor spin speed [2, 3]. Hence, the rotor speed may get caught at the resonance with excessive vibration or whirl amplitude.
There is always an energy interaction between the source (drive) and the rotor system, and any real drive (motor, engine, etc.) has power saturation behaviour. These drives follow specific torque-speed characteristic and can deliver a limited amount of torque/power at a given speed. Therefore, the output torque/power of such a drive is influenced by the load and such a drive is often termed as a non-ideal drive/source to distinguish it from an ideal drive that can provide unlimited amount of power output at any speed. In a non-ideally driven rotor, as the rotor speed approaches a critical speed with gradually increasing input power, the rate of increase in rotor speed slows down (almost remains constant) and the vibration amplitudes start to increase at a faster rate. For passage through the resonance or to accelerate through the critical speed, the rotor requires a minimum (just sufficient) amount of power supply from the drive, termed as the critical power. If the available power is a little less than this critical power limit then the rotor speed remains nearly at the critical speed with large vibration amplitude, and a slightly higher power causes the rotor speed to attain a much higher value with a corresponding reduction in thee vibration amplitude. Similar phenomenon is also present during gradual rotor speed reduction from a speed above the critical speed. This non-linear jump phenomenon is called the Sommerfeld effect. In fact, there exists a missing speed range in the neighbourhood of a critical speed which is neither reached during the rotor coast up (speed increase) nor during coast down (speed reduction). Three different kinds of Sommerfeld effect due to large vibration amplitudes or load, and consequent drive power saturation in non-ideally driven rotor dynamic systems will be discussed in this chapter.
Arnold Sommerfeld is credited with being the first to study non-ideal sources [4]. The power saturation phenomenon was first experimentally observed by Sommerfeld in 1902 and it has been named in his honor as the Sommerfeld effect [5]. Sommerfeld’s observation was that the structural response of the system to which a non-ideal source, such as an electric motor, is connected may act like energy sink under certain conditions so that a part of the energy supplied by the source is spent to vibrate the structure rather than to increase the drive speed. Sommerfeld put it as “the plant owner spends expensive coal not to rotate his shaft, but rather to shake the foundation”. Further to that, Kononenko [6] described an experiment where a cantilever beam supports a non-ideal energy source (i.e., an unbalanced motor) at its free end and exhibits large amplitude motions in the region of resonance for a sufficiently large range of motor power increase and it is then followed by a sudden amplitude reduction on increasing the input power beyond the critical power input. Sommerfeld effect has been a subject of discussion in several books [2, 3, 7,8,9].
2 Types of Sommerfeld Effect
Generally, the Sommerfeld effect is described by the dynamics of an unbalanced electric motor, particularly a DC motor, placed on an elastic support [10,11,12]. With increase in the input voltage to the motor (coast up operation), the motor speed increases almost proportionally at the beginning. Due to the unbalance in the rotor, resonance effect sets in as the motor speed approaches the elastic foundation’s natural frequency. Therein, the high vibration amplitude of foundation produces a large dynamic load on the motor and hence, the input power supply from motor goes to the foundation to overcome this. If the motor supply voltage is increased and still the motor output power is insufficient to overcome the power diverted to the foundation then the motor speed remains perpetually caught near the resonance speed. In fact, a large amount of motor power is delivered to increase the support’s flexural vibration rather than to increase the motor speed [13]. There is a critical amount of motor power beyond which a non-linear jump phenomenon occurs. This results in a sudden jump of motor/rotor speed to a higher speed with a simultaneous sudden reduction in the foundation vibration amplitude. This jump phenomenon is termed as the Sommerfeld effect of first kind. Similar jump phenomenon occurs during coast down operation, however, the transition points for this kind of sudden jump are different for coast up and coast down operations. This non-linear jump phenomenon is characterized by the inability to obtain certain common motor steady-state speeds near the resonance frequency [14, 15].
Sommerfeld effect of first kind has been widely studied for mechanical engineering applications in [16,17,18,19]. Moreover, several techniques to encourage passage through resonance with a limited power supply and to prevent the growth of large amplitude vibration, thereby extending the machine life, has been proposed in [6, 20]. Tuned Sommerfeld effect suppression is proposed in [21], where the effect of a vibration absorber near the zone of the Sommerfeld effect is described. Sommerfeld effect in wind turbine [22], vehicle dynamics [23] and slider-crank mechanism are also reported in [24]. Balthazar and his co-workers [25,26,27,28,29,30,31] have published several studies on different kinds of non-ideal source and system interactions leading to Sommerfeld effect of first kind. Sommerfeld effect of first kind can also appear without rotor unbalance. One example is resonance in the torsional vibration modes due to fluctuating input speed or load [32].
Many rotor dynamic systems exhibit parametric instability. In some specific rotor dynamic applications, the cross-section of the shaft is purposefully designed to be non-circular (asymmetric). Considerable amount of research has been reported on the dynamics of asymmetric rotor shaft mounted on rigid or flexible supports [33,34,35,36,37,38]. One unstable speed region appears between the two major critical speeds for a flexible asymmetric rotor shaft with a centrally placed rotor disc and rigid/ideal support bearings at the shaft ends [36, 39]. The asymmetry in shaft bending stiffness combined with flexible and asymmetric supports produce many additional unstable regions near at the combined parametric resonance regions, as reported by several researchers [37, 40,41,42]. The lumped parameter model of asymmetric shaft-rotor system is studied in both rotating and inertial frames in [43, 44]. These studies assume that the rotor can be driven to and through the unstable regions to reach any operating desired speed, i.e. those do not consider the drive dynamics. The situation under real drive conditions is significantly different due to drive power saturation. The power scarcity to escape through the parametric instability regimes leads to a different kind of Sommerfeld effect, which is termed here as the Sommerfeld effect of second kind [45]. Parametric instabilities occur in other types of rotor assemblies, such as geared shaft systems and shafts with universal joints and flexible foundation, and thus, there can be Sommerfeld effect of second kind present in many as yet unsolved problems.
When the rotor shaft has material damping, it exhibits a permanent instability at certain threshold speed. Such permanent instability thresholds also exist in shafts with internal friction such as splined joints, and shafts supported on journal bearings [46,47,48,49,50]. Fluid film forces from bearings and Alford forces on bladed disc systems produce non-conservative circulatory forces and lead to rotor system instability. The permanent instability threshold is a speed above which there is no further stable operating speed. A real rotor cannot operate at any speed higher than this permanent instability speed and shows saturation behaviour termed as the Sommerfeld effect of third kind [51].
The nature of the above-mentioned three types of Sommerfeld effects is detailed with example applications in the following sections.
3 The Sommerfeld Effect of First Kind Due to Lateral Vibrations
Most studies on Sommerfeld effect reported in literature have focused on the unbalance-induced excitation of natural frequencies with forward precession modes only, while considering the synchronous critical speeds. However, a backward precession mode can also be excited by using just the rotor unbalance as the chief driving force. This has been documented before in some crucial works in this area [52,53,54,55,56,57]. The occurrence of such a backward whirl response is strongly dependent on stiffness asymmetry at the support ends. Therefore, Sommerfeld effect can also exist at various speed ranges in addition to that at the forward critical speed.
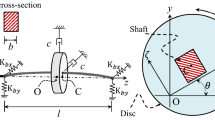
The influence of anisotropy in support flexibility of a rigid rotor shaft on the rotor whirl dynamics is studied here for the case when the rotor shaft carries single unbalanced rotor disc and is driven by a permanent magnet DC (PMDC) motor, as shown in Fig. 1. The rigid disc is firmly placed away from the middle portion of the rigid rotor shaft and this introduces a strong gyroscopic coupling to the rotor dynamic formulation. The rotor dynamic system is studied here for the chosen parameter values listed in Table 1.
Non-ideal rotor dynamic system with anisotropic bearings
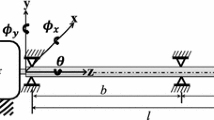
The rotor shaft’s length is \(l\) and as the rotor disc is placed asymmetrically at one-third of shaft length from the left end support. The rigid hollow shaft has a uniform circular cross-section. The disc mass is \(m\) and the position of the mass centre of the rotor disc is assumed to be at a distance \(e\) from the shaft geometric centre. The position of the mass centre M is given as \((x\_m,y\_m )\) and that of the geometric centre G as \((x,y)\) according to the co-ordinate axes shown in Fig. 2. Thus, the coordinates of mass centre \((x\_m,y\_m )\) are expressed as
Positions of the geometric and mass centre of the rotor disc
where \(\theta\) is the angle of rotation of the rotor disc about the spin axis (i.e. z-axis) and \(\varphi\) is a constant phase corresponding to the initial position of the mass centre of the disc. The angles \(\phi \_x\) and \(\phi \_y\) describe the small angular motions of the rotor about the positive \(x\) and \(y\) directions, respectively. In steady state, the unbalance response is a synchronous whirl at same frequency as the constant angular speed \(\omega\) about the spin or z-axis. The instantaneous angle between the x-axis and the line passing from origin to the geometric centre is then expressed as \(\theta =\omega t\).
With reference to Fig. 1, \(l\_1\) and \(l\_2\) are the distance of disc from the left and the right support ends, respectively. \(K\_x\) and \(R\_x\) are the bearing stiffness and damping in the x-direction for both ends of the shaft; whereas, \(K\_y\) and \(R\_y\) represent the same in the y-direction. For the disc, \(R\_e\) and \(R\_e\phi\) represent the external translational and rotational damping values acting at the geometric centre of the disc, respectively. \(I\_p\) is the rotary inertia of disc about the spin axis and \(I\_d\) is the disc diametral moment of inertia. For this analysis, the disc is assumed to be thin and laterally symmetric, which implies \(I\_p=2{I}_{d}\).
3.1 Modal Analysis
A constant angular speed \(\upomega\) about the spin z-axis, which is the synchronous frequency, is assumed to analyse the ideal drive system. The equations of motion for the rotor disc system (excluding the non-ideal motor) are obtained as
These equations are then written in state-space form by excluding the excitation forces and the critical speeds of the system are obtained from the Campbell diagram, as shown in Fig. 3, through modal or eigenvalue analysis. The first backward and the first forward critical speeds of the shaft are \({\omega }_{cr1}=48.97\) rad/s and \({\omega }_{cr1}=68.9\) rad/s, respectively.
Campbell diagram showing critical speed versus shaft spin speed (\(\omega\))
The frequency response plots for the system (operating at constant speed) are obtained by assuming harmonic solutions in the form \(x=A\mathrm{cos}\left(\omega t+\alpha \right)\), \(y=B\mathrm{sin}\left(\omega t+\beta \right)\), \({\phi }_{x}=-C\mathrm{sin}\left(\omega t+\gamma \right)\), and \({\phi }_{y}=D\mathrm{cos}\left(\omega t+\delta \right)\), where \(A\), \(B\), \(C\) and \(D\) are whirl amplitudes and \(\alpha\), \(\beta\), \(\gamma\) and \(\delta\) are the phases. Substitution of these harmonic solutions into Eq. (2) and separation of sine and cosine terms give eight equations which are then solved to determine the eight unknown variables, i.e. the four amplitudes and four phase angles, at any given speed \(\upomega\). Further details on these frequency responses are available in [58]. The normalized whirl amplitudes are defined as \({x}^{*}=0.33{\left({\omega }_{cr1}\right)}^{2}A\left(\omega \right)/g\) \({y}^{*}=0.4{\left({\omega }_{cr1}\right)}^{2}B\left(\omega \right)/g\), \({\phi }_{x}^{*}=100C\left(\omega \right)\) and \({\phi }_{y}^{*}=120D\left(\omega \right)\), where and \(g\) is the acceleration due to gravity. The spin speed is also normalized as \({\omega }^{*}=\omega /{\omega }_{cr1}\). The steady-state amplitudes of the rotor at various constant operating speeds, as would happen in an ideal system, are obtained in the form of frequency response plots presented in Fig. 4.
Normalized steady state whirl amplitudes versus spin speed \(\left({\omega }^{*}\right)\)
3.2 Interfacing the Non-ideal Drive
The permanent type DC motor, whose parameter values are given in Table 2, is considered here as the non-ideal drive. The DC motor produces torque to rotate the rotor shaft instead of a constant speed motor considered for ideal drive. The power developed by a DC motor is given as
with \({\tau }_{m}={k}_{m}{i}_{m}\), \({i}_{m}=\frac{{V}_{i}-{V}_{e}}{{R}_{m}}=\frac{\left({V}_{i}-{k}_{m}\dot{\theta }\right)}{{R}_{m}}\), where \({V}_{i}\) is the voltage supplied across the motor terminal, \({V}_{e}\) is the back emf developed in motor coils, \({k}_{m}\) is the motor characteristic (torque or speed) constant, \({i}_{m}\) is the armature current, \({R}_{m}\) is the armature resistance of the coils,\({\tau }_{m}\) is the mechanical torque developed by the motor and \(\dot{\theta }\) is the rotor angular velocity.
Under steady state conditions, \(\dot{\theta }=\omega\); with no angular accelerations. Since the synchronous whirl response is periodic, an energy balance is carried out by integrating the motor power and dissipated power over a cycle, i.e. a complete whirl orbit. The steady state response presented in Fig. 4 is then used in an averaged steady state energy balance between the energy produced by non-ideal DC motor and the energy dissipated through the rotor whirl. The energy dissipation occurs through the external damping \({R}_{e}\) and \({R}_{e\phi }\), and also through the damping in the bearings, i.e. \({R}_{x}\) and \({R}_{y}\). In addition, some dissipation also occurs at the bearings in the motor and spin resistance in the support bearings, which is represented by a viscous resistance \({R}_{b}\). Overall, the net work done by all the dissipative forces over a fixed cycle can be expressed as
where
\({P}_{d,\mathrm{left}}={\dot{q}}_{L}^{T}\left[\begin{array}{cc}\begin{array}{cc}{R}_{x}& 0\end{array}& \begin{array}{cc} 0& 0\end{array}\\ \begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c} 0\\ \begin{array}{c} 0\\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}{R}_{y}\\ 0\end{array}\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\end{array}\right]{\dot{q}}_{L}\), \({P}_{d,\mathrm{right}}={\dot{q}}_{R}^{T}\left[\begin{array}{cc}\begin{array}{cc}{R}_{x}& 0\end{array}& \begin{array}{cc} 0& 0\end{array}\\ \begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c} 0\\ \begin{array}{c} 0\\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}{R}_{y}\\ 0\end{array}\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\end{array}\right]{\dot{q}}_{R}\),
\({P}_{d,\mathrm{disc}}={\dot{q}}_{d}^{T}\left[\begin{array}{cc}\begin{array}{cc}{R}_{e}& 0\end{array}& \begin{array}{cc} 0& 0\end{array}\\ \begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c} {R}_{e\phi }\\ \begin{array}{c} 0\\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}{R}_{e}\\ 0\end{array}\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ {R}_{e\phi }\end{array}\end{array}\end{array}\end{array}\right]{\dot{q}}_{d}\),
\({\dot{q}}_{L}^{T}=\left[\begin{array}{cc}\begin{array}{cc}\left(\dot{x}-{l}_{1}{\dot{\phi }}_{y}\right)& 0\end{array}& \begin{array}{cc}\left(\dot{y}+{l}_{1}{\dot{\phi }}_{x}\right)& 0\end{array}\end{array}\right]\),
The energy supplied by the motor in each cycle is given by
The steady state energy balance
Equation (6) is expanded by using the assumed harmonic solutions and treating the whirl amplitudes (\(A, B, C, D\)) and phases (\(\alpha\), \(\beta\), \(\gamma\), \(\delta\)) as constants at any given steady-state speed \(\omega\) during the integrations mentioned in Eq. (4). Further simplification and reorganization of Eq. (6) gives
For a fixed speed \(\omega\), and given parameter values and computed parameters of the frequency response, Eq. (7) is used to compute the motor supply voltage \({V}_{i}\). Interestingly, it is found that there are ranges of speed where three \(\omega\) values give the same \({V}_{i}\), i.e. the map from \({V}_{i}\) to \(\omega\) is not unique. Out of those three solutions, two are stable (attainable) and one is not. The solutions that satisfy the condition \(d\left({W}_{m}-{W}_{d}\right)/d\omega <0\) are attainable [18].
Accordingly, the non-ideal rotor system’s response is predicted and multiple jump phenomena due to Sommerfeld effect in the non-ideal system are revealed at the forward and backward critical speeds as shown in Fig. 5. Therein two jumps in the rotor speed, which correspond to the two resonance zones are shown– the first occurs from first backward whirl critical speed \({\omega }_{cr1}\) to \(\omega =57.07\mathrm{ rad}/\mathrm{s }\) (i.e. near \({\omega }^{*}=1\)) and the second takes place from the first forward whirl critical speed \({\omega }_{cr2}\) to \(\omega =89.1\) rad/s (i.e. near \({\omega }^{*}=1.41\)).
Normalized spin speed (\({\omega }^{*}\)) versus voltage supply \({V}_{i}\)
During the rotor coast up operation, the rotor speed continues to increase almost linearly until it reaches point ‘a’. Thereafter, further increase in supply voltage does not result in appreciable change in rotor speed. For the region ‘a’ to ‘b’, although the supply voltage is being increased, the rotor speed does not increase and is stuck at the first backward critical speed for the voltage range 26.43 V to 28.81 V. When the voltage is increased above 28.81 V, the rotor speed suddenly jumps from point ‘b’ to a much higher value at point ‘g’. Afterwards, by increasing voltage, the shaft speed again increases linearly till point ‘c’ (at 37.7 V). This is the zone for the first forward critical speed. Here, the rotor speed is stuck again, from ‘c’ to ‘d’ i.e. for the voltage range 37.77 V to 44.83 V. Subsequently, the second jump takes place from ‘d’ to ‘e’. Thereafter, from point ‘e’ onwards, the speed increases linearly with increase in voltage. The Sommerfeld effect is thus observed for both the first backward and first forward whirl modes of the system; thus, it is termed as ‘Multi-Sommerfeld effect’. Between the two, the jump size is comparatively higher for the first forward critical speed.
On the other hand, during coast down operation from a very high speed, the spin speed reduces linearly as the supply voltage is decreased along the line connecting points ‘e’ to ‘f’. As the voltage is reduced just below 37.77 V (point ‘f’), the speed jumps from point ‘f’ to ‘c’, i.e. there is a sudden reduction in the speed. On further voltage reduction, the voltage-speed curve traces the path along the line joining points ‘c’ to ‘h’ and a second jump occurs from point ‘h’ to ‘a’.
Note that there are three possible rotor speeds for the voltage ranges ‘a’ to ‘b’ and ‘c’ to ‘d’. However, the speed ranges 48.79 to 51.1 rad/s and 68.9 to 72.7 rad/s, are not physically achievable either during rotor coast-up or coast-down. This is because the branches in between ‘d’ to ‘f’ and ‘b’ to ‘h’ are unstable in nature [60, 69]. As a result, only two possible speeds exist near the resonance region; one of these can be reached during rotor coast-up and the other during rotor coast-down.
Further note that the whirl amplitudes are also functions of speed. As a direct consequence, there is an amplitude jump associated with the speed jump at the respective resonance zones. Near the resonance, the energy from the non-ideal motor is not used to increase the spin speed; instead, this energy is transferred to the vibration or whirl amplitudes. Consequently, as speed saturation occurs on approaching a critical speed during the rotor coast up, the whirl amplitudes increase. Such continuous large amplitudes of vibration may severely affect the performance of the rotor and its support structures. This happens for a voltage range in the immediate pre-jump scenario. Afterwards, as the speed jumps to a higher value, the whirl amplitudes promptly reduce. Likewise, during rotor coast down, the discrete jump in speed from a higher value to a lower value is associated with a discrete jump in amplitude from a lower value to a higher value. This dependency comes from the energy balance.
The tendency to get stuck near resonance, also called resonance capture, which occurs due to power saturation, is a typical feature of non-ideal systems. The motor energy \({W}_{m}\) for different supply voltages and the dissipated energy \({W}_{d}\) are plotted against the normalized rotor speed \({\omega }^{*}\) in Fig. 6. The \({W}_{m}\) curve for 28.81 V supply voltage grazes the dissipated energy curve at \({\omega }^{*}=1\) and intersects it at \({\omega }^{*}=1.19\). Likewise, the \({W}_{m}\) curve for 44.83 V supply voltage grazes the dissipated energy curve \({W}_{d}\) at \({\omega }^{*}=1.41\) and intersects it at \({\omega }^{*}=1.85\). The grazing or intersecting points indicate exact energy balance equation \({W}_{m}={W}_{d}\) given in Eq. (6) and hence those are the possible steady-state operating points. There can be one or two or three operating points. One operating point indicates that the operation is away from the resonance regime, two means operation at the exact point from which jumps occur. When there are three intersection points, the one giving the middle speed is an unstable solution. As an example of one operating point, the \({W}_{m}\) curve for 25 V intersects the \({W}_{d}\) curve once and it is at a point below first backward critical speed, and the \({W}_{m}\) curve for 35 V intersects the \({W}_{d}\) curve once and it is at a point below first forward critical speed. If the input voltage is increased slowly from 25 V or 35 V, then there is a resonance capture at the respective critical speeds. On the other hand, the \({W}_{m}\) curve for 40 V intersects the dissipated energy \({W}_{d}\) curve at three points, out of which two are stable [59] and there is resonance capture during rotor coast up at the lowest of the three speed values corresponding to the intersection points.
Energy versus Normalized spin speed \(\left({\omega }^{*}\right)\)
The inset in Fig. 6 shows a zoomed view of the resonance condition at 2BW critical speed. It is seen that the energy dissipation at 2BW critical speed and its neighbourhood is too small, and hence, no Sommerfeld effect is observed at 2BW critical speed. However, with a weakly damped bearing support system and large translational and small rotational damping on the rotor disc, it is possible to encounter Sommerfeld effect the 2BW speed. High damping often suppresses Sommerfeld effect [18]. The net external damping in 1FW and 1BW modes comes from the bearing supports and the translational external damping (\({R}_{e}\)) whereas the net external damping on 2BW and 2FW modes some from the bearing supports and the rotational external damping.
The steady state analysis of the non-ideal system is valid only if the rotor acceleration is negligible, i.e. when voltage increment is done gradually or the rotor disc has large polar moment of inertia. For step input voltages, the steady-state analysis may not give accurate results. To address that, a separate transient analysis for the rotor-motor system, with non-ideal source loading, is carried out.
3.3 Transient Analysis
The frequency response and power balance are obtained analytically, but with the assumption that the rotor system operates at a steady-state. These analytical results are then validated through direct numerical simulations of the non-ideal system. To include interaction with the non-ideal drive, the equations of motion are modified with introduction of angular acceleration terms as well as one additional equation describing the spin dynamics of the motor/rotor. From Eq. (1), it can be shown that \(m{\ddot{x}}_{m}=m\ddot{x}-me{\dot{\theta }}^{2}\mathrm{cos}\left(\theta +\varphi \right)-me\ddot{\theta }\mathrm{sin}\left(\theta +\varphi \right)\) and \(m{\ddot{y}}_{m}=m\ddot{y}-me{\dot{\theta }}^{2}\mathrm{sin}\left(\theta +\varphi \right)+me\ddot{\theta }\mathrm{cos}\left(\theta +\varphi \right)\). These inertia forces produce reactive moment about the axis of the motor rotation. The new set of equations are then given as
The above equation of motion is numerically integrated to obtain the transient response of the system. The initial phase \(\varphi\) does not influence the key aspects of the results and can be taken zero during the analysis. In Fig. 7a, the transient response amplitude for a step input voltage of \({V}_{i}=28.8\) V is shown, for which the shaft speed is stuck at \({\omega }^{*}=1\), i.e. at the first backward critical speed. Note that the line styles and colors used to plot the variables are mentioned in the y-axis label of these graphs. At this point, with a slight increase of input voltage to \({V}_{i}=28.81\) V, the first jump is detected as shown in Fig. 7b. It can be seen that the normalized amplitudes \({x}^{*}\) and \({\phi }_{y}^{*}\) are comparatively larger than \({y}^{*}\) and \({\phi }_{x}^{*}\). Similarly, the second jump is also detected when supply voltage is increased from \({V}_{i}=44.73\) V (Fig. 8a) to \({V}_{i}=44.74\) V (Fig. 8b). This is the resonance zone corresponding to the first forward critical speed. Here, i.e. in the second resonance zone, the normalized amplitudes \({y}^{*}\) and \({\phi }_{x}^{*}\) are larger than \({x}^{*}\) and \({\phi }_{y}^{*}\)
Transient response during coasting up for a constant \({V}_{i}=28.8\) V and b constant Vi = 28.81 V, showing resonance capture and escape through the 1st critical speed
.
Transient response during coasting up for a constant Vi = 4.73 V and b constant Vi = 44.74 V, showing resonance capture and escape through the 2nd critical speed
The numerical simulation results differ a little from the analytically predicted results. Numerical simulations show that the voltage required to escape resonance capture can be slightly less than the theoretically predicted values through steady state analysis. In fact, the discrepancy can be more when the rotary inertia of the rotor disc and the shaft is too small. For large rotary inertia of rotor disc, it acts like a flywheel that reduces the angular accelerations (speed variation due to load transients) and hence, the simulation results tend to be more agreeable with the steady state analysis results.
The severity of the Sommerfeld effect of first kind depends on the system parameters. Especially, if the support and external damping are small then there can be resonance capture for a significantly large range of input power variation. In fact, in the absence of damping in the system, a rotor cannot be operated above the critical speed because it would theoretically require infinite amount of energy to do so. With very high values of damping in the system, Sommerfeld effect can disappear at one or more of the critical speeds. The influence of system damping on the Sommerfeld effect is detailed in [18].
Another interesting phenomenon occurs in the considered system when the two critical speeds are closely spaced and the system is weakly damped. In that case, escape from the 1BW critical speed directly leads to resonance capture at the 1FW critical speed. More such interesting results can be seen in [58].
4 Sommerfeld Effect of First Kind Due to Torsional Vibrations
Universal joints (U-joints) or Cardan joints are used for power transmission while accommodating parallel or angular misalignment between the input and output shafts. Torsional dynamics of rotor-shafts with a single U-joint driveline and small misalignment angle was analysed in [61,62,63]. The single U-joint transmission shaft system with lateral vibrations leads to parametric resonance, quasi-periodic and chaotic motions in certain speed ranges [64,65,66]. Double U-joints driveline also shows parametric instabilities [67]. Only very recently, the resonance capture phenomenon in a Double U-joints driveline is reported by [68] under combined torsional and lateral vibrations. However, the analysis of Sommerfeld effect purely due to resonance in torsional vibrations in the presence of large U-joint angle and large twist of the elastic shaft has not been studied so far.
Now, we discuss another system of double Cardan joint driveline which shows the Sommerfeld effect of first kind. The schematic representation of the system under consideration is shown in Fig. 9. A non-ideal motor (DC motor) drives a short and rigid input shaft which transmits power to the drive shaft through a U-joint. The hollow drive shaft is long and makes an angle β with the input shaft. The drive shaft is assumed to be flexible and it is connected to a short and rigid output shaft at its other end. The input and output shafts have parallel misalignment due to which the double U-joint configuration is called Z-configuration. A heavy rotor disc is mounted on the output shaft. It is assumed that the coupler shaft is massless and its flexural vibrations are prevented by suitably placed idealized rigid bearings. Furthermore, the idealized rigid bearings supporting the shafts (including the coupler shaft) and the spline joint (which is needed for in-phase assembly) are supposed to prevent warping /buckling of the shaft due to combined torsion and bending. Therefore, only torsional vibrations of the system will be considered here. Furthermore, the rotary inertia of the U-joints, clearance/backlash and friction effects are neglected. The two U-joints are assumed to be initially in phase, i.e. the yokes are initially aligned in a plane. Here, the input shaft is driven by either an open-loop controlled torque or a torque applied by a DC motor.
Schematic representation of double U-joint transmission system with parallel offset
4.1 Equations of Motion
The torque applied by the DC motor is denoted by \({T}_{i}\) and the angular velocity of the input shaft of the transmission line is \({\omega }_{i}={\dot{\theta }}_{i}\). The angular velocity of the output shaft is \({\omega }_{o}={\dot{\theta }}_{o}\). The angular speed of the motor and load sides (input and output shaft sides) of the coupler shaft are denoted by \({\dot{\theta }}_{ic}\) and \({\dot{\theta }}_{oc}\), respectively. It is assumed that while the shaft angle of twist \({\theta }_{t}={\theta }_{ic}-{\theta }_{oc}\) can be large, the maximum dynamic shear stress remains well within the yield stress, and preferably within the endurance limit (for fatigue). The angular velocities at the two ends of the coupler shaft are given by using the transmission ratio at the U-joints as
Further, by assuming no power loss (friction) at the universal joint, the reaction torque on the input shaft \({T}_{i}\) and active torque \({T}_{o}\) on the output shaft are given, respectively, as
where \({T}_{c}={k}_{t}{\theta }_{t}+{c}_{t}{\dot{\theta }}_{t}\) is the torque transmitted through the coupler shaft, and \({k}_{t}\) and \({c}_{t}=\lambda {k}_{t}\), with \(\lambda\) as a material constant, are the torsional stiffness and damping of the coupler shaft, respectively. The equations of motion of this two-degrees-of-freedom mechanical sub-system are given as
where, \(T\) (or \({T}_{i}\)) is the motor torque that applied on the input shaft.
4.2 Numerical Simulation Results
A representative set of parameter values given in Table 3 is chosen for this system. The natural frequency of torsional vibration is \({\omega }_{n0}=\sqrt{{k}_{t}\left(1/{J}_{m}+1/{J}_{d}\right)}\), which, for the given data, turns out to be 176.21 rad/s, when \(\beta =0\) or the input, output and coupler shafts are perfectly aligned in a line. For the considered parameter values in Table 3, numerical simulations are done for the different constant input torque values (\(T=200\) Nm, 300 Nm and 474 Nm) and the respective results for the input side rotor speed, the output side rotor speed and angle of twist of the coupler shaft are shown in Fig. 10.
The angular velocities of input side rotor \({\dot{\theta }}_{m}\) and output side rotor \({\dot{\theta }}_{d}\), and angle of twist of the coupler shaft \({\theta }_{t}\) for constant input torque. Column 1: \(T=200\) N.m, Column 2: \(T=300\) N.m and Column 3: \(T=474\) N.m
Due to flywheel effect, the angular velocity of the bigger rotor is steadier with respect to that of the rotor of the motor. At this nearly steady speed of the output rotor, a ball park estimate of the average speed can be obtained as \({\overline{\Omega } }_{o}=T/{R}_{d}\) and the actual average output shaft speed \({\Omega }_{o}\). Since, the input shaft is directly connected to the geared motor the speed of the output shaft of the motor, the motor output speed \({\dot{\theta }}_{m}={\omega }_{i}={\dot{\theta }}_{i}\). Likewise, since the rotor disc is rigidly fixed to the output drive shaft, the rotor disc speed \({\dot{\theta }}_{d}={\omega }_{o}={\dot{\theta }}_{o}\).
The results show that the output shaft speed almost reaches the estimated speed for low values of torque. For example, consider the simulation results presented in Fig. 10 for a constant input toque \(T=200\) Nm. With chosen value \({R}_{d}\) = 3 Nms/rad (see Table 3), the estimated output shaft speed \({\overline{\Omega } }_{o}\) is 66.67 rad/s whereas the simulation results show that the average actual speed of output shaft \({\Omega }_{o}\) is less, about 62.1 rad/s (see Fig. 10). The estimation error is about 4.5 rad/s or about 7%. This is because a part of the energy is lost through damping in torsional vibration (see Fig. 10). Also, the output shaft speed has less fluctuation due to heavy rotor inertia whereas there is significant fluctuation in the input shaft speed.
When the torque is increased to \(T=300\) Nm, the estimated output shaft speed \({\overline{\Omega } }_{o}\) is 100 rad/s. However. The corresponding results given in Fig. 10 show that the average output shaft speed \({\Omega }_{o}\) is about 78.5 rad/s; i.e. the estimation error is about 21.5 rad/s or 27%. This increase in error is due to the increased torsional vibration amplitude. In this case, the output shaft speed is closer to half of the torsional natural frequency of the zero-offset configuration (\(\beta =0\)) of the system. Apparently, the high torsional vibration amplitudes are due to approaching the resonance speed (twice the shaft speed is closer to the zero-offset configuration natural frequency). In fact, this shows that a kind of saturation phenomena is starting to take hold and more and more energy from the source is being wasted in torsional vibrations rather than being used to accelerate the output shaft.
For \(T=474\) Nm, the estimated output shaft speed \({\overline{\Omega } }_{o}\) is 158 rad/s. However, the actual average output shaft speed \({\Omega }_{o}\) is 94.7 rad/s as shown in simulation results in Fig. 10. The torsional vibration amplitudes have reached peak twist of 0.38 rad and that vibration amplitude persists thereafter. Therefore, with the increase in torque \(T\) from 300 to 474 Nm, the output shaft speed has changed by a small margin because the additional energy is diverted to sustain the torsional vibrations. This is a classic symptom associated with the Sommerfeld effect of first kind and is termed as the capture at the resonance or resonance capture.
If input torque is increased to \(T=480\) Nm, the estimated output shaft speed is 160 rad/s and the simulated average output shaft speed (see Fig. 11a) is 148.5 rad/s. Hence by increasing the input torque up to the critical value, system has escaped the resonance capture at about 20 s which is associated with an upward speed jump, together with a simultaneous reduction in torsional vibration amplitude and speed fluctuations of the input shaft. As soon as there is escape from resonance, less drive power is lost in torsional vibrations and the extra power is able to accelerate the output shaft rotor disc. An important observation is that during the rotor coast up, the range of steady average output shaft speeds between 94.7 to 148.5 rad/s are unreachable (excluding the transient period). The resonance capture and escape at this sub-critical speed would be henceforth referred to as Zone-A dynamics.
a The angular velocities of input side rotor \({\dot{\theta }}_{m}\) and output side rotor \({\dot{\theta }}_{d}\), b angle of twist of the coupler shaft \({\theta }_{t}\), for constant input torque \(T=480\) N.m
When the torque is increased further, the output shaft speed continues to increase in a nonlinear manner showing a second speed saturation or resonance capture. The response of the system for \(T=540\) N.m given in Fig. 12 shows that after escaping Zone-A capture, the output shaft speed initially increases to 170 rad/s and then reduces to approximately steady mean speed of 156 rad/s (marked as Zone-B in the Fig. 12).
The angular velocities of input side rotor \({\dot{\theta }}_{m}\) and output side rotor \({\dot{\theta }}_{d}\), and angle of twist of the coupler shaft \({\theta }_{t}\) for constant input torque. Column 1: \(T=540\) N.m, Column 2: \(T=765\) N.m and Column 3: \(T=770\) N.m
The estimated average output shaft speed at \(T=540\) Nm is 180 rad/s. When the input torque is increased further, there is very little increase in the approximate steady average output shaft speed. For example, with \(T=765\) Nm, the estimated output shaft speed is 255 rad/s whereas the actual average output shaft speed initially reaches 225 rad/s and then reduces to a steady average output shaft speed of 166 rad/s (see Fig. 12). Thus, for input torque changing from 480 Nm (see Fig. 11) to 765 Nm (see Fig. 12) or about 60%, the average output shaft speed has changed from 148.5 to 166 rad/s or about 12%. This indicates presence of another resonance capture in the neighbourhood of the critical speed of the straight-line assembly configuration of the system, which is 176.21 rad/s.
Figure 12 also shows the transient response of the system for constant input torque \(T=770\) Nm, where the resonance capture is escaped and the average output shaft speed reaches 237 rad/s. So, an abrupt speed increase or jump of more than 70 rad/s is obtained with a small increase in torque from 765 to 770 Nm. Moreover, the torque change from 480 to 770 Nm (about 60.4%) produces 148.5 to 237 rad/s speed change (about 60%). Such almost commensurate change occurs when the resonance capture is avoided.
Further, note that the upward speed jump is associated with a corresponding reduction in torsional vibration amplitude. In fact, the peak vibration amplitude (almost 1 rad) at \(T=765\) Nm exceeds the allowable limit and the steady vibration amplitude is large enough to cause quick fatigue failure. However, if the applied torque is more than the threshold value (\(T\ge 770\) Nm) to escape the resonance capture then the peak as well as steady torsional vibration amplitudes reduce significantly and the system can be operated safely. This establishes the need for dynamic analysis of the system because an undersized actuator can lead to resonance capture and system failure.
In addition to the resonance capture and escapes seen during rotor coast up, discrete speed jumps are also observed for this system during rotor coast down. More such results can be consulted in [32]. In this section, a pre-computed open-loop controlled torque \(T={\overline{\Omega } }_{o}{R}_{d}\) is applied for any desired mean speed \({\overline{\Omega } }_{o}\). Similar phenomena are also observed in the case the drive is a non-ideal source, such as a DC motor. To include the DC motor dynamics in the model, the following set of modified system equations are considered.
where the motor torque that applied on the input shaft is given as \(T={k}_{m}{i}_{a}\), \({i}_{a}\) is the armature current, \({k}_{m}\) is the effective motor characteristic constant, and \({L}_{m}\) and \({R}_{m}\) are, respectively, the motor armature coil inductance and resistance. The two-way coupling between Eqs. (14) and (17) establishes an energy transfer pipeline. Note that while many authors do not consider the inductance term \({L}_{m}\) in the model, here it is important to retain it because of large speed fluctuations of the input shaft which is connected to the rotor of the motor [26, 69,70,71,72]. The motor is assumed to be geared and hence a large motor characteristic constant \({k}_{m}=5\) Nm/A is chosen here. The other chosen motor parameters are \({L}_{m}=0.01\) H and \({R}_{m}=10\Omega\). The motor supply voltage \(V\) is the controllable input.
A consolidated result showing gradual coast up and coast down dynamics is given in Fig. 13. Here, the motor input voltage is increased @50 V/s till 80 s, held at 4 kV for the next 40 s and then reduced @50 V/s for the next 80 s.
a The angular velocities of input side rotor \({\dot{\theta }}_{m}\) and output side rotor \({\dot{\theta }}_{d}\), and motor current \(i\), and b angle of twist of the coupler shaft \({\theta }_{t}\), when the DC motor voltage is ramped up @50 V/s from \(t=0\) s to 80 s, held constant at 4 kV up to \(t=120\) s and then ramped down @50 V/s up to \(t=200\) s
The trend for average output shaft speed, in time sequence, shows escape through Zone-A resonance capture at sub-critical speed, a small downward speed jump at the onset of resonance capture at the critical speed (Zone-B1), gradual speed increase at a slow rate followed by a sudden upward speed jump to escape resonance capture at the critical speed (Zone-B2), constant speed for the duration of constant input torque, gradually decreasing speed and then a sudden downward speed jump through the critical speed (Zone-C) and a small downward jump through the sub-critical speed resonance (Zone-D). Note that sudden speed jumps in Zones A and C are not clearly visible in this result due to faster rate of input voltage ramp. The resonance capture and escape symptoms are also present in the motor current signature. Interested readers may refer to [32] for more such information.
Hence, two instances of Sommerfeld effect were observed in the system for large joint angle at the U-joints. If a so-called critical speed is defined as the fundamental torsional vibration natural frequency of the system with zero joint angle then these Sommerfeld effects occur in the neighborhood of half of the so-called critical speed, termed sub-critical speed resonance capture and escape, and further in the vicinity of the critical speed itself, called critical speed resonance capture and escape. The zone of the resonance can be determined through a simplification by assuming the mean output shaft speed to be \({\overline{\Omega } }_{o}\), and initially neglecting the small fluctuations over it. Then the angular speed fluctuations in the output shaft side of the coupler shaft are obtained from Eq. (9), which is periodic with time period \(\tau =2\pi /{\overline{\Omega } }_{o}\) and can be expanded as a Fourier series
where
All the sin(.) terms of regular Fourier series are absent because the function is even and odd coefficients (\(i=\mathrm{1,3},\dots\)) of cos(.) terms also vanish on integration; thus only even coefficients are shown as \({a}_{2i}\) (\(i=0..n\)) in Eq. (18). These coefficients depend only on the value of \(\beta\). For the chosen value \(\beta =1\) rad, a good convergence is obtained by considering the first five coefficients \({a}_{0}=2\), \({a}_{2}=0.5969\), \({a}_{4}=0.1781\), \({a}_{6}=0.0532\) and \({a}_{8}=0.0159\). From Eq. (18), it is evident that the mean \({\dot{\theta }}_{oc}\) is \(\frac{{a}_{0}}{2}{\overline{\Omega } }_{o}={\overline{\Omega } }_{o}\) and the fluctuating parts have frequencies \(2{\overline{\Omega } }_{o}\), \(4{\overline{\Omega } }_{o}\), \(6{\overline{\Omega } }_{o}\), … Thus, resonance occurs when the average output shaft speed approaches natural frequency or any of its even fractions. However, Sommerfeld effect is not observed at all those speeds because of the presence of damping in the system. If the system has smaller torsional damping and/or stiffness, then it is possible to obtain resonance capture and escape at further subcritical speed ranges. On the other hand, Sommerfeld effect may disappear at lower values of angular misalignment and higher values of shaft stiffness and damping. Thus, the severity of Sommerfeld effect in the considered system depends on a whole lot of system parameters, mostly the torsional stiffness and damping, motor constant and the shaft misalignment angle.
5 The Sommerfeld Effect of Second Kind
There are some specific applications in rotor dynamic systems, in which the rotor shaft is designed with non-circular or asymmetric cross section. For example, rotor shafts of multi-pole electric motors, twisted brush motors, shafts with keyways or flats to allow coupling, spade drill bits, rotary broaches, etc. Due to this rotating asymmetry, the vibrational characteristics of the rotor system have unstable dynamics in certain conditions. The asymmetry appears in the form of different bending stiffness or different moment of inertia of rotor shaft or rotor disc along the principal axes in the shaft cross-section. A rotor system with asymmetry in its bending flexibility has unstable speed range near the vicinity of the natural frequencies. The dynamics of such a system is governed by differential equations with time-varying parametric coefficients which lead to parametric instability in certain rotor speed range. Therefore, the unstable speed range is bounded by a lower stable speed range and an upper stable speed range.
However, to reach the upper stable speed range, the rotor system has to transit through the unstable speeds. This consideration is not made when mathematical analysis of the system is done with an ideal drive assumption. In reality, the whirl amplitudes grow exponentially at any speed lying in the unstable speed range and such whirl loads the drive, thereby limiting the amount of energy available to accelerate the shaft spin. The transition from the lower stable range to higher stable range would require the rotor spin to accelerate quickly through the unstable speed range before the whirl amplitudes grow substantially and create energy scarcity for rotor spin acceleration. As a consequence, when rotor spin escapes the unstable speed range, it would reach a substantially higher speed with decaying whirl amplitudes. Similar behavior occurs during rotor coast down through unstable speed range. This kind of non-linear jump phenomena is termed as the Sommerfeld effect of second kind. Unlike regular Sommerfeld effect (of first kind) where the power scarcity at the resonance is the cause of speed capture, Sommerfeld effect of the second kind relates to power scarcity at the parametric instability regions.
5.1 Flexible Asymmetric Rotor Shaft with Rigid Supports
We consider an asymmetric flexible rotor shaft which is mounted on two ideal or rigid bearings at its two ends and carries a heavy centrally placed rotor disc. A permanent magnet type DC motor is used to drive the rotor. A schematic representation of this rotor dynamic system is shown in Fig. 14, in which the shaft’s cross-section is rectangular. The two ends of the rotor shaft, where the shaft is supported on the rigid bearings, are cylindrical for negligibly small lengths. The rotor shaft mass is referred to the rotor disc position, as it is common in a Jeffcott rotor model, and the torsional vibrations are neglected.
Rectangular flexible rotor shaft with central rotor disc driven by a DC motor
A rotating coordinate frame is aligned parallel to the principal axes in the shaft cross-section so that the shaft bending stiffness remains constant in that reference frame. In the fixed or inertial coordinate frame, the shaft bending stiffness change with time as the shaft rotates. Here, \(x\), \(y\), \(z\) is the fixed coordinate system and \(\eta\), \(\zeta\), \(z\) is the rotating coordinate system, as shown in Fig. 14, with the rotation \(\theta\) about the common or parallel z-axis defining the angle between the two coordinate systems at any particular time and \(\Omega =\dot{\theta }\) is the angular rotational speed of shaft about z-axis (shaft spin axis). The coordinates (\(x\), \(y\)) and (\(\eta\), \(\zeta\)) refer to position of deflected shaft centre C in the respective frames. The shaft stiffness in \(\eta\), \(\zeta\)—directions are \({k}_{\eta }\) and \({k}_{\zeta }\), respectively.
An overall viscous damping c is assumed to act at the geometric centre C of the rotor disc. Since the rotor disc is symmetrically mounted on the rotor shaft and the rotor whirls in cylindrical mode, only two degrees of freedom of the system are considered. For studying the Sommerfeld effect of second kind, there is no need for rotor disc eccentricity. However, if the system is ideally at equilibrium (zero whirl amplitude) then it cannot show exponential whirl amplitude growth at instability. Therefore, one needs to disturb the system from equilibrium to initiate the whirl. This disturbance is naturally present in a real working environment. However, for simulation or analysis, this disturbance can be given as an initial condition such as impact or as small residual unbalance [73]. An ideal coupling which is flexible in bending and rigid in torsion is assumed between the DC motor and the rotor shaft. Since the torsion of the rotor shaft is neglected, the motor torque is directly applied to the rotor disc.
5.2 Equations of Motion of the System
Only lateral displacements of the disc in the first bending (whirl) mode of the rotor shaft are considered with no rotation of the disc about diametral (\(\eta -\zeta\)) axes. To derive the stability domain of the rotor system at various rotor spin speeds, initially, the rotor speed is assumed to be constant; i.e., \(\theta\) = \(\Omega t\), \(\dot{\theta }=\Omega\) and \(\ddot{\theta }=0\). The equations of motion of the rotor in the lateral directions can be written as
where mass matrix \(\mathbf{M}=m\mathbf{I}\), damping matrix \(\mathbf{D}=c\mathbf{I}\), I is a 2 × 2 identity matrix, \({\stackrel{\sim }{\mathbf{k}}}_{\mathbf{s}}\) is a time-varying shaft bending stiffness matrix, rotor’s lateral displacement vector in the fixed frame \(\mathbf{z}={\left[\begin{array}{cc}x& y\end{array}\right]}^{T}\), \(\mathbf{f}\) is a forcing vector which is zero in the present case, \(m\) is rotor disc mass (including referred shaft mass) and c is the viscous damping coefficient at the rotor disc position. At constant spin speed, the rotation matrix from rotating to fixed frame is \(\mathbf{R}=\left[\begin{array}{cc}\mathrm{cos\Omega }t& -\mathrm{sin\Omega }t\\ \mathrm{sin\Omega }t& \mathrm{cos\Omega }t\end{array}\right]\). If \(\mathbf{t}={\left[\begin{array}{cc}\eta & \zeta \end{array}\right]}^{T}\) is the rotor’s lateral displacement vector then the restoring force vector in rotating frame is \({\mathbf{k}}_{\mathbf{s}}\mathbf{t}={\mathbf{k}}_{\mathbf{s}}{\mathbf{R}}^{T}\mathbf{z}\) where \({\mathbf{k}}_{\mathbf{s}}=\left[\begin{array}{cc}{k}_{\eta }& 0\\ 0& {k}_{\zeta }\end{array}\right]\). Transformation of the restoring forces from rotating coordinate system to fixed coordinate system gives the restoring force vector in fixed frame as \({\mathbf{R}\mathbf{k}}_{\mathbf{s}}{\mathbf{R}}^{T}\mathbf{z}={\stackrel{\sim }{\mathbf{k}}}_{\mathbf{s}}\mathbf{z}\) where time varying matrix \({\stackrel{\sim }{\mathbf{k}}}_{\mathbf{s}}=\mathbf{R}{\mathbf{k}}_{\mathbf{s}}{\mathbf{R}}^{\mathbf{T}}\)\(=\)\(\left[\begin{array}{cc}{k}_{s}+{\Delta k}_{s}\mathrm{cos}2\Omega t& {\Delta k}_{s}\mathrm{sin}2\Omega t\\ {\Delta k}_{s}\mathrm{sin}2\Omega t& {k}_{s}-{\Delta k}_{s}\mathrm{cos}2\Omega t\end{array}\right]\) with \({k}_{s}=\frac{{k}_{\eta }+{k}_{\zeta }}{2}\) as the mean shaft bending stiffness and \({\Delta k}_{s}=\frac{{k}_{\eta }-{k}_{\zeta }}{2}\) as the deviatoric shaft bending stiffness. Thus the equation of motion in fixed coordinate system is obtained as
where \({\mathbf{K}}_{\mathbf{o}}=\left[\begin{array}{cc}{k}_{s}& 0\\ 0& {k}_{s}\end{array}\right]\), \({{\varvec{\Delta}}\mathbf{K}}_{1}=\left[\begin{array}{cc}{\Delta k}_{s}& 0\\ 0& {-\Delta k}_{s}\end{array}\right]\), \({{\varvec{\Delta}}\mathbf{K}}_{2}=\left[\begin{array}{cc}0& {\Delta k}_{s}\\ {\Delta k}_{s}& 0\end{array}\right]\) and \(\stackrel{\sim }{\Omega }=2\Omega\).
It can be seen that Eq. (20) is a second order differential equation containing time dependent coefficients. Usually, the boundaries of unstable regions of systems described by differential equations with parametric coefficients are determined by using Floquet theory. Hence, the state space form of Eq. (20) is first obtained as
where \(\mathbf{S}\left(t\right)=\left[\begin{array}{cccc}-c/m& 0& -\left({k}_{s}+{\Delta k}_{s}\mathrm{cos}2\Omega t\right)/m& -\left({\Delta k}_{s}\mathrm{sin}2\Omega t\right)/m\\ 0& -c/m& -\left({\Delta k}_{s}\mathrm{sin}2\Omega t\right)/m& -\left({k}_{s}-{\Delta k}_{s}\mathrm{cos}2\Omega t\right)/m\\ 1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right] .\)
As \(\mathbf{S}\left(t\right)\) is \(T\)-periodic with \(T=2\pi /\Omega\), the monodromy matrix is obtained by numerical integration of Eq. (21) from 0 to T with initial conditions set to \({\left[I\right]}_{4\times 4}\) (4×4 identity matrix) and then the eigenvalues \({\sigma }_{i} (i=1..4)\) of the monodromy matrix are used to conclude the stability of the system. The real parts of the eigenvalues \(\sigma\), i.e. \({\sigma }_{\mathrm{Re}}\), indicate the system’s stability. Positive real part indicates instability whereas negative real part indicates stability. The parameter values chosen for this study are listed in Table 4.
5.3 Numerical Results
In the absence of external damping (\(c=0\)), available theoretical results indicate instability speed range appears between the non-rotating beam natural frequencies in principal directions, i.e. between \({\Omega }_{\eta }=\sqrt{\left({k}_{s}-\Delta {k}_{s}\right)/m}=\) 89.44 rad/s and \({\Omega }_{\zeta }=\sqrt{\left({k}_{s}+\Delta {k}_{s}\right)/m}=\) 126.49 rad/s. The eigenvalues are evaluated numerically in the frequency range of interest. The real parts of the eigenvalues are plotted with respect to rotor spin speed in Fig. 15. In Fig. 15, real parts of all the four eigenvalues are equal and negative everywhere except between a narrow region identified as \({\mathrm{U}}_{\mathrm{I}}\). The absolute values of eigenvalues are plotted Fig. 16, in which the region for \(\Vert \sigma \Vert >1\) indicates instability.
Real parts of eigenvalues versus rotor spin speed from \(x-y\) frame model
Absolute values of eigenvalues versus rotor spin speed from \(x-y\) frame model
Hence for the chosen parameter values given in Table 4, the unstable speed range is 89.63 to 126.2 rad/s. It is evident that the system has one unstable region \({\mathrm{U}}_{\mathrm{I}}\) which appears near the critical speeds of system, as previously reported in [39, 74]. Only principal parametric resonance appears, in which the instability boundaries are near the major natural frequencies, i.e. \({\Omega }_{\eta }\) and \({\Omega }_{\zeta }\). The combined resonance and other parametric resonances do not appear for this system with rigid supports.
Let us introduce a shaft non-circularity parameter \(\kappa ={\Delta k}_{s}/{k}_{s}\) and a non-dimensional rotor speed \({\Omega }^{*}=\Omega /{\Omega }_{avg}\) with \({\Omega }_{avg}^{2}=\left({\Omega }_{\eta }^{2}+{\Omega }_{\zeta }^{2}\right)/2\). The stability domain for constant zero damping \(c=0\) Ns/m, evaluated from Eq. (21), is shown in Fig. 17, wherein the hatched area shows the unstable region which has two boundaries. From Fig. 17, it is observed that unstable speed range increases as the shaft stiffness asymmetry or non-crcularity (\(\kappa\)) increases. It is known that increasing system damping reduces the parametric instability region [75]. As \(c\) increases, the unstable zone starts shrinking in size. In the present model with \(\kappa =1/3\), for damping value \(c=365\) Ns/m, the unstable zone vanishes completely (absolute magnitude of the eigenvalues \(\le\) 1) as shown in Fig. 18.
Shaft non-circularity \(\kappa\) versus non-dimensional rotor speed \({\Omega }^{*}\) and \(c=0\) Ns/m
Absolute magnitude of eigenvalues versus rotor speed, \(\kappa =1/3\) and \(c=365\) Ns/m
Let us introduce a damping coefficient ratio \(\xi =c/\left(2m{\Omega }_{avg}\right)\). The stability domain variation with shaft non-circularity \(\kappa\), damping coefficient ratio \(\xi\) and non-dimensional rotor spin speed \({\Omega }^{*}\) is shown in Fig. 19. Note that Fig. 17 is a cross-section of Fig. 19 at \(\xi =0\).
Stability domain of rotor for different values of \(\kappa\), \(\xi\) and \({\Omega }^{*}\)
5.4 Transient Analysis of the Non-ideal System
The permanent type DC motor is considered here as the non-ideal drive with suitable motor parameters needs to be considered, as given in Table 3. The DC motor produces torque to rotate the rotor shaft instead of a constant speed motor considered for ideal drive.
It can be shown that the reactive load torque applied on the motor is \({\Gamma }_{l}=2\Delta {k}_{s}\eta \zeta =\left({k}_{\eta }-{k}_{\zeta }\right)\left(x\mathrm{cos}\theta +y\mathrm{sin}\theta \right)\left(-x\mathrm{sin}\theta +y\mathrm{cos}\theta \right)\) [45]. Thus, the equations of motion for transient analysis are given as
where \(J\) is the rotary inertia of the rotor disc (including the rotor of the motor and the rotor shaft) about the spin axis, \({k}_{m}\) is the motor constant, \({i}_{a}\) is the armature current, \({L}_{m}\) and \({R}_{m}\) are, respectively, the motor armature coil inductance and resistance, and \({V}_{i}\) is the voltage applied across the motor terminals. The parameters of the DC motor chosen for the transient analysis are given in Table 5.
The theoretical analysis provides the stable and unstable speed ranges, but does not reveal the process to reach stable speed regions beyond the unstable regions when the energetic coupling between the motor and the rotor is considered. Thus, the transition through the unstable speed ranges is analyzed here through numerical simulations. The power supply by motor is used to overcome the load produced by rotor system. If the amount of available power is insufficient then the rotor may get stuck in boundary of the unstable zone. So it is essential to determine the critical amount of power to smoothly escape the instability for the motor sizing and overall system design perspectives.
The transient analysis of the rotor system with a non-ideal DC motor is carried out through numerical simulation; therein an initial momentum of 1 kg.m/s is given to the rotor disc in x-direction. Note that the dynamics of the system is governed by the initial conditions because the excitation here is of multiplicative nature. If there is no whirl in the rotor (\(\eta =0\) or \(\zeta =0\)) then there is no load on the motor. Even a small residual unbalance is sufficient to initiate the load on the motor. The rotor speed response and amplitude response are plotted with time for coast up operation, as shown in Figs. 20 and 21.When constant input voltage is applied, the speed saturation starts to occur from about \({V}_{i}=44.83\) V. Such saturation behavior continues up to \({V}_{i}=83\) V (see Fig. 21). When the speed is saturated, i.e. captured at the lower instability bound (89.66 rad/s), the whirl amplitude increases with applied voltage (see Fig. 21) and more and more energy is dissipated through the external viscous damping. During transient phase, the maximum speed does not exceed the upper instability bound.
Rotor speed response for motor supply voltages \({V}_{i}=83\) V and 83.1 V showing passage through parametric instability
Rotor amplitude response for motor supply voltages \({V}_{i}=83\) V and 83.1 V showing passage through parametric instability
At the steady-state, the motor power is balanced by the dissipated power. The steady-state whirl amplitude depends on the excess motor power, i.e., it is zero at \({V}_{i}=44.83\) V and increases as \({V}_{i}\) increases, until it reaches 83 V, where the whirl amplitudes are very large and the system is still captured at the lower instability threshold.
When the supply voltage reaches or exceeds a critical value, \({V}_{i}=83.1\) V, then the rotor system escapes from capture at the lower instability threshold and reaches a higher speed. Thus, between \({V}_{i}=83\) V and \({V}_{i}=83.1\) V, there is a sudden speed jump. Also, the whirl amplitude converges to 0 at \({V}_{i}=83.1\) V, i.e. there is also an associated amplitude jump (see Fig. 21). Note that at \({V}_{i}=83\) V, the rotor speed just about reaches the upper instability threshold speed \(\Omega =126.2\) rad/s (indicated by dashed line in Fig. 20).
When the voltage is reduced from a value \({V}_{i}>83.1\) V or above, there is also a similar jump phenomenon where the rotor speed suddenly jumps from the upper instability threshold to the lower instability threshold (see Figs. 22 and 23), but there is no speed capture at the upper stability threshold. The results in Figs. 22 and 23 are obtained under the initial conditions that correspond to initial rotor spin speed 200 rad/s (above the upper stability threshold) and 0.1 m/s initial velocity of the rotor disc in x-direction. The initial input voltage is 100 V and it is reduced suddenly (a step drop) to a lower value.
Rotor speed response for motor supply voltages \({V}_{i}=63\) V and 63.1 V showing passage through parametric instability
Rotor amplitude response for motor supply voltages \({V}_{i}=63\) V and 63.1 V showing passage through parametric instability
Note that in this case, the induced emf is initially larger than the supplied voltage to the motor and hence, the motor applies brake or negative torque on the rotor. Up to \({V}_{i}>63.1\) V, the whirl amplitude converges to zero and the steady rotor speed reaches \({V}_{i}/{k}_{m}>126.2\) rad/s. When \({V}_{i}\) is reduced just below \(63.1\) V, the rotor becomes unstable and whirl amplitudes start growing. This causes dissipation of energy through the viscous damping on the rotor and hence the rotor speed reduces until it reaches the lower instability threshold speed, i.e. 89.66 rad/s and it remains captured there until the motor supply voltage is reduced below 49.83 V. The bending stresses in the rotor shaft remain below yield stress when there is smooth passage through instability; whereas, capture at the lower instability threshold may lead to failure of the rotor shaft.
5.5 Jump Phenomena Characteristics
From the results, there is a clear similarity with the Sommerfeld effect of the first kind, although the Sommerfeld effect of the second kind happens here due to instability of whirl mode. This characteristic of the non-linear jump phenomena is shown in Fig. 24. During the rotor coast up (speed increase), the steady-state rotor speed follows the path \(o\to a\to b\to c\to d\) containing a capture at lower stability threshold in the path \(a\to b\) and a jump \(b\to c\), as shown in Fig. 24. During rotor coast down (speed decrease), the steady-state rotor speed follows the path \(d\to e\to f\to a\to o\) containing a capture at lower stability threshold in the path \(f\to a\) and a jump \(e\to f\), as shown in Fig. 24. Note that there is no speed capture at the upper instability threshold speed. Further note that steady-state speeds in the range lying between points a to e, i.e. the unstable speed range, can neither be reached during rotor coast-up nor during rotor coast-down.
Characterization of the Sommerfeld effect of second kind in asymmetric rotor
Additionally, the plot between the non-circularity \(\kappa\) and the rotor speed \(\Omega\) is presented together with plot between input voltage supply \({V}_{i}\) and the rotor speed \(\Omega\), for coast up and coast down operation in Figs. 25 and 26, respectively. In Fig. 25, the blue colored lines indicate stability boundaries for different values of \(\kappa\). Here, the Sommerfeld effect is shown for a fixed value \(\kappa\)\(=\)0.4 and \(c=0\) Ns/m, for which the shaded area is unstable speed range (69.28 rad/s to 105.8 rad/s). During coast up operation, the input voltage and speed variation (red line) takes the linear path a to b till the voltage reaches 34.6 V and speed reaches 69.28 rad/s. After point b, i.e. at the stability boundary, the rotor speed gets stuck at 69.28 rad/s even as the input voltage is increased. During this period, the vibration amplitude increases as the energy supplied by motor contributes to increase in the whirl amplitude. At point c, for the input voltage of 102 V, enough energy is available to escape from this unstable region and a sudden speed jump occurs from c to d, i.e. the rotor speed increases to 204 rad/s from 69.28 rad/s (shown by dashed line). After that, the rotor speed increases linearly with the input voltage along the path d to e.
Non-circularity versus rotor speed (stability map), and motor supply voltage versus rotor speed with \(\kappa\) = 0.4 for coast up dynamics
Non-circularity versus rotor speed (stability map), and motor supply voltage versus rotor speed with \(\kappa\)=0.4 for coast down dynamics
Similarly, for the coast down operation, the variation of the rotor speed with voltage follows the path \(\mathrm{e}\to \mathrm{d}\to \mathrm{c}\to \mathrm{b}\to \mathrm{a}\) as shown in Fig. 26. Once the rotor speed reaches the speed corresponding to the upper stability boundary (point d, 105.8 rad/s at 54.5 V), further reduction in voltage reduces the rotor speed to that corresponding to the lower stability boundary (point c, 69.28 rad/s at 54.5 V). Further reduction in voltage up to 34.6 V does not change the rotor speed and thereafter, a linear reduction in speed with voltage occurs in the path b to a.
Mathematically, the location of points c and d depend on the initial conditions during rotor coast up. With large rotor inertia and sufficiently high constant supply voltage, realistic initial disturbances die out by the time the rotor speed starts from zero and reaches the stability boundary. Thus, the whirl amplitude is usually small at point b if sufficient time has elapsed to reach there and then point c appears closer to point b. However, for large initial conditions or rotor unbalance, the whirl amplitude on reaching point b can be large and then it grows very fast at the stability boundary. In that case, point c shifts upwards. Likewise, if the supply voltage is gradually increased then the rotor speed gets permanently captured at the stability boundary, i.e. the voltage at point c in Fig. 25 tends to infinity. On the other hand, location of points b, c and d during rotor coast down are mostly unaffected by the initial conditions.
6 The Sommerfeld Effect of Third Kind
Rotor systems become permanently unstable beyond a certain threshold speed due to the effect of non-conservative circulatory forces, which can arise out of shaft material/internal damping, anti-symmetric bearing stiffness, Alford forces, etc. These physical phenomena create an energy pipeline for continuous pumping of motor power to the rotor whirl. In fact, the material damping increases the effective damping for rotor speeds below the shaft natural frequency and the destabilizing effect (effective damping reduction) starts for rotor speeds after the shaft natural frequency [76]. The material damping effect is present during asynchronous rotor whirl and it vanishes during synchronous rotor whirl. The material damping is modeled in a rotating frame just like the asymmetric shaft stiffness and for higher frequencies, it is found to be proportional to the shaft’s stiffness, with the proportionality constant \(\lambda\). Here, the material damping parameter \(\lambda =0.002\) s−1, which is a standard material constant, is chosen for the steel rotor shaft.
6.1 Flexible Asymmetric Rotor Shaft Mounted on Rigid Support
Here, we consider the same asymmetric rotor shaft system as in the previous section (Sect. 5). The material damping of the shaft \({\mathbf{C}}_{\mathbf{s}\mathbf{i}}\) is given as \(\left[\begin{array}{cc}{c}_{\eta i}& 0\\ 0& {c}_{\zeta i}\end{array}\right]\) in rotating coordinate system where, \({c}_{\eta i}=\lambda {k}_{\eta }\) and \({c}_{\zeta i}=\lambda {k}_{\zeta }\). Thus, the force due to shaft’s material damping in fixed coordinate system is determined as \({\stackrel{\sim }{\mathbf{C}}}_{\mathbf{s}\mathbf{i}}^{1}\dot{\mathbf{z}}+{\varvec{\Omega}}{\stackrel{\sim }{\mathbf{C}}}_{\mathbf{s}\mathbf{i}}^{2}\mathbf{z}\) where,
\({c}_{si}=\frac{{c}_{\eta i}+{c}_{\zeta i}}{2}\) is mean shaft material damping and \(\Delta {c}_{si}=\frac{{c}_{\eta i}-{c}_{\zeta i}}{2}\) is deviatoric shaft material damping. Finally, in form of matrices and vectors representation, the system’s equation in fixed coordinate system is obtained as.
where, \(\mathbf{D}=\left[\begin{array}{cc}c& 0\\ 0& c\end{array}\right]\),\({\mathbf{K}}_{\mathbf{o}}=\left[\begin{array}{cc}{k}_{s}& 0\\ 0& {k}_{s}\end{array}\right]\), \({\mathbf{C}}_{\mathbf{o}}=\left[\begin{array}{cc}{c}_{si}& 0\\ 0& {c}_{si}\end{array}\right]\), \({\mathbf{C}}_{0}^{1}=\left[\begin{array}{cc}0& {c}_{si}\\ -{c}_{si}& 0\end{array}\right]\), \({{\varvec{\Delta}}\mathbf{C}}_{1}=\left[\begin{array}{cc}{\Delta c}_{si}& 0\\ 0& -\Delta {c}_{si}\end{array}\right]\), \({{\varvec{\Delta}}\mathbf{C}}_{2}=\left[\begin{array}{cc}0& {\Delta c}_{si}\\ {\Delta c}_{si}& 0\end{array}\right]\) and \(\stackrel{\sim }{\Omega }=2\Omega\).
6.2 Stability Analysis
The boundaries of unstable regions of system are determined by using Floquet theory. Hence, Eq. (26) written in state space form as \({\dot{\mathbf{A}}}^{\mathrm{T}}=\mathbf{P}\left(t\right){\mathbf{A}}^{\mathrm{T}}\).
and, \({p}_{11}=c+{c}_{si}+\Delta {c}_{si}\mathrm{cos}2\Omega t\), \({p}_{12}=\Delta {c}_{si}\mathrm{sin}2\Omega t\), \({p}_{13}={k}_{s}+\Delta {k}_{s}\mathrm{cos}2\Omega t-\mathrm{\Omega \Delta }{c}_{si}\mathrm{sin}2\Omega t\), \({p}_{14}=\Omega {c}_{si}+\mathrm{\Omega \Delta }{c}_{si}\mathrm{cos}2\Omega t+\Delta {k}_{s}\mathrm{sin}2\mathrm{\Omega t}\), \({p}_{21}=\Delta {c}_{si}\mathrm{sin}2\Omega t\), \({p}_{22}=c+{c}_{si}-\Delta {c}_{si}\mathrm{cos}2\Omega t\), \({p}_{23}=-\Omega {c}_{si}+\mathrm{\Omega \Delta }{c}_{si}\mathrm{cos}2\Omega t+\Delta {k}_{s}\mathrm{sin}2\mathrm{\Omega t}\), and \({p}_{24}={k}_{s}-\Delta {k}_{s}\mathrm{cos}2\Omega t+\Delta {c}_{si}\mathrm{sin}2\Omega t\).
As the monodromy matrix is obtained by numerical integration of \(\mathbf{P}\left(t\right)\) and then the eigenvalues \({\sigma }_{i} (i=1..4)\) of the monodromy matrix are used to conclude the stability of the system by inputting the values of parameters that are given in Table 4. The real parts of the eigenvalues \({\sigma }_{\mathrm{Re}}\) are plotted with respect to rotor spin speed without considering the internal damping in Fig. 27. It can be seen that only one unstable region (UI) due to parametric instability appears in entire speed range of the rotor. The real parts of the eigenvalues \({\sigma }_{\mathrm{Re}}\) are plotted for the same parameters with internal damping (\(\lambda =0.002\) s−1) in Fig. 28. Now, there is a similar unstable operation region due to parametric instability (speeds \({u}_{1}\) to \({u}_{2}\) i.e., 89.7 to 126.2 rad/s, corresponding to region UI) and another permanent instability region (from 133.2 rad/s i.e., \({u}_{3}\) onwards). Thus, the instability threshold speed \({\Omega }_{\mathrm{th}}=133.2\) rad/s and there is no stable operating speed beyond this permanent instability threshold. The range of parametric instability and the onset of permanent flutter instability strongly depend upon the damping in the system. For example, if the external damping is increased to \(c=100\) Ns/m then the system has parametric instability region from \({u}_{1}=90\) rad/s to \({u}_{2}=125.7\) rad/s, i.e. there is a very small change in the unstable speed range, whereas the permanent instability threshold value increases significantly to \({u}_{3}=151.9\) rad/s.
Real parts of eigenvalues versus rotor speed for the rotor and \(\lambda =0 {\mathrm{s}}^{-1}\)
Real parts of eigenvalues versus rotor speed for the rotor and \(\lambda =0.002\, {\mathrm{s}}^{-1}\)
6.3 Transient Analysis of Non-ideal System
Some sample simulation results are discussed here corresponding to the stability behavior shown in Fig. 28 where the parametric instability region appears for speed range 89.7–126.2 rad/s, and the stability threshold speed is 133.2 rad/s. The excitation to initiate rotor whirl is provided by the initial momentum of 1 kg-m/s in x-direction of disc centre. The rotor speed reaches the desired steady-state value \(\Omega ={V}_{i}/{k}_{m}\) for \({V}_{i}\le 44.9\) V. The results show that the rotor spin speed is stuck at 89.65 rad/s (near lower unstable boundary \({\mathrm{U}}_{1}\)) for \({V}_{i}=45\mathrm{V}\). After that, it never escapes through the unstable regions for any further increase in the supply voltage. This is because the when there is sufficient power given to accelerate the rotor speed outside the capture at the parametric instability boundary, the rotor speed would actually reach a value beyond the permanent stability threshold (133.2 rad/s, here). Thus, the vibration amplitudes start to increase and reduce the shaft speed back to the lower limit of the parametric instability boundary. Such a behavior is observed when the permanent instability speed is very close to the parametric instability region.
For the case of higher value of external–damping, i.e. \(c=100\) Ns/m, there is sufficient gap between the parametric instability regions (\(90{-}125.7\) rad/s) and stability threshold (\(151.9\) rad/s). In this case, the rotor speed reaches the desired steady-state value \(\Omega ={V}_{i}/{k}_{m}\) for \({V}_{i}\le 45.1\) V. For the supply voltage range \({V}_{i}=45.1\) to 69.8 V, the rotor speed is captured at the lower stability threshold of parametric instability zone \({u}_{1}\), i.e. at the average speed of 90 rad/s. The system escapes from the parametric instability for \({V}_{i}\ge 69.9\) V (see Fig. 29), reaches the desired steady-state value \(\Omega ={V}_{i}/{k}_{m}\) and the whirl amplitudes reduces (see Fig. 30).
Rotor speed response during capture at and escape through parametric instability for the rotor with c = 100 Ns/m and material damping
Rotor whirl amplitudes during capture at and escape through parametric instability for the rotor with c = 100 Ns/m and material damping
On further increasing the supply voltage, at \({V}_{i}=75.9\) V, the rotor speed gets stuck at 151.9 rad/s (near threshold value of permanent instability \({\Omega }_{\mathrm{th}}\)) with large bounded amplitudes of vibration. Hence, on reaching the stability threshold for \({V}_{i}\ge 75.9\), there is a permanent capture of rotor speed at average speed of 151.9 rad/s and the whirl amplitude continues to increase with any further increase in voltage, as shown for two such supply voltages in Figs. 31 and 32. Note that in Fig. 32, the whirl amplitude appears unsteady because of the simultaneous presence of synchronous and asynchronous whirls.
Rotor speed response during capture at stability threshold for the rotor with material damping
Rotor whirl amplitudes during capture at stability threshold for the rotor with material damping
This permanent capture at stability threshold is termed as the Sommerfeld effect of third kind. It has been discussed previously in various articles [19, 48,49,50,51, 77, 78]. Note that permanent capture at the stability threshold does not give steady whirl amplitude. In fact, there is a synchronous whirl and an asynchronous whirl present at the same time. In rotor dynamic systems, various means have been proposed to increase the stable operating speed regions, such as squeeze film dampers, impact dampers, and visco-elastic supports, all of which attempt to increase the effective external damping in the system. However, effective external damping cannot be increased arbitrarily in a system because it is also related to the vibration isolation capacity of the foundation and the energy efficiency of the non-ideal motor, as has been recently described in [79].
References
El-Badawy, A.A.: Behavioral investigation of a nonlinear nonideal vibrating system. J. Vib. Control 13(2), 203–217 (2007). ISSN 1077–5463. https://doi.org/10.1177/1077546307073674
Kononenko, V.O.: Vibrating Systems with Limited Excitation [in Russian]. Nauka, Moscow (1964)
Nayfeh, A., Mook, D.: Nonlinear Oscillations. Wiley-Interscience, NY (1979)
Sommerfeld, A.: Beiträge Zum Dynamischen Ausbau Der Festigkeitslehe. Physikal Zeitschr 3, 266–286 (1902)
Eckert, M.: The Sommerfeld effect: theory and history of a remarkable resonance phenomenon. Europ. J. Phys. 17(5), 285–289 (1996)
Kononenko, V.O.: Vibrating Systems with Limited Excitation, English Translation from Russian. (Illife Books) (1969)
Timoshenko, S.: Vibration Problems in Engineering. Van Nostrand, Princeton, NJ (1961)
Blekhman, I.I.: Vibrational Mechanics: Nonlinear Dynamic Effects, General Approach, Applications. World Scientific, Singapore (2000)
Alifov, A.A., Frolov, K.V.: Interaction of Non-linear Oscillatory Systems with Energy Sources. Taylor & Francis, London (1990)
Hübner, W.: Die Wechsetwirkung zwischen Schwinger und Antrieb bei Schwingungen. Ingenieur-Archive 34, 411–422 (1965)
Rand, R.H., Kinsey, R.J., Mingori, D.L.: Dynamics of spinup through resonance. Int. J. Non-Linear Mech. 27(3), 489–502 (1992)
Ryzhik, A., Amer, T., Duckstein, H., Sperling, L.: Zum Sommerfeldeffect beim selbsttätigen Auswuchten in einer Ebene. Tech. Mech. 21(4), 297–312 (2001)
Yamanaka, H., Murakami, S.: Optimum designs of operating curves for rotating shaft systems with limited power supplier. In: Chung, H. (ed.), Current Topics in Structural Mechanics, pp. 181–185 (1989)
Christ, H.: Stationärer und Instatioärer Betrieb Eines Federnd Gelagerten, Unwuchtigen Motors, Ph.D. Thesis, Universität Karlsruhe (1966)
Frolov, K.V., Krasnopol’skaya, T.S.: Sommerfeld effect in systems without internal damping. Prikladnaya Mekhanika 23(12), 19–24 (1987)
Dimentberg, M.F., McGovern, L., Norton, R.L., Chapdelaine, J., Harrison, R.: Dynamics of an unbalanced shaft interacting with a limited power supply. Nonlinear Dyn. 13, 171–187 (1997)
Cveticanin, L.: Dynamics of the non-ideal mechanical systems: a review. J. Serbian Soc. Comput. Mech. 4(2), 75–86 (2010)
Samantaray, A.K., Dasgupta, S., Bhattacharyya, R.: Sommerfeld effect in rotationally symmetric planar dynamical systems. Int. J. Eng. Sci. 48(1), 21–36 (2010)
Dasgupta, S.S., Samantaray, A.K., Bhattacharyya, R.: Stability of an internally damped non-ideal flexible spinning shaft. Int. J. Non-linear Mech. 45(3), 286–293 (2010)
Dimentberg, M.F.: Vibration of a rotating shaft with randomly varying internal damping. J. Sound Vib. 285(3), 759–765 (2005). https://doi.org/10.1016/j.jsv.2004.11.025
Kovriguine, D.A.: Synchronization and sommerfeld effect as typical resonant patterns. Arch. Appl. Mech. 82(5), 591–604 (2012)
Hu, W.H., Thöns, S., Rohrmann, R.G., Said, S., Rücker, W.: Vibration-based structural health monitoring of a wind turbine system. Part I: Reson. Phenomenon. Eng. Struct. 89, 260–272 (2015)
Blekhman, I.I., Kremer, E.: Vibrational resistance to vehicle motion due to road unevenness. J. Sound Vib. 405, 306–313 (2017)
Sinha, A., Bharti, S.K., Samantaray, A.K., Chakraborty, G., Bhattacharyya, R.: Sommerfeld effect in an oscillator with a reciprocating mass. Nonlinear Dyn. 93(3), 1719–1739 (2018)
Balthazar, J.M., Mook, D.T., Weber, H.I., Fenili, A., Belato, D., de Mattos, M.C., Wieczorek, S.: On vibrating systems with a limited power supply and their applications to engineering sciences. In: Honig, C.S. (ed.) 49th Brazilian Seminar of Mathematical Analysis, pp. 137–277. State University of Campinas, Campinas, SP, Brazil (1999)
Balthazar, J.M., Mook, D.T.: Brasil, R.M.L.R.F., Weber, H.I., Fenili, A., Belato, D., Felix, J.L.P., Recent results on vibrating problems with limited power supply. In: Awrejcewicz, J., Brabski, J., Nowakowski, J. (eds.) Sixth Conference on Dynamical Systems Theory and Applications, pp. 27–50. Lodz, Poland (2001)
Balthazar, J.M., Mook, D.T., Brasil, R.M.L.R.F., Fenili, A., Belato, D., Felix, J.L.P., Weber, H.I.: Recent results on vibrating problems with limited power supply. Meccanica 330(7), 1–9 (2002)
Balthazar, J.M., Brasil, R.M.L.R.F., Garzeri, F.J.: On non-ideal simple portal frame structural model: experimental results under a non-ideal excitation. Appl. Mech. Mater. 1–2, 51–58 (2004)
Dantas, M.J.H., Balthazar, J.M.: On the appearance of a Hopf bifurcation in a non-ideal mechanical problem. Mech. Res. Commun. 30(5), 493–503 (2003)
Bolla, M.R., Balthazar, J.M., Felix, J.L.P., Mook, D.T.: On an approximate analytical solution to a nonlinear vibrating problem, excited by a nonideal motor. Nonlinear Dyn. 50(4), 841–847 (2007)
numerical and analytical approaches: Felix, J.L.P., Balthazar, J.M., Brasil, R.M.L.R.F. Comments on nonlinear dynamics of a non-ideal duffing-rayleigh oscillator. J. Sound Vib. 319, 1136–1149 (2009)
Bharti, S.K., Samantaray, A.K.: Resonant capture and Sommerfeld effect due to torsional vibrations in a double Cardan joint driveline. Commun. Nonlinear Sci. Numer. Simul. 97, 105728 (2021)
Taylor, H.D.: Critical-speed behavior of unsymmetrical shafts. J. Appl. Mech. 7(2), 71–79 (1940)
Dimentberg, F.M.: Flexural Vibrations of Rotating Shaft. Butterworths, London (1961)
Brosens, P.J., Crandall, S.H.: Whirling of unsymmetrical rotors. Trans. ASME. J. Appl. Mech. 28(3), 355–362 (1961)
Yamamoto, T., Ota, H.: On the unstable vibrations of the shaft carrying an unsymmetrical rotor. J. Appl. Mech. 31(3), 515–522 (1964)
Yamamoto, T., Yasuda, K.: Unstable Vibrations of an unsymmetrical rotor supported by flexible bearing pedestals. Bullet. JSME 15(87), 1063–1073 (1972)
Ikeda, T., Murakami, S.: Dynamic response and stability of a rotating asymmetric shaft mounted on a flexible base. Nonlinear Dyn. 20(1), 1–19 (1999)
Srinath, R., Sarkar, A., Sekhar, A.S.: Instability of asymmetric shaft system. J. Sound Vib. 362, 276–291 (2016)
Foote, W.R., Poritsky, H., Slade, J.J.: Critical speeds of a rotor with unequal shaft flexibilities, mounted in bearings of unequal flexibility—I. J. Appl. Mech. 10, A77–A84 (1943)
Messal, E.E., Bonthron, R.J.: Subharmonic rotor instability due to elastic asymmetry. J. Eng. Indus. 94(1), 185–192 (1972)
Ardayfio, D., Frohrib, D.A.: Instabilities of an asymmetric rotor with asymmetric shaft mounted on symmetric elastic supports. Trans. ASME J. Eng. Indus. 98(4), 1161–1165 (1976)
Lee, C.W.: Vibration Analysis of Rotors. Springer Science & Business Media, 21 (1993)
Boru, F.E.: Numerical and Experimental Response and Stability Investigations of Anisotropic Rotor-Bearing Systems. Kassel University press GmbH (2010)
Bharti, S.K., Sinha, A., Samantaray, A.K., Bhattacharyya, R.: The Sommerfeld effect of second kind: passage through parametric instability in a rotor with non-circular shaft and anisotropic flexible supports. Nonlinear Dyn. 100, 3171–3197 (2020)
Samantaray, A.K., Bhattacharyya, R., Mukherjee, A.: An investigation into the physics behind the stabilizing effects of two-phase lubricants in journal bearings. J. Vib. and Control 12(4), 425–442 (2006)
Samantaray, A.K., Mukherjee, A., Bhattacharyya, R.: Some studies on rotors with polynomial type nonlinear external and internal damping. Int. J. Non-linear Mech. 41, 1007–1015 (2006)
Samantaray, A.K., Dasgupta, S.S., Bhattacharyya, R.: Bond graph modeling of an internally damped nonideal flexible spinning shaft. J. Dyn. Syst. Measur. Control 132(6), 061502 (2010)
Samantaray, A.K., A note on internal damping induced self-excited vibration in a rotor by considering source loading of a DC motor drive, Int. J. Non-Linear Mech. 43(9), 1012–1017 (2008)
Samantaray, A.K.: Steady state dynamics of a non-ideal rotor with internal damping and gyroscopic effects. Nonlinear Dyn. 56(4), 443–451 (2009)
Mukherjee, A., Karmakar, R., Samantaray, A.K.: Modelling of basic induction motors and source loading in rotor-motor systems with regenerative force field. Simul. Pract. Theory 7(5), 563–576 (1999)
Kirk, R.G., Gunter, E.J.: The effect of support flexibility and damping on the synchronous response of a single-mass flexible rotor. J. Eng. Indus. Trans. ASME 94, 221–232 (1972)
Gunter, E. J.: The influence of internal friction on the stability of high speed rotors. J. Eng. Indus. Trans. ASME Ser. B 89(4), 683–688 (1967)
Vance, J.M., Rotordynamics of Turbomachinery. New York, Wiley (1988)
Genta, G.: Dynamics of Rotating Systems. Springer (2005)
Greenhill, Lyn, M., Guillermo, A.: Cornejo.: critical speeds resulting from unbalance excitation of backward whirl modes. Design Eng. Techn. Conf. 3, part 3, ASME (1995)
Muszynska, A.: Forward and backward precession of a vertical anisotropically supported rotor. J. Sound Vib. 192(1), 207–222 (1996)
Bharti, S.K., Bisoi, A., Sinha, A., Samantaray, A.K., Bhattacharyya, R.: Sommerfeld effect at forward and backward critical speeds in a rigid rotor shaft system with anisotropic supports. J. Sound Vib. 442, 330–349 (2019)
Karthikeyan, M., Bisoi, A., Samantaray, A.K., Bhattacharyya, R.: Sommerfeld effect characterization in rotors with non-ideal drive from ideal drive response and power balance. Mech. Mach. 91, 269–288 (2015)
Bisoi, A., Samantaray, A.K., Bhattacharyya, R.: Sommerfeld effect in a two-disk rotor dynamic system at various unbalance conditions. Meccanica 53(4), 681–701 (2018)
Porter, B.: A theoretical analysis of the torsional oscillation of a system incorporating a Hooke’s joint. J. Mech. Eng. Sci. 3(4), 324–329 (1961)
Porter, B., Gregory, R.W.: Non-linear torsional oscillation of a system incorporating a Hooke’s joint. J. Mecha. Eng. Sci. 5(2), 191–200 (1963)
Porter, B.: Non-linear torsional oscillation of a two-degree-of-freedom system incorporating a Hooke joint. Proc. R. Soc. Lond. Ser. A 277(1368), 92–106 (1964)
Asokanthan, S.F., Hwang, M.C.: Torsional instabilities in a system incorporating a Hooke’s joint. J. Vib. Acoust. 118(3), 368–374 (1996)
Asokanthan, S.F., Meehan, P.A.: Non-linear vibration of a torsional system driven by a Hooke’s joint. J. Sound Vib. 233(2), 297–310 (2000)
Bulut, G.: Dynamic stability analysis of torsional vibrations of a shaft system connected by a Hooke’s joint through a continuous system model. J. Sound Vib. 333(16), 3691–3701 (2014)
De Smidt, H.A., Wang, K.W., Smith, E.C.: Multi-harmonic adaptive vibration control of AMB-driveline systems with non-constant velocity flexible couplings. Int. Design Eng. Techn. Conf. Comput. Inform. Eng. Conf. 37033, 1995–2005 (2003)
Yao, W., DeSmidt, H.. Nonlinear coupled torsion/lateral vibration and Sommerfeld behavior in a double U-joint driveshaft. J. Vib. Acoust. 143(3), 031011 (2021)
Lima, R., Soize, C., Sampaio, R.: Robust design optimization with an uncertain model of a nonlinear vibro-impact electro-mechanical system. Commun. Nonlinear Sci. Numer. Simul. 23(1–3), 263–273 (2015)
Lima, R., Sampaio, R.: Two parametric excited nonlinear systems due to electromechanical coupling. J. Braz. Soc. Mech. Sci. Eng. 38(3), 931–943 (2016)
Tsuchida, M., Guilherme, K.L., Balthazar, J.M., Silva G.N., Cheshancov, B.I.. On regular and irregular vibrations of a non-ideal system with two degree of freedom. 1:1 resonance. J. Sound Vib. 260, 949–960 (2003)
Tsuchida, M., Guilherme, K.L., Balthazar, J.M.: On chaotic vibrations of a non-ideal system with two degrees of freedom: 1:2 resonance and Sommerfeld effect. J. Sound Vib. 282, 1201–1207 (2005)
Quinn, D.D.: Resonant dynamics in a rotordynamic system with nonlinear inertial coupling and shaft anisotropy. Nonlinear Dynam. 57(4), 623–633 (2009)
Song, Z., Chen, Z., Li, W., Chai, Y.: Parametric instability analysis of a rotating shaft subjected to a periodic axial force by using discrete singular convolution method. Meccanica 52(4–5), 1159–1173 (2017)
Bones, J.A., Hannam, R.G.: Whirling of shafts with asymmetric stiffness. J. Mech. Eng. Sci. 8(4), 437–447 (1966)
Genta, G.: On a persistent misunderstanding of the role of hysteretic damping in rotordynamics. J. Vib. Acoust. Trans. ASME 126(3), 459–461 (2004)
Wettergren, H.L., Olsson, K.O.: Dynamic instability of a rotating asymmetric shaft with internal viscous damping supported in anisotropic bearings. J. Sound Vib. 195(1), 75–84 (1996)
Sinha, A., Bharti, S.K., Bhattacharyya, R., Samantaray, A.K.: Discussion on A novel approach to study effects of asymmetric stiffness on parametric instabilities of multi-rotor-system, Jain et al. J. Sound Vib. 413(2018) 159–172, J. Sound Vib. 442(3), 268–280 (2019)
Samantaray, A.K.: Efficiency considerations for Sommerfeld effect attenuation. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 0954406221991584 (2021)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Samantaray, A.K. (2022). Three Kinds of Sommerfeld Effect in Rotor Dynamics. In: Balthazar, J.M. (eds) Nonlinear Vibrations Excited by Limited Power Sources. Mechanisms and Machine Science, vol 116. Springer, Cham. https://doi.org/10.1007/978-3-030-96603-4_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-96603-4_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-96602-7
Online ISBN: 978-3-030-96603-4
eBook Packages: EngineeringEngineering (R0)