The Sommerfeld effect of second kind: passage through parametric instability in a rotor with non-circular shaft and anisotropic flexible supports

Abstract

A rotor system with asymmetry in its bending flexibility as well as in its support bearings has many stable and unstable speed ranges. The dynamics of such a system is governed by differential equations with time-varying parametric coefficients which lead to parametric instability in certain rotor speed ranges. In this study, an asymmetric rotor shaft having a rotor disc placed firmly on its centre is considered. The rotor shaft is mounted on two bearings at its two ends having stiffness asymmetry. A permanent magnet-type DC motor is used to drive the rotor. When rotor approaches the lower limit of any unstable speed range, the rotor spin speed is captured at that speed with increasing whirl amplitudes and the rotor speed does not respond to an increase in the motor power, unless there is sufficient surplus power to accelerate the rotor through the corresponding unstable speed range. With this surplus power, the escape from lower instability limit speed to a much higher stable speed takes place as a nonlinear jump phenomenon. In certain situations, escape from one unstable speed range may lead to capture at another unstable speed range or simultaneous escape from the next unstable range. This specifically occurs due to the presence of the non-ideal drive and is termed here as the Sommerfeld effect of second kind. Unlike regular Sommerfeld effect (of first kind) where the power scarcity at the resonance is the cause of speed capture; there is, ideally, no need for a residual rotor unbalance in the Sommerfeld effect of second kind. In both the cases of speed capture, the excess motor power is spent to increase the whirl amplitudes. The Sommerfeld effect of the first kind relates to the resonance at the synchronous rotor whirl (critical speeds), whereas that of the second kind relates to instability of the rotor whirl. Due to such nonlinear jumps, some of the speed ranges where the rotor is theoretically stable under ideal or mathematical conditions may not be reached in practice, i.e. with a real drive which is naturally non-ideal. The dynamics of this rotor system is analytically and numerically studied in this article. The numerical simulations are performed with a multi-energy domain bond graph model which guarantees energetic consistency of the model.

1 Introduction

In some specific rotor dynamic applications, the cross section of the shaft is purposefully designed to be non-circular. For example, rotor shafts of multi-pole electric motors, twisted brush motors, shafts with keyways or flats to allow coupling, drill bits, rotary broaches, etc. Due to this non-circularity, asymmetry may appear in the form of different bending stiffness of shaft along the principal axes in the shaft cross section of the rotor [1,2,3,4]. Due to this asymmetry in a flexible asymmetric shaft with a centrally placed disc supported rigidly at its ends, an unstable region appears between the major critical speeds [5,6,7]. Additional unstable regions appear when, in addition to the asymmetry in the shaft stiffness, the supports are also flexible and asymmetric [8,9,10]. The effect of asymmetric parameters on the unstable regions of the rotor is analysed in [11, 12].

Modelling aspects of asymmetric shaft systems with elastic support are addressed by many researchers [13, 14]. The instabilities of a flexible asymmetric shaft with internal viscous damping and anisotropic bearings are studied by employing Floquet theory in [15, 16]. Various researchers [17,18,19] have used the finite element method (FEM) to model continuous rotor system to study the asymmetric anisotropic rotor-bearing systems. Modal analysis by using Floquet theory [20], FEM with time-based matrix method and Floquet theory [21], asymptotic methods [22], normal forms [23], etc., are some other methods applied to study stability of asymmetric rotor shaft systems.

Almost all published studies on asymmetric shaft-rotor system consider an ideal energy source which is unaffected by the dynamics of the shaft-rotor system. But in reality, the drives are non-ideal where the variable load due to dynamics of the shaft-rotor system influences the power delivery from the energy source. Examples are DC motor, induction machine, hydraulic pump, etc. With a non-ideal drive, the rotor system may get captured at the synchronous whirl critical speed with excessive vibration levels, thereby damaging the rotor shaft, bearings and other structures [24,25,26,27,28]. With substantial excess power input from the non-ideal drive, the rotor speed can escape the resonance speed with a corresponding reduction in the vibration amplitudes. It is a nonlinear jump phenomenon known as the Sommerfeld effect [29,30,31,32,33,34]. Mostly, the Sommerfeld effect is found in rotor dynamic systems with eccentric disc and non-ideal drives [24,25,26,27,28, 35,36,37,38,39,40]. Sommerfeld effect in wind turbine [41], vehicle dynamics [42] and slider-crank mechanism are also reported [43]. In this article, this well-known effect is termed as the Sommerfeld effect of first kind.

At the stability threshold of a rotor system, the asynchronous whirl, at a frequency different from the rotor spin speed, becomes unstable. Reasons for such loss of stability are internal or material damping of the shaft [44], friction in spline joints, Alford forces on turbine blades, and oil whip in hydrodynamic bearing, etc. If the drive output power is increased after reaching the rotor stability threshold speed, then the motor/rotor speed gets entrapped at the stability threshold speed and the asynchronous whirl amplitudes increase [45,46,47]. Though this behaviour is similar to Sommerfeld effect of first kind, the stability threshold is inescapable.

Parametric instability in rotor dynamic systems gives one or more unstable speed ranges lying between stable speed ranges. Therefore, each unstable speed range is bounded by a lower stable speed range and an upper stable speed range. However, to reach the upper stable speed range, the rotor system has to transit through the unstable speeds. This consideration is not made when mathematical analysis of the system is done with an ideal drive assumption. In reality, the transition from the lower stable range to higher stable range would require the rotor spin to accelerate quickly through the unstable speed range before the whirl amplitudes grow substantially and create energy scarcity for rotor spin acceleration. As a consequence, when rotor spin escapes the unstable speed range, it would reach a substantially higher speed with decaying whirl amplitudes. Similar behaviour occurs during rotor coast down through unstable speed range. In [27], a rotor dynamic system with asymmetric shaft stiffness due to cracked rotor shaft is studied with non-ideal drive and it is shown that the stall torque not only depends on the parameter values but also on the initial conditions. Thus, prima facie, there is a nonlinear jump as well as a missing speed range, as would be investigated herein. In this article, such kind of nonlinear jump phenomena is termed as the Sommerfeld effect of second kind. This phenomenon is distinctly different from the usual Sommerfeld effect (of first kind) because it is related to instability of the rotor whirl rather than the resonance in the synchronous rotor whirl. In fact, appearance of the Sommerfeld effect of first kind requires unbalance in the rotor to excite the synchronous whirl as a forcing function or additive excitation, whereas appearance of the Sommerfeld effect of the second kind does not require any rotor unbalance because it is a multiplicative excitation which requires a small disturbance from the equilibrium position. During the Sommerfeld of second kind, if the motor power output is slowly increased after reaching any of the lower stability boundaries, then the vibration amplitudes can grow to suck up all the excess power and the rotor spin speed will be perpetually caught at the corresponding speed, i.e. it would not be possible to transit through the resonance. Therefore, judicious actuator sizing or design is needed to smoothly transit/accelerate through the unstable speed ranges while limiting the whirl amplitudes within acceptable bounds during that transient process.

In the present work, the Sommerfeld effect of second kind in a flexible asymmetric rotor shaft which is rigidly fixed with a circular rotor disc at its centre, mounted on anisotropic bearings at its two ends, and driven by a permanent magnet DC motor (a non-ideal drive), is studied. The asymmetries in the rotor system give rise to so-called parametric instabilities containing one or more stable and unstable regions. The Floquet theory based on Hill’s infinite determinant is used to determine the stability domains. The complete electro-mechanical system is modelled in bond graph (BG) form for numerical simulation. The critical or threshold values of input voltages for smooth passage or escape through the various unstable speed ranges are numerically studied. Initially, a rigid support is considered as a special case and then the insights are extended to the full system. Subsequently, the Sommerfeld effect of second kind is revealed for the present rotor system and its characterization is done for the particular rotor system parameters.

2 System description and analysis

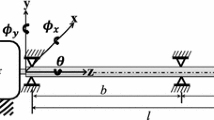
A flexible rectangular rotor shaft carries a heavy rotor disc fixed at its mid-section as shown in Fig. 1. Negligibly small lengths at the two ends of the rotor shaft are cylindrical where the shaft is supported on the bearings, out of which one is a roller bearing allowing axial sliding of the shaft. The rotor shaft mass is referred to the rotor disc position and the two bearings, as it is common in a Jeffcott rotor model. Twisting of the rotor shaft is neglected. There is no constraint force along the shaft axis, i.e. the shaft is not stretched axially, and the slenderness ratio of the rotor shaft is large. The shaft has asymmetric bending stiffness due to rectangular cross section. A rotating coordinate frame is aligned parallel to the principal axes in the shaft cross section so that the shaft stiffness remains constant in that reference frame. In a fixed or inertial coordinate frame, these stiffnesses change with time. Here, $x,y,z$ is the fixed coordinate system ($\Phi$) and $\eta ,\zeta ,z$ is the rotating coordinate system ($\varPsi$), as shown in Fig. 1, with the rotation $\theta$ about the common or parallel z-axis defining the angle between the two coordinate systems at any particular time and $\Omega = \dot{\theta }$ the angular rotational speed of shaft about z-axis (shaft spin axis). The coordinates $\left( {x,y} \right)$ and $\left( {\eta ,\zeta } \right)$ refer to position of deflected shaft centre C in the respective frames. The corresponding shaft stiffness in $\eta ,\zeta$-directions in $\varPsi$ are $k_{\eta }$ and $k_{\zeta }$, respectively. The flexible supports are anisotropic with $K_{bx}$ and $K_{by}$ being the stiffness in x and y directions, respectively. The damping at the supports and the material damping in the shaft are neglected. However, an overall viscous damping c is assumed to act at the geometric centre C of the rotor disc.

Fig. 1

Schematic diagram of the non-circular flexible rotor driven by non-ideal DC motor

For studying the Sommerfeld effect of second kind, there is no need for rotor disc eccentricity. However, one needs to disturb the system from equilibrium to initiate the whirl, i.e. to set up the multiplicative excitation. This disturbance is naturally present in real working environment. However, for simulation or analysis, this disturbance can be given as an initial condition such as impact or as residual unbalance [27]. An ideal coupling which is flexible in bending and rigid in torsion is assumed between the DC motor and the rotor shaft. Since the torsion of the rotor shaft is neglected, the motor torque is directly applied to the rotor disc.

2.1 Equations of motion

Since, the disc is placed on the middle of the flexible shaft, only lateral the displacements of the disc in the first bending (whirl) mode of the rotor shaft are considered with no rotation of the disc about diametral ($\eta { - }\xi$) axes. To derive the stability domain of the rotor system at various rotor spin speeds, initially, the rotor speed is assumed to be constant; i.e. $\dot{\theta } = \Omega$ and $\ddot{\theta } = 0$. The steady-state dynamics as well as stability domains do not depend on the value of initial configuration of the infinitely small eccentricity and hence, initial $\theta$ is taken as zero without any loss of generality. For large slenderness ratio and no axial stretching of the rotor shaft, linear Jeffcott rotor model is used here. The equations of motion of the rotor in the lateral directions can be written as

$$ {\mathbf{M}}{\ddot{\mathbf{z}}} + {\mathbf{D}}{\dot{\mathbf{z}}}+ {\tilde{\mathbf{K}}}_{bs} {\mathbf{z}} = {\mathbf{f}}, $$

(1)

where mass matrix ${\mathbf{M}} = m{\mathbf{I}}$ is damping matrix ${\mathbf{D}} = c{\mathbf{I}}$, I is a 2 × 2 identity matrix, ${\tilde{\mathbf{K}}}_{{{\mathbf{bs}}}}$ is time-variant combined stiffness matrix, rotor’s lateral displacement vector in the fixed frame ${\mathbf{z}} = \left[ {\begin{array}{*{20}c} x & y \\ \end{array} } \right]^{{\rm T}}$, and forcing vector ${\mathbf{f}}$ is an forcing vector which is zero in the present case. At constant spin speed, the rotation matrix from $\varPsi$ to $\Phi$, ${\mathbf{R}} = \left[ {\begin{array}{*{20}c} {\cos \Omega t} & { - \sin \Omega t} \\ {\sin \Omega t} & {\cos \Omega t} \\ \end{array} } \right]$. If ${\mathbf{t}} = \left[ {\begin{array}{*{20}c} \eta & \zeta \\ \end{array} } \right]^{{\rm T}}$ is the rotor’s lateral displacement vector in $\varPsi$, then the restoring force vector in $\varPsi$ is ${\mathbf{k}}_{{\mathbf{s}}} {\mathbf{t}} = {\mathbf{k}}_{{\mathbf{s}}} {\mathbf{R}}^{\text{T}} {\mathbf{z}}$ where ${\mathbf{k}}_{{\mathbf{s}}} = \left[ {\begin{array}{*{20}c} {k_{\eta } } & 0 \\ 0 & {k_{\zeta } } \\ \end{array} } \right]$. Transformation of the restoring forces from $\varPsi$ to $\Phi$ gives the restoring force vector in $\Phi$ as ${\mathbf{Rk}}_{{\mathbf{s}}} {\mathbf{R}}^{\text{T}} {\mathbf{z}} = {\tilde{\mathbf{k}}}_{{\mathbf{s}}} {\mathbf{z}}$ where time-varying matrix ${\tilde{\mathbf{k}}}_{{\mathbf{s}}} = {\mathbf{Rk}}_{{\mathbf{s}}} {\mathbf{R}}^{\text{T}} = \left[ {\begin{array}{*{20}c} {k_{s} + \Delta k_{s} \cos 2\Omega t} & {k_{s} + \Delta k_{s} \sin 2\Omega t} \\ {k_{s} + \Delta k_{s} \sin 2\Omega t} & {k_{s} - \Delta k_{s} \cos 2\Omega t} \\ \end{array} } \right]$ with $k_{s} = \frac{{k_{\eta } + k_{\zeta } }}{2}$ as the mean shaft bending stiffness and $\Delta k_{s} = \frac{{k_{\eta } - k_{\zeta } }}{2}$ as the deviatoric shaft bending stiffness. The bearing stiffness ${\mathbf{k}}_{b} = \left[ {\begin{array}{*{20}c} {k_{bx} } & 0 \\ 0 & {k_{by} } \\ \end{array} } \right]$ at the both ends, which is parallel to the shaft’s lateral stiffness. Neglecting the bearing mass and any shaft mass referred to the bearing end, the combined lateral stiffness of the rotor shaft system in $\Phi$ is represented as ${\tilde{\mathbf{K}}}_{bs}$ where $\left( {{\tilde{\mathbf{K}}}_{bs} } \right)^{ - 1} = \left( {2{\mathbf{k}}_{b} } \right)^{ - 1} + \left( {{\tilde{\mathbf{k}}}_{s} } \right)^{ - 1}$. Thus,

$$ {\tilde{\mathbf{K}}}_{bs} = \left[ {\begin{array}{*{20}c} {K_{obx} } & 0 \\ 0 & {K_{oby} } \\ \end{array} } \right] + \frac{{\Delta k_{s} }}{{k_{s}^{2} }}\left[ {\begin{array}{*{20}c} {K_{obx}^{2} \cos 2\Omega t} & {K_{obx} K_{oby} \sin 2\Omega t} \\ {K_{obx} K_{oby} \sin 2\Omega t} & { - K_{oby}^{2} \cos 2\Omega t} \\ \end{array} } \right], $$

(2)

where $K_{obx} = \frac{{2k_{s} k_{bx} }}{{2k_{bx} + k_{s} }}$ and $K_{oby} = \frac{{2k_{s} k_{by} }}{{2k_{by} + k_{s} }}$.

Substitution of Eq. (2) into Eq. (1), the equation of motion in $\Phi$ is obtained as

$$ {\mathbf{M}}{\ddot{\mathbf{z}}} + {\mathbf{D}}{\dot{\mathbf{z}}} +{\mathbf{K}}_{{\mathbf{o}}} {\mathbf{z}} + \varvec{\Updelta}{\mathbf{K}}_{{\mathbf{1}}} {\mathbf{z}}\cos \left( {\tilde{\Omega }t}\right) + \varvec{\Updelta}{\mathbf{K}}_{{\mathbf{2}}} {\mathbf{z}}\sin \left({\tilde{\Omega }t} \right) = {\mathbf{0}}, $$

(3)

with ${\mathbf{K}}_{{\mathbf{o}}} = \left[ {\begin{array}{*{20}c} {K_{obx} } & 0 \\ 0 & {K_{oby} } \\ \end{array} } \right]$,$\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} = \left[ {\begin{array}{*{20}c} {\alpha K_{obx}^{2} } & 0 \\ 0 & { - \alpha K_{oby}^{2} } \\ \end{array} } \right]$,$\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{2}}} = \left[ {\begin{array}{*{20}c} 0 & {\alpha K_{obx} K_{oby} } \\ {\alpha K_{obx} K_{oby} } & 0 \\ \end{array} } \right]$,$\alpha = \Delta k_{s} /k_{s}^{2}$ and $\tilde{\Omega } = 2\Omega.$

2.2 Stability analysis

It can be seen that Eq. (3) is a second-order differential equation containing time-dependent coefficients. Usually, the boundaries of unstable regions of systems described by differential equations with parametric coefficients are determined by using Floquet theory [48, 49], similar to the analysis for Mathieu–Hill equation. To solve the homogenous part of Eq. (3), the solution is assumed as ${\mathbf{z}} = {\tilde{\varvec{\Upgamma }}}e^{\Lambda t}$, where periodic function ${\tilde{\varvec{\Upgamma }}}$ can be written as the sum of simple sinusoidal functions by using a Fourier series as ${\tilde{\varvec{\Upgamma }}} = \sum\nolimits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}}$, with j as the imaginary variable. Noting that $\sin \left( {\tilde{\Omega }t} \right) = \frac{{e^{{j\tilde{\Omega }t}} - e^{{ - j\tilde{\Omega }t}} }}{2j}$ and $\cos \left( {\tilde{\Omega }t} \right) = \frac{{e^{{j\tilde{\Omega }t}} + e^{{ - j\tilde{\Omega }t}} }}{2}$, the homogenous form of Eq. (3), i.e. without forcing terms, is rewritten as

$$ {\mathbf{M}}{\ddot{\mathbf{z}}} + {\mathbf{D}}{\dot{\mathbf{z}}} + {\mathbf{K}}_{{\mathbf{o}}} {\mathbf{z}} + \left\{ {{\mathbf{K}}_{{{\mathbf{ + 12}}}} e^{{j\tilde{\Omega }t}} + {\mathbf{K}}_{{{\mathbf{ - 12}}}} e^{{ - j\tilde{\Omega }t}} } \right\}{\mathbf{z}} = {\mathbf{0}}, $$

(4)

where ${\mathbf{K}}_{{{\mathbf{ + 12}}}} = \left( {\frac{{\varvec{\Updelta}{\mathbf{ K}}_{1} - j\varvec{\Updelta}{\mathbf{ K}}_{2} }}{2}} \right)$ and ${\mathbf{K}}_{{{\mathbf{ - 12}}}} = \left( {\frac{{\varvec{\Updelta}{\mathbf{ K}}_{1} + j\varvec{\Updelta}{\mathbf{ K}}_{2} }}{2}} \right)$.

Substitution of the assumed solution (${\mathbf{z}} = {\tilde{\varvec{\Upgamma }}}e^{\Lambda t}$,${\dot{\mathbf{z}}}$ and ${\ddot{\mathbf{z}}}$) in Eq. (4) yields

$$ e^{\Lambda t} \left\{ \begin{aligned} {\mathbf{M}}\sum\limits_{n = - \infty }^{\infty } {\left( { - n^{2} \tilde{\Omega }^{2} + 2\Lambda jn\tilde{\Omega } + \Lambda^{2} } \right){\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}} \hfill \\ + {\mathbf{D}}\sum\limits_{n = - \infty }^{\infty } {\left( {jn\tilde{\Omega } + \Lambda } \right){\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}} + {\mathbf{K}}_{{\mathbf{o}}} \sum\limits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}} \hfill \\ + \left\{ {{\mathbf{K}}_{{{\mathbf{ + 12}}}} e^{{j\tilde{\Omega }t}} + {\mathbf{K}}_{{{\mathbf{ - 12}}}} e^{{ - j\tilde{\Omega }t}} } \right\}\sum\limits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}} \hfill \\ \end{aligned} \right\} = {\mathbf{0}}. $$

(5)

Equation (5) contains the matrices and vectors in infinite dimension. Thus to find the eigenvalues $\Lambda$ and the stability ranges, a finite index (n) of summation limit in place of infinity can be taken without incurring significant errors. Since the system has two degrees of freedom, $2\left( {2n + 1} \right) \times 2\left( {2n + 1} \right)$ size matrices and $2\left( {2n + 1} \right) \times 1$ size vectors are obtained. Selecting coefficients of $e^{{jn\tilde{\Omega }t}}$ terms from Eq. (5), the system of linear equations involving complex elements is obtained. For example, if $n = 1$, then the equation containing $6 \times 6$ size matrices and $6 \times 1$ size vectors is obtained as

$$ \left\{ {\left[ {\begin{array}{*{20}c} {\mathbf{M}} & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{M}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{M}} \\ \end{array} } \right]\Lambda^{2} + \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{{{\mathbf{11}}}} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{D}}_{{{\mathbf{22}}}} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{D}}_{{{\mathbf{33}}}} } \\ \end{array} } \right]\Lambda + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{{\mathbf{11}}}} } & {{\mathbf{K}}_{{{\mathbf{ - 12}}}} } & {\mathbf{0}} \\ {{\mathbf{K}}_{{{\mathbf{ + 12}}}} } & {{\mathbf{K}}_{{{\mathbf{22}}}} } & {{\mathbf{K}}_{{{\mathbf{ - 12}}}} } \\ {\mathbf{0}} & {{\mathbf{K}}_{{{\mathbf{ + 12}}}} } & {{\mathbf{K}}_{{{\mathbf{33}}}} } \\ \end{array} } \right]} \right\}\left\{ {\begin{array}{*{20}c} {{\varvec{\Upgamma}}_{{{\mathbf{ - 1}}}} } \\ {{\varvec{\Upgamma}}_{{\mathbf{0}}} } \\ {{\varvec{\Upgamma}}_{{\mathbf{1}}} } \\ \end{array} } \right\} = {\mathbf{0}}, $$

(6)

where ${\mathbf{D}}_{{{\mathbf{11}}}} = - 2j\tilde{\Omega }{\mathbf{M}} + {\mathbf{D}}$, ${\mathbf{D}}_{{{\mathbf{22}}}} = {\mathbf{D}}$, ${\mathbf{D}}_{{{\mathbf{33}}}} = 2j\tilde{\Omega }{\mathbf{M}} + {\mathbf{D}}$, ${\mathbf{K}}_{{{\mathbf{11}}}} = - \tilde{\Omega }^{2} {\mathbf{M}} - j\tilde{\Omega }{\mathbf{D}} + {\mathbf{K}}_{{\mathbf{o}}}$, ${\mathbf{K}}_{{{\mathbf{22}}}} = {\mathbf{K}}_{{\mathbf{o}}}$, and ${\mathbf{K}}_{{{\mathbf{33}}}} = - \tilde{\Omega }^{2} {\mathbf{M}} - j\tilde{\Omega }{\mathbf{D}} + {\mathbf{K}}_{{\mathbf{o}}}$.

The real parts of the eigenvalues $\Lambda$, i.e. $\Lambda_{\text{Re}}$, of Eq. (6) indicate the system’s stability. Positive real part indicates instability, whereas negative real part indicates stability. The eigenvalues are evaluated numerically. The eigenvalues are evaluated by choosing $n = 1,2, \ldots$ until the eigenvalues indicating unstable ranges in the frequency range of interest converge at each selected frequency $\tilde{\Omega }$ or $\Omega$.

2.3 Numerical results

The parameter values chosen for this study are listed in Table 1. Note that the smallest slenderness ratio (out of $l/b$ and $l/h$) turns out to be 42.65. Initially the special case of rigid bearings and then the case of flexible bearings are taken up.

Table 1 The rotor disc system parameters

2.3.1 Special case and validation of formulation

Initially, we will consider a special case where the rotor shaft is flexible but the bearings are rigid. For the special case, the bearing stiffness in both directions is given large values $k_{bx} = k_{by} = 10^{12}$ N/m. The eigenvalues $\Lambda$ are obtained from Eq. (6) by inputting the other parameter values given in Table 1. It turns out that $n = 1$ is sufficient for convergence up to 3rd decimal place.

The eigenvalues for the simplified special case problem can be obtained differently. Noting that ${\mathbf{z}} = {\mathbf{Rt}}$, ${\dot{\mathbf{z}}} = {\mathbf{R\dot{t}}} + {\dot{\mathbf{R}}\mathbf{t}}$ and ${\ddot{\mathbf{z}}} = {\mathbf{R}}{\ddot{\mathbf{t}}} + 2{\dot{\mathbf{R}}}{\dot{\mathbf{t}}} + {\ddot{\mathbf{R}}}{\mathbf{t}}$, Eq. (1) for the unforced case with rigid bearings can be written as

$$ {\mathbf{M}}\left( {\mathbf{R}}{\ddot{\mathbf{t}}} + 2{\dot{\mathbf{R}}}{\dot{\mathbf{t}}} + {\ddot{\mathbf{R}}}{\mathbf{t}} \right) + {\mathbf{D}}\left( {\mathbf{R}}{\dot{\mathbf{t}}} + {\dot{\mathbf{R}}}{\mathbf{t}} \right) + {\mathbf{K}}_{{\mathbf{s}}} {\mathbf{t}} = {\mathbf{0}} . $$

(7)

Multiplying Eq. (7) by ${\mathbf{R}}^{{\mathbf{T}}}$, one gets

$$ \left( {\mathbf{R}}^{{\mathbf{T}}} {\mathbf{MR}}{\ddot{\mathbf{t}}} + 2{\mathbf{R}}^{{\mathbf{T}}} {\mathbf{M}}{\dot{\mathbf{R}}}{\dot{\mathbf{t}}} + {\mathbf{R}}^{{\mathbf{T}}} {\mathbf{M}}{\ddot{\mathbf{R}}}{\mathbf{t}} \right) + \left( {\mathbf{R}}^{{\mathbf{T}}} {\mathbf{DR}}{\dot{\mathbf{t}}} + {\mathbf{R}}^{{\mathbf{T}}} {\mathbf{D}}{\dot{\mathbf{R}}}{\mathbf{t}} \right) + {\mathbf{K}}_{{\mathbf{s}}} {\mathbf{t}} = {\mathbf{0}} . $$

(8)

Substituting the expanded forms of ${\mathbf{R}}^{{\mathbf{T}}}$, ${\dot{\mathbf{R}}}$ and ${\ddot{\mathbf{R}}}$ in Eq. (8), and noting that ${\mathbf{R}}^{{\mathbf{T}}} {\mathbf{R}} = {\mathbf{I}}_{2 \times 2}$, the equations of motion for the special case in rotating coordinate frame $\varPsi$, without forcing turn out to be

$$ \left\{ {\begin{array}{*{20}c} {\ddot{\eta }} \\ {\ddot{\zeta }} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {c^{\prime}} & {2\Omega } \\ { - 2\Omega } & {c^{\prime}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{\eta }} \\ {\dot{\zeta }} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\Omega_{\eta }^{2} - \Omega^{2} } & {\Omega c^{\prime}} \\ { - \Omega c^{\prime}} & {\Omega_{\zeta }^{2} - \Omega^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} \eta \\ \zeta \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\} $$

(9)

where $\Omega_{\eta }^{2} = k_{\eta s} /m$, $\Omega_{\zeta }^{2} = k_{\zeta s} /m$ and $c^{\prime} = c/m$. For stability analysis, assume a solution of Eq. (9) in the form

$$ {\mathbf{t}} = \left\{ {\begin{array}{*{20}c} {\hat{\eta }_{r} } \\ {\hat{\zeta }_{r} } \\ \end{array} } \right\}e^{\Lambda t} ,\quad {\text{where}}\;\Lambda = \Lambda_{\text{Re}} + j\Lambda_{\text{Im}} . $$

(10)

Substituting Eq. (10) into Eq. (9) gives the eigenvalue problem (with $\Lambda$ as eigenvalue)

$$ \left[ {\begin{array}{*{20}c} {\Lambda^{2} + c^{\prime}\Lambda + \Omega_{\eta }^{2} - \Omega^{2} } & {2\Omega \Lambda + c^{\prime}\Omega } \\ { - 2\Omega \Lambda - c^{\prime}\Omega } & {\Lambda^{2} + c^{\prime}\Lambda + \Omega_{\zeta }^{2} - \Omega^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\hat{\eta }_{r} } \\ {\hat{\zeta }_{r} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\}. $$

(11)

For the chosen parameter values (with implicit rigid bearings, i.e. approximated through high stiffness $k_{bx} = k_{by} = 10^{12}$ N/m), the eigenvalues from Eq. (6) with $n = 1$ are sufficiently close (up to third decimal place) to the eigenvalues obtained from the explicit rigid bearing formulation in Eq. (11).

Let us introduce shaft non-circularity parameter $\kappa = {{\Delta k_{s} } \mathord{\left/ {\vphantom {{\Delta k_{s} } {k_{s} }}} \right. \kern-0pt} {k_{s} }}$ and non-dimensional rotor speed $\Omega^{ * } = \Omega /\Omega_{{\rm avg}}$ with $\Omega_{{\rm avg}}^{2} = {{\left( {\Omega_{\eta }^{2} + \Omega_{\zeta }^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {\Omega_{\eta }^{2} + \Omega_{\zeta }^{2} } \right)} 2}} \right. \kern-0pt} 2}$. The real and imaginary parts of the eigenvalues are plotted with respect to rotor spin speed as represented in Figs. 2 and 3, respectively. In Fig. 2, real parts of all the four eigenvalues are same and negative everywhere except between a narrow region identified as ${\text{U}}_{\text{I}}$. The corresponding critical points (start points s₁ to s₄ and end points e₁ to e₄) in Fig. 2 are mapped to Fig. 3 so that the root movements are clearly visible. The branch from $s_{4}$ to e₄ turns out to contain purely real positive eigenvalues and indicates the presence of unstable solution. For the chosen parameter values, the unstable speed range is 89.63–126.2 rad/s. The real part of eigenvalues computed from $x - y$ and $\eta - \zeta$ frame models remain the same, whereas the imaginary parts differ by ${{\Omega }}$. The whirl frequency in ${\text{U}}_{\text{I}}$ region is zero in $\eta - \zeta$ frame, i.e. a synchronous whirl at frequency ${{\Omega }}$ takes place in $x - y$ frame. In fact, the imaginary part of eigenvalues computed from the corresponding $x - y$ frame model in the speed range 89.63–126.2 rad/s lie on 1X line.

Fig. 2

Real parts of eigenvalues versus rotor spin speed for rigid bearings from $\eta - \zeta$ frame model

Fig. 3

Imaginary parts of eigenvalues versus rotor spin speed for rigid bearings from $\eta - \zeta$ frame model

It is evident that the system has one unstable region ${\text{U}}_{\text{I}}$ which appears near the critical speeds of system, as previously reported in [7, 50]. For the present special case, only principal parametric resonance appears, in which the instability boundaries are near the major natural frequencies, i.e.$\Omega_{\eta }$ and $\Omega_{\zeta }$. The combined resonance and other parametric resonances do not appear for this system with rigid supports [50].

In the absence of external damping ($c = 0$), available theoretical results indicate instability speed range between the non-rotating beam natural frequencies in principal directions, i.e. between $\Omega_{\eta } = \sqrt {{{\left( {k_{s} - \Delta k_{s} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{s} - \Delta k_{s} } \right)} m}} \right. \kern-0pt} m}} = 89.44$ rad/s and $\Omega_{\zeta } = \sqrt {{{\left( {k_{s} + \Delta k_{s} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{s} + \Delta k_{s} } \right)} m}} \right. \kern-0pt} m}} = 126.49$ rad/s. The stability domain for constant damping c = 0 Ns/m, evaluated from Eq. (11), is shown in Fig. 4, wherein the hatched area shows the unstable region. Eigenvalue analysis and numerical simulation results with $c = 0$ and shaft non-circularity parameter $\kappa = 1/3$ validate the instability region in the frequency range $\Omega_{\eta }$ to $\Omega_{\zeta }$.

Fig. 4

Shaft non-circularity $\kappa$ versus non-dimensional rotor speed $\Omega^{ * }$ for rigid bearings and $c = 0$ Ns/m

From Fig. 4, it is observed that unstable speed range increases as the shaft stiffness asymmetry ($\kappa$) increases. The unstable region has two boundaries. It is known that increasing system damping reduces the parametric instability region [7, 51]. As $c$ increases, the unstable zone starts shrinking in size. In the present model with $\kappa = 1/3$, for damping value $c = 365$ Ns/m, the complete unstable zone vanishes (real part of none of the eigenvalues are positive) as shown in Fig. 5.

Fig. 5

Real parts of the eigenvalues versus rotor speed for rigid bearings, $\kappa = 1/3$ and $c = 365$ Ns/m

Let us introduce a damping coefficient ratio $\xi = {c \mathord{\left/ {\vphantom {c {\left( {2m\Omega_{{\rm avg}} } \right)}}} \right. \kern-0pt} {\left( {2m\Omega_{{\rm avg}} } \right)}}$. The stability domain variation with shaft non-circularity $\kappa$, damping coefficient ratio $\xi$ and non-dimensional rotor spin speed $\Omega^{ * }$ is shown in Fig. 6. Note that Fig. 4 is a cross section of Fig. 6 at $\xi = 0$.

Fig. 6

Stability domain of rotor with rigid supports for different values of $\kappa$, $\xi$ and $\Omega^{ * }$

2.3.2 General case

The real part of eigenvalues for the general case with flexible supports is shown in Fig. 7 and corresponding imaginary parts are shown in Fig. 8. Note that the number of terms in expansion is $n = 1$ because higher values of $n$ only affect the eigenvalues in the third decimal place. More than one unstable regions are observed for the rotor system with flexible supports, which is commensurate with the observations made in [52, 53]. In Fig. 7, the specific feature observed in region a_I is amplified as the rotor speed increases (regions a_II, a_III, U_I, U_II and U_III, in order). Regions a_I to a_III contain eigenvalues with negative real part. In regions U_I to U_III, the real part of one of the eigenvalues becomes positive for some frequency range, which is indicated by hatched portions in Fig. 7. The transition points are marked as $a_{1} ,a_{2} ,b_{1} ,b_{2} ,c_{1} ,c_{2} ,d_{1}$ and $d_{2}$. In region U_II, two roots cross the zero line in Fig. 7 at the same frequency. If the external damping in the system is reduced then parts of the regions belonging to a_I–a_III may show instability, and likewise, increased external damping can make parts of the regions U_I–U_III stable.

Fig. 7

Real parts of eigenvalues versus rotor speed for the general case data in Table 1

Fig. 8

Magnitude of imaginary parts of eigenvalues versus rotor speed for the general case data in Table 1

For the parameters values shown in Table 1, the unstable speed ranges of the rotor are $\text{U}_{I}$($\Omega_{{a_{1} }} =$ 74.1 to $\Omega_{{a_{2} }} =$ 78.5 rad/s), $\text{U}_{II}$($\Omega_{{b_{1} }} = \Omega_{{d_{1} }} =$ 87.6 to $\Omega_{{b_{2} }} = \Omega_{{d_{2} }} =$ 96.4 rad/s) and $\text{U}_{III}$($\Omega_{{c_{1} }} =$ 101.6 to $\Omega_{{c_{2} }} =$ 118.3 rad/s). In Fig. 8, it can be seen that between $a_{1} - a_{2}$, the imaginary parts of eigenvalues $\Lambda_{\text{Im}}$ merge into single value at $a_{1}$ and then they split after $a_{2}$. The same happens in the branch $c_{1} - c_{2}$. The dashed 1X line shows that the imaginary part of unstable eigenvalue is synchronous with rotor speed between $a_{1} - a_{2}$ and $c_{1} - c_{2}$, leading to principal parametric resonance; whereas the imaginary part of unstable eigenvalue is asynchronous with rotor speed between $b_{1} - b_{2}$ and $d_{1} - d_{2}$, leading to principal combination resonance.

In multi-degree of freedom parametrically excited systems, unstable behaviour occurs in a wider range of intervals of the parametric excitation frequency [54]. With the combined effects of anisotropic supporting structure and parametric vibration, the unstable regions are often found in vicinity of the natural frequencies. The lower and upper limits of undamped fundamental natural frequencies of the rotor system are found to be $\Omega_{1} = \sqrt {K_{obx} /m}$ = 77.46 rad/s and $\Omega_{2} = \sqrt {K_{oby} /m}$ = 109.54 rad/s, respectively. The principal parametric resonance at $\Omega_{i,k}^{PR} = \Omega_{i} /k,k = 1,2,\ldots$ destabilizes the system which is associated with only one of the natural frequencies. The additive (or summation-type) principal parametric combined resonance occurs at $\Omega_{ij,k}^{PCR} = \frac{{\Omega_{i} + \Omega_{j} }}{k},k = 1,2,\ldots$, with $\Omega_{i}$ and $\Omega_{j}$ being the fundamental natural frequencies of the system. This resonance has same nature of unstable behaviour as parametric resonance, but it is associated with more natural frequencies. Hence the principal parametric resonances $\left( {{\text{for }}k = 1} \right)$, $\Omega_{1,1}^{PR}$ and $\Omega_{2,1}^{PR}$ have been calculated as 77.46 and 109.54 rad/s, respectively. The principal parametric combined resonance $\Omega_{12,2}^{PCR}$ is determined as 93.5 rad/s. As per the theorem presented in [55] for a class of dynamic systems to which the present system [Eq. (3)] belongs, only summation-type principal parametric combined resonances occur in the system and difference-type principal parametric combined resonances at are absent.

It is found that the first and third unstable regions appear near the principal parametric resonances $\Omega_{1,1}^{PR}$ and $\Omega_{2,1}^{PR}$, respectively. The second unstable region appears near the principal parametric combined resonance $\Omega_{12,2}^{PCR}$. Hence, the parametric instability occurs near the shaft critical speeds and near the half of the sum of these critical speeds. The same result was also observed in [56]. Note that ${\text{a}}_{\text{I}}$, ${\text{a}}_{\text{II}}$ and ${\text{a}}_{\text{III}}$ regions (shown in Fig. 7) appear near $\Omega_{1,2}^{PR}$, $\Omega_{12,4}^{PCR}$ and $\Omega_{2,2}^{PR}$, respectively, but those are stable operating regions. For the parameter values given in [57], the stability domains calculated from our analysis exactly match those presented for linear stiffnesses given in Fig. 2 of [57]. The instability at some of these parametric resonance regions disappears due to the damping present in the system, as has been observed earlier in [9, 16,17,18].

The steady-state results for asymmetric rotor shaft with imbalance in the rotor disc are given in [20, 21, 58] by using harmonic balance method, modulated coordinate method, and parametric quasi modes. But in the case of non-ideally driven rotor system the whirl amplitude cannot grow indefinitely since the source and system interaction limits overall power supply to the system. In this case, the amplitude responses are always bounded and invariably reach a steady state. In the next sections, the dynamic analysis of the non-ideally driven rotor system will be used to determine the source power requirement for the rotor to transit through the parametric instabilities and to ensure that the whirl amplitudes remain small during the transition process for safe operation of the system.

3 Transient analysis of non-ideal system

The permanent type DC motor is considered here as the non-ideal drive. The DC motor, as a non-ideal source, produces torque to rotate the rotor shaft instead of a constant speed motor considered for ideal drive. The spin speed of rotor is decided by the interaction between the load on the system and the motor. Therefore, for the non-ideally driven rotor, another equation of motion is introduced as

$$ J\ddot{\theta } = \varGamma_{m} - \varGamma_{l} , $$

(12)

where $T_{m}$ is the motor torque, $J$ is the rotary inertia of the rotor disc (including the rotor of the motor and the rotor shaft) about the spin axis and $\varGamma_{l} = 2\Delta k_{s} \eta \zeta$ is the load torque. The motor torque is product of motor constant $k_{m}$ and the armature current $i_{a}$, i.e. $\varGamma_{m} = k_{m} i_{a}$ where the armature current is determined from the voltage applied across the motor terminals $V_{i}$, the induced electro-motive force (emf) $k_{m} \dot{\theta }$ and the armature resistance $R_{a}$ as $i_{a} = {{\left( {V_{i} - k_{m} \dot{\theta }} \right)} \mathord{\left/ {\vphantom {{\left( {V_{i} - k_{m} \dot{\theta }} \right)} {R_{a} }}} \right. \kern-0pt} {R_{a} }}$ [59,60,61]. This is valid when the motor has small speed fluctuations, which mostly happens for large value of J. For large angular accelerations or fluctuation of motor speed, the motor’s armature inductance $L_{m}$ has significant effect [62,63,64,65,66,67]. Thus, one more differential equation is introduced as

$$ L_{m} \frac{{\text{d} i_{a} }}{{\text{d} t}} + R_{a} i_{a} + k_{m} \dot{\theta } = V_{i} \;{\text{or}}\;\dot{\varGamma }_{m} = k_{U} V_{i} - k_{\theta } \dot{\theta } - k_{\varGamma } \varGamma_{m} $$

(13)

where $k_{U} = k_{m} /L_{m}$, $k_{\theta } = k_{m}^{2} /L_{m}$ and $k_{{{\Gamma }}} = R_{a} /L_{m}$.

The load torque can be determined through various approaches such as from simple free-body-diagram. Here, it will be derived from a bond graph model, and some insights related to the physics of the problem will be drawn thereof. Note that for simplifying the problem, the rotational damping on the rotor is neglected. This extra load can be included in the formulation as given in [25, 40, 60].

3.1 The bond graph modelling of the rotor-motor system

The bond graph is well-known for energy consistent model structure [68, 69] which facilitates multi-energy domain modelling. Bond graph modelling has been used in the past to model rotor dynamics problems with non-ideal drive [70, 71]. The theory and other applications of bond graph modelling may be consulted in [72,73,74,75]. To start with, the bond graph model corresponding to the special case problem (asymmetric rotor shaft with rigid support) is given in Fig. 9.

Fig. 9

Bond graph model of the special case problem

In the bond graph model, the constraints are modelled by 1 and 0 junctions, where 1 represents common flow (current, velocity, angular velocity, etc.) and 0 represents common effort (voltage, force, torque, etc.). Note that junctions being power-conserving constraints, as a corollary, 1 junction also models a constraint on the sum of efforts and 0 junction models a constraint on sum of flows. The TF elements in the model represent power-conserving scaling of effort and flow variables. The following representations are made in the model: SE:$V_{i}$ for the voltage across the DC motor terminals, R:$R_{a}$ for the armature resistance, I:${\text{L}}_{m}$ for the armature inductance, GY:$k_{m}$ for the electro-mechanical coupling, I:$J$ for rotary inertia at disc, I:$m$ for disc mass, R:$c$ for external viscous damping, and C:$k_{\eta }$ and C:$k_{\zeta }$ for shaft stiffness in $\eta$ and $\zeta$ directions, respectively. The flow detectors Df are used to obtain the rotor disc’s angle of rotation and the x and y deflections at $1_{{\dot{\theta }}}$, $1_{{\dot{x}}}$ and $1_{{\dot{y}}}$ junctions, respectively. From ${\mathbf{t}} = {\mathbf{R}}^{{\mathbf{T}}} {\mathbf{z}}$ and ${\dot{\mathbf{t}}} = {\mathbf{R}}^{{\mathbf{T}}} {\dot{\mathbf{z}}} + {\dot{\mathbf{R}}}^{{\mathbf{T}}} {\mathbf{z}}$, $\dot{\eta } = \dot{x}\cos \theta + \dot{y}\sin \theta - \dot{\theta }x\sin \theta + \dot{\theta }y\cos \theta$ and $\dot{\zeta } = - \dot{x}\sin \theta + \dot{y}\cos \theta - \dot{\theta }x\cos \theta - \dot{\theta }y\sin \theta$. This coordinate transformation is performed by the model structure shown within dashed lines and will be henceforth be referred to as the CTF sub-model. Some of the bond numbers are indicated within circles in Fig. 9 for referencing. The effort variables $e_{\eta }$ and $e_{\zeta }$ indicate the shaft restoring efforts (forces) in $\eta$ and $\zeta$ directions, respectively.

The load on the motor is the effort (reaction torque) in bond number 1 and it is computed from the bond graph model [74, 75] as

$$ \varGamma_{l} = e_{1} = e_{2} + e_{3} = e_{\eta } \left( { - x\sin \theta + y\cos \theta } \right) + e_{\zeta } \left( { - x\cos \theta - y\sin \theta } \right). $$

(14)

Noting that $e_{\eta } = k_{\eta } \eta$, $e_{\zeta } = k_{\zeta } \zeta$, $\eta = x\cos \theta + y\sin \theta$ and $\zeta = - x\sin \theta + y\cos \theta$, Eq. (14) is simplified to

$$ \varGamma_{l} = \left( {k_{\eta } - k_{\zeta } } \right)\eta \zeta = 2\Delta k_{s} \eta \zeta . $$

(15)

Some key observations can be made from the simple relation in Eq. (15). For a symmetric shaft, i.e. $k_{\eta } = k_{\zeta }$, there is no load on motor for whatsoever whirl. For $\Delta k_{s} > 0$, the motor supplies power to the load when $\eta \zeta > 0$, whereas it draws power from the load when $\eta \zeta < 0$, and the opposite happens for $\Delta k_{s} < 0$. A steady circular whirl orbit in $x - y$ frame maps to a point in the $\eta - \zeta$ frame and it produces a constant load on the motor resulting in constant steady motor speed.

The bond graph model of the general case problem is shown in Fig. 10. The bond graph model, in its mechanical system part, considers five degrees of freedom of the rotor disc, i.e. its linear velocities in x–y frame, its spin, and its rotational velocities about two diametral axes denoted by $\dot{\phi }$ and $\dot{\psi }$. Thus, the model is more generic in the sense that it models both cylindrical and conical modes of the rotor.

Fig. 10

Bond graph model of the general case problem

In the model, CTF blocks represent the coordinate transformation, as discussed earlier with reference to Fig. 9. At $1_{{\dot{\phi }}}$ and $1_{{\dot{\psi }}}$ junctions, I:$I_{d}$ models the diametral moment of inertia. Similarly, I:$m_{b}$, C:$k_{bx}$ and C:$k_{bx}$ model the bearing mass, and bearing/support stiffness in x and y directions of the fixed $x - y$ frame. Note that the bearing mass $m_{b}$ is a small parameter ($m_{b} = 0.01$ kg during the simulation) which is required for causal consistency in the model. The left and right supports are modelled separately. Therefore, half the shaft lies between the rotor disc and the left support and the remaining half lies between the rotor disc and the right support. Accordingly, C:${{k_{\eta } } \mathord{\left/ {\vphantom {{k_{\eta } } 2}} \right. \kern-0pt} 2}$ and C:${{k_{\zeta } } \mathord{\left/ {\vphantom {{k_{\zeta } } 2}} \right. \kern-0pt} 2}$ model the stiffness of half of the shaft in the rotating $\eta - \zeta$ frame. The gyroscopic moments acting on the diametral axes of the disc are modelled by GY: $J\dot{\theta }$ element where $J\dot{\theta }$ is the spin angular momentum of the rotor disc. The TF elements in the model represent kinematic transformations for rotor disc’s rotation about diametral axes. The relative motions between the shaft ends and the bearings/supports are modelled at the 0 junctions and these relative motions indicate the shaft bending, which are transformed to the rotating frame through CTF and the shaft asymmetric stiffness are then modelled in the rotating frame. The forces in the rotating frame are transformed to the inertial frame through the same CTF elements, and those forces (at the respective common effort or 0 junctions) are then transferred to the bearings/supports, to the rotor disc’s linear dynamics and as moments to the rotor disc’s rotational dynamics about its diametral axes, in $x - y$ frame.

For centrally placed rotor at the mid-span, $\dot{\phi } = \dot{\psi } = 0$ in cylindrical mode motion. The analysis done in the previous sections consider this situation. Therefore, $1_{{\dot{\phi }}}$ and $1_{{\dot{\psi }}}$ junctions along with all the bonds and elements connected to those, i.e. I:$I_{d}$, GY:$J\dot{\theta }$ and TF:$\pm l/2$, may be removed to simplify the model structure. Eventually, the left and right side CTFs and shaft bending stiffness can be combined, and the left and right bearings can as well be combined.

Note the load torque on the motor still remains $\varGamma_{l} = \left( {k_{\eta } - k_{\zeta } } \right)\eta \zeta = 2\Delta k_{s} \eta \zeta .$ The viscous damping on the transverse motions of the rotor disc does not directly load the motor. The power from the motor goes through the shaft bending stiffness to produce a whirling motion and then it is dissipated by the damper R:c.

3.2 Determination of unstable region by simulation

The unstable regions are obtained analytically earlier in Sec. 2. However to match these results by simulation, the constant speed source SF: $\Omega$ is used at $1_{{\dot{\theta }}}$-junction, instead of the model of DC motor in Figs. 9 and 10. Parameter values mentioned in Table 1 are used in the simulations. The unstable operating speed range of the rotor with rigid support was found to be 89.66–126.2 rad/s which is identical to the results found from the eigenvalue analysis. The unstable operating speed ranges of the rotor with flexible supports are found to be 74.0–78.3 rad/s in ${\text{U}}_{\text{I}}$, 86.8–95.4 rad/s in ${\text{U}}_{\text{II}}$, and 100.2–117.1 rad/s in $\text{U}_{III}$. The small mismatch between the analytical and simulation results for the flexible supports case is mostly due to the truncation of Hill’s infinite determinant to finite order.

4 Sommerfeld effect characterization

To study the non-ideal drive dynamics with present rotor system, motor parameters given in Table 2 are considered.

Table 2 DC motor specifications

It is seen that for the present study, one unstable region appears for the rotor with rigid supports and three regions appear for the rotor with flexible supports. These regions are bounded by stable regions. The theoretical analysis provides the stable and unstable speed ranges, but does not reveal which stable speed ranges are reachable in practice when the energetic coupling between the motor and the rotor is considered. Thus, the transition through the unstable speed ranges is analysed here through numerical simulations. Particularly, the growth of the vibration amplitudes during the transition is considered so that the rotor shaft does not fail. The power supply by motor is used to overcome the load produced by rotor system. If the amount of available power is insufficient then the rotor may get stuck in boundary of the unstable zone. Thus, it is essential to determine the critical amount of power to smoothly escape the instability.

4.1 Transient analysis of non-ideal rotor system

The transient analysis of non-ideal motor-rotor is carried out by numerically integrating the differential equations derived from the BG models given in Figs. 9 and 10. The BG modelling and simulation is performed through Symbol-Shakti software [76]. The displacement $\left( {\sqrt {\eta^{2} + \zeta^{2} } } \right)$ responses are enveloped through Hilbert transform to obtain the corresponding amplitudes of vibration. We do not normalize the responses because often normalization hides the fact that some of the values may be grossly out of range from a practical viewpoint.

4.2 Sommerfeld effect for asymmetric shaft with rigid supports

The unstable operating speed range of the considered rotor with rigid support is 89.66–126.2 rad/s. An initial momentum of 1 kg.m/s, i.e. 0.1 m/s initial velocity, was given to the rotor disc in x-direction. When constant input voltage is applied, the speed saturation starts to occur from about $V_{i} = 44.83$ V. Such saturation behaviour continues up to $V_{i} = 83$ V (see Fig. 11). When the speed is saturated, i.e. captured at the lower instability bound, the whirl amplitude increases (see Fig. 12) and it dissipates more and more energy through the external viscous damping.

Fig. 11

Rotor speed response for motor supply voltages $V_{i} = 83$ V and 83.1 V showing passage through parametric instability

Fig. 12

Rotor amplitude response for motor supply voltages $V_{i} = 83$ V and 83.1 V showing passage through parametric instability

At the steady state, the motor power is balanced by the dissipated power. The steady-state whirl amplitude depends on the excess motor power, i.e. it is zero at $V_{i} = 44.83$ V and increases as $V_{i}$ increases, until it reaches 83 V, where the whirl amplitudes are large and the system is still captured at the lower instability threshold.

When the supply voltage reaches or exceeds a critical value, $V_{i} = 83.1$ V, the rotor system escapes from capture at the lower instability threshold and reaches a higher speed. Thus, between $V_{i} = 83$ V and $V_{i} = 83.1$ V, there is a sudden speed jump. Also, the whirl amplitude converges to 0 at $V_{i} = 83.1$ V, i.e. there is also an associated amplitude jump (see Fig. 12). Such speed and amplitude jumps are also discussed and experimentally validated in [6]. Note that at $V_{i} = 83$ V, the maximum transient rotor speed just about reaches the upper instability threshold speed ${{\Omega }} = 126.2$ rad/s (indicated by dashed line in Fig. 11). It falls further short of that limit when $V_{i} < 83$ V. If the rotor speed manages to exceed the upper instability threshold then it reaches a stable equilibrium where $\ddot{\theta } = 0$, $\varGamma_{m} = k_{m} i_{a} = 0$, the steady speed ${{\Omega }} = V_{i} /k_{m}$ [see Eq. (13)] and the whirl amplitude becomes 0.

If the voltage is reduced from a value $V_{i} > 83.1$ V to reduce rotor speed (rotor coast down), then there is also a similar jump phenomenon where the rotor speed suddenly jumps from the upper instability threshold to the lower instability threshold (see Figs. 13, 14), but there is no speed capture at the upper instability threshold. The results in Figs. 13 and 14 are obtained for initial rotor spin speed 200 rad/s (above the upper stability threshold) and 0.1 m/s initial velocity of the rotor disc in x-direction. The initial input voltage is 100 V and it is reduced by a step to a lower value. Note that in this case, the induced emf is initially larger than the supplied voltage to the motor and hence, the motor applies brake or negative torque on the rotor. If $V_{i} > 63.1$ V, then the whirl amplitude converges to zero and the steady rotor speed reaches $V_{i} /k_{m} > 126.2$ rad/s. If $V_{i}$ is reduced below $63.1$ V, then the rotor becomes unstable and whirl amplitudes start growing. This causes larger dissipation of energy through the viscous damping on the rotor, and hence the rotor speed reduces until it reaches the lower instability threshold speed, i.e. 89.66 rad/s, and it remains captured there. The excess motor power is spent to sustain the whirl amplitudes. Such capture ends for $V_{i} <$ 44.83 V, i.e. $V_{i} /k_{m} < 89.66$ rad/s.

Fig. 13

Rotor speed response for motor supply voltages $V_{i} = 63$ V and 63.1 V showing passage through parametric instability

Fig. 14

Rotor amplitude response for motor supply voltages $V_{i} = 63$ V and 63.1 V showing passage through parametric instability

The results during the rotor coast up can be better illustrated from the transient torque-speed response. As seen from Fig. 11, if the rotor speed exceeds the upper stability threshold ($126.2$ rad/s) during transient dynamics, then it is possible to escape speed capture at the lower instability threshold (89.66 rad/s). Figure 15 shows the same dynamics as in Fig. 11 in terms of different variables. In Fig. 15, the motor output mechanical torque ${{\Gamma }}_{m}$ and the load torque ${{\Gamma }}_{l}$ due to rotor whirl are plotted versus the rotor speed. A clear bifurcation in the dynamics is visible when the constant motor supply voltage is changed from 83 and 83.1 V. This transition is shown in the zoomed inset of Fig. 15.

Fig. 15

Motor and load torque versus speed transient response for motor supply voltages $V_{i} = 83$ V and 83.1 V showing escape through parametric instability

The appearance of jump phenomena is schematically represented in Fig. 16 for explanation purpose. The steady-state motor torque versus speed diagram is a straight line [see Eq. (13)] which intersects the load curve at one, two or three points. Only one operating speed remains when the maximum rotor speed is below the lower stability threshold; otherwise two or three operating points are possible.

Fig. 16

Schematic representation of steady-state motor and load torque versus speed at different motor supply voltages to determine the stable operating points

Out of these operating points, say $a_{1}$, $b_{1}$ and $c_{1} ,$ for a given motor voltage $V_{1}$ (see Fig. 16), points $a_{1}$ and $c_{1}$ are stable equilibriums and point $b_{1}$ is an unstable equilibrium. This can be determined from straight-forward perturbation from the equilibrium point. This perturbation can be based on power or even torque, as described in [25]. For the present case, when the system is perturbed from equilibrium at $a_{1}$, there is a small change in ${{\Gamma }}_{m}$, but ${{\Gamma }}_{l}$ increases by large amount (up along the vertical line in direction $a_{1}$ to $a_{2}$). As a consequence, $\frac{\text{d}}{{{\text{d}}\omega }}\left( {{{\Gamma }}_{m} - {{\Gamma }}_{l} } \right) < 0$ and the equilibrium point is stable. On the other hand, at point $b_{1}$, with small change in ${{\Gamma }}_{m}$, there is large reduction in ${{\Gamma }}_{l}$ (almost becomes 0). Thus, $\frac{\text{d}}{{{\text{d}}\omega }}\left( {{{\Gamma }}_{m} - {{\Gamma }}_{l} } \right) > 0$ and the equilibrium point is unstable. At point $c_{1}$, $\frac{\text{d}}{{{\text{d}}\omega }}\left( {{{\Gamma }}_{m} - {{\Gamma }}_{l} } \right) < 0$ and the equilibrium point is stable. Thus, during transient dynamics, if the system escapes from an equilibrium in the branch indicated by $a_{0}$, $a_{1}$, $a_{2}$ …, then it reaches the other equilibrium point in the branch $c_{0}$, $c_{1}$, $c_{2}$ …, i.e. there is a kind of jump phenomenon with a range of missing speeds. Note that during rotor coast down (motor speed reduction or power down), jump from operating point $c_{0}$ to $a_{0}$ is compulsory because the solution cannot evolve along the unstable branch $c_{0}$, $b_{1}$, $b_{2}$ …. However, during rotor coast up, the solution can evolve either along the branch $a_{0}$, $a_{1}$, $a_{2}$ … or jump to the branch $c_{0}$, $c_{1}$, $c_{2}$ …. This jump is governed by the transient phenomena (influenced by parameters such as rotary inertia, motor inductance, etc., which are absent in the steady-state analysis) and at present, the conditions for this jump cannot be determined analytically for this complex system.

4.2.1 Jump phenomena

The foregoing results indicate that there is a clear similarity with the Sommerfeld effect of first kind, although the Sommerfeld effect of second kind occurs here due to instability of whirl. This characteristic of the nonlinear jump phenomena is shown in Fig. 17. During the rotor coast up (speed increase), the steady-state rotor speed follows the path $o \to a \to b \to c \to d$ containing a capture at lower stability threshold in the path $a \to b$ and a jump $b \to c$, as shown in Fig. 17. During rotor coast down (speed decrease), the steady-state rotor speed follows the path $d \to e \to f \to a \to o$ containing a capture at lower stability threshold in the path $f \to a$ and a jump $e \to f$, as shown in Fig. 17. Note that there is no speed capture at the upper instability threshold speed.

Fig. 17

Characterization of the Sommerfeld effect of second kind in asymmetric rotor supported on rigid bearings

The location of points b and c in Fig. 17 depends on the initial conditions. In the absence of eccentricity, for zero initial velocity or displacement of the rotor disc, points b, c, e and f merge to point a, i.e. the rotor can pass through all the speeds and would not feel the instability. For large initial conditions, point b (and c) shifts to the right; whereas, it shifts to the left towards point f as the initial disturbance is reduced. Points a, e and f are fixed. However, if large disturbance is given during voltage/speed reduction in the branch c–e, there can be premature jump to the branch b–f. For infinitesimally small initial disturbance, jump at b–c shifts towards left and merges with jump at e–f. Such shift of jump points due to initial condition variation would be demonstrated in the next section. In practice, there is no need for the initial conditions; the residual eccentricity in the rotor disc itself is enough to setup the whirl amplitudes that grow upon entering the unstable speed range and consequently, load the motor. Note that steady-state speeds in the range lying between points a to e, i.e. the unstable speed range, can neither be reached during rotor coast up nor during rotor coast down.

Let us say there is a requirement to operate the rotor at speed at 140 rad/s which lies between points c and e. A simple design gives the required supply voltage to be 70 V. If a motor with maximum voltage capacity of 75 V is chosen then it would not be possible to reach the operating point through the path $o \to a \to b \to c \to e$. The voltage capacity of the motor, for the considered example in Fig. 17, should be at least about 85 V. This is how the study of the Sommerfeld effect in this case is useful in actuator sizing for the application.

4.2.2 Whirl amplitude estimation and validation

It is the whirl amplitude growth that sucks the power from the motor and prevents enough power to be diverted to accelerate the rotor spin. Successful escape through the instability requires rotor acceleration before the whirl amplitudes grow large enough. In the numerical studies shown here, constant step input voltage is given to the motor. If, however, the input voltage is given as a ramp input with small slope or in other words, the voltage increment is done quasi-statically, then the rotor system gets perpetually caught at the lower instability threshold. The vibration amplitudes, when the rotor is caught at the lower or upper instability threshold are determined from simple load balance. From Figs. 2 and 3, the imaginary part of the unstable eigenvalue is zero. Thus, in the steady state, the constant whirl amplitude $A$ may be related to constant deflections in $\eta - \zeta$ frame so that $\eta = A\cos \beta$ and $\zeta = A\sin \beta$, with $\beta$ as a constant phase. Consequently, with $\dot{\eta } = \dot{\zeta } = 0$, one gets $x = \eta \cos \theta - \zeta \sin \theta$, $y = \eta \sin \theta + \zeta \cos \theta$, $\dot{x} = \left( { - \eta \sin \theta - \zeta \cos \theta } \right)\dot{\theta }$, and $\dot{y} = \left( {\eta \cos \theta - \zeta \sin \theta } \right)\dot{\theta }$, where steady-state constant spin speed $\Omega = \dot{\theta }$. The load torque from viscous damping acting on the rotor disc turns out to be

$$ \varGamma_{d} \hat{k} = \left( {x\hat{i} + y\hat{j}} \right) \times \left( {c\dot{x}\hat{i} + c\dot{y}\hat{j}} \right) = c\left( {x\dot{y} - y\dot{x}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} = cA^{2} \Omega \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} , $$

(16)

where $\hat{i}$, $\hat{j}$ and $\hat{k}$ are the unit vectors in Cartesian coordinates. Further, in steady state, the motor torque is given by

$$ \varGamma_{m} = k_{m} i_{a} = {{k_{m} \left( {V_{i} - k_{m} \Omega } \right)} \mathord{\left/ {\vphantom {{k_{m} \left( {V_{i} - k_{m} \Omega } \right)} {R_{a} }}} \right. \kern-0pt} {R_{a} }}. $$

(17)

From load balance and by using Eqs. (15–17), $\varGamma_{m} = \varGamma_{l} = \varGamma_{d}$, one obtains

$$ A^{2} \Delta k_{s} \sin \left( {2\beta } \right) = \frac{{k_{m} \left( {V_{i} - k_{m} \Omega } \right)}}{{R_{a} }} = cA^{2} \Omega . $$

(18)

For $A = 0$, i.e. stable zone, we get $\Omega = {{V_{i} } \mathord{\left/ {\vphantom {{V_{i} } {k_{m} }}} \right. \kern-0pt} {k_{m} }}$. Otherwise, for $A > 0$, $c > 0$ and $\Delta k_{s} \ne 0$, simplification of Eq. (18) gives

$$ \beta = \frac{1}{2}\sin^{ - 1} \left( {\frac{c\Omega }{{\Delta k_{s} }}} \right)\quad {\text{and}}\quad A = \frac{{k_{m} }}{{\sqrt {cR_{a} } }}\sqrt {\left( {\frac{{V_{i} }}{{k_{m} \Omega }} - 1} \right)} . $$

(19)

It is evident from Eq. (19) that unless and otherwise the system escapes through the instability region, increasing $V_{i}$ increases $A$. Also, for $c \to 0$ Ns/m, escape through instability is impossible because the whirl amplitude, theoretically, becomes infinite during the transition period. If $\left| {c{{\Omega }}/{{\Delta }}k_{s} } \right|$ is small, as in the present case, then $\beta \cong 0$ for ${{\Delta }}k_{s} > 0$ or $\beta \cong \pi$ for ${{\Delta }}k_{s} < 0$, and mostly the rotor shaft deflection occurs in the weaker shaft section, i.e. in $\eta -$ direction.

For the chosen values ($c = 60$ Ns/m, $k_{m} = 0.5$ Nm/A, $R_{a} = 5\,{{\Omega }}$), when the system is captured at the lower instability bound ($\Omega = 89.66$ rad/s) with $V_{i} = 83$ V (near point b in Fig. 17) then use of Eq. (19) yields $A = 0.0266$ m, i.e. 26.6 mm. Simulation results in Fig. 12 show exactly the same steady-state amplitude (after the initial transient phase). Likewise, when the system is captured at the lower instability bound ($\Omega = 89.66$ rad/s) with $V_{i} = 63$ V (near point f in Fig. 17), then use of Eq. (19) yields $A = 0.0184$ m, i.e. 18.4 mm which is exactly the same steady-state amplitude as shown in Fig. 14. These numerical simulation results validate the formulations for steady-state amplitude given in Eq. (19).

4.3 Sommerfeld effect for asymmetric shaft with flexible supports

The simulation results for the asymmetric rotor on flexible foundation (parameters values given in Tables 1 and 2) corresponding to four different motor supply voltages and 1 kg m/s initial momentum given in x-direction are shown in Figs. 18 and 19. In the results plotted here, amplitude refers to the enveloped (Hilbert transformed [72]) relative whirl magnitude $\sqrt {\eta^{2} + \zeta^{2} }$ between the supports and the rotor disc. It is seen that from $V_{i} = 37.05$ V to $39.1$ V, the rotor speed is captured at the lower instability threshold of unstable zone $\text{U}_{I}$ at speed 74.1 rad/s (see point $a_{1}$ in Fig. 8) and it escapes $\text{U}_{I}$ when $V_{i} \ge 39.2$ V. When the rotor is captured at speed 74.1 rad/s, at steady state, there is an elliptical whirl orbit in $\eta - \zeta$ frame which can be defined as $\eta = \eta_{0} + A\cos \left( {2{{\Omega }}t - \beta } \right)$ and $\zeta = \zeta_{0} - B\sin \left( {2{{\Omega }}t - \beta } \right)$, with $\beta$ as a phase of major axis with $\eta -$ axis, $\left( {\eta_{0} ,\zeta_{0} } \right)$ as centre of the ellipse, and $A$ and $B$ being the length of major and minor axes. Averaging the torques from motor, flexure of the rotor shaft and the external damping on the rotor shaft over one cycle of steady orbit or time window of $2\pi /{{\Omega }}$, the following relations can be worked out:

$$ \begin{aligned} & 2\Delta k_{s} \eta_{0} \zeta_{0} = \frac{{k_{m} \left( {V_{i} - k_{m} \Omega } \right)}}{{R_{a} }} \\ & = c\Omega \left( {k_{1} k_{3} \eta_{o}^{2} + k_{2} k_{4} \zeta_{o}^{2} + \frac{{A^{2} + B^{2} }}{2} + \left( {k_{1} k_{4} + k_{2} k_{3} } \right)AB + \frac{1}{2}\left( {k_{1} k_{4} - k_{2} k_{3} } \right)\left( {A\zeta_{o} \sin \beta + B\eta_{o} \cos \beta } \right)} \right), \\ \end{aligned} $$

(20)

where $k_{1}$ = $\left( {1 + k_{\eta } /k_{bx} } \right)$, $k_{2}$ = $\left( {1 + k_{\zeta } /k_{bx} } \right)$, $k_{3}$ = $\left( {1 + k_{\eta } /k_{by} } \right)$, and $k_{4}$ = $\left( {1 + k_{\zeta } /k_{by} } \right)$. Equation (20) is satisfied when simulated values are substituted in it. Moreover, in the limiting case for rigid supports, i.e. $k_{bx} ,k_{by} \to \infty$, and $k_{1} = k_{2} = k_{3} = k_{4} \approx 1$ with $A = B \approx 0$, Eq. (20) reduces to Eq. (19).

Fig. 18

Rotor speed response showing critical supply voltages to pass through the first and second unstable ranges for asymmetric rotor on flexible supports

Fig. 19

Rotor whirl amplitudes during capture and passage through the first and second unstable ranges for asymmetric rotor on flexible supports

It is seen that from Fig. 18 that for $V_{i} = 43.8$ V to $47.8$ V, the rotor speed is captured at the lower instability threshold of unstable zone $\text{U}_{II}$ at average speed 87.6 rad/s (see points $b_{1}$ and $d_{1}$ in Fig. 8) and it escapes $\text{U}_{II}$ when $V_{i} \ge 47.9$ V. The rotor speed as well as whirl amplitude has small fluctuations when the rotor speed is captured in the neighbourhood of the lower stability threshold of $\text{U}_{II}$. In fact, the 1X line does not pass through points $b_{1}$ and $d_{1}$ in Fig. 8 and $\text{U}_{II}$ is a combination resonance zone lying between two principal parametric resonances. The frequency mixing is evident from the phase plots given in Fig. 20 and the fast Fourier transform (FFT) of $\eta$-displacement shown in Fig. 21. Note that in Fig. 21, ${{\Omega }}_{b1} = 100.9$ rad/s and ${{\Omega }}_{d1} = 74.3$ rad/s correspond to the imaginary part of the eigenvalues at points $b_{1}$ and $d_{1}$, respectively, at rotor speed ${{\Omega }} = {{\Omega }}_{b1} = {{\Omega }}_{d1} = 87.6$ rad/s, in Fig. 8. Also, in Fig. 21, $\Delta {{\Omega }} = {{\Omega }}_{b1} - {{\Omega }} = {{\Omega }} - {{\Omega }}_{d1} = \left( {{{\Omega }}_{b1} - {{\Omega }}_{d1} } \right)/2$.

Fig. 20

Phase plots in $x - y$ and $\eta - \zeta$ frames when the system is captured at the boundary of combination resonance (lower stability threshold of ${\text{U}}_{\text{II}}$)

Fig. 21

Fast Fourier transform (FFT) of the $\eta$-displacement when the system is captured at the boundary of combination resonance for $V_{i} = 47.8$ V

For the supply voltage range $V_{i} = 47.9$ V to $55.3$ V, the rotor speed reaches predicted steady-state speed ${{\Omega }} = V_{i} /k_{m}$. With further increase in voltage, the rotor speed reaches the unstable zone $\text{U}_{III}$ and the results given in Figs. 22 and 23 show that it escapes $\text{U}_{III}$ smoothly with low whirl amplitudes during transient period when $V_{i} \ge 60.5$ V.

Fig. 22

Rotor speed response showing critical supply voltages to pass through the third unstable range for asymmetric rotor on flexible supports

Fig. 23

Rotor whirl amplitudes during capture and passage through the third unstable range for asymmetric rotor on flexible supports

When the system is unable to accelerate through $\text{U}_{III}$, there is a complex capture phenomena with highly fluctuating rotor speed and whirl amplitude. In fact, the rotor speed fluctuations indicate that the system repeatedly transits through the unstable zones $\text{U}_{I}$, $\text{U}_{II}$, lower boundary of $\text{U}_{III}$ and the stable zones. The Poincaré map (a sample case for $V_{i} = 57$ V) shown in Fig. 24 reveals that behaviour of the system is chaotic and the whirl amplitudes are excessive. However, for $V_{i} \ge 60.5$ V, the transient period whirl amplitudes are well within the allowable limits and the steady speed is achieved smoothly.

Fig. 24

Poincaré map in $x - \dot{x}$ plane for $V_{i} = 57$ V. Here, each point is taken at $\int {{\Omega d}}t = 2n\pi , n \in {\mathbb{N}}$ after excluding few initial points and retaining about 250,000 final points

The previously presented results were obtained for 0.1 m/s initial velocity given in $x$-direction (initially aligned with $\eta$-direction). The corresponding results for 1 m/s initial velocity given in $x$-direction are given in Figs. 25, 26 and 27. It is seen from Fig. 25 that the voltage requirement to transit through the first unstable region remains unaffected as compared to the results in Fig. 18. This is because with small input voltage, the rotor torque is small and it accelerates slowly. As a consequence, the initial disturbance dies out much before reaching the unstable regime.

Fig. 25

Rotor speed response showing critical supply voltages to pass through the first unstable range for asymmetric rotor on flexible supports with large initial disturbance

Fig. 26

Rotor whirl amplitudes during capture and passage through the first unstable range for asymmetric rotor on flexible supports with large initial disturbance

Fig. 27

Rotor speed response showing critical supply voltages to pass through the second (and simultaneously, third) unstable range for asymmetric rotor on flexible supports with large initial disturbance

When the rotor is captured at the lower instability threshold of unstable zone $\text{U}_{I}$ at speed 74.1 rad/s (see point $a_{1}$ in Fig. 8), the steady whirl amplitudes as shown in Fig. 26 are same as those in Fig. 19. However, for $V_{i} = 43.8$ V to $64.2$ V, the rotor speed is captured at the lower instability threshold of unstable zone $\text{U}_{II}$ at average speed 87.6 rad/s (see points $b_{1}$ and $d_{1}$ in Fig. 8) and it escapes $\text{U}_{II}$ as well as $\text{U}_{III}$ (see Figs. 27, 28) with small transient whirl amplitudes when $V_{i} \ge 64.2$ V. The stable speed range between the upper bound of $\text{U}_{II}$ and the lower bound of $\text{U}_{III}$ is never reached. These results are markedly different from those in Figs. 18, 19, 22 and 23 where there was individual capture and escape from unstable zones $\text{U}_{II}$ and $\text{U}_{III}$.

Fig. 28

Rotor whirl amplitudes during capture and passage through the second (and simultaneously, third) unstable range for asymmetric rotor on flexible supports with large initial disturbance

4.4 Effect of residual unbalance in the rotor

The Sommerfeld effect of second kind, as presented here, does not require any unbalance in the rotor disc. However, the system responses are shown to be dependent on the initial conditions [27]. In practice, a rotor cannot be perfectly balanced and some small residual unbalance always remains. This residual unbalance sets up small amplitude synchronous rotor whirl which can grow and saturate the non-ideal motor power input, as the system enters into unstable operating zones. Therefore, small residual rotor unbalance can be used as a forcing to study the system behaviour rather than arbitrary initial conditions. To study the system behaviour with rotor unbalance, the bond graph model in Fig. 10 is simplified. As mentioned earlier, the rotations about the diametral axes of rotor disc are neglected. The simplified bond graph model is shown in Fig. 29. The position of the mass centre of the rotor disc is assumed to be at a distance $e$ from the shaft geometric centre and aligned with the weaker shaft section, i.e. $\eta$-direction, to simulate the worst case scenario. Therefore, the inertial-frame velocity of the mass centre of the disc can be written as $\dot{x}_{m} = \dot{x} - e\dot{\theta }\sin \theta$ and $\dot{y}_{m} = \dot{y} + e\dot{\theta }\cos \theta$ where $\theta$ is the angle between the fixed and the rotating frames. Two new TF elements connected to $1_{{\dot{\theta }}}$-junction and the two new 0-junctions in Fig. 29 model this kinematic relation as well as the additional torque on the motor produced by the inertial forces [40, 70].

Fig. 29

Bond graph model of the general case problem with eccentricity in the rotor disc

The simulation results for $e = 0.1$ mm (which is a reasonable value for residual unbalance in a 10 kg rotor disc) and various input voltages are given in Figs. 30 and 31. In stable operation at constant speed when the rotor speed is not captured at any instability threshold, the steady-state amplitude (synchronous whirl amplitude) corresponds to a constant point $\left( {\eta_{0} ,\zeta_{0} } \right)$ in $\eta - \zeta$ frame. The rotor speed is captured at the lower threshold speed of unstable principal parametric resonance region $\text{U}_{I}$ for $V_{i} = 37.05$ to 40.2 V, at the lower threshold speed (on the average) of unstable combination resonance region $\text{U}_{II}$ for $V_{i} = 43.8$ to 48.9 V and chaotically (with large speed fluctuation) for $V_{i} = 55.3$ to 62.1 V. These speed capture and escape characteristics are similar to those presented in Figs. 18, 19. 20, 21, 22 and 23. To escape unstable regions $\text{U}_{I}$, $\text{U}_{II}$ and $\text{U}_{III}$, the critical voltages are 40.3 V, 49 V and 62.2 V, respectively.

Fig. 30

Rotor speed response showing critical supply voltages to pass through the first to third unstable ranges for asymmetric rotor on flexible supports with eccentricity in the rotor disc

Fig. 31

Rotor whirl amplitudes during capture and passage through the first to third unstable ranges for asymmetric rotor on flexible supports with eccentricity in the rotor disc

5 Four-degree-of-freedom rotor with shaft internal/material damping

It would be prudent to recall here that in the foregoing analyses the electro-mechanical system including the non-ideal drive has four degrees of freedom, two for the shaft-rotor system [Eq. (1)] and two more given by Eqs. (6) and (7) signifying shaft rotation and armature current behaviour, respectively. The bearing/support mass has been neglected in the analytical formulations and as a consequence, an equivalent stiffness [see Eq. (2)] could be defined. This approach has been adopted by various researchers for undamped supports [14, 16]. However, when material damping in the rotor shaft and/or bearing damping is considered, it is not possible to define the equivalent stiffness as in Eq. (2). Therefore, two more degrees of freedom are introduced to represent the motion of the bearing/support. Here, $x_{b}$ and $y_{b}$ represent the cylindrical mode displacement (rotations of the rotor disc about diametral axes are neglected) of the bearing/support in inertial, i.e. $x - y$ frame, and $m_{b}$ is the equivalent lumped bearing/support mass at each end of the rotor shaft.

The material or internal damping in the rotor shaft causes permanent instability of the rotor system beyond a threshold speed. In fact, the material damping increases the effective damping for rotor speeds below the shaft natural frequency but the destabilizing effect (effective damping reduction) starts for speeds after the shaft natural frequency [77]. The material damping effect is present during asynchronous rotor whirl but vanishes during synchronous whirl. The material damping is modelled in a rotating frame just like the asymmetric shaft stiffness. Here, the material damping parameter $\lambda = 0.002$ s⁻¹, which is a standard material constant, is chosen for the steel rotor shaft. The damping coefficient is proportional to the stiffness with $\lambda$ being the constant of proportionality.

The equations of motion for the ideal (constant speed) rotor system with material damping in the rotor shaft can be written as

$$ \begin{aligned} {\mathbf{Mq}} + {\mathbf{D}}{\dot{\mathbf{q}}} + \left( {\mathbf{K}}_{{\mathbf{o}}} + \Omega {\mathbf{C}}_{{\mathbf{o}}} \right){\mathbf{q}} + \lambda \varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} {\dot{\mathbf{q}}}\cos \left( {\tilde{\Omega }t} \right) + \lambda \varvec{\Updelta}{\mathbf{ K}}_{2} {\dot{\mathbf{q}}}\sin \left( {\tilde{\Omega }t} \right) \hfill \\ + \varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} {\mathbf{q}}\cos \left( {\tilde{\Omega }t} \right) + \varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{2}}} {\mathbf{q}}\sin \left( {\tilde{\Omega }t} \right) + \Omega \lambda \varvec{\Updelta}{\mathbf{ K}}_{2} {\mathbf{q}}\cos \left( {\tilde{\Omega }t} \right) - \Omega \lambda \varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} {\mathbf{q}}\sin \left( {\tilde{\Omega }t} \right) = {\mathbf{0}} \hfill \\ \end{aligned} $$

(21)

where ${\mathbf{q}} = \left[ {\begin{array}{*{20}l} x \hfill & y \hfill & {x_{b} } \hfill & {y_{b} } \hfill \\ \end{array} } \right]^{{\rm T}}$, $\tilde{\Omega } = 2\Omega$, ${\mathbf{I}}$ is $2 \times 2$ identity matrix, ${\mathbf{M}} = \left[ {\begin{array}{*{20}c} {m{\mathbf{I}}} & {\mathbf{0}} \\ {\mathbf{0}} & {2m_{b} {\mathbf{I}}} \\ \end{array} } \right]$, ${\mathbf{D}} = \left[ {\begin{array}{*{20}c} {c{\mathbf{I}}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right] + \lambda \left[ {\begin{array}{*{20}c} {k_{s} {\mathbf{I}}} & { - k_{s} {\mathbf{I}}} \\ { - k_{s} {\mathbf{I}}} & {k_{s} {\mathbf{I}}} \\ \end{array} } \right]$, ${\mathbf{K}}_{{\mathbf{o}}}^{{}} = \left[ {\begin{array}{*{20}c} {k_{s} {\mathbf{I}}} & { - k_{s} {\mathbf{I}}} \\ { - k_{s} {\mathbf{I}}} & {k_{s} {\mathbf{I}} + 2{\mathbf{k}}_{{\mathbf{b}}} } \\ \end{array} } \right]$, ${\mathbf{k}}_{{\mathbf{b}}} = \left[ {\begin{array}{*{20}c} {k_{bx} } & 0 \\ 0 & {k_{by} } \\ \end{array} } \right]$${\mathbf{C}}_{{\mathbf{o}}}^{{}} = \lambda \left[ {\begin{array}{*{20}c} {k_{s} {\mathbf{I}}_{{\mathbf{1}}} } & { - k_{s} {\mathbf{I}}_{{\mathbf{1}}} } \\ { - k_{s} {\mathbf{I}}_{{\mathbf{1}}} } & {k_{s} {\mathbf{I}}_{{\mathbf{1}}} } \\ \end{array} } \right]$, ${\mathbf{I}}_{{\mathbf{1}}} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 1} & 0 \\ \end{array} } \right]$, $\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} = \left[ {\begin{array}{*{20}c} {\Delta k{\mathbf{I}}_{{\mathbf{2}}} } & { - \Delta k{\mathbf{I}}_{{\mathbf{2}}} } \\ { - \Delta k{\mathbf{I}}_{{\mathbf{2}}} } & {\Delta k{\mathbf{I}}_{{\mathbf{2}}} } \\ \end{array} } \right]$, ${\mathbf{I}}_{{\mathbf{2}}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & { - 1} \\ \end{array} } \right]$, $\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{2}}} = \left[ {\begin{array}{*{20}c} {\Delta k{\mathbf{I}}_{{\mathbf{3}}} } & { - \Delta k{\mathbf{I}}_{{\mathbf{3}}} } \\ { - \Delta k{\mathbf{I}}_{{\mathbf{3}}} } & {\Delta k{\mathbf{I}}_{{\mathbf{3}}} } \\ \end{array} } \right]$ and ${\mathbf{I}}_{{\mathbf{3}}} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 1 & 0 \\ \end{array} } \right]$.

The above homogenous equation can be rewritten as

$$ \begin{aligned} {\mathbf{M}}{\ddot{\mathbf{q}}} + {\mathbf{D}}{\dot{\mathbf{q}}} + \left( {{\mathbf{K}}_{{\mathbf{o}}} + \Omega {\mathbf{C}}_{{\mathbf{o}}} } \right){\mathbf{q}} + \lambda \left\{ {{\mathbf{K}}_{{{\mathbf{ + 12}}}} e^{{j\tilde{\Omega }t}} + {\mathbf{K}}_{{{\mathbf{ - 12}}}} e^{{ - j\tilde{\Omega }t}} } \right\}{\dot{\mathbf{q}}} \hfill \\ + \left\{ {{\mathbf{K}}_{{{\mathbf{ + 12}}}} e^{{j\tilde{\Omega }t}} + {\mathbf{K}}_{{{\mathbf{ - 12}}}} e^{{ - j\tilde{\Omega }t}} } \right\}{\mathbf{q}} + \Omega \lambda \left\{ {{\mathbf{K}}_{{{\mathbf{ - 21}}}} e^{{j\tilde{\Omega }t}} + {\mathbf{K}}_{{{\mathbf{ + 21}}}} e^{{ - j\tilde{\Omega }t}} } \right\}{\mathbf{q}} = {\mathbf{0}} \hfill \\ \end{aligned} $$

(22)

where ${\mathbf{K}}_{{{\mathbf{ + 12}}}} = \left( {\frac{{\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} - j\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{2}}} }}{2}} \right)$, ${\mathbf{K}}_{{ - {\mathbf{12}}}} = \left( {\frac{{\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} + j\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{2}}} }}{2}} \right)$,${\mathbf{K}}_{{{\mathbf{ - 21}}}} = \left( {\frac{{\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{2}}} + j\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} }}{2}} \right)$, and ${\mathbf{K}}_{{ + {\mathbf{21}}}} = \left( {\frac{{\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{2}}} - j\varvec{\Updelta}{\mathbf{ K}}_{{\mathbf{1}}} }}{2}} \right)$.

The solution of the homogenous part of Eq. (22) is assumed as ${\mathbf{q}} = {\tilde{\varvec{\Upgamma }}}e^{\Lambda t} = e^{\Lambda t} \sum\nolimits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}}$. By substituting ${\mathbf{q}}$,${\dot{\mathbf{q}}}$, and ${\ddot{\mathbf{q}}}$ in Eq. (22), one obtains

$$ e^{\Lambda t} \left\{ \begin{aligned} {\mathbf{M}}\sum\limits_{n = - \infty }^{\infty } {\left( { - n^{2} \tilde{\Omega }^{2} + 2\Lambda jn\tilde{\Omega } + \Lambda^{2} } \right){\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}} + {\mathbf{D}}\sum\limits_{n = - \infty }^{\infty } {\left( {jn\tilde{\Omega } + \Lambda } \right){\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}} + \left( {{\mathbf{K}}_{{\mathbf{o}}} + \Omega {\mathbf{C}}_{{\mathbf{o}}} } \right)\sum\limits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{jn\tilde{\Omega }t}} \hfill \\ + \lambda \left\{ {{\mathbf{K}}_{{{\mathbf{ + 12}}}} \sum\limits_{n = - \infty }^{\infty } {\left( {jn\tilde{\Omega } + \Lambda } \right){\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{j\left( {n + 1} \right)\tilde{\Omega }t}} + {\mathbf{K}}_{{{\mathbf{ - 12}}}} \sum\limits_{n = - \infty }^{\infty } {\left( {jn\tilde{\Omega } + \Lambda } \right){\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{j\left( {n - 1} \right)\tilde{\Omega }t}} } \right\} \hfill \\ + \left\{ {{\mathbf{K}}_{{{\mathbf{ + 12}}}} \sum\limits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{j\left( {n + 1} \right)\tilde{\Omega }t}} + {\mathbf{K}}_{{{\mathbf{ - 12}}}} \sum\limits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{j\left( {n - 1} \right)\tilde{\Omega }t}} } \right\} + \Omega \lambda \left\{ {{\mathbf{K}}_{{{\mathbf{ - 21}}}} \sum\limits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{j\left( {n + 1} \right)\tilde{\Omega }t}} + {\mathbf{K}}_{{{\mathbf{ + 21}}}} \sum\limits_{n = - \infty }^{\infty } {{\varvec{\Upgamma}}_{{\mathbf{n}}} } e^{{j\left( {n - 1} \right)\tilde{\Omega }t}} } \right\} \hfill \\ \end{aligned} \right\} = {\mathbf{0}} $$

(23)

Considering a finite index of summation limit $n = - 2$ to $2$ in Eq. (22) to approximate Hill’s infinite determinant while ensuring convergence, dividing with $e^{\Lambda t}$ and equating $e^{{jn\tilde{\Omega }t}}$ terms in both sides of above equation, a system of linear equations having the matrices of order $20 \times 20$ and vectors of order $20 \times 1$ is obtained as

$$ \left\{ {\left[ {\begin{array}{*{20}l} {\mathbf{M}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{M}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{M}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{M}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{M}} \hfill \\ \end{array} } \right]\Lambda^{2} + \left[ {\begin{array}{*{20}l} {{\mathbf{D}}_{{{\mathbf{11}}}} } \hfill & {{\mathbf{D}}_{{{\mathbf{12}}}} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {{\mathbf{D}}_{{{\mathbf{21}}}} } \hfill & {{\mathbf{D}}_{{{\mathbf{22}}}} } \hfill & {{\mathbf{D}}_{{{\mathbf{23}}}} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{D}}_{{{\mathbf{32}}}} } \hfill & {{\mathbf{D}}_{{{\mathbf{33}}}} } \hfill & {{\mathbf{D}}_{{{\mathbf{34}}}} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{D}}_{{{\mathbf{43}}}} } \hfill & {{\mathbf{D}}_{{{\mathbf{44}}}} } \hfill & {{\mathbf{D}}_{{{\mathbf{45}}}} } \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{D}}_{{{\mathbf{54}}}} } \hfill & {{\mathbf{D}}_{{{\mathbf{55}}}} } \hfill \\ \end{array} } \right]\Lambda + \left[ {\begin{array}{*{20}l} {{\mathbf{K}}_{{{\mathbf{11}}}} } \hfill & {{\mathbf{K}}_{{{\mathbf{12}}}} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {{\mathbf{K}}_{{{\mathbf{21}}}} } \hfill & {{\mathbf{K}}_{{{\mathbf{22}}}} } \hfill & {{\mathbf{K}}_{{{\mathbf{23}}}} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{K}}_{{{\mathbf{32}}}} } \hfill & {{\mathbf{K}}_{{{\mathbf{33}}}} } \hfill & {{\mathbf{K}}_{{{\mathbf{34}}}} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{K}}_{{{\mathbf{43}}}} } \hfill & {{\mathbf{K}}_{{{\mathbf{44}}}} } \hfill & {{\mathbf{K}}_{{{\mathbf{45}}}} } \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{K}}_{{{\mathbf{54}}}} } \hfill & {{\mathbf{K}}_{{{\mathbf{55}}}} } \hfill \\ \end{array} } \right]} \right\}\left\{ {\begin{array}{*{20}l} {{\varvec{\Upgamma}}_{{{\mathbf{ - 2}}}} } \hfill \\ {{\varvec{\Upgamma}}_{{{\mathbf{ - 1}}}} } \hfill \\ {{\varvec{\Upgamma}}_{{\mathbf{0}}} } \hfill \\ {{\varvec{\Upgamma}}_{{\mathbf{1}}} } \hfill \\ {{\varvec{\Upgamma}}_{{\mathbf{2}}} } \hfill \\ \end{array} } \right\} = {\mathbf{0}} $$

(24)

where

${\mathbf{D}}_{{{\mathbf{11}}}} = {\mathbf{D}} - 4j\tilde{\Omega }{\mathbf{M}}$, ${\mathbf{D}}_{{{\mathbf{12}}}} = \lambda {\mathbf{K}}_{{{\mathbf{ - 12}}}}$, ${\mathbf{D}}_{{{\mathbf{21}}}} = \lambda {\mathbf{K}}_{{{\mathbf{ + 12}}}}$, ${\mathbf{D}}_{{{\mathbf{22}}}} = {\mathbf{D}} - 2j\tilde{\Omega }{\mathbf{M}}$, ${\mathbf{D}}_{{{\mathbf{23}}}} = \lambda {\mathbf{K}}_{{{\mathbf{ - 12}}}}$,${\mathbf{D}}_{{{\mathbf{32}}}} = \lambda {\mathbf{K}}_{{{\mathbf{ + 12}}}}$, ${\mathbf{D}}_{{{\mathbf{33}}}} = {\mathbf{D}}$, ${\mathbf{D}}_{{{\mathbf{34}}}} = \lambda {\mathbf{K}}_{{{\mathbf{ - 12}}}}$, ${\mathbf{D}}_{{{\mathbf{43}}}} = \lambda {\mathbf{K}}_{{{\mathbf{ + 12}}}}$, ${\mathbf{D}}_{{{\mathbf{44}}}} = {\mathbf{D}} + 2j\tilde{\Omega }{\mathbf{M}}$, ${\mathbf{D}}_{{{\mathbf{45}}}} = \lambda {\mathbf{K}}_{{{\mathbf{ - 12}}}}$, ${\mathbf{D}}_{{{\mathbf{54}}}} = \lambda {\mathbf{K}}_{{{\mathbf{ + 12}}}}$, ${\mathbf{D}}_{{{\mathbf{55}}}} = {\mathbf{D}} + 4j\tilde{\Omega }{\mathbf{M}}$, ${\mathbf{K}}_{{{\mathbf{11}}}} = \left( {{\mathbf{K}}_{{\mathbf{o}}} + \Omega {\mathbf{C}}_{{\mathbf{o}}} } \right) - 4\tilde{\Omega }^{2} {\mathbf{M}} - 2j\tilde{\Omega }{\mathbf{D}}$, ${\mathbf{K}}_{{{\mathbf{12}}}} = {\mathbf{K}}_{{{\mathbf{ - 12}}}} + \Omega \lambda {\mathbf{K}}_{{{\mathbf{ + 21}}}} - j\tilde{\Omega }\lambda {\mathbf{K}}_{{{\mathbf{ - 12}}}}$, ${\mathbf{K}}_{{{\mathbf{21}}}} = {\mathbf{K}}_{{{\mathbf{ + 12}}}} + \Omega \lambda {\mathbf{K}}_{{{\mathbf{ - 21}}}} - 2j\tilde{\Omega }\lambda {\mathbf{K}}_{{{\mathbf{ + 12}}}}$, ${\mathbf{K}}_{{{\mathbf{22}}}} = \left( {{\mathbf{K}}_{{\mathbf{o}}} + \Omega {\mathbf{C}}_{{\mathbf{o}}} } \right) - \tilde{\Omega }^{2} {\mathbf{M}} - j\tilde{\Omega }{\mathbf{D}}$, ${\mathbf{K}}_{{{\mathbf{23}}}} = {\mathbf{K}}_{{{\mathbf{ - 12}}}} + \Omega \lambda {\mathbf{K}}_{{{\mathbf{ + 21}}}}$, ${\mathbf{K}}_{{{\mathbf{32}}}} = {\mathbf{K}}_{{{\mathbf{ + 12}}}} + \Omega \lambda {\mathbf{K}}_{{{\mathbf{ - 21}}}} - j\tilde{\Omega }\lambda {\mathbf{K}}_{{{\mathbf{ + 12}}}}$, ${\mathbf{K}}_{{{\mathbf{33}}}} = \left( {{\mathbf{K}}_{{\mathbf{o}}} + \Omega {\mathbf{C}}_{{\mathbf{o}}} } \right)$, ${\mathbf{K}}_{{{\mathbf{34}}}} = {\mathbf{K}}_{{{\mathbf{ - 12}}}} + \Omega \lambda {\mathbf{K}}_{{{\mathbf{ + 21}}}} + j\tilde{\Omega }\lambda {\mathbf{K}}_{{{\mathbf{ - 12}}}}$, ${\mathbf{K}}_{{{\mathbf{43}}}} = {\mathbf{K}}_{{{\mathbf{ + 12}}}} + \Omega \lambda {\mathbf{K}}_{{{\mathbf{ - 21}}}}$, ${\mathbf{K}}_{{{\mathbf{44}}}} = \left( {{\mathbf{K}}_{{\mathbf{o}}} + \Omega {\mathbf{C}}_{{\mathbf{o}}} } \right) - \tilde{\Omega }^{2} {\mathbf{M}} + j\tilde{\Omega }{\mathbf{D}}$, ${\mathbf{K}}_{{{\mathbf{45}}}} = {\mathbf{K}}_{{{\mathbf{ - 12}}}} + \Omega \lambda {\mathbf{K}}_{{{\mathbf{ + 21}}}} + 2j\tilde{\Omega }\lambda {\mathbf{K}}_{{{\mathbf{ - 12}}}}$, ${\mathbf{K}}_{{{\mathbf{54}}}} = {\mathbf{K}}_{{{\mathbf{ + 12}}}} + \Omega \lambda {\mathbf{K}}_{{{\mathbf{ - 21}}}} + j\tilde{\Omega }\lambda {\mathbf{K}}_{{{\mathbf{ + 12}}}}$, and ${\mathbf{K}}_{{{\mathbf{55}}}} = \left( {{\mathbf{K}}_{{\mathbf{o}}} + \Omega {\mathbf{C}}_{{\mathbf{o}}} } \right) - 4\tilde{\Omega }^{2} {\mathbf{M}} + 2j\tilde{\Omega }{\mathbf{D}}$.

In the above four-degree-of-freedom bearing-shaft-rotor model, the bearing mass appears explicitly. In fact, the bearing mass significantly changes the system stability. While we have neglected the bearing mass in the previous analysis, a proper value will be used in the subsequent analysis. With shaft material (alloy steel) density taken as 7850 kg/m³, the rotor shaft mass turns out to be approximately 2.2 kg and hence, 0.55 kg mass may be assumed to be lumped at each bearing. By accounting for the mass of the bearing, its housing and pedestal, it is assumed that the effective mass at each bearing $m_{b} =$ 1 kg. Here, support stiffness $k_{by}$ corresponds to the vertical stiffness of the pedestal and the bearing, and it is usually very high as considered in Table 1. The bearing/support stiffness $k_{bx}$ includes the bending stiffness of the pedestal. With increased pedestal mass, we assume $k_{bx} = 12 \times 10^{4}$  N/m which is double of that considered in Table 1. The real parts of eigenvalues of the system without and with material damping in the rotor shaft are plotted in Figs. 32 and 33, respectively, where the line colours indicate the ordering of the eigenvalues in MATLAB. The increased bearing stiffness and mass removes the symptoms in zones ${\text{a}}_{\text{I}} - {\text{a}}_{\text{III}}$ of Fig. 7 and combines the parametric instability zones ${\text{U}}_{\text{I}} - {\text{U}}_{\text{III}}$ therein to a single parametric instability zone ${\text{U}}_{\text{I}}$ in Fig. 32. Also, two narrow parametric instability zones ${\text{U}}_{\text{II}}$ and ${\text{U}}_{\text{III}}$, and a significantly wide new parametric instability zone ${\text{U}}_{\text{IV}}$ appear in Fig. 32 in comparison with Fig. 7.

Fig. 32

Real parts of eigenvalues versus rotor speed for the rotor with additional degree of freedom for bearing and $\lambda = 0 \;{\text{s}}^{ - 1}$

Fig. 33

Real parts of eigenvalues versus rotor speed for the rotor with additional degree of freedom for bearing and $\lambda = 0.002 \;{\text{s}}^{ - 1}$

It is found that the parametric instability zones (${\text{U}}_{\text{I}} - {\text{U}}_{\text{IV}}$) appearing in Fig. 32 disappear when rotor shaft material damping is introduced (Fig. 33). Moreover, a permanent instability threshold at ${{\Omega }} = {{\Omega }}_{\text{th}}$ appears in Fig. 33 and there is no stable operating speed beyond ${{\Omega }}_{\text{th}}$. All flexible rotor shaft systems have a definite stability threshold (as in Fig. 33) and therefore, studies which do not consider rotor shaft material damping, as in Figs. 7 and 32 here, and results in several other literature [7, 8, 11, 12] are of less practical use. Here, the permanent instability occurs due to non-conservative curl forces [78] which arise from the rotating material damping [15, 45]. Even a rotor system with rigid or almost rigid shaft may exhibit instability due to non-conservative curl forces arising from oil whip in journal bearings [79] and clearance changes (Alford forces [80]) around the periphery of a turbine rotor.

For transient analysis of the system behaviour, minor modifications are made in the bond graph model given in Fig. 29. Two resistances ${\text{R}}:\lambda k_{n}$ and ${\text{R}}:\lambda k_{\zeta }$ are connected to the two 1-junctions where ${\text{C}}:k_{n}$ and ${\text{C}}:k_{\zeta }$ are connected, respectively. Thus, both asymmetric shaft stiffness and its material damping are modelled in the rotating $n - \zeta$ frame.

Some sample simulation results are presented here corresponding to the system behaviour shown in Fig. 33 where the parametric instability region appears for speed range 81.6–104.8 rad/s, and the stability threshold speed is 182.5 rad/s. The excitation to initiate rotor whirl is provided by the small eccentricity $e = 0.1$ mm. The rotor speed reaches the desired steady-state value ${{\Omega }} = V_{i} /k_{m}$ for $V_{i} \le 40.8$ V. For the supply voltage range $V_{i} = 40.9$–64.3 V, the rotor speed is captured at the lower stability threshold of parametric instability zone U_I, i.e. at 81.6 rad/s on the average (see Fig. 34). The system escapes from the parametric instability for $V_{i} \ge 64.4$ V, reaches the desired steady-state value ${{\Omega }} = V_{i} /k_{m}$ and the whirl amplitudes reduces (see Fig. 35).

Fig. 34

Rotor speed response during capture at and escape through parametric instability for the rotor with additional degrees of freedom (for bearing) and material damping

Fig. 35

Rotor whirl amplitudes during capture at and escape through parametric instability for the rotor with additional degrees of freedom and material damping

However, on reaching the stability threshold for $V_{i} \ge 91.25$ V, there is a permanent capture of rotor speed at 182.5 rad/s. This permanent capture of rotor speed at the stability threshold has been discussed previously in various articles [15, 45,46,47, 59, 81, 82]. In fact, there has been a persistent misunderstanding between parametric instability due to stiffness asymmetry and permanent super-critical instability due to material damping as has been pointed out in a recent discussion [83]. When the motor supply voltage is increased above 91.25 V, the motor speed remains stuck at 182.5 V and the whirl amplitude continues to increase, as shown for two such supply voltages in Figs. 36 and 37. Note that permanent capture at the stability threshold does not give steady whirl amplitude. In fact, there is a synchronous whirl and an asynchronous whirl present at the same time. The frequency of the asynchronous whirl is determined from imaginary part of the eigenvalue at 182.5 rad/s, which turns out to be 95 rad/s. The whirl occurs at a mixture of predominant frequency components such as $182.5 - 95 = 87.5$ rad/s, $182.5 + 95 = 227.5$ rad/s, and other frequencies as in Fig. 21. The capture at stability threshold may be termed as the Sommerfeld effect of third kind and there needs to be further investigations on the system dynamics thereof beyond the analysis presented here and in [15, 45,46,47, 59, 81, 82].

Fig. 36

Rotor speed response during capture at permanent stability threshold for the rotor with additional degrees of freedom (for bearing) and material damping

Fig. 37

Rotor whirl amplitudes during capture at permanent stability threshold for the rotor with additional degrees of freedom and material damping

6 Conclusions

Flexible rotor shafts with non-circular cross section and mounted on rigid support have one parametric instability speed region, whereas those mounted on flexible asymmetric supports have more than one parametric instability speed regions. When material damping in the rotor shaft is introduced, a super-critical stability threshold appears. When such a rotor system is driven by a non-ideal or limited power source, such as a DC motor, depending upon the motor power, saturation behaviours are seen at the boundaries of stability-instability speed regions. Below a certain amount of power, the rotor speed is captured near the parametric instability boundary with large whirl amplitudes; and when the motor power is increased, there is a discrete jump in the rotor speed with an associated decrease in the whirl amplitudes. For sufficiently more power than the required minimum power to escape through the parametric instability, the rotor accelerates almost smoothly through the unstable region and the whirl amplitudes remain significantly small.

However, such an escape through instability region is not possible through the super-critical stability threshold which results from the effect of material damping on asynchronous rotor whirl. At the permanent stability threshold, any increase in the motor power does not change the rotor speed and any surplus motor power simply contributes towards increased whirl amplitudes.

Depending upon the number of parametric instability regions and the desired operating speed, a number of transitions through the unstable (parametric instability) regions are observed. Sometimes, there is a combined transition through more than one region. Moreover, the dynamics of capture and transition is shown to be dependent on the initial conditions. Likewise, the speed capture at the stability-instability boundary is often unsteady and spans a wide range of speed containing stable and unstable speeds; which gives rise to bounded, but chaotic response.

One of the key findings from this research is that when encountering an unstable zone in a parametrically excited system, the steady-state rotor speed is always captured at the lower instability boundary unless there is sufficient power to escape through the instability. Figure 17 illustrates this behaviour as well as the influence of the initial conditions. For rotor coast up, as the rotor speed reaches the lower instability boundary and the motor power is increased further in steps, then the rotor speed increases and enters unstable speed range which increases the whirl amplitudes, dissipates more motor power and consequently brings down the rotor speed back to the lower instability boundary to maintain a balance. On the other hand, as the motor power is reduced from a speed above the higher instability boundary during rotor coast down, as the rotor speed enters the unstable region, the whirl amplitude grows and the increase in dissipated power further reduces the rotor speed until the speed reaches the lower instability boundary. Thus, there is a capture phenomenon only at the lower instability boundary. Also, for quasi-static increase of motor power, such as a slow rate ramp input, the rotor speed cannot escape the lowest stability threshold of the system. During rotor coast up, high motor power as step input (so-called full steam ahead) and low initial disturbance (and/or eccentricity) promote passage through the unstable speed ranges with lower whirl amplitude. Often, depending upon the desired motor speed, it may be necessary to reduce the motor power immediately after passage through a specific unstable speed range as illustrated for the speeds lying between points c to e in Fig. 17.

The capture at various parametric instabilities and stability threshold may be utilized in different ways for engineering design. For rotor systems designed to operate at stable operating speeds, the analysis presented here is useful for actuator sizing, i.e. selecting the motor power rating to reach the desired stable operating speed. Also, the sequence to reach a stable operating speed is equally important because it may require higher input power to first reach a higher speed by transiting through a parametric instability and then reducing the motor power to reach the desired speed. On the other hand, for vibrating machines such as particle separators, vibrating screens, washing machine dryers, etc., the actuators can be sized to operate at the threshold of parametric and permanent unstable ranges while restricting the whirl amplitudes within tolerable range; thereby giving a few discrete operating speeds. In fact, chaotic speed and amplitude variations (e.g. Figs. 22, 23, 30, 31) within tolerable ranges may be desirable for some vibrating devices, such as mixers. Therefore, there needs to be more exploration of chaos and bifurcations in the system, especially the kind of situations depicted in Figs. 22, 23 and 24. Moreover, there are many parameters in the considered system and changes in those parameter values, such as due to parametric or measurement uncertainty or external disturbance, can affect the stability regions as well as transient responses. Therefore, detailed sensitivity analysis with respect to the parameters as well as initial conditions can be taken up for future research. Moreover, various other systems that exhibit parametric resonance can be considered to be driven by non-ideal drive. Specifically, in the field of rotor dynamics, this study can be extended to non-ideal engine/motor driven transmission shaft with universal/Cardan joint [84, 85], cracked rotor shaft with fixed or breathing crack [86, 87], and asymmetric rotor shaft with stretching nonlinearity [88,89,90]. Also, active and passive vibration suppression devices [6] and their optimization to control rotor whirl can be taken up as future research.