Keywords

16.1 Introduction

Mass-spring models are a common tool in mechanics due to their simplicity and ability to address rather complicated phenomena. For example, in work [1], the oscillator model is coupled with finite element method to address the acoustic emission studies of rocks.

Oscillator chains were considered in works by L. Slepyan and his co-workers [2]; however, this approach considers infinite oscillator chains. Moreover, the chain models are successfully used to study peculiar heat conduction effects in crystals. Two-dimensional models have been also used to address the effects encountered in dynamic crack propagation problems. For example, in work [3], the crack velocity oscillations are explained using a lattice model, while in [4], a bi-material model is studied in order to investigate various regimes of the interface crack propagation. The chain models have been also used to address martensitic phase transformations as seen from work [5].

Simple mass-spring models have been effectively applied to study rate sensitivity of materials and inverse rate sensitivity in particular [6].

In this paper, dynamic fracture effects related to discreetness of the oscillator chain system are discussed. First, an analytic solution for the system of differential equations governing the chain movement is obtained. This solution is then compared to the solution of a one-dimensional wave equation, which describes wave propagation in an elastic rod—a continuous analogue of the oscillator chain.

16.2 Static Preload with Abrupt Link Failure

16.2.1 Analytic Solution of the Chain Problem

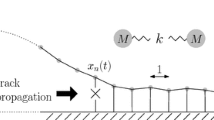
Consider a uniformly deformed chain consisting of \(N+1\) equal linear oscillators with both ends fixed.

If the masses are taken equal m, stiffnesses of the springs-c, the following system of differential equations coupled with initial conditions describes the chain motion:

$$\begin{aligned} \begin{array}{c} \boldsymbol{M}\ddot{\boldsymbol{Q}}+\boldsymbol{CQ}\boldsymbol{=}\boldsymbol{0} \\ q_i\left( t=0\right) -q_{i-1}\left( t=0\right) =l_c \\ \dot{q_i}\left( t=0\right) =0 \\ q_0\left( t\right) =0 \end{array} \end{aligned}$$
(16.1)

where \(\boldsymbol{Q}=(q_1,q_2,\ldots ,q_N)\) is a vector containing relative mass displacements, \(\boldsymbol{M}\) is the mass matrix and \(\boldsymbol{C}\) is a stiffness matrix and \(l_c\) is critical link deformation. Moreover, it is supposed that link with number \(N+1\) (dashed link in Fig. 16.1) does not bear this load and breaks abruptly at \(t=0\) initiating a release wave. The following fracture conditions are used: \(\left| q_i-q_{i-1}\right| >l_c,\ \ i=1\ldots N\). Matrices \(\boldsymbol{M}\) and \(\boldsymbol{C}\) read as (\(\boldsymbol{E}\) is identity matrix):

$$\begin{aligned} \boldsymbol{M}=m\boldsymbol{E} ; \boldsymbol{C}=c\left( \begin{array}{ccccc} 2 &{} -1 &{} \cdots &{} 0 &{} 0 \\ -1 &{} 2 &{} -1 &{} \cdots &{} 0 \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ 0 &{} &{} -1 &{} 2 &{} -1 \\ 0 &{} 0 &{} \cdots &{} -1 &{} 1 \end{array} \right) =c\boldsymbol{K}\boldsymbol{'}. \end{aligned}$$
(16.2)
Fig. 16.1
figure 1

Uniformly deformed chain with an abruptly failing link

Full size image

One of the chain ends remains fixed, and therefore \(q_0\left( t\right) =0\ \forall t\). The substitution \(t'=t\sqrt{{c}/{m}}\) yields the dimensionless problem with the mass matrix equaling identity matrix and the stiffness matrix \(\boldsymbol{K'}=\frac{1}{c}\boldsymbol{C}\) from Eq. 16.2. Additionally, normalized deformations of the chain links are introduced according to equation \(u_i={q_i-q_{i-1}}/{l_c},\ i=1\ldots N\) resulting in a modified stiffness matrix \(\boldsymbol{K}=\boldsymbol{SK}\boldsymbol{'}{\boldsymbol{S}}^{-1}\) with S being a matrix of coordinates transformation. The fracture condition has the form: \(\left| u_i\left( t\right) \right| >1,\ i=1\ldots N\). This way, the following problem is solved if vector \(\boldsymbol{U}=(u_1,u_2,\ldots ,\ u_N)\) is introduced:

$$\begin{aligned} \begin{array}{c} \ddot{\boldsymbol{U}}+\boldsymbol{KU}\boldsymbol{=}\boldsymbol{0} \\ u_i\left( t=0\right) =1 \\ \dot{u_i}\left( t=0\right) =0 \\ u_0\left( t\right) =0 \\ \left| u_i\left( t\right) \right| >1. \end{array} \end{aligned}$$
(16.3)

Solution of the system Eq. 16.3 is sought in form

$$\begin{aligned} \boldsymbol{U}\left( \boldsymbol{t}\right) =\sum ^n_{j=1}{c_j{\boldsymbol{R}}_{\boldsymbol{j}}\mathrm {cos}\mathrm {}({\omega }_jt)} \end{aligned}$$
(16.4)

where \({\omega }_j\) are the system eigenfrequencies, \({\boldsymbol{R}}_{\boldsymbol{j}}\boldsymbol{=}{\left( r^{\left( j\right) }_1,r^{\left( j\right) }_2,\ldots ,r^{\left( j\right) }_N\right) }^{\boldsymbol{T}}\) are corresponding eigenvectors and \(c_j\) is the set constants evaluated using the initial conditions.

The eigenfrequencies are calculated from eigenvalues \({\lambda }_j\) of the system stiffness matrix \(\boldsymbol{K}\): \({\omega }_j=\sqrt{{\lambda }_j}\). The eigenvalues of \(\boldsymbol{K}\) are calculated from equation

$$\begin{aligned} Det\left( \boldsymbol{K}-\lambda \boldsymbol{E}\right) =Det\left( \boldsymbol{K}\boldsymbol{'}-\lambda \boldsymbol{E}\right) =0. \end{aligned}$$
(16.5)

If we put \(\alpha =2-\lambda \), (5) can be rewritten explicitly in the following way:

$$\begin{aligned} \left| \begin{array}{ccccc} \alpha &{} -1 &{} \cdots &{} 0 &{} 0 \\ -1 &{} \alpha &{} -1 &{} \cdots &{} 0 \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ 0 &{} &{} -1 &{} \alpha &{} -1 \\ 0 &{} 0 &{} \cdots &{} -1 &{} \alpha -1 \end{array} \right| =D_N=0. \end{aligned}$$
(16.6)

In Eq. 16.6, \(D_N\) is determinant of order N. One may note that a recursive equation can be composed for a determinant of order k:

$$\begin{aligned} D_k=\ \alpha D_{k-1}-D_{k-2} \end{aligned}$$
(16.7)

and the following relations hold: \(D_0=1,\ D_1=\alpha -1\). Equation 16.7 is reduced to a quadratic equation \(p^2-\alpha p+1=0\) with roots \(p_{1,2}\) using substitution \(D_k=p^k\). This way the following expression is obtained:

$$\begin{aligned} D_N=\ b_1p^N_1+b_2p^N_2=0 \end{aligned}$$
(16.8)

where \(b_1\) and \(b_2\) are constants to be evaluated using conditions \(D_0=1,\ D_1=\alpha -1\) and substitution \(\alpha =2\mathrm {cos}\mathrm {}(\theta )\). Equation 16.8 yields the following formula for eigenvalues of the stiffness matrix:

$$\begin{aligned} {\lambda }_k=2-2cos\left( \frac{\pi \left( 2k-1\right) }{2N+1}\right) ,\ k=1\ldots N \end{aligned}$$
(16.9)

and thus, we obtain the formula for eigenfrequencies of the studied system:

$$\begin{aligned} {\omega }_k=2sin\left( \frac{\pi (2k-1)}{4N+2}\right) ,\ k=1\ldots N. \end{aligned}$$
(16.10)

For components of the eigenvectors of matrix \(\boldsymbol{K}\) the following equation holds:

$$\begin{aligned} r^j_i=P_{i-1}\left( x_j\right) -P_{i-2}\left( x_j\right) \end{aligned}$$
(16.11)

where \(x_j=\left( {2-\lambda }_j\right) /2\) and \(P_k(x)\) is a k-order Chebyshev polynomial of second kind, which can be expressed in the following way:

$$\begin{aligned} P_k\left( y\right) =\frac{\mathrm {sin}\mathrm {}((k+1){\mathrm {arccos} \left( y\right) })}{\mathrm {sin}\mathrm {}({\mathrm {arccos} \left( y\right) })}. \end{aligned}$$
(16.12)

Thus, the following expression can be obtained for the components of eigenvectors \({\boldsymbol{R}}_{\boldsymbol{j}}\):

$$\begin{aligned} r^j_i=\frac{cos\left( \frac{\pi (2i-1)(2j-1)}{4N+2}\right) }{cos\left( \frac{\pi (2j-1)}{4N+2}\right) },\ i=1\ldots N. \end{aligned}$$
(16.13)

In order to evaluate constants \(c_j\) to satisfy the initial conditions the following system should be solved accounting for Eq. 16.11:

$$\begin{aligned} \begin{array}{cc} \left( \begin{array}{cccc} P_0\left( x_1\right) &{} P_0\left( x_2\right) &{} \cdots &{} P_0\left( x_N\right) \\ P_1\left( x_1\right) -P_0\left( x_1\right) &{} P_1\left( x_2\right) -P_0\left( x_2\right) &{} \cdots &{} P_1\left( x_N\right) -P_0\left( x_N\right) \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ P_{N-1}\left( x_1\right) -P_{N-2}\left( x_1\right) &{} P_{N-1}\left( x_2\right) -P_{N-2}\left( x_2\right) &{} \cdots &{} P_{N-1}\left( x_N\right) -P_{N-2}\left( x_N\right) \end{array} \right) \left( \begin{array}{c} c_1 \\ c_2 \\ \begin{array}{c} \vdots \\ c_N \end{array} \end{array} \right) =\\ =\left( \begin{array}{c} 1 \\ 1 \\ \begin{array}{c} \vdots \\ 1 \end{array} \end{array} \right) =\left( \begin{array}{c} P_0(1) \\ P_1\left( 1\right) -P_0\left( 1\right) \\ \begin{array}{c} \vdots \\ P_{N-1}\left( 1\right) -P_{N-2}\left( 1\right) \end{array} \end{array} \right) . \end{array} \end{aligned}$$
(16.14)

If the second-order Chebyshev polynomials are explicitly written and elementary matrix operations are performed, the system Eq. 16.14 is reduced to the system with a Vandermonde matrix:

$$\begin{aligned} \left( \begin{array}{cccc} 1 &{} 1 &{} \cdots &{} 1 \\ x_1 &{} x_2 &{} \cdots &{} x_N \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {x_1}^{N-1} &{} {x_2}^{N-1} &{} \cdots &{} {x_N}^{N-1} \end{array} \right) \left( \begin{array}{c} c_1 \\ c_2 \\ \begin{array}{c} \vdots \\ c_N \end{array} \end{array} \right) =\left( \begin{array}{c} 1 \\ 1 \\ \begin{array}{c} \vdots \\ 1 \end{array} \end{array} \right) . \end{aligned}$$
(16.15)

Constants \(c_j\) can be evaluated from Eq. 16.15 using Cramer rule and formula for the determinant of the Vandemonde matrix:

$$\begin{aligned} c_j=\frac{(1-x_1)\cdots (1-x_{j-1})(1-x_{j+1})\cdots (1-x_N)}{(x_j-x_1)\cdots (x_j-x_{j-1})(x_j-x_{j+1})\cdots (x_j-x_N)}. \end{aligned}$$
(16.16)

Let’s put \(M_N\left( x\right) =2^N\prod ^N_{k=1}{(x-x_k)}\). Then Eq. 16.16 can be rewritten:

$$\begin{aligned} c_j=\frac{M_N\left( 1\right) }{{M_N}^\prime (x_j)(1-x_j)}. \end{aligned}$$
(16.17)

Considering the fact that \(M_N\left( x\right) \) has zeros at points \(x_j\) and multiplier \(2^N\), one may conclude that \(M_N\left( x\right) =P_N\left( x\right) -P_{N-1}\left( x\right) \) and thus one can deduce formula for constants \(c_j\) taking into account that \(M_N\left( 1\right) =1\):

$$\begin{aligned} c_j=\frac{{(-1)}^{j+1}2\mathrm {sin}\left( \frac{\pi (2j-1)}{2n+1}\right) \mathrm {cos}\left( \frac{\pi (2j-1)}{4n+2}\right) }{(2n+1)\left( 1-cos\left( \frac{\pi (2j-1)}{2n+1}\right) \right) }. \end{aligned}$$
(16.18)

Now general solution of the problem Eq. 16.3 is the following:

$$\begin{aligned} \begin{array}{cc} u_i\left( t\right) =\frac{2}{(2N+1)}\sum ^n_{j=1}{\frac{{(-1)}^{j+1}\mathrm {sin}\left( {\beta }_j\right) \mathrm {cos}\left( \frac{{\beta }_j}{2}(2i-1)\right) }{\left( 1-\mathrm {cos}\left( {\beta }_j\right) \right) }}{\mathrm {cos} \left( {\omega }_jt\right) } \\ {\beta }_j=\frac{\pi (2j-1)}{2N+1}. \end{array} \end{aligned}$$
(16.19)

In Eq. 16.19, \(u_i\left( t\right) \) stands for deformation of the chain link with number i.

16.2.2 Forced Chain Oscillations, Inhomogeneous System of Equations

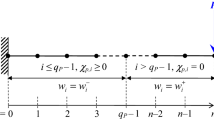
The following problem is considered: a chain of oscillators with N links and a fixed end is loaded with an arbitrary force f(t) applied to the chain free end (Fig. 16.2).

Fig. 16.2
figure 2

Chain loaded with an arbitrary force f(t)

Full size image

The system of dimensionless equations describing deformation of the chain links is the following:

$$\begin{aligned} \begin{array}{cccc} \ddot{\boldsymbol{U}}+\boldsymbol{KU}=\boldsymbol{F}\left( \boldsymbol{t}\right) ={\left( 0,0,\ldots ,f\left( t\right) \right) }^T \\ u_i\left( t=0\right) =0 \\ \dot{u_i}\left( t=0\right) =0 \\ u_0\left( t\right) =0. \end{array} \end{aligned}$$
(16.20)

In Eq. 16.20, \(\boldsymbol{U}=(u_1,u_2,\ldots ,\ u_N)\) and \(i=1\ldots N\). In order to solve system Eq. 16.20, an auxiliary homogeneous system of differential equations with modified initial conditions is introduced and solved following Duhamel’s method (system inhomogeneity is transferred to the initial conditions [7]:

$$\begin{aligned} \begin{array}{cccc} \ddot{\boldsymbol{W}}+\boldsymbol{KW}\boldsymbol{=}\boldsymbol{0} \\ w_i\left( t=0\right) =0 \\ \dot{w_i}\left( t=0\right) =0 \\ \dot{w_N}\left( t=0\right) =f(p)\\ w_0\left( t\right) =0. \end{array} \end{aligned}$$
(16.21)

In Eq. 16.21, \(\boldsymbol{W}=(w_1,w_2,\ldots ,\ w_N)\) and \(i=1\ldots N\) and p is an arbitrary real number. Systems, Eqs. 16.20 and 16.21, share stiffness matrix \(\boldsymbol{K}\) with the system solved in the previous section. Solution of Eq. 16.20 is further obtained using solution of Eq. 16.21.

Solution steps for Eq. 16.21 are similar to those for Eq. 16.3. The general solution is sought in form

$$\begin{aligned} \boldsymbol{W}\left( \boldsymbol{t}\right) =\sum ^N_{j=1}{a_j{\boldsymbol{R}}_{\boldsymbol{j}}\mathrm {sin}\mathrm {}({\omega }_jt)} \end{aligned}$$
(16.22)

where eigenfrequencies and eigenvectors \({\omega }_j\) and \({\boldsymbol{R}}_{\boldsymbol{j}}\) are evaluated according to formulas Eqs. 16.10 and 16.13. In order to obtain the solution, constants \(a_j\) should be calculated satisfying the initial conditions. Let’s put \(b_j=a_j{\omega }_j\). Then the system for \(b_j\) reads as:

$$\begin{aligned} \begin{array}{cc} \left( \begin{array}{cccc} P_0(x_1) &{} P_0(x_2) &{} \cdots &{} P_0(x_N) \\ P_1\left( x_1\right) -P_0(x_1) &{} P_1\left( x_2\right) -P_0(x_2) &{} \cdots &{} P_1\left( x_N\right) -P_0(x_N) \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ P_{N-1}\left( x_1\right) -P_{N-2}(x_1) &{} P_{N-1}\left( x_2\right) -P_{N-2}(x_2) &{} \cdots &{} P_{N-1}\left( x_n\right) -P_{N-2}(x_N) \end{array} \right) \cdot \\ \cdot \left( \begin{array}{c} b_1 \\ b_2 \\ \begin{array}{c} \vdots \\ b_N \end{array} \end{array} \right) =\left( \begin{array}{c} 0 \\ 0 \\ \begin{array}{c} \vdots \\ f(p) \end{array} \end{array} \right) \end{array} \end{aligned}$$
(16.23)

In Eq. 16.23 \(x_j=\left( {2-\lambda }_j\right) /2\) and \(P_k(x)\) is a k-order Chebyshev polynomial of second kind. As in the previous case, Eq. 16.23 is reduced to a system with a Vandermonde matrix:

$$\begin{aligned} \left( \begin{array}{cccc} 1 &{} 1 &{} \cdots &{} 1 \\ x_1 &{} x_2 &{} \cdots &{} x_N \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {x_1}^{N-1} &{} {x_2}^{N-1} &{} \cdots &{} {x_N}^{N-1} \end{array} \right) \left( \begin{array}{c} b_1 \\ b_2 \\ \begin{array}{c} \vdots \\ b_N \end{array} \end{array} \right) =\left( \begin{array}{c} 0 \\ 0 \\ \begin{array}{c} \vdots \\ f\left( p\right) /2^{N-1} \end{array} \end{array} \right) \end{aligned}$$
(16.24)

If the Cramer’s rule is applied and function \(M_N\left( x\right) =2^N\prod ^N_{k=1}{(x-x_k)}\) is introduced, the following formula holds:

$$\begin{aligned} b_j=\frac{2f(t)}{M_N'\left( x_j\right) }. \end{aligned}$$
(16.25)

Thus, if \(M_N\left( x\right) \) is expressed using \(P_k(x)\), final formula for the constants \(a_j\) can be written:

$$\begin{aligned} b_j=\frac{{\left( -1\right) }^{j+1}4{{\mathrm {cos}}^2 \left( \frac{\pi \left( 2j-1\right) }{4N+2}\right) f(t)}}{\left( 2N+1\right) }. \end{aligned}$$
(16.26)

Since the auxiliary system is explicitly solved, solution to the initial system Eq. 16.20 can be written:

$$\begin{aligned} \boldsymbol{U}\left( \boldsymbol{t}\right) =\sum ^N_{j=1}{a_j{\boldsymbol{R}}_{\boldsymbol{j}}\int ^t_0{{\mathrm {sin} \left( {\omega }_j\left( t-s\right) \right) }f\left( s\right) ds}}. \end{aligned}$$
(16.27)

The considered loading function f(t) is shown in Fig. 16.3.

Fig. 16.3
figure 3

Loading function: pulse with duration T

Full size image

Then Eq. 16.27 is transformed into the following expression:

$$\begin{aligned} \boldsymbol{U}\left( \boldsymbol{t}\right) =\left\{ \begin{array}{c} \sum ^N_{j=1}{\frac{a_j{\boldsymbol{R}}_{\boldsymbol{j}}}{{\omega }_j}}\left( 1-{\mathrm {cos} \left( {\omega }_jt\right) }\right) ,\ t<T \\ \sum ^N_{j=1}{\frac{a_j{\boldsymbol{R}}_{\boldsymbol{j}}}{{\omega }_j}}\left( {\mathrm {cos} \left( {\omega }_j\left( t-T\right) \right) }-{\mathrm {cos} \left( {\omega }_jt\right) }\right) ,t\ge T \end{array}. \right. \end{aligned}$$
(16.28)

Thus, Eq. 16.28 is a formula for the deformation of links of the chain subjected to pulse load.

16.3 Results. Comparison with Solutions for an Elastic Rod

In this section formulas, Eqs. 16.19 and 16.28 will be used to evaluate deformations in particular chain links. Moreover, these solutions will be compared to deformations of an elastic rod, subjected to similar loads. The rod can be regarded as a continuous counterpart of the chain.

A prestressed elastic rod is a complete analogue of the chain problem considered in 2.1. A release wave propagation in the homogeneously deformed elastic rod of length l with model material parameters (elastic modulus and density equal 1) is considered. If displacements of the rod points are described by function \(U\left( x,t\right) \) and deformations by \(\varepsilon (x,t)\) and sealing of the rod end \(x=0\) is supposed, the following initial boundary value problem can be stated:

$$\begin{aligned} \begin{array}{ccccc} \begin{array}{c} \frac{{\partial }^2U(x,t)}{\partial x^2}=\frac{{\partial }^2U(x,t)}{\partial t^2} \\ U\left( x,0\right) =x\Rightarrow \varepsilon \left( x,t\right) =1 \\ \begin{array}{c} {\left. \frac{\partial U(x,t)}{\partial t}\right| }_{t=0}=0 \\ U\left( 0,t\right) =0 \end{array} \\ {\left. \frac{\partial U(x,t)}{\partial x}\right| }_{x=l}=H(-t) \end{array}. \end{array} \end{aligned}$$
(16.29)

Additionally, the following fracture condition is set: fracture takes place if \(\left| \varepsilon \left( x,t\right) \right| >1\). Solution of Eq. 16.29 can be obtained as a combination of travelling and reflected waves. In Fig. 16.4, deformation of the first link and deformation of the rod sealing are shown. It is clear that deformations of the elastic rod never exceed the initial value 1 and thus fracture never takes place, while deformation of the first link of the chain exceeds critical value by about 50% leading to the system failure. This way, equal loading conditions result in fracture for the discrete system, while its continuous analogue remains intact.

Fig. 16.4
figure 4

Deformation of the first chain link (solid line) and deformation of rod in a sealed point (dashed line). Arrow indicates the link fracture. Results for 50 links and a rod with length \(l=50\) are shown

Full size image

Now the rod is supposed to be loaded by a deformation pulse. Model material is used and the rod is supposed to be sealed from one end. Thus, the initial boundary value problem reads as:

$$\begin{aligned} \begin{array}{ccccc} \begin{array}{c} \frac{{\partial }^2\varepsilon (x,t)}{\partial x^2}=\frac{{\partial }^2\varepsilon (x,t)}{\partial t^2} \\ \varepsilon \left( x,0\right) =0 \\ \begin{array}{c} {\left. \frac{\partial \varepsilon (x,t)}{\partial t}\right| }_{t=0}=0 \\ U\left( 0,t\right) =0 \end{array} \\ \varepsilon \left( l,t\right) =f\left( t\right) =H\left( t\right) \mathrm {-}H\left( t\mathrm {-}T\right) \end{array}. \end{array} \end{aligned}$$
(16.30)

If d’Alembert method is applied, one can find that an undistorted deformation pulse \(f\left( t\right) \) travels through the rod and no fracture occurs, since \(\left| \varepsilon \left( x,t\right) \right| >1\) fracture condition is considered. On the contrary, solution for the chain shows distortion of the pulse, which leads to failure of the link with number N. This phenomenon is shown in Fig. 16.5 for a chain consisting of 100 links, pulse duration \(T=10\) and rod with length \(l=100\).

Fig. 16.5
figure 5

Deformation of the chain link with number N (solid line) and rod deformation at point x \(=\) l (dashed line). Link fracture is indicated by an arrow. In this case number of links \(N=100\) and rod length \(l=100\)

Full size image

This way pulse load applied to a discrete system may lead to failure, while the continuous system remains intact for the identical load.

16.4 Conclusion

Dynamic fracture of linear oscillator chains is considered in the work. In particular, the effect related to discreetness of the system is studied. Two load cases are considered: abrupt release of a prestressed chain and pulse loading of an undeformed chain. For both cases, analytical solutions for the chain link deformations are obtained. These solutions are compared to the results for a continuous analogue of chain—elastic rod. It is demonstrated that the wave travelling through a chain (resulting either from abrupt release or from deformation pulse applied) is distorted comparing to an elastic rod, which can result in fracture. On the contrary, such effect is not possible for the continuous system.

This effect can be accounted for when structures with explicit discreetness and periodicity are designed and studied, e.g. construction facilities in civil engineering. A railway train could serve as another example of possible application of the studied discrete problem. A railway train moving with a constant velocity can be modelled by a statically uniformly deformed chain of oscillators. Thus, a sudden break of a damaged or worn coupling device can potentially lead to the failure of normally functioning coupling devices.