Bending of an elastoplastic Hencky bar-chain: from discrete to nonlocal continuous beam models

Abstract

The static behavior of an elastoplastic one-dimensional lattice system in bending, also called a microstructured elastoplastic beam or elastoplastic Hencky bar-chain (HBC) system, is investigated. The lattice beam is loaded by concentrated or distributed transverse monotonic forces up to the complete collapse. The phenomenon of softening localization is also included. The lattice system is composed of piecewise linear hardening–softening elastoplastic hinges connected via rigid elements. This physical system can be viewed as the generalization of the elastic HBC model to the nonlinear elastoplasticity range. This lattice problem is demonstrated to be equivalent to the finite difference formulation of a continuous elastoplastic beam in bending. Solutions to the lattice problem may be obtained from the resolution of piecewise linear difference equations. A continuous nonlocal elastoplastic theory is then built from the lattice difference equations using a continualization process. The new nonlocal elastoplastic theory associated with both a distributed nonlocal elastoplastic law coupled to a cohesive elastoplastic model depends on length scales calibrated from the spacing of the lattice model. Differential equations of the nonlocal engineering model are solved for the structural configurations investigated in the lattice problem. It is shown that the new micromechanics-based nonlocal elastoplastic beam model efficiently captures the scale effects of the elastoplastic lattice model, used as the reference. The hardening–softening localization process of the nonlocal continuous model strongly depends on the lattice spacing which controls the size of the nonlocal length scales.

List of symbols

	Parameters	Dimension	Relative dimensionless parameter
a	Element length	(L)	$a^{*} = {a \mathord{\left/ {\vphantom {a L}} \right. \kern-0pt} L} = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}$
$k_{p}^{ + }$	Hardening plastic bending modulus	(M L3 T−2)	$k_{p}^{ + *} = {{k_{p}^{ + } } \mathord{\left/ {\vphantom {{k_{p}^{ + } } {EI}}} \right. \kern-0pt} {EI}}$
$k_{p}^{ - }$	Softening plastic bending modulus	(M L3 T−2)	$k_{p}^{ - *} = {{k_{p}^{ - } } \mathord{\left/ {\vphantom {{k_{p}^{ - } } {EI}}} \right. \kern-0pt} {EI}}$
C	Elastic rotation stiffness of hinge: C = EI/a	(M L2 T−2)	–
$C_{p}^{ + }$	Hardening plastic rotation stiffness	(M L2 T−2)	–
$C_{p}^{ - }$	Softening plastic rotation stiffness	(M L2 T−2)	–
E	Young modulus of the beam	(M L−1 T−2)	–
I	Area moment of inertia	(L4)	–
L	Length of the beam	(L)	–
l 0	Limit of the plastic zone	(L)	$l_{0}^{*} = {{l_{0}^{{}} } \mathord{\left/ {\vphantom {{l_{0}^{{}} } L}} \right. \kern-0pt} L}$
l c	Characteristic length	(L)	$l_{c}^{*} = {{l_{c}^{{}} } \mathord{\left/ {\vphantom {{l_{c}^{{}} } L}} \right. \kern-0pt} L}$
M	Bending moment	(M L2 T−2)	$\mu = {{ML} \mathord{\left/ {\vphantom {{ML} {EI}}} \right. \kern-0pt} {EI}}$
M*	Additional hardening–softening moment	(M L2 T−2)
M p	Yield bending moment (Mp = EIκy)	(M L2 T−2)	$\mu_{p}^{{}} = {{M_{p}^{{}} L} \mathord{\left/ {\vphantom {{M_{p}^{{}} L} {EI = }}} \right. \kern-0pt} {EI = }}\kappa_{y}^{*}$
m	Ultimate to yield moment ratio	–	$m = {{M_{u} } \mathord{\left/ {\vphantom {{M_{u} } {M_{p} }}} \right. \kern-0pt} {M_{p} }}$
n	Number of elements	–
q	Number of plastic hinges	–
P	Single transverse load applied at the tip	(M L T−2)	$P = {{\beta_{P} EI\kappa_{y} } \mathord{\left/ {\vphantom {{\beta_{P} EI\kappa_{y} } L}} \right. \kern-0pt} L} = {{\beta_{P} ES\varepsilon_{y} } \mathord{\left/ {\vphantom {{\beta_{P} ES\varepsilon_{y} } n}} \right. \kern-0pt} n}$
Q	Uniformly distributed load	(M T−2)	$Q = {{2\beta_{Q} EI\kappa_{y} } \mathord{\left/ {\vphantom {{2\beta_{Q} EI\kappa_{y} } L}} \right. \kern-0pt} L}^{2} = {{2\beta_{Q} ES\varepsilon y} \mathord{\left/ {\vphantom {{2\beta_{Q} ES\varepsilon y} {nL}}} \right. \kern-0pt} {nL}}$
w	Deflection (transversal displacement)	(L)	$w^{*} = {w \mathord{\left/ {\vphantom {w L}} \right. \kern-0pt} L}$
x	Longitudinal coordinate	(L)	$x^{*} = {x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}$
β P	Dimensionless concentrated tip load	–	$\beta_{P} = {{PL} \mathord{\left/ {\vphantom {{PL} {EI\kappa_{y} }}} \right. \kern-0pt} {EI\kappa_{y} }} = {{nP} \mathord{\left/ {\vphantom {{nP} {ES\varepsilon_{y} }}} \right. \kern-0pt} {ES\varepsilon_{y} }}$
β Q	Dimensionless distributed load	–	$\beta_{Q} {{ = QL^{2} } \mathord{\left/ {\vphantom {{ = QL^{2} } {2EI\kappa_{y} }}} \right. \kern-0pt} {2EI\kappa_{y} }} = {{nQL} \mathord{\left/ {\vphantom {{nQL} {2ES\varepsilon_{y} }}} \right. \kern-0pt} {2ES\varepsilon_{y} }}$
δ	Tip deflection (free end)	(L)	$\delta_{{}}^{*} = {{w\left( L \right)} \mathord{\left/ {\vphantom {{w\left( L \right)} L}} \right. \kern-0pt} L} = w^{*} \left( 1 \right)$
κ y	Elastic limit curvature of the beam	(L−1)	$\kappa_{y}^{*} = \kappa_{y}^{{}} L$
κ c	Plastic curvature for M = Mu	(L−1)	$\kappa_{c}^{*} = \kappa_{c}^{{}} L = \left( {m - 1} \right){{\kappa_{y}^{*} } \mathord{\left/ {\vphantom {{\kappa_{y}^{*} } {k_{p}^{ + *} }}} \right. \kern-0pt} {k_{p}^{ + *} }}$
μ	Dimensionless moment	–
θ	Angle (incline) of element	–
Δθ	Total hinge rotation	–
Δθp	Plastic hinge rotation	–
χ	Total curvature of the beam	(L−1)	$\chi^{*} = \chi L$

Subscripts

K	Kinematic (boundary condition)
P	Concentrated load at the tip
Q	Uniformly distributed load
S	Static-equivalent (boundary condition)
i	At the node i or in the ith hinge
p	Plastic
u	Ultimate value
y	Yield elastic value

1 Introduction

This paper focuses on the link between discrete elastoplasticity and nonlocal continuum elastoplasticity through a paradigmatic lattice system. In the present work, we derive a new micromechanics-based (or discrete-based) nonlocal elastoplasticity model from an elastoplastic lattice model. Understanding the source of nonlocal plasticity is of primary interest for an accurate capture of scale effects of small-scale structures, for a consistent multiscale analysis of microstructured solids, and for physically controlling the localization processes, especially in the presence of softening materials. It is demonstrated in this paper that hardening–softening elastoplastic lattice systems may behave in the same manner as one-dimensional nonlocal elastoplastic systems, using rational arguments for bridging both models at the micro and the macro level.

Elastic lattices, as opposed to elastoplastic lattices, have been thoroughly investigated in engineering physics [1, 2] and relatively recently have been shown to be related to some nonlocal elastic continua, see for instance [3,4,5,6]. For example, Eringen et al. [3] calibrated bilinear nonlocal integral kernels from the dynamics of a linear axial lattice. Eringen introduced in 1983 [5] a stress gradient model with a length scale also calibrated from axial lattice wave dispersion characteristics. Most of the results focus on the dynamics of axial chains, but the results may be generalized to strings, rods in torsion, or even in-plane or out-of-plane beam behavior [7]. It is only recently that the length scale calibration of Eringen’s stress gradient model [5] has been justified from a so-called continualization process of the lattice difference equations [8]. The continualization process consists in approximating the finite difference operators of the lattice model by differential operators using the Taylor-based expansion [9] or rational expansion [10]. Using such a continualization process, it has been recently demonstrated that bending of elastic chain also called Hencky Bar-Chain (HBC) system can be approximated using Eringen’s nonlocal elasticity beam mechanics [8, 11]. The nonlocal length scale has been identified from the lattice spacing, thus giving a type of physical support for justifying nonlocal elastic beam mechanics. However, these results have been mainly derived for linear elastic interactions. Even if nonlinear lattice systems can also be continualized for the wave propagation of an axial chain [9, 10, 12, 13], very few results are available for the nonlocal behavior of nonlinear beam problems, especially in statics. The study by Triantafyllidis and Bardenhagen [14] is noted for the static behavior of a nonlinear hyperelastic axial chain and its link with the strain gradient elasticity model. Cohesive elasticity laws have been derived from discrete elasticity models, with convex and non-convex energy [15,16,17]. In these models, the convex part of the elastic energy gives rise to a “local” distributed elasticity inside the element, whereas the concave part associated to the softening phenomenon can be captured by the cohesive behavior with discontinuous kinematics. Braides and Gelli [16] and Gelli and Royer-Carfagni [17] asymptotically obtained local elasticity laws coupled to zero-length cohesive elasticity using so-called Γ-convergence results (variational convergence that ensures convergence of the minimum problem). In the latter methods, the elasticity inside the nonlocalized element was preserved in a local format. Hérisson et al. [18] investigated the possible use of nonlocal mechanics based on strain and stress gradient elasticity (including Eringen’s nonlocal model) for capturing scale effects in nonlinear elastic axial lattices. The considered nonlinearity is of a material type and the nonlocal elasticity inside the element is coupled with a nonlocal cohesive behavior in the softening range. Geometrically nonlinear HBC lattices have been also studied [19] from a nonlocal continualized model under stress gradient. Dell’Isola et al. [20] generalized the geometrically nonlinear HBC lattice by including both axial and bending elastic interactions. More general HBC lattices with axial, bending and shear interactions have been recently developed by Turco et al. [21] and Kocsis and Challamel [22] including geometrical nonlinearities. With respect to inelastic lattices, Challamel et al. [23] built a nonlocal Continuum Damage beam model from a lattice made of Discrete Damage hinges in bending.

In this paper, we examine an elastoplastic lattice in bending with the piecewise linear hardening–softening law, following the methodology of Challamel et al. [24] initially applied at the continuum beam level in terms of nonlocal elastoplastic bending–curvature constitutive law. The lattice elastoplastic model can be viewed as a type of elastoplastic Hencky’s model composed of elastoplastic hinges linked to rigid elements. Hencky developed in 1920 [25] his chain theory for lattice systems with linear elastic interaction. The piecewise nature of the constitutive law leads to linear difference equations for both elastic and plastic region, whose connection may be achieved from continuity conditions. As exact solutions of linear difference equations are available in standard textbooks [26, 27], the solution to the present piecewise linear difference problem will also be sought in an exact form. Wood’s paradox [28, 29] of elastic unloading in the presence of softening is solved with an equivalent lattice-based nonlocal model, and the softening localization zone is shown to depend firmly on the lattice spacing. In a continuous beam with a local softening behavior, the length of elements vanishes, and the global response after the maximum load tends toward the complete unloading elastic response.

It is the first time, to our knowledge, that a nonlocal elastoplastic beam model is built from elastoplastic lattices. In Challamel et al. [8], nonlocal elastic beam models have been built from elastic lattices, using Hencky bar-chain model. The generalization to nonlocal Continuum Damage beam models from elastic-damage Hencky bar-chain model is due to Challamel et al. [23]. This study is devoted to the transition from discrete elastoplastic beam model to nonlocal continuous elastoplastic beam models, using a rigorous continualization process. Analytical solutions for both the discrete and the nonlocal continuous elastoplastic systems are derived. Efficiency of the nonlocal continuous approaches to capture the scale effects of the elastoplastic lattices is presented.

2 A discrete plasticity mechanics problem in bending

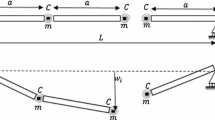
The microstructured elastoplastic cantilever beam is examined in Figs. 1 and 2. The beam is composed of n rigid elements of length a connected to elastoplastic hinges (or rotational spring), and connected to the clamped section. The total length of the cantilever beam is denoted by L, such as L = na. This microstructured beam is loaded by a concentrated force P at the free end, (see Fig. 1), or a uniform distributed loading Q along the microstructured beam, (see Fig. 2). The constitutive law in each elastoplastic joint may be written from the bending moment–rotation relationship as:

$$M_{i} = C\left( {\Delta \theta_{i} - \Delta \theta_{p,i} } \right)\;{\text{with}}\;\Delta \theta_{i} = \frac{{w_{i + 1} - 2w_{i} + w_{i - 1} }}{a}\;{\text{and}}\;\Delta \theta_{p,i} = a\chi_{p,i}$$

(1)

where $M_{i}$ is the bending moment in the ith elastoplastic hinge, C is the elastic rotational stiffness, Δθ_i is the relative rotation between two adjacent segments, and Δθ_p,i is the plastic rotation which can be expressed with respect to the plastic curvature from Δθ_p,i = aχ_p,i. Furthermore, the discrete to continuous scale transition is based on C = EI/a where E is Young’s modulus and I is the area moment of inertia of the equivalent continuous beam, asymptotically obtained for an infinite number of periodic cells. This model is exactly the same as the HBC system without the plasticity phenomena [25]. C = EI/a, where a plays the role of a small parameter, can be understood to be a rescaling of rigidity or normalization procedure, as used by Hencky [25] for pure bending systems or more recently by Dell’Isola et al. [20] for coupled axial-bending systems.

Fig. 1

Microstructured cantilever beam loaded by a concentrated transverse load, P, applied at its tip, according to the lattice approach

Fig. 2

Microstructured cantilever beam loaded by a uniformly distributed transverse load, Q, according to the lattice approach

The elastoplastic constitutive law can be rewritten as:

$$M_{i} = EI\left( {\frac{{w_{i + 1} - 2w_{i} + w_{i - 1} }}{{a^{2} }} - \chi_{p,i} } \right)$$

(2)

A piecewise linear hardening–softening plasticity loading function is considered in each elastoplastic hinge, whose plasticity loading function is written as:

$$f\left( {M_{i} ,M_{i}^{*} } \right) = \left| {M_{i} } \right| - \left( {M_{p} + M_{i}^{*} } \right) \le 0$$

(3)

where M_p is the plastic moment and $M_{i}^{*}$ is an additional static variable which controls the hardening–softening process. M_i is the bending moment which is assumed to remain positive during the bending test, so that |M_i| = M_i.

The loading functions in the hardening and softening phase are respectively written as:

$$\begin{aligned} & M_{i}^{*} = k_{p}^{ + } \chi_{p,i} \quad{\text{if}}\quad\chi_{p,i} \in \left[ {0;\kappa_{c} } \right]\;{\text{with}}\;\kappa_{c} = \left( {m - 1} \right){{M_{p} } \mathord{\left/ {\vphantom {{M_{p} } {k_{p}^{ + } }}} \right. \kern-0pt} {k_{p}^{ + } }} \\ & M_{i}^{*} = M_{u} - M_{p} + k_{p}^{ - } \left( {\chi_{p,i} - \kappa_{c} } \right)\quad{\text{if}}\quad\chi_{p,i} \ge \kappa_{c} \;{\text{with}}\;M_{u} = mM_{p} \\ \end{aligned}$$

(4)

where $k_{p}^{ + } \ge 0$ and $k_{p}^{ - } \le 0$ are the hardening and the softening plastic bending modulus, (see Fig. 3), M_u is the ultimate bending moment and m is the ultimate to yield bending moment ratio (i.e. m = M_u/M_p).

Fig. 3

Elastoplastic bending moment–curvature law of each element with a linear hardening (if $\Delta \theta_{p} \in \left[ {0;a\kappa_{c} } \right]$, $M = M_{p} + C_{p}^{ + } \Delta \theta_{p}$ with $C_{p}^{ + } > 0$) and a linear softening (if $\Delta \theta_{p} \ge a\kappa_{c}$, $M = M_{u} + C_{p}^{ - } \left( {\Delta \theta_{p} - a\kappa_{c} } \right)$ with $C_{p}^{ - } < 0$)

The loading–unloading conditions (Kuhn–Tucker conditions) are defined by:

$$f\left( {M_{i} ,M_{i}^{*} } \right) \le 0,\;\dot{\chi }_{p,i} \ge 0,\;f\left( {M_{i} ,M_{i}^{*} } \right)\dot{\chi }_{p,i} = 0$$

(5)

During the examination of the monotonic test, once plasticity is initiated, the bending moment (or the generalized stress) remains on the yield surface and the loading criterion is satisfied i.e. $f\left( {M_{i} ,M_{i}^{*} } \right) = 0$, except for the unloading phase in presence of softening, and then:

$$M_{i} = M_{p} + M_{i}^{*}$$

(6)

The equilibrium equation inside the beam lattice can also be written in a discrete form as:

$$\frac{{M_{i + 1} - 2M_{i} + M_{i - 1} }}{{a^{2} }} = Q$$

(7)

It is worth mentioning that the coupled system of difference equations associated with the elastoplastic lattice corresponds exactly to the finite difference formulation of a “local” continuous elastoplastic beam. The associated “local” continuous constitutive law whose finite difference formulation is formulated in Eq. (2) is based on the following elastoplastic bending moment—curvature:

$$M = EI\left( {w^{\prime\prime} - \chi_{p} } \right)$$

(8)

where w″ is the second-order derivative of the deflection with respect to x, the longitudinal coordinate. In the so-called local framework, the bending moment depends on the total curvature and the plastic curvature, a property which won’t be valid anymore for the nonlocal elastoplastic constitutive law considered in the continualization process of the lattice equations.

The plasticity loading function of the “local” continuous model is obtained from Eq. (3) and is written as:

$$f\left( {M,M^{*} } \right) = \left| M \right| - \left( {M_{p} + M^{*} } \right) \le 0$$

(9)

where M* is an additional static variable which controls the hardening–softening process, [see Eq. (3)]. Finally, the “local” equilibrium equation of the associated continuous beam (with an infinite number of periodic cells i.e. in absence of scale effects) is written from Eq. (7) as:

$$M^{\prime\prime} = Q$$

(10)

where M″ is the second-order derivative of M with respect to x.

Thereafter, the following dimensionless parameters, normalized with respect to the physical characteristics of the beam, i.e., L, E and I are introduced to correspond to: longitudinal coordinate, x*; limit of the plasticized zone, $l_{0}^{*}$; characteristic length, λ_c; deflection, w*; hardening plastic bending modulus, $k_{p}^{ + *}$; softening plastic bending modulus $k_{p}^{ - *}$; plastic curvature, $\chi_{p}^{*}$; yield curvature, $\kappa_{Y}^{*}$; normalized concentrated load at the free end, β_P and normalized uniformly distributed load, β_Q, see Figs. 1 and 2 with discrete systems or Figs. 8 and 9 with continuous beams.

$$\begin{aligned} & x_{{}}^{*} = \frac{x}{L};\;l_{0}^{*} = \frac{{l_{0}^{{}} }}{L};\;\lambda_{c}^{{}} = \frac{{l_{c}^{{}} }}{L};\;w_{{}}^{*} = \frac{w}{L} \\ & k_{p}^{ + *} = \frac{{k_{p}^{ + } }}{EI};\;k_{p}^{ - *} = \frac{{k_{p}^{ - } }}{EI};\;\chi_{p}^{*} = \chi_{p}^{{}} L;\;\kappa_{Y}^{*} = \kappa_{Y}^{{}} L = \frac{{M_{p} L}}{EI} \\ & \beta_{P} = \frac{P}{{P_{y} }} = \frac{PL}{{M_{p} }} = \frac{PL}{{EI\kappa_{y} }};\;\beta_{Q} = \frac{Q}{{Q_{y} }} = \frac{{QL^{2} }}{{2M_{p} }} = \frac{{QL^{2} }}{{2EI\kappa_{y} }} \\ \end{aligned}$$

(11)

In the next two sections, all the parameters that have been used and their associated dimensionless parameters can be found in the nomenclature provided. It should be noted that the derivatives of all dimensionless parameters are hereafter considered with respect to the dimensionless coordinate, x*, (i.e., ${\partial \mathord{\left/ {\vphantom {\partial {\partial x^{*} }}} \right. \kern-0pt} {\partial x^{*} }}$).

3 Elastoplastic lattice system in bending

The discrete elasticity law Eq. (2), can be written as:

$$\frac{{M_{i} }}{{\Delta \theta_{y} }} = C\left( {\frac{{\Delta \theta_{i} }}{{\Delta \theta_{y} }} - \frac{{\Delta \theta_{p,i} }}{{\Delta \theta_{y} }}} \right)\;{\text{with}}\;C = \frac{EI}{a}$$

(12)

In the hardening regime, the discrete loading function derived from Eq. (4) can be written as:

$$\begin{aligned} & M_{i} = M_{p} + C_{p}^{ + } \Delta \theta_{p,i} \;{\text{if}}\;\Delta \theta_{p,i} \in \left[ {0;a\kappa_{c} } \right]\;{\text{with}}\;\kappa_{c} = \left( {m - 1} \right)\frac{{M_{p} }}{{k_{p}^{ + } }}\;{\text{and }}C_{p}^{ + } = \frac{{k_{p}^{ + } }}{a} \\ & M_{i} = C\Delta \theta_{i} \quad {\text{if}}\quad \Delta \theta_{p,i} = 0 \\ \end{aligned}$$

(13)

Figure 3 shows the bilinear elastoplastic bending moment–curvature law and states the various parameters considered.

In the plasticity zone, i.e. for x ∈ [0;l₀], χ_p,i ≥ 0, the deflection is thereafter annotated w⁻, while it is annotated w⁺, in the elastic zone, i.e. for x ∈ [l₀;L], where χ_p,i = 0.

3.1 Exact deflection solution in the hardening regime

In the case of a concentrated load, P, at the free end of the cantilever beam, (see Fig. 1), the moment M_i is equal to P(L − ai). For sufficiently small rotations, as far as elasticity is preserved along the lattice, this system corresponds to the HBC one, as previously investigated by Hencky [25]. Plasticity occurs if PL ≥ M_P. The plasticity propagates along the beam from the clamped section if x_i/L ≤ (1 − M_p/PL).

In the cantilever beam under uniformly distributed load, Q, plasticity occurs if M_i = QL²/2 ≥ M_P, (see Fig. 2). Plasticity propagates along the beam from the clamped end if ${{x_{i} } \mathord{\left/ {\vphantom {{x_{i} } L}} \right. \kern-0pt} L} \le 1 - \sqrt {{{2M_{p} } \mathord{\left/ {\vphantom {{2M_{p} } {QL^{2} }}} \right. \kern-0pt} {QL^{2} }}}$.

Thereafter, the loading case P corresponds to concentrated load at the tip and the loading case Q corresponds to uniformly distributed load. The subscripts _P or _Q are used to refer the parameters to the corresponding loading case.

The plasticity propagates along the beam from the clamped section. In a continuous elastoplastic beam, the plasticity zone ranges from x = 0 to x = l₀, where l₀ = l_0P or l₀ = l_0Q according to the considered loading case P or Q, is the limit of the plasticity zone that can also be written in a dimensionless form according to the dimensionless concentrated load β with β = β_P or β = β_Q:

$$l_{0P}^{*} = 1 - \frac{1}{{\beta_{P} }}\;{\text{or}}\;l_{0Q}^{*} = 1 - \frac{1}{{\sqrt {\beta_{Q} } }}$$

(14)

The number of plasticized hinges q can be defined as

$$\frac{q}{n} \le l_{0}^{*} < \frac{q + 1}{n} \Rightarrow q = \left\lfloor {nl_{0}^{*} } \right\rfloor + 1$$

(15)

where $\left\lfloor x \right\rfloor$ is the smallest integer (or floor) function of the real value x.

The maximum length of the plasticity zone is reached in a continuous beam when the moment M₀ at the clamped end is equal to M_u, i.e., when the dimensionless load parameter reaches its maximum value: β_P = m or β_Q = m, (see Fig. 3). Once this dimensionless load reaches the peak, m, the softening stage controls the post-localization process in the first hinge while all the other hinges discharge elastically without any additional propagation of plasticity along the beam. The maximum number of plasticized hinges, q _max, can then be defined:

$$q_{P\text{ max} } = \left\lfloor {n\left( {1 - \frac{1}{m}} \right)} \right\rfloor + 1\;{\text{ or }}\;q_{Q\text{ max}} = \left\lfloor {n\sqrt {1 - \frac{1}{m}} } \right\rfloor + 1$$

(16)

The discrete activation of the plastic hinges with respect to the load parameter is shown in Figs. 4 and 5 for different values of n, namely for n = 4 and n = 12 in the hardening phase. Clearly, Fig. 4 as Fig. 5 shows that the discrete problem is a non-smooth problem, which can be efficiently represented by the smooth continuous model but only for a sufficiently large number of elastoplastic hinges.

Fig. 4

Evolution of the q_P active elastoplastic hinges beyond the elastic point with 5 and 25 elements-systems in the case of concentrated tip load, P

Fig. 5

Evolution of the q_Q active elastoplastic hinges beyond the elastic point with 5 and 25 elements-systems in the case of uniformly distributed load, Q

In the first part of the beam, for x ∈ [0; l₀[, plasticity occurs, χ_p > 0, and the deflection is annotated w⁻, while it is annotated w⁺, in the elastic zone, i.e., for x ∈ [l₀; L] where χ_p = 0. The difference problem can be then expressed for i ∈  [0;q − 1] according to Eqs. (2) and (4)–(6) with

$$\begin{aligned} & M_{i} = P\left( {L - ai} \right)\;{\text{and}}\;\chi_{p,i} = \frac{{\left( {L - ai} \right)P - M_{p} }}{{k_{p}^{ + } }}\;{\text{or}}\;\frac{{\chi_{p,i}^{*} }}{{\kappa_{y}^{*} }} = \frac{1}{{k_{p}^{ + *} }}\left[ {\beta_{P} \left( {1 - \frac{i}{n}} \right) - 1} \right] \\ & M_{i} = \frac{Q}{2}\left( {L - ai} \right)^{2} \;{\text{and}}\;\chi_{p,i} = \frac{{\left( {L - ai} \right)^{2} {Q \mathord{\left/ {\vphantom {Q 2}} \right. \kern-0pt} 2} - M_{p} }}{{k_{p}^{ + } }}\;{\text{or}}\;\frac{{\chi_{p,i}^{*} }}{{\kappa_{y}^{*} }} = \frac{1}{{k_{p}^{ + *} }}\left[ {\beta_{Q} \left( {1 - \frac{i}{n}} \right)^{2} - 1} \right] \\ \end{aligned}$$

(17)

leading to the linear second-order difference equation expressed for i > 0 with:

$$\begin{aligned} & \frac{{w_{i + 1}^{ - } - 2w_{i}^{ - } + w_{i - 1}^{ - } }}{{a^{2} }} = P\left( {L - ai} \right)\left( {\frac{1}{EI} + \frac{1}{{k_{p}^{ + } }}} \right) - \frac{{M_{p} }}{{k_{p}^{ + } }}\;{\text{or}} \\ & \frac{{w_{i + 1}^{ - } - 2w_{i}^{ - } + w_{i - 1}^{ - } }}{{a^{2} }} = \frac{Q}{2}\left( {L - ai} \right)^{2} \left( {\frac{1}{EI} + \frac{1}{{k_{p}^{ + } }}} \right) - \frac{{M_{p} }}{{k_{p}^{ + } }} \\ \end{aligned}$$

(18)

with the lattice-based boundary conditions at the clamped end: w₀ = 0 and w₁ = w₋₁. Determining the lattice moment definition at the first node and using the lattice-based boundary conditions gives the moment at the clamped end, M₀, with respect to the deflection of the first node w₁, (see Fig. 3):

$$\begin{aligned} & M_{0} = \frac{{CC_{p}^{ + } }}{{C + C_{p}^{ + } }}\left( {\frac{{2w_{1} }}{a} + \frac{{M_{p} }}{{C_{p}^{ + } }}} \right) = PL\quad \Rightarrow \quad w_{1} = a^{2} \left[ {\frac{PL}{2}\left( {\frac{1}{EI} + \frac{1}{{k_{p}^{ + } }}} \right) - \frac{{M_{p} }}{{2k_{p}^{ + } }}} \right]{\text{or}} \\ & M_{0} = \frac{{CC_{p}^{ + } }}{{C + C_{p}^{ + } }}\left( {\frac{{2w_{1} }}{a} + \frac{{M_{p} }}{{C_{p}^{ + } }}} \right) = \frac{{QL^{2} }}{2}\quad \Rightarrow \quad w_{1} = a^{2} \left[ {\frac{{QL^{2} }}{4}\left( {\frac{1}{EI} + \frac{1}{{k_{p}^{ + } }}} \right) - \frac{{M_{p} }}{{2k_{p}^{ + } }}} \right] \\ \end{aligned}$$

(19)

It should be noted that in the elastic regime, i.e., if $k_{p}^{ + } \to \infty$ (no plasticity rotation), the elastoplastic moment-rotation law is written as $M_{0} = 2Cw_{0} /a$, which means that the first hinge at the clamped section is considered to be twice as stiff as the others, i.e., C₀ = 2C as already assumed by Hencky [25] and detailed in [8].

In case of concentrated tip load, P, the exact solution of this second-order difference equation can be sought from the cubic shape function: w_i = A₀ + A₁i + A₂i² + A₃i³, where A₀ to A₃ are unknown constants [8, 27]. The clamped boundary condition for w₀ leads to the vanishing of the constant term A₀, whereas the second boundary condition for w₁ (w₁ = w_–1 leads to A₁ = − A₃) gives the unknown parameter A₂. Insertion of this function into Eq. (18) leads to the exact dimensionless deflection at nodes i of the discrete elastoplastic system:

$$\frac{{w_{i,P}^{ - *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{P} }}{{6n^{3} }}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left( {i - i^{3} } \right) + \left[ {\beta_{P} \left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - \frac{1}{{k_{p}^{ + *} }}} \right]\frac{{i^{2} }}{{2n^{2} }}$$

(20)

In the elastic regime, if β_P ≤ 1 or i ≥ q_P, χ_p,i = 0, Eq. (20) can be considered with $k_{p}^{ + } \to \infty$. The dimensionless deflection $w_{i}^{ +*}$ at the node i of the discrete elastic system differs slightly from the continuous elastic solution (see [8]). In the case of a concentrated load at the tip, the yield tip deflection, δ_y,P, obtained for β_P = 1, is given by:

$$\frac{{\delta_{y,P} }}{L} = w_{n}^{ + *} = \frac{{\kappa_{y}^{*} }}{3}\left( {1 + \frac{1}{{2n^{2} }}} \right)$$

(21)

The ratio of the dimensionless tip deflection to the one of the yield’s is used hereafter to normalize the results, as shown in Figs. 6 and 10.

Fig. 6

Dimensionless load-tip displacement of elastoplastic discrete bending system with m = 2, $k_{p}^{ + *} = 0.2$ and $k_{p}^{ - *} = 0.2$ and various numbers of constitutive elements, n, in the case of a concentrated load at the tip, P

In case of uniformly distributed load, Q, the solution of the second-order difference equation given in Eq. (18) can be obtained again from a quartic function: w_i = B₀ + B₁i + B₂i² + B₃i³ + B₄i⁴ where B₀ to B₄ are unknown constants. The boundary conditions of the discrete clamp-free problem lead to the vanishing of the constant term B₀, (w₀ = 0), whereas the second boundary condition for w₁ gives the unknown constant B₁ according to B₃ (w₁ = w_–1 → B₁ = − B₃). Insertion of this solution into Eq. (18) also leads to the identification of the constants B₂, B₃, and B₄, regardless of the size n of the system. The dimensionless deflection of the discrete elastoplastic system is then calculated exactly as:

$$\begin{aligned} & \frac{{w_{i,Q}^{ - *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{Q} }}{{3n^{3} }}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left( {i - i^{3} } \right) + \frac{{\beta_{Q} }}{12}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\frac{{i^{4} }}{{n^{4} }} \\ & \quad \quad \quad + \left[ {\beta_{Q} \left( {1 - \frac{1}{{6n^{2} }}} \right)\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - \frac{1}{{k_{p}^{ + *} }}} \right]\frac{{i^{2} }}{{2n^{2} }} \\ \end{aligned}$$

(22)

In the elastic regime, if β_Q ≤ 1 or i ≥ q_Q, χ_p,i = 0, Eq. (20) has to be considered with $k_{p}^{ + } \to \infty$ to obtain the dimensionless deflection $w_{i}^{+^{*}}$ at the node i of the discrete elastic system as already formulated with such an elastic discrete system (see Challamel et al. [8]). It should be noted that the yield tip deflection in the case of a uniformly distributed load, δ_y,Q, is then given by:

$$\frac{{\delta_{y,Q} }}{L} = w_{n}^{ + *} = \frac{{\kappa_{y}^{*} }}{4}\left( {1 + \frac{1}{{n^{2} }}} \right)$$

(23)

The ratio of the tip deflection to the one of the yield’s is used hereafter to normalize the results, as shown in Figs. 7 and 11.

Fig. 7

Dimensionless load-tip displacement of elastoplastic discrete bending system with m = 2, $k_{p}^{ + *} = 0.2$ and $k_{p}^{ - *} = 0.2$ and various numbers of constitutive elements, n, in the case of a uniformly distributed load, Q

3.2 Iterative computation of the full hardening–softening response of the elastoplastic lattice beam

As shown in Fig. 3, in the elastic, hardening, and the softening phase, the constitutive law is given by:

$$\begin{aligned} & M_{i} = EI\chi_{i} \quad {\text{if}}\quad \chi_{i} \le \kappa_{y} \;{\text{and if}}\quad \chi_{p,i} = 0 \\ & M_{i} = M_{p} + k_{p}^{ + } \chi_{p,i} \quad {\text{if}}\quad \chi_{p,i} \in \left[ {0;\kappa_{c} } \right]\;{\text{with}}\;\kappa_{c} = \left( {m - 1} \right)\frac{EI}{{k_{p}^{ + } }}\kappa_{y} \\ & M_{i} = M_{u} + k_{p}^{ - } \left( {\chi_{p,i} - \kappa_{c} } \right)\quad {\text{if}}\quad \chi_{p,i} \ge \kappa_{c} \;{\text{with}}\;M_{u} = mM_{p} \;{\text{and}}\;M_{p} = EI\kappa_{y} \\ \end{aligned}$$

(24)

The dimensionless discrete moment μ_i at the node i can be written according to the loading case, see Eq. (17), as:

$$\mu_{i,P}^{{}} = \beta_{P}^{{}} \left( {1 - \frac{i}{n}} \right)\;{\text{or}}\;\mu_{i,Q}^{{}} = \beta_{Q} \left( {1 - \frac{i}{n}} \right)^{2}$$

(25)

In the hardening regime, the boundary conditions at the clamped section, i.e., w₀ = 0 and w₁ = w_–1, give the dimensionless deflection of the first node $w_{1}^{ - *}$:

$$w_{1}^{ - *} = \frac{{\kappa_{y}^{*} }}{{2n^{2} }}\left[ {\mu_{0} \left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - \frac{1}{{k_{p}^{ + *} }}} \right]\;{\text{with}}\;\mu_{0 } = \mu_{0,P} = \beta_{P} \;{\text{or}}\;\mu_{0} = \mu_{0,Q} = \beta_{Q}$$

(26)

Iteratively, the other dimensionless node deflections in the plastic zone, $w_{i}^{ - *}$, can be computed as follows:

$$w_{i + 1}^{* - } = \frac{{\kappa_{y}^{*} }}{{n^{2} }}\left[ {\mu_{i} \left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - \frac{1}{{k_{p}^{ + *} }}} \right] + 2w_{i}^{* - } - w_{i - 1}^{* - }$$

(27)

with μ_i = μ_i,P and i ∈ [0; q_P − 2] or μ_i = μ_i,Q and i ∈ [0; q_Q − 2].

At the elastic–elastoplastic interface, i.e., for i = q − 1 with q = q_P or q = q_Q, the continuity condition of the deflection gives $w_{q - 1}^{* - } = w_{q - 1}^{* + }$ and $w_{q}^{* - } = w_{q}^{* + }$. The expression of the discrete elastoplastic moment–curvature in the (q − 1)th and qth hinges gives the following matching equations:

$$\begin{aligned} & w_{q}^{* + } = \frac{{\kappa_{y}^{*} }}{{n^{2} }}\left[ {\mu_{q - 1} \left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - \frac{1}{{k_{p}^{ + *} }}} \right] + 2w_{q - 1}^{* - } - w_{q - 2}^{* - } \;{\text{and}} \, w_{q + 1}^{* + } = \frac{{\kappa_{y}^{*} }}{{n^{2} }}\mu_{q} + 2w_{q}^{* + } - w_{q - 1}^{* - } \\ \end{aligned}$$

(28)

with μ_q = μ_q,P and q = q_P or μ_q = μ_q,Q and q = q_Q.

The dimensionless deflection of the nodes in the elastic zone, $w_{i}^{ + *}$, can be iteratively obtained from the following equation:

$$w_{i + 1}^{* + } = \frac{{\kappa_{y}^{*} }}{{n^{2} }}\mu_{i} + 2w_{i}^{* + } - w_{i - 1}^{* + }$$

(29)

with μ_i = μ_i,P and i ∈ [q_P + 2; n] or with μ_i = μ_i,Q and i ∈ [q_Q + 2; n].

Once β_P or β_Q reaches m, the first hinge behaves with a negative plastic bending modulus. The boundary conditions at the clamped section give the dimensionless deflection of the first node in the softening regime according to Eq. (24):

$$w_{1}^{ - *} = \frac{{\kappa_{y}^{*} }}{{2n^{2} }}\left[ {\mu_{0} \left( {1 + \frac{1}{{k_{p}^{ - *} }}} \right) + \frac{m - 1}{{k_{p}^{ + *} }} - \frac{m}{{k_{p}^{ - *} }}} \right]$$

(30)

where μ₀ = μ_0,P = β_P or μ₀ = μ_0,Q = β_Q according to the considered load distribution.

The other hinges, in the plasticity part, for i < q_P max or i < q_Q max, unload elastically while the plasticity curvature reached at the maximum load remains constant during the unloading process. The dimensionless node deflections can then be computed iteratively from the first node:

$$\begin{aligned} & w_{i + 1}^{* - } = \frac{{\kappa_{y}^{*} }}{{n^{2} }}\left[ {\left( {\beta_{P}^{{}} + \frac{m}{{k_{p}^{ + *} }}} \right)\left( {1 - \frac{i}{n}} \right) - \frac{1}{{k_{p}^{ + *} }}} \right] + 2w_{i}^{* - } - w_{i - 1}^{* - } \;{\text{or}} \\ & w_{i + 1}^{* - } = \frac{{\kappa_{y}^{*} }}{{n^{2} }}\left[ {\left( {\beta_{Q}^{{}} + \frac{m}{{k_{p}^{ + *} }}} \right)\left( {1 - \frac{i}{n}} \right)^{2} - \frac{1}{{k_{p}^{ + *} }}} \right] + 2w_{i}^{* - } - w_{i - 1}^{* - } \\ \end{aligned}$$

(31)

In this softening regime, the dimensionless deflection of the nodes in the pure elastic part of the chain, for i ≥ q_P max or i ≥ q_Q max, can be computed according to Eq. (28) from the continuity condition at the elastic–elastoplastic interface. The normalized dimensionless tip deflection ${{w^{ + *} \left( 1 \right)} \mathord{\left/ {\vphantom {{w^{ + *} \left( 1 \right)} {\kappa_{y}^{*} }}} \right. \kern-0pt} {\kappa_{y}^{*} }}$ of the full softening-hardening process of the discrete elastoplastic bending system is plotted in Figs. 6 and 7 with various numbers of elements in each loading case. For sufficiently large values of n, a snap-back occurs, which is controlled by the size of the first element a with respect to the total size of the beam L, with a/L = 1/n.

When the number of elements tends towards an infinity, i.e. n → ∞, the continuous softening beam is asymptotically obtained while the size of the first element vanishes. Then, as shown in Figs. 6 and 7, the global response after the maximum load tends toward the complete unloading elastic response, known as Wood’s paradox, for the continuous softening beam.

4 Continualization of elastoplastic interactions in bending

The discrete equations are extended to an equivalent continuum via a continualization method, for the displacement, the plastic curvature, and the moment. In this section, a representative continualized elastoplastic beam model is established in order to capture the specific scale effects of the microstructured elastoplastic problem. The propagation of plasticity in the hardening range is then captured within a nonlocal continuous elastoplastic model. This continuum is shown as a fully coupled nonlocal elastoplastic beam model able to capture, for instance, the propagation of the plasticity along the beam in the case of hardening.

4.1 Continualization method for nonlocal elastoplastic laws

The following relationship between the discrete and the equivalent continuous system $w_{i} = w\left( {x = ia} \right)$, $\chi_{pi} = \chi_{p,i} \left( {x = ia} \right)$ and $M_{i} = M\left( {x = ai} \right)$ holds for a sufficiently smooth deflection and plastic curvature as:

$$w\left( {x + a} \right) = \sum\limits_{k = 0}^{\infty } {\frac{{a^{k} \partial_{x}^{k} }}{k\,!}} w\left( x \right) = e^{{a\partial_{x} }} w\left( x \right)$$

$$\chi_{p} \left( {x + a} \right) = \sum\limits_{k = 0}^{\infty } {\frac{{a^{k} \partial_{x}^{k} }}{k\,!}} \chi_{p}^{{}} \left( x \right) = e^{{a\partial_{x} }} \chi_{p}^{{}} \left( x \right)$$

$${\text{and}}\;M\left( {x + a} \right) = \sum\limits_{k = 0}^{\infty } {\frac{{a^{k} \partial_{x}^{k} }}{k\,!}} M\left( x \right) = e^{{a\partial_{x} }} M\left( x \right)$$

(32)

where $\partial_{x} = {\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}$ is the spatial differentiation and $e^{{a\partial_{x} }}$ is a pseudo differential operator as introduced for example in [10, 30,31,32]. The principle of deriving higher-order continuous equations from lattice interactions is old and has been already used during the XIXth century by Piola for elastic materials (see [33] for an extensive analysis of the works of Piola with respect to this question).

By expanding the finite difference operator using Eq. (32), Eq. (2) can be continualized as

$$M = EI\left[ {\frac{4}{{a^{2} }}\sinh^{2} \left( {\frac{a}{2}\partial_{x} } \right)w - \chi_{p} } \right]$$

(33)

For a sufficiently smooth variation of the considered variable, the pseudo-differential operator can be approximated by the following Taylor expansion:

$$\frac{4}{{a^{2} }}\sinh^{2} \left( {\frac{a}{2}\partial_{x} } \right) = \partial_{x}^{2} + \frac{{a^{2} }}{12}\partial_{x}^{4} + O\left( {a^{4} } \right)$$

(34)

which leads to a gradient-type moment–curvature elastoplastic law:

$$M = EI\left[ {w^{\prime\prime} + \frac{{a^{2} }}{12}w^{\left( 4 \right)} - \chi_{p} } \right] + O\left( {a^{4} } \right)$$

(35)

A typical gradient-type curvature-driven model is recognized, with the square of characteristic length, $l_{c}^{2}$, equal to a²/12. A numerical solution could be directly computed from the second-order continualized equation using higher-order boundary conditions. However, the pseudo-differential operator can also be efficiently approximated by Padé’s approximant, to compute dynamic responses [10, 30,31,32] or a quasi-static response in the case of pure elasticity [8] or damage mechanics [23]. To avoid the difficulties associated with higher-order boundary conditions in the resolution of such continualized schemes [34], Padé’s approximation of the finite difference Laplacian operator is used:

$$\frac{4}{{a^{2} }}\sinh^{2} \left( {\frac{a}{2}\partial_{x} } \right) = \frac{{\partial_{x}^{2} }}{{1 - \frac{{a^{2} }}{12}\partial_{x}^{2} }} + \cdots \;{\text{with}}\;l_{c}^{2} = \frac{{a^{2} }}{12}$$

(36)

Equation (35) can be turned into the following analytical relationship:

$$M - l_{c}^{2} M^{\prime\prime} = EI\left( {w^{\prime\prime} - \chi_{p} + l_{c}^{2} \chi_{p}^{\prime \prime } } \right)$$

(37)

The continualized nonlocal constitutive law at the cross section level can then be written from the discrete bending moment–elastic curvature relationship given in Eq. (2). The new nonlocal elastoplastic law contains scale effects which affect the moment and the plastic curvature gradients. In a certain sense, the scale effect affects the internal variables of both the elasticity and the plasticity. We note that this nonlocal law is valid for monotonic or cyclic loadings. An Eringen’s type nonlocal elastic law is recognized when the plastic curvature can be ignored (see [8] for the application of Eringen’s stress gradient theory to the bending behavior of nonlocal elastic Euler–Bernoulli beam models). This nonlocal law can also be viewed as a fully coupled nonlocal elastoplastic bending moment curvature law. In the hardening and softening regime, the loading function, derived from Eq. (24), is simply given by:

$$\begin{aligned} M = M_{p} + k_{p}^{ + } \chi_{p} \;{\text{for}}\;\chi_{p} \in \left[ {0;\kappa_{c} } \right]\;{\text{with}}\;M_{p} = EI\kappa_{y} \hfill \\ M = M_{u} + k_{p}^{ - } \left( {\chi_{p} - \kappa_{c} } \right)\;{\text{for}}\;\chi_{p} \ge \kappa_{c} \;{\text{with}}\;M_{u} = mM_{p} \hfill \\ \end{aligned}$$

(38)

It is worth mentioning that the elastoplastic constitutive law is nonlocal both from the bending moment gradient and from the plastic curvature gradient, whereas the loading function is kept in a local form due to the continualization of the moment and the plastic curvature at the same points.

In the first stage, two parts of the nonlocal elastoplastic beam need to be considered separately, as mentioned in Sects. 3.1 and 3.2. In the first part, ranging from the clamped section to l₀, plasticity occurs, since χ_p ≠ 0 where x ∈ [0;l₀]. The displacement is annotated with the superscript “−”, as u⁻, whereas in the second part, beyond l₀, a pure elastic behavior takes place, since χ_p = 0 where x ∈ [l₀;L] it is annotated with the superscript “+” as u⁺.

The continualized nonlocal elastoplastic law is valid for propagating elastoplastic zones. The continualized finite length cohesive law is also derived from a continualization procedure in the presence of discontinuous kinematic variables, [Δθ], and is written by:

$$M = EI\left( {\frac{{\left[ {\Delta \theta } \right]}}{a} - \chi_{p} } \right)\;{\text{with}}\;\left[ {\Delta \theta } \right] = \theta^{ + } - \theta^{ - } = \left[ {\frac{{w\left( {x + a} \right) - w\left( x \right)}}{a}} \right] - \left[ {\frac{{w\left( x \right) - w\left( {x - a} \right)}}{a}} \right]$$

(39)

where the cohesive loading function in the hardening and the softening range is similar to Eq. (38). This cohesive law associated with some kinematic discontinuities will be used at the clamped boundary in both the hardening and the softening elastoplastic phases. It plays a crucial role in the softening regime as it will be detailed in this paper, in Sects. 4.3 and 4.4. To summarize, both the distributed nonlocal elastoplastic constitutive law and the associated cohesive law depend on the lattice spacing denoted by “a”. They can be considered as nonlocal, in the sense that the constitutive law does not depend only on the state variable but also includes its gradient, or its value at another point.

4.2 Boundary conditions for the nonlocal elastoplastic beam and elastoplastic interface continuity

Two types of boundary conditions can be considered in such discrete-based continuous systems, named hereafter as the local kinematic boundary condition or the static-equivalent boundary condition.

• The local type of kinematic boundary condition at the clamped section posits that the continuous rotation is vanishing, i.e., w^−′(0) = 0.

• The so-called static-equivalent boundary condition uses the cohesive law expressed at the clamped boundary. It posits that the bending moment, expressed in the first hinge (or rotational spring), can be expressed as a function of the displacement at the first node, for the full hardening–softening response [23, 34]. This relationship is actually derived from the nonlocal kinematic boundary condition, i.e. w⁻(a) = w⁻(− a), which defines the displacement of the closest node of the clamped end as a function of the load β:

$$\begin{aligned} M\left( 0 \right) &= EI\left[ {\frac{2w\left( a \right)}{{a^{2} }} - \chi_{p} \left( 0 \right)} \right]\;{\text{with}}\;M\left( 0 \right) = M_{p} + k_{p}^{ + } \chi_{p} \left( 0 \right) \\ \; \Rightarrow \frac{{w_{{}}^{ - *} \left( {{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}} \right)}}{{\kappa_{y}^{*} }} &= \frac{1}{{2n^{2} }}\left[ {\beta + \frac{1}{{k_{p}^{ + *} }}\left( {\beta - 1} \right)} \right]\;{\text{with}}\;\beta = \beta_{P} \;{\text{or}}\;\beta = \beta_{Q} \\ \end{aligned}$$

(40)

The dimensionless deflection of the beam for x = a or x* = 1/n, can also be equivalently computed from the exact lattice solution given in Eq. (20) or in Eq. (22) according to the loading configuration.

Once the load reaches the peak, i.e., β_P = m or β_Q = m, the softening stage occurs and is controlled by the negative plastic bending modulus. Softening occurs in the clamped section, at x = 0 while the beam unloads elastically even in the rest of the plasticity zone. In such conditions, the local kinematic boundary condition cannot be considered at this stage. Only static-equivalent boundary conditions, within the frame of a nonlocal cohesive model, are consistent.

Within the plasticity zone that is extended to its maximum length, i.e., for l_0P = 1 − 1/m or l_0Q = 1 − m^−1/2, the plastic bending reached at the load peak, χ_P max, remains constant. According to Eq. (24) and using the same methodology, the exact deflection for x = a can be defined as:

$$\frac{{w_{{}}^{ - *} \left( {{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}} \right)}}{{\kappa_{y}^{*} }} = \frac{1}{{2n^{2} }}\left[ {\beta + \frac{1}{{k_{p}^{ + *} }}\left( {m - 1} \right) + \frac{1}{{k_{p}^{ - *} }}\left( {\beta - m} \right)} \right]\;{\text{with}}\;\beta = \beta_{P} \;{\text{or}}\;\beta = \beta_{Q}$$

(41)

At the elastic–elastoplastic interface, at x = l₀, both static-equivalent and non-local kinematic boundary conditions lead to the same consequence, in both the hardening and the softening stages. The continualization assumes that the elastic–elastoplastic interface abscissa, x = l₀, continuously increases with load, with l₀ = l_0P or l₀ = l_0Q. The following conditions derived from the discrete continualized equations are considered:

• Deflection continuity: w⁻(l₀) = w⁺(l₀).

• Discrete bending moment continuity:

  w⁻(l₀ − a) + w⁻(l₀ + a) = w⁺(l₀ − a) + w⁺(l₀ + a) since χ_p(l₀) = 0 and w⁻(l₀) = w⁺(l₀), see Eq. (2).

• Discrete rotation continuity: w⁻(l₀ + a) − w⁻(l₀ − a) = w⁺(l₀ + a) − w⁺(l₀ − a).

These conditions lead to w⁻(l₀) = w⁺(l₀) and w⁻(l₀ − a) = w⁺(l₀ − a) and/or w⁻(l₀ + a) = w⁺(l₀ + a) as previously shown and tested in the case of continualized nonlocal damage mechanics beam models [23]. Examination of only two of these three continuity conditions in l₀ − a, l₀ and l₀ + a gives exactly the same analytical solution of continualized deflection, w⁺(x), in the elastic part. As a consequence, the deflection is continuous along the continualized nonlocal beam but its derivative, i.e., its rotation is no longer continuous in the vicinity of the elastoplastic interface.

4.3 Deflection of the nonlocal elastoplastic beam in the hardening regime

The continuous beam model is represented in Figs. 8 and 9 according to the loading case P and Q respectively.

Fig. 8

Continuous cantilever beam loaded by a concentrated transverse load, P, applied at its tip

Fig. 9

Continuous cantilever beam loaded by a uniformly distributed transverse load, Q

In the case of a concentrated tip load, P, the bending moment varies linearly according to x and then $M^{\prime\prime} = 0$. Deriving the loading consistency condition given in Eq. (8) $M^{\prime \prime } = M^{*\prime\prime } = k_{p}^{ + } \chi^{\prime \prime }_{p}$ and using $M^{\prime\prime} = 0$ leads to a plastic curvature constraint: $\chi_{p} ^{\prime \prime } = 0$. Therefore, the nonlocal continuous elastoplastic model established in Eq. (37) leads to the local constitutive law given in Eq. (8). For such a loading configuration, the continualized model leads to the same differential equations as the local one: the continualized model and the local elastoplastic model are identical, except eventually when considering the boundary conditions, as discussed later. The continuous problem can be formulated as a second-order differential equation with respect to the dimensionless deflection $w_{P}^{ - *}$:

$$\frac{{w_{P}^{ - *\prime \prime }}}{{\kappa_{y}^{*} }} = \beta_{P} \left( {1 - x^{*} } \right)\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - \frac{1}{{k_{p}^{ + *} }}$$

(42)

In the case of uniformly distributed load, Q, the bending moment is parabolic according to x and $M^{\prime \prime } = Q$. The loading consistency condition leads to $\chi_{p}^ {\prime \prime } = Q/k_{p}^{{}}$ and then the elastoplastic constitutive law is corrected, according to Eq. (37), by the small length terms as:

$$M - l_{c}^{2} Q = EI\left( {w_{Q}^ {\prime \prime } - \chi_{p} + l_{c}^{2} \frac{Q}{{k_{p} }}} \right)$$

(43)

If $x^{*} \in \left[ {0;l_{0Q}^{*} } \right]$, the nonlocal continuous elastoplastic model established in Eq. (37) leads to a second-order differential equation for the deflection that can be presented in a dimensionless format as:

$$\frac{{w_{Q}^{ - *\prime \prime }}}{{\kappa_{y}^{*} }} = \beta_{Q} \left( {1 - x^{*} } \right)^{2} \left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - 2\beta_{Q} l_{c}^{*2} \left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - \frac{1}{{k_{p}^{ + *} }}\;{\text{with}}\;l_{c}^{*2} = \frac{1}{{12n^{2} }}$$

(44)

where β_Q is the dimensionless load parameter introduced in Eq. (11).

Then, integrating Eq. (42) twice, and using the boundary condition at the fixed end w⁻(0) = 0, the following deflection equation is given in the plasticity part of the beam model, for $x^{*} \in \left[ {0;l_{0}^{*} } \right]$ where $l_{0}^{*} = l_{0P}^{*}$ or $l_{0}^{*} = l_{0Q}^{*}$ according to the considered model with a local or nonlocal kinematic boundary condition.

4.3.1 Load-induced deflection into the elastoplastic part of the beam

• In the case of local kinematic boundary condition, w⁻′(0) = 0, the dimensionless deflection solution $w_{P,K}^{ - *}$ and $w_{Q,K}^{ - *}$ in the plasticity zone are written as:

$$\frac{{w_{P,K}^{ - *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{P} }}{6}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left[ {\left( {1 - x^{*} } \right)^{3} - 1} \right] - \frac{{x^{*2} }}{{2k_{p}^{ + *} }} + \frac{{\beta_{P} }}{2}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)x^{*}$$

$$\begin{aligned} \frac{{w_{Q,K}^{ - *} }}{{\kappa_{y}^{*} }} & = \frac{{\beta_{Q} }}{12}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left[ {\left( {1 - x^{*} } \right)^{4} - 1} \right] \\ & \quad - \left[ {2l_{c}^{*2} \beta_{Q} \left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) + \frac{1}{{k_{p}^{ + *} }}} \right]\frac{{x^{*2} }}{2} + \frac{{\beta_{Q} }}{3}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)x^{*} \\ \end{aligned}$$

(45)

For the loading case composed of the concentrated load only, it is worth noting that the elastoplastic response is independent of the number of elements n and is, as a consequence, equivalent to the local response of the considered elastoplastic beam. This insensitivity to the microstructure is no more verified in presence of distributed loading.

• Using the cohesive law (also called static-equivalent) expressed at the clamped section, and based on w⁻(a) = w⁻(− a), leads to the alternative solution of $w_{P}^{ - *}$ and $w_{Q}^{ - *}$:

$$\frac{{w_{P,S}^{ - *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{P} }}{6}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left[ {\left( {1 - x^{*} } \right)^{3} - 1} \right] - \frac{{x^{*2} }}{{2k_{p}^{ + *} }} + \frac{{\beta_{P} }}{2}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left( {1 + \frac{1}{{3n^{2} }}} \right)x^{*}$$

$$\begin{aligned} & \frac{{w_{Q,S}^{ - *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{Q} }}{12}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left[ {\left( {1 - x^{*} } \right)^{4} - 1} \right] \\ & \quad \quad \quad - \left[ {2l_{c}^{*2} \beta_{Q} \left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) + \frac{1}{{k_{p}^{ + *} }}} \right]\frac{{x^{*2} }}{2} + \frac{{\beta_{Q} }}{3}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left( {1 + \frac{1}{{n^{2} }}} \right)x^{*} \\ \end{aligned}$$

(46)

It should be noted that when n → ∞, i.e., when the local case can be considered, both kinematic and static-equivalent boundary conditions yield the same results.

In the case of the static-equivalent boundary condition, it is worth noting that introducing x* = j/n where j is an integer as j ≤ q_0P or j ≤ q_0Q into Eq. (46) produces the exact lattice solution of the deflection at the node j previously established in Eq. (20) or in Eq. (22).

4.3.2 Deflection in the purely elastic part of the beam

The deflection in the whole of the nonlocal beam can be obtained by the integration of the curvature in the elastic part, whose integration constants are calculated from the kinematics boundary conditions at the elastic-elastoplastic interface. In the elastic part, the integration of the governing differential equation needs two boundary conditions, namely the kinematics continuity at the elastic–elastoplastic interface. The limit between the plastic and elastic part is located at x = l₀ where l₀ has already been defined as l_0P or l_0Q in the dimensionless relationship given in Eq. (14).

The deflection is assumed to be continuous at the elastic–elastoplastic interface, i.e., w⁻(l₀) = w⁺(l₀). Integrating the curvature twice from the bending moment curvature relationship in the elastic zone and taking into account this kinematic continuity condition gives the following equation of the dimensionless deflection $w_{P}^{ + *}$ and $w_{Q}^{ + *}$ within the elastic part:

$$\frac{{w_{P,K}^{ + *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{P} }}{6}\left[ {\left( {1 - x^{*} } \right)^{3} - \left( {1 - l_{0P}^{*} } \right)^{3} } \right] + B_{P1} \left( {x^{*} - l_{0P}^{*} } \right) + \frac{{w_{P}^{ - *} \left( {l_{0P}^{*} } \right)}}{{\kappa_{y}^{*} }}$$

$$\frac{{w_{Q,K}^{ + *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{Q} }}{12}\left( {1 - x^{*} } \right)^{4} - \beta_{Q} l_{c}^{*2} \left( {x^{*2} - l_{0Q}^{*2} } \right) + B_{Q1} \left( {x^{*} - l_{0Q}^{*} } \right) + \frac{{w_{Q}^{ - *} \left( {l_{0Q}^{*} } \right)}}{{\kappa_{y}^{*} }} - \frac{1}{{12\beta_{Q} }}$$

(47)

where B_P1 and B_Q1 are constant parameters to be defined according to the second boundary condition, which has to remain consistent with the condition considered in the plasticity zone.

• The local kinematic model simply considers the continuity of the rotation at the interface:$w^{ - \prime }\left( {l_{0}^{{}} } \right) = w^{ + \prime }\left( {l_{0}^{{}} } \right)$, and gives:

$$\begin{aligned} & B_{P1} = B_{PK} = \frac{{w_{P}^{ - * \prime }\left( {l_{0P}^{*} } \right)}}{{\kappa_{y}^{*} }} + \frac{1}{{2\beta_{P} }} = \frac{{\beta_{P} }}{2}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) + \frac{1}{{k_{p}^{ + *} }}\left( {\frac{1}{{2\beta_{P} }} - 1} \right)\;{\text{or}} \\ & B_{Q1} = B_{QK} = \frac{{\beta_{Q} }}{3}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right) - \frac{1}{{k_{p}^{*} }}\left[ {\frac{1}{{3\sqrt {\beta_{Q} } }} + \left( {1 - \frac{1}{{\sqrt {\beta_{Q} } }}} \right)\left( {2\beta_{Q} l_{c}^{*2} + 1} \right)} \right] \\ \end{aligned}$$

(48)

It should be noted that, in the loading case P, the complementary elastic deflection is independent of the number of elements n since it is equivalent to the local response. As a consequence, the kinematic boundary conditions, in such a case, lead to an elastoplastic response of the lattice system equivalent to the one of the local elastoplastic constitutive law, i.e., for n → ∞, plotted in Figs. 6 as 10, or in Fig. 7 as in Fig. 11.

Fig. 10

Comparison of the load-tip displacement of the full hardening–softening process of the elastoplastic bending lattice (n = 5) with the continualized model and with the local law in the case of a concentrated tip load, P

Fig. 11

Comparison of the load-tip displacement of the full hardening–softening process of the elastoplastic bending lattice (n = 5) with the continualized models and with the local law in the case of a uniformly distributed load, Q

In the loading case Q, at the yield point, β_Q → 1 leads to l_0Q → 0 and to B_QK → 1/3. As a consequence, Eq. (47) leads to:

$$w_{Q,K}^{ - *} (1) = \frac{{\kappa_{y}^{*} }}{4}\left( {1 - \frac{1}{{3n^{2} }}} \right)$$

(49)

As a consequence, unlike the loading case P, the local elastoplastic response obtained for n → ∞ and plotted in Fig. 7 departs from the local kinematic response, as shown in Fig. 11. This surprising stiffening result, already obtained in other studies of Eringen’s nonlocal beam response under distributed loading [8], slightly differs from the softening effect of the discreteness of the lattice system presented in Eq. (23). Actually, a nonlocal effect appears here in the elastic process with such a distributed load whereas it does not exist with a concentrated load [8]. As a consequence, the continualized nonlocal model with a local kinematic boundary condition does not give satisfactory results as compared to the exact lattice solution, see Figs. 11 and 16. The use of a static-based boundary condition formulated in terms of a cohesive law at the boundary is recommended to avoid this paradox.

• Static-equivalent conditions (viewed as non-local kinematic boundary conditions) lead to the same condition at the elastic–elastoplastic interface: w⁻(l₀ − a) = w⁺(l₀ − a), and/or w⁻(l₀ + a) = w⁺(l₀ + a), as previously shown and tested in the case of damage mechanics [23], which gives:

$$\begin{aligned} & B_{P1} = B_{PS} = \frac{1}{{k_{p}^{ + *} }}\left( {\frac{{\beta_{P} }}{2} + \frac{1}{{2\beta_{P} }} - 1} \right) + \frac{{\beta_{P} }}{2}\left( {1 + \frac{1}{{3n^{2} }}} \right)\;{\text{or}} \\ & B_{Q1} = B_{QS} = \frac{{\beta_{Q} }}{3}\left( {1 + \frac{1}{{k_{p}^{ + *} }}} \right)\left( {1 + \frac{1}{{n^{2} }}} \right) - \frac{1}{{3k_{p}^{ + *} \sqrt {\beta_{Q} } }}\left( {1 + \frac{{\beta_{Q} }}{{n^{2} }}} \right) - \frac{{2\beta_{Q} l_{c}^{*2} + 1}}{{k_{p}^{ + *} }}\left( {1 - \frac{1}{{\sqrt {\beta_{Q} } }}} \right) \\ \end{aligned}$$

(50)

Note that β_P → 1 leads to B_PS → (1 + 1/3n²)/2 and β_Q → 1 leads to B_QS → (1 + 1/n²)/3. As a consequence, Eq. (47) is in perfect accordance with Eqs. (21) and (23) since the yield tip deflection exactly matches the one of the discrete system. In this load distribution case, as already observed in a previous study [8], the nonlocal model obtained by continualization of the discrete system gives the exact response in the elastic process, but only if static-equivalent boundary conditions are considered (or lattice-based nonlocal boundary conditions, equivalent to cohesive boundary conditions).

Beyond the elastic point, the complementary elastic deflection, for $x^{*} \in \left[ {l_{0}^{*} ;1} \right]$ with $l_{0}^{*} = l_{0P}^{*}$ or $l_{0}^{*} = l_{0Q}^{*}$, can then be computed from Eq. (47) with the parameter B_PK or B_PS instead of B_P1 or with the parameter B_QK or B_QS instead of B_Q1, according to the loading case and the model examined. With such loading, the dimensionless normalized tip deflection ${{w^{ + *} } \mathord{\left/ {\vphantom {{w^{ + *} } {\kappa_{y}^{*} }}} \right. \kern-0pt} {\kappa_{y}^{*} }}$ is plotted in Figs. 10 and 11. It is possible to verify that in both cases, local kinematic or static, a perfect match between the elasticity and the elastoplastic solutions is obtained.

As previously mentioned in Sect. 4.3.1, at the nodes abscissa, the solution of the static equivalent model leads to the exact deflection of the discrete system in elastoplastic part as well as into the elastic part. As a consequence, if $\beta_{P} = {n \mathord{\left/ {\vphantom {n {\left( {n - j} \right)}}} \right. \kern-0pt} {\left( {n - j} \right)}}$, in case of concentrated tip load, P, or if $\beta_{Q} = \sqrt {{n \mathord{\left/ {\vphantom {n {\left( {n - j} \right)}}} \right. \kern-0pt} {\left( {n - j} \right)}}}$ in case of uniformly distributed load, Q, the limit between the elastic and the elastoplastic parts matches with a node coordinate, i.e., $l_{0P}^{*} = \left( {q_{0P} - 1} \right)/n$ or $l_{0Q}^{*} = \left( {q_{0Q} - 1} \right)/n$, the continualized nonlocal elastoplastic solution at the node abscissa perfectly matches the exact lattice response for both P and Q loading cases as shown in Figs. 10, 11, 12, 13, 14 and 15. Therefore, when the load increases into the elastoplastic range, l₀, the elastoplastic interface grows starting from the clamped section. When it matches with a node abscissa, the tip deflection computed with the static equivalent continualized equations are strictly equivalent with the response of the discrete system, see Fig. 16. For instance, this case can be specifically observed along the whole beam with β_P = 2/3 and n = 5 in Fig. 14.

Fig. 12

Deflection field along the whole elastoplastic bending lattice (n = 5) for three concentrated tip load values, β_P, ranging into the hardening stage

Fig. 13

Deflection field along the whole elastoplastic bending lattice (n = 5) for three uniformly distributed load values, β_Q, ranging into the hardening stage

Fig. 14

Difference between the deflection fields of the discrete system (n = 5) and those obtained from the continualized models for three concentrated tip load values, β_P, ranging into the hardening stage

Fig. 15

Difference between the exact deflection fields of the discrete system (n = 5) and those obtained from the continualized models for three uniformly distributed load values, β_Q, ranging into the hardening stage

Fig. 16

Relative difference between δ_sys., the load-tip displacement of the discrete system (n = 5) and δ, the tip displacements obtained from the continualized elastoplastic models, in both loading cases in the hardening stage

Note that for n → ∞, i.e., in the local case, with l_c → 0, and according to Eq. (50), B_PS → B_PK and B_QS → B_QK. As a consequence, as an asymptotic property of both nonlocal models, both boundary conditions lead to the same local model in the plastic and the elastic part of the beam. The dimensionless tip deflection computed according to this local model is also plotted as a reference in Fig. 10, 11, 12, 13, 14 and 15.

4.4 Complete collapse of the nonlocal elastoplastic beam: softening regime

After the peak load, a softening phase controls the behavior of the beam, composed of a softening cohesive law at the clamped boundary, a plasticity zone in unloading and an elastic complementary zone. The so-called cohesive boundary condition at the clamped section, (also previously presented as static equivalent boundary condition), has then to be considered in the softening regime.

4.4.1 Deflection in the elastoplastic part of the beam

Within the plasticity zone that is extended to its maximum length, i.e., for x* ≤ 1 − 1/m in case P or for x* ≤ 1 − m^−1/2 in case Q, the plastic curvature reached at the load peak remains constant and is equal to the maximum plastic curvature reached at the peak load, χ _max. In the softening range, for x* ∈ ]0;1 − 1/m] (concentrated tip load) or for $x^{*} \in \left[ {0;1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt m }}} \right. \kern-0pt} {\sqrt m }}} \right]$ (uniformly distributed load), the beam unloads elastically, and the following equation prevails:

$$\begin{aligned} & w_{P}^{ - \prime \prime } = \frac{PL}{EI}\left( {1 - \frac{x}{L}} \right) + \chi_{p\text{\,max} } \Rightarrow \frac{{w_{P}^{ - * \prime \prime }}}{{\kappa_{y}^{*} }} = \left( {\beta_{P} + \frac{m}{{k_{p}^{ + *} }}} \right)\left( {1 - x^{*} } \right) - \frac{1}{{k_{p}^{ + *} }} \\ & \frac{{w_{Q}^{ - * \prime \prime }}}{{\kappa_{y}^{*} }} = \left( {\beta_{Q} + \frac{m}{{k_{p}^{ + *} }}} \right)\left( {1 - x^{*} } \right)^{2} - 2\left[ {l_{c}^{*2} \left( {\beta_{Q} + \frac{m}{{k_{p}^{ + *} }}} \right) + \frac{1}{{2k_{p}^{ + *} }}} \right]\;{\text{with}}\;l_{c}^{2} = \frac{{a^{2} }}{12} \\ \end{aligned}$$

(51)

If the deflection at the clamped section is vanishing, i.e., w⁻(0) = 0, the dimensionless deflections $w_{P}^{ - *}$ and $w_{Q}^{ - *}$ within the plasticity part, assuming the second boundary condition (cohesive or static equivalent) relative to the known deflection of w⁻(a) or $w_{{}}^{ - *} \left( {{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}} \right)$ determined into Eq. (40), can be written as:

$$\begin{aligned} & \frac{{w_{P,S}^{* - } \left( {x^{*} } \right)}}{{\kappa_{y}^{*} }} = \frac{1}{6}\left( {\beta_{P} + \frac{m}{{k_{p}^{ + *} }}} \right)\left[ {\left( {1 - x^{*} } \right)^{3} - 1} \right] - \frac{1}{{2k_{p}^{ + *} }}x^{*2} + S_{P1} x^{*} \\ & {\text{with}}\;S_{P1} = \frac{n}{6}\left( {\beta_{P} + \frac{m}{{k_{p}^{ + *} }}} \right)\left[ {1 - \left( {1 - \frac{1}{n}} \right)^{3} } \right] + \frac{{\beta_{P} }}{2n}\left( {1 + \frac{1}{{k_{p}^{ - *} }}} \right) + \frac{m}{2n}\left( {\frac{1}{{k_{p}^{ + *} }} - \frac{1}{{k_{p}^{ - *} }}} \right) \\ \end{aligned}$$

and

$$\begin{aligned} & \frac{{w_{Q,S}^{ - *} }}{{\kappa_{y}^{*} }} = \frac{1}{12}\left( {\beta_{Q} + \frac{m}{{k_{p}^{ + *} }}} \right)\left[ {\left( {1 - x^{*} } \right)^{4} - 1} \right] - \left[ {l_{c}^{*2} \left( {\beta_{Q} + \frac{m}{{k_{p}^{ + *} }}} \right) + \frac{1}{{2k_{p}^{ + *} }}} \right]x^{*2} + S_{Q1} x^{*} \;{\text{with}} \\ & S_{Q1} = \left( {\beta_{Q} + \frac{m}{{k_{p}^{ + *} }}} \right)\left[ {\frac{{l_{c}^{*2} }}{n} + \frac{n}{12}\left( {1 - \left( {1 - \frac{1}{n}} \right)^{4} } \right)} \right] + \frac{{\beta_{Q} }}{2n}\left( {1 + \frac{1}{{k_{p}^{ - *} }}} \right) + \frac{m}{2n}\left( {\frac{1}{{k_{p}^{ + *} }} - \frac{1}{{k_{p}^{ - *} }}} \right) \\ \end{aligned}$$

(52)

where S_P1 and S_Q1 are constant parameters.

4.4.2 Deflection in the purely elastic part of the beam

The behavior remains purely elastic for $x^{*} \in \left[ {l_{0}^{*} ;1} \right]$ (where $l_{0}^{*} = l_{0P}^{*}$ or $l_{0}^{*} = l_{0Q}^{*}$) without any plastic curvature in this elastic domain. In the elastic part of the beam, the deflection can be easily computed from the bending moment–curvature constitutive law knowing the boundary conditions at the elastic–elastoplastic interface. The static-equivalent boundary conditions, as previously presented in Sect. 4.2, assume the deflection continuity as the first condition, i.e., $w_{P,S}^{ - *} \left( {1 - {1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0pt} m}} \right) = w_{P,S}^{ + *} \left( {1 - {1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0pt} m}} \right)$ or $w_{Q,S}^{ - *} \left( {1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt m }}} \right. \kern-0pt} {\sqrt m }}} \right) = w_{Q,S}^{ + *} \left( {1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt m }}} \right. \kern-0pt} {\sqrt m }}} \right)$ leading to:

$$\begin{aligned} & \frac{{w_{P,S}^{ + *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{P} }}{6}\left[ {\left( {1 - x^{*} } \right)^{3} - \frac{1}{{m^{3} }}} \right] + U_{P1} \left[ {x^{*} - \left( {1 - \frac{1}{m}} \right)} \right] + w_{P,S}^{ + *} \left( {1 - \frac{1}{m}} \right) \\ & \frac{{w_{Q,S}^{ + *} }}{{\kappa_{y}^{*} }} = \frac{{\beta_{Q} }}{12}\left[ {\left( {1 - x^{*} } \right)^{4} - \frac{1}{{m^{2} }}} \right] - \beta_{Q} l_{c}^{*2} \left[ {x^{*2} - \left( {1 - \frac{1}{\sqrt{m}}} \right)^{2} } \right] \\ & \quad \quad \quad + U_{Q1} \left( {x^{*} - 1 + \frac{1}{\sqrt{m}}} \right) + \frac{{w_{Q,S}^{ + *} \left( {1 - \frac{1}{\sqrt{m}}} \right)}}{{\kappa_{y}^{*} }} \\ \end{aligned}$$

(53)

where U_P1 and U_Q1 are constant parameters, defined according to the loading case P or Q respectively. The second boundary condition, of a static-equivalent type, i.e., $w_{P,S}^{ - *} \left( {1 - {1 \mathord{\left/ {\vphantom {1 {m + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}}} \right. \kern-0pt} {m + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}}} \right) = w_{P,S}^{ + *} \left( {1 - {1 \mathord{\left/ {\vphantom {1 {m + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}}} \right. \kern-0pt} {m + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}}} \right)$ or $w_{Q,S}^{ - *} \left( {1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt m + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}}} \right. \kern-0pt} {\sqrt m + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}}} \right) = w_{Q,S}^{ + *} \left( {1 - {1 \mathord{\left/ {\vphantom {1 {\sqrt m + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}}} \right. \kern-0pt} {\sqrt m + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}}} \right)$ gives.

$$\begin{aligned} & U_{P1} = \frac{nm}{{6k_{p}^{ + *} }}\left[ {\left( {\frac{1}{m} - \frac{1}{n}} \right)^{3} - \frac{1}{{m^{3} }}} \right] - \frac{1}{{k_{p}^{ + *} }}\left( {1 - \frac{1}{m}} \right) - \frac{1}{{2nk_{p}^{ + *} }} + S_{P1} \;{\text{and}} \\ & U_{Q1} = \frac{nm}{{12k_{p}^{ + *} }}\left[ {\left( {\frac{1}{\sqrt{m} } - \frac{1}{n}} \right)^{4} - \frac{1}{{m^{2} }}} \right] - \left( {2ml_{c}^{*2} + 1} \right)\left( {1 - \frac{1}{\sqrt{m}} + \frac{1}{2n}} \right)\frac{1}{{k_{p}^{ + *} }} + S_{Q1} \\ \end{aligned}$$

(54)

where S_P1 and S_Q1 are the constant parameters previously defined into Eq. (52).

The dimensionless deflection can then be computed during the softening stage in the complementary elastic part of the beam. The normalized dimensionless tip deflection, δ/δ_y, of the full hardening–softening process are presented with respect to the dimensionless load parameter β_P and β_Q in Figs. 10 and 11. It should be noted that if unloading or softening occurs when the elastoplastic interface, i.e. l₀, matches a node abscissa, the tip deflection obtained with static equivalent continualized model is exactly equivalent to the one of the discrete system during unloading or in the softening regime.

In the local case, n → ∞, l_c→ 0, the softening plastic zone tends to vanish and the elastic unloading prevails. The dimensionless deflection, computed from Eqs. (53) and (54) when n → ∞, confirms that ${{\partial \delta_{y,P}^{*} } \mathord{\left/ {\vphantom {{\partial \delta_{y,P}^{*} } {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} = {{\kappa_{y}^{*} } \mathord{\left/ {\vphantom {{\kappa_{y}^{*} } 3}} \right. \kern-0pt} 3}$ and ${{\partial \delta_{y,Q}^{*} } \mathord{\left/ {\vphantom {{\partial \delta_{y,Q}^{*} } {\partial \beta }}} \right. \kern-0pt} {\partial \beta }} = {{\kappa_{y}^{*} } \mathord{\left/ {\vphantom {{\kappa_{y}^{*} } 4}} \right. \kern-0pt} 4}$ as obtained initially with the exact elastic solution in Eqs. (21) and (23). As shown in Figs. 6 and 7, the softening response of the system strongly depends on the number of elements, n. For sufficiently large values of n, the snap-back response is observed with a complete unloading behavior. This phenomenon, known as Wood’s paradox [28, 29], is also clearly exhibited in both loading cases, in Fig. 10 as in Fig. 11.

5 Discussion of the results

With the linear hardening of elastoplastic lattices, the continuous nonlocal elastoplastic moment–curvature law coupled with the cohesive-type boundary conditions is the most efficient of the nonlocal continualization process. In the presented cases, the static equivalent continualized model always gives the deflection or displacement, in the elastoplastic zone, at the node abscissa of the discrete system used as a reference. Furthermore, if the load makes the elastic–elastoplastic interface coincides with a node abscissa, in the elastic part, the solution in the overall beam coincides at the lattice nodes for both the lattice and the nonlocal continuous systems. As a consequence, when the maximum load makes this interface coincide with a node abscissa, the continualized softening tip deflection also exactly matches the discrete response, which is not the case in Figs. 10 and 11 as shown in detail in Fig. 16.

In the nonlinear hardening case, these specific properties would not be valid anymore. As already observed in the case of unidimensional elastic damage lattices [8], static-equivalent boundary conditions would give the most consistent results, while the exact deflection or displacement of the equivalent continuous media at the node abscissa departs slightly from the discrete system in the non-linear part.

This formulation is able to capture the scale effects of such lattices. It clearly shows that the characteristic length scale of the equivalent nonlocal continuous media is intrinsic for each microstructured system. It is load independent. It is also expected that the nonlocal length scale could depend on the physics (discreteness of the matter in a small scale) and the order of the difference equations associated with the inelastic lattice mechanics.

As a possible extension to this study, a one-dimensional axial problem has to be considered in order to show that characteristic length is associated with the square length of the considered periodic elements, a², of the discrete system.

According to the physical parameter examined, such as the axial displacement of the stretched fiber inside the beam or its whole deflection, the characteristic length scale of the equivalent continuous media is intrinsic for each microstructured system and is load independent. However, it should strongly depend on the degree of the differential equation linking the physical values of the macroscopic continuous medium, asymptotically obtained for an infinite number of cells.

6 Conclusion

In this paper, we have investigated the bending of an elastoplastic lattice beam (also called elastoplastic Hencky Bar-Chain or HBC system) for different loading configurations. The lattice system is composed of piecewise linear hardening–softening elastoplastic hinges (or rotational springs) connected to some rigid elements. This lattice system may be referred to as a lattice system that includes only the nearest neighbors for the elastoplastic interaction. Solutions of the elastoplastic lattice equations have been obtained exactly for the piecewise linear hardening–softening law.

A nonlocal elastoplastic theory has been built from the lattice difference equations using a continualization process. It has been demonstrated that the new nonlocal elastoplastic theory depends on additional length scale rigorously calibrated from the spacing of the lattice model. This nonlocal elastoplastic system has not been derived in the literature to the authors’ knowledge. A lattice-dependent cohesive elastoplastic law governs the response in the softening regime. The new micromechanics-based model possesses some nonlocality for the constitutive law, but preserves the local nature of the plasticity loading function. A comparison of the results obtained from the new engineering beam model with the lattice model illustrates the efficiency of the new nonlocal elastoplastic model, especially for capturing the scale effects inherent in the lattice model (considered to be the reference model). The hardening–softening localization process strongly depends on the lattice spacing.

General elastoplastic interactions at the microlevel can be examined, in order to derive a more general nonlocal elastoplasticity model. The results presented in this paper, valid for elastoplastic HBC systems, may be extended to axial elastoplastic lattices. This study can be seen as a first step towards the foundation of a more general theory of lattice-based nonlocal elastoplastic structural models.