Multibody dynamics system with energy dissipation by hardening and softening plasticity

Abstract

In this work we present a multibody dynamics system composed of geometrically exact nonlinear beams with inelastic behavior, representing flexible system components. The main focus of the work is to introduce advanced energy dissipation models using hardening and softening plasticity into such beam models and to show how they can also recover a vibration amplitude decay typical of viscous damping. The damping model is represented by the constitutive behavior of the flexible beam element chosen as an elasto-viscoplastic response with linear isotropic hardening and subsequent softening plasticity. The formulation is cast within the mixed variational framework, where the strong embedded discontinuity is introduced into displacement/rotation fields in the softening phase leading to localized plastic deformation. We also aim to ensure model capabilities to deliver results for long-term loading simulations, which is of interest for quantifying the risk of fatigue failure for such flexible system component. The corresponding numerical implementation combines the space discretization based on the finite element method with the time discretization based upon energy-conserving or energy-decaying integration schemes. The results of several numerical simulations are presented in the dynamics of flexible-rigid multi-body systems to illustrate a very satisfying performance of the proposed model.

1 Introduction

In this paper we propose the model that can be used for studying the integrity and durability of flexible multibody dynamics systems exposed to long-term loads including extreme events that can also lead to very large motion. To develop a predictive model for large motion, we use an extension of the geometrically exact beam (e.g., [5, 6, 13, 22]). The main novelty introduced here concerns the development of a damping model that is based on viscoplastic constitutive behavior that can also recover typical vibration amplitude decay by including the system material heterogeneities [20, 21]). We also aim at using the proposed model in durability studies by time-integration schemes. Thus, to ensure the stability of long-term computation needed to provide the fatigue failure estimates, we also revisit the time-integration schemes for energy-conserving and energy decaying (e.g., [3, 4, 9, 15, 16, 19, 26, 27]) to carry out the novel developments pertinent to viscoplasticity with both hardening and softening behavior. We note that the choice of viscoplasticity plays a crucial role in enforcing this extension that guarantees the computation stability for second-order schemes, with no operator split as in the previous works (e.g., [1, 14]).

The first main novelty concerns the inelastic constitutive material response of the combined hardening and softening plasticity developed for multibody system with flexible beam components in the dynamics framework. This development is more demanding from the previous version available for small strain case [14] for it has to handle the nonlinear kinematics setting of geometrically exact beam. We note that the softening response produces localized plastic behavior similar to those of plastic beam hinges, which can be used to replace revolute joints. The classical manner of introducing kinematic constraints corresponding to different kinds of joints in a multibody system (e.g., see [18]) employs the Lagrange multiplier method. In comparison with the perfect kinematic joints [18], we utilize nonlinear material formulation to develop a plastic hinge that gradually turns into a perfect joint (with no resistance), seeking to represent an emergency stop. The corresponding formulation is based upon the incompatible modes approach, where we choose to enrich the rotation field of the two-node beam element. Such an approach offers the possibility to include different types of nonlinear material behavior inside the hinge. The chosen fracture energy for the beam hinge will determine its particular response, whether as the plastic hinge with resistance or as a kinematic revolute joint without any resistance with respect to rotation.

The second main novelty pertains to enforcing the computations stability over a long time period where an inelastic response of the flexible multibody system can occur. The classical Newmark time integration scheme and other related schemes do not remain stable for long-time computations since they do not provide a suitable choice when dealing with stiff problems (with a large difference in tangent stiffness components), which can be introduced by the difference between plastic loading and elastic unloading. A partially successful solution is provided by the energy-conserving time integration scheme, which was discussed in several previous works on 3D beams in elastodynamics (e.g., see [3, 9, 17, 19]). Such a scheme is using a mid-point algorithm to time-integrate equations of motion while enforcing the energy conservation in the discrete approximation setting, which ensures that the computations can be carried out over a long period of time. The occurrence of high-frequency modes in the calculation of stiff problems can reduce the robustness of the energy-conserving scheme, especially if the stress computations are of interest, which is the case in plasticity. The pollution of output results by high-frequency oscillation was shown in [19] for elastodynamics, where an energy-decaying algorithm was proposed. This development serves as the starting point of the development presented herein, where we adapt the energy decaying scheme to inelasticity.

The crucial choice for the time-integration accuracy pertains to choosing the rate-dependent viscoplastic behavior in dynamics, characterizing the constitutive model of the flexible beam. By choosing the viscoplastic behavior, we can integrate simultaneously the global motion equations and local viscoplastic evolution equations to ensure the second-order accuracy. The computations in viscoplasticity are based upon Duvaut–Lions approach [8, 14], which is more robust (for a large value of viscosity) than an alternative Perzyna viscoplasticity model [14, 28]. The plastic dissipation in inelastic response can be considered as a physically-based damping model, which can recover the exponential decay when we account for heterogeneities (e.g., see [20, 21]).

The paper outline is as follows. The variational formulation of the geometrically exact beam in the dynamics framework is constructed by employing mixed Hu–Washitzu functional presented in Sect. 2. The highly nonlinear problem in the sense of kinematics and material behavior is restricted to finite strain theory. The numerical implementation and corresponding solution schemes, which ensure long-term computation in dynamics, are given in Sect. 3. Several numerical examples that pertain to static and dynamic responses, which verify beam behavior, are illustrated in Sect. 4. In Sect. 5 we offer a discussion of the obtained results and draw conclusions.

2 Variational formulation of geometrically exact beam

In this section we briefly present governing equations of the geometrically exact beam fitting within the large gradient displacement framework by extending previous works on Reissner’s beam development by Ibrahimbegovic and co-workers [17]. Here we propose the mixed variational formulation to provide a mere sound formulation to embedded discontinuity approach that allowed the development of elastoplastic hinge in statics. We present an extension of the elastoplastic Reissner’s beam to dynamics. This requires the novel development of nonlinear material behavior where a viscoplastic model is used to be able to provide the second-order scheme suitable for long-term simulations. The viscoplasticity is also related to the development of a new damping model based on inelastic material behavior in hardening and softening.

2.1 Beam kinematics

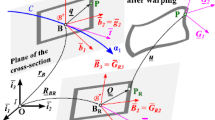
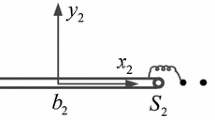
The initial beam configuration of the length $L$ is described by the neutral axis position $s$ and the corresponding cross-section $A$. The beam volume is generated by sweeping the cross-section $A$ along beam neutral axis domain $s \in [0,L]$, see Fig. 1. Let the beam domain $\Omega$ be an open bounded set with a piece-wise smooth boundary such that $\partial \Omega=\partial \Omega_{u} \cup \partial \Omega_{\sigma}$ and $\emptyset =\partial \Omega_{u} \cap \partial \Omega_{\sigma}$. The intrinsic parametrization of the shear-flexible beam is done with a set of generalized coordinates $u(x)$, $v(x)$, and $\psi (x)$, which describe the beam cross-section position and its orientation. The beam initial configuration is specified by position vector $\textbf{x}$, which describes a point on the neutral axis and orthonormal basis in the initial configuration with unit vectors $\textbf{e}_{i}$. We choose unit vector $\textbf{e}_{1}$ is orthogonal to the beam cross-section in the initial configuration of the beam. The neutral axis tangent then can be written as

$$ \textbf{e}_{1} = \textbf{x}'; \quad \textbf{e}_{2}^{T} \cdot \textbf{e}_{1} = 0, $$

(1)

where notation $(\bullet )'=\partial{(\bullet )}/{\partial s}$ indicates derivative with respect to $s\equiv x$. The deformed configuration produced by the planar motion of the beam to a new position is described by position vector $\boldsymbol{\upphi}$ defined as

$$ \boldsymbol{\upphi}=\boldsymbol{\upvarphi} + x_{2}\textbf{t}_{2}; \quad \boldsymbol{\upvarphi} = (x+u)\textbf{e}_{1}+(y+v)\textbf{e}_{2}, $$

(2)

where $\boldsymbol{\upvarphi}: \Omega \rightarrow \mathbb{R}^{2}$, $\textbf{t}_{2}$ and $x_{2}\in A$ are, respectively, a position vector of the neutral axis in the deformed configuration, a unit vector placed in the cross-sectional plane, and the corresponding cross-sectional parameter. By taking into account the shear flexibility of the beam, we note that Eq. (1) no longer holds in the deformed configuration since the neutral axis tangent $\boldsymbol{\upvarphi}'$ and the unit normal vector $\textbf{t}_{2}$ placed in the cross-section are no longer orthogonal

$$ \textbf{t}_{2}^{T}\cdot \boldsymbol{\upvarphi}' \neq 0; \quad \boldsymbol{\upvarphi}'=\left (1+\frac{\partial u}{\partial x}\right ) \textbf{e}_{1} + \frac{\partial v}{\partial x}\textbf{e}_{2} $$

(3)

The orthogonal transformation $SO(2)$ that brings basis $\text{e}_{i}$ to $\text{t}_{i}$ resolved can be represented by rotation tensor $\boldsymbol{\Lambda}(\psi ): \text{e}_{i} \rightarrow \text{t}_{i}$ with the components that are given as follows:

$$ \boldsymbol{\Lambda}=\textbf{t}_{i}\otimes \textbf{e}_{i} \quad \Rightarrow \quad \textbf{t}_{i}=\boldsymbol{\Lambda}\textbf{e}_{i}; \quad \boldsymbol{\Lambda}= \begin{bmatrix} \cos{\psi} & -\sin{\psi} \\ \sin{\psi} & \cos{\psi} \end{bmatrix} . $$

(4)

The spatial strain measure for shear flexible beams with curvature represents the difference between beam neutral axis tangent $\boldsymbol{\varphi}'$ and cross-section unit normal $\textbf{t}_{1}$ (see Fig. 1), which is defined as

$$ \begin{aligned} \boldsymbol{\upvarepsilon}= \begin{Bmatrix} \boldsymbol{\epsilon} \\ \boldsymbol{\kappa} \end{Bmatrix} = \begin{Bmatrix} \boldsymbol{\upvarphi}' - \textbf{t}_{1} \\ \psi ' \textbf{e}_{3} \end{Bmatrix}, \end{aligned} $$

(5)

where $\boldsymbol{\epsilon}$ and $\boldsymbol{\kappa}$ represent axial, shear, and curvature strain components in the deformed configuration, respectively. The material form of the strain measure can be obtained through a pull-back operation [25] applied to the spatial strain measure given in Eq. (5)

$$ \begin{aligned} \textbf{E}&=\boldsymbol{\Lambda}^{T} \boldsymbol{\epsilon}; \\ K&=\kappa ; \end{aligned} \quad \Rightarrow \quad \textbf{E}= \begin{Bmatrix} E_{1} \\ E_{2} \end{Bmatrix} = \begin{Bmatrix} \left (1+ \frac{\partial u}{\partial x} \right ) \cos \psi + \frac{\partial v}{\partial x} \sin \psi - 1 \\ -(1+\frac{\partial u}{\partial x})\sin \psi + \frac{\partial v}{\partial x} \cos \psi \end{Bmatrix} . $$

(6)

Fig. 1

Beam kinematics: Initial and deformed configuration

2.2 Constitutive equations

By employing the simplest constitutive law of linear elasticity, one can state stress resultant forces $N$ and moment $M$ in the material description

$$ \begin{aligned} \textbf{N}&=\mathbb{C}_{n}\textbf{E}; \quad \mathbb{C}_{n}=diag(EA, GA) \\ M&=\mathbb{C}_{m} K; \quad \mathbb{C}_{m}=EI, \end{aligned} $$

(7)

where the strains $\textbf{E}$ and $M$ are given in (6). The spatial forces $\textbf{n}$ and moment $\textbf{m}$ representation can be expressed by pushing forward material stress resultants in (7)

$$ \begin{aligned} \textbf{n}&=\boldsymbol{\Lambda}\textbf{N}; \\ \textbf{m}&=M\textbf{e}_{3}; \end{aligned} \quad \quad \quad \begin{aligned} \boldsymbol{\epsilon}&=\boldsymbol{\Lambda}\textbf{E}; \\ \boldsymbol{\kappa}&=K\textbf{e}_{3}; \end{aligned} $$

(8)

where the work conjugate strain measures in spatial description are $\boldsymbol{\epsilon}$ and $\boldsymbol{\kappa}$. The internal strain energy of the geometrically exact beam can be stated by using the result in Eq. (6)

$$ \begin{aligned} \Pi^{int} &=\frac{1}{2} \int _{L} {\left ( \boldsymbol{\epsilon}^{T} \cdot \textbf{n} + \boldsymbol{\kappa}^{T} \cdot \textbf{m}\right )}ds \\ &=\frac{1}{2}\int _{L} {\left ( \textbf{E}^{T} \cdot \textbf{N} + K M \right )} ds \\ &=\frac{1}{2}\int _{L} {\left (E_{1}N_{1}+E_{2}N_{2}+KM\right )} ds. \end{aligned} $$

(9)

The internal virtual work can be recast in an alternative form of material strain measure proposed by Reissner [29] $\boldsymbol{\Sigma}=\left (\Sigma , \Gamma , K \right )^{T}$. To obtain the Biot strain measure, we begin with the spatial strain measure $\boldsymbol{\epsilon}$ as shown in Eq. (5):

$$ \begin{aligned} \boldsymbol{E} &= \boldsymbol{\Lambda}^{T} \boldsymbol{\epsilon} \\ K &=\kappa \end{aligned} \quad \Rightarrow \quad \begin{aligned} \textbf{H} = \begin{bmatrix} \Sigma - x_{2}K & 0 \\ \Gamma & 0 \end{bmatrix} . \end{aligned} $$

(10)

Applying a pull-back transformation to the first Piola–Kirchhoff stress $\textbf{P}$, we can obtain work conjugate Biot stress $\textbf{T}$ to the Biot strain measure $\textbf{H}$:

$$ \textbf{T}\textbf{e}_{1} = \boldsymbol{\Lambda}^{T} \textbf{P}\textbf{e}_{1} \quad \Rightarrow \quad \begin{Bmatrix} T^{11} \\ T^{21} \end{Bmatrix} = \boldsymbol{\Lambda}^{T} \begin{Bmatrix} P^{11} \\ P^{21} \end{Bmatrix} . $$

(11)

The corresponding form of internal virtual work is given as follows:

$$ \begin{aligned} G^{int}&:= \int _{L} \int _{A} {{\delta \textbf{F} : \textbf{P}}dA}ds= \int _{L} \int _{A} {{\delta \textbf{H} : \textbf{T}}dA}ds \\ & = \int _{L} {\left ( \delta \Sigma N + \delta \Gamma V + \delta K M \right )}ds, \end{aligned} $$

(12)

where $\delta \textbf{F}$ and $\delta \textbf{H}$ are virtual deformation gradient and Biot strain tensor, respectively. The internal vector of forces and moment $\textbf{r}=\left (N,V,M \right )^{T}$ in Eq. (12) is defined as follows:

$$ N=\int _{A} {T^{11}}dA; \quad V=\int _{A} {T^{21}}dA; \quad M=-\int _{A} {x_{2}T^{11}}dA. $$

(13)

2.3 Extension to the dynamics

Here we present an extension of Reissner’s beam model to fit within the dynamics framework. The inertial velocity vector of the material point can be found by taking the time derivative of the position vector in Eq. (2)

$$ \dot{\boldsymbol{\upphi}} = \dot{\boldsymbol{\upvarphi}}+ x_{2} \dot{\textbf{t}}_{2}, $$

(14)

where the notation $\dot{(\bullet )}=\partial (\bullet ) \ \partial t$ indicates derivative with respect to time. The time derivative of position vector $\boldsymbol{\upvarphi}$ represents the material velocity of points located on the neutral axis, for which one can write

$$ \dot{\boldsymbol{\upvarphi}}= \dot{u}\textbf{e}_{1}+\dot{v}\textbf{e}_{2}, $$

(15)

while direction change of unit base vectors $\textbf{t}_{i}$ in time represents material velocity of rotating frame. It can be shown that the time derivative of the orthogonal matrix $\boldsymbol{\Lambda}$ is given by the skew-symmetric matrix $\textbf{W}$

$$ \begin{aligned} \dot{\boldsymbol{\Lambda}}=\dot{\psi} \frac{\partial \boldsymbol{\Lambda}}{\partial \psi}=\dot{\psi} \textbf{W} \boldsymbol{\Lambda}; \quad \textbf{W}= \begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}. \end{aligned} $$

(16)

The result in Eq. (16) leads to a time derivative of unit vectors $\textbf{t}_{i}$, which can be stated

$$ \begin{aligned} \dot{\textbf{t}}_{i} &=\dot{\psi} \frac{\partial \boldsymbol{\Lambda}}{\partial t} \textbf{e}_{i}= \dot{\psi} \textbf{W} \boldsymbol{\Lambda} \textbf{e}_{i}=\dot{\psi} \textbf{W} \textbf{t}_{i} \quad \Rightarrow \quad \begin{Bmatrix} \dot{\textbf{t}}_{1} \\ \dot{\textbf{t}}_{2} \end{Bmatrix} = \dot{\psi} \begin{Bmatrix} \textbf{t}_{2} \\ -\textbf{t}_{1} \end{Bmatrix} . \end{aligned} $$

(17)

With the help of the result in Eq. (15) and (17), the kinetic energy of the beam can be written as a quadratic form

$$ \begin{aligned} K=\frac{1}{2} \int _{L} {\int _{A} {\rho \dot{\boldsymbol{\upphi}}^{T} \cdot \dot{\boldsymbol{\upphi}}}dA}ds = \frac{1}{2} \int _{L} \left ( A_{\rho}\dot{\boldsymbol{\upvarphi}}^{T} \cdot \dot{\boldsymbol{\upvarphi}} + J_{\rho} \dot{\psi}^{2} \right )ds, \end{aligned} $$

(18)

where $A_{\rho} = \int _{A} {\rho} dA$ and $J_{\rho} = \int _{A} {x_{2}^{2}\rho}dA$ are the mass of the beam and the cross-section moment of inertia, respectively. The total system energy is constructed as a Hamiltonian functional or a sum of kinetic and potential energy as a function of the generalized coordinates and their time derivatives:

$$ H(\boldsymbol{\upvarphi},\psi ;\dot{\boldsymbol{\upvarphi}}, \dot{\psi})= K(\dot{\boldsymbol{\upvarphi}},\dot{\psi})+\Pi( \boldsymbol{\upphi},\psi ). $$

(19)

Dynamic equilibrium can be obtained by finding a variation of the energy functional in Eq. (19), and by applying Hamilton’s principle, we can state the weak form of equilibrium equations in spatial description

$$ \begin{aligned} G(\boldsymbol{\upvarphi},\psi ;\delta \boldsymbol{\upvarphi},\delta \psi ) &:= \int _{L} {\left (\delta \boldsymbol{\upvarphi}^{T} \cdot A_{\rho} \ddot{\boldsymbol{\upvarphi}} + \delta \psi \cdot J_{\rho} \ddot{\psi}\right )}ds \\ &+ \int _{L} {\left ( \mathcal{L}_{\delta} (\boldsymbol{\epsilon})^{T} \cdot \textbf{n} + \mathcal{L}_{\delta} (\boldsymbol{\kappa})^{T} \cdot \textbf{m} \right )}ds - G^{ext}=0, \end{aligned} $$

(20)

where the virtual part of spatial strains $\mathcal{L}_{\delta} (\boldsymbol{\epsilon})$ and $\mathcal{L}_{\delta} (\boldsymbol{\epsilon})$ is obtained by push-forward (e.g., see [12]) variation of material strains defined in Eq. (6)

$$ \begin{aligned} \mathcal{L}_{\delta} (\boldsymbol{\epsilon}) &= \boldsymbol{\Lambda} \frac{d}{dt} \left [ \boldsymbol{\Lambda}_{t}^{T} (\upvarphi - \textbf{t}_{1,t}) \right ]|_{t=0} = \delta \boldsymbol{\upvarphi}' - \delta \psi \textbf{W} \boldsymbol{\upvarphi}' \\ \mathcal{L}_{\delta} (\boldsymbol{\epsilon}) &= \textbf{I}\frac{d}{dt} \left [ \textbf{I} \psi \right ]|_{t=0} =\delta \psi ' \textbf{e}_{3} . \end{aligned} $$

(21)

The time derivative of the material strains in Eq. (6) can be computed as follows:

$$ \dot{\textbf{E}}= \boldsymbol{\Lambda}^{T} (\textbf{v}' - \textbf{W} \boldsymbol{\upvarphi}' \omega ); \quad \dot{K}=\omega ', $$

(22)

where $\textbf{v}=\dot{\boldsymbol{\upvarphi}}$ and $\omega =\dot{\psi}$ are linear and angular velocities, respectively. By using the result in Eq. (22), we can rewrite the weak equilibrium in Eq. (20)

$$ 0 = \int _{L} {\left (\textbf{v}^{T} \cdot A_{\rho} \dot{\textbf{v}} + \omega \cdot J_{\rho} \dot{\omega}\right )}ds + \int _{L} {\left ( \dot{\textbf{E}}^{T} \cdot \textbf{N} + \dot{K} \cdot M \right )}ds, $$

(23)

which further yields the important property of conservation of total energy in Eq. (19):

$$ \frac{\partial}{\partial t} H(\boldsymbol{\upvarphi},\psi ; \dot{\boldsymbol{\upphi}},\dot{\psi})= G(\boldsymbol{\upvarphi},\psi ; \dot{\boldsymbol{\upphi}},\dot{\psi})=0 \quad \Rightarrow \quad H( \boldsymbol{\upvarphi},\psi ;\dot{\boldsymbol{\upphi}},\dot{\psi})= cst. $$

(24)

2.4 Mixed variational functional of multibody with elastoplastic joints

We first recall that the standard multibody system, e.g., the system with revolute joint, can be introduced by the Lagrange multiplier method as an additional kinematic constraint, e.g., we refer to the previous works of Ibrahimbegovic and co-workers (see [18, 23]). Here we are seeking to accommodate the supplement of a perfect plastic hinge. To achieve this, we propose an elastoplastic hinge with a softening behavior, which is used to control dissipation and damping to reduce vibrations. We present the implementation of such a hinge with an embedded discontinuity approach in the finite strain setting by enriching the polynomial basis of the beam element. Assuming that the displacement gradient $\nabla \textbf{u}$ is given as a separate dependent variable $\textbf{D}$

$$ \textbf{D} = \nabla \textbf{u} \quad \Rightarrow \quad \nabla \boldsymbol{ \upphi} = \textbf{I} + \textbf{D,} $$

(25)

with a convenient choice of enhancement of strain field, we can exploit a feature of increased order of interpolation without increasing the number of nodes, see (Fig. 2). This will provide more robustness of the element with respect to the distortion. The mixed form of variational (Hu–Washitzu) functional defined with three independent fields can be written as follows:

$$ \begin{aligned} \Pi (\boldsymbol{\upphi},\textbf{D},\textbf{P}) &= \int _{L} {\int _{A} { W\left (\textbf{I} + \textbf{D} \right )}dA} ds \\ & + \int _{L} {\int _{A} {\textbf{P}: \left (\nabla \boldsymbol{\upphi} - \left (\textbf{I} + \textbf{D} \right )\right )}dA}ds - \Pi^{ext}(\boldsymbol{\upphi}) \end{aligned} $$

(26)

where $\nabla \boldsymbol{\upphi} \in \mathcal{F}$, $\textbf{D} \in \mathcal{D}$, and $\textbf{P} \in \mathcal{P}$ are respectively trial deformation gradient, enhanced displacement gradient, and internal stress resultant field. The variational functional in Eq. (26) is less demanding with respect to the regularity of the internal stress field $\textbf{P}$ and displacement gradient $\textbf{D}$, which needed not be continuous, but only square integrable over the domain $\Omega$, which is denoted as $L_{2} (\Omega)$

$$ \begin{aligned} \mathcal{D}=\left \lbrace \textbf{D}|\textbf{D} \in L_{2} ( \Omega) \right \rbrace ; \quad \mathcal{P}=\left \lbrace \textbf{P}| \textbf{P} \in L_{2} (\Omega) \right \rbrace . \end{aligned} $$

(27)

However, the displacement field $\boldsymbol{\upphi}$ must belong to the $H_{0}^{1}(\Omega)$ with square-integrable derivatives

$$ \begin{aligned} \mathcal{F}=\left \lbrace \boldsymbol{\upphi}| \boldsymbol{\upphi} \in H_{0}^{1}(\Omega) \right \rbrace \end{aligned} . $$

(28)

The corresponding Euler–Lagrange equations can be obtained by taking variations with respect to the displacement $\boldsymbol{\upphi}$, displacement gradient $\textbf{D}$, and stress field $\textbf{P}$

$$ \begin{aligned} G_{\upphi} (\boldsymbol{\upphi},\textbf{D},\textbf{P}; \delta \boldsymbol{\upphi}) &:= \int _{L} { \int _{A} {\textbf{P} : \delta \nabla \boldsymbol{\upphi}} dA} ds - G^{ext}(\delta \boldsymbol{\upphi}) \\ G_{D} (\boldsymbol{\upphi},\textbf{D},\textbf{P};\delta \textbf{D}) &:= \int _{L} {\int _{A}{\left ( \frac{\partial W\left (\textbf{I}+ \textbf{D} \right )}{\partial \textbf{D}} - \textbf{P}\right ):\delta \textbf{D}}dA} ds \\ G_{P} (\boldsymbol{\upphi},\textbf{D},\textbf{P};\delta \textbf{P}) &:= \int _{L} {\int _{A}{\delta \textbf{P} : \left ( \nabla \boldsymbol{\upphi} - (\textbf{I} + \textbf{D})\right )}dA} ds, \end{aligned} $$

(29)

where $\delta \boldsymbol{\upphi}$, $\delta \textbf{D}$, and $\delta \textbf{P}$ are, respectively, virtual displacement, virtual displacement gradient, and virtual stress. We chose here virtual displacement gradient as the sum of the compatible and incompatible part

$$ \textbf{D} = \nabla \bar{\boldsymbol{\upphi}} + \bar{\bar{\textbf{D}}}. $$

(30)

After inserting Eq. (30) into Eq. (26), a new variational formulation is obtained, in which displacement and internal stress resultant serve as independent state variables, which can be written as follows:

$$ \Pi (\bar{\boldsymbol{\upphi}},\bar{\bar{\textbf{D}}}, \textbf{P}) := \int _{L} {\int _{A}{W \left (\textbf{I} + \nabla \bar{\boldsymbol{\upphi}} + \bar{\bar{\textbf{D}}} \right )}dA} ds - \int _{L} {\int _{A}{\textbf{P} : \bar{\bar{\textbf{D}}}}dA} ds - \Pi^{ext}(\boldsymbol{\upphi}). $$

(31)

To be consistent with notation, we denote by $(\bar{\bullet})$ and $(\bar{\bar{\bullet}})$ compatible and incompatible parts, respectively. The corresponding weak form of the equilibrium equations can be obtained from the modified Hu–Washitzu functional in Eq. (31)

$$ \begin{aligned} G_{\bar{\upphi}} (\bar{\boldsymbol{\upphi}}, \bar{\bar{\textbf{D}}},\textbf{P};\delta \bar{\boldsymbol{\upphi}}) &:= \int _{L} { \int _{A} { \frac{\partial W \left ( \textbf{I} + \nabla \bar{\boldsymbol{\upphi}} + \bar{\bar{\textbf{D}}}\right )}{\partial \nabla \bar{\boldsymbol{\upphi}}} : \delta \nabla \bar{\boldsymbol{\upphi}}}dA} ds - G^{ext}(\delta \bar{\boldsymbol{\upphi}}) \\ G_{\bar{\bar{ D}}} (\bar{\boldsymbol{\upphi}},\bar{\bar{\textbf{D}}}, \textbf{P};\delta \bar{\bar{\textbf{D}}}) &:= \int _{L}{\int _{A} { \left ( \frac{\partial W \left ( \textbf{I} + \nabla \bar{\boldsymbol{\upphi}} + \bar{\bar{\textbf{D}}}\right )}{\partial \bar{\bar{\textbf{D}}}} - \textbf{P}\right ):\delta \bar{\bar{\textbf{D}}}}dA}ds \\ G_{P} (\bar{\boldsymbol{\upphi}},\bar{\bar{\textbf{D}}},\textbf{P}; \delta \textbf{P}) &:=\int _{L} {\int _{A} {\delta \textbf{P} : \bar{\bar{\textbf{D}}}}dA } ds. \end{aligned} $$

(32)

We enforce orthogonality between the enhanced strain and the internal force in Eq. (31) to make sure no work is produced when coupling these two fields. The minimum requirement is to enforce this condition $\textbf{P}=cst$., which ensures the patch test (see more in [31]) enforcement

$$ \begin{aligned} \int _{L} {\int _{A} {\underbrace{\delta \textbf{P}}_{=cst.} : \bar{\bar{\textbf{D}}}}dA }ds=0 \\ \int _{L} {\int _{A} {\delta \bar{\bar{\textbf{D}}}: \underbrace{\textbf{P}}_{=cst.}}dA}ds=0 \end{aligned} \quad \Rightarrow \quad \begin{aligned} \int _{L} {\int _{A} {\bar{\bar{\textbf{D}}}}dA}ds = \int _{L} {\int _{A}{ \delta \bar{\bar{\textbf{D}}}}dA}ds = 0. \end{aligned} $$

(33)

Finally, having the result from Eq. (32), we are able to restate weak equilibrium as presented in Eq. (30):

$$ \begin{aligned} G_{\bar{\upphi}} (\bar{\boldsymbol{\upphi}}, \bar{\bar{\textbf{D}}};\delta \bar{\boldsymbol{\upphi}}) &:= \int _{L} {\int _{A} { \frac{\partial W \left ( \textbf{I} + \nabla \bar{\boldsymbol{\upphi}} + \bar{\bar{\textbf{D}}}\right )}{\partial \nabla \boldsymbol{\upphi}} : \nabla \delta \bar{\boldsymbol{\upphi}}}dA } ds - G^{ext}(\delta \bar{\boldsymbol{\upphi}}) \\ G_{\bar{\bar{D}}} (\bar{\boldsymbol{\upphi}},\bar{\bar{\textbf{D}}}; \delta \bar{\bar{\textbf{D}}}) &:= \int _{L}{ \int _{A} { \frac{\partial W \left ( \textbf{I} + \nabla \bar{\boldsymbol{\upphi}} + \bar{\bar{\textbf{D}}}\right )}{\partial \bar{\bar{\textbf{D}}}} : \delta \bar{\bar{\textbf{D}}}}dA}ds. \end{aligned} $$

(34)

Fig. 2

Embedded discontinuity introduced into rotation field

2.5 Beam elasto-viscoplastic constitutive behavior

We present here a strain rate dependent material model where constitutive elasto-viscoplastic behavior of flexible beam exhibits a linear isotropic hardening model (for rate independent version see [10, 11]). By using the strain measure result in Eq. (10) together with work conjugate stress resultants in Eq. (11), written in vector form $\boldsymbol{\Sigma}= \left (\Sigma , \Gamma , K \right )^{T}$ and $\textbf{r}=\left ( N,V,M \right )^{T}$, one can state Helmholtz free energy potential:

$$ \begin{aligned} \Psi (\boldsymbol{\Sigma}, \boldsymbol{\Sigma}^{vp}, \boldsymbol{\zeta}):= \frac{1}{2}(\boldsymbol{\Sigma}- \boldsymbol{\Sigma}^{vp})^{T} \cdot \mathbb{C}(\boldsymbol{\Sigma}- \boldsymbol{\Sigma}^{vp}) + \frac{1}{2} \boldsymbol{\zeta}^{T}\cdot \mathbb{K}\boldsymbol{\zeta}, \end{aligned} $$

(35)

where $\boldsymbol{\Sigma}^{vp}$, $\zeta$, and $\mathbb{K}$ represent the viscoplastic component of generalized strains, an internal variable that governs hardening, and the corresponding hardening modulus, respectively. The local dissipation produced by inelastic behavior can be stated according to the second thermodynamic principle

$$ \mathcal{D}_{loc}^{vp}:=\left (\textbf{r} - \frac{\partial \Psi}{\partial \boldsymbol{\Sigma}}\right )^{T} \cdot \frac{\partial \boldsymbol{\Sigma}}{\partial t} - \left ( \frac{\partial \Psi}{\partial \boldsymbol{\Sigma}^{vp}} \right )^{T} \cdot \frac{\partial \boldsymbol{\Sigma}^{vp}}{\partial t} - \left ( \frac{\partial \Psi}{\partial \boldsymbol{\zeta}}\right )^{T} \cdot \frac{\partial \boldsymbol {\zeta}}{\partial t} $$

(36)

such that the viscoplastic part of the dissipation must remain positive

$$ 0 \leq \mathcal{D}^{vp}:= \textbf{r}^{T} \cdot \frac{\partial \boldsymbol{\Sigma}^{vp}}{\partial t} + \textbf{q}^{T} \cdot \frac{\partial \boldsymbol {\zeta}}{\partial t}. $$

(37)

We can recast the yield function in terms of dual variables

$$ \boldsymbol{\mathcal{\phi}} (\textbf{r},\textbf{q}) := |\textbf{r}| - \left ( \textbf{r}_{y} - \textbf{q} \right ); \quad \textbf{q}=- \mathbb{K}\boldsymbol{\zeta}, $$

(38)

where $\textbf{r}$ and $\textbf{r}_{y}$ are internal force and yield force. Note that during the elastic step, no modification of internal variables will occur when $\boldsymbol{\mathcal{\phi}} (\textbf{r,q}) \leq \textbf{0}$. The rheological model of viscoplastic behavior describes rate-sensitive deformation by viscous dash-pot, which leads to the increase of resistance in the plastic phase. Thus one can define excessive stress taken by dash-pot

$$ \boldsymbol{\mathcal{\phi}} := < \boldsymbol{\mathcal{\phi}}>= \boldsymbol{\eta} \frac{\partial \boldsymbol{\Sigma}^{vp}}{\partial t} \quad \Rightarrow \quad < \boldsymbol{\mathcal{\phi}}>:= \frac{\boldsymbol{\mathcal{\phi}}+|\boldsymbol{\mathcal{\phi}}|}{2}, $$

(39)

where $\eta$ is the viscosity coefficient. In general, all stress values that maximize the viscoplastic dissipation are admissible, but those outside the elastic domain are penalized by additional term $\mathcal{P}(\cdot )$ directly proportional to the penalty factor $\frac{1}{\eta}$. The viscoplasticity computation can be formulated as a penalty version of the constrained minimization problem, where the plastic admissibility constraint is relaxed and handled by the penalty method. By employing the Lagrange multiplier method, the constrained minimization can be re-defined as the corresponding unconstrained minimization problem:

$$ \text{max}_{\frac{\partial \boldsymbol{\gamma}}{\partial t}} \text{min}_{\forall \textbf{r,q}} \mathcal{L}^{vp} \left ( \textbf{r,q}, \frac{\partial \boldsymbol{\gamma}}{\partial t} \right ) = - \mathcal{D}^{vp} (\textbf{r,q}) + \eta ^{-1} \mathcal{P} ( \boldsymbol{\mathcal{\phi}} (\textbf{r,q})). $$

(40)

We use here the simplest choice of the penalty term as a quadratic functional placing a higher penalty on the stress outside of the elastic domain

$$ \begin{aligned} \mathcal{P} (\boldsymbol{\mathcal{\phi}}) = \textstyle\begin{cases} \frac{1}{2} \boldsymbol{\mathcal{\phi}}^{2}, &\text{if} \quad \boldsymbol{\mathcal{\phi}} \geq \textbf{0} \\ \textbf{0}, &\text{if} \quad \boldsymbol{\mathcal{\phi}} < \textbf{0} \end{cases}\displaystyle \quad \Rightarrow \quad \frac{d \mathcal{P}}{d \boldsymbol{\mathcal{\phi}}} = < \boldsymbol{\mathcal{\phi}}>:= \textstyle\begin{cases} \boldsymbol{\mathcal{\phi}}, &\text{if} \quad \boldsymbol{\mathcal{\phi}} \geq \textbf{0} \\ \textbf{0}, &\text{if} \quad \boldsymbol{\mathcal{\phi}}< \textbf{0} \end{cases}\displaystyle , \end{aligned} $$

(41)

where <⋅> is the Macaulay bracket. The Kuhn–Tucker optimality conditions for the problem in Eq. (40) will provide evolution equations of plastic strain and hardening variables as a rate form for both loading/unloading conditions:

$$ \begin{aligned} \frac{\partial \mathcal{L}^{vp}}{\partial \textbf{r}} &= - \frac{\partial \boldsymbol{\Sigma}^{vp}}{\partial t} + \eta ^{-1} \frac{\partial \mathcal{P}}{\partial \boldsymbol{\mathcal{\phi}}} \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial \textbf{r}}= \textbf{0} \quad \Rightarrow \quad \frac{\partial \boldsymbol{\Sigma}^{vp}}{\partial t}=\eta ^{-1} < \boldsymbol{\mathcal{\phi}}> \frac{\textbf{r}}{|\textbf{r}|} \\ \frac{\partial \mathcal{L}^{vp}}{\partial \textbf{q}} &=- \frac{\partial \boldsymbol{\zeta}}{\partial t} + \eta ^{-1} \frac{\partial \mathcal{P}}{\partial \boldsymbol{\mathcal{\phi}}} \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial \textbf{q}}= \textbf{0} \quad \Rightarrow \quad \frac{\partial \boldsymbol{\zeta}}{\partial t}=\eta ^{-1} < \boldsymbol{\mathcal{\phi}}> \\ \frac{\partial \boldsymbol{\gamma}}{\partial t} & = \eta ^{-1} \frac{ \partial \mathcal{P}}{\partial \boldsymbol{\mathcal{\phi}}} = \eta ^{-1} < \boldsymbol{\mathcal{\phi}}> \geq \textbf{0}; \quad \boldsymbol{\mathcal{\phi}}\leq \textbf{0}; \quad \frac{\partial \boldsymbol{\gamma}}{\partial t} \boldsymbol{\mathcal{\phi}} = \textbf{0.} \end{aligned} $$

(42)

We note that the operator split solution procedure for viscoplasticity remains the same as in the standard plasticity model with isotropic hardening except computation of the plastic multiplier. The appropriate value of the plastic multiplier in the local phase can be computed directly from the trial stress:

$$ \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial t} := \frac{\partial \boldsymbol {\mathcal{\phi}}}{\partial \textbf{r}} \mathbb{C} \frac{\partial \boldsymbol {\Sigma}}{\partial t} - \frac{\partial \boldsymbol {\gamma}}{\partial t} \left ( \frac{\partial \boldsymbol {\mathcal{\phi}}}{\partial \textbf{r}} \mathbb{C} \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial t} + \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial \textbf{q}} \mathbb{K} \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial t} \right ). $$

(43)

By introducing result in Eq. (43) into Eq. (42c), we can express the value of plastic multiplier

$$ \frac{\partial \boldsymbol {\gamma}}{\partial t}= \frac{\frac{\partial \boldsymbol {\mathcal{\phi}}}{\partial \textbf{r}} \mathbb{C} \frac{\partial \boldsymbol {\Sigma}}{\partial t}}{ \frac{\eta}{\Delta t} + \frac{\partial \boldsymbol {\mathcal{\phi}}}{\partial \textbf{r}} \mathbb{C} \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial t} + \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial \textbf{q}} \mathbb{K} \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial t} }. $$

(44)

The proposed model of viscoplasticity is a suitable choice for a very small value of viscosity parameter, and thus it will recover a similar response as the standard plasticity model. Hence, we choose here an alternative approach (see [8]) that can handle limit values of the viscosity parameter in a more robust manner. This computation model is considered to be an appropriate modification of the result calculated by standard plasticity due to stress relaxation. Based on that, one can recast the evolution equation for viscoplastic deformation in terms of stress:

$$\begin{array}{rl}\begin{array}{c}\frac{\partial \mathbf{\text{r}}}{\partial t}=\mathbb{C}(\frac{\partial \mathbf{\Sigma }}{\partial t}-\frac{\partial {\mathbf{\Sigma }}_{vp}}{\partial t})\\ \frac{\partial {\mathbf{\Sigma }}^{vp}}{\partial t}={\mathit{\tau }}^{-1}{\mathbb{C}}^{-1}(\mathbf{\text{r}}-{\mathbf{\text{r}}}_{\mathrm{\infty }})\end{array}\Rightarrow \frac{\partial \mathbf{\text{r}}}{\partial t}+{\mathit{\tau }}^{-1}\mathbf{\text{r}}& =\mathbb{C}\frac{\partial \mathbf{\Sigma }}{\partial t}-{\mathit{\tau }}^{-1}{\mathbf{\text{r}}}_{\mathrm{\infty }};\end{array}$$

(45)

where $\textbf{r}_{\infty}$ and ${\boldsymbol{\tau}}$ are stress produced by the standard plasticity model with isotropic hardening and its relaxation period defined as

$$ \begin{aligned} \boldsymbol{\tau} := \eta \left ( \frac{\partial \boldsymbol {\mathcal{\phi}}}{\partial \textbf{r}} \mathbb{C} \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial t} + \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial \textbf{q}} \mathbb{K} \frac{\partial \boldsymbol{\mathcal{\phi}}}{\partial t} \right )^{-1}. \end{aligned} $$

(46)

We can express stress rate equation for viscoplasticity with linear isotropic hardening as a linear combination of trial stress and computed stress of the standard plasticity model

$$ \frac{\partial \textbf{r}}{\partial t} = \textstyle\begin{cases} \mathbb{C} \frac{\partial \boldsymbol{\Sigma}}{\partial t}; & \text{if} \quad \frac{\partial \boldsymbol{\gamma}}{\partial t} = \textbf{0} \\ \frac{1}{1+\frac{\Delta t}{\boldsymbol{\tau}}} \frac{\partial \boldsymbol {\mathcal{\phi}}}{\partial \textbf{r}} \mathbb{C} \frac{\partial \boldsymbol {\Sigma}}{\partial t} + \frac{\frac{\Delta t}{\boldsymbol{\tau}}}{1+\frac{\Delta t}{\boldsymbol{\tau}}} \frac{\frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{r}} \mathbb{C} \mathbb{K} \frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{r}} }{\frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{r}} \mathbb{C} \frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{r}} + \frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{q}} \mathbb{K} \frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{q}} } \frac{\partial \boldsymbol{\Sigma}}{\partial t}; & \text{if} \quad \frac{\partial \boldsymbol {\gamma}}{\partial t}> \textbf{0} \end{cases}\displaystyle , $$

(47)

where the corresponding weighting factors are functions of relaxation period. The viscoplastic tangent modulus can also be given as a linear combination in Eq. (46)

$$ \frac{\partial \textbf{r}}{\partial \boldsymbol{\Sigma}} = \textstyle\begin{cases} \mathbb{C}; & \text{if} \quad \frac{\partial \boldsymbol{\gamma}}{\partial t} = \textbf{0} \\ \frac{1}{1+\frac{\Delta t}{\boldsymbol{\tau}}} \frac{\partial \boldsymbol {\mathcal{\phi}}}{\partial \textbf{r}} \mathbb{C} + \frac{\frac{\Delta t}{\boldsymbol{\tau}}}{1+\frac{\Delta t}{\boldsymbol{\tau}}} \frac{\frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{r}} \mathbb{C} \mathbb{K} \frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{r}} }{\frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{r}} \mathbb{C} \frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{r}} + \frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{q}} \mathbb{K} \frac{\partial \boldsymbol {\mathcal{\phi}} }{\partial \textbf{q}} }; & \text{if} \quad \frac{\partial \boldsymbol {\gamma}}{\partial t}> \textbf{0} \end{cases}\displaystyle . $$

(48)

2.6 Beam hinge softening behavior

To represent softening constitutive behavior at the discontinuity, we assume that the Helmholtz free energy potential is equal to the following strain energy function:

$$ \begin{aligned} \Psi (\bar{\boldsymbol{\Sigma}}, \bar{\boldsymbol{\Sigma}}^{vp},\bar{\boldsymbol{\zeta}}, \bar{\bar{\boldsymbol{\zeta}}})=\bar{\Psi}( \bar{\boldsymbol{\Sigma}},\bar{\boldsymbol{\Sigma}}^{vp}, \bar{\boldsymbol{\zeta}}) + \delta _{\bar{x}} \bar{\bar{\Psi}}(\bar{\bar{\boldsymbol{\zeta}}}); \quad \bar{\bar{\Psi}}(\bar{\bar{\boldsymbol{\zeta}}})= \frac{1}{2} \bar{\bar{\boldsymbol{\zeta}}}^{T} \cdot \mathbb{K}^{s} \bar{\bar{\boldsymbol{\zeta}}}, \end{aligned} $$

(49)

where $\mathbb{K}^{s}<0$ and $\bar{\bar{\boldsymbol{\zeta}}}\geq 0$ represent the softening modulus and the plastic variable related to softening, respectively. The plastic part of the dissipation at the discontinuity can be obtained from softening potential $\bar{\bar{\Psi}}(\bar{\bar{\zeta}})$, where we write

$$ 0 \leq \bar{\bar{\mathcal{D}}}^{p}:= \textbf{t}^{T} \cdot \frac{\partial \bar{\bar{\boldsymbol{\upphi}}}}{\partial t} + \bar{\bar{\textbf{q}}}^{T} \cdot \frac{\partial \bar{\bar{\boldsymbol {\zeta}}}}{\partial t}; \quad \bar{\bar{\textbf{q}}} = \bar{\bar{\boldsymbol{\zeta}}} \mathbb{K}^{s}, $$

(50)

where $\textbf{t}$ and $\bar{\bar{\boldsymbol{\upphi}}}$ are traction at the discontinuity and incompatible mode variable, respectively. The corresponding yield function that controls plasticity process activation during inelastic time step is given as follows:

$$ \textbf{0} \geq \boldsymbol{\mathcal{\phi}}^{s} (\textbf{t}, \bar{\bar{\boldsymbol{\zeta}}}) := |\textbf{t}| - \left ( \textbf{t}_{u} - \bar{\bar{\textbf{q}}}\right ), $$

(51)

where $\textbf{t}$ and $\textbf{t}_{u}$ are traction force and ultimate yield force or moment at discontinuity, respectively. The softening law in this development is adopted as a nonlinear function

$$ \bar{\bar{\textbf{q}}}(\bar{\bar{\boldsymbol{\zeta}}})=-\textbf{t}_{u} \left (1-\exp{\left (-\frac{\textbf{t}_{u}}{\textbf{G}_{f}} \bar{\bar{\boldsymbol{\zeta}}}\right )}\right ), $$

(52)

which introduces fracture energy $\textbf{G}_{f}$. Finding the first variation of Eq. (52) with respect to plastic variable $\bar{\bar{\boldsymbol{\zeta}}}$, one can obtain softening modulus

$$ \frac{d\bar{\bar{\textbf{q}}}}{d\bar{\bar{\boldsymbol{\zeta}}}}= \mathbb{K}^{s} \quad \Rightarrow \quad \mathbb{K}^{s} = - \frac{\textbf{t}_{u}^{2}}{\textbf{G}_{f}}\exp{\left (- \frac{\textbf{t}_{u}}{\textbf{G}_{f}} \bar{\bar{\boldsymbol{\zeta}}} \right )}\leq 0. $$

(53)

The algorithm during softening time step will pick only admissible candidates $(\textbf{t}, \bar{\bar{\boldsymbol{\zeta}}})$ that maximize plastic dissipation or, in other words, satisfy the following criteria $\bar{\bar{\boldsymbol{\phi}}}(\textbf{t}, \bar{\bar{\boldsymbol{\zeta}}}) \leq 0$:

$$ \text{max}_{ \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t}} \text{min}_{\forall \textbf{t},\bar{\bar{\textbf{q}}}} \mathcal{L}^{s} \left ( \textbf{t},\bar{\bar{\textbf{q}}}, \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} \right ) = -\mathcal{D}^{s} (\textbf{t},\bar{\bar{\textbf{q}}}) + \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} \boldsymbol{\mathcal{\phi}} (\textbf{t},\bar{\bar{\textbf{q}}}), $$

(54)

where $\frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} \geq \textbf{0}$ is the plastic multiplier. This can be solved as an unconstrained minimization problem from where one can cast the following evolution equations:

$$ \begin{aligned} \frac{\partial \mathcal{L}^{s}}{\partial \textbf{t}} &= - \frac{\partial \bar{\bar{\boldsymbol{\upphi}}}}{\partial t} + \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} \frac{\partial \boldsymbol{\mathcal{\phi}}^{s}}{\partial \textbf{t}}= \textbf{0} \quad \Rightarrow \quad \frac{\partial \bar{\bar{\boldsymbol{\upphi}}} }{\partial t}= \frac{\textbf{t}}{|\textbf{t}|} \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} \\ \frac{\partial \mathcal{L}^{s}}{\partial \bar{\bar{\textbf{q}}}} &= - \frac{\partial \bar{\bar{\boldsymbol{\zeta}}}}{\partial t} + \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} \frac{\partial \boldsymbol{\mathcal{\phi}}^{s}}{\partial \bar{\bar{\textbf{q}}}}= \textbf{0} \quad \Rightarrow \quad \frac{\partial \bar{\bar{\boldsymbol{\zeta}}}}{\partial t}= \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} \\ \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} & \geq \textbf{0}; \quad \boldsymbol{\mathcal{\phi}}^{s} \leq \textbf{0}; \quad \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t} \boldsymbol{\mathcal{\phi}}^{s} = \textbf{0}. \end{aligned} $$

(55)

The corresponding plastic multiplier can be expressed from the plastic consistency condition for inelastic time step

$$ \frac{\partial \boldsymbol{\mathcal{\phi}}^{s}}{\partial t} := \textbf{0} \quad \Rightarrow \quad \frac{\partial \bar{\bar{\boldsymbol{\gamma}}}}{\partial t}= \frac{\frac{\partial \boldsymbol {\mathcal{\phi}}^{s}}{\partial \textbf{t}} \mathbb{C} \frac{\partial \boldsymbol {\Sigma}}{\partial t}}{\frac{1}{L^{e}}\frac{\partial \boldsymbol {\mathcal{\phi}}^{s}}{\partial \textbf{t}} \mathbb{C} \frac{\partial \boldsymbol{\mathcal{\phi}}^{s}}{\partial t} + \frac{\partial \boldsymbol{\mathcal{\phi}}^{s}}{\partial \bar{\bar{\textbf{q}}}} \mathbb{K}^{s} \frac{\partial \boldsymbol{\mathcal{\phi}}^{s}}{\partial t} }. $$

(56)

2.7 Damping model based on nonlinear material response

Here we propose an innovative damping model based on energy dissipation by plastic processes. Namely, during inelastic response system changes its momentum, where total energy given as Hamiltonian in Eq. (19) is decreasing. Such a change that corresponds to plastic dissipation is handled via already introduced expressions for hardening and softening, respectively, Eq. (36) and Eq. (50). In this manner, we propose to employ a plastic hinge formulation as a damping device. We note that for a linear elastic response, the system recalls the basic damping model. Thus, we can rewrite in a simple manner the MDOF equation of motion in Eq. (20) with dissipative viscous damping term

$$ \begin{aligned} \textbf{M}\ddot{\boldsymbol{\upphi}}(t) + \textbf{C} \dot{\boldsymbol{\upphi}}(t) + \textbf{K}\boldsymbol{\upphi}(t)= \textbf{f}(t). \end{aligned} $$

(57)

Equation (57) can further be modified by multiplying with orthonormal eigenvectors $\textbf{V}_{m}$ obtained with the fixed mass matrix $\textbf{M}$ and reference stiffness value, which allows us to obtain the following set of equations of motion:

$$ \begin{aligned} \textbf{I}\textbf{a} + \boldsymbol{\Lambda}_{C}\textbf{v} + \boldsymbol{\Lambda}_{K}\boldsymbol{\upphi}= \textbf{0}, \end{aligned} $$

(58)

where $\boldsymbol{\Lambda}_{C}=diag(2 \zeta _{n} \omega _{n})$ and $\boldsymbol{\Lambda}_{K}=diag(\omega _{n}^{2})$ are diagonalized damping and stiffness matrix, respectively. By knowing the damping ratio $\zeta _{n}$ and the natural frequency $\omega _{n}$, we can compute system response. The total damped energy for any arbitrary time period $[0,\bar{t}]$ can be calculated as follows:

$$ Q (\dot{\boldsymbol{\upvarphi}},\dot{\psi})= \int _{0}^{\bar{t}} { \begin{Bmatrix} \dot{\boldsymbol{\upvarphi}} \\ \dot{\psi} \end{Bmatrix} ^{T} \cdot \textbf{C} \begin{Bmatrix} \dot{\boldsymbol{\upvarphi}} \\ \dot{\psi} \end{Bmatrix} } dt. $$

(59)

With the previous, we can perform computations for linear elastic behavior. Instead of putting an effort into defining an approximative damping model that can reliably represent decay in inelasticity, we switch here to a known formulation of nonlinear behavior which introduces energy dissipation through a stiffness matrix. Such a model can verify different outputs in dependence of hinge material parameters $\textbf{K}(\bar{\boldsymbol{\Sigma}},\bar{\boldsymbol{\Sigma}}_{vp}, \bar{\boldsymbol{\zeta}}, \bar{\bar{\boldsymbol{\zeta}}}_{s}, \mathbb{K},\mathbb{K}_{s},G_{f})$. The amount of damped energy in Eq. (59) can be modified by taking into account plastic dissipation where we can state the following equality:

$$ Q (\dot{\boldsymbol{\upvarphi}},\dot{\psi}) = \mathcal{D}^{vp} + \mathcal{D}^{p}_{s}. $$

(60)

Since we seek to quantify the relationship between damping ratio $\zeta$ and the parameters of the proposed damping model, we choose to apply a mathematical method of logarithmic decrement $\delta$ and analyze output results. We mention that it is quite a laborious task to find analytic relationships due to many nonlinearities and approximations. The logarithmic decrement takes into account the ratio of output amplitudes for arbitrary two successive peaks in the time domain, and thus one can write

$$ \delta = \frac{1}{n} \text{ln} \frac{\boldsymbol{\upphi}(t)}{\boldsymbol{\upphi}(t+nT)}. $$

(61)

This measure becomes a reliable tool in the computation of the damping ratio for underdamped systems with $\zeta <0.5$, while for greater values of coefficient, it becomes less precise. The damping ratio can be expressed by using the result in Eq. (61)

$$ \zeta = \frac{1}{\sqrt{1 + \left ( \frac{2\pi}{\delta}\right )^{2}}}. $$

(62)

3 Numerical implementation

In this chapter we present a numerical implementation of the previously presented theoretical formulation, which consists of corresponding linearization of the nonlinear problem, space discretization, and static condensation of the 1D beam finite element. We also present energy-conserving and decaying time-integration solution schemes for this transient problem to provide a more robust model and deal with high-frequency modes.

3.1 Consistent linearization of the weak formulation

To find the solution to a highly nonlinear dynamic problem, we employ Newton’s method, which will ensure a quadratic convergence rate. Taking into account that equilibrium is attained for the previous time step, we can obtain by linearizing the internal work of weak equilibrium equations defined in Eq. (12) the following form:

$$ \begin{aligned} &Lin[G_{\Pi}] = G_{\Pi} + \int _{L} { \begin{Bmatrix} \delta \boldsymbol{\upvarphi}' \\ \delta \psi \end{Bmatrix} ^{T} \cdot \begin{bmatrix} 0 & \textbf{Wn} \\ \textbf{(Wn)}^{T} & -\textbf{n}^{T} \cdot \boldsymbol{\upvarphi}' \end{bmatrix} \begin{Bmatrix} \Delta \boldsymbol{\upvarphi}' \\ \Delta \psi \end{Bmatrix} }ds \\ &+\int _{L} { \begin{Bmatrix} \delta \boldsymbol{\upvarphi}' - \textbf{W}\boldsymbol{\upvarphi}' \delta \psi \\ \delta \psi ' \textbf{e}_{3} \end{Bmatrix} ^{T} \cdot \begin{bmatrix} \boldsymbol{\Lambda} \mathbb{C}_{n} \boldsymbol{\Lambda}^{T} & 0 \\ 0 & \mathbb{C}_{m} \end{bmatrix} \begin{Bmatrix} \Delta \boldsymbol{\upvarphi}' - \textbf{W} \boldsymbol{\upvarphi}' \Delta \psi \\ \Delta \psi '\textbf{e}_{3} \end{Bmatrix} }ds , \end{aligned} $$

(63)

where $\Delta \boldsymbol{\upvarphi}$ and $\Delta \psi$ are incremental displacements and rotation, respectively. It can be noticed that in Eq. (63) we get material $\textbf{K}_{m}$ and geometric part $\textbf{K}_{g}$ of tangent stiffness as a product of consistent linearization, such that $\textbf{K}=\textbf{K}_{m}+\textbf{K}_{g}$. To obtain the corresponding linearization of dynamic equilibrium, we need to linearize the inertia term in Eq. (18), which yields

$$ Lin[G_{K}] = G_{K} + \int _{L} { \begin{Bmatrix} \delta \boldsymbol{\upvarphi} \\ \delta \psi \end{Bmatrix} ^{T} \cdot \begin{bmatrix} A_{\rho} \textbf{I} & 0 \\ 0 & J_{\rho} \end{bmatrix} \begin{Bmatrix} \Delta \ddot{\boldsymbol{\upvarphi}} \\ \Delta \ddot{\psi} \end{Bmatrix} }ds. $$

(64)

By using results in Eq. (63) and (64), we can state linearized dynamic equilibrium equations in Eq. (12) with introduced strong discontinuity, where one can write the following expression according to Eq. (34a):

$$ \begin{aligned} Lin&[G_{\bar{\upphi}}]= G_{\bar{\upphi}} + \int _{L} { \begin{Bmatrix} \delta \bar{\boldsymbol{\upvarphi}} \\ \delta \bar{\psi} \end{Bmatrix} ^{T} \cdot \textbf{M} \begin{Bmatrix} \Delta \ddot{\boldsymbol{\upvarphi}} \\ \Delta \ddot{\psi} \end{Bmatrix} }ds \\ & + \int _{L} { \begin{Bmatrix} \delta \bar{\boldsymbol{\upvarphi}}' - \textbf{W} \bar{\boldsymbol{\upvarphi}}' \delta \bar{\psi} \\ \delta \bar{\psi}' \textbf{e}_{3} \end{Bmatrix} ^{T} \cdot \textbf{K}_{m} \begin{Bmatrix} \Delta \tilde{\boldsymbol{\upvarphi}}' - \textbf{W} \bar{\boldsymbol{\upvarphi}}' \Delta \bar{\psi} \\ \Delta \tilde{\psi}'\textbf{e}_{3} \end{Bmatrix} }ds \\ & + \int _{L} { \begin{Bmatrix} \delta \bar{\boldsymbol{\upvarphi}} \\ \delta \bar{\psi} \end{Bmatrix} ^{T} \cdot \textbf{K}_{g} \begin{Bmatrix} \Delta \tilde{\boldsymbol{\upvarphi}}' \\ \Delta \tilde{\psi} \end{Bmatrix} }ds -\int _{L} {\delta \bar{\boldsymbol{\upphi}}^{T} \cdot \Delta \textbf{f}} ds - \left [ \delta \bar{\boldsymbol{\upphi}}^{T} \cdot \Delta \textbf{t} \right ]_{x=L} =0, \end{aligned} $$

(65)

while linearization of the additional equilibrium equation in Eq. (34b) gives

$$ \begin{aligned} Lin&[G_{\bar{\bar{D}}}]=G_{\bar{\bar{D}}} + \int _{L} { \begin{Bmatrix} \delta \bar{\bar{\boldsymbol{\upvarphi}}}' - \textbf{W} \bar{\boldsymbol{\upvarphi}}' \delta \bar{\bar{\psi}} \\ \delta \bar{\bar{\psi}}' \textbf{e}_{3} \end{Bmatrix} ^{T} \cdot \textbf{K}_{m} \begin{Bmatrix} \Delta \tilde{\boldsymbol{\upvarphi}}' - \textbf{W} \bar{\boldsymbol{\upvarphi}}' \Delta \bar{\psi} \\ \Delta \tilde{\psi}'\textbf{e}_{3} \end{Bmatrix} }ds \\ &+ \int _{L} { \begin{Bmatrix} \delta \bar{\bar{\boldsymbol{\upvarphi}}} \\ \delta \bar{\bar{\psi}} \end{Bmatrix} ^{T} \cdot \textbf{K}_{g} \begin{Bmatrix} \Delta \tilde{\boldsymbol{\upvarphi}}' \\ \Delta \tilde{\psi} \end{Bmatrix} }ds + \underbrace{\frac{\partial \textbf{t}}{\partial \bar{\bar{\boldsymbol{\upvarphi}}}}}_{ \mathbb{K}^{s} \frac{\textbf{t}}{|\textbf{t}|}}\Delta \bar{\bar{\boldsymbol{\upvarphi}}}=0, \end{aligned} $$

(66)

where $\textbf{M}$, $\textbf{K}_{m}$, and $\textbf{K}_{g}$ are, respectively, mass matrix, material part of stiffness matrix, and geometrical part of stiffness matrix, with the following matrix form:

$$ \begin{aligned} \textbf{M}= \begin{bmatrix} A_{\rho} \textbf{I} & 0 \\ 0 & J_{\rho} \end{bmatrix}; \quad \textbf{K}_{m}= \begin{bmatrix} \boldsymbol{\Lambda} \mathbb{C}_{n} \boldsymbol{\Lambda}^{T} & 0 \\ 0 & \mathbb{C}_{m} \end{bmatrix}; \quad \textbf{K}_{g}= \begin{bmatrix} 0 & \textbf{Wn} \\ \textbf{(Wn)}^{T} & -\textbf{n}^{T} \cdot \bar{\boldsymbol{\upvarphi}}' \end{bmatrix}. \end{aligned} $$

(67)

3.2 Space discretization

We can adopt any order of shape functions for the displacement field discretization. However, for the sake of simplicity, we use the lowest order polynomial approximation. Let us consider a domain $\Omega\in \mathbb{R}$ that is represented by a standard discrete linear mesh as a set ℐ of nonzero length linear elements $\Omega^{e}$ such that $\Omega=\cup _{\Omega^{e}\in \mathcal{I}} \Omega^{e}$. The isoparametric shape functions are used to construct real and virtual displacement field, and for a given element $\Omega^{e}$, one can write

$$ \begin{aligned} N_{a}^{e}(\xi )&=\frac{1}{2}(1+\xi _{a}\xi ), \quad \xi _{a}= \textstyle\begin{cases} -1, &a=1 \\ 1,&a=2 \end{cases}\displaystyle , \quad \xi \in [-1,1]; \\ M^{e}(\xi )&= \textstyle\begin{cases} -\frac{1}{2} (1+\xi ), & \text{ if } \xi \in [-1,0] \\ \frac{1}{2}(1-\xi ), & \text{ if } \xi \in [0,1], \end{cases}\displaystyle \end{aligned} $$

(68)

where $N_{a}^{e}(\xi )$ and $M^{e}(\xi )$ represent linear piece-wise and incompatible mode shape functions, respectively. Among many possibilities, we choose to introduce Heaviside (step) $H(\xi )$ function in the middle of element length $\xi =0$ to represent incompatible mode compliance. Since we are only interested in rotational beam hinge behavior, we introduce embedded discontinuity only in the rotation field

$$ \begin{aligned} u^{h}(\xi ,t)&=\sum _{a=1}^{2} {N_{a}^{e}(\xi )\bar{u}_{a}^{e}(t)}; \\ v^{h}(\xi ,t)&=\sum _{a=1}^{2} {N_{a}^{e}(\xi )\bar{v}_{a}^{e}(t)}; \\ \psi ^{h}(\xi ,t)&= \underbrace{\sum _{a=1}^{2} {N_{a}^{e}(\xi )\bar{\psi}_{a}^{e}(t)} + N_{2}^{e}(\xi )\bar{\bar{\psi}}_{a}^{e}(t)}_{ \tilde{\psi}^{e} (t)} + \underbrace{ \left (H^{e}(\xi ) - N^{e}_{2}(\xi )\right )}_{M^{e}( \xi )} \bar{\bar{\psi}}^{e}(t) \\ &= \tilde{\psi}^{e} (t) + M^{e}(\xi )\bar{\bar{\psi}}^{e}(t), \end{aligned} $$

(69)

while the corresponding strain fields as a necessary part of beam formulation can be calculated as follows:

$$ \begin{aligned} \frac{du^{h}(\xi ,t)}{d x} &=\sum _{a=1}^{2} {B_{a}^{e}( \xi )\bar{u}_{a}^{e}(t)}; \\ \frac{dv^{h}(\xi ,t)}{d x}&=\sum _{a=1}^{2} {B_{a}^{e}(\xi )\bar{v}_{a}^{e}(t)}; \\ \frac{d\psi ^{h}(\xi ,t)}{d x}&= \underbrace{\sum _{a=1}^{2} {B_{a}^{e}(\xi )\bar{\psi}_{a}^{e}(t)} + G^{e}(\xi )\bar{\bar{\psi}}^{e}(t)}_{ \frac{\partial \tilde{\psi}^{e}}{\partial x}} + \delta _{\bar{x}} \bar{\bar{\psi}}^{e} (t) = \frac{\partial \tilde{\psi}^{e} (\xi ,t)}{\partial x} + \delta _{ \bar{x}} \bar{\bar{\psi}}^{e} (t) . \end{aligned} $$

(70)

The shape function derivatives are given as follows:

$$ \begin{aligned} B_{a}(\xi )=\frac{dN_{a}^{e}(\xi )}{d\xi}= \frac{(-1)^{a}}{l^{e}};\quad G^{e}(\xi )= \textstyle\begin{cases} -\frac{1}{l^{e}}, & \text{ if } \xi \in [-1,0) \cup (0,1] \\ \frac{1}{l^{e}}+\delta _{0}, & \text{ if } \xi =0 \end{cases}\displaystyle , \end{aligned} $$

(71)

where $\delta _{0}$ is Dirac (jump) delta function positioned in the center of an element. We mention that the standard two-point linear shape functions are employed for discretization of velocity and acceleration fields.

3.3 Static condensation

The linearized governing equations in Eq. (65) and (66) can be rewritten now in matrix notation as discrete element contribution with unknown vectors of incremental displacement and rotation $\Delta \boldsymbol{\upphi}=(\Delta \boldsymbol{\upvarphi}, \Delta \psi )^{T}$, velocity $\Delta \textbf{v}=\Delta \dot{\boldsymbol{\upphi}}=(\Delta \dot{\boldsymbol{\upvarphi}}, \Delta \dot{\psi})^{T}$, and acceleration $\Delta \textbf{a}=\Delta \ddot{\boldsymbol{\upphi}}=(\Delta \ddot{\boldsymbol{\upvarphi}}, \Delta \ddot{\psi})^{T}$, we obtain

$$ \begin{aligned} \mathbb{A}_{e=1}^{nel} \begin{bmatrix} -\textbf{M}_{ab}^{e} \ &\textbf{0} \\ \textbf{0} \ &\textbf{0} \end{bmatrix} \begin{bmatrix} \Delta \ddot{\bar{\boldsymbol{\upphi}}} \\ \Delta \ddot{\bar{\bar{\boldsymbol{\upphi}}}} \end{bmatrix} +\mathbb{A}_{e=1}^{nel} \begin{bmatrix} \textbf{K}_{ab}^{e} & {\textbf{F}_{ab}^{e}}^{T} \\ \textbf{F}_{ab}^{e} & {\textbf{H}_{ab}^{e}} \end{bmatrix} \begin{bmatrix} \Delta \bar{\boldsymbol{\upphi}}^{e} \\ \Delta \bar{\bar{\boldsymbol{\upphi}}}^{e} \end{bmatrix} =\mathbb{A}_{e=1}^{nel} \begin{bmatrix} \textbf{f}_{b}^{e} \\ \textbf{0} \end{bmatrix}, \end{aligned} $$

(72)

where matrices $\textbf{K}_{ab}^{e}$, $\textbf{F}_{ab}^{e}$, $\textbf{H}_{ab}^{e}$, $\textbf{M}_{ab}^{e}$, and $\textbf{f}_{b}^{e}$ are

$$ \begin{aligned} \textbf{K}_{ab}^{e} &=\int _{L^{e}} {\textbf{B}_{a}^{e^{T}} \textbf{D}\textbf{B}_{b}^{e}}ds; \quad \textbf{F}_{ab}^{e} =\int _{L^{e}} {\textbf{G}_{a}^{e^{T}}\textbf{D}\textbf{B}_{b}^{e}}ds; \\ \textbf{H}_{ab}^{e} &=\int _{L^{e}} {\textbf{G}_{a}^{e^{T}}\textbf{D} \textbf{G}_{b}^{e}}ds; \quad \textbf{M}_{ab}^{e} =\int _{L^{e}} { \textbf{N}_{a}^{e^{T}}\rho \textbf{N}_{b}^{e}}ds; \\ \textbf{f}_{b}^{e} &=\int _{L^{e}} {\textbf{N}_{a}^{e}\textbf{b}}ds+ \left [\textbf{N}_{a}^{e}\textbf{t}\right ]_{\partial \Omega ^{e}}. \end{aligned} $$

(73)

To eliminate incompatible mode parameters $\Delta \bar{\bar{\boldsymbol{\upphi}}}^{e}$, we need to carry out static condensation, which can be done on element level before approaching to the final stiffness matrix assembly. By using the result in Eq. (72b), we can obtain

$$ \begin{aligned} \Delta \bar{\bar{\boldsymbol{\upphi}}}^{e}=-{\textbf{H}_{ab}^{e}}^{-1} \textbf{F}_{ab}^{e} \Delta \bar{\boldsymbol{\upphi}}^{e} \quad \Rightarrow \quad \left (\textbf{K}_{ab}^{e}-{\textbf{F}_{ab}^{e}}^{T} { \textbf{H}_{ab}^{e}}^{-1}{\textbf{F}_{ab}^{e}}\right ) \Delta \bar{\boldsymbol{\upphi}}^{e}=\textbf{f}_{b}^{e}, \end{aligned} $$

(74)

thus condensed stiffness matrix has the following form:

$$ \tilde{\textbf{K}}_{ab}^{e}=\textbf{K}_{ab}^{e}-{\textbf{F}_{ab}^{e}}^{T} {\textbf{H}_{ab}^{e}}^{-1}{\textbf{F}_{ab}^{e}} \quad \Rightarrow \quad \tilde{\textbf{K}}_{ab}^{e}\Delta \bar{\boldsymbol{\upphi}}^{e}= \textbf{f}_{b}^{e}, $$

(75)

where finally we can rewrite the result in Eq. (72)

$$ \begin{aligned} \mathbb{A}_{e=1}^{nel} \begin{bmatrix} -\textbf{M}_{ab}^{e}\Delta \ddot{\bar{\boldsymbol{\upphi}}} + \bar{\textbf{K}}_{ab}^{e}\Delta \bar{\boldsymbol{\upphi}}^{e} \end{bmatrix} = \mathbb{A}_{e=1}^{nel} \begin{bmatrix} \textbf{f}_{b}^{e} \end{bmatrix}. \end{aligned} $$

(76)

3.4 Energy-conserving solution scheme

For the purpose of ensuring computation stability over a long time period, we present here the development of an energy-conserving (EC) scheme for the present nonlinear dynamic problem. Integration of nodal quantities is done by the mid-point scheme to maintain second-order solution $O(\Delta t^{3})$ accurate. The nodal displacement, velocity, and acceleration approximation at the time step $t_{n+1/2}$ can be written as follows:

$$ \begin{aligned} \boldsymbol{\upvarphi}_{n+1/2}&= \frac{1}{2} \left ( \boldsymbol{\upvarphi}_{n+1} + \boldsymbol{\upvarphi}_{n}\right ); \quad \psi _{n+1/2} =\frac{1}{2} \left ( \psi _{n+1} + \psi _{n} \right ) \\ \textbf{v}_{n+1/2}&=\frac{1}{\Delta t} \left ( \boldsymbol{\upvarphi}_{n+1}- \boldsymbol{\upvarphi}_{n} \right ); \quad \omega _{n+1/2}= \frac{1}{\Delta t} \left ( \psi _{n+1}-\psi _{n} \right ) \\ \textbf{a}_{n+1/2}&=\frac{1}{\Delta t} \left ( \textbf{v}_{n+1}- \textbf{v}_{n} \right ); \quad \alpha _{n+1/2}=\frac{1}{\Delta t} \left ( \omega _{n+1}-\omega _{n} \right ). \end{aligned} $$

(77)

Having the result Eq. (77), we can state mid-point approximation of weak form of equilibrium equations in Eq. (20)

$$ \begin{aligned} &G(\boldsymbol{\upvarphi}_{n+1},\psi _{n+1},\delta \boldsymbol{\upvarphi},\delta \psi ) := \int _{L} {\left (\delta \boldsymbol{\upvarphi}^{T} \cdot A_{\rho} \textbf{a}_{n+1/2} + \delta \psi \cdot J_{\rho} \alpha _{n+1/2}\right )}ds \\ & + \int _{L} {\left ((\delta \boldsymbol{\upvarphi}' - \delta \psi \textbf{W} \boldsymbol{\upvarphi}'_{n+1/2})^{T} \cdot \textbf{n}_{n+1/2} + \delta \psi ' \textbf{e}_{3}^{T} \cdot \textbf{m}_{n+1/2} \right )}ds - G^{ext}_{n+1/2}. \end{aligned} $$

(78)

For the mid-point algorithm of weak equilibrium equations, we enforce the energy conservation feature by introducing an approximation of the displacement and rotation increment, which are given as follows:

$$ \begin{aligned} \Delta \boldsymbol{\upvarphi}&=\frac{1}{2}\Delta t ( \textbf{v}_{n+1}-\textbf{v}_{n}) \quad \Rightarrow \quad \textbf{v}_{n+1} = - \textbf{v}_{n} + \frac{2}{\Delta t} \left ( \boldsymbol{\upvarphi}_{n+1} - \boldsymbol{\upvarphi}_{n} \right ), \\ \Delta \psi &=\frac{1}{2}\Delta t (\omega _{n+1}-\omega _{n}) \quad \Rightarrow \quad \omega _{n+1} = - \omega _{n} + \frac{2}{\Delta t} \left ( \psi _{n+1} - \psi _{n} \right ). \end{aligned} $$

(79)

By choosing a test displacement vector $\delta \boldsymbol{\upvarphi}$ and rotation $\delta \psi$ as $\Delta \boldsymbol{\upvarphi}$ and $\Delta \psi$, respectively, a work done by both internal and external forces can be elaborated from the weak balance equation in Eq. (78):

$$ \begin{aligned} 0&:= - G^{ext}_{n+1/2} + \int _{L} {\left (\Delta \boldsymbol{\upvarphi}^{T} \cdot A_{\rho} \textbf{a}_{n+1/2} + \Delta \psi \cdot J_{\rho} \alpha _{n+1/2}\right )}ds \\ & + \int _{L} {\left ((\Delta \boldsymbol{\upvarphi}' - \Delta \psi \textbf{W} \boldsymbol{\upvarphi}'_{n+1/2})^{T} \cdot \textbf{n}_{n+1/2} + \Delta \psi ' \textbf{e}_{3}^{T} \cdot \textbf{m}_{n+1/2} \right )}ds. \end{aligned} $$

(80)

The first term in Eq. (80) represents the kinetic energy term, which can be simplified in the following manner by employing results in Eq. (79) and (77):

$$ \begin{aligned} \Delta K &=\int _{L} {\left (\Delta \boldsymbol{\upvarphi}^{T} \cdot A_{\rho} \textbf{a}_{n+1/2} + \Delta \psi \cdot J_{\rho} \alpha _{n+1/2}\right )}ds \\ &=\frac{1}{2}\int _{L}{\left ({\textbf{v}_{n+1}}^{T} \cdot A_{\rho} \textbf{v}_{n+1} + {\omega _{n+1}} \cdot J_{\rho}\omega _{n+1} \right )ds} - \frac{1}{2}\int _{L}{\left (\textbf{v}_{n}^{T} \cdot A_{\rho} \textbf{v}_{n} + \omega _{n} \cdot J_{\rho}\omega _{n}\right )ds} \\ &=K_{n+1}-K_{n}. \end{aligned} $$

(81)

To calculate the second term in Eq. (80), which pertains to potential energy conservation, we need to obtain spatial strain

$$ \begin{aligned} \boldsymbol{\Lambda}_{n+1/2}^{T}\left (\Delta \boldsymbol{\upvarphi}' - \Delta \psi \textbf{W} \boldsymbol{\upvarphi}'_{n+1/2}\right )&=\boldsymbol{\Lambda}_{n+1}^{T} \boldsymbol{\upvarphi}'_{n+1} - \boldsymbol{\Lambda}_{n}^{T} \boldsymbol{\upvarphi}'_{n} \\ &=\textbf{E}_{n+1} - \textbf{E}_{n}, \end{aligned} $$

(82)

while internal force at time $t_{n+1/2}$ can be stated accordingly to the nonlinear dynamics algorithmic form calculated from the mid-point configuration

$$ \begin{aligned} \textbf{N}_{n+1/2}&=\frac{1}{2}\mathbb{C}_{n} \left ( \textbf{E}_{n+1} + \textbf{E}_{n} \right ) \\ M_{n+1/2}&=\frac{1}{2}\mathbb{C}_{m} \left (K_{n+1} + K_{n} \right ). \end{aligned} $$

(83)

The work done by potential forces

$$ \begin{aligned} \Delta \Pi &=\int _{L} {\left ((\Delta \boldsymbol{\upvarphi}' - \Delta \psi \textbf{W} \boldsymbol{\upvarphi}'_{n+1/2})^{T} \cdot \textbf{n}_{n+1/2} + \Delta \psi ' \textbf{e}_{3}^{T} \cdot \textbf{m}_{n+1/2} \right )}ds \\ &=\frac{1}{2}\int _{L} { \left (\textbf{E}_{n+1}^{T} \cdot \mathbb{C}_{n} \textbf{E}_{n+1} + K_{n+1} \cdot \mathbb{C}_{m} K_{n+1} \right ) ds} - \frac{1}{2}\int _{L} { \left (\textbf{E}_{n}^{T} \cdot \mathbb{C}_{n} \textbf{E}_{n} + K_{n} \cdot \mathbb{C}_{m} K_{n} \right ) ds} \\ &=\Pi_{n+1}-\Pi_{n}. \end{aligned} $$

(84)

As a final step in the proof, the tangent may be written in a general form:

$$ \begin{aligned} (K_{n+1}+\Pi_{n+1})-(K_{n}+\Pi_{n})&=( \boldsymbol{\upphi}_{n+1}-\boldsymbol{\upphi}_{n})^{T} \cdot \textbf{f}_{ext} \\ \Rightarrow E_{n+1} - E_{n} &= \Delta W. \end{aligned} $$

(85)

We thus conclude that the result in Eq. (84) is implying on the conservation property of the system total energy for any external loading obtained from potential. This property leads to an unconditionally stable algorithm.

3.5 Energy-decaying solution scheme

In this section we construct a modification of algorithmic constitutive equations of a mid-point scheme that is capable to dissipate the energy of high-frequency modes. Such a scheme has a strong practical interest in stress computation accuracy. By adding the dissipative term in result Eq. (77), the increment of displacement can be computed:

$$ \begin{aligned} \Delta \boldsymbol{\upvarphi}=\boldsymbol{\upvarphi}_{n+1/2}^{cons} + \beta \Delta t (\textbf{v}_{n+1}-\textbf{v}_{n}) \\ \Delta \psi =\psi _{n+1/2}^{cons} + \beta \Delta t (\omega _{n+1}- \omega _{n}), \end{aligned} $$

(86)

and thus one can express velocities at the end of time interval $n+1$

$$ \begin{aligned} \textbf{v}_{n+1}&=\Delta \boldsymbol{\upvarphi} \frac{1}{\Delta t \left (\frac{1}{2} + \beta \right )} - \textbf{v}_{n} \frac{\left (\frac{1}{2} - \beta \right )}{\left (\frac{1}{2} + \beta \right )} \\ \omega _{n+1}&=\Delta \psi \frac{1}{\Delta t \left (\frac{1}{2} + \beta \right )} - \omega _{n} \frac{\left (\frac{1}{2} - \beta \right )}{\left (\frac{1}{2} + \beta \right )} , \end{aligned} $$

(87)

where $\beta \in [0, \frac{1}{2}]$ is the kinetic energy dissipation coefficient. The work done by inertia force can be simplified

$$ \begin{aligned} \Delta K &=\int _{L} {\left (\Delta \boldsymbol{\upvarphi}^{T} \cdot A_{\rho} \textbf{a}_{n+1/2} + \Delta \psi \cdot J_{\rho} \alpha _{n+1/2}\right )}ds \\ &=\frac{1}{2}\int _{L}{\left ({\textbf{v}_{n+1}}^{T} \cdot A_{\rho} \textbf{v}_{n+1} + {\omega _{n+1}} \cdot J_{\rho}\omega _{n+1} \right )ds} - \frac{1}{2}\int _{L}{\left (\textbf{v}_{n}^{T} \cdot A_{\rho} \textbf{v}_{n} + \omega _{n}\cdot J_{\rho}\omega _{n}\right )ds} \\ &+\beta \int _{L} {\left ( \left (\textbf{v}_{n+1}-\textbf{v}_{n} \right )^{T} \cdot A_{\rho} \left (\textbf{v}_{n+1}-\textbf{v}_{n} \right ) + J_{\rho} \left (\omega _{n+1}-\omega _{n}\right )^{2} \right )}ds \\ &=K_{n+1}-K_{n}+D_{K}. \end{aligned} $$

(88)

Similarly, we modify internal force algorithmic equations in Eq. (79):

$$ \begin{aligned} \textbf{N}_{n+1/2}&=\textbf{N}_{n+1/2}^{cons} + \alpha \mathbb{C}_{n}\left (\textbf{E}_{n+1} - \textbf{E}_{n} \right ) \\ M_{n+1/2}&=M_{n+1/2}^{cons} + \alpha \mathbb{C}_{m} \left (K_{n+1} - K_{n} \right ), \end{aligned} $$

(89)

where $\alpha \in [0,\frac{1}{2}]$ is the internal energy dissipation coefficient. The work done by potential forces can be rewritten as follows:

$$ \begin{aligned} \Delta \Pi&=\int _{L} {\left ((\textbf{E}_{n+1}- \textbf{E}_{n})^{T} \cdot \frac{1}{2}\mathbb{C}_{n} \left (\textbf{E}_{n+1} + \textbf{E}_{n} \right ) + \frac{1}{2}\mathbb{C}_{m} \left (K_{n+1}^{2} - K_{n}^{2} \right ) \right .} \\ &{\left . + \alpha (\textbf{E}_{n+1}-\textbf{E}_{n})^{T} \cdot \mathbb{C}_{n} \left (\textbf{E}_{n+1} - \textbf{E}_{n} \right ) + \alpha \mathbb{C}_{m} \left (K_{n+1} - K_{n} \right )^{2} \right ) ds} \\ &=\frac{1}{2}\int _{L} {\left (\textbf{E}_{n+1}^{T} \cdot \mathbb{C}_{n} \textbf{E}_{n+1} + \mathbb{C}_{m} K_{n+1}^{2} \right ) ds}-\frac{1}{2} \int _{L} {\left (\textbf{E}_{n}^{T} \cdot \mathbb{C}_{n}\textbf{E}_{n} + \mathbb{C}_{m}K_{n}^{2} \right ) ds} \\ & + \alpha \int _{L} {\left (\left (\textbf{E}_{n+1}-\textbf{E}_{n} \right )^{T} \cdot \mathbb{C}_{n}\left (\textbf{E}_{n+1}-\textbf{E}_{n} \right ) + \mathbb{C}_{m} \left (K_{n+1} - K_{n} \right )^{2} \right ) ds} \\ &=\Pi_{n+1}-\Pi_{n} + D_{\Pi}, \end{aligned} $$

(90)

where $D_{\Pi}\geq 0$ is a positive definite quadratic form of internal force dissipation term if $\alpha$ coefficient is taken positively.

$$ \begin{aligned} (K_{n+1}+\Pi_{n+1})-(K_{n}+\Pi_{n}) + D_{K}+D_{ \Pi}&=(\boldsymbol{\upphi}_{n+1}-\boldsymbol{\upphi}_{n})^{T} \cdot \textbf{f}_{ext} \\ \Rightarrow E_{n+1} - E_{n} + D_{K}+D_{\Pi} &= \Delta W. \end{aligned} $$

(91)

The result in Eq. (91) confirms that for any positive value of coefficients $\beta$ and $\alpha$, the system energy will be dissipated. A closer inspection of the algorithmic constitutive equation in (89) above reveals that the energy dissipation will most likely affect high-frequency modes for which a more significant change from energy-conserving equation will occur with a reasonable choice of time step granting computational accuracy.

4 Numerical examples

In this section we present numerical examples, which are firstly related to element verification and comparison with already known examples, while the second group of examples present new development. The element development and computation are done inside FEAP software [30].

4.1 Straight cantilever under imposed end rotation

In this example, we present different types of a response for a cantilever beam with imposed rotation $\psi =\pi$ at the right free-end, see Fig. 3a. The example consists of a separate analysis of linear elastic, elasto-viscoplastic with hardening, and elasto-viscoplastic with softening response. We chose to verify the model by considering that initially straight cantilever is constructed of several beam elements, 2, 4, and 8. The rest of chosen mechanical and geometry properties of the cantilever are set as follows: cross-section area $A=2$ $\text{cm}^{2}$, moment of inertia $I=0.1667$ $\text{cm}^{4}$, Young’s modulus $E=73$ GPa, hardening modulus $K=2$ GPa, yielding bending moment $M_{y}=5$ kNcm, ultimate bending moment $M_{u}=8$ kNcm, unit softening fracture energy $G_{f}=10\cdot 10^{3}$ kJ, and viscoplastic coefficients $\eta _{1}=1 \cdot 10^{6}$ Pas and $\eta _{2}=2\cdot 10^{7}$ Pas. The output results of computations are given in Table 1, and the last can be verified analytically according to the bending moment formula for linear elasticity $M_{e}=\pi \cdot EI/L$, elastoplasticity $M_{vp}=(\pi -\psi _{y})\cdot EK/((E+K)L) + \psi _{y}\cdot EI/L$ and elasto-viscoplasticity $M_{evp}=M_{ep} + \eta \cdot \dot{\varepsilon}_{y}I$. Elasto-viscoplastic computations are performed for different finite strain rates, see Fig. 3b, where we applied smaller $\eta _{1}$ and larger $\eta _{2}$ viscoplastic parameter.

Fig. 3

Straight cantilever under imposed end rotation: (a) Input geometry; (b) Input loading program; Output configurations: (c) Viscoplasticity, (d) Softening behavior

Table 1 Straight cantilever under imposed end rotation: Comparison between analytical and computed values of bending moment

The output configurations are given in Fig. 3c. The bending moment-strain relationship with respect to the different number of elements as well as for different strain rates is shown in Fig. 4. The other part of the example presents an analysis of elasto-viscoplastic response with softening phase, where the localized failure is placed in the middle of the cantilever. We consider one element of length $L=20$ cm to be the place of failure localization when it reaches the ultimate bending moment $M_{u}$. The output response, which includes softening, is depicted in Fig. 5a, where it can be seen that response is indifferent with respect to a number of elements. By varying the strain rate with an enforced constant value of unit fracture energy in softening, we show different results due to viscoplastic behavior in hardening, Fig. 5b.

Fig. 4

Straight cantilever under imposed end rotation: Output bending moment-strain relationship: (a) Linear elasticity, (b) Isotropic hardening, (c) Standard viscoplastic model, (d) Duvaut et Lions viscoplastic model

Fig. 5

Straight cantilever under imposed end rotation: Elasto-viscoplasticity with softening behavior for: a) $\eta = 0$ b) $\eta =2 \cdot 10^{7}$ Pas

4.2 Rigid flexible manipulator

This example was proposed in the previous works of Ibrahimbegovic [18], and it is selected to demonstrate the versatility of the presented development. The multibody system consists of rigid and flexible elements, which are connected by a revolute joint, see Fig. 6. We show here hinge with a nonlinear material profile that made the transition from plastic to perfect hinge can yield identical output results in comparison with the kinematic revolute joint [20]. The input data of flexible components are set $EA=GA=10^{6}$, $EI=GJ=10^{5}$, and $A=1$, while geometry is given in Fig. 6a. The rigid components are introduced as flexible ones, but with significantly increased parameters related to axial and bending stiffness (roughly ${EA}_{rigid}/{EA}_{flexible}>10^{3}$ and ${EI}_{rigid}/{EI}_{flexible}>10^{3}$).

Fig. 6

Rigid flexible manipulator: (a) Input geometry; (b) Output configurations

The weight of the components is considered very small, and thus we neglect the inertial effect. The planar mechanism is set in motion by applying the constant angular velocity $\omega =10$ rad/s to the rigid component, where the system undergoes vibrations. We note that computations are performed with small time steps $\Delta t=0.001$ s to capture the development of internal plasticity variables. Several discretizations are employed in computations for one, two, four, and eight beam elements. We employed two-phase computation to simulate a perfect hinge response. The first phase pertains to plastic hinge transition to perfect hinge $t\in [0,1]$ s (see Fig. 8), while in the second we compute system response for applied loading programme $t\in [1,3]$ s. The successive deformed configurations are taken at every time instant $\Delta t=2\pi /10$ s for one period, which is illustrated in Fig. 6b.

By comparing output displacements with respect to a different number of elements in Fig. 8, it can be seen that results are almost imperceptible. The plastic dissipation of the system in the second phase of the planar movement shows that there are no plastic processes, see Fig. 7, and indicates that a plastic hinge can behave like a true revolute joint.

Fig. 7

Rigid flexible manipulator: (a) Material profile of the hinge; (b) Plastic dissipation of the system

Fig. 8

Rigid flexible manipulator: Output results in case of 1,2,4, and 8 elements: (a) Horizontal, (b) Vertical displacement. Comparison of output results of kinematic joint and present formulation: (c) Horizontal, (d) Vertical displacement

4.3 Four-beam swing

To illustrate the performance of the proposed time-conserving scheme, we present here an example already discussed in [17, 19]. The problem pertains to the nonlinear dynamics of the planar mechanism, which consists of rigid and flexible elements depicted in Fig. 9a. The initially horizontal flexible beam is constructed of four finite elements with lumped mass $m$ placed in the half length of the flexible beam. The rigid components are modeled as a flexible finite element but with increased axial and bending stiffness ${EA}_{rigid}/{EA}_{flexible}>10^{2}$ and ${EI}_{rigid}/{EI}_{flexible}>10^{2}$, respectively.

Fig. 9

Four-beam swing: (a) Input geometry; (b) Input loading program; (c) Output configurations

The rest of the input data are set $E=73$ $\text{GN/m}^{2}$, $A=5x1$ $\text{mm}^{2}$, and $\rho =2700$ $\text{kg/m}^{3}$, while geometry is given in Fig. 9a. The connection between rigid and flexible elements is considered a revolute joint when the beam hinge passes through the plastic process. Therefore, the hinge with nonlinear softening law has the following mechanical properties: yielding moment $M_{y}=100$ MPa, ultimate moment $M_{u}=150$ MPa, and unit fracture energy $G_{f}=1.2 \cdot 10^{6}$ kNm. The system is set into motion by applying triangular load impulse $p$ on lumped mass $m=0.5$ kg in horizontal direction Fig. 9b. The four-beam mechanism undergoes vibrations where the response is captured in time interval $t\in [0,2.5]$ s for both time integration schemes. The plastic dissipation of beam hinges is modeled to have small fracture energy to not significantly affect total energy during vibrations, see Fig. 11d.

The output displacement of point $B$ (see Fig. 9a) is shown in Fig. 10a,b, where it can be noticed that system activates high-frequency modes at the time 0.64 s. Such frequencies pollute output results of axial and shear forces, see Fig. 10c,d. These vibrations remain preserved due to energy conservation property until the end of the computation, see Fig. 11a. The energy dissipation of high frequencies introduced via coefficients $\alpha =\beta =0.01$ reduces the noise of such modes at expense of the system energy (see Fig. 11b,c). This modification of the computation algorithm tends to stabilize output results, see Fig. 10d. In other words, the decaying scheme penalizes high frequencies by taking their energy until they are within an acceptable tolerance. The computation by energy decaying algorithm returns energy conservation property when the energy of high oscillations is dissipated, Fig. 10c.

Fig. 10

Four-beam swing: Output results at point B: (a) Horizontal displacement; (b) Vertical displacement; (c) Axial reaction; (d) Shear reaction

Fig. 11

Four-beam swing: The system energy: (a) Energy-conserving scheme, (b) Energy decaying scheme; (c) Comparison of the total system energy; (d) Plastic dissipation

Another important finding can be deduced from Fig. 10a,b, which pertains to the adoption of parameters $\alpha$ and $\beta$. Namely, by finding suitable parameters, we can obtain optimal performance of the energy decaying algorithm, where the high frequencies are damped out, but without significant deterioration of the output results, see Fig. 10a,b.

4.4 Vibrating frame

We propose this example to present the damping effect generated by the inelastic material response. The frame consists of three linear elastic beams, where the top-right connection of beams is modeled as a plastic hinge, see Fig. 12a. Here we choose the material profile of the plastic hinge that corresponds to linear elasticity with softening response. By selecting different amounts of unit fracture energy $G_{f}$, we can obtain different responses from the system. The chosen properties of the joint connection between beams: cross-section area $A=10$ $\text{cm}^{2}$, moment of inertia $I=1$ $\text{cm}^{4}$, Young’s modulus $E=1$ GPa, hardening modulus $K=500$ MPa, yielding bending moment $M_{y}=300$ kNcm, ultimate bending moment $M_{u}=315$ kNcm, and fracture energy $G_{f}=600$ kNcm.

Fig. 12

Vibrating frame: (a) Input geometry; (b) Input loading program; (c) Output total displacement field

The impulse $p$ is applied in a horizontal direction on the top-left corner of the frame for all computations. We use energy-conserving scheme to compute the response for time period $t \in [0,15]$ s with chosen time step $\Delta t=0.001$ s. The output configurations are shown in Fig. 12b, and they are captured for each time instant 0.1 s until the computation reaches 2 s. The horizontal and vertical displacements of the frame top-right corner are given in Fig. 13a,b with respect to the amount of fracture energy $G_{f}$. It can be easily noticed decay in displacement Fig. 13a,b and total energy Fig. 14a,b,c by decreasing the amount of fracture energy. The corresponding relationship between fracture energy $G_{f}$ and damping ratio $\zeta$ for horizontal and vertical displacement is given in Table 2

Fig. 13

Vibrating frame: The output displacement of the point A: (a) Horizontal direction, (b) Vertical direction

Fig. 14

Vibrating frame: Total system energy decay for: (a) $G_{f} = 6000$ kNcm, (b) $G_{f} = 600$ kNcm; (c) Relationship between displacement decay and amount of fracture energy; (d) Plastic dissipation

Table 2 Vibrating frame: Corresponding relationship between damping ratios $\zeta$ and fracture energy $G_{f}$ computed via logarithmic decrement method

In other words, by increasing fracture energy, see Fig. 14a, the damped energy is reduced since the total energy is not dissipated on plastic processes, and thus the frame remains vibrating in elasticity. This can be justified by considering the nonlinear softening law where it can be seen that fracture energy directly contributes to the value of the softening modulus, plastic multiplier and stress resultant, which consequently determine plastic dissipation. The critical amount of fracture energy needed to stop oscillations is related to the accumulated energy of the vibrating frame, see Fig. 14b. By varying the fracture energy, we present a family of curves where each of them describes total energy decay Fig. 14c, as well as plastic dissipation in Fig. 14d.

4.5 Damping model replacement of Rayleigh damping

The damping model of viscoplasticity can also be given a multi-scale interpretation, which allows to illustrate how the fine-scale processes stochastically upscale to coarse scale in dynamics. This is further illustrated with a simple example problem of a 1D beam multi-scale model (see Fig. 15).

Fig. 15

Simple problem to illustrate stochastic upscaling in the dynamical system: (a) Multi-scale 1D beam model; (b) Experimental stress-strain hysteresis loops; (c) Numerical model hysteresis loops

First option is to use a macro-scale 1D beam with homogenized elastic behavior, where eventual energy dissipation can be represented by viscoelastic behavior and classical Rayleigh damping. Such a damping effect is proportional to velocity with a damping matrix ${\mathbf{C}}$ as a linear combination of structure mass ${\mathbf{M}}$ and stiffness matrices ${\mathbf{K}}$ [7]; see Fig. 92. Next, to model simplicity with only one model parameter, the so-called damping ratio $\xi$, the main advantage of Rayleigh damping is in matching the experimentally observed exponential decay of the vibration amplitude that can be quantified by the logarithmic decrement $\delta$, which is proportional to the damping ratio, see Fig. (92). The main deficiency of Rayleigh damping is that the damping ratio $\xi$ is a structural property, which pertains only to a particular structure size, characterized by its stiffness and mass matrices (e.g., see [7]).

$$ \textstyle\begin{array}{l} {\mathbf{M}} \ddot{\boldsymbol{\upphi}}(t) + {\mathbf{C}} \dot{\boldsymbol{\upphi}}({t}) + {\mathbf{K}} \boldsymbol{\upphi}({t}) = { \mathbf{f}}({t}) \ ; \ {\mathbf{C}}={a}_{0} {\mathbf{M}}+{a}_{1} {\mathbf{K}}, \\ \xi ={a}_{0} / 2 \omega _{{n}} \ ; \ \xi =a_{1} \omega _{{n}} / 2 \ ; \ \delta \equiv \ln \frac{v_{n}}{v_{n+1}}= \frac{2 \pi \xi}{\sqrt{1-\xi ^{2}}} . \end{array} $$

(92)

An alternative option is to use the material model with fine-scale plasticity, where the damping ‘ratio’ can be used for a different structure size without the need for new experiments. Namely, we use a multi-scale model of energy dissipation, which can deal with all progressive stages of dynamic fracture (with hardening and softening) and also capture the size effect. In particular, we will use a cyclic-plasticity with combined hardening and softening at micro-scale beam model to reproduce the area of experimentally observed hysteresis loops, see Fig. 15.

For computational efficiency, in each particular fiber we keep linear evolution equations of corresponding internal variables (plastic strain ${\epsilon}^{\mathrm{p}}$ hardening variables for plasticity ${\xi}^{\mathrm{p}}$, and variables that handle softening phase, both for plasticity $\bar{\bar{\upphi}}^{\mathrm{p}}$, see Eq. (93). With this simple choice, we cannot match experimental hysteresis loops in terms of their shape, but rather in terms of the enclosed area representing the energy dissipated in each hysteresis loop, see Fig. 15.

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \dot{\epsilon}^{\mathrm{p}} = \dot{\gamma}^{\mathrm{p}} \frac{\partial \phi ^{\mathrm{p}}}{\partial \sigma} ; & \dot{\xi}^{ \mathrm{p}}=\dot{\gamma}^{\mathrm{p}} \frac{\partial \phi ^{\mathrm{p}}}{\partial q^{\mathrm{p}}}; & {\phi}^{ \mathrm{p}}(\sigma , \overline{q}^{\mathrm{p}}, \overline{\kappa}^{ \mathrm{p}}) =|\sigma +\overline{\kappa}^{\mathrm{p}}|-(\sigma _{y}- \overline{q}^{\mathrm{p}}) \\ \dot{\bar{\bar{\upphi}}}^{\mathrm{p}} = \dot{\overline{\overline{\gamma}}}^{\mathrm{p}} \frac{\partial {\overline{\overline{\phi}}}^{\mathrm{p}}}{\partial \overline{\overline{t}}^{\mathrm{p}}} ; & \dot{\overline{\overline{\xi}}}^{\mathrm{p}} = \dot{\overline{\overline{\gamma}}}^{\mathrm{p}} \frac{\partial \overline{\overline{\phi}}^{\mathrm{p}}}{\partial \overline{\overline{q}}^{\mathrm{p}}} ; & \overline{\overline{\phi}}^{\mathrm{p}}({t}, \overline{\overline{q}}^{\mathrm{p}})= |{t}| -(\sigma _{u}^{c}- \overline{\overline{q}}^{\mathrm{p}}). \end{array} $$

(93)

The multi-scale approach combines these micro-scale evolution equations with a hybrid displacement-stress formulation for macro-scale state variables, and with their independent interpolation with an additive decomposition of internal variable contributions that simplify tangent stiffness computations

$$ \textstyle\begin{array}{l} \sum _{f} A_{f} \int _{L}\left (\tilde{w} \rho \frac{\partial ^{2} \tilde{\upphi}}{\partial t^{2}} + \frac{\partial \tilde{w}}{\partial x} \sigma _{f}\right ) \, dx - G^{ \mathrm{ext}}=0 \\ \int _{L} \tau _{f}\left (\frac{\partial \tilde{\upphi}}{\partial x}-{ \epsilon}^{{\mathrm{p}}}-{\overline{\overline{\upphi}}}^{{\mathrm{p}}} \frac{d \varphi _{i}}{\, dx}\right ) \, dx = 0, \quad \forall f \end{array} $$

(94)

with

$$ \textstyle\begin{array}{l} \left .\tilde{\upphi}^{h}({\mathbf{x}}, t)\right |_{{\mathbf{x}} \in \Omega ^{e}}={ \mathbf{N}}({\mathbf{x}}) {\upphi}^{e}(t) \\ \left .\sigma ^{f, h}(x, t)\right |_{{\mathbf{x}} \in \Omega ^{e}}={\mathbf{S}}(x) \beta ^{f}(t). \end{array} $$

The proposed approach results in a very efficient multi-scale computational model combining global and local equations that is capable of capturing energy dissipation in each particular stage of the beam ductile failure, with a cost that is comparable to the solution of Eq. (92) with a standard time stepping scheme.

$$ \textstyle\begin{array}{l} {\mathbf{M}} \ddot{{\boldsymbol{\upphi}}}(t) + \mathbb{A}_{f=1}^{n_{f}} { \mathbf{f}}_{f}^{int} (t) = {\mathbf{f}}^{ext}(t) \\ \dot{\gamma}^{\mathrm{p}} \geq 0, \phi ^{\mathrm{p}} \leq 0, \dot{\gamma}^{\mathrm{p}} \phi ^{\mathrm{p}}=0 , \\ \dot{\overline{\overline{\gamma}}}^{\mathrm{p}} \geq 0, \overline{\overline{\phi}}^{\mathrm{p}} \leq 0, \dot{\overline{\overline{\gamma}}}^{\mathrm{p}} { \overline{\overline{\phi}}}^{\mathrm{p}}=0 . \end{array} $$

(95)

The final step is to consider the probability distribution of structure heterogeneities, as illustrated in Fig. 16a for the case of a plastic component with simple Gaussian distribution of the yield stress $\sigma _{y}$ for each fiber. We note that such an assumption is equivalent to assuming a random field distribution of the beam structure macro-scale properties, given the beam bending problem with linear stress distribution. A larger beam structure size (with a more likely concentration of initial and induced defects) results in stronger heterogeneities and thus a larger standard deviation $\tau$. For such a large (heterogeneous) structure, we show in Fig. 16b the multi-scale model ability to recover exponential amplitude decay, as opposed to linear amplitude decay for a smaller (homogeneous) structure with almost constant yield stress everywhere; (linear amplitude decay is characteristic of frictional energy dissipation [24], which confirms the equivalence between plasticity and friction [14]). In conclusion, the multi-scale model of damping can represent the size effect through the crucial role of the probability distribution of structure-scale heterogeneities.

Fig. 16

Simple problem to illustrate stochastic upscaling in the dynamical system: (a) Gaussian probability distribution of yield stress $\sigma _{y}$ as a random variable with $\tau$ as a standard deviation; (b) Amplitude decay computed with the proposed multi-scale model, indicating a transition from linear amplitude decay for homogeneous structure (bottom graph with $\tau =0.01$) towards exponential amplitude decay for heterogeneous structure (top graph with $\tau =1.06$), adapting energy dissipation to structure size with more likely heterogeneities for larger structures

5 Conclusion

Some of the most salient features of the developments presented herein are as follows. We employed mixed variational formulation of geometrically exact beams to introduce strong discontinuity into the rotation field to model nonlinear material softening behavior. We extended formulation to dynamics where we used the second-order scheme, which demands rate-dependent plasticity formulation that allows integrating the rate equations and equations of motion simultaneously.

In particular, the viscoplastic material model is introduced for isotropic hardening. Since the standard model for computation of viscoplasticity is not a suitable choice for vanishing values of viscosity parameter, we chose Duvaut and Lions [8, 14] approach over Perzyna model [14, 28] to compute the stresses in the local phase of computation. The proposed formulation can also handle the softening behavior and thus handle all different stages of response leading towards an emergency stop activation under extreme loads.

The performance of the proposed finite element model is tested under both static and transient loading for both linear and nonlinear response to illustrate the model robust performance. Of particular interest for model robustness is the energy-conserving solution scheme that offers the stability of numerical computation over a long time period. The stress computation accuracy can be achieved even with fairly coarse mesh by eliminating the contribution of high-frequency modes by using the energy-decaying scheme.

In particular, we have demonstrated that, by including the heterogeneities in viscoplastic behavior of the material, one can obtain the same exponential decay of vibration amplitude in free vibration phase as for viscoelasticity model [2], which allows us to replace the simple Rayleigh damping model not representative of real material behavior [14].

Finally, we note that the proposed methodology carries over to the 3D case, which requires dealing with a more demanding consideration of nonvectorial character of 3D finite rotations [12, 13]. The details of such developments are left for subsequent publication.