Cohesive Zone Model Analysis, Development, and Application in Mixed-Mode Arterial Dissection

Abstract

Recent studies have presented evidence that aortic dissection entails mode II and mixed-mode crack growth. In the present chapter we analyze the mixed-mode behavior of two exponentially softening path-dependent cohesive zone models (CZMs). We demonstrate that these models provide physically realistic tractions and positive incremental dissipation during proportional and non-proportional loading paths. In contrast, we demonstrate that potential-based path-independent CZMs can potentially result in the calculation of physically unrealistic repulsive normal tractions and negative incremental dissipation. Our recent experiments suggest that mode II fracture strength of the aorta in the circumferential-axial plane is significantly higher than the mode I strength in the same plane. We demonstrate that such anisotropic interface behavior renders potential-based CZMs unsuitable for simulation of aortic dissection. Using our new non-potential path-dependent CZM we simulate aortic dissection due to the presence of a notch in the radial-axial plane of the aorta. Simulations suggest that significant dissection propagation only occurs in cases of extreme hypertension. Additionally, we demonstrate that blood pressure loading in a false lumen will result in a mixed-mode traction state at the crack tip, with significant crack-tip blunting acting as a toughening mechanism against significant propagation of the false lumen.

From an early stage in my career I have closely followed Gerhard’s seminal work on anisotropic soft tissue behavior. His rigorous and fundamental mechanistic advances have been key to the establishment of the field of computational biomechanics. Gerhard has been a generous and inspirational mentor and friend, and there have been many highlights over the years. He invited me to present at his special symposium on soft tissue modeling at ESMC in Madrid, after which we had some truly excellent discussions. I was particularly honored when Gerhard traveled to Galway to deliver a wonderful keynote lecture when I chaired the National Irish Bioengineering Conference in 2016. I was truly delighted when Gerhard appointed me as Visiting Professor at TU Graz in 2017, allowing me to spend two wonderful weeks at his Institute for Biomechanics. This was a memorable experience; in addition to delivering a graduate module, I had the pleasure of working with Gerhard on the development of a micromechanical model of the myocardium. Gerhard also gave me fantastic experience of Austrian culture and cuisine, in addition to a unique St. Patrick’s day celebration in Graz! Gerhard, thank you always for your generosity, support and friendship. Patrick

Gerhard has been my role model since I started my masters in the field of solid mechanics in 2009. Five years later, I first met Gerhard in Graz when I had the honor of a six month visit to his institute as a visiting researcher. I had the pleasure of working with Gerhard on the development of a mechanobiological model for growth of arterial tissue. He gave me a deep insight into the field of continuum thermodynamics. I was particularly honored when Gerhard accepted to be my PhD co-supervisor. Gerhard, I appreciate all of your supports and kindness. I look forward to continue collaboration in the future. Behrooz

I attended Professor Holzapfel’s Summer School at the Institute of Biomechanics in Graz in 2016. It was a truly inspirational and memorable experience. Thank you for providing this wonderful opportunity. Brian

1 Introduction

The progression and pathogenesis of aortic dissection (AD)  is relatively poorly understood compared to other cardiovascular diseases (Vilacosta et al. 2009; Criado 2011). For example, several clinical studies suggest that AD occurs as a result of initial damage to the intima, with such damage referred to in clinical literature as an ‘intimal tear’  or ‘entry tear’ (Larson and Edwards 1984; Criado 2011; Lemaire and Russel 2011; Kim et al. 2014). However, a number of clinical studies report AD without an intimal tear (Lui et al. 1992; Eichelberger 1994; Utoh et al. 1997; Colli et al. 2018). Conversely, an intimal tear may present without extensive AD, indicating early arrest of tear propagation (Svensson et al. 1999). AD is typically characterized in the clinical literature as the occurrence of a true and false lumen separated by an intraluminal septum (Hasleton and Leonard 1979; Sayer et al. 2008; Nienaber et al. 2010; Huang et al. 2015). The end point of the false lumen is typically used to indicate the extent of the AD, which may be as short as 1 cm from the original entry tear (Svensson et al. 1999) or as long as the entire aorta and iliac vessels (${>}1$ m) (Dotter et al. 1950; Hagan et al. 2000; Dake et al. 2013; Qiao et al. 2015; Gambardella et al. 2017).

In recent years there have been a myriad of numerical studies examining the fluid dynamics of AD, and more recently, studies examining AD from a fluid-structure interaction standpoint (Cheng et al. 2013, 2014; Alimohammadi et al. 2015; Doyle and Norman 2016; Ryzhakov et al. 2019; Bäumler et al. 2020; Xiong et al. 2020; Zorrilla et al. 2020). Many of these studies explore subject matter such as the effect of bypassing the false lumen on fluid flow using a bypass graft (Qiao et al. 2015), development of patient-specific models (Alimohammadi et al. 2015; Xiong et al. 2020), and analysis of intraluminal septum rigidity (Bonfanti et al. 2018). However, to the authors’ knowledge, no study to date has examined the risk of false lumen propagation from a fracture mechanics standpoint. In the present chapter we investigate the application of mixed-mode cohesive zone models  (CZMs) to analyze AD risk. We begin the chapter with an analysis of mixed-mode cohesive zone formulations. Cohesive zone models have been extensively used to describe an interface undergoing separation (Barenblatt 1959; Xu and Needleman 1993; van den Bosch et al. 2006; McGarry et al. 2014). CZMs have been used to model crack propagation in ductile metals (Nielsen 2012), polyethylene (Ivankovic et al. 2004), porous materials (Nakamura and Wang 2001) and concrete beams (Aure and Ioannides 2010). They have also been used to model the delamination of cells from substrates (McGarry and McHugh 2008), polymer coatings from stents (Hopkins et al. 2010; McGarry et al. 2014), inter-laminar failure in carbon-fiber laminates (Gallagher et al. (2018, 2019)), failure of coatings of diamond-coated cutting tools (Hu et al. 2008), and separation of arterial layers (Gasser and Holzapfel (2006, 2007); Ferrara and Pandolfi 2010; Wang et al. 2017; Noble et al. 2017; Gültekin et al. 2019; FitzGibbon and McGarry 2020). The calibration of CZM parameters requires experimental testing data (Ivankovic et al. 2004; Di Leo et al. 2014; Wu et al. 2016). The primary outputs of these tests are interface strength and fracture energy. It is extremely difficult to measure the stiffness of interfaces in highly elastic materials. The characteristic length $(\delta )$ or the modulus (K) of the initial elastic region of some CZMs often dictates the fracture energy (G) and vice versa. This is common in exponential CZM formulations as seen in Xu and Needleman (1993), van den Bosch et al. (2006) and Dimitri et al. (2015). Therefore, the choice of fracture energy may anomalously influence the stiffness and characteristic length of the interface.

Piecewise CZMs allow for the specification of K (and by extension $\delta$) and G independently (Camanho et al. 2003; Park et al. 2009). Choice of CZM should be motivated by experimental data and boundary conditions. CZMs may be coupled or uncoupled. In a coupled CZM the traction depends on the separation vector which will include both normal and tangential opening $(\Delta _\mathrm {n}, \Delta _\mathrm {t})$, whereas in an uncoupled CZM the normal traction $(T_\mathrm {n})$ depends only on the normal opening $(\Delta _\mathrm {n})$. Most engineering applications involve mixed separation and therefore should implement mixed-mode (coupled) CZMs. Achieving a physically realistic mixed-mode response is important in such applications. Many constitutive relationships of traction-separation laws have been proposed, these include but are not limited to, linear softening (Camacho and Ortiz 1996), bilinear softening, cubic polynomial, exponential (Xu and Needleman 1993; van den Bosch et al. 2006; McGarry et al. 2014), exponential softening, and trapezoidal (Tvergaard and Hutchinson 1992).

In the first part of this chapter we investigate the suitability of several cohesive zone formulations for mixed-mode dissection. We firstly consider exponential softening model and introduce a feature whereby tangential interface strength can be augmented as a function of compressive normal traction. We also explore the extension of such exponential softening models to a potential-based formulation. We demonstrate that the derivation of path-independent tractions separation relationships from a potential function results in non-physical behavior. In the second part of this chapter we apply our mixed-mode exponential softening CZM to the analysis of AD. We consider the evolution of AD due to pre-existing intraluminal septum and a patent false lumen. Simulations suggest that extensive propagation of a false lumen will not occur at a slightly hypertensive systolic pressure  of 140 mmHg in a healthy aorta. Even in extreme hypertensive loading conditions AD propagation is arrested due to blunting of the crack tip and an increase in the mode angle towards mode II. We also investigate if an intimal tear (radial notch) will result in extensive AD under physiological and super-physiological lumen blood pressure. Simulations suggest that propagation of an intimal tear is not predicted for pressures less than $p=275$ mmHg in a healthy aorta.

2 Analysis of CZMs in Mixed-Mode Dissection

2.1 Development of Non-Potential Based Mixed-Mode CZMs with Exponential Damage and Overclosure Penalization (CZM1 and CZM2)

For  a given interface displacement vector ${\boldsymbol{\Delta }}$ with normal and tangential (shear) components $\Delta _\mathrm {n}$ and $\Delta _\mathrm {t}$, respectively, the corresponding displacement magnitude is given as $\Delta _\mathrm {m}=\left( {\Delta _\mathrm {n}}^2+{\Delta _\mathrm {t}}^2\right) ^{1/2}$ and the mode angle is given as $\varphi =\tan ^{-1}{\left( {\Delta _\mathrm {t}}/{\Delta _\mathrm {n}}\right) }$. The magnitude of the interface traction is expressed as a function of $\Delta _{\mathrm n}$ and $\varphi$ by the following formulation:

$$\begin{aligned} T_\mathrm {m}\left( \mathrm {\Delta }_\mathrm {m},\varphi \right) = \left\{ \begin{array}{lc} K_\mathrm {m} \Delta _\mathrm {m}, \quad &{} \Delta _\mathrm {m} < T_\mathrm {m}^{\mathrm {max}}(\varphi )/K_\mathrm {m}. \\ K_\mathrm {m} T_\mathrm {m}^{\mathrm {max}}(\varphi )/K_\mathrm {m} \Psi (\varphi ), \quad &{} \Delta _\mathrm {m} \ge T_\mathrm {m}^{\mathrm {max}}(\varphi )/K_\mathrm {m}. \end{array} \right. \end{aligned}$$

(1)

We refer to $\Psi$ as the integrity of the interface (i.e. $\Psi =(1-D)$, where D is referred to as the interface damage). $\Psi$ monotonically decreases from 1 to 0 with increasing interface separation, such that

$$\begin{aligned} \Psi (\varphi )=\exp {\left( -\frac{\mathrm {\Delta }_\mathrm {m}^{\mathrm {max}}-T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) /K_\mathrm {m}}{\delta _\mathrm {m}^*\left( \varphi \right) }\right) }\left. \ \frac{\Delta _\mathrm {m}}{\Delta _\mathrm {m}^{\mathrm {max}}},\right. \end{aligned}$$

(2)

where $K_\mathrm {m}$ is the intrinsic elastic stiffness of the interface. $K_\mathrm {m}$ is assumed to be mode-independent. $T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right)$ is the specified mode-dependent interface strength; the corresponding displacement ${(\delta }_\mathrm {m}^{\mathrm {el}}\left( \varphi \right) =T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) /K_\mathrm {m})$ represents the elastic limit of interface separation at the point of damage initiation. The mode-dependent parameter $\delta _\mathrm {m}^*\left( \varphi \right)$ governs the rate of softening in the damage region $\Delta _\mathrm {m} \ge T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) /K_\mathrm {m}$. The interface strength is defined as a function of the mode as follows:

$$\begin{aligned} \displaystyle T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) =\tau _{\mathrm {max}}-\left[ \frac{\tau _{\mathrm {max}}-\sigma _{\mathrm {max}}}{1-\exp {\left( -\left. \ \frac{\pi /2}{\Omega ^\mathrm{T}}\right. \right) }}\right] \left[ 1-\exp {\left( -\left. \ \frac{\varphi }{\Omega ^\mathrm{T}}\right. \right) }\right] , \end{aligned}$$

(3)

where $\tau _{\mathrm {max}}$ is the mode II interface strength, $\Omega ^\mathrm{T}$ sets the nonlinearity of the transition from mode II to mode I, and $\sigma _{\mathrm {max}}$ is the mode I interface strength. The mode mixity of the initial interface damage parameter $\delta _\mathrm {m}^*\left( \varphi \right)$ is obtained from

$$\begin{aligned} \delta _\mathrm {m}^*\left( \varphi \right) =\frac{G_\mathrm {m}\left( \varphi \right) \ }{T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) }-\frac{T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) }{2K_\mathrm {m}}, \end{aligned}$$

(4)

where $G_\mathrm {m} (\varphi )$ is the mode-dependent fracture energy

$$\begin{aligned} G_\mathrm {m}\left( \varphi \right) =&\frac{1}{2} K_\mathrm {m} {\delta _\mathrm {m}^{\mathrm {el}} \left( \varphi \right) }^2 + \int _{T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) /K_\mathrm {m}}^{\infty } { T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) \exp {\left( -\frac{\mathrm {\Delta }_\mathrm {m}^{\mathrm {max}}-T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) /K_\mathrm {m}}{\delta _\mathrm {m}^*}\right) }\mathrm {d}\Delta _\mathrm {m} } . \end{aligned}$$

(5)

We may specify the mode-dependence of $G_\mathrm {m} (\varphi )$ using the following function:

$$\begin{aligned} G_\mathrm {m}\left( \varphi \right) =G_{\mathrm t}^0-\left[ \frac{G_{\mathrm t}^0-G_{\mathrm n}^0}{1-\exp {\left( -\left. \ \frac{\pi /2}{\Omega ^\mathrm{G}}\right. \right) }}\right] \left[ 1-\exp {\left( - \frac{\varphi }{\Omega ^\mathrm{G}}\right) }\right] , \end{aligned}$$

(6)

where $G_{\mathrm t}^0$ is the mode II fracture energy and $G_{\mathrm n}^0$ is the mode I fracture energy. $\Omega ^\mathrm{G}$ sets the nonlinearity of the transition from mode II to mode I. Finally, we complete the description of the cohesive zone formulation by decomposing $T_\mathrm {m}$ into the normal and tangential components, $T_{\mathrm n}$ and $T_{\mathrm t}$, respectively, such that

$$\begin{aligned} T_{\mathrm n}= \left\{ \begin{array}{lc} K_{\mathrm {{n_{oc}}}} \Delta _{\mathrm n}, &{} \quad \Delta _{\mathrm n} < 0, \\ T_\mathrm {m} \sin {\varphi }, &{} \quad \Delta _{\mathrm n} \ge 0, \end{array} \qquad T_{\mathrm t}=T_\mathrm {m} \cos (\varphi ),\right. \end{aligned}$$

(7)

where $K_{\mathrm {{n_{oc}}}}$ is the overclosure penalty stiffness. We include a dependence of the mode II interface strength, $\tau _{\mathrm {max}}$, on normal compression at the interface, such that

$$\begin{aligned} \tau _{\mathrm {max}}(T_{\mathrm n})= \left\{ \begin{array}{lc} \tau _{\mathrm {max}}^{\mathrm {nc}} (T_{\mathrm n}), \quad &{} \Delta _{\mathrm n} < 0, \\ \tau _{\mathrm {max}}^{0}, \quad &{} \Delta _{\mathrm n} \ge 0, \end{array} \right. \end{aligned}$$

(8)

as described in Eq. (9). The mode II interface strength increases with increasing (negative) normal traction, such that

$$\begin{aligned} \tau _{\mathrm {max}}^{\mathrm {nc}}(T_{\mathrm n})=\tau _{\mathrm {max}}^0\ +\tau _{\mathrm {max}}^0(F_{\mathrm {oc}}-1) \left[ 1-\exp \left( \frac{T_{\mathrm n}K_{\mathrm {{n_{oc}}}}^*/\sigma _{\mathrm {max}}}{K_\mathrm {m}}\right) \right] , \end{aligned}$$

(9)

where $\tau _{\mathrm {max}}^{\mathrm {nc}} (\Delta _{\mathrm n})$ is the increased value of tangential strength due to a normal compression at the interface. $\tau _{\mathrm {max}}^0$ is the maximum tangential strength, as encountered during a pure mode II separation when $\Delta _{\mathrm n}=0$ and $T_{\mathrm n}=0$. The parameter $F_{\mathrm {oc}}$ prescribes the maximum (plateau) value of increased shear strength due to compressive normal tractions at the interface. The parameter $K_{\mathrm {{n_{oc}}}}^*$ governs the sensitivity of maximum (plateau) shear stress to compressive normal tractions. Unless otherwise stated, we assume that $\tau _{\mathrm {max}}{=\tau }_{\mathrm {max}}^0$, i.e. maximum tangential strength is not increased due to normal compression at the interface.

2.2 Alternative Form of Damage and Softening (CZM2)

To demonstrate that alternative forms of damage softening laws can be readily incorporated into our CZM framework, we next present a small modification of Eq. (2) whereby in which exponential damage is assumed to depend on the square of the interface separation. Again, starting with Eq. (1), and the integrity of the interface, $\Psi$ is now defined as

$$\begin{aligned} \Psi (\varphi )=\exp {\left[ -\left( \frac{\mathrm {\Delta }_\mathrm {m}^{\mathrm {max}} - T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) / K_\mathrm {m}}{\delta _\mathrm {m}^*\left( \varphi \right) }\right) ^2\right] } \frac{\Delta _\mathrm {m}}{\Delta _\mathrm {m}^{\mathrm {max}}}. \end{aligned}$$

(10)

We make use of the same relation of $G(\varphi )=\int _{0}^{\infty }{T_\mathrm {m}\left( \Delta _\mathrm {m},\varphi \right) \mathrm {d}\Delta _\mathrm {m}}$ in order to obtain an expression for $\delta _\mathrm {m}^*$. The description of $G_\mathrm {m}(\varphi )$ is given as follows

$$\begin{aligned} \begin{aligned} G_\mathrm {m}\left( \varphi \right) =\,&\frac{1}{2}K_\mathrm {m}{\delta _\mathrm {m}^{\mathrm {el}}\left( \varphi \right) }^2 \\&+\int _{T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) /K_\mathrm {m}}^{\infty }{T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) \exp {\left[ -\left( \frac{\mathrm {\Delta }_\mathrm {m}^{\mathrm {max}} - T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) / K_\mathrm {m}}{\delta _\mathrm {m}^*\left( \varphi \right) }\right) ^2\right] }\mathrm {d}\Delta _\mathrm {m}}. \end{aligned} \end{aligned}$$

(11)

Integrating we get the following expression which includes the error function

$$\begin{aligned} G_\mathrm {m}=\frac{1}{2}K_\mathrm {m}{\delta _\mathrm {m}^{\mathrm {el}}\left( \varphi \right) }^2+T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) \left\{ \lim _{\Delta _\mathrm {m}\rightarrow \infty }{\left[ \frac{1}{2}\sqrt{\pi }\ \delta _\mathrm {m}^*\left( \varphi \right) {\left( \frac{\mathrm {\Delta }_\mathrm {m} - T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) / K_\mathrm {m}}{\delta _\mathrm {m}^*\left( \varphi \right) }\right) }\right] }\right\} . \end{aligned}$$

(12)

As $\Delta _\mathrm {m}\rightarrow \infty$ we arrive at the final expression for $\delta _\mathrm {m}^*(\varphi )$, i.e.

$$\begin{aligned} \delta _\mathrm {m}^*(\varphi )=-\frac{T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) }{K_\mathrm {m}\sqrt{\pi }}+\frac{2G_\mathrm {m}(\varphi )}{\sqrt{\pi }T_\mathrm {m}^{\mathrm {max}}\left( \varphi \right) }. \end{aligned}$$

(13)

2.3 Exploration of CZM1 and CZM2 Behavior

We firstly present the response of CZM1 and CZM2 to pure mode II loading, as shown in Fig. 1a. Normalized tangential traction $T_{\mathrm t}/\tau _{\mathrm {max}}$ is presented as a function of normalized tangential separation $\Delta _{\mathrm t}/\delta _{\mathrm t}^{\mathrm {el}}$. Traction increases according to the interfacial stiffness $K_\mathrm {m}$ until the prescribed mode II strength $\tau _{\mathrm {max}}$ is reached. Further deformation results in damage and softening. Due to the form of the respective exponential damage laws, CZM1 initially softens at a faster rate than CZM2. An expression for the instantaneous incremental energy dissipation (Cazes et al. 2009) is given as $\mathrm {d}\phi _i= 0.5 ( \mathbf{T}\mathrm {d}{\boldsymbol{\Delta }}- {\boldsymbol{\Delta }}\mathrm {d}\mathbf{T})$. As shown in Fig. 1b, positive instantaneous incremental energy dissipation is observed throughout the mode II separation for both CZM1 and CZM2.

Fig. 1

(a) Normalized traction separation curves for a mode II separation for both formulations of the proposed model ($K_\mathrm {m}=10$ MPa, $\tau _{\mathrm {max}}=5$ MPa, $G_{\mathrm t}^0=10$ N/mm); (b) instantaneous incremental energy dissipation ${\mathrm d}\phi _i/\phi _{\mathrm t}$ as a function of normalized tangential separation for CZM1 and CZM2 during a mode II displacement

Fig. 2

(a) Influence of compressive normal tractions on tangential fracture; (b) maximum tangential traction shown as a function of the $F_{\mathrm {oc}}$ parameter

In Fig. 2a we explore the influence of normal compressive tractions on tangential fracture. An increase in magnitude of a compressive normal traction $T_{\mathrm n}$ (with $T_{\mathrm n}<0$) results in an increase in $\tau _{\mathrm {max}}^{\mathrm {nc}} (T_{\mathrm n})$, up to a plateau value of $\tau _{\mathrm {max}}^0 F_{\mathrm {oc}}$ as $T_{\mathrm n}\rightarrow -\infty$. Figure 2b further explores the influence of a fixed applied normal separation on the maximum tangential traction, $T_{\mathrm {max}}$, encountered during a subsequent tangential separation. As expected, normal interface separation $\Delta _{\mathrm n}>0$ results in a reduction in $T_{\mathrm {max}}$. In contrast, if $\Delta _{\mathrm n}<0$ a negative normal traction $T_{\mathrm n}<0$ is obtained through the overclosure penalty term (Eq. (8)). This results in an increase in $\tau _{\mathrm {max}}^{\mathrm {nc}} (T_{\mathrm n})$ up to a plateau value with increasingly negative normal traction.

Fig. 3

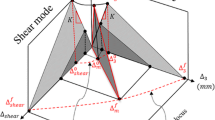
Mixed-mode response of each CZM undergoing proportional loading ranging from mode II to mode I. Normalized traction versus separation in the normal direction (b), (d) and tangential direction (a), (c) for CZM1 (a), (b), CZM2 (c), (d) undergoing proportional loading. $K_\mathrm {m}=10$ MPa, $\tau _{\mathrm {max}}=5 \sigma _{\mathrm {max}}$, $G_{\mathrm t}= 5 G_{\mathrm n}$

Proportional loading paths: CZM1 and CZM2 are examined under mixed-mode proportional loading conditions whereby $\Delta _\mathrm {m}$ increases at a constant mode angle $\varphi$. Computed traction-separation responses are presented in Fig. 3 for the case of $K_\mathrm {m}=10$ MPa, $\tau _{\mathrm {max}}=5 \sigma _{\mathrm {max}}$, $G_{\mathrm t}= 5 G_{\mathrm n}$, $\Omega ^\mathrm{T}=\pi /16$, $\Omega ^\mathrm{G}=\Omega ^\mathrm{T}$ for both models. CZM1 is shown in Fig. 3a, b and CZM2 in Fig. 3c, d. Consistent mixed-mode behavior is observed for both formulations, with a gradual transition from mode II behavior to mode I behavior. In accordance with Eqs. (3) and (6), identical fracture energy is obtained for both formulations for such proportional loading paths, as shown in Fig. 4. The computed total fracture energy $G_{\mathrm {total}}$ monotonically increases from $G_{\mathrm n}^0$ to $G_{\mathrm t}^0$.

Fig. 4

Computed fracture energy as a function of mode angle $\varphi$ for CZM1 and CZM2 under proportional loading in the case of $K_\mathrm {m}=10$ MPa, $\tau _{\mathrm {max}}=5 \sigma _{\mathrm {max}}$, $G_{\mathrm t}= 5 G_{\mathrm n}$, $\Omega ^\mathrm{T}=\pi /16,\Omega ^\mathrm{G}=\Omega ^\mathrm{T}$

Fig. 5

Normalized traction versus separation in the normal direction (b), (d) and tangential direction (a), (c) for CZM1 (a), (b) and CZM2 (c), (d) undergoing non-proportional loading. Each simulation involves incrementally increasing tangential displacements beginning at $\Delta _{\mathrm t}/\delta _{\mathrm t}=0$ and increasing until the interface is fully debonded in the tangential direction followed by a complete normal separation ($\Delta _{\mathrm n}/\delta _{\mathrm n}=50$. $K_\mathrm {m}=10$ MPa, $\tau _{\mathrm {max}}=5 \sigma _{\mathrm {max}}, G_{\mathrm t}= 5 G_{\mathrm n}$)

Non-proportional loading paths: We next consider non-proportional loading path whereby the interface undergoes an initial mode II separation to a prescribed value of $\Delta _{\mathrm t}=\Delta _{\mathrm t}^{\mathrm {max}}$, followed by a subsequent normal separation to complete failure. Figure 5 shows the traction-separation response, again for the case of $K_\mathrm {m}=10$ MPa, $\tau _{\mathrm {max}}=5 \sigma _{\mathrm {max}}$, $G_{\mathrm t}= 5 G_{\mathrm n}$, $\Omega ^\mathrm{T}=\pi /16$, $\Omega ^\mathrm{G}=\Omega ^\mathrm{T}$ for both models. CZM1 is shown in Fig. 5a, b and CZM2 in Fig. 5c, d. Consistent behavior is again observed for both models. If significant damage is computed during the initial mode II separation, the maximum normal traction computed during subsequent normal separation is reduced. This demonstrates that sensible mixed-mode coupling is provided by both CZM1 and CZM2. Computed fracture energy is presented in Fig. 6 for the same non-proportional loading paths as those presented in Fig. 5. While identical fracture energy is not obtained for both formulations, a monotonic increase as a function of increasing $\Delta _{\mathrm t}^{\mathrm {max}}$ is computed both formulations. Additionally, monotonically increasing/decreasing tangential/normal fracture energy contributions are also computed.

Fig. 6

Fracture energy (G) for CZM1 (a) and CZM2 (b) undergoing non-proportional loading paths of varying initial tangential separation $\Delta _{\mathrm t}$ followed by normal separation $\Delta _{\mathrm n}$ until complete failure. Parameters are the same as those implemented in Fig. 5

Fig. 7

Instantaneous incremental energy dissipation of CZM1 (a), (c) and CZM2 (b), (d) under proportional loading (a), (b) and non-proportional loading (c), (d)

Fig. 8

Loading-unloading path (a); demonstration of the interface integrity variable in CZM1 (b), (d) and CZM2 (c), (e) for a series of proportional loading modes ranging from mode II to mode I ($K_\mathrm {m}=10$ MPa, $\tau _{\mathrm {max}}=5 \sigma _{\mathrm {max}}$, $G_{\mathrm t}= 5 G_{\mathrm n}$). Instantaneous incremental dissipation is shown in (f), (g) for CZM1 and CZM2, respectively

The dissipation of CZM1 is presented in Fig. 7a, c and CZM2 is presented in Fig. 7b, d for the proportional loading (Fig. 7a, b) and non-proportional loading (Fig. 7c, d). Positive instantaneous incremental dissipation is computed throughout each of the analyses presented. The response of CZM1 and CZM2 to load-unload boundary conditions is demonstrated in Fig. 8. Specifically, as shown in Fig. 8a, a mixed-mode proportional loading path is followed so that partial damage is computed. The interface is then unloaded along the same mode angle, until it returns to its original configuration $(\Delta _{\mathrm n}=\Delta _{\mathrm t}=0)$. The interface is then subjected to the same mode angle in the reverse direction $(\Delta _{\mathrm t}<0)$ to failure. As shown in Fig. 8b–d, consistent behavior is obtained for all mode angles. In all cases, the prescribed strength for the given mode angle is exceeded and softening/damage is computed. Reversal of loading results in elastic unloading at a reduced/damaged interface stiffness. Reversal of the direction of tangential loading direction for the final mixed-mode component of the loading path results in a continuation of elastic deformation at the reduced damaged interface stiffness. Eventually, the tangential traction reaches the reduced/damaged tangential strength and further interface softening proceeds during ultimate mode II separation and failure. Similar consistent trends are computed for both CZM1 and CZM2. Figure 8f, g demonstrate that instantaneous incremental dissipation is positive throughout the entire mixed-mode loading histories shown in Fig. 8b–e.

2.4 Comparison of CZM1 and CZM2 with Abaqus Exponential Softening Formulation (CZM3)

The commercial finite element software Abaqus provides a cohesive zone functionality in which damage evolution may be specified in terms of mixed-mode fracture energy. In this section we describe this formulation, which we refer to as CZM3, and we provide critical comparisons with CZM1 and CZM2. The constitutive law for the traction is specified as follows

$$\begin{aligned} \mathbf{T}= \begin{pmatrix} T_{\mathrm n} \\ T_{\mathrm t}\\ \end{pmatrix} = \begin{bmatrix} K_{\mathrm {nn}}&{}0\\ 0&{}K_{\mathrm {tt}}\\ \end{bmatrix} \begin{pmatrix} \Delta _{\mathrm n}\\ \Delta _{\mathrm t}\\ \end{pmatrix} = \mathbf{K}{\boldsymbol{\Delta }}, \end{aligned}$$

(14)

where $K_{\mathrm {nn}}$ is a prescribed mode I stiffness and $K_{\mathrm {tt}}$ is a prescribed mode II stiffness. The traction increases elastically in accordance with Eq. (14) until the chosen damage initiation criterion is met. As an example, the quadratic failure criterion (Tsai and Wu 1971) can readily be chosen, such that damage initiates when

$$\begin{aligned} \left( \frac{\left\langle \left. T_{\mathrm n}\right\rangle \right. }{\sigma _{\mathrm {max}}}\right) ^2 + \left( \frac{T_{\mathrm t}}{{\tau _{\mathrm t}}_{\mathrm {max}}}\right) ^2=1, \end{aligned}$$

(15)

where brackets describe the ramp function

$$\begin{aligned} \left\langle \left. T_{\mathrm n}\right\rangle \right. = \left\{ \begin{array}{lc} 0, \quad &{} T_{\mathrm n} < 0, \\ T_{\mathrm n}, \quad &{} T_{\mathrm n} \ge 0. \end{array} \right. \end{aligned}$$

(16)

Once the damage initiation criterion is satisfied, the scalar damage variable D increases monotonically from 0 to 1 with increasing separation until complete failure of the interface occurs. The traction during damage evolution is given as

$$\begin{aligned} \mathbf{T}= \left( 1-D\right) \overline{\mathbf{T}}, \end{aligned}$$

(17)

where $\overline{\mathbf{T}}$ is the peak elastic traction calculated in the absence of damage according to Eq. (14). This applies in both tangential directions, however, in normal displacement the traction is given as follows

$$\begin{aligned} T_{\mathrm n}= \left\{ \begin{array}{lc} (1-D) \overline{T}_{\mathrm n}, \quad &{} \overline{T}_{\mathrm n} \ge 0, \\ \overline{T}_{\mathrm n}, \quad &{} \overline{T}_{\mathrm n} < 0. \end{array} \right. \end{aligned}$$

(18)

This ensures the stiffness of the interface in overclosure cannot be affected by the damage variable D whilst allowing stiffness of the interface in normal opening $K_{\mathrm {nn}}$ to be affected in the same manner as Eq. (17). For exponential damage evolution specified according to energy the damage variable D reduces to

$$\begin{aligned} D=\int _{\delta _\mathrm {m}^{\mathrm {el}}}^{\delta _\mathrm {m}^*}\frac{T_\mathrm {m} \mathrm {d} \Delta _\mathrm {m}}{G_\mathrm {m}-G_0}, \end{aligned}$$

(19)

where $T_\mathrm {m}$ is the effective traction and $\Delta _\mathrm {m}$ is the effective separation, $G_0$ is the stored-elastic energy at damage initiation and $G_\mathrm {m}$ is the mixed-mode fracture energy. In Fig. 9a we show the response of CZM3 to a simple mode II separation. The computed tangential traction exceeds the prescribed mode II fracture strength of the interface, providing a non-physical prediction. In contrast, CZM1 and CZM2 correctly reproduce the prescribed mode II fracture strength, in addition to the prescribed mode II fracture energy. Figure 9b shows the computed tangential traction for CZM3 as a function of the damage ($D=(1-\Psi )$, where $\Psi$ is the interface integrity) during a mode II separation. The relationship is non-monotonic, whereby the mode II interface strength incorrectly increases with increasing interface damage. Peak tangential traction occurs when the scalar damage variable $D \approx 0.3$. Furthermore, the tangential traction does not decrease to the specified mode II fracture strength until $D \approx 0.7$, i.e. when the interface is $70\%$ damaged. In contrast, tangential tractions are correctly computed to decrease monotonically with increasing interface damage for CZM1 and CZM2.

Fig. 9

(a) Normalized traction-separation response of CZM3 (Abaqus exponential softening) formulation presented with CZM1 and CZM2 for a pure mode II separation. Note $T_{\mathrm t} > \tau _{\mathrm {max}}$ for the Abaqus exponential softening ($K_\mathrm {m}=10$ MPa, $\tau _{\mathrm {max}}=5$ MPa , $G=10$ N/mm); (b) normalized tangential traction as a function of damage D (where $D=(1-\Psi )$). Monotonic reduction is mode II interface strength with increasing damage for CZM1 and CZM2, but not for CZM3

Such anomalous behavior in CZM3 is further exposed in Fig. 10. Figure 10a shows the computed maximum normal traction as a function of mode angle during proportional mixed-mode separation. In the case of CZM1 and CZM2 the prescribed mode I strength is reached only for a pure mode I, as expected. However, for CZM3 the prescribed mode I strength is incorrectly exceeded for a wide range of applied mode angles. Similar results are presented in Fig. 10b for non-proportionate mixed-mode loading paths.

Fig. 10

(a) Normalized normal traction ${T_{\mathrm n}}_{\mathrm {max}}/\sigma _{\mathrm {max}}$ as a function of mode angle $\varphi$ for the three models in proportional loading scenarios (as seen in Fig. 3); (b) normalized traction as a function of maximum normalized tangential displacement prior to complete normal separation (as seen in Fig. 5). The dotted grey curve indicates $\sigma _{\mathrm {max}}$ in both (a) and (b). Note the non-monotonic behavior of the Abaqus exponential softening model

2.5 Construction of a Potential-Based CZM

Several previous studies have used traction-separation laws derived from a potential function (Xu et al. 1993; Park et al. 2009), so that the work of separation associated with a given interface separation vector should be path independent. A study by McGarry et al. (2014) uncovered problematic behavior associated with potential-based CZMs, such as repulsive tractions during mixed-mode loading paths. To further demonstrate this limitation of potential-based CZMs, we construct a potential surface by integrating the traction magnitude-separation magnitude relationships specified for CZM1 along proportional loading paths for ${0\le \varphi }\le {\pi }/{2}$, giving the following piece-wise expression potential function

$$\begin{aligned} \phi \left( \mathrm {\Delta }_\mathrm {m},\varphi \right) = \left\{ \begin{array}{lc} \frac{1}{2}K_\mathrm {m} \Delta _\mathrm {m}^2, &{} \Delta _\mathrm {m} < T_\mathrm {m}^{\mathrm {max}}(\varphi )/K_\mathrm {m}, \\ \frac{1}{2} K_\mathrm {m} \delta _\mathrm {m}^{\mathrm {el}}(\varphi )^2 - \\ T_\mathrm {m}^{\mathrm {max}}(\varphi )\delta _\mathrm {m}^*(\varphi )\left[ \exp \left( -\frac{\Delta _\mathrm {m}-\delta _\mathrm {m}^{\mathrm {el}}(\varphi )}{\delta _\mathrm {m}^*(\varphi )} \right) -1 \right] , &{} \Delta _\mathrm {m} \ge T_\mathrm {m}^{\mathrm {max}}(\varphi )/K_\mathrm {m}. \end{array} \right. \end{aligned}$$

(20)

We refer to this formulation as PF-CZM1 (potential function extension of CZM1). The traction separation relationships are derived from $T_{(i={\mathrm n},{\mathrm t})}=\partial \varphi /\partial \Delta _i$. Figure 11a shows $\varphi$ for PF-CZM1 for the case where the specified mode II fracture energy is two times higher than the mode I fracture energy. The potential function ($\varphi$) of the PPR model (2009) and the Xu-Needleman model (1993) are also shown for comparison. Figure 12a shows the normal traction $\partial \phi /\partial \Delta _{\mathrm n}$ derived from the PF-CZM1 potential function $\phi$ as a function of normal separation $\Delta _{\mathrm n}$ and tangential separation $\Delta _{\mathrm t}$. As clearly shown in Fig. 12b repulsive tractions are computed for increasing tangential separation, even when no normal separation exists ($\Delta _{\mathrm n}=0$).

Fig. 11

Potential surfaces shown as a function of normal separation and tangential separation: (a) PF-CZM1 ($K=1, \varphi _{\mathrm t}=2 \varphi _{\mathrm n},\tau _{\mathrm {max}}=\sigma _{\mathrm {max}}, \varphi ^0=\pi /8$); (b) PPR ($\sigma _{\mathrm {max}}=\tau _{\mathrm {max}},\varphi _{\mathrm t}=2 \varphi _{\mathrm n},\delta _{\mathrm n}=\delta _{\mathrm t}$); (c) Xu-Needleman ($r=0, q=2$)

Fig. 12

(a) Normal traction derived from the potential function $\varphi (\Delta _{\mathrm n},\Delta _{\mathrm t})$ seen in Fig. 11. Note repulsive normal tractions exist for increasing tangential opening even for $\Delta _{\mathrm n}=0$; (b) repulsive normal tractions are further demonstrated for a proportional loading of $\Delta _{\mathrm t}=2 \Delta _{\mathrm n}$. The transparent surface indicates $\partial {\phi }/\partial \Delta _{\mathrm n}=0$

Fig. 13

PPR model subject to a proportional loading path where $\varphi ={45}^\circ$. Model parameters are the same as those seen in Fig. 5 ($\tau _{\mathrm {max}}=5\sigma _{\mathrm {max}},\ {\ \phi }_{\mathrm t}=5\phi _{\mathrm n},\ \delta _{\mathrm t}=0.5,\ \delta _{\mathrm n}=\delta _{\mathrm t}/5$): (a) normalized normal traction $T_{\mathrm n}/\sigma _{\mathrm {max}}$ as a function of normal separation $\Delta _{\mathrm n}$. Repulsive (negative) tractions are computed; (b) normalized tangential traction $T_{\mathrm t}/\tau _{\mathrm {max}}$ as a function of tangential separation $\Delta _{\mathrm t}$. Tractions remain positive throughout; (c) instantaneous incremental energy dissipation ${\mathrm d}\phi _i/\phi _{\mathrm n}$ as a function of normal separation $\Delta _{\mathrm n}$. Negative instantaneous incremental energy dissipation is observed during the loading history; (d) decomposition of the instantaneous incremental energy dissipation (c) into normal and tangential components presented as a function of normal separation $\Delta _{\mathrm n}$

Figure 13 illustrates the response of the PF-CZM1, XN and PPR potential-based formulations when subjected to a mixed-mode monotonic loading path with $\varphi ={45}^\circ$. In all cases tangential strength is higher than the normal strength ($\tau _{\mathrm {max}}=5 \sigma _{\mathrm {max}}$) and the tangential work of separation is higher than the corresponding normal value (${\phi }_{\mathrm t}=5 \phi _{\mathrm n}$). In all cases significant repulsive normal tractions are computed from the potential function during the monotonic deformation path, while tangential tractions remain positive (non-repulsive). Negative instantaneous incremental dissipation is computed for the XN model, whereas such a violation of the second law is avoided for the PF-CZM1 and the PPR model simply due to the dominance of the positive dissipation of the tangential contribution over the negative normal contributions. However, Fig. 13 illustrates that potential-based models can result in repulsive normal tractions and negative instantaneous incremental dissipation during mixed-mode loading paths.

3 CZM Simulation of Mixed-Mode Aortic Dissection

In the previous section we demonstrated the advantages of path-dependent exponential softening CZM1 and CZM2 formulations. In this section we use CZM1 to investigate mixed-mode AD.

3.1 Examination of an Artery with an Intimal Tear

We first examine the risk of dissection propagation in an artery with a pre-existing intimal tear in the form of a radial notch. Figure 14e shows an illustration of the intimal tear highlighted in red on the arterial geometry. In order to assess the risk of the intimal tear propagating under a luminal pressure load a cohesive zone is prescribed in the circumferential plane around the intimal tear, as shown by the red surface in Fig. 14e. In order to determine an upper limit of allowable lumen pressure a super-physiological blood pressure of 500 mmHg is applied in the lumen. A $10\%$ axial stretch is applied to the artery prior to lumen pressurization. Hyperelastic anisotropic fiber-reinforced material behavior is prescribed to the artery according to the bilinear fiber model proposed by Fereidoonnezhad et al. (2020). The shear strength of the CZM interface is taken as $\tau _{\mathrm {max}}=1.6$ MPa, as determined in the experimental-computational study of mode II dissection (Fig. 15) by FitzGibbon and McGarry (2020). The normal strength of the interface is taken as $\sigma _{\mathrm {max}}=0.2$ MPa, based on standard peel test experiments (FitzGibbon and McGarry 2020).

Fig. 14

(a) Illustration of the dissected geometry with the paraboloid flow profile . The intraluminal septum is shown; (b) velocity magnitude (mm s$^{-1}$) streamline plot of the dissected geometry; (c) blunting of the crack tip in the axisymmetric cohesive zone finite element analysis; (d) mode at the crack tip in (c) is shown as a function of the lumen pressure; (e) illustration of the intimal tear in the artery. The surface of the CZM is shown in red; (f) maximum principal stress in the aorta subject to 500 mmHg of lumen pressure; (g) interface strength ($\tau ^{\mathrm {max}}$) as a function of pressure at crack propagation ($p^{\mathrm {init}}$). Four regions of blood pressure are shown: hypotensive, normotensive, hypertensive, and super-physiological. In summary, this analysis suggests that propagation of an intimal tear of the aorta will occur only in cases of extreme hypertensive pressures (${\ge }275$ mmHg). Extensive propagation of a false lumen is not predicted at a slightly hypertensive blood pressure of 140 mmHg. Even in extreme hypertensive loading conditions propagation is arrested due to mixed-mode blunting of the crack tip and an increase in the mode angle towards mode II

Fig. 15

(a) Computational fit of the bilinear fiber model to the experimental results (adapted from FitzGibbon and McGarry 2020); (b) calibrated cohesive zone shear interface strength parameters (adapted from FitzGibbon and McGarry 2020)

Figure 14f shows the max principal stress in the aorta at a lumen pressure of 500 mmHg. The crack initiates at a pressure of 275 mmHg and continues to propagate with increasing applied pressure. The final crack growth is $\sim$ $5.75$ mm at a pressure of 500 mmHg. No crack propagation is recorded at lumen pressures below 275 mmHg. The crack initiates and propagates in a pure mode II due to compressive tractions at the medial interface caused by the hypertensive blood pressure. Figure 14g shows the interface strength as a function of the lumen pressure at the point of intimal tear propagation. $\tau ^{\mathrm {max}}/\tau ^{\mathrm {exp}}=1$ indicates the interface strength is the experimentally recorded value of $\tau ^{\mathrm {max}}=1.6$ MPa (FitzGibbon and McGarry 2020). As shown, a $50\%$ reduction in interface strength will lead to an intimal tear propagation under a typical hypertensive blood pressure load of p $\approx$ 190 mmHg. A further reduction in interface strength ($\tau ^{\mathrm {max}}/\tau ^{\mathrm {exp}}=0.25$) results in tear propagation in the normotensive blood pressure range. The highest recorded blood pressure in humans is 480/350 mmHg during heavy-resistance exercise (MacDougall et al. 1985), these are referred to here as super-physiological. Our results seem to suggest under such blood pressure conditions an intimal tear is likely to propagate in a mode II in a healthy artery.

3.2 Examination of a Dissected Artery with a Patent False Lumen

We next explore the risk of a false lumen propagating further in an artery with a pre-existing patent false lumen, as shown in Fig. 14a. Computational fluid dynamics simulations are implemented to determine the loading on the vessel wall and on the intimal flap. A parabolic flow profile is prescribed at the inlet boundary (Fig. 14a). A zero-velocity (no-slip) condition is imposed at the wall for the fluid. Physiologically accurate transient flow profiles are implemented. A pressure boundary condition is imposed at the outlet boundary. Using a one-way fluid-structure-interaction approach, computed pressure distributions are applied to a solid finite element, including CZM interfaces, to simulate propagation of the false lumen (Fig. 14c). Velocity streamlines in the aorta are shown in Fig. 14b. Maximum velocity occurs above the intraluminal septum and minimum velocities occur in the false lumen. Figure 14c, d explores crack arrest due to blunting of the crack tip. While recent studies demonstrate that initiation of AD is a pure mode II process (Haslach et al. 2018; Gültekin et al. 2019; FitzGibbon and McGarry 2020), the simulations presented in Fig. 14c suggests that the eventual formation of a false lumen, following mode II initiation, will result in mixed-mode conditions at the crack-tip. A form of toughening of the crack tip is also evident in Fig. 14d as the mode angle at the crack tip increases (tending towards mode II propagation) with increasing pressure. As the mode II strength has been shown to be eight times higher than mode I strength (FitzGibbon and McGarry 2020), such an increase in the mode angle with increasing pressure will be accompanied by a significant increase fracture resistance. Such a toughening mechanism is incorporated into our model through our calibrated mixed-mode CZM formulation.

4 Conclusion

In the present chapter we analyze two new exponentially softening path-dependent cohesive zone formulations. An extensive exploration of the mixed-mode coupling in proportional and non-proportional loading paths is presented. Physically realistic mixed-mode behavior of a CZM is of fundamental importance for applications in materials with anisotropic fracture properties. Our recent experimental work demonstrates that the mode II fracture strength of the aorta in the circumferential-axial plane is eight times higher than the mode I strength in the same plane (FitzGibbon and McGarry 2020). Recent studies have presented evidence that initiation of aortic dissection is predominantly a mode II fracture process (Haslach et al. 2018; Gültekin et al. 2019) while the further propagation of aortic dissection is suspected to occur in a mixed-mode, as demonstrated in the finite element cohesive zone analysis presented in Fig. 14c, d.

Accurate cohesive zone simulation of these complex fractures cannot be achieved without robust analysis of the mixed-mode behavior of the cohesive zone under a range of boundary conditions and material properties. This is clearly demonstrated in the simulation presented in Fig. 14c, d. Accurate simulation of the crack tip blunting in the false lumen, as presented in Fig. 14c, d, requires the use of a cohesive zone formulation with robust mixed-mode behavior (CZM1). As previously demonstrated by McGarry et al. (2014), the use of potential-based cohesive zone formulations in mixed-mode applications results in problematic repulsive normal tractions. This is clearly demonstrated in Fig. 13 where repulsive tractions are calculated for three different potential-based models subject to a proportional separation at a mode angle of $\varphi =\pi /4$ (Xu and Needleman 1993; Park et al. 2009). The newly proposed PF-CZM1 is subject to the same limitations as previously proposed potential-based CZMs despite its robust mixed-mode basis. Furthermore, the use of potential-based models may result in the calculation of residual tractions after separation has occurred. The analysis presented in the present chapter clearly demonstrates the importance of using a non-potential-based cohesive zone formulation with robust mixed-mode behavior in the simulation of aortic dissection.