Keywords

12.1 Introduction

Arterial tissue failure leads to a number of potentially life-threatening clinical conditions such as atherosclerotic plaque rupture and aortic dissection, which often occur suddenly and unpredictably in vivo. Atherosclerotic plaque rupture is responsible for roughly 75 % of all newly developed and recurring myocardial infarctions, which affect approximately 1.1 million people in the USA per year with a 40 % fatality rate [1].

Clinical autopsy studies have shown that plaque rupture often occurs at two sites: (1) the center of the plaque, where the fibrous cap may be very thin, and (2) the shoulder region, where the interface between the plaque and the underlying vascular wall is located [2]. Relevant to the second plaque rupture site, the interface strength of the bond between the plaque and vascular wall is important for the stability of the plaque. The local critical energy release rate, which is the energy required to delaminate a unit area of the plaque from the underlying vascular wall, provides a measure for quantifying the interface strength. As such, it is important to understand catastrophic arterial failures in order to develop effective approaches for treatment and intervention. To understand the atherosclerotic plaque rupture phenomena we have developed a finite element simulation procedure and applied the procedure to plaque delamination in mouse aorta.

An important part of finite element simulation studies is the modeling of material behavior. In the literature aorta has been modeled as a linearly elastic material in finite element analysis of the distribution of the circumferential stress in ruptured and stable atherosclerotic lesions [3]. In the evaluation of the impact of calcification on plaque structural stability, the finite element method has been applied to the study of human coronary atherosclerotic lesions using an isotropic, incompressible, Mooney-Rivlin finite-strain elasticity material model [4]. A composite material model has been proposed in the literature to capture the nonlinear properties of arterial wall, in which each arterial layer is treated as a fiber-reinforced material with the fibers corresponding to the collagenous component embedded in a non-collagenous matrix [5]. To account for the distribution of collagen fibers, an additional structure parameter has been added in the composite material model [6].

Atherosclerotic plaque is composed of a plaque core (which may contain a lipid core and calcifications in advanced lesions) and the underlying arterial wall, including a media layer and an adventitia layer. Plaque rupture is similar to the common delamination damage phenomenon in laminated fiber-reinforced composites between composite layers because of the relatively weak interlaminar strength. Methods based on the cohesive zone model (CZM) have been proven to be an effective way of modeling delamination failure in composite materials [7]. In an application of CZM to arterial tissue failure [8], the arterial wall is described as an anisotropic, heterogeneous, highly deformable, incompressible material, and arterial tissue failure is represented by a strong discontinuity kinematics. This approach was also applied to model the propagation of dissection of human aortic media [9]. In another study [10], the dissection of aortic media was simulated using an anisotropic cohesive law in order to distinguish between the cohesive responses along different directions of the cohesive surface.

The present study is focused on understanding the atherosclerotic plaque rupture phenomenon by modeling and simulating experiments performed on mouse aorta specimens in which a plaque is peeled off from an arterial wall.

12.2 Material Model

Under physiological conditions, arteries are regards as nearly incompressible material. Healthy arteries behave as highly deformable composite structures and exhibit a nonlinear stress–strain response with typical stiffening at the physiological strain level [10]. To simulate atherosclerotic plaque delamination in mouse aorta, we adopt the Holzapfel model [5] for the bulk material behavior and the cohesive zone model (CZM) [11] for the delamination behavior along the plaque-media interface. In the Holzapfel model, each artery layer is treated as a fiber-reinforced material with the fibers symmetrically disposed with respect to the axial direction of the aorta. In the CZM, delamination is governed by a traction-separation law.

12.2.1 Bulk Material for the Mouse Aorta

Holzapfel model assumes that the mean orientation of collagen fibers has no out-of-plane component [6], and state that the preferred orientation of the 3D collagen fiber network lies parallel to the aorta wall, although in mouse aorta there are some fiber orientations with an out-of-plane component to prevent out-of-plane shearing [12].

The anisotropic hyper-elastic potential ψ(C, H 1, H 2) for an arterial layer can be represented by a superposition of the isotropic potential ψ g (C) for the non-collagenous ground-matrix (indicated by subscript ‘g’), and the two transversely isotropic potentials ψ f1 , ψ f2, for two families of embedded collagen fibers (with subscript ‘f’). Thus, the free-energy function [7, 13], is

$$ \psi \left( C,{H}_1,{H}_2\right)={\psi}_g(C)+\left[{\psi}_{f1}\left( C,{H}_1\left({a}_{01},\kappa \right)\right)+{\psi}_{f2}\left( C,{H}_2\left({a}_{02},\kappa \right)\right)\right] $$
(12.1)

where C is the right Cauchy–Green strain tensor. The structure tensors H 1, H 2 depend on the direction vectors a 01 , a 02, and have the following forms in a cylindrical coordinate system, in matrix notation,

$$ {H}_1\left({a}_{01},\kappa \right)=\kappa I+\left(1-3\kappa \right)\left({a}_{01}\otimes {a}_{01}\right) $$
(12.2)
$$ {H}_2\left({a}_{02},\kappa \right)=\kappa I+\left(1-3\kappa \right)\left({a}_{02}\otimes {a}_{02}\right) $$
(12.3)
$$ \left[{a}_{01}\right]=\left[\begin{array}{c}\hfill 0\hfill \\ {}\hfill cos\beta \hfill \\ {}\hfill sin\beta \hfill \end{array}\right],\kern1em \left[{a}_{02}\right]=\left[\begin{array}{c}\hfill 0\hfill \\ {}\hfill cos\beta \hfill \\ {}\hfill - sin\beta \hfill \end{array}\right] $$
(12.4)

The non-collagenous ground-matrix is represented by means of an incompressible isotropic neo-Hookean model,

$$ {\psi}_g(C)=\frac{\mu}{2}\left({I}_1-3\right) $$
(12.5)

where I 1 = tr(C) and μ denotes the first invariant of C and the neo-Hookean parameter, respectively. The transversely isotropic free-energy functions for the two families of collagen fibers are as follows

$$ {\psi}_{f1}\left( C,{H}_1\left({a}_{01},\kappa \right)\right)=\frac{k_1}{2{k}_2}\left[{e}^{k_2{\left[ tr\left({H}_1 C\right)-1\right]}^2}-1\right] $$
(12.6)
$$ {\psi}_{f2}\left( C,{H}_2\left({a}_{02},\kappa \right)\right)=\frac{k_1}{2{k}_2}\left[{e}^{k_2{\left[ tr\left({H}_2 C\right)-1\right]}^2}-1\right] $$
(12.7)
$$ tr\left({H}_1 C\right)= tr\left({H}_2 C\right)=\kappa {I}_1+\left(1-3\kappa \right){I}_4 $$
(12.8)

where I 4 = a 01 ⋅ Ca 01 = a 02 ⋅ Ca 02 = λ 21 cos 2 β + λ 22 sin 2 β, and λ 1 and λ 2 are the stretch ratios along the axial direction and circumferential direction of the arterial wall. Then ψ(C, H 1, H 2) is reduced to

$$ \psi \left( C,{H}_1,{H}_2\right)=\frac{\mu}{2}\left({I}_1-3\right)+\frac{k_1}{k_2}\left[{e}^{k_2{\left[\kappa {I}_1+\left(1-3\kappa \right){I}_4-1\right]}^2}-1\right] $$
(12.9)

Note that the constitutive parameter μ is the shear modulus of the solid without fibers; k 1 is a stress-like parameter to be determined from mechanical tests of the tissue, which is related to the relative stiffness of the fibers in the small stretch ratio region; and k 2 is a dimensionless stiffness parameter that is related to the large strain stiffening behavior of the fibers; κ is the dispersion parameter which denotes the distribution of the collagen fibers within the two families of fibers. The lower limit of the dispersion parameter κ is 0, which describes the ideal alignment of collagen fibers, whereas the upper limit of the dispersion parameter κ is 1/3, which represents the isotropic distribution of the collagen fibers [6].

12.2.2 Cohesive Model

The use of a CZM in this study is realized through a user implementation of a UEL subroutine in ABAQUS [14]. The failure mechanism in a cohesive element as described by a traction-separation law involves three steps: (1) Damage initiation, (2) damage evolution and (3) element removal [14]. Damage initiation refers to the start of degradation of the cohesive element when an effective peak traction τ c is reached; damage evolution refers to the period after damage initiation but before complete failure and is controlled; and element removal occurs after the cohesive traction reaches zero at a critical effective separation value.

In CZM, the failure criteria is defined as part of the cohesive element degradation properties [15]. Kenane and Benzeggagh [13] proposed a failure criterion which, in some cases, fits experimental results accurately:

$$ {G}_c={G}_T $$
(12.10)

where G T is obtained from

$$ {G}_T={G}_I+{G}_{I I}+{G}_{I I I} $$
(12.11)

and

$$ {G}_c={G}_{Ic}+\left({G}_{IIc}-{G}_{Ic}\right){\left(\frac{G_{shear}}{G_T}\right)}^{\alpha} $$
(12.12)
$$ {G}_{shear}={G}_{II}+{G}_{II I} $$
(12.13)

In the above G I , G II and G III represent the mode I, mode II and mode III energy release rate, respectively; G Ic , G IIc and G IIIc are the corresponding fracture toughness values of the material; and α is a parameter determined by fitting Eq. (12.12) to experimental data. Failure occurs when the energy release rate G T is equal to G c .

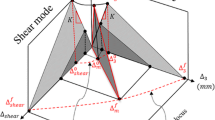
The cohesive law that governs material separation can be written as:

$$ {\tau}_i=\tau \left({\Delta}_i\right) $$
(12.14)
$$ {\Delta}_3^0={T}_3^0/ K $$
(12.15)
$$ {\Delta}_{shear}^0={T}_{shear}^0/ K $$
(12.16)

where τ i is the cohesive traction; Δ i is the displacement jump in the local coordinates which is required for modeling the behavior of the material discontinuity; K is the tangential stiffness of pure Mode I triangular cohesive law; Δ 03 and Δ 0 shear are the displacement jumps of the initial cohesive element damage under pure Mode I and Mode II, respectively; and T 03 and T 0 shear are the strengths of the cohesive interface along the normal direction and tangential direction, respectively. Derivation of the finite element discretization is provided by Turon [7], and a finite element-based cohesive zone model is implemented as a UEL subroutine in ABAQUS [14].

12.3 Numerical Simulations of Atherosclerotic Plaque Delamination

12.3.1 Experimental Process and Simulation Model

In the plaque delamination experiment [16] modeled in this study, 6-week old apolipoprotein E-knockout (apo E-KO) male mice were used. The mice were fed a high-fat (42 % of total calories) Western-style diet for 8 months to develop atherosclerosis throughout the aorta [17]. To initiate surface separation (delamination) between the plaque and the media layer of the aorta, a small initial flaw was carefully introduced at the proximal end of the plaque. The plaques were delaminated in situ, so that the tissues surrounding and underlying the aorta provide considerable structural support, restricting the outward motion of the aorta during mechanical loading. For the thoracic aorta, the intercostal branches prevented the outward motion of the aorta. For the abdominal aorta, bent insect pins were placed at both ends of an atherosclerotic plaque to prevent excessive outward motion of the aorta due to the lack of dorsally-oriented vascular branches like thoracic aorta [16].

A schematic of the atherosclerotic plaque delamination experimental setup is shown in Fig. 12.1. A mouse carcass with exposed aorta was fastened to a small plate connected to the load cell of a Bose ELF 3200 for load data recording. The small delamination on the proximal end of the plaque was gripped by a pair of micro-clamps connected to the Bose ELF 3200 actuator which applies sequential loading–unloading cycles. The delamination process of plaque was recorded by a computer vision system. For each experiment, a load–displacement curve with multiple loading–unloading cycles was obtained. Histological analyses of the specimens were performed, which show that the delamination interface in the mouse atherosclerotic lesions is located between the plaque (a relatively acellular tissue) and the underlying internal elastic lamina (IEL), instead of within the media.

Fig. 12.1
figure 1

The atherosclerotic plaque delamination experiment: (a) A mouse specimen on a loading table; (b) a schematic of the experimental process represented by a finite element model

Full size image

Considering the complexity of the geometry of atherosclerotic plaque, the difficulty to measure accurately the dimensions of the small aorta, and the lack of data from the experiments that were performed before the modeling study was initiated, it is not possible to reconstruct an exact geometric model for the test specimen in the current study. As such, an approximate geometry model will be built in this study based on limited and incomplete data from multiple sources. In building the model, several conclusions have been made based on available information, for example: (1) the atherosclerotic plaque specimen is not flat, and (2) the plaque shape is irregular, with a changing width and a rough and uneven surface. Accordingly, the resulting geometric model that best approximate the actual specimen contains an asymmetrical atherosclerotic plaque, as shown by the finite element model in Fig. 12.1b. The widths of plaque at different locations along the longitudinal direction of arterial wall are measured from experimental images, and the thickness of the plaque is taken to be constant because the total delamination length during one loading–unloading cycle is around 0.2 mm, which is a very small distance.

12.3.2 Parameter Identification

12.3.2.1 Material Properties of Holzapfel Model

Due to the lack of mechanical properties for the mouse aorta, the values of the material parameters in the Holzapfel model for the bulk artery material, which is employed in the current study, were determined based on values suggested in the literature and by matching simulation predictions with measurements using the first loading–unloading cycle of the load–displacement curve. The arterial wall and the plaque are treated as two layers of homogeneous materials, and their material parameters are shown in Table 12.1. This set of parameter values allows the predicted first loading–unloading cycle of the load–displacement curve to match reasonably well with the measured curve, as shown in Fig. 12.2.

Table 12.1 Material parameters of mice arterial wall and plaque
Full size table
Fig. 12.2
figure 2

The simulation predicted load–displacement curve of the first loading–unloading cycle during delamination is compared with the measured curve. The delamination cycle includes the loading process in which the plaque is pulled in order to cause delamination of the plaque, and the unloading process in which the plaque is returned to the initial position

Full size image

The parameter β represents the angle between the mean fiber orientation and the circumferential direction of the aorta. The dispersion parameter κ describes the alignment of collagen fibers [6].

12.3.2.2 CZM Material Properties

The cohesive parameter values G Ic and G IIc are based on the experimental data of atherosclerotic plaque delamination from reference [16]. The plaque delamination experiment is basically a Mode I process, in which the tensile cohesive traction normal to plane of delamination is the dominant cohesive traction. As such, G IIc is simply set to be equal to G Ic , since the shear component is negligible. The value of G Ic from experimental measurements is found to vary with the amount of delamination [16], possibly due to variations in the geometry of the plaque and material heterogeneities along the longitudinal direction. The measured G Ic are used in the CZM model.

The rest of the CZM parameter values are selected based on values suggested in the literatures, such as the tensile strength of the interface between plaque and the underlying tissue (arterial wall) [9], and by matching simulation predictions with measurements using the first loading–unloading cycle of the load–displacement curve, as described earlier for determining parameter values of the Holzapfel model for bulk mouse arterial wall and plaque behavior. The resulting CZM parameter values are shown in Table 12.2.

Table 12.2 CZM parameter values
Full size table

In the finite element simulations using the CZM approach, special care has been made so that (1) the cohesive element size is sufficiently small compared to the cohesive zone length [18], and (2) the initial stiffness of the cohesive element is sufficiently high to avoid introducing a fictitious structural compliance.

12.4 Prediction and Validation

To avoid the effects of variations and uncertainties in specimen geometry and material properties from one experiment to another, the second and third loading–unloading cycles of the measured load–displacement curve from the same experiment as the one used to determine the material and CZM parameter values are utilized to validate the simulation predictions.

Fig. 12.3
figure 3

Comparisons of the predicted and measured load–displacement curves for loading–unloading cycle 2 and cycle 3

Full size image

In the validation predictions for the second and third loading–unloading cycles, the same Holzapfel model parameter values for the arterial wall and the plaque, the same CZM parameter values (except for the critical energy release rate, which is taken from experimental measurements directly), and the same boundary conditions used for the first cycle were employed. Comparisons of the predicted and measured load–displacement curves for cycle 2 and cycle 3 are shown in Fig. 12.3. Although there are some differences between the predictions and measurements, overall a reasonably good agreement is achieved, which provides a validation for the CZM based simulation approach for the plaque delamination process.

12.5 Conclusions

Plaque dissection of arterial tissue often happens at the shoulder region of the fibrous cap, which is frequently observed in clinical operations. Mouse atherosclerotic plaque delamination experiments provide a way to investigate the underlying mechanism of tissue damage in order to understand the process of vascular tissue failure. Although the finite element method have been used to analyze the stress–stain behavior and tissue separation inside the arterial material during the process of plaque delamination, few studies have focused on the biomechanics of atherosclerotic plaque rupture.

In the present work, the finite element method and cohesive zone model approach has been employed to model and simulate atherosclerotic plaque delamination process. This study focused on plaque delamination experiments performed on mouse aorta specimens. Approximations of the specimen geometry were made based on limited and incomplete data from multiple sources. The bulk mouse arterial wall and plaque behavior were modeled based on a Holzapfel model in which each artery layer is treated as a fiber-reinforced material with the fibers symmetrically disposed with respect to the axial direction of the aorta. The plaque-media interface was modeled using cohesive elements. Holzapfel model and CZM parameter values were determined based on values suggested in the literature and by matching simulation prediction of the first loading–unloading cycle of the load–displacement curve with the measured curve. As validation of the CZM approach, these parameter values were then used in simulations of the second and third loading–unloading cycles of the plaque delamination experiment, and the simulation predictions of the second and third cycles match reasonably well with the measured load–displacement curve.