Effective Transport Properties

Abstract

Porous media are an integral part of electrochemical energy conversion and storage devices, including fuel cells, electrolyzers, redox flow batteries and lithium-ion batteries, among others. The calculation of effective transport properties is required for designing more efficient components and for closing the formulation of macroscopic continuum models at the cell/stack level. In this chapter, OpenFOAM is used to determine the effective transport properties of virtually-generated fibrous gas diffusion layers. The analysis focuses on effective properties that rely on the fluid phase, diffusivity and permeability, which are determined by solving Laplace and Navier-Stokes equations at the pore scale, respectively. The model implementation (geometry generation, meshing, solver settings and postprocessing) is described, accompanied by a discussion of the main results. The dependence of orthotropic effective transport properties on porosity is examined and compared with traditional correlations.

1 Introduction

Macroscopic continuum models are based on a volume-averaged formulation of mass, momentum, species, charge and energy conservation equations (Weber et al. 2014; Wang 2004; Goshtasbi et al. 2019; García-Salaberri et al. 2017). The model is closed through appropriate constitutive relationships that define the various effective properties of the cell components (García-Salaberri et al. 2018). Effective transport properties include the absolute permeability used in Darcy’s law, the tortuosity factor used to correct Fick’s law of diffusion, or the effective electrical and thermal conductivities used in Ohm’s and Fourier’s laws. However, effective properties are challenging to determine in practice due to the thin nature of the porous components used in electrochemical devices ($\mathrm{thickness}\sim 10-1000~\mu \mathrm{m}$), such as gas diffusion layers and catalyst layers in fuel cells and active electrodes in batteries (García-Salaberri et al. 2015a, b; Kashkooli et al. 2016; Liu et al. 2019). These porous media must fulfill several critical functions, such as providing a transport pathway for reactants/products through their pore volume and ensuring charge and heat conduction through their solid structure. Catalyst layers and active electrodes have the added functionality of providing a reactive surface area. Therefore, as a complement to experimentation, numerical simulation at the pore scale has become increasingly common. Pore-scale simulations in porous media provide direct insight into the impact of the microstructure on transport processes, allowing one to determine effective transport properties and explore specific transport phenomena (see, e.g., García-Salaberri et al. 2019; Hack et al. 2020; Sabharwal et al. 2016; Zhang et al. 2020; Gostick et al. 2007; Gostick 2013; Tranter et al. 2018; Belgacem et al. 2017; Aghighi and Gostick 2017). A thorough understanding of the mass, charge and heat transport properties of porous components is crucial for achieving improved performance and durability.

Two main pore-scale modeling approaches are widely used: pore-network modeling (PNM) and direct numerical simulation (DNS) (Arvay et al. 2012). PNMs idealize the pore space as a network of pore bodies interconnected by throats, whose size and connectivity are determined from the microstructure of the porous media (Gostick et al. 2007; García-Salaberri 2021). Some authors have also presented dual networks that include both the solid phase and the standard fluid phase (Aghighi and Gostick 2017). Different transport processes can be simulated on the network, including capillary transport, convection, diffusion and heat conduction. In contrast, DNS solves the transport equations (e.g., species conservation or Navier-Stokes equations) in computational meshes generated on tomography images or virtually-generated microstructures of porous media. Numerical methods used to solve conservation equations at the pore scale include the lattice Boltzmann method (LBM) or more conventional techniques such as the finite-element (FEM) or finite-volume (FVM) methods. Unlike the LBM, higher convergence rates are achieved with the FEM or FVM using steady-state solvers, although the time invested in mesh generation can represent a significant portion of the overall simulation (García-Salaberri et al. 2015a, b; Liu et al. 2019; Sabharwal et al. 2016). DNS only requires the input of the bulk properties of the constituents of the material (e.g., the bulk diffusion coefficient for effective diffusivity or the kinematic viscosity for absolute permeability), providing direct insight into the impact of microstructure on transport. Hence, the information that can be potentially extracted from DNS is higher, even though the computational cost is significantly higher than PNM.

Previous works that used OpenFOAM to simulate pore-scale transport phenomena in porous components of electrochemical energy conversion and storage devices are reviewed below. The literature survey includes works focused both on polymer electrolyte fuel cells (PEFCs) and solid oxide fuel cells (SOFCs).

In terms of PEFCs, James et al. (2012) examined the effect of inhomogeneous assembly compression on the effective electrical/thermal conductivity and diffusivity in a commercial GDL (SGL SIGRACET 30BA). The microstructure was extracted by means of X-ray computed tomography, then triangulated using the marching-cubes algorithm, and finally converted into a volumetric mesh for simulation. The numerical results showed that assembly compression significantly affects the effective transport properties between the under-the-land and under-the-channel regions. In addition, a notable decrease of the effective gas diffusivity was found compared to that predicted by widely used correlations, such as Bruggeman correlation (Bruggeman 1935) and the random fibre model of Tomadakis and Sotirchos (1993). Pharoah et al. (2011) analyzed the effective electrical/ionic conductivity and gas diffusivity of catalyst layers as a function of the volume fraction of carbon/Pt, ionomer and fluid phases. The microstructure was virtually-generated using spherical particles. It was found that Knudsen numbers in the pore space varied between the transition regime and Knudsen regime, with higher pore radius leading to lower Knudsen number. In a subsequent work, Khakaz-Babol et al. (2012) studied the coupling between transport and electrochemical kinetics on microstructural representations of catalyst layers that were generated using a similar algorithm to that of Pharoah et al. (2011). Different Pt loadings were created by randomly exchanging Pt particles with carbon particles, so that the base geometries were identical for each Pt loading. The results showed that both the transport of protons and oxygen significantly affect performance, with increased local losses in the ionomer at reduced Pt loading.

Regarding SOFCs, Choi et al. (2009) analyzed the effective electrical and ionic conductivity and gas diffusivity (including Knudsen diffusion) of the anode and cathode electrodes. The microstructures were made of randomly distributed and overlapping spheres with particle size distributions that matched those of ceramic powders. The numerical results were compared against experimental data and theoretical correlations. Gunda et al. (2011) examined the effective transport properties (electrical conductivity and gas diffusivity) of ceramic lanthanum strontium manganite (LSM) electrodes, whose microstructures were acquired using dual-beam focused ion beam-scanning electron microscopy (FIB-SEM). The sensitivity of different image processing steps (threshold value, median filter radius, morphological operators, surface triangulation, etc.) was examined. In addition, the work showed that the effective transport properties determined by FIB-SEM reconstruction were more anisotropic than those determined by numerical reconstruction. Next, Choi et al (2011) presented a numerical framework for the computation of effective transport properties of SOFC porous electrodes from 3D reconstructions of the microstructure based on measured parameters, such as porosity and particle size distribution. Three different types of grids were considered: cartesian, octree, and body-fitted/cut-cell with successive levels of surface refinement. OpenFOAM was used to compute the effective transport properties in the three phases of the electrode (pore, electron and ion). The model, validated with results from random walk simulations, was used to investigate microstructures with monosized particle distributions, as well as polydisperse particle size distributions similar to those found in SOFC electrodes. Bertei et al. (2014) presented a modeling framework, based on random sequential-addition packing algorithms, for the particle-based reconstruction of SOFC infiltrated electrodes. Key parameters, such as the connected triple-phase boundary length, effective electrical conductivity and effective diffusivity, were evaluated on the reconstructed electrodes by using geometric analysis, FVM and random-walk methods. A parametric study showed that the critical loading (i.e., the percolation threshold) increases as the backbone porosity decreases and the nanoparticle diameter increases. Large triple-phase boundary length, specific surface area and good effective conductivity can be reached by infiltration, without detrimental effect on effective transport properties of the fluid phase.

In this chapter, DNS in porous media using OpenFOAM is introduced. Diffusion and convection are simulated in virtually-generated GDLs formed by a 2D arrangement of randomly-oriented fibres. The organization of the chapter is as follows. In Sect. 2, the physical model is presented, including the governing equations, boundary conditions and calculation of effective transport properties, namely, effective diffusivity and permeability. In Sect. 3, the model implementation is described with a focus on the geometry generation, meshing, solution procedure and post-processing. In Sect. 4, the results are discussed, including the effect of porosity on the computed orthotropic transport properties and a comparison with traditional correlations.

2 Physical Model

Diffusion and convection in the fluid phase of fibrous GDLs are examined. The conservation equations and the expressions used to determine the corresponding effective transport properties, effective diffusivity and absolute permeability, are presented below.

Effective Transport Properties of Solid Phase

Effective properties that rely on the solid phase (e.g., electrical conductivity) can be determined using a similar procedure to that presented in this chapter, but changing the phase of interest.

2.1 Diffusion: Effective Diffusivity

Species molar concentration C is determined from the steady-state species conservation equation (i.e., Laplace’s equation)

$$\begin{aligned} \nabla \cdot \left( -D\nabla C\right) =0 \end{aligned}$$

(1)

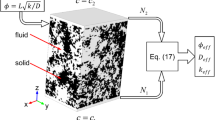
where D is the bulk diffusivity. This equation is subject to Dirichlet boundary conditions ($C=C^\mathrm{in}$ and $C=C^\mathrm{out}$) on the external faces of the domain perpendicular to the direction of interest i ($i=x, y~\mathrm{or}~z$) to create a concentration gradient. $C^\mathrm{in}$ and $C^\mathrm{out}$ are the inlet and outlet concentrations, respectively. A no-flux boundary condition ($\partial C/\partial \boldsymbol{n}=0$) is set on the remaining faces of the domain and internal fluid-solid interfaces. A schematic representation of the external boundary conditions is shown in Fig. 1.

Fig. 1

Schematic of the computational domain and boundary conditions used to determine effective transport properties in the in-plane direction (x-direction). Similar boundary conditions are applied to compute effective transport properties in other directions. Effective diffusivity and permeability are determined from the computed average diffusive flux and velocity in the direction of interest, respectively

According to Fick’s first law, the effective diffusivity of an anisotropic porous medium is given by a second-order tensor, whose diagonal and non-diagonal components can be determined by changing the direction of interest in the calculations

$$\begin{aligned} \langle \boldsymbol{j}\rangle =-\boldsymbol{\bar{\bar{D}}^\mathrm{eff}}\nabla C;\quad \boldsymbol{\bar{\bar{D}}^\mathrm{eff}}= \begin{pmatrix} D_{xx}^\mathrm{eff} &{} D_{xy}^\mathrm{eff} &{} D_{xz}^\mathrm{eff} \\ D_{yx}^\mathrm{eff} &{} D_{yy}^\mathrm{eff} &{} D_{yz}^\mathrm{eff} \\ D_{zx}^\mathrm{eff} &{} D_{zy}^\mathrm{eff} &{} D_{zz}^\mathrm{eff} \end{pmatrix} \end{aligned}$$

(2)

where the symbol $\langle * \rangle$ denotes volume-average quantities. In this case, the volume-average diffusive flux.

Since the flux vanishes in the solid region (s) of the porous medium, i.e., $\boldsymbol{j_s}=0$, the diagonal components of the normalized effective diffusivity tensor (e.g., the zz-component) are given by

$$\begin{aligned} \dfrac{D_{ii}^\mathrm{eff}}{D}=\dfrac{\frac{1}{V_t}\int _{V_t} j_i dV}{\frac{D\Delta C}{L_i}}=\dfrac{\frac{V_f}{V_t}\left[ \frac{1}{V_f}\int _{V_f} j_i dV\right] }{\frac{D \Delta C}{L_i}}=\varepsilon \dfrac{{\langle {j}_{i,f}\rangle }}{\frac{D\Delta C}{L_i}} \end{aligned}$$

(3)

where $V_t$ and $V_f$ are the total and fluid (f) volume of the porous medium, respectively, $L_i$ is the length of the domain in the direction of interest i, $\varepsilon =V_f/V_t$ is the porosity, and $j_i=-D\partial _i C$ is the diffusive flux in i-direction. Non-diagonal components were not determined since they are typically small in the fibrous materials examined (see the note below).

! Non-Diagonal Components

The full effective diffusivity tensor $\boldsymbol{\bar{\bar{D}}^\mathrm{eff}}$ can be determined from three simulations (1,2,3) of diffusive flux fields $\left( j_{x}^1,j_{y}^1,j_z^1\right)$, $\left( j_{x}^2,j_{y}^2,j_z^2\right)$ and $\left( j_{x}^3,j_{y}^3,j_z^3\right)$, corresponding to imposed concentration gradients in the x-, y- and z-direction, ${\nabla C_x^1}$, ${\nabla C_y^2}$ and ${\nabla C_z^3}$, respectively.

Using Fick’s first law, the components of the tensor are obtained by solving the following system of equations

$$\begin{aligned} - \begin{pmatrix} D_{xx}^\mathrm{eff} &{} D_{xy}^\mathrm{eff} &{} D_{xz}^\mathrm{eff} \\ D_{yx}^\mathrm{eff} &{} D_{yy}^\mathrm{eff} &{} D_{yz}^\mathrm{eff} \\ D_{zx}^\mathrm{eff} &{} D_{zy}^\mathrm{eff} &{} D_{zz}^\mathrm{eff} \end{pmatrix} \begin{pmatrix} {\nabla C_x^1} &{} {\nabla C_x^2} &{} {\nabla C_x^3} \\ {\nabla C_y^1} &{} {{\nabla C_y^2}} &{} {\nabla C_y^3} \\ {\nabla C_z^1} &{} {\nabla C_z^2} &{} {{\nabla C_z^3}} \end{pmatrix} = \begin{pmatrix} \langle j_x^1 \rangle &{} \langle j_x^2 \rangle &{} \langle j_x^3 \rangle \\ \langle j_y^1 \rangle &{} \langle j_y^2 \rangle &{} \langle j_y^3 \rangle \\ \langle j_z^1 \rangle &{} \langle j_z^2 \rangle &{} \langle j_z^3 \rangle \end{pmatrix} \end{aligned}$$

(4)

where ${\nabla C_x^2}$, ${\nabla C_x^3}$, ${\nabla C_y^1}$, ${\nabla C_y^3}$, ${\nabla C_z^1}$ and ${\nabla C_z^2}$ are the average concentration gradients computed in the transverse directions.

Note that although a local no-flux boundary condition is prescribed at the sidewalls of the domain, the average concentration gradients and volume-average diffusive fluxes in the transverse directions are in general different from zero. Similar considerations apply for the permeability tensor (see Guibert et al. (2016) for further details).

2.2 Convection: Permeability

Convection is modeled through the steady-state mass conservation and Navier-Stokes equations for an incompressible Newtonian fluid

$$\begin{aligned} \begin{aligned}&\nabla \cdot \boldsymbol{u}=0\\&\nabla \cdot (\boldsymbol{u}\boldsymbol{u})= -\nabla \tilde{p} + \nabla \cdot \left( \nu \left( \nabla \boldsymbol{u} + \nabla \boldsymbol{u}^\intercal \right) \right) \end{aligned} \end{aligned}$$

(5)

where $\boldsymbol{u}$ is the velocity vector, $\nu$ is the kinematic viscosity, p is the static pressure and $\tilde{p}=p/\rho$ is the kinematic pressure, with $\rho$ the density. Similar to diffusion, Dirichlet boundary conditions are prescribed for pressure on the external faces of the domain in i-direction, $\tilde{p}=\tilde{p}^\mathrm{in}$ and $\tilde{p}=\tilde{p}^\mathrm{out}$. An impermeable no-slip boundary condition ($\boldsymbol{u}=0$) is set on the remaining faces of the domain and interior fluid-solid interfaces of the porous medium.

According to Darcy’s law,

$$\begin{aligned} \langle \boldsymbol{u}\rangle =-\dfrac{\boldsymbol{\overline{\overline{K}}}}{\nu }\nabla \tilde{p};\quad \boldsymbol{\overline{\overline{K}}}= \begin{pmatrix} K_{xx} &{} K_{xy} &{} K_{xz} \\ K_{yx} &{} K_{yy} &{} K_{yz} \\ K_{zx} &{} K_{zy} &{} K_{zz} \end{pmatrix}, \end{aligned}$$

(6)

the diagonal components of the permeability tensor, $K_{i i}$, are determined as

$$\begin{aligned} K_{i i}=\dfrac{\nu \left[ \frac{1}{V_t}\int _{V_t} u_i dV\right] }{\frac{\Delta \tilde{p}}{L_i}}=\dfrac{\nu \frac{V_f}{V_t} \left[ \frac{1}{V_f}\int _{V_f} u_i dV\right] }{\frac{\Delta \tilde{p}}{L_i}}= \varepsilon \nu L_i \dfrac{{\langle {u}_{if}}\rangle }{\Delta \tilde{p}} \end{aligned}$$

(7)

where $\Delta \tilde{p} = \tilde{p}^\mathrm{in}-\tilde{p}^\mathrm{out}$ is the prescribed kinematic pressure difference and $u_i$ is the i-component of the velocity vector.

Calculations of absolute permeability are usually performed in physical units, considering $\Delta \tilde{p}=1~\mathrm m^2/s^2$ ($\tilde{p}^\mathrm{in}=1~\mathrm m^2/s^2$, $\tilde{p}^\mathrm{out}=0$), while $\nu$ is adjusted to ensure that the flow is in the creeping regime, i.e.,

$$\begin{aligned} Re=\dfrac{\langle {\Vert \boldsymbol{u}\Vert }\rangle d_f}{\nu } \approx \dfrac{\langle {u}_{i} \rangle d_f}{\nu } \ll 1 \end{aligned}$$

(8)

where ${\langle \Vert \boldsymbol{u}\Vert \rangle }$ is the average modulus of the velocity and $d_f$ is the diameter of the mono-sized fibres. Using these values, the expression of permeability is reduced to

$$\begin{aligned} K_{i,i}=\varepsilon \nu L_i \langle {u}_{i,f}\rangle \end{aligned}$$

(9)

where $\langle {u}_{i,f}\rangle$ is the average velocity in i-direction in the fluid phase.

Darcy’s Law

Darcy’s law can be verified by varying $\Delta \tilde{p}$, while keeping constant the value of $\nu$. The linear relationship between $\Delta \tilde{p}/L_i$ and Re shows that inertia is not important and the flow is indeed in the creeping regime, $Re\ll 1$.

3 Model Implementation

The main steps followed for the calculation of the effective transport properties are presented in this section, including the geometry generation, meshing routine, solver selection and post-processing. An example of the bash script used to run the simulations of effective diffusivity (and permeability) is presented below. The number of processors in the parallel execution is given as an argument to the script. Before running the script, the user must generate the triangulated geometry of the porous medium (facets.stl) using the gdl.cpp code. In addition to the solution fields, the output results include the volume-average diffusive fluxes (or velocity components) in each direction, which are saved periodically (as indicated in controlDict) and in the last iteration. The computed values are written into the postProcessing folder. The average quantities corresponding to the last iteration are used to determine the effective transport properties through Eqs. (3) and (9). The dimensions of the domain, porosity and bulk properties are known in advance.

Managing Computational Simulations

Since the meshing step is time consuming, it is recommended to use the decomposed mesh for calculations in other directions. The boundary conditions (i.e., the direction of the imposed gradient) must be changed as desired in the 0.orig folder.

3.1 Geometry

The microstructure of porous media can be obtained from (1) tomography images (García-Salaberri et al. 2015a, b, 2018, 2019) or can be (2) generated virtually using numerical algorithms (Choi et al. 2009; Choi et al 2011; Bertei et al. 2014). Volume-averaged quantities (e.g., composition fraction) and statistical descriptors (e.g., pore size distribution, n-point correlation functions, lineal path function, and chord length function) can be used as objective variables (Pant et al. 2014). Usually, the first method provides a higher degree of fidelity to reality, even though sometimes it is difficult to determine the constituents present in the images. An example is the differentiation of carbon fibres/binder and polytetrafluoroethylene (PTFE) in GDLs due to their similar X-ray absorption properties García-Salaberri et al. (2018). The virtual generation of materials allows one to overcome this issue, although the creation of realistic microstructures can be challenging in some circumstances. An example is the complex multi-component, multi-scale geometry of catalyst layers. Here, fibrous porous materials with a 2D arrangement of randomly-oriented fibres similar to carbon-paper GDLs were used as an illustrative example.

For a specified number of cylindrical fibres, $N_f$, of diameter $d_f=10~\mathrm{\mu m}$, the steps followed for the generation of the material microstructure in a box of size $[0-{S}_x$, $0-{S}_y$, $0-{S}_z]$ ($S_x=S_y=1.5~\mathrm{mm}$, $S_z=0.25~\mathrm{mm}$), are as follows:

• 1. The 3D coordinates, $\boldsymbol{P_1}$ and $\boldsymbol{P_2}$, of the axial endpoints of the cylindrical fibres are generated randomly inside the box of material. The same z-coordinate is prescribed for the endpoints of each fibre ($P_{1,z}=P_{2,z}$) to achieve a 2D arrangement.

• 2. The x and y coordinates of the axial endpoints are translated $-0.25~\mathrm{mm}$, so there is some extra material around the cropped domain of size $[0-{L}_x$, $0-{L}_y$, $0-{L}_z]$ that is used in the simulations ($L_x=L_y=1~\mathrm{mm}$, $L_z=0.25~\mathrm{mm}$). This step removes edge effects.

• 3. Once the position of all the axial endpoints is fixed, the lateral surface of the cylindrical fibres is triangulated using a spacing in the axial and azimuthal directions, $\boldsymbol{\Delta x}=(\boldsymbol{P_2} - \boldsymbol{P_1})/10$ and $\Delta \phi = 2\pi /20$, respectively. The unit normal vectors perpendicular to each triangle are also determined.

• 4. The vertices and normals of the triangles that define the lateral surface of the cylindrical fibres are written into an STL file (facets.stl).

• 5. The endcaps of the cylindrical fibres are triangulated using a spacing in the azimuthal direction equal to that used for the lateral surface ($\Delta \phi = 2\pi /20$).

• 6. The vertices and normals of the triangles that define the endcaps are added to the facets.stl file (an example of a triangulated geometry is shown in Fig. 2).

Fibre Intersections

Fibre intersection is not explicitly taken into account in the geometry generation. However, when the fluid region is selected in the meshing step with snappyHexMesh, the mesh is adapted to the external fibres surface and the intersections among them. The solid regions inside the fibres and their intersections are removed, since they are unreachable from the fluid region.

Fig. 2

Geometry composed of cylindrical fibres of $10~\mu$m in diameter with random orientations in the material plane (x-y plane) used to mimic the microstructure of binder-free carbon-paper GDLs. The close-up view shows the triangulated geometry

3.2 Meshing

The meshing utility snappyHexMesh is used to mesh the pore space enclosed within the external surfaces of the domain and the geometry of the cylindrical fibres. A background mesh composed of cubes is first created with blockMesh. Then, the resulting mesh is refined with snappyHexMesh using the facets.stl file as an input. Castellated meshes were considered here, suppressing the surface snapping and layer addition steps. The resulting meshes had around 5.5 millions of cells depending on the number of fibres $N_f$ in the sample (i.e., the porosity). The maximum number of cells was achieved for intermediate porosities around $\varepsilon \approx 0.6$. An example of the generated meshes is shown in Fig. 3, including a close-up view of the refined mesh close to the fibres surface. The level of refinement used in snappyHexMesh was set equal to (2 4).

Practical Advice

The following guidelines should be taken into account during the meshing step:

• 1. Introduce a small gap slightly higher than the fibre radius near the boundary faces in the z-direction, so that the axial endpoints of the fibres do not touch the boundary faces. This practice facilitates the selection of a point inside the fluid region during the meshing step.

• 2. Set the size of the cubic cells in the background mesh similar to the fibre diameter ($d_f=10~\mathrm{\mu m}$). This size ensures that the geometry of the fibres is properly captured during the refinement of the mesh with snappyHexMesh. No significant differences were found in the results using background cells of $5~\mathrm{\mu m}$.

Fig. 3

Castellated mesh generated with snappyHexMesh using a background mesh with cubic cells of $10~\mu$m in size (equal to the fibre diameter, $d_f$). The close-up view shows the refined mesh around the fibres surface

3.3 Solver and Post-processing

Laplace and Navier-Stokes equations used to simulate diffusion and convection are solved in OpenFOAM with the steady-state solvers laplacianFoam and simpleFoam, respectively. A laminar simulationType with a Newtonian transportModel is used in simpleFoam. The remaining solver settings can be kept similar to those commonly used in OpenFOAM.

For post-processing, the topoSet utility is used to create a cell zone that includes the entire computational domain (i.e., the fluid region of the porous medium). Then, the volume-average diffusive fluxes (or velocity components) in each direction are calculated using the postProcess utility, defining function objects in controlDict. The volAverage operation is used for volume averaging.

Calculation of Effective Transport Properties

The pre-factors multiplying the average diffusive flux (or velocity component) in Eqs. (3) and (9) (such as the length $L_i$ or the porosity $\varepsilon$) can be included as a scaling factor in the function objects implemented in controlDict. The porosity can be easily determined by dividing the volume of the fluid region (provided by the postProcess utility) by the total volume of the domain (which is known in advance). Alternatively, the pre-factors can be introduced when the results are plotted, for example, using Python.

Fig. 4

Concentration fields, C(x, y, z), corresponding to calculations of the through-plane effective diffusivity for two different porosities, $\varepsilon$ (number of fibres, $N_f$): (left) $\varepsilon =0.8$ ($N_f=1500$), (right) $\varepsilon =0.6$ ($N_f=3500$)

Fig. 5

Concentration fields, C(x, y, z), corresponding to calculations of the in-plane effective diffusivity. See caption to Fig. 4 for further details

Fig. 6

Kinematic pressure fields, $\tilde{p}(x,y,z)$, and streamlines (colored by pressure level) corresponding to calculations of the through-plane absolute permeability for two different porosities, $\varepsilon$ (number of fibres, $N_f$): (left) $\varepsilon =0.8$ ($N_f=1500$), (right) $\varepsilon =0.6$ ($N_f=3500$)

Fig. 7

Kinematic pressure, $\tilde{p}(x,y,z)$, and streamlines (colored by pressure level) corresponding to calculations of the in-plane absolute permeability. See caption to Fig. 6 for further details

Fig. 8

Computed through- (TP) and in-plane (IP) normalized effective diffusivities, $D^\mathrm{eff}/D$, as a function of porosity, $\varepsilon$. The Bruggeman correlation Bruggeman (1935), $D^\mathrm{eff}/D=\varepsilon ^{1.5}$, and the anisotropic random fibre model of Tomadakis and Sotirchos (1993) (see Eq. (12)) are also shown

4 Results

In this section, the computed results for the effective diffusivity and permeability are discussed. The results in both the through- and in-plane directions are presented given the anisotropy of the generated carbon-paper GDLs. One representative direction (x-direction) is analyzed in the material plane (x-y plane). Figures 4 and 5 show some illustrative examples of the species concentration distributions corresponding to effective diffusivity calculations for two different porosities (i.e., number of fibres). The pressure distributions and streamlines corresponding to permeability calculations are shown in Figs. 6 and 7. The porosities are in the range typically observed for uncompressed ($\varepsilon \approx 0.8$) and mid-compressed ($\varepsilon \approx 0.6$) GDLs. Higher transport properties are found in the in-plane direction due to the 2D arrangement of carbon fibres (and pores), which facilitates transport in this direction.

The overall diffusive flux across the material (at the same concentration gradient) decreases with decreasing porosity and increasing tortuosity of transport pathways. The increment of tortuosity with porosity leads to non-linearities in the dependence between the normalized effective diffusivity, $D^{\mathrm{eff}}/D$, and the porosity, $\varepsilon$, as given by the relationship García-Salaberri et al. (2015b):

$$\begin{aligned} \dfrac{D^{\mathrm{eff}}}{D}=\dfrac{\varepsilon }{\tau } \end{aligned}$$

(10)

where $\tau$ is the diffusion tortuosity factor. For example, $\tau =\varepsilon ^{-1/2}$ ($D^{\mathrm{eff}}/D=\varepsilon ^{1.5}$) in the traditional Bruggeman correction for porous media consisting of small, spherical solid inclusions (Bruggeman 1935; Tjaden et al. 2016).

Permeability is influenced by hydraulic radius, porosity and tortuosity, resulting in a non-linear variation as a function of porosity Holzer et al. (2017). The Carman-Kozeny equation has been successfully applied to describe the variation of GDL permeability with porosity Gostick et al. (2006).

$$\begin{aligned} K = \dfrac{d_f^2\varepsilon ^3}{16k_{ck}(1-\varepsilon )^2} \end{aligned}$$

(11)

where $k_{ck}$ is the Carman-Kozeny constant, which is used as a fitting parameter depending on the microstructure of the porous medium.

The variations of the normalized effective diffusivity and permeability as a function of porosity are shown in Figs. 8 and 9, respectively. The normalized effective diffusivity is lower than that predicted by the Bruggeman correlation, $D^{\mathrm{eff}}/D=\varepsilon ^{1.5}$, due to the more complex geometry of fibrous GDLs. Moreover, it is somewhat lower than the correlation proposed by Tomadakis and Sotirchos (1993) for random fibre structures

$$\begin{aligned} \dfrac{D^\mathrm{eff}}{D}= \varepsilon \left( \dfrac{\varepsilon -0.11}{1-0.11}\right) ^{n} \end{aligned}$$

(12)

where $n=0.785~\text {and}~n=0.521$ for the through- and in-plane directions, respectively.

Fig. 9

Computed through- (TP) and in-plane (IP) absolute permeabilities, K, as a function of porosity, $\varepsilon$. The curves corresponding to various Carman-Kozeny constants, $k_{ck}$, are also shown (see Eq. (11))

The differences between both models are ascribed to the different methodology used for the generation of the fibrous geometry. For instance, the values computed here approach those reported for binder-free GDLs, such as Freudenberg carbon paper, being $D^{\mathrm{eff}}/D\approx 0.36$ for $\varepsilon \approx 0.65$ (Hack et al. 2020; Hwang and Weber 2012).

The permeability is well correlated as a function of porosity using Eq. (11) with $k_{ck}=2-4$. A steeper decrease of the permeability is found for porosities below $\varepsilon \lesssim 0.5$, which drops around two orders of magnitude in the range $\varepsilon =0.1-0.5$ compared to the ten-fold descent in the range $\varepsilon =0.5-0.85$. The non-linear behaviour arises from the sensitivity of permeability to small microstructural differences near the percolation threshold. Similar results were reported in previous works for fibrous porous media (Tomadakis and Robertson 2005; Nabovati et al. 2009).

Effective Diffusivity and Permeability of Commercial GDLs

For a given porosity, the effective diffusivity and permeability of commercial GDLs (Toray, SGL Carbon Group and Freudenberg carbon papers) highly depends on their microstructure. In fact, the volume fraction and porosity of binder have been identified as key parameters that influence the effective transport properties of GDLs (García-Salaberri et al. 2018; Mathias et al. 2003; Zenyuk et al. 2016). For example, Toray TGP-H series carbon papers show lower effective diffusivities in the through-plane direction than those computed here due to the more complex pore structure that arises from the addition of an almost non-porous binder (García-Salaberri et al. 2015a, b); $D^\mathrm{eff}/D\sim 0.22-0.28$ (Toray TGP-H) vs. $D^\mathrm{eff}/D\sim 0.45$ (present work) at $\varepsilon \approx 0.72$.