1 Introduction

Polymer electrolyte membrane fuel cells (PEMFCs) are one of the leading candidates to replace the internal combustion engines. Operating on hydrogen and air, they guarantee zero greenhouse gas emissions if the hydrogen is produced from a renewable source. The main appeal of PEMFCs is their high power and energy density, as well as short refueling times which make them suitable for transport, mobile, and vehicular applications. A typical PEMFC stack consists of a proton exchange membrane (PEM), catalyst layers (CL), gas diffusion layers (GDL), and flow field plates. Each cell in a PEM is a sandwich of porous layers on both sides of a thin polymer electrolyte membrane, referred to as a membrane electrode assembly (MEA). The GDLs are carbon fiber papers which allow gaseous reactants to reach regions of the CLs under the ribs, and provides electron access for the CLs over the channels. The PEM acts as an ionic conductor and allows protons generated at the anode to be transported to the cathode. It also prevents direct mixing of oxygen and hydrogen since it is essentially impermeable to the gas. The catalyst layer is composed of a mixture of ionomer and carbon-supported platinum particles, which are adhered to the surface of the membrane. The ionomer phase acts as pathway for protons to reach the reactive sites, while the carbon provides electron access. The bipolar plates, which are made from graphite or metal to promote conductivity, sandwich the porous assembly and distribute reactants across the cell. A microporous layer (MPL), which is a mixture of carbon black and PTFE, is usually applied to the side of the GDL facing the CL. It has been shown that the MPL improves mass transfer and creates more effective electrical and thermal contact between the CL and the GDL [1, 2].

The production of liquid water is a major engineering challenge because it must be removed from the cell as it is generated. Accumulation of water inside the cell results in flooding of the internal porous electrode structures, specifically the GDL, and prevents gaseous reactants from reaching catalyst sites. Achieving a balance between water rejection from the cell to sustain high mass transfer rates and maintaining sufficient moisture inside the cell to ensure membrane hydration is a challenging task and referred to as water management [3,4,5]. Unfortunately, the goal of maintaining the water content inside the cell at the optimum value is not practically achievable for several reasons. Because water is generated inside the cell, the relative humidity of the air stream increases as it passes through the cell, creating a distribution of humidity conditions throughout the cell. There are also temperature and current density variations across the active area, creating altered humidity conditions from location to location. Another difficulty is the transient nature of the fuel cell operation under a duty cycle, which creates variable internal water contents at any given time. The result is that ideal or optimum conditions can only be expected in limited locations and at certain operating conditions. Since currently available membranes do not perform well when dry, it is necessary to supply highly humidified feed gases and design the cell to handle liquid water [6, 7].

Understanding the effect of liquid water on PEM fuel cell performance has been a major goal of fuel cell modeling research. In the recent years, numerous models have been published, attempting to use continuum models to simulate multiphase flow in the MEA [8, 9]. It has been found that because of the atypical properties of GDL, such as high porosity, fibrous structure, anisotropy, and thinness, testing of GDL transport properties is challenging compared to the other traditional porous media. The past decade has seen the development of numerical simulations and suitable techniques for measuring relevant experimental transport data; however, their availability did not improve the applicability of the volume averaging continuum models but rather called their results into question [10,11,12]. Aghighi et al. have provided an overview of the limitation of this modeling approach [13].

Pore network modeling (PNM) is receiving interest as an alternative approach in this field. In PNMs, the media is represented as a set of connected pores and throats, capillary behavior of the liquid is modeled by applying percolation theory, and transport is modeled using a resistor network analogy. Pore network models have been widely used to model porous materials for the last three decades [14,15,16]. Applying PNMs for media like PEMFCs electrodes is appealing for several reasons: Firstly, it is possible to capture a full unit cell (rib-channel-rib and full thickness) in all dimensions using PNM and easily incorporate two-phase flow, and since the water invasion is capillary dominated, simple percolation algorithms are sufficient to model the movement of liquid water. Thus, they can efficiently track discrete water configurations and allow the study of the local impacts of water blockages on other transport processes. And secondly, the thinness of these materials makes multiphase transport parameters difficult to measure. But PNMs do not need any constitutive relationships, instead they require only structural information. Moreover, it can be shown that the volume-averaged approach is technically questionable and small differences in the location of water blobs can have a significant impact on the cell performance, but these features are missed by volume-averaged models [11, 13]. PNMs have long been used in the study of porous media [17,18,19], but only recently has been fruitfully applied to fuel cell electrodes [20,21,22,23]. For instance, Gostick et al. applied a cubic pore network model to study multiphase mass transfer and capillary properties of GDL to estimate experimentally challenging properties such as relative permeability and effective diffusivity [24]. Since then, many other PNMs have been developed to study multiphase transport processes in PEMFCs applying various types of networks and operational parameters to study cell performance [25,26,27,28]. There have been efforts to combine PNM and continuum approach. Recently [29], methods have been presented for coupling pore network modeling with a continuum model and proposed different coupling schemes depending on the applied simulation parameters. On the other hand, Aghighi et al. [13] introduced the first PNM to simulate the entire membrane electrode assembly of fuel cell and highlighted the strength of PNMs to resolve discrete water blockages in the electrodes.

The majority of pore network models in the PEMFC literature have focused on the capillary invasion of liquid water injecting into the face of the GDL from the CL. This type of invasion process is simple to model with PNMs, and these studies have shed light on various aspects fuel cell performance. It has become apparent, however, that diffusion of water vapor from the CL into the GDL and subsequent condensation in the GDL is an important source of liquid water. In fact, it has been argued that this is the only way liquid water can enter the GDL when an MPL is present since the MPL is so hydrophobic [30,31,32]. Some experiments using in situ synchrotron-based X-ray radiography [30, 31] and neutron radiography [33] show that, in addition to a peak of saturation near the CL–GDL interface, which might be expected when water invaded from the CL, there is a second peak within the GDL near the flow field. Gostick et al. [6]. demonstrated that this profile could be reproduced in a pore network model if condensation was also occurring at the bipolar plate, but their condensation model was purely heuristic and did not incorporate any heat or mass transfer. Clearly, any model of multiphase flow in the GDL must include phase change (both evaporation and condensation) in addition to capillary invasion. Generally, phase change in porous media has been well studied [34], but the bulk of the literature utilizes the continuum modeling approach, which is not suitable for simulating phase change in GDL as mentioned earlier. Generally, incorporation of phase change into a network is complicated because of the coupling of the liquid, vapor, and heat transport equations. Some researchers have extensively studied drying phenomena in porous media using pore networks [35,36,37,38]. The importance of condensation in PEMFCs has been shown in several recent experimental studies [3, 39]. Louriou et al. [40] have presented simulations and visualization experiments for bubble growth in a porous media, which is analogous to condensation where bubbles are analogous to liquid droplets. They were able to achieve good agreement between the numerical procedures and their experiments indicating that phase change processes can be realistically captured with the PNM approach. Medici and Allen [41] have presented a network model of evaporation with the addition of heat transfer and vapor transport coupled with the liquid percolation. They have extended this evaporation model to include a more elaborate film evaporation model with the consideration of pore geometry, interfacial properties, heat and mass transfer, and microscale fluid flows [42]. Gostick et al. [6] modeled condensation over the channel lands (assumed to be the coldest location in the GDL) by artificially seeding invading clusters of water and letting them grow until they reached an outlet pore over the channel. This approach reproduced some experimentally determined saturation profiles. Hinebaugh et al. [43] developed a two-dimensional dynamic pore network model to simulate condensation in hydrophobic GDL. Similar to Gostick et al. they did not consider heat and mass transfer, but they did study the effect of nucleation location on the resulting saturation pattern.

Boillat et al. [44] introduced an experimental method combined with high-resolution dynamic neutron imaging for studying the effects of liquid water on mass transfer limitations. Their study suggests that water accumulation near the GDL surface has a significant impact on the cell performance and bulk diffusion. In another experimental study, Oberholzer et al. [45] used high-resolution in-plane imaging to visualize the water distribution for paper-type and cloth-type GDLs. In their study, the in-plane water distribution profiles under different operational conditions indicate the crucial impact of accumulation of water in the channel/rib region of the cathode GDL on flooding and cell performance.

Also in the last 3 years, Prat et al. have applied pore network models [46, 47] for condensation in the presence of imposed temperature gradient across the GDL. More recently [48], they simulated a coupled condensation model which links the heat/mass transport to electrochemical reactions at the catalyst layer. Their results show that at a sufficiently high-temperature water vapor enters the GDL in vapor and liquid water appears near the rib region of the cathode. However, the impact of latent heat on the temperature distribution within the network was not been considered. Moreover, they did not explore condensation over the full range of operating voltages of the cell. In this work, we present a methodology for simulating phase change inside the cathode side of PEMFC based on a pore network model, with both condensation and evaporation allowed to occur naturally depending on the local humidity conditions. This work offers several key improvements over the recently published works coming from the Prat group. Firstly, the present work considers the full polarization behavior of the cell so examines the process as a function of current density. Secondly, this model includes both of the catalyst layers and membrane as well as the GDL, building on our previous work [13]. Finally, this work implements the solid phase heat transfer using a novel ‘dual network’ where the solid phase is modeled using a distinct network that interpenetrates the standard void network. As a case study for this algorithm, the present work investigated a variety of relative humidity conditions for the reactant gas at the cathode side. This led to condensed water clusters and ultimately allowed to the study of these local effect on the overall polarization performance of the cell.

2 Model development

The domain for this simulation is depicted in Fig. 1. This work focuses on the water management in the cathode GDL, so does not consider the anode GDL or CL; however, to create more realistic cell performance results including Ohmic loss, the membrane was included. This arrangement will be discussed in more detail below. In the model presented here, the channel and rib areas of the flow field plate are included as boundary conditions to the gas diffusion and electron conduction problems, respectively. The GDL is modeled as a cubic pore network representative of Toray TGP-H-120 as outlined in the previous work [24]. The CL, MPL, and the membrane are treated as continua. The continua simplification was due to the large-scale difference between the GDL and CL–MPL pore sizes [49]. This approach has been used previously to simulate gas diffusion through the GDL–MPL/GDL–CL [1, 13]. PNMs are essentially resistor-networks, so the transport equations in these sub-domains are solved using the same finite-difference framework used to solve transport in the pore network.

Fig. 1
figure 1

Schematic view of the modeling domain with indication of the variables corresponding to each section. \({{\phi}_{{m}}}\) is the ionomer potential and \({\eta}~\) is the overvoltage

Full size image

2.1 Network generation

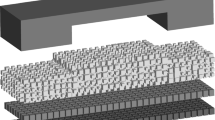
For a PNM to represent the material to be modeled, it is necessary that the pores and throats of the model have the same physical properties as the material, including size distribution, aspect ratios, connectivity, and spatial correlations. If done correctly for the GDL, the PNM simulations should reproduce the known physical and transport properties of material, such as porosity, capillary drainage curves, absolute permeability, and effective diffusivity. In 2007, Gostick et al. [24] provided the first fully calibrated model of the GDL, including several adaptations to account for the fibrous nature of the materials, and these model parameters were used in the present work as well, except for the spatial correlations to create anisotropic media. The individual networks for the GDL, CL, MPL, and membrane domains are stitched together to form a single modeling domain as shown in Fig. 2. The stitching occurs in such a way that the pores on the adjacent interfaces between the networks are connected via throats that span across the interface. In the case of adjacent layers with different spacing, each larger pore is connected to multiple nodes on the neighboring domain.

Fig. 2
figure 2

Illustration of interconnections between the GDL, MPL, and the neighboring CL domain for both solid and pore network of the cathode side. Blue and red spheres represent pore and solid node centers, respectively. The lattice spacing of the GDL was 40 µm while the spacing of the CL–MPL–PEM nodes was 8 µm. (Color figure online)

Full size image

In this study, a unique dual network arrangement was used to enable the modeling of transport in the void phase on one network and through the solid phase on the other one. Unlike the recent work by Prat et al. [48], the networks in here are not collocated but instead are interpenetrating to make the domain more realistic. The nodes of this secondary solid network are located at the interstitial locations of the void network, so the pores/nodes of these 6-connected lattices are connected to each other in the diagonal directions. Geometrical parameters of the solid network are then calculated considering the properties of the pore network, so there is less solid surrounding a large pore or instance. The cathode side of the MEA domain includes a GDL network with a lateral (in-plane) size of 30 × 30 pores which are spaced 40 µm apart. The center of the domain is masked by the flow field rib. The ratio of rib/channel was set to 4/6. The GDL was eight pores thick or 320 µm and the catalyst domain was 150 × 150 × 1 nodes with 8 µm spacing. The MPL layer is also added with the same topological properties as the CL. The CL and MPL were each treated as single layer of nodes, but they had physical depth since every node was 8 µm deep, so transport resistance into the CL/MPL was included. The proposed numerical scheme is fully applicable to MPL/CL with more layers of nodes, but the simple case of one layer for each one of them was sufficient for the present aim of demonstrating the numerical scheme. The MEA also consists of the membrane layer with a size of 150 × 150 × 6 nodes, also with 8 µm spacing. Another boundary layer similar to the cathode CL had been added for the sake of anode boundary conditions. Using the OpenPNM package [50, 51], it was possible to run each algorithm only for the desired subdomain, and thus significantly facilitates simulation and speeds up the solution procedure.

2.2 Model equations

The channel pressure was set to 110,000 (Pa) and this was assumed constant throughout the entire electrode. It is also assumed that the mass transfer simulation was equivalent to binary diffusion of \({{\text{O}}_2}/{{\text{H}}_2}{\text{O}}\) through a stagnant film of \({{\text{N}}_2}\) and \({{\text{H}}_2}{\text{O}}\), rather than accounting for the multicomponent mass transfer.

The model presented in what follows adopts the same equations as in [13] in regard to coupling mass transfer and electrochemical reaction which are briefly explained here again. The transport in the GDL is modeled using established pore-scale physics [24]. Diffusion of A through stagnant B, based on Fick’s law using the finite-difference scheme, can be obtained by:

$${n_i}=\mathop \sum \limits_{{j=1}}^{N} {g_{d,ij}}\left( {\ln \left( {{x_{B,j}}} \right) - \ln ({x_{B,i}})} \right)=~\mathop \sum \limits_{{j=1}}^{N} {g_{d,ij}}\left( {{X_{B,j}} - {X_{B,i}}} \right)$$
(1)

with \({g_d}\) given by

$${g_d}=\frac{{c{\mathcal{D}_{{\text{AB}}}}{{(2r)}^2}}}{L}$$
(2)

where \({n_i}\) is the mass transfer rate through the throat between pore \(i\) and pore \(j\); \({x_{{\text{B}},j}}\) is the mole fraction of the stagnant species \({\text{B}}\) in the neighboring pore \(j\); \({x_{{\text{B}},j}}\) is the mole fractions of \({\text{B}}\) in pore \(i\); and \({g_d}\) is the diffusive conductance of the conduit. In this equation, \(c\) is the total molar concentration of the gas; \({\mathcal{D}_{AB}}\) is the binary diffusion coefficient; \(2r\) is the width of the conduit; and \(L\) is the conduit length. The total diffusive conductance for diffusion between two adjacent pore bodies is taken as the net conductance for diffusion through half of body \(i\), the connecting throat and half of body \(j\). The \({g_d}\) for each section is calculated and the total conductance for the pore-throat-pore assembly is found by

$$\frac{1}{{{g_{d,ij}}}}=\frac{1}{{{g_{d,i}}}}+\frac{1}{{{g_{d,t}}}}+\frac{1}{{{g_{d,j}}}}$$
(3)

Applying Eqs. (1–3) for each pore in the network yields a system of linear equations that can be solved with the applied boundary condition on each side of the network to give the concentration distribution across the network. The effective diffusivity for each node in the CL/MPL region is treated as a porous block with a fixed porosity of 0.50 using the following:

$${D_{eff}}={\mathcal{D}_{AB}}\frac{\epsilon }{\tau },{\text{ }}\tau ={\text{}}{\ \epsilon ^{ - 0.5}}$$
(4)

where \(\epsilon\) is the porosity and \(\tau\) is the tortuosity calculated using the Bruggeman relation [52] for lack of a more specific model. So, the effective diffusive conductance between two nodes of this region is

$${g_{d,{\text{CL}}}}=\frac{{c{D_{{\text{eff}}}}\,A}}{L}$$
(5)

where \(L\) and \(A\) are length and area of each porous block are set by the node spacing. The same analogy can be applied to ion transport in the ionomer phase (both in the CL and membrane) inside the MEA:

$${g_p}=\frac{{\sigma _{p}^{{{\text{eff}}}}~\,A}}{L}$$
(6)

where \({g_p}\) is the ionic conductance between the neighboring nodes, which is a function of the node spacing and intrinsic conductivity of the ionomer. The following relation for the effective proton conductivity \(\sigma _{p}^{{{\text{eff}}}}\) is used:

$$\sigma _{p}^{{{\text{eff}}}}=~~\sigma _{p}^{{{\text{bulk}}}}{({\phi _p})^{1.5}}$$
(7)

where \({\phi _p}\) is the ionomer volume fraction and \(\sigma _{p}^{{{\text{bulk}}}}\) is the conductivity of the ionomer. The preceding two equations could be used to get the electronic conductivity of the CL, but in the present work the voltage loss due to electron transport was neglected due the high conductivity of the carbon phase. The validity of this assumption was checked for some initial simulations, and it was confirmed that the electronic voltage drop was less than 1 mV. At the CL-membrane interface, the protonic resistance was the sum of half of a CL node and half of a membrane node, which is the typical pore-network formulation for a conductance between nodes. For the GDL–MPL interface throats, however, the resistance of the GDL pore was neglected which assumes that the GDL pore is well mixed; thus, diffusion into the MPL was only hindered by the resistance of half of a MPL node.

The kinetics in the fuel cell and therefore the reaction rate was modeled using the following form of Butler–Volmer equations for the cathode reactions at the CLs [53]:

$${J_c}=j_{0}^{c}~{A_v}\left( {\frac{{{C_{{O_2}}}}}{{C_{{{O_2}}}^{*}}}} \right)\left[ {\exp \left( {\frac{{\alpha \cdot {z_{{O_2}}} \cdot F}}{{RT}} \cdot {\eta _c}} \right) - \exp \left( { - \frac{{\left( {1 - \alpha } \right) \cdot {z_{{O_2}}} \cdot F}}{{RT}} \cdot {\eta _c}} \right)} \right]=~{k_c}{x_{{O_2}}}$$
(8)

where \(\alpha\) is the transfer coefficient describing the symmetry of the reaction; \({z_{{O_2}}}\)are the number of electrons involved in the cathode reactions; \({j_0}\) is exchange current density; \({C^*}\) is the reference concentration; \({A_v}\) is the catalyst reactive surface area per unit volume; \(F\) is the Faraday constant; \({\eta _c}\) describes the activation overvoltage of the cathode reactions; \(R\) is the ideal gas constant; \(T\) the temperature; and \(J\) is the current production/consumption rate \((A{\text{ m}}_{{cat}}^{{ - 3}})\).

In terms of fuel cell operation, drainage of a wetting phase by invasion of a non-wetting phase corresponds to the flow of liquid water into the pores of the GDL [25]. This behavior can be described by percolation theory. A modified percolation algorithm, known as invasion percolation (IP), was developed specifically for immiscible displacements of a non-wetting phase into a porous medium. An invasion percolation of liquid water algorithm is considered by simulating a drainage process of the water into porous electrodes, using the Washburn equation to relate throat size and entry pressure [54]:

$${P_{c,i}}=~ - 2\sigma \frac{{cos\theta }}{{{r_i}}}$$
(9)

where \({P_{c,i~}}\) is capillary entry pressure of pore \(i\) with radius \({r_i;}\) \(\theta\) is the contact angle of water with the carbon phase; and \(\sigma\) is the surface tension of water. It has been shown that the Purcell model is more suitable to quantitatively predict the capillary invasion pressure in fibrous media [25]; however, in this work, it is only the invasion patter of liquid water that is of interest so Eq. [9] is suitable for simplicity. IP [55,56,57] is used to simulate volume controlled injection into a sample where fluid flows into the material in a pore-by-pore fashion, following the path of least resistance. IP is a dynamic process since at each time step, the algorithm searches in all of the neighbor throats of an invaded pore to find the throat with the minimum entry pressure. The algorithm continues by adding the throats connected to the newly invaded pore to the list of accessible throats, and so on [58]. Depending on the conditions prevailing around a water cluster the total vapor rate to a cluster can be positive (condensation) or negative (evaporation). During condensation, a water cluster grows applying the IP by the addition of water from the vapor phase. During evaporation, the water cluster shrinks so percolation must proceed in the opposite direction, which is technically imbibition of air. This must be more difficult to model; however, so in the present work the invasion of air was also treated as drainage which is one interpretation of the experimental data on air–water capillary pressure behavior in GDLs [59].

2.3 Iterative algorithm

A major part of this work was the development of an algorithm that is able to solve the various coupled transport equations for the physics occurring at the cathode side. The standard PNM framework requires that each transport process is solved independently, and the coupling of different processes occurs through an iterative scheme where results from one solution are used as boundary conditions for another. Applied boundary conditions required for simulation of an operating MEA are as follows:

  • Constant RH at the GDL/flow channels interface

  • Zero mass rate of \({{\text{H}}_2}{\text{O}}\) and \({{\text{O}}_2}\) at the membrane/CL interface and at the flow field rib

  • Zero rate of protons at the CL/GDL interface

  • Constant voltage boundary conditions applied at the flow field rib

  • Constant temperature at the GDL/rib interface

  • Constant values for \({\eta _a}\) at the CL/GDL interface of the anode side

The iterative algorithm for this simulation as depicted in Fig. 3 is consisted of two main steps: (1) transport phenomena and electrochemical reactions and (2) phase change and cluster growth. The procedure for the first part is as follows: The values for \({\eta _c}\) are guessed. An initial guess for these values can be obtained by solving a 1D simplified system with spatially averaged properties of the network. But in this study, the boundary values for \({\eta _a}\) and initial guesses for \({\eta _c}\) have been selected from [13]. In the next iteration, the results of the last step are used and provide an excellent estimation. Once \({\eta _c}\) are known in every pore, the reaction constants \({k_c}\) can be found for Eq. 8. Based on Faraday’s Law of Electrolysis, the source/sink terms in the unit volume of catalyst layer will be

$${S_c}=\frac{{{k_c}}}{{{z_{{O_2}}}F}}{x_{{O_2}}}$$
(10)

Then using the overvoltage values and Eqs. (1) and (10), the rates of oxygen diffusion are computed through the cathode from the flow channels to the catalyst layer. The mass diffusion for oxygen and vapor in cathode is computed independently. Once the mole fractions are found, the local current per unit volume is determined from the computed local concentration and the kinetic constants based on the current guesses of \({\eta _c}\) in Eq. [8]:

$$I_{{{\text{local}}}}^{c}={k_c}~{x_{{O_2}}}$$
(11)

By applying the local currents as boundary conditions to the solid phase electron conduction, voltage gradient from the separator plates to the reactive sites can be found. From this step, the ionomer potentials (\({\phi _{m,a}}\) and \({\phi _{m,c}}\)) can be obtained by using the solid phase potentials \({\phi _{s,a}}\) and \({\phi _{s,c}}\), and the definition of overvoltage:

$${\eta _a}={\phi _{s,a}} - {\phi _{m,a}}~$$
(12)

and

$${\eta _c}={\phi _{s,c}} - {\phi _{m,c}} - {V_{{\text{OC}}}}$$
(13)

Due to high conductivity of the carbon phase in the GDL and the CL, the voltage distribution will be nearly identical to the respective boundary conditions at each side. The calculation of electron transport can therefore be safely skipped by assuming the voltage at the flow field rib prevails throughout the solid matrix to reduce the number of steps in the algorithm and sped up the solution. With \({\phi _{m,a}}\) and \({\phi _{m,c}}\) values known, the protonic conduction through the CL/MEM can be computed for the cathode sides.

The difficulty of this algorithm lies in the step 2 shown in Fig. 3, which tries to couple heat transfer and mass transfer results that control cluster growth. Modeling phase change in the GDL adds considerable complexity to the transport calculations. Although, it is feasible to couple the transient heat and mass transport equations and solve them simultaneously, it is not trivial or obvious how to incorporate phase change effects, growth and shrinkage of percolating clusters, and tracking of the air–water interfaces in the pore network. Figure 4 displays a schematic 2D view of a pore network showing the main transport mechanisms to be considered in this model. The first main change required by this model was the superposition of a solid phase network onto the pore space, which is required to model the thermal conditions in the domain. The temperature distribution will affect the local equilibrium conditions, which indicate whether condensation or evaporation will occur and at which rate. The second significant challenge was to include the transient nature of the various processes. The following general approach for coupling heat/mass transfer should be taken: (1) Solve the steady-state heat and mass transfer based on the electrochemical reactions at CL, and then solve the invasion percolation problem separately. (2) Reevaluate the conditions in the network (e.g., alter the relative humidity based on the temperature profile, calculate the mass transfer rate to or from a water cluster, and account for latent heat of the phase change). (3) Index the time and reiterate until some stopping criteria (i.e., steady-state cluster configuration) is reached. This approach is referred to as pseudo-transient, and it implies that the growth of the water clusters happens slowly, giving time for the other phenomena to reach new steady-state conditions.

Fig. 3
figure 3

Algorithm diagram of the iterative computational procedure, starting with initial guesses for \({\eta}{_{{c}}}\), and ultimately obtaining \({{I}_{{total}}}\)

Full size image
Fig. 4
figure 4

Schematic view of the cross section of the 3D pore network used for the phase change model

Full size image

For the sake of simplicity, it is also assumed that the fluids are in thermal equilibrium with the surrounding solid, and that all heat transfer occurs as solid phase conduction since its thermal conductivity is much higher than the fluid phases. The temperature profile in the solid phase is found by considering heat conduction through the solid network using Fourier’s law:

$${\dot {Q}_{ij}}=\frac{{{T_i} - {T_j}}}{{{R_{ij}}}},\quad R=\frac{l}{{{k_T}A}}$$
(14)

where \(i\) and \(j\) are two adjacent solid nodes, and \({\dot {Q}_{ij}}\), \(R\), \(l\), \({k_T}\) , and \(A\) are the heat conduction rate, the thermal resistance, the distance, the thermal conductivity of fibers, and the cross-sectional area between \(i\) and \(j\), respectively. The thermal conductivity of GDLs has been measured in the literature, so calibration data are available [60, 61]. The geometrical properties of the solid matrix present in each pore were found by subtracting the pore and throat volumes from the unit cell. This means that around a large pore there was less solid material and vice versa. The value of thermal conductivity was then found by trial and error until the effective thermal conductivity of the solid network matched the experimentally measured values. The temperature profile in the GDL is of course a function of the thermal boundary conditions, e.g., prescribed channel rib temperatures and the heat source terms at the CL. These heat sources can be calculated by using the ORR enthalpy of reaction or the produced power at the catalyst layer for each node. The temperature profile will also be impacted by another sink/source term which is the liberated or absorbed latent heat due to phase change in each pore. Applying an energy balance around node i in the solid network gives

$$\mathop \sum \limits_{{j=1}}^{{{N_s}}} {\dot {Q}_{ij}}+\mathop \sum \limits_{{k=1}}^{{{N_p}}} \frac{{{n_{ik}}\Delta {h_l}}}{{{N_{s,k}}}}~=0$$
(15)

where \({n_{ik}}\) is the rate at which mass evaporates or condenses in pore \(k\), and will only be non-zero for pores in which phase change occurs. \({N_p}\)and \({N_s}\) are the number of neighboring pores and solid nodes, respectively. \(\Delta {h_l}\) is the molar enthalpy of evaporation; the term \({n_{ik}}\Delta {h_l}\) is the rate of energy absorbed/liberated in pore \(~k\); and solid node \(i\) is assumed only to receive \(1/N_{{s,k}}\) of this energy since it is divided evenly between the solid nodes neighboring the pore \(~k\). Applying the above equation to each node in the solid network yields a system of linear equations that can be solved with the appropriate boundary conditions to give the temperature distribution across the solid network. Since the fluids are in thermal equilibrium with the solid, it is assumed that temperature at each pore are the average temperature of its surrounding solid nodes. Once the temperature profile is established, then by using vapor compositions from the mass transfer algorithm, the nucleation sites can be located as described next.

To find the nucleation sites for condensation, firstly the relative humidity distribution should be found from the results of heat/mass transfer algorithms. The pores with RH > 1 are considered as the potential pores for condensation. Assuming liquid–vapor equilibrium for the nucleation sites, the vapor partial pressure will be changed to saturation vapor pressure; thus, in the selected pores RH will be equal to 1. Then, to determine condensation rate applying Fickian diffusion for a nucleation site \(p\) shown in Fig. 5 gives

Fig. 5
figure 5

A pore with relative humidity higher than 1 which is considered as a nucleation site and then reaches the equilibrium after condensation

Full size image
$$\left. {\begin{aligned}{~~~~~~{r_1}=\mathop \sum \limits_{{k=1}}^{N} ~{g_{d,kp}}\left( {{X_{B,k}} - {X_{B,p}}} \right)} \\ {~~~~~~{r_2}=\mathop \sum \limits_{{k=1}}^{N} ~{g_{d,kp}}\left( {X_{{B,k}} - {X_{B,p}^{s}}} \right)} \end{aligned}} \right\} \to ~{r_2} - {r_1}=~{r_{c,p}}=\sum\limits_{{k=1}}^{N} {{g_{d,kp}}\left( {{X_{B,p}} - X_{{B,p}}^{s}} \right)}$$
(16)

Each nucleation site is considered as a new cluster (most of these small clusters join together in the next time steps and create larger clusters). Once all liquid water clusters are established, it is assumed that the water at the water–air interface is in equilibrium with the vapor at the local temperature. Because the liquid water distribution is known and fixed for each time step, the pores at the water–air interface will be treated as Dirichlet boundary conditions at 100% RH. Total flux between a water filled pore k and its neighboring pores is described by

$${n_k}=\sum\limits_{{p=1}}^{{{N}}} {{g_{d,kp}}\left( {\ln ({x_{B,p}}) - \ln ({x^*}_{{B,k}})} \right)} =\sum\limits_{{p=1}}^{{{N}}} {{g_{d,kp}}\left( {{X_{B,p}} - X_{{B,k}}^{s}} \right)}$$
(17)

where \({g_{kp}}\) (diffusion conductivity between pores \(k\) and \(p\)) will be calculated by Eq. [2]; \(B\) is the stagnant film of oxygen and nitrogen; and \({x^*}_{{A,k}}=1 - {x^*}_{{B,k}}\) is the saturation composition of water vapor in pore \(k\) at \({T_i}\) obtained by Antoine equation. This equation is identical in form to that for dry pores, with the exception that mass accumulates in wet pores. The flux between two wet pores is 0, since liquid water transport is accounted by percolation theory, rather than mass transfer. The cumulative water gained or lost by each cluster must be tracked to determine if the cluster is growing or shrinking. Mass flux into cluster c is found as the sum of all fluxes into the pores in cluster c:

$${n_{{\text{net}},c}}=\mathop \sum \limits_{{k=1}}^{N} {n_k}$$
(18)

where \({n_{{\text{net}},c}}\) is the net condensed/evaporated rate for cluster c; \(N\) is the total number of pores in this cluster; and \({n_k}\) is the same as defined by Eq. 17. Once this is known, the IP algorithm will be used to determine which pore should be filled for cluster growth (condensation) or drained for cluster shrinkage (evaporation). In this way, the IP algorithm releases the accumulated mass in wet pores. In case of condensation, liquid water is invading phase and the air is defending phase, but as for IP algorithm of the evaporation air is invading phase and liquid water is defending.

The amount and location of the latent heat liberated or absorbed are found from \({n_k}\) and fed back into the heat transfer solution as local sources or sinks of heat in the next time step. This results in a new temperature distribution in the network, which will in turn affect the humidity conditions, and so on. The algorithm in Fig. 3 is repeated until a steady-state condition is reached, which requires that (a) all clusters have ceased growing or have reached the outlet over the channel and (b) the temperature distribution in the network is constant.

One key element of this simplified pseudo-transient approach is the determination of a suitable time step. A convenient time step is the amount of time required to fill (or drain) one pore. This is complicated since there will be multiple clusters in the network growing simultaneously. As such, a time step (\(\Delta t\)) for each cluster c must be calculated by using the volume of the invaded/imbibed pore and throat in that cluster:

$$\Delta t=\frac{{{v_l}}}{{{n_{{\text{net}},~c}}}}$$
(19)

where \({n_{{\text{net}},c}}\) is the net condensed/evaporated rate for cluster c. \(l\) refers to the next pore in cluster c to be drained or filled, which can be determined by IP algorithm in each time step. \({v_l}\) is the total volume required for cluster c to grow or shrink by pore \(l\), which includes volume of pore \(l\), the connecting throat between pore \(l\) and cluster c and filling partially occupied pores in the cluster from the last time step. The overall time step for the system will be the minimum \(\Delta t\) for all the clusters, and a new time step will be found on each iteration. Including the time step in this way allows for the evolution and redistribution of latent heat, and the growth or shrinkage of water clusters as a function of local equilibrium conditions. The main parameters and properties used in this simulation are summarized in Table 1.

Table 1 Summary of the main parameters and properties used in the simulation
Full size table

3 Results and discussion

In general, fuel cells are subject to performance cycles that result in large humidity and temperature variations in both time and space. As mentioned in the previous sections, recent studies show that liquid water might not enter the network solely at the GDL–MEA interface, and that condensation should be considered as an important source of liquid water formation within the bulk of the GDL. Since liquid water in the GDL has a negative impact on fuel cell performance, it is vital to develop a modeling framework that can fully simulate the movement of liquid water inside the cell. The iterative algorithm described in the previous section was applied to demonstrate the ability of pore network modeling to simulate a phase change in the cathode side of PEMFC.

The two-step procedure can be applied for various operating conditions. In the case study shown in Fig. 6, the simulation results at 350.15 (K) for different RH values are presented. As the polarization and saturation curves in Fig. 6a suggest, increasing the RH leads reduced limiting current values caused by mass transfer limitations. A certain fraction of this performance loss is due the reduced oxygen content in the channel as it is displaced by water vapor, falling from 21 at 0% RH to near 10 at 100% RH for the temperature used here. The remainder of the performance loss is due to the presence of liquid water in the GDL blocking the oxygen transport. These effects can be deconvoluted to show the relative impact of each. Figure 7a shows the limiting current as a function of humidity for the case with no liquid water present and with condensed water. The decrease in oxygen content in the channels as the RH increases from 50 to 100% leads to a nearly 20% drop in the limiting current, while the presence of liquid water in the GDL causes an additional decrease due to the transport resistance. At 50% RH, a water saturation of 7% adds an additional 10% drop in limiting current, while at 100% RH the saturation is 17% and the drop in limiting current is nearly 19% of the dry case. One caveat of this analysis is that the model does not include the effect of humidity on the Nafion conductivity and proton transfer. Since these membranes do not perform well when dry, it is expected that supplying feed gases with low RH limits cell performance drastically, so the enhanced performance at 0% RH is exaggerated.

Fig. 6
figure 6

Simulation results at 350.15 (K) for different RH values: a polarization curves for various RH values and b liquid saturation inside the GDL for the same set of RH values

Full size image
Fig. 7
figure 7

The impact of condensed liquid water on performance and transport properties of the cell at 350.15 (K). a The limiting current as a function of relative humidity with and without liquid water. b The normalized effective diffusivity of oxygen in the cell as function of GDL water saturation at RH = 1.0

Full size image

Figure 6b shows the total water saturation in the GDL versus current at various RH. At low currents, the saturation is essentially 0 for all RH values, because the vapor production rate is not sufficient to create the first nucleation sites. But by increasing the current, the vapor and temperature gradients increase creating nucleation sites, and larger RH gradients inside the network lead to larger clusters and consequently higher GDL saturation. The increase in the saturation qualitatively tracks the increase in mass transfer losses seen in the polarization curves. However, in the study by Iranzo et al. [68], it is observed that liquid water saturation increases up to mid-range currents, but slightly decreases at high currents. There are several plausible sources of this disagreement. Firstly, their results include membrane simulation which will certainly vary in water content at different conditions. Secondly, the effect of the anode is considerable, which introduces the osmotic drag and back-diffusion processes that are not included in our model. Thirdly, in their work much of the water was in the channels, and assuming that the flow rate was proportional to the current density, the gas flow was 2.5 times higher at 25 (A). This presumably removed liquid water droplets from the channel much more effectively that at 10 (A). Figure 7b shows the effective diffusivity of oxygen at 100% RH from the channel to the catalyst layer as a function of GDL saturation, normalized by the effective diffusivity of a dry cell. This is similar to the traditional ‘effective diffusivity’ plots that are produced by pore network models and experiments [24, 69], but includes the impact of the rib blocking half of the inlets, and the fact that the water formation is highly localized under the rib due to condensation. This figure is quite interesting since it shows that at low saturations the water, which is entirely concentrated under the rib, has almost no noticeable impact on the transport of oxygen. As for the saturations above 10%, there are sufficiently large water clusters to block gas phase transport.

Several different 3D visualizations of the conditions inside the cell are shown in Fig. 8 for the simulation results of the mentioned case study at 0.5 (V) and 80% RH. Parts (a), (b), and (c) show distribution of oxygen mole fraction in the PNM, distribution of water vapor mole fraction in the PNM, and the temperature profile in the solid network, respectively. Figure 8d depicts the liquid water cluster as the result of condensation inside the cathode network and the missing pores in (a) and (b) are the pores blocked due to the presence of this liquid cluster. Also, Fig. 8c also shows the minor temperature difference in the regions around the water blob which is the result of including latent heat in the simulation. To our knowledge, this is the first pore network model of phase change which considers the latent heat. As shown in the part (d) of Fig. 8, the liquid water forms in the GDL due to the condensation of the vapor mostly below the ribs in the colder zones of the network. This prediction regarding the behavior and location of liquid water cluster is in good agreement with the recent experimental studies [44, 45]. From these results, it can be seen that the temperature gradient inside the network leads to condensation of vapor in the colder zones under the rib, as expected.

Fig. 8
figure 8

Simulation results at 350.15 (K) and 0.5 (V) for 80% RH: a Distribution of Oxygen mole fraction in the PNM. b Distribution of water vapor mole fraction in the PNM. c Temperature distribution in the solid network. d Liquid water cluster as the result of condensation inside the cathode network. In a and b, the missing pores are those blocked due to the presence of liquid water

Full size image

Perhaps the most vital finding of these simulations, as well as those recently produced by Prat’s group [48], is that the fuel cell can clearly operate entirely by vapor diffusion from the CL. Virtually all previous attempts to model liquid water flow in the electrode have assumed that liquid water invaded into the GDL from the CL. The present results clearly show that, even for a thick GDL with an MPL present and including mass transfer resistance of the CL itself, the rate of vapor diffusion from the CL is sufficient to expel all produced water without condensation in the CL under a wide range of conditions. And moreover, the presence of liquid water observed in operating fuel cells can be explained entirely by condensation.

A through-plane slice of the pore network is also depicted in Fig. 9 which shows the RH profile through the cathode from the CL to the channel. The missing pores are the ones blocked by liquid water, and as can be seen the neighboring pores around the water cluster show higher RH values than the other regions. As mentioned in the previous section, the mass transfer rate between the cluster and these pores will determine that the occurred phase change is condensation or evaporation. It can be seen that the liquid water cluster(s) essentially grow from the rib into the GDL. The liquid water cluster does not reach the CL, because (a) the higher temperatures near the CL induce evaporation of any water that may percolate there, and/or (b) the cluster growth stops once a stable path to the channel is formed.

Fig. 9
figure 9

A through-plane slice of the pore network at 350.15 (K) and 0.5 (V) which shows the RH distribution through the cathode from the CL to the channel. The missing pores are blocked by liquid water

Full size image

Figure 10 shows the relative humidity and local rate distribution at the CL/PEM interface for the same temperature and RH of 350.15 (K) and 80%. Relative humidity across the CL does not change significantly, but there is a noticeable difference between the regions under the rib and under the channels. Accumulation of the liquid water under the ribs results in longer diffusion paths, affects the CL reaction sites under this region, and thus leads to a lower current and heat production in this region which explains the slightly higher RH in this part. Figure 10b shows the local oxygen consumption rates at CL/PEM interface which is also proxy for the local water generation rates. As shown in Fig. 10a, RH is lower in the regions over the channels even though the rate of water production is locally higher there because the water vapor can more easily diffuse away from the CL. One might have hypothesized that regions of highest reaction rate would become the most humid and potentially experience local condensation; however, it appears that regions of the high reaction rate occur where the oxygen transport rate is high, and thus so is water vapor’s ability to exit the cell. This is all the more impressive considering that the oxygen is highly depleted in the regions over the rib so the local mole fraction of water vapor and thus RH is increased even further.

Fig. 10
figure 10

Simulation results at 350.15 (K) and 0.5 (V) for 80% RH: a Relative humidity distribution at the CL/MEM interface, b Oxygen consumption rate at the CL/MEM interface

Full size image

4 Conclusion

Limited understanding of the coupled transport processes occurring inside the cells has been one of the main roadblocks to commercialization of PEMFCs. It is also well known that the presence of the liquid water in the porous electrodes can negatively impact performance. To properly model liquid water’s movement in the MEA, a numerical simulation for coupling multiple transport processes within the cell is essential. Pore network simulations have proven to be particularly useful tools for tracking the liquid water configuration and provide computationally efficient ways to include multiphase flow using percolation algorithms. In this work, an iterative algorithm for phase change was presented that captures the cathode side of PEMFC using a multi-domain pore network model to describe each part of the membrane electrode assembly. The proposed method applied a constant voltage boundary condition, and coupled the transport occurring on the cathode sides of the cell. The model included an algorithm for solving pseudo-transient multiphase heat, mass, and electrical transfer equations combined with invasion percolation of the liquid water using pore network model. The gas diffusion layer region was modeled using pore-scale physics, while the CL and MPL were treated as porous continuum. The algorithm was able to predict the phase change under different operating conditions and to capture the local water configuration within the cathode. It was shown that spatial temperature and vapor gradients led to the condensation in the colder zones especially under the rib. Modeling of phase change inside GDL based on more realistic transport processes opens the new route to improving water management in PEMFCs by providing the insight into fuel cell operation and enhancing the applicability of numerical simulations. Aside from defining a robust framework for multiphysics modeling in pore networks, this work illustrated conclusively that vapor diffusion from the CL was sufficiently fast under all conditions considered that condensation in or near the CL was never observed.

Future work should incorporate the impact of local humidity on the membrane hydration and ionic conductivity in particular. It would also be beneficial to model the process at different cell temperatures, but many of the transport and kinetic parameters are temperature dependent so this requires substantially more input data than are currently available. Additionally, the pseudo-transient treatment of the transport processes should be handled as actually transient models, but again this requires materials properties such as heat capacity and densities that are not well known. Finally, it would be better to model the MPL and CL as pore networks of their own, but the computational demands of modeling so many pores (probably in the trillions across all the scales) are simply not feasible.