Efficient Personalized Influential Community Search in Large Networks

Abstract

Community search, which aims to retrieve important communities (i.e., subgraphs) for a given query vertex, has been widely studied in the literature. In the recent, plenty of research is conducted to detect influential communities, where each vertex in the network is associated with an influence value. Nevertheless, there is a paucity of work that can support personalized requirement. In this paper, we propose a new problem, i.e., maximal personalized influential community (MPIC) search. Given a graph G, an integer k and a query vertex u, we aim to obtain the most influential community for u by leveraging the k-core concept. To handle larger networks efficiently, two algorithms, i.e., top-down algorithm and bottom-up algorithm, are developed. To further speedup the search, an index-based approach is proposed. We conduct extensive experiments on 6 real-world networks to demonstrate the advantage of proposed techniques.

1 Introduction

Retrieving communities and exploring the latent structures in the networks can find many applications in different fields, such as protein complex identification, friend recommendation, event organization, etc.  [8, 10]. There are two essential problems in community retrieval, that is community detection and community search. Generally, given a graph, community detection problem aims to find all or top-r communities from the graph  [12, 16], while community search problem is to identify the cohesive communities that contain the given query vertex  [6, 18]. In this paper, we focus on the category of community search problem, which is very important for personalized applications. For instance, we can conduct better friend recommendation by identifying the important community that contains the query users. Similarly, we can make better event organization by retrieving the community, which contains the user that we want to invite.

In the literature, lots of research tries to find personalized communities by emphasizing the structure cohesiveness. While, in many cases, we also need to consider the influence of obtained communities. Recently, there are some research that tries to find communities with large influence, e.g.,  [1, 2, 14]. In  [14], Li et al. propose a novel community model called k-influential community, where each vertex is associated with a weight (i.e., influence value) in the graph. A community (i.e., subgraph) is essential when it is cohesive and has large influence value. Efficient algorithms are developed to obtain the top-r communities with the largest influence value. Given the importance of the problem, [1, 2] try to speedup the search from different aspects. Since influence value is user’s natural property, by considering the influence value, it can lead us to identify more significant communities.

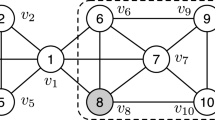
Nevertheless, the existing works on influential community detection mainly focus on finding all or top-r influential communities. The personalized situation is not considered. To fill this gap, in this paper, we propose the maximal personalized influential community (MPIC) search problem. Given a graph G, an integer k and a query vertex q, the MPIC is the community with the largest influence value that contains q, and satisfies the k-core (i.e., the degree of each vertex inside is no less than k), connectivity (i.e., the subgraph is connected) and maximal (i.e., no other supergraph satisfies the previous criteria) constraints. As defined in the previous work  [14], the influence value of a community is the minimum weight of all the vertices in the community. Given the graph in Fig. 1, if $k=3$ and the query vertex is $v_8$, then the vertices in the dotted line is the corresponding MPIC. Note that, the k-core model is also used in the previous works to measure the cohesiveness of the community  [1, 2, 14].

Challenges. The main challenges of the problem lie in the following two aspects. Firstly, the real-world networks, such as social networks, are usually large in size. It is critical for the algorithms to scale for large networks. Secondly, since we investigate the personalized scenario, there may be plenty of queries generated by users in real applications, it is important that the developed algorithms can meet the online requirements.

Contributions. To the best of our knowledge, we are the first to investigate the maximal personalized influential community (MPIC) search problem. The contributions of this paper are summarized as follows.

• We formally define the MPIC search problem.

• To handle large networks, two algorithms, i.e., top-down algorithm and the bottom-up algorithm, are developed based on different searching orders.

• An index-based method is proposed in order to meet the online requirements.

• We conduct extensive experiments on 6 real-world networks to evaluate the performance of proposed techniques. As shown, the developed techniques can significantly speedup the search compared with the baseline.

Fig. 1.

Running example (The number in the vertex denotes its weight)

2 Problem Definition

We consider a network $G=(V, E, \omega )$ as an undirected graph, where V and E denote the vertex set and edge set, respectively. Each vertex $u \in V$ is associated with a weight denoted by $\omega (u)$, representing the influence of vertex u. The vertex weight can be its PageRank score or other user defined value. Without loss of generality, we use the same setting as the previous work for vertex weight, where different vertices have different weights  [14]. Note, if that is not the case, we use the vertex id to break the tie. We denote the number of vertices by $n=|V|$ and the number of edges by $m=|E|$. A subgraph $S = (V_S, E_S)$ is an induced subgraph of G, if $V_S \subseteq V$ and $E_S = \{(u,v)|u,v\in V_S, (u,v)\in E\}$. Given a subgraph S, the neighbors of $u \in V_S$ is denoted by $N(u,S)=\{v|v\in V_S, (u, v)\in E_S\}$, and deg(u, S) represents the degree of u in S, i.e., $deg(u,S)=|N(u,S)|$. In this paper, we utilize the k-core model to represent the cohesiveness of a community, which is also widely used in the literature  [1, 14].

Definition 1

(k-core). Given a graph G and a positive integer k, a subgraph $S \subseteq G$ is the k-core of G, denoted by $C_{k}(G)$, if S satisfies the following conditions. (i) $deg(u,S) \ge k$ for each vertex u in S. (ii) S is maximal, i.e., any subgraph $S' \supset S$ is not a k-core.

To compute the k-core of a graph, we can remove the vertex whose degree is less than k recursively. The time complexity of computing k-core is O(m)  [20] and the detailed algorithm is shown in Algorithm 1. To identify important communities, we consider both the cohesiveness and the influence of a community. We employ the widely used influence value to measure the influence of a community  [1, 14].

Definition 2 (Influence value)

Given an induced subgraph S of G, the influence value of S is the minimum weight of the vertex in $V_{S}$, denoted as f(S), i.e., $f(S)=\min _{u\in V_{S}}\omega (u)$.

In the previous works, people usually focus on finding all or top-r influential communities  [1, 2, 14]. While, as discussed, in real applications, it is also essential to identify the personalized influential communities for different user queries. Given this requirement, we define the maximal personalized influential community as follows.

Definition 3 (Maximal Personalized Influential Community (MPIC))

Given a graph G, a positive integer k and a query vertex q, a maximal personalized influential community, short as MPIC, is an induced subgraph S of G, which meets all the following constraints.

• Connectivity: S is connected;

• Cohesiveness: each vertex in S has degree at least k;

• Personalized: query vertex q is contained in S, i.e., $q \in V_S$;

• Maximal: there is no other induced subgraph $S'$ that (i) satisfies the first three constraints (i.e., connectivity, cohesiveness and personalized constraints), (ii) is a supergraph of S, i.e., $S' \supset S$, and (iii) has the same influence value as S, i.e., $f(S) = f(S')$;

• Largest: S is the one with the largest influence value and satisfies the previous constraints.

Problem Definition. Given a graph $G=(V, E, \omega )$, a query vertex q and a positive integer k, we aim to develop efficient algorithm to find the maximal personalized influential community (MPIC) for the query, denoted by MPIC(q ,  k).

Example 1

As shown in Fig. 1, the number in each vertex is the corresponding weight. Suppose k = 3 and query vertex is $v_{8}$. Then we can see that the subgraph $S_1 =$ $\{v_{6}$, $v_{7}$, $v_{8}$, $v_{9}$, $v_{10}\}$ in the dotted line is the corresponding MPIC with influence value of 6. While the subgraph $S_2 =$ $\{v_{1}$, $v_{2}$, $v_{3}$, $v_{4}$, $v_{5}$, $v_{6}$, $v_{7}$, $v_{8}$, $v_{9}$, $v_{10}\}$, which satisfies the first four constraints of MPIC with influence value of 1, is not the MPIC, because it is not the one with the largest influence value.

3 Solutions

In this section, we first introduce some properties about the maximal personalized influential community. Then we develop two approaches, top-down method and bottom-up method by verifying the vertices in different orders. Finally, to support efficient online processing and scale for large networks, an index-based method is proposed based on the bottom-up framework.

3.1 Properties of Maximal Personalized Influential Community

Lemma 1

Given a graph G, an integer k and a query vertex q, then the influence value of MPIC(q, k) is at most the weight of q, i.e., $f(\text {MPIC}(q,k)) \le \omega (q)$.

Proof

MPIC(q, k) must contain q. Based on the definition of influence value, we have $f(\text {MPIC}(q,k)) = \min _{u \in \text {MPIC}(q,k)} \omega (u) \le \omega (q)$. Thus, the lemma holds.

Lemma 2

Given a graph G and two induced subgraphs $S_1$ and $S_2$, we have $V_{S_2} \subset V_{S_1}$ and $V_{S_1} = V_{S_{2}} \cup \{u\}$. If the weight of u is smaller than the influence value of $S_2$ (i.e., $\omega (u) < f(S_2)$), then the influence value of $S_1$ is smaller than that of $S_2$ (i.e., $f(S_1) < f(S_2)$).

Proof

Based on the definition of influence value, $f(S_1) =$ $\min _{v \in V_{S_1}} \omega (v)$ $\le \omega (u)$ $< f(S_2)$. Therefore, the lemma holds.

3.2 Top-Down Algorithm

In this section, we present the top-down algorithm which is inspired by the existing influential community detection method  [1]. According to Lemma 1, the influence value of the identified MPIC is at most $\omega (q)$. To find the community with the largest influence value, we can first add all the vertices whose weight is no less than $\omega (q)$ and check if we can obtain a community that satisfies the first four constraints of MPIC. If so, we can output the identified community. Otherwise, we can add some vertices with weight smaller than $\omega (q)$ to find the MPIC. The detailed algorithm is shown in Algorithm 2.

In Algorithm 2, we first compute the k-core of G, denoted by $C_{k}(G)$. Since the MPIC must be inside $C_{k}(G)$, if q does not belong to the k-core, error code is returned in Line 3, which means we cannot find a MPIC containing q. Otherwise, due to the connectivity constraint, we only need to keep the connected component that contains q. Then we sort the survived vertices in descending order by their weights and store them in S (Lines 4–5). We load the query q and the vertices ranked above q into Q (Lines 7–10). If the k-core $C_{k}(Q)$ of Q contains q, then we return the connected component containing q, which can be obtained by conducting a BFS from q (Lines 11–12). Otherwise, we add the remaining vertices in S one by one to Q until the k-core of Q contains the query vertex q, and the connected component is returned (Lines 14–18).

Example 2

Consider the graph in Fig. 1. Suppose k = 3 and the query vertex is $v_{8}$. Following the top-down algorithm, we first compute the k-core of G. Thus, $v_{11}$ and $v_{12}$ are deleted, because they violate the degree constraint. Then we add $v_{8}$ and the vertices ranked higher (i.e., {$v_{10}$, $v_{9}$}) than $v_{8}$ into Q. However, they cannot form a 3-core. Then we insert vertex one by one into Q. Until $v_6$ is added, there is a 3-core containing query $v_{8}$, i.e., {$v_{10}$, $v_{9}$, $v_{8}$, $v_{7}$, $v_{6}$}, which is the MPIC returned.

3.3 Bottom-Up Algorithm

In the top-down algorithm, we first add all the vertices ranked higher than q into Q. After that, by adding each vertex into Q, we need to invoke the k-core computation procedure. Even though the time complexity of k-core computation is O(m), in the worst case, we need to repeat the process n times, which can be time-consuming. Ideally, we can add more vertices into Q for each iteration. However, in order to guarantee the correctness of the algorithm, it is difficult to determine the appropriate number of vertices to be added. If too many vertices are added, we may need a lot of computations to shrink the result. Otherwise, we still need to compute the k-core plenty of times. To reduce the computation cost, in this section, the bottom-up method is proposed, which can avoid computing the k-core repeatedly.

According to Lemma 2, for a given induced subgraph, we can increase its influence value by removing the vertex with the smallest weight. Intuitively, since we aim to find the MPIC, we can iteratively remove the vertices with the smallest weight and keep tracking the other constraints of MPIC, until the MPIC is found. Different from the top-down approach, in the bottom-up method, we visit the vertices in ascending order and remove the unpromising vertices iteratively. The detailed algorithm is shown in Algorithm 3.

For the algorithm, the first three steps are exactly the same as the top-down method (Lines 1–4). Then, we sort the survived vertices in ascending order by the weight of vertex and store them in S (Line 5). Then we try to remove the vertex with the current smallest weight one by one until the query vertex q is met (Lines 6–10). For each vertex u processed, we invoke the Delete procedure, which details are shown in Lines 11–26. For each processed vertex u, we need to ensure the remained subgraph satisfies the k-core constraint. After deleting a vertex, it may cause its neighbors to have less than k neighbors. Then we remove these vertices as well (Lines 17–20). We put the vertices that violate the degree constraint into R and process them iteratively. When $w = q$ (Line 15), it means either (i) the input vertex u of Delete procedure is q, or (ii) deg(q, S) becomes less than k because of the deletion u. In this case, the remained subgraph S and D (i.e, $S\cup D$) form the MPIC. This is because, when we remove the input vertex u, it will cause the remained subgraph does not contain q or q violates the degree constraint. The reason that we keep tracking the deleted vertices D for each Delete procedure is for case when ii situation happens. Since the identified community should satisfy the connectivity constraint, we can safely remove the connected components in S that do not contain q (Lines 23–25).

Example 3

Consider the graph in Fig. 1. Suppose k = 3 and the query vertex is $v_{8}$. Following the bottom-up approach, $v_{11}$ and $v_{12}$ are firstly deleted due to the k-core computation. After deleting the vertex $v_1$ with the smallest weight, the remained graph are separated into two connected components. Therefore, we can safely remove the connected component $\{v_{2}$, $v_{3}$, $v_{4}$, $v_{5}\}$ from S since it does not contain the query vertex. Then, we process $v_6$. As we can see, when processing $v_6$ in the Delete procedure, it will result in $v_8$ violating the degree constraint. Then we can stop and output $\{v_{6}$, $v_{7}$, $v_{8}$, $v_{9}$, $v_{10}\}$ as the result.

3.4 Index-Based Algorithm

In the bottom-up approach, we invoke the k-core computation at the beginning of the algorithm and the total cost of checking degree constraint in Delete only takes O(m) time, which avoids lots of computations compared to the top-down method. However, the bottom-up approach still has some limitations. (i) When deleting the vertices, it still costs a lot for processing very large graphs. (ii) For real applications, different users may have different requirements and there may exist a large amount of queries. Therefore, it is hard for it to meet the online requirement.

Motivated by the requirements, in this section, we propose an index-based algorithm by leveraging the bottom-up framework. In the bottom-up method, for a given k, we try to delete the vertex u with the smallest weight in each iteration by Delete procedure. Then we can obtain the MPIC for certain vertices, such as the vertex u and the vertices removed when processing u. If we process the vertices in order, we can obtain the MPICs for all the vertices. Therefore, we can build a tree structure index according to the processing order. Let $k_{\max }$ be the largest core number, i.e., the largest k value for any k-core. If we build a tree index for each k value, then we can answer any given query efficiently. In Algorithm 4, we present the details of how to index the visited vertices effectively. Then we show how to answer a query by utilizing the index.

Index Construction. In Algorithm 4, we build a tree index for each k value from 1 to $k_{max}$ (Lines 1–5). In each iteration, we first compute the corresponding k-core, and for each connected component, we construct the indexed tree nodes by invoking BuildNode procedure. The details of BuildNode procedure are shown in Lines 6–20. The BuildNode procedure is very similar to the Delete procedure in Algorithm 3. It starts by processing the vertex with the smallest weight (Line 7). When we process a vertex u, it will cause some other vertices violating the degree constraints (Lines 11–14) and we add them and u into D (Line 16). According to the bottom-up method, it means the vertices in D belong to the same MPIC. Then we construct an intermediate node crn that contains the vertices in D, and append it to its parent node rn (Lines 17–18). Then we recursively call the BuildNode to process each connected component $S'$ of the remained subgraph S (Lines 19–20). After processing each k, the index is constructed. Based on the construction process, we can see that the MPIC of a vertex consists of its belonged intermediate node and its children nodes in the index.

Fig. 2.

Example for index construction

Example 4

Figure 2 shows the constructed index for the graph in Fig. 1 when $k = 1,2,3$. The ER node is the empty root node. It is for the case when the computed k-core in Line 2 of Algorithm 4 is not connected. For $k=1$, the constructed index is shown in Fig. 2(a). We first process $v_1$ which will result in 2 connected components. Then we remove $v_2$ and $v_3$ and create two intermediate nodes for them, since the removal of them does not make other vertices violate the degree constraint. When deleting $v_4$, the degree of $v_5$ becomes less than 1. Then we construct an intermediate node that contains $v_4$ and $v_5$. We conduct similar procedure for the other connected component, and the constructed index is shown in the right branch. Similar procedure is conducted for $k=2,3$, where the corresponding index are shown in Figs. 2(b) and 2(c).

Query Processing. As we can see, for a given query, the MPIC consists of the intermediate node that contains the query vertex and all its children nodes in the corresponding k index. If we maintain $k_{\max }$ pointers for each vertex to its corresponding intermediate nodes, we can efficiently locate the vertex’s intermediate node for a given k and traverse the index to return the result. For a given query, if we cannot find its intermediate node in the index, it means it does not has a MPIC for the query.

Example 5

Consider the graph in Fig. 1. The constructed index is shown in Fig. 2 for $k=1,2,3$. Given the query vertex $v_8$, the MPIC is the vertices in the dotted line for $k=1,2,3$ respectively.

Discussion. If we do not need to retrieve the specific vertices in MPIC, the index can answer the query in O(1) time by just returning the pointer for the intermediate node. Otherwise, we need to traverse from the intermediate node to obtain all the vertices. In this paper, we use the second case in the experiments, since the first two algorithms will obtain all the vertices in MPIC.

4 Experiments

In this section, we conduct extensive experiments on real-world networks to evaluate the performance of proposed techniques.

4.1 Experiment Setup

Algorithms. Since there is no previous work for the proposed problem, we conduct experiments with the proposed three algorithms, i.e., top-down algorithm, bottom-up algorithm and index-based algorithm. The top-down algorithm serves as the baseline method.

Datasets. We evaluate the algorithms on 6 real-world datasets, i.e., Email, Brightkite, Gowalla, YouTube, Wiki and Livejournal. Table 1 shows the statistic details of the datasets. The datasets are downloaded from the Stanford Network Analysis Platform¹, which are public available. Similar as previous work, we use the PageRank value to serve as the vertex weight  [14].

Table 1. Statistics of datasets

Fig. 3.

Index construction time

Parameter and Workload. To evaluate the performance of proposed techniques, we vary the weight of query vertex and k. To generate the query vertices, we sort the vertices according to the weight and divide them into 5 buckets. For each bucket, we randomly select 200 vertices as query vertices. For k, we vary k from 5 to 25 with 10 as the default value. For each setting, we run the algorithms 10 times and report the average response time.

All algorithms are implemented in C++ with GNU GCC 7.4.0. Experiments are conducted on a PC with Intel Xeon 3.2 GHz CPU and 32 GB RAM using Ubuntu 18.04 (64-bit).

4.2 Experiment Result

Results of Index Construction. We first present the index construction time for all datasets, the results are shown in Fig. 3. As we can observe, the index construction phase is very efficient. It only takes 0.290 seconds for Brightkite dataset. For the largest network Livejournal, which has more than 34 million edges, it only takes 325.656 s for constructing the index.

Fig. 4.

Experiment results by varying query vertex weight

Results of Varying Query Vertex Weight. By varying the query vertex weight, we conduct the experiments on all the datasets. The response time is shown in Fig. 4, where k is set as the default value. As observed, the bottom-up method is much faster than the top-down method, since the top-down method may compute the k-core many times. Among all, the index-based method runs fastest, due to the novel index structure proposed. In the two largest datasets, i.e., Wiki and Livejournal, the index-based method achieves up to 6 orders of magnitudes speedup compared with the top-down method. As we can see, the bottom-up and index-based methods are not sensitive to the weight of query vertex. While, for the top-down method, the response time increases when the weight increases. This is because, for query vertex with larger weight, it may compute the k-core more times when adding vertices one by one.

Fig. 5.

Experiment results by varying k

Results of Varying k. We conduct the experiments on all the datasets by varying the query parameter k. The results of response time are shown in Fig. 5, where similar trend can be observed. The bottom-up and index-based methods are significantly faster than the top-down method, and the index-based method is the fastest one for all cases. In the largest dataset, i.e., Livejournal, the index-based method can achieve up to 6 orders of magnitudes speedup compared with the top-down method. With the increase of k, the response time of top-down method decreases. This is because, for larger k, the identified MPIC tends to be smaller. As shown, the bottom-up and index-based methods can scale well for the parameter k.

Summary. As demonstrated in the experiments, both bottom-up and index-based methods are significantly faster than the top-down method, and they can scale well for different query parameters. Especially for the index-based method, it usually can achieve orders of magnitudes speedup. Given the experiment results, in real applications, users can make a trade-off when selecting algorithms. If index construction is allowed by the applied platform, it would be better to use the index-based method. Otherwise, users can select the bottom-up method, which can also provide competitive performance.

5 Related Work

We present the related work from the following three aspects, i.e., cohesive subgraph mining, community search and influential community detection.

Cohesive Subgraph Mining. Cohesive subgraph mining is a very important tool for graph analysis and can find many applications in different fields  [4, 17]. In the literature, different models are proposed to measure the cohesiveness of a subgraph, such as k-core  [20], k-truss  [21], clique  [5], etc. There are also some works that try to identify cohesive subgraph on special graphs, such as identifying k-core and k-truss over uncertain graphs  [11, 19].

Community Search. For cohesive subgraph mining, people usually focus on finding all or high ranked cohesive subgraphs. Given a graph G and query vertices, the community search problem aims to identify a densely connected subgraph that contains the query vertices  [8]. To measure the cohesiveness of a community, different models are used. In [6, 18], authors use the minimum degree to serve as the metric, which is similar to the k-core constraint. [18] proposes a global search framework to identify the community. Cui et al.   [6] develop a local search method to avoid visiting too many vertices. Huang et al.   [9] leverage the k-truss model and propose the triangle-connected k-truss community problem. It designs a triangle connectivity-preserving index to efficiently search the k-truss communities. There is lots of research for other kinds of graphs, e.g., attribute graphs and profile graphs  [3, 7]. [8] presents a comprehensive survey of recent advanced methods for community search problems.

Influential Community Detection. In traditional community detection/search problems, the influence value of a community has been neglected. In  [14], Li et al. present a novel community model called k-influential community. Given a graph G, each vertex is associated with a weight, i.e., influence value. It aims to find the top-r k-influential communities, where the cohesiveness is measured based on the k-core model. In  [2], Chen et al. propose the backward searching technique to enable early termination. Recently, Bi et al.   [1] develop a local search method, which can overcome the deficiency of accessing the whole graph. Li et al.   [15] present an I/O-efficient algorithm to compute the top-r influential communities. In  [13], authors further investigate the case when each user is associated with multiple weights. However, as observed, these works aim to identify the influential communities for the whole network, while the personalized case has not been considered.

6 Conclusion

In this paper, we investigate the maximal personalized influential community search problem, which is an important tool for many applications, such as personalized friend recommendation, social network advertisement, etc. In order to scale for large networks, two algorithms, i.e., top-down algorithm and bottom-up algorithm, are developed based on different vertex accessing orders. To fulfill the requirement of online searching, an index based method is proposed. Finally, comprehensive experiments are conducted to verify the advantage of developed techniques on 6 real world datasets.