Personalized Top-n Influential Community Search over Large Social Networks

Abstract

User-centered analysis is one of the aims of online community search. In this paper, we study personalized top-n influential community search that has a practical application. Given an evolving social network, where every edge has a propagation probability, we propose a maximal pk-Clique community model, that uses a new cohesive criterion. The criterion requires that the propagation probability of each edge or each maximal influence path between two vertices that is considered as an edge, is greater than p. The maximal clique problem is an NP-hard problem, and the introduction of this cohesive criterion makes things worse, as it may add new edges to existing networks. To conduct personalized top-n influential community search efficiently in such networks, we first introduce a search space refinement method. We then present pruning based and heuristic based search approaches. The proposed algorithms more than double the efficiency of the search performance for basic solutions. The effectiveness and efficiency of our algorithms have been verified using four real datasets.

1 Introduction

Online community analysis aims to find communities that have certain relationships with a query node in an online manner. As the communities for different vertices residing in a network may have very different characteristics, the ability for personalized community detection, which online community search provides, is more meaningful.

In this paper, we study modeling and querying of the top-n influential communities to a specific query node, termed as personalized top-n influential community search. As the influential communities around a user represent the social contexts for that user, top-n influential community search provides a useful tool for other analytical tasks, such as influential social community discovery and accurate community influence modeling. The following is a example.

Example

(User-centered influential community discovery). Users in social networks are usually surrounded by many communities. Suppose that Mr. Spike is a Twitter user. Though he does not belong to any music community yet, he is surrounded by many music fans. So, to learn which are influential music communities for Spike we conduct a top-n influential community search.

But we face challenges in this study. The first challenge is how to identify all communities around a user in evolving and dynamic social networks. The second is how to calculate the influence of all these communities efficiently.

To address these two challenges, we model a social network as a graph G with vertices representing individuals and edges representing connections or relationships between any two individuals. While influence is propagated in the network according to a stochastic cascade model, such as Independent Cascade (IC) model [5], each edge (u, v) in the network is associated with a propagation probability w(u, v). With cliques [1], we propose the concept of a maximal pk-Clique community. A k-clique is a complete subgraph that includes at least k vertices, and is not contained in any other complete subgraph. A maximal pk-Clique community is a community in a social network that has edges between nodes u and v in the graph that can either be original edges in the social network or a path from u to v, and its corresponding maximum influence probability is greater than p. We argue that, with propagation probability of every edge greater than a specific value p, users are well-connected with each other in such a community. A maximal pk-Clique ensures that a discovered community is connected and cohesive. We also develop pruning based and heuristic search based algorithms to efficiently find top-n influential communities with the support of an auxiliary data structure. Our contributions can be summarized as follows:

Table 1. Notations

• We propose a novel cohesive criterion to define an explicit community model in evolving and dynamic social networks;

• A search space that contains all communities surrounding a user is identified. We also propose two search approaches that reduce time complexity by more than two times, while preserving the robustness of the search approaches;

• The experimental results from four real datasets confirm that our algorithms are correct and show that the proposed algorithms significantly outperform the baseline algorithm (Table 1).

2 Preliminaries

Consider a directed graph $G = (V, E)$ with an edge labeled $w: E \rightarrow (0, 1]$, where V is a set of vertices representing users of a social network and E is a set of edges between vertices representing user-to-user connections. For every edge $(u, v) \in E$, weight w(u, v) denotes the propagation probability of the edge, which is the probability that v is influenced by u through the edge (u, v).

To model the influence process, we adopt the IC model [5] in this paper. For a path $P =\langle v_0,v_1,\ldots ,v_k \rangle$ in G, we define the propagation probability of the path as the product of the weights of its constituent edges:

$$\begin{aligned} w(P)= \prod _{i=0}^{k-1} w(v_i,v_{i+1}) \end{aligned}$$

(1)

There may be more than one path between one vertex and the other, and different paths may have a different propagation probability. We use the Maximum Influence Path (MIP) to approximate the real influence from one vertex to another within the social network. A maximum influence path from vertex u to vertex v is defined as any path P with a maximal weight w(P).

Definition 1

(pk-Clique Community)

Given a graph G, and two parameters p and k, a pk-Clique community is an induced subgraph $C_{pk} = (V_{pk}, E_{pk})$ of G that satisfies the following requirements:

• Any two vertices in $C_{pk}$ can be reached via an MIP between them in the subgraph $C_{pk}$, and the weight of every MIP is greater than p. And there are at least k vertices in $C_{pk}$.

• A pk-Clique community is maximal if $C_{pk}$ is not a subgraph of any other pk-Clique community.

The difference in this study from previous community models [7, 12, 14] is that, for the first time, we model the relationship between users in a community with an edge as a dynamic propagation probability. We argue this is an appropriate measurement of cohesiveness in a community.

Existing maximal clique enumeration algorithms suffer from exploring a huge search space [18]. Though the cohesiveness measurement used in pk-Clique is reasonable, the introduction of pk-Clique will add more new edges to a network, thus leading to an increased number and size of cliques. These cliques usually have high similarity, as many cliques share a large portion of vertices. In order to obtain comprehensive knowledge of communities around a query node, it is inappropriate to report all these cliques for this is redundant. We define the concept of l-diversity for returned cliques.

Definition 2

(l-diversified and l-similar)

Given two maximal cliques $C_i$, $C_j$ in graph G and a parameter $l(0\le l \le 1)$. We define the diversity of two maximal cliques $C_i$ and $C_j$ as

$$\begin{aligned} D(C_i,C_j)= \frac{\mid C_i \cap C_j \mid }{\mid C_i \cup C_j \mid } \end{aligned}$$

(2)

If $D(C_i,C_j) \ge l$, then cliques $C_i$ and $C_j$ are l-diversified, otherwise cliques $C_i$ and $C_j$ are l-similar.

Given a vertex s and a pk-Clique community in the graph, we will use aggregated influence, which is the weight union of the MIPs from nodes in a community to s, to estimate the influence from the community to s. We also use a threshold $\varepsilon$ to filter out vertices with little influence.

To calculate the influence of a community, the problem is that a vertex can be influenced by another vertex through different paths. Many works [12] adopt a model known as an “expectation model” to simplify the paths by supposing a dependence between paths, and mostly the MIP is the path that is adopted. In this work we are mainly concerned with the relationship between two vertices. We always assume that the paths between a different pair of vertices are independent. That is, even if two paths that share a sub-path lead to the same destination. We also assume that there are virtually two independent paths from two sources to the destination. This approximation simplifies the calculation of the aggregated influence of a community.

Definition 3

(Aggregated Influence of Community)

Aggregated influence of a maximal pk-Clique community to a vertex s, is defined as the influence probability that s is influenced by any vertices in this community, and the weight of every maximum influence path from these vertices to vertex s is greater than $\varepsilon$. Denote aggregated influence as $Pr(v \mid V(C))$ by the IC model, it is calculated as

$$\begin{aligned} Pr(v \mid V(C))= 1-\prod _{v \in V(c)}(1-w(P_{v \rightarrow s}))) \end{aligned}$$

(3)

Definition 4

(Top-n Influential Community Search)

Suppose $\mathbb {C}$ is the set of influential maximal pk-Clique communities around s. The top-n influential community search can be defined as a query to find n maximal pk-Cliques in $\mathbb {C}$,

Top-$n$ $(s) = \langle C_1,C_2,\ldots ,C_n \rangle$ where $Pr(C_1) \> Pr(C_2)>\ldots > Pr(C_n)$ if $\mid \mathbb {C} \mid >n$.

In this work, we explore top-n influential community search, and we also require that the returned communities are l-diversified.

Example 3

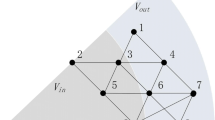
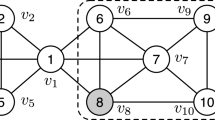
(Top-3 maximal pk-Cliques in Fig. 1). Figure 1 illustrates a subgraph surrounding a query node s. Suppose the vertices residing in the dark grey area have influence over s greater than $\varepsilon$ (say, 0.2). To simplify the illustration, we set all their influence to s at 0.3; When calculating aggregated influence of a clique, we ignore the vertices residing in the light grey area with an influence of less than $\varepsilon$. But when we check whether a group of vertices is a pk-Clique, these vertices make sense, since a maximal pk-Clique may include the vertices where the influence over s is less than $\varepsilon$. Having done the search, we present all maximal pk-Cliques and their aggregated influence in Table 2. With the setting l-diversified ($l=0.5$), we obtain cliques {2, 3, 5}, {6, 8, 5}, and {6, 8, 9, 7}.

Fig. 1.

A query example of node s.

Table 2. Maximal pk-cliques (example 3)

3 Basic Solution

3.1 Search Space

In contrast to community detection that aims to find all communities in a graph, personalized search of top-n influential communities only considers communities “near” a given vertex in the social graph. We take the word “near” to mean a vertex that can be reached by a specific community with a probability above a fixed threshold. So we only examine communities that include at least one vertex such that the MIP between this vertex and the query node is above the threshold $\varepsilon$.

We adopt single-source shortest-path algorithms such as Dijkstra algorithm to find all vertices around a query node where the weight of their MIPs is above $\varepsilon$. A modified version of Dijkstra algorithm is used that will stop at a vertex when the propagation probability of the MIP between this vertex and the query node is less than $\varepsilon$.

We denote the vertices where the propagation probability to a query node is above $\varepsilon$ as $V_{in}$. From previous discussions we are also aware that a maximal pk-Clique community C, said to be influential to a query node, must include at least one vertex that is included in $V_{in}$. If we denote this vertex as v, to determine whether C is a maximal pk-Clique, we must examine every vertex where the propagation probability of the MIP between these vertices to v is greater than p.

We derive the following lemma.

Lemma 1

(Given a maximal pk-Clique that has influence on s, the minimum propagation probability of an MIP between a vertex in the clique and the query node s is $p \varepsilon$.)

Given a graph $G = (V, E)$ with influence function $w:E \rightarrow (0, 1]$, probability $p, \varepsilon$, and a query node s, for any vertex u, if the MIP between vertex u and node s is less than $p \varepsilon$, it will not be included by any maximal pk-Clique that has influence on s.

Proof

Suppose u is a vertex with $w(P_{us}) < p \varepsilon$. And $P_ {us}= \langle u,v_1,v_2,\ldots ,v_k,s \rangle$ is a maximal influential path from u to s. There will be a node $v_i (1 \le i \le k)$ that is the last node along path P with $w(P_{v_is}) \ge \varepsilon$. In other words, node $v_i$ is the last node in set $V_{in}$ along path P.

Suppose node $v_i$ is included in a maximal pk-Clique denoted by C and path P can be decomposed into $P_{uv_i}$ and $P_{v_is}$. We know that sub-paths of a maximal influential path are maximum influence paths. Then, paths $P_{uv_i}$ and $P_{v_is}$ are maximum influence paths. Because with $w(P_{v_is}) \ge \varepsilon$, we have $w(P_{uv_i})< p$. According to Definition 1, vertex u will not be included in C.

With Lemma 1 and Definition 1, we propose Algorithm 1, that returns a candidate subgraph $G'$, including all vertices around a query node s with influence to s greater than $p \varepsilon$.

Algorithm 1 obtains all the vertices consisting of $V_{in}$ and $V_{out}$, and any edge between these vertices remains unchanged in graph $G'$. Since we use a modified version of Dijkstra’s algorithm to retrieve influential vertices at lines 1–2, the time complexity of identifying $V_{in}$ and $V_{out}$ is $O(\mid E' \mid lg \mid V'\mid )$.

3.2 Basic Algorithm

In this and following sections we will use the terms maximal pk-Clique and maximal clique interchangeably. Using social networks related to a query node s, the first step of a top-n Influential Community Search (ICS) is to identify the subgraph, including all candidate cliques, by executing Algorithm 1. Then the ICS enumerates all maximal cliques in this area. Among all these returned maximal cliques, we filter out those cliques where the size is less than k, calculate the integrated influence of each community, and then push it into a heap. When all the maximal cliques have been put in the heap, the algorithm selects l-diversified top-n maximal cliques in the heap and returns the result list.

The procedure of the top-n influential community search is presented in Algorithm 2. Algorithm 2 uses the procedure, Maximal Cliques Enumerate (MCE), to generate all maximal cliques in a graph. MCE is an implementation of maximal clique enumeration method proposed by Bron-Kerbosch [1]. Its performance is discussed in [17]. MCE takes $G'$ as input. Where $G'$ is originally obtained from Algorithm 1. But before being fed into Algorithm 2, it is transformed into an undirected graph. After collecting all maximal cliques at line 3, Algorithm 2 pushes every maximal clique into a data structure heap. As its name implies, heap uses the heap to manage maximal cliques during the insertion. The sort key is the aggregated influence of each clique. Lines 5–6 finish this operation. After we have the ordered cliques, the next step is to select l-diversified results. Lines 8–12 check each clique to see whether it is l-diversified with the previous appended cliques in the list, if it is, it will also be appended to the list.

Algorithm 2 achieves the worst-case time complexity of $O(3^{|V|/3})$ for a |V|-vertex graph [17]. Using d-degenerate order in the first-round iteration, the complexity is reduced to $O(|V| 3^{d/3})$ [4].

4 Efficient Influential Community Search

Algorithm 2 is a functionally correct procedure, but we are unlikely to be satisfied with its performance, particularly with the large social networks that now exist.

4.1 Search Space Refinement

The first possible method for accelerating the entire work is to remove all vertices where the degree is less than k. From the perspective of each vertex in the graph, if a vertex’s degree is less than k, then it absolutely will not be a member of any maximal pk-Clique. We make the following observation.

Observation 1:

A vertex with a degree less than k will not be a member of any maximal pk-Clique.

Many core decomposition algorithms use a bottom-up approach to determine a vertex’s class. That is, what kind of maximal clique dose this vertex belong to? We adopt such a bottom-up approach to remove all vertices, so they will not be included in any maximal pk-Clique, and conduct search space refinement. We use Algorithm 3 for this purpose.

With binary sort to order vertices, this refinement can be done in $O(|V'| + |E'|)$ time complexity.

4.2 Pruning Based Algorithm

Recalling Definition 3, the aggregated influence of the community is defined as the probability that s is influenced by any vertex in a maximal pk-Clique community. Algorithm 2 calculates the aggregated influence of each identified community. Is it possible to derive an upper bound of aggregated influence of to-be-found communities in advance? With this bound, can we prune unnecessary search branches in the graph? To this end, we propose Definition 5, following Observation 2.

Definition 5

(Aggregated Influence of vertex set)

The aggregated influence of a set of vertices to a vertex s, is defined as the probability that s is influenced by any vertex in this set. The calculation is the same as that in Definition 3.

Suppose a node set $V_{s}$ and all maximal pk-Clique communities it includes. Denote all these communities as $\mathbb {C}$, and for any $C \in \mathbb {C}$, we have

$$\begin{aligned} \begin{aligned}&Pr(v \mid v\in V_{s}) - Pr(v \mid v \in C \ ) \\&= 1-\prod _{v \in V_{s}}(1-w(P_{v \rightarrow s})) -(1-\prod _{v \in C}(1-w(P_{v \rightarrow s}))) \\&= \prod _{v \in C}(1-w(P_{v \rightarrow s}))(1-\prod _{v \in V_{s}-C}(1-w(P_{v \rightarrow s})))\\&>0 \end{aligned} \end{aligned}$$

(4)

With the above inequation, we obtain Observation 2.

Observation 2:

The aggregated influence of a vertex set is bigger than any maximal clique residing in it.

With Observation 2, we have the upper bound of the aggregated influence of maximal cliques in a subgraph. This upper bound will help us make the right decision before exploring the branch of a search tree. The remaining question is how to calculate this upper bound.

In the previous subsection, Algorithm 3 removes the vertices where the degree was less than k. It is important to notice that it decreases the number of vertices, leading to a reduced search space, but it does not ensure that there are no maximal cliques left with a size less than k. Thus we also have a lower size bound of expected maximal cliques, that is k. Now we have Algorithm 4.

Algorithm 4, Pruning Based Top-n ICS, calls Algorithm 5, MCP (Maximal Cliques with Pruning), to complete the top-n influential community search. Then it selects l-diversified n maximal cliques. If the number of previous returned top-n maximal cliques is less than n after the selection, Algorithm 5 calls MCP once again, but this time it will enlarge the result set to twice its previous one. That is, it will set parameter n to 2n and pass to procedure MCP. Until we have arrived at n maximal pk-Cliques which are l-diversified in the returned list.

Algorithm 5 MCP takes more inputs than Algorithm 3 MCE. Parameter q keeps track of currently found top-n influential communities. MCP uses an efficient global priority queue to manage the cliques found while running it.

The second main difference between MCP and MCE is lines 5–7. Vertex set T denotes a union of vertex sets, including C, $\{v\}$, and $(P \cup X) \cap \varGamma (v)$. Set C includes the vertices that are part of maximal cliques to be found. $\{v\}$ is currently an expanding vertex. And $(P \cup X) \cap \varGamma (v)$ includes the vertices to be extended. According to Observation 2, the aggregate influence of set T is the upper bound of any pk-Cliques to be retrieved. Thus, if the aggregate influence of set T is less than the minimum aggregate influential pk-Cliques in the queue, for instance, clique q[n], there is no need to undergo further searches along this branch. For the same reason, if the size of T is less than k, there is no need to conduct further searches either. This is the pruning based top-n influential community search. When a maximal clique is found, it is inserted into q. This operation is executed with line 2. At the end of MCP, we have a queue with n maximal pk-Cliques.

Theorem 1

(Correctness of algorithm Pruning Based Top-n ICS)

Given a graph $G = (V, E) (V \ne \emptyset )$ and a query node s, the algorithm Pruning Based Top-n ICS generates top-n l-diversified maximal pk-cliques without duplication.

Proof

It has been proofed in [17], that MCE generates all, and only, maximal cliques without duplication that contain all vertices in C, some vertices in P, and no vertices in X, without duplication. MCP follows MCE, and just skips over some branches that do not lead to top-n maximal cliques. Thus MCP returns the top-n maximal cliques with input vertex sets P, X, C as well.

With the statements at lines 10–14, the returned cliques in list are l-diversified.

Now we come to analyze its time complexity. In the best case, MCP finds top-n maximal pk-Cliques first. Thus the time complexity is O(n). But in the worst case, MCP finds top-n maximal pk-Cliques at the last moment. If the returned top-n maximal pk-Cliques are not l-diversified, it will call MCP once again, until n is greater than $|\mathbb {C}|$. The time complexity in this case is $O(3^{|V|/3)}log_2^{|\mathbb {C}|})$.

4.3 Heuristic Based Algorithm

According to Eq. 3, if the probability distribution of each node’s influence in $V_{in}$ is uniform, then the more nodes that reside in $V_{in}$ for a clique, the bigger the aggregated influence it will acquire. This leads to Observation 3.

Observation 3:

It is generally expected that a vertex $u \in V$ such that $V=V_{in} \cup V_{out}$ and $u=max\{|V_{in} \cap \varGamma (u)|\}$ has a high probability of being included in an influential maximum clique.

With Observation 3, we propose Algorithm 6, Heuristic MCP(HMCP). To minimize $P \setminus \varGamma (u)$, MCP chooses a pivot $u \in P \cup X$ that maximizes $|P \cap \varGamma (u)|$ at line 3 of Algorithm 5. In contrast to MCP, HMCP chooses a pivot that maximizes $|V_{in} \cap P \cap \varGamma (u)|$. That is, expending of a subtree that has a high probability of leading to influential maximum cliques becomes a priority.

The heuristic based top-n ICS maintains an additional list which keeps the sets of all vertices that are in $V_{in}$ and adjacent to v in $G' = (V',E')$. Note that the rather time-consuming calculation at this step is carried out only at the beginning of the main program and not in HMCP. Therefore, the total time required to select the pivot is very small.

Example 4

(An execution of a heuristic search). With the settings left the same as in Example 3, it is easy to find a heuristic based search that will perform the outermost recursive calls in the order of {5, 7, 1}, instead of {6, 2, 1} in MCP.

5 Experimental Study

In this section, we study the performance of the proposed algorithms over four real datasets. All the algorithms are implemented with Python2.7 and run on a CentOS server (Intel i7-7700 3.6 GHz CPU and 32 GB RAM).

A. Data sets

We used four real social network datasets available at https://snap.stanford.edu. For each dataset, we selected one of the vertices with the most neighbors, that is, vertex 2070 in Facebook, vertex 349932090 in Twitter, vertex 104***590 in Google+, and vertex 1 in Epinions as query nodes. For those with no propagation probability with each edge in the original datasets, we set a random value which uniformly distributed (0, 1) to each edge and took this value as their propagation probability. Experiments in this work focused on the scenario when $\varepsilon =0.2$, $p=0.6$, and $n=3$.

B. Evaluation of the maximal pk -Clique model

The Label Propagation Algorithm (LPA) is considered to be an accurate model in detecting communities in social networks [19]. Wang et al. [19] also proposed that Normalized Mutual Information (NMI) [3] is a popular criterion for evaluating the accuracy of community detection models. The score of NMI stands for the agreement of two results. We compute the score of NMI for the results of our maximal pk-Clique model and the LPA model in this experiment. The scores we achieved were about 83% for Twttier, 58% for Google+, 67% for Facebook, and 63% for Epinions.

C. The necessity to l -diversify

Figure 2 presents the redundancy over different maximal pk-Clique sizes. It indicates that similarity increases as the size of maximal clique increases.

Fig. 2.

Similarity between communities

D. Evaluation of search space refinement

Given a social network and a parameter k, early removal of vertices where the degree is less than k will lead to a smaller search space. The results presented in Table 3 show that the refinement approach works in different networks, but the effectiveness varies and depends on the topology of the graph in an actual situation.

Table 3. Vertices removed in a refined search space

E. Efficiency of proposed algorithms

We implemented a search space refinement in all three algorithms for fair comparison between results. Tables 4, 5, 6 and 7 illustrate the results (time in seconds) obtained from different datasets, where PS denotes Pruning based top-n ICS, HS denotes Heuristic based top-n ICS and BS denotes Basic Search algorithm.

Table 4. Efficiency over Twitter

Table 5. Efficiency over Google+

It is clear that proposed pruning based PS and heuristic based HS algorithms appear far more efficient than the basic solution, both in time and space costs. It also shows that the HS performs better than the PS in most cases. We notice that time cost does not decrease dramatically as vertices are progressively removed.

Table 6. Efficiency over Facebook

Table 7. Efficiency over Epinions

Table 8. Space cost over Twitter

Table 9. Space cost over Google+

Table 10. Space cost over Facebook

Table 11. Space cost over Epinions

Tables 8, 9, 10 and 11 compare the space cost (in kbytes) of different algorithms. The results show that the PS and the HS require less memory than the BS in each case.

F. Evaluation of scalability

To further test the performance of proposed algorithms, we enlarged the search space over Facebook and Epinions datasets. The results are presented in Tables 12 and 13. The cost increases as the number of vertices increases in both cases.

Table 12. Scalability over Facebook

Table 13. Scalability over Epinions

Table 14. Top-3 influential communities for Alexanderm T

G.Case Study

We built a co-author network from the DBLP (DataBase systems and Logic Programming) data set for this case study. The diameter of the network is 6. A vertex represents an author and an edge is added between two authors if they are co-authors. The propagation probability is calculated according the frequency of co-authorships. We performed a top-3 ICS ($\varepsilon =0.2, p=0.8, k=5$) query for “Alexanderm T”, the results are shown in Table 14.

6 Related Work

The detection of community, which is defined as natural divisions of network nodes into densely connected subgroups [15], has been widely studied in biological networks and social networks [8, 15, 16, 20].

Concepts relating to graph properties like k-clique, k-core and so on have been extensively studied in random graphs. Recently, implicit community models k-core [14], kr-Clique [12] have been proposed to discover communities.

An online community search, which finds communities around a query vertex online, recently attracted a lot of attentions, for example, [2].

In considering models for the spread of influence through a social network, a dynamic cascade model called the Independent Cascade (IC) model, was first investigated by Goldenberg et al. [5]. Granovetter et al. [6] were among the first to propose another Linear Threshold (LT) model. Kempe et al. [9] discussed maximizing the spread of influence problem with these models in social network analysis. Based on these works, there appears to be a lots of proposals focusing on the spread of influence problem, for example, [10, 11, 13].

7 Conclusions

In this paper, we study the personalized top-n influential community search problem in social networks. In particular, we propose a novel community model based on the maximal pk-Clique concept which uses a new cohesive criterion. We first present search space refinement. Then we introduce a pruning approach and a heuristic search approach. Extensive experiments over real social networks verify the effectiveness and efficiency of our search algorithms.