Finding influential communities in massive networks

Abstract

Community search is a problem of finding densely connected subgraphs that satisfy the query conditions in a network, which has attracted much attention in recent years. However, all the previous studies on community search do not consider the influence of a community. In this paper, we introduce a novel community model called k-influential community based on the concept of k-core to capture the influence of a community. Based on this community model, we propose a linear time online search algorithm to find the top-r k-influential communities in a network. To further speed up the influential community search algorithm, we devise a linear space data structure which supports efficient search of the top-r k-influential communities in optimal time. We also propose an efficient algorithm to maintain the data structure when the network is frequently updated. Additionally, we propose a novel I/O-efficient algorithm to find the top-r k-influential communities in a disk-resident graph under the assumption of ${{\mathcal {U}}}=O(n)$, where ${{\mathcal {U}}}$ and n denote the size of the main memory and the number of nodes, respectively. Finally, we conduct extensive experiments on six real-world massive networks, and the results demonstrate the efficiency and effectiveness of the proposed methods.

1 Introduction

Many real-world networks, such as social networks and biological networks, contain community structures. Discovering communities in a network is a fundamental problem in network science, which has attracted much attention in recent years [13, 30]. Another related but different problem is community search where the goal is to find the most likely community that contains the query node [11, 25]. The main difference between these two problems is that the community discovery problem is to identify all communities in a network by optimizing some pre-defined criterions [13], while the community search problem is a query-dependent variant of the community discovery problem, which aims to find the community that contains the query node [25].

In all the previous studies on these problems, a community is defined as a densely connected subgraph which ignores another important aspect, namely the influence (or importance) of a community. However, in many application domains, we are interested in finding the most influential communities. For example, in the co-authorship network, we may want to find the well-connected communities that contain many highly cited researchers, as these communities play the leading roles in their corresponding research areas. In the web graph, we may wish to discover the densely connected subgraphs that include many high PageRank web pages, because these dense subgraphs hold a broad catalog of authoritative information that the web users want to find. In the social network, we would like to detect the cohesive subgroups that consist of many celebrities, as these subgroups act important roles for information dissemination and spread over the network.

In this paper, we study, for the first time, the influential community search problem in large networks. To study this issue, we present a new community model called k-influential community based on the well-known concept of k-core [24]. In our definition, we model a network as an undirected graph $G=(V, E)$ where each node in G is associated with a weight, denoting the influence (or importance) of the node. A community is defined as a connected induced subgraph in which each node has a degree at least k, where the parameter k measures the cohesiveness of the community. Unlike the traditional definition of k-core [24], our definition of community is not necessary the maximal induced subgraph that satisfies such a degree constraint (i.e., each node has degree at least k). The influence value of a community is defined as the minimum weight of the nodes in that community. An influential community is one that has a large influence value. We call an influential community with parameter k a k-influential community.

The intuition behind our definition is that each node in an influential community should have a large weight, indicating that every member in an influential community is an influential individual. Another possible measure of influence of a community is the average weight of all the nodes. However, this measure has a drawback that it is not robust to the outliers, because by this measure, an influential community with a high average weight may include some low-weight nodes (outliers) which are not influential. Therefore, in this paper, we use the minimum weight to measure the influence value of a community, as it captures the intuitive idea of influential community. In addition, we require that a k-influential community cannot be contained in a k-influential super-community with equivalent influence value. Because if that is the case, the latter will dominate the former on both size and influence value. Based on this novel k-influential community model, the goal of the influential community search problem is to find the top-r k-influential communities with the highest influence value in a network.

Straightforward searching the top-r k-influential communities in a large network is impractical, because there could be a large number of communities that satisfy the degree constraint, and for each community, we need to check whether it is a k-influential community. By an in-depth analysis of the structure of k-influential communities, we discover that all the k-influential communities can be obtained by iteratively deleting the smallest weight node of the maximal k-core (Here the maximal k-core means that there is no super-graph that is also a k-core). Based on this finding, we propose a depth-first-search (DFS)-based algorithm to search the top-r k-influential communities online. We show that the DFS-based algorithm consumes linear time and space with respect to (w.r.t.) the graph size.

For very large graphs, however, the linear time DFS-based algorithm is still inefficient. To further accelerate the influential community search algorithm, we design a novel data structure, called influential community-preserved structure ($\mathsf {ICPS}$), to store all the pre-calculated k-influential communities. The $\mathsf {ICPS}$ preserves all the k-influential communities, and it takes only linear space w.r.t. the graph size. Based on the $\mathsf {ICPS}$, the query of the top-r k-influential communities can be computed in linear time w.r.t. the answer size only; thus, it is optimal. To construct the $\mathsf {ICPS}$, we devise an efficient algorithm that takes $O(\rho m)$ time and O(m) space, where $\rho$ and m denote the arboricity [8] and the number of edges of a graph, respectively. The arboricity of a graph is the minimum number of spanning forests that are needed to cover all the edges of the graph. Note that the arboricity of a graph is no larger than $O(\sqrt{m})$ even in the worst-case [8], and it has shown to be much smaller than the worst case bound in many real-world sparse graphs [15, 20]. When the graph is frequently updated, we also propose an efficient algorithm to incrementally maintain the $\mathsf {ICPS}$. In addition, when the graph cannot be stored in the main memory, we develop a novel I/O-efficient algorithm to find the top-r k-influential communities under the assumption of ${{\mathcal {U}}}=O(n)$, where ${{\mathcal {U}}}$ and n denote the size of the main memory and the number of nodes respectively. The I/O cost of the proposed algorithm is O(sort(m)), where sort(m) denotes the I/O cost to sort the edges of a graph using the standard external sort algorithm. More details of the I/O-efficient algorithm can be found in Sect. 6.

We conduct extensive experiments over six web-scale real-world graphs to evaluate the efficiency of the proposed algorithms. The results show that the $\mathsf {ICPS}$-based algorithm is several orders of magnitude faster than the DFS-based online search algorithm. The query time of the $\mathsf {ICPS}$-based algorithm is from one millisecond for small k and r to a few seconds for large k and r in four large graphs with more than one billion edges. Moreover, the results show that the $\mathsf {ICPS}$ is compact and can be constructed efficiently. The results also indicate that the proposed $\mathsf {ICPS}$ maintenance algorithm is very efficient which is at least four orders of magnitude faster than the baseline algorithm in large graphs. When the memory size is limited, the results show that our I/O-efficient algorithm can create the $\mathsf {ICPS}$ in reasonable time, and the query processing time of our I/O-efficient algorithm is around one second in web-scale graphs. In addition, we also conduct comprehensive case studies on a co-authorship network to evaluate the effectiveness of the k-influential community model. The results demonstrate that using our community model is capable of finding meaningful influential communities in a network, which cannot be identified by using the k-truss community model [16].

The rest of this paper is organized as follows. We formulate the influential community search problem in Sect. 2. The DFS-based algorithm is presented in Sect. 3. We design a new $\mathsf {ICPS}$ and propose two $\mathsf {ICPS}$ construction algorithms in Sect. 4. We devise an efficient $\mathsf {ICPS}$ update algorithm in Sect. 5. We propose the I/O-efficient algorithm in Sect. 6. Extensive experiments are reported in Sect. 7. We review related work and conclude this paper in Sects. 8 and  9, respectively.

2 Problem statement

Consider an undirected graph $G=(V, E)$, where V and E denote the node set and edge set, respectively. Denote by $n = |V|$ the number of nodes and by $m = |E|$ the number of edges in G. Let d(v, G) be the degree of a node v in graph G. A graph $H = (V_H, E_H)$ is an induced subgraph of G if $V_H \subseteq V$ and $E_H = \{(u, v)|u, v \in V_H, (u, v) \in E\}$. In this paper, we refer to an induced subgraph H such that each node v in H has degree at least k (i.e., $d(v,H)\ge k$ ) as a k-core. The maximal k-core $H^\prime$ is a k-core that no super-graph H of $H^\prime$ is also a k-core. Note that the maximal k-core of a graph G is unique and can be a disconnected graph. For a node $u\in V$, the core number of u, denoted by $c_u$, is the maximal k value such that a k-core contains u.

In the literature, the maximal k-core is widely used to represent cohesive communities of a graph [2, 5, 19, 25]. Instead of general cohesive communities, in this work, we seek to find influential communities in a graph. Specifically, in our setting, each node u in G has a weight $w_u$ (such as PageRank or any other user-defined attributes), indicating the influence (or importance) of u. Additionally, we assume without loss of generality that the weight vector $W=(w_1, w_2, \ldots , w_n)$ forms a total order, i.e., for any two nodes $v_i$ and $v_j$, if $i \ne j$, then $w_i \ne w_j$. Note that if that is not the case, we use the node identity to break ties for any $w_i = w_j$. Before proceeding further, we give the definition of influence value of an induced subgraph as follows.

Definition 1

Given an undirected graph $G=(V, E)$ and an induced subgraph $H=(V_H, E_H)$ of G, the influence value of H denoted by f(H) is defined as the minimum weight of the nodes in H, i.e., $f(H) = \mathop {\min }\nolimits _{u \in {V_H}} \{ {w_u}\}$.

By Definition 1, if the influence value of an induced subgraph H (i.e., f(H)) is large, then the weight of every node in H should be a large value, indicating that H is an influential subgraph. Below, we give a brief discussion of why we define f as the minimum weight of the nodes. Regarding the choice of f(H), we need to consider functions that capture the influence (weight) of nodes in H. Moreover, we want the influence value f(H) to be a large value if the induced subgraph H is influential. Except the minimum weight of the nodes in H, one potential definition of f(H) is the average weight of the nodes in H, i.e., $f(H) = \sum \nolimits _{u \in {V_H}} {{w_u}} /|{V_H}|$. However, this definition has a drawback that it is not robust to outliers. Specifically, by this definition, an influential subgraph may include low-weight nodes (outliers), albeit it has a high average weight. Another potential definition of f(H) is the median of the weights of all the nodes in H. However, the community based on this definition may also include many low-weight nodes. For example, suppose that the community H includes 100 nodes, and there are 51 nodes in H that have weights larger than 1000, and the remaining 49 nodes have weights smaller than 10. Clearly, the median is high (${\ge }1000$) in this example, but H contains too many low-weight nodes. In this paper, we define f(H) as the minimum weight of nodes in H based on the following reasons. First, it is robust to the low-weight nodes. Second, it admits an elegant algorithmic framework to solve the influential community search problem (see Sects. 3 and  4). Third, using the definition of the minimum weight can effectively find influential communities as shown in our experiments (see Sect. 7).

Intuitively, an influential community should not only have a large influence value, but it is also a cohesive induced subgraph. Based on this intuition, we give the definition of k-influential community, where the parameter k controls the cohesiveness of the community.

Definition 2

Given an undirected graph $G=(V, E)$ and an integer k. A k-influential community is an induced subgraph $H^k=(V_H^k, E_H^k)$ of G that meets all the following constraints.

• Connectivity: $H^k$ is connected;

• Cohesiveness: each node u in $H^k$ has degree at least k;

• Maximal structure: there is no other induced subgraph ${{\tilde{H}}}$ such that (1) ${\tilde{H}}$ satisfies connectivity and cohesiveness constraints, (2) ${{\tilde{H}}}$ contains $H^k$, and (3) $f({{\tilde{H}}}) = f(H^k)$.

Clearly, the cohesiveness constraint indicates that the k-influential community is a k-core. With the connectivity and cohesiveness constraints, we can ensure that the k-influential community is a connected and cohesive subgraph. And with the maximal structure constraint, we can guarantee that any k-influential community cannot be contained in a k-influential super-community with equivalent influence value. The following example illustrates the definition of k-influential community.

Fig. 1

Running example (the numbers denote the weights)

Example 1

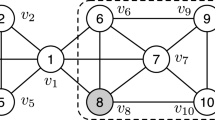
Consider the graph shown in Fig. 1. Suppose, for instance, that $k=2$, then by definition the subgraph induced by node set $\{v_{12}, v_{13}, v_{14}, v_{15}\}$ is a 2-influential community with influence value 12, as it meets all the constraints in Definition 2. Note that the subgraph induced by node set $\{v_{12}, v_{14}, v_{15}\}$ is not a 2-influential community. This is because it is contained in a 2-influential community induced by node set $\{v_{12}, v_{13}, v_{14}, v_{15}\}$ whose influence value equals its influence value, thus fail to satisfy the maximal structure constraint. $\square$

In many practical applications, we are typically interested in the most influential communities whose influence values are larger than those of all other influential communities. In this paper, we aim to find such communities in a large graph efficiently. Below, we formulate two influential community search problems.

Problem 1

Given a graph $G=(V, E)$, a weight vector W, and two parameters k and r, the problem is to find the top-r k-influential communities with the highest influence value. Formally, let $\small {{\mathcal {H}}}^k=\{H^k(1), H^k(2), \ldots , H^k(l)\}$ be the complete set of k-influential communities. If $l \ge r$, the problem is to find a subset $\small {{\mathcal {R}}}^k=\{H^k(i_1), \ldots , H^k(i_r)\}$ of $\small {{\mathcal {H}}}^k$ with cardinality r such that for any k-influential community $H^k$ in $\small {{\mathcal {H}}}^k$ but not in $\small {{\mathcal {R}}}^k$ (i.e., $\small H^k \in {{\mathcal {H}}}^k \backslash {{\mathcal {R}}}^k$), we have $\small f(H^k) \le f(H^k(i_j))$ for any $\small H^k(i_j) \in {{\mathcal {R}}}^k$. Otherwise, the problem outputs the complete set of k-influential communities, i.e., $\small {{\mathcal {H}}}^k$.

For Problem 1, a k-influential community may be contained in another k-influential community in the top-r results. For example, in Fig. 1, we can easily verify that the top-2 2-influential communities are the subgraphs induced by $\{ v_{13}, v_{14}, v_{15}\}$ and $\{v_{12}, v_{13}, v_{14}, v_{15}\}$, respectively. Clearly, in this example, the second 2-influential community contains the first 2-influential community. To avoid the inclusion relationships in the top-r results, in the following, we consider a problem of finding the top-r non-containing k-influential communities.

Definition 3

Given a graph $G=(V, E)$ and an integer k. A non-containing k-influential community $H^k=(V_H^k, E_H^k)$ is a k-influential community that meets the following constraint.

• Non-containment: $H^k$ cannot contain a k-influential community ${{\bar{H}}}^k$ such that $f({{\bar{H}}}^k) > f(H^k)$.

We illustrate Definition 3 in the following example.

Example 2

Let us reconsider the graph shown in Fig. 1. Assume that $k=2$. By Definition 3, we can see that the subgraphs induced by $\{ v_{3}, v_{4}, v_{5}\}$, $\{v_8, v_9, v_{11}\}$ and $\{ v_{13}, v_{14}, v_{15}\}$ are non-containing 2-influential communities. However, the subgraph induced by $\{ v_{12}, v_{13}, v_{14}, v_{15}\}$ is not a non-containing 2-influential community, because it includes a 2-influential community (the subgraph induced by $\{ v_{13}, v_{14}, v_{15}\}$) with a larger influence value. $\square$

Problem 2

Given a graph $G=(V, E)$, a weight vector W, and parameters k and r, the problem is to find the top-r non-containing k-influential communities with the highest influence value. Here, the definition of top-r is similar to the definition given in Problem 1.

Note that with the Non-containment constraint, there is no inclusion relationship in the top-r non-containing k-influential communities; thus, no redundant results are introduced. In other words, Problem 2 tends to find the sub-communities if they haver larger influence values than their corresponding super-communities.

Challenges A k-influential community is different from the maximal k-core in two aspects. First, a k-influential community must be a connected subgraph, whereas the maximal k-core does not impose such a constraint. Second, with the maximal structure constraint, a k-influential community $H^k$ requires that there is no super-graph of $H^k$ which is a connected k-core with influence value equivalent to $f(H^k)$. However, the maximal k-core H only requires that there is no super-graph of H which is also a k-core. For a non-containing k-influential community, it further imposes a non-containment constraint. Due to these differences, given a graph G, the maximal k-core of G is unique, whereas there are multiple (non-containing) k-influential communities in G. Thus, the methods for computing the maximal k-core cannot be directly used for computing the top-r (non-containing) k-influential communities.

A straightforward method to compute the top-r (non-containing) k-influential communities is first to compute the set of subgraphs that satisfy the connectivity and cohesiveness constraints. For each subgraph, we further check whether it satisfies the maximal structure constraint and the non-containment constraint (for non-containing k-influential communities). Finally, the top-r (non-containing) k-influential communities with the highest influence value are returned. Obviously, such a method is inefficient since the number of potential subgraphs that satisfy the connectivity and cohesiveness constraints can be exponentially large, and for each potential subgraph, we need to check the maximal structure constraint, which is costly. In the following sections, we will present several efficient algorithms to tackle these challenges.

3 Online search algorithms

In this section, we focus on developing online search algorithms for Problem 1 and then discuss how to generalize the proposed algorithms for Problem 2. Note that we refer to our algorithms proposed in this section as the online search algorithms because all the algorithms do not require any pre-computations. In the following section, we will propose a new algorithm that is based on a pre-computed data structure. Before we proceed further, we give three useful lemmas as follows.

Lemma 1

For any graph G, each maximal connected component of the maximal k-core of G is a k-influential community.

Proof

The proof can be easily obtained by definition. $\square$

Lemma 2

For any k-influential community $H^k=(V_{H}^k, E_H^k)$, if we delete the smallest weight node in $H^k$ and the resulting subgraph still contains a k-core, each maximal connected component of the maximal k-core in the resulting graph, denoted by $C^k=(V_C^k, E_C^k)$, is a k-influential community.

Proof

Without loss of generality, we consider a maximal connected component (MCC) of $C^k$. The following arguments hold for each MCC of $C^k$. In particular, we let ${{\bar{C}}}^k=(V_{{\bar{C}}}^k, E_{{\bar{C}}}^k)$ be a MCC of $C^k$. First, ${{\bar{C}}}^k$ satisfies the connectivity constraint. Second, by the definition of maximal k-core, ${{\bar{C}}}^k$ satisfies the cohesiveness constraint. Finally, we show that ${{\bar{C}}}^k$ also meets the maximal structure constraint. We prove it by contradiction. Suppose to the contrary that there is an induced subgraph ${{\tilde{C}}}=(V_{{\tilde{C}}}, E_{{\tilde{C}}})$ such that (1) ${{\tilde{C}}}$ satisfies connectivity and cohesiveness constraints, (2) ${{\tilde{C}}}$ contains ${{\bar{C}}}^k$, and (3) $f({{\tilde{C}}}) = f({{\bar{C}}}^k)$. Further, we have that $f({{\tilde{C}}}) = f({{\bar{C}}}^k) \ge f(C^k) > f(H^k)$, because $C^k$ is obtained after deleting the smallest weight node in $H^k$. By $f({{\tilde{C}}}) > f(H^k)$, we can conclude that ${{\tilde{C}}}$ does not contain $H^k$. Then, we can construct a subgraph ${{\tilde{H}}}^k=(V_{{\tilde{H}}}^k, E_{{\tilde{H}}}^k)$ which is induced by the nodes in $V_{{\tilde{C}}} \cup V_{H}^k$. Since both the induced subgraphs ${{\tilde{C}}}$ and $H^k$ satisfy the cohesiveness constraint, thus ${{\tilde{H}}}^k$ also meets the cohesiveness constraint. Moreover, we know that ${{\bar{C}}}^k$ is a subgraph of both ${{\tilde{C}}}$ and $H^k$. Since both ${{\tilde{C}}}$ and $H^k$ are connected induced subgraphs and $V_{{\tilde{C}}} \cap V_{H}^k$ is nonempty, ${{\tilde{H}}}^k$, which is the union of ${{\tilde{C}}}$ and $H^k$, is also a connected induced subgraph. As a result, the induced subgraph ${{\tilde{H}}}^k$ satisfies cohesiveness and cohesiveness constraint, and ${{\tilde{H}}}^k$ contains $H^k$. Moreover, by our definition, $f({{\tilde{H}}}^k)= \mathop {\min }\nolimits _{u \in {V_{{\tilde{C}}} \cup V_{H}^k}} \{ {w_u}\} = \mathop {\min }\nolimits _{u \in {V_{H}^k}} \{ {w_u}\}=f(H^k)$, where the second equality is due to $f({\tilde{C}})>f(H^k)$. Thus, we obtain that $H^k$ does not meet the maximal structure constraint, which is a contradiction. Putting it all together, we can conclude that ${{\bar{C}}}^k$ is a k-influential community. $\square$

Lemma 3

For any k-influential community $H^k=(V_{H}^k, E_H^k)$, if we delete the node in $H^k$ with the smallest weight and the resulting subgraph does not contain a k-core, then $H^k$ is a non-containing k-influential community.

Proof

The proof can be easily obtained by definition. $\square$

Based on the above lemmas, we are ready to devise efficient algorithms for Problems 1 and  2. Below, we first develop a basic algorithm for our problems and then propose an optimized algorithm based on depth-first-search (DFS), which is much more efficient than the basic one.

3.1 The basic algorithm

The basic idea of our algorithm is described below. First, for a given k, we compute the maximal k-core of the graph G denoted by $C^k(G)$. Then, we iteratively invoke the following procedure until the resulting graph does not contain a k-core. The procedure consists of two steps. Let $G_i$ be the resulting graph in the i-th iteration, and $C^k(G_i)$ be the maximal k-core of $G_i$. The first step is to delete the smallest weight node in $C^k(G_{i-1})$, which results in a graph $G_{i}$. The second step is to compute the maximal k-core $C^k(G_{i})$ of $G_{i}$. The detailed description is outlined in Algorithm 1.

Below, we first show that all the $H^k(j)$ ($0 \le j \le i - 1$) obtained by Algorithm 1 are k-influential communities. Then, based on this fact, we will prove that Algorithm 1 correctly outputs the top-r k-influential communities in Theorem 2.

Theorem 1

Let ${\mathcal {H}}^k=\{H^k(0), \ldots , H^k(i - 1)\}$ be a set including all the $H^k(j)$ ($0 \le j \le i - 1$) obtained by Algorithm 1. Then, for $0 \le j \le i - 1$, $H^k(j)$ is a k-influential community.

Proof

The proof can be easily obtained based on Lemmas 1 and  2. $\square$

Theorem 2

Algorithm 1 correctly finds the top-r k-influential communities.

Proof

By Algorithm 1, $H^k(j + 1)$ is obtained after deleting the smallest weight node in the maximal k-core that includes $H^k(j)$; thus, we have $f(H^k(j)) \ge f(H^k(j + 1))$ for $0 \le j \le i - 2$. Recall that we have assumed without loss of generality that the weight vector W forms a total order. Thus, we have $f(H^k(0))< f(H^k(1))<\cdots < f(H^k(i-1))$. To prove the theorem, it remains to show that the set $\mathcal {H}^k$ includes all the k-influential communities in G. We prove it by contradiction. Suppose to the contrary that there is a k-influential community ${{\tilde{H}}}^k$ such that ${{\tilde{H}}}^k \notin \mathcal {H}^k$. On the one hand, since ${{\tilde{H}}}^k$ is a k-influential community, it meets the connectivity and cohesiveness constraints, and therefore, it must be contained in a maximal connected component (MCC) of the maximal k-core of G (i.e., $C^k(G_0)$). Since $H^k(0)$ is the MCC of $C^k(G_0)$ with the smallest influence value, we have $f({{\tilde{H}}}^k) > f(H^k(0))$. On the other hand, we have $f({{\tilde{H}}}^k) < f(H^k(i-1))$. The reason is as follows. By our algorithm, if we delete the smallest weight node in $H^k(i-1)$, there is no k-core in $G_i$; thus, there is no k-influential community whose influence value is larger than $f(H^k(i-1))$. As a consequence, we have $f(H^k(0))< f({{\tilde{H}}}^k) < f(H^k(i-1))$. Since $f(H^k(0))< f(H^k(1))<\cdots < f(H^k(i-1))$, there must be a j ($0 \le j < i - 1$) such that $f(H^k(j))< f({{\tilde{H}}}^k) < f(H^k(j+1))$. Note that after deleting the smallest weight node u in $H^k(j)$, the algorithm obtains a subgraph $G_{j+1}$. Since $f(H^k(j))< f({{\tilde{H}}}^k)$, the subgraph ${{\tilde{H}}}^k$ is still contained in $G_{j+1}$. However, after this deletion operation, the algorithm obtains $H^k(j+1)$ which is the k-influential community with the smallest influence value. Thus, we have $f({{\tilde{H}}}^k) > f(H^k(j+1))$, which contradicts to $f({{\tilde{H}}}^k) < f(H^k(j+1))$. Hence, $\mathcal {H}^k$ includes all the k-influential communities in G. Putting it all together, we conclude that Algorithm 1 correctly outputs the top-r k-influential communities. $\square$

By Theorem 2, we have a corollary as shown below.

Corollary 1

Given a graph G with n nodes. The number of k-influential communities in G is bounded by n.

Proof

Recall that in Algorithm 1, each k-influential community except $H^k(0)$ is obtained by deleting one node in G. Since there are n nodes in G, the number of k-influential communities in G is bounded by n. $\square$

We analyze the time and space complexity of Algorithm 1 in the following theorem.

Theorem 3

The time complexity of Algorithm 1 is $O(N_km)$ bounded by O(nm), where $N_k$ denotes the number of k-influential communities. The space complexity of Algorithm 1 is $O(n+m)$.

Proof

In each iteration, the most time-consuming step is to compute the maximal k-core which takes O(m) time complexity [2]. There is $O(N_k)$ iterations in total, because in each iteration Algorithm 1 computes one k-influential community. As a consequence, the total time cost of Algorithm 1 is $O(N_km)$. Note that by Corollary 1, for every k, $O(N_k)$ is bounded by O(n), thus $O(N_km)$ is bounded by O(nm). Also, we can easily derive that the space complexity of Algorithm 1 is $O(m+n)$. $\square$

Note that we can slightly modify Algorithm 1 to obtain the top-r non-containing k-influential communities. Specifically, we only need to add one line behind line 6 in Algorithm 1 to check whether $H^k(i)$ includes a k-core or not. If $H^k(i)$ does not include a k-core, then by Lemma 3, $H^k(i)$ is a non-containing k-influential community, and we mark such a $H^k(i)$ as a candidate result. Finally, in line 9, we only output the top-r results that are marked as candidate results. It is easy to show that the time and space complexity of this algorithm is the same as those of Algorithm 1.

3.2 The DFS-based algorithm

As shown in the previous subsection, Algorithm 1 is very expensive which is clearly impractical for most real-world graphs. Here, we present a much more efficient algorithm based on depth-first-search (DFS). The detailed description of the algorithm is shown in Algorithm 2. Similar to Algorithm 1, Algorithm 2 also iteratively computes the k-influential communities one by one. Unlike Algorithm 1, in each iteration, Algorithm 2 does not recompute the maximal k-core. Instead, in each iteration, Algorithm 2 recursively deletes all the nodes that are definitely excluded in the subsequent k-influential communities. In particular, when Algorithm 2 deletes the smallest weight node in the k-influential community $H^k(i)$ (line 6), the algorithm recursively deletes all the nodes that violate the cohesiveness constraint by a DFS procedure (lines 9–14). This is because, when we delete the smallest weight node u, the degrees of u’s neighbor nodes decrease by 1. This may result in that some of u’s neighbors violate the cohesiveness constraint; thus, they cannot be included in the subsequent k-influential communities, and therefore, we have to delete them. Similarly, we also need to verify the other hop (e.g., 2-hop, 3-hop, etc.) neighbors whether they satisfy the cohesiveness constraint. Clearly, we can use a DFS procedure to identify and delete all those nodes. The correctness of Algorithm 2 is shown in Theorem 4.

Theorem 4

Algorithm 2 correctly finds the top-r k-influential communities.

Proof

Since Algorithm 1 is correct, to prove the theorem, we only need to show that in the iteration i of Algorithm 2, the resulting subgraph $C^k(G)$ before invoking DFS(u) (line 6 in Algorithm 2) is the maximal k-core $C^k(G_{i})$ of the graph $G_{i}$ in Algorithm 1. We prove it by induction. First, when $i=0$, we have $C^k(G)=C^k(G_0)$. Second, assume that in the iteration i of Algorithm 2, we have $C^k(G)=C^k(G_{i})$. Then, in the iteration $i+1$ of Algorithm 2, $C^k(G)$ will be updated after invoking DFS(u), where u is the smallest weight node. To avoid confusion, we denote the updated $C^k(G)$ by ${\tilde{C}}^k(G)$. Our goal is to show ${\tilde{C}}^k(G) = C^k(G_{i+1})$. In Algorithm 2, DFS(u) recursively deletes all the nodes whose degrees are smaller than k. When DFS(u) terminates, the resulting subgraph ${\tilde{C}}^k(G)$ is a k-core, because every node in the resulting subgraph has a degree at least k. We claim that this k-core is the maximal k-core of the subgraph $C^k(G) \backslash u$. We prove this claim by a contradiction. Suppose to the contrary that there is another k-core ${\bar{C}}^k$ of $C^k(G) \backslash u$ with $|{\bar{C}}^k| > |{\tilde{C}}^k(G)|$. Then, there is a node $v \in {\bar{C}}^k$ and $v \notin {\tilde{C}}^k(G)$. Since v is in a k-core of $C^k(G) \backslash u$, v’s degree is no less than k after invoking DFS(u). Otherwise, v cannot be included in any k-core of $C^k(G) \backslash u$. Note that by Algorithm 2, such a node v must be included in ${\tilde{C}}^k(G)$, which contradicts to $v \notin {\tilde{C}}^k(G)$. Therefore, ${\tilde{C}}^k(G)$ is the maximal k-core of $C^k(G) \backslash u$. On the other hand, in Algorithm 1, $C^k(G_{i+1})$ is obtained by first deleting u from $C^k(G_{i})=C^k(G)$ (induction assumption) and then computing the maximal k-core. Thus, we can conclude that ${\tilde{C}}^k(G) = C^k(G_{i+1})$. $\square$

We analyze the complexity of Algorithm 2 in the following theorem.

Theorem 5

The time complexity and space complexity of Algorithm 2 are both $O(m+n)$.

Proof

First, we can pre-compute all the maximal k-cores of G for every k by an O(m)-time core decomposition algorithm [2]. Second, we can sort all the nodes based on their weights in advance; thus, getting the smallest weight node (line 5) can be done in constant time. Third, in the “while loop” of Algorithm 2, the most time-consuming step is to invoke the procedure DFS(u). For each edge $(u, v) \in E$, Algorithm 2 only visits it once in the DFS procedure. This is because, when the algorithm visits an edge, the algorithm will delete it (line 11), and this edge will no longer be visited in the subsequent DFS steps. Therefore, the total time cost taken in all the DFS steps is bounded by the number of edges. As a result, the time complexity of Algorithm 2 is $O(m+n)$. The algorithm only needs to store the graph G and maintains the k-core $C^k(G)$ and a sorted node list, which uses $O(m+n)$ space complexity. $\square$

Similarly, we can easily modify Algorithm 2 for Problem 2. In particular, we only need to add one line behind line 6 in Algorithm 2 to check whether all nodes in $H^k(i)$ are deleted or not. If that is the case, $H^k(i)$ is a non-containing k-influential community (by Lemma 3), and we mark such a $H^k(i)$ as a candidate result. Finally, in line 8, we only output the top-r results that are marked. It is easy to show that the time complexity and space complexity of this algorithm are the same as those of Algorithm 2.

4 $\mathsf {ICPS}$-based search algorithms

Although Algorithm 2 is much more efficient than Algorithm 1, it takes $O(m+n)$ time for each query which is still inefficient for very large graphs. In this section, we present a much more efficient algorithm whose time complexity is proportional to the size of the top-r results; thus, it is optimal. The general idea is that the algorithm first pre-computes all k-influential communities for every k and then uses a space-efficient data structure to store all such k-influential communities in memory. Based on this data structure, the algorithm outputs the top-r results in optimal time. The challenges of this algorithm are twofold: (1) how to devise a space-efficient structure to store all the k-influential communities and (2) how to efficiently construct such a structure. This is because there could be O(n) k-influential communities for each k (see Corollary 1), and thus, there could be $O(k_{\max }n)$ k-influential communities in total, where $k_{\max }$ is the maximal core number of the nodes in G. Obviously, it is impractical to directly store all such k-influential communities for very large graphs. To tackle these challenges, we will present a novel linear space structure, called influential community-preserved structure ($\mathsf {ICPS}$), to compress and store all the k-influential communities, and then, we propose two algorithms to efficiently construct the $\mathsf {ICPS}$.

4.1 The influential community-preserved structure ($\mathsf {ICPS}$)

The idea of the $\mathsf {ICPS}$ is based on the following observation. Observation For each k, the k-influential communities form an inclusion relationship. Based on such an inclusion relationship, all the k-influential communities can be organized by a tree-shape (or a forest-shape) structure.

Recall that Lemma 2 implies an inclusion relationship in the k-influential communities. More specifically, based on Lemma 2, we can see that a k-influential community $H^k$ contains all k-influential sub-communities which are the MCCs of the maximal k-core of $H^k \backslash \{u\}$, where u is the smallest weight node in $H^k$. Note that all these k-influential sub-communities are disjoint, because they are different MCCs. Clearly, we can use a two-level tree structure to characterize the inclusion relationships among all these k-influential communities. The parent vertex is $H^k$, and each child vertex is a MCC of the maximal k-core of $H^k \backslash \{u\}$ which is also a k-influential community. Note that the result of Lemma 2 can be recursively applied in each k-influential sub-community. Thus, we can obtain a tree structure for an initial k-influential community, where each vertex of the tree corresponds to a k-influential community. To organize all the k-influential communities of a graph G, we can set the initial k-influential communities as the MCCs of the maximal k-core of G. As a consequence, we are able to use a tree (or forest¹) structure to organize all the k-influential communities, where the root vertex of a tree is a MCC of the maximal k-core of G. Additionally, by Lemma 3, it is easy to see that each leaf vertex in such a tree corresponds to a non-containing k-influential community. To avoid confusion, in the rest of this paper, we use the term vertex to denote a node in a tree.

Compression method Based on the inclusion relationship between the parent vertex and child vertex in the tree (or forest) structure, we can compress all k-influential communities. Our compression solution is described as follows. For each non-leaf vertex in the tree which corresponds to a k-influential community, we only store the nodes of the k-influential community that are not included in it’s k-influential sub-communities (i.e, it’s child vertices in the tree). The same idea is recursively applied to all the non-leaf vertices of the tree following a top-down manner. For each leaf vertex which corresponds to a non-containing k-influential community, we store all the nodes of that non-containing k-influential community. The following example illustrates the tree organization of all the k-influential communities.

Example 3

Reconsider the graph shown in Fig. 1. Let us consider the case of $k=2$. Clearly, the entire graph is a connected 2-core, thus it is a 2-influential community. Therefore, the root vertex of the tree corresponds to the entire graph. After deleting the smallest weight node $v_1$, we get three 2-influential communities which are the subgraphs induced by the node sets $\{v_3, v_4, v_5\}$, $\{v_6, \ldots , v_{11}\}$, and $\{v_{12}, \ldots , v_{15}\}$, respectively. Thus, we create three child vertices for the root vertex which corresponds to the three 2-influential communities, respectively. Since $v_1$ and $v_2$ are not included in these three 2-influential communities, we store them in the root vertex. The same idea is recursively applied in all the three 2-influential communities. For instance, for the 2-influential community induced by $\{v_3, v_4, v_5\}$, we can find that it is a non-containing 2-influential community. By our compression method, we store the nodes $\{v_3, v_4, v_5\}$ in the corresponding tree vertex. For the other child vertices of the root, we have a similar process. Also, similar processes can be used for other k values. Figure 2 shows the tree organization for all k for the graph shown in Fig. 1. $\square$

We refer to the above tree-shape structures for all k from 1 to $k_{max}$ as the $\mathsf {ICPS}$. Below, we analyze the space complexity of the $\mathsf {ICPS}$ in Theorem 6.

Theorem 6

The space complexity of the $\mathsf {ICPS}$ is O(m).

Proof

By our compression method, each node u in G is only stored once in the tree (or forest) for a given k. Moreover, by our solution, each node u with a core number $c_u$ can only be stored in at most $c_u$ trees (or forests). Thus, the total space overhead of the $\mathsf {ICPS}$ is bounded by $\sum \nolimits _{u \in V} {{c_u}} \leqslant \sum \nolimits _{u \in V} {{d(u,G)}} = 2m$. $\square$

Fig. 2

Tree organization of all the k-influential communities. a k=1, b k=2, c k=3

By Theorem 6, the $\mathsf {ICPS}$ takes linear space w.r.t. the graph size; thus, it can be used for very large graphs. Below, we present two algorithms to construct the $\mathsf {ICPS}$.

4.2 The basic $\mathsf {ICPS}$ construction algorithm

The basic $\mathsf {ICPS}$ construction algorithm is to invoke the DFS-based algorithm (Algorithm 2) $k_{\max }$ times, where $k_{\max }$ is the maximal core number of the nodes in G. Specifically, the basic algorithm consists of two steps. In the first step, the algorithm iteratively calls Algorithm 2 to compute all the tree vertices for each k ($k=1, \ldots , k_{\max }$). Then, in the second step, the algorithm invokes a tree construction algorithm to build the $\mathsf {ICPS}$. The detailed description of the algorithm is outlined in Algorithm 3. Note that in line 8 of Algorithm 3, all the nodes deleted after invoking DFS(u) must be stored in a tree vertex. The reason is that the nodes deleted by DFS(u) are excluded in any k-influential sub-communities of the current k-influential community. Moreover, only these nodes in the current k-influential community are excluded in its k-influential sub-communities. Thus, by our compression method, we need to create a tree vertex that contains all these nodes (line 9 of Algorithm 3). After generating all the tree vertices for all k, the algorithm calls Algorithm 4 to construct the $\mathsf {ICPS}$ (line 11 of Algorithm 3).

Specifically, Algorithm 4 works in a bottom-up manner. To build a tree (or forest) structure for each k ($k=1, \ldots , k_{\max }$), the algorithm first builds a single-vertex tree for each tree vertex generated in the previous step (lines 1–2 of Algorithm 4). Then, for each k, the final tree (or forest) structure can be obtained by iteratively merging two subtrees (lines 3–9). Here, the merge operation between two subtrees $T_1$ and $T_2$ is defined as follows. Let $r_1$ and $r_2$ be the roots of subtrees $T_1$ and $T_2$, respectively. Assume that $f(r_1) < f(r_2)$ where $f(r_i)=\mathop {\min }\nolimits _{u \in {r_i}} \{ {w_u}\}$ for $i=1,2$. Then, the merge operation between $T_1$ and $T_2$ is to set the root of $T_2$ as a child vertex of the root of $T_1$. Note that this subtree merge operation can be efficiently implemented by using a union-find structure [10]. Moreover, we find that such a bottom-up tree construction algorithm for all k can be done via traversing the graph once, following a decreasing order of the node weight (lines 3-9 of Algorithm 4). The detailed implementation is depicted in Algorithm 4. We prove the correctness of Algorithm 4 in Theorem 7.

Theorem 7

Algorithm 4 correctly creates the tree-shape structures for all k ($k=1, \ldots , k_{\max }$).

Proof

First, it is easy to verify that for each k, the final merged structure produced by Algorithm 4 must be a tree. Thus, to prove the theorem, we need to show that the resulting tree structure is exactly the tree structure defined in Sect. 4.1. Below, we focus on proving the theorem for one k, and similar arguments can also be used for other k values. In addition, for convenience, we refer to the tree generated by Algorithm 4 as ${\tilde{T}}$, and denote the tree defined in Sect. 4.1 by T. Our goal is to show ${\tilde{T}} = T$. Let $r_u$ be a tree vertex, and $f(r_u)=\mathop {\min }\nolimits _{u \in {r_u}} \{ {w_u}\}$ be the weight of the tree vertex $r_u$. We sort all the tree vertices in an decreasing order based on their weights (i.e., $f(r_1)> \cdots , > f(r_{N_k})$). Then, we prove the theorem by an induction argument. First, the subtree induced by $r_1$ of ${\tilde{T}}$ is clearly the subtree induced by $r_1$ of T. Second, we denote the subtree (or sub-forest) induced by the vertices $\{r_1, \ldots , r_j\}$ of ${\tilde{T}}$ by ${\tilde{T}}_j$, and denote the subtree (or sub-forest) induced by the vertices $\{r_1, \ldots , r_j\}$ of T by $T_j$. We make an induction assumption that ${\tilde{T}}_i = T_i$ for all $1< i \le j$. Based on this, we aim to prove ${\tilde{T}}_{j+1} = T_{j+1}$. Specifically, to prove ${\tilde{T}}_{j+1} = T_{j+1}$, we only need to prove that for each edge $e=(r_{j+1}, r_i)$ in $T_{j+1}$ with $i<j+1$, it is also in ${\tilde{T}}_{j+1}$. With $e=(r_{j+1}, r_i) \in T_{j+1}$ and the property of $T_{j+1}$, we know that the k-influential community induced by the subtree rooted by vertex $r_{j+1}$ must contain the k-influential community induced by the subtree rooted by vertex $r_i$. As a result, there must exist an edge (u, v) in G such that u is included in vertex $r_{j+1}$ and v is contained in a vertex of the subtree rooted by $r_{i}$. Assume without loss of generality that $w_u < w_v$. When Algorithm 4 visits a node u, the algorithm will traverse the edge (u, v), and then, the algorithm will merge the subtree rooted by vertex $r_{j+1}$ and the subtree that includes v. Note that at this moment, the subtree produced by Algorithm 4 with root vertex containing v is $r_i$ (by induction assumption). Thus, Algorithm 4 creates an edge between the vertex $r_{j+1}$ and $r_i$ in ${\tilde{T}}_{j+1}$. This completes the proof. $\square$

The correctness of Algorithm 3 can be guaranteed by Theorems 4 and  7. Below, we give an example to show how Algorithm 3 works.

Example 4

Consider the graph shown in Fig. 1. For each k, by invoking the DFS-based algorithm, Algorithm 3 generates all the tree vertices shown in Table 1. Then, the algorithm calls Algorithm 4 to build the tree structure. First, for each k ($k=1, 2,3$), the Algorithm 4 creates a tree for each vertex. For instance, for $k=1$, the algorithm generates 11 trees, because in Table 1 (row 1), there are 11 vertices when $k=1$. Then, the algorithm processes the node $v_{15}$, as it is the largest weight node. As can be seen, $v_{15}$ has four neighbor nodes $\{v_1, v_{12}, v_{13}, v_{14}\}$. But the weights of all of them are smaller than $w_{15}$; thus, the algorithm continues to process node $v_{14}$. Since $v_{14}$ has a neighbor $v_{15}$ whose weight exceeds $w_{14}$, the algorithm traverses the edge $(v_{14}, v_{15})$ (line 4 of Algorithm 4). Since the core numbers of $v_{14}$ and $v_{15}$ are 3, these two nodes must be included in the vertices of the trees of $k=1, 2, 3$. Thus, for each k ($k=1,2,3$), the algorithm first finds the root vertices of the trees including $v_{14}$ and $v_{15}$, respectively (lines 6–7 of Algorithm 4). Since both $v_{14}$ and $v_{15}$ are included in the same vertex for all k, no merge operation will be done. For the remaining nodes, we use the same procedure, and we will obtain the tree-shape structures shown in Fig. 2 when the algorithm terminates. $\square$

Table 1 Tree vertices for all k

We analyze the time complexity of Algorithms 3 and 4 as follows.

Theorem 8

The time complexities of Algorithms 3 and  4 are $O(k_{\max }(m+n))$ and $O(\rho m)$, respectively, where $\rho$ is the arboricity [8] of a graph G.

Proof

We first analyze the time complexity of Algorithm 3. For each k ($k=1, \ldots , \min \{c_u, c_v\}$), the most time-consuming step is to compute the maximal k-core which takes $O(m+n)$ time. Therefore, the total cost for computing all the tree vertices is $O(k_{\max }(m+n))$. Since the tree construction algorithm takes $O(\rho m)$ time and $\rho \le k_{\max }$ [17], the total time complexity of Algorithm 3 is $O(k_{\max }(m+n))$.

Then, we analyze the time complexity of Algorithm 4 as follows. First, since the space complexity of the $\mathsf {ICPS}$ is O(m), the total number of vertices in the $\mathsf {ICPS}$ is bounded by O(m). Second, we can use a union-find structure to efficiently implement the root-finding operation (lines 6–7 of Algorithm 4) as well as the tree-merge operation (line 9 of Algorithm 4). It is well known that the amortized time per operation of a union-find structure is $O(\alpha (n))$, where $\alpha (n)$ is the inverse Ackermann function which is less than 5 for all practical values of n [10]. Thus, each union-find operation can be done in O(1) time. Based on these results, lines 1–2 in Algorithm 4 take O(m) time, and lines 3–9 take $O(\rho m)$ time. The reason is as follows. For each edge (u, v), the algorithm performs at most $\min \{c_u, c_v\}$ tree-merge operations (lines 5–9 of Algorithm 4). Since each merge operation can be done in O(1) time by the union-find structure, the time cost taken in lines 3–9 is bounded by $\sum \nolimits _{(u,v) \in E} {\min \{ {c_u},{c_v}\} } \le \sum \nolimits _{(u,v) \in E} {\min \{ {d(u,G)},{d(v,G)}\} }$. Based on the result shown in [8], $O(\sum \nolimits _{(u,v) \in E} {\min \{ {d(u,G)},{d(v,G)}\} } )$ is bounded by $O(\rho m)$, where $\rho$ is the arboricity of a graph G. Therefore, the time complexity of Algorithm 4 is $O(\rho m)$. $\square$

In addition, the space complexity of Algorithm 3 is $O(m+n)$, which is linear w.r.t. the graph size.

4.3 The new $\mathsf {ICPS}$ construction algorithm

As shown in the previous subsection, the time complexity of the basic $\mathsf {ICPS}$ construction algorithm is $O(k_{\max }(m+n))$ which is inefficient when the graph size and $k_{\max }$ are very large. Here, we propose a much more efficient algorithm to construct the $\mathsf {ICPS}$.

Recall that in Algorithm 3, the most time-consuming step is to generate all the tree vertices for all k. Thus, to reduce the time overhead, we strive to reduce the time cost of the tree vertices generation procedure. Unlike Algorithm 3 which creates all tree vertices following the increasing order of k (i.e., $k=1, \ldots , k_{\max }$), the key idea of our new algorithm is that it generates all tree vertices following the increasing order of node weights. Specifically, the new algorithm iteratively deletes the nodes following the increasing order of their weights. When the algorithm removes a node u in an iteration, the algorithm will generate the tree vertices containing u for all k. Thus, if all the nodes are deleted, all tree vertices are generated. After creating all tree vertices, the algorithm calls Algorithm 4 to build the $\mathsf {ICPS}$. The rationale behind the new algorithm is as follows. We observe in Algorithm 3 that for each k, all the tree vertices are generated based on the increasing order of node weights. Since all the tree generation procedures for $k=1, \ldots , k_{\max }$ share the same node order, we can simultaneously create all the tree vertices for all k by following this order.

The challenge of the new algorithm is how to correctly create the tree vertices for all k when deleting a node. Note that a node u with core number $c_u$ is included in $c_u$ different vertices in the trees with $k=1, 2, \ldots , c_u$, respectively. Thus, if u is deleted, the new algorithm must simultaneously creates $c_u$ different tree vertices. Since each tree vertex containing u may also include other nodes, the algorithm also needs to find these nodes and add them into the tree vertex that includes u. Furthermore, after deleting a node, the core numbers of some other nodes may be updated. Therefore, when the algorithm deletes node u, the current core number of u denoted by ${\tilde{c}}_u$ may not be the original $c_u$, as it may be updated after a node is deleted. This gives rise to a new challenge to devise such a tree vertices generation algorithm.

To overcome the above challenges, we develop an algorithm that can correctly create the tree vertices for all k when deleting a node. The idea of our algorithm is that when the algorithm deletes a node u in an iteration, it creates ${\tilde{c}}_u$ (i.e., the current core number of u) tree vertices and dynamically maintains the core numbers of the other nodes after deleting u. By an in-depth analysis of our algorithm, we can show that all the tree vertices containing u that are not created in this iteration have already been generated before deleting u. The detailed description of our algorithm is shown in Algorithm 5.

Algorithm 5 iteratively deletes the nodes by following the increasing order of their weights (line 5). In each iteration, the algorithm creates ${\tilde{c}}_u$ tree vertices when deleting u, where ${\tilde{c}}_u$ is the updated core number of node u (lines 6–7). Note that in Algorithm 5, the algorithm does not explicitly delete a node. Instead, the algorithm sets the core number of a node to $-1$, indicating that the node is deleted (line 8). After deleing a node, the algorithm calls Algorithms 6 and 7 to dynamically maintain the core numbers of the remaining nodes (lines 10–11). Notice that Algorithms 6 and 7 generalize the core maintenance algorithm independently proposed in [19, 23] to handle the case of node deletion². Here, we implement this core maintenance algorithm by dynamically updating the support of each node u (denoted by $x_u$), which is defined as the number of neighbors whose updated core numbers are no smaller than ${\tilde{c}}_u$. When the support of a node u is smaller than it’s current core number (i.e., $x_u < {\tilde{c}}_u$), the core number of u must be updated (lines 9–11 of Algorithm 6). Note that the core numbers of all the remaining nodes decrease by at most 1 after removing a node. In addition, after deleing a node u, the neighbor nodes of u with core numbers larger than ${\tilde{c}}_u$ may need to update their core number (line 4 of Algorithm 6). Moreover, in the core number maintenance procedure (Algorithm 6), the algorithm also needs to add the nodes whose core numbers are updated into the corresponding tree vertices (line 2 of Algorithm 6). The correctness of Algorithm 5 is shown in Theorem 9.

Theorem 9

Algorithm 5 correctly creates the $\mathsf {ICPS}$.

Proof

We prove the theorem by an induction argument. Denote by $\{v_1, v_2, \ldots , v_n\}$ a sorted node list where $w_i < w_j$ if and only if $1 \le i < j \le n$. When $i=1$ (the first iteration), Algorithm 5 processes node $v_1$ and creates $c_1={\tilde{c}}_1$ tree vertices for it, which are denoted by $S_1, \ldots , S_{c_1}$. Note that here $S_l$ ($l=1, \ldots c_1$) denotes the tree vertex included in the tree of $k=l$. When deleting $v_1$ (i.e., ${\tilde{c}}_1 \leftarrow -1$), the algorithm calls Algorithm 6 to maintain the core numbers of all the remaining nodes. For a node $v_l$ whose core number is updated by Algorithm 6, the algorithm adds $v_l$ to $S_{c_l}$. Note that by using a result proved in [19, 23], the core maintenance algorithm (Algorithms 6 and 7) is correct. Moreover, we know that when the algorithm deletes $v_1$, only the nodes whose core numbers are no larger than $c_1$ may be updated. Thus, there exists a tree vertex $S_{c_l}$, as $c_l \le c_1$. It remains to show that for each $S_{c_l}$, it is exactly the one that includes $v_1$ defined in our tree structure. Let us consider the maximal $c_l$-core. Clearly, $v_1$ is contained in that core, as $c_l \le c_1$. After the algorithm deletes $v_1$, in the maximal $c_l$-core, only the nodes whose core numbers have been updated are inserted into $S_{c_l}$. Note that this procedure is equivalent to a procedure of invoking DFS($v_1$) in Algorithm 3, and all the nodes deleted by DFS($v_1$) are added into $S_{c_l}$ in our case. Thus, $S_{c_l}$ is indeed the tree vertex that includes $v_1$ defined in our tree-shaped structure. For other $S_l$ ($l=1, \ldots , c_1$), we can get the same conclusion. As a result, when $i=1$, the algorithm correctly generates all tree vertices that contains node $v_1$. Second, we make an induction hypothesis that for all $j \le i$, the algorithm correctly generates all tree vertices that contains node $v_j$. Now, we prove that for $j=i+1$, the algorithm correctly creates all tree vertices including $v_{i+1}$. On the one hand, if ${\tilde{c}}_{i+1} = c_{i+1}$, by using a similar argument used to prove the case of $i=1$, we can get that the algorithm correctly creates all tree vertices including $v_{i+1}$. On the other hand, if ${\tilde{c}}_{i+1} < c_{i+1}$, the algorithm correctly generates the tree vertices $S_1, \ldots S_{{\tilde{c}}_{i+1}}$ that contains $v_{i+1}$ by using a similar argument used to prove the case of $i=1$. It remains to show that for the tree vertices $S_{{\tilde{c}}_{i+1} + 1}, \ldots , S_{c_{i+1}}$ including $v_{i+1}$ must be generated before deleting $v_{i+1}$. Note that by our algorithm, there must exist a node $v_l$ with $l < i+1$ such that when the algorithm deletes $v_l$, the core number of $v_{i+1}$ decreases from ${\tilde{c}}_{i+1} + 1$ to ${\tilde{c}}_{i+1}$. This implies that when the algorithm deletes $v_l$, $v_{i+1}$’s core number is updated; thus, $v_{i+1}$ must be inserted into a tree vertex of the tree of $k={\tilde{c}}_{i+1} + 1$ that also includes $v_l$. Since $l<i+1$, such a tree vertex must be correctly generated by the induction assumption. Clearly, such a tree vertex is indeed $S_{{\tilde{c}}_{i+1} + 1}$, as each node can only be included in one vertex of a tree. Similarly, for the case that the core number of $v_{i+1}$ decreases from ${\tilde{c}}_{i+1} + 2$ to ${\tilde{c}}_{i+1}+1$, we can derive that $S_{{\tilde{c}}_{i+1} + 2}$ is correctly created. Iteratively using this procedure, we can get a similar conclusion when the core number of $v_{i+1}$ decreases from $c_{i+1}$ to $c_{i+1}-1$. As a consequence, when $j=i+1$, the algorithm correctly creates all tree vertices including $v_{i+1}$.

$\square$

The following example illustrates how Algorithm 5 works.

Example 5

Consider the graph shown in Fig. 1. In the first iteration of Algorithm 5, the algorithm processes node $v_1$. Since ${\tilde{c}}_1=3$, the algorithm creates three tree vertices that include $v_1$, which is denoted by $S_1(v_1)$, $S_2(v_1)$, and $S_3(v_1)$, respectively (lines 6–7). Note that here $S_i(v_1)$ ($i=1, 2, 3$) denotes a tree vertex that belongs to the tree of $k=i$. Subsequently, the algorithm sets the core number of $v_1$ to $-1$, indicating that $v_1$ is deleted. Then, the algorithm invokes Algorithm 6 to update the core numbers of the remaining nodes. After invoking Algorithm 6, we can find that $v_2$ is inserted into the tree vertex $S_2(v_1)$, and $v_8$ is added into the tree vertex $S_3(v_1)$. Moreover, the core numbers of $v_2$ and $v_8$ are updated to 1 and 2 respectively. After that, all the tree vertices containing $v_1$ have been generated, which is consistent with the tree vertices shown in Table 1. In the second iteration, the algorithm continues to deal with node $v_2$ by following the increasing order of node weights. Since the current core number of $v_2$ is 1, in this iteration, the algorithm only creates one tree vertex $S_1(v_2)$ that contains $v_2$ (lines 6–7). Likewise, the algorithm sets the core number of $v_2$ to $-1$, denoting that $v_2$ is removed. Then, the algorithm calls Algorithm 6 to update the core numbers of the remaining nodes. After invoking Algorithm 6, we can see that no node needs to update its core number. Therefore, in this iteration, the algorithm generates only one tree vertex $S_1(v_2)$ that contains only one node $v_2$. Up to this iteration, all the tree vertices that includes $v_2$ is created. Other iterations are processed similarly. After processing all nodes, the algorithm correctly generates all tree vertices shown in Table 1. Finally, the algorithm calls Algorithm 4 to construct the $\mathsf {ICPS}$. $\square$

The time complexity of Algorithm 5 is shown in Theorem 10.

Theorem 10

The time complexity of Algorithm 5 is $O(\rho m)$, where $\rho$ is the arboricity of the graph.

Proof

First, in line 1, computing the core numbers for all nodes can be done in O(m). In lines 2–3, the algorithm takes O(m) time to initialize the support and the current core number for each node. Second, lines 6–7 and lines 12–13 take at most O(m) time cost for all node $u \in V(G)$ in total. The most time-consuming steps are lines 10–11, which invokes the core number maintenance algorithm. The time complexity analysis for these two steps is very tricky. Let us consider an edge (u, v). Assume without loss of generality that $c_u \le c_v$. When deleting u, then Algorithm 6 traverses all u’s neighbors (line 4 of Algorithm 6), as ${\tilde{c}}_u = -1$. Thus, to visit all neighbors for all the deleted nodes, the total time cost is O(m). However, when deleting u, the algorithm may also recursively visit the other nodes. For an edge (u, v), we first consider the node u. Note that u’s core number is updated at most $c_u$ times, because for each update, the core number decreases by 1. When the algorithm updates u’s core number, it traverses the edge (u, v) once (see line 4 of Algorithm 6), because ${\tilde{c}}_u \le c_u \le c_v$. Therefore, for updating the core number of u, the edge (u, v) will be traversed by Algorithm 5 at most $c_u$ times. On the other hand, we consider the node v. When the core number v is updated, the algorithm also traverses the edge (v, u) at most $c_u$ times. This is because the algorithm traverses the edge (v, u) only when ${\tilde{c}}_v \le c_u$ (line 4 of Algorithm 6), thus the number of visit of (v, u) is bounded by $c_u$. In summary, for each edge (u, v), Algorithm 5 traverses it at most $2 \times \min \{c_u, c_v\}$ times. As a result, for all nodes, the total time cost for invoking Algorithm 6 is bounded by $2 \sum \nolimits _{(u,v) \in E} {\min \{ {c_u},{c_v}\} } \leqslant 2 \sum \nolimits _{(u,v) \in E} {\min \{ {d(u,G)},{d(v,G)}\} } = O(\rho m)$. Note that to efficiently implement line 4 of Algorithm 6, for each node u, we can first sort all u’s neighbors in a decreasing order of their core numbers by using a bin-sort algorithm, which takes O(d(u, G)) time. Hence, for all nodes, the sort procedure takes O(m) time in total. Then, to visit every u’s neighbor v with ${\tilde{c}}_u \le c_v$ (line 4 of Algorithm 6), we can linearly scan the sorted neighbors until ${\tilde{c}}_u > c_v$. This procedure only traverses all the edges (u, v) that satisfy ${\tilde{c}}_u \le c_v$. By a similar analysis, the total time cost for invoking Algorithm 7 can be bounded by $2\sum \nolimits _{(u,v) \in E} {\min \{ {c_u},{c_v}\} } \leqslant 2 \sum \nolimits _{(u,v) \in E} {\min \{ {d(u,G)},{d(v,G)}\} } = O(\rho m)$. In addition, Algorithm 4 takes $O(\rho m)$ time. Putting it all together, the time complexity of Algorithm 5 is $O(\rho m)$.

$\square$

Remark 1

According to Chiba and Nishizeki [8], the arboricity of a graph is never larger than $O(\sqrt{m} )$ in the worst case, and it has shown to be very small in many real-world graphs [15, 20]. Thus, the time cost of Algorithm 5 is much lower than the worst-case bound, which is also confirmed in our experiments. $\square$

In addition, it is very easy to show that the space complexity of Algorithm 5 is $O(m+n)$.

4.4 Query processing algorithm

Based on the $\mathsf {ICPS}$, the query processing algorithm is straightforward. For Problem 1, to compute the top-r k-influential communities, the algorithm first finds the tree corresponding to k from the $\mathsf {ICPS}$ and then outputs the nodes in the top-r subtrees with the highest weights (the weight of a subtree is the minimum weight of nodes in its root vertex). This is because in our $\mathsf {ICPS}$, the nodes included in a subtree of the tree corresponding to k exactly form a k-influential community. Similarly, for Problem 2, the algorithm outputs nodes in the top-r leaf vertices with the highest weights in the tree corresponding to k, as the nodes in each leaf vertex form a non-containing k-influential community. The time complexity of the query processing algorithm for both Problems 1 and  2 is linear w.r.t. the answer size³; thus, it is optimal.

Discussions Our models and algorithms can also be extended to handle the edge-weighted graph, in which each edge (not the node) of the graph is associated a weight. Instead of iteratively deleting the smallest weight node, we can simply delete the smallest weight edge in each iteration to find the influential communities in the edge-weighted graph. Likewise, we can also extend our models and algorithms to directed graphs by using the generalized core model [3], which defines the k-core based on the in-degree or out-degree of a node in the directed graph. Since the generalized core model is very similar to k-core, all the techniques proposed in this paper can be easily extended to handle the generalized core case.

5 Update in the dynamic network

Many real-world networks are frequently updated. Clearly, when the network is updated, both the $\mathsf {ICPS}$ and the top-r results also need to be updated. The challenge is that a single edge insertion or deletion may trigger updates in a number of tree vertices of the $\mathsf {ICPS}$. This can be an expensive operation because the corresponding tree vertices need to be recomputed. For example, consider a graph shown in Fig. 1. After inserting an edge $(v_{10}, v_{11})$, the tree vertex $\{v_9,v_{10},v_{11}\}$ in the tree of $k=1$ (see Table 1) needs to be split into two tree vertices $\{v_9\}$ and $\{v_{10}, v_{11}\}$. In the tree of $k=2$, the two tree vertices $\{v_7, v_{10}\}$ and $\{v_8, v_9, v_{11}\}$ are updated by three tree vertices which are $\{v_7\}$, $\{v_8\}$, and $\{v_9, v_{10}, v_{11}\}$. In the tree of $k=3$, no update is needed. To overcome this challenge, we will propose an efficient algorithm for dynamically maintaining the tree vertices of the $\mathsf {ICPS}$ when the network is updated. Note that we can also efficiently answer the query by using the tree vertices only (without the tree structure). Specifically, we can first find the top-r tree vertices and then only search the neighbors of the nodes in the tree vertices to construct the answer (i.e., the tree structure is implicitly constructed online). It is easy to show that the time complexity of this algorithm is the same as the time complexity of the previous tree-based algorithm to construct the top-r results (include edges). Therefore, in this paper, we mainly focus on updating the tree vertices. Below, we consider two types of updates: edge insertion and edge deletion.

Before we proceed further, we define some useful and frequently used notations. Let $r_{\max }$ be the maximal r in the queries posed by the users. For example, we can set $r_{\max }=100,000$, because users typically are not interested in the results beyond top-100, 000. It should be noted that compared to a large $r_{\max }$ (e.g., $r_{\max }=100,000$), the pruning performance of our algorithm is much better when $r_{\max }$ is small (e.g., $r_{\max }=100$). In other words, our algorithm prefers a small $r_{\max }$. In the experiments, we will show that even for a large $r_{\max }=100,000$, our algorithm is still two orders of magnitude faster than the baseline algorithm. Therefore, we believe that setting $r_{\max }=100,000$ is sufficient in practice.

For convenience, we refer to the tree of $k=i$ in the $\mathsf {ICPS}$ as tree-i. Let ${{\tilde{r}}}_u$ be the rank of u in the sorted list of nodes with the increasing order by weights. For simplicity, we assume that the rank of a node is based on the property of the node itself, which is independent of edge updates. For each tree-i ($i=1,\ldots , k_{\max }$), we assign a time stamp for every tree vertex when it is generated by Algorithm 2. Here, the time stamp is an integer ranging from 1 to $n_i$, where $n_i$ denotes the number of vertices in tree-i. Note that by definition, a tree vertex with a large time stamp implies that the tree vertex has a large influence value. Denote by $R_u^{(i)}$ the time stamp of the tree vertex that contains node u in tree-i. For convenience, we also refer to $R_u^{(i)}$ as the time stamp of node u in tree-i when the definition is clear. Let ${{\tilde{r}}}_{\max }^{(i)}$ be the rank of the smallest weight node in the tree vertex with time stamp $n_i - r_{\max }+1$. For example, reconsider the graph shown in Fig. 1. We can see that ${{\tilde{r}}}_{v_9} = 9$. In tree-1, $R_{v_9}^{(1)} = 8$, because $v_9$ is included in the tree vertex $\{v_9, v_{10}, v_{11}\}$ whose time stamp is 8 (see Table 1). Assume that $r_{\max }=4$. Then, ${{\tilde{r}}}_{\max }^{(1)} = 9$, because in tree-1, the tree vertex with time stamp $n_1 - r_{\max }+1$ (equals 8) is $\{v_9, v_{10}, v_{11}\}$, where the rank of the smallest weight node ($v_9$) is 9.

5.1 Handling edge insertion

Here, we consider the case of inserting an edge (u, v). The straightforward method is to re-compute all tree vertices using Algorithm 5 when the graph is updated. Clearly, this method is inefficient for large graphs. Below, we first present two basic updating rules and then propose a minimum tree re-computation method to further reduce the computational cost for edge insertion.

The basic updating rules: we give two basic updating rules below.

Rule 1: let $c_{\min } \ = \min \{c_u, c_v\}$ (i.e., the minimum core number of u and v). Then, after inserting (u, v), every tree-i for $i > c_{\min } + 1$ will not be updated. This is because when inserting an edge, the core numbers of the nodes increase by at most one [19]. As a result, each i-influential community for $i>c_{\min }+1$ does not change, and thus, every tree-i remains unchanged.

Rule 2 (Lazy update): the key idea of the lazy update rule is that we only maintain the tree vertices when they affect the top-r results for $r \le r_{\max }$. Formally, we have the following lemma.

Lemma 4

For each tree-i ($i=1,\ldots , k_{\max }$), if ${{\tilde{r}}}_u < {{\tilde{r}}}_{\max }^{(i)}$ or ${{\tilde{r}}}_v < {{\tilde{r}}}_{\max }^{(i)}$, the tree vertices in the top-r results for $r \le r_{\max }$ keep unchanged when the graph is updated by inserting or deleting an edge (u, v).

Based on the above lemma, when inserting an edge (u, v), we first check the conditions ${{\tilde{r}}}_u < {{\tilde{r}}}_{\max }^{(i)}$ and ${{\tilde{r}}}_v < {{\tilde{r}}}_{\max }^{(i)}$. If one of them holds, we do not perform any update operation for the tree vertices in tree-i, because their updates do not affect the top-r results for $r \le r_{\max }$.

The minimum tree re-computation method Besides the basic updating rules, here we present a method which can achieve minimum tree re-computation when an edge is inserted. The method, as verified in our experiments, can largely reduce the computational cost for edge insertion even after Rules 1 and 2 are applied. Recall that after inserting an edge (u, v), all tree-i with $i > c_{\min } + 1$ do not change (by Rule 1); thus, we only need to update all tree-i with $i = 1, \ldots , c_{\min }+1$. Specifically, we consider two cases: (1) all tree-i with $i = 1, \ldots , c_{\min }$, and (2) tree-$(c_{\min } + 1)$.

For case (1), we let $l_w^{i}$ be the number of w’s neighbors whose time stamps are no less than w after inserting (u, v), i.e., $l_w^{i}= |\{x| x \in N(w, G) \wedge R_x^{(i)} \ge R_w^{(i)}\}|$. By this definition, $l_w^{i}$ denotes the degree of w in the i-core after deleting all nodes whose time stamps are smaller than w. We assume without loss of generality that $R_u^{(i)} \le R_v^{(i)}$ in tree-i. Let $IT_i[R_u^{(i)}]$ be the tree vertex containing u and ${\bar{u}}$ be the smallest weight node in $IT_i[R_u^{(i)}]$. After inserting (u, v), for each tree-i with $i = 1, \ldots , c_{\min }$ (case (1)), we study whether $IT_i[R_u^{(i)}]$ needs to be updated. To this end, we recover the procedure of generating the tree vertex $IT_i[R_u^{(i)}]$. In particular, we perform a similar DFS procedure as Algorithm 2 to recursively delete the nodes in $IT_i[R_u^{(i)}]$. Unlike Algorithm 2, here we use $l_w^{i}$ as the degree of node w, and the DFS procedure only traverses the nodes in $IT_i[R_u^{(i)}]$ and their neighbors as well. Similar to Algorithm 2, the DFS procedure initially traverses node ${\bar{u}}$. When a neighbor node of w for $w \in IT_i[R_u^{(i)}]$ is deleted, $l_w^{i}$ decreases by 1, and when $l_w^{i}$ is smaller than i, w is deleted. If node u is deleted when the DFS procedure terminates, the tree vertex $IT_i[R_u^{(i)}]$ does not need to be updated, and therefore, all tree vertices keep unchanged. The reason is as follows. First, the insertion of edge (u, v) does not affect the tree vertices with time stamps smaller than $R_u^{(i)}$. Second, if u is deleted, all the other nodes in $IT_i[R_u^{(i)}]$ must be deleted (by the definition of tree vertex), and thus, the tree vertex $IT_i[R_u^{(i)}]$ does not change. Third, if u is deleted, all u’s outgoing edges are also deleted, and thus, inserting the edge (u, v) does not affect the tree vertices with time stamps larger than $R_u^{(i)}$. On the other hand, if node u fails to be removed by the DFS procedure, then we re-compute all the tree vertices for tree-i. Below, we give a sufficient and necessary condition for updating the tree vertices in tree-i.

Lemma 5

For each tree-i with $i=1, \ldots , c_{\min }$, the tree vertices in tree-i need to be updated after inserting (u, v) ($R_u^{(i)} \le R_v^{(i)}$ ), if and only if u is not deleted by the DFS procedure.

Proof

First, by definition, if u is not deleted by the DFS procedure, the original vertex $IT_i[R_u^{(i)}]$ (before inserting the edge (u, v)) in tree-i that includes u must be revised, as u is no longer in that tree vertex. Therefore, tree vertices in tree-i need to be updated. Second, suppose that there exists a tree vertex in tree-i that is updated. Then, the tree vertex including u must be updated. This is because if the original tree vertex $IT_i[R_u^{(i)}]$ including u does not update, no tree vertex in tree-i will be updated after inserting (u, v). Assume to the contrary that u is deleted by the DFS procedure, then all the other nodes in $IT_i[R_u^{(i)}]$ must be removed by definition, and thus, $IT_i[R_u^{(i)}]$ does not update, which is a contradiction. $\square$

By Lemma 5, a sufficient and necessary condition for updating the tree vertices in tree-i is that u is not deleted by the DFS procedure. Thus, our algorithm, which is based on such a sufficient and necessary condition, is optimal in the sense that the number of tree re-computations by our algorithm is minimum.

For case (2) (tree-$(c_{\min } + 1)$), if u or v’s core number is updated, we use Rule 2 to update the tree vertices in tree-$(c_{\min } + 1)$. Otherwise, no update is needed.

The algorithm for handling edge insertion is depicted in Algorithm 8, which integrates both the basic updating rules and the minimum tree re-computation method. In lines 4–5 and lines 9–10, we use Rule 2 for updating. In lines 6–7, we apply the minimum tree re-computation method to update the tree vertices. In the main loop (line 3), we use Rule 1 for updating. In lines 11–17, the procedure IsRecompute is used to determine whether u (assume $R_u^{(i)} \le R_v^{(i)}$) is deleted by the DFS procedure (InsertionDFS, lines 18–24) or not. Note that in the InsertionDFS procedure, we set $l_u^k = -1$ to denote that u is deleted. The correctness of Algorithm 8 can be guaranteed by Lemma 4 and Lemma 5. The time complexity for checking the tree re-computation conditions in Algorithm 8 (line 6) is $O(\sum \nolimits _{i=1} ^{c_{\min }}{\sum \nolimits _{u \in IT[R_u^{(i)}] } {{d_u}}})$. In the experiments, we will show that our algorithm is at least four orders of magnitude faster than the straightforward re-computation based algorithm in large graphs.

5.2 Handling edge deletion

Consider the case of deleting an edge (u, v). Similarly, we have two basic updating rules. First, for Rule 1, each tree-i with $i>c_{\min }$ ($c_{\min }=\min \{c_u, c_v\}$) will not be updated after deleting an edge (u, v), because all i-influential communities for $i>c_{\min }$ remain unchanged after removing (u, v). Second, for Rule 2, we can also use Lemma 4 to handle the edge deletion case. To further improve the efficiency, we also propose a minimum tree re-computation method. For each tree-i with $i=1, \ldots , c_{\min }$, we let $l_w^{i}$ be the number of w’s neighbors whose time stamps are no less than w after deleting (u, v), i.e., $l_w^{i}= |\{x| x \in N(w, G) \wedge R_x^{(i)} \ge R_w^{(i)}\}|$. Below, we give a sufficient and necessary condition for updating the tree vertices.

Lemma 6

For each tree-i with $i=1, \ldots , c_{\min }$, the tree vertices in tree-i need to be updated after deleing (u, v), if and only if $l_u^{i} < i$ or $l_v^{i} < i$.

Proof

First, if $l_u^{i} < i$ or $l_v^{i} < i$ after deleting (u, v), the number of neighbors of u (or v) that are deleted after u (or v) by the DFS algorithm is smaller than i, and thus, u (or v) cannot be in the i-core after deleting all the nodes with time stamps smaller than $R_u^{(i)}$ (or $R_v^{(i)}$). This result implies that the time stamp of u (or v) after deleting (u, v) must be smaller than the original time stamp $R_u^{(i)}$ (or $R_v^{(i)}$); thus, the tree vertex in tree-i must be updated. Second, suppose that there exists a tree vertex in tree-i that is updated, then the tree vertex including u (i.e., $IT_i[R_u^{(i)}]$) must be updated. Suppose to the contrary that $l_u^{i} \ge i$ and $l_v^{i} \ge i$ after deleting (u, v). Then, u and v must be in the i-core after deleting all the nodes with time stamps smaller than $R_u^{(i)}$ and $R_v^{(i)}$. This result implies that all the tree vertices does not change after deleting (u, v), which is a contradiction. $\square$

Based on Lemma 6, we can use $l_u^{i}$ and $l_v^{i}$ to determine whether the tree vertices in tree-i need to be updated. The algorithm for handling edge deletion is outlined in Algorithm 9, which integrates both the basic updating rules and the minimum tree re-computation method. In lines 4–5, we use Rule 2 for updating, and in lines 6–8, we use the minimum tree re-computation method to update the tree vertices. In the main loop (line 3), we use Rule 1 for updating. The time complexity for checking all re-computation conditions in Algorithm 9 (lines 6–7) is $O(d_u+d_v)$. In addition, it is worth mentioning that both Algorithms 8 and 9 do not increase the space complexity for top-r k-influential communities search.

Remark 2

Recall that in our algorithm, we assume that the rank of the nodes does not change when the edges update. In some real-world applications, when the edges of the graph frequently update, the weights of the nodes may also update. Fortunately, this issue does not largely affect our algorithm. The reasons are as follows. First, our algorithm relies on the rank (not the weight) of the node. Thus, even if the weight of a node is updated, its rank may not change. Second, even when the rank of a node is updated, if it is not in the top-r results, we also do not need to update the results based on the lazy update rule. Third, if a node in the top-r results and its rank is updated, we can use the following reduction to reduce this case to a series of edge updating. Specifically, we can first delete the node whose weight is updated and then add the same node with the updated weight into the graph. Note that the node deletion and insertion can be transformed to a series of edge deletions and insertions. As a result, we can also use our algorithm to handle this case.

6 The I/O efficient algorithm

In this section, we develop an I/O-efficient algorithm for the influential community search problem when the network cannot be completely stored in the main memory. We assume that all the nodes of a network, and the top-r results can be kept in the memory, i.e., the memory size (${\mathcal {U}}$) is at least O(n). This assumption is reasonable in practice, and it is also widely adopted in semi-external memory algorithms to handle massive graph data [32, 33]. For example, in the well-known SNAP⁴ datasets (including 79 real-world networks), the largest network consists of 64 million nodes, and it contains 1.8 billion edges. In the well-known KONET⁵ datasets (including 230 real-world networks), the largest network contains 68 million nodes and 2.6 billion edges. Clearly, in these massive networks, the main memory of a typical PC (e.g., 8GB main memory) can accommodate all the nodes but not all edges. On the other hand, devising an algorithm for the influential community search problem under this assumption is a nontrivial task, because we cannot access all the edges in the main memory, and thus, all our algorithms proposed in the previous sections cannot work under this setting. Below, we will develop an interesting algorithm to tackle this challenge.

Recall that all the influential communities can be organized by a tree-shaped structure where each influential community is represented by a tree vertex (as shown in Fig. 2). Therefore, to solve the influential community search problem, the key is to compute the corresponding tree vertices for all influential communities. Below, we devise a sequential algorithm, which is I/O-efficient, to compute all the tree vertices for a given k value.

The key idea of the sequential algorithm is that it computes the tree vertices following the decreasing order of their weights, and the tree vertices (as well as the edges in the corresponding influential communities) with large weights can be safely deleted without affecting the correctness of the algorithm to compute the tree vertices with small weights. Specifically, we let $w(e)=\min \{w_u, w_v\}$ be the weight of an edge $e=(u, v)$. The algorithm first sorts the edges in a non-increasing order of their weights using the standard external memory sort algorithm (we can use the node ID to break ties). Then, following this order, the algorithm loads the edges into the main memory up to the memory limit. Subsequently, the algorithm invokes Algorithm 2 to compute the influential communities in the main memory (and thus obtains the tree vertices). After that, the algorithm deletes the computed influential communities as well as the associated edges from the main memory and then sequentially loads new edges into the main memory until reaches the memory limit. The algorithm iteratively performs this procedure until all the edges are scanned. Note that in each iteration, the algorithm only works on a partial graph, which is loaded in the main memory. To guarantee the correctness, we use an array, called deposit, to dynamically record the number of associated edges that are deleted from each node. Let ${\underline{d}} _u$ be the degree of a node u in the partial graph, called partial degree of node u, and ${{\tilde{d}}}_u$ be the effective degree of a node u such that ${{\tilde{d}}}_u={\underline{d}} _u + deposit(u)$. Then, in each iteration, we use the effective degree to compute the k-core and the influential communities in Algorithm 2. In each iteration, when we delete the computed influential communities and their associated edges, we update the deposit array. It should be noted that the deposit array is kept in the main memory, because the memory size is at least O(n) by our assumption. The detailed description of the algorithm is depicted in Algorithm 10. Note that in Algorithm 10, we use $\mathcal {M}$ to denote the set of edges that are loaded into the memory (line 6). In each iteration, the algorithm works on the partial graph generated by the edges $\mathcal {M}$ and invokes Algorithm 2 to compute the influential communities (also tree vertices) in the main memory (lines 5–11). The following example illustrates how the algorithm works.

Table 2 Running example of Algorithm 10 ($k=2$, $|\mathcal {M}| \le 10$)

Example 6

Let us reconsider the graph shown in Fig. 1. Assume that $k=2$ and the memory can hold at most 10 edges (except for storing all the nodes and the deposit array), i.e., $|\mathcal {M}| \le 10$. The detailed running procedure is shown in Table 2 and Fig. 3.

Initially, the deposit array is set to be a zero array. In the first iteration, the top-10 edges (with the highest w(e)) are loaded into the memory. The corresponding partial graph in the memory is depicted in Fig. 3a). The states of the ${\underline{d}}$ array (partial degree) and ${{\tilde{d}}}$ array (effective degree) are shown in Table 2 (the top part). Based on the effective degree, the algorithm computes the influential communities on the partial graph in the main memory. Clearly, in this iteration, the algorithm obtains three influential communities, and the corresponding tree vertices are $\{v_{13}, v_{14}, v_{15}\}$, $\{v_{12}\}$, and $\{v_8, v_9, v_{11}\}$ (see Table 2). After computing the tree vertices, the algorithm removes all the edges in the influential communities. It is easy to verify that all the edges except for $(v_9, v_{10})$ are deleted from the memory in this iteration. Then, the algorithm updates the deposit array. The updated deposit array is shown in Table 2. For instance, $deposit(v_9)=2$, because there are two edges (i.e., $(v_8, v_9)$ and $(v_9, v_{11})$) associated with $v_9$ that are deleted.

In the second iteration, the algorithm loads 9 new edges into the memory, as there is already an edge $(v_9, v_{10})$ in the memory. The partial graph is shown in Fig. 3b. The partial degree and effective degree of all the nodes are given in Table 2 (the middle part). Note that for each node, the effective degree is equal to its current partial degree plus the updated deposit value in the first iteration. For example, ${\tilde{d}}_{v_9}=4$, because ${\underline{d}}_{v_9}=2$ and $deposit(v_9)=2$ (the updated deposit value in the first iteration). In this iteration, the algorithm gets three tree vertices which are $\{v_7, v_{10}\}$, $\{v_6\}$, and $\{v_3, v_4, v_5\}$. Finally, the algorithm deletes the edges in the influential communities and updates the deposit array (see Table 2). In this iteration, all the 10 edges are deleted.

In the third iteration, the algorithm loads all the remainder 6 edges into the memory. The results are shown in Fig. 3c and Table 2 (the bottom part). The procedure is very similar to the first and second iterations; thus, we omit the details for brevity. $\square$

Fig. 3

Partial graphs in the memory ($k=2$, $|\mathcal {M}| \le 10$)

Analysis of the algorithm First, we analyze the I/O cost of Algorithm 10. In line 2, the algorithm needs to sort the edges of the graph; thus, the I/O cost is O(sort(m)), where O(sort(m)) denotes the I/O cost of the $\mathsf {External}$-$\mathsf {Sort}$ algorithm. In lines 4–11, the algorithm only needs to scan the graph once; thus, the I/O cost is O(m / B), where B denotes the block size. Therefore, the I/O cost the algorithm is O(sort(m)). Second, we analyze the correctness of the algorithm. Suppose that the algorithm can successfully terminate. Then, the following theorem shows that the algorithm is correct.

Theorem 11

If Algorithm 10 successfully terminates, the algorithm correctly finds the influential communities and the corresponding tree vertices for a given k.

Proof

Since the algorithm computes the influential communities following the decreasing order of their weights, the deletion of the influential communities with high weights does not affect the algorithm to compute the influential communities with low weights based on the effective degree of nodes. Assume that the edge (u, v) has weight $w_0$, and it is the last edge that is loaded into the memory in the i-th iteration. Let ${\tilde{G}}_{\ge w_0}$ be a graph such that all the edges with weights smaller than $w_0$ are deleted (here we assume that the weights of the edges form a total order; otherwise, we can use the node ID to break the ties). By definition, it is easy to check that the effective degree for any node u in the i-th iteration is equal to the degree of u in ${\tilde{G}}_{\ge w_0}$. Thus, in the i-th iteration, the influential community $H^k$ computed in the partial graph is the same as the influential community computed in ${\tilde{G}}_{\ge w_0}$. Clearly, adding any edge with weight smaller than $w_0$ into ${\tilde{G}}_{\ge w_0}$ does not affect the influential community $H^k$; thus, $H^k$ is also the influential community in G. The above arguments hold for any iteration. Consequently, any influential community found by the algorithm must be a correct influential community in G. On the other hand, it is easy to show that any influential community $H^k$ in G will be found by the algorithm when the smallest weight edge in $H^k$ is loaded into the memory. Put it all together, we conclude that the theorem holds. $\square$

It should be noted that when $|\mathcal {M}|$ (the maximal number of edges that can be kept in memory) is very small, the algorithm may fail to terminate. This is because in a certain iteration, the partial graph in $\mathcal {M}$ may not contain any influential community, and thus, no edge can be deleted in this iteration, which makes the algorithm fail to terminate. However, by our assumption, the memory size is at least O(n); thus, $|\mathcal {M}|$ can be as large as O(n) without violating the assumption. In other words, the algorithm can hold a partial graph with size O(n) in the memory. In most real-world networks, any O(n)-size partial graph typically contains an influential community. Therefore, under these assumptions, the algorithm can successfully terminate for most real-world graphs. With Theorem 11, the algorithm can correctly compute the influential communities as well as the corresponding tree vertices. In our experiments, we set the maximal memory size only to be 3GB (including store all nodes and the deposit array), and Algorithm 10 can correctly calculate all the influential communities for all k values on the graphs with more than one billion edges.

Armed with Algorithm 10, we can devise both online search and $\mathsf {ICPS}$-based algorithms for finding the top-r k-influential communities (and non-containing k-influential communities). Specifically, for the online search algorithm, we can invoke Algorithm 10 with a parameter k, and the algorithm can early terminate if there are r k-influential communities that are outputted. This is because the algorithm calculates the k-influential communities following the decreasing order by their weights. For the $\mathsf {ICPS}$-based algorithm, we can invoke Algorithm 10 $k_{\max }$ times to compute the $\mathsf {ICPS}$. Clearly, the worst-case I/O cost for constructing the $\mathsf {ICPS}$ is $O(sort(m)+k_{\max }\times m/B)$. To speed up the query processing, we can compute the core number for each node using the fast I/O-efficient core decomposition algorithm [29]. Let $c(e)=\min \{c_u, c_v\}$ be the core number of an edge. We sort the edges in a non-decreasing order by their core numbers using the $\mathsf {External}$-$\mathsf {Sort}$ algorithm. For a query with parameters k and r, we first load the top-r tree vertices into memory and then sequentially load the associated edges whose core numbers are no smaller than k into the memory to generate the influential communities (since the edges are sorted, we can sequentially load the edges). Both the online search and $\mathsf {ICPS}$-based algorithms can be easily modified to find the top-r non-containing k-influential communities. In Algorithm 10, we can use the deposit array to determine the tree vertex if it corresponds to a non-containing influential community. Specifically, in an iteration, if the deposit values (before updating) of all the nodes in that tree vertex are 0, then the tree vertex corresponds to a non-containing influential community. This is because no edge associated with those nodes is deleted; thus, the tree vertex must be a leaf vertex in the tree of the $\mathsf {ICPS}$, which corresponds to a non-containing influential community.

Comparison with Algorithm 2 Clearly, Algorithm 10 is correct when the graph is completely contained in the main memory. Assume that the edges are previously sorted; then, the time complexity of the algorithm is $O(m+n)$, which is the same as the DFS-based algorithm (Algorithm 2). Also, the space complexity of the algorithm is $O(m+n)$. Compared to Algorithm 2 (which works in a top-down manner), Algorithm 10 computes the tree vertices following in a bottom-up manner, which first computes the tree vertices with higher weights followed by the tree vertices with lower weights.

7 Performance studies

We conduct extensive experiments to evaluate the proposed algorithms. To construct the $\mathsf {ICPS}$, we implement both the basic (Algorithm 3) and the new (Algorithm 5) algorithms, denoted by $\mathsf {Basic}$ and $\mathsf {New}$ respectively. For query processing, we implement four algorithms, named $\mathsf {Online}$-$\mathsf {All}$, $\mathsf {Online}$-$\mathsf {NCT}$, $\mathsf {ICPS}$-$\mathsf {All}$, and $\mathsf {ICPS}$-$\mathsf {NCT}$, respectively. $\mathsf {Online}$-$\mathsf {All}$ and $\mathsf {Online}$-$\mathsf {NCT}$ are the DFS-based online search algorithms (Algorithm 2) which are used to compute the top-r k-influential communities and the top-r non-containing k-influential communities, respectively; similarly, $\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$ are the $\mathsf {ICPS}$-based algorithms used to compute the top-r k-influential communities and the top-r non-containing k-influential communities, respectively. Note that we do not implement the basic online search algorithm (Algorithm 1), as it is impractical for many real-world graphs. All algorithms are implemented in C++. All experiments are conducted on a computer with 3.46GHz Intel Xeon X5690 (6-core) CPU and 96GB memory running Red Hat Enterprise Linux 6.4 (64-bit). Unless otherwise specified, in all experiments, both the graph and the $\mathsf {ICPS}$ are resident in the main memory. We will evaluate the I/O-efficient algorithms in Sect. 7.2, where the graph is resident in the disk.

Datasets. We use six web-scale real-world graphs in our experiments. The detailed statistics of our datasets are shown in Table 3. The first five datasets in Table 3 are downloaded from (http://law.di.unimi.it/datasets.php), and the FriSter dataset is downloaded from (http://snap.stanford.edu). Among the six graphs, UK, Arabic, WebBase, and SK are web graphs, and Twitter and FriSter are social networks.

Parameters. In all the experiments, without otherwise specified, we use the PageRank score of node u to denote its weight, as PageRank is a widely used model to measure the influence (or importance) of the nodes. For each dataset, we vary 4 parameters: r (denoting the parameter of top-r), k (denoting the parameter of k-influential community), the percentage of nodes n, and the percentage of edges m. The range of the parameters and their default values are shown in Table 4. When varying m (or n) for scalability testing, we extract subgraphs of $20\%$, $40\%$ $60\%$, $80\%$ and $100\%$ edges (or nodes) of the original graph with a default value of $100\%$, using the uniform random edge sampling algorithm (random node sampling). When varying a certain parameter, the values for all the other parameters are set to their default values.

Table 3 Datasets

Table 4 Parameters

7.1 Testing main memory algorithms

$\mathsf {ICPS}$ Construction We build the $\mathsf {ICPS}$ for six graphs using both $\mathsf {Basic}$ and $\mathsf {New}$. The $\mathsf {ICPS}$ construction time is shown in Fig. 4a. $\mathsf {New}$ is 5–10 times faster than $\mathsf {Basic}$ in all datasets. Moreover, we can see that $\mathsf {New}$ is very efficient which takes only 1,477 s (<25  min) in the Twitter dataset (more than 1 billion edges and 41 million nodes). This is because $\mathsf {New}$ can avoid computing influential communities for all k values one by one, which saves much computational cost. The result is also consistent with the theoretical analysis shown in Theorems 8 and  10. We further compare the size of the $\mathsf {ICPS}$ with the size of the original graph. The results are depicted in Fig. 4b. Over all the datasets, the sizes of $\mathsf {ICPS}$ are almost the same as the size of the original graph. This result confirms the theoretical analysis shown in Theorem 6.

Query processing (Vary k ). We vary k from 2 to 256 and evaluate the query processing time for the four proposed algorithms by fixing $r=40$. The results are reported in Fig. 5. In all datasets, when k increases, the processing time of $\mathsf {Online}$-$\mathsf {All}$ and $\mathsf {Online}$-$\mathsf {NCT}$ decreases. This is because when k increases, the size of the maximal k-core decreases, and the time complexity of $\mathsf {Online}$-$\mathsf {All}$ and $\mathsf {Online}$-$\mathsf {NCT}$ is dominated by traversing the maximal k-core. Instead, when k increases, the processing time of both $\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$ increases. This is because when k increases, the size of the top-r results increases, and thus it takes more time to calculate the top-r results for both $\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$. When k is small, $\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$ is several orders of magnitude faster than $\mathsf {Online}$-$\mathsf {All}$ and $\mathsf {Online}$-$\mathsf {NCT}$, respectively. When k is large, the advantages of $\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$ are not significant. The reason is that, when k increases, the time cost for traversing the k-core decreases, while the time spent on outputting the top-r results increases. For instance, in UK, when the core number increases to 256, the time overhead for outputting the top-r results dominates the whole query processing time for all algorithms. Thus, the processing time of all the algorithms are similar.

Fig. 4

$\mathsf {ICPS}$ testing. a $\mathsf {ICPS}$ construction time, b $\mathsf {ICPS}$ size

Fig. 5

Query processing testing (Vary k) a UK (vary k), b Arabic (vary k), c WebBase (vary k) d Twitter (vary k), e SK (vary k), f FriSter (vary k)

Fig. 6

Query processing testing (Vary r). a UK (vary r), b Arabic (vary r), c WebBase (vary r), d Twitter (vary r), e SK (vary r), f FriSter (vary r)

Fig. 7

Scalability testing ($\mathsf {ICPS}$ construction time). a Twitter (vary m), b Twitter (vary n), c SK (vary m), d SK (vary n), e FriSter (vary m), f FriSter (vary n)

Query processing (Vary r ) We vary the parameter r from 5 to 320 and evaluate the query processing time of the four algorithms by fixing $k=16$. The results are shown in Fig. 6. Over all datasets, we can see that the processing time of all the algorithms increases with increasing r. For $\mathsf {Online}$-$\mathsf {All}$ and $\mathsf {Online}$-$\mathsf {NCT}$, the processing time increases very slowly. This is because for both $\mathsf {Online}$-$\mathsf {All}$ and $\mathsf {Online}$-$\mathsf {NCT}$, the dominant cost is spent on traversing the maximal k-core other than outputting the top-r results. For $\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$, when r is small, the processing time increases slowly. However, when r is large, the processing time of $\mathsf {ICPS}$-$\mathsf {All}$ increases while the processing time of $\mathsf {ICPS}$-$\mathsf {NCT}$ still keeps stable. The reason is that when r increases, the size of the r-th answer in the top-r results for the $\mathsf {ICPS}$-$\mathsf {All}$ algorithm tends to increase. Thus, when r is large, a large number of redundant subgraphs are outputted in the top-r results. For $\mathsf {ICPS}$-$\mathsf {NCT}$, when r increases, the size of the r-th answer in the top-r results does not significantly increase; thus, the processing time of $\mathsf {ICPS}$-$\mathsf {NCT}$ keeps stable. For example, in the FriSter dataset, when r increases to 320, the processing time of $\mathsf {ICPS}$-$\mathsf {All}$ approaches the processing time of $\mathsf {Online}$-$\mathsf {NCT}$ and $\mathsf {Online}$-$\mathsf {All}$, indicating that a large number of redundant subgraphs are computed in $\mathsf {ICPS}$-$\mathsf {All}$. However, in this case, $\mathsf {ICPS}$-$\mathsf {NCT}$ is still very efficient, which is four orders of magnitude faster than $\mathsf {ICPS}$-$\mathsf {All}$.

Scalability for $\mathsf {ICPS}$ construction We vary the number of edges (m) and nodes (n) in Twitter, SK, and FriSter datasets to study the scalability of the $\mathsf {ICPS}$ construction algorithms: $\mathsf {Basic}$ and $\mathsf {New}$. The results are reported in Fig. 7. As can be seen, both $\mathsf {Basic}$ and $\mathsf {New}$ scale near linearly in most datasets. Moreover, we can see that $\mathsf {New}$ is around one order of magnitude faster than $\mathsf {Basic}$, which is consistent with the previous observations. In addition, we also report the scalability results for the $\mathsf {ICPS}$ size in Fig. 8. We can see that the $\mathsf {ICPS}$ size is nearly the same as the graph size over all testing cases, which confirms the theoretical analysis shown in Sect. 4.

Fig. 8

Scalability testing ($\mathsf {ICPS}$ size). a Twitter (vary m), b Twitter (vary n), c SK (vary m), d SK (vary n), e FriSter (vary m), f FriSter (vary n)

Fig. 9

Scalability testing (Query processing time). a Twitter (vary m), b Twitter (vary n), c SK (vary m) d SK (vary n), e FriSter (vary m), f FriSter (vary n)

Scalability for query processing. We vary the number of edges (m) and nodes (n) in Twitter, SK, and FriSter datasets to evaluate the scalability of the proposed query processing algorithms. Fig. 9 depicts the results. As desired, the query processing time for the online search algorithms ($\mathsf {Online}$-$\mathsf {All}$ and $\mathsf {Online}$-$\mathsf {NCT}$) increases with increasing graph size. However, for the $\mathsf {ICPS}$-based algorithms ($\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$), the query processing time does not significantly increase when the graph size increases. The reason is that the processing time of $\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$ are mainly dependent on the size of the top-r communities, and the size of the top-r communities is not largely affected by the size of the graph. As a result, in all testing cases, $\mathsf {ICPS}$-$\mathsf {All}$ and $\mathsf {ICPS}$-$\mathsf {NCT}$ are at least one order of magnitude faster than $\mathsf {Online}$-$\mathsf {All}$ and $\mathsf {Online}$-$\mathsf {NCT}$, respectively.

Table 5 Update time per edge (in seconds)

Dynamic update In this experiment, we evaluate the efficiency of the proposed $\mathsf {ICPS}$ updating algorithms. We compare three algorithms which are $\mathsf {Ba}$, $\mathsf {Ne}$, and $\mathsf {Recompute}$. $\mathsf {Ba}$ is the algorithm using two basic updating rules; $\mathsf {Ne}$ is the algorithm using both two basic updating rules and the minimum tree re-computation method (Algorithms 8 and 9); $\mathsf {Recompute}$ is the straightforward updating algorithm which uses Algorithm 5 to re-compute all tree vertices when the graph is updated by an edge insertion/deletion. In all testings, we set $r_{\max }=100,000$. For each dataset, we randomly delete 1K edges, and update the $\mathsf {ICPS}$ after every deletion, and then, we insert the same 1K edges and update the $\mathsf {ICPS}$ after every insertion. The average update time per edge insertion/deletion is reported in Table 5. From Table 5, we can make the following observations. Compared to $\mathsf {Recompute}$, $\mathsf {Ba}$ can significantly reduce the cost of maintaining the tree vertices. For example, in WebBase, $\mathsf {Ba}$ only takes 0.5 s to maintain all the tree vertices for either insertion or deletion, while $\mathsf {Recompute}$ requires more than 330 s. However, only applying the basic updating rules may be still inefficient. For example, in Twitter, $\mathsf {Ba}$ needs more than 60 s for each edge insertion/deletion which is inefficient. $\mathsf {Ne}$, however, can significantly cut the updating time of $\mathsf {Ba}$ by applying the minimum tree re-computation method. For instance, in the Twitter dataset, by using $\mathsf {Ne}$, the updating time for an edge insertion/deletion is reduced from 66.5/64.9 s to 0.035/0.001 s. For $\mathsf {Ne}$, handling edge deletion is more efficient than handling edge insertion, because checking the re-computation condition for edge insertion needs to invoke a DFS procedure (see Algorithm 8). In general, we can see that the updating time of $\mathsf {Ne}$ is several orders of magnitude faster than the straightforward re-computation based method ($\mathsf {Recompute}$) over all datasets, which confirms the theoretical analysis in Sect. 5.

7.2 Testing I/O efficient algorithms

In this subsection, we test the performance of our I/O efficient algorithms. We set the maximum available memory used for each algorithm to be 3 GB for all tests in this subsection. We choose the largest four datasets WebBase, Twitter, SK, and FriSter in Table 3 for testing. To load the entire graph in memory, the four datasets require 6.37 , 8.96 , 13.49 , and 13.46 GB memory, respectively. Therefore, all the main memory algorithms cannot be used to process this four graphs with the limited 3 GB memory. We use $\mathsf {Online}$-$\mathsf {All}$+, $\mathsf {Online}$-$\mathsf {NCT}$+, $\mathsf {ICPS}$-$\mathsf {All}$+, and $\mathsf {ICPS}$-$\mathsf {NCT}$+ to denote the I/O-efficient versions for algorithms $\mathsf {Online}$-$\mathsf {All}$, $\mathsf {Online}$-$\mathsf {NCT}$, $\mathsf {ICPS}$-$\mathsf {All}$, and $\mathsf {ICPS}$-$\mathsf {NCT}$, respectively, all of which are based on the Algorithm 10.

$\mathsf {ICPS}$ Construction performance The $\mathsf {ICPS}$ construction performance of the I/O-efficient algorithm on the four datasets WebBase, Twitter, SK, and FriSter are shown in Fig. 10. Specifically, Fig. 10a shows the results for $\mathsf {ICPS}$ construction time and Fig. 10b shows the results for the number of I/Os. As desired, the $\mathsf {ICPS}$ construction time and I/Os of the algorithm roughly increases with increasing graph size. As an exception, Twitter requires more $\mathsf {ICPS}$ construction time and I/Os than SK, which is larger than Twitter. This is because when k increases, the size of the k-core in Twitter reduces slowly than the size of the k-core in SK, which results in the high $\mathsf {ICPS}$ construction time and I/Os in Twitter.

Fig. 10

$\mathsf {ICPS}$ testing for the I/O-efficient algorithm. a $\mathsf {ICPS}$ construction time, b $\mathsf {ICPS}$ construction I/Os

Query processing time (Vary k ) The testing results of query processing time for $\mathsf {Online}$-$\mathsf {All}$+, $\mathsf {Online}$-$\mathsf {NCT}$+, $\mathsf {ICPS}$-$\mathsf {All}$+, and $\mathsf {ICPS}$-$\mathsf {NCT}$+ when varying k are shown in Fig. 11. As can be seen, the query processing time of $\mathsf {ICPS}$-$\mathsf {All}$+ ($\mathsf {ICPS}$-$\mathsf {NCT}$+) consumes around 1 second over all the datasets, and it is two orders of magnitude faster than $\mathsf {Online}$-$\mathsf {All}$+ ($\mathsf {Online}$-$\mathsf {NCT}$+). Generally, the performance of all the algorithms are not largely influenced by k. The results in SK (Fig. 11 c and FriSter (Fig. 11 d are similar to those in WebBase and Twitter, respectively, because SK and WebBase are both web graphs with similar graph properties and FriSter and Twitter are both social networks with similar graph properties. These results confirm the efficiency of the proposed algorithms.

Fig. 11

Query processing time for I/O efficient algorithms (Vary k). a WebBase (vary k), b Twitter (vary k), c SK (vary k), d FriSter (vary k)

Query processing I/Os (Vary k ) The results of the number of I/Os consumed by $\mathsf {Online}$-$\mathsf {All}$+, $\mathsf {Online}$-$\mathsf {NCT}$+, $\mathsf {ICPS}$-$\mathsf {All}$+, and $\mathsf {ICPS}$-$\mathsf {NCT}$+ when varying k are shown in Fig. 12. Since the results in four datasets are similar, we mainly analyze the results in the WebBase dataset. Specifically, from Fig. 12a, we can see that the I/O costs of $\mathsf {Online}$-$\mathsf {All}$+ and $\mathsf {Online}$-$\mathsf {NCT}$+ are robust with varying k. However, the I/O consumptions of $\mathsf {ICPS}$-$\mathsf {All}$+ and $\mathsf {ICPS}$-$\mathsf {NCT}$+ are unstable when k increases. This is because the number of I/Os consumed by $\mathsf {ICPS}$-$\mathsf {All}$+ and $\mathsf {ICPS}$-$\mathsf {NCT}$+ depends on the size of the top-r communities, which is unstable when k increases. Additionally, we can observe that $\mathsf {ICPS}$-$\mathsf {All}$+ ($\mathsf {ICPS}$-$\mathsf {NCT}$+) consumes 100 to 1000 times less I/Os than $\mathsf {Online}$-$\mathsf {All}$+ ($\mathsf {Online}$-$\mathsf {NCT}$+), which further confirms that the $\mathsf {ICPS}$-based algorithms are much more efficient than the online search algorithms.

Query processing time (Vary r ) In this experiment, we test the query processing time for $\mathsf {Online}$-$\mathsf {All}$+, $\mathsf {Online}$-$\mathsf {NCT}$+, $\mathsf {ICPS}$-$\mathsf {All}$+, and $\mathsf {ICPS}$-$\mathsf {NCT}$+ when varying r. The results are shown in Fig. 13. From Fig. 13, we can see that the query processing time of $\mathsf {Online}$-$\mathsf {All}$+ and $\mathsf {Online}$-$\mathsf {NCT}$+ are robust with varying r in all datasets. This is because the top-r results can be computed by $\mathsf {Online}$-$\mathsf {All}$+ and $\mathsf {Online}$-$\mathsf {NCT}$+ when loading the same set of edges into the memory. In the social network datasets (Twitter and FriSter), $\mathsf {Online}$-$\mathsf {All}$+ is much more efficient than $\mathsf {Online}$-$\mathsf {NCT}$+. This is because, in social networks, the tree structure of all the influential communities may be very high, and thus finding the top-r non-containing k-influential communities (the leaves of the tree) requires to load a large number of edges into the memory. As desired, the $\mathsf {ICPS}$-based algorithms ($\mathsf {ICPS}$-$\mathsf {All}$+ and $\mathsf {ICPS}$-$\mathsf {NCT}$+) are much more efficient than the online search algorithms ($\mathsf {Online}$-$\mathsf {All}$+ and $\mathsf {Online}$-$\mathsf {NCT}$+). These results are consistent with our previous results.

Fig. 12

Query processing I/Os for I/O efficient algorithms (Vary k). a WebBase (vary k), b Twitter (vary k), c SK (vary k), d FriSter (vary k)

Note that in FriSter (Fig. 13d, the query processing time of $\mathsf {ICPS}$-$\mathsf {All}$+ is even faster than that of $\mathsf {ICPS}$-$\mathsf {All}$ shown in Fig. 6f. This is because in $\mathsf {ICPS}$-$\mathsf {All}$+, we obtain the set of edges of the top-r communities by computing the corresponding induced subgraphs in the k-core of the original graph, which is kept in the disk. However, in $\mathsf {ICPS}$-$\mathsf {All}$, we obtain the set of edges of the top-r communities by computing the induced subgraphs directly from the original graph in the memory. Since the size of the k-core is typically much smaller than the size of the original graph and the set of top-r k-influential communities may largely overlap, computing the induced subgraphs from the k-core can avoid large redundant computational costs compared to computing the induced subgraphs from the original graph.

Query processing I/Os (Vary r ). In this experiment, we test the I/O cost for $\mathsf {Online}$-$\mathsf {All}$+, $\mathsf {Online}$-$\mathsf {NCT}$+, $\mathsf {ICPS}$-$\mathsf {All}$+, and $\mathsf {ICPS}$-$\mathsf {NCT}$+ when varying r. The testing results are shown in Fig. 14. The curves for the number of I/Os in all datasets are consistent with those for the processing time shown in Fig. 13, respectively. Specifically, similar to the results for query processing time, the I/O cost of $\mathsf {Online}$-$\mathsf {All}$+ and $\mathsf {Online}$-$\mathsf {NCT}$+ are robust with varying r in all datasets. As desired, when r increases, the I/O overhead for $\mathsf {ICPS}$-$\mathsf {All}$+ and $\mathsf {ICPS}$-$\mathsf {NCT}$+ increases. $\mathsf {ICPS}$-$\mathsf {All}$+ ($\mathsf {ICPS}$-$\mathsf {NCT}$+) is much more efficient than $\mathsf {Online}$-$\mathsf {All}$+ ($\mathsf {Online}$-$\mathsf {NCT}$+) for various r values over all datasets. For example, in FriSter (Fig. 14 d, $\mathsf {ICPS}$-$\mathsf {NCT}$+ is four orders of magnitude more I/O-efficient than $\mathsf {Online}$-$\mathsf {NCT}$+. These results further confirm the efficiency of the proposed algorithms.

Fig. 13

Query processing time for I/O efficient algorithms (Vary r). a WebBase (vary r), b Twitter (vary r), c SK (vary r) d FriSter (vary r)

Fig. 14

Query processing I/Os for I/O efficient algorithms (Vary r). a WebBase (vary r), b Twitter (vary r), c SK (vary r), d FriSter (vary r)

Fig. 15

Case study: results for different k and r. a top-1 for $k=4$, b top-2 for $k=4$, c top-3 for $k=4$, d top-1 for $k=6$, e top-2 for $k=6$, f top-3 for $k=6$, g top-1 for $k=8$, h top-2 for $k=8$, i top-3 for $k=8$, j top-1 for $k=10$, k top-2 for $k=10$, l top-3 for $k=10$

7.3 Case studies

We use a co-authorship network extracted from ArnetMiner (http://arnetminer.org) for case studies. The dataset consists of authors in different research areas including database, data mining, semantic web, machine learning, information retrieval, Bayesian network, and so on. The graph contains 5411 nodes and 17,477 edges. Each author (node) is associated with a label, denoting the research area of that author. Based on this dataset, we conduct three various case studies to evaluate the effectiveness of the k-influential community model.

Results for different k and r. In this case study, we use the number of publications to denote the weight of an author. We vary k from 4 to 10 and generate the top-3 non-containing k-influential communities for each k value. The results are depicted in Fig. 15. As can be seen, for a certain k, the top results of the non-containing k-influential communities tend to cover high influential researchers in different research areas. For example, when $k=4$, the top-1 result includes high-influential researchers in database area, the top-2 result contains high-influential researchers in data mining area, and the top-3 result consists of high-influential researchers in semantic web area. The researchers in each community are highly connected with each other, and each of them plays an leading role in the specific research area. These results indicate that the k-influential community model is indeed capable of capturing both influence and cohesiveness of a community.

In addition, we can see that the parameter k can balance the trade-off between influence and cohesiveness of a community. In general, the influence value of a community decreases with increasing k. For instance, comparing Fig. 15a with Fig. 15d, when k increases from 4 to 6, some high influential researchers such as “H. V. Jagadish” and “Beng Chin Ooi” leave the community, while some other researchers are added into the community, forming a more cohesive but relatively lower influential community. The reason is that when k increases, the cohesiveness constraint in the k-influential community model becomes more strict, which may exclude some high influential nodes from the community and thus may reduce the influence of the community. For a practical recommendation, if the user wants to find a high influential community, a small k is preferred, while if the user aims at finding a high cohesive but relatively low influential community, a large k is preferred.

Fig. 16

Top-3 results using labels for weights ($k=6$). a top-1 (ML), b top-2 (IR), c top-3 (BN)

Fig. 17

Four truss communities containing “Jiawei Han.” a $C_1$, b $C_2$, e $C_3$, d $C_4$

Fig. 18

Comparison with truss community ($k=4$, $r=1, 2, \ldots , 6$)

Using labels for weights In this case study, we use the labels for weights to study the effectiveness of the k-influential community model. Specifically, we first give different weights for different labels. Then, we rank the nodes based on the weights, and break ties based on the number of publications. Fig. 16 reports the results for $k=6$ given that the weights of different labels are ranked as “Machine Learning (ML)” > “Information Retrieval (IR)” > “Bayesian Network (BN),” and so on. Similar results can also be observed for different k values (e.g., $k=8$) and different weighting methods. From Fig. 16, we can see that the top-3 results are consistent with our weighting method (the top-1 result is a “Machine Learning” community, the top-2 result is a “Information Retrieval” community, and the top-3 result is a “Bayesian Network” community). These results suggest that the k-influential community model can also capture user-specified definition of influence. In practice, the users can define the influence based on their preferences, and our proposed methods can be applied to identify the influential communities based on user-defined influence.

Comparison with truss community Here, we compare the proposed community model with the truss community model [16], which is successfully applied to find query-dependent cohesive communities in a large network. Here, a k-truss is the maximal subgraph in which each edge is contained in at least $k-2$ triangles. For a fair comparison, we compare the k-influential community with the $k+1$ truss community. This is because a $k+1$ truss is a k-core [27], and our k-influential community is based on k-core. Below, we consider the case when $k=4$. Similar conclusions can also be made for other k values. Fig. 17 depicts four 5-truss communities containing “Jiawei Han.” From Fig. 17, we can see that the 5-truss communities mainly contains professor Jiawei Han’s students or research fellows. However, in our 4-influential community model, professor Jiawei Han’s community (see Fig. 15b) includes many other influential researchers in data mining area who have a co-author relationship with “Jiawei Han.” The reason is that the k-truss community only captures the cohesiveness of a community, while our k-influential community not only captures the cohesiveness, but it also considers the influence of a community.

We also perform a user study to compare our model with the k-truss community. To this end, we recruit ten first-year graduate students (majoring in computer science) from Shenzhen University in China as human raters to rate the resulting communities. All the ten human raters are aware of the research on community detection and search. For each resulting community, each rater is asked to give two integer scores from 0 to 5 to evaluate the cohesiveness and influence of the community, respectively (the higher score means a better community). The detailed instruction can be found in (http://www1.se.cuhk.edu.hk/~rhli/paper/Instruction_vldbj.pdf) due to space limit. The resulting score is obtained by taking the average score over all 10 scores given by the 10 raters. We fix $k=4$ and similar results can also be observed for other k values. We first find the top-r communities obtained by our model, denoted by $H_1, \ldots , H_r$. Then, for each node u in $H_i$ ($i=1, \ldots , r$), we find the $k+1$-truss community that contains u. Since we may generate a set of $k+1$ truss communities for each $H_i$, we take the average cohesiveness and influence scores as the scores of the $k+1$-truss community. Then, we compare the cohesiveness and influence scores of $H_i$ with the average scores of the corresponding $k+1$-truss community. Fig. 18 depicts the results. As can be seen, the cohesiveness scores of our model and the k-truss community model are comparable, whereas the influence scores of our model are significantly higher than those of the k-truss community model with different r. These results further confirm that our model is much better than the k-truss community model to capture both the cohesiveness and the influence of a community.

8 Related work

Community search and discovery Sozio et al. [25] studied the community search problem in social networks where the goal is to find the maximal connected k-core with maximal k value that contains the query nodes. In [25], the authors proposed a linear time algorithm to solve the community search problem. Recently, Cui et al. [12] proposed a more efficient local search algorithm for the same problem. Except the maximal k-core-based model, Cui et al. [11] proposed an $\alpha$-adjacency $\gamma$-quasi-k-clique model to study the overlap community search problem. More recently, Huang et al. [16] studied the community search problem based on a k-truss community model. In addition, another related but different problem is community discovery, which is to discover all the communities in a network. This issue is extensively studied in the literature. Two surveys on this topic can be found in [13, 30]. All the mentioned work do not consider the influence of a community. In our preliminary work [18], we studied the influential community search problem and proposed several efficient algorithms to find the most influential communities in a network. In the present work, we substantially extend our previous work. In particular, we develop a novel I/O-efficient algorithm (under the assumption of ${{\mathcal {U}}}=O(n)$) for the influential community search problem when the graph cannot be stored in the main memory. We conduct comprehensive I/O testings to evaluate the proposed I/O-efficient algorithm, and the results demonstrate the efficiency of our algorithm.

Cohesive subgraph mining Cohesive subgraph is an important concept in social network analysis. There are many different definitions of cohesive graphs in the literature, which consists of maximal clique [6, 7], k-core [5, 19, 24], k-truss [9, 27], DN-graph [28], maximal k-edge connected subgraph [1, 4, 35], and so on. Due to a large number of applications, the cohesive subgraph mining problem has attracted much attention in recent years. For example, James et al. proposed a series of external memory algorithms for finding and enumerating maximal clique [6, 7], and for k-core [5] and k-truss [27] decomposition in massive graphs. Interestingly, many equivalent concepts of k-truss were independently proposed in different papers. For instance, in [22], Saito and Yamada termed the k-truss k-dense community, and this term was also followed in [14]; In [26], k-truss is termed k-brace; In [31], Zhang and Parthasarathy termed the k-truss triangle k-core, and in [34], Zhao and Tung termed the k-truss k-mutual-friend subgraph. DN-graph was proposed in [28] which is closely related k-truss. Unlike k-truss, the problem of mining the DN-graphs is NP-hard. The maximal k-edge connected subgraph (MkCS), also called structural cohesion in sociology [21], is typically more cohesive than k-core and k-truss. Recently, several efficient algorithms were proposed to compute the MkCS. For instance, in [35], Zhou et al. proposed several pruning techniques to speed up the MkCS mining algorithm. In [4], Chang et al. presented a linear time algorithm based on a graph decomposition framework. In [1], Akiba et al. proposed a linear time randomized algorithm for the same problem based on a random edge contraction technique.

9 Conclusion

We study a problem of finding the top-r influential communities in a network. We propose a new community model called k-influential community to capture the influence of a community. To find the top-r k-influential communities efficiently, we propose a linear time online search algorithm and an optimal $\mathsf {ICPS}$-based algorithm. The $\mathsf {ICPS}$ (influential community-preserved structure) only takes linear space, and can be constructed efficiently. We also develop an efficient algorithm to maintain the $\mathsf {ICPS}$ when the network is frequently updated. Additionally, we devise an I/O-efficient algorithm to find the top-r k-influential communities in a disk-resident graph under the assumption of ${{\mathcal {U}}}=O(n)$. Finally, extensive experiments on six web-scale real-world networks demonstrate the efficiency and effectiveness of our algorithms. For a future direction, it would be interesting to develop a distributed or parallel algorithm to compute the $\mathsf {ICPS}$. Since the proposed algorithm is a sequential algorithm, it is very difficult to generalize it to the distributed or parallel setting. We believe that devising such a distributed or parallel algorithm requires new techniques, which deserves to further investigate.