Piecewise Continuous Stepanov-Like Almost Automorphic Functions with Applications to Impulsive Systems

Abstract

In this chapter, we discuss Stepanov-like almost automorphic function in the framework of impulsive systems. Next, we establish the existence and uniqueness of such solution of a very general class of delayed model of impulsive neural network. The coefficients and forcing term are assumed to be Stepanov-like almost automorphic in nature. Since the solution is no longer continuous, so we introduce the concept of piecewise continuous Stepanov-like almost automorphic function. We establish some basic and important properties of these functions and then prove composition theorem. Composition theorem is an important result from the application point of view. Further, we use composition result and fixed point theorem to investigate existence, uniqueness and stability of solution of the problem under consideration. Finally, we give a numerical example to illustrate our analytical findings.

4.1 Introduction

The introduction of almost periodic functions (AP) by H. Bohr [11] in the year 1924–1925 led to various important generalizations of this concept. One important generalization is the concept of almost automorphic function (AA) given by S. Bochner [10]. This concept is further generalized to several other concepts out of which one important generalization is the concept of Stepanov-like almost automorphic function introduced by N’Guérékata and Pankov [21]. Several authors have discussed several classes of almost automorphic functions and their extensions with application to differential equations [13, 14, 20]. It has been observed that one of the natural questions in the field of differential equations is: if the forcing function possesses a special characteristic, then whether the solution possesses the same characteristic or not? Motivated by this many researchers have studied the existence of Stepanov-like almost automorphic solutions of differential equations (see, for example, [14, 20] and the references therein). While studying the behaviour of many physical and biological phenomena, it has been observed that many phenomenons exhibit regularity behaviour which is not exactly periodic. These kind of phenomenons can be modelled by considering more general notions such as almost periodic, almost automorphic, or Stepanov-like almost automorphic. We have the following inclusion AP ⊂ AA _u ⊂ AA ⊂ BC, where AA _u stands for uniformly almost automorphic and BC is the space of bounded and continuous functions. If we consider the class of Stepanov-like almost automorphic, then it covers more functions than almost automorphic functions. So, if the underlying behaviour of the systems is not almost automorphic, it may be possible that it is Stepanov-like almost automorphic or it belongs to other more general class of functions. For more work on Stepanov-like almost automorphic and its generalizations, we refer to [2, 4, 15, 16] and the references therein.

Impulsive differential equations involve differential equations on continuous time interval as well as difference equations on discrete set of times. It provides a real framework of modelling the systems, which undergo through abrupt changes like shocks, earthquake, harvesting, etc. Recent years have seen tremendous work in this area due to its applicability in several fields. There are few excellent monographs and literatures on impulsive differential equations [7,8,9, 19, 24]. As we know that impulses are sudden interruptions in the systems, in neural case, we can say that these abrupt changes are in the neural state. Its effect on humans will depend on the intensity of the change. In signal processing, the faulty elements in the corresponding artificial network may produce sudden changes in the state voltages and thereby affect the normal transient behaviour in processing signals or information. Neural networks have been studied extensively, but the mathematical modelling of dynamical systems with impulses is very recent area of research [1, 3, 5, 6, 25,26,27,28,29,30,31].

To the best of our knowledge, the existences, uniqueness and stability of Stepanov-like almost automorphic solution of impulsive differential equations is rarely discussed. In this work, we introduce piecewise continuous Stepanov-like almost automorphic function. We prove composition theorem, which is very important result. As an application we study the existence, uniqueness and stability of Stepanov-like almost automorphic solution of the following impulsive delay differential equations arising from neural network modelling,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dx_{i}(t)}{dt} &\displaystyle =&\displaystyle \sum_{j=1}^{n}a_{ij}(t)x_{j}(t)+\sum_{j=1}^{n}\alpha _{ij}(t)f_{j}(x_{j}(t)) + \sum_{j=1}^{n}\beta _{ij}(t)f_{j}(x_{j}(t-\alpha ))\notag \\ &\displaystyle +&\displaystyle \gamma _{i}(t),\quad t \neq t_k,\ \alpha >0, \notag \\ \Delta (x(t_k)) &\displaystyle =&\displaystyle A_{k}x(t_k)+I_{k}(x(t_k))+\gamma _{k}, \notag \\ x(t_k-0) &\displaystyle =&\displaystyle x(t_k),\quad x(t_k+0)=x(t_k)+\Delta x(t_k), \quad k \in \mathbb{Z},\ t\in \mathbb{R}, \notag \\ x(t) &\displaystyle =&\displaystyle \Psi _{0}(t),\quad t\in \lbrack -\alpha ,0], {} \end{array} \end{aligned} $$

(4.1.1)

where $a_{ij},\alpha _{ij},\beta _{ij},f_{j},\gamma _{i}\in \mathcal {C}(\mathbb {R},\mathbb {R})$ for i = 1, 2, ⋯ , n, j = 1, 2, ⋯ , n. The coefficient $A_{k}\in \mathbb {R}^{n\times n},$ the function $I_{k}(x)\in \mathcal {C}(\Omega ,\mathbb {R}^{n})$ and the constant $\gamma _{k}\in \mathbb {R}^{n}.$ The symbol Ω denotes a domain in $\mathbb {R}^{n}$ and $\mathcal {C}(X,Y)$ denotes the set of all continuous functions from X to Y.

The organization of this work is as follows: In Sect. 4.2, we give some basic definitions and results. In Sect. 4.3, we establish composition theorem. In Sect. 4.4, we study existence and stability of piecewise continuous Stepanov-like almost automorphic solutions of impulsive differential equations with delay. In Sect. 4.5, we present an example with numerical simulation.

4.2 Preliminaries

Throughout the manuscript, the symbol $\mathbb {R}^n$ denotes the n dimensional space with norm $\|x\|=\max \{|x_i|;i=1,2,\cdots ,n\}.$ We denote $PC(\mathbb {J}, \mathbb {R}^n),$ space of all piecewise continuous functions from $J \subset \mathbb {R}$ to $\mathbb {R}^n$ with points of discontinuity of first kind t _k where it is left continuous.

For smooth reading of the manuscript, we first define the following class of spaces,

• $S^{p}AA_{pc}(\mathbb {R}, \mathbb {R}^n) = \Big \{\phi \in PC(\mathbb {R}, \mathbb {R}^n): \phi \ \mbox{is a piecewise continuous Stepanov-} \ \\ \quad \quad \ \mbox{like almost automorphic function} \ \Big \}$

• $S^{p}AA_{pc}(\mathbb {R}\times \mathbb {R}^n, \mathbb {R}^n) = \Big \{\phi \in PC(\mathbb {R}\times \mathbb {R}^n, \mathbb {R}^n): \phi \ \mbox{is a piecewise continuous } \ \\ \quad \quad \ \mbox{Stepanov-like almost automorphic function} \ \Big \}$

• $S^{p}AAS(\mathbb {Z}, \mathbb {R}) = \Big \{\phi :\mathbb {Z}\rightarrow \mathbb {R}: \phi \ \mbox{is a Stepanov-like almost automorphic } \ \\ \quad \quad \ \mbox{sequence} \ \Big \}$

Note that the definition of almost automorphic operator is given by N’Gu$\acute {e}$r$\acute {e}$ kata and Pankov [22]. Now we give the following definitions in the framework of impulsive systems motivated by the work of [12, 17, 28].

Definition 4.2.1 ([18])

A function $f \in PC(\mathbb {R},\mathbb {R}^{n})$ is called a PC-almost automorphic if

• (i) sequence of impulsive moments {t _k} is an almost automorphic sequence,

• (ii) for every real sequence (s _n), there exists a subsequence $(s_{n_k})$ such that $g(t)=\lim _{n\to \infty }f(t+s_{n_k})$ is well defined for each $t\in \mathbb {R}$ and $\lim _{n\to \infty }g(t-s_{n_k})=f(t)$ for each $t\in \mathbb {R}.$

We denote $AA_{pc}(\mathbb {R},\mathbb {R}^{n})$ the set of all such functions.

Definition 4.2.2 ([18])

A function $f \in PC(\mathbb {R}\times \mathbb {R}^{n},\mathbb {R}^{n})$ is called PC-almost automorphic in t uniformly for x in compact subsets of X if

• (i) sequence of impulsive moments {t _k} is an almost automorphic sequence,

• (ii) for every compact subset K of X and every real sequence (s _n), there exists a subsequence $(s_{n_k})$ such that $g(t,x)=\lim _{n\to \infty }f(t+s_{n_k},x)$ is well defined for each $t\in \mathbb {R}$, x ∈ K and $\lim _{n\to \infty }g(t-s_{n_k},x)=f(t,x)$ for each $t\in \mathbb {R}$, x ∈ K.

We denote $AA_{pc}(\mathbb {R}\times \mathbb {R}^{n},\mathbb {R}^{n})$ the set of all such functions.

Definition 4.2.3

A sequence of continuous functions, $I_k: \mathbb {R}^{n} \to \mathbb {R}^{n}$ is almost automorphic, if for integer sequence $\{k_n^{\prime } \}$, there exist a subsequence {k _n} such that $\lim _{n\to \infty }I_{(k+k_n)}(x) = I_k^*(x)$ and $\lim _{n\to \infty }I_{(k-k_n)}^*(x) = I_k(x)$ for each k and x ∈ X.

Definition 4.2.4

A bounded sequence $x:\mathbb {Z}^+ \to \mathbb {R}^{n}$ is called an almost automorphic sequence, if for every real sequence $(k_{n}^{\prime })$, there exists a subsequence (k _n) such that y(k) =lim_n→∞x(k + k _n) is well defined for each $m\in \mathbb {Z}$ and lim_n→∞y(k − k _n) = x(k) for each $k\in \mathbb {Z}^+$. We denote $AAS(\mathbb {Z}, \mathbb {R}^{n}),$ the set of all such sequences.

Definition 4.2.5 ([23])

The Bochner transform f ^b(t, s), $t\in \mathbb {R}$, s ∈ [0, 1] of a function $f: \mathbb {R} \to \mathbb {R}^{n}$ is defined by f ^b(t, s) := f(t + s).

Definition 4.2.6 ([23])

Let p ∈ [1, ∞). The space $BS^p(\mathbb {R}^{n})$ of all Stepanov bounded functions, with the exponent p, consists of all measurable functions f on $\mathbb {R}$ with values in $\mathbb {R}^{n}$ such that $f^b\in L^\infty \big (\mathbb {R}, L^p((0,1), d\tau )\big )$. This is a Banach space when it is equipped with the norm defined by

$$\displaystyle \begin{aligned}\|f\|{}_{S^p}=\|f^b\|{}_{L^\infty(\mathbb{R},L^p)} =\sup_{t\in\mathbb{R}}\Big(\int_t^{t+1}\|f(\tau)\|{}^p\,d\tau\Big)^{1/p}.\end{aligned}$$

Definition 4.2.7

A bounded piecewise continuous function $f \in PC(\mathbb {R}, \mathbb {R}^n)$ is called a piecewise continuous Stepanov-like almost automorphic if

• (i) sequence of impulsive moments {t _k} is a Stepanov-like almost automorphic sequence,

• (ii) for every real sequence (s′ _n), there exists a subsequence (s _n) such that

  $$\displaystyle \begin{aligned} \lim_{n\to\infty}\left(\int_0^1\|f(t+s_n+s)-g(t+s)\|{}^pds\right)^{\frac{1}{p}} = 0 \end{aligned}$$

  is well defined for each $t\in \mathbb {R}$ and

  $$\displaystyle \begin{aligned} \lim_{n\to\infty}\left(\int_0^1\|g(t-s_n+s)-f(t+s)\|{}^pds\right)^{\frac{1}{p}} = 0 \end{aligned}$$

  for each $t\in \mathbb {R}$.

The space of all such functions is denoted by $S^{p}AA_{pc}(\mathbb {R}, \mathbb {R}^n)$.

Definition 4.2.8

A bounded piecewise continuous function $f \in PC(\mathbb {R}\times \mathbb {R}^n, \mathbb {R}^n)$ is called a piecewise continuous Stepanov-like almost automorphic in t uniformly in x in compact subsets of $\mathbb {R}^n$ if

• (i) the sequence of impulsive moments {t _k} is a Stepanov-like almost automorphic sequence,

• (ii) for every compact subset K of $\mathbb {R}^n$ and every real sequence (s′ _n), there exists a subsequence (s _n) such that

  $$\displaystyle \begin{aligned} \lim_{n\to\infty}\left(\int_0^1\|f(t+s_n+s,x)-g(t+s,x)\|{}^pds\right)^{\frac{1}{p}} = 0 \end{aligned}$$

  is well defined for each $t\in \mathbb {R}$ and

  $$\displaystyle \begin{aligned} \lim_{n\to\infty}\left(\int_0^1\|g(t-s_n+s,x)-f(t+s,x)\|{}^pds\right)^{\frac{1}{p}} = 0 \end{aligned}$$

  for each $t\in \mathbb {R}$.

The space of all such functions is denoted by $S^{p}AA_{pc}(\mathbb {R}\times \mathbb {R}^n, \mathbb {R}^n).$

Definition 4.2.9

A bounded sequence $x:\mathbb {Z}^+ \to \mathbb {R}^n$ is called Stepanov-like almost automorphic if for every real sequence (k′ _n), there exists a subsequence (k _n) and a sequence $y:\mathbb {Z}^+ \to \mathbb {R}^n$ such that

$$\displaystyle \begin{aligned} \left(\sum_{n=0}^1\|x(m+n_k+n)-y(m+n)\|{}^p\right)^{\frac{1}{p}} \to 0 \ \mbox{as} \ k \to 0 \end{aligned}$$

is well defined for each $m\in \mathbb {Z}$ and

$$\displaystyle \begin{aligned} \left(\sum_{n=0}^1\|y(m-n_k+n)-x(m+n)\|{}^p\right)^{\frac{1}{p}} \to 0 \ \mbox{as} \ k \to 0 \end{aligned}$$

for each $m\in \mathbb {Z}^+.$

We denote $S^{p}AAS(\mathbb {Z}^+,\mathbb {R}^n),$ the set of all such sequences.

We finish this section by defining few examples of Stepanov-like almost automorphic functions below.

• (i) Consider $x=(x_n)_{n\in \mathbb {Z}},$ an almost automorphic sequence and the function:

  $$\displaystyle \begin{aligned} a(t)= \begin{cases} x_n,\quad t \in (n-\epsilon,n+\epsilon), n \in \mathbb{Z}, \\ 0, \quad \ \mbox{otherwise} \ \end{cases} \end{aligned}$$
• (ii)
  $$\displaystyle \begin{aligned} b(t)= \begin{cases} \sin \Big(\frac{1}{2+\sin{}(n)+\sin{}(\sqrt{2}n)}\Big),\quad t \in \left(n-\frac{1}{4},n+\frac{1}{4}\right), n \in \mathbb{Z}, \\ 0, \quad \ \mbox{otherwise} \ \end{cases} \end{aligned}$$
• (iii)
  $$\displaystyle \begin{aligned} c(t)= \begin{cases} \cos \Big(\frac{1}{2+\cos{}(n)+\cos{}(\sqrt{2}n)}\Big),\quad t \in \left(n-\frac{1}{4},n+\frac{1}{4}\right), n \in \mathbb{Z}, \\ 0, \quad \ \mbox{otherwise} \ \end{cases} \end{aligned}$$

4.3 Composition Theorem

Lemma 4.3.1

Let $I_k: \mathbb {R}^n \to \mathbb {R}^n$ be a sequence of Stepanov-like almost automorphic functions and $K \subset \mathbb {R}^n$ be a compact subset. If I _k satisfies Lipschitz condition on $\mathbb {R}^n$ , i.e.

$$\displaystyle \begin{aligned} \|I_k(x)-I_k(y)\| \le L\|x-y\|, \forall x, y \in \mathbb{R}^n, \forall k, \end{aligned}$$

then the sequence {I _k(x) : x ∈ K} is Stepanov-like almost automorphic.

Proof

Since I _k is Lipschitz continuous over a compact set K, its range is also compact. Hence every sequence $I_{k+k_n}(x)$ has a convergent subsequence. So using the fact that I _k is Stepanov almost automorphy, the Stepanov almost automorphy of I _k(x) for x ∈ K is ensured. □

Lemma 4.3.2

Let $I_k: \mathbb {R}^n \to \mathbb {R}^n$ be a sequence of Stepanov-like almost automorphic functions and $\phi \in S^{p}AA_{pc}(\mathbb {R},\mathbb {R}^n).$ If I _k satisfies Lipschitz condition on $\mathbb {R}^n$ , i.e.

$$\displaystyle \begin{aligned} \|I_k(x)-I_k(y)\| \le L\|x-y\|, \forall x, y \in \mathbb{R}^n, \forall k, \end{aligned}$$

then the sequence {I _k(ϕ(t _k))} is Stepanov-like almost automorphic.

Proof

Since I _k is a sequence of Stepanov-like almost automorphic functions, there exists $I_k^*$ such that $I_{k+k_n}(x(t_{k}))\rightarrow I_{k}^*(x(t_{k}))$ and $I^*_{k-k_n}(x(t_{k}))\rightarrow I_{k}(x(t_{k})).$ By the above property and Lipschitz continuity of I _k, we obtain

$$\displaystyle \begin{aligned} \|I_{k+k_n}(x(t_{k+k_n}))-I_{k}^*(x(t_{k}))\| & \le \|I_{k+k_n}(x(t_{k+k_n}))-I_{k+k_n}(x(t_{k}))\| \\ &+ \|I_{k+k_n}(x(t_{k}))-I_{k}^*(x(t_{k}))\| \\ & \le L\|x(t_{k+k_n})-x(t_{k})\| \\ & + \|I_{k+k_n}(x(t_{k}))-I_{k}^*(x(t_{k}))\|. {} \end{aligned} $$

(4.3.1)

Using Lemma 4.3.1 and the above expression (4.3.1), the sequence {I _k(ϕ(t _k))} is Stepanov-like almost automorphic. □

Lemma 4.3.3

If $f, f_1, f_2 \in S^{p}AA_{pc}(\mathbb {R},\mathbb {R}^n),$ then the following are true:

• (i) $f_1+f_2 \in S^{p}AA_{pc}(\mathbb {R},\mathbb {R}^n),$

• (ii) $cf \in S^{p}AA_{pc}(\mathbb {R},\mathbb {R}^n)$for any scalar c,

• (iii) $f_a(t)-f(t+a) \in S^{p}AA_{pc}(\mathbb {R},\mathbb {R}^n)$ for any $a \in \mathbb {R},$

• (iv) $R_f=\{f(t): t \in \mathbb {R}\}$ is relatively compact.

Proof

Proof of (i), (ii), (iii) is obvious from definition of Stepanov-like almost automorphic function. For the proof of (iv) consider a sequence f(t + s′ _n) ∈ R _f, then using definition of Stepanov-like almost automorphic function, there exists a function g such that $\lim _{n\to \infty }(\int _0^1\|f(t+s_n+s,x)-g(t+s,x)\|ds)^{\frac {1}{p}} = 0.$ And hence R _f is relatively compact. □

Now we prove our main result of this section.

Lemma 4.3.4 (Composition Theorem)

Let $f\in S^{p}AA_{pc}(\mathbb {R}\times \mathbb {R}^n,\mathbb {R}^n)$ is uniformly continuous with respect to x on any compact subset of $\mathbb {R}^n.$ If $\phi \in S^{p}AA_{pc}(\mathbb {R},\mathbb {R}^n),$ then $f(\cdot , \phi (\cdot ))\in S^{p}AA_{pc}(\mathbb {R},\mathbb {R}^n).$

Proof

From the assumption f is uniformly continuous with respect to x on any compact subset of $\mathbb {R}^n, i.e.$ for 𝜖 > 0, there exists δ > 0 such that ∥x − y∥ < δ ⇒∥f(⋅, x) − f(⋅, y)∥ < 𝜖.

Also, the range of function ϕ is relatively compact, i.e. $K=\overline {\{\phi (t): t \in \mathbb {R}\}}$ is compact and hence there exists a finite number of open balls O _k, k = 1, 2, ⋯ , n centred at $x_k \in \{\phi (t): t \in \mathbb {R}\}$ with radius δ such that

$$\displaystyle \begin{aligned} \{\phi(t): t \in \mathbb{R}\} \subset \cup_{k=0}^nO_k \end{aligned}$$

Define B _k such that

$$\displaystyle \begin{aligned} B_k=\{s \in \mathbb{R}: \phi(s) \in O_k\}, \mathbb{R} =\cup_{k=0}^nB_k \end{aligned}$$

and set

$$\displaystyle \begin{aligned} E_1=B_1, E_k=B_k/\cup_{j=1}^{k-1}B_j \end{aligned}$$

Consider a step function $\bar {x} : \mathbb {R}^{n} \to \mathbb {R}^{n}$ by

$$\displaystyle \begin{aligned} \bar{x}(s)=x_k, s\in E_k, \ \mbox{we can see that} \ \|x(s)-\bar{x}\|\leq\delta. \end{aligned}$$

Further using the definition of Stepanov-like almost automorphy of f and ϕ, that is for each sequence {s′ _n} there exist subsequence {s _n} and functions g and ψ such that

$$\displaystyle \begin{aligned} & \int_0^1\Big(\|f(t+s+s_n,x)-g(t+s,x)\|{}^pds\Big)^{\frac{1}{p}} \to 0, {}\\ & \ \int_0^1\Big(\|g(t+s-s_n,x)-f(t+s,x)\|{}^pds\Big)^{\frac{1}{p}} \to 0 \ \mbox{as} \ n\to \infty \ \mbox{pointwise on} \ \mathbb{R}, \notag \end{aligned} $$

(4.3.2)

and

$$\displaystyle \begin{aligned} & \int_0^1\Big(\|\phi(t+s+s_n)-\psi(t+s)\|{}^pds\Big)^{\frac{1}{p}} \to 0, {} \\ & \int_0^1\Big(\|\psi(t+s-s_n)-\psi(t+s)\|{}^pds\Big)^{\frac{1}{p}} \to 0 \ \mbox{as} \ n\to \infty \ \mbox{pointwise on} \ \mathbb{R}. \notag \end{aligned} $$

(4.3.3)

Calculating the Stepanov norm of f, we have

$$\displaystyle \begin{aligned} & \int_0^1\Big(\|f(t+s,x(t+s))\|{}^p ds\Big)^{\frac{1}{p}} \\ & \leq \int_0^1\Big(\|f(t+s,x(t+s))-f(t+s,\bar{x}(t+s))\|{}^p ds\Big)^{\frac{1}{p}} \\ & + \int_0^1\Big(\|f(t+s,\bar{x}(t+s))\|{}^pds\Big)^{\frac{1}{p}} \\ & \le \int_t^{t+1}\Big(L\|x(s)-\bar{x}(s)\|{}^pds\Big)^{\frac{1}{p}}+ \int_t^{t+1}\Big(\|f(s,x_k)\|{}^pds\Big)^{\frac{1}{p}} \\ & \le L\|x(s)-\bar{x}(s)\|{}_{S^p} + \sum_{k=1}^n\int_{E_k\cap [t,t+1]}\Big(\|f(s,x_k)\|{}^pds\Big)^{\frac{1}{p}}. \end{aligned} $$

Using Eqs. (4.3.2) and (4.3.3), we obtain

$$\displaystyle \begin{aligned} & \int_0^1\Big(\|f(t+s+s_n,\phi(t+s+s_n))-g(t+s,\psi(t+s))\|{}^pds\Big)^{\frac{1}{p}} \\ & \le \int_0^1\Big(\|f(t+s+s_n,\phi(t+s+s_n))-f(t+s+s_n,\psi(t+s))\|{}^pds\Big)^{\frac{1}{p}} \\ & + \int_0^1\Big(\|f(t+s+s_n,\psi(t+s))-g(t+s,\psi(t+s))\|{}^pds\Big)^{\frac{1}{p}} \\ & \le \int_0^1\Big(L\|\phi(t+s+s_n)-\psi(t+s)\|{}^pds\Big)^{\frac{1}{p}}\\ & + \int_0^1\Big(\|f(t+s+s_n,\psi(t+s))-g(t+s,\psi(t+s))\|{}^pds\Big)^{\frac{1}{p}} \\ & < (L+1)\epsilon. \end{aligned} $$

Similarly

$$\displaystyle \begin{aligned}\int_0^1\Big(\|g(t+s-s_n,\psi(t+s-s_n))-f(t+s,\phi(t+s))\|{}^pds\Big)^{\frac{1}{p}} <(L+1) \epsilon.\end{aligned}$$

Hence f(⋅, ϕ(⋅)) is Stepanov almost automorphic. □

4.4 Impulsive Delay Differential Equations

We can easily see that the Eq. (4.1.1) can be written in the following compact form:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dx(t)}{dt}&\displaystyle =&\displaystyle A(t)x(t)+f(t,x(t),x(t-\alpha)) \quad t \neq t_k \notag \\ \Delta x(t_k)&\displaystyle =&\displaystyle A_kx(t_k)+I_k(x(t_k)), \ k\in \mathbb{Z}, \ t \in \mathbb{R}, {} \end{array} \end{aligned} $$

(4.4.1)

where A(t) = (a _ij(t))_nxn, i, j = 1, 2, ⋯ , n, f = (f ₁, f ₂, ⋯ , f _n)^T and

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{i}(t,x(t),x(t-\alpha)) =\sum_{j=1}^{n}\alpha _{ij}(t)f_{j}(x_{j}(t)) +\sum_{j=1}^{n}\beta _{ij}(t)f_{j}(x_{j}(t-\alpha ))+\gamma_i(t), \end{array} \end{aligned} $$

for i = 1, 2, ⋯ , n. In order to prove our results, we need the following assumptions:

• (H1) The function $A(t)\in \mathcal {C}(\mathbb {R},\mathbb {R}^{n})$ is a piecewise continuous Stepanov-like almost automorphic function,

• (H2) $\det (I+A_{k})\neq 0$ and the sequences A _k and t _k are Stepanov-like almost automorphic.

It is well known that if U _k(t, s) is the Cauchy matrix associated with the system

$$\displaystyle \begin{aligned} \frac{dx(t)}{dt}=A(t)x(t)\quad t_{k-1}\leq t\leq t_{k}, \end{aligned}$$

then the Cauchy matrix of the system (4.4.1) is given by

$$\displaystyle \begin{aligned} U(t,s)= \begin{cases} U_{k}(t,s),\quad t_{k-1}\leq t\leq t _{k}, \\ U_{k+1}(t,t _{k}+0)(I+A_{k})U_{k}(t,s), \\ \quad t_{k-1}<s<t_{k}<t<t _{k+1}, \\ U_{k+1}(t,t _{k}+0)(I+A_{k})U_{k}(t_{k},t_{k}+0) \\ \cdots (I+A_{i})U_{i}(t_{i},s), \\ \text{for}\quad t_{i-1}<s\leq t _{i}<t _{k}<t<t_{k+1}. \end{cases} \end{aligned}$$

For the above Cauchy matrix, the solution of the corresponding homogenous system could be written as x(t, t ₀, x ₀) = U(t, t ₀)x ₀, where x ₀ is the initial condition at the initial point t ₀. Let us further assume the followings:

• (H3) There exist positive constants K and δ such that ∥U(t, s)∥≤ Ke ^−δ(t−s), which further implies that $\|U(t+t_{n_{k}},s+t_{n_{k}})-U(t,s)\|\leq M\epsilon e^{-\frac {\delta }{2}(t-s)}$ for any 𝜖 > 0 and positive constant M.

• (H4) The functions α _ij, β _ij are Stepanov-like almost automorphic such that

  $$\displaystyle \begin{aligned} \begin{array}{rcl} -\infty <{\alpha _{ij}}_{\ast }\leq \alpha _{ij}(t)\leq \alpha _{ij}^{\ast }<\infty , \quad \quad -\infty <{\beta _{ij}}_{\ast }\leq \beta _{ij}(t)\leq \beta _{ij}^{\ast }<\infty . \end{array} \end{aligned} $$

• (H5) The function f _j is Stepanov-like almost automorphic with $0<\sup _{t\in \mathbb {R}}f_{j}(t)<\infty$ and satisfies |f _j(t) − f _j(s)|≤ L _j|t − s|, j = 1, 2, ⋯ , n.

• (H6) The function γ _i is Stepanov-like almost automorphic and satisfies $-\infty <{\gamma _{i}}_{\ast }\leq \gamma _{i}(t)\leq \gamma _{i}^{\ast }<\infty .$

• (H7) The sequence I _k is Stepanov-like almost automorphic and there exists a positive constant L such that $\|I_{k}(x)-I_{k}(y)\|\leq L\|x-y\|, \ \mbox{for} \ k\in \mathbb {Z},x,y\in \Omega \subset \mathbb {R}^{n}.$

Now we have made enough background to prove the main results of this paper, which are presented below.

Lemma 4.4.1

Under the properties of Cauchy matrix U(t, s), the impulsive differential Eq.(4.4.1) is equivalent to the following integral equation:

$$\displaystyle \begin{aligned} \begin{array}{rcl} x(t) =\int_{-\infty }^{t}U(t,s)f(s,x(s),x(s-\alpha)) ds +\sum_{t>t_k}U(t,t_{k}) I_{k}(x (t _{k})). {}\quad \end{array} \end{aligned} $$

(4.4.2)

Proof

For t ∈ [0, t ₁], we claim that the following function is the solution of system (4.1.1)

$$\displaystyle \begin{aligned} \begin{array}{rcl} x(t) =\int_{-\infty }^{t}U(t,s)f(s,x(s),x(s-\alpha))ds. \end{array} \end{aligned} $$

Differentiating both sides with respect to t, we get

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dx(t)}{dt} = \int_{-\infty }^{t}\frac{\partial U(t,s)}{\partial t}f(s,x(s),x(s-\alpha))ds + f(t,x(t),x(t-\alpha)) , \ x(0)=\psi_0(0) \end{array} \end{aligned} $$

$$\displaystyle \begin{aligned}\begin{array}{rcl} \Leftrightarrow \frac{dx(t)}{dt} &\displaystyle =&\displaystyle A(t)x(t) + f(t,x(t),x(t-\alpha)), \quad x(0)=\psi_0(0). \end{array} \end{aligned} $$

For t ∈ (t ₁, t ₂], define

$$\displaystyle \begin{aligned} \begin{array}{rcl} x(t) &\displaystyle =&\displaystyle \int_{-\infty }^{t}U(t,s)f(s,x(s),x(s-\alpha))ds + U(t,t_{1})(I_{1}x (t _{1})) \\ \Leftrightarrow x(t) &\displaystyle =&\displaystyle U(t,t_{1})\Big(I_{1}(x (t _{1}))+ \int_{-\infty }^{t_1}U(t_1,s)f(s,x(s),x(s-\alpha))ds\Big) \\ &\displaystyle &\displaystyle + \int_{t_1 }^{t}U(t,s)f(s,x(s),x(s-\alpha))ds \\ \Leftrightarrow x(t) &\displaystyle =&\displaystyle U(t,t_{1})x(t_1^+) + \int_{t_1 }^{t}U(t,s)f(s,x(s),x(s-\alpha))ds , \\ x(t_1^+) &\displaystyle =&\displaystyle I_{1} (x (t_{1}))+ \int_{-\infty }^{t_1}U(t_1,s)f(s,x(s),x(s-\alpha))ds. \end{array} \end{aligned} $$

Differentiating both sides of the above relation with respect to t, we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dx(t)}{dt} &\displaystyle =&\displaystyle \frac{\partial U(t,t_1)}{\partial t}x(t_1^+) + \int_{t_1 }^{t}\frac{\partial U(t,s)}{\partial t}f(s,x(s),x(s-\alpha))ds \\ &\displaystyle &\displaystyle + f(t,x(t),x(t-\alpha)), \\ x(t_1^+) &\displaystyle =&\displaystyle A_1x (t_1) + I_{1}(x (t_1))+ \int_{-\infty }^{t_1}U(t_1,s)f(s,x(s),x(s-\alpha))ds \\ \Leftrightarrow \frac{dx(t)}{dt} &\displaystyle =&\displaystyle A(t)\Big(U(t,t_1)x(t_1^+) + \int_{t_1 }^{t}U(t,s)f(s,x(s),x(s-\alpha))ds\Big) \\ &\displaystyle &\displaystyle + f(t,x(t),x(t-\alpha)), \\ \Delta x(t_1) &\displaystyle =&\displaystyle A_1x (t_1) + I_{1}(x (t_1)) \\ \Leftrightarrow \frac{dx(t)}{dt} &\displaystyle =&\displaystyle A(t)x(t) + f(t,x(t),x(t-\alpha)), \quad \Delta x(t_1) = A_1x (t_1) + I_{1}(x (t_1)). \end{array} \end{aligned} $$

⋮

For t ∈ (t _k, t _k+1], define

$$\displaystyle \begin{aligned} \begin{array}{rcl} x(t) &\displaystyle =&\displaystyle \int_{-\infty }^{t}U(t,s)f(s,x(s),x(s-\alpha))ds + U(t,t_{k})(I_{1}x (t_k)) \\ \Leftrightarrow x(t) &\displaystyle =&\displaystyle U(t,t_{k})(I_{k}(x (t_k))+ \int_{-\infty }^{t_k}U(t_k,s)f(s,x(s),x(s-\alpha))ds \\ &\displaystyle &\displaystyle + \int_{t_k }^{t}U(t,s)f(s,x(s),x(s-\alpha))ds \\ \Leftrightarrow x(t) &\displaystyle =&\displaystyle U(t,t_{k})(x(t_k^+) + \int_{t_k }^{t}U(t,s)f(s,x(s),x(s-\alpha))ds , \\ x(t_k^+) &\displaystyle =&\displaystyle I_{k}(x (t_k))+ \int_{-\infty }^{t_k}U(t_k,s)f(s,x(s),x(s-\alpha))ds. \end{array} \end{aligned} $$

Again differentiating both sides of the above relation with respect to t, we get

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dx(t)}{dt} &\displaystyle =&\displaystyle \frac{\partial U(t,t_{k})}{\partial t}(x(t_k^+) + \int_{t_k }^{t}\frac{\partial U(t,s)}{\partial t}f(s,x(s),x(s-\alpha))ds \\ &\displaystyle &\displaystyle + f(t,x(t),x(t-\alpha)), \\ x(t_k^+) &\displaystyle =&\displaystyle A_kx (t_k) + I_{k}(x (t_k))+ \int_{-\infty }^{t_k}U(t_k,s)f(s,x(s),x(s-\alpha))ds \\ \Leftrightarrow \frac{dx(t)}{dt} &\displaystyle =&\displaystyle A(t)\Big(U(t,t_{k})x(t_k^+) + \int_{t_k }^{t}U(t,s)f(s,x(s))ds\Big) + f(t,x(t),x(t-\alpha)) \\ \Delta x(t_k) &\displaystyle =&\displaystyle A_kx (t_k) + I_{k}(x (t_k)), \\ \Leftrightarrow \frac{dx(t)}{dt} &\displaystyle =&\displaystyle A(t)x(t) + f(t,x(t),x(t-\alpha)) \quad \Delta x(t_k) = A_kx (t_k) + I_{k}(x (t_k)). \end{array} \end{aligned} $$

⋮

Similarly the result holds for any interval (t _l, t _l+1]. □

Lemma 4.4.2

If $f:\mathbb {R}\rightarrow \mathbb {R}^{n}$ is a Stepanov-like almost automorphic function, then $\int _{-\infty }^{t}U(t,s)f(s) ds +\sum _{t>t_{k}}U(t,t_{k}) I_{k}(x (t_{k}))$ is Stepanov-like almost automorphic.

Proof

Since f is Stepanov-like almost automorphic, for each sequence {t _n} there exist a subsequence $\{t_{n_k}\}$ and function g such that

$$\displaystyle \begin{aligned} \lim_{k\rightarrow \infty} f(t+t_{n_k}) =g(t), \quad \lim_{k\rightarrow \infty} g(t-t_{n_k}) =f(t) \quad \forall t \in \mathbb{R} \ \mbox{in} \ L^p(\mathbb{R},\mathbb{R}^n). \end{aligned}$$

We define

$$\displaystyle \begin{aligned} F(t)=\int_{-\infty }^{t}U(t,s)f(s) ds +\sum_{t>t_{k}}U(t,t_{k}) I_{k}(x (t_{k})) \end{aligned}$$

and

$$\displaystyle \begin{aligned} G(t)=\int_{-\infty}^t U(t,s)g(s)ds + \sum_{t>t_k}U(t,t_k)I^*_k(x(t_k)). \end{aligned}$$

Using continuity of U(t, s) and Lebesgue’s dominated convergence theorem, we obtain

$$\displaystyle \begin{aligned} \int_{-\infty}^t U(t,s)f(s+t_{n_k})ds \rightarrow \int_{-\infty}^t U(t,s)g(s)ds \ \mbox{in} \ L^p(\mathbb{R},\mathbb{R}^n). {} \end{aligned} $$

(4.4.3)

Moreover,

$$\displaystyle \begin{aligned} \sum_{t+t_{n_k}>t_k}U(t+t_{n_k},t_k)I_k(x(t_k)) &= \sum_{t>t_k}U(t+t_{n_k},t_k+t_{n_k})I_k(x(t_k+t_{n_k})) \\ & \rightarrow \sum_{t>t_k}U(t,t_k)I^*_k(x(t_k)) \ \mbox{in} \ L^p(\mathbb{R},\mathbb{R}^n). {} \end{aligned} $$

(4.4.4)

Thus using Eqs. (4.4.3) and (4.4.4), we get

$$\displaystyle \begin{aligned} \lim_{k\rightarrow \infty} \left(\int_0^1\|F(t+t_{n_k}+s)-G(t+s)\|{}^pds\right)^{\frac{1}{p}} = 0 \ \mbox{in } \quad \forall t \in \mathbb{R}. \end{aligned} $$

Similarly, we can prove that

$$\displaystyle \begin{aligned} \lim_{k\rightarrow \infty} \left(\int_0^1\|G(t-t_{n_k}+s)-F(t+s)\|{}^pds\right)^{\frac{1}{p}} = 0 \quad \forall t \in \mathbb{R}. \end{aligned} $$

Hence F is piecewise Stepanov-like almost automorphic. □

Theorem 4.4.3

Under the hypotheses (H1)–(H7), there exists a unique piecewise continuous Stepanov-like almost automorphic solution of Eq.(4.1.1) provided

$$\displaystyle \begin{aligned} K\left(\max_i\left(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast }\right)L^* (p\delta)^{-\frac{1}{p}}+L(1-e^{-p\delta})^{-\frac{1}{p}} \right) <1. \end{aligned} $$

Proof

Define the operator

$$\displaystyle \begin{aligned} \Lambda \phi (t) =\int_{-\infty }^{t}U(t,s)f(s,\phi (s),\phi(s-\alpha))ds +\sum_{t> t_k}U(t,t_{k})I_{k}(\phi (t _{k})). \end{aligned} $$

we denote $B \subset S^{p}AA_{pc}(\mathbb {R}, \mathbb {R}^n),$ the set of all Stepanov-like almost automorphic functions satisfying $\|\phi \|{ }_{S^p} \leq K_{1},$ where $\|\phi \|{ }_{S^p} =\sup _{t\in \mathbb {R}}(\int _t^{t+1}\|\phi (s)\|{ }^pds)^{\frac {1}{p}}$ and $K_{1}=KC\Big ((p\delta )^{-\frac {1}{p}}+(1-e^{-p\delta })^{-\frac {1}{p}}\Big ).$ Using composition theorem, it is not difficult to see that Λϕ is Stepanov-like almost automorphic as ϕ is Stepanov-like almost automorphic. As the function $f\in S^{p}AA_{pc}(\mathbb {R}\times \mathbb {R}^{n},\mathbb {R}^n),$ define u(⋅) = f(⋅, x(⋅), x(⋅− α)). Again using composition Theorem 4.3.4 and Lemma 4.4.2, we conclude

$$\displaystyle \begin{aligned} \begin{array}{rcl} \Lambda _{1}\phi =\int_{-\infty }^{t}U(t,s)f(s,\phi (s),\phi(s-\alpha))ds \in S^{p}AA_{pc}(\mathbb{R},\mathbb{R}^n). \vspace{-3pt}\end{array} \end{aligned} $$

Further using Stepanov-like almost automorphy of sequence $I_{k}\in C(\mathbb {R}^n,\mathbb {R}^n),$ we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{t_k<t+t_{n_{k}}}U(t+t_{n_{k}},t_{k})I_{k}(\phi (t_{k})) \notag &\displaystyle &\displaystyle =\sum_{t_k<t}U(t+t_{n_{k}},t_{k}+t_{n_{k}})I_{k}(\phi (t_{k}+t_{n_{k}})) \notag \\ &\displaystyle &\displaystyle \rightarrow \sum_{t_k<t}U(t,t_{k})I_{k}^{\ast }(\phi (t_{k})) \ \mbox{in} \ L^p(\mathbb{R},\mathbb{R}^n).\notag \end{array} \end{aligned} $$

Similarly

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{t_k<t-t_{n_{k}}}U(t-t_{n_{k}},t_{k})(I_{k}^{\ast } \phi (\tau _{k})) \notag &\displaystyle &\displaystyle =\sum_{t_k<t}U(t-t_{n_{k}},t_{k}-t_{n_{k}})(I_{k}^{\ast } \phi (t_k-t_{n_{k}})) \notag \\ &\displaystyle &\displaystyle \rightarrow \sum_{t_k<t}U(t,t_{k})(I_{k}(\phi (t_{k})) \ \mbox{in} \ L^p(\mathbb{R},\mathbb{R}^n).\notag \end{array} \end{aligned} $$

The above analysis implies $\Lambda \phi \in S^{p}AA_{pc}(\mathbb {R}, \mathbb {R}^n).$

Let us denote

$$\displaystyle \begin{aligned} B\supset B^{\ast }=\Big\{\phi \in B:\|\phi\|{}_{S^p} \leq \frac{rK_{1} }{1-r}\Big\}, \end{aligned}$$

where

$$\displaystyle \begin{aligned} \phi _{0}(t)=\int_{-\infty }^{t}U(t,s)\gamma (s)ds+\sum_{t_{k}<t}U(t,t_{k})\gamma _{k}. \end{aligned}$$

Now first we calculate the norm of ϕ ₀, which is as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \|\phi _{0}\|{}_{S^p} \notag \\ &\displaystyle =&\displaystyle \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\|\int_{-\infty }^{s}U(s,z)\gamma(z)dz\|{}^pds\Big)^{\frac{1}{p}} +\sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\|\sum_{t_k<s}U(s,t_k)\gamma_{k}\|{}^pds\Big)^{\frac{1}{p}} \notag \\ &\displaystyle \le &\displaystyle \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\|\int_0^{\infty}U(s,s-z)\gamma(s-z)dz\|{}^pds\Big)^{\frac{1}{p}} +\sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\sum_{t_k<s}\|U(s,t_k)\|{}^p \notag \\ &\displaystyle \times &\displaystyle \|\gamma_{k}\|{}^pds\Big)^{\frac{1}{p}} \notag \\ &\displaystyle \le &\displaystyle K\sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\int_0^{\infty}e^{-p\delta z}\|\gamma(s-z)dz\|{}^pds\Big)^{\frac{1}{p}} +K\sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\sum_{t_k<s}e^{-p\delta (s-t_k)} \notag \\ &\displaystyle \times &\displaystyle \|\gamma_{k}\|{}^pds\Big)^{\frac{1}{p}} \notag \\ &\displaystyle \le &\displaystyle \|\gamma\|{}_{S^p} K\sup_{t\in \mathbb{R}}\Big(\int_0^{\infty}e^{-p\delta z}dz\Big)^{\frac{1}{p}} +\|\gamma_k\|K\sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\sum_{t_k<s}e^{-p\delta (s-t_k)}ds\Big)^{\frac{1}{p}} \notag \\ &\displaystyle \le &\displaystyle KC\Big((p\delta)^{-\frac{1}{p}}+(1-e^{-p\delta})^{-\frac{1}{p}}\Big)=K_1. \end{array} \end{aligned} $$

(4.4.5)

Hence for any ϕ ∈ B ^∗, we get

$$\displaystyle \begin{aligned} \|\phi\|{}_{S^p} \le \|\phi-\phi_0\|{}_{S^p}+\|\phi_0\|{}_{S^p} \le \frac{rK_{1}}{1-r}+K_{1}=\frac{K_{1}}{1-r}. \end{aligned}$$

Our next aim is to prove that Λ maps set B ^∗ to B ^∗.

In order to achieve this, let us first observe that

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \|\Lambda \phi-\phi_0\|{}_{S^p} \\ &\displaystyle &\displaystyle \quad \leq \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\|\int_{-\infty }^{s}U(s,z)f(z,\phi(z),\phi(z-\alpha))dz\|{}^pds\Big)^{\frac{1}{p}} \\ &\displaystyle &\displaystyle \qquad +\sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\|\sum_{t_k<s}U(s,t_k)\times I_k(\phi(t_k))\|{}^pds\Big)^{\frac{1}{p}} \\ &\displaystyle &\displaystyle \quad \leq \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\max_i\int_{-\infty }^{s}\|U(s,z)\|{}^p\sum_{j=1}^{n}\alpha _{ij}^{\ast }\|f_{j}(\phi _{j}(s-z))\|{}^pdzds\Big)^{\frac{1}{p}} \\ &\displaystyle &\displaystyle \qquad + \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\max_i\int_{-\infty }^{s}\|U(s,z)\|{}^p\sum_{j=1}^{n}\beta _{ij}^{\ast }\|f_{j}(\phi _{j}(s-z-\alpha))\|{}^pdzds\Big)^{\frac{1}{p}} \\ &\displaystyle &\displaystyle \qquad + \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\sum_{t_k<s}\|U(s,t_k)\|{}^p\|I_k(\phi(t_k))\|{}^pds\Big)^{\frac{1}{p}} \\ &\displaystyle &\displaystyle \quad \leq \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\max_i\int_{-\infty }^{s}\|U(s,z)\|{}^p\sum_{j=1}^{n}\alpha _{ij}^{\ast }((L^*)^p\|\phi _{j}(s-z))\|{}^p\\ &\displaystyle &\displaystyle \qquad +\|f_j(0)\|{}^p)dzds\Big)^{\frac{1}{p}} \\ &\displaystyle &\displaystyle \qquad +\sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\max_i\int_{-\infty }^{s}\|U(s,z)\|{}^p\|f_j(0)\|{}^p\sum_{j=1}^{n}\beta _{ij}^{\ast }((L^*)^p\|\phi _{j}(s-z-\alpha))\|{}^p \\ &\displaystyle &\displaystyle \qquad +\|f_j(0)\|{}^p)dzds\Big)^{\frac{1}{p}} +\sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\sum_{t_k<s}\|U(s,t_k)\|{}^p(L^p\|\phi(t_k)\|{}^p\\&\displaystyle &\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\|I_k(0)\|{}^p)ds\Big)^{\frac{1}{p}}, \end{array} \end{aligned} $$

where $L^{\ast }=\max \{L_{i},i=1,2,\cdots ,n\}.$ In order to have zero as an equilibrium solution of the system (4.1.1), we assume that f _j(0) = I _k(0) = 0. Thus we have

(4.4.6)

Thus we conclude that Λϕ ∈ B ^∗.

Now we prove that Λ is a contraction. For any ϕ ₁, ϕ ₂ ∈ B ^∗, we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \| \Lambda \phi _{1}-\Lambda \phi _{2}\|{}_{S^p} \notag \\ &\displaystyle &\displaystyle \quad \leq \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\|\int_{-\infty }^{s}U(s,z)(f(z,\phi_1(z),\phi_1(z-\alpha))\\ &\displaystyle &\displaystyle \qquad -f(z,\phi_2(z),\phi_2(z-\alpha)))dz\|{}^pds\Big)^{\frac{1}{p}} \notag \\ &\displaystyle &\displaystyle \qquad + \sup_{t\in \mathbb{R}}\Big(\int_t^{t+1}\|\sum_{t_k<s}U(s,t_k)(I_k(\phi_1(t_k))-I_k(\phi_2(t_k))\|{}^pds\Big)^{\frac{1}{p}} \notag \\ &\displaystyle &\displaystyle \quad \le K\left(\max_i\left(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast }\right)L^* \Big(\int_0^{\infty}e^{-p\delta z}dz\Big)^{\frac{1}{p}}\right.\notag\\ &\displaystyle &\displaystyle \qquad \left. +\, L\Big(\sum_{t_k<s}e^{-p\delta (s-t_k)}\Big)^{\frac{1}{p}}\right)\|\phi_1-\phi_2\|{}_{S^p} \notag \\ &\displaystyle &\displaystyle \quad \le K\left(\max_i\left(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast }\right)L^* (p\delta)^{-\frac{1}{p}}+L(1-e^{-p\delta})^{-\frac{1}{p}} \right)\|\phi_1-\phi_2\|{}_{S^p} \notag \\ &\displaystyle &\displaystyle \quad =r\|\phi_1-\phi_2\|{}_{S^p} . \notag \end{array} \end{aligned} $$

Using the assumptions, we obtain

$$\displaystyle \begin{aligned} r=K\left(\max_i\left(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast }\right)L^* (p\delta)^{-\frac{1}{p}}+L(1-e^{-p\delta})^{-\frac{1}{p}} \right)<1. \end{aligned}$$

Thus the mapping Λ is a contraction. Hence using Banach contraction principle, we conclude that there exists a unique piecewise continuous Stepanov-like almost automorphic solution of Problem (4.1.1). □

Our next theorem is about asymptotic stability of the system (4.1.1).

Theorem 4.4.4

Under the hypotheses (H1)–(H7), the solution of the system (4.1.1) is asymptotically stable provided

$$\displaystyle \begin{aligned} p^2\delta^2 > 8K^p{L^*}^p\left(\max_i\left(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast }\right)\right). \end{aligned}$$

Proof

For any two solutions x(t) and y(t) of the system (4.1.1) with initial values x ₀ and y ₀, we define V (t) = x(t) − y(t). Using the property (∥x∥ + ∥y∥)^p ≤ 2^p−1(∥x∥^p + ∥y∥^p) and calculating p −th norm of V (t), we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \|V(t)\|{}^p &\displaystyle =&\displaystyle \|x(t)-y(t)\|{}^p \notag \\ &\displaystyle \leq &\displaystyle 2^{p-1}\big[ 2^{p-1}\|U(t,0)\|{}^p\|x_{0}-y_{0}\|{}^p \notag \\ &\displaystyle &\displaystyle + \int_0^t\|U(t,s)\|{}^p\|f(s,x(s),x(s-\alpha))-f(s,y(s),y(s-\alpha))\|{}^pds \notag \\ &\displaystyle &\displaystyle + 2^{p-1}\sum_{0<t_k<t}\|U(t,t_k)\|{}^p\|I_k(x(t_k))-I_k(y(t_k))\|{}^p \big], \notag\\ &\displaystyle \leq &\displaystyle 2^{p-1}\big[2^{p-1} K^pe^{-p\delta t}\|x_{0}-y_{0}\|{}^p + K^p\int_0^t e^{-\frac{p\delta (t-s)}{2}}ds \\ &\displaystyle &\displaystyle \times \int_0^t e^{-\frac{p\delta (t-s)}{2}}\|f(s,x(s),x(s-\alpha))-f(s,y(s),y(s-\alpha))\|{}^pds \\ &\displaystyle &\displaystyle +2^{p-1} \sum_{0<t_k<t}\|U(t,t_k)\|{}^p\|I_k(x(t_k))-I_k(y(t_k))\|{}^p \big] \notag\\ &\displaystyle \leq &\displaystyle 2^{p-1}\big[2^{p-1} K^pe^{-p\delta t}\|x_{0}-y_{0}\|{}^p\\ &\displaystyle &\displaystyle + 2\frac{K^p{L^*}^p\left(\max_i\left(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast }\right)\right)}{p\delta} \notag \\ &\displaystyle &\displaystyle \times \int_0^t e^{-\frac{p\delta (t-s)}{2}}\|x(s)-y(s)\|{}^pds \notag \\ &\displaystyle &\displaystyle + 2^{p-1}\sum_{0<t_k<t}K^pL^p e^{-p\delta (t-t_k)}\|x(t_k)-y(t_k)\|{}^p \big]. \notag \end{array} \end{aligned} $$

From the assumption

$$\displaystyle \begin{aligned} p^2\delta^2 > 2^p K^p{L^*}^p\left(\max_i\left(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast }\right)\right), \end{aligned}$$

there exists an 𝜖 ∈ (0, δ) such that

$$\displaystyle \begin{aligned} p\delta\left(\frac{p\delta}{2} -\epsilon\right) > 2^{p-1}K^p{L^*}^p\left(\max_i\left(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast }\right)\right). \end{aligned}$$

We further define X(t) = ∥x(t) − y(t)∥^pe ^𝜖t. Integrating both sides of X(t), we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_0^{\tau}X(s)ds &\displaystyle \leq &\displaystyle \frac{2^{2p-2}K^p}{p\delta - \epsilon}X(0)+\frac{2^{p-1}K^p{L^*}^p(\max_i(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast })}{p\delta(\frac{p\delta}{2} -\epsilon)}\times\notag\\ &\displaystyle \times&\displaystyle \int_0^{\tau}X(s)ds + \sum_{0<t_k<\tau}\frac{2^{2p-2}K^pL^p}{p\delta -\epsilon} X(t_k)\notag \\ \int_0^{\tau}X(s)ds &\displaystyle \leq &\displaystyle \frac{p\delta(\frac{p\delta}{2} -\epsilon)}{p\delta(\frac{p\delta}{2} -\epsilon)-2^{p-1}K^p{L^*}^p(\max_i(\sum_{j=1}^{n}\alpha _{ij}^{\ast } + \sum_{j=1}^{n}\beta _{ij}^{\ast })}\times\notag\\ &\displaystyle \times&\displaystyle \Big(\frac{2^{2p-2}K^p}{p\delta - \epsilon} + \Big(1+\frac{2^{2p-2}K^pL^p}{p\delta -\epsilon}\Big)^{i(0,\tau)}\Big)X(0). {} \end{array} \end{aligned} $$

(4.4.7)

Here i(0, τ) is the number of points t _k in the interval (0, τ) and the product $\prod _{0<t_k<\tau }\Big (1+\frac {2^{2p-2}K^pL^p}{p\delta - \epsilon }\Big ) = \Big (1+\frac {2^{2p-2}K^pL^p}{p\delta -\epsilon }\Big )^{i(0,\tau )}$ is convergent because of $\Big (1+\frac {2^{2p-2}K^pL^p}{p\delta - \epsilon }\Big ) \leq \Big (1+L^p\Big )^{\frac {2^{2p-2}K^p}{p\delta - \epsilon }}.$ Since RHS of inequality (4.4.7) is independent of τ ∈ [0, T) as well as of T, and hence the LHS integral of inequality (4.4.7) exists in [0, ∞). In particular, we have

$$\displaystyle \begin{aligned} X(t) \to 0 \ \mbox{as} \ t \to \infty. \end{aligned}$$

Eventually, the Stepanov-like almost automorphic solution is asymptotically stable. □

4.5 Examples

As an example of Problem (4.1.1), consider the following classical model of Hopefield neural network model,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dx_{i}(t)}{dt} &\displaystyle =&\displaystyle -a_{i}(t)x_{i}(t)+\sum_{j=1}^{n}\alpha _{ij}f_{j}(x_{j}(t)) + \sum_{j=1}^{n}\beta _{ij}f_{j}(x_{j}(t-\alpha ))+\gamma _{i}(t), t \neq t_k, \notag \\ \Delta (x(t_k)) &\displaystyle =&\displaystyle A_{k}x(t_k)+I_{k}(x(t_k))+\gamma _{k}, \notag \\ x(t_k-0) &\displaystyle =&\displaystyle x(t_k),\quad x(t_k+0)=x(t_k)+\Delta x(t_k), \quad k \in \mathbb{Z},\ t\in \mathbb{R}, \notag \\ x(t) &\displaystyle =&\displaystyle \phi _{0}(t),\quad t\in \lbrack -\alpha ,0], \ \alpha >0, {} \end{array} \end{aligned} $$

(4.5.1)

where $a_{i},f_{j},\gamma _{i}\in \mathcal {C}(\mathbb {R},\mathbb {R}),\ \alpha _{ij},\beta _{ij} \in \mathbb {R}$ for i = 1, 2, ⋯ , n, j = 1, 2, ⋯ , n. The coefficient $A_{k}\in \mathbb {R}^{n\times n},$ the function $I_{k}(x)\in \mathcal {C}(\Omega , \mathbb {R}^{n})$ and the constant $\gamma _{k}\in \mathbb {R}^{n},$ where Ω a domain in $\mathbb {R}^{n}.$ In this case our matrix A(t) is a diagonal matrix with diagonal entire − a ₁(t), ⋯ , −a _n(t). We assume that a _i(t) are Stepanov-like almost automorphic and choose a _i(t) = 1 for each i = 1, 2, ⋯ , n. One can easily verify the hypotheses (H1) and (H2) for this case and we assume the hypothesis (H3). Now under all the conditions of Theorem 4.4.3, there exists a Stepanov-like almost automorphic solution of the Problem (4.5.1).

Let us choose the following set of parameters for the Problem (4.5.1) in $\mathbb {R}^2$:

$$\displaystyle \begin{aligned} \begin{array}{rcl} a_1(t) &\displaystyle =&\displaystyle signum(\cos 2\pi t\theta ), \ \beta_{12}=0.2, \ \gamma_{1}(t)=2\sin \sqrt{2t}, \\ a_2(t) &\displaystyle =&\displaystyle \cos\Big(\frac{1}{2+\sin{}(t)+\sin{}(\sqrt{2}t)}\Big), \ \beta_{21}=signum(\cos 2\pi t\theta ), \ \gamma_{2}(t)=c(t), \\ A_{k} &\displaystyle =&\displaystyle \begin{pmatrix} -0.3 &\displaystyle 0 \\ 0 &\displaystyle -0.3 \end{pmatrix}, \\ I_{k}(x) &\displaystyle =&\displaystyle 0.9|x|, \ x_1(s)=1=x_2(s), s \in [-0.1,0], \ \gamma_k = \begin{pmatrix} 0.25 \\ 0.25 \end{pmatrix} . \end{array} \end{aligned} $$

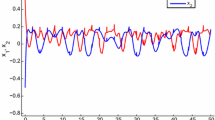
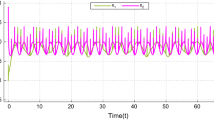
These parameters clearly satisfy the conditions of our Theorem 4.4.3. The graph of the solution of (4.5.1) corresponding to these parametric values is depicted in Fig. 4.1. It can be easily seen that the nature of the graph is Stepanov almost automorphic.

Fig. 4.1

Stepanov-like almost automorphic solution of 4.5.1

4.6 Discussion

The class of Stepanov-like almost automorphic functions covers larger class of functions and hence more complicated behaviour can be expressed in terms of these functions. It already contains the class of almost periodicity, automorphy as a subclass and hence it is more general in nature. One natural question one can always ask in the neural network theory is that what will be the nature of the output when all the parameters are Stepanov-like almost automorphic. In this work, we answered this question under certain condition. The asymptotic stability of solution is also established under certain conditions on the parameters. One can easily see the truth of this claim in the numerical simulation section. The obtained results can be easily generalized to other general class of systems such as neutral system, integro-differential system and systems with deviated arguments.