Oblique Impact of a Droplet on a Textured Substrate

Abstract

This study presents the modelling of an oblique drop impact on a textured substrate using the multiphase lattice Boltzmann method to understand the conditions under which the lamella lifts off the substrate and generates a satellite droplet. Depending on the impact angle and the Weber number, four various outcomes are observed: asymmetric spreading, bilateral splashing including a prompt splash and a corona splash, one-sided coronal splashing and asymmetric break-up. To obtain a better understanding of when splashing is likely to occur, a graph which shows splashing thresholds for a range of normal Weber numbers and impact angles between 5° and 45° is presented. Numerical results show that an increasing proportion of the droplet bounces off the surface in the form of satellite droplets for increasingly tangential impacts. Furthermore, the influence of substrate texture parameters such as the height of posts and wettability of the substrate are investigated. Results show that splashing vanishes as the wettability of the substrate increases. Also, the space between posts and the height of posts is shown to play an important role on the occurrence of splashing.

11.1 Introduction

The impact of droplets onto solid surfaces has been extensively studied over the past due to its importance in a range of applications such as inject printing or spray coating but also because it encompasses some of the most difficult modelling challenges in fluid mechanics such as a free surface, a wetting front or topography changes. The current state of the knowledge is comprehensively reviewed by Josserand and Thoroddsen [1]. Better understanding how the droplet wets a solid surface after impact is critical to obtaining a better control in practical applications. For example, one may wish to avoid lamella break-up and the production of satellite droplets post-impact in the application of pesticide on foliage.

For normal impacts on solid surfaces, Rioboo et al. proposed that the wetting outcomes can be broken down into five categories: deposition, rebound, receding break-up, prompt splash and corona splash [2]. The regime of interest here is the splashing because this phenomena, observed in many applications, still remains less understood. As a droplet impacts on a solid surface, the kinetic energy of the droplet is transformed into surface energy (potential energy) and dissipated by the viscous shear. If kinetic energy overcomes surface energy, the lamella may either generate tiny droplets at the contact line (prompt splash) or lifts off and detaches away from the substrate and generates satellite droplets (corona splash). Simple dimensional analysis reveals that the main dimensionless number expressing the ratio of inertia forces to surface tension forces is the Weber number:

$$ {\text{We}} = \frac{{\rho V^{2} D}}{\sigma } $$

(11.1)

where $\rho$ and $\sigma$ are the density and surface tension of the liquid, respectively. D denotes the diameter of the droplet and V refers to the impact velocity.

Several studies have described the dynamics of a droplet which impacts normally onto a textured substrate [3,4,5,6]. Generally, at a high enough Weber number, increment of the roughness amplitude of substrates leads eventually to prompt splash [3]. Experiments also demonstrated that the presence of a small vertical obstacle promotes corona splash [4]. Furthermore, the drop splashing threshold is dependent on geometrical parameters of the textured substrate [5]. In addition to surface morphology, the ambient pressure may affect the dynamics of the wetting front so that the splashing vanishes with a decrease in the ambient pressure [6].

In spite of the large number of important applications, the understanding of oblique impacts is, on the other hand, a lot less advanced. For oblique impacts, both the normal and tangential components of the impact velocity are considered and therefore the behaviour of the lamella spreading is more complex. In particular, an important question is how the tangential component of the impact velocity influences the dynamics of the contact line. To address this question, several researchers studied vertical impact onto an inclined stationary surface [7,8,9,10] and others investigated the vertical impact of droplets onto a moving surface which equally resulted in a tangential component of the impact velocity [11,12,13]. Another case for which the tangential component of the impact velocity matters is oblique impact on a horizontal surface. For such impacts, the role of the impact velocity components on the wetting outcomes has not to this day been investigated systematically.

The wettability of the substrate and the impact parameters such as the impact angle and the Weber number may affect the wetting outcome of oblique droplet impacts. Few studies exist on the oblique impact of droplets on super-hydrophobic surfaces. For example; Yeong et al. [8] performed an investigation of the impact and rebound dynamics of droplet impacting at an angle onto a super-hydrophobic surface and reported that the maximum spread of the droplet is a function of both the normal and tangential components of the impact velocity. Aboud and Kietzig [13] carried out oblique drop impacts onto tilted moving surfaces with various wettability including super-hydrophobic surfaces to obtain the oblique splashing threshold. Although the wettability of the surface was considered in the above studies, the effect of the geometrical parameters of the textured hydrophobic surface such as the space between posts, the height of the posts have not been investigated.

On the other hand, the aforementioned efforts in the literature have been experimental and therefore a numerical modelling of the dynamics of the lamella resulting from the oblique impact of a droplet onto a horizontal textured substrate has not performed yet. Thus, this work is a first attempt to simulate the behaviour of the lamella and investigate numerically the conditions under which it breaks-up and generates a satellite droplet. Furthermore, the influence of geometrical parameters of the textured substrate as well as the impact parameters is studied systematically. Thus, the aim of this contribution is to provide a greater understanding of the relation between the splashing, the impact parameters, and the substrate texture. To achieve this goal, we have developed a two-dimensional multiphase lattice Boltzmann code following the Shan-Chen model [14]. In recent years, the lattice Boltzmann method (LBM) which is based on the mesoscopic kinetic equation has been developed as a powerful tool for simulating multiphase fluid systems.

The remainder of the paper is structured as follows. Section 11.2 describes the multiphase lattice Boltzmann method in details. Then, a validation case is presented in Sect. 11.3. In this section, we perform simulations to calculate the maximum spread of an oblique impacting droplet onto a smooth surface and compare the numerical results with a correlation reported by Yeong et al. [8]. Section 11.4 represents the various possible splashing outcomes of the oblique impact of a droplet onto a textured substrate and investigates the effects of the impact angle, Weber number and wettability of the textured substrate. Finally, Sect. 11.5 presents concluding remarks.

11.2 Computational Algorithm

In the LBM, the simulation domain is divided into lattices which are occupied by either a fluid (liquid or gas) or a solid. The main variable is the density distribution function $f_{k} \left( {\varvec{x},t} \right)$ which represents the state of the particle collection. The lattice position vector at time t is represented by x and the velocity direction is denoted by the label k. The density distribution function is discretised using the typical D2Q9 lattice arrangement [15]. This velocity model involves nine microscopic velocity vectors in two space dimensions. For this model, the microscopic velocity vectors $\varvec{e}_{k}$ and weights $\omega_{k}$ are defined as follows:

$$ \varvec{e}_{k} = \left\{ {\begin{array}{*{20}l} {(0,0)} \hfill & {k = 0} \hfill \\ {c\left( {\cos \left( {\frac{{\left( {k - 1} \right)\pi }}{2}} \right),\sin \left( {\frac{{\left( {k - 1} \right)\pi }}{2}} \right)} \right)} \hfill & {k = 1,2,3,4} \hfill \\ {\sqrt 2 c\left( {\cos \left( {\frac{{\left( {k - \frac{9}{2}} \right)\pi }}{2}} \right),\sin \left( {\frac{{\left( {k - \frac{9}{2}} \right)\pi }}{2}} \right)} \right)} \hfill & {k = 5,6,7,8} \hfill \\ \end{array} } \right. $$

(11.2)

$$ \omega_{k} = \left\{ {\begin{array}{*{20}l} {4/9} \hfill & {k = 0} \hfill \\ {1/9} \hfill & {k = 1,2,3,4} \hfill \\ {1/36} \hfill & {k = 5,6,7,8} \hfill \\ \end{array} } \right. $$

(11.3)

In the above, c denotes the lattice speed which is given by $c = \frac{\Delta x}{\Delta t}$ where $\Delta x$ and $\Delta t$ are the lattice unit (lu) and the time step (ts), respectively. Within the LBM, a fluid is modelled as a fraction of the distribution functions which streams with $\varvec{e}_{k}$ from x to its neighbouring lattice $\varvec{x} + \varvec{e}_{k} \Delta t$ via certain directions k at the following time step $\Delta t$. This process is named the streaming step. Another process which is called the collision step occurs since a portion of other particles is moving from various directions to the same lattice simultaneously. The collision step which takes account of the rate of change in the particle distribution can be simplified to the Bhathagar-Gross-Krook (BGK) single relaxation time approximation [15]. Both above-mentioned steps are embodied by the discretized Boltzmann equation:

$$ f_{k} \left( {\varvec{x} + \varvec{e}_{k} \Delta t , t + \Delta t} \right) - f_{k} \left( {\varvec{x}, t} \right) = \frac{\Delta t}{\tau }\left[ {f_{k}^{eq} \left( {\varvec{x}, t} \right) - f_{k} \left( {\varvec{x}, t} \right)} \right] $$

(11.4)

The left hand side of the Eq. 11.4 expresses the streaming step and the right hand side represents the collision step where $\tau$ is the relaxation time adjusted to 1. The kinematic viscosity which is related to the relaxation time is defined as $\upsilon = c_{s}^{2} \left( {\tau - 0.5} \right)\Delta t$ where the sound speed is determined as $c_{s}^{2} = \frac{{c^{2} }}{3}$. In the collision step, the equilibrium distribution function $f_{k}^{eq}$ is calculated as:

$$ f_{k}^{eq} = \omega_{k} \rho \left[ {1 + \frac{{\varvec{e}_{k} .\varvec{u}}}{{c_{s}^{2} }} + \frac{1}{2}\left( {\frac{{\varvec{e}_{k} .\varvec{u}}}{{c_{s}^{2} }}} \right)^{2} - \frac{{\varvec{u} .\varvec{u}}}{{2c_{s}^{2} }}} \right] $$

(11.5)

where $\rho$ and u denote the fluid density and velocity, respectively. These quantities can be determined from the density distributions:

$$ \rho = \sum\limits_{k = 0}^{8} {f_{k} } $$

(11.6)

$$ \varvec{u} = \frac{1}{\rho }\sum\limits_{k = 0}^{8} {f_{k} \varvec{e}_{k} } $$

(11.7)

For fluid nodes, an initial velocity $u_{0}$ needs to be assigned as well as an initial density $\rho_{0}$ which is either the gas density $\rho_{g}$ or the liquid density $\rho_{l}$. The following initial assumption can be applied as the relaxation time is unity:

$$ f_{k} \left( {\varvec{x},t = 0} \right) = f_{k}^{eq} \left( {\varvec{x},t = 0} \right) = f_{k}^{eq} \left( {\rho_{0} ,\varvec{u}_{0} } \right) $$

(11.8)

Following Benzi et al. [16], the solid nodes possess an artificial wall density $\rho_{w}$ where $\rho_{g} \le \rho_{w} \le \rho_{l}$ to tune the substrate contact angle [17]. It is also important to note that for the lateral sides of the bounding box, periodic boundary conditions are applied for which the distribution functions carry on the opposite wall once they reach the end of the region. We also consider bounce-back boundary conditions at the solid-liquid interface as the known distribution functions from the streaming process hit the wall and scatter back to the fluid via its incoming lattice link. To obtain the inter-particle forces, the single component multiphase Shan-Chen model [14] is used as follows:

$$ \varvec{F}\left( {\varvec{x}, t} \right) = - G\psi \left( {\varvec{x}, t} \right)\sum\limits_{k = 0}^{8} {\omega_{k} \psi \left( {\varvec{x} + \varvec{e}_{\varvec{k}} \Delta t, t} \right)\varvec{e}_{k} } $$

(11.9)

where G denotes the attraction strength factor and creates the liquid-gas interface with constant surface tension, density gradient and interface thickness. $\psi$ denotes the mean field potential term and is a function of density such that [18]:

$$ \psi (\rho ) = \sqrt {\frac{{2\left( {P - c_{s }^{2} \rho } \right)}}{{c_{s }^{2} G}}} $$

(11.10)

where P denotes the pressure and is determined from the Carnahan-Starling (C-S) equation of state (EOS) [19]:

$$ P = \rho \gamma T\frac{{1 + \frac{\beta \rho }{4} + \left( {\frac{\beta \rho }{4}} \right)^{2} - (\frac{\beta \rho }{4})^{3} }}{{\left( {1 - \frac{\beta \rho }{4}} \right)^{3} }} - \alpha \rho^{2} $$

(11.11)

where T denotes the temperature and can be obtained by $T = 0.0943T_{0}$ as α = 1 $lu^{5} /(mu.ts^{2} )$, β = 4 $lu^{3} /mu$ and $\upgamma = 1\,lu^{2} /(ts^{2} .tu)$ [19]. mu and tu are the mass unit and the temperature unit, respectively.

An alternative velocity named the equilibrium velocity is considered for calculating the equilibrium distribution function [14]:

$$ \varvec{u}^{eq} = \varvec{u} + \frac{{\varvec{F }\tau }}{\rho } $$

(11.12)

where $\varvec{u}^{eq}$ denotes the equilibrium velocity and replaces u in Eq. 11.5.

After collision, a new collection of distribution functions can leave this collision lattice and another streaming step starts. These steps are performed until a final desired time is reached. Finally, the density contours can be plotted to show the liquid behaviour during its interaction with the gas and the solid. During our simulation, default values of the liquid density and gas density are $0.285\,mu/lu^{3}$ and $0.0285\,mu/lu^{3}$, respectively. Furthermore, the effect of gravity is neglected as it is assumed to be negligible compared to inertia and surface tension.

11.3 Validation

The maximum spread which occurs when an impacting droplet deforms to its largest extent along a substrate is considered as a validation case. For an oblique impact, the maximum spread is the outcome of an asymmetric behaviour created by the tangential component of the impact velocity. Since the tangential momentum affect such drop impacts, a normal and tangential Weber number is defined through the normal impact velocity $V_{n}$ and the tangential impact velocity $V_{t}$:

$$ {\text{We}}_{n} = \frac{{\rho V_{n}^{2} D}}{\sigma } $$

(11.13)

$$ {\text{We}}_{t} = \frac{{\rho V_{t}^{2} D}}{\sigma } $$

(11.14)

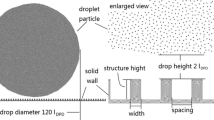
The impact angle, illustrated in Fig. 11.3, is defined as:

$$ \varPhi = \tan^{ - 1} \frac{{V_{n} }}{{V_{t} }} $$

(11.15)

Yeong et al. [8] obtained a relationship between the normalized maximum spread $D_{max} /D$ and the Weber numbers:

$$ \left( {D_{max} /D} \right) = 0.9\,{\text{We}}_{n}^{0.25} + C\,{\text{We}}_{t} $$

(11.16)

where C is a constant equal to 0.005. It should be noted that this correlation is valid for $We_{n} < 60$ since break-up occurs beyond this value.

We now model the impact of a droplet with a diameter of $D = 200\,lu$ and impact velocity V under an initial impact angle Φ = 30° onto a smooth substrate with an equilibrium contact angle of $\theta = 150{^\circ }$. Figure 11.1 shows the droplet at maximum spread when the Weber number is 50. For this case, the non-dimensional maximum spread calculated via correlation 15 yields 3.14, while our simulation gives 3.17 (error is around 1%).

Fig. 11.1

Numerical simulation of the maximum spread of a droplet when the normal Weber number and the impact angle are 50° and 30°, respectively

Numerical simulations are performed for a various range of the normal Weber numbers from 10 to 50. A comparison between the normalized maximum spread determined numerically (the blue line) and Eq. 11.16 (the black spot) is shown in Fig. 11.2. It can be seen that a good agreement is found. The maximum error is 3.7% as Φ = 10°.

Fig. 11.2

Comparison between the current numerical simulations and the correlation reported by Yeong et al. [8] for the maximum spread of an oblique impact drop on a super-hydrophobic surface when the impact angle is 30°

11.4 Results and Discussion

11.4.1 Outcomes Classification

We consider now an oblique droplet impacts on a textured substrate as is shown in Fig. 11.3. The size of the droplet is $D = 200 lu$ during all simulations and because of its diagonal motion, the impact velocity of the droplet contains two components: $V_{n} = V\sin \Phi$ and $V_{t} = V\cos \Phi$. The textured substrate features an array of identical posts. To restrict the number of independent parameters, posts have unit aspect ratio and unit spacing ratio. Therefore the width of posts W, the space between posts S, and the height of posts H are equal and such that $W = S = H = 10\,lu$. The equilibrium contact angle of the substrate is set to $\theta = 150^{^\circ }$ which is referred to a super-hydrophobic surface.

Fig. 11.3

Schematic of an oblique impacting droplet with a diameter of D and an impact angle Φ onto a substrate. V, $V_{n}$ and $V_{t}$ denote the impact velocity, the normal component and tangential components of the impact velocity, respectively

First, we investigate the possible outcomes which are observed during our simulations. Four possible outcomes are illustrated in Fig. 11.4: (a) an asymmetric spreading occurs as the lamella may spread onto substrate in an asymmetrically without splashing, (b) bilateral splashing including a prompt splash which generates tiny droplets onto the substrate from the receding contact line of the lamella and a corona splash which launches a satellite droplet from the advancing contact line of the lamella, (c) one-sided corona splashing which only occurs at the advancing contact line of the lamella and finally (d) an asymmetric break-up which takes place as an air pocket appears and grows underneath the lamella and causes a break-up at maximum spread. It is also worth noting that the combination outcome of (c) and (d) in Fig. 11.4 may occur. This combination happens when the normal Weber number increases in Case (d) and as a consequence in addition to the occurrence of the asymmetric break-up, the one-sided corona splashing also takes places in the separated right hand part of the lamella.

Fig. 11.4

Four various possible outcomes of the oblique impact of a droplet onto a super-hydrophobic textured substrate: a asymmetric spreading (${\text{We}}_{n} = 125$ and $\varPhi = 30{^\circ }$), b bilateral splashing includes simultaneous occurrence of both the prompt splash and the corona splash (${\text{We}}_{n} = 140$ and $\varPhi = 20{^\circ }$), c one-sided corona splashing (${\text{We}}_{n} = 140$ and $\varPhi = 30{^\circ }$) and d asymmetric break-up (${\text{We}}_{n} = 690$ and $\varPhi = 60{^\circ }$)

11.4.2 Effect of Impact Parameters on Splashing

The impact angle of the droplet as well as its normal Weber number lead to different wetting outcomes as mentioned in previous section. Numerical results demonstrate that the asymmetric spreading can be observed so long as the normal weber number is insufficient to trigger splashing. Therefore, such outcome may occur for any impact angle. If the normal Weber number is high enough, splashing and asymmetric break-up take place. While bilateral splashing only takes place as long as the impact angle is $\varPhi \le 20{^\circ }$, the one-sided corona splashing happens for an impact angle between $25{^\circ } \le \varPhi \le 45{^\circ }$. When the impact angle becomes $\varPhi \ge 50{^\circ }$ the asymmetric break-up can occur.

Figure 11.5 illustrates the splashing threshold values for an oblique impact with an impact angle of $5{^\circ } \le \varPhi \le 45{^\circ }$. There is no splash in the area located on the left hand side of the line. It can be seen that splashing is likely to occur with a decrease in the impact angle (i.e. increasingly tangential impact). In other words, with a lower normal weber number, splashing takes place for smaller impact angles.

Fig. 11.5

Corona splashing threshold for an oblique impact with a range of the impact angle between 5° and 45°. On left hand side of the line splashing does not occur

During corona splashing, amount of the mass which detaches away from the lamella is also an interesting quantity. In thermal spraying and for a smooth surface, Sobolev and Guilemany [20] reported that the ratio χ of the mass of the droplet which remains onto the substrate to the initial mass of the droplet is dependent on the impact angle as follows:

$$ \chi \sim \sin \varPhi $$

From the above relation, it is obvious that the loss of the droplet mass due to splashing decreases as the impact angle increases. To confirm this trend, we compared two different cases with the same normal Weber number $({\text{We}}_{n} = 140)$ and different impact angles ($\varPhi = 20{^\circ }$ Case (b) and $\varPhi = 30{^\circ }$ for Case (c) in Fig. 11.4). It can be seen that with an increase in the impact angle from $\varPhi = 20{^\circ }$ to $\varPhi = 30{^\circ }$, the mass of the satellite droplet generated during splashing decreases as predicted.

11.4.3 Effect of Texture Parameters on Splashing

In addition to the impact parameters, the substrate parameters such as texture and wettability may influence on splashing. In this section, the normal Weber number and the impact angle are kept constant and equal to ${\text{We}}_{n} = 140$ and $\varPhi = 30{^\circ }$ (Case (c) in Fig. 11.4) and numerical simulation were performed for a range of substrate parameters.

First of all, the effect of texture on splashing is investigated. When the substrate does not feature posts, splashing does not occur for a contact angle of 150° with ${\text{We}}_{n} = 140$ and $\varPhi = 30{^\circ }$ as seen in Fig. 11.6. Conversely, the presence of texture with $W = S = H = 10\,lu$ was shown to trigger the splash for the same conditions (Case c in Fig. 11.4). To understand the role of the space between posts (S), the height of post (H), and the wettability of the substrate $(\theta )$ in appearance of splashing, we now simulate six different cases as are reported in Table 11.1 and compare these numerical results with Case (c) in Fig. 11.4. The simulation results for Case 1 and Case 2 for which only the space between posts is varied are depicted in Fig. 11.7. It can be seen that with S equal to 5 lu (Case 1) the splashing is unlikely to occur (see Fig. 11.7a), whereas with an increase in this parameter to 20 lu (Case 2) the splashing is observed (see Fig. 11.7b) as was seen for Case (c) for which S was 10 lu. The difference between Case 2 and Case (c) is that splashing occurs earlier (17,000 ts for Case 2 against 20,000 ts for Case (c)). This means that the space between posts affects the time and the likelihood of splashing.

Fig. 11.6

Although the equilibrium contact angle of the substrate is $\theta = 150{^\circ }$ splashing does not occur for an oblique impact on a smooth substrate with the impact parameters ${\text{We}}_{n} = 140$ and $\varPhi = 30{^\circ }$

Table 11.1 Six simulation cases with different substrate parameters

Fig. 11.7

The effect of the space between posts (S) on the occurrence of splashing for an oblique impact with ${\text{We}}_{n} = 140$ and $\varPhi = 30{^\circ }$ on a textured substrate with an equilibrium contact angle $\theta = 150{^\circ }$: a the splashing is does not occur for Case 1 for which S = 5 lu and the height of posts (H) and the width of posts (W) are 10 lu but b splashing occurs for Case 2 which S = 20 lu and $H = W = 10\,lu$

Beside the space between posts, the height of the posts also plays an important role in splashing. Our numerical results demonstrate that for Case 3 for which the height of posts is $H = 5\,lu$ splashing does not happen as shown in Fig. 11.8a, while as previously observed in Fig. 11.4c splashing occurs when $H = 10\,lu$. Splashing takes place until $H = 20\,lu$ (Case 4). When the height of posts reaches $H = 25\,lu$ (Case 5), splashing is once more prevented as shown in Fig. 11.8b. Thus, splashing occurs between two thresholds of post height. To investigate the effect of the wettability of the substrate on splashing, we consider another case (Case 6) for which the impact parameters (${\text{We}}_{n} = 140$ and $\varPhi = 30{^\circ }$) and texture parameters ($W = S = H = 10\,lu$) are similar to Case c in Fig. 11.4. The equilibrium contact angle of the substrate is set to $\theta = 110{^\circ }$. Figure 11.4c showed that splashing occurs when the equilibrium substrate contact angle is 150°. With a reduction in the contact angle from 150° to 110°, the splashing is seen to be prevented since wettability of the substrate increases (Fig. 11.9).

Fig. 11.8

For an oblique impacting droplet with ${\text{We}}_{n} = 140$ and $\varPhi = 30{^\circ }$ onto a textured substrate with $S = W = 10\,lu$, the splashing is unlikely to occur as the height of the posts are either a $H = 5\,lu$ or b $H = 25\,lu$

Fig. 11.9

Simulation result for an oblique impacting droplet with an impact angle of 30° and normal Weber number of 140. The equilibrium contact angle of the substrate is θ = 110°. The numerical results show that the splashing vanishes with an increase in wettability of the substrate to θ = 110°

11.5 Conclusion

In this numerical study, we have developed a multiphase lattice Boltzmann code to investigate how the lamella of an oblique impacting droplet behaves onto a textured super-hydrophobic substrate. For oblique impacts, an asymmetric behaviour has been observed due to the tangential component of the impact velocity. First, as a validation case, we have performed simulations to calculate the maximum spread for an oblique impacting droplet onto a smooth surface. The numerical results have been compared with a correlation reported by Yeong et al. [8] and a good agreement has been found.

Then, numerical simulations were performed for oblique impacts on a textured substrate. Four various wetting outcomes have been identified for such impacts. The asymmetric spreading happens for any impact angle $\varPhi$ as the normal Weber is sufficiently low such that surface tension prevents splashing. Depending on the impact angle, other wetting outcome occur with an increase in the normal Weber number. Bilateral splashing including prompt and corona splash is observed for an impact angle $\varPhi \le 20{^\circ }$, one-sided corona splash for $25{^\circ } \le \varPhi \le 45{^\circ }$ and the asymmetric break-up for $\varPhi \ge 50{^\circ }$. We have also presented a graph which illustrates splashing threshold values for impact angles $5{^\circ } \le \varPhi \le 45{^\circ }$. Results show that splashing is more likely to occur for smaller impact angle. Moreover, we have demonstrated that the mass of the satellite droplet generated during corona splashing decreases as the impact angle increases as predicted by others. In addition to the impact parameters, we have studied the influence of the geometrical parameters of the textured substrate (the space between posts and the height of the posts) and also the wettability of the surface on the occurrence of splashing. We observed that the time and the occurrence of splashing are influenced by the distance between posts. Furthermore, corona splashing only occurs in a limited range of post heights. Finally, our result show that with a decrease of the substrate contact angle from θ = 150° to θ = 110°, splashing is prevented as intuitively expected.