1 Introduction

Superhydrophobic surfaces are of great technical interest because of their non-wetting behavior. Recently, it has been shown that superhydrophobic surfaces with macro-scale features with dimensions between \(10^{-1}\) and \(10^{0}\) mm can enhance water repellency by reducing the contact time between a water droplet and the solid surface. In particular, Bird et al. [1] have shown that the contact time for a droplet impacting on a superhydrophobic surface with a ridge was shorter than the contact time on a flat superhydrophobic surface because of the changed impact morphology. Gauthier et al. [2] found a relationship between contact time and number of liquid sub-units formed during impact for droplet impacting on a superhydrophobic surface with a wire. The same trend between contact time and number of liquid sub-units was reproduced by Regulagadda et al. [3] for a drop impacting on the top and between superhydrophobic triangular ridges. The majority of literature dealing with contact time reduction on superhydrophobic surfaces with submillimetric- and millimetric-scale features consists of experimental studies. Chantelot et al. [4] performed both experiments and lattice Boltzmann simulations for drop impact on a superhydrophobic surface with a small spherical feature. Shen et al. [5] have presented experimental and numerical results for a drop bouncing on short cones. More numerical research exists for drop impact on superhydrophobic curved surfaces. Khojasteh et al. [6] have studied drop impact on hydrophobic and superhydrophobic spheres of different diameters. They used a Level-Set method for their simulations. Liu et al. [7] studied experimentally and numerically with a lattice Boltzmann method drop rebound on a cylindrical surface and analyzed the total momentum distribution in the directions parallel and perpendicular to the surface curvature. A numerical study on drop impact on hydrophobic and superhydrophobic cylinders at different wettabilites and impact velocities was also performed by Liu et al. [8]. It is apparent that only very few numerical research has dealt with drop impact on superhydrophobic surfaces with small scale features. This manuscript explain the method used in Free Surface 3D (FS3D) for predicting drop impact on textured surfaces. FS3D is a program for the Direct Numerical Simulation (DNS) of incompressible multi-phase flows, which was originally created at the Institute of Aerospace Thermodynamics at the University of Stuttgart and it is continuously being improved with new features. Up to now, FS3D has successfully been used for the prediction of various phenomena such as evaporation of oscillating droplets [9], drop collisions impact [10], jet break-up [11], ice formation [12] and sublimation [13]. Rauschenberger et al. [14] implemented a method to represent the motion of rigid particles immersed in a continuous fluid phase. However, until recently FS3D could not handle the motion of a fluid interface on a rigid body of arbitrary shape. Therefore, a prerequisite of our study was a method to represent arbitrary-shaped boundaries in a Cartesian grid. In this paper, after an illustration of FS3D’s numerical fundamentals, we will discuss two methods for the implementation of solid boundaries embedded in a Cartesian grid; a first approximate method and a second more rigorous method inspired by the work of Popinet [15]. With the first method, which was developed as a simplified approach, we introduced the necessary data structures and routines that later enabled us to develop the more rigorous method. After having illustrated the concepts on which the preliminary approach is based, we will discuss its problematics which led to the development of the second approach. After this, the second more rigorous method will be explained. Finally in Sect. 4 we compare results for a water drop impacting on a superhydrophobic surface with macro-ridges obtained with the two approaches.

2 Numerical Methods

In this section, the numerical fundamentals of FS3D are illustrated briefly; the work of Eisenschmidt et al. [16] provides a broader overview. Here we focus on the case of an incompressible Newtonian fluid of a single liquid phase immersed in a continuous gas phase. The flow is assumed to be isothermal without phase change. Thus, the energy equation does not need to be considered. The governing equations of the flow are then the conservation of mass:

$$\begin{aligned} \nabla \cdot \varvec{u} = 0\,\text {,} \end{aligned}$$
(1)

and momentum transport:

$$\begin{aligned} \frac{\partial (\rho \varvec{u})}{\partial t}+\nabla \cdot (\rho \varvec{u}\otimes \varvec{u})=-\nabla p + \nabla \cdot \mathbb {S}+\rho \varvec{g}+\mathbf {f}_{\sigma }\,\text {.} \end{aligned}$$
(2)

The \(\mathbf {f}_{\sigma }\) term in Eq. (2) represents the surface tension force per unit volume which is different from zero only at the interface. This term is modeled with the Continuum Surface Stress (CSS) model of Lafaurie et al. [17]. A further equation is necessary for interface tracking. In FS3D, this equation is obtained with the Volume of Fluid (VOF) method of Hirt and Nichols [18]. The liquid disperse phase is represented by a colour function \(\chi (\varvec{x})\) defined as follows:

$$\begin{aligned} \chi (\varvec{x})={\left\{ \begin{array}{ll} 1 \quad \text {inside the liquid phase}\\ 0 \quad \text {outside the liquid phase} \end{array}\right. }\,\text {.} \end{aligned}$$
(3)

It is assumed that each material property of the flow \(\psi \), as for example density \(\rho \) or dynamic viscosity \(\mu \), is constant within each phase and is given by

$$\begin{aligned} \psi (\varvec{x}) = \psi _{\text {f}}\chi (\varvec{x})+(1-\chi (\varvec{x}))\psi _{\text {g}} \,\text {,} \end{aligned}$$
(4)

where \(\psi _{\text {f}}\) and \(\psi _{\text {g}}\) are the material property constant values in the liquid and gas phase, respectively. The equation for interface tracking is obtained by considering the volume fraction \(f=(1/\Omega )\int _{\Omega }\chi (\varvec{x})d\varvec{x}\), where \(\Omega \) is an arbitrary control volume. The transport equation for f is:

$$\begin{aligned} \frac{\partial f}{\partial t}=-\nabla \cdot (f\varvec{u})\,\text {.} \end{aligned}$$
(5)

In a space discretized domain,  \(f_{\varvec{i}}\) denotes the liquid volume fraction within the computational cell of index \(\varvec{i}=i\varvec{e}_{1}+j\varvec{e}_{2}+k\varvec{e}_{3}\). The interface is then located by identifying those cells in which \(0<f_{\varvec{i}}<1\) and reconstructed with the Piecewise Linear Interface Calculation (PLIC) scheme of Rider and Kothe [19]. Thus, in each interface cell the interface is approximated by a plane of direction \(-\hat{\varvec{n}}=\nabla f / \left\Vert \nabla f\right\Vert \) and position determined analytically by the values of f.

2.1 FS3D’s Advection Scheme

In FS3D two different methods are implemented for the numerical treatment of advection, a split and an unsplit scheme. Here the discussion is limited to the split scheme, since it was used for the presented results in this paper. Let us consider the advection equation for a generic scalar variable \(\phi \):

$$\begin{aligned} \frac{\partial \phi }{\partial t} + \varvec{u}\cdot \nabla \phi =0\,\text {,} \end{aligned}$$
(6)

which can also be written as:

$$\begin{aligned} \frac{\partial \phi }{\partial t} = - \nabla \cdot (\phi \varvec{u}) + \phi \nabla \cdot \varvec{u}\,\text {.} \end{aligned}$$
(7)

The variable \(\phi \) can be the fluid volume fraction f or a component of momentum \(\rho \varvec{u} = \rho ( u\varvec{e}_{1}+v\varvec{e}_{2}+w\varvec{e}_{3})\). The advection of \(\phi \) is then carried out in each direction separately in three different steps (or sweeps) [19, 20]. Time integration of Eq. (7) is carried out subsequently for each sweep. For example, in \(\varvec{e}_{1}\) direction and for the first sweep one obtains:

$$\begin{aligned} \frac{\phi ^*-\phi ^{n}}{\Delta t} = -\frac{\partial ( \phi u)}{\partial x}+[(1-\beta )\phi ^{n}+\beta \phi ^{*}]\frac{\partial u}{\partial x}\,\text {,} \end{aligned}$$
(8)

where the superscript \(*\) indicates an intermediate auxiliary time step. The second term on the right hand side is the divergence correction [19, 20], and \(0\le \beta \le 1\) a coefficient which indicates its implicit or explicit nature [20]. Space discretization of Eq. (7) leads to the discretized sweep equations. For example, in \(\varvec{e}_{1}\)-direction:

$$\begin{aligned}&\Omega \frac{\overline{\phi ^{*}}_{\varvec{i}}-\overline{\phi ^{n}}_{\varvec{i}}}{\Delta t} = -A_{\varvec{e}_{1}}\Big \{ \left( F_{\varvec{i}+\frac{1}{2}\varvec{e}_{1}}(\varvec{u},\,\phi )-F_{\varvec{i}-\frac{1}{2}\varvec{e}_{1}}(\varvec{u},\,\phi )\right) \nonumber \\&+\left[ (1-\beta )\overline{\phi ^{n}}_{\varvec{i}}+\beta \overline{\phi ^{*}}_{\varvec{i}}\right] \left( u_{\varvec{i}+\frac{1}{2}\varvec{e}_{1}}-u_{\varvec{i}-\frac{1}{2}\varvec{e}_{1}}\right) \Big \}\,\text {,} \end{aligned}$$
(9)

where \(\Omega =(\Delta x\varvec{e}_{1}\times \Delta y\varvec{e}_{2})\cdot \Delta z\varvec{e}_{3}=\Delta x \Delta y \Delta z\) is a Cartesian control volume, \(A_{\varvec{e}_{1}}=\left\Vert \Delta y \varvec{e}_{2}\times \Delta z \varvec{e}_{3}\right\Vert =\Delta y \Delta z\) its face perpendicular to \(\varvec{e}_{1}\). In Eq. (9), it was assumed that \(\int _{\Omega }\phi \nabla \cdot \varvec{u}d\varvec{x}\approx \overline{\phi }\int _{\Omega }\nabla \cdot \varvec{u}d\varvec{x} = \overline{\phi }[\Delta y \Delta z(u_{\varvec{i}+\frac{1}{2}\varvec{e}_{1}}-u_{\varvec{i}-\frac{1}{2}\varvec{e}_{1}})\varvec{e}_{1}+\Delta z \Delta x(v_{\varvec{i}+\frac{1}{2}\varvec{e}_{2}}-v_{\varvec{i}-\frac{1}{2}\varvec{e}_{2}})\varvec{e}_{2}+\Delta x \Delta y(w_{\varvec{i}+\frac{1}{2}\varvec{e}_{3}}-w_{\varvec{i}-\frac{1}{2}\varvec{e}_{3}})\varvec{e}_{3}]\). The terms \(F_{\varvec{i}\pm \frac{1}{2}\varvec{e}_{1}}(\varvec{u},\,\phi )\) in Eq. (9) denote the numerical fluxes. These are discretized with a second order Godunov scheme for the case of momentum components [20], whereas the geometrical procedure indicated by Rider and Kothe [19] is used to calculate the f-fluxes.

2.2 Solution of the Discretized Poisson Problem

Because the flow is incompressible, an equation for pressure is needed to solve Eq. (2). This equation is obtained by applying the divergence-free condition of the velocity field to the time-discretized Eq. (2). One obtains:

$$\begin{aligned} \frac{\nabla \cdot \tilde{\varvec{u}}}{\Delta t}=\frac{\nabla ^{2} p}{\rho }\,\text {,} \end{aligned}$$
(10)

where \(\tilde{\varvec{u}}=\tilde{u}\varvec{e}_{1}+\tilde{v}\varvec{e}_{2}+\tilde{w}\varvec{e}_{3}\) is an auxiliary velocity field where all acceleration terms of Eq. (2) but the pressure gradient have been added. By integrating Eq. (10) over a control volume \(\Omega \) and using of the Gauss theorem one obtains:

$$\begin{aligned} \int _{\partial \Omega }\frac{\tilde{\varvec{u}}\cdot \hat{\varvec{n}}}{\Delta t} d\varvec{x} = \int _{\partial \Omega } \frac{\nabla p\cdot \hat{\varvec{n}}}{\rho } d\varvec{x}\,\text {,} \end{aligned}$$
(11)

where \(\hat{\varvec{n}}\) denotes the normal vector to the surface \(\partial \Omega \). Discretization of Eq. 11 leads to a system of equations of the form:

$$\begin{aligned} \mathbf {A}\overline{p} =\mathbf {b}\,\text {,} \end{aligned}$$
(12)

where \(\mathbf {A}\) is the system matrix with dimension \(N_{cell}\times N_{cell}\), \(\overline{p}\) and \(\mathbf {b}\) are the vectors for the discrete p values and for the right hand side, respectively. Because the pressure gradient in Eq. (11) is discretized with central finite differences, on each line of the system corresponding to the control volume of index \(\varvec{i}\) all coefficients of \(\mathbf {A}\) are zero but for the ones with positions \(S_{\mathbf {A}}=\left\{ 0,\pm \varvec{e}_{1},\pm \varvec{e}_{2},\pm \varvec{e}_{3} \right\} \) with respect to \(\varvec{i}\). \(S_{\mathbf {A}}\) is called the structure of \(\mathbf {A}\) [21]. Equation (12) is solved by a multigrid solver embedded into FS3D which is specialized to deal with matrices which have the structure \(S_{\mathbf {A}}=\left\{ 0,\pm \varvec{e}_{1},\pm \varvec{e}_{2},\pm \varvec{e}_{3} \right\} \) for each computational cell.

3 Treatment of Embedded Boundaries

3.1 The Simplified Approach

To represent embedded boundaries, an additional volume fraction variable \(f_{b}\) is introduced and the boundary surface is also approximated with the PLIC scheme. Embedded boundaries are then treated as rigid bodies of infinite density. This is obtained by setting to zero all coefficients of Eq. (12), which correspond to momentum control volumes in which \(f_{b}>0\). This is equivalent to solving Eq. (12) for the stair-step approximation of the boundary (see Fig. 1a). As a consequence however, the velocities on all faces of the vast majority of the boundary-cut cells are set to zero. One a-posteriori treatment of the velocity field is then necessary to advect the fluid volume fraction in these cells. Boundary-cut cells with zero velocities on all their faces are marked as slaves and linked to the neighbor in the direction of the largest component of \(\hat{\varvec{n}}_b\), which becomes their master (see Fig. 1b). This is made possible by the apposite structured data type boundary cell:

$$ {{\mathbf {\mathtt{{boundary cell}}}}} {\left\{ \begin{array}{ll} \texttt {type(boundary cell), pointer:} &{} master, slave\\ \texttt {integer(1:3):} &{} \varvec{i} = i\varvec{e}_1+j\varvec{e}_2+k\varvec{e}_3\\ \end{array}\right. } $$

which is allocated in each boundary-cut cell and in its neighborhood. The advection of f is then carried out on the total volume of master-slave pairs using an averaged velocity field. The averaging of the velocity field after the solution of the Poisson equation causes an error in mass conservation. Even if those errors are very small in our simulations, this approach is fundamentally not conservative. With the purpose of improving conservativeness, we started the development of a new approach.

Fig. 1
figure 1

The simplified approach to embed solid structures in a Cartesian grid. a Stair-step approximation of embedded boundaries. b Merging of critical cells with the neighbor in the direction of the largest normal component \(\hat{\varvec{n}}_b\).

Full size image

3.2 The New Approach

As in the simplified approach described in Sect. 3.1, embedded boundaries are represented by their volume fraction \(f_{b}\) and their surface is approximated with the PLIC scheme. However, instead of being treated as rigid bodies of infinite density, the boundaries are cut-off from the computational domain. Following the approach of Popinet [15], the discretized equations for momentum transport (Eq. 2) and pressure (Eq. 10) are rewritten in terms of boundary-cut cell volume and faces. The same treatment is applied to the equations for interface transport (Eq. 5) and mass conservation (Eq. 1). Information about “free” volume and lateral “free” faces, as well as the orientation \(\varvec{n}_{b}\) and position \(l^*\) of the plane approximating the surface must then be stored for each boundary-cut control volume. The structured data type boundary cell is then modified as follows:

$$ {{\mathbf {\mathtt{{boundary cell}}}}} {\left\{ \begin{array}{ll} {\texttt {real}:} &{} l^{*}_{b},\,f_b\\ {\texttt {real(1:3):}} &{} \hat{\varvec{n}}_b \\ {\texttt {real(1:3,1:2):}} &{} a_{b\,\varvec{i}}\\ {\texttt {type(boundary cell), pointer:}} &{} master,\,slave\\ {\texttt {integer(1:3):}} &{} \varvec{i} = i\varvec{e}_1+j\varvec{e}_2+k\varvec{e}_3\\ \end{array}\right. } $$

where \(a_{b\,\varvec{i}}\) are the ratios of the lateral free to whole faces. For example:

$$\begin{aligned} a_{b\,\varvec{i}}(1,1)\equiv a^{-}_{b\,\varvec{e}_{1}} = \frac{A^{-}_{\varvec{i}\,\varvec{e}_{1}}}{A_{\varvec{i}\,\varvec{e}_{1}}}\,\text {,}\qquad a_{b\,\varvec{i}}(1,2)\equiv a^{+}_{b\,\varvec{e}_{1}} = \frac{A^{+}_{\varvec{i}\,\varvec{e}_{1}}}{A_{\varvec{i}\,\varvec{e}_{1}}}\,\text {.} \end{aligned}$$
(13)

where \(A^{\pm }_{\varvec{i}\,\varvec{e}_{1}}\) are the “free” lateral areas at positions \(\varvec{i}\pm \frac{1}{2}\varvec{e}_{1}\). The master and slave pointer attribute are still needed to avoid problems caused by very small cut-cells, which we will address in Sect. 3.2.1. Since the grid is staggered, the structured data type boundary cell has to be allocated in staggered control volumes as well. Therefore, the new data type boundary cell array, is introduced:

$$ {{\mathbf {\mathtt{{boundary cell array}}}}} {\left\{ \begin{array}{ll} {\texttt {type(boundary cell):}} &{}bcell_{c}\\ {\texttt {type(boundary cell):}} &{}bcell_{x}\\ {\texttt {type(boundary cell):}} &{}bcell_{y}\\ {\texttt {type(boundary cell):}} &{}bcell_{z}\\ \end{array}\right. } $$

This data structure serves as container for boundary cell data types, one for each control volume associated with a position of index \(\varvec{i}\) of the computational domain (one scalar control volume and three staggered control volumes). The boundary cell array is allocated in each position of the computational domain, in which at least one of the associated control volumes is intercepted by the boundary surface and in its neighborhood. Since phase change is not considered here, the treatment of the advection term is the point of interest for interface tracking (Eq. 5). In the case of momentum transport (Eq. 2), apart for advection and pressure, other terms have to be considered: the viscous stresses \(\nabla \cdot \mathbb {S}\), the body forces \(\rho \varvec{g}\), and the surface tension force \(\mathbf {f}_{\sigma }\). For the surface tension force no special treatment is needed, since it only depends on the interface orientation \(\hat{\varvec{n}}\). Body forces and viscous stresses are calculated by using material properties calculated on boundary-cut cell volumes. That is

$$\begin{aligned} \psi _{\varvec{i}}=\mathbf {min}\left( \left| \frac{f_{\varvec{i}}}{1-f_{b,\,\varvec{i}}}\right| ,1 \right) \psi _{l}+\left( 1-\mathbf {min}\left( \left| \frac{f_{\varvec{i}}}{1-f_{b,\,\varvec{i}}}\right| ,1 \right) \right) \psi _{g}\text {,} \end{aligned}$$
(14)

where \(0<f_{b,\,\varvec{i}}<1\) and \(\psi \) is a material property as density \(\rho \) or viscosity \(\mu \). Apart for this, the usual FS3D schemes for calculating viscous terms and body forces are used. This is equivalent to consider computational nodes on whole cell centres instead of boundary-cut cell centres. Of course, this simplification comes at the cost of slightly reduced accuracy, but it spares the computational overhead of calculating the barycentres of boundary-cut cells and the distance between the barycentres to compute gradients and linear interpolations of needed variables.

3.2.1 Advection in Boundary-Cut Cells

The split advection scheme, illustrated in Sect. 2.1, is also used on boundary-cut cells. Here Eq. (9) takes the form:

$$\begin{aligned}&\Omega (1-f_{b,\,\varvec{i}})\frac{\overline{\phi ^{*}}_{\varvec{i}}-\overline{\phi ^{n}}_{\varvec{i}}}{\Delta t} =\nonumber \\&-A_{\varvec{e}_{1}}\big (a^{+}_{b\,\varvec{e}_{1}}F_{\varvec{i}+\frac{1}{2}\varvec{e}_{1}}(\varvec{u},\,\phi )-a^{-}_{b\,\varvec{e}_{1}}F_{\varvec{i}-\frac{1}{2}\varvec{e}_{1}}(\varvec{u},\,\phi )\big )\nonumber \\&+\big [(1-\beta )\overline{\phi ^{n}}_{\varvec{i}}+\beta \overline{\phi ^{*}}_{\varvec{i}}\big ] \big (V_{\varvec{i}+\frac{1}{2}\varvec{e}_{1}}-V_{\varvec{i}-\frac{1}{2}\varvec{e}_{1}}\big ) \,\text {,} \end{aligned}$$
(15)

where \(a^{\pm }_{b\,\varvec{e}_{1}}\) are the free to whole area ratio at positions \(\varvec{i}\pm \frac{1}{2}\varvec{e}_{1}\) and V denotes an altered form of the divergence correction. For momentum advection, \(V_{\varvec{i}\pm \frac{1}{2}\varvec{e}_{1}}=A_{\varvec{e}_{1}}a^{\pm }\varvec{u}_{\varvec{i}\pm \frac{1}{2}\varvec{e}_{1}}\), for f-advection, V is calculated geometrically and it corresponds to the ratio of the cut cell volume enclosed by \(A_{\varvec{e}_{1}}\varvec{u}_{\varvec{i}\pm \frac{1}{2}\varvec{e}_{1}}\Delta t\) in upwind control volumes to the time step \(\Delta t\). FS3D’s usual schemes are used to compute the numerical fluxes. As already mentioned in Sect. 3.2, this is equivalent to considering computational nodes on whole cell centres and, consequently, faces. In the case of f-advection, the volume of arbitrary polyhedra has to be calculated in order to compute the fluxes. For this, geometrical algorithms similar to these proposed by Pathak and Raessi [22] are used. The interface position is calculated iteratively until the volume of the polyhedron representing the liquid phase corresponds to the liquid volume fraction f. As reported by Popinet [15], the occurrence of very small cells leads to prohibitively small time steps in order to satisfy the Courant-Friedrichs-Lewy (CFL) condition. Small cells are then marked as slaves and merged to the neighbor in the direction of the largest normal component, which becomes their master. Advection is then carried out in the whole master-slave control volume.

3.2.2 Discretization of the Poisson Problem on Boundary-Cut Cells

Discretization of Eq. (10) on boundary-cut volumes leads to:

$$\begin{aligned} \sum _{k}\left( Aa_{b}\frac{\nabla p}{\rho }\right) _{k}=\frac{1}{\Delta t}\sum _{k}\left( Aa_{b}u\right) _{k} \end{aligned}$$
(16)

where \(k=\varvec{i}\pm \frac{1}{2}\varvec{e}_{1,\,2,\,3}\) are the positions of the faces of the considered scalar control volume. As already mentioned in Sects. 3.1 and 3.2.1, we consider computational nodes on whole face centres instead of boundary-cut cell centres. The pressure gradient \((\nabla p)_{k}\) can then be discretized by finite differences. Then, the formulation of Eq. (16) for each control volume leads to a system of equations analogously to Eq. (12). We observed that the use of whole-face centres may cause inaccurate values of the velocity field at very small boundary-cut cells. Better accuracy may be achieved by discretizing the pressure gradient differently, as indicated by Johansen and Colella [23]. However, this would change the structure of the system matrix \(\mathbf {A}\), requiring a modification of the multigrid solver.

4 Results

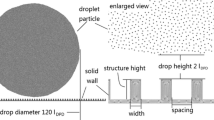
In this section, a comparison of the two methods is shown for the case of a water drop impacting on the valley between two trapezoidal ribs at a Weber number \(We=(\rho R U_{0}^2)/\sigma =11.2\) (see Fig. 2). This setup is analogous to one of the cases studied by Regulagadda et al. [24]. Because of the symmetry of the problem, only a quarter of the computational domain was simulated with a total of \(N_{x}\times N_{y}\times N_{z}= 192\times 192\times 192\) computational cells. The mesh was refined near the impact area.

Fig. 2
figure 2

Setup of the investigated case, which is analogous to one used in the experiments of Regulagadda et al. [24]

Full size image
Fig. 3
figure 3

Simulation results for drop impact on the valley between two trapezoidal ribs at \(We=11.2\). a Approximate approach. b New approach

Full size image
Fig. 4
figure 4

Mass conservation error over time

Full size image

In Fig. 3a comparison of the results obtained with the two methods is shown for different times during impact. It can be noted how the whole velocity field is affected by the choice of the method. Indeed, a difference is visible even before the drop touches the ribs. This is probably caused by the different treatment of the discretized elliptic Poisson equation. The impact occurs at a higher velocity in the new method, even if both simulations were initialized identically. Indeed, in Fig. 3b the droplet rim is thinner and faster and reaches a larger extension in the direction parallel to the ribs. The major differences however take place during the retraction phase. In both methods, the droplet assumes a three-lobed shape while retracting; in the approximate method however, these liquid sub-units merge just before take-off. The different impact morphology also explains the difference in contact time prediction. Indeed, according to Richard [25], the contact time \(t_{0}\) on a flat superhydrophobic surface does not depend on impact velocity. Instead, it scales with the inertial-capillary time scale \(\tau =\sqrt{\rho R^{3}/\sigma }\). For the case of a droplet impacting on a wire, Gauthier et al. [2] found that the contact time \(t_{c}\) was approximately \(t_{0}/\sqrt{N_{l}}\), where \(N_{l}\) denotes the number of liquid sub-units formed during impact. The same trend was confirmed by Regulagadda et al. [3] for a drop impacting on the top and between triangular ribs. For the new approach, \(t_{c}/t_{0}\) is closer to \(1/\sqrt{(}3)\), as expected from the number of liquid sub-units. The formation of three lobes was also observed by Regulagadda et al. for impact on the valley between two triangular ribs at higher impact velocities. Both methods however underestimate the contact time for this case, which is close to \(2\tau =13.316\) ms, as can be seen from a further publication from the same authors [24]. For both cases, we observe an un-physical rupture of the lamella at \(t\approx 6\) ms, which in the new approach comes together with the ejection of a very small secondary droplet. This occurs probably because the grid used for the comparison is too large to capture the thin film on the top of the solid surface. With the new method, a significant improvement in mass conservation was obtained. In Fig. 4 the mass error \(E_{m}=(m(t)-m_{0})/m_{0}\) is shown for both simulations as a function of time. The sudden step in the mass error for the new approach at \(t\approx 9.2\) ms is due to the ejection of the satellite droplet. It can be seen that the error in mass conservation could be reduced of about a factor of 3. We have indeed \(E_{m,\,\infty ,\,old}=\left\Vert (m(t)-m_{0})/m_{0}\right\Vert _{\infty } = 3.27\times 10^{-4}\) for the approximate approach and \(E_{m,\,\infty ,\,new} = 1.01\times 10^{-4}\) for the new one. This is a remarkable achievement considering the fact that the contact time between liquid and ribs is short. Better performances are expected for cases in which the interaction between droplet and solid structures has a longer duration. Further investigation on the causes of the residual error in mass conservation is planned.

5 Conclusions

Two methods to embed boundaries of arbitrary shape in a Cartesian grid have been presented, one approximate and a more rigorous one. A comparison between the two approaches for the case of a droplet impacting between two trapezoidal ribs has shown a considerable difference in impact dynamics. The cause of this discrepancy still needs to be clarified, but we expect it to be due to the different treatment of the discretized Poisson problem. Even if the newer approach has shown a slightly larger discrepancy for the contact time prediction for the case under consideration, further research is needed to assess its accuracy for other surface geometries and impact velocities. On the other hand, a remarkable reduction of the mass conservation error was obtained. Small error in mass conservation are still present however, the cause of which will be addressed by further research.