Higher Order Thermo-mechanical Gradient Plasticity Model: Nonproportional Loading with Energetic and Dissipative Components

Abstract

In this chapter, two cases of thermodynamic-based higher order gradient plasticity theories are presented and applied to the stretch-surface passivation problem for investigating the material behavior under the nonproportional loading condition. This chapter incorporates the thermal and mechanical responses of microsystems. It addresses phenomena such as size and boundary effects and in particular microscale heat transfer in fast-transient processes. The stored energy of cold work is considered in the development of the recoverable counterpart of the free energy. The main distinction between the two cases is the presence of the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$. Fleck et al. (Soc. A-Math. Phys. 470:2170, 2014, ASME 82:7, 2015) noted that ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ always gives rise to the stress jump phenomenon, which causes a controversial dispute in the field of strain gradient plasticity theory with respect to whether it is physically acceptable or not, under the nonproportional loading condition. The finite element solution for the stretch-surface passivation problem is also presented by using the commercial finite element package ABAQUS/standard (User’s Manual (Version 6.12). Dassault Systemes Simulia Corp., Providence, 2012) via the user-subroutine UEL. The model is validated by comparing with three sets of small-scale experiments. The numerical simulation part, which is largely composed of four subparts, is followed. In the first part, the occurrence of the stress jump phenomenon under the stretch-surface passivation condition is introduced in conjunction with the aforementioned three experiments. The second part is carried out in order to clearly show the results to be contrary to each other from the two classes of strain gradient plasticity models. An extensive parametric study is presented in the third part in terms of the effects of the various material parameters on the stress-strain response for the two cases of strain gradient plasticity models, respectively. The evolution of the free energy and dissipation potentials are also investigated at elevated temperatures. In the last part, the two-dimensional simulation is given to examine the gradient and grain boundary effect, the mesh sensitivity of the two-dimensional model, and the stress jump phenomenon. Finally, some significant conclusions are presented.

Introduction

It is well known that the classical continuum plasticity theory cannot capture the size effect of the microstructure during the course of plastic deformation. Aifantis (1984) incorporated a material length scale into the conventional continuum plasticity model to capture the size effect and proposed a modified flow rule by including the gradient term β∇²ε^p into the conventional flow rule as follows:

$$ {\tau}_{{\textit{ef\ f}}}=R\left({\varepsilon}^p\right)-\beta {\nabla}^2{\varepsilon}^p $$

(1)

where τ_eff is the effective stress and is calculated by ${\tau}_{\textit{ef\ f}}=\sqrt{3{\tau}_{ij}{\tau}_{ij}/2}$ with the deviatoric stress tensor τ_ij, R(ε^p) > 0 is the conventional flow resistance, ε^p is the accumulated plastic strain, β >0 is a material coefficient, and ∇² = Div∇ is the Laplacian operator. Hereafter, a number of mechanisms associated with geometrically necessary dislocations (GNDs) have been proposed within the framework of the strain gradient plasticity (SGP) theory. Generally, there are two different kinds of viewpoints in SGP theory in terms of the origin of the strengthening effect. Firstly, there is a specific argument that the strain gradient strengthening is purely energetic in the sense that GNDs originate in the blockage by grain boundaries and the pile-ups of dislocations has a backstress associated with the energetic strengthening (Fleck and Willis 2015). For example, Kuroda and Tvergaard (2010) argued that the term τ_eff + β∇²ε^p calculated in Eq. 1 represents a total stress at the material point that activates the plastic straining, i.e., the generation and movement of dislocations. They also pointed out that the thermodynamic requirement on the plastic dissipation $\mathcal{D}$ is evaluated by $\mathcal{D}=\left({\tau}_{\textit{ef\ f}}+\beta {{\nabla}}^2{\varepsilon}^p\right){\dot{\varepsilon}}^p>0$. This demonstration shows that the nonlocal term β∇²ε^p is naturally interpreted as an energetic quantity, which is consistent with the interpretation in Gurtin and Anand (2009) that the nonlocal term in Aifantis’ formulation should be energetic. Secondly, there is another point of view that GNDs combine with the statistically stored dislocations (SSDs) to provide the forest hardening, which in turn, lead to the dissipative strengthening. For example, in Fleck and Hutchinson (2001), gradient term is implicitly considered as a dissipative quantity that causes the theory to violate the thermodynamic requirement on plastic dissipation. Fleck and Willis (2009a) developed a mathematical basis for phenomenological gradient plasticity theory corresponding to both rate dependent/independent behavior with the scalar plastic multiplier. The plastic work in Fleck and Willis (2009a) is taken to be purely dissipative in nature, and the thermodynamic microstresses are assumed to be dissipative. In their incremental form of plasticity theory, an associated plastic flow rule is assumed by means of the convex yield function, consequently, the positive plastic work is ensured. Fleck and Willis (2009b) developed a phenomenological flow theory version of SGP theory by extending their theory in Fleck and Willis (2009a) to isotropic and anisotropic solids with tensorial plastic multiplier. Fleck and Willis (2009b) argued that the microstress quantities should include a dissipative part; thus, it has been proposed that the term β∇²ε^p is additively decomposed into an energetic (⋅)_en and dissipative (⋅)_dis in order to develop a kinematic hardening theory. The dissipative stresses satisfy a yield condition with an associated flow plastic rule, while the free energy provides the standard kinematic hardening.

There has been a debate between Fleck, Willis, and Hutchinson (Fleck et al. 2014, 2015; Hutchinson 2012) and Gudmundson et al. (Gudmundson 2004; Gurtin and Anand 2009) for the last 15 years or so. Fleck and Hutchinson (2001) developed a phenomenological SGP theory using higher order tensors with a similar framework to that proposed by Aifantis (1984) and Muhlhaus and Aifantis (1991). Higher order stresses and additional boundary conditions have been involved in the theory to develop a generalization of the classical rate-independent J₂ flow theory of gradient plasticity. However, they do not discuss the compatibility of their theory with thermodynamic requirements on the plastic dissipation. Gudmundson (2004) and Gurtin and Anand (2009) pointed out that the formulation of Fleck and Hutchinson (2001) violates thermodynamic requirements on the plastic dissipation. Gurtin and Anand (2009) discussed the physical nature of nonlocal terms in the flow rules developed by Fleck and Hutchinson (2001) under isothermal condition and concluded that the flow rule of Fleck and Hutchinson (2001) does not always satisfy the thermodynamic requirement on plastic dissipation unless the nonlocal term is dropped. A formulation of Fleck and Hutchinson (2001) has been modified to meet this thermodynamic requirement by partitioning the higher order microstresses into energetic and dissipative components (Hutchinson 2012). In addition, Hutchinson (2012) classified the strain gradient version of J₂ flow theories into two classes: incremental theory developed by Fleck and Hutchinson and nonincremental theory developed by Gudmundson et al. (c.f. see Fleck et al. (2014, 2015), Gudmundson (2004), Gurtin and Anand (2005, 2009), and Hutchinson (2012) for details). The specific phenomenon in the nonincremental theory that exhibits a finite stress jump due to infinitesimal changes in plastic strain that may occur under the nonproportional loading is noted and its physical acceptance is also discussed in the work of Fleck et al. (2014, 2015). Hutchinson (2012) concluded that discontinuous changes with infinitesimal changes in boundary loads are physically suspect. (Despite the argument of J.W. Hutchinson, Acta Mech. Sin. 28, 4 (2012), there is another viewpoint to look at the stress jump phenomenon. The perspective taken in N.A. Fleck, J.R. Willis, ibid. 31, (2015) is that it is premature at this moment in time to judge whether a formulation associated with the stress jump is physically acceptable or not, therefore, an in-depth study of dislocation mechanism and microscale experiments with non-proportional loading history is needed.) Fleck et al. (2014, 2015) have shown this phenomenon with two plane strain problems, stretch-passivation problem, and stretch-bending problem, for nonproportional loading condition. In their work, it is noted that the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ always generate the stress jump for nonproportional loading problems.

In this chapter, two different cases of the high order SGP model with and without the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ are presented based on the new forms of the free energy and the dissipation potentials for eliminating an elastic loading gap. The presented model is applied to the stretch-surface passivation problem in order to compare the behavior of each case under the nonproportional loading condition. For this, the finite element solution for the stretch-surface passivation problem is presented by using the commercial finite element package ABAQUS/standard (2012) via the user-subroutine UEL and validated by comparing with three sets of small-scale experiments, which have been conducted by Han et al. (2008), Haque and Saif (2003), and Xiang and Vlassak (2006). An extensive numerical work is also carried out based on the one-dimensional and two-dimensional codes in order to compare the results from the two cases of the SGP model and to analyze the characteristics of the stress jump phenomenon.

Principle of Virtual Power

The principle of virtual power is used to derive the local equation of motion and the nonlocal microforce balance for volume V as well as the equations for local traction force and nonlocal microtraction condition for the external surface S, respectively. In the presence of varying temperature fields at the microstructure level, the formulation should incorporate the effects of the temperature gradient on the thermo-mechanical behavior of the material due to the microheterogeneous nature of material (Forest and Amestoy 2008). In this sense, it is assumed here that the plastic strain, plastic strain gradient, temperature, and temperature gradient contribute to the power per unit volume.

Moreover, as it is mentioned in section “Introduction,” the effect of the interface plays a crucial role for the plastic behavior of the material at the microscale. An interface (grain boundary) separating grains ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ is taken into account here, and it is assumed that the displacement field is continuous, i.e. ${u}_i^{{\mathcal{G}}_1}={u}_i^{{\mathcal{G}}_2}$, across the grain boundary (Fig. 1). As shown in this figure, a dislocation moving toward the grain boundary in grain ${\mathcal{G}}_1$ cannot pass through the grain boundary, but it is trapped and accumulated at the grain boundary due to the misalignment of the grains ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ that are contiguous to each other. In this sense, the grain boundary acts as an obstacle to block the dislocation movement; therefore, the yield strength of the material increases as the number of grain boundaries increases. By assuming that the interface surface energy depends on the plastic strain rate at the interface of the plastically deforming phase, the internal part of the principle of virtual power for the bulk P_int and for the interface ${P}_{\mathrm{int}}^I$ are expressed in terms of the energy contributions in the arbitrary subregion of the volume V and the arbitrary subsurface of the interface S^I, respectively, as follows:

$$ {P}_{\mathrm{int}}=\int_{V}\left({\sigma}_{ij}{\dot{\varepsilon}}_{ij}^e+{\mathcal{X}}_{ij}{\dot{\varepsilon}}_{ij}^p+{\mathcal{S}}_{ijk}{\dot{\varepsilon}}_{ij,k}^p+\mathcal{A}\dot{T}+{\mathrm{\mathcal{B}}}_i{\dot{T}}_{,i}\right)dV $$

(2)

$$ {P}_{\mathrm{int}}^I={\int}_{S^I}\left({\mathbb{M}}_{ij}^{I{\mathcal{G}}_1}{{\dot{\varepsilon}}_{ij}^{pI{\mathcal{G}}_1}}+{\mathbb{M}}_{ij}^{I{\mathcal{G}}_2}{{\dot{\varepsilon}}_{ij}^{pI{\mathcal{G}}_2}}\right){dS}^I $$

(3)

Fig. 1

The schematic illustration of the spatial lattice of two contiguous grains, ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$, along with a single slip in grain ${\mathcal{G}}_1$ (Reprinted with permission from Voyiadjis et al. 2017)

where the superscripts “e,” p,” and “I” are used to express the elastic state, the plastic state, and the interface, respectively. The internal power for the bulk in the form of Eq. 2 is defined using the Cauchy stress tensor σ_ij, the backstress ${\mathcal{X}}_{ij}$ conjugate to the plastic strain rate ${\dot{\varepsilon}}_{ij}^p$, the higher order microstress S_ijk conjugate to the gradients of the plastic strain rate ${\dot{\varepsilon}}_{ij,k}^p$, and the generalized stresses $\mathcal{A}$ and $\mathcal{B}_{i}$ conjugate to the temperature rate $\dot{T}$ and the gradient of the temperature rate ${\dot{T}}_{,i}$, respectively. The internal power for the interface in the form of Eq. 3 is defined using the interfacial microscopic moment tractions ${\mathbb{M}}_{ij}^{I{\mathcal{G}}_1}$ and ${\mathbb{M}}_{ij}^{I{\mathcal{G}}_2}$ expending power over the interfacial plastic strain rates ${{\dot{\varepsilon}}_{ij}^{pI\mathcal{G}_{1}}}$ at ${S}^{I{\mathcal{G}}_1}$ and ${{\dot{\varepsilon}}_{ij}^{pI{\mathcal{G}}_2}}$ at ${S}^{I{\mathcal{G}}_2}$, respectively.

Moreover, since the plastic deformation, which is accommodated by the generation and motion of the dislocation, is influenced by the interfaces, Eq. 3 results in higher order boundary conditions generally consistent with the framework of a gradient type theory. These extra boundary conditions should be imposed at internal and external boundary surfaces or interfaces between neighboring grains (Aifantis and Willis 2005; Gurtin 2008). The internal power for the bulk is balanced with the external power for the bulk expended by the tractions on the external surfaces S and the body forces acting within the volume V as shown below:

$$ {P}_{\mathrm{ext}}={\int}_V{b}_i{v}_idV+{\int}_S\left({t}_i{v}_i+{m}_{ij}{\dot{\varepsilon}}_{ij}^p+a\dot{T}\right)dS $$

(4)

where t_i and b_i are traction and the external body force conjugate to the macroscopic velocity v_i, respectively. It is further assumed here that the external power has terms with the microtraction m_ij and a, conjugate to the plastic strain rate ${\dot{\varepsilon}}_{ij}^p$ and the temperature rate $\dot{T}$_, respectively, since the internal power in Eq. 2 contains the terms of the gradients of the plastic strain rate ${\dot{\varepsilon}}_{ij,k}^p$ and the gradients of the temperature rate ${\dot{T}}_{,i}$, respectively.

Making use of the principle of virtual power that the external power is equal to the internal power (P_int = P_ext) along with the integration by parts on some terms in Eq. 2, and utilizing the divergence theorem, the equations for balance of linear momentum and nonlocal microforce balance can be represented, respectively, for volume V, as follows:

$$ {\sigma}_{ij,j}+{b}_i=0 $$

(5)

$$ {\mathcal{X}}_{ij}-{\tau}_{ij}-{\mathcal{S}}_{ijk,k}=0 $$

(6)

$$ \operatorname{div}{\mathrm{\mathcal{B}}}_i-\mathcal{A}=0 $$

(7)

where τ_ij = σ_ij − σ_kkδ_ij/3 is the deviatoric part of the Cauchy stress tensor and δ_ij is the Kronecker delta.

On the external surface S, the equations for local surface traction conditions and nonlocal microtraction conditions can be written, respectively, with the outward unit normal vector to S, n_k, as follows:

$$ {t}_j={\sigma}_{ij}{n}_i $$

(8)

$$ {m}_{ij}={\mathcal{S}}_{ijk}{n}_k $$

(9)

$$ a={\mathrm{\mathcal{B}}}_i{n}_i $$

(10)

In addition, the interfacial external power ${P}_{\mathrm{ext}}^I$, which is balanced with the interfacial internal power ${P}_{\mathrm{int}}^I$, is expended by the macrotractions ${\sigma}_{ij}^{{\mathcal{G}}_1}(-{n}_j^I)$ and ${\sigma}_{ij}^{{\mathcal{G}}_2}({n}_j^I)$ conjugate to the macroscopic velocity v_i, and the microtractions ${\mathbb{S}}_{ijk}^{I{\mathcal{G}}_1}\left(-{n}_k^I\right)$ and ${\mathbb{S}}_{ijk}^{I{\mathcal{G}}_2}\left({n}_k^I\right)$ that are conjugate to ${{\dot{\varepsilon}}_{ij}^{pI{\mathcal{G}}_1}}$ and ${{\dot{\varepsilon}}_{ij}^{pI{\mathcal{G}}_2}}$, respectively, as follows:

$$ {P}_{\mathrm{ext}}^I={\int}_{S^I}\left\{\left({\sigma}_{ij}^{{\mathcal{G}}_2}{n}_j^I-{\sigma}_{ij}^{{\mathcal{G}}_1}{n}_j^I\right){v}_i+{\mathbb{S}}_{ijk}^{I{\mathcal{G}}_2}{n}_k^I{{\dot{\varepsilon}}_{ij}^{pI{\mathcal{G}}_2}}-{\mathbb{S}}_{ijk}^{I{\mathcal{G}}_1}{n}_k^I{{\dot{\varepsilon}}_{ij}p^{I{\mathcal{G}}_1}}\right\}{dS}^I $$

(11)

By equating ${P}_{\mathrm{int}}^I={P}_{\mathrm{ext}}^I$ with considering the arbitrary variation of the plastic strain at the interface, the interfacial macro- and microforce balances can be obtained as follows:

$$ \left({\sigma}_{ij}^{{\mathcal{G}}_1}-{\sigma}_{ij}^{{\mathcal{G}}_2}\right){n}_j^I=0 $$

(12)

$$ {\mathbb{M}}_{ij}^{I{\mathcal{G}}_1}+{\mathbb{S}}_{ijk}^{I{\mathcal{G}}_1}{n}_k^I=0 $$

(13)

$$ {\mathbb{M}}_{ij}^{I{\mathcal{G}}_2}-{\mathbb{S}}_{ijk}^{I{\mathcal{G}}_2}{n}_k^I=0 $$

(14)

The microforce balance conditions in Eqs. 13 and 14 represent the coupling behavior in the grain interior at the interface to the behavior of the interface, since the microtractions ${\mathbb{S}}_{ijk}^{I{\mathcal{G}}_1}{n}_k^I$ and ${\mathbb{S}}_{ijk}^{I{\mathcal{G}}_2}{n}_k^I$ are the special cases of Eq. 8 for the internal surface of the interface.

Thermodynamic Formulation with Higher Order Plastic Strain Gradients

The first law of thermodynamics , which encompasses several principles including the law of conservation of energy, is taken into account in this chapter in order to develop a thermodynamically consistent formulation accounting for the thermo-mechanical behavior of small-scale metallic volumes during the fast transient process. In order to consider micromechanical evolution in the first law of thermodynamics, the enhanced SGP theory with the plastic strain gradient is employed for the mechanical part of the formulation, whereas the micromorphic model is employed for the thermal counterpart as follows (see the work of Forest and co-workers (Forest and Amestoy 2008; Forest and Sievert 2003)):

$$ \rho \dot{\mathrm{e}}={\sigma}_{ij}{\dot{\varepsilon}}_{ij}^e+{\mathcal{X}}_{ij}{\dot{\varepsilon}}_{ij}^p+{\mathcal{S}}_{ijk}{\dot{\varepsilon}}_{ij,k}^p+\mathcal{A}\dot{T}+{\mathrm{\mathcal{B}}}_i{\dot{T}}_{,i}-div{q}_i $$

(15)

$$ {\dot{e}}^I={\mathbb{M}}_{ij}^I{\dot{\varepsilon}}_{ij}^{pI}+{q}_i^I{n}_i^I $$

(16)

where ρ is the mass density, e is the specific internal energy, e^I is the internal surface energy density at the contacting surface, and q_i and ${q}_i^I$ are the heat flux vectors of the bulk and the interface, respectively.

The second law of thermodynamics, or entropy production inequality as it is often called, yields a physical basis that accounts for the distribution of GNDs within the body along with the energy carrier scattering and requires that the free energy increases at a rate not greater than the rate at which work is performed. Based on this requirement, entropy production inequalities for the bulk and the interface can be expressed, respectively, as follows:

$$\rho \dot{\mathcal{s}}T-\rho \dot{\mathrm{e}}+{\sigma }_{\mathrm{ij}}{\dot{\epsilon }}_{\mathrm{ij}}^e+{\mathcal{X}}_{\mathrm{ij}}{\dot{\epsilon }}_{\mathrm{ij}}^p+{\mathcal{S}}_{\mathrm{ijk}}{\dot{\epsilon }}_{\mathrm{ij},k}^p-q_i\frac{T_{,i}}{T}+\mathcal{A}\dot{T}+{\mathrm{ℬ}}_i{\dot{T}}_{,i}\ge 0$$

(17)

$${\dot{\mathcal{s}}}^I{T}^I-q_i^I{n}_i^I\ge 0$$

(18)

where is the specific entropy and is the surface density of the entropy of the interface.

The Energetic and Dissipative Components of the Thermodynamic Microstresses

Internal ene rgy e, temperature T, and entropy describing the current state of the material can be attributed to the Helmholtz free energy Ψ (per unit volume) such as

(19)

By taking the time derivative of Eq. 19 for the bulk and the interface and substituting each into Eqs. 17 and 18, respectively, the nonlocal free energy (i.e., Clausius-Duhem) inequality for the bulk and the interface can be obtained as follows:

(20)

(21)

In order to derive the constitutive equations within a small-scale framework, an attempt to account for the effect of nonuniform distribution of the microdefection with temperature on the homogenized response of the material is carried out in this chapter with the functional forms of the Helmholtz free energy in terms of its state variables. By assuming the isothermal condition for the interface (i.e., ${\dot{T}}^I=0$), the Helmholtz free energy for the bulk and the interface are given, respectively, by

$$ \varPsi =\varPsi \left({\varepsilon}_{ij}^e,{\varepsilon}_{ij}^p,{\varepsilon}_{ij,k}^p,T,{T}_{,i}\right) $$

(22)

$$ {\varPsi}^I={\varPsi}^I\left({\varepsilon}_{ij}^{pI}\right) $$

(23)

where the function Ψ is assumed to be smooth and the function Ψ¹ is assumed to be convex with respect to a plastic strain at the interface ${\varepsilon}_{ij}^{pI}$.

Taking time derivative of the Helmholtz free energy for the bulk $\dot{\varPsi}$ and the interface ${\dot{\varPsi}}^I$ give the following expressions, respectively

$$ \dot{\varPsi}=\frac{\partial \varPsi }{\partial {\varepsilon}_{ij}^e}{\dot{\varepsilon}}_{ij}^e+\frac{\partial \varPsi }{\partial {\varepsilon}_{ij}^p}{\dot{\varepsilon}}_{ij}^p+\frac{\partial \varPsi }{\partial {\varepsilon}_{ij,k}^p}{\dot{\varepsilon}}_{ij,k}^p+\frac{\partial \varPsi }{\partial T}\dot{T}+\frac{\partial \varPsi }{\partial {T}_{,i}}{\dot{T}}_{,i} $$

(24)

$$ {\dot{\varPsi}}^I=\frac{\partial {\varPsi}^I}{\partial {\varepsilon}_{ij}^{pI}}{\dot{\varepsilon}}_{ij}^{pI} $$

(25)

By substituting Eq. 24 into Eq. 20 for the bulk and Eq. 25 into Eq. 21 for the interface, and factoring out the common terms, one obtains the following inequalities:

(26)

$$ {\mathbb{M}}_{ij}^I{\dot{\varepsilon}}_{ij}^{pI}-\rho \frac{\partial {\Psi}^I}{\partial {\varepsilon}_{ij}^{pI}}{\dot{\varepsilon}}_{ij}^{pI}\ge 0 $$

(27)

Guided by Eqs. 26 and 27, it is further assumed that the thermodynamic microstress quantities ${\mathcal{X}}_{ij}$, ${\mathcal{S}}_{ijk}$, $\mathcal{A}$, and ${\mathbb{M}}_{ij}^I$ are decomposed into the energetic and the dissipative components such as (Voyiadjis and Deliktas 2009; Voyiadjis and Faghihi 2012; Voyiadjis et al. 2014):

$$ {\mathcal{X}}_{ij}={\mathcal{X}}_{ij}^{\mathrm{en}}+{\mathcal{X}}_{ij}^{\mathrm{dis}} $$

(28)

$$ {\mathcal{S}}_{ijk}={\mathcal{S}}_{ijk}^{\mathrm{en}}+{\mathcal{S}}_{ijk}^{\mathrm{dis}} $$

(29)

$$ \mathcal{A}={\mathcal{A}}^{\mathrm{en}}+{\mathcal{A}}^{\mathrm{dis}} $$

(30)

$$ {\mathbb{M}}_{ij}^I={\mathbb{M}}_{ij}^{I,\mathrm{en}}+{\mathbb{M}}_{ij}^{I,\mathrm{dis}} $$

(31)

The components ${\mathbb{M}}_{ij}^{I,\mathrm{en}}$ and ${\mathbb{M}}_{ij}^{I,\mathrm{dis}}$ represent the mechanisms for the pre- and postslip transfer and thus involve the plastic strain at the interface prior to the slip transfer ${\varepsilon_{ij}^{p^{I\left(\mathrm{pre}\right)}}}$ and the one after the slip transfer ${\varepsilon_{ij}^{p^{I\left(\mathrm{post}\right)}}}$, respectively. The overall plastic strain at the interface can be obtained by the summation of both plastic strains such as:

$$ {\varepsilon_{ij}^p}^I={\varepsilon_{ij}^{p^{I\left(\mathrm{pre}\right)}}}+{\varepsilon_{ij}^{p^{I\left(\mathrm{post}\right)}}} $$

(32)

Substituting Eqs. 28, 29, and 30 into Eq. 26 for the bulk and Eq. 31 into Eq. 27 for the interface and rearranging them in accordance with the energetic and the dissipative parts give the following expressions:

(33)

$$ \left({\mathbb{M}}_{ij}^{I,\mathrm{en}}-\rho \frac{\partial {\varPsi}^I}{\partial {\varepsilon}_{ij}^{pI}}\right){\dot{\varepsilon}}_{ij}^{pI}+{\mathbb{M}}_{ij}^{I,\mathrm{dis}}{\dot{\varepsilon}}_{ij}^{pI}\ge 0 $$

(34)

From the above equations with the assumption that the fifth term in Eq. 33 is strictly energetic, one can retrieve the definition of the energetic part of the thermodynamic microstresses as follows:

(35)

$$ {\mathbb{M}}_{ij}^{I,\mathrm{en}}=\rho \frac{\partial {\varPsi}^I}{\partial {\varepsilon}_{ij}^{pI}} $$

(36)

Hence, the residual respective dissipation is then obtained as:

$$ \mathcal{D}={\mathcal{X}}_{ij}^{\mathrm{dis}}{\dot{\varepsilon}}_{ij}^p+{\mathcal{S}}_{ijk}^{\mathrm{dis}}{\dot{\varepsilon}}_{ij,k}^p+{\mathcal{A}}^{\mathrm{dis}}\dot{T}-\frac{q_i}{T}{T}_{,i}\ge 0 $$

(37)

$$ {\mathcal{D}}^I={\mathbb{M}}_{ij}^{I,\mathrm{dis}}{\dot{\varepsilon}}_{ij}^{pI}\ge 0 $$

(38)

where $\mathcal{D}$ and ${\mathcal{D}}^I$ are the dissipation densities per unit time for the bulk and the interface, respectively. The definition of the dissipative thermodynamic microstresses can be obtained from the complementary part of the dissipation potentials $\mathcal{D}\left({\dot{\varepsilon}}_{ij}^p,{\dot{\varepsilon}}_{ij,k}^p,\dot{T},{T}_{,i}\right)$ and ${\mathcal{D}}^I\left({\dot{\varepsilon}}_{ij}^{pI}\right)$ such as

$$ {\mathcal{X}}_{ij}^{\mathrm{dis}}=\frac{\partial \mathcal{D}}{\partial {\dot{\varepsilon}}_{ij}^p};{\mathcal{S}}_{ijk}^{\mathrm{dis}}=\frac{\partial \mathcal{D}}{\partial {\dot{\varepsilon}}_{ij,k}^p};{\mathcal{A}}^{\mathrm{dis}}=\frac{\partial \mathcal{D}}{\partial \dot{T}};-\frac{q_i}{T}=\frac{\partial \mathcal{D}}{\partial {T}_{,i}} $$

(39)

$$ {\mathbb{M}}_{ij}^{I,\mathrm{dis}}=\frac{\partial {\mathcal{D}}^I}{\partial {\dot{\varepsilon}}_{ij}^{pI}} $$

(40)

One now proceeds to present the constitutive laws for both the energetic and the dissipative parts which are achieved by employing the free energy and the dissipation potentials, which relate the stresses to their work-conjugate generalized stresses. The functional forms of the Helmholtz free energy and dissipation potential and the corresponding energetic and dissipative thermodynamic microstresses for the aforementioned two different cases of the model, i.e., the case with the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ and the one without ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$, are presented in the following sections.

Helmholtz Free Energy and Energetic Thermodynamic Microstresses

Defining a specific form of the Helmholtz free energy function Ψ is t remendously important since it constitutes the bases in deriving the constitutive equations. In this chapter, the Helmholtz free energy function is put forward with three main counterparts, i.e., elastic, defect, and thermal energy, as follows (Voyiadjis and Song 2017):

$$ \begin{aligned}\Psi &=\substack{\underbrace{\left\{\frac{1}{2\rho }{\varepsilon}_{ij}^e{E}_{ij{kl}}{\varepsilon}_{{kl}}^e-\frac{\alpha_t}{\rho}\left(T-{T}_r\right){\varepsilon}_{ij}^e{\delta}_{ij}\right\}}\\ \Psi^e\left({elastic}\right)}\nonumber\\ &\quad+\left\{\substack{\underbrace{\frac{1}{\rho}\left(\substack{\underbrace{\frac{h}{r+1}\left(1-{\left(\frac{T}{T_y}\right)}^n\right){\varepsilon}_p^{r+1}}\\{\varPsi_1^d}}+\substack{\underbrace{\frac{G}{2}{\ell}_{{en}}^2{\varepsilon}_{{lm},n}^p{\varepsilon}_{{lm},n}^p}\\{\varPsi_2^d}}\right)}\\ {\varPsi^d\left({defect}\right)}}\right\}\nonumber\\ &\quad +\substack{\underbrace{\left\{-\frac{1}{2}\frac{c_{\varepsilon }}{T_r}{\left(T-{T}_r\right)}^2-\frac{1}{2\rho }a{T}_{,i}{T}_{,i}\right\}}\\{\varPsi^t\left({thermal}\right)}}\end{aligned} $$

(41)

where E_ijkl is the elastic modulus tensor, α_t is the coefficient of linear thermal expansion, T_r is the reference temperature, h is the hardening material constant corresponding to linear kinematic hardening, r (0 < r < 1) is the isotropic hardening material constant, ${\varepsilon}_p=\sqrt{\varepsilon_{ij}^p{\varepsilon}_{ij}^p}$ is the accumulated plastic strain, T_y and n are the thermal material constants that need to be calibrated by comparing with the experimental data, ℓ_en is the energetic length scale that describes the feature of the short-range interaction of GNDs, G is the shear modulus for isotropic linear elasticity, c_ε is the specific heat capacity at constant stress, and a is a material constant accounting for the interaction between energy carriers such as phonon-electron. The term (1 − (T/T_y)ⁿ) in Eq. 41 accounts for the thermal activation mechanism for overcoming the local obstacles to dislocation motion.

The first term of the defect energy ${\varPsi}_1^d$ characterizes the interaction between slip systems, i.e., the forest dislocations leading to isotropic hardening. This term is further assumed to be decomposed into the recoverable counterpart ${\varPsi}_1^{d,R}$ and nonrecoverable counterpart ${\varPsi}_1^{d,\mathrm{NR}}$. The establishment of the plastic strain gradient independent stored energy of cold work with no additional material parameters is achievable with this decomposition.

The recoverable counterpart, ${\varPsi}_1^{d,R}$, accounts for the stored energy of cold work. When the elasto-plastic solid is cold-worked, most of the mechanical energy is converted into heat, but the remaining contributes to the stored energy of cold work through the creation and rearrangement of crystal defects such as dislocations, point defects, line defects, and stacking faults (Rosakis et al. 2000). In this chapter, the plastic strain-dependent free energy, ${\varPsi}_1^{d,R}$, accounting for the stored energy of cold work is derived by assuming that the stored energy is related to the energy carried by dislocations. Mollica et al. (2001) investigated the inelastic behavior of the metals subject to loading reversal by linking the hardening behavior of the material to thermo-dynamical quantities such as the stored energy due to cold work and the rate of dissipation. In the work of Mollica et al. (2001), it is assumed that the stored energy depends on the density of the dislocation network that increases with monotonic plastic deformation until it is saturated at some point. This points out that the material stores this energy for a certain range of the accumulated plastic strain, after which the material will mainly dissipate the external work supply.

For the derivation of the stored energy of cold work, one assumes that the energetic microstress ${\mathcal{X}}_{ij}^{\mathrm{en}}$, given later by Eq. 52, can be expressed by separation of variables as follows:

$$ {\mathcal{X}}_{ij}^{\mathrm{en}}\left({\varepsilon}_{ij}^p,T\right)=\sum \left({\varepsilon}_{ij}^p\right)\mathcal{T}(T) $$

(42)

with $\sum \left({\varepsilon}_{ij}^p\right)=h{\varepsilon}_{ij}^p{\varepsilon}_p^{r-1}$ and $\mathcal{T}(T)=\left(1-{\left(T/{T}_y\right)}^n\right)$.

On the other hand, instead of using the plastic strain at the macroscale level to describe the plastic deformation, Σ can be defined at the microscale level using the Taylor law, which gives a simple relation between the shear strength and the dislocation density, as follows:

$$ \sum =\varsigma \mathrm{Gb}\sqrt{\rho_t} $$

(43)

where ς is the statistical coefficient accounting for the deviation from regular spatial arrangements of the dislocation populations, b is the magnitude of the Burgers vector, and ρ_t is the equivalent total dislocation density and can be obtained by (Σ/ςGb)² from Eq. 43.

Here, it is assumed that the stored energy of cold work, the result of energy carried by each dislocation, results in an extra latent hardening which is recoverable and temperature independent. Thus, the recoverable energy of cold work can be put forward as follows:

$$ {\varPsi}_1^{d,R}=\mathbb{U}{\rho}_t $$

(44)

where $\mathbb{U}$ is the elastic deformation energy of a dislocation and can be approximately given by

$$ \mathbb{U}=\frac{{\mathrm{Gb}}^2}{4\pi}\operatorname{ln}\left(\frac{R}{R_0}\right) $$

(45)

where R is the cut-off radius (R ≈ 10³b) and R₀ is the internal radius (b < R₀ < 10b) (Meyers and Chawla 2009). By substituting ρ_t = (Σ/ςGb)² into Eq. 45 along with Eq. 42, one can obtain the stored energy of cold work as follows:

$$ {\varPsi}_1^{d,R}=\vartheta {h}^2{\varepsilon}_p^{2r} $$

(46)

where by comparing the aforementioned ranges for R, R₀, and ς to the shear modulus G, ϑ can be expressed by

$$ \vartheta =\frac{1}{4{\pi \varsigma}^2G}\operatorname{ln}\left(\frac{R}{R_0}\right)\approx \frac{1}{G} $$

(47)

The nonrecoverable counterpart ${\varPsi}_1^{d,\mathrm{NR}}$ accounting for the energetically based hardening rule that mimics the dissipative behavior by describing irreversible loading processes can then be derived as follows (Gurtin and Reddy 2009):

$$ {\varPsi}_1^{d,\mathrm{NR}}=\frac{h}{r+1}\left(1-{\left(\frac{T}{T_y}\right)}^n\right){\varepsilon}_p^{r+1}-\vartheta {h}^2{\varepsilon}_p^{2r} $$

(48)

where ϑ is a constant that depends on the material microstructure.

The second term of the defect energy ${\varPsi}_2^d$ characterizes the short-range interactions between coupling dislocations moving on close slip planes and leads to the kinematic hardening. This defect energy ${\varPsi}_2^d$ is recoverable in the sense that by starting at any value of the accumulated plastic strain gradients, ${\varPsi}_2^d$ returns to its original value as the accumulated plastic strain gradients return to their original value.

One can now obtain the energetic thermodynamic forces by using the definitions in Eq. 35 along with the Helmholtz free energy given by Eq. 41 as follows:

$$ {\sigma}_{ij}={E}_{ij\mathrm{kl}}{\varepsilon}_{\mathrm{kl}}^e-{\alpha}_t\left(T-{T}_r\right){\delta}_{ij} $$

(49)

(50)

$$ {\mathrm{\mathcal{B}}}_i=-{{aT}}_{,i} $$

(51)

$$ {\mathcal{X}}_{ij}^{\mathrm{en}}=h{\varepsilon}_{ij}^p\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\ {\varepsilon}_p^{r-1} $$

(52)

$$ {\mathcal{S}}_{ijk}^{\mathrm{en}}=G{\ell}_{\mathrm{en}}^2{\varepsilon}_{ij,k}^p $$

(53)

Here, according to the aforementioned decomposition of the first term of the defect energy into the recoverable and nonrecoverable counterparts, ${\mathcal{X}}_{ij}^{\mathrm{en}}$ can be further decomposed into recoverable $\left({\mathcal{X}}_{ij}^{\mathrm{en},R}\right)$ and nonrecoverable $\left({\mathcal{X}}_{ij}^{\mathrm{en},\mathrm{NR}}\right)$ counterparts as follows:

$$ {\mathcal{X}}_{ij}^{\mathrm{en},R}=2 r\vartheta {h}^2{\varepsilon}_{ij}^p{\varepsilon}_p^{2r-2} $$

(54)

$$ {\mathcal{X}}_{ij}^{\mathrm{en},\mathrm{NR}}=\mathrm{h}{\varepsilon}_{ij}^p\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\ {\varepsilon}_p^{r-1}-2 r\vartheta {h}^2{\varepsilon}_{ij}^p{\varepsilon}_p^{2r-2} $$

(55)

From the aforementioned physical interpretations of ${\varPsi}_1^{d,R}$ and ${\varPsi}_1^{d,\mathrm{NR}}$, as well as ${\mathcal{X}}_{ij}^{\mathrm{en},R}$ and ${\mathcal{X}}_{ij}^{\mathrm{en},\mathrm{NR}}$ can be defined as the terms describing the reversible loading due to the energy carried by dislocations and the energetically based hardening rule that mimics dissipative behavior by describing irreversible loading processes, respectively.

Meanwhile, it is well known that the interface plays a role as the barrier to plastic slip in the early stages of plastically deforming phase, while it acts as a source of the dislocation nucleation in the later stages. The energetic condition in the area around the interface is affected by the long-range internal stress fields associated with constrained plastic flow which leads to the accumulated and pile-up of dislocations near the interface. Thus, the condition at the interface is determined by a surface energy that depends on the plastic strain state at the interface (Fredriksson and Gudmundson 2005).

The interfacial Helmholtz free energy per unit surface area of the interface is put forward under the guidance of Fredriksson and Gudmundson (2005) work such as (It should be noted that it is possible to introduce another form of the surface energy if it is convex in, ${\varepsilon}_{ij}^{pI}$.):

$$ {\varPsi}^I=\frac{1}{2}G{\ell}_{\mathrm{en}}^I{\varepsilon_{ij}^{p^{I\left(\mathrm{pre}\right)}}}{\varepsilon_{ij}^{p^{I\left(\mathrm{pre}\right)}}} $$

(56)

where ${\ell}_{\mathrm{en}}^I$ is the interfacial recoverable length scale.

By substituting the interfacial Helmholtz free energy per unit surface given by Eq. 56 into Eq. 36, the interfacial recoverable microstresses ${\mathbb{M}}_{ij}^{I,\mathrm{en}}$ can be obtained as follows:

$$ {\mathbb{M}}_{ij}^{I,\mathrm{en}}=G{\ell}_{\mathrm{en}}^I{\varepsilon_{ij}^{p^{I\left(\mathrm{pre}\right)}}} $$

(57)

As can be seen in Eq. 57, ${\mathbb{M}}_{ij}^{I,\mathrm{en}}$ does not involve the plastic strain rate, which is related to the dislocation slip, and the temperature since the interfacial recoverable microstresses are activated by the recoverable stored energy.

Dissipation Potential and Dissipative Thermodynamic Microstresses

In this section, the dissipation potential functions for the aforementioned two cases of the SGP model are postulated, respectively. The first case is derived from the dissipation potential dependent on the plastic strain gradient, which leads to the nonzero dissipative thermodynamic microstress${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, while the other case is derived from the dissipa tion potential that is independent on the plastic strain gradient, which leads to ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$.

Coleman and Gurtin (1967) pointed out that the dissipation potential function is composed of two parts, the mechanical part which is dependent on the plastic strain and its gradient and the thermal counterpart which shows the purely thermal effect such as the heat conduction. In this sense, and in the context of Eq. 37, the functional form of the dissipation potential, which is dependent on ${\dot{\varepsilon}}_{ij,k}^p$, for the former class can be put forward as (Voyiadjis and Song 2017):

$$\begin{array}{l}\mathcal{D}=\frac{{\sigma }_y}{2\dot{\mathcal{p}}}\left\{{\left(\frac{\dot{\mathcal{p}}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\left({\dot{\epsilon }}_{\mathrm{ij}}^p{\dot{\epsilon }}_{\mathrm{ij}}^p\right)+{\ell }_{\mathrm{dis}}^2{\left(\frac{\dot{\mathcal{p}}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\left({\dot{\epsilon }}_{\mathrm{lm},k}^p{\dot{\epsilon }}_{\mathrm{lm},k}^p\right)\right\}\\ -\frac{b}{2}{\dot{T}}^2-\frac{1}{2}\frac{k\left(T\right)}{T}{T}_{,i}{T}_{,i}\ge 0\end{array}$$

(58)

where σ_y is a material constant accounting for the yield strength, m is a nonnegative material constant for the rate sensitivity parameter, in which the limit m → 0 corresponds to rate-independent material behavior, is a constant for the reference flow rate, ℓ_dis is the dissipative length scale that corresponds to the dissipative effects in terms of the gradient of the plastic strain rate, b is the material constant accounting for the energy exchange between phonon and electron, and k(T) is the thermal conductivity coefficient. The generalized dissipative effective plastic strain measure is defined as a function of the plastic strain rate, the gradient of the plastic strain rate, and the dissipative length scale as follows:

$$\dot{\mathcal{p}}=\sqrt{{\dot{\epsilon }}_{\mathrm{ij}}^p{\dot{\epsilon }}_{\mathrm{ij}}^p+{\ell }_{\mathrm{dis}}^2{\dot{\epsilon }}_{\mathrm{lm},k}^p{\dot{\epsilon }}_{\mathrm{lm},k}^p}$$

(59)

By using the dissipation potential given in Eq. 58 along with Eq. 39 and the assumption k(T)/T = k₀ = constant, the dissipative thermodynamic forces for the former case (Case I) can be obtained as follows:

$${\mathcal{X}}_{\mathrm{ij}}^{\mathrm{dis}}={\sigma }_y{\left(\frac{\dot{\mathcal{p}}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\frac{{\dot{\epsilon }}_{\mathrm{ij}}^p}{\dot{\mathcal{p}}}$$

(60)

$${\mathcal{S}}_{\mathrm{ijk}}^{\mathrm{dis}}={\sigma }_y{\ell }_{\mathrm{dis}}^2{\left(\frac{\dot{\mathcal{p}}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\frac{{\dot{\epsilon }}_{\mathrm{ij},k}^p}{\dot{\mathcal{p}}}$$

(61)

$$ {\mathcal{A}}^{\mathrm{dis}}=-\mathrm{b}\dot{\mathrm{T}} $$

(62)

$$ {q}_i=-{k}_0{T}_{,i} $$

(63)

On the other hand, the functional form of the dissipation potential, which is independent of ${\dot{\varepsilon}}_{ij,k}^p$, for the latter case (Case II) can be postulated by setting ℓ_dis = 0 in Eq. 58 as follows:

$$\mathcal{D}=\frac{{\sigma }_y}{2}{\left(\frac{{\dot{\mathcal{p}}}_{{\ell }_{\mathrm{dis}}=0}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right){\dot{\mathcal{p}}}_{{\ell }_{\mathrm{dis}}=0}-\frac{b}{2}{\dot{T}}^2-\frac{1}{2}\frac{k\left(T\right)}{T}{T}_{,\mathrm{i}}{T}_{,i}\ge 0$$

(64)

where is given by $\sqrt{{\dot{\varepsilon}}_{ij}^p{\dot{\varepsilon}}_{ij}^p}$ by setting ℓ_dis = 0 in Eq. 59. By substituting Eq. 64 into Eq. 39, the dissipative thermodynamic forces for the latter case (Case II) can be obtained as follows:

$${\mathcal{X}}_{\mathrm{ij}}^{\mathrm{dis}}={\sigma }_y{\left(\frac{{\dot{\mathcal{p}}}_{{\ell }_{\mathrm{dis}}=0}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\frac{{\dot{\epsilon }}_{\mathrm{ij}}^p}{{\dot{\mathcal{p}}}_{{\ell }_{\mathrm{dis}}=0}}$$

(65)

$$ {\mathcal{S}}_{ijk}^{\mathrm{dis}}=0 $$

(66)

$$ {\mathcal{A}}^{\mathrm{dis}}=-\mathrm{b}\dot{\mathrm{T}} $$

(67)

$$ {q}_i=-{k}_0{T}_{,i} $$

(68)

Meanwhile, Gurtin and Reddy (2009) pointed out that the classical isotropic hardening rule, which is dissipative in nature, may equally well be characterized via a defect energy since this energetically based hardening rule mimics the dissipative behavior by describing loading processes that are irreversible. In this sense, as it was mentioned previously in this chapter, the energetic microstress ${\mathcal{X}}_{ij}^{\mathrm{en}}$ is further decomposed into ${\mathcal{X}}_{ij}^{\mathrm{en},\mathrm{NR}}$ that describes an irreversible loading process and ${\mathcal{X}}_{ij}^{\mathrm{en},R}$ that describes a reversible loading process due to the energy carried by the dislocations. The present framework follows the theorem of Gurtin and Reddy (2009) in that the theory without a defect energy is equivalent to the theory with a defect energy by replacing the dissipation $\mathcal{D}$ by an effective dissipation ${\mathcal{D}}_{\mathrm{eff}}$, which is defined as follows:

$$ {\mathcal{D}}_{\mathrm{eff}}=\left({\mathcal{X}}_{ij}^{\mathrm{dis}}+{\mathcal{X}}_{ij}^{\mathrm{en},\mathrm{NR}}\right){\dot{\varepsilon}}_{ij}^p+{\mathcal{S}}_{ijk}^{\mathrm{dis}}{\dot{\varepsilon}}_{ij,k}^p+{\mathcal{A}}^{\mathrm{dis}}\dot{T}-\frac{q_i}{T}{T}_{,i} $$

(69)

where ${\mathcal{X}}_{ij}^{{en},{NR}}$ may be viewed as the effectively dissipative microforce since it satisfies an effective dissipation inequality.

There are two main mechanisms affecting the energy dissipation during the dislocation movement in the grain boundary area. The first mechanism is related to an energy change in the grain boundary region. The macroscopic accumulated plastic strain at the grain boundary can be connected to the microscopic deformation of the grain boundary through the quadratic mean of the deformation gradient. Thus, the energy change after the onset of slip transmission to the adjacent grain is able to be approximately determined by a quadratic function of the deformation gradient at the microscale and hence the interfacial plastic strain at the macroscale. The other mechanism introduces the energy involved in the deformation of the grain boundary. This energy is mainly due to the energy dissipation during the dislocation movement and can be taken as a linear function of the interfacial plastic strain.

The interfacial dissipation potential ${\mathcal{D}}^I$ in the current study is postulated by combing the above-mentioned mechanisms as follows:

$${\mathcal{D}}^I=\frac{{\ell }_{\mathrm{dis}}^I}{m^I+1}\left({\sigma }_y^I+h^I{\epsilon }_p^{I\left(\text{post}\right)}\right){\left(1-\frac{T^I}{T_y^I}\right)}^{n^I}{\left(\frac{{\dot{\epsilon }}_p^{I\left(\text{post}\right)}}{{\dot{\mathcal{p}}}_0^I}\right)}^{m^I}{\dot{\epsilon }}_p^{I\left(\text{post}\right)}\ge 0$$

(70)

where ${\ell}_{\mathrm{dis}}^I$ is the interfacial dissipative length scale, m^I and are the viscous related material parameters, ${\sigma}_y^I$ is a constant accounting for the interfacial yield stress at which the interface starts to deform plastically, h^I is an interfacial hardening parameter representing the slip transmission through the interface, ${T}_y^I$ is the scale-independent interfacial thermal parameter at the onset of yield, n^I is the interfacial thermal parameter, and ${\varepsilon}_{p}^{I\left(\mathrm{post}\right)}=\sqrt{{\varepsilon_{ij}^{p^{I\left(\mathrm{post}\right)}}}{\varepsilon_{ij}^{p^{I\left(\mathrm{post}\right)}}}}$ and ${\dot{\varepsilon}}_{p}^{I\left(\mathrm{post}\right)}=\sqrt{{\dot{\upvarepsilon}_{ij}^{p^{I\left(\mathrm{post}\right)}}}{\dot{\varepsilon}_{ij}^{p^{I\left(\mathrm{post}\right)}}}}$ are defined, respectively, with the plastic strain at the interface after the slip transfer ${\varepsilon_{ij}^{p^{I\left(\mathrm{post}\right)}}}$ and its rate ${{\dot{\varepsilon}}_{ij}^{p^{I\left(\mathrm{post}\right)}}}$. The rate-dependency and temperature-dependency of the interfacial dissipation energy are clearly shown in Eq. 70 through the terms and ${\left(1-{T}^I/{T}_y^I\right)}^{n^I}$, respectively.

The interfacial dissipative microstresses ${\mathbb{M}}_{ij}^{I,\mathrm{dis}}$ can be obtained by substituting Eq. 70 into Eq. 40 as follows:

$${\mathbb{M}}_{\mathrm{ij}}^{I,\mathrm{dis}}=\frac{{\ell }_{\mathrm{dis}}^I}{m^I+1}\left({\sigma }_y^I+h^I{\epsilon }_p^{I\left(\text{post}\right)}\right){\left(1-\frac{T^I}{T_y^I}\right)}^{n^I}{\left(\frac{{\dot{\epsilon }}_p^{I\left(\text{post}\right)}}{{\dot{\mathcal{p}}}_0^I}\right)}^{m^I}\frac{{{\dot{\epsilon }}_{\mathrm{ij}}^p}^{I\left(\text{post}\right)}}{{\dot{\epsilon }}_p^{I\left(\text{post}\right)}}$$

(71)

By substituting Eqs. 71 and 57 into Eq. 31, one can obtain the interfacial microtraction ${\mathbb{M}}_{ij}^I$ as follows:

$$\begin{array}{l}{\mathbb{M}}_{\mathrm{ij}}^I=G{\ell }_{\mathrm{en}}^I{{\epsilon }_{\mathrm{ij}}^p}^{I\left(\mathrm{pre}\right)}\\ +\frac{{\ell }_{\mathrm{dis}}^I}{m^I+1}\left({\sigma }_y^I+h^I{\epsilon }_p^{I\left(\text{post}\right)}\right){\left(1-\frac{T^I}{T_y^I}\right)}^{n^I}{\left(\frac{{\dot{\epsilon }}_p^{I\left(\text{post}\right)}}{{\dot{\mathcal{p}}}_0^I}\right)}^{m^I}\frac{{{\dot{\epsilon }}_{\mathrm{ij}}^p}^{I\left(\text{post}\right)}}{{\dot{\epsilon }}_p^{I\left(\text{post}\right)}}\end{array}$$

(72)

As can be seen in Eq. 72, a free surface, i.e., microfree boundary condition, at the grain boundary can be described by setting ${\ell}_{{en}}^I={\ell}_{{dis}}^I=0$ and it is also possible to describe a surface passivation, i.e., microclamped boundary condition, by setting ${\ell}_{{en}}^I\to \infty$ and ${\ell}_{{dis}}^I\to \infty$.

Flow Rule

The flow rule in the present framework is established based on the nonlocal microforce balance, Eq. 6, augmented by thermodynamically consistent constitutive relations for both energetic and dissipative microstresses. By substituting Eqs. 51, 53, 60, and 61 into Eq. 6, one can obtain a second-order partial differential form of the flow rule as follows (The flow rule, Eq. 73, corresponds to the SGP model (Case I), in which the functional form of the dissipation potential is dependent on ${\dot{\varepsilon}}_{ij,k}^p\left({\mathcal{S}}_{ijk}^{{dis}}\ne 0\right)$. One can easily obtain the flow rule for the other case (Case II) of the SGP model, i.e. with ${\mathcal{S}}_{ijk}^{{dis}}=0$, by setting ℓ_dis = 0.) (Voyiadjis and Song 2017):

$$\begin{array}{l}{\tau }_{\mathrm{ij}}-\underset{-{\mathcal{S}}_{\mathrm{ijk},k}^{\mathrm{en}}}{\underbrace{\left(-G{\ell }_{\mathrm{en}}^2{\epsilon }_{\mathrm{ij},\mathrm{kk}}^p\right)}}\\ =h{\epsilon }_{\mathrm{ij}}^p\left(1-{\left(\frac{T}{T_y}\right)}^n\right){\epsilon }_p^{r-1}+{\sigma }_y{\left(\frac{\dot{\mathcal{p}}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\frac{{\dot{\epsilon }}_{\mathrm{ij}}^p}{\dot{\mathcal{p}}}\\ -\left({\sigma }_y{\ell }_{\mathrm{dis}}^2{\left(\frac{\dot{\mathcal{p}}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\frac{{\dot{\epsilon }}_{\mathrm{ij},\mathrm{kk}}^p}{\dot{\mathcal{p}}}\right)\end{array}$$

(73)

where the under-braced term ${\mathcal{S}}_{ijk,k}^{{en}}$ represents a backstress due to the energy stored in dislocations and results in the Bauschinger effect observed in the experiments (Liu et al. 2015; Nicola et al. 2006; Xiang et al. 2005; Xiang and Vlassak 2006) and discrete dislocation plasticity (Nicola et al. 2006; Shishvan et al. 2010, 2011).

Thermo-mechanical Coupled Heat Equation

The evolution of the temperature field is govern ed by t he law of conservation of energy (the first law of thermodynamics). The terms addressing heating as a result of the inelastic dissipation and thermo-mechanical coupling are involved for describing the evolution of the temperature field. The equation for the conservation of energy in this chapter is put forward as follows:

$$ {\sigma}_{ij}{\dot{\varepsilon}}_{ij}^e+{\mathcal{X}}_{ij}{\dot{\varepsilon}}_{ij}^p+{\mathcal{S}}_{ijk}{\dot{\varepsilon}}_{ij,k}^p+\mathcal{A}\dot{T}+{{\mathcal{B}}}_i{\dot{T}}_{,i}-\operatorname{div}\ {q}_i+\rho {{\mathcal{H}}}_{\mathrm{EXT}}-\rho \dot{e}=0 $$

(74)

where ℋ_EXT is the specific heat from the external source.

By considering the effective dissipation potential given in Eq. 69 along with the equations for the entropy production (the second law of thermodynamics) previously described in Eq. 17, the relationship for the evolution of the entropy, which describes the irreversible process, can be derived as follows:

$$\rho \dot{\mathcal{s}}T={\mathcal{D}}_{\mathrm{eff}}+\rho {\mathrm{\mathscr{H}}}_{\mathrm{EXT}}$$

(75)

By using Eq. 50 for solving the rate of the entropy the evolution of the temperature field can be obtained as follows:

$$\begin{array}{c}\rho c_0\dot{\mathcal{𝒯}}=\underset{172}{\underbrace{{\mathcal{𝒳}}_{\mathrm{ij}}^{\mathrm{dis}}{\dot{𝜀}}_{\mathrm{ij}}^p+{\mathcal{𝒳}}_{\mathrm{ij}}^{\mathrm{en},\mathrm{IR}}{\dot{𝜀}}_{\mathrm{ij}}^p+{\mathcal{𝒮}}_{\mathrm{ijk}}^{\mathrm{dis}}{\dot{𝜀}}_{\mathrm{ij},k}^p}}+\underset{173}{\underbrace{\frac{k\left(T\right)}{2T}{T}_{,i}{T}_{,i}+𝔞T_r{Ṫ}_{,\mathrm{ii}}-{\mathrm{bT}}_r\ddot{T}}}\\ -\underset{174}{\underbrace{{\alpha }_t{\dot{𝜀}}_{\mathrm{ij}}^e{\delta }_{\mathrm{ij}}T}}\\ \underset{175}{\underbrace{-\left\{h{𝜀}_p^{r-1}\left(\frac{n}{T_y}{\left(\frac{T}{T_y}\right)}^{n-1}\right){\dot{𝜀}}_{\mathrm{ij}}^p+\frac{h{𝜀}_p^{r+1}}{r+1}\left(\frac{n\left(n-1\right)}{T_y^2}{\left(\frac{T}{T_y}\right)}^{n-2}\right)Ṫ\right\}T}}\\ +\underset{176}{\underbrace{\rho {\mathcal{\mathscr{H}}}_{\mathrm{EXT}}}}\end{array}$$

(76)

where c₀ is the specific heat capacity at constant volume and is given by c₀ = constant ≅ c_εT/T_r. As shown in Eq. 76, the following terms are depicted, ① irreversible mechanical process, ② generalized heat conduction, ③ thermo-elastic coupling, ④ thermo-plastic coupling, and ⑤ heat source, which are involved in the evolution of the temperature. The third-order mixed derivation term $\mathfrak{a}{T}_r{T}_{,\mathrm{ii}}$ in part ② introduces the microstructural interaction effect into the classical heat equation, in addition, the second-order time derivative term ${\mathrm{bT}}_r\ddot{T}$ gives the thermal wave behavior effect in heat propagation.

By substituting the constitutive equations of the energetic microstresses given by Eqs. 49, 50, 51, 52, and 53 and the dissipative microstresses given by Eqs. 60, 61, 62, and 63 into Eq. 76 and defining three additional terms , and , the evolution of temperature for the model, in which the functional form of the dissipation potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$, i.e., ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, can be obtained as follows (Voyiadjis and Song 2017):

$$\begin{array}{l}\left[1+\frac{h{\epsilon }_p^{r+1}}{\rho c_v\left(r+1\right)}\left(\frac{n\left(n-1\right)}{T_y}{\left(\frac{T}{T_y}\right)}^n\right)\right]\dot{T}\\ =\frac{{\dot{\epsilon }}_{\mathrm{ij}}^p}{\rho c_v}\left[\left\{h{\epsilon }_p^{r-1}\left(1-{\left(\frac{T}{T_y}\right)}^n\right)-2\mathit{r\vartheta }{h}^2{\epsilon }_p^{2r-1}-\mathrm{nh}{\epsilon }_p^{r-1}{\left(\frac{T}{T_y}\right)}^n\right\}{\epsilon }_{\mathrm{ij}}^p+{\sigma }_y{\left(\frac{\dot{\mathcal{p}}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\frac{{\dot{\epsilon }}_{\mathrm{ij}}^p}{\dot{\mathcal{p}}}\right]\\ +\frac{1}{\rho c_v}\left[{\sigma }_y{\ell }_{\mathrm{dis}}^2{\left(\frac{\dot{\mathcal{p}}}{{\dot{\mathcal{p}}}_0}\right)}^m\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\frac{{\dot{\epsilon }}_{\mathrm{ij},k}^p{\dot{\epsilon }}_{\mathrm{ij},k}^p}{\dot{\mathcal{p}}}-{\alpha }_t{\dot{\epsilon }}_{\mathrm{ij}}^e{\delta }_{\mathrm{ij}}T+\rho {\mathrm{\mathscr{H}}}_{\mathrm{EXT}}\right]+\left[{\mathcal{t}}_{\mathrm{eff}}{T}_{,\mathrm{ii}}+{\mathcal{t}}_{\mathrm{eff}}{\mathcal{t}}^{\mathrm{en}}{\dot{T}}_{,\mathrm{ii}}-{\mathcal{t}}^{\mathrm{dis}}\ddot{T}\right]\end{array}$$

(77)

In the absence of the mechanical terms, Eq. 77 turns to the generalized heat equation including and . The evolution of temperature for the other case (Case II) of SGP model, i.e., with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$ can be obtained by setting ℓ_dis = 0 in Eq. 77.

Finite Element Implementation of the Strain Gradient Plasticity Model

In this section, first a one-dimensional finite element model for the SGP model by Voyiadjis and Song (2017) is presented to investigate the size dependent behavior in the microscopic structures under macroscopically uniform uniaxial tensile stress. In a one-dimensional finite element implementation, the macroscopic partial differential equations for balance of linear momentum Eq. 5 with the macroscopic boundary conditions, u_{x = 0} = 0 and u_x = L = u^† (prescribed), and the microscopic partial differential equations for nonlocal force balance Eq. 6 with the microscopic boundary conditions, ${\left({\mathbb{M}}^I-\mathcal{S}\right)}_{x=0}=0$ and ${\left({\mathbb{M}}^I-\mathcal{S}\right)}_{x=L}=0$, yield the following expressions in a global weak form, respectively (The finite element solutions, in this section, depend on the x-direction. A single crystal with the size of L bounded by two grain boundaries is analyzed (see Fig. 7 for details). Also a two dimensional case is presented for solving the problem of the square plate in the latter part of this chapter:

$$ \substack{\overset{L}{\int }\\{0}}\left(\sigma {\tilde{u}}_{,x}\right)\mathrm{dx}=0 $$

(78)

$$ {\int}_0^L\left[\left(\mathcal{X}-\tau \right){\tilde{\varepsilon}}^p+\mathcal{S}{\tilde{\varepsilon}}_{,x}^p\right]\mathrm{dx}+{\mathbb{M}}^I{\tilde{\varepsilon}}_{x=L}^p-{\mathbb{M}}^I{\tilde{\varepsilon}}_{x=0}^p=0 $$

(79)

where the arbitrary virtual fields $\tilde{u}$ and ${\tilde{\varepsilon}}^p$ are assumed to be kinematically admissible weighting functions in the sense that ${\tilde{u}}_{x=0}={\tilde{u}}_{x=L}=0$. (In the case of micro-clamped boundary condition, ${\tilde{\varepsilon}}_{x=0}^p={\tilde{\varepsilon}}_{x=L}^p=0$ is imposed at the grain boundaries to enforce the complete blockage of dislocations at the interface. In the case of micro-free boundary condition, on the other hand, the dislocations are free to move across the interface, which in turn, the present grain boundary flow rule is imposed.)

The user-element subroutine UEL in the commercial finite element package ABAQUS/standard (2012) is presented in this chapter in order to numerically solve the weak forms of the macroscopic and microscopic force balances, Eqs. 78 and 79, respectively. In this finite element solution, the displacement field u and the plastic strain field ε^p are discretized independently and both of the fields are taken as fundamental unknown nodal degrees of freedom. In this regard, the displacement field and corresponding strain field ε, and the plastic strain field and corresponding plastic strain gradient field ${\varepsilon}_{,x}^p$ can be obtained by using the interpolation as follows:

$$ u(x)=\sum_{\xi =1}^{n_u}{\mathrm{\mathbb{N}}}_u^{\xi }{\mathcal{U}}_u^{\xi}\ \ \varepsilon (x)=\frac{\partial u(x)}{\partial x}=\sum_{\xi =1}^{n_u}{{\mathrm{\mathbb{N}}}_u^{\xi}}_{,x}{\mathcal{U}}_u^{\xi } $$

(80)

$$ \begin{array}{cc}\hfill {\varepsilon}^p(x)=\sum\limits_{\xi =1}^{n_{\varepsilon^p}}{\mathrm{\mathbb{N}}}_{\varepsilon^p}^{\xi }{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi}\hfill & \hfill {\varepsilon}_{,x}^p(x)=\frac{\partial {\varepsilon}^p(x)}{\partial x}=\sum\limits_{\xi =1}^{n_{\varepsilon^p}}{{\mathrm{\mathbb{N}}}_{\varepsilon^{p,x}}^{\xi}}{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi}\hfill \end{array} $$

(81)

where ${\mathrm{\mathbb{N}}}_u^{\xi }$ and ${\mathrm{\mathbb{N}}}_{\varepsilon^p}^{\xi }$ are the shape functions, and ${\mathcal{U}}_u^{\xi }$ and ${\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi }$ are the nodal values of the displacements and the plastic strains at node ξ, respectively. The terms n_u and ${n}_{\varepsilon^p}$ represent the number of nodes per a single element for the displacement and the plastic strain, respectively. (If a one-dimensional three-noded quadratic element is employed, n_u and ${n}_{\varepsilon^p}$ are set up as three. On the other hand, these parameters are set up as two in the case that a one-dimensional two-noded linear element is used. It should be noted that n_u and ${n}_{\varepsilon^p}$ do not necessarily have to be same as each other in the present finite element implementation, even though both the displacement field and the plastic strain fields are calculated by using the standard isoparametric shape functions.)

Substituting Eqs. 80 and 81 into Eqs. 78 and 79 give the nodal residuals for the displacement r_u and the plastic strain ${r}_{\varepsilon^p}$ for each finite element el as follows:

$$ {\left({r}_u\right)}_{\xi }={\int}_{\mathrm{el}}\left(\sigma {{\mathrm{\mathbb{N}}}_u^{\xi}}_{,x}\right)\mathrm{dx} $$

(82)

$$ {\left({r}_{\varepsilon^p}\right)}_{\xi }={\int}_{\mathrm{el}}\left[\left(\mathcal{X}-\tau \right){\mathrm{\mathbb{N}}}_{\varepsilon^p}^{\xi }+{{\mathcal{S}\mathrm{\mathbb{N}}}_{\varepsilon^p}^{\xi}}_{,x}\right]\mathrm{dx}+{\mathbb{M}}^I{\mathrm{\mathbb{N}}}_{\varepsilon^p}^{\xi } $$

(83)

where the term ${\mathbb{M}}^I{\mathrm{\mathbb{N}}}_{\varepsilon^p}^{\xi }$ is applied only for the nodes on the interface which is at x = 0 and x = L.

The global coupled system of equations, (r_u)_ξ = 0 and ${\left({r}_{\varepsilon^p}\right)}_{\xi }=0$, are solved using ABAQUS/standard (2012) based on the Newton-Raphson iterative scheme. Occasionally, the modified Newton-Raphson method, referred to as quasi Newton-Raphson method, is employed in the case that the numerical solution suffers a divergence during the initial increment immediately after an abrupt change in loading. The Taylor expansion of the residuals with regard to the current nodal values can be expressed by assuming the nodal displacement and the plastic strain in iteration ζ as ${\mathcal{U}}_u^{\upzeta}$ and ${\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}$, respectively, as follows:

$$ \begin{array}{l}{\left({\left.{r}_u\right|}_{{\mathcal{U}}_u^{\upzeta +1},{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta +1}}\right)}_{\xi }={\left({\left.{r}_u\right|}_{{\mathcal{U}}_u^{\upzeta},{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}}\right)}_{\xi }+\left({\left.\frac{\partial {r}_u}{\partial {\mathcal{U}}_u^{\xi }}\right|}_{{\mathcal{U}}_u^{\upzeta}}\right)\Delta {\mathcal{U}}_u^{\xi }+\left({\left.\frac{\partial {r}_u}{\partial {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi }}\right|}_{{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}}\right)\Delta {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi}\\ \quad\quad+\mathcal{O}\left({\left(\Delta {\mathcal{U}}_u^{\xi}\right)}^2,{\left(\Delta {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi}\right)}^2\right)\end{array} $$

(84)

$$ \begin{array}{l}{\left({\left.{r}_{\varepsilon^p}\right|}_{{\mathcal{U}}_u^{\upzeta +1},{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta +1}}\right)}_{\xi}\\ \quad\quad={\left({\left.{r}_{\varepsilon^p}\right|}_{{\mathcal{U}}_u^{\upzeta},{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}}\right)}_{\xi }+\left({\left.\frac{\partial {r}_{\varepsilon^p}}{\partial {\mathcal{U}}_u^{\xi }}\right|}_{{\mathcal{U}}_u^{\upzeta}}\right)\Delta {\mathcal{U}}_u^{\xi }+\left({\left.\frac{\partial {r}_{\varepsilon^p}}{\partial {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi }}\right|}_{{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}}\right)\Delta {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi}\\ \quad\quad +\mathcal{O}\left({\left(\Delta {\mathcal{U}}_u^{\xi}\right)}^2,{\left(\Delta {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi}\right)}^2\right)\end{array} $$

(85)

where $\Delta {\mathcal{U}}_u^{\xi }={\left({\mathcal{U}}_u^{\upzeta +1}\right)}_{\xi }-{\left({\mathcal{U}}_u^{\upzeta}\right)}_{\xi }$, $\Delta {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi }={\left({\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta +1}\right)}_{\xi }-{\left({\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}\right)}_{\xi }$, and $\mathcal{O}\left({\left(\Delta {\mathcal{U}}_u^{\xi}\right)}^2,{\left(\Delta {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi}\right)}^2\right)$ are the big $\mathcal{O}$ notation to represent the terms of higher order than the second degree. The residual is ordinarily calculated at the end of each time step, and the values of the nodal displacements and the plastic strains are updated during the iterations. The increments in nodal displacements and the plastic strains can be computed by solving the system of linear equations shown in Eq. 86 with the Newton-Raphson iterative method:

$$ \substack{\underbrace{ \left[\begin{array}{cc}\hfill {K}_{\mathrm{uu}}^{\mathrm{el}}\hfill & \hfill {K}_{u{\varepsilon}^p}^{\mathrm{el}}\hfill \\ \hfill {K}_{{\varepsilon^p}_u}^{\mathrm{el}}\hfill & \hfill {K}_{\varepsilon^p{\varepsilon}^p}^{\mathrm{el}}\hfill \end{array}\right] }\\{{\boldsymbol{K}}^{\mathbf{el}}}} \left\{\begin{array}{c}\hfill \Delta {\mathcal{U}}_u^{\xi}\hfill \\ \hfill \Delta {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill {\left({\left.{r}_u\right|}_{{\mathcal{U}}_u^{\upzeta},{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}}\right)}_{\xi}\hfill \\ \hfill {\left({\left.{r}_{\varepsilon^p}\right|}_{{\mathcal{U}}_u^{\upzeta},{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}}\right)}_{\xi}\hfill \end{array}\right\} $$

(86)

where K^el is the Jacobian (stiffness) matrix that needs to be defined in the user-subroutine for each element.

From Eqs. 84 and 85 along with the discretization for the displacements given by Eq. 80 and the plastic strains given by Eq. 81 at the end of a time step, and the functional forms of the energetic and dissipative higher order stresses defined in the previous sections, the Jacobian matrix for the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$ can be obtained as follows:

$$ {K}_{\mathrm{uu}}^{\mathrm{el}}=-{\left.\frac{\partial {r}_u}{\partial {\mathcal{U}}_u^{\xi }}\right|}_{{\mathcal{U}}_u^{\upzeta}}=-{\int}_{\mathrm{el}}\left(E{{\mathrm{\mathbb{N}}}_u^{\xi}}_{,x}{{\mathrm{\mathbb{N}}}_u^{\xi}}_{,x}\right)\mathrm{dx} $$

(87)

$$ {K}_{u{\varepsilon}^p}^{\mathrm{el}}=-{\left.\frac{\partial {r}_u}{\partial {\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\xi }}\right|}_{{\mathrm{\mathcal{E}}}_{\varepsilon^p}^{\upzeta}}={\int}_{\mathrm{el}}\left(E{\mathrm{\mathbb{N}}}_{\varepsilon^p}^{\xi }{{\mathrm{\mathbb{N}}}_u^{\xi}}_{,x}\right)\mathrm{dx} $$

(88)

$$ {K}_{{\varepsilon^p}_u}^{\mathrm{el}}=-{\left.\frac{\partial {r}_{\varepsilon^p}}{\partial {\mathcal{U}}_u^{\xi }}\right|}_{{\mathcal{U}}_u^{\upzeta}}={\int}_{\mathrm{el}}\left(E{{\mathrm{\mathbb{N}}}_u^{\xi}}_{,x}{\mathrm{\mathbb{N}}}_{\varepsilon^p}^{\xi}\right)\mathrm{dx} $$

(89)

$$\begin{array}{l}{\left(K_{{\epsilon }^p{\epsilon }^p}^{\mathrm{el}}\right)}_{{\mathcal{S}}_{\mathrm{ijk}}^{\mathrm{dis}}\ne 0}={\left(-{\left.\frac{\partial r_{{\epsilon }^p}}{\partial {\mathrm{ℰ}}_{{\epsilon }^p}^{\xi }}\right|}_{{\mathrm{ℰ}}_{{\epsilon }^p}^{\mathrm{\zeta }}}\right)}_{{\mathcal{S}}_{\mathrm{ijk}}^{\mathrm{dis}}\ne 0}\\ =\underset{\mathrm{for}\text{bulk}}{\underbrace{{\int }_{\mathrm{el}}\left[\left\{E+\left(\mathrm{rh}{\left({\epsilon }^p\right)}^r+\frac{{\sigma }_y{\left(\dot{\mathcal{p}}\right)}^{m-1}}{\mathrm{\Delta }t{\left({\dot{\mathcal{p}}}_0\right)}^m}\right)\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\right\}{\mathrm{\mathbb{N}}}_{{\epsilon }^p}^{\xi }{\mathrm{\mathbb{N}}}_{{\epsilon }^p}^{\xi }\right.}}\\ +\underset{\mathrm{for}\text{bulk}}{\underbrace{\left.\left\{\left(G{\ell }_{\mathrm{en}}^2+\frac{{\sigma }_y{\ell }_{\mathrm{dis}}^2{\left(\dot{\mathcal{p}}\right)}^{m-1}}{\mathrm{\Delta }t{\left({\dot{\mathcal{p}}}_0\right)}^m}\right)\left(1-{\left(\frac{T}{T_y}\right)}^n\right)\right\}{{\mathrm{\mathbb{N}}}_{{\epsilon }^p}^{\xi }}_{,x}{{\mathrm{\mathbb{N}}}_{{\epsilon }^p}^{\xi }}_{,x}\right]\mathrm{dx}}}\\ +\underset{\mathrm{for}\text{interface}}{\underbrace{\left[G{\left({\ell }_{\mathrm{en}}^I\right)}^2+\frac{{\sigma }_y^I{\left({\ell }_{\mathrm{dis}}^I\right)}^2{\left({\dot{\mathcal{p}}}^I\right)}^{m^I-1}}{\mathrm{\Delta }t{\left({\dot{\mathcal{p}}}_0^I\right)}^{m^I}}\left(1-{\left(\frac{T}{T_y^I}\right)}^{n^I}\right)\right]{\mathrm{\mathbb{N}}}_{{\epsilon }^p}^{\xi }{\mathrm{\mathbb{N}}}_{{\epsilon }^p}^{\xi }}}\end{array}$$

(90)

where Δt is a time step. The Jacobian matrix for the other case, i.e. ${\left({K}_{\varepsilon^p{\varepsilon}^p}^{\mathrm{el}}\right)}_{{\mathcal{S}}_{ijk}^{\mathrm{dis}}=0}$, can be obtained by setting ℓ_dis = 0 in Eq. 90. The interfacial terms in ${\left({K}_{\varepsilon^p{\varepsilon}^p}^{\mathrm{el}}\right)}_{{\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0}$ and ${\left({K}_{\varepsilon^p{\varepsilon}^p}^{\mathrm{el}}\right)}_{{\mathcal{S}}_{ijk}^{\mathrm{dis}}=0}$ are applied only for the nodes on the interface which is at x = 0 and x = L in this chapter.

Experimental Validation of the Strain Gradient Plasticity Model

In this section, the present SGP model and corresponding finite element code by Voyiadjis and Song (2017) are validated by comparing with the experimental results from three sets of size effect experiments. In addition, the comparison between the SGP model by Voyiadjis and Song (2017) and Voyiadjis and Faghihi (2014) is carried out to show the increase in accuracy of the model by Voyiadjis and Song (2017). To examine the applicability of the present finite element implementation to the various kinds of materials, it is considered that each set of three experiments involves the three different materials, viz. aluminum (Al), copper (Cu), and nickel (Ni).

Haque and Saif (2003) developed Micro-Electro Mechanical Systems (MEMS)-based testing techniques for uniaxial tensile testing of nanoscale freestanding Al thin films to explore the effect of strain gradient in 100 nm, 150 nm, and 485 nm thick specimens with average grain size of 50 nm, 65 nm, and 212 nm, respectively. The specimens with 99.99% pure sputter-deposited freestanding Al thin films are 10 μm wide and 275 μm long. All experiments are carried out in situ in SEM and the stress and strain resolutions for the tests are set 5 Mpa and 0.03%, respectively. In particular, the comparison between the present SGP model by Voyiadjis and Song (2017) and Voyiadjis and Faghihi (2014) is carried out to show the increase in accuracy of the present model. The calibrated material parameters as well as the general material parameters for the Al are presented in Table 1, and the numerical results from both the present model by Voyiadjis and Song (2017) and Voyiadjis and Faghihi (2014) are shown in Fig. 2 in conjunction with the experimental data of Haque and Saif (2003). As it is clearly shown in this figure, the size effect: Smaller is Stronger is observed on the stress-strain curves of the Al thin films. Furthermore, the calculated results of the present SGP model by Voyiadjis and Song (2017) display a tendency to be more coincident to the experimental data than those of Voyiadjis and Faghihi (2014).

Fig. 2

The validation of the present strain gradient plasticity model by comparing the numerical results from the present model by Voyiadjis and Song (2017) with those from Voyiadjis and Faghihi (2014) and the experimental measurements from Haque and Saif (2003) on the stress-strain response of the sputter-deposited Al thin films (Reprinted with permission from Voyiadjis and Song 2017)

Table 1 The general and calibrated material parameters used for the validation of the proposed strain gradient plasticity model (Reprinted with permission from Voyiadjis and Song 2017)

Xiang and Vlassak (2006) investigated the size effects with a variety of film thicknesses on the plastic behavior of the freestanding electroplated Cu thin films by performing the plane strain bulge test. In this plane strain bulge test, the rectangular freestanding membranes surrounded by a rigid silicon (Si) frame are deformed in plane strain by applying a uniform pressure to one side of the membrane as shown in Fig. 3. The displacement and pressure resolutions for this bulge tests system are 0.3 μm and 0.1 kpa, respectively.

Fig. 3

Schematic representation of the plane strain bulge test technique presented by Xiang and Vlassak (2006). The stress-strain response of either a single material membrane or a stack of multiple material membranes adhered on a rigid Si frame is able to be obtained by using the following equations: σ = P(d² + Δ²)/2tΔ andε = ε_r + {(d² + Δ²)/2dΔ} arcsin(2dΔ/d² + Δ²) − 1 where ε_r is a residual strain in the membrane (Reprinted with permission from Voyiadjis and Song 2017)

As can be seen in the work of Xiang and Vlassak (2006), the stress-strain curves of the Cu thin films with a passivation layer on both surfaces clearly show the size effects due to the presence of a boundary layer with high dislocation density near the film-passivation layer interfaces. In this sense, the bulge test of electroplated Cu thin films with both surfaces passivated by 20 nm of titanium (Ti) is considered here for the experimental validation of the present SGP model. In order to describe the passivation effect, the microclamped condition, which causes the dislocations to be completely blocked at the grain boundary, is imposed at both surfaces of the Cu thin films. Meanwhile, the experiments are performed with the various thicknesses of the Cu thin films of 1.0 μm, 1.9 μm, and 4.2 μm. The average grain sizes in all cases are given by 1.5 ± 0.05 μm, 1.51 ± 0.04 μm, and 1.5 ± 0.05 μm, respectively, which mean almost equal to each other.

The calibrated and general material parameters for the copper are presented in Table 1, and the comparison between the experimental measurements from the bulge tests and the calculated results from the present SGP model by Voyiadjis and Song (2017) is shown in Fig. 4. As it is clearly shown in this figure, the size effects according to the variation of the Cu thin film thicknesses is well observed in both the present SGP model and the experimental work of Xiang and Vlassak (2006). Moreover, the numerical results of the present model by Voyiadjis and Song (2017) are in good agreement with the experimental measurements.

Fig. 4

The validation of the present strain gradient plasticity model by comparing to the experimental measurements from Xiang and Vlassak (2006) on the stress-strain response of the electroplated Cu thin films with the passivated layers on both sides (Reprinted with permission from Voyiadjis and Song 2017)

Han et al. (2008) developed the microscale tensile testing system, which is composed of a high temperature furnace, a micro motor actuator and the Digital Image Correlation (DIC) system, for evaluating the mechanical properties of the Ni thin films at high temperatures. Dogbone-shaped specimens used in their experiments were made by Micro-electro mechanical system (MEMS) processes and the primary dimensions of the specimen are shown in Fig. 5.

Fig. 5

The specimen dimensions for the experimental validation (Reprinted with permission from Voyiadjis and Song 2017)

The calibrated material parameters as well as the general parameters for Ni are presented in Table 1. The results of the microscale tensile tests at four different temperatures, i.e., 25 °C, 75 °C, 145 °C, and 218 °C, and corresponding numerical results from the present model (Voyiadjis and Song 2017) are shown in Fig. 6. As shown in this figure, it is clear from both the experimental and numerical results that the Young’s modulus is not affected by variations in temperature, while the yield and tensile strength decrease as the specimen temperature increases. In addition, Fig. 6 clearly shows that the Bauschinger effect is not affected very much by variations in the specimen temperature. Meanwhile, the calculated results of the present model (Voyiadjis and Song 2017) compare better to the experimental data than those of Voyiadjis and Faghihi (2014) (Fig. 6).

Fig. 6

The validation of the present strain gradient plasticity model (Voyiadjis and Song 2017) by comparing the numerical results with the model by Voyiadjis and Faghihi (2014) and the experimental measurements from Han et al. (2008) on the stress-strain response of Ni thin films (Reprinted with permission from Voyiadjis and Song 2017)

Stretch-Passivation Problem

The numerical solutions for the stretch-passivation problem with the two cases of the SGP model are presented in this section. The frameworks presented in this chapter represent the nonlocal flow rules in the form of partial differential equations when the microscopic force balances are integrated with the thermodynamically consistent constitutive equations. To interpret and analyze the physical phenomena characterized by the current frameworks is very complicated; in this sense, a one-dimensional numerical solution is presented first and extended to the two-dimensional one later in this chapter.

An initially uniform single grain with the size of L is used with two grain boundaries as shown in Fig. 7. The grain is assumed to be infinitely long along the x-direction and initially homogeneous; therefore, the solution depends only on the x-direction. In the one-dimensional stretch-passivation problem, the grain is deformed into the plastic regime by uniaxial tensile stretch with no constraint on plastic flow at the grain boundaries. At a certain point, the plastic flow is then constrained by blocking off the dislocations from passing out of the grain boundary, which leads the further plastic strain not to occur at the grain boundary.

Fig. 7

One-dimensional model for a single grain with two grain boundaries (Reprinted with permission from Voyiadjis et al. 2017)

Numerical Results

In this section, an extensive numerical work is carried out based on the validated code in order to compare the results from the aforementioned two cases of the SGP model and to analyze the characteristics of the stress jump phenomenon. This section is largely composed of four subparts. In the first part, the occurrence of the stress jump phenomenon under the stretch-surface passivation condition is introduced in conjunction with three experiments used in section “Experimental Validation of the Strain Gradient Plasticity Model.” The second part is focused on indicating that the results are contrary to each other for the two cases of the SGP model. An extensive parametric study is also conducted in terms of the various material parameters, and the evolution of the free energy involving the stored energy of cold work and the dissipation potentials during the plastic deformation are discussed in the third part. In the last part, the two-dimensional simulation is also given to examine the gradient and grain boundary effect, the mesh sensitivity of the two-dimensional model, and the stress jump phenomenon.

The numerical results on the stress-strain behaviors of Al and Cu thin films for the SGP model with the corresponding dissipative microstress quantities are presented in Figs. 8 and 9, respectively. In both simulations, a significant stress jump is observed at the onset of passivation. In particular, it is shown that the very first slopes immediately after the passivation increase as the film thicknesses decrease, viz. the dissipative length scales increase, in both simulations. Thus, the stress jump phenomenon is revealed to be highly correlated with the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$.

Fig. 8

A finite stress jump due to infinitesimal changes in the plastic strain. The numerical implementation of the SGP model with the dissipative potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$, i.e., ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, is carried out based on the experiments of Haque and Saif (2003) with the various thicknesses of the Al thin films of 100 nm, 150 nm, and 485 nm (Reprinted with permission from Voyiadjis and Song 2017)

Fig. 9

A finite stress jump due to infinitesimal changes in the plastic strain. The numerical implementation of the SGP model with the dissipative potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$, i.e., ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, is carried out based on the experiments of Xiang and Vlassak (2006) with the various thicknesses of the Cu thin films of 1.0 μm, 1.9 μm, and 4.2 μm (Reprinted with permission from Voyiadjis and Song 2017)

Figure 10 shows the numerical results on the stress-strain behavior of Ni thin films for the SGP model with the dissipative microstress quantities. As shown in this figure, the magnitudes of the stress jump are less than expected in all cases since the dissipative length scale ℓ_dis is set 0.1 which is much smaller than the energetic length scale ℓ_en = 1.0. Nevertheless, the very first slopes immediately after the passivation are calculated as E_25℃ = 58.0 GPa, E_75℃ = 59.2 GPa, E_145℃ = 72.6 GPa, and E_218℃ = 105.0 GPa, respectively, and this shows the responses immediately after the passivation gets gradually closer to the elastic response E = 115 GPa as the temperature increases.

Fig. 10

A finite stress jump due to infinitesimal changes in the plastic strain. The numerical implementation of the SGP model with the dissipative potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$, i.e., ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, is carried out based on the experiments of Han et al. (2008) at the various temperatures of the Ni thin films of 25 °C, 75 °C, 145 °C, and 218 °C. The circles on the curve indicate the passivation point (Reprinted with permission from Voyiadjis and Song 2017)

The numerical implementations to specify whether or not the stress jump phenomenon occurs under the stretch-surface passivation have been hitherto conducted within the framework of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$. Hereafter, the numerical simulations are given more focus on the direct comparison of the material response on the stress-strain curves between the two cases of the SGP models. The material parameters used for these implementations are presented in Table 2.

Table 2 Material parameters for the numerical simulation (Reprinted with permission from Voyiadjis and Song (2017))

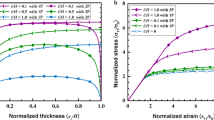
Figure 11 clearly shows this point by comparing the results from the two cases. The behavior of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$ is in stark contrast with that of the SGP case with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$ after the passivation point. A significant stress jump with the slope E_passivation similar to the modulus of elasticity E is shown in the SGP case with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$. On the other hand, no elastic stress jump is observed in the SGP case with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$. This result is exactly in agreement with the prediction in Fleck et al. (2014, 2015). In the case that the dissipative potential is independent of ${\dot{\varepsilon}}_{ij,k}^p$, the contribution from the plastic strain gradients is entirely energetic as can be seen in section “Dissipation Potential and Dissipative Thermodynamic Microstresses.” Both the increase in the yield strength in the early stages of passivation and subsequent hardening due to the effects of the plastic strain gradient are observed along with the increase of the energetic length scale as shown in Fig. 11.

Fig. 11

Comparison of the results from two different cases of the present SGP model with the dissipation potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$, i.e., ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0,$ and with the dissipative potential independent on ${\dot{\varepsilon}}_{ij,k}^p$, i.e., ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$. The results for the latter case are computed with three different values of energetic length scales ℓ_en = 0.1 , 0.2 and 0.3 (Reprinted with permission from Voyiadjis and Song 2017)

The comparison of the results from the case of the present SGP model by Voyiadjis and Song (2017) with the dissipative potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$ is shown in Fig. 12a with various dissipative length scales, i.e., ℓ_dis = 0.1 , 0.3 , 0.5 , 1.0 , 1.5 , and 2.0. As can be seen in this figure, the magnitude of the stress jump significantly increases as the dissipative length scale increases, on the other hand, the stress jump phenomenon disappears as the dissipative length scale tends to zero. This is because the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$, which is the main cause of the stress jump, vanishes when the dissipative length scale ℓ_dis is equal to zero. It is worth noticing that the very first behavior immediately after the passivation indicates a substantial difference with varying dissipative length scales. As the dissipative length scales increase from 0.1 to 2.0, the corresponding slopes of the very first response E also increase from 13.3 to 198.4 GPa. The main reason of this phenomenon in terms of the dissipative length scale is also because the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ sharply increases with increasing ℓ_dis.

Fig. 12

Comparison of the results from the case of the present SGP model with the dissipative potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$, i.e., ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$: (a) with various dissipative length scales (ℓ_dis = 0.1 , 0.3 , 0.5 , 1.0 , 1.5 , and 2.0) and (b) for various passivation points (ε = 20.2%, 0.3%, 0.4%, 0.5%, and 0.6% with identical energetic and dissipative length scales) (Reprinted with permission from Voyiadjis and Song 2017)

The comparison of the results from the case of the SGP model with the dissipative potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$ is shown in Fig. 12b for various passivation points. The energetic and dissipative length scales are set identical in all cases. The magnitudes of the stress jump with the magnitudes of ε = 20.2%, 0.3%, 0.4%, 0.5%, and 0.6% are obtained as 13.8 MPa, 16.2 MPa, 18.6 MPa, 21.1 MPa, and 23.5 MPa, respectively, and the values normalized by the value of the magnitude ε = 20.2% are calculated as 1.00, 1.17, 1.35, 1.52, and 1.70, respectively. The normalized higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ with the magnitudes of ε = 20.2%, 0.3%, 0.4%, 0.5%, and 0.6% are obtained as 1.00, 1.17, 1.30, 1.40, and 1.48, respectively, as shown in Fig. 12b. Thus, it is worth noticing that the stress jump phenomenon is highly correlated with the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$. In addition, the very first responses immediately after the passivation also make a substantial difference with varying passivation points. The slopes of the very first responses for the magnitudes of ε = 0.2%, 0.3%, 0.4%, 0.5%, and 0.6% are calculated as 64.8 GPa, 87.1 GPa, 109.7 GPa, 132.5 GPa, and 155.5 GPa, respectively.

The effects of various parameters on the mechanical behavior of the stretch-surface passivation problem are investigated by using a one-dimensional finite element. The numerical results reported in this parametric study are obtained by using the values of the material parameters in Table 2 unless it is differently mentioned.

The stress-strain graphs for various values of the hardening material parameter h are shown in Fig. 13a with two different cases of the SGP model. For the case with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, the slopes of the very first response immediately after the passivation are obtained as E_h = 109.7 GPa in all simulations, and the corresponding magnitudes of the stress jump for each simulation are, respectively, obtained as ${\sigma}_{h=100\mathrm{MPa}}^{\prime }=18.6\;\mathrm{MPa}$, ${\sigma}_{h=200\mathrm{MPa}}^{\prime }=18.6\;\mathrm{MPa}$, ${\sigma}_{h=300\mathrm{MPa}}^{\prime }=18.7\;\mathrm{MPa}$, ${\sigma}_{h=400\mathrm{MPa}}^{\prime }=18.7\;\mathrm{MPa}$, and ${\sigma}_{h=500\mathrm{MPa}}^{\prime }=18.7\;\mathrm{MPa}$. There is little difference between all the simulations. For the case with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$, no stress jump phenomena are observed in all simulations.

Fig. 13

Comparison of the results from the case of the present SGP model with the dissipative potential dependent on ${\dot{\varepsilon}}_{ij,k}^p$, i.e., ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$ with the effects of: a the hardening material parameter h (100 MPa, 200 MPa, 300 MPa, 400 MPa, and 500 MPa), b the nonnegative rate sensitivity parameter m (0.2, 0.25, 0.3, and 0.35), c the temperature sensitivity parameter n (0.4, 0.6, 0.8, and 1.0), d the thermal material parameter T_y (500°K, 1,000°K, 1,500°K, and 2,000°K), e the interfacial temperature sensitivity parameter n^I (0.1, 0.2, 0.3 and 0.5), f the interfacial thermal material parameter ${T}_y^I$ (600°K, 700°K, 1,000°K, and 11,300°K) (Reprinted with permission from Voyiadjis and Song 2017)

The effects of the nonnegative rate sensitivity parameter m on the stress-strain behavior for the two cases of the SGP model are represented in Fig. 13b. It is clearly shown in this figure that by increasing the rate sensitivity parameter, the stress jump phenomena are significantly manifested in the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$ in terms of both the slope of the very first response immediately after the passivation and the corresponding magnitude of the stress jump. In the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$, on the other hand, the material behavior is not affected a lot by the rate sensitivity parameter m. In the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, the slopes of the very first response immediately after the passivation (E_m) and the corresponding magnitudes of the stress jump $({\sigma}_m^{\prime})$ are obtained as E_{m = 0.2} = 96.7 GPa, E_{m = 0.25} = 103.0 GPa, E_{m = 0.3} = 109.7 GPa, E_{m = 0.35} = 116.5 GPa and ${\sigma}_{m=0.2}^{\prime }=14.8\;\mathrm{MPa}$, ${\sigma}_{m=0.25}^{\prime }=16.7\;\mathrm{MPa}$, ${\sigma}_{m=0.3}^{\prime }=18.6\;\mathrm{MPa}$, ${\sigma}_{m=0.35}^{\prime }=20.6\;\mathrm{MPa}$_, respectively. Thus, it is clearly shown that both the slope of the very first response immediately after the passivation and the corresponding magnitude of the stress jump increase as the nonnegative rate sensitivity parameter m increases.

The effects of the temperature sensitivity parameter n on the stress-strain behavior for the two cases of the SGP model are represented in Fig. 13c. It is clearly shown in this figure that the yield stress significantly increases as the temperature sensitivity parameter n increases, while the strain hardening is not influenced a lot by this parameter. This is because the temperature affects the strain hardening mechanism through the dislocation forest barriers, while the backstress, i.e., energetic gradient hardening, is almost independent of the temperature. Meanwhile, the temperature sensitivity parameter n significantly affects the stress-strain response in the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$. In this case, the slopes of the very first response immediately after the passivation are obtained as E_{n = 0.4} = 112.5 GPa, E_{n = 0.6} = 109.7 GPa, E_{n = 0.8} = 107.8 GPa, and E_{n = 1.0} = 106.6 GPa, and the corresponding magnitudes of the stress jump are obtained as ${\sigma}_{n=0.4}^{\prime }=16.6\;\mathrm{MPa}$, ${\sigma}_{n=0.6}^{\prime }=18.6\;\mathrm{MPa}$, ${\sigma}_{n=0.8}^{\prime }=19.7\;\mathrm{MPa}$, and ${\sigma}_{n=1.0}^{\prime }=20.4\;\mathrm{MPa}$, respectively. Thus, in contrast with the rate sensitivity parameter m, the slope of the very first response immediately after the passivation decreases, while the corresponding magnitude of the stress jump increases as the temperature sensitivity parameter n increases.

The effects of the thermal material parameter T_y on the stress-strain behavior with the two cases of the SGP model are represented in Fig. 13d. Similar to the temperature sensitivity parameter n, the yield stress significantly increases as the thermal material parameter T_y increases, while the strain hardening is not influenced a lot by this parameter. In the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, the slopes of the very first response immediately after the passivation $({E}_{T_y})$ and the corresponding magnitudes of the stress jump $({\sigma}_{T_y}^{\prime})$ are obtained as ${E}_{T_y=500 ^{\circ}K}=111.9\;\mathrm{GPa}$, ${E}_{T_y=1000 ^{\circ}K}=109.7\;\mathrm{GPa}$, ${E}_{T_y=1500 ^{\circ}K}=108.7\;\mathrm{GPa}$, ${E}_{T_y=2000 ^{\circ}K}=108.1\;\mathrm{GPa}$ and ${\sigma}_{T_y=500 ^{\circ}K}^{\prime }=17.1\;\mathrm{MPa}$, ${\sigma}_{T_y=1000 ^{\circ}K}^{\prime }=18.6\;\mathrm{MPa}$, ${\sigma}_{T_y=1500 ^{\circ}K}^{\prime }=19.2\;\mathrm{MPa}$, ${\sigma}_{T_y=2000 ^{\circ}K}^{\prime }=19.6\;\mathrm{MPa}$, respectively. These results from the simulations with various thermal material parameter T_y are very similar to those with the temperature sensitivity parameter n, in the sense that the slope of the very first response immediately after the passivation decreases, while the corresponding magnitude of the stress jump increases as the temperature sensitivity parameter n increases.

The effects of the interfacial temperature sensitivity parameter n^I on the stress-strain behavior for the two cases of the SGP model are presented in Fig. 13e. It is clearly shown in this figure that increasing interfacial temperature sensitivity parameter makes the grain boundary (interface) harder and results in less variation of the stress jump in both cases of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$ and ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$. In the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, the slopes of the very first response immediately after the passivation are obtained as ${E}_{n^I=0.1}=109.7\;\mathrm{GPa}$, ${E}_{n^I=0.2}=80.4\;\mathrm{GPa}$, ${E}_{n^I=0.3}=70.3\;\mathrm{GPa}$, and ${E}_{n^I=0.5}=62.1\;\mathrm{GPa}$, and the corresponding magnitudes of the stress jump are obtained as ${\sigma}_{n^I=0.1}^{\prime }=18.6\;\mathrm{MPa}$, ${\sigma}_{n^I=0.2}^{\prime }=17.6\;\mathrm{MPa}$, ${\sigma}_{n^I=0.3}^{\prime }=17.1\;\mathrm{MPa}$, and ${\sigma}_{n^I=0.5}^{\prime }=16.4\;\mathrm{MPa}$, respectively. From these results, it is easily observed that the slope of the very first response after the passivation and the corresponding magnitude of the stress jump increase as the interfacial temperature sensitivity parameter n^I decreases. In addition, the variations along with the different cases are shown to be more drastic by decreasing the interfacial temperature sensitivity parameter n^I. Similarly, for the case of the SGP model with ${\mathcal{S}}_{ijk}=0$, decreasing the interfacial temperature sensitivity parameter makes the variation more radically as shown in Fig. 13e.

The effects of the interfacial thermal material parameter ${T}_y^I$ on the stress-strain behavior for the two cases of the SGP model are represented in Fig. 13f. As can be seen in this figure, the overall characteristic from the simulation results with various ${T}_y^I$ is similar to those with various n^I in the sense that increasing ${T}_y^I$ makes the grain boundary (interface) harder and results in less variation of the stress jump in both cases of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$ and ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$. In the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, the slopes of the very first response immediately after the passivation are obtained as ${E}_{T_y^I=600 ^{\circ}K}=114.0\;\mathrm{GPa}$, ${E}_{T_y^I=700 ^{\circ}K}=109.7\;\mathrm{GPa}$, ${E}_{T_y^I=1000 ^{\circ}K}=101.7\;\mathrm{GPa}$, and ${E}_{T_y^I=1300 ^{\circ}K}=97.1\;\mathrm{GPa}$, and the corresponding magnitudes of the stress jump are obtained as ${\sigma}_{T_y^I=600 ^{\circ}K}^{\prime }=18.7\;\mathrm{MPa}$, ${\sigma}_{T_y^I=700 ^{\circ}K}^{\prime }=18.6\;\mathrm{MPa}$, ${\sigma}_{T_y^I=1000 ^{\circ}K}^{\prime }=18.4\;\mathrm{MPa}$, and ${\sigma}_{T_y^I=1300 ^{\circ}K}^{\prime }=18.3\;\mathrm{MPa}$, respectively.

Based on the calibrated model parameters of Ni (Table 1), the evolution of the various potentials during the plastic deformation are investigated with four different temperatures, i.e., 25 °C, 75 °C, 145 °C, and 218 °C, in this section. Figure 14 shows (a) the variation of the plastic strain dependent free energies $({\varPsi}_1^d,{\varPsi}_1^{d,R}\mathrm{and}{\varPsi}_1^{d,\mathrm{NR}})$, (b) plastic strain dependent dissipation rate ${\mathcal{D}}_1$ (i.e., plastic strain dependent term in Eq. 58), (c) plastic strain gradient-dependent free energy $({\varPsi}_2^d)$ and dissipation rate ${\mathcal{D}}_2$ (i.e., plastic strain gradient dependent term in Eq. 58), and (d) amount of stored energy $({\varPsi}_1^d+{\varPsi}_2^d)$ and dissipated energy $(\mathbb{D}=\int ({\mathcal{D}}_1+{\mathcal{D}}_2)\mathrm{dt})$.

Fig. 14

The evolution of free energy and dissipation potentials based on the calibrated model parameters (Han et al. 2008): (a) plastic strain-dependent free energy, (b) plastic strain-dependent dissipation rate, (c) plastic strain gradient-dependent free energy and dissipation rate (The primary y-axis on the LHS: ${\mathcal{D}}_2$, the secondary y-axis on the RHS: ${\varPsi}_2^d$), and (d) amount of stored and dissipated energies (Reprinted with permission from Voyiadjis and Song 2017)

As can be seen in Fig. 14a, both free energies ${\varPsi}_1^d$ and ${\varPsi}_1^{d,\mathrm{NR}}$ decrease as the temperature increases. The stored energy of cold work ${\varPsi}_1^{d,R}$ is also presented in this figure. One can observe that ${\varPsi}_1^d$ and ${\varPsi}_1^{d,\mathrm{NR}}$ have a strong temperature dependency, while the stored energy of cold work has no variation with varying temperatures. In addition, the stored energy of cold work tends to saturate after some critical point since the stored energy of cold work is proportional to the dislocation density that remains constant after the aforementioned critical point. Meanwhile, it is shown in Fig. 14b,c that rates of dissipation, ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$, are dependent on the temperature such that both ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$ increase with decreasing temperatures while ${\varPsi}_2^d$ shows no temperature dependency. The amount of stored and dissipated energies is shown in Fig. 14d. As it is shown in this figure, the amount of stored energy is larger than the dissipated energy and both decrease as the temperature increases.

Lastly, the one-dimensional finite element implementation is extended to the two-dimensional one. The simple tension problem of the square plate is solved to study the strain gradient effects, the mesh sensitivity of the model with the three cases according to the number of elements (100, 400, and 1,600 elements), and the stress jump phenomena under the abrupt surface passivation. Each edge of the plate has a length of w and the material parameters in Table 2 are used again for these simulations.

Figure 15a, b shows the stress-strain behavior of the plate with the various energetic length scales (ℓ_en/w = 0.0, 0.1, 0.3, 0.5, 0.7, and 1.0 with ℓ_dis/w = 0.0) and dissipative length scales (ℓ_dis/w = 0.0, 0.1, 0.2, 0.3, 0.4, and 0.5 with ℓ_en/w = 0.0), respectively. In common with the one-dimensional simulations, the numerical results show the energetic hardening as the energetic length scale increases as well as the dissipative strengthening as the dissipative length scale increases.

Fig. 15

The stress-strain behavior of the square plate: (a) the energetic hardening, (b) the dissipative strengthening, (c) the grain boundary effect, (d) the mesh sensitivity with varying ℓ_en, (e) the mesh sensitivity with varying ℓ_dis, and (f) the stress jump phenomenon (Fig. 15c, f: Reprinted with permission from Voyiadjis and Song (2017))

Figure 15c shows the grain boundary effect of the square plate. It is well known that the grain boundary blocks the dislocation movement, which, in turn, leads to the strengthening of the material. The energetic and dissipative length scales reported in these simulations are set zero and the microclamped condition is imposed at the grain boundary, which is indicated by the bold line in the figure. The strengthening caused by increasing the grain boundary area is well observed as expected. For the simulations presented in Fig. 15a–c, 20 × 20 elements are used.

The mesh sensitivity of the two-dimensional numerical model is examined in terms of the energetic and dissipative length scales with 10 × 10, 20 × 20 and 40 × 40 mesh elements in Fig. 15d, e, respectively. Figure 15d shows the stress-strain behavior of the plate with the various energetic length scales (ℓ_en/w = 0.1, 0.5 and 1.0 with ℓ_dis/w = 0) compared to those in the absence of the gradient effects (ℓ_en/w = ℓ_dis/w = 0). The numerical results without the gradient terms significantly show the mesh sensitivity as expected, while for all nonzero values of ℓ_en/w, the numerical solutions show the mesh-independent behavior. In addition, Fig. 15d also shows the energetic hardening as the energetic length scale increases. The mesh-independent behavior is also observed with varying dissipative length scales ℓ_dis/w = 0.1 , 0.2 and 0.3 with ℓ_en/w = 0 in Fig. 15e as with the case for the energetic length scale. The dissipative strengthening is also observed in this figure.

The stress jump phenomenon hitherto extensively studied in the one-dimensional finite element implementation is also examined for the two-dimensional simulation; 20 × 20 elements with ℓ_en/w = 0.0 and ℓ_dis/w = 0.2 are used for this simulation. Figure 15f shows the material behaviors of the unpassivated plate, the passivated plate, and the plate abruptly passivated at some point. As can be seen in this figure, the stress jump is significantly observed by the numerical results, which are identical to the one-dimensional case.

Conclusions

In this chapter, a phenomenological thermodynamic-based higher order gradient plasticity theory is presented and applied to the stretch-surface passivation problem for investigating the material behavior under the nonproportional loading condition. The thermodynamic potentials such as the Helmholtz free energy and the dissipation potential are established based on the concepts of the dislocation interaction mechanism and the thermal activation energy. The microstructural interface effect between two grains is also incorporated into the formulation, such that the present interfacial flow rule is able to account for the energy storage at the interface caused by the dislocation pile up as well as the energy dissipation through the interface caused by the dislocation transfer. The formulation is tested for two cases in the presence of the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$. In the first case, the dissipation potential is dependent on the gradients of the plastic strain rate ${\dot{\varepsilon}}_{ij,k}^p$; as a result, ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ does not have a value of zero in this formulation. In the second case the dissipation potential is independent of ${\dot{\varepsilon}}_{ij,k}^p$, which in turn, ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ does not exist. It is noticed by Fleck et al. (2014, 2015) that ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ always gives rise to the stress jump phenomenon, which causes a controversial dispute in the field of SGP theory with respect to whether it is physically acceptable or not, under the nonproportional loading condition.

Prior to exploring the effect of the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$ on the stress-strain behavior for the two cases of the SGP model with and without ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$, the present model and corresponding finite element code by Voyiadjis and Song (2017) are validated by comparing with three sets of small-scale experiments. Particularly, each set of three experiments involving Al, Cu, and Ni are selected, respectively, to examine the applicability of the present finite element implementation to the various kinds of materials. The first experiment, which was performed by Haque and Saif (2003), is the uniaxial tensile testing of nanoscale freestanding Al thin films to explore the effect of strain gradient in 100 nm, 150 nm, and 485 nm thick specimens with average grain size of 50 nm, 65 nm, and 212 nm, respectively. The results clearly show the size effect on the stress-strain curves of the Al thin films; in addition, the calculated results of the present SGP model display a tendency to be more coincident to the experimental data than those of Voyiadjis and Faghihi (2014). For the second experimental validation, the experimental work of Xiang and Vlassak (2006) on the size effect in electroplated Cu thin films with various microscale thicknesses is selected since the effect of passivation on the stress-strain behavior of the Cu thin film is also considered in their work. The stress-strain curves from the numerical results of the present SGP (Voyiadjis and Song 2017) model are in good agreement with the experimental measurements. The size effect according to the variation of the film thicknesses is also well observed from the results. For the third experimental validation, the microtensile test on the temperature effect on Ni thin films by Han et al. (2008) is employed since, in the nano- or microsystems, the effect of the higher order gradient on temperature also needs to be considered for the fast transient behavior. From both the experimental and numerical results, it is shown that the Young’s modulus is not affected by the variations in temperature, while the yield and tensile strength decrease as the specimen temperature increases. The calculated results of the present model (Voyiadjis and Song 2017) compare better to the experimental data than those of Voyiadjis and Faghihi (2014).

The numerical simulation part is largely composed of four subparts. The main purpose of the first part is to examine the occurrence of the stress jump phenomenon under the stretch-surface passivation condition in conjunction with the aforementioned three experiments. In all simulations, a stress jump is clearly observed at the onset of passivation. The second part is carried out in order to clearly show the results to be contrary to each other from the two cases of the SGP model. The conclusion in this part is drawn such that a significant stress jump with the slope E_passivation similar to the modulus of elasticity E is shown in the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, on the other hand, no elastic stress jump is observed in the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$. This result is exactly in agreement with the predictions in Fleck et al. (2014, 2015).

In the third part, an extensive parametric study is presented in terms of the effects of the dissipative length scale ℓ_dis, the onset point of passivation, the hardening material parameter h, the nonnegative rate sensitivity parameter m, the temperature sensitivity parameter n, the thermal material parameter T_y, the interfacial temperature sensitivity parameter n^I, and the interfacial thermal material parameter ${T}_y^I$ on the stress-strain response for the two SGP cases, respectively. There are a number of conclusions worth mentioning here, namely: (1) the magnitude of the stress jump significantly increases as the dissipative length scale increases, on the other hand, the stress jump phenomenon disappears as the dissipative length scale comes closer to zero, (2) the slopes of the very first response E immediately after the passivation also increase as the dissipative length scales increase, (3) the stress jump phenomenon is highly correlated with the dissipative higher order microstress quantities ${\mathcal{S}}_{ijk}^{\mathrm{dis}}$, in addition, the very first responses immediately after the passivation also make a substantial difference with varying passivation points, (4) the hardening material parameter h does not affect the stress jump significantly in the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, (5) both the slope of the very first response immediately after the passivation and the corresponding magnitude of the stress jump substantially increase as the nonnegative rate sensitivity parameter m increases in the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, (6) as the temperature-related parameters for the bulk such as the temperature sensitivity parameter n and the thermal material parameter T_y increase, the slope of the very first response immediately after the passivation decreases and the corresponding magnitude of the stress jump increases in the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, (7) the slope of the very first response after the passivation, the corresponding magnitude of the stress jump increases and the variations along with the cases are shown more drastically by decreasing the temperature-related parameters for the interface, such as the interfacial temperature sensitivity parameter n^I and the interfacial thermal material parameter ${T}_y^I$ in the case of the SGP model with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}\ne 0$, and finally (8) no stress jump is observed in all cases with ${\mathcal{S}}_{ijk}^{\mathrm{dis}}=0$.

Meanwhile, the plastic strain-dependent free energy accounting for the stored energy of cold work is derived in this chapter by assuming that the stored energy is related to the energy carried by dislocations. Accordingly, the variation of free energies and dissipation potentials during the plastic deformation are investigated with four different temperatures, i.e. 25 °C, 75 °C, 145 °C, and 218 °C. From the numerical results, it is shown that the stored energy of cold work has no temperature dependency; in addition, the stored energy of cold work tends to saturate after some critical point since the stored energy of cold work is proportional to the dislocation density that remains constant after the aforementioned critical point.

Lastly, the two-dimensional tension problem of the square plate (Voyiadjis and Song 2017) is solved to examine the mesh sensitivity of the model. The effects of the strain gradient and grain boundary are also studied. As expected, a strong mesh-dependence stress-strain behavior is observed in the case of no gradient effects, while the numerical results with the gradient effects show the mesh-independent behavior. The energetic hardening, the dissipative strengthening, the grain boundary strengthening, and the stress jump phenomena are well observed in common with the results from the one-dimensional simulation.