On dissipative gradient effect in higher-order strain gradient plasticity: the modelling of surface passivation

Abstract

The phenomenological flow theory of higher-order strain gradient plasticity proposed by Fleck and Hutchinson (J. Mech. Phys. Solids, 2001) and then improved by Fleck and Willis (J. Mech. Phys. Solids, 2009) is used to investigate the surface-passivation problem and micro-scale plasticity. An extremum principle is stated for the theory involving one material length scale. To solve the initial boundary value problem, a numerical scheme based on the framework of variational constitutive updates is developed for the strain gradient plasticity theory. The main idea is that, in each incremental time step, the value of the effective plastic strain is obtained through the variation of a functional in regard to effective plastic strain, provided the displacement or deformation gradient. Numerical results for elasto-plastic foils under tension and bending, thin wires under torsion, are given by using the minimum principle and the numerical scheme. Implications for the role of dissipative gradient effect are explored for three non-proportional loading conditions: (1) stretch-passivation problem, (2) bending-passivation problem, and (3) torsion-passivation problem. The results indicate that, within the Fleck–Hutchinson–Willis theory, the dissipative length scale controls the strengthening size effect, i.e. the increase of initial yielding strength, while the surface passivation gives rise to an increase of strain hardening rate.

Graphic abstract

1 Introduction

A number of experiments at small scales have revealed that metallic materials display significant size effects related to plastic deformation involving plastic strain gradients [1,2,3,4,5,6,7,8,9,10]. It is well known that conventional (local) plasticity theories cannot capture the experimentally observed change in the mechanical behavior with diminishing size. One way to predict size effects in polycrystalline metals is to introduce gradient effects in the governing equations. To date, various strain gradient theories of isotropic plasticity have been developed, mainly based on the relationship between geometrically necessary dislocations (GNDs) and the gradient of plastic strain [11, 12], see for example, Aifantis [13], Fleck and Hutchinson [14, 15], Fleck and Willis [16, 17], Gudmundson [18], Gudmundson and Dahlberg [19], Gurtin and Anand [20, 21], Gurtin [22], Nix and Gao [23], Gao et al. [24], Kuroda and Tvergaard [25], Chen and Wang [26], etc. In most of these theories, one or more material length scales are introduced through the definition of the gradient-enhanced effective plastic strain, which combines the contributions from the effective plastic strain and the effective plastic strain gradient. A general review of strain gradient plasticity (SGP) in both theoretical and experimental aspects has been recently given by Voyiadjis and Song [27].

It is now well accepted that the strain gradient plasticity theory should be higher-order [15, 28], not only by incorporating strain gradient into the frameworks but also in possessing higher-order stresses which are work-conjugate to the plastic strain gradients. The higher-order theories open up one way to model the extra boundary conditions beyond the scope of conventional plasticity theory. In each theory some measure of the plastic strain (rate) and its spatial gradient enter a statement of the principle of virtual power, see the works of Gudmundson [18], Gurtin et al. [29], and Voyiadjis and Song [27] in detail. An attractive formulation of higher-order strain gradient plasticity is the one proposed by Fleck and Hutchinson [14]. The Fleck–Hutchinson theory [14] is a phenomenological extension of the classic $J_{2}$ flow theory, which shares several common features with an earlier model developed by Muhlhaus and Aifantis [30]. However, Gudmundson [18] and Gurtin and Anand [31] found that, under non-proportional straining, the Fleck–Hutchinson theory violates the thermodynamic requirement that plastic dissipation must be non-negative. The theory has then been improved by Fleck and Willis [17] and Hutchinson [15] for satisfying the thermodynamic restriction. To ensure a positive plastic dissipation, the requirement of energetic (or recoverable) and dissipative (or unrecoverable) gradient contributions is needed for the vast majority of the modern SGP formulations. However, as indicated by Fleck and Willis [32], the degree to which size effects are mainly energetic or dissipative remains an open issue. On the one hand, GNDs may be considered to translate into an increase in free energy of the solid [33]. On the other hand, experiments suggest that the core energy of dislocations stored during plastic deformation is much smaller than the plastic work dissipated in dislocation motion, such that GNDs movement in the lattice may contribute more to plastic dissipation [17]. The different qualitative responses with decreasing size have been observed in experiments at micron-meter scale. For example, the torsion experiments on thin metallic wires by Fleck et al. [1] and Liu et al. [2] reveal a significant increase in the yield strength; while additional hardening is seen in other measurements [7, 34]. Moreover, some experiments, e.g. the micro-bending tests [8] and micro-torsion tests [3], even show a combination of strengthening and hardening. The role of higher-order energetic and dissipative stresses has been numerically investigated in several works [35,36,37,38,39,40,41,42]. It is shown that the higher-order energetic stresses lead to higher strain hardening while the dissipative counterparts increase the yield strength. Also, the role of higher-order boundary conditions has been highlighted by Evans and Hutchinson [28], Panteghini and Bardella [43], and Niordson and Hutchinson [44]. However, the role of dissipative gradient effect on the boundary passivation problem remains to be investigated in detail.

Recent theoretical and experimental works demonstrate that the appearance of the passivated layer significantly elevates the yield strength and (or) the strain hardening of thin foils and wires [28, 32, 34, 39, 40, 45,46,47,48]. However, the strengthening of small-scale structures due to surface passivation cannot be captured by the standard continuum plasticity theory or the lower-order SGP theory since the boundary conditions imposed by the classical or lower-order SGP theory make no difference between conditions at the unpassivated surface and at the passivated surface [28, 46]. Additional boundary conditions are requisite for plastic strains or higher-order stresses, which make it possible to enhance the description of the solid near interfaces or surface boundary [49].

In this paper, the role of dissipative gradient contribution is assessed within the higher-order strain gradient plasticity theory developed by Fleck and Hutchinson [14] and Fleck and Willis [17]. The basic problems including tension of thin foils, bending of thin foils, and torsion of thin wires are analyzed under micro-free (unpassivated) and micro-hard (passivated) boundary conditions. The effect of surface passivation on the mechanical responses of thin wires and foils under different loading conditions is highlighted. The current work is structured as follows. The theory basis is briefly introduced in Sect. 2. The constitutive model and the associated minimum principle for the elasto-plastic solid are stated. In Sect. 3, the numerical method based on the framework of variational constitutive updates is introduced to solve the initial boundary value problem for Fleck–Hutchinson–Willis theory. The theoretical analyses of foil tension, foil bending, and wire torsion problems are carried out in Sect. 4. Numerical results and discussion are given in Sect. 5. Finally, some conclusions are provided in Sect. 6.

2 Theory basis

2.1 Principle of virtual work and balance equations

We introduce the Fleck–Hutchinson–Willis higher-order SGP theory [14, 17] briefly. The theory is a natural extension of $J_{2}$ flow theory for the classical elastic–plastic solid. Small strain, rate-independent plasticity is assumed throughout the paper. With $\dot{u}_{i}$ as the rate of displacement vector, $\dot{\varepsilon }_{ij} = \tfrac{1}{2}\left( {\dot{u}_{i,j} + \dot{u}_{j,i} } \right)$ is the strain rate, and $\dot{\varepsilon }_{ij} = \dot{\varepsilon }_{ij}^{\text{EL}} + \dot{\varepsilon }_{ij}^{\text{PL}}$, where $\dot{\varepsilon }_{ij}^{\text{EL}}$ is elastic strain rate and $\dot{\varepsilon }_{ij}^{\text{PL}}$ plastic strain rate; $\dot{\varepsilon }_{\text{P}} = \sqrt {{{2\dot{\varepsilon }_{ij}^{\text{PL}} \dot{\varepsilon }_{ij}^{\text{PL}} } \mathord{\left/ {\vphantom {{2\dot{\varepsilon }_{ij}^{\text{PL}} \dot{\varepsilon }_{ij}^{\text{PL}} } 3}} \right. \kern-0pt} 3}}$ is the rate of effective plastic strain, and $\varepsilon_{\text{P}} = \int {\dot{\varepsilon }_{\text{P}} {\text{d}}t}$; $\sigma_{ij}$ is the symmetric Cauchy stress, $s_{ij}$ is its deviator, and the effective stress $\sigma_{\text{e}} = \sqrt {{{3s_{ij} s_{ij} } \mathord{\left/ {\vphantom {{3s_{ij} s_{ij} } 2}} \right. \kern-0pt} 2}}$. In a domain with non-vanished $\varepsilon_{\text{P}}$, the principle of virtual power for the body with volume $V$ and surface $S$ reads

$$\int_{V} {\left( {\sigma_{ij} \dot{\varepsilon }_{ij}^{\text{EL}} + q\dot{\varepsilon }_{\text{P}} + \tau_{i} \dot{\varepsilon }_{{{\text{P}},i}} } \right){\text{d}}V} = \int_{S} {\left( {T_{i} \dot{u}_{i} + t\dot{\varepsilon }_{\text{P}} } \right){\text{d}}S} ,$$

(1)

where $q$ is a scalar microstress power-conjugate to $\dot{\varepsilon }_{\text{P}}$, $\tau_{i}$ is a vector microstress power-conjugate to $\dot{\varepsilon }_{{{\text{P}},i}}$. Both the conventional traction $T_{i}$ and the high-order traction $t$ contribute to the external virtual power when applied on the boundary $S$.

A main hypothesis of the Fleck–Hutchinson–Willis theory is the conventional co-directionality constraint. That is, the direction of the plastic strain rate $\dot{\varepsilon }_{ij}^{\text{PL}}$ coincides with the direction of the deviatoric Cauchy stress $s_{ij}$, i.e.

$$\dot{\varepsilon }_{ij}^{\text{PL}} = \dot{\varepsilon }_{\text{P}} m_{ij} \;\;{\text{where}}\;\;m_{ij} \equiv \tfrac{3}{2}\tfrac{{s_{ij} }}{{\sigma_{\text{e}} }}.$$

(2)

Here, $m_{ij}$ denotes the direction of the plastic strain increment. The local balance equations and traction conditions follow directly from the principle of virtual power

$$\sigma_{ij,j} = 0, \, q - \tau_{i,i} = \sigma_{\text{e}} \;\;{\text{in}}\;\;V,$$

(3)

$$\sigma_{ij} n_{j} = T_{i} , \, \tau_{i} n_{i} = t\;\;{\text{on}}\;\;S,$$

(4)

and $n_{i}$ is the unit normal on the boundary. By the second law of thermodynamics under isothermal conditions, Fleck and Hutchinson [14] achieve the requirement of positive plastic work at each point within $V$,

$$q\dot{\varepsilon }_{\text{P}} + \tau_{i} \dot{\varepsilon }_{{{\text{P}},i}} \ge 0.$$

(5)

It should be mentioned that, as noted by Gudmundson [18] and Gurtin and Anand [31], the requirement Eq. (5) may be violated for certain non-proportional strain histories. However, as discussed by Hutchinson [15], such a requirement can be always met for the plastic loading condition which we focus on here.

2.2 Generalized effective plastic strain rates

Two versions of generalized effective plastic strain rates are considered. One is introduced by Aifantis [13, 50], which is expressed as

$$\dot{E}_{\text{P}} = \sqrt {\dot{\varepsilon }_{\text{P}}^{2} + \ell^{2} \dot{\varepsilon }_{{{\text{P}},i}} \dot{\varepsilon }_{{{\text{P}},i}} } .$$

(6)

It contains one dissipative material length scale, $\ell$, which is required for dimensional consistency. The other is the three-parameter version introduced by Fleck and Hutchinson [14], which is defined as

$$\dot{E}_{\text{P}} = \sqrt {\dot{\varepsilon }_{\text{P}}^{2} + \sum\limits_{I = 1}^{3} {\left( {\ell_{I} } \right)^{2} \rho_{ijk}^{(I)} \rho_{ijk}^{(I)} } } .$$

(7)

Here, $\ell_{I} \left( {I = 1,2,3} \right)$ are three dissipative material length scales, $\rho_{ijk} = \dot{\varepsilon }_{ij,k}^{\text{PL}}$ is the plastic strain gradient tensor, and $\rho_{ijk} = \rho_{jik}$, $\rho_{iik} = 0$. According to Smyshlyaev and Fleck [51], $\rho_{ijk}$ can be decomposed into three orthogonal tensors $\rho_{ijk}^{(I)}$, i.e.

$$\rho_{ijk} = \sum\limits_{I = 1}^{3} {\rho_{ijk}^{(I)} } ,\;{\text{and}}\;\;\rho_{ijk}^{(I)} \rho_{ijk}^{(J)} = 0\;\;{\text{if}}\;\;I \ne J,$$

(8)

The explicit expressions of $\rho_{ijk}^{(I)}$ for $I = 1,2{\text{ or 3}}$ in terms of $\rho_{ijk}$ have been provided by Fleck and Hutchinson [14]. Considering Eq. (2), we have the relation

$$\dot{\varepsilon }_{ij,k}^{\text{PL}} = \rho_{ijk} = m_{ij} \dot{\varepsilon }_{{{\text{P}},k}} + m_{ij,k} \dot{\varepsilon }_{\text{P}} .$$

(9)

By performing the orthogonal decomposition (8) of $\rho_{ijk}$ and considering Eq. (9), one can recast the generalized effective plastic strain rate as

$$\dot{E}_{\text{P}} = \left( {\dot{\varepsilon }_{\text{P}}^{2} + A_{ij} \dot{\varepsilon }_{{{\text{P}},i}} \dot{\varepsilon }_{{{\text{P}},i}} + B_{i} \dot{\varepsilon }_{{{\text{P}},i}} \dot{\varepsilon }_{\text{P}} + C\dot{\varepsilon }_{\text{P}}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} .$$

(10)

The coefficients $A_{ij}$, $B_{i}$, and $C$ are dependent on three material length scales $\ell_{I}$ and on $m_{ij}$. Explicit expressions for these coefficients can be found in Ref. [14]. As indicated by Fleck and Hutchinson [14], the one-length scale version (6) is not a special case of Eq. (7), but formally included in Eq. (10) by assuming $A_{ij} = \ell_{ *}^{2} \delta_{ij}$, $B_{i} = 0$ and $C = 0$. For convenience, Fleck and Willis [17] simplify the above notations by introducing the four-dimensional strain rate vectors $\dot{\varvec{e}} = \left[ {\dot{\varepsilon }_{\text{P}} ,\dot{\varepsilon }_{{{\text{P}},1}} ,\dot{\varepsilon }_{{{\text{P}},2}} ,\dot{\varepsilon }_{{{\text{P}},3}} } \right]$. Then, Eqs. (6) and (10) can be rewritten in the form

$$\dot{E}_{\text{P}} = \left( {\bar{A}_{IJ} \dot{e}_{I} \dot{e}_{J} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\;\left( {I,J} \right)\;\;{\text{sum over }}0, 1, 2, 3,$$

(11)

where the coefficients in the symmetric, positive definite $4 \times 4$ matrix $\left[ {\bar{A}_{IJ} } \right]$ are related straightforwardly to $\left( {A_{IJ} ,B_{I} ,C} \right)$ through $\bar{A}_{00} = 1 + C$, $\bar{A}_{0I} = \bar{A}_{I0} = \tfrac{1}{2}B_{I}$ for $I \in \left\{ {1,2,3} \right\}$, and $\bar{A}_{IJ} = A_{JI}$ for $I,J \in \left\{ {1,2,3} \right\}$. By choosing reasonable parameters $\ell_{I}$, Eq. (10) can be reduced to the form containing one length scale, whereas it is different from Eq. (6) in some cases, see discussion in Appendix in detail. It should be noted that we don’t intend to discuss the physical interpretation or the magnitude of the length scale introduced in the strain gradient plasticity. Several attempts in this direction can be found in works [28, 52, 53]. Here, we are simply trying to clarify the role of dissipative length scale, especially for the passivated cases. Following other works [14, 15, 17,18,19, 24, 36,37,38,39,40,41], we employ the dimensionless ratio between the material length scale and the geometrical dimension (e.g. the foil thickness, the wire radius, etc.), instead of giving a specific value of the length scale, to analyze the problems in what follows.

2.3 Constitutive equations and minimum principle

We restrict our attention to the dissipative model and emphasize that neither $\varepsilon_{ij}^{\text{PL}}$ nor $\varepsilon_{ij,k}^{\text{PL}}$ contributes to a free energy. An isotropic elasto-plastic constitutive model is assumed that accounts for internal energy storage due to elastic straining, and for dissipation due to plastic straining and its spatial gradient. The elastic behavior is characterized by

$$\sigma_{ij} = \frac{{\partial U\left( {\varepsilon_{ij}^{\text{EL}} } \right)}}{{\partial \varepsilon_{ij}^{\text{EL}} }} = L_{ijkl} \varepsilon_{kl}^{\text{EL}} = L_{ijkl} \left( {\varepsilon_{kl} - \varepsilon_{kl}^{\text{PL}} } \right),$$

(12)

where $U\left( {\varepsilon_{ij}^{\text{EL}} } \right)$ is the internal energy density of the solid, and $L_{ijkl}$ is an isotropic elastic stiffness tensor.

It is assumed that the plastic dissipation depends upon $\dot{E}_{\text{P}}$ within $V$. The notation can be further simplified by introducing a four-dimensional stress vector $\varvec{r} = \left[ {q,\tau_{1} ,\tau_{2} ,\tau_{3} } \right]$, where $\tau_{i}$ is the higher-order stress, and $q$ is the microstress work-conjugate to the effective plastic strain $\varepsilon_{\text{P}}$ [17, 54]. Fleck and Willis [17] refined the generalized effective stress for satisfying the thermodynamics requirement. In the original Fleck–Hutchinson model [14], the generalized effective stress is exactly work-conjugate to $\varepsilon_{\text{P}}$, while in the Fleck–Willis model [17], it comprises both the work-conjugate to $\varepsilon_{\text{P}}$ and the work-conjugate to $\varepsilon_{{{\text{P}},i}}$. Correspondingly, the generalized effective stress is given by

$$S = \left( {D_{IJ} r_{I} r_{J} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,$$

(13)

where $\varvec{D} \equiv \bar{\varvec{A}}^{ - 1}$. For the incremental plasticity, we have

$$r_{I} = \frac{S}{{\dot{E}_{\text{P}} }}\bar{A}_{IJ} \dot{e}_{J} .$$

(14)

In order to guarantee a positive dissipation, an associative plastic flow is assumed, whereby the strain-rate vector $\dot{e}_{I}$ is taken to be normal to a convex yield surface defined in the space of stress vectors. So,

$$f\left( {r_{I} ;E_{\text{P}} } \right) = S - \sigma_{y} \left( {E_{\text{P}} } \right) = 0.$$

(15)

Here, $\sigma_{y} \left( {E_{\text{P}} } \right)$ is the uniaxial flow strength of the solid, evaluated at $E_{\text{P}} = \int {\dot{E}_{\text{P}} {\text{d}}t}$. The strength is therefore enhanced by the presence of plastic strain gradients. Note that $\dot{S} = {{\dot{r}_{I} r_{I} } \mathord{\left/ {\vphantom {{\dot{r}_{I} r_{I} } S}} \right. \kern-0pt} S}$ is the projection of the generalized stress rate on the yield surface. During plastic loading, $\dot{S} > 0$ and the continued yield implies the consistency relation $\dot{S} = h\left( {E_{\text{P}} } \right)\dot{E}_{\text{P}}$ with $h\left( {E_{\text{P}} } \right)$ being the hardening modulus of the material. Therefore, the dissipation rate is $r_{I} \dot{e}_{I} = \sigma_{y} \left( {E_{\text{P}} } \right)\dot{E}_{\text{P}} \ge 0$, as required by thermodynamics. The solid with $h\left( {E_{\text{P}} } \right) \le 0$ needs a special treatment which is not considered here.

2.3.1 Minimum principle

The minimum principle for the incremental boundary value problem for the theory is similar in structure to that for classical $J_{2}$ flow theory except that it involves the contributions from the gradients of plastic strain rate. Following Fleck and Hutchinson [14], we obtain the minimum principle which requires that the functional $I$ to be minimized with respect to $\dot{u}_{i}$ and $\dot{\varepsilon }_{\text{P}}$, i.e.

$$I\left( {\dot{u}_{i} ,\dot{\varepsilon }_{\text{P}} } \right) = \frac{1}{2}\int_{V} {\left[ {\left( {\dot{\varepsilon }_{ij} - m_{ij} \dot{\varepsilon }_{\text{P}} } \right)L_{ijkl} \left( {\dot{\varepsilon }_{kl} - m_{kl} \dot{\varepsilon }_{\text{P}} } \right) + h\left( {E_{\text{P}} } \right)\dot{E}_{\text{P}}^{2} } \right]{\text{d}}V} - \int_{{S_{T} }} {\left( {\dot{T}_{i}^{0} \dot{u}_{i} + \dot{t}^{0} \dot{\varepsilon }_{\text{P}} } \right){\text{d}}S} .$$

(16)

Here, the first term in $V$ represents the elastic part of the work, and the second term represents the plastic expenditure of work, due to a gradient enhanced measure of effective plastic strain $E_{\text{P}}$. $\dot{T}_{i}^{0}$ and $\dot{t}^{0}$ are given traction rates on $S_{T}$.

2.4 Kinematic boundary conditions

The classical kinematic boundary conditions are

$$\dot{u}_{i} = \dot{u}_{i}^{0} \;\;{\text{on}}\;\;S_{u} .$$

(17)

Specifically, we consider essential higher-order kinematic boundary conditions, called microscopically hard boundary conditions by Gurtin and Anand [21], asserting that

$$\dot{\varepsilon }_{\text{P}} = 0\;\;{\text{on}}\;S_{u}^{\text{hard}} .$$

(18)

The microscopically hard condition Eq. (18) corresponds to a boundary surface which cannot pass dislocations. So, Eq. (18) can be used to model the passivation problem in which, for example, the surface of the solid is passivated by a hard layer that deforms elastically, but not plastically.

3 Numerical method

The minimization of functional $I$ can be implemented on basis of framework of variational constitutive updates [55]. The displacement rate $\dot{u}_{i}$ is assumed to be tentatively provided, which suggests that the strain rate $\dot{\varepsilon }_{ij}$ is determined. By Eq. (16), one can see that the effective plastic strain rate is the only primary kinematic variable to be determined. Correspondingly, during the finite element implementation, it is not necessary to solve any classical displacement equilibrium equations.

A one-dimensional, linear (two-noded) element with fully integration (two Gauss points) is used here. The effective plastic strain increment at point x is written in terms of the shape functions $N_{a}$ and the associated nodal unknowns $\Delta \xi_{a}$, i.e.

$$\Delta \xi = \sum\limits_{a = 1}^{2} {N_{a} \Delta \xi_{a} } .$$

(19)

The Backward-Euler time integration scheme is adopted. The effective plastic strain at the end of each time step is calculated as

$$\xi^{t + \Delta t} = \xi^{t} + \Delta \xi .$$

(20)

Given the foregoing spatial and time discretization, Eq. (16) can be written in the finite element formulation,

$$\begin{aligned} I\left( {\Delta \xi } \right) & = \frac{1}{2}\int_{V} {E\left( {\Delta \varepsilon - N_{a} \Delta \xi_{a} } \right)\left( {\Delta \varepsilon - N_{b} \Delta \xi_{b} } \right){\text{d}}V} \\ & \quad + \frac{1}{2}\int_{V} {h\left( {E_{\text{P}}^{t} } \right)\left( {\Delta E_{\text{P}} } \right)^{2} {\text{d}}V} , \end{aligned}$$

(21)

where $\Delta \varepsilon$ is the increment of applied effective strain, $E$ is the Young’s modulus, and

$$\Delta E_{\text{P}} = \left( {\omega_{1} N_{a} \Delta \xi_{a} N_{b} \Delta \xi_{b} + \omega_{2} N_{a,i} \Delta \xi_{a} N_{b,i} \Delta \xi_{b} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

(22)

is the generalized effective plastic strain increment. Here, $N_{a,i}$ denotes the derivative of the shape function with respect to the local coordinate, and the coefficients $\omega_{1}$ and $\omega_{2}$ are given in Appendix. Similar to Eq. (20), we have

$$E_{\text{P}}^{t + \Delta t} = E_{\text{P}}^{t} + \Delta E_{\text{P}} .$$

(23)

In order to achieve the minimization, we need to determine the nodal residuals $\varvec{R}$, defined as the differentiation of Eq. (21) with respect to the incremental nodal variables,

$$R_{a} = - \int_{V} {E\Delta \varepsilon N_{a} {\text{d}}V} + \int_{V} {\left[ {\left( {E + h\omega_{1} } \right)N_{a} N_{b} \Delta \xi_{b} + \omega_{2} N_{a,i} N_{b,i} \Delta \xi_{b} } \right]{\text{d}}V} .$$

(24)

One can obtain the increment of the effective plastic strain $\Delta \xi$ by setting $\varvec{R} = {\mathbf{0}}$ and solving a system of linear equations

$$K_{ab} \Delta \xi_{b} = F_{a} ,$$

(25)

where the consistent stiffness matrix $\varvec{K}$ is obtained by differentiating $\varvec{R}$ with respect to the incremental nodal variables, and

$$K_{ab} = \int_{V} {\left[ {\left( {E + h\omega_{1} } \right)N_{a} N_{b} + \omega_{2} N_{a,i} N_{b,i} } \right]{\text{d}}V} ,$$

(26)

$$F_{a} = \int_{V} {E\Delta \varepsilon N_{a} {\text{d}}V} .$$

(27)

If the strain increment is tentatively prescribed, the effective plastic increment can be consistently obtained by Eq. (25). Here, we adopt $E_{\text{P}}^{t}$ instead of $E_{\text{P}}^{t + \Delta t}$ at step $t$ to achieve a relatively simple formulation. It has been proved that this choice makes no difference for the convergence of the results [55]. Furthermore, we set a critical value of $E_{\text{P}}$ as a truncation, e.g. $tr = 1 0^{ - 10}$, in order to launch the simulation at the first step. The convergence of the computation has been carefully checked by increasing the number of nodes until the results are not affected by further mesh refinement.

4 Numerical examples

Three benchmark problems, foil tension, foil bending and wire torsion, are studied. Attention is specifically paid to the microscopically hard condition for elucidating the role of surface passivation. We work in the rate-independent plasticity and the monotonic loading condition. Plane-strain conditions and material incompressibility ($\nu = 0.5$) are assumed. The hardening function in Eq. (16) can be described by the Ramberg–Osgood relation

$${\varepsilon \mathord{\left/ {\vphantom {\varepsilon {\varepsilon_{0} }}} \right. \kern-0pt} {\varepsilon_{0} }} = {\sigma \mathord{\left/ {\vphantom {\sigma {\sigma_{0} }}} \right. \kern-0pt} {\sigma_{0} }} + \left( {{\sigma \mathord{\left/ {\vphantom {\sigma {\sigma_{0} }}} \right. \kern-0pt} {\sigma_{0} }}} \right)^{n} ,$$

(28)

where $\sigma_{0} = E\varepsilon_{0}$ is a flow stress, and $n = {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0pt} N}$ is a hardening exponent. For this choice, Eq. (28) can be reformulated as $\sigma_{y} \left( {E_{\text{P}} } \right) = \sigma_{0} \left( {{{E_{\text{P}} } \mathord{\left/ {\vphantom {{E_{\text{P}} } {\varepsilon_{0} }}} \right. \kern-0pt} {\varepsilon_{0} }}} \right)^{N}$, and the hardening modulus reads

$$h\left( {E_{\text{P}} } \right) = NE\left( {{{E_{\text{P}} } \mathord{\left/ {\vphantom {{E_{\text{P}} } {\varepsilon_{0} }}} \right. \kern-0pt} {\varepsilon_{0} }}} \right)^{N - 1} .$$

(29)

Upon loading, plasticity generally evolves from the outset throughout the specimen, so that no elastic–plastic boundary exists.

4.1 Foil tension

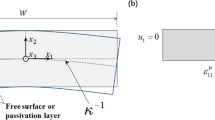
A foil of thickness $H$ with one or two passivated layers (shaded area) is stretched along the $x_{1}$-axis to a prescribed strain $\varepsilon_{11}$, as shown in Fig. 1. The strain is imposed at the ends of the foil. The components of the plastic strain rate are functions of $x_{2}$. The non-vanishing strain components can be expressed as

Fig. 1

Schematic of the thin foil under plane-strain tension. a One passivated surface, and b two passivated surfaces

$$\dot{\varepsilon }_{11}^{\text{PL}} = - \dot{\varepsilon }_{22}^{\text{PL}} = \tfrac{\sqrt 3 }{2}\dot{\varepsilon }_{\text{P}} \left( {x_{2} } \right),$$

(30)

$$\dot{\sigma }_{11} = 2\dot{\sigma }_{33} = \tfrac{2}{\sqrt 3 }\dot{\sigma }_{\text{e}} .$$

(31)

A monotonically increasing uniaxial strain $\dot{\varepsilon }_{11}$ is applied. By Eq. (10), the generalized effective plastic strain rate has the form of

$$\dot{E}_{\text{P}} = \sqrt {\dot{\varepsilon }_{\text{P}}^{2} + \left( {\ell \dot{\varepsilon^{\prime}}_{\text{P}} } \right)^{2} } ,$$

(32)

where $\left( \cdot \right)^{\prime } \equiv {{{\text{d}}\left( \cdot \right)} \mathord{\left/ {\vphantom {{{\text{d}}\left( \cdot \right)} {{\text{d}}x}}} \right. \kern-0pt} {{\text{d}}x}}_{2}$. The tensile stress at the cross-section of the foil is

$$\sigma_{11} = \frac{4}{3}E\left( {\varepsilon_{11} - \varepsilon_{11}^{\text{PL}} } \right).$$

(33)

In this case, the functional Eq. (16) is reduced to be

$$I\left( {\dot{\varepsilon }_{\text{P}} } \right) = \frac{1}{2}\int_{0}^{H} {\left[ {E\left( {\frac{2}{\sqrt 3 }\dot{\varepsilon }_{11} - \dot{\varepsilon }_{\text{P}} } \right)^{2} + h\left( {E_{\text{P}} } \right)\dot{E}_{\text{P}}^{2} } \right]{\text{d}}x_{2} } .$$

(34)

Plastic strain gradients come into play in this problem only if the top and/or bottom boundaries are assumed to constrain the plastic flow. The simulation of this situation must require the plastic strain rate to vanish at such a boundary, i.e. $\dot{\varepsilon }_{\text{P}} = 0$ at $x_{2} = 0$ or $H$.

4.2 Foil bending

A foil of thickness $2H$ which is bent around the $x_{3}$-axis to a curvature $\kappa$ is shown in Fig. 2. A Cartesian coordinate system is embedded with the $x_{1}$-axis along the neutral axis and the $x_{2}$-axis perpendicular to the neutral axis in the plane of deformation. Following Stölken and Evans [7], we assume that curvature is imposed via displacement boundary conditions at the ends of the foil. The traction-free boundary conditions are adopted at the top and bottom surfaces of the foil, i.e. $\dot{T}_{i}^{0} = \dot{t}^{0} = 0$ at $x_{2} = \pm H$. We concentrate on the top half of the foil, i.e. on the domain $0 \le x_{2} \le H$, for simplicity. The only non-zero components of the total and plastic strain-rate tensors can be written as

Fig. 2

Schematic of a thin foil under bending

$$\dot{\varepsilon }_{11} = - \dot{\varepsilon }_{22} = \dot{\kappa }x_{2} ,$$

(35)

$$\dot{\varepsilon }_{11}^{\text{PL}} = - \dot{\varepsilon }_{22}^{\text{PL}} = \tfrac{\sqrt 3 }{2}\dot{\varepsilon }_{\text{P}} \left( {x_{2} } \right).$$

(36)

The stress components and the generalized effective plastic strain rate are identical to Eqs. (31) and (32), as discussed in Appendix. The functional Eq. (16) for this situation is written as

$$I\left( {\dot{\varepsilon }_{\text{P}} } \right) = \frac{1}{2}\int_{0}^{H} {\left[ {E\left( {\frac{2}{\sqrt 3 }\dot{\kappa }x_{2} - \dot{\varepsilon }_{\text{P}} } \right)^{2} + h\left( {E_{\text{P}} } \right)\dot{E}_{\text{P}}^{2} } \right]{\text{d}}x_{2} } .$$

(37)

The distribution of plastic strain rate $\dot{\varepsilon }_{\text{P}} \left( {x_{2} } \right)$ can then be obtained by using the numerical scheme stated in Sect. 3. The bending moment is evaluated as the standard expression

$$M = 2\int_{0}^{H} {\sigma_{ 1 1} x_{2} {\text{d}}x_{2} } .$$

(38)

4.3 Wire torsion

We now consider a cylindrical wire of radius $R$ twisted monotonically, as shown in Fig. 3. Here, $\alpha$ is the twist per unit length. In the cylindrical coordinates system, the only non-zero components of the total and plastic strain-rate tensors are given by

Fig. 3

Schematic of wire under torsion and the corresponding coordinate systems

$$\dot{\varepsilon }_{\theta z} = - \dot{\varepsilon }_{z\theta } = \frac{{\dot{\alpha }r}}{2}\;\;{\text{and}}\;\;\dot{\varepsilon }_{\theta z}^{\text{PL}} = \dot{\varepsilon }_{z\theta }^{\text{PL}} = \frac{\sqrt 3 }{2}\dot{\varepsilon }_{\text{P}} \left( r \right).$$

(39)

The shear stress is

$$\sigma_{\theta z} = \frac{2}{3}E\left( {\varepsilon_{\theta z} - \varepsilon_{\theta z}^{\text{PL}} } \right).$$

(40)

The functional Eq. (16) governing this problem for the distribution of the plastic strain rate is expressed as

$$I\left( {\dot{\varepsilon }_{\text{P}} } \right) = \frac{1}{2}\int_{0}^{R} {\left[ {E\left( {\frac{{\dot{\alpha }r}}{\sqrt 3 } - \dot{\varepsilon }_{\text{P}} } \right)^{2} + h\left( {E_{\text{P}} } \right)\dot{E}_{\text{P}}^{2} } \right]2\uppi r{\text{d}}r} ,$$

(41)

with

$$\dot{E}_{\text{P}} = \sqrt {\left( {1 + \ell^{2} r^{ - 2} } \right)\dot{\varepsilon }_{\text{P}}^{2} + \left( {\ell \dot{\varepsilon }^{\prime}_{\text{P}} } \right)^{2} } .$$

(42)

Here, $\left( \cdot \right)^{\prime } \equiv {{\text{d} \left( \cdot \right)} \mathord{\left/ {\vphantom {{\text{d} \left( \cdot \right)} {\text{d} r}}} \right. \kern-0pt} {\text{d} r}}$. For a wire with unpassivated surface, the natural boundary condition associated with the variational principle is $\tau_{i} n_{i} = 0$, which requires $\dot{\varepsilon }^{\prime}_{\text{P}} = 0$ at $r = R$. While for a wire with passivated surface, a more appropriate boundary condition would be $\dot{\varepsilon }_{\text{P}} = 0$ at $r = R$. The torque reads

$$Q = 2\uppi \int_{0}^{R} {\sigma_{\theta z} r^{2} {\text{d}}r} .$$

(43)

5 Results and discussion

Passivated boundary conditions are considered as a full constraint on the plastic flow. As discussed in Sect. 2.4, within the higher-order SGP theory, this situation can be modeled as the plastic strain vanishes on the boundaries, i.e. $\dot{\varepsilon }_{\text{P}} = 0$. This is an appropriate condition that models the fact that dislocations cannot penetrate the boundary surface. In the following, numerical results are obtained by choosing the parameter $N = 0.1$ [54, 56].

5.1 Tension of thin foil with passivation

In the tension experiment of Xiang and Vlassak [34], the surface of the Cu foils was passivated with a thin Si₃N₄/TaN layer. Therefore, when the foil is stretched, the dislocations can not escape from the foil surface easily. That is, only elastic deformation occurs on the passivated layer. The measurements show that the flow stress of the passivated foils is much higher than that of unpassivated ones. We now simulate this phenomenon within Fleck-Hutchinson-Willis SGP theory.

The plastic strain distribution is determined uniquely from minimizing the Eq. (34) with a prescribed strain $\varepsilon_{11} = 5\varepsilon_{0}$. Figure 4 shows the distributions of the normalized plastic strain across the foil thickness for the one-surface passivated case and two-surface passivated case, respectively. It can be seen that the plastic strain near the passivation layer is greatly constrained, while the plastic strain far from the passivation layer remain uniform along the thickness. Interestingly, the thickness of the boundary layer(s) at the bottom or top surface remains the same as ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ decreases. Results predicted by the classical model, i.e. ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H} = 0$, are also plotted in Fig. 4a, b for comparison. We found that the classical plasticity predicts a constant plastic strain throughout the thickness, where no gradients emerge. The distributions of the normalized plastic strain gradient along the foil thickness for one-surface passivation and two-surface passivation are displayed in Fig. 4c, d, respectively. In Fig. 4d, only a half thickness of the foil ($0 \le x_{2} \le {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0pt} 2}$) is shown for symmetry reasons. The uniform distribution of the plastic strain near the free surface is a consequence of the higher-order boundary condition which demands a zero higher-order traction, and hence a vanishing plastic strain gradient appears, as seen in Fig. 4c. A large plastic strain gradient appears near the passivation interface ($x_{2} = 0$) by employing a passivation condition, $\dot{\varepsilon }_{\text{P}} = 0$ at $x_{2} = 0$. Interestingly, the width of the boundary layer is almost independent of the foil thickness. An obvious decrease in the plastic strain gradient is found for the ratio ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H} = 1$ in the two-surface passivation case (see Fig. 4d). A vanishing plastic strain gradient for any values of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ at $x_{2} = {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0pt} 2}$ can be seen due to the symmetric boundary conditions.

Fig. 4

Distributions of the normalized plastic strain and its gradient across the thickness at $\varepsilon_{11} = 5\varepsilon_{0}$ for various values of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$. a, c One-passivated surface; b, d two-passivated surfaces

Plots of normalized stress versus normalized strain for different values of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ are shown in Fig. 5. For a prescribed strain, the average stress is evaluated as $\left( {{1 \mathord{\left/ {\vphantom {1 H}} \right. \kern-0pt} H}} \right)\int_{0}^{H} {\sigma_{11} {\text{d}}x_{2} }$. The applied strain $\varepsilon_{11}$ is assumed to be increased monotonically from zero to $10\varepsilon_{0}$. From Fig. 5, one can see that both the flow stress and the strain-hardening rate increase as ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ increases. Comparing Fig. 5a and b, one may find that a relatively smaller size effect is predicted for the one-surface passivated case than that for the two-surface passivated case. It is because that the passivated layer constraints the dislocation motion more severely for the two-surface passivation than that for the one-surface passivation.

Fig. 5

Normalized stress versus normalized strain with various values of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ for thin foil under tension. a One-surface passivated case, and b two-surface passivated case

Results for the foils with one passivated surface and with two passivated surfaces under tension are given in Fig. 6. It is shown that, for the same ratio of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$, the normalized plastic strain for the one-surface passivated case is generally larger than that for the two-surface passivated case. The difference between the two cases diminishes as the ratio ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ decreases. Again, it confirms that the two passivated surfaces constraint the plastic flow much more severely than the one passivated surface. For a given normalized strain, the normalized stress for the two-surface passivated case is greater than that of one-surface passivated case, as shown in Fig. 6b. This result is consistent with the formation of a boundary layer of high dislocation density near the interface.

Fig. 6

Comparison between the 1P (one passivated surface) case and 2P (two passivated surfaces) case with various values of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$. a Distributions of normalized plastic strain across the foil thickness at $\varepsilon_{11} = 5\varepsilon_{0}$; b normalized stress versus normalized strain

The boundary value problem is characterized by imposing microhard boundary conditions at the foil top and bottom surfaces or micro-free conditions. Fleck et al. [45] found that, after switching the higher-order boundary conditions, the non-incremental SGP theory (e.g. Gudmundson [18], and Gurtin [22]) predicts an unexpected delay in plastic flow, referred to as an “elastic gap” by Fleck et al. [57], while the incremental SGP theory (e.g. Fleck and Hutchinson [14], Hutchinson [15]) does not suffer this apparent drawback. It should be mentioned the difference between non-incremental and incremental theories lies in the fact that the constitutive law for the non-incremental theory has certain stress variables expressed in terms of strain increments, whereas the incremental theory expresses stress increments in terms of strain increments. Similar to Fleck et al. [45], we perform an analysis on the stretch-passivation problem by switching the higher-order boundary conditions, from micro-free to micro-hard, after an amount of plastic deformation. The simulation results are shown in Fig. 7. Figure 7a shows the normalized stress–strain curve in which, at $\varepsilon_{11} = 5\varepsilon_{0}$, the increase in strain hardening rate due to passivation is evident. Also, the numerical evalution of the ratio ${{\Delta \varepsilon_{11}^{\text{PL}} } \mathord{\left/ {\vphantom {{\Delta \varepsilon_{11}^{\text{PL}} } {\Delta \varepsilon_{11} }}} \right. \kern-0pt} {\Delta \varepsilon_{11} }}$ across the foil thickness immediately after switching the higher-order boundary conditions is illustrated in Fig. 7b. Prior to passivation, the stress and strain distributions are uniform. After passivation the distributions become non-uniform and the problem needs an incremental step-by-step solution procedure. The results in Fig. 7 confirm the findings of Fleck et al. [45, 57]. The “incremental” Fleck–Hutchinson–Willis theory predicts no elastic gap in plastic straining following passivation, while the passivation mainly gives rise to a rapid rise in strain hardening.

Fig. 7

Effect of the application of a passivation layer at $\varepsilon_{11} = 5\varepsilon_{0}$ for ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H} = 0.5$. a Normalized stress versus normalized strain, and b normalized plastic strain increment along the thickness immediately after passivation

5.2 Bending of thin foil

In this section, we explore the dependence of bending response on the ratio of material length scale $\ell$ to the half thickness of foil, $H$, with accounting for the effect of surface passivation. The distributions of the normalized plastic strain across the foil thickness for different values of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ are shown in Fig. 8. Here, the surface strain is assumed to be $\kappa H = 40\varepsilon_{0}$. Generally, the plastic strain $\varepsilon_{11}^{\text{PL}}$ increases with decreasing the value of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$. For the classical plasticity theory (${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H} = 0$), the plastic strain is found to be linear with the thickness. For the unpassivated cases, as shown in Fig. 8a, one may find that there is a prominent decrease in the slope of $\varepsilon_{11}^{\text{PL}} \left( {x_{2} } \right)$ with $x_{2}$ as ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ increases. For a given value of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$, the plastic strain $\varepsilon_{11}^{\text{PL}} \left( {x_{2} } \right)$ increases linearly with $x_{2}$ at the beginning, and then tends to a plateau around the free surface. This is a consequence of the homogeneous micro-free boundary conditions which require $\varepsilon_{11,2}^{\text{PL}} = 0$ at $x_{2} = H$. This fact means that there must be an elastic boundary layer develops near the top or bottom surface of foil. As ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ approaches to zero, the strain gradient effect becomes less important, the distribution of the pastic strain across the thickness of the foil is similar to the conventional result, as shown in Fig. 8a. If the surfaces of foil are passivated, due to the restriction of the micro-hard boundary condition, there must be a sharp decline in the value of $\varepsilon_{11}^{\text{PL}} \left( {x_{2} } \right)$ near the passivated surface, as shown in Fig. 8b. Accordingly, distinct boundary layers appear in the plastic-strain distributions.

Fig. 8

Distributions of normalized plastic strain accross thickness with various values of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ at $\kappa = {{40\varepsilon_{0} } \mathord{\left/ {\vphantom {{40\varepsilon_{0} } H}} \right. \kern-0pt} H}$. a Unpassivated surface, and b passivated surface

Plots of bending moment versus curvature, normalized by $\sigma_{0} H^{2}$ and ${{\varepsilon_{0} } \mathord{\left/ {\vphantom {{\varepsilon_{0} } H}} \right. \kern-0pt} H}$, respectively, for different values of ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ are shown in Fig. 9. The response predicted by the classical $J_{2}$ flow theory (i.e. ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H} = 0$) is also given. For both unpassivated (Fig. 9a) and passivated (Fig. 9b) cases, a significant size effect with increasing ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ on the initial yielding and the flow stress is present. For example, the flow stress at deep plastic deformation ${{\kappa H} \mathord{\left/ {\vphantom {{\kappa H} {\varepsilon_{0} }}} \right. \kern-0pt} {\varepsilon_{0} }} = 40$ is elevated by a factor about two for the unpassivated case, while a factor about four for the passivated case, as the ratio ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$ increases from zero to unity. This is in agreement with the elevation of strength observed in Ni foils [7, 58] and Cu thin beams [59]. Comparing Fig. 9a and b, one can see that a lager bending moment is required for the passivated foil to reach the same curvature as the unpassivated foil. Taking the ratio ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H} = 1$ as an example, for a prescribed strain ${{\kappa H} \mathord{\left/ {\vphantom {{\kappa H} {\varepsilon_{0} }}} \right. \kern-0pt} {\varepsilon_{0} }} = 40$, the magnitude of bending moment for the passivated foil is nearly twice lager than the unpassivated one.

Fig. 9

Normalized moment versus curvature for various ratios ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H}$. a Unpassivated surface, and b passivated surface

The numerical results for the bending problem after switching the higher-order boundary conditions at $\kappa = {{10\varepsilon_{0} } \mathord{\left/ {\vphantom {{10\varepsilon_{0} } H}} \right. \kern-0pt} H}$ are displayed in Fig. 10. Here, an unpassivated foil in plane strain is first bent into the plastic range with no surface constraint followed by surface passivation and continued bending. An enhancement of the flow stress after passivation is clearly indicated, as shown in Fig. 10a. In general, the dislocations are forced to pile up around the passivated surface by imposing the micro-hard boundary conditions. The distribution of the incremental plastic strain along the thickness of the foil immediately after passivation is given in Fig. 10b. Here, the incremental plastic strain is described in terms of $\Delta \varepsilon_{11}^{\text{PL}} = \Delta t\dot{\varepsilon }_{11}^{\text{PL}}$, with $\Delta t$ being the time increment, and it is normalized by $\Delta \kappa H = \Delta t\dot{\kappa }H$. It is revealed that setting the dissipative length scale $\ell > 0$ leads to an increase of the strain hardening after formation of the passivation layer. The plastic strain increment across the upper or lower half of the foil is nonlinear, in which the plastic strain increment approaches to zero near the foil surface.

Fig. 10

Pure bending in plane strain with no passivation followed by continued bending with passivation at $\kappa = {{10\varepsilon_{0} } \mathord{\left/ {\vphantom {{10\varepsilon_{0} } H}} \right. \kern-0pt} H}$ for ${\ell \mathord{\left/ {\vphantom {\ell H}} \right. \kern-0pt} H} = 0.5$. a Normalized moment versus curvature, and b normalized plastic strain increment along the thickness of the foil after passivation

As pointed out by Hutchinson [15] and Fleck et al. [45], the dissipative higher-order micro-forces in non-incremental theory always cause the significant elastic gap or stress jump under the non-proportional loading conditions. For instance, based on Gurtin’s non-incremental theory [22], Martínez-Pañeda et al. [40] studied a thin foil that is bent into the plastic range, passivated, and then subject to further bending. It is found that, if the dissipative gradient effect is considered, plastic flow would be interrupted after passivation. In other words, there is a purely elastic incremental response after passivation. By contrast, as an incremental theory, the Fleck–Hutchinson–Willis theory here predicts that plastic flow is not interrupted by passivation, only constrained, giving rise to an increase in effective incremental stiffness, as shown in Fig. 10. From a physical standpoint, the elastic gap predicted by non-incremental theory seems unacceptable since infinitesimal changes in strains lead to finite changes in stress [15]. Therefore, the incremental theory developed by Fleck, Hutchinson and Willis [14, 15, 17, 45] is favored. However, critical experiments are needed for further clarify the physical relevance of the incremental and non-incremental theories.

5.3 Torsion of thin wire

The distributions of the normalized plastic shear strain with the radial coordinate predicted by Eq. (41) for torsion of thin wires with and without surface passivation are given in Fig. 11a, b, respectively. For the passivated wires, the normalized plastic shear strain decreases with increasing the ratio ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R}$ for a given normalized radius, as shown in Fig. 11a. For the classical plasticity (i.e. ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R} = 0$), the normalized plastic shear strain increases linearly with the radial coordinate in the plastic zone. While for the cases with accounting for strain gradient effect, the plastic shear strain increases linearly with the radial coordinate initially, and then tends to a plateau around the surface (see the insert of Fig. 11a in detail). The slope of the plastic shear strain versus the radial coordinate vanishes around the free surface of the wire. This behavior is similar to that observed in foil bending, as seen in Fig. 8. It also agrees with our assumption that the higher-order traction at the wire surface is zero. The presence of a elastic-strain layer around the free surface is confirmed, as discussed by Liu et al. [60]. For the passivated wires, the plastic shear strain increases linearly with the radial coordinate firstly, and then, around the wire surface, decreases sharply to be zero, as shown in Fig. 11b. The vanishment of the plastic shear strain around the passivated surface is because the passivation layer of a negligible thickness prohibits dislocations strongly. It corresponds to the micro-hard boundary condition, Eq. (18). Comparing Fig. 11a, b, one may find that the effect of passivation on the distribution of plastic shear strain in torsion is significant since yielding initiates at the wire surface whereby plasticity is rigorously restrained. While, there is no constraint on plastic shear strain for the unpassivated surface. Therefore, the plastic shear strain for the passivated wires decreases more sharply than that for the unpassivated wires. It should be mentioned that, for a small value ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R}$, much more finite elements are needed to ensure the convergence. Otherwise, the plastic strain would be discontinuous near the surface for the passivated cases. Actually, we use 400 elements for the bending and torsion problems, while 100 elements for the tension problem. The issue of convergence has also been examined for the wire torsion. Since the exact solution is unknown, we conduct simulations with increasing number of elements until a satisfactory result is achieved, i.e. when there is no obvious change. The numerical results from the simulations with 50, 100, 200 and 400 elements are employed to examine the convergence. In Fig. 11c, the distributions of the plastic shear strain for the un-passivated wire with ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R} = 0.5$ are plotted. It is shown that the convergence is evident, which also demonstrates the robustness of the numerical formulation.

Fig. 11

Distributions of the normalized plastic shear strain across the radius for various values of ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R}$ at $\alpha = {{40\varepsilon_{0} } \mathord{\left/ {\vphantom {{40\varepsilon_{0} } R}} \right. \kern-0pt} R}$. a Unpassivated surface, b passivated surface, and c convergence of the plastic shear strain

The dependence of torsional response on the ratio of ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R}$ is investigated for both unpassivated and passivated wires. Plots of the normalized torque versus normalized twist for different values of ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R}$ are shown in Fig. 12. The case ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R} = 0$ corresponds to the conventional plasticity theory without strain gradient effect. The results for both cases show a strong size effect, whereby both the initial yielding point and the flow stress increase with increasing ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R}$. For instance, the flow stress deep in the plastic range is elevated by a factor about 2.5 as the value of ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R}$ increases from zero to unity. Taking the case $\ell = 5$ μm as an example, the torsional strength of wire with $R = 10$ μm is predicted to be 1.6 times larger than that of thick wire. This is on the order of size effect found in thin Cu wires [2,3,4, 61]. However, the elastic response predicted by the theory is independent of wire diameter since the contribution due to elastic strain gradient is not considered. Similar results for thin wires under torsion predicted by SGP theories have also been provided by many other authors, e.g. Fleck and Hutchinson [14], Fleck et al. [1], Idiart and Fleck [56], Liu et al. [2, 5], Bardella [39], Gudmundson [18], etc. However, the passivation effect has not yet considered in detail in previous studies, except the works by Bardella [39], Gudmundson and Dahlberg [19], and Liu et al. [41]. The previous work [41] focuses on the energetic gradient effects based on the reduced version of Gudmundson theory and the Polizzotto theory. Only analytical solution for the wire torsion problem is provided therein. Here, we perform one-dimensional finite element implementation on three benchmark examples based on the Fleck–Hutchinson–Willis theory. The roles of dissipative gradient effects are highlighted, by which one can predict the size effect at initial yielding and simulate the passivation effect due to dissipative plastic strain gradients.

Fig. 12

Normalized torque versus the normalized twist with various ratios ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R}$ for a unpassivated surface and b passivated surface

Figure 13a shows the normalized torque-twist curve in which, at the applied twist level ${{\alpha R} \mathord{\left/ {\vphantom {{\alpha R} {\varepsilon_{0} }}} \right. \kern-0pt} {\varepsilon_{0} }} = 10$, the abrupt change in strain hardening rate due to switching the higher-order boundary conditions is obvious. It can be seen how the torque-twist curve significantly changes for the passivated and unpassivated surface. Such an apparent difference corresponds to a very different mechanical response. This is illustrated in Fig. 13b, which displays the numerical evaluation of the ratio ${{\Delta \gamma_{\text{P}} } \mathord{\left/ {\vphantom {{\Delta \gamma_{\text{P}} } {\left( {\Delta \alpha R} \right)}}} \right. \kern-0pt} {\left( {\Delta \alpha R} \right)}}$ along the radial coordinate immediately after switching the higher-order boundary conditions. One can see that the passivation leads to an increase of the plastic strain increment firstly, and then a sharp decline of the plastic strain increment around the passivated surface. For the unpassivated wire, the plastic strain increment increases monotonously with the radial coordinate. It should be emphasized that the dissipative SGP theory used here allows for an immediate development of plasticity inside the wire within the very first twist increment after passivation, which is very different from the results predicted by “non-incremental” SGP theories [39, 45]. For example, by using Gurtin’s theory, Bardella and Panteghini [39] investigated a cylindrical wire that is twisted into the plastic range, passivated, and then subject to further twist. It is shown that plastic flow is interrupted after passivation. In other words, a purely elastic incremental response is observed after formation of the passivation layer. By contrast, the Fleck–Hutchinson–Willis theory used here predicts that plastic flow is not interrupted by passivation, only constrained, giving rise to an increase in effective incremental stiffness, as shown in Fig. 13.

Fig. 13

Torsion with no passivation followed by continued torsion with passivation at $\alpha = {{10\varepsilon_{0} } \mathord{\left/ {\vphantom {{10\varepsilon_{0} } R}} \right. \kern-0pt} R}$ for ${\ell \mathord{\left/ {\vphantom {\ell R}} \right. \kern-0pt} R} = 0.5$. a Normalized torque versus normalized twist, and b normalized plastic strain increment along the radial coordinate after immediate passivation

6 Conclusions

A numerical formulation of the variational constitutive updates for the Fleck-Hutchinson-Willis higher-order SGP theory has been constructed to solve the initial boundary value problems. The numerical scheme is relatively simple and general in form, which allows for an efficient finite element implementation of the problem with a uniform displacement field. By using this method, three benchmark problems, i.e. the stretch-passivation problem, the foil bending, and the wire torsion, have been studied to reveal the role of the dissipative strain gradient and the effect of surface passivation. It is shown that the dissipative gradient term controls the strengthening size effect, i.e. the increase of initial yielding strength, while the surface passivation mainly gives rise to an increase of strain hardening rate. In the present incremental SGP theory, no elastic gap occurs after passivation in the plastic regime. The theory predicts continued plastic flow following passivation, although reduced by the constraint imposed by surface passivation. The examples considered here provide some insights for the interpretation of experiments on surface passivation. Critical experiments are required in future to better understand the passivation effect in the plastic flow due to specific non-proportional loading conditions.

Appendix

Three material length scales can be introduced to the Fleck–Hutchinson–Willis theory as seen in Eq. (10). We restrict attention to the simplest model, containing a single material length scale. Following Danas et al. [62], we introduce a particular choice for the relative magnitude of the length scales $\ell_{I}$ by allowing

$$\ell_{1} = \sqrt {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}} \ell ,\;\;\ell_{2} = \sqrt {{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0pt} 6}} \ell \;\;{\text{and}}\;\;\ell_{3} = {\ell \mathord{\left/ {\vphantom {\ell 2}} \right. \kern-0pt} 2}.$$

(44)

With this choice, one can write the length scales $\ell_{I}$ in terms of a single length scale $\ell$.

For the cases of foil tension and bending, the generalized effective plastic strain rate Eq. (10) is written as

$$\dot{E}_{\text{P}} = \sqrt {\dot{\varepsilon }_{\text{P}}^{2} + \left( {\tfrac{1}{2}\ell_{1}^{2} + \tfrac{8}{3}\ell_{3}^{2} } \right)\dot{\varepsilon }_{\text{P}}^{{{\prime }2}} } ,$$

(45)

where the second material length parameter $\ell_{2}$ does not enter the expression. By (44), Eq. (45) is reduced to be

$$\dot{E}_{\text{P}} = \sqrt {\dot{\varepsilon }_{\text{P}}^{2} + \ell^{2} \dot{\varepsilon }_{\text{P}}^{{{\prime }2}} } .$$

(46)

In Eq. (22), the coefficients read

$$\omega_{1} = 1, \, \omega_{2} = \ell^{2} .$$

(47)

For the case of wire torsion, the generalized effective plastic strain rate Eq. (10) is expressed as

$$\dot{E}_{\text{P}} = \sqrt {c_{1} \dot{\varepsilon }_{\text{P}}^{2} + c_{2} \dot{\varepsilon }_{\text{P}} \dot{\varepsilon }_{\text{P}}^{{\prime }} + c_{3} \dot{\varepsilon }_{\text{P}}^{{{\prime }2}} } ,$$

(48)

with

$$\left\{ \begin{aligned} & c_{1} = 1 + \left( {\tfrac{1}{2}\ell_{1}^{2} + 4\ell_{2}^{2} } \right)r^{ - 2} \hfill \\ & c_{2} = \left( { - \ell_{1}^{2} + 4\ell_{2}^{2} } \right)r^{ - 1} \hfill \\ & c_{3} = \left( {\tfrac{1}{2}\ell_{1}^{2} + 4\ell_{2}^{2} } \right) \hfill \\ \end{aligned} \right.,$$

(49)

where $\ell_{3}$ is not involved in the expression. By (44), Eq. (48) is reduced to be

$$\dot{E}_{\text{P}} = \sqrt {\left( {1 + \ell^{2} r^{ - 2} } \right)\dot{\varepsilon }_{\text{P}}^{2} + \ell^{2} \dot{\varepsilon }_{\text{P}}^{{{\prime }2}} } .$$

(50)

In Eq. (22), the coefficients become

$$\omega_{1} = 1 + \ell^{2} r^{ - 2} , \, \omega_{2} = \ell^{2} .$$

(51)