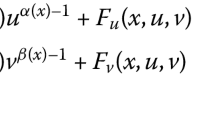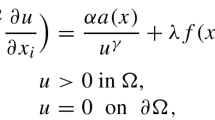Abstract
In this manuscript an existence result for an anisotropic variable problem which is related to several applications is proved. By considering suitable hypotheses, the multiplicity of solutions is obtained. Examples of applicability of the results are also presented. The arguments are based on appropriated \(L^{\infty }\) estimates, sub-supersolutions, and the mountain pass theorem.
Similar content being viewed by others
1 Introduction and main results

where Ω, unless otherwise stated, is a bounded domain in \({\mathbb{R}}^{N} (N \geq 3)\) with smooth boundary \(p_{i} \in C(\overline{\Omega }), 2 \leq p_{i}(x) \leq p_{+}(x) < { \overline{p}}^{\star }(x), i=1,\ldots,N, p_{+}(x):= \max \{p_{1} (x),\ldots,p_{N}(x) \}\) for any \(x \in \overline{\Omega } \) with \({\overline{p}}(x):= N / \sum_{i=1}^{N}(1/p_{i} (x))\) and \({\overline{p}}^{*}(x)={N\overline{p}(x)}/{(N-\overline{p}(x))}\) if \(\overline{p}(x)< N\) and \({\overline{p}}(x)=+\infty \) if \(N\geq p(x)\), \(\alpha \in C(\overline{\Omega })\) is a nonnegative function with \(1 \leq \alpha (x)\) for all \(x\in \overline{\Omega }\), \(f: {\Omega } \times [0,+\infty ) \rightarrow \mathbb{R}\) is a continuous function and
- (H):
-
\(a \in L^{\infty }(\Omega )\) with \(a(x) >0\) a.e. in Ω;
- (\(f_{1}\)):
-
There is \(\delta >0\) such that \(f(x,t)\geq (1-t^{\alpha (x)-1})a(x) \) for all \((x,t) \in \Omega \times [0,\delta ] \);
- (\(f_{2}\)):
-
There exists \(r \in C(\overline{\Omega })\) such that \(1 < r(x)\) for any \(x \in \overline{\Omega }\) and \(|f(x,t)|\leq a(x)(1 + |t|^{r(x)-1})\) for all \((x,t) \in \Omega \times [0,+\infty ) \).
We say that \(u \in W^{1,{\overrightarrow{p}(x)}}_{0} (\Omega )\) is a weak solution for \((P)\) if
for all \(\phi \in W^{1,\overrightarrow{p}(x)}_{0} (\Omega )\).
Denoting by \(\| \cdot \|_{\infty }\) the norm in \(L^{\infty }(\Omega )\), we obtain, by means of sub-supersolutions and minimization arguments, the result described below.
Theorem 1.1
Consider that hypotheses \((H), (f_{1})\), and \((f_{2})\) hold. Then problem \((P)\) has a solution for \(\| a\|_{\infty }\) small enough.
Define \(p_{\infty }(x) = \max \{\overline{p}^{\star }(x), p_{+}(x)\}, p_{-}(x) = \min \{p_{1}(x),\ldots,p_{n}(x)\}, x \in \overline{\Omega }\) and denote \(q^{-}:= \operatorname{inf}_{\Omega } q \) and \(q^{+}:= \operatorname{sup}_{\Omega } q \) for a function \(q \in C(\overline{\Omega })\). Considering the Ambrosetti–Rabinowitz type condition:
- (\(f_{3}\)):
-
It holds that \(\alpha ^{-} >1\), \(\alpha ^{+}, r^{+} < p^{-}_{\infty } \) with \(\alpha ^{+} < p^{-}_{-}\) or \(p^{+}_{+} < \alpha ^{-}\), and there are \(t_{0} >0\) and \(\theta > p^{+}_{+}\) such that
$$\begin{aligned} 0< \theta F(x,t)\leq f(x,t)t, \quad\text{a.e. in } \Omega, \text{ for all } t \geq t_{0}, \end{aligned}$$
we have the multiplicity result below.
Theorem 1.2
Consider that hypotheses \((H)\), \((f_{1})\)–\((f_{3})\) hold. Then problem \((P)\) has two solutions for \(\| a\|_{\infty }\) small enough.
Consider \(s_{0}>0\). The function
satisfies \((f_{1})\) and \((f_{2})\) for \(\delta \in (0,s_{0}]\) and \(r \in C(\overline{\Omega })\) with \(r_{-}>1 \) for all \(x \in \overline{\Omega }\). Note that \((f_{1})\)–\((f_{3})\) hold if \(1 < \alpha ^{+}< p^{-}_{\infty }\) and \(p^{+}_{+} < r^{-}\) with \(\alpha ^{+} < p^{-}_{-}\) or \(p^{+}_{+} < \alpha ^{-}\).
Anisotropic partial differential equations have attracted the attention of several researchers in the last years due to their applicability in several areas of science. For example, in the classical paper [1] the authors considered a model which was applied for both image enhancement and denoising in terms of anisotropic PDEs as well as allowing the preservation of significant image features. In physics, anisotropic problems arise in models that describe the dynamics of fluids with different conductivities in different directions. We also point out that anisotropic equations can be applied in models that describe the spread of epidemic disease in heterogeneous environments. For more details regarding the mentioned applications, see for instance [2–4].
On the other hand, problems involving variable exponents can be also applied to consider several important models. A classical application is in the study of electrorheological fluids. The study of electrorheological fluids started when fluids that stop spontaneously, which are known in the literature as Bingham fluids, were discovered. We also mention the important work [5] due to W. Winslow, where the first major discovery regarding electrorheological fluids was presented. A notable fact is that under the presence of an eletrical field, parallel and string-like formations arise in this kind of fluid. Such behavior is known as Winslow effect. As mentioned in the interesting paper [6], several experiments with such fluids have been considered in NASA due to their applicability in space technology and robotics.
We also mention that, from the mathematical viewpoint, anisotropic problems and equations with variable exponents are very interesting. For example, in the reference [7], regularity results for a system which arise in the study of electrorheological fluids are proved. In [8], the authors generalize several results of elliptic equations for the variable exponents setting. In the classical manuscript [9] the author considers problems with an anisotropic operator with variable exponents. We also quote the interesting references [10–19] and the paper [20] which provides an overview of recent results concerning elliptic variational problems with nonstandard growth conditions and related to different kinds of nonuniformly elliptic operators. For a complete treatment of problems involving variable exponents, see [21, 22].
Problem \((P)\) is motivated by [23], where the authors obtained versions of Theorems 1.1 and 1.2 with \(\alpha \equiv 2\) for an anisotropic operator.
The rest of the manuscript is organized as follows: in Sect. 2 we present some preliminaries regarding spaces with variable exponents; in Sect. 3 we obtain an auxiliary \(L^{\infty }\) estimate which will play an important role in our arguments; in Sects. 5 and 6 the proofs of Theorems 1.1 and 1.2 are provided, respectively.
2 Preliminaries
Let \(\Omega \subset \mathbb{R}^{N} ( N \geq 1)\) be a bounded domain. Given \(p\in C_{+}(\overline{\Omega }):= \{p \in C(\overline{\Omega }); \inf_{ \Omega } p > 1\}\), we define the Lebesgue space
with the norm
It holds that \((L^{p(x)}(\Omega ), \|\cdot \|_{{p(x)}})\) is a Banach space.
The results below, which can be found for example in [24], will be often used.
Proposition 2.1
Consider \(p \in C_{+}(\overline{\Omega })\) and define \(\rho (u): =\int _{\Omega }|u|^{p(x)}\,dx\). For \(u, u_{n}\in L^{p(x)}(\Omega ), n \in \mathbb{N}\), the statements below hold.
-
(i)
If \(u\neq 0\) in \(L^{p(x)}(\Omega )\), then \(\|u\|_{{p(x)}}=\lambda \Leftrightarrow \rho (\frac{u}{\lambda })=1\);
-
(ii)
If \(\|u\|_{{p(x)}}< 1 (= 1; > 1)\), then \(\rho (u) < 1 (= 1; > 1)\);
-
(iii)
If \(\|u\|_{{p(x)}}> 1 \), then \(\|u\|_{p(x)}^{p^{-}}\leq \rho (u)\leq \|u\|_{p(x)}^{p^{+}}\);
-
(iv)
If \(\|u\|_{{p(x)}}< 1 \), then \(\|u\|_{{p(x)}}^{p^{+}}\leq \rho (u)\leq \|u\|_{{p(x)}}^{p^{-}}\).
Theorem 2.2
Consider \(p,q\in C_{+}(\overline{\Omega })\). The assertions below hold.
-
(i)
If \(\frac{1}{q(x)}+\frac{1}{p(x)}=1\) in Ω, then \(\vert \int _{\Omega }uv\,dx \vert \leq (\frac{1}{p^{-}}+ \frac{1}{q^{-}} )\|u\|_{{p(x)}}\|v\|_{{q(x)}} \);
-
(ii)
If \(q(x)\leq p(x)\) in Ω and \(|\Omega |<\infty \), then \(L^{p(x)}(\Omega )\hookrightarrow L^{q(x)}(\Omega )\).
In what follows we recall some results on anisotropic variable exponents which can be found for example in [9]. Consider \(p_{i} \in C_{+}(\overline{\Omega }), i=1,\ldots,N\). Denote
and define
The anisotropic variable exponent Sobolev space given by
is a Banach space with respect to the norm
If \(p^{-}_{i} >1, i=1,\ldots,N\), then \(W^{1,\overrightarrow{p(x)}}(\Omega )\) is reflexive, see [9, Theorem 2.2].
By \(W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) we denote the Banach space defined by the closure of \(C_{0}^{\infty }(\Omega )\) in \(W^{1,\overrightarrow{p}}(\Omega )\) with respect to the norm (2.2).
Consider \({\overline{p}}(x):= N / \sum_{i=1}^{N}(1/p_{i} (x))\) and \({\overline{p}}^{*}(x)={N\overline{p}(x)}{(N-\overline{p}(x))}\) if \(\overline{p}(x)< N\) and \({\overline{p}}(x)=+\infty \) if \(N\geq p(x)\). If \(p(x) < {\overline{p}}^{*}(x)\) for all \(x \in \overline{\Omega }\), then the following Poincaré type inequality holds:
where C is a positive constant independent of \(u \in W^{1,\overrightarrow{p(x)}}_{0} (\Omega )\). Thus, the norm
is equivalent to the norm given in (2.2).
If \(q \in C_{+}(\overline{\Omega })\) and \(q(x) < p_{\infty }(x)\) for all \(x \in \overline{\Omega }\), where \(p_{\infty }(x):= \max \{\overline{p}^{\star }(x), p_{+}(x)\}\), then there exists a compact embedding \(W^{1,\overrightarrow{p(x)}}_{0}(\Omega ) \hookrightarrow L^{q(x)}( \Omega )\).
3 Auxiliary results
In what follows we present an existence result for a linear problem and a weak comparison principle which generalize Lemmas 2.1 and 2.2 of [23] respectively.
Lemma 3.1
Consider \(a \in L^{\infty }(\Omega )\). The problem
has a unique solution in \(W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\).
Proof
The continuous nonlinear map \(T:W_{0}^{1,\overrightarrow{p(x)}}(\Omega )\rightarrow (W_{0}^{1, \overrightarrow{p(x)}}(\Omega ))'\) is defined by
Since \(p_{i} > 1, i=1,\ldots,N\), we have from the inequality (see for example [25, page 97])
for all \(x, y \in \mathbb{R}^{N}\) and \(l\geq 2\), where \(\langle \cdot, \cdot \rangle \) denotes the usual inner product in \(\mathbb{R}^{N}\), that
Consider \((u_{n}) \subset W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) a sequence with \(\|u_{n}\|\to +\infty \). As in the proof of [21, Theorem 36], for each \(i\in \{1,\ldots,N\}\) and \(n \in \mathbb{N}\), we define
Since \((a_{1} +\cdots + a_{N})^{\beta } \leq C(a^{\beta }_{1} +\cdots + a^{\beta }_{N})\) for \(\beta \geq 1\) and \(a_{i} \geq 0, i=1,\ldots,N\), for some constant C, we have
where \(C_{1},C_{2},C_{3} >0\) are constants that do not depend on \(n \in \mathbb{N}\). Therefore
Thus, it follows from the Minty–Browder theorem [26, Theorem 5.16] that there is a unique function \(u \in W_{0}^{1,\overrightarrow{p(x)}}(\Omega )\) such that \(Tu=a\). □
Lemma 3.2
Let \(u,v \in W_{0}^{1,\overrightarrow{p(x)}}(\Omega )\) satisfy
where \(u \leq v\) on ∂Ω means that \((u-v)^{+}:= \max \{0,u-v\} \in W^{1,\overrightarrow{p}(x)}_{0} ( \Omega )\). Then \(u(x)\leq v(x)\) a.e. in Ω.
Proof
Using the test function \(\phi = (u-v)^{+}:=\max \{u-v,0\}\in {W_{0}^{1,\overrightarrow{p}(x)}( \Omega )}\), it follows that
for \(x, y \in \mathbb{R}^{N}\). Thus, it follows from (3.1) that
for \(i=1,\ldots,N\), which allows to conclude that \(\frac{\partial }{\partial x_{i}} (u - v)^{+}(x) =0 \) a.e. in Ω for \(i=1,\ldots,N\). Applying (2.3) we obtain that \((u - v)^{+}(x) =0\) a.e. in Ω, which finishes the proof of the result. □
4 An auxiliary \(L^{\infty }\) estimate
Consider \(\Omega \subset \mathbb{R}^{N} (N \geq 2 )\) to be an admissible and bounded domain, that is, there exists a continuous embedding \(W^{1,1}_{0}(\Omega ) \hookrightarrow L^{\frac{N}{N-1}}(\Omega )\). The best constant of such an embedding will be denoted by \(C_{0}\), which depends on only Ω and N. Then it follows that
for all \(u \in W^{1,1}_{0}(\Omega )\), where \(\| u\|_{W^{1,1}_{0} (\Omega )}: = \| \!|\nabla u|\!\|_{L^{1}}\). Adapting the ideas of [27, Lemma 4.1], we obtain an \(L^{\infty }\) estimate that will be applied in the construction of appropriate sub-supersolutions, which is provided below.
Lemma 4.1
Consider \(\lambda >0\) and \(u_{\lambda } \in W^{1,\overrightarrow{p(x)}}_{0} (\Omega )\) to be the unique solution of the problem

Consider \(h:= \frac{p^{-}_{-}}{2 |\Omega |^{\frac{1}{N}}} C_{0} \). If \(\lambda \geq h\), then \(u \in L^{\infty }(\Omega )\) with \(\| u\|_{L^{\infty }(\Omega )} \leq C^{\star } \lambda ^{ \frac{1}{p^{-}_{-}-1}}\) and \(\| u\|_{L^{\infty }(\Omega )} \leq C_{\star } \lambda ^{ \frac{1}{p^{+}_{+} -1}}\) when \(\lambda < h\), where \(C^{\star }\) and \(C_{\star }\) are positive constants which depend only on \(\Omega, N\) and \(p_{i},i=1,\ldots,N\).
Proof
Note that \(u_{\lambda }\) is a nonnegative function with \(u\not \equiv 0 \). Consider \(k \geq 0\) and define the set \(A_{k}:= \{x \in \Omega; u(x)>k\}\). Let \(0<\epsilon <1\). Applying in \((P_{\lambda })\) the test function \((u-k)^{+} \in W^{1,\overrightarrow{p(x)}}_{0} (\Omega )\), we obtain from (4.1) and Young’s inequality that
We have that
where \(p_{-} \) was defined in (2.1). Consider \(h:= \frac{p^{-}_{-}}{2|\Omega |^{\frac{1}{N}} C_{0}}\) and suppose that \(\lambda \geq h\). Define
We have \(\epsilon \leq 1 \) and
Thus it follows from (4.2) and (4.3) that
where
which provides that
From the \(L^{\infty }\) estimates in [28, Lemma 5.1-Chap. 2], we obtain that
where \(C^{\star }\) is a constant that does not depend on \(u_{\lambda }\). If \(\lambda < h\), then the result follows by applying the previous arguments with
□
5 Proof of Theorem 1.1
Below we describe the notion of sub-supersolution that will be considered for \((P)\) and a related result.
It will be considered that \((\underline{u}, \overline{u}) \in W^{1,\overrightarrow{p(x)}}_{0}( \Omega ) \times W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) is a sub-supersolution pair for \((P)\) if \(\underline{u}\) and u̅ belong to \(L^{\infty }(\Omega )\), \(0 < \underline{u}(x) \leq \overline{u}(x)\) a.e. in Ω and
for all \(\varphi \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) with \(\varphi (x) \geq 0\) a.e. in Ω.
Lemma 5.1
Consider that hypotheses \((H)\) and \((f_{1})\)–\((f_{2})\) hold. There is \(\iota >0\) such that if \(\|a\|_{L^{\infty }(\Omega )}< \iota \), then \((P)\) has a sub-supersolution pair \((\underline{u},\overline{u}) \in (W^{1,\overrightarrow{p(x)}}_{0}( \Omega ) \cap L^{\infty }(\Omega )) \times (W^{1,\overrightarrow{p(x)}}_{0}( \Omega ) \cap L^{\infty }(\Omega ))\) with \(\|\underline{u}\|_{\infty }\leq \delta \), where δ is provided in \((f_{1})\).
Proof
From Lemmas 3.1 and 4.1, there are unique nonnegative solutions \(\underline{u}, \overline{u} \in W^{1,\overrightarrow{p(x)}}_{0}( \Omega ) \cap L^{\infty }(\Omega )\), respectively, for
such that \(\|\underline{u}\|_{\infty } \leq \max \{C^{\star }\| a\|^{ \frac{1}{p^{-}_{-}-1}}_{\infty },C_{\star }\| a\|^{ \frac{1}{p^{+}_{+}-1}}_{\infty }\}\), where \(C^{\star },C_{\star }>0\) are the constants given in Lemma 4.1. Thus, there is \(\eta >0\), which depends only on \(C^{\star }\) and \(C_{\star }\), such that \(\|\underline{u}\|_{\infty }\leq \delta /2\) for \(\|a\|_{\infty }<\eta \). From Lemma 3.2 we have \(0< \underline{u}(x) \leq \overline{u}(x)\) a.e. in Ω.
Let \(\phi \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) be such that \(\phi (x) \geq 0\) a.e. in Ω. Applying \((f_{1})\) and (5.2) we obtain that
From \((f_{2})\) we have
where \(K:=\max \{ \|\overline{u}\|^{\alpha ^{+}}_{\infty },\|\overline{u}\|^{ \alpha ^{-}}_{\infty }\} +\max \{ \|\overline{u}\|^{r^{+}-1}_{\infty }, \|\overline{u}\|^{r^{-}-1}_{\infty }\}\). Considering, if necessary, \(\iota >0\) smaller such that \(K\|a\|_{\infty }\leq 1\) for \(\|a\|_{\infty }<\iota \), it follows that the right-hand side in the last inequality is nonnegative, which provides the result. □
Proof of Theorem 1.1
Consider the functions \(\underline{u}, \overline{u} \in W^{1,\overrightarrow{p(x)}}_{0}( \Omega )\) defined in Lemma 5.2. Define
for \((x,t) \in \Omega \times \mathbb{R}\) and the problem
whose solutions are the critical points of the \(C^{1}\) functional defined by
where \(W(x,t):= \int _{0}^{t}w(x,s) \,ds\). Note that J is coercive and sequentially weakly lower semicontinuous. We have that \(K:= \{u \in W^{1,\overrightarrow{p(x)}}_{0} (\Omega ); \underline{u} (x) \leq u(x) \leq \overline{u}(x) \text{ a.e. in } \Omega \}\) is closed and convex and hence weakly closed in \(W^{1,\overrightarrow{p(x)}}_{0} (\Omega )\). Thus, it follows that \(J{ |}_{K}\) attains its minimum at some \(u_{0} \in K\). Reasoning as in [29, Theorem 2.4], we get \(J^{\prime }(u_{0})=0\), which provides the result. □
6 Proof of Theorem 1.2
Consider \(\underline{u} \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) given in Lemma 5.1 and the function
and the auxiliary problem
whose solutions are given by the critical points of the \(C^{1}\) functional
where \(H(x,t):= \int _{0}^{t}h(x,s) \,ds\).
Lemma 6.1
The functional S satisfies the Palais–Smale condition.
Proof
Consider \((u_{n}) \subset W^{1,\overrightarrow{p(x)}}_{0}(\Omega ) \) to be a sequence with \(S^{\prime }(u_{n})\rightarrow 0\) and \(S(u_{n})\rightarrow c\) for some \(c \in \mathbb{R}\).
We will start by considering the case \(p^{+}_{+} < \alpha ^{-}\). Note that \((f_{3})\) holds for \(\widetilde{\theta } >0\) such that \(p^{+}_{+} < \widetilde{\theta }<\min \{\alpha ^{-},\theta \}\). Reasoning as in (3.2) and applying \((f_{2})\)–\((f_{3})\), the boundedness of \(\underline{u}\), and the continuous embedding \(W^{1,\overrightarrow{p(x)}}_{0}(\Omega ) \hookrightarrow L^{1} ( \Omega )\), we obtain positive constants \(C_{1}, C_{2}, C_{3}>0\) such that
which provides the boundedness of \((u_{n})\) in \(W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\).
In the case \(\alpha ^{+} < p^{-}_{-}\) we can apply \((f_{2})\), \((f_{3})\), Proposition 2.1, the boundedness of \(\underline{u}\), and the continuous embedding \(W^{1,\overrightarrow{p(x)}}_{0}(\Omega ) \hookrightarrow L^{1} ( \Omega ) \) to obtain that
where \(C_{1},C_{2},C_{3}, C_{4} >0\) are constants. Applying the embedding \(W^{1,p(x)}_{0}(\Omega ) \hookrightarrow L^{\alpha (x)}(\Omega )\), we have
Since \(\alpha ^{+} < p^{-}_{-}\), we obtain that \((u_{n})\) is bounded in \(W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\).
Thus, up to a subsequence, we get
for all \(\nu \in C(\overline{\Omega })\) with \(1 < \nu ^{-}\leq \nu ^{+} < p^{-}_{\infty }\) and some \(u \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\). Combining (6.1) and Lebesgue’s dominated convergence theorem it follows that
which provides the result. □
Lemma 6.2
Consider that \((H)\), \((f_{1})\)–\((f_{3})\) hold. If \(\|a\|_{L^{\infty }(\Omega )}\) is small enough, then the claims below hold.
-
(i)
There are constants \(R, \lambda >0\) with \(R > \|\underline{u}\|\) such that
$$\begin{aligned} S(\underline{u}) < 0 < \lambda \leq \inf_{u \in \partial B_{R}(0)} S(u). \end{aligned}$$ -
(ii)
There is \(e \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega ) \setminus \overline{B_{2R}(0)}\) with \(S(e) < \lambda \).
Proof
From (5.1) and since \(p^{-}_{-}>1\), we have \(S(\underline{u}) <0\). Consider \(u \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) with \(\| u\| \geq 1 \). Arguing as in (3.2), applying Proposition 2.1 and the continuous embedding \(W^{1,\overrightarrow{p(x)}}_{0}(\Omega ) \hookrightarrow L^{\alpha (x)}( \Omega )\), we obtain that
for positive constants \(K_{1}, K_{2}, K_{3}, K_{4}>0\). If necessary, decrease \(\| a\|_{\infty }\) in such a way that \(\| \underline{u}\|< 1\), which is possible by considering the test functions \(\phi = \underline{u}\) in (5.1) and applying Lemma 4.1. Consider \(\lambda >0\) and fix \(R> 1 \) such that \(K_{1} R^{p^{-}_{-}} - K_{2} R - K_{4} \geq 2\lambda \). Considering \(\|a\|_{\infty }\) small enough satisfying \(K_{3} \|a\|_{\infty } ( R^{\alpha ^{+}} + R^{r^{+}})\leq \lambda \), it follows that \(L(u)\geq \lambda \) for all \(u \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) with \(\| u\|=R\), which finishes the proof of (i).
With respect to (ii), note that \((f_{3})\) implies the existence of constants \(C_{1}, C_{2}, C_{3}, C_{4}>0\) and \(t>0\) such that \(S(t\underline{u}) \leq C_{1} t^{p^{+}_{+}} - C_{2}t^{\alpha ^{-}} - C_{3} t^{\theta } + C_{4} <0\) with \(\| t \underline{u}\| > 2R\). □
Proof of Theorem 1.2
Consider \(\underline{u}, \overline{u} \in W^{1,\overrightarrow{p(x)}}_{0}( \Omega )\) given in Lemma 5.1 and \(u_{1} \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) the solution of \((P)\) obtained in Theorem 1.1, which provides the minimum of \(J\vert _{K}\), where
and J is the functional defined in (5.3). From Lemmas 6.1 and 6.2 we obtain that the hypotheses of the mountain pass theorem [30, Theorem 2.1] are satisfied by S. Therefore
is a critical value of S, that is, \(S^{\prime }(u_{2} ) = 0\) and \(L(u_{2})=c\) for some \(u_{2} \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\). Note that \(J(u)=S(u)\) for \(u \in \{w \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega ); 0\leq w(x) \leq \overline{u}(x) \text{ a.e. in } \Omega \}\). Thus, \(S(u_{1}) = \inf_{u \in K} J(u)\). If \(u_{2} (x)\geq \underline{u}(x)\) a.e. in Ω, it follows that problem \((P)\) has two weak solutions \(u_{1},u_{2} \in W^{1,\overrightarrow{p(x)}}_{0}(\Omega )\) with \(S(u_{1})\leq S(\underline{u})<0<\lambda \leq c:= S(u_{2})\), where \(\lambda >0\) was provided in Lemma 6.2.
We claim that \(u_{2} (x)\geq \underline{u}(x)\) a.e. in Ω. In fact, by considering the function \((\underline{u} - u_{2})^{+} \in W^{1,\overrightarrow{p(x)}}_{0}( \Omega )\), we get
Thus, it follows from (3.1) that
for \(i=1,\ldots,N\), which implies that \(\frac{\partial }{\partial x_{i}} (\underline{u} - u_{2})^{+}(x) =0 \) a.e. in Ω for \(i=1,\ldots,N\). From Proposition 2.1 and (2.3) we have \((\underline{u} - u_{2})^{+}(x) =0\) a.e. in Ω, which proves the claim. □
Availability of data and materials
Not applicable.
References
Perona, P., Malik, J.: Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 12, 629–639 (1990)
Antontsev, S.N., Diaz, J.I., Shmarev, S.: Energy Methods for Free Boundary Problems. Progress in Nonlinear Differential Equations and Their Applications, vol. 48. Birkhauser, Boston (2002)
Bear, J.: Dynamics of Fluids in Porous Media. Elsevier, New York (1972)
Bendahmane, M., Karlsen, K.H.: Renormalized solutions of an anisotropic reaction-diffusion advection system with L1 data. Commun. Pure Appl. Anal. 5, 733–762 (2006)
Winslow, W.: Induced fibration of suspensions. J. Appl. Phys. 20, 1137–1140 (1949)
Rǎdulescu, V.D.: Nonlinear elliptic equations with variable exponent: old and new. Nonlinear Anal. 121, 336–369 (2015)
Acerbi, E., Mingione, G.: Regularity results for stationary electro-rheological fluids. Arch. Ration. Mech. Anal. 164, 213–259 (2002)
Fan, X., Zhang, Q., Zhao, Y.: A strong maximum principle for \(p(x)-\)Laplace equations. Chin. J. Contemp. Math. 21, 1–7 (2000)
Fan, X.: Anisotropic variable exponent Sobolev spaces and \(\overrightarrow{p(x)}-\)Laplacian equations. Complex Var. Elliptic Equ. 56, 623–642 (2011)
Benslimane, O., Aberqi, A., Bennouna, J.: Existence results for double phase obstacle problems with variable exponents. J. Elliptic Parabolic Equ. 7, 875–890 (2021)
Benslimane, O., Aberqi, A., Bennouna, J.: The existence and uniqueness of an entropy solution to unilateral Orlicz anisotropic equations in an unbounded domain. Axioms 9(3), 109 (2020)
Benslimane, O., Aberqi, A., Bennouna, J.: Existence and uniqueness of entropy solution of a nonlinear elliptic equation in anisotropic Sobolev–Orlicz space. Rend. Circ. Mat. Palermo 2(70), 1579–1608 (2021)
Goodrich, C.S., Ragusa, M.A., Scapellato, A.: Partial regularity of solutions to \(p(x)-\)Laplacian PDEs with discontinuous coefficients. J. Differ. Equ. 268, 5440–5468 (2020)
Papageorgiou, N.S., Scapellato, A.: Nonlinear Robin problems with general potential and crossing reaction. Rend. Lincei Mat. Appl. 30, 1–29 (2019)
Cencelj, M., Rǎdulescu, V.D., Repovš, D.: Double phase problems with variable growth. Nonlinear Anal. 177, 270–287 (2018)
Ragusa, M.A., Tachikawa, A.: Partial regularity of the minimizers of quadratic functionals with VMO coefficients. J. Lond. Math. Soc. (2) 72, 609–620 (2005)
Ragusa, M.A., Tachikawa, A.: Regularity for minimizers for functionals of double phase with variable exponents. Adv. Nonlinear Anal. 9, 710–728 (2020)
Ragusa, M.A., Tachikawa, A.: On continuity of minimizers for certain quadratic growth functionals. J. Math. Soc. Jpn. 57, 691–700 (2005)
Rǎdulescu, V.D., Saiedinezhad, R.: A nonlinear eigenvalue problem with \(p(x)\)-growth and generalized Robin boundary value condition. Commun. Pure Appl. Anal. 17, 39–52 (2018)
Mingione, G., Rǎdulescu, V.: Recent developments in problems with nonstandard growth and nonuniform ellipticity. J. Math. Anal. Appl. 501, 125197 (2021)
Rǎdulescu, V., Repovš, D.: Partial Differential Equations with Variable Exponents: Variational Methods and Qualitative Analysis. CRC Press, Boca Raton (2015)
Růžička, M.: Electrorheological Fluids: Modeling and Mathematical Theory. Springer, Berlin (2000)
dos Santos, G.C.G., Figueiredo, G., Silva, J.R.S.: Multiplicity of positive solutions for an anisotropic problem via sub-supersolution method and mountain pass theorem. J. Convex Anal. 27(4), 1363–1374 (2020)
Fan, X., Zhao, D.: On the spaces \(L^{p(x)}(\Omega )\) and \(W^{m,p(x)}(\Omega )\). J. Math. Anal. Appl. 163, 424–446 (2001)
Lindqvist, P.: Notes on the Stationary p-Laplace Equation. SpringerBriefs in Mathematics. Springer, Cham (2019)
Brézis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, New York (2011)
dos Santos, G.C.G., Figueiredo, G., Tavares, L.S.: Existence of solutions for a class of nonlocal problems driven by an anisotropic operator via sub-supersolutions. J. Convex Anal. 29(1), 291–320 (2022)
Ladyzenskaya, O.A., Uraltseva, N.N.: Linear and Quasilinear Elliptic Equations. Academic Press, New York (1968)
Struwe, M.: Variational Methods. Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 2nd edn. Ergebnisse der Mathematik und Ihrer Grenzgebiete, vol. 34. Springer, Berlin (1996)
Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973)
Acknowledgements
The author would like to thank the referees for the comments which improved the manuscript.
Funding
No funding was received for this study.
Author information
Authors and Affiliations
Contributions
The author proved all the results of the paper and wrote the whole manuscript. He also read and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tavares, L.S. Multiplicity of solutions for an anisotropic variable exponent problem. Bound Value Probl 2022, 10 (2022). https://doi.org/10.1186/s13661-022-01591-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-022-01591-4