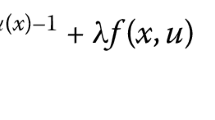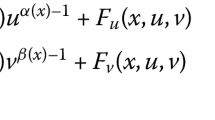Existence and multiplicity of solutions for a singular anisotropic problem with a sign-changing term

Abstract

In this paper we investigate the existence and multiplicity of solutions for a class of singular anisotropic problems involving a weight and a term that may change sign. The approach is based on sub-supersolutions and the Mountain Pass Theorem.

1 Introduction

In this manuscript we are interested in existence and multiplicity results for the weighted singular anisotropic problem

where $\Omega \subset {\mathbb {R}}^N (N \ge 3)$, unless stated otherwise, is a bounded smooth domain, $\alpha ,\lambda ,\gamma >0,$ $f: {\overline{\Omega }} \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ and $a: \Omega \rightarrow {\mathbb {R}}$ are functions satisfying certain conditions and $2 \le p_1 \le ... \le p_N < {\overline{p}}^{\star }$ with $\overline{p} < N,$ where $\overline{p} =N/ \sum _{i=1}^{N} \frac{1}{p_i}$ and ${\overline{p}}^{\star }{:}{=} \displaystyle \frac{N \overline{p}}{N-\overline{p}}.$

In the last decades Partial Differential Equations involving anisotropic operators has drawn the attention of several researchers due to their applicability in several areas of Science and Technology. Several types of applications were considered in the literature, among them we point out models that can describe the dynamics of fluids with different conductivities in different directions, in the study of the spread of an epidemic disease in heterogeneous environments and in the study of image noise reduction. For more details see for instance [6, 8, 9, 24].

In other direction, arisen from the classical theory of the Lebesgue and Sobolev spaces, we have the development of the anisotropic spaces $W^{1,\overrightarrow{p}}$ where $\overrightarrow{p}$ is a vector with constant components $\overrightarrow{p} = (p_1,p_2,...,p_N),$ see for instance [5, 10, 14, 19, 25, 29] and its references. Regarding the applicability of such spaces, several problems involving anisotropic operators were considered and they were motivated from differential equations with the classical Laplacian operator, see for instance [1, 2, 20, 22]. For example, in [2] the authors studied the problem

$$\begin{aligned} \left\{ \begin{array}{rcl} -\displaystyle \sum ^{N}_{i=1}\frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial u}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial u}{\partial x_{i}}\Big )\ &{}=&{}h(x,u) \text{ in } \Omega \text{, }\\ u&{}>&{}0 \text{ in } \Omega \text{, }\\ u&{}=&{}0 \text{ on } \partial \Omega \text{, } \end{array} \right. \end{aligned}$$

where $h: \Omega \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ is a Carathedory function satisfying certain conditions.

There are few works that consider singular problems involving anisotropic operators. We cite below some articles that treat this kind of problems which were inspirational for the present paper.

In the reference [20], the authors considered, by means of sub-supersolution technique combined with an application of the Schaefer’s Fixed Point Theorem, the problem

where $\gamma \in (0,1), \beta >0$ and $f: {\overline{\Omega }} \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ is a continuous function. In [20], it was proved the existence of a solution depending on the values of $\beta$ and of the behaviour of f. In [27], using approximation arguments to control for the singular term, the authors proved results of existence and regularity of solution to $(P_{\gamma })$ with $\lambda =0$ and a(x) in suitable Lebesgue space. The same problem and techniques of [27] were considered in [30], but with the constant $\gamma$ replaced by a function $\gamma (x).$

On other hand, singular problems for the $p-$Laplacian operator has drawn the attention of several researchers in the last decades, see for instance [3, 7, 11,12,13, 15, 28, 31]. A related equation to (P),  which was studied in [31], is the problem

where $\Delta _p u {:}{=} div( |\nabla u|^{p-2}\nabla u),p>1$ denotes the $p-$Laplacian operator and $a:\Omega \rightarrow {\mathbb {R}}$ and $f:\Omega \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ are functions satisfying some conditions. The approach is mainly based in classical regularity results, the Vazquez’s Strong Maximum Principle, sub-supersolutions and Variational Methods.

An important point regarding $(P_{\gamma })$ is the lack of homogeneity of the anisotropic operator, which implies in serious obstacles in the study of $(P_{\gamma })$ when one intends to consider a sub-supersolution approach. Another mathematical difficulty, and the main one, is the fact that the regularity results used in [31] are not available for the anisotropic setting. Due to the mentioned problems, the approach considered in [31] is not applicable to $(P_{\gamma }).$ Therefore, compared to [20] and [31], the study of $(P_{\gamma })$ requires new arguments and knowledge of relevant topics of nonlinear functional analysis, particularly the theory of anisotropic spaces. Thus motivated by all these papers, mainly by [20, 27, 30, 31], we propose the study of existence and multiplicity of solutions for $(P_{\gamma })$, which, to the best of our knowledge, was not considered previously in the literature. The approach relies on the explicit construction of appropriate sub-supersolutions (see (3)) and Variational Methods. The first difficulty, is handled by considering explicit constructions of sub-supersolutions. Moreover, such argument is different from the one considered in [20]. With respect to the second one, which is applied to obtain the multipicity of solutions, we consider truncated problems and apply a minimax argument in convex sets and the Mountain Pass Theorem [4] to the associated energy functionals. Since truncated problems are considered, fine estimates are needed to apply the variational approach. Thus, our research are based the sub-supersoution method and variational arguments. As mentioned before the sub-supersolution technique, which is rare in the anisotropic setting., cannot be easily implemented due to the presence of the anisotropic operator and such fact imply that that such explicit construction can be of independent interest.

With respect to the contributions of this work we quote that the results of [31] can be obtained partially in the anisotropic case. We also improve the results of [20, 27, 30] in the sense that it is possible to obtain, in the weighted anisotropic singular case, the existence of a solution. Moreover, under some additional conditions, it is possible to obtain multiplicity results, which was not considered in the mentioned papers and differently from [20], here our results include the case $\gamma >1.$

The rest of the paper is organized as follows: Sect. 2 is focused in the presentation of the results of this manuscript. Section 3 is devoted to the needed properties of the anisotropic spaces. In Sect. 4 we prove the results of this paper.

2 Presentation of the results

In order to state the results of this paper some definitions are needed. Considering that $f:{\overline{\Omega }}\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a continuous function and $a(x)>0$ a.e in $\Omega$ we say what $u \in W^{1,\overrightarrow{p}}_{0}(\Omega )$ with $\overrightarrow{p}{:}{=}(p_1,...,p_N)$ is a solution of $(P)_{\gamma }$ if, for all $\varphi \in W^{1,\overrightarrow{p}}_{0}(\Omega )$ the following equality holds true

$$\begin{aligned} \displaystyle \int _{\Omega }\sum ^{N}_{i=1}\Big \vert \frac{\partial u}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial u}{\partial x_{i}} \frac{\partial \varphi }{\partial x_{i}} =\int _{\Omega }\left( \frac{\alpha a(x)}{u^{\gamma }}+ \lambda f(x,u)\right) \varphi . \end{aligned}$$

Consider the function $d(x) = dist (x,\partial \Omega ),x \in \Omega$ and the hypotheses below.

$({H_a})$:

The function a satisfies $\displaystyle \frac{a}{d^\gamma } \in L^{\infty } (\Omega ).$

$(H^{\prime }_{a})$:

The function a satisfies $(H_a)$ and $a(x) \ge K {d(x)}^{\tau }, \tau \ge \gamma$ near the boundary, that is, there exist $K,{\widetilde{\delta }}>0$ such that $a(x) \ge K {d(x)}^{\tau },$ for all $x \in \Omega _{{\widetilde{\delta }}}$ where $\Omega _{{\widetilde{\delta }}} = \{x \in \Omega ; d(x) < {\widetilde{\delta }}\}.$

$(H_f)$:

There exists $\delta >0$ such that $f(x,t) \ge - c a(x), \text{ for } \text{ all } 0\le t\le \delta \text{, } \text{ a.e } \text{ in } \Omega$ and for some constant $c>0 .$

$(H^{\prime }_{f})$:

The function f satisfies $(H_f)$ and there exist $r>1$ and a constant $C > 0$ such that $f(x,t)\le C(t^{r-1}+1) \ \text{ a.e } \text{ in } \Omega \text{ for } \text{ every } t \ge 0.$

Remark 1

Note that $(H_a)$ imply that $a \in L^{\infty }(\Omega )$. In particular, $(H_f)$ tells us that f may change sign on $[0, \delta ].$

Our first result is as follows:

Theorem 1

Suppose that $(H_a)$ and $(H_f)$ hold true. The following assertions are true.

• (i) There exist $\alpha _0>0,\lambda _0>0$ such that $(P_\gamma )$ admits solution, for all $\alpha \ge \alpha _0$ and $\lambda \in (0,\lambda _0).$

• (ii) If, in addition, $(H^{\prime }_{a})$ is also verified then given $\alpha >0,$ there exists ${\lambda _0}^{\prime }>0$, depending only on $\alpha ,$ such that $(P_\gamma )$ admits solution, for all $\lambda \in (0,{\lambda _0}^{\prime }).$

Consider the function $F(x, t) =\displaystyle \int _{0}^{t}f(x,s) ds.$ By considering an Ambrosetti-Rabinowitz type condition it is possible to prove a multiplicity result for $(P_{\gamma }).$ The condition is given below.

$(H_{AR})$ The function f satisfies $(H^{\prime }_{f})$ with $r \in (1,{\overline{p}}^{\star })$ and there exists $t_0 >0$ and $\theta > p_N$ such that $0 <\theta F(x,t) \le tf(x,t),$ for all $t \ge t_0, \ \ \text {a.e in} \ \Omega .$

Theorem 2

Suppose that $(H_a)$ and $(H_{AR})$ hold and let $\alpha _0,\lambda _0$ and ${\lambda _0}^{\prime }$ as in Theorem 1. The following assertions are true.

• (i) The problem $(P_\gamma )$ has two solutions, for all $\lambda \in (0,\widetilde{\lambda _0})$ for some $0< \widetilde{\lambda _0}\le \lambda _0$ and $\alpha \ge \alpha _0.$

• (ii) If $(H^{\prime }_{a})$ is also verified, then given $\alpha >0,$ there exists $0<\lambda ^{\prime \prime }_{0} \le \lambda ^{\prime }_{0}$ depending only on $\alpha ,$ such that $(P_\gamma )$ admits two solutions, for all $\lambda \in (0,{\lambda _0}^{\prime \prime }).$

Remark 2

The functions $a(x) = d(x)^{\gamma } + d(x)^{\tau }, \tau \ge \gamma$ and $f(x,t) = a(x)(|t|^{r-1} - \beta ^{r-1} )$ with $r \in (p_N, {\overline{p}}^{\star })$ satisfies $(H^{\prime }_{a})$ and $(H_{AR})$ for $\beta >0$ and $t_0=t_0(\beta )>0$ sufficiently large respectively.

3 Preliminaries

In this section we present some basic facts regarding anisotropic spaces and results that will be used in this work. For more informations on anisotropic spaces we quote [2, 18, 19, 21, 26, 33].

Let $1<p_1\le p_2 \le ... \le p_N$ be real numbers and denote by $\overrightarrow{p}$ the vector $\overrightarrow{p}{:}{=} (p_1,...,p_N) \in {\mathbb {R}}^N.$ We denote by $W^{1,\overrightarrow{p}}(\Omega )$ the space defined by

$$\begin{aligned} W^{1,\overrightarrow{p}}(\Omega ){:}{=} \left\{ u \in L^{p_N}(\Omega ); \frac{\partial u}{\partial x_i} \in L^{p_i}(\Omega ), i=1,...,N\right\} , \end{aligned}$$

which is a Banach space when endowed with the norm

$$\begin{aligned} \Vert u\Vert _{1,\overrightarrow{p}}{:}{=} \Vert u\Vert _{L^{p_N}} + \displaystyle \sum _{i=1}^{N} \left\| \frac{\partial u}{\partial x_i}\right\| _{L^{p_i}}, \end{aligned}$$

(1)

where $\Vert \cdot \Vert _{L^{p_i}}$ denotes the usual norm of $L^{p_i}(\Omega ).$ It will be denoted by $W^{1,\overrightarrow{p}}_{0}(\Omega )$ the Banach space defined by the closure of $C_{0}^{\infty }(\Omega )$ in $W^{1,\overrightarrow{p}}(\Omega )$ with respect to the norm $\Vert \cdot \Vert _{1,\overrightarrow{p}}.$

Consider $\overline{p}$ the harmonic mean of $p_i,i=1,...,N$ given by $\overline{p}{:}{=} N/ \sum _{i=1}^{N} \frac{1}{p_i}$ and define ${{\overline{p}}^{\star }}{:}{=} \displaystyle \frac{N \overline{p}}{N-\overline{p}}$ for $\overline{p} < N.$ From [19] we have that there exists an embedding $W^{1,\overrightarrow{p}}_{0}(\Omega ) \hookrightarrow L^{q}(\Omega )$ which is continuous for $q\in [1,{{\overline{p}}^{\star }}]$ and compact in the case $q\in [1,{{\overline{p}}^{\star }}).$ Thus the norm

$$\begin{aligned} \Vert u \Vert {:}{=} \displaystyle \sum _{i=1}^{N} \left\| \frac{\partial u}{\partial x_i}\right\| _{L^{p_i}}, u \in W^{1,\overrightarrow{p}}_{0}(\Omega ) \end{aligned}$$

(2)

is equivalent to the norm given in (1).

The next result can be found in [16, Lemma 2.1].

Lemma 1

Let $a \in L^{\infty }(\Omega )$ and $p_1\ge 2 .$ There exists a unique solution $u \in W_{0}^{1,\overrightarrow{p}}(\Omega )$ of the problem

Remark 3

It is worthwhile to say that if $a \in L^{\infty }(\Omega )$ is a positive constant, then the only solution of $(P_a)$ is strictly positive in $\Omega$. See [20, Lemma 3.1].

The next two results can be found in [16, Lemma 2.4] and [16, Lemma 2.1], respectively.

Lemma 2

Let $u\in W_{0}^{1,\overrightarrow{p}}(\Omega )$ be a solution to problem

$$\begin{aligned} \left\{ \begin{array}{rcl} -\displaystyle \sum ^{N}_{i=1}\frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial u}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial u}{\partial x_{i}}\Big )\ &{}=&{}f \text{ in } \Omega \text{, }\\ u&{}=&{}0 \text{ on } \partial \Omega \text{, } \end{array} \right. \end{aligned}$$

such that $f\in L^{r}(\Omega )$ with $r>\overline{p}^{*}/(\overline{p}^{*}-p_{1}).$ Then $u\in L^{\infty }(\Omega ).$ Moreover,

$$\begin{aligned} \Vert u\Vert _{\infty }\le \frac{C\Vert f\Vert _{r}^{\frac{1}{p_{1}-1}}|\Omega |^{\frac{\beta -1}{\alpha }}}{S^{\frac{1}{p_{1}-1}}}, \end{aligned}$$

where $\beta , \alpha , S$ and C are constants that does not depend on u.

Lemma 3

Consider $u,v \in W_{0}^{1,\overrightarrow{p}}(\Omega )$ satisfying

$$\begin{aligned} \left\{ \begin{array}{rcl} -\displaystyle \sum ^{N}_{i=1}\frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial u}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial u}{\partial x_{i}}\Big )\ &{} \le &{}-\displaystyle \sum ^{N}_{i=1}\frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial v}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial v}{\partial x_{i}}\Big )\ \;\;\text{ in }\;\; \Omega , \\ u &{} \le &{} v\;\;\text{ on }\;\;\partial \Omega , \end{array} \right. \end{aligned}$$

where $u \le v$ on $\partial \Omega$ means that $(u-v)^{+} \in W^{1,\overrightarrow{p}}_{0}(\Omega ).$ Then $u(x)\le v(x)$ a.e in $\Omega$.

4 Proof of Theorems 1 and 2

The goal of this section is to prove Theorems 1 and 2. The approach is based on the sub-supersolution technique combined with the variational method.

We say that $({\underline{u}}, \overline{u}) \in (W^{1,\overrightarrow{p}}_{0}(\Omega ) \cap L^{\infty }(\Omega ) )\times (W^{1,\overrightarrow{p}}_0(\Omega ) \cap L^{\infty }(\Omega ))$ is a sub-supersolution for $(P_{\gamma })$ if ${\underline{u}}(x) \le \overline{u}(x)$ a.e. in $\Omega$ and

$$\begin{aligned} \displaystyle \int _{\Omega }\sum ^{N}_{i=1}\Big \vert \frac{\partial {\underline{u}}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial {\underline{u}}}{\partial x_{i}} \frac{\partial \varphi }{\partial x_{i}} \le \int _{\Omega }\left( \frac{\alpha a(x)}{{{\underline{u}}}^{\gamma }}+ \lambda f(x,{\underline{u}})\right) \varphi \end{aligned}$$

and

$$\begin{aligned} \displaystyle \int _{\Omega }\sum ^{N}_{i=1}\Big \vert \frac{\partial \overline{u}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial \overline{u}}{\partial x_{i}} \frac{\partial \varphi }{\partial x_{i}} \ge \int _{\Omega }\left( \frac{\alpha a(x)}{{\overline{u}}^{\gamma }}+ \lambda f(x,\overline{u})\right) \varphi , \end{aligned}$$

for all nonnegative functions $\varphi \in W^{1,\overrightarrow{p}}_{0}(\Omega ).$

The next lemma plays a key role in the proofs of our results:

Lemma 4

The following assertions are true.

• (i) If $(H_a)$ and $(H_f)$ hold true, then there exist $\alpha _0>0,$ $\lambda _0 >0$ and ${\underline{u}},\overline{u} \in W^{1,\overrightarrow{p}}_{0}(\Omega ) \cap L^{\infty }(\Omega )$ such that $a {{\underline{u}}}^{-\gamma } \in L^{\infty } (\Omega ),$ $\Vert {\underline{u}}\Vert _{L^{\infty }} \le \delta$ with the pair $({\underline{u}},\overline{u})$ being a sub-supersolution for $(P_\gamma )$, for all $\alpha \ge \alpha _0$ and $\lambda \in (0,\lambda _0).$

• (ii) If $(H_a),(H_f)$ and $(H^{\prime }_{a})$ hold true, then given $\alpha >0$ there exist $\lambda _0>0,$ depending only on $\alpha$, and ${\underline{u}},\overline{u} \in W^{1,\overrightarrow{p}}_{0}(\Omega ) \cap L^{\infty }(\Omega )$ such that $a {{\underline{u}}}^{-\gamma } \in L^{\infty } (\Omega ),$ $\Vert {\underline{u}}\Vert _{L^{\infty }} \le \delta$ with the pair $({\underline{u}},\overline{u})$ being a sub-supersolution for $(P_\gamma ),$ for all $\lambda \in (0,\lambda _0).$

Proof

(i) We will begin by considering the function ${\underline{u}}.$ Since $\partial \Omega$ is of class $C^2$ then there exists ${\overline{\delta }}>0$ such that $d \in C^2 (\overline{\Omega _{3{\overline{\delta }}}} )$ with $|\nabla d| \equiv 1$ in $\overline{\Omega _{3{\overline{\delta }}}},$ see for example [23, Lemma 14.16] and its proof.

For $k >0$ and $2\sigma \in (0,{\overline{\delta }})$ with $\sigma {:}{=} \frac{ln 2}{k}$ consider the function, which was introduced in [17], given by

$$\begin{aligned} \phi (x) = {\left\{ \begin{array}{ll} e^{k d(x)} -1&{} \quad \text {if} \quad d(x)< \sigma ,\\ e^{k \sigma } -1 + \displaystyle \int _{\sigma }^{d(x)} ke^{k\sigma } \left( \frac{2\delta -t}{\sigma }\right) ^{2} dt&{} \quad \text {if} \quad \sigma \le d(x) < 2\sigma ,\\ e^{k \sigma } -1 + \displaystyle \int _{\sigma }^{2\sigma } ke^{k\sigma } \left( \frac{2 \delta -t}{ \sigma }\right) ^{2}dt, &{}\quad \text {if} \quad 2\sigma \le d(x). \end{array}\right. } \end{aligned}$$

(3)

Note that $\phi \in C^{1}({\overline{\Omega }})$ and $\phi = 0$ on $\partial \Omega .$ If $p_N >p_1$ define $\mu {:}{=} \frac{1}{k^{\iota }},$ where

$$\begin{aligned} \frac{p_N - p_1 +1}{p_N - p_1}> \iota > 1. \end{aligned}$$

In the case $p_N =p_1$ consider $\mu {:}{=} \frac{1}{k^{\iota }}$ where $\iota > 1$ is an arbitrary number.

The inequality $e^{x} -1 \ge x,x \ge 0$ combined with the condition $(H_a)$ imply that $a (\mu \phi )^{-\gamma } \in L^{\infty }(\Omega ).$ If $d(x) <\sigma$ we have that $\mu \phi (x) \le \mu (e^{kd(x)} -1 ) \le \mu (e^{k\sigma } -1 ) = \frac{1}{k^{\iota }}.$ In the case $\sigma \le d(x)$ we have

$$\begin{aligned} \begin{aligned} \mu \phi&\le \mu \left( e^{k \sigma } -1 + \displaystyle \int _{\sigma }^{2\sigma } ke^{k\sigma } \left( \frac{2 \delta -t}{ \sigma }\right) ^{2}dt\right) \\&= \mu \left( 2 -1 + \frac{2k}{3}\left( \left( \frac{2\delta -\sigma }{\sigma }\right) ^{3} - \left( \frac{2\delta -2\sigma }{\sigma }\right) ^{3}\right) \right) . \end{aligned} \end{aligned}$$

(4)

If $k\rightarrow +\infty$ we have $\sigma \rightarrow 0^{+}$. Since $\lim _{\sigma \rightarrow 0^{+}} \left( \frac{2\delta -\sigma }{\sigma }\right) ^{3} - \left( \frac{2\delta -2\sigma }{\sigma }\right) ^{3} < + \infty ,$ it follows from (4) that $\mu \phi \le \frac{C_0}{k^{\iota }} \left( 1 + k \right)$ for some constant $C_0>0$ which does not depend on k. Then we obtain that $\Vert \mu \phi \Vert _{L^{\infty }} \le \delta$ for $k>0$ large enough.

A straightforward calculation shows that if $x \in \Omega$ satisfy $d(x) < \sigma$ with $\frac{\partial d (x)}{\partial x_i} \ne 0,$ then

$$\begin{aligned} \begin{aligned}&-\sum _{i=1}^{N}\frac{\partial }{\partial x_i} \left( \left| \frac{\partial (\mu \phi )}{\partial x_i}\right| ^{p_i-2} \frac{\partial (\mu \phi )}{\partial x_i}\right) \\&\quad =-\displaystyle \sum _{i=1}^{N}(k \mu )^{p_i -1} \left( e^{k d(x)(p_i -1)} k(p_i -1) \left| \frac{\partial d}{\partial x_i}\right| ^{p_i} + e^{kd(x)(p_i -1)} \left| \frac{\partial d}{\partial x_i}\right| ^{p_i -2} \frac{\partial ^2 d}{\partial x^{2}_{i}} \right) \\&\quad {:}{=} B(x). \end{aligned}\nonumber \\ \end{aligned}$$

(5)

In the case $\sigma< d(x) < 2\sigma$ we have

$$\begin{aligned} \begin{aligned}&-\sum _{i=1}^{N}\frac{\partial }{\partial x_i} \left( \left| \frac{\partial (\mu \phi )}{\partial x_i}\right| ^{p_i-2} \frac{\partial (\mu \phi )}{\partial x_i}\right) \\&\quad = \sum _{i=1}^{n}(\mu k e^{k\sigma })^{p_i -1}\theta (p_i -1) \left( \frac{2\sigma -d(x)}{\sigma }\right) ^{2(p_i -1) -1} \frac{1}{\sigma } \left| \frac{\partial d }{\partial x_i}\right| ^{p_i -1} \\&\qquad + \sum _{i=1}^{n} (\mu k e^{k\sigma })^{p_i -1}\left( \frac{2\sigma - d(x)}{\sigma }\right) ^{2(p_i -1)} \left| \frac{\partial d}{\partial x_i}\right| ^{p_i -2}\left( - \frac{\partial ^2 d }{\partial x^{2}_{i}}\right) \\&\quad {:}{=}C(x). \end{aligned} \end{aligned}$$

(6)

From (5) and (6) we get

$$\begin{aligned} \int _{\Omega } \displaystyle \sum _{i=1}^{N} \left| \frac{\partial (\mu \phi )}{\partial x_i}\right| ^{p_i -2} \frac{\partial (\mu \phi )}{\partial x_i} \frac{\partial \varphi }{\partial x_i} = \int _{\Omega } A \varphi , \forall \varphi \in W^{1,\overrightarrow{p}}_{0}(\Omega ), \end{aligned}$$

where $A(x)= B(x),$ if $d(x)<\sigma$ and $\frac{\partial d (x)}{\partial x_i} \ne 0$, $A(x)= C(x),$ if $\sigma<d(x)<2\sigma$ and $\frac{\partial d (x)}{\partial x_i} \ne 0$ and A(x) is defined to be zero if one of the conditions is satisfied $\frac{\partial d (x)}{\partial x_i} = 0, d(x) \ge 2\sigma$ or $d(x) = \sigma .$

From now on consider $k\mu \le 1$ which occurs for k large enough. Now we will obtain some estimates for the function A. Let $x \in \Omega$ with $d(x) < \sigma .$ Therefore $|\nabla d(x)|=1$. Note that

$$\begin{aligned} \begin{aligned} -(k\mu )^{p_i -1} e^{kd(x)(p_i - 1)} k(p_i -1 ) \left| \frac{\partial d}{\partial x_i} \right| ^{p_i}&\le -(k \mu )^{p_N -1} e^{k d(x) (p_i - 1)} k(p_1 -1) \left| \frac{\partial d}{\partial x_i}\right| ^{p_N}\\&\le -(k \mu )^{p_N -1} k(p_1 -1) \left| \frac{\partial d}{\partial x_i}\right| ^{p_N}. \end{aligned}\nonumber \\ \end{aligned}$$

(7)

Thus we obtain from (7) that

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^{N} -(k\mu )^{p_i -1} e^{kd(x) (p_i - 1)} k(p_i -1 ) \left| \frac{\partial d}{\partial x_i} \right| ^{p_i} \le \sum _{i=1}^{N}-(k\mu )^{p_i -1} k(p_1 -1) \left| \frac{\partial d}{\partial x_i}\right| ^{p_i}\\&\quad \le \sum _{i=1}^{N}-(k\mu )^{p_i -1} k(p_1 -1) \left| \frac{\partial d}{\partial x_i}\right| ^{p_N}. \end{aligned} \end{aligned}$$

(8)

Using in (8) the inequality $(a + b)^{p_N} \le C_1 (a^{p_N} + b^{p_N}),$ for all $a,b \ge 0$, where $C_1>0$ is a constant that does not depend on a and b, we get

$$\begin{aligned}{} & {} \sum _{i=1}^{N} -(k\mu )^{p_i -1} e^{kd(x) (p_i - 1)} k(p_i -1 ) \left| \frac{\partial d}{\partial x_i} \right| ^{p_i}\nonumber \\ {}{} & {} \le - (k\mu )^{p_N -1} k (p_1 -1) \left( \sum _{i=1}^{N} \left| \frac{\partial d}{\partial x_i}\right| \right) ^{p_N} C_1. \end{aligned}$$

(9)

Since $\sum \nolimits _{i=1}^{N} |a_i| \ge C_2 \sqrt{\sum \nolimits _{i=1}^{N}a^{2}_{i}},$ for all $a_i \ge 0 , i=1,...,N$ with $C_2 >0$ being a constant that does not depend on $a_i ,$ we obtain from (9) that

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{N} -(k\mu )^{p_i -1} e^{kd(x) (p_i - 1)} k(p_i -1 ) \left| \frac{\partial d}{\partial x_i} \right| ^{p_i}&\le - (k\mu )^{p_N -1} k (p_1 -1) |\nabla d|^{p_N} C_2 \\&\le - (k\mu )^{p_N -1} k (p_1 -1) C_2, \end{aligned}\nonumber \\ \end{aligned}$$

(10)

because $|\nabla d| \equiv 1$ near the boundary with $C_2 >0$ being a constant which does not depend on $k>0 .$

Since $d(x) < \sigma ,$ we have for all $i=1,...,N$ that

$$\begin{aligned}{} & {} \left| \sum _{i=1}^{N}(k \mu )^{p_i - 1} e^{kd(x)(p_i -1)} \left| \frac{\partial d}{\partial x_i}\right| ^{p_i -2} \left( - \frac{\partial ^2 d}{\partial x^{2}_{i}}\right) \right| \nonumber \\{} & {} \le \sum _{i=1}^{N} (k \mu )^{p_i -1} e^{k d(x) (p_N -1)} \left| \frac{\partial d}{\partial x_i}\right| ^{p_i -2} \left| \frac{\partial ^2 d}{\partial x^{2}_{i}}\right| \nonumber \\{} & {} \le \sum _{i=1}^{N} (k \mu )^{p_1 -1} e^{(p_N -1)ln2} \left| \frac{\partial d}{\partial x_i}\right| ^{p_i -2} \displaystyle \sup _{\begin{array}{c} x \in \Omega _{\delta } \nonumber \\ i=1,.,,,N \end{array}} \left\{ \left| \frac{\partial ^2 d}{\partial x^{2}_{i}}\right| \right\} \nonumber \\{} & {} \le (k \mu )^{p_1 -1} C_3,\nonumber \\ \end{aligned}$$

(11)

where $C_3 >0$ is a constant that does not depend on k. Thus by (5), (10) and (11), we obtain that

$$\begin{aligned} A(x) \le - (k\mu )^{p_N -1} k (p_1 -1) C_2 + (k \mu )^{p_1 -1} C_3 , d(x) < \sigma . \end{aligned}$$

(12)

If $p_N >p_1$ we have

$$\begin{aligned} \begin{aligned} A(x)&\le (k\mu )^{p_1 -1}(C_3 - (k\mu )^{p_N -1 - (p_1 -1)} k (p_1 -1)C_2) \\&= (k\mu )^{p_1 -1} (C_3 - k^{(1-\iota )(p_N - p_1 )) +1} (p_1 -1 )C_2), \ \text {if} \ d(x) < \sigma . \end{aligned} \end{aligned}$$

(13)

The inequality $\frac{p_N -p_1 +1}{p_N-p_1} > \iota$ implies that $(1-\iota )(p_N -p_1)+1 >0 .$ Thus if $p_N >p_1 ,$ we have from (13) that $A(x) \le 0$ for $k>0$ large enough, for all $x \in \Omega$ with $d(x) < \sigma .$

If $p_N = p_1$ we have from (12) that

$$\begin{aligned} A(x) \le (k\mu )^{p_N -1} (-k (p_1 -1)C_2 + C_3), \ \text {if} \ d(x) <\sigma . \end{aligned}$$

(14)

Using (13) and (14), we can conclude in all cases that

$$\begin{aligned} A(x)\le 0, \ \text {if} \ d(x)<\sigma \ \text {or} \ 2\sigma < d(x), \end{aligned}$$

(15)

for k large.

Consider the case $\sigma< d(x) < 2\sigma .$ Since $d \in C^2 (\overline{\Omega _{3{\overline{\delta }}}} )$ with $|\nabla d(x)| \equiv 1$ in $\overline{\Omega _{2{\overline{\delta }}}}$ and $\mu k\le 1$ for $k>0$ large we have from (6) that

$$\begin{aligned} \begin{aligned} |A(x)|&\le \displaystyle \max _{i=1,...,N}\{(\mu k e^{k\sigma })^{p_i -1}\} \frac{C_4}{\sigma }&\le C_5 k. \end{aligned} \end{aligned}$$

(16)

where $C_4 , C_5 >0$ are constants that do not depend on k. Define $\mu \phi {:}{=}{\underline{u}}$ with $k_0{:}{=} k$ such that (15) and (16) occur and $\Vert \mu \phi \Vert _{L^{\infty }} \le \delta .$ Consider $x \in \Omega$ with $d(x) < \sigma$ or $d(x) > 2\sigma$ and $\lambda \in (0,1).$ From $(H_f)$ we have

$$\begin{aligned} \frac{ \alpha a(x)}{{{\underline{u}}}^{\gamma }} + \lambda f(x,{\underline{u}}){} & {} \ge \frac{\alpha a(x)}{\delta ^{\gamma }} - \lambda a(x) c\nonumber \\{} & {} \ge a(x)\left( \frac{\alpha }{\delta ^{\gamma }} - c\right) \nonumber \\{} & {} \ge 0\nonumber \\{} & {} \ge -\displaystyle \sum _{i=1}^{N} \frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial {\underline{u}}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial {\underline{u}}}{\partial x_{i}}\Big ),\nonumber \\ \end{aligned}$$

(17)

for $\alpha >0$ large enough, which does not depend on $k_0.$

Consider the case $\sigma< d(x) < 2\sigma .$ Fix $k_0{:}{=}k > 0$ such that (16) and (17) are verified. Define $\displaystyle \inf _{x \in W_{k_0}} a(x) {:}{=}a_{k_0},$ where $\{x \in \Omega ; \sigma< d(x) < 2\sigma \}{:}{=} W_{k_0}.$ In this case we have by (16) that

$$\begin{aligned} \begin{aligned} \frac{ \alpha a(x)}{{{\underline{u}}}^{\gamma }} + \lambda f(x,{\underline{u}})&\ge a(x) \left( \frac{\alpha }{\delta ^{\gamma }} - \lambda c\right) \\&\ge a_{k_0} \left( \frac{\alpha }{\delta ^{\gamma }} - c\right) \\&\ge C_5 k_0 \\&\ge -\displaystyle \sum _{i=1}^{N} \frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial {\underline{u}}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial {\underline{u}}}{\partial x_{i}}\Big ), \end{aligned} \end{aligned}$$

for $\alpha >0$ large enough, which depends only on $\delta ,c,\gamma$ and $k_0 .$

Since $a{\underline{u}}^{-\gamma } \in L^{\infty }(\Omega ),$ by Lemma 1 there exists $\overline{u} \in W^{1,\overrightarrow{p}}_0 (\Omega )$ such that

$$\begin{aligned} \left\{ \begin{array}{rcl} -\displaystyle \sum ^{N}_{i=1}\frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial \overline{u}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial \overline{u}}{\partial x_{i}}\Big )\ &{}=&{}\displaystyle \frac{\alpha a(x)}{{\underline{u}}^{\gamma }}+ C_5 k_0 \text{ in } \Omega \text{, }\\ \overline{u}&{}=&{}0 \text{ on } \partial \Omega \text{, } \end{array} \right. \end{aligned}$$

is verified. Using (16) and the fact that $A(x)\le 0$ in the cases $d(x) <\sigma$ or $d(x) > 2\sigma$ we can infer by Lemma 3 that ${\underline{u}}(x) \le \overline{u}(x)$ a.e. in $\Omega .$ Since $\lambda$ does not depend on $k_0$ we have

$$\begin{aligned}&-\displaystyle \sum ^{N}_{i=1}\frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial \overline{u}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial \overline{u}}{\partial x_{i}}\Big )\ - \frac{\alpha a(x)}{{\overline{u}}^{\gamma }} - \lambda f(x,\overline{u}) \ge \alpha a(x)\left( \frac{1}{{\underline{u}}^{\gamma }} - \frac{1}{\overline{u}^{\gamma }} \right) \nonumber \\&\qquad +C_5 k_0-\lambda f(x,\overline{u})\nonumber \\&\quad \ge C_5 k_0 - |\lambda | \sup _{x \in \Omega } |f(x,\overline{u})|,\nonumber \\&\quad \ge 0, \end{aligned}$$

(18)

for all $\lambda \in (0,\lambda _0),$ for some $0<\lambda _0<1$ depending only on $k_0.$

(ii) The argument will be based on nontrivial modifications of (i). Since $\iota >1$ there exists $\xi >0$ such that $(1-\iota )(p_1 -1) + \xi (1+\tau ) <0 .$ Consider $\phi ,\mu ,\delta$ as before with $\displaystyle \frac{\ln 2}{k^{\xi }}{:}{=}\sigma$. Note that $a(\mu \phi )^{-\gamma } \in L^{\infty }(\Omega )$ with $\Vert \mu \phi \Vert _{L^{\infty }} \le \delta$ for $k{:}{=}k_0>0$ large enough. Consider $0<\lambda ^{\prime }_{0}<1,$ depending only on $\alpha$, with $\displaystyle \frac{\alpha }{\delta ^{\gamma }} - \lambda ^{\prime }_{0} c >0.$

Arguing as in (15) and (16) we obtain

$$\begin{aligned} \begin{aligned} -\sum _{i=1}^{N}\frac{\partial }{\partial x_i} \left( \left| \frac{\partial (\mu \phi )}{\partial x_i}\right| ^{p_i-2} \frac{\partial (\mu \phi )}{\partial x_i}\right)&\le 0 , \ \text {if} \ d(x)< \sigma \ \text {or} \ 2\sigma< d(x) \\ -\sum _{i=1}^{N}\frac{\partial }{\partial x_i} \left( \left| \frac{\partial (\mu \phi )}{\partial x_i}\right| ^{p_i-2} \frac{\partial (\mu \phi )}{\partial x_i}\right)&\le C_6 (\mu k)^{p_1-1} k^{\xi }, \ \text {if} \ \sigma< d(x) <2\sigma , \end{aligned} \end{aligned}$$

(19)

for $k{:}{=}k_0$ large enough, where $C_6 >0$ is a constant which does not depend on k. If necessary consider a larger $k_0$ satisfying

$$\begin{aligned} \left( \frac{K \ln 2}{{k_0}^{\xi }}\right) ^{\tau } \left( \frac{\alpha }{\delta ^{\gamma }} - \lambda ^{\prime }_{0} c\right) \ge C_6{k_0}^{(1-\iota )(p_1 -1)+\xi }, \end{aligned}$$

(20)

where $K>0$ is the constant given in $(H^{\prime }_{a}),$ which is possible because $(1-\iota )(p_1 -1) + \xi (1+\tau ) <0 .$ Denoting by $\mu \phi {:}{=}{\underline{u}}$ we get

$$\begin{aligned} \begin{aligned} \frac{ \alpha a(x)}{{{\underline{u}}}^{\gamma }} + \lambda f(x,{\underline{u}})\ge a(x)\left( \frac{\alpha }{\delta ^{\gamma }} - \lambda c\right) \ge a(x)\left( \frac{\alpha }{\delta ^{\gamma }} - \lambda ^{\prime }_{0} c\right)&\ge 0 \\&\ge -\displaystyle \sum _{i=1}^{N} \frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial {\underline{u}}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial {\underline{u}}}{\partial x_{i}}\Big ), \end{aligned} \end{aligned}$$

for all $\lambda \in (0,\lambda ^{\prime }_{0})$ and $d(x) < \sigma$ or $2\sigma < d(x)$. In the case $\sigma< d(x) < 2\sigma$ we derive from (19), (20) and $(H^{\prime }_{a})$ that

$$\begin{aligned} \begin{aligned}&\frac{ \alpha a(x)}{{{\underline{u}}}^{\gamma }} + \lambda f(x,{\underline{u}}) \ge a(x) \left( \frac{\alpha }{\delta ^{\gamma }} - \lambda c\right) \ge (K d(x))^{\tau } \left( \frac{\alpha }{\delta ^{\gamma }} - \lambda c\right) \ge (K\sigma )^{\tau } \left( \frac{\alpha }{\delta ^{\gamma }} - \lambda c\right) \\&\quad \ge \left( \frac{K \ln 2}{{k_0}^{\xi }}\right) ^{\tau } \left( \frac{\alpha }{\delta ^{\gamma }} - \lambda ^{\prime }_{0} c\right) \ge C_6 {k_0}^{(1-\iota )(p_1 -1) + \xi } \\&\quad \ge -\displaystyle \sum _{i=1}^{N} \frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial {\underline{u}}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial {\underline{u}}}{\partial x_{i}}\Big ), \end{aligned} \end{aligned}$$

for all $\lambda \in (0,\lambda ^{\prime }_{0}).$ Let $\overline{u}\in W^{1,\overrightarrow{p}}_{0}(\Omega )$ be the only solution of the problem

$$\begin{aligned} \left\{ \begin{array}{rcl} -\displaystyle \sum ^{N}_{i=1}\frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial \overline{u}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial \overline{u}}{\partial x_{i}}\Big )\ &{}=&{}\displaystyle \frac{\alpha a(x)}{{\underline{u}}^{\gamma }}+ C_6 {k_0}^{(1-\iota )(p_1- 1) + \xi } \text{ in } \Omega \text{, }\\ \overline{u} &{} = &{} 0\;\;\text{ on }\;\;\partial \Omega . \end{array} \right. \end{aligned}$$

Note that $0 \le {\underline{u}}(x) \le \overline{u}(x)$ a.e. in $\Omega .$ If necessary by considering a smaller $\lambda ^{\prime }_{0}$ it is possible to argue as in (18) to obtain that

$$\begin{aligned} -\displaystyle \sum ^{N}_{i=1}\frac{\partial }{\partial x_{i}}\Big ( \Big \vert \frac{\partial \overline{u}}{\partial x_{i}}\Big \vert ^{p_i-2}\frac{\partial \overline{u}}{\partial x_{i}}\Big )\ - \frac{\alpha a(x)}{\overline{u}^{\gamma }} \ge 0, \end{aligned}$$

for all $\lambda \in (0,\lambda ^{\prime }_{0}),$ where $\lambda ^{\prime }_{0}$ depends only on $\alpha >0$ and $k_0$. $\square$

Proof of Theorem 1

As pointed in Lemma 4 we have the existence of a sub-supersolution in each case stated in the theorem. We will prove the existence of a solution $u \in W^{1,\overrightarrow{p}}_{0}(\Omega )\cap L^{\infty }(\Omega )$ satsifying $0 < {\underline{u}}(x)\le u(x)\le \overline{u}(x) \ \text {a.e. in } \ \Omega .$

Define the function

$$\begin{aligned} g(x,t)=\left\{ \begin{array}{ll} \displaystyle \frac{\alpha a(x)}{{\overline{u}}^{\gamma }} + \lambda f(x,\overline{u}(x)), &{} t> \overline{u}(x), \\ \displaystyle \frac{\alpha a(x)}{{t}^{\gamma }} + \lambda f(x,t), &{} {\underline{u}}(x)\le t\le \overline{u}(x), \\ \displaystyle \frac{\alpha a(x)}{{{\underline{u}}}^{\gamma }} + \lambda f(x,{\underline{u}}(x)), &{} t < {\underline{u}}(x), \end{array} \right. \end{aligned}$$

(21)

for $(x,t) \in {\overline{\Omega }} \times {\mathbb {R}}$ and the functional

$$\begin{aligned} J_{\alpha ,\lambda }(u){:}{=} \int _{\Omega } \sum _{i=1}^{N}\frac{1}{p_i}\left| \frac{\partial u}{\partial x_i}\right| ^{p_i} dx - \int _{\Omega } G(x,u) dx , u \in W^{1,\overrightarrow{p}}_{0}(\Omega ), \end{aligned}$$

(22)

where $G(x,t){:}{=} \displaystyle \int _{0}^{t}g(x,s) ds.$ Let us consider the space $W^{1,\overrightarrow{p}}_{0}(\Omega )$ equipped with the norm given in (2). Using the continuity of f and that ${\underline{u}},\overline{u},a {\overline{u}}^{-\gamma },a {{\underline{u}}}^{-\gamma } \in L^{\infty }(\Omega )$ it follows that exists $K>0$ such that $|g(x,t)| \le C_7,$ for all $(x,t) \in {\overline{\Omega }} \times {\mathbb {R}}.$ Thus, we obtain that $J_{\alpha ,\lambda } \in C^{1}(W^{1,\overrightarrow{p}}_{0}(\Omega ), {\mathbb {R}})$ with

$$\begin{aligned} J^{\prime }_{\alpha ,\lambda }(u)v = \int _{\Omega } \sum _{i=1}^{N}\left| \frac{\partial u}{\partial x_i} \right| ^{p_i -2} \frac{\partial u}{\partial x_i} \frac{\partial v}{\partial x_i} dx - \int _{\Omega }g(x,u)v dx, u,v \in W^{1,\overrightarrow{p}}_{0}(\Omega ). \end{aligned}$$

Note that $J_{\alpha ,\lambda }$ is coercive. In fact, by using the continuous embedding $W^{1,\overrightarrow{p}}_0 (\Omega ) \hookrightarrow L^{1}(\Omega ),$ the boundedness of g and the inequalities $|t|^{p_i}\ge 1 +|t|^{p_1}, t \in {\mathbb {R}}, (a_1+\cdots +a_N)^{b} \le C_8 (a^{b}_{1}+\cdots +a^{b}_{N}), a_i\ge 0,i=1,...,N,b\ge 1,$ where C depends only on N and b, we obtain that

$$\begin{aligned} \begin{aligned} J_{\alpha ,\lambda }(u)&\ge \frac{1}{p_N} \sum _{i=1}^{N}\left\| \frac{\partial u}{\partial x_i}\right\| ^{p_i}_{L^{p_i}} dx - C_9\int _{\Omega }|u| dx \ge \frac{1}{p_N} \sum _{i=1}^{N}\left\| \frac{\partial u}{\partial x_i}\right\| ^{p_1}_{L^{p_i}} - C_{10} (\Vert u \Vert +1)\\&\ge \frac{1}{p_N} \left( \sum _{i=1}^{N}\left\| \frac{\partial u}{\partial x_i}\right\| _{L^{p_i}}\right) ^{p_1} - C_{10} (\Vert u \Vert +1), \end{aligned} \end{aligned}$$

which proves the coerciveness of $J_{\alpha ,\lambda }.$ Since $g \in L^{\infty }(\Omega ),$ we have that $J_{\alpha ,\lambda }$ is weak lower semicontinuous. The set

$$\begin{aligned} {\mathcal {C}}{=}{:}\bigl \{v\in W^{1,\overrightarrow{p}}_0(\Omega ): {\underline{u}}(x)\le v(x)\le \overline{u}(x) \ \text{ a.e } \text{ in } \ \Omega \bigl \} \end{aligned}$$

is closed and convex in $W^{1,\overrightarrow{p}}_0(\Omega ),$ thus the reflexivity of $W^{1,\overrightarrow{p}}_0(\Omega )$ and [32, Theorem 1.2] imply that the restriction $J_{\alpha ,\lambda }\bigl |_{{\mathcal {C}}}$ attains its infimum at a point u in ${\mathcal {C}}$. Arguing as in [32, Theorem 2.4], we see that u is a weak solution of the problem

$$\begin{aligned} \left\{ \begin{array}{rcl} -\displaystyle \sum _{i=1}^{N} \displaystyle \frac{\partial }{\partial x_i}\left( \left| \displaystyle \frac{\partial w}{\partial x_i}\right| ^{p_i -2} \displaystyle \frac{\partial w}{\partial x_i}\right) &{} = &{} g(x,w)\;\;\text{ in }\;\;\Omega , \\ w &{} = &{} 0\;\;\text{ on }\;\;\partial \Omega . \end{array} \right. \end{aligned}$$

(23)

Since $u\in {\mathcal {C}}$ it follows from the definition of g given in (21) that u solves $(P_{\gamma })$. $\square$

Let ${\underline{u}} \in W^{1,\overrightarrow{p}}_{0}(\Omega )$ be as in Lemma 4 and consider ${\widetilde{g}}$ the continuous function defined on ${\overline{\Omega }} \times {\mathbb {R}}$ by

$$\begin{aligned} {\widetilde{g}}(x,t)=\left\{ \begin{array}{ll} \displaystyle \frac{\alpha a(x)}{t^{\gamma }} + \lambda f(x,t), &{} t\ge {\underline{u}}(x), \\ \displaystyle \frac{\alpha a(x)}{{{\underline{u}}(x)}^{\gamma } }+ \lambda f(x,{\underline{u}}(x)) &{} t < {\underline{u}}(x). \end{array} \right. \end{aligned}$$

(24)

Consider the auxiliary problem

$$\begin{aligned} \left\{ \begin{array}{rcl} -\displaystyle \sum _{i=1}^{N} \frac{\partial }{\partial x_i} \left( \left| \frac{\partial u}{\partial x_i}\right| ^{p_i -2} \frac{\partial u}{\partial x_i}\right) &{} = &{} {\widetilde{g}}(x,u)\;\;\text{ in }\;\;\Omega , \\ u &{} = &{} 0\;\;\text{ on }\;\;\partial \Omega , \end{array} \right. \end{aligned}$$

(25)

and the functional associated to (25), whose formula is

$$\begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }(u){:}{=} \int _{\Omega }\sum _{i=1}^{N} \frac{1}{p_i}\left| \frac{\partial u}{\partial x_i}\right| ^{p_i} - \int _{\Omega } {\widetilde{G}}(x,u) , u \in W^{1,\overrightarrow{p}}_{0}(\Omega ), \end{aligned}$$

(26)

where ${\widetilde{G}}(x,t){:}{=} \displaystyle \int _{0}^{t}{\tilde{g}}(x,s) ds.$ We have that ${\widetilde{J}}_{\alpha ,\lambda }\in C^{1}(W^{1,\overrightarrow{p}}_{0}(\Omega ),{\mathbb {R}})$ with

$$\begin{aligned} {{\widetilde{J}}}^{\prime }_{\alpha ,\lambda }(u)\varphi = \int _{\Omega }\sum _{i=1}^{N} \left| \frac{\partial u}{\partial x_i}\right| ^{p_i -2} \frac{\partial u}{\partial x_i} \frac{\partial \varphi }{\partial x_i} - \int _{\Omega } {\widetilde{g}}(x,u) \varphi , u,\varphi \in W^{1,\Phi }_{0}(\Omega ). \end{aligned}$$

Now we will focus our attention in the proof of (i) of Theorem 2. The next Lemma is needed.

Lemma 5

Suppose that $(H_a)$ and $(H_f)$ hold and consider the notation of Lemma 4 and Theorem 2. Given $\alpha \ge \alpha _0$ there exists $0<\widetilde{\lambda _{0}}\le \lambda _0,$ depending only on $\alpha >0$, such that the following properties are satisfied:

(i) There are constants R and ${\widetilde{\eta }}$ with $R > \Vert {\underline{u}}\Vert ,$ which depends only on $\alpha$ , such that

$$\begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }({\underline{u}}) \le \eta < {\widetilde{\eta }} \le \inf _{u \in \partial B_R(0)} {\widetilde{J}}_{\alpha ,\lambda }(u), \end{aligned}$$

for all $\lambda \in (0,\widetilde{\lambda _{0}}),$ where $\eta$ is a constant that does not depend on $\alpha .$

(ii) There exists $e_{\alpha ,\lambda } \in W^{1,\overrightarrow{p}}_{0}(\Omega ) \setminus \overline{B_R(0)},$ depending only on $\alpha \ge \alpha _0$ and $\lambda \in (0,\widetilde{\lambda _{0}})$, such that ${\widetilde{J}}_{\alpha ,\lambda }(e_{\alpha ,\lambda }) < {\widetilde{\eta }}.$

Proof

(i) Fix $\alpha \ge \alpha _0$ and $\lambda \in (0,\lambda _0).$ Using $(H_f),$ Lemma 4 and the fact that ${\widetilde{G}}(x,{\underline{u}}(x)) \ge \lambda {\underline{u}}(x)f(x,{\underline{u}}(x))$ a.e. in $\Omega$ we obtain that

$$\begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }({\underline{u}})&\le \int _{\Omega } \sum _{i=1}^{N}\frac{1}{p_1} \left| \frac{\partial {\underline{u}}}{\partial x_i}\right| ^{p_i} - \lambda \int _{\Omega } {\underline{u}}(x) f(x,{\underline{u}}(x)) \le \sum _{i=1}^{N}\frac{1}{p_1} \left| \frac{\partial {\underline{u}}}{\partial x_i}\right| ^{p_i} + \lambda c \int _{\Omega } {\underline{u}}(x) \nonumber \\&\le \sum _{i=1}^{N}\frac{1}{p_1} \left| \frac{\partial {\underline{u}}}{\partial x_i}\right| ^{p_i} + \lambda _0 c \int _{\Omega } {\underline{u}}(x){:}{=}\eta . \end{aligned}$$

(27)

From the definition of ${\widetilde{g}}$ we obtain that ${\widetilde{g}}(x,t) \le \alpha \left\| \displaystyle \frac{a}{{\underline{u}}^{\gamma }}\right\| _{L^{\infty }} +\lambda C(|t|^{r-1}+1),$ for all $(x,t) \in {\overline{\Omega }} \times {\mathbb {R}}.$ Then by direct computations combined with the continuous embedding $W^{1,\overrightarrow{p}}_0 (\Omega ) \hookrightarrow L^{q}(\Omega ), q\in [1,{\overline{p}}^{\star }]$ we obtain that

$$\begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }(u)\ge C_{11} \Vert u\Vert ^{p_1} - C_{12}(\Vert u\Vert + \lambda \Vert u\Vert ^{r}), u \in W^{1,\overrightarrow{p}}_{0} (\Omega ), \end{aligned}$$

(28)

where $C_{12}$ is constant that depends only on $\alpha .$ Fix ${\overline{\eta }} > \eta .$ Consider $R > \Vert {\underline{u}} \Vert ,$ depending only on $\alpha$, such that $C_{11} R^{p_1} - C_{12} R > 2 {\overline{\eta }}.$ Let $0<\widetilde{\lambda _{0}}\le \lambda _0$ such that $C_{11} R^{p_1} - C_{12} R - \widetilde{\lambda _{0}}C_{12}R \ge {\overline{\eta }}.$ The choices of $\eta ,{\overline{\eta }},R$ and $\widetilde{\lambda _{0}}$ combined with (27) and (28) imply that the condition (i) is satisfied.

(ii) Recall that $\Vert {\underline{u}}\Vert _{L^{\infty }} \le \delta$ thus by using the previous inequality and $(H_f)$ we obtain for $t\ge 1$ that

$$\begin{aligned} \begin{aligned} {\widetilde{G}}(x,t{\underline{u}}(x))&= \int _{0}^{ {\underline{u}}(x)} {\widetilde{g}}(x,s) ds + \int _{{\underline{u}}(x)}^{ t {\underline{u}}(x)} {\widetilde{g}}(x,s) ds \\&\ge \int _{0}^{{\underline{u}}(x)} \lambda f(x,{\underline{u}}(x)) ds + \int _{{\underline{u}}(x)}^{t {\underline{u}}(x)} \lambda f(x,s) ds \\&\ge -c a(x){\underline{u}}(x) + \lambda (F(x,t{\underline{u}}(x)) -F(x,{\underline{u}}(x))). \end{aligned} \end{aligned}$$

From $(H_{AR})$ we have $F(x,t)\ge C_{13} t^{\theta }-C_{14},$ for all $t \ge 0$ a.e. in $\Omega$ with $C_{13},C_{14}$ positive constants.

Thus we obtain for $t \ge 1$ that

$$\begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }(t {\underline{u}}) \le C_{15} t^{p_N} - C_{16}t^{\theta } - C_{17}, \end{aligned}$$

where $C_{15},C_{16}$ and $C_{17}$ are positive constants. Since $p_N < \theta$ we have the result. $\square$

Lemma 6

The functional ${\widetilde{J}}_{\alpha ,\lambda }$ satisfies the Palais-Smale condition at any level $c \in {\mathbb {R}}.$

Proof

Let $t\in {\mathbb {R}}$ and $x\in \Omega$ with $t <{\underline{u}}(x).$ Since $\theta>p_N >1$ we have

$$\begin{aligned} {\widetilde{g}}(x,t)t-\theta {\widetilde{G}}(x,t)&= (1-\theta )t\left( \frac{\alpha a(x)}{{{\underline{u}}(x)}^{\gamma }} +\lambda f(x,{\underline{u}}(x))\right) \nonumber \\&\ge (1-\theta )|t|(\alpha \Vert a {{\underline{u}}}^{-\gamma }\Vert _{L^{\infty }} + \lambda \displaystyle \sup _{x \in \Omega } |f(x,{\underline{u}}(x))|). \end{aligned}$$

(29)

If $t \ge {\underline{u}}(x)$ we have

$$\begin{aligned}&{\widetilde{g}}(x,t)t-\theta {\widetilde{G}}(x,t) = \left( \frac{\alpha a(x)}{t^{\gamma }} + \lambda f(x,t)\right) t-\theta \int _{0}^{t} {\widetilde{g}}(x,s) ds\nonumber \\&\qquad \left( \frac{\alpha a(x)}{t^{\gamma }} + \lambda f(x,t)\right) t - \theta \left( \int _{0}^{{\underline{u}}(x)} {\widetilde{g}}(x,s) ds + \int _{{\underline{u}}(x)}^{t}{\widetilde{g}}(x,s) ds\right) \nonumber \\&\quad =\left( \frac{\alpha a(x)}{t^{\gamma }}+\lambda f(x,t)\right) t-\theta {\underline{u}}(x)\left( \frac{\alpha a(x)}{{{\underline{u}}(x)}^{\gamma }} + \lambda f(x,{\underline{u}}(x))\right) \nonumber \\&\qquad -\theta \left( \int _{{\underline{u}}(x)}^{t}\frac{\alpha a(x)}{s^{\gamma }} +\lambda f(x,s) ds\right) . \end{aligned}$$

(30)

Case $\gamma \ne 1$:

In this case we have from (30) that

$$\begin{aligned} \begin{aligned}&{\widetilde{g}}(x,t)t-\theta {\widetilde{G}}(x,t) \ge \alpha a(x)t^{1-\gamma } +\lambda f(x,t)t \\&\qquad -\theta (\alpha \Vert a {{\underline{u}}}^{1-\gamma }\Vert _{L^{\infty }} +\lambda \Vert f(\cdot , {\underline{u}}(\cdot )) {\underline{u}}\Vert _{L^{\infty }} + \lambda \Vert F(\cdot , {\underline{u}}(\cdot ))\Vert _{L^{\infty }})\\&\qquad -\theta \left( \frac{\alpha a(x)}{1-\gamma } t^{1-\gamma } - \frac{\alpha a(x) {{\underline{u}}(x)}^{1-\gamma }}{1-\gamma } + \lambda F(x,t) \right) \\&\quad \ge \alpha a(x)\left( 1 - \frac{\theta }{1-\gamma } \right) t^{1-\gamma } + \lambda (f(x,t)t - \theta F(x,t)) - \frac{\alpha a(x) {{\underline{u}}(x)}^{1-\gamma }}{1-\gamma } \\&\qquad -C_{18}, \end{aligned} \end{aligned}$$

(31)

where $C_{18}$ is a positive constant.

If $\gamma >1$ we have that $\frac{1}{1-\gamma } <0.$ Since a and ${\underline{u}}$ are nonnegative functions we obtain from (31) and $(H_{AR})$ that

$$\begin{aligned} \begin{aligned} {\widetilde{g}}(x,t)t-\theta {\widetilde{G}}(x,t) \ge - C_{19}, \end{aligned} \end{aligned}$$

(32)

for some positive constant $C_{19}.$

Consider the case $0<\gamma <1 .$ Since $\theta> p_N > 1$ we obtain that $1- \frac{\theta }{1-\gamma } <0 .$ Thus by using the inequality $|t| + 1 \ge |t|^{1-\gamma }, t \in {\mathbb {R}},$ (31) and $(H_{AR})$ it follows that

$$\begin{aligned} {\widetilde{g}}(x,t)t-\theta {\widetilde{G}}(x,t) \ge - C_{20}t- C_{21}, \end{aligned}$$

(33)

for positive constants $C_{20}$ and $C_{21}.$

Case $\gamma = 1$:

From (30) we have

$$\begin{aligned} \begin{aligned} {\widetilde{g}}(x,t)t-\theta {\widetilde{G}}(x,t)&=\alpha a(x) + \lambda f(x,t)t - \theta \alpha a(x) \ln \left( \frac{t}{{\underline{u}}(x)}\right) -\theta \lambda F(x,t)\\&\quad - \theta (\alpha a(x) - \lambda F(x,{\underline{u}}(x)) + {\underline{u}}f(x,{\underline{u}}(x)). \end{aligned} \end{aligned}$$

(34)

By using (34), the inequalities $\ln t < t , t >0,$ the fact that $a {{\underline{u}}}^{-\gamma }\in L^{\infty } (\Omega )$ and $(H_{AR})$ it follows that

$$\begin{aligned} \begin{aligned} {\widetilde{g}}(x,t)t-\theta {\widetilde{G}}(x,t)&\ge \lambda (f(x,t)t - \theta F(x,t)) - \theta \alpha \frac{a(x)}{{{\underline{u}}(x)}}t - C_{22}\\&\ge - C_{23}t - C_{24}, \end{aligned} \end{aligned}$$

(35)

for all $t \ge t_0 ,$ where $C_{23}$ and $C_{24}$ are positive constants.

Thus by using (29), (32), (33) and (35) it follows that

$$\begin{aligned} {\widetilde{g}}(x,t)t-\theta {\widetilde{G}}(x,t) \ge -C_{25} |t| - C_{26}, t \in {\mathbb {R}},\ \text {a.e. in } \ \Omega , \end{aligned}$$

(36)

where $C_{25}$ and $C_{26}$ are positive constants.

Let $(u_n) \subset W^{1,\overrightarrow{p}}_{0}(\Omega )$ be a sequence with ${\widetilde{J}}_{\alpha ,\lambda }(u_n) \rightarrow c$ and ${{\widetilde{J}}}^{\prime }_{\alpha ,\lambda }(u_n) \rightarrow 0.$ There exists a constant $C_{27}>0$ such that

$$\begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }(u_n) - \frac{1}{\theta }{{\widetilde{J}}}^{\prime }_{\alpha ,\lambda }(u_n) u_n \le C_{27} (1+ \Vert u_n\Vert ), \end{aligned}$$

(37)

for all $n \in {\mathbb {N}}.$ On other hand we have

$$\begin{aligned} \begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }(u_n) - \frac{1}{\theta }{{\widetilde{J}}}^{\prime }_{\alpha ,\lambda }(u_n) u_n&\ge \left( \frac{1}{p_N} - \frac{1}{\theta } \right) \int _{\Omega } \sum _{i=1}^{N} \left| \frac{\partial u_n}{\partial x_i} \right| ^{p_i} + \int _{\Omega }\frac{1}{\theta } {\widetilde{g}}(x,u_n)u_n - {\widetilde{G}}(x,u_n)\\&\ge C_{27} \Vert u\Vert ^{p_1} + \int _{\Omega }\frac{1}{\theta } {\tilde{g}}(x,u_n)u_n - {\tilde{G}}(x,u_n). \end{aligned} \end{aligned}$$

(38)

Using (36), (37), (38) and the continuous embedding $W^{1,\overrightarrow{p}}_0 (\Omega ) \hookrightarrow L^{q}(\Omega ), q\in [1,{\overline{p}}^{\star }]$ we get $\Vert u_n\Vert ^{p_1} \le C_{28}(1+ \Vert u_n\Vert )$ which implies that $(u_n)$ is bounded in $W^{1,\overrightarrow{p}}_0 (\Omega )$. Since the embedding $W^{1,\overrightarrow{p}}_0 (\Omega ) \hookrightarrow L^{q}(\Omega ), q\in [1,{\overline{p}}^{\star })$ is compact we have, up to a subsequence, that

$$\begin{aligned} \left\{ \begin{array}{rcl} &{}u_n&{} \rightharpoonup u \ \text {in} \ W^{1,\overrightarrow{p}}_{0}(\Omega ), \\ &{}u_n&{} \rightarrow u \ \text {in} \ L^{q}(\Omega ), 1 \le q < {\overline{p}}^{\star } ,\\ &{}u_n(x)&{} \rightarrow u(x) \ \text {a.e. in} \ \Omega , \end{array} \right. \end{aligned}$$

(39)

for some $u \in W^{1,\overrightarrow{p}}_{0}(\Omega ).$ We have

$$\begin{aligned} \begin{aligned}&\int _{\Omega } \sum _{i=1}^{N}\left( \biggl |\frac{\partial u_n }{\partial x_{i}}\biggl |^{p_{i}-2}\frac{\partial u_n }{\partial x_{i}}-\biggl |\frac{\partial u }{\partial x_{i}}\biggl |^{p_{i}-2} \frac{\partial u }{\partial x_{i}}\right) \left( \frac{\partial u_n }{\partial x_{i}}-\frac{\partial u }{\partial x_{i}}\right) = {{\widetilde{J}}}^{\prime }_{\alpha ,\lambda }(u_n)(u_n - u) \\&+ \int _{\Omega }{\widetilde{g}}(x,u_n)(u_n -u) dx - \int _{\Omega } \sum _{i=1}^{N} \left| \frac{\partial u}{\partial x_i}\right| ^{p_i -2}\frac{\partial u}{\partial x_i} \frac{\partial (u_n - u)}{\partial x_i} . \end{aligned} \end{aligned}$$

(40)

Since ${{\widetilde{J}}}^{\prime }_{\alpha ,\lambda } (u_n) \rightarrow 0$ and $(u_n)$ is bounded in $W^{1,\overrightarrow{p}}_0(\Omega )$ we obtain that

$$\begin{aligned} {{\widetilde{J}}}^{\prime }_{\alpha ,\lambda } (u_n)(u_n -u) \rightarrow 0. \end{aligned}$$

(41)

From the weak convergence of (39) we get

$$\begin{aligned} \int _{\Omega }\sum _{i=1}^{N} \left| \frac{\partial u}{\partial x_i}\right| ^{p_i -2}\frac{\partial u}{\partial x_i} \frac{\partial (u_n - u)}{\partial x_i} \rightarrow 0. \end{aligned}$$

(42)

Using $(H^{\prime }_{f})$, (39) and the Lebesgue Dominated Convergence Theorem we get

$$\begin{aligned} \int _{\Omega }{\widetilde{g}}(x,u_n)(u_n -u) \rightarrow 0. \end{aligned}$$

(43)

From (40), (41), (42) and (43) we have

$$\begin{aligned} \int _{\Omega } \sum _{i=1}^{N}\left( \biggl |\frac{\partial u_n }{\partial x_{i}}\biggl |^{p_{i}-2}\frac{\partial u_n }{\partial x_{i}}-\biggl |\frac{\partial u }{\partial x_{i}}\biggl |^{p_{i}-2} \frac{\partial u }{\partial x_{i}}\right) \left( \frac{\partial u_n }{\partial x_{i}}-\frac{\partial u }{\partial x_{i}}\right) \rightarrow 0, \end{aligned}$$

which implies that $u_n \rightarrow u$ in $W^{1,\overrightarrow{p}}_0(\Omega ).$ $\square$

Proof of Theorem 2

It will be proved (i). Consider the notation provided in Lemma 5. Using (21) and (24) we get $g(x,t)={\widetilde{g}}(x,t)$ for $t\in [0,\overline{u}(x)],$ thus it follows that $J_{\alpha ,\lambda }(u)={\widetilde{J}}_{\alpha ,\lambda }(u)$ for $u\in [0,\overline{u}],$ where $[0,\overline{u}]{:}{=}\{v\in W^{1,\overrightarrow{p}}_{0}(\Omega ):0\le u(x)\le \overline{u}(x) \ \text {a.e. in}\ \Omega \}$ with $J_{\alpha ,\lambda }(u),{\widetilde{J}}_{\alpha ,\lambda }(u)$ given in (22) and (26), respectively. Consider u the solution of (23) provided by Theorem 1. Then,

$$\begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }(u)=\inf _{{\mathcal {C}}}{\widetilde{J}}_{\alpha ,\lambda }(v), \end{aligned}$$

where ${\mathcal {C}}=[{\underline{u}},\overline{u}]$ is given in the proof of Theorem 1.

Using Lemma 5, we conclude, with the Mountain Pass Theorem [4], that ${\tilde{c}}=\displaystyle \inf _{w \in \Gamma }\max _{t \in [0,1]} {\widetilde{J}}_{\alpha ,\lambda }(w(t))$ is a critical value of ${\widetilde{J}}_{\alpha ,\lambda },$ where

$$\begin{aligned} \Gamma =\{w \in C\bigl ([0,1], W^{1,\overrightarrow{p}}_{0}(\Omega )\bigl ): w(0)={\underline{u}},\ w(1)=e_{\lambda }\}. \end{aligned}$$

Therefore, the problem $(P_{\gamma })$ has two weak solutions $u,v\in W_{0}^{1,\overrightarrow{p}}(\Omega ),$ such that

$$\begin{aligned} {\widetilde{J}}_{\alpha ,\lambda }(u)\le {\widetilde{J}}_{\alpha ,\lambda }({\underline{u}})\le \eta <\ {\widetilde{\eta }}\le {\widetilde{J}}_{\alpha ,\lambda }(v)= {\tilde{c}}. \end{aligned}$$

The other part can be obtained by proving a suitable version of Lemma 5 by adapting its reasoning and the proof of (i).