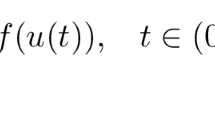Existence and multiplicity of positive solutions for one-dimensional prescribed mean curvature equations

Abstract

In this work, we establish the existence and multiplicity results of positive solutions for one-dimensional prescribed mean curvature equations. Our approach is based on fixed point index theory for completely continuous operators which leave invariant a suitable cone in a Banach space of continuous functions.

MSC:34B10, 34B18.

1 Introduction

The prescribed mean curvature problems like

$$\{\begin{array}{l}-div(\frac{Du}{\sqrt{1+\kappa {(Du)}^2}})=f(x,u),x\in \mathrm{\Omega },\\ u=0,x\in \partial \mathrm{\Omega }\end{array}$$

have attracted much attention in recent years, see [1–4] and the references therein. Since the problem is quasilinear non-uniformly elliptic, it is more difficult to study the existence of classical solutions. The greatest obstacle is the lack of gradient estimate, such kind of estimate does not hold in general and boundary gradient blow-up may occur. This leads to some new phenomena very different from those in semilinear problems. Many well-known results of semilinear problems have to be reconsidered for this quasilinear problem. Motivated by the search for solutions of the above problem, many authors (see [5–13]) studied the existence of (positive) solutions for one-dimensional prescribed mean curvature equations with Dirichlet boundary conditions

$$\{\begin{array}{l}-{(\frac{u^{\prime }}{\sqrt{1+\kappa {(u^{\prime })}^2}})}^{\prime }=\lambda f(u),x\in (0,1),\\ u(0)=u(1)=0,\end{array}$$

(1.1)

where $\kappa >0$ is a constant, $f\in C([0,\mathrm{\infty }),[0,\mathrm{\infty }))$ and $f(u)>0$ for $u>0$ and $x\in [0,1]$.

Note that if $\kappa =0$, problem (1.1) is degenerate to the second-order ordinary differential equation boundary value problems

$$\{\begin{array}{l}-u^{″}=\lambda f(u),x\in (0,1),\\ u(0)=u(1)=0.\end{array}$$

(1.2)

The existence of (positive) solutions of (1.1) has been well known with various qualitative assumptions of the nonlinearity f, see [14, 15] and the references therein.

If $\kappa =1$, Bonheure et al. [6], Habets and Omari [9], Kusahara and Usami [10], Pan and Xing [12, 13] studied the existence of (positive) solutions of (1.2) by using the variational method, lower and upper solutions method and time mapping method, respectively.

However, to the best of our knowledge, the existence and multiplicity of positive solutions for (1.1) are relatively few by the fixed point index theory. In this paper, based on the fixed point index theory, we shall investigate the existence and multiplicity of positive solution of (1.1) when f is ϕ-superlinear and ϕ-sublinear at 0 and ∞, respectively, here $\varphi (s)=\frac{s}{\sqrt{1+\kappa s^2}}$.

Let $\varphi (s)=\frac{s}{\sqrt{1+\kappa s^2}}$. Then (1.1) can be rewritten as

$$\{\begin{array}{l}-{(\varphi (u^{\prime }))}^{\prime }=\lambda f(u(x)),x\in (0,1),\\ u(0)=u(1)=0.\end{array}$$

(1.3)

Obviously, $\varphi :\mathbb{R}\to (-\frac{1}{\sqrt{\kappa }},\frac{1}{\sqrt{\kappa }})$ is an odd, increasing homeomorphism with $\varphi (0)=0$.

For convenience, we introduce some notations

$$f_0=\underset{u\to 0}{lim}\frac{f(u)}{\varphi (u)}\text{and}{f}_{\mathrm{\infty }}=\underset{u\to \mathrm{\infty }}{lim}\frac{f(u)}{\varphi (u)}.$$

We will also need the function $f^{\ast }(u)={max}_{0\le t\le u}\{f(t)\}$, and let $f_0^{\ast }={lim}_{u\to 0}\frac{f^{\ast }(u)}{\varphi (u)}$. By a similar method in [[14], Lemma 2.8], it is not difficult to verify that $f_0^{\ast }=f_0$.

In the rest of this paper, we shall study the existence of positive solutions of (1.3) by using the fixed point index theory to give a brief and clear proof for the existence of positive solutions of (1.1). More concretely, we shall prove the following.

Theorem 1.1 Assume that $f\in C([0,\mathrm{\infty }),[0,\mathrm{\infty }))$ and $f(u)>0$ for $u>0$.

• (i) If $f_0=0$, then there exists $0<{\lambda }_{\ast }<{\lambda }^{\ast }$ such that (1.1) has a positive solution for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$.

• (ii) If $f_0=\mathrm{\infty }$, then there exists ${\lambda }_0>0$ such that (1.1) has a positive solution for $0<\lambda <{\lambda }_0$.

• (iii) If $f_0=f_{\mathrm{\infty }}=0$, then there exists $0<{\lambda }_{\ast }<{\lambda }^{\ast }$ such that (1.1) has at least two positive solutions for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$.

• (iv) If $f_0=f_{\mathrm{\infty }}=\mathrm{\infty }$, then there exists $0<{\lambda }_{\ast }<{\lambda }^{\ast }$ such that (1.1) has at least two positive solutions for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$.

Corollary 1.2 Assume that $f\in C([0,\mathrm{\infty }),[0,\mathrm{\infty }))$ and $f(u)>0$ for $u>0$.

• (a) If $f_0=0$ and $f_{\mathrm{\infty }}=\mathrm{\infty }$, then there exists $0<{\lambda }_{\ast }<{\lambda }^{\ast }$ such that (1.1) has a positive solution for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$.

• (b) If $f_0=\mathrm{\infty }$ and $f_{\mathrm{\infty }}=0$, then there exists ${\lambda }_0>0$ such that (1.1) has a positive solution for $0<\lambda <{\lambda }_0$.

Remark 1.1 The results of Theorem 1.1 and Corollary 1.2 are different with the case $\kappa =0$ which is the classical Dirichlet boundary value problem (1.2). This phenomenon is a striking feature of problem (1.1), which is just the reason why we study the existence of positive solutions of problem (1.1). It is pointed out that in equation of (1.1), having replaced $f(u)$ with $f(x,u)$, Theorem 1.1 and Corollary 1.2 also hold as well as all of the proofs with obvious changes.

2 Preliminaries

Throughout the paper $|\cdot |$ will denote absolute value, and let

$$E=\{u\in C[0,1]\mid u(0)=u(1)=0\}.$$

Then E is a Banach space endowed with the norm ${\parallel u\parallel }_{\mathrm{\infty }}={max}_{x\in [0,1]}|u(x)|$.

We first establish some preliminary results to prove our main result. An easy but useful property of ϕ and ${\varphi }^{-1}$ is the following one.

Lemma 2.1 Let $\varphi (s)=\frac{s}{\sqrt{1+\kappa s^2}}$. Then $\varphi :\mathbb{R}\to (-\frac{1}{\sqrt{\kappa }},\frac{1}{\sqrt{\kappa }})$ is an odd, increasing homeomorphism with $\varphi (0)=0$. Moreover, ϕ has the following properties:

• (i) ϕ is convex up on $[0,\mathrm{\infty })$ and ${\varphi }^{-1}$ is concave up on $(0,\frac{1}{\sqrt{\kappa }})$.

• (ii) For each $c\ge 1$, there exists ${\hat{A}}_c\ge c$ such that $\varphi (cs)\le {\hat{A}}_c\varphi (s)$, $\mathrm{\forall }s\ge 0$ with ${lim}_{c\to \mathrm{\infty }}{\hat{A}}_c=\mathrm{\infty }$ and for each $0<c\le 1$, there exists $0<{\hat{B}}_c\le c$ such that $\varphi (cs)\ge {\hat{B}}_c\varphi (s)$, $\mathrm{\forall }s\ge 0$ with ${lim}_{c\to 0}{\hat{B}}_c=0$.

• (iii) For each $0<c\le 1$, there exists $B_c\ge c$ such that ${\varphi }^{-1}(cs)\le B_c{\varphi }^{-1}(s)$, $\mathrm{\forall }s\in (0,\frac{1}{\sqrt{\kappa }})$. For each $c\ge 1$ with $-\frac{1}{\sqrt{\kappa }}<cs<\frac{1}{\sqrt{\kappa }}$, there exists $A_c\le c$ such that ${\varphi }^{-1}(cs)\ge A_c{\varphi }^{-1}(s)$, $\mathrm{\forall }s\in (0,\frac{1}{\sqrt{\kappa }})$.

Proof By a simple computation, it follows that $\varphi (-s)=-\varphi (s)$ and ${\varphi }^{\prime }(s)=\frac{1}{\sqrt{{(1+\kappa s^2)}^3}}>0$. So ϕ is an odd, increasing homeomorphism with $\varphi (0)=0$. Moreover, from ${\varphi }^{″}(s)=\frac{-3\kappa s}{\sqrt{{(1+\kappa s^2)}^5}}$, we get that ϕ is convex up on $[0,\mathrm{\infty })$. Notice that ${\varphi }^{-1}(s)=\frac{s}{\sqrt{1-\kappa s^2}}$ is also an odd, increasing homeomorphism with $\varphi (0)=0$. It is easy to verify that ${\varphi }^{-1}$ is concave up on $(0,\frac{1}{\sqrt{\kappa }})$.

• (ii) For each $0<c\le 1$, there exists ${\hat{B}}_c\le c$ such that

  $$\varphi (cs)=\frac{cs}{\sqrt{1+\kappa c^2{s}^2}}\ge {\hat{B}}_c\frac{s}{\sqrt{1+\kappa s^2}},\mathrm{\forall }s\ge 0;$$

and for each $c\ge 1$, there exists ${\hat{A}}_c\ge c$ such that

$$\varphi (cs)=\frac{cs}{\sqrt{1+\kappa c^2{s}^2}}\le {\hat{A}}_c\frac{s}{\sqrt{1+\kappa s^2}},\mathrm{\forall }s\ge 0.$$

• (iii) By a similar argument, it is not difficult to compute that for each $0<c\le 1$, there exists $B_c\ge c$ such that ${\varphi }^{-1}(cs)\le B_c{\varphi }^{-1}(s)$, $\mathrm{\forall }s\in (0,\frac{1}{\sqrt{\kappa }})$. For each $c\ge 1$ with $-\frac{1}{\sqrt{\kappa }}<cs<\frac{1}{\sqrt{\kappa }}$, there exists $A_c\le c$ such that ${\varphi }^{-1}(cs)\ge A_c{\varphi }^{-1}(s)$, $\mathrm{\forall }s\in (0,\frac{1}{\sqrt{\kappa }})$. □

Lemma 2.2 Let $h\in C([0,1],[0,\mathrm{\infty }))$ with $h\not\equiv 0$. Assume that w is the solution of

$$\{\begin{array}{l}-{(\varphi (u^{\prime }))}^{\prime }=h(x),x\in (0,1),\\ u(0)=u(1)=0.\end{array}$$

(2.1)

Then $w>0$ on $(0,1)$ and ${\parallel w^{\prime }\parallel }_{\mathrm{\infty }}\le {\varphi }^{-1}(M)$, where $M=min\{\frac{1}{\sqrt{\kappa }},{sup}_{x\in [0,1]}|h(x)|\}$.

Proof By integrating, it follows that (2.1) has the unique solution given by

$$w(x)={\int }_0^x{\varphi }^{-1}(C-{\int }_0^{s}h(t)dt)ds,$$

where C is such that $w(1)=0$. Hence we must have $0<C<{\int }_0^{1}h(t)dt$. Further, since $\varphi (u^{\prime })\in (-\frac{1}{\sqrt{\kappa }},\frac{1}{\sqrt{\kappa }})$, by using $\varphi (w^{\prime }(x))=C-{\int }_0^{x}h(t)dt$, we obtain $-M\le \varphi (w^{\prime }(x))\le M$, $\mathrm{\forall }x\in [0,1]$ and ${\parallel w^{\prime }\parallel }_{\mathrm{\infty }}\le {\varphi }^{-1}(M)$ follows, here $M=min\{\frac{1}{\sqrt{\kappa }},{sup}_{x\in [0,1]}|h(x)|\}$.

Since $w(0)=w(1)=0$, there exists $x_0\in (0,1)$ such that $w^{\prime }(x_0)=0$ and it follows from $-{(\varphi (w^{\prime }))}^{\prime }\ge 0$ that $\varphi (w^{\prime })$ is decreasing on $(0,1)$. Then $w^{\prime }(x)>0$ for $x<x_0$ and $w^{\prime }(x)<0$ for $x>x_0$. Hence, $w>0$ on $(0,1)$. □

Note that from Lemma 2.2, there exists ${\tau }_i\in (0,\frac{1}{2})$, $i=1,2$, such that ${min}_{x\in [{\tau }_1,1-{\tau }_2]}w(x)\ge \sigma {\parallel w\parallel }_{\mathrm{\infty }}$ with $0<\sigma <1$ depending on ${\tau }_i$. Define the cone P in E by

$$P=\{u\in E|u(x)\ge 0\text{ on }[0,1]\text{ and }\underset{x\in [{\tau }_1,1-{\tau }_2]}{min}u(x)\ge \sigma {\parallel u\parallel }_{\mathrm{\infty }}\},$$

and for $r>0$, let ${\mathrm{\Omega }}_r=\{u\in P\mid {\parallel u\parallel }_{\mathrm{\infty }}<r\}$.

Lemma 2.3 ([[11], Lemma 4.1 and Lemma 4.2])

For each $h\in C[0,1]$, (2.1) has a unique solution given by

$$u(x)={\int }_0^x{\varphi }^{-1}(C-{\int }_0^{s}h(t)dt)ds=:T_h(u)(x),$$

where C is such that $u(1)=0$ with $0<C<{\int }_0^{1}h(t)dt$. Moreover, the operator $T_h:E\to E$ is continuous and sends equicontinuous sets in $C[0,1]$ into a relatively compact set in E.

We next state the fixed point index theorem which will be used to prove our results.

Lemma 2.4 ([[16], Chapter 6])

Let E be a Banach space and P be a cone in E. Assume that Ω is a bounded open subset of E with $0\in \mathrm{\Omega }$, and let $T:P\cap \overline{\mathrm{\Omega }}\to P$ be a completely continuous operator such that $Tu\ne u$, $u\in \partial \mathrm{\Omega }\cap P$.

• (i) If $\parallel Tu\parallel \le \parallel u\parallel$, $u\in \partial \mathrm{\Omega }\cap P$, then $i(A,\mathrm{\Omega }\cap P,P)=1$.

• (ii) If $\parallel Tu\parallel \ge \parallel u\parallel$, $u\in \partial \mathrm{\Omega }\cap P$, then $i(A,\mathrm{\Omega }\cap P,P)=0$.

From Lemma 2.2, problem (1.3) is equivalent to the fixed point problem

$$u(x)={\int }_0^x{\varphi }^{-1}(C_0-\lambda {\int }_0^{s}f(u(t))dt)ds:=T_{\lambda }(u)(x)$$

in the space E, where $C_0$ is such that $u(1)=0$ with $0<C_0<\lambda {\int }_0^{1}f(u(t))dt$, since otherwise,

$$u(1)={\int }_0^1{\varphi }^{-1}(C_0-\lambda {\int }_0^{s}f(u(t))dt)ds\ge {\int }_0^1{\varphi }^{-1}\left(\lambda {\int }_s^{1}f(u(t))dt\right)ds>0,$$

which is a contradiction. This together with Lemma 2.3 implies that $T_{\lambda }:E\to E$ is a completely continuous mapping. Moreover, for any fixed $u\in P$, we have

$$T_{\lambda }(u)(x)={\int }_0^x{\varphi }^{-1}(C_0-\lambda {\int }_0^{s}f(u(t))dt)ds\ge 0,x\in [0,1]$$

(2.2)

and $T_{\lambda }(u)(0)=T_{\lambda }(u)(1)=0$. In addition, from Lemma 2.2, it follows that $T_{\lambda }(u)(x)>0$ on $(0,1)$ and there exist ${\tau }_i\in (0,\frac{1}{2})$, $i=1,2$, such that ${min}_{x\in [{\tau }_1,1-{\tau }_2]}{T}_{\lambda }u\ge \sigma {\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}$. So $T_{\lambda }:P\to P$ is a completely continuous operator.

Lemma 2.5 Let $r>0$ be given. If there exists $\epsilon >0$ small enough with $B_{\lambda \epsilon }<1$ such that $f^{\ast }(r)\le \epsilon \varphi (r)$, then

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\le B_{\lambda \epsilon }{\parallel u\parallel }_{\mathrm{\infty }}\mathit{\text{for }}u\in \partial {\mathrm{\Omega }}_r,$$

where $B_{\lambda \epsilon }$ is defined as in Lemma  2.1(iii).

Proof From the definition of $T_{\lambda }$, for any $u\in \partial {\mathrm{\Omega }}_r$, we have

$$\begin{array}{rl}{\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}& =\underset{x\in [0,1]}{max}\left|{\int }_0^x{\varphi }^{-1}(C_0-\lambda {\int }_0^{s}f(u(t))dt)ds\right|\\ \le {\int }_0^1{\varphi }^{-1}\left(\lambda {\int }_s^{1}f(u(t))dt\right)ds\le {\int }_0^1{\varphi }^{-1}(\lambda {\int }_s^1{f}^{\ast }(r)dt)ds\\ \le {\int }_0^1{\varphi }^{-1}(\lambda \epsilon \varphi (r))ds\le B_{\lambda \epsilon }r.\end{array}$$

 □

Lemma 2.6 Let $\eta >0$ be given. If $u\in P$ and $f(u(x))\ge \eta \varphi (u(x))$ for $x\in [0,1]$, then

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\ge \sigma x_{\ast }{\varphi }^{-1}(\lambda (1-\sigma )x_{\ast }\eta \varphi \left(\sigma {\parallel u\parallel }_{\mathrm{\infty }}\right)),$$

where $x_{\ast }=min\{x_0,1-x_0\}$ and $u(x_0)={max}_{x\in [0,1]}u(x)={\parallel u\parallel }_{\mathrm{\infty }}$.

Proof From problem (1.3), since $u(0)=u(1)=0$, it follows that there exists $x_0\in (0,1)$ such that $u^{\prime }(x_0)=0$. Let ${\parallel u\parallel }_{\mathrm{\infty }}=u(x_0)$. Then u satisfies the following boundary value problem:

$$\{\begin{array}{l}-{(\varphi (u^{\prime }(x)))}^{\prime }=\lambda f(u(x)),x\in (0,x_0),\\ u(0)=0,u(x_0)={\parallel u\parallel }_{\mathrm{\infty }}.\end{array}$$

(2.3)

Let v be the solution of the problem

$$\{\begin{array}{l}-{(\varphi (v^{\prime }(x)))}^{\prime }=0,x\in (0,x_0),\\ v(0)=0,v(x_0)={\parallel u\parallel }_{\mathrm{\infty }}.\end{array}$$

(2.4)

Then we have

$$\{\begin{array}{l}-{(\varphi (u^{\prime }(x))-\varphi (v^{\prime }(x)))}^{\prime }=\lambda f(u(x)),x\in (0,x_0),\\ (u-v)(0)=0,(u-v)(x_0)=0,\end{array}$$

(2.5)

and by a comparison argument, we get that $u>v$ on $(0,x_0)$. In fact, from $(u-v)(0)=0$, $(u-v)(x_0)=0$, there exists $\hat{x}\in (0,x_0)$ such that ${(u-v)}^{\prime }(\hat{x})=0$, i.e., $u^{\prime }(\hat{x})=v^{\prime }(\hat{x})$. Thus, by a simple computation, we have that

$$\varphi (u^{\prime }(x))=\varphi (v^{\prime }(x))+{\int }_x^{\hat{x}}\lambda f(u(t))dt\ge \varphi (v^{\prime }(x))\text{for }x\in (0,\hat{x})$$

and

$$\varphi (v^{\prime }(x))=\varphi (u^{\prime }(x))+{\int }_{\hat{x}}^x\lambda f(u(t))dt\ge \varphi (u^{\prime }(x))\text{for }x\in (\hat{x},x_0).$$

This together with ϕ is an increasing homeomorphism implies that

$$u^{\prime }(x)\ge v^{\prime }(x)\text{for }x\in (0,\hat{x}),$$

(2.6)

$$v^{\prime }(x)\ge u^{\prime }(x)\text{for }x\in (\hat{x},x_0).$$

(2.7)

Integrating from 0 to x for (2.6) and integrating from x to $x_0$ for (2.7), respectively, we have that $u(x)\ge v(x)$ for $x\in [0,x_0]$.

Note that

$$v(x)={\parallel u\parallel }_{\mathrm{\infty }}-{\int }_x^{x_0}{\varphi }^{-1}(C_1)ds,$$

where $C_1$ is such that $v(0)=0$, and hence ${\parallel u\parallel }_{\mathrm{\infty }}={\int }_0^{x_0}{\varphi }^{-1}(C_1)ds$. If $C_1>\varphi (\frac{{\parallel u\parallel }_{\mathrm{\infty }}}{x_0})$, then it follows that

$${\parallel u\parallel }_{\mathrm{\infty }}={\int }_0^{x_0}{\varphi }^{-1}(C_1)ds>{\int }_0^{x_0}{\varphi }^{-1}\left(\varphi \left(\frac{{\parallel u\parallel }_{\mathrm{\infty }}}{x_0}\right)\right)ds\ge {\parallel u\parallel }_{\mathrm{\infty }},$$

which is a contradiction. Thus, $0\le C_1\le \varphi (\frac{{\parallel u\parallel }_{\mathrm{\infty }}}{x_0})$. Moreover, we have

$$\begin{array}{rl}v(x)& ={\parallel u\parallel }_{\mathrm{\infty }}-{\int }_x^{x_0}{\varphi }^{-1}(C_1)ds\ge {\parallel u\parallel }_{\mathrm{\infty }}-(x_0-x){\varphi }^{-1}\left(\varphi \left(\frac{{\parallel u\parallel }_{\mathrm{\infty }}}{x_0}\right)\right)\\ =\frac{x}{x_0}{\parallel u\parallel }_{\mathrm{\infty }},x\in [x_1,x_0],\end{array}$$

where $x_1=\sigma x_0$. Consequently, $u(x)\ge v(x)\ge \sigma {\parallel u\parallel }_{\mathrm{\infty }}$ for $x\in [x_1,x_0]$. Obviously,

$$u(x)={\int }_0^x{\varphi }^{-1}(C_2-\lambda {\int }_0^{s}f(u(t))dt)ds,$$

where $C_2$ satisfies $u^{\prime }(x_0)=0$. It follows from ${\varphi }^{-1}(C_2-\lambda {\int }_0^{x_0}f(u(t))dt)=0$ that $C_2=\lambda {\int }_0^{x_0}f(u(t))dt$. Therefore,

$$u(x)={\int }_0^x{\varphi }^{-1}\left(\lambda {\int }_s^{x_0}f(u(t))dt\right)ds=T_{\lambda }u(x),x\in [0,x_0].$$

(2.8)

If $x_0\ge \frac{1}{2}$, then

$$\begin{array}{rl}{\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}& \ge {\int }_0^{x_1}{\varphi }^{-1}\left(\lambda {\int }_s^{x_0}f(u(t))dt\right)ds\ge {\int }_0^{x_1}{\varphi }^{-1}\left(\lambda {\int }_{x_1}^{x_0}\eta \varphi (u(t))dt\right)ds\\ \ge {\int }_0^{x_1}{\varphi }^{-1}(\lambda (x_0-x_1)\eta \varphi \left(\sigma {\parallel u\parallel }_{\mathrm{\infty }}\right))ds\ge \sigma x_0{\varphi }^{-1}(\lambda (1-\sigma )x_0\eta \varphi \left(\sigma {\parallel u\parallel }_{\mathrm{\infty }}\right)).\end{array}$$

If $x_0\le \frac{1}{2}$, let w be the solution of

$$\begin{array}{r}-{\left(\varphi (w^{\prime }(x))\right)}^{\prime }=0,x\in (x_0,1),\\ w(x_0)={\parallel u\parallel }_{\mathrm{\infty }},w(1)=0.\end{array}$$

(2.9)

Then

$$w(x)={\parallel u\parallel }_{\mathrm{\infty }}+{\int }_{x_0}^x{\varphi }^{-1}(C_3)ds,$$

where $C_3<0$ satisfies $w(1)=0$, i.e., ${\parallel u\parallel }_{\mathrm{\infty }}=-{\int }_{x_0}^1{\varphi }^{-1}(C_3)ds$. If $C_3<-\varphi (\frac{{\parallel u\parallel }_{\mathrm{\infty }}}{1-x_0})$, then

$${\parallel u\parallel }_{\mathrm{\infty }}=-{\int }_{x_0}^1{\varphi }^{-1}(C_3)ds>-{\int }_{x_0}^1{\varphi }^{-1}(-\varphi \left(\frac{{\parallel u\parallel }_{\mathrm{\infty }}}{1-x_0}\right))ds\ge {\parallel u\parallel }_{\mathrm{\infty }},$$

which is contradiction. Hence $-\varphi (\frac{{\parallel u\parallel }_{\mathrm{\infty }}}{1-x_0})\le C_3\le 0$.

By a similar argument as before, it follows that $u\ge w$ on $(x_0,1)$. Moreover,

$$\begin{array}{rl}w(x)& ={\parallel u\parallel }_{\mathrm{\infty }}+{\int }_{x_0}^x{\varphi }^{-1}(C_3)ds\ge {\parallel u\parallel }_{\mathrm{\infty }}+(x-x_0){\varphi }^{-1}(-\varphi \left(\frac{{\parallel u\parallel }_{\mathrm{\infty }}}{1-x_0}\right))\\ =\frac{1-x}{1-x_0}{\parallel u\parallel }_{\mathrm{\infty }},x\in [x_0,x_2],\end{array}$$

where $x_2=1-\sigma (1-x_0)$. So $u(x)\ge w(x)\ge \sigma {\parallel u\parallel }_{\mathrm{\infty }}$, $x\in [x_0,x_2]$. Therefore, we have

$$u(x)={\int }_x^1{\varphi }^{-1}\left(\lambda {\int }_{x_0}^{s}f(u(t))dt\right)ds=T_{\lambda }u(x),x\in [x_0,1],$$

(2.10)

and subsequently,

$$\begin{array}{rl}{\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}& \ge {\int }_{x_2}^1{\varphi }^{-1}\left(\lambda {\int }_{x_0}^{s}f(u(t))dt\right)ds\ge {\int }_{x_2}^1{\varphi }^{-1}\left(\lambda {\int }_{x_0}^{x_2}\eta \varphi (u(t))dt\right)ds\\ \ge {\int }_{x_2}^1{\varphi }^{-1}(\lambda (x_2-x_0)\eta \varphi \left(\sigma {\parallel u\parallel }_{\mathrm{\infty }}\right))ds\\ \ge \sigma (1-x_0){\varphi }^{-1}(\lambda (1-\sigma )(1-x_0)\eta \varphi \left(\sigma {\parallel u\parallel }_{\mathrm{\infty }}\right)).\end{array}$$

Let $x_{\ast }=min\{x_0,1-x_0\}$. Then

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\ge \sigma x_{\ast }{\varphi }^{-1}(\lambda (1-\sigma )x_{\ast }\eta \varphi \left(\sigma {\parallel u\parallel }_{\mathrm{\infty }}\right)).$$

 □

Lemma 2.7 Let $r>0$ be given. If $u\in \partial {\mathrm{\Omega }}_r$, then

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\le {\varphi }^{-1}(\lambda M_r),$$

where $M_r=1+{max}_{0\le u\le r}\{f(u)\}>0$.

Proof Obviously, for any $u\in \partial {\mathrm{\Omega }}_r$, it follows that $f(u(x))\le M_r$ for $x\in [0,1]$. So we have

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\le {\int }_0^1{\varphi }^{-1}\left(\lambda {\int }_s^{1}f(u(t))dt\right)ds\le {\varphi }^{-1}(\lambda M_r).$$

 □

Lemma 2.8 Let $r>0$ be given. If $u\in \partial {\mathrm{\Omega }}_r$, then

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\ge \sigma x_{\ast }{\varphi }^{-1}(\lambda (1-\sigma )x_{\ast }{m}_r),$$

where $m_r={min}_{\sigma r\le u\le r}\{f(u)\}>0$ and $x_{\ast }=min\{x_0,1-x_0\}$.

Proof By using a similar argument of the proof of Lemma 2.6, we have that $u(x)\ge \sigma {\parallel u\parallel }_{\mathrm{\infty }}$ for $x\in [x_1,x_2]$. Meanwhile, (2.8) is true. If $x_0\ge \frac{1}{2}$, then we can get that

$$\begin{array}{rl}{\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}& \ge {\int }_0^{x_1}{\varphi }^{-1}\left(\lambda {\int }_s^{x_0}f(u(t))dt\right)ds\ge {\int }_0^{x_1}{\varphi }^{-1}\left(\lambda {\int }_{x_1}^{x_0}{m}_{r}dt\right)ds\\ \ge {\int }_0^{x_1}{\varphi }^{-1}(\lambda (x_0-x_1)m_r)ds\ge x_1{\varphi }^{-1}(\lambda (x_0-x_1)m_r)\\ =\sigma x_0{\varphi }^{-1}(\lambda (1-\sigma )x_0{m}_r).\end{array}$$

If $x_0\le \frac{1}{2}$, then (2.10) holds and it follows that

$$\begin{array}{rl}{\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}& \ge {\int }_{x_2}^1{\varphi }^{-1}\left(\lambda {\int }_{x_0}^{s}f(u(t))dt\right)ds\ge {\int }_{x_2}^1{\varphi }^{-1}\left(\lambda {\int }_{x_0}^{x_2}{m}_{r}dt\right)ds\\ \ge {\int }_{x_2}^1{\varphi }^{-1}(\lambda (x_2-x_0)m_r)ds\ge (1-x_2){\varphi }^{-1}(\lambda (x_2-x_0)m_r)\\ =\sigma (1-x_0){\varphi }^{-1}(\lambda (1-\sigma )(1-x_0)m_r).\end{array}$$

Let $x_{\ast }=min\{x_0,(1-x_0)\}$, then

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\ge \sigma x_{\ast }{\varphi }^{-1}(\lambda (1-\sigma )x_{\ast }{m}_r).$$

 □

3 Proof of the main results

Proof of Theorem 1.1 (i) Choose a suitable number $r_1>0$. By Lemma 2.8, we have

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}>{\parallel u\parallel }_{\mathrm{\infty }}\text{for }u\in \partial {\mathrm{\Omega }}_{r_1}\text{ and }{\lambda }_{\ast }<\lambda <{\lambda }^{\ast },$$

where

$${\lambda }^{\ast }\le \frac{1}{\sqrt{\kappa }(1-\sigma )x_{\ast }{m}_{r_1}}\text{and}{\lambda }_{\ast }\ge \frac{1}{(1-\sigma )x^{\ast }{m}_{r_1}}\varphi \left(\frac{r_1}{\sigma x^{\ast }}\right).$$

If $f_0=0$, then $f_0^{\ast }=0$, and so we can choose $r_2\in (0,r_1)$ such that $f^{\ast }(r_2)\le \epsilon \varphi (r_2)$, where $\epsilon >0$ small enough satisfies

$$B_{\lambda \epsilon }<1.$$

(3.1)

Then Lemma 2.5 implies that

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}<{\parallel u\parallel }_{\mathrm{\infty }}\text{for }u\in \partial {\mathrm{\Omega }}_{r_2}.$$

From Lemma 2.4, it follows that $i(T_{\lambda },{\mathrm{\Omega }}_{r_1},P)=0$ and $i(T_{\lambda },{\mathrm{\Omega }}_{r_2},P)=1$. By using the additivity-excision property of the fixed point index [16], we have that

$$i(T_{\lambda },{\mathrm{\Omega }}_{r_1}\mathrm{\setminus }{\overline{\mathrm{\Omega }}}_{r_2},P)=i(T_{\lambda },{\mathrm{\Omega }}_{r_1},P)-i(T_{\lambda },{\mathrm{\Omega }}_{r_2},P)=-1.$$

Therefore, $T_{\lambda }$ has a fixed point in ${\overline{\mathrm{\Omega }}}_{r_1}\mathrm{\setminus }{\mathrm{\Omega }}_{r_2}$. Consequently, (1.1) has a positive solution for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$.

• (ii) Choose a suitable number $r_1>0$. By Lemma 2.7, there exists

  $$0<{\lambda }_0\le min\{\frac{1}{\sqrt{\kappa }{M}_{r_1}},\frac{\varphi (r_1)}{M_{r_1}}\}=\frac{\varphi (r_1)}{M_{r_1}}$$

such that ${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}<{\parallel u\parallel }_{\mathrm{\infty }}$ for $u\in \partial {\mathrm{\Omega }}_{r_1}$ and $0<\lambda <{\lambda }_0$. That is, $i(T_{\lambda },{\mathrm{\Omega }}_{r_1},P)=1$.

If $f_0=\mathrm{\infty }$, then there exists $r_2\in (0,r_1)$ such that $f(u)\ge \eta \varphi (u)$ for $0\le u\le r_2$, where $\eta >0$ is chosen large enough so that

$$\lambda (1-\sigma )x_{\ast }\eta \varphi (\sigma r_2)<\frac{1}{\sqrt{\kappa }}\text{and}{\sigma }^2\lambda (1-\sigma )x_{\ast }^2\eta >1.$$

(3.2)

Clearly, $f(u)\ge \eta \varphi (u(x))$ for $u\in \partial {\mathrm{\Omega }}_{r_2}$, $x\in [0,1]$. From Lemma 2.6, we get that

$$\begin{array}{r}{\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\ge \sigma x_{\ast }{\varphi }^{-1}(\lambda (1-\sigma )x_{\ast }\eta \varphi \left(\sigma {\parallel u\parallel }_{\mathrm{\infty }}\right))\ge {\sigma }^2\lambda (1-\sigma )x_{\ast }^2\eta {\parallel u\parallel }_{\mathrm{\infty }}>{\parallel u\parallel }_{\mathrm{\infty }}\\ \text{for }u\in \partial {\mathrm{\Omega }}_{r_2}.\end{array}$$

This together with Lemma 2.4 implies $i(T_{\lambda },{\mathrm{\Omega }}_{r_2},P)=0$. By using the additivity-excision property of the fixed point index [16], we have

$$i(T_{\lambda },{\mathrm{\Omega }}_{r_1}\mathrm{\setminus }{\overline{\mathrm{\Omega }}}_{r_2},P)=i(T_{\lambda },{\mathrm{\Omega }}_{r_1},P)-i(T_{\lambda },{\mathrm{\Omega }}_{r_2},P)=1.$$

Therefore, $T_{\lambda }$ has a fixed point in ${\overline{\mathrm{\Omega }}}_{r_1}\mathrm{\setminus }{\mathrm{\Omega }}_{r_2}$. Consequently, (1.1) has a positive solution for $0<\lambda <{\lambda }_0$.

• (iii) Since ϕ is a bounded operator, multiplying (1.3) by $u^{\prime }$ and integrating from 0 to $x_0$, we get that

  $$\lambda {\int }_0^{u(x_0)}f(u)du=\frac{1}{\kappa }[1-\frac{1}{\sqrt{1+\kappa {(u^{\prime }(0))}^2}}]\to \frac{1}{\kappa }\text{as }{u}^{\prime }(0)\to \mathrm{\infty }.$$

Let ${\lambda }^{\ast }>0$ be the solution of $\lambda {\int }_0^{r^{\ast }}f(u)du=\frac{1}{\kappa }$. Then there exists $\overline{r}:=r^{\ast }-ϵ>0$ such that

$$\lambda {\int }_0^{\overline{r}}f(u)du<\frac{1}{\kappa }$$

(3.3)

with $\overline{r}=u(x_0)={\parallel u\parallel }_{\mathrm{\infty }}$.

Choose two numbers $0<r_3<r_4<\overline{r}$ satisfying

$$\varphi \left(\frac{r_3}{\sigma x_{\ast }}\right)<\frac{(1-\sigma )x_{\ast }{m}_{r_3}}{M_{\overline{r}}}\varphi (\overline{r})\text{and}\varphi \left(\frac{r_4}{\sigma x_{\ast }}\right)<\frac{(1-\sigma )x_{\ast }{m}_{r_4}}{M_{\overline{r}}}\varphi (\overline{r}).$$

By Lemma 2.8, there exist

$${\lambda }_{\ast }=max\{\frac{\varphi (\frac{r_3}{\sigma x^{\ast }})}{(1-\sigma )x^{\ast }{m}_{r_3}},\frac{\varphi (\frac{r_4}{\sigma x^{\ast }})}{(1-\sigma )x^{\ast }{m}_{r_4}}\}$$

and

$${\lambda }^{\ast }=min\{\frac{1}{\sqrt{\kappa }{M}_{\overline{r}}},\frac{\varphi (\overline{r})}{M_{\overline{r}}},\frac{1}{(1-\sigma )x_{\ast }{m}_{r_3}\sqrt{\kappa }},\frac{1}{(1-\sigma )x_{\ast }{m}_{r_4}\sqrt{\kappa }}\}=\frac{\varphi (\overline{r})}{M_{\overline{r}}}$$

such that for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$, we have

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}>{\parallel u\parallel }_{\mathrm{\infty }}\text{for }u\in \partial {\mathrm{\Omega }}_{r_i},i=3,4.$$

This together with Lemma 2.4 implies $i(T_{\lambda },{\mathrm{\Omega }}_{r_i},P)=0$, $i=3,4$.

Since $f_0=0$, from the proof of the case (i), it follows that we can choose $r_1\in (0,\frac{r_3}{2})$ such that $i(T_{\lambda },{\mathrm{\Omega }}_{r_1},P)=1$. Subsequently,

$$i(T_{\lambda },{\mathrm{\Omega }}_{r_3}\mathrm{\setminus }{\overline{\mathrm{\Omega }}}_{r_1},P)=i(T_{\lambda },{\mathrm{\Omega }}_{r_3},P)-i(T_{\lambda },{\mathrm{\Omega }}_{r_1},P)=-1.$$

On the other hand, $f_{\mathrm{\infty }}=0$, $\lambda <{\lambda }^{\ast }$ and (3.3) together with Lemma 2.7 implies

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\le {\varphi }^{-1}(\lambda M_{\overline{r}})<{\parallel u\parallel }_{\mathrm{\infty }}\text{for any }u\in \partial {\mathrm{\Omega }}_{\overline{r}}.$$

That is, $i(T_{\lambda },{\mathrm{\Omega }}_{\overline{r}},P)=1$. Subsequently,

$$i(T_{\lambda },{\mathrm{\Omega }}_{\overline{r}}\mathrm{\setminus }{\overline{\mathrm{\Omega }}}_{r_4},P)=i(T_{\lambda },{\mathrm{\Omega }}_{\overline{r}},P)-i(T_{\lambda },{\mathrm{\Omega }}_{r_4},P)=1.$$

Therefore, $T_{\lambda }$ has two fixed points $u_1$ and $u_2$ such that $u_1\in {\overline{\mathrm{\Omega }}}_{r_3}\mathrm{\setminus }{\mathrm{\Omega }}_{r_1}$ and $u_2\in {\overline{\mathrm{\Omega }}}_{\overline{r}}\mathrm{\setminus }{\mathrm{\Omega }}_{r_4}$. These are the desired distinct positive solutions of (1.1) for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$ satisfying

$$r_1\le {\parallel u_1\parallel }_{\mathrm{\infty }}\le r_3<r_4\le {\parallel u_2\parallel }_{\mathrm{\infty }}\le r_2.$$

(3.4)

• (iv) Choose two numbers $0<r_3<r_4<\overline{r}$ satisfying

  $$\varphi (r_3)>\frac{M_{r_3}}{(1-\sigma )x_{\ast }{m}_{\overline{r}}}\varphi \left(\frac{\overline{r}}{\sigma x_{\ast }}\right)\text{and}\varphi (r_4)>\frac{M_{r_4}}{(1-\sigma )x_{\ast }{m}_{\overline{r}}}\varphi \left(\frac{\overline{r}}{\sigma x_{\ast }}\right).$$

By Lemma 2.7, there exists $0<{\lambda }_0\le min\{\frac{\varphi (r_3)}{M_{r_3}},\frac{\varphi (r_4)}{M_{r_4}}\}$ such that for $0<\lambda <{\lambda }_0$, we have

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}<{\parallel u\parallel }_{\mathrm{\infty }}\text{for }u\in \partial {\mathrm{\Omega }}_{r_i},i=3,4.$$

That is, $i(T_{\lambda },{\mathrm{\Omega }}_{r_3},P)=1$ and $i(T_{\lambda },{\mathrm{\Omega }}_{r_4},P)=1$.

Since $f_0=\mathrm{\infty }$, from the proof of the case (ii), choose $r_1\in (0,\frac{r_3}{2})$ such that $i(T_{\lambda },{\mathrm{\Omega }}_{r_1},P)=0$. Consequently,

$$i(T_{\lambda },{\mathrm{\Omega }}_{r_3}\mathrm{\setminus }{\overline{\mathrm{\Omega }}}_{r_1},P)=i(T_{\lambda },{\mathrm{\Omega }}_{r_3},P)-i(T_{\lambda },{\mathrm{\Omega }}_{r_1},P)=1.$$

On the other hand, $f_{\mathrm{\infty }}=\mathrm{\infty }$ and (3.3) together with Lemma 2.8 implies that

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}\ge \sigma x_{\ast }{\varphi }^{-1}(\lambda (1-\sigma )x_{\ast }{m}_{\overline{r}}).$$

Let ${\lambda }_{\ast }=\frac{\varphi (\frac{\overline{r}}{\sigma x_{\ast }})}{(1-\sigma )x_{\ast }{m}_{\overline{r}}}$ and ${\lambda }^{\ast }=min\{{\lambda }_0,\frac{1}{\sqrt{\kappa }(1-\sigma )x_{\ast }{m}_{\overline{r}}}\}$. Then, for any ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$, we have

$${\parallel T_{\lambda }u\parallel }_{\mathrm{\infty }}>{\parallel u\parallel }_{\mathrm{\infty }}\text{for any }u\in u\in \partial {\mathrm{\Omega }}_{\overline{r}}.$$

That is, $i(T_{\lambda },{\mathrm{\Omega }}_{\overline{r}},P)=0$. Subsequently,

$$i(T_{\lambda },{\mathrm{\Omega }}_{\overline{r}}\mathrm{\setminus }{\overline{\mathrm{\Omega }}}_{r_4},P)=i(T_{\lambda },{\mathrm{\Omega }}_{\overline{r}},P)-i(T_{\lambda },{\mathrm{\Omega }}_{r_4},P)=-1.$$

Therefore, $T_{\lambda }$ has two fixed points $u_1$ and $u_2$ such that $u_1\in {\overline{\mathrm{\Omega }}}_{r_3}\mathrm{\setminus }{\mathrm{\Omega }}_{r_1}$ and $u_2\in {\overline{\mathrm{\Omega }}}_{\overline{r}}\mathrm{\setminus }{\mathrm{\Omega }}_{r_4}$. These are the desired distinct positive solutions of (1.1) for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$ satisfying (3.4). □

Proof of Corollary 1.2 It is easy to show by the result of Theorem 1.1(i) and (ii). □

Example 3.1 Let us consider the following problem:

$$\{\begin{array}{l}-{(\frac{u^{\prime }}{\sqrt{1+\kappa {(u^{\prime })}^2}})}^{\prime }=\lambda e^u,x\in (0,1),\\ u(0)=u(1)=0.\end{array}$$

(3.5)

Obviously, $f_0={lim}_{u\to 0}\frac{e^u}{\varphi (u)}=\mathrm{\infty }$ and $f_{\mathrm{\infty }}={lim}_{u\to \mathrm{\infty }}\frac{e^u}{\varphi (u)}=\mathrm{\infty }$. From Theorem 1.1(iv), there exists $0<{\lambda }_{\ast }<{\lambda }^{\ast }$ such that (3.5) has at least two positive solutions for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$.

Example 3.2 Let us consider the following problem:

$$\{\begin{array}{l}-{(\frac{u^{\prime }}{\sqrt{1+\kappa {(u^{\prime })}^2}})}^{\prime }=\lambda u^p,x\in (0,1),\\ u(0)=u(1)=0.\end{array}$$

(3.6)

Obviously, we divided the discussion into two cases as follows.

Case 1. $p>1$

In this case, $f(u)=u^p$ is convex, and $f_0={lim}_{u\to 0}\frac{u^p}{\varphi (u)}=0$ and $f_{\mathrm{\infty }}={lim}_{u\to \mathrm{\infty }}\frac{u^p}{\varphi (u)}=\mathrm{\infty }$. From Corollary 1.2(a), there exists $0<{\lambda }_{\ast }<{\lambda }^{\ast }$ such that (3.6) has at least one positive solution for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$.

Case 2. $p<1$

In this case, $f(u)=u^p$ is concave, and $f_0={lim}_{u\to 0}\frac{u^p}{\varphi (u)}=\mathrm{\infty }$ and $f_{\mathrm{\infty }}={lim}_{u\to \mathrm{\infty }}\frac{u^p}{\varphi (u)}=\mathrm{\infty }$. From Theorem 1.1(iv), there exists $0<{\lambda }_{\ast }<{\lambda }^{\ast }$ such that (3.6) has at least two positive solutions for ${\lambda }_{\ast }<\lambda <{\lambda }^{\ast }$.

Remark 3.1 It is worth to point out that our results only partly generalize the results of Habet and Omari [9] and Pan [12], since $f(u)$ is more general than $e^u$, $u^p$ and due to the limitation of the fixed point index method.

Remark 3.2 Since $f(u)$ in (1.1) is autonomous, it is not difficult to show that the solutions of (1.1) are symmetric around $\frac{1}{2}$, see [2, 12]. It follows that $x_0=\frac{1}{2}$ in the proof of Theorem 1.1, and we can set ${\tau }_i=\frac{1}{4}$, $i=1,2$ and $\sigma =\frac{1}{2}$.