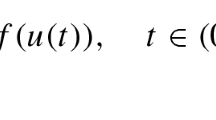Multiplicity and Calabi–Bernstein type asymptotic property of positive solutions for one-dimensional Minkowski-curvature problems

Abstract

In this paper, we first consider the existence and multiplicity of positive solutions to a Minkowski-curvature problem when nonlinearity is sublinear. We then study the nonexistence and multiplicity of positive solutions for the corresponding one-parameter problem in which its nonlinear function has m zeros in the interval $(0,\frac{1}{2})$ by proving that the problem has no and $m+1$ positive solutions for suitably small and large parameter, respectively. Furthermore, we investigate the Calabi–Bernstein type asymptotic property of each positive solution of the one-parameter problem as the parameter goes to infinity, showing that the ith solution converges to a function whose shape is isosceles trapezoid when $1 \le i\le m$ and isosceles triangle when $i=m+1$.

1 Introduction and main results

We first consider the existence of one or two positive solutions of the following one-dimensional Minkowski-curvature problem

where $\phi (y)=\frac{y}{\sqrt{1-y^2}}$, $y\in (-1,1)$, weight function r satisfies $r\ge 0$, $r\not \equiv 0$ on any compact subinterval of (0, 1) and $r\in {\mathcal {A}}_q$ a class of functions given as

$$\begin{aligned} {\mathcal {A}}_q\triangleq \Big \{r\in L_{loc}^1((0,1),[0,\infty )):\int _0^1 \tau ^q(1-\tau )^qr(\tau )d\tau <\infty ,q\ge 1\Big \}. \end{aligned}$$

As an example, consider $r(t)=t^{-\frac{5}{2}},$ then $r\notin L^1 (0,1)$ but $r\in {\mathcal {A}}_2$ ($q=2$ in ${\mathcal {A}}_q$). $f:[0,\alpha )\rightarrow [0,\infty )$ with $\alpha > \frac{1}{2}$ is a continuous function and $f\not \equiv 0$ on any compact subinterval of $(0,\frac{1}{2})$.

We say u a solution of problem (P) if $u\in C[0,1]\cap C^1(0,1)$, $|u'(t)|<1$ for $t\in (0,1)$, and $\phi (u')$ is absolutely continuous on any compact subinterval of (0, 1), and u satisfies the equation and the boundary conditions in problem (P). Moreover, we say u is a positive solution of problem (P) if solution u satisfies $u(t)\ge 0$ and $u(t)\not \equiv 0$ on (0, 1).

This type of problem is related to mean curvature operator in flat Minkowski space endowed with the Lorentzian metric, which has a wide range of applications in physics and geometry. Physically, it naturally appears in Dirichlet p-branes of string theory (see [22]) and nonlinear electrodynamics model of the Born–Infeld theory, see for instance [9,10,11,12]. Geometrically, it plays a significant role in determining existence and regularity properties of maximal and constant mean curvature hypersurfaces (see [4, 21, 35]) and cosmological model, see [5, 33] and references therein. In recent decades, many researchers have studied the nonexistence, existence and multiplicity of solutions for boundary value problems of nonlinear Minkowski-curvature equations (see [6,7,8, 15, 16, 19, 20, 30, 34, 40]).

We detail some existence and multiplicity results of solutions for Minkowski-curvature problems with singular nonlinear terms. Specially, Coelho–Corsato–Obersnel–Omari [15] studied the existence and multiplicity of positive solutions for the 0-Dirichlet boundary problem

where $f:[0,T] \times {{\mathbb {R}}} \rightarrow {{\mathbb {R}}}$ satisfies the $L^1$-Carathéodory conditions. Under some more assumptions on f, mainly by variational and topological methods, they proved the existence of either one, or two, or three, or infinitely many positive solutions.

In a subsequent paper, Coelho–Corsato–Rivetti [16] studied the existence and multiplicity of positive radial solutions for the null Dirichlet problem of the Minkowski-curvature equation

where $\phi _N(y)=\frac{y}{\sqrt{1-|y|^2}}$, $y\in {\mathbb {R}}^N$, $N\ge 2$, $R>0$ and $B_R$ is a ball in ${\mathbb {R}}^N$, $f:[0,R] \times {{\mathbb {R}}} \rightarrow {{\mathbb {R}}}$ satisfies the $L^1$-Carathéodory conditions. By variational methods, they proved the existence of either one, two or three positive solutions according to the behaviour of f(r, s) near s=0. A model example is $f(r,s)=\lambda a(r)s^p+\mu b(r)s^q$, $0<p<1<q$. Their work extended partially the results for one-dimensional problem (S) obtained in [15] to the radial problem (G).

Recently, Yang–Lee–Sim [38, 40] studied the existence of positive or nodal radial solutions for the following problem defined on an exterior domain

where $\Omega =\{x\in {\mathbb {R}}^N:|x|>R\}$ and $N\ge 3,$ $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is a continuous and odd function satisfying $f(s)s>0$ for $s\ne 0$, and a function K satisfies

(HK):

$K\in L^1([R,\infty ),[0,\infty ))$ is not identically zero on any subinterval in $(R,\infty )$ and satisfies $\int _{R}^\infty rK(r)dr<\infty$.

After introducing variables $|x|=r$, $v(x)=u(r)$ and $t=(\frac{r}{R})^{-(N-2)},$ problem $(E_\lambda )$ is transformed into one-dimensional problem of the form

where functions $\beta$ and h are given by

$$\begin{aligned} \beta (t)=\frac{R}{N-2}t^{-\frac{N-1}{N-2}}, \ \ h(t)=\beta ^2(t)K\big (Rt^{-\frac{1}{N-2}}\big ). \end{aligned}$$

We note that weight function h is singular at $t=0$ and if K in $(E_\lambda )$ satisfies (HK), then corresponding h in $(D_\lambda )$ satisfies $h\in L^1 _{loc} ((0,1),[0,\infty ))$ with $\int _0 ^1 \tau h(\tau )d\tau <\infty .$ Under assumptions $0<f_0^1<\infty$ and $f_\infty ^1=0$, where $f_0^1\triangleq \lim \nolimits _{s\rightarrow 0}\frac{f(s)}{s}$ and $f_\infty ^1\triangleq \lim \nolimits _{|s|\rightarrow \infty }\frac{f(s)}{s}$, they proved that for each $k\in {\mathbb {N}}$, there exists $\lambda _*\in (0,\frac{\lambda _k(h)}{f_0}]$ such that problem $(D_\lambda )$ has no $(k-1)$-nodal solution for all $\lambda \in (0,\lambda _*)$ and at least two $(k-1)$-nodal solutions for all $\lambda \in (\frac{\lambda _k(h)}{f_0},\infty )$, where $\lambda _k(h)$ is the kth eigenvalue of corresponding second order linearized problem and for $k=1$, the 0-nodal solution is a positive solution or a negative solution.

Very recently, Bartolo–Caponio–Pomponio [3] considered the existence of a spacelike solution of the exterior Dirichlet problem

where $\Omega _c={\mathbb {R}}^N\setminus {\bar{\Omega }}$ is an exterior domain in ${\mathbb {R}}^N$, $N\ge 3$, $\varphi :\partial \Omega \rightarrow {\mathbb {R}}$ and $H:\Omega _c\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function satisfying

(Hh):

there exists $h\in L^s(\Omega _c)\cap L_{loc}^{\infty }(\Omega _c)$, $s\in [1,\frac{2N}{N+2}]$, such that

$$\begin{aligned} n|H(x,t)|\le h(x)~\mathrm{for~ a.e.~} x\in \Omega _c~\mathrm{and~ all~}t\in {\mathbb {R}}. \end{aligned}$$

They gave a necessary and sufficient condition for the existence of a spacelike solution of problem (H).

In the study of [38, 40], a novel class of weight functions is generally defined as

$$\begin{aligned} {\mathcal {A}}_1\triangleq \{r\in L_{loc}^1((0,1),[0,\infty )):\int _0^1 \tau (1-\tau )r(\tau )d\tau <\infty \}, \end{aligned}$$

admitting the singularity of weight function at $t=0$ or $t=1.$ In fact, we can easily check that $L^1((0,1),[0,\infty ))\subset {\mathcal {A}}_1\subset {\mathcal {A}}_q$ for $q>1.$ The singularity in nonlinear term may affect the compactness of solution space for such a problem. In paper [41], authors classified the solutions by introducing ”non $\frac{\pi }{4}$-tangential solution” defined as $u\in C^1[0,1]$, $|u'(0)|<1$ and $|u'(1)|<1$ and ”$\frac{\pi }{4}$-tangential solution” defined as $u\in C^1[0,1]$, $|u'(0)|=1$ or $|u'(1)|=1$. When weight function in nonlinear term belongs to $L^1$-class, all solutions of problem (P) are non $\frac{\pi }{4}$-tangential, while solutions of problem (P) may be $\frac{\pi }{4}$-tangential if weight function is of ${\mathcal {A}}_q$-class and meanwhile, solution operator may loss of compactness. To guarantee compactness of solution operator in this paper, the asymptotic behaviour of f(s) near $s=0$ is linear or sublinear, which will be specified later. It is also interesting to note that studies of the existence and multiplicity of positive solutions for problem (P), specially with nonlinearity f satisfying $0\le f_0 < \infty$ and weight function r of ${\mathcal {A}}_q$-class are rare before this paper as far as the authors know. In the present paper, we will deal with the existence and multiplicity of positive solutions of problem (P) using the Krasnoselskii’s theorem of cone expansion and compression, a different approach to the one in [3, 15, 16, 38, 40].

We now give a relation between weight function r and nonlinear function f.

(F):

there exist $\delta \in (0,\frac{1}{2})$ and $\rho \in (0,\delta M_{\delta })$ such that

$$\begin{aligned} f(s)\ge \phi \left( \frac{s}{\delta M_{\delta }}\right) ~\textrm{for}~s\in [\delta \rho ,\rho ], \end{aligned}$$

where $M_{\delta }=\min \left\{ \int _\delta ^{\frac{1}{2}}\phi ^{-1}\left( \int _s^{\frac{1}{2}}r(\tau )d\tau \right) ds,\int ^{1-\delta }_{\frac{1}{2}}\phi ^{-1}\left( \int ^s_{\frac{1}{2}}r(\tau )d\tau \right) ds\right\}$.

Remark 1.1

Condition (F) is first introduced in [39] and there is a large number of functions satisfying condition (F), one can refer to [39].

Denote $f_0\triangleq \lim \nolimits _{s\rightarrow 0^+}\frac{f(s)}{s^{q}}$, where q is from ${\mathcal {A}}_q$. The following proposition is an existence result of one positive solution to problem (P).

Proposition 1.1

Assume $r\in {\mathcal {A}}_q$, (F) and $0\le f_0<\infty$. Then problem (P) has at least one positive solution u satisfying $\rho<\Vert u\Vert _\infty <\frac{1}{2}$.

Our existence result of two positive solutions to problem (P) is the following.

Theorem 1.2

Assume $r\in {\mathcal {A}}_q$, (F) and $f_0=0$. Then problem (P) has at least two positive solutions $u_1$ and $u_2$ such that $0<\Vert u_1\Vert _\infty<\rho<\Vert u_2\Vert _\infty <\frac{1}{2}$.

Next, we consider the corresponding one-parameter problem

where $\lambda >0$, weighted function r satisfies the same conditions as the ones in problem (P), $g:[0,\alpha )\rightarrow [0,\infty )$ is a continuous function with $\alpha > \frac{1}{2}$ and $g\not \equiv 0$ on $(0,\frac{1}{2})$. A multiplicity result of the one-parameter problem is the following, which shows that the number of solutions of problem $(P_\lambda )$ is related to the number of interior zeros of function g on $(0,\frac{1}{2})$.

Theorem 1.3

Assume $r\in {\mathcal {A}}_q$ and $0\le g_0<\infty$. Also assume that there exist numbers $0(=a_0)<a_1<a_2<\cdots<a_{m}<\frac{1}{2}(= a_{m+1})$ such that $(\frac{1}{2}+a_i)a_i>2a_{i-1}$ for all $i\in \{1,2,\cdots ,m+1\}$, $\sum \nolimits _{i=0}^{m}g(a_i)=0$ and $g>0$ on the set $I\triangleq (0,\frac{1}{2})\setminus \{a_i\}_{i=1}^{m}$. Then there exist $0<\lambda _*\le \lambda ^*<\infty$ such that problem $(P_\lambda )$ has no positive solution for all $\lambda <\lambda _*$ and at least $m+1$ distinct positive solutions $\{u_{\lambda ,i}\}_{i=1}^{m+1}$ for all $\lambda \ge \lambda ^*$, which satisfy

• (i) $u_{\lambda ,i}(t)>0$ for $t\in (0,1)$;

• (ii) $0<b_1\le \Vert u_{\lambda ,1}\Vert _\infty \le a_1<b_2\le \Vert u_{\lambda ,2}\Vert _\infty \le a_2<\cdots \le a_{m-1}<b_m\le \Vert u_{\lambda ,m}\Vert _\infty \le a_m<b_{m+1}\le \Vert u_{\lambda ,m+1}\Vert _\infty <\frac{1}{2}$, where $b_1,b_2,\cdots ,b_{m+1}$ are constants.

Remark 1.2

• (i) The condition $(\frac{1}{2}+a_i)a_i>2a_{i-1}$ is crucial to guarantee a suitable interval length between $a_{i-1}$ and $a_i$. If such condition is $a_i^2>\frac{1}{4}a_{i-1}$, by a similar fashion, the result is also valid. Previous work on nonlinear problems with nonlinear function which has many zeros has been done in [25, 36]. In [25], the author proved $2m-1$ positive solutions result for a nonlinear elliptic eigenvalue problem, in which nonlinear function is of $C^1$-class and may be negative in some subintervals. Paper [36] is concerned with those quasilinear equations where operators satisfy a homeomorphism condition. Condition $\sum \nolimits _{i=0}^{m}g(a_i)=0$ is equivalent to $g(a_0)=g(a_1)=\cdots =g(a_m)=0$.

• (ii) The number $m+1$ of positive solutions is sharp in Theorem 1.3. Specially, situation 1: when $m=0$, $0<g_0<\infty$ and $\frac{g(s)}{s}$ is strictly decreasing on $(0,\frac{1}{2})$, problem $(P_\lambda )$ has exact one positive solution for suitably large $\lambda$. For readers’ convenience, we give a brief explanation here. Indeed, by a similar argument of Theorem 2.4 in [37], problem $(P_\lambda )$ has at most one positive solution for any fixed $\lambda >0$. And together with the result of Corollary  1.1 in [29], we conclude that there exists $\lambda ^*>0$ such that problem $(P_\lambda )$ has a unique positive solution for all $\lambda \ge \lambda ^*$; situation 2: when $m=0$ and $g_0=0$, similar to Corollary 1.2 in [29], problem $(P_\lambda )$ has at least two positive solutions for suitably large $\lambda$.

The existence, uniqueness and regularity for spacelike hypersurface with zero or constant mean curvature are classical and important problems in general relativity (see [1, 2, 13, 14, 18, 35] and references therein). There are some well-known results in this perspective which are so called Calabi–Bernstein problem in Minkowski spacetime. In 1968, Calabi [13] studied the maximal spacelike hypersurface equation

$$\begin{aligned} (1-|\nabla u|^2)\sum _{i=1}^N\frac{\partial ^2u}{\partial x_i^2}+\sum _{i,j=1}^N\frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_j}\frac{\partial ^2u}{\partial x_i\partial x_j}=0, \end{aligned}$$

(1.1)

and found a remarkable result that Eq. (1.1) has the Bernstein-type property by proving that (1.1) has only linear entire solutions in dimension $N\le 4$. In 1976, Cheng–Yau [18] extended the result to all N. In [17, 27], authors studied Calabi–Bernstein-type problem for the maximal surface equation in a Robertson–Walker spacetime. Note that the above references [13, 17, 18, 27] considered the equations with zero mean curvature. In a recent paper [29], authors studied bifurcation and Calabi–Bernstein type asymptotic property of one-sign solutions of problem $(P_\lambda )$ as parameter $\lambda$ goes to $\infty$ when nonlinear function g has no interior zero on the interval $(0,\frac{1}{2})$ and proved that one-sign solutions on two bifurcation branches converge to two linear functions. Our next aim is to investigate Calabi–Bernstein type asymptotic property of multiplicity solutions of problem $(P_\lambda )$ as $\lambda$ goes to $\infty$ when nonlinearity g has m zeros on the interval $(0,\frac{1}{2})$.

The Calabi–Bernstein type asymptotic property result of multiplicity solutions for problem $(P_\lambda )$ is given as follows.

Theorem 1.4

Under the assumptions in Theorem 1.3, the solutions $\{u_{\lambda ,i}\}_{i=1}^{m+1}$ of problem $(P_\lambda )$, obtained from Theorem 1.3, satisfy

• (i) $u_{\lambda ,i}(t)$ is continuous with respect to $\lambda$ $(\ge \lambda ^*)$, that is, there exist a sequence $\{(\lambda _n,u_{\lambda _n,i})\}$ and $({\tilde{\lambda }},u_{{\tilde{\lambda }},i})$ such that $\Vert u_{\lambda _n,i}-u_{{\tilde{\lambda }},i}\Vert _{\infty }\rightarrow 0$ as $\lambda \rightarrow {\tilde{\lambda }}$, here notation $(\lambda ,u_\lambda )$ means a solution pair that $u_\lambda$ is a solution of problem $(P_\lambda )$ at $\lambda$;

• (ii) $\lim \nolimits _{\lambda \rightarrow \infty } u_{\lambda ,i}'(t)= 1~uniformly~on~[0,a_i-\varepsilon ]$, for sufficiently small $\varepsilon >0$, $i\in \{1,2,\cdots ,m+1\}$;

• (iii) $\lim \nolimits _{\lambda \rightarrow \infty } u_{\lambda ,i}'(t)=- 1~uniformly~on~[1-a_i+\varepsilon ,1]$, for sufficiently small $\varepsilon >0$, $i\in \{1,2,\cdots ,m+1\}$;

• (iv) $\lim \nolimits _{\lambda \rightarrow \infty } u_{\lambda ,i}'(t)=0~uniformly~on~[a_i+\varepsilon ,1-a_i-\varepsilon ]$, for sufficiently small $\varepsilon >0$, $i\in \{1,2,\cdots ,m\}$;

• (v) $\lim \nolimits _{\lambda \rightarrow \infty } \Vert u_{\lambda ,i}\Vert _\infty =a_i$, $i\in \{1,2,\cdots ,m+1\}$.

Note that Theorem 1.4 (i) shows that the solution pairs $(\lambda ,u_{\lambda ,i}),$ $i=1,2,\cdots ,m+1$, of problem $(P_\lambda )$ may form at least $m+1$ connected curves, name ${\mathcal {C}}_i(\lambda ,u_{\lambda ,i})$, going through $(\lambda ,u_{\lambda ,i})$, which can extend to infinity in $\lambda$-direction. The results $(ii)-(v)$ in Theorem 1.4 manifests that solution $u_{\lambda ,i}(t)$ ($i\in \{1,\cdots ,m+1\}$) of problem $(P_\lambda )$ converges to the following function as $\lambda$ goes to $\infty$, whose shape is isosceles trapezoid when $1\le i\le m$ and isosceles triangle when $i=m+1$,

$$\begin{aligned} u_i(t)= {\left\{ \begin{array}{ll} t, ~&{}t\in [0,a_i),\\ a_i,~&{}t\in [a_i,1-a_i],\\ 1-t,~&{}t\in (1-a_i,1]. \end{array}\right. } \end{aligned}$$

It is worth mentioning that in a recent paper [26], Hong-Yuan studied the existence and uniqueness of solution to the exterior Dirichlet problem of the Minkowski spacetime and proved asymptotic properties of the exterior solution at infinity, which shows that the linear growth rate of the exterior solution at infinity is uniformly less that one. Compared with the asymptotic results of Hong-Yuan, the asymptotic property in Theorem 1.4 is concerned with stable state of solution with respect to a parameter near infinity in a bounded domain.

The rest of this paper is organized as follows. In Sect. 2, we prove Proposition 1.1 and Theorem 1.2. In Sect. 3, we prove Theorems 1.3–1.4.

2 Multiplicity result for problem (P)

In this section, we prove Proposition 1.1 and Theorem  1.2 which deal with the existence and multiplicity of positive solutions for problem (P), respectively.

Let $E=C[0,1]$ be the Banach space with supremum norm $\Vert \cdot \Vert _\infty$ and denote $K=\{u\in E: \ u(0)=u(1)=0 \ \textrm{and } \ u$ is concave on $(0,1) \}.$ Then K is a cone in E.

We will mainly use the Krasnoselskii’s theorem of cone expansion and compression to prove the existence and multiplicity results in this section.

Lemma 2.1

([23]) Let E be a Banach space and let K be a cone in E. Assume that $\Omega _1$ and $\Omega _2$ are bounded open subsets of E such that $0\in \Omega _1\subset \overline{\Omega _1}\subset \Omega _2$, and let $T:K\cap (\overline{\Omega _2}\setminus \Omega _1)\rightarrow K$ be a completely continuous operator such that either

• (i) $\Vert Tx\Vert \le \Vert x\Vert$ for $x\in K\cap \partial \Omega _1$ and $\Vert Tx\Vert \ge \Vert x\Vert$ for $x\in K\cap \partial \Omega _2$, or

• (ii) $\Vert Tx\Vert \ge \Vert x\Vert$ for $x\in K\cap \partial \Omega _1$ and $\Vert Tx\Vert \le \Vert x\Vert$ for $x\in K\cap \partial \Omega _2$.

Then T has a fixed point in $K\cap (\overline{\Omega _2}\setminus \Omega _1)$.

Remark 2.1

Assume $r\in {\mathcal {A}}_q$ and $0\le f_0<\infty$, then $r(\cdot )f(u(\cdot ))\in L^1(0,1)$ and every solution u of problem (P) is of $C^1[0,1]$ and $\Vert u'\Vert _\infty <1$ implying $\Vert u\Vert _\infty <\frac{1}{2}$, refer to Theorem 2.1 in [41].

For $u\in K$ and fixed $\sigma \in (0,1)$ in an arbitrary manner, we define an integral operator $T:K\rightarrow E$ as

$$\begin{aligned} (Tu)(t)= {\left\{ \begin{array}{ll} \int _0^t\phi ^{-1}\left( \alpha +\int _s^{\sigma }r(\tau )f(u(\tau ))d\tau \right) ds,~&{} t\in (0,\sigma ],\\ \int ^1_t\phi ^{-1}\left( -\alpha +\int ^s_{\sigma }r(\tau )f(u(\tau ))d\tau \right) ds,~&{} t\in [\sigma ,1), \end{array}\right. } \end{aligned}$$

(2.1)

where $\alpha$ satisfies

$$\begin{aligned} \int _0^\sigma \phi ^{-1}\left( \alpha +\int _s^\sigma r(\tau )f(u(\tau ))d\tau \right) ds=\int _\sigma ^1\phi ^{-1}\left( -\alpha +\int ^s_\sigma r(\tau )f(u(\tau ))d\tau \right) ds. \end{aligned}$$

We easily check by a standard argument that $T(K)\subset K$ and T is completely continuous. Moreover, we can check that u is a solution of problem (P) if and only if $u\in K$ satisfies $u=Tu$. For $u\in K$, Tu is concave and satisfies the Dirichlet boundary condition. Thus we may assume that there exists $t^*\in (0,1)$, a maximal point of Tu, such that $\Vert Tu\Vert _\infty =(Tu)(t^*)$ and $(Tu)'(t^*)=0$. Here $t^*$ need not be unique.

From the fact $(Tu)'(t^*)=0$, we obtain

$$\begin{aligned} \alpha =-\int _{t^*}^\sigma r(\tau )f(u(\tau ))d\tau . \end{aligned}$$

Since $r\in L^1(t^*-\delta ,t^*+\delta )$ for any small $\delta$, replacing $\sigma$ with $t^*$, we get $\alpha =0$ and Tu can be written as

$$\begin{aligned} (Tu)(t)= {\left\{ \begin{array}{ll} \int _0^t\phi ^{-1}\left( \int _s^{t^*}r(\tau )f(u(\tau ))d\tau \right) ds,~&{} t\in (0,t^*],\\ \int ^1_t\phi ^{-1}\left( \int ^s_{t^*}r(\tau )f(u(\tau ))d\tau \right) ds,~&{} t\in [t^*,1). \end{array}\right. } \end{aligned}$$

(2.2)

This operator is first introduced in [39].

Remark 2.2

• (i) If there exist $0<t_1<t_2<1$ such that $u'(t_1)=u'(t_2)=0$, then the operator T defined in (2.2) is independent of the choice of $t^*\in [t_1,t_2]$. In fact, by the concavity of u, we see that $u'(t)\equiv 0$ for $t\in [t_1,t_2]$ and thus $u(t)\equiv$ constant for $t\in [t_1,t_2]$. We calculate the first equation in problem (P) and get

  $$\begin{aligned} -\frac{u''(t)}{\left( \sqrt{1-|u'(t)|^2}\right) ^3}=r(t)f(u(t)), ~t\in [t_1,t_2]. \end{aligned}$$

  Thus $r(t)f(u(t))\equiv 0$ for $t\in [t_1,t_2]$ implying that $\int _{s_1}^{s_2}r(\tau )f(u(\tau ))d\tau =0$ for any $s_1, s_2\in [t_1,t_2]$.

• (ii) If we find a nontrivial fixed point u of T in K, then $u(t)>0$ for $t\in (0,1)$ mainly by concavity and double zero property ($u(t)=u'(t)=0$) of solution u of problem (P) (see Lemma 2.3 in [38]).

We now start to prove Proposition 1.1, an existence result of problem (P).

Proof of Proposition 1.1

Define $\Omega _\rho =\{u\in E:\Vert u\Vert _\infty <\rho \}$ and consider $u\in K\cap \partial \Omega _\rho .$ Let $\delta \in (0,\frac{1}{2})$ be from condition (F). Recall Tu defined in (2.2). If $t^*\in [\frac{1}{2},1)$, then

$$\begin{aligned} \Vert Tu \Vert _{\infty }=(Tu)(t^*)&=\int _0^{t^*}\phi ^{-1}\left( \int _s^{t^*}r(\tau )f(u(\tau ))d\tau \right) ds\\&\ge \int _{\delta }^{\frac{1}{2}}\phi ^{-1}\left( \int _s^{\frac{1}{2}}r(\tau )f(u(\tau ))d\tau \right) ds. \end{aligned}$$

Since $u\in K\cap \partial \Omega _\rho$, we see

$$\begin{aligned} \frac{u(t)}{\Vert u\Vert _\infty }\ge \frac{t}{t^*}>\delta , ~\textrm{for}~t\in [\delta ,t^*], \end{aligned}$$

implying $u(t)\in [\delta \rho ,\rho ]$ for $t\in [\delta ,t^*]$. Applying (F), we get

$$\begin{aligned} \int _{\delta }^{\frac{1}{2}}\phi ^{-1}\left( \int _s^{\frac{1}{2}}r(\tau )f(u(\tau ))d\tau \right) ds&\ge \int _{\delta }^{\frac{1}{2}}\phi ^{-1}\left( \int _s^{\frac{1}{2}}r(\tau )\phi \left( \frac{u(\tau )}{\delta M_{\delta }}\right) d\tau \right) ds\\&\ge \int _{\delta }^{\frac{1}{2}}\phi ^{-1}\left( \int _s^{\frac{1}{2}}r(\tau )\phi \left( \frac{\Vert u\Vert _\infty }{M_{\delta }}\right) d\tau \right) ds\\&> \int _{\delta }^{\frac{1}{2}}\phi ^{-1}\left( \int _s^{\frac{1}{2}}r(\tau )d\tau \right) ds\frac{\Vert u\Vert _\infty }{M_{\delta }} \ge \Vert u\Vert _\infty , \end{aligned}$$

where we used the property $\phi ^{-1}(xy)> \phi ^{-1}(x)\phi ^{-1}(y)$ for $x,y>0$ in the above inequality. Thus $\Vert Tu\Vert _\infty > \Vert u\Vert _\infty$ for $u\in K\cap \partial \Omega _\rho$. By a similar argument to the case $t^*\in (0,\frac{1}{2})$, we also get

$$\begin{aligned} (Tu)(t^*)> \Vert u\Vert _\infty , ~\textrm{for}~u\in K\cap \partial \Omega _\rho . \end{aligned}$$

This implies that $\Vert Tu\Vert _\infty > \Vert u\Vert _\infty$ for $u\in K\cap \partial \Omega _\rho .$ Denote $\Omega _{1/2}=\{u\in E:\Vert u\Vert _\infty <\frac{1}{2}\}$. Consider $u\in K\cap \partial \Omega _{1/2}$. From Remark 2.1, we see $\Vert Tu\Vert _\infty < \Vert u\Vert _\infty$ for any $u\in K\cap {{\overline{\Omega }}}_{1/2}$. Therefore, by Lemma 2.1, operator T has a fixed point in $K\cap ({{{\overline{\Omega }}}_{1/2}}\setminus \Omega _\rho )$, which is a positive solution, name ${\widetilde{u}}$, of problem (P) satisfying $\rho \le \Vert {\widetilde{u}}\Vert _\infty \le \frac{1}{2}$. Also noticing that $Tu\ne u$ for $u\in \partial \Omega _\rho \cup \partial \Omega _{1/2}$, we get $\rho<\Vert {\widetilde{u}}\Vert _\infty <\frac{1}{2}$ and the proof is completed. $\square$

We prove Theorem 1.2, an existence result of two positive solutions for problem (P) below.

Proof of Theorem 1.2

By following the proof of Theorem 3.1 in [39] with obvious modifications and combining with the fact $Tu\ne u$ for $u\in \partial \Omega _\rho$, problem (P) has a positive solution, name $u_1$, such that $0<\Vert u_1\Vert _\infty <\rho$. Moreover, from Proposition 1.1, we see that problem (P) also has one positive solution $u_2$ (name ${\widetilde{u}}$ in Proposition  1.1) such that $\rho<\Vert u_2\Vert _\infty <\frac{1}{2}$. Therefore, problem (P) has at least two positive solutions $u_1$ and $u_2$ satisfying $0< \Vert u_1\Vert _{\infty }<\rho<\Vert u_2\Vert _{\infty }<\frac{1}{2}$. The proof is done. $\square$

3 Multiplicity and asymptotic property for $(P_\lambda )$

In this section, we show the nonexistence, multiplicity and Calabi–Bernstein type asymptotic property of positive solutions to the one-parameter problem $(P_\lambda )$ under condition $0\le g_0<\infty$. We first show a nonexistence result of positive solutions for problem $(P_\lambda )$.

Theorem 3.1

Assume $r\in {\mathcal {A}}_q$. Also assume that there is a positive constant $c_0$ such that

$$\begin{aligned} \frac{g(s)}{s^q}\le c_0, \end{aligned}$$

(3.1)

for all $s\in [0,\frac{1}{2}].$ Then problem $(P_\lambda )$ has no positive solution for all $\lambda \in (0,\lambda _0]$ with $\lambda _0=\frac{1}{c_02^{q-1}\int _0^1 t^q(1-t)^qr(t)dt}$.

Proof

Let $\lambda >0$ and u be a positive solution of problem $(P_\lambda )$. Under conditions $r\in {\mathcal {A}}_q$ and (3.1), by Theorem 2.1 in [41], we know $u\in C^1[0,1]$ and $|u'(t)|<1$ for $t\in [0,1]$.

Together with the boundary conditions, we obtain

$$\begin{aligned} |u(t)|=\left| \int _0^tu'(\tau )d\tau \right| \le t\Vert u'\Vert _\infty \le 2t(1-t)\Vert u'\Vert _\infty ,~\mathrm{for~} t\in (0,\frac{1}{2}], \end{aligned}$$

and

$$\begin{aligned} |u(t)|=\left| \int _t^1u'(\tau )d\tau \right| \le (1-t)\Vert u'\Vert _\infty \le 2t(1-t)\Vert u'\Vert _\infty ,~\mathrm{for~} t\in [\frac{1}{2},1). \end{aligned}$$

Thus,

$$\begin{aligned} |u(t)|\le 2t(1-t)\Vert u'\Vert _\infty ,~\mathrm{for~} t\in [0,1]. \end{aligned}$$

(3.2)

To eliminate the integration $\int _0^1|u'(\tau )|^2d\tau$ later, we now bound $|u(t)|^2$ by $\int _0^1|u'(\tau )|^2d\tau$. Applying the Hölder’s inequality, we obtain

$$\begin{aligned} |u(t)|\le \int _0^t|u'(\tau )|d\tau \le t^{\frac{1}{2}}\left( \int _0^t|u'(\tau )|^2d\tau \right) ^{\frac{1}{2}},~\forall t\in [0,1]. \end{aligned}$$

Thus,

$$\begin{aligned} (1-t)|u(t)|^2\le t(1-t)\left( \int _0^t|u'(\tau )|^2d\tau \right) ,~\forall t\in [0,1]. \end{aligned}$$

(3.3)

Similarly, we also obtain

$$\begin{aligned} t|u(t)|^2\le t(1-t)\left( \int _t^1|u'(\tau )|^2d\tau \right) ,~\forall t\in [0,1]. \end{aligned}$$

(3.4)

Adding (3.3) and (3.4), we get

$$\begin{aligned} |u(t)|^2\le t(1-t)\left( \int _0^1|u'(\tau )|^2d\tau \right) ,~\forall t\in [0,1]. \end{aligned}$$

(3.5)

Multiplying the first equation in problem $(P_\lambda )$ by u and then integrating it over (0, 1), we obtain

$$\begin{aligned} \int _0^1\Big (\phi (u'(t))\Big )u'(t)dt=\lambda \int _0^1 r(t)g(u(t))u(t)dt. \end{aligned}$$

(3.6)

Note that the integration on the right-hand side of (3.6) makes sense, since $r(\cdot )g(u(\cdot ))\in L^1(0,1)$ by (3.1) and (3.2). Combining (3.2), (3.5) and (3.6), we deduce

$$\begin{aligned} \int _0^1|u'(t)|^2dt&<\int _0^1\Big (\phi (u'(t))\Big )u'(t)dt \nonumber \\&=\lambda \int _0^1 r(t)g(u(t))u(t)dt \nonumber \\&\le \lambda c_0\int _0^1 r(t)|u(t)|^{q+1}dt \nonumber \\&=\lambda c_0\int _0^1 r(t)|u(t)|^{q-1}|u(t)|^2dt \nonumber \\&\le \lambda c_02^{q-1}\int _0^1 r(t)t^q(1-t)^qdt\Vert u'\Vert _{\infty }^{q-1}\left( \int _0^1|u'(\tau )|^2d\tau \right) . \end{aligned}$$

It yields $\lambda >\lambda _0$ and the proof is completed. $\square$

The following lemma shows that a nontrivial solution of problem $(P_\lambda )$ has no interior zero on (0, 1).

Lemma 3.1

Let u be a nontrivial solution of problem $(P_\lambda )$, then $u(t)>0$ for $t\in (0,1)$.

Proof

Since u is a nontrivial solution of problem $(P_\lambda )$, by the definition of function g and 0-Dirichlet boundary conditions, u is concave and $u\ge 0$ on (0, 1). If u has an interior zero on (0, 1), then the interior zero is a double zero of u. Now, we claim that u has no double zero on (0, 1). Then $u(t)>0$ for $t\in (0,1)$ and the proof is done.

Suppose on the contrary that $t_0\in (0,1)$ is a double zero of u, that is $u(t_0)=u'(t_0)=0$. Integrating the first equality in problem $(P_\lambda )$ over $(t,t_0)$ for $t\in [0,1]$, we obtain

$$\begin{aligned} u'(t)=\phi ^{-1}\left( \int ^{t_0}_{t}\lambda r(\tau )g(u(\tau ))d\tau \right) . \end{aligned}$$

Thus, $u'(t)\ge 0$ for $t\in [0,t_0)$ and $u'(t)\le 0$ for $t\in (t_0,1]$. Together with the fact $u(0)=u(t_0)=u(1)=0$, we deduce $u\equiv 0$ on [0, 1], a contradiction. Therefore, solution u has no double zero on [0, 1]. $\square$

Before proving the multiplicity result of Theorem 1.3, we introduce a new family of truncation functions $g^i$, $i=1,2,\cdots ,m+1$, by

$$\begin{aligned} g^i(s)= {\left\{ \begin{array}{ll} g(s),&{} 0\le s\le a_i,\\ 0,&{}s> a_i, \end{array}\right. } \end{aligned}$$

(3.7)

and consider the following auxiliary family

where r is given in problem $(P_\lambda )$.

Similar to the operator T introduced in (2.2), we define the operator $T^i_\lambda :K\rightarrow K$ as

$$\begin{aligned} (T^i_\lambda u)(t)= {\left\{ \begin{array}{ll} \int _0^t\phi ^{-1}\left( \lambda \int _s^{t_i^*}r(\tau )g^i(u(\tau ))d\tau \right) ds,~&{} t\le t_i^*,\\ \int ^1_t\phi ^{-1}\left( \lambda \int ^s_{t_i^*}r(\tau )g^i(u(\tau ))d\tau \right) ds,~&{} t\ge t_i^*, \end{array}\right. } \end{aligned}$$

(3.8)

where $t_i^*\in (0,1)$ is a zero of function $G^i_\lambda :(0,1)\rightarrow {\mathbb {R}}$ with

$$\begin{aligned} G^i_\lambda (t)=\int _0^{t}\phi ^{-1}\left( \lambda \int _s^{t}r(\tau )g^i(u(\tau ))d\tau \right) ds-\int ^1_{t}\phi ^{-1}\left( \lambda \int ^s_{t}r(\tau )g^i(u(\tau ))d\tau \right) ds. \end{aligned}$$

Then $T^i_\lambda$ is completely continuous and $u\in K$ is a positive fixed point of $T^i_\lambda$ if and only if u is a positive solution of problem $(P_\lambda ^i)$.

We consider properties of solutions of problem $(P_\lambda ^i)$ in the following two lemmas.

Lemma 3.2

Let g satisfy the assumptions in Theorem 1.3. If $u_i\in K$ is a solution of problem $(P^i_\lambda )$, then $\Vert u_i\Vert _\infty \le a_i$ and $u_i$ is also a solution of problem $(P_\lambda )$.

Proof

Let $u_i$ be a solution of problem $(P_\lambda ^i)$. Obviously, $u_i(0)=0=u_i(1)$. From the first equation in problem $(P_\lambda ^i)$, we have

$$\begin{aligned} -\frac{u_i''}{\left( \sqrt{1-|u_i'(t)|^2}\right) ^3}=\lambda r(t) g^i(u_i(t)), ~&t\in (0,1). \end{aligned}$$

Thus $u_i$ is concave on (0, 1). By the mean value theorem, there exists $t^*_i\in (0,1)$ such that $u_i'(t^*_i)=0$, implying that $u_i(t^*_i)=\Vert u_i\Vert _\infty$. Suppose on the contrary that $\Vert u_i\Vert _\infty > a_i$. Then, combining with the continuity of $u_i$, there exists a subinterval $(t_i^1,t_i^2)\subset (0,1)$ satisfying $t_i^*\in (t_i^1,t_i^2)$, $u(t)>a_i$ for $t\in (t_i^1,t_i^2)$ and $u_i(t_i^1)=u_i(t_i^2)=a_i.$ Recalling the condition $g^i(s)=0$ for $s\ge a_i$, we have

$$\begin{aligned} -\Big (\phi (u_i'(t))\Big )'=0, ~&t\in [t_i^1,t_i^2]. \end{aligned}$$

Thus, $\phi (u_i')$ is a constant on $[t_i^1,t_i^2]$ and so $u_i'(t)$ is a constant on $[t_i^1,t_i^2]$. Together with the fact $u_i'(t_i^*)=0$, we deduce $u_i'(t)\equiv 0$ for $t\in [t_i^1,t_i^2]$. Hence, $u_i(t)=u_i(t_i^1)= a_i$ for $t\in [t_i^1,t_i^2]$, a contradiction showing $\Vert u_i\Vert _\infty \le a_i$. Due to (3.7), $g^i(u_i)=g(u_i)$ for $0\le u_i\le a_i$. Thus, $u_i$ is also a solution of problem $(P_\lambda )$. The proof is completed. $\square$

Denote $\Omega _{R}=\{u\in E:\Vert u\Vert _\infty <R\}$.

Lemma 3.3

Let g satisfy the assumptions in Theorem 1.3 and $b_i>0$ be such that $\frac{1}{2}(\frac{1}{2}+b_i)b_i \in \left( a_{i-1},\frac{1}{2}(\frac{1}{2}+a_i)a_i\right)$, for any $i\in \{1,2,\cdots ,m+1\}$. Then, there exists $0<\lambda _i^{*}<\infty$ such that

$$\begin{aligned} \Vert T^i_\lambda u\Vert _\infty > \Vert u\Vert _\infty ,~\mathrm{for~all}~ \lambda \ge \lambda _i^{*} \mathrm{~and}~u\in K\cap \partial \Omega _{b_i}. \end{aligned}$$

Proof

From assumptions on $b_i$ for any $i\in \{1,2,\cdots ,m+1\}$, we see $[\frac{1}{2}(\frac{1}{2}+b_i)b_i,b_i]\subset (a_{i-1},a_i)$. Select

$$\begin{aligned} \lambda _i^{*}=\frac{\phi \left( \frac{8b_i}{1+6b_i}\right) }{g^i_{min}\min \left\{ \int _{\frac{1}{2}(\frac{1}{2}+b_i)}^{\frac{1}{2}}r(\tau )d\tau ,\int ^{1-\frac{1}{2}(\frac{1}{2}+b_i)}_{\frac{1}{2}}r(\tau )d\tau \right\} }, \end{aligned}$$

where

$$\begin{aligned} g^i_{min}=\min \limits _{s\in [\frac{1}{2}(\frac{1}{2}+b_i)b_i,b_i]}g^i(s). \end{aligned}$$

Then, $g^i_{min}>0$ from the condition $g^i(s)>0$ for $s\in [\frac{1}{2}(\frac{1}{2}+b_i)b_i,b_i]\subset (a_{i-1},a_i)$, and thus $0<\lambda _i^{*}<\infty$.

Let $u\in K\cap \partial \Omega _{b_i}$ and $t^*_i\in (0,1)$ be such that $u_i'(t^*_i)=0$. Then from the definition of $T_{\lambda }^iu$ in (3.8), $(T_\lambda ^iu)(t_i^*)$ is the maximum value of $T_\lambda ^iu$ on [0, 1]. Obviously, $t^*_i\in (0,\frac{1}{2})$ or $t^*_i\in [\frac{1}{2},1)$. Without loss of generality, we consider the case $t_i^*\in [\frac{1}{2},1)$. The argument would be similar for the case $t_i^*\in (0,\frac{1}{2})$ and we omit its details here. Let us fix $\lambda \ge \lambda _i^{*}$ below.

For $t_i^*\in [\frac{1}{2},1)$ and any $\delta \in (0,\frac{1}{2})$, we have

$$\begin{aligned} \Vert T^i_\lambda u \Vert _{\infty }=(T^i_\lambda u)(t_i^*)&=\int _0^{t_i^*}\phi ^{-1}\left( \lambda \int _s^{t_i^*} r(\tau )g^i(u(\tau ))d\tau \right) ds\\&\ge \int _0^{\frac{1}{2}}\phi ^{-1}\left( \lambda _i^*\int _s^{\frac{1}{2}}r(\tau )g^i(u(\tau ))d\tau \right) ds\\&\ge \int _0^{\delta }\phi ^{-1}\left( \lambda _i^*\int _{\delta }^{\frac{1}{2}}r(\tau )g^i(u(\tau ))d\tau \right) ds\triangleq I_0. \end{aligned}$$

By the concavity of u, we obtain

$$\begin{aligned} u(t)\ge \frac{t}{t_i^*}\Vert u\Vert _{\infty }\ge \frac{\delta }{t_i^*}\Vert u\Vert _{\infty }>\delta \Vert u\Vert _{\infty },~\mathrm{~ for}~ t\in [\delta ,t_i^*]. \end{aligned}$$

Specially, setting $\delta =\frac{1}{2}(\frac{1}{2}+b_i)$, we get $u(t)\in (\frac{1}{2}(\frac{1}{2}+b_i)b_i, b_i]$ for $t\in [\frac{1}{2}(\frac{1}{2}+b_i),\frac{1}{2}]$. Hence,

$$\begin{aligned} I_0&>\int _{\frac{1}{4}(\frac{1}{2}-b_i)}^{\frac{1}{2}(\frac{1}{2}+b_i)}\phi ^{-1}\left( \lambda _i^{*}\int _{\frac{1}{2}(\frac{1}{2}+b_i)}^{\frac{1}{2}}r(\tau )g^i(u(\tau ))d\tau \right) ds\\&= \frac{1+6b_i}{8}\phi ^{-1}\left( \lambda _i^{*}\int _{\frac{1}{2}(\frac{1}{2}+b_i)}^{\frac{1}{2}}r(\tau )g^i(u(\tau ))d\tau \right) \\&\ge \frac{1+6b_i}{8}\phi ^{-1}\left( \lambda _i^{*}g^i_{min}\int _{\frac{1}{2}(\frac{1}{2}+b_i)}^{\frac{1}{2}}r(\tau )d\tau \right) \\&\ge b_i=\Vert u\Vert _{\infty }. \end{aligned}$$

Therefore, $\Vert T_{\lambda }^iu\Vert _\infty > \Vert u\Vert _\infty$ for $\lambda \ge \lambda _i^{*}$ and $u\in K\cap \partial \Omega _{b_i}$. The proof is completed. $\square$

Proof of Theorem 1.3

Let $b_i>0$ be such that $\frac{1}{2}(\frac{1}{2}+b_i)b_i \in \left( a_{i-1},\frac{1}{2}(\frac{1}{2}+a_i)a_i\right)$ for any $i\in \{1,2,\cdots ,m+1\}$. Then by Lemma 3.3, there exists $0<\lambda _i^{*}<\infty$ such that $\Vert T^i_\lambda u\Vert _\infty > \Vert u\Vert _\infty$ for $\lambda \ge \lambda _i^{*}$ and $u\in K\cap \partial \Omega _{b_i}$. On the other hand, by Lemma 3.2, $\Vert T^i_\lambda u\Vert _\infty \le \Vert u\Vert _\infty$ for $u\in K\cap \partial \Omega _{a_i}$. Therefore, by Lemma 2.1, for any $\lambda \ge \lambda _i^*$, operator $T^i_\lambda$ has a fixed point in $K\cap (\overline{\Omega _{a_i}}\setminus \Omega _{b_i})$, which is a positive solution of problem $(P_\lambda ^i)$, denoted by $u_{\lambda ,i}$, satisfying

$$\begin{aligned} a_{i-1}<b_i\le \Vert u_{\lambda ,i}\Vert _\infty \le a_i. \end{aligned}$$

(3.9)

Now we focus on problem $(P_\lambda )$. By Theorem 3.1, there exists $\lambda _*>0$, such that problem $(P_\lambda )$ has no positive solution for all $\lambda <\lambda _*$. Recall that any solution $u_{\lambda ,i}$ of problem $(P_\lambda ^i)$ is also a solution of problem $(P_\lambda )$ in Lemma 3.2. Combining with Lemma 3.1, we know $u_{\lambda ,i}(t)>0$ for $t\in (0,1)$ and so Theorem 1.3 (i) is derived. We set $\lambda ^*=\max \nolimits _{1\le i\le m+1}\lambda _i^*$, then problem $(P_\lambda )$ has at least $m+1$ distinct positive solutions $\{u_{\lambda ,i}\}_{i=1}^{m+1}$ for $\lambda \ge \lambda ^*$, which satisfy

$$\begin{aligned} 0&<b_1\le \Vert u_{\lambda ,1}\Vert _\infty \le a_1<b_2\le \Vert u_{\lambda ,2}\Vert _\infty \le a_2<\cdots \\&<b_m\le \Vert u_{\lambda ,m}\Vert _\infty \le a_m<b_{m+1}\le \Vert u_{\lambda ,m+1}\Vert _\infty <\frac{1}{2}, \end{aligned}$$

and thus Theorem 1.3 (ii) is deduced. The proof is completed. $\square$

We begin to investigate Calabi–Bernstein type asymptotic property of solution $u_{\lambda ,i}$, $i\in \{1,2,\cdots , m+1\}$, of Theorem  1.3. Before showing it, we give some lemmas for later use. The following lemma is essential to show the continuity of solutions of problem $(P_\lambda )$ with respect to $\lambda$.

Lemma 3.4

Let $\{(\lambda _n,u_{\lambda _n,i})\}$ $(n\in {\mathbb {N}})$ be a sequence of solution pairs of problem $(P_\lambda )$ such that $\lambda _n\rightarrow {\tilde{\lambda }}$ as $n\rightarrow \infty$. Then there exists a solution $u_{{\tilde{\lambda }},i}$ of problem $(P_\lambda )$ such that $\Vert u_{\lambda _n,i}-u_{{\tilde{\lambda }},i}\Vert _{\infty }\rightarrow 0$ as $n\rightarrow \infty$.

Proof

Since $\{(\lambda _n,u_{\lambda _n,i})\}$ is a sequence of solution pairs of problem $(P_\lambda )$ with $\lambda _n\rightarrow {\tilde{\lambda }}$, combining with the fact $\Vert u_{\lambda _n,i}\Vert _\infty <\frac{1}{2}$ and by Arzelà-Ascoli theorem, we obtain a subsequence, say $\{u_{\lambda _n,i}\}$ again and a function $u_{{\tilde{\lambda }},i}\in C[0,1]$ such that $u_{\lambda _n,i}\rightarrow u_{{\tilde{\lambda }},i}$ in C[0, 1]. We still need to show that $u_{{\tilde{\lambda }},i}$ is a solution of problem $(P_\lambda )$ at $\lambda ={\tilde{\lambda }}$. Similar to Remark 2.1, we see $r(\cdot )g(u(\cdot ))\in L^1(0,1)$. It suffices to show that $u_{{\tilde{\lambda }},i}$ is a fixed point of operator $T_\lambda$ at $\lambda ={\tilde{\lambda }}$, where $T_\lambda : K \rightarrow K$ is obtained after replacing f by $\lambda g$ in T given in (2.1), that is,

$$\begin{aligned} (T_\lambda u)(t)= {\left\{ \begin{array}{ll} \int _0^t\phi ^{-1}\left( \alpha +\int _s^{\sigma }\lambda r(\tau )g(u(\tau ))d\tau \right) ds,~&{} t\in (0,\sigma ],\\ \int ^1_t\phi ^{-1}\left( -\alpha +\int ^s_{\sigma }\lambda r(\tau )g(u(\tau ))d\tau \right) ds,~&{} t\in [\sigma ,1), \end{array}\right. } \end{aligned}$$

where $\sigma \in (0,1)$ is fixed in any fashion and $\alpha \left( \triangleq \alpha (\lambda rg(u))\right) :L^1(0,1)\rightarrow {\mathbb {R}}$ satisfies

$$\begin{aligned} \int _0^\sigma \phi ^{-1}\left( \alpha +\int _s^\sigma \lambda r(\tau )g(u(\tau ))d\tau \right) ds=\int _\sigma ^1\phi ^{-1}\left( -\alpha +\int ^s_\sigma \lambda r(\tau )g(u(\tau ))d\tau \right) ds. \end{aligned}$$

(3.10)

Indeed, $\alpha$ is continuous with respect to $\lambda rg(u)$ and maps equi-integrable sets of $L^1$ into bounded sets, similar continuous functions were constructed in [24, 28, 31, 32] and also $T_\lambda$ is completely continuous.

From the definition of sequence $\{(\lambda _n,u_{\lambda _n,i})\}$ and (3.10), together with the continuity of $\alpha$, we get a sequence $\{\alpha _n\}\left( \alpha _n\triangleq \alpha _n(\lambda _n rg(u_{\lambda _n,i}))\right)$ satisfying $\alpha _n\rightarrow {\tilde{\alpha }}\left( \triangleq {\tilde{\alpha }}({\tilde{\lambda }} rg(u_{{\tilde{\lambda }},i}))\right)$. Obviously, ${\tilde{\alpha }}$ satisfies

$$\begin{aligned} \int _0^\sigma \phi ^{-1}\left( {\tilde{\alpha }}+\int _s^\sigma {\tilde{\lambda }} r(\tau )g(u_{{\tilde{\lambda }},i}(\tau ))d\tau \right) ds=\int _\sigma ^1\phi ^{-1}\left( -{\tilde{\alpha }}+\int ^s_\sigma {\tilde{\lambda }} r(\tau )g(u_{{\tilde{\lambda }},i}(\tau ))d\tau \right) ds. \end{aligned}$$

By the Lebesgue dominated convergence theorem, it follows from the fact $u_{\lambda _n,i}=T_{\lambda } u_{\lambda _n,i}$ at $\lambda =\lambda _n$ that

$$\begin{aligned} u_{{\tilde{\lambda }},i}&=\lim \limits _{n\rightarrow \infty }u_{\lambda _n,i}=\lim \limits _{n\rightarrow \infty }(T_{\lambda } u_{\lambda _n,i})(t)\\&= {\left\{ \begin{array}{ll} \int _0^t\lim \limits _{n\rightarrow \infty }\phi ^{-1}\left( \alpha _n+\int _s^{\sigma }\lambda _n r(\tau )g(u_{\lambda _n,i}(\tau ))d\tau \right) ds,~&{} t\in (0,\sigma ],\\ \int ^1_t\lim \limits _{n\rightarrow \infty }\phi ^{-1}\left( -\alpha _n+\int ^s_{\sigma }\lambda _n r(\tau )g(u_{\lambda _n,i}(\tau ))d\tau \right) ds,~&{} t\in [\sigma ,1), \end{array}\right. } \\ {}&= {\left\{ \begin{array}{ll} \int _0^t\phi ^{-1}\left( \lim \limits _{n\rightarrow \infty }\alpha _n+\int _s^{\sigma }\lim \limits _{n\rightarrow \infty }\lambda _n r(\tau )g(u_{\lambda _n,i}(\tau ))d\tau \right) ds,~&{} t\in (0,\sigma ],\\ \int ^1_t\phi ^{-1}\left( -\lim \limits _{n\rightarrow \infty }\alpha _n+\int ^s_{\sigma }\lim \limits _{n\rightarrow \infty }\lambda _n r(\tau )g(u_{\lambda _n,i}(\tau ))d\tau \right) ds,~&{} t\in [\sigma ,1), \end{array}\right. } \\ {}&= {\left\{ \begin{array}{ll} \int _0^t\phi ^{-1}\left( {\tilde{\alpha }}+\int _s^{\sigma }{\tilde{\lambda }} r(\tau )g(u_{{\tilde{\lambda }},i}(\tau ))d\tau \right) ds,~&{} t\in (0,\sigma ],\\ \int ^1_t\phi ^{-1}\left( -{\tilde{\alpha }}+\int ^s_{\sigma }{\tilde{\lambda }} r(\tau )g(u_{{\tilde{\lambda }},i}(\tau ))d\tau \right) ds,~&{} t\in [\sigma ,1). \end{array}\right. } \end{aligned}$$

Therefore, $u_{{\tilde{\lambda }},i}$ is a fixed point of $T_\lambda u$ at $\lambda ={\tilde{\lambda }}$ and the proof is done. $\square$

From Theorem 1.3 and Lemma 3.4, we conclude that positive solution pairs $(\lambda ,u_{\lambda ,i})$ of problem $(P_\lambda )$ may form at least $m+1$ connected curves for all $\lambda \ge \lambda ^*$ in which any element is a positive solution pair of problem $(P_\lambda ^i)$ and of problem $(P_\lambda )$ as well. Let us denote ${\mathcal {C}}_i\triangleq {\mathcal {C}}_i(\lambda ,u_{\lambda ,i})$, $i\in \{1,2,\cdots ,m+1\}$ as the connected curve going through solution pair $(\lambda , u_{\lambda ,i})$ in which $u_{\lambda ,i}$ comes from Theorem 1.3. Then ${\mathcal {C}}_i$ goes to infinity in $\lambda$-direction.

Note that any positive solution $u_{\lambda ,i}$ of problem $(P_\lambda )$ is concave on (0, 1). Using 0-Dirichlet boundary conditions and the mean value theorem, $u_{\lambda ,i}'$ has at least one zero on (0, 1). Denote ${\underline{t}}_{i,0}^{\lambda }(u_{\lambda ,i}',\lambda )\triangleq \inf \{t\in (0,1):u_{\lambda ,i}'(t)=0\}$ and ${\overline{t}}_{i,0}^{\lambda }(u_{\lambda ,i}',\lambda )\triangleq \sup \{t\in (0,1):u_{\lambda ,i}'(t)=0\}$. For simplicity, we denote ${\underline{t}}_{i,0}^{\lambda }(u_{\lambda ,i}',\lambda )$, ${\overline{t}}_{i,0}^{\lambda }(u_{\lambda ,i}',\lambda )$ by ${\underline{t}}_{i,0}^{\lambda }$, ${\overline{t}}_{i,0}^{\lambda }$, respectively.

In the following lemma, we consider some properties related to solution $u_{\lambda ,i}$ of problem $(P_\lambda ^i)$ for fixed $\lambda$ and to be concise, we denote $u_{\lambda ,i}$ by $u_i$ with no confusion.

Lemma 3.5

Let $0\le g_0^i<\infty$ and $u_i$ be a positive solution of problem $(P_\lambda ^i)$, then $0<{\underline{t}}_{i,0}^{\lambda }\le {\overline{t}}_{i,0}^{\lambda }<1$.

Proof

The proof is inspired by the one of Theorem 2.1 in [41]. We only prove ${\underline{t}}_{i,0}^{\lambda }>0.$ The rest can be obtained after suitable modifications. On the contrary, suppose ${\underline{t}}_{i,0}^{\lambda }=0$ (a similar argument can be applied for the case ${\overline{t}}_{i,0}^{\lambda }=1$). Then there exists a sequence $\{t_n\}$ with $t_n\in (0,1)$ satisfying $u_i'(t_n)=0$ and $t_n\rightarrow 0$ as $n\rightarrow \infty$. By the mean value theorem, there exists $\xi \in (0,t)$ for any $t\in (0,1)$ such that

$$\begin{aligned} u_i(t)=|u_i(t)-u_i(0)|=|u_i'(\xi )|t< t,~\textrm{for}~t\in (0,1), \end{aligned}$$

and combining with the boundary conditions, we obtain

$$\begin{aligned} u_i(t)\le t,~\textrm{for}~t\in [0,1]. \end{aligned}$$

(3.11)

Similarly,

$$\begin{aligned} u_i(t)\le 1-t,~\textrm{for}~t\in [0,1]. \end{aligned}$$

(3.12)

By the condition $0\le g_0^i<\infty$, we obtain, for some $c\triangleq c(\Vert u_i\Vert _\infty )>0$,

$$\begin{aligned} g^i\big (u_i(t)\big )\le cu_i(t)^{q},~\textrm{for}~t\in [0,1]. \end{aligned}$$

(3.13)

Since $r\in {\mathcal {A}}_q$, we choose a small constant $\gamma _0>0$ satisfying

$$\begin{aligned} c\int _0^{\gamma _0} \lambda \tau ^{q} r(\tau )d\tau <1. \end{aligned}$$

(3.14)

We take ${N_0} \in {\mathbb {N}}$ large enough such that $0<t_n<\gamma _0$ for all $n\ge {N_0}$ and consider terms $t_n's$ for all $n\ge {N_0}$. Integrating the first equation in problem $(P_\lambda ^i)$ on $(t, t_n)$ for $t\in (0,t_n)$, we obtain

$$\begin{aligned} \phi (u_i'(t))=\int ^{t_n}_t \lambda r(\tau )g^i\big (u_i(\tau )\big ){d}\tau . \end{aligned}$$

It follows that

$$\begin{aligned} u_i'(t)=\phi ^{-1}\left( \int ^{t_n}_t \lambda r(\tau )g^i\big (u_i(\tau )\big ){d}\tau \right) . \end{aligned}$$

(3.15)

Integrating the above equation on (0, t) for $t\in (0,t_n)$, we get

$$\begin{aligned} u_i(t)=\int _0^t \phi ^{-1}\left( \int ^{t_n}_s \lambda r(\tau )g^i\big (u_i(\tau )\big ){d}\tau \right) ds. \end{aligned}$$

By (3.11) and (3.13), for $t\in (0,t_n)$, setting $\Vert u_i\Vert _{t_n,\infty }\triangleq \max \nolimits _{0\le t\le t_n}|u_i(t)|$ and applying the Fubini’s theorem, we have

$$\begin{aligned} |u_i(t)|&\le \int _0^t c\int ^{t_n}_s \lambda r(\tau )|u_i(\tau )|^{q}{d}\tau ds\\&\le c \int _0^{t_n} \int ^{t_n}_s \lambda r(\tau )|u_i(\tau )|^{q}{d}\tau ds\\&= c \int ^{t_n}_0 \lambda \tau r(\tau )|u_i(\tau )|^{q}{d}\tau \\&\le c \int ^{t_n}_0 \lambda \tau ^{q} r(\tau ){d}\tau \Vert u_i\Vert _{t_n,\infty }. \end{aligned}$$

Using (3.14), we obtain $\Vert u_i\Vert _{t_n,\infty }= 0$ for all $n\ge {N_0}$, i.e., $u_i$ is identically zero on $[0,t_n]$ for all $n\ge {N_0}$. Thus we may assume that $u_i(t_n) = u_i'(t_n) =0$ for sufficiently large n. For $t\in [t_n,1]$, by (3.12) and (3.13), using the Fubini’s theorem again, we obtain

$$\begin{aligned} |u_i(t)|&=\left| \int ^{t}_{t_n}\phi ^{-1}\left( \int ^{s}_{t_n}\lambda r(\tau )g^i\big (u_i(\tau )\big ){d}\tau \right) ds\right| \\&\le \int ^{t}_{t_n}\int ^{s}_{t_n}\lambda r(\tau )\left| g^i\big (u_i(\tau )\big )\right| d\tau ds\\&=\int ^{t}_{t_n}\lambda (t-\tau )r(\tau )\left| g^i\big (u_i(\tau )\big )\right| d\tau \\&\le c\int ^{t}_{t_n}\lambda (1-\tau )r(\tau )|u_i(\tau )|^{q}d\tau \\&\le c\int ^{t}_{t_n}\lambda (1-\tau )^{q}r(\tau )|u_i(\tau )|d\tau . \end{aligned}$$

By the Gronwall–Bellman inequality, we obtain $u_i(t)= 0$ for $t\in [t_n,1]$. Thus, $u_i\equiv 0$ on [0, 1] and this is a contradiction. Hence, ${\underline{t}}_{i,0}^{\lambda }>0$ and the proof is done. $\square$

Lemma 3.6

Let $(\lambda ,u_{\lambda ,i})\in {\mathcal {C}}_i$, then $0<\liminf \nolimits _{\lambda \rightarrow \infty }{\underline{t}}_{i,0}^{\lambda }\le \limsup \nolimits _{\lambda \rightarrow \infty }{\underline{t}}_{i,0}^{\lambda }<1$ and $0<\liminf \nolimits _{\lambda \rightarrow \infty }{\overline{t}}_{i,0}^{\lambda }\le \limsup \nolimits _{\lambda \rightarrow \infty }{\overline{t}}_{i,0}^{\lambda }<1$.

Proof

Without loss of generality, we take an arbitrary element in the set $\{\liminf \nolimits _{\lambda \rightarrow \infty }{\underline{t}}_{i,0}^{\lambda }, \limsup \nolimits _{\lambda \rightarrow \infty }{\underline{t}}_{i,0}^{\lambda }, \liminf \nolimits _{\lambda \rightarrow \infty }{\overline{t}}_{i,0}^{\lambda },\limsup \nolimits _{\lambda \rightarrow \infty }{\overline{t}}_{i,0}^{\lambda }\}$, denoted as $\beta$. Claim that $0<\beta <1$. Then the results will be obtained.

We now show $\beta >0$. To prove it by contradiction, we suppose on the contrary that $\beta =0$. Then there exist sequences $\{(\lambda _n,u_{\lambda _n,i})\}\subset {\mathcal {C}}_i$ $(n\in {\mathbb {N}})$ of solution pairs of problem $(P_\lambda ^i)$ and $\{t_{i,0}^{n}\}$ of zeros of the corresponding $\{u_{\lambda _n,i}'\}$ satisfying

• (i) $\lambda _n\rightarrow \infty$ as $n\rightarrow \infty$;

• (ii) $a_{i-1}<b_i\le \Vert u_{\lambda _n,i}\Vert _\infty \le a_i$;

• (iii) $t_{i,0}^{n}\in (0,1)$ and $t_{i,0}^{n}\rightarrow 0$ as $n\rightarrow \infty$.

From definitions of ${\mathcal {C}}_i$ and $\beta$, sequences $\{(\lambda _n,u_{\lambda _n,i})\}$ and $\{t_{i,0}^{n}\}$ make sense.

Using the fact $\Vert u'_{\lambda _n,i}\Vert _{\infty }<1$ for any $n\in {\mathbb {N}}$ and definition of $\{t_{i,0}^{n}\}$, we get

$$\begin{aligned} \Vert u_{\lambda _n,i}\Vert _{\infty }=u_{\lambda _n,i}(t_{i,0}^{n}) = \int _0^{t_{i,0}^{n}} u'_{\lambda _n,i}(\tau )d\tau < t_{i,0}^{n}. \end{aligned}$$

Since $t_{i,0}^{n}\rightarrow 0$ as $n\rightarrow \infty$, we infer $\Vert u_{\lambda _n,i}\Vert _{\infty }\rightarrow 0$ as $n\rightarrow \infty$, which contradicts the above (ii) and thus $\beta >0$. Similarly, we can prove $\beta <1$ and the proof is done. $\square$

Lemma 3.7

Assume that there exists a sequence $\{(\lambda _n,u_{\lambda _n,i})\}\subset {\mathcal {C}}_i$ $(n\in {\mathbb {N}})$ satisfying

• (i) $\lambda _n\rightarrow \infty$ as $n\rightarrow \infty$;

• (ii) $a_{i-1}<b_i\le \Vert u_{\lambda _n,i}\Vert _\infty \le a_i$.

Denote ${\underline{t}}_{i,0}^{n}\triangleq \inf \{t\in (0,1):u_{\lambda _n,i}'(t)=0\}$. Also assume $\lim \nolimits _{n\rightarrow \infty }{\underline{t}}_{i,0}^{n}=\beta$. Then $\lim \nolimits _{n\rightarrow \infty }u_{\lambda _n,i}'(t)=1~uniformly~on~[0,\beta -\varepsilon ]$, for sufficiently small $\varepsilon >0$.

Proof

By Lemma 3.6, $0<\beta <1$. Directly from the definition of $\beta$, for any small $\varepsilon _0>0$, there exists $N\in {\mathbb {N}}$ such that $\beta -\varepsilon _0<{\underline{t}}_{i,0}^{n}<\beta +\varepsilon _0$ for all $n>N.$ By (ii), $\Vert u_{\lambda _n,i}\Vert _\infty \ge b_i$ for all $n>N$ and together with Lemma 3.1, $u_{\lambda _n,i}(t)>0$ for $t\in (0,1)$ and all $n>N$. Since $u_{\lambda _n,i}$ is concave and $u_{\lambda _n,i}'(t)$ is nonincreasing on (0, 1), we see

$$\begin{aligned} \Vert u_{\lambda _n,i}\Vert _\infty =u_{\lambda _n,i}({\underline{t}}_{i,0}^{n})=\max \limits _{t\in [0,{\underline{t}}_{i,0}^n]}u_{\lambda _n,i}(t)=\max \limits _{[{\underline{t}}_{i,0}^n,1]}u_{\lambda _n,i}(t). \end{aligned}$$

Moreover,

$$\begin{aligned} u_{\lambda _n,i}(t)\ge \frac{t}{{\underline{t}}_{i,0}^n}\Vert u_{\lambda _n,i}\Vert _\infty ,~t\in [0,{\underline{t}}_{i,0}^n]. \end{aligned}$$

(3.16)

Specially, setting $t\ge \frac{2a_{i-1}}{a_{i-1}+b_i}{\underline{t}}_{i,0}^n$ in (3.16), we get

$$\begin{aligned} u_{\lambda _n,i}(t)\ge \frac{2a_{i-1}b_i}{a_{i-1}+b_i}>a_{i-1}, \end{aligned}$$

for $t\in [\frac{2a_{i-1}}{a_{i-1}+b_i}{\underline{t}}_{i,0}^n,{\underline{t}}_{i,0}^n]$. Let us fix $\varepsilon _0\in (0,\frac{b_i-a_{i-1}}{4a_{i-1}+2b_i}\beta )$ and $\varepsilon _1\in \left( \frac{2a_{i-1}}{a_{i-1}+b_i}(\beta +\varepsilon _0),\beta -2\varepsilon _0\right)$. Then from (3.16), we deduce

$$\begin{aligned} \min \limits _{t\in [\varepsilon _1,{\underline{t}}_{i,0}^n]}u_{\lambda _n,i}(t)\ge \frac{\varepsilon _1}{{\underline{t}}_{i,0}^{n}}\Vert u_{\lambda _n,i}\Vert _\infty \ge \frac{2a_{i-1}(\beta +\varepsilon _0)}{(a_{i-1}+b_i){\underline{t}}_{i,0}^{n}}\Vert u_{\lambda _n,i}\Vert _\infty> \frac{2a_{i-1}b_i}{a_{i-1}+b_i}>a_{i-1}, \end{aligned}$$

for all $n>N$. Let $t\in [\varepsilon _1,\beta -\varepsilon _0]$. Obviously, $t\in [\varepsilon _1,{\underline{t}}_{i,0}^{n}]$ for all $n>N$ since $\beta -\varepsilon _0<{\underline{t}}_{i,0}^{n}.$ Since $u_{\lambda _n,i}$ is strictly increasing on $(0,{\underline{t}}_{i,0}^{n})$, we get

$$\begin{aligned} a_{i-1}<u_{\lambda _n,i}(t)<a_i,~ \mathrm{for \ all} \ t\in [\varepsilon _1,\beta -\varepsilon _0]. \end{aligned}$$

Hence there exists $M_0(=M_0(\varepsilon _1))>0$ such that

$$\begin{aligned} g^i(u_{\lambda _n,i}(t))>M_0,~ \mathrm{for \ all} \ t\in [\varepsilon _1,\beta -\varepsilon _0]. \end{aligned}$$

Let us first consider $t\in [\varepsilon _1,\beta -2\varepsilon _0]$, then we get

$$\begin{aligned} \int _t^{\beta -\varepsilon _0}r(\tau )g^i(u_{\lambda _n,i}(\tau ))d\tau>M_0\int _{\beta -2\varepsilon _0}^{\beta -\varepsilon _0}r(\tau )d\tau >0, \end{aligned}$$

which implies

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\lambda _n\int _t^{\beta -\varepsilon _0}r(\tau )g^i(u_{\lambda _n,i}(\tau ))d\tau =\infty , \end{aligned}$$

for $t\in [\varepsilon _1,\beta -2\varepsilon _0].$ Similar to (3.15),

$$\begin{aligned} u_{\lambda _n,i}'(t)=\phi ^{-1}\left( \lambda _n\int _t^{{\underline{t}}_{i,0}^n}r(\tau )g^i(u_{\lambda _n,i}(\tau ))d\tau \right) . \end{aligned}$$

Since

$$\begin{aligned} \phi ^{-1}\left( \lambda _n\int _t^{{\underline{t}}_{i,0}^n}r(\tau )g^i(u_{\lambda _n,i}(\tau ))d\tau \right) \ge \phi ^{-1}\left( \lambda _n\int _t^{\beta -\varepsilon _0}r(\tau )g^i(u_{\lambda _n,i}(\tau ))d\tau \right) , \end{aligned}$$

and $\phi ^{-1}\left( \lambda _n\int _t^{\beta -\varepsilon _0}r(\tau )g^i(u_{\lambda _n,i}(\tau ))d\tau \right) \rightarrow 1$ as $n\rightarrow \infty$, it follows that $\lim \nolimits _{n\rightarrow \infty }u_{\lambda _n,i}'(t)\ge 1$ for all $t\in [\varepsilon _1,\beta -2\varepsilon _0]$. Since $u_{\lambda _n,i}'(t)<1$ for $t\in [0,1]$ and any n, it yields

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }u_{\lambda _n,i}'(t)=1,~\mathrm{uniformly~ on}~ [\varepsilon _1,\beta -2\varepsilon _0]. \end{aligned}$$

(3.17)

For $t\in [0,\varepsilon _1]$, from the fact

$$\begin{aligned} u_{\lambda _n,i}'(t)&=\phi ^{-1}\left( \lambda _n\big (\int _t^{\varepsilon _1}+\int _{\varepsilon _1}^{{\underline{t}}_{i,0}^n}\big )r(s)g^i(u_{\lambda _n,i}(s))ds\right) \\&\ge \phi ^{-1}\left( \lambda _n\int _{\varepsilon _1}^{{\underline{t}}_{i,0}^n}r(s)g^i(u_{\lambda _n,i}(s))ds\right) =u'_{\lambda _n,i}(\varepsilon _1), \end{aligned}$$

we have

$$\begin{aligned} \lim \nolimits _{n\rightarrow \infty }u_{\lambda _n,i}'(t)=1~\mathrm{uniformly~ on}~ [0,\varepsilon _1]. \end{aligned}$$

(3.18)

By combining (3.17) and (3.18), we obtain $\lim \nolimits _{n\rightarrow \infty }u_{\lambda _n,i}'(t)=1,$ uniformly on $[0,\beta -2\varepsilon _0],$ and we conclude

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }u_{\lambda _n,i}'(t)=1~\mathrm{uniformly~ on}~ [0,\beta -\varepsilon ], ~\mathrm{for~ sufficiently~ small}~ \varepsilon >0. \end{aligned}$$

$\square$

Similar to Lemma 3.7, we get the following lemma.

Lemma 3.8

Assume that there exists a sequence $\{(\lambda _n,u_{\lambda _n,i})\}\subset {\mathcal {C}}_i$ $(n\in {\mathbb {N}})$ satisfying

• (i) $\lambda _n\rightarrow \infty$ as $n\rightarrow \infty$;

• (ii) $a_{i-1}<b_i\le \Vert u_{\lambda _n,i}\Vert _\infty \le a_i$.

Denote ${\overline{t}}_{i,0}^{n}\triangleq \sup \{t\in (0,1):u_{\lambda _n,i}'(t)=0\}$. Also assume $\lim \nolimits _{n\rightarrow \infty }{\overline{t}}_{i,0}^{n}=\beta$. Then $\lim \nolimits _{n\rightarrow \infty }u_{\lambda _n,i}'(t)=-1~uniformly~on~[\beta +\varepsilon ,1]$, for sufficiently small $\varepsilon >0$.

Lemma 3.9

Let $(\lambda ,u_{\lambda ,i})\in {\mathcal {C}}_i$, then

• (a) $\liminf \nolimits _{\lambda \rightarrow \infty }{\underline{t}}_{i,0}^{\lambda }=\limsup \nolimits _{\lambda \rightarrow \infty }{\underline{t}}_{i,0}^{\lambda }=a_i$ and $\liminf \nolimits _{\lambda \rightarrow \infty }{\overline{t}}_{i,0}^{\lambda }=\limsup \nolimits _{\lambda \rightarrow \infty }{\overline{t}}_{i,0}^{\lambda }=1-a_i$, $i\in \{1,2,\cdots ,m+1\}$;

• (b) $\lim \nolimits _{\lambda \rightarrow \infty } u_{\lambda ,i}'(t)=0~uniformly~on~[a_i+\varepsilon ,1-a_i-\varepsilon ]$, for sufficiently small $\varepsilon >0$, $i\in \{1,2,\cdots ,m\}$;

• (c) $\lim \nolimits _{\lambda \rightarrow \infty } \Vert u_{\lambda ,i}\Vert _\infty =a_i$, $i\in \{1,2,\cdots ,m+1\}$.

Proof

Let $\{(\lambda _n,u_{\lambda _n,i})\}\subset {\mathcal {C}}_i$ be a sequence of solution pairs of problem $(P_\lambda ^i)$ such that

• (i) $\lim \nolimits _{n\rightarrow \infty }\lambda _n=\infty$;

• (ii) $a_{i-1}<b_i\le \Vert u_{\lambda _n,i}\Vert _\infty \le a_i$.

From Theorem 1.3, we see that such sequence makes sense. Then, we can get two sequences $\{{\underline{t}}_{i,0}^{n}\}$ and $\{{\overline{t}}_{i,0}^{n}\}$ where ${\underline{t}}_{i,0}^{n}\triangleq \inf \{t\in (0,1):u_{\lambda _n,i}'(t)=0\}$ and ${\overline{t}}_{i,0}^{n}\triangleq \sup \{t\in (0,1):u_{\lambda _n,i}'(t)=0\}$. Due to the fact that $\Vert u_{\lambda _n,i}'\Vert _{\infty }\le 1$ and Arzelà–Ascoli theorem, we obtain a subsequence, say $\{u_{\lambda _n,i}\}$ again and a function $v\in C[0,1]$ such that $u_{\lambda _n,i}\rightarrow v$ in C[0, 1] as $n\rightarrow \infty$. Correspondingly, we obtain two subsequences, named $\{{\underline{t}}^{n}_{i,0}\}$ and $\{{\overline{t}}^{n}_{i,0}\}$ again. It follows from Lemma 3.6 that

$$\begin{aligned}&0<\liminf \nolimits _{n\rightarrow \infty }{\underline{t}}_{i,0}^{n}\le \limsup \nolimits _{n\rightarrow \infty }{\underline{t}}_{i,0}^{n}<1~\mathrm{~and}\\&0<\liminf \nolimits _{n\rightarrow \infty }{\overline{t}}_{i,0}^{n}\le \limsup \nolimits _{n\rightarrow \infty }{\overline{t}}_{i,0}^{n}<1. \end{aligned}$$

To prove $\liminf \nolimits _{n\rightarrow \infty }{\underline{t}}_{i,0}^{n}=\limsup \nolimits _{n\rightarrow \infty }{\underline{t}}_{i,0}^{n}=a_i$ and $\liminf \nolimits _{n\rightarrow \infty }{\overline{t}}_{i,0}^{n}=\limsup \nolimits _{n\rightarrow \infty }{\overline{t}}_{i,0}^{n}=1-a_i$, it suffices to show that any two subsequences of $\{{\underline{t}}_{i,0}^n\}$ and $\{{\overline{t}}_{i,0}^n\}$ converge to $a_i$ and $1-a_i$, respectively. We consider subsequences, name $\{{\underline{t}}_{i,0}^n\}$ and $\{{\overline{t}}_{i,0}^n\}$ again, if necessary in the following. Denote

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } {\underline{t}}_{i,0}^n={\underline{t}}_{i,0}^{\infty }~\textrm{and}~ \lim \nolimits _{n\rightarrow \infty } {\overline{t}}_{i,0}^n={\overline{t}}_{i,0}^{\infty }. \end{aligned}$$

We divide the rest into four steps:

Step 1. Claim that $0<{\underline{t}}_{i,0}^{\infty }\le a_i$ and $1-a_i\le {\overline{t}}_{i,0}^{\infty }<1$, for any $i\in \{1,2,\cdots ,m+1\}$.

Without loss of generality, we prove $0<{\underline{t}}_{i,0}^{\infty }\le a_i$ and the other can be proved by a similar argument after suitable modifications. Suppose on the contrary that ${\underline{t}}_{i,0}^{\infty }>a_i$. Recall the result in Lemma 3.7 that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }u_{\lambda _n,i}'(t)=1,\mathrm{~uniformly~on~} [0,{\underline{t}}_{i,0}^{\infty }-\varepsilon _1], \mathrm{~for ~sufficiently ~small~} \varepsilon _1>0. \end{aligned}$$

(3.19)

For any small $\varepsilon _0>0$, there exists $N(\varepsilon _0)\in {\mathbb {N}}$ such that

$$\begin{aligned} {\underline{t}}_{i,0}^n>{\underline{t}}_{i,0}^\infty -\varepsilon _0, ~\mathrm{for~ all}~ n\ge N(\varepsilon _0). \end{aligned}$$

Specially, we set $0<\varepsilon _1<\frac{{\underline{t}}_{i,0}^\infty -a_i}{2}$ and $\varepsilon _0=\varepsilon _1$ in the following proof. Noting $u_{\lambda _n,i}'(t)\ge 0$ for $t\in [0,{\underline{t}}_{i,0}^n]$, we get

$$\begin{aligned} u_{\lambda _n,i}({\underline{t}}_{i,0}^n)&=\int _{0}^{{\underline{t}}_{i,0}^n}u_{\lambda _n,i}'(\tau )d\tau \ge \int _0^{{\underline{t}}_{i,0}^n-\varepsilon _1}u_{\lambda _n,i}'(\tau )d\tau \nonumber \\&\ge \int _{0}^{{\underline{t}}_{i,0}^\infty -2\varepsilon _1}u_{\lambda _n,i}'(\tau )d\tau , ~\mathrm{for~ all}~ n\ge N(\varepsilon _1). \end{aligned}$$

(3.20)

Taking $\varepsilon _2>0$ sufficiently small satisfying

$$\begin{aligned} 0<\varepsilon _2<\frac{{\underline{t}}_{i,0}^\infty -2\varepsilon _1-a_i}{{\underline{t}}_{i,0}^\infty -2\varepsilon _1}, \end{aligned}$$

by applying (3.19), we may choose $N(\varepsilon _2)>0$ such that

$$\begin{aligned} 1-\varepsilon _2<u_{\lambda _n,i}'(t)<1~\mathrm{~for~ all} ~n>N(\varepsilon _2)~ \mathrm{~and} ~t\in [0,{\underline{t}}_{i,0}^\infty -\varepsilon _1]. \end{aligned}$$

Since $\varepsilon _2$ satisfies $(1-\varepsilon _2)({\underline{t}}_{i,0}^\infty -2\varepsilon _1)>a_i$, from (3.20), we have

$$\begin{aligned} u_{\lambda _n,i}({\underline{t}}_{i,0}^n)\ge \int _0^{{\underline{t}}_{i,0}^\infty -2\varepsilon _1}u_{\lambda _n,i}'(\tau )d\tau>(1-\varepsilon _2)({\underline{t}}_{i,0}^\infty -2\varepsilon _1)>a_i, \end{aligned}$$

for all $n\ge \max \{N(\varepsilon _1),N(\varepsilon _2)\}.$ Thus we get

$$\begin{aligned} a_i\ge v({\underline{t}}_{i,0}^\infty )=\lim \limits _{n\rightarrow \infty }u_{\lambda _n,i}({\underline{t}}_{i,0}^n)>a_i. \end{aligned}$$

This contradiction proves ${\underline{t}}_{i,0}^{\infty }\le a_i$. Similarly, we can show $1-a_i\le {\overline{t}}_{i,0}^{\infty }<1$.

Step 2. Claim that ${\underline{t}}_{i,0}^{\infty }= a_i$ and ${\overline{t}}_{i,0}^{\infty }= 1-a_i$, for any $i\in \{1,2,\cdots ,m+1\}$.

Suppose that $0<{\underline{t}}_{i,0}^{\infty }<a_i$. Then, for $0<\varepsilon _3<\frac{a_i-{\underline{t}}_{i,0}^{\infty }}{4}$, there exists $N(\varepsilon _3)\in {\mathbb {N}}$ such that

$$\begin{aligned} {\underline{t}}_{i,0}^{\infty }-\varepsilon _3<{\underline{t}}_{i,0}^n<{\underline{t}}_{i,0}^{\infty }+\varepsilon _3,~\mathrm{for~ all}~ n>N(\varepsilon _3). \end{aligned}$$

Similarly, for $0<\varepsilon _4<\frac{1-a_i-{\underline{t}}_{i,0}^{\infty }}{4}$, there exists $N(\varepsilon _4)\in {\mathbb {N}}$ such that

$$\begin{aligned} {\overline{t}}_{i,0}^{\infty }-\varepsilon _4<{\overline{t}}_{i,0}^n<{\overline{t}}_{i,0}^{\infty }+\varepsilon _4, ~\mathrm{for~ all}~ n>N(\varepsilon _4). \end{aligned}$$

Recall that $1-a_i\le {\overline{t}}_{i,0}^{\infty }<1$ in Step 1 and denote $N_3\triangleq \max \{N(\varepsilon _3),N(\varepsilon _4)\}$. Then, for $n>N_3$, we have

$$\begin{aligned} {\underline{t}}_{i,0}^n<\frac{a_i+3{\underline{t}}_{i,0}^{\infty }}{4}<\frac{3(1-a_i)+{\underline{t}}_{i,0}^{\infty }}{4}<{\overline{t}}_{i,0}^n. \end{aligned}$$

Since

$$\begin{aligned} u_{\lambda _n,i}({\underline{t}}_{i,0}^n)=\int _{0}^{{\underline{t}}_{i,0}^n}u_{\lambda _n,i}'(\tau )d\tau<{\underline{t}}_{i,0}^n<\frac{a_i+3{\underline{t}}_{i,0}^{\infty }}{4}<a_i, ~\mathrm{for~ all}~ n\ge N_3, \end{aligned}$$

we get $b_i\le \Vert u_{\lambda _n,i}\Vert _{\infty }<a_i$ for all $n\ge N_3$. Combining with the concavity of $u_{\lambda _n,i}$ on [0, 1], we deduce

$$\begin{aligned} u_{\lambda _n,i}'(t)=0,~u_{\lambda _n,i}(t)=\Vert u_{\lambda _n,i}\Vert _{\infty }\in [b_i,a_i)~\mathrm{~ on}~ t\in [{\underline{t}}_{i,0}^n,{\overline{t}}_{i,0}^n],~\mathrm{for~ all}~ n, \end{aligned}$$

and so $g^i(u_{\lambda _n,i})>0$ on $t\in [{\underline{t}}_{i,0}^n,{\overline{t}}_{i,0}^n]$, for all $n\ge N_3$. However, from the calculation

$$\begin{aligned} 0=u_{\lambda _n,i}'({\overline{t}}_{i,0}^n)=-\phi ^{-1}\left( \lambda _n\int ^{{\overline{t}}_{i,0}^n}_{{\underline{t}}_{i,0}^n}r(s)g^i(u_{\lambda _n,i}(s))ds\right) <0, ~~\mathrm{for~ all}~n\ge N_3, \end{aligned}$$

we get a contradiction. Hence ${\underline{t}}_{i,0}^{\infty }= a_i$. By a similar fashion, we also conclude ${\overline{t}}_{i,0}^{\infty }= 1-a_i$. Consequently, result (a) is obtained.

Step 3. Prove that $\lim \nolimits _{n\rightarrow \infty } u_{\lambda _n,i}'(t)=0~uniformly~on~[a_i+\varepsilon ,1-a_i-\varepsilon ]$, for sufficiently small $\varepsilon >0$, $i\in \{1,2,\cdots ,m\}$.

By the concavity of $u_{\lambda _n,i}$ on [0, 1], we know that $u_{\lambda _n,i}'=0$ on $[{\underline{t}}_{i,0}^n,{\overline{t}}_{i,0}^n]$, for all n. Since ${\underline{t}}_{i,0}^{\infty }= a_i$, for small $0<\varepsilon <\frac{1-2a_i}{2}$, there exists $N_1(\varepsilon )\in {\mathbb {N}}$ such that

$$\begin{aligned} a_i-\varepsilon<{\underline{t}}_{i,0}^n<a_i+\varepsilon ,~\mathrm{for~ all}~ n>N_1(\varepsilon ). \end{aligned}$$

Similarly, thanks to ${\overline{t}}_{i,0}^{\infty }= 1-a_i$, there exists $N_2(\varepsilon )\in {\mathbb {N}}$ such that

$$\begin{aligned} 1-a_i-\varepsilon<{\overline{t}}_{i,0}^n<1-a_i+\varepsilon ,~\mathrm{for~ all}~ n>N_2(\varepsilon ). \end{aligned}$$

Thus, $[a_i+\varepsilon ,1-a_i-\varepsilon ]\subset [{\underline{t}}_{i,0}^n,{\overline{t}}_{i,0}^n]$ for $n>N_4\triangleq \max \{N_1(\varepsilon ),N_2(\varepsilon )\}$ and we have

$$\begin{aligned} u_{\lambda _n,i}'=0,~\textrm{on}~ [a_i+\varepsilon ,1-a_i-\varepsilon ],~\mathrm{for~ all}~ n>N_4. \end{aligned}$$

Further, we obtain

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } u_{\lambda _n,i}'(t)=0~\mathrm{uniformly~on}~[a_i+\varepsilon ,1-a_i-\varepsilon ], \end{aligned}$$

for sufficiently small $\varepsilon >0$, $i\in \{1,2,\cdots ,m\}$, which is result (b).

Step 4. Prove that $\lim \nolimits _{n\rightarrow \infty } \Vert u_{\lambda _n,i}\Vert _\infty =a_i$ for any $i\in \{1,2,\cdots ,m+1\}$.

From (3.20), for any $n\ge N(\varepsilon _1)$, we obtain

$$\begin{aligned} \Vert u_{\lambda _n,i}\Vert _\infty =u_{\lambda _n,i}({\underline{t}}_{i,0}^n)\ge \int _0^{{\underline{t}}_{i,0}^\infty -2\varepsilon _1}u_{\lambda _n,i}'(\tau )d\tau . \end{aligned}$$

Since ${\underline{t}}_{i,0}^{\infty }=a_i$ as proved in previous steps, by using Lemma 3.7 and the bounded convergence theorem, we get

$$\begin{aligned}&\lim \limits _{n\rightarrow \infty } \Vert u_{\lambda _n,i}\Vert _\infty \ge \lim \limits _{n\rightarrow \infty } \int _0^{{\underline{t}}_{i,0}^\infty -2\varepsilon _1}u_{\lambda _n,i}'(\tau )d\tau \\&\quad =\int _0^{a_i-2\varepsilon _1}\lim \limits _{n\rightarrow \infty }u_{\lambda _n,i}'(\tau )d\tau =a_i-2\varepsilon _1. \end{aligned}$$

Thus by the arbitrariness of $\varepsilon _1$, we get $\lim \nolimits _{n\rightarrow \infty } \Vert u_{\lambda _n,i}\Vert _\infty \ge a_i.$ On the other hand, we know from Lemma 3.2 that $\Vert u_{\lambda _n,i}\Vert _\infty \le a_i$ for all n. Therefore, we conclude $\lim \nolimits _{n\rightarrow \infty } \Vert u_{\lambda _n,i}\Vert _\infty =a_i$. Specially, $\lim \nolimits _{n\rightarrow \infty }\Vert u_{\lambda _n,m+1}\Vert _\infty =\frac{1}{2}$. Result (c) is deduced and the proof is completed. $\square$

Proof of Theorem 1.4

By Lemma 3.4, we deduce (i). By Lemmas  3.5–3.9, assertions $(ii)-(iv)$ are verified. The proof is completed. $\square$

Finally, we give an example to illustrate the applicability of our multiplicity and asymptotic property results.

Example 3.1

We consider the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Big (\phi (u'(t))\Big )'=\lambda t^{-2}u^2(t)\left| (u(t)-\frac{1}{64})(u(t)-\frac{1}{16})(u(t)-\frac{1}{4})\right| , ~&{}t\in (0,1),\\ u(0)=0=u(1). \end{array}\right. } \end{aligned}$$

(3.21)

Note that $r(t)=t^{-2}$ and $g(s)=s^2|(s-\frac{1}{64})(s-\frac{1}{16})(s-\frac{1}{4})|$ as in problem $(P_\lambda )$. It is obvious that $r\in {\mathcal {A}}_2$ and $g_0=\lim \nolimits _{s\rightarrow 0}\left| (s-\frac{1}{64})(s-\frac{1}{16})(s-\frac{1}{4})\right| =\frac{1}{4096}$. Let $a_0=0$, $a_1=\frac{1}{64}$, $a_2=\frac{1}{16}$, $a_3=\frac{1}{4}$ and $a_4=\frac{1}{2}$. Then we can check $\sum \nolimits _{i=0}^{3}g(a_i)=0$ and $g(s)>0$ on $(0,\frac{1}{2})\setminus \{a_i\}_{i=1}^{3}$. Thus, assumptions in Theorem 1.3 are satisfied and by applying Theorem 1.3, there exist $0<\lambda _*\le \lambda ^*<\infty$ such that problem (3.21) has no positive solution for all $\lambda \in (0,\lambda _*)$ and at least four positive solutions $u_{\lambda ,1}$, $u_{\lambda ,2}$, $u_{\lambda ,3}$ and $u_{\lambda ,4}$ for all $\lambda \in (\lambda ^*,\infty )$. Combining with Theorem 1.4, $u_{\lambda ,i}$ ($i\in \{1,2,3,4\}$) convergences to function $u_i$ given below as $\lambda$ goes to $\infty$,

$$\begin{aligned} u_i(t)= {\left\{ \begin{array}{ll} t, ~&{}t\in [0,a_i),\\ a_i,~&{}t\in [a_i,1-a_i],\\ 1-t,~&{}t\in (1-a_i,1]. \end{array}\right. } \end{aligned}$$

The shape of $u_i$ is isosceles trapezoid when $1\le i\le 3$ and isosceles triangle when $i=4$.