1 Introduction

Sustainable energy sources are clean and constitute an alternative resolution to meet the needs of the actual society. These renewable energy sources offer advantages because they are sustainable and reduce the CO2 coming from the combustion of fossil fuels [1].Among these energy sources, we find wind energy. The doubly fed Induction generator (DFIG) has an important role in modern wind energy conversion systems [2] because it can generate reactive current and produces constant-frequency electric power at variable speed operation. In this perspective, various techniques have been employed to control wind turbine systems based on DFIG by applying field oriented control (FOC) also known as the vector control technique, its principle is to make DFIG similar to a DC machine, where the flux and torque are independently controlled. Various control schemes adopted the field oriented control (FOC). In [3], classical PI controllers are used for the decoupled control of the active and reactive powers; the controller lacks strong dynamics and is not fully resistant to wind a fluctuation [1], which reduces the quality of energy produced. In [4], the fuzzy PI controllers are investigated to enhance the performance of the PI controller. Sliding mode control is used in [5], the controller can easily control instantaneous active and reactive power without a rotor current control loop and synchronous coordinate transformation [5]. However, these strategies do not consider the dynamics of DFIG-based wind energy systems because these systems are complex and nonlinear. In this control approach, the changes in wind speed have a negative impact on system performance. Therefore, the field oriented control scheme becomes powerless, unable to account for certain phenomena and, often gives less efficient results. To overcome this problem, the current research trend has been carried out in the field of nonlinear control systems. Many methods have been proposed in this field. The feedback linearization technique has been and still is one of the most used. This technique is used to cancel the nonlinear terms and linearize the system [6]. In this context, several works have shown that this nonlinear control technique has revealed interesting properties regarding decoupling and parametric robustness. In [7], a feedback linearization technique is used to control DC-based DFIG systems, to ameliorate the dynamic response of the system [7].In [8], the same control strategy is used to control the stator power of the DFIG wind turbine under unbalanced grid voltage in which the oscillations of generator torque and active power can be considerably reduced. While [9] proposes a mathematical formulation of the feedback linearization control technique of the DFIG wind turbine considering magnetic saturation which gives better dynamic performance. A Sliding mode control combined with feedback linearization is presented in [10] to improve the system's robustness. The searches presented in [7,8,9,10] are based on the simplified model of DFIG (The currents, the stator voltage, and the stator flux are expressed in the stator flux-oriented reference frame) and controlled by feedback linearization algorithm combined with the classical PI controller. The success of these controllers counts on the suitable choice of PI gains [11]. The adjustment of the PID gains using conventional trial and error techniques to achieve the best performance takes time and is almost tiring, particularly for non-linear systems [12].Recently, intelligent optimization techniques have been effectively applied as optimization tools in various applications such as grey wolf optimizer (GWO), particle swarm optimization (PSO), and artificial bee colony (ABC) [13].In [14], the author used a cuckoo search algorithm (CSA) for maximum power point tracking of solar PV systems under partial shading conditions. In [15], a genetic algorithm (GA), GWO and ABC algorithm are employed for the optimal control of the pitch angle of the wind turbine.

In this paper, feedback linearization controller based on the proposed MOTs algorithm is investigated and tested in control for DFIG Wind turbine. The feedback linearization strategy is applied to the nonlinear mathematical model of DFIG to independently control the active and reactive power. The difference between the current method and the methods in previous studies is to propose MOTs algorithms to tune and generate the optimal gains (\(K_{P}\) and \(K_{I}\)) of the feedback linearization controller, to overcome the drawbacks of the old tuning methods, which rely on conventional trial and error techniques, in order to improve the performance of FLC-DFIG response such as reducing overshoot and minimizing the steady-state errors and settling time.

The main contributions of this research can be summarized are as:

  • To design and use a feedback linearization controller (FLC) based on the nonlinear model of the DFIG integrated into a wind system to control the active and reactive powers, in order to capture the maximum power from the wind.

  • To apply MOTs algorithms (GWO, ABC) to determine and generate the optimal gains (\(K_{P}\) and \(K_{I}\)) of the feedback linearization controller of wind turbines in order to achieve maximum performance.

  • To compare the simulation results obtained using optimized feedback linearization control FLC tuned by GWO and ABC with the conventional feedback linearization control which is based on traditional tuning methods.

2 Problem Formulation

The correct tuning of the PI gains is necessary to obtain the required performances according to the characteristics of the system. The transfer function of a PI controller is:

$$F_{C} (s) = K_{P} + \frac{{K_{I} }}{s}$$
(1)

where \(K_{P}\) and \(K_{I}\) are the proportional and integral gains respectively. These parameters for active and reactive powers control of the DFIG according to the criterion of the performance index. The problem of optimization is formulated in the form of objective function for adjusting the gains controllers of rotor side converter (RSC) to track the reference values of the stator powers and to ameliorate the dynamic behavior of the system [13].

The objective function is to improve the overall system dynamic behavior via minimizing the error objective function that refers to the performance index [16].

This function is based on the relation of the system performance when analyzing a set point response, criteria used to describe how well the system responds to the change including the steady state error, settling time, rise time, and the maximum overshoot ratio [13]. The Integration of the time weighted square error (ITWSE) is objective function. In this paper, the error signal is the active power and reactive power errors respectively.

$$ITWES = \int\limits_{0}^{\infty } {\left[ {C_{1} (t(P_{sre} )^{2} )C_{2} (t(Q_{sre} )^{2} )} \right]}$$
(2)

where the \(P_{sre}\) and \(Q_{sre}\) are the RSC active and reactive powers regulation error, \(C_{1}\) and \(C_{2}\) are positive, their values are selected according to optimization technique. Fig. 1 shows the successive steps for estimating the values of the optimal gain for the PI controller [16]. PI controllers are then taken into account in the loop to regulate the stator powers [17] then, ABC and GWO algorithms are used for estimating the optimal values of PI controller via the performance index minimization [18]. The results of the different optimization algorithms will be compared through the overall system dynamic response.

Fig. 1
figure 1

Steps for optimal gain search

Full size image

3 Studied System Modeling

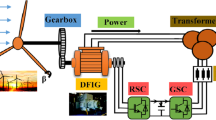
The studied system (Fig. 2) consists in a wind turbine comprising three blades of length \(R\), fixed on a drive shaft which is connected to a gain multiplier \(G\). This multiplier drives DFIG. Its stator is connected to the electric grid, while its rotor is connected to the electric grid but via a back-to-back two-level converter. The rotor side converter RSC is used to control the active and reactive stator powers issued by the WECS to the electric grid. The regulation of DC voltage to the desired value is assured by the grid side converter (GSC).

Fig. 2
figure 2

DFIG Wind turbine system

Full size image

3.1 Turbine Model

The general expression of the aerodynamic power produced by the turbine is given by:

$$P_{t} = \frac{1}{2}\rho .Cp\left( {\lambda ,\beta } \right)\pi R^{2} V^{3}$$
(3)

where:\(\rho\) is the air density,\(Cp\left( {\lambda ,\beta } \right)\) is the power coefficient of the turbine,\(\lambda\) is the tip speed ratio and \(\beta\) is the pitch angle (deg),\(V\) is the wind speed (m/s).

The tip speed ratio is defined by:

$$\lambda = \frac{{R\omega_{t} }}{V}$$
(4)

where: \(\omega_{t}\) is the speed turbine (rad/s).

Figure 3 shows the \(Cp\left( {\lambda ,\beta } \right)\) characteristic for different values of \(\beta\).

Fig. 3
figure 3

Typical \(Cp\left( {\lambda ,\beta } \right)\) curve

Full size image

where

$$Cp\left( {\lambda ,\beta } \right) = (0.44 - 0.0167\beta )\sin \left( {\frac{\pi (\lambda + 0.1)}{{14 - 0.44\beta }}} \right) - 0.00184(\lambda - 3)\beta$$
(5)

3.2 Dynamique Model of DFIG

The DFIG is modeled in Park frame by the following equations

$$\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}c} {v_{ds} = R_{s} i_{ds} + \frac{{d\phi_{ds} }}{dt} - \omega_{s} \phi_{qs} } \\ {v_{qs} = R_{s} i_{qs} + \frac{{d\phi_{qs} }}{dt} + \omega_{s} \phi_{ds} } \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} {v_{dr} = R_{r} i_{dr} + \frac{{d\phi_{dr} }}{dt} - (\omega_{s} - \omega )\phi_{qr} } \\ {v_{qr} = R_{s} i_{qr} + \frac{{d\phi_{qr} }}{dt} + (\omega_{s} - \omega )\phi_{dr} } \\ \end{array} } \hfill \\ \end{array} } \right.$$
(6)
$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\phi_{ds} = L_{s} i_{ds} + Mi_{dr} } \\ {\phi_{qs} = L_{s} i_{qs} + Mi_{qr} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\phi_{dr} = L_{r} i_{dr} + Mi_{ds} } \\ {\phi_{qr} = L_{r} i_{qr} + Mi_{qs} } \\ \end{array} } \\ \end{array} } \right.$$
(7)

The DFIG stat model according to the rotor components is given by

$$\left\{ {\begin{array}{*{20}l} {\frac{{di_{{dr}} }}{{dt}} = - a_{1} i_{{dr}} + \omega _{s} i_{{qr}} + a_{2} \phi _{{dr}} - a_{3} \omega \phi _{{qr}} - a_{4} v_{{ds}} + a_{3} v_{{dr}} } \hfill \\ {\frac{{di_{{qr}} }}{{dt}} = - \omega _{s} i_{{dr}} - a_{1} i_{{qr}} + a_{2} \phi _{{qr}} + a_{3} \omega \phi _{{dr}} - a_{4} v_{{qs}} + a_{3} v_{{qr}} } \hfill \\ {\frac{{d\phi _{{dr}} }}{{dt}} = - R_{r} i_{{dr}} + \omega _{s} \phi _{{qr}} - \omega \phi _{{qr}} + v_{{dr}} } \hfill \\ {\frac{{d\phi _{{qr}} }}{{dt}} = - R_{r} i_{{qr}} - \omega _{s} \phi _{{dr}} + \omega \phi _{{dr}} + v_{{qr}} } \hfill \\ \end{array} } \right.$$
(8)

where

$$a_{1} = \left( {\frac{1}{{\sigma T_{r} }} + \frac{1}{{\sigma T_{s} }}} \right),\,a_{2} = \frac{1}{{\sigma L_{r} T_{s} }},\,a_{3} = \frac{1}{{\sigma L_{r} }},\,a_{4} = \frac{1 - \sigma }{{\sigma M}},\,\sigma = 1 - \frac{{1 - M^{2} }}{{L_{s} L_{r} }}\,b = R_{r} ,\,C_{1} = \frac{{P^{2} }}{J},\,C_{2} = \frac{P}{J},\,T_{s} = \frac{{L_{s} }}{{R_{s} }},\,T_{r} = \frac{{L_{r} }}{{R_{r} }}$$

The mechanical equation is given by

$$\frac{d\omega }{{dt}} = C_{1} (\phi_{qr} i_{dr} - \phi_{dr} i_{qr} ) + C_{2} (C_{vis} + C_{G} )$$
(9)

where \(P\),\(J\),\(C_{G}\), \(C_{vis}\) represents the number of pole pairs, the inertia of the shaft, the torque on the generator, all frictions on the shaft, respectively.

We put

$$(i_{dr} ,i_{qr} ,\phi_{dr} ,\phi_{qr} ,\omega ) = (x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} )$$
(10)

The system (8) is then written in the form:

$$\mathop x\limits^{.} = f(x) + g(x)u$$
(11)

where

$$f(x) = \left\{ {\begin{array}{*{20}l} {\frac{{dx_{1} }}{dt} = f_{1} (x) + a_{3} v_{dr} } \hfill \\ {\frac{{dx_{2} }}{dt} = f_{2} (x) + a_{3} v_{qr} } \hfill \\ {\frac{{dx_{3} }}{dt} = f_{3} (x) + v_{dr} } \hfill \\ {\frac{{dx_{4} }}{dt} = f_{4} (x) + v_{dr} } \hfill \\ {\frac{{dx_{5} }}{dt} = f_{5} (x)} \hfill \\ \end{array} } \right.$$
(12)
$$u = \left[ {\begin{array}{*{20}c} {v_{qr} } & {v_{dr} } \\ \end{array} } \right]^{T} ,\,u = \left[ {\begin{array}{*{20}c} {a_{3} } & 0 & 1 & 0 & 0 \\ 0 & {a_{3} } & 0 & 1 & 0 \\ \end{array} } \right]^{T}$$
(13)

and

$$f_{1} (x) = - a_{1} x_{1} + \omega_{s} x_{2} + a_{2} x_{3} - a_{3} x_{5} x_{4} - a_{4} v_{ds}$$
$$f_{2} (x) = - \omega_{s} x_{1} - a_{1} x_{2} + a_{2} x_{4} + a_{3} x_{5} x_{3} - a_{4} v_{qs}$$
$$f_{3} (x) = - bx_{1} + \omega_{s} x_{4} - x_{5} x_{4}$$
$$f_{4} (x) = - bx_{2} - \omega_{s} x_{3} + x_{5} x_{3}$$
$$f_{5} (x) = C_{1} (x_{4} x_{1} - x_{3} x_{2} ) + C_{2} (C_{vis} + C_{G} )$$

4 Feedback Linearization Control

This strategy uses an inverse transformation to get the required control law for the nonlinear system and attain a decoupled power control [19].

The command vector is \(\left[ {\begin{array}{*{20}c} {v_{qr} } & {v_{dr} } \\ \end{array} } \right]^{T}\) and the output vector is \(\left[ {\begin{array}{*{20}c} {P_{s} } & {Q_{s} } \\ \end{array} } \right]^{T}\) defined by:

$$\left\{ {\begin{array}{*{20}c} {P_{s} = v_{qs} i_{qs} + v_{ds} i_{ds} } \\ {Q_{s} = v_{qs} i_{ds} - v_{ds} i_{qs} } \\ \end{array} } \right.$$
(14)

Substituting \(i_{ds}\) and \(i_{qs}\) in (14) by their counterparts extracted from the two last equations of (7), one has [20]:

$$\left\{ {\begin{array}{*{20}c} {P_{s} = v_{qs} (\frac{{\phi_{qr} - L_{r} i_{qr} }}{M}) + v_{ds} (\frac{{\phi_{dr} - L_{r} i_{dr} }}{M})} \\ {Q_{s} = v_{qs} (\frac{{\phi_{dr} - L_{r} i_{dr} }}{M}) - v_{ds} (\frac{{\phi_{qr} - L_{r} i_{qr} }}{M})} \\ \end{array} } \right.$$
(15)

Arranging (15)

$$\left\{ {\begin{array}{*{20}c} {P_{s} = \frac{{\phi_{qr} }}{M}v_{qs} - \frac{{L_{r} i_{qr} }}{M}v_{qs} + \frac{{\phi_{dr} }}{M}v_{ds} - \frac{{L_{r} i_{dr} }}{M}v_{ds} } \\ {Q_{s} = \frac{{\phi_{dr} }}{M}v_{qs} - \frac{{L_{r} i_{dr} }}{M}v_{qs} - \frac{{\phi_{qr} }}{M}v_{ds} + \frac{{L_{r} i_{qr} }}{M}v_{ds} } \\ \end{array} } \right.$$
(16)

Differentiating (16) until an input appears

$$\left\{ {\begin{array}{*{20}c} {\mathop {P_{s} }\limits^{.} = \frac{{\mathop {\phi_{qr} }\limits^{.} }}{M}v_{qs} - \frac{{\mathop {L_{r} i_{qr} }\limits^{.} }}{M}v_{qs} + \frac{{\mathop {\phi_{dr} }\limits^{.} }}{M}v_{ds} - \frac{{\mathop {L_{r} i_{dr} }\limits^{.} }}{M}v_{ds} } \\ {\mathop {Q_{s} }\limits^{.} = \frac{{\mathop {\phi_{dr} }\limits^{.} }}{M}v_{qs} - \frac{{\mathop {L_{r} i_{dr} }\limits^{.} }}{M}v_{qs} - \frac{{\mathop {\phi_{qr} }\limits^{.} }}{M}v_{ds} + \frac{{\mathop {L_{r} i_{qr} }\limits^{.} }}{M}v_{ds} } \\ \end{array} } \right.$$
(17)

From (12) and (17), we obtain:

$$\left\{ {\begin{array}{*{20}c} \begin{aligned} \mathop {P_{s} }\limits^{.} = & \frac{{(f_{3} - L_{r} f_{1} )}}{M}v_{ds} + \frac{{(f_{4} - L_{r} f_{2} )}}{M}v_{qs} \\ & + \frac{{(1 - a_{3} L_{r} )}}{M}v_{ds} v_{dr} + \frac{{(1 - a_{3} L_{r} )}}{M}v_{qs} v_{qr} \\ \end{aligned} \\ \begin{aligned} \mathop {Q_{s} }\limits^{.} = & \frac{{(L_{r} f_{2} - f_{4} )}}{M}v_{ds} + \frac{{(f_{3} - L_{r} f_{1} )}}{M}v_{qs} \\ & + \frac{{(1 - a_{3} L_{r} )}}{M}v_{qs} v_{dr} + \frac{{(a_{3} L_{r} - 1)}}{M}v_{ds} v_{qr} \\ \end{aligned} \\ \end{array} } \right.$$
(18)

The objective is to force the output \(P_{s}\) and \(Q_{s}\) to follow their references values \(P_{sref}\) and \(Q_{sref}\),respectively.

The power errors are defined as follows:

$$\left\{ {\begin{array}{*{20}c} {e_{1} = P_{sref} - P_{s} } \\ {e_{2} = Q_{sref} - Q_{s} } \\ \end{array} } \right.$$
(19)

The control input is defined as:

$$u = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {v_{qr} } & {v_{dr} } \\ \end{array} } \right]^{T}$$
(20)

Rewriting (18) in the matrix form

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\mathop {P_{s} }\limits^{.} } \\ {\mathop {Q_{s} }\limits^{.} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} {\frac{{(f_{3} - L_{r} f_{1} )}}{M}v_{ds} + \frac{{(f_{4} - L_{r} f_{2} )}}{M}v_{qs} } \\ {\frac{{(L_{r} f_{2} - f_{4} )}}{M}v_{ds} + \frac{{(f_{3} - L_{r} f_{1} )}}{M}v_{qs} } \\ \end{array} } \right] \\ & + \left[ {\begin{array}{*{20}c} {\frac{{(1 - a_{3} L_{r} )}}{M}v_{qs} } & {\frac{{(1 - a_{3} L_{r} )}}{M}v_{ds} } \\ {\frac{{(a_{3} L_{r} - 1)}}{M}v_{ds} } & {\frac{{(1 - a_{3} L_{r} )}}{M}v_{qs} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] \\ \end{aligned}$$
(21)

A new control input is defined as

$$\left\{ {\begin{array}{*{20}c} {\mathop {P_{s} }\limits^{.} = V_{1} } \\ {\mathop {Q_{s} }\limits^{.} = V_{2} } \\ \end{array} } \right.$$
(22)

The expression of control will be defined as

$$\left[ {\begin{array}{*{20}c} {v_{dr} } \\ {v_{qr} } \\ \end{array} } \right] = E(x)^{ - 1} \left[ { - A(x) + \left[ {\begin{array}{*{20}c} {V_{1} } \\ {V_{2} } \\ \end{array} } \right]} \right]$$
(23)

where

$$A(x) = \left[ {\begin{array}{*{20}c} {\frac{{(f_{3} - L_{r} f_{1} )}}{M}v_{ds} + \frac{{(f_{4} - L_{r} f_{2} )}}{M}v_{qs} } \\ {\frac{{(L_{r} f_{2} - f_{4} )}}{M}v_{ds} + \frac{{(f_{3} - L_{r} f_{1} )}}{M}v_{qs} } \\ \end{array} } \right]$$

and

$$E(x) = \left[ {\begin{array}{*{20}c} {\frac{{(1 - a_{3} L_{r} )}}{M}v_{qs} } & {\frac{{(1 - a_{3} L_{r} )}}{M}v_{ds} } \\ {\frac{{(a_{3} L_{r} - 1)}}{M}v_{ds} } & {\frac{{(1 - a_{3} L_{r} )}}{M}v_{qs} } \\ \end{array} } \right]$$

The goal is stabilized the output at \(\left[ {\begin{array}{*{20}c} {P_{sref} } & {Q_{sref} } \\ \end{array} } \right]^{T}\), a PI controller is used to the system (23). Hence, the new control is given by

$$\left[ {\begin{array}{*{20}c} {V_{1} } \\ {V_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\dot{P}_{sref}^{*} - K_{pP - reg} e_{1} - K_{iP - reg} \int {e_{1} } dt} \\ {\dot{Q}_{sref}^{*} - K_{pQ - reg} e_{2} - K_{iQ - reg} \int {e_{2} } dt} \\ \end{array} } \right]$$
(24)

The control is stable if the gains \(K_{pP - reg}\),\(K_{iP - reg}\), \(K_{pQ - reg}\), \(K_{iQ - reg}\) of the polynomial (25) obtained by Eqs. (22) and (24) are greater than zero. The tracking error converges and the system remains stable [21].

$$\left\{ {\begin{array}{*{20}c} {\mathop {e_{1} }\limits^{..} + K_{pP - reg} \mathop {e_{1} }\limits^{.} + K_{iP - reg} e_{1} = 0} \\ {\mathop {e_{2} }\limits^{..} + K_{pQ - reg} \mathop {e_{2} }\limits^{.} + K_{iQ - reg} e_{2} = 0} \\ \end{array} } \right.$$
(25)

5 Meta-Heuristic Optimization Techniques

Recently, several meta-heuristic optimization algorithms have been used to resolve complex computational problems [15]. Some of the most famous are: genetic algorithm (GA), particle swarm optimization (PSO), gravitational search algorithm (GSA), magnetic optimization algorithm (MOA), charged system search (CSS), ant colony optimisation (ACO), teaching learning-based optimization (TLBO) and biogeography-based optimisation (BBO). The classical optimization techniques cannot resolve effectively and flexibly deal different problems. For this cause, the metaheuristic optimisation techniques (MOTs) have been applied to several domains. In addition, it has been proved that there is no MOT that can resolve all optimization problems [22]. The existing methods give good results in solving some problems, but not all.Therefore, various new heuristic algorithms are proposed every year, and research in this discipline is active [22].

5.1 Grey Wolf Optimization

GWO has been developed by Seyedali Mirjalili et al. [23].The principle of this algorithm is detailed in [23].This is simulate by democratic behaviour and the hunting mechanism of grey wolves [24]. Grey wolves favor to dwell in a group of 5–12 members they have a very strict hierarchy as in Fig. 4 [25]. It consists of four levels as follows.

Fig. 4
figure 4

Hierarchy of grey wolf

Full size image

The leader wolf is called α. He is responsible for making decisions concerning predatory and defensive activities and resting [26].β wolf helps α to make decisions and the main responsibility of the β is the feedback suggestions. δ performs as sentinels scouts caretakers elders and hunters. The δ wolves have to submit to α and β, but they control the ω. The omega wolves must obey all the pack. α, β, and δ, orientates the hunting operation and ω follows them [27].

The encircle behaviour of GWO can be given as [16].

$$\mathop D\limits^{ \to } = \left| {\mathop C\limits^{ \to } . X_{p} (t) - \mathop X\limits^{ \to } (t)} \right|$$
(26)
$$\mathop X\limits^{ \to } (t + 1) = X_{p} (t) - \mathop A\limits^{ \to } .\mathop D\limits^{ \to }$$
(27)

where \(t\) is the iterations number, \(\mathop A\limits^{ \to }\) and \(\mathop C\limits^{ \to }\) are coefficient vectors, \(\overrightarrow{{\mathrm{X}}_{\mathrm{p}}}\) is the position vector of the prey and \(\overrightarrow{\mathrm{X}}\) denotes the position vector of a wolf [28]. The vectors \(\mathop A\limits^{ \to }\) and \(\mathop C\limits^{ \to }\) are denoted as:

$$\mathop C\limits^{ \to } = 2.\mathop {r_{2} }\limits^{ \to }$$
(28)
$$\mathop A\limits^{ \to } = 2.\mathop a\limits^{ \to } .\mathop {r_{1} }\limits^{ \to } - \mathop a\limits^{ \to }$$
(29)

where \(\mathop a\limits^{ \to }\) is linearly decreased from 2 to 0 over the course of iterations. \(\mathop {r_{1} }\limits^{ \to }\) and \(\mathop {r_{2} }\limits^{ \to }\) are random vectors in [0,1].

The other research agents (including the ω wolves) must adjust their placements in accordance with the research agents' best positions provided the first best solutions. Figure 5 depicts the GWO algorithm's position updating [15].

$$\left\{ {\begin{array}{*{20}c} {\mathop {D_{\alpha } }\limits^{ \to } = \left| {\mathop C_{1} .\mathop X_{\alpha } - \mathop X\limits^{ \to } } \right|} \\ {\mathop {D_{\beta } }\limits^{ \to } = \left| {\mathop C_{2} .\mathop X_{\beta } - \mathop X\limits^{ \to } } \right|} \\ {\mathop {D_{\delta } }\limits^{ \to } = \left| {\mathop C_{3} .\mathop X_{\delta } - \mathop X\limits^{ \to } } \right|} \\ \end{array} } \right.$$
(30)
$$\left\{ {\begin{array}{*{20}c} {\mathop {X_{1} }\limits^{ \to } = \mathop X_{\alpha } - \mathop {A_{1} }\limits^{ \to } .\mathop D_{\alpha } } \\ {\mathop {X_{2} }\limits^{ \to } = \mathop X_{\beta } - \mathop {A_{2} }\limits^{ \to } .\mathop D_{\beta } } \\ {\mathop {X_{3} }\limits^{ \to } = \mathop X_{\delta } - \mathop {A_{3} }\limits^{ \to } .\mathop D_{\delta } } \\ \end{array} } \right.$$
(31)
$$\mathop X\limits^{ \to } (t + 1) = \frac{{\mathop {X_{1} }\limits^{ \to } + \mathop {X_{2} }\limits^{ \to } + \mathop {X_{3} }\limits^{ \to } }}{3}$$
(32)
Fig. 5
figure 5

Position updating in GWO

Full size image

Figure 5 depicts how a search agent updates its location in the search region based on, α, β and δ. The final location of the search agent in the search area will be in a random position based on α, β and δ placements. Evidently, the prey's position is determined by α, β, δ and other wolves modify their places around the prey randomly [15].

The social hierarchy associated with the GWO hunting technique is mathematically simulated in a flowchart as shown in Fig. 6.

Fig. 6
figure 6

GWO algorithm

Full size image

5.2 Artificial Bee Colony Algorithm

Artificial bee colony algorithm (ABC) has been developed by Karaboga in 2005.The principle of this algorithm is detailed in [29] is motivated by the intelligent behavior of the bee swarm [30]. In this optimization method, the bees are divided into three groups based on their tasks: employed, scout bee groups and onlooker [18]. 50% of the colony is possessed by employed bees and the other 50% composed of onlooker bees [30].

While other bees wait in the hive, the employed bees locate the food. Moreover, the onlookers’process the information and determine the best food place [16]. While the task of scout bees is the launch random search of the food source.The search could be done in three dimensions with the three groups, with the results being shared between them to reach an optimal solution rapidly and facilely [18].The ABC flowchart are shown in Fig. 7.

Fig. 7
figure 7

ABC algorithm

Full size image

To transfer the onlooker bee to the position of the employed bee, we can use the Eq. (33)

$$X_{i(k + 1)} = X_{i(k)} + \frac{{\phi \times (d_{\max } - d_{\min } )}}{{\frac{{N_{p} }}{2} - 1}}$$
(33)

where k denotes to the iteration number, i and j are randomly chosen indexes (i ≠ j), ∅ randomly variable. In [−1 1]. Each employed bee's location is updated in the neighborhood using:

$$X_{i(k + 1)} = X_{i(k)} + \phi (X_{i(k)} - X_{j(k)} )$$
(34)

The scheme of the optimized control system is shown in Fig. 8.

Fig. 8
figure 8

Optimized control scheme of the DFIG

Full size image

6 Simulations Results

To validate the feedback linearization controller designed by PI,simulations were performed using Matlab™/Simulink. The proposed control strategy of the DFIG's RSC, using the ABC and GWO algorithms based feedback linearization PI control is tested.

The ABC-PI and GWO-PI are used on the system of the 1.5 MW WT-DFIG the parameters of DFIG are given in the Appendix. In this test, the system's controller parameters can be separated into four proportional-integral gains for RSC controllers, namely. (\(K_{pP - reg}\),\(K_{iP - reg}\)), (\(K_{pQ - reg}\), \(K_{iQ - reg}\)) that deal with the controller gains of the active and reactive powers regulator respectively. The optimal gain scheduling of the DFIG as shown in Table 1.

Table 1 Proposed controllers gains (GWO&ABC)
Full size table

Figure 9 clearly shows the area of high agent density where the optimal gains of the PI controllers will be found.

Fig. 9
figure 9

Trace of search agents for different MOTs

Full size image

Figures 10 and 11 illustrate(s) the performance of feedback linearization controller. These figures show(s) the stator active and reactive powers responses when the speed varies from 1450 to 1600 rpm at 8 s.The optimization algorithms ABC-PI and GWO-PI achieve excellent tracking of the control variables and close to zero steady state error. The active and reactive powers ripples are reduced considerably with the GWO-PI compared with that of ABC-PI and conventional PI controller and the GWO-PI has best dynamic performance than the ABC-PI concerning the steady state error and overshoot adequate.

Fig. 10
figure 10

Active power of the DFIG

Full size image
Fig. 11
figure 11

Reactive power of the DFIG

Full size image

Figures 12 and 13 show the DFIG rotor current time responses (\(i_{dr}\),\(i_{qr}\)) respectively for GWO-PI and ABC-PI. The rotor current damping with GWO tuned PI controller is decreased as compared with that of ABC-PI and the conventional PI controller or the over-current in the rotor circuit is reduced when using GWO-PI comprehensible.

Fig. 12
figure 12

Direct rotor current

Full size image
Fig. 13
figure 13

Quadrature rotor current

Full size image

In [9] and [31],the success of controllers counts on the suitable choice of PI gains (\(K_{p}\) and \(K_{I}\)).The adjustment of the PI coefficients using conventional trial and error techniques to achieve the best performance takes time and is almost tiring. Same remark for the choice of the gains for the fuzzy controller presented in [20].

Table 2 summarizes the comparison of previous researchs and our proposal. It should be noted that it is very difficult to find numerical results for the proposed technique in previous research to compare with the results of the current paper because they do not refer to the same conditions.

Table 2 Comparison of the proposed paper with previous researchs
Full size table

7 Conclusion

In this paper, the nonlinear control using a feedback linearization based on MOTs has been used to obtain the best performance for nonlinear control of DFIG active/ reactive power. The importance of this work is the determination of the optimal proportional integral (PI) controller’s gains for the control of DFIG Wind system.

The ABC and GWO techniques are introduced in order to ameliorate the dynamic performance WT-DFIG. The introduced GWO-PI and ABC-PI have provided more efficiency in seeking for the global optimum PI parameters with respect to the desired performance indices compared to the conventional PI controller. Therefore, both GWO and ABC are successfully used for optimizing the control parameters of the RSC for DFIG-based WECS under variable speed conditions.These two optimization techniques give better performance compared to the classical method. For the overshoot, the ABC algorithm provided the best overshoot value, outperforming GWO and the manual method by 6.82% and 43.85%, respectively. For the settling time, the GWO algorithm yielded the best settling time value, outperforming ABC and the manual method by 9.38% and 87.85% respectively. An identical observation is made for the steady-state error, the GWO algorithm provided the best steady-state error value, outperforming ABC and the manual method by 210% and more than 3e3% respectively. According to the simulation results based on the newly proposed tuning method using MOTs, the main improvements presented in this paper are:

  • Reduction of the maximum overshoot of the response of the active and reactive powers in a transient state.

  • Minimization of the settling time.

  • Decreasing the steady-state error of the system's dynamic behavior.