Optimal Tuning of a New Multi-input Multi-output Fuzzy Controller for Doubly Fed Induction Generator-Based Wind Energy Conversion System

Abstract

Wind energy is one of the world’s leading promising renewable energy sources, due to that there is a prediction that wind generation systems will provide maximum power supply and have good integration with the electric grid. To fulfill the increasing power demand, wind power generation systems need more advanced, novel, and robust control approaches to achieve a more stable operation of the controller and to improve the overall efficiency of the system. This paper presents an optimal design and tuning of fuzzy logic controllers (FLC) for a 1.5-MW doubly fed induction generator (DFIG), grid-connected, wind energy conversion system (WECS) using intelligent methodologies such as particle swarm optimizer (PSO), the gray wolf optimization (GWO), moth-flame optimizer (MFO), and multi-verse optimizer (MVO). FLC scaling factors are optimized for both dc-link voltage controller and current regulators of the grid-side converter and rotor-side converter of the back to back of DFIG wind turbine. A multi-objective optimization methodology is proposed which aims to minimize the steady-state errors of these controllers to improve the dynamic operation of the DFIG wind energy system subjected to variable wind speed conditions. Finally, a comparison is carried out between the different optimization techniques for FLC using PSO, GWO, MFO, and MVO, also between the proposed optimized controller and PI controller. The main contribution of this study is that it proposes a new control methodology for a DFIG-based WECS. This strategy is to optimize multi-input multi-output MIMO-FLC scaling factors by applying PSO, GWO, MFO, and MVO algorithms to control the d-q component of rotor and stator currents to control the active and reactive power of the DFIG. The operation of the proposed controller is tested under variable wind speed to investigate the DFIG behavior in case of transition from low to high gust and it is found by comparing the different techniques that the best-optimized controller is MFO-FLC which gives a very good behavior under variable wind speed conditions.

1 Introduction

The current vision of the world is directed toward renewable energy sources, in which wind power is one of the most essential and promising sources and has advanced rapidly over the last three decades. because it is clean, cost-effective, renewable, and friendly to the environment contributing to the reduction of C02 emissions [1, 2]. With the rising use of renewable energy resources especially wind, it is expected at the end of 2021 that wind capacity installed worldwide will be reached over 800 GW [3, 4]. The main differences between WECS technologies are in the design of the controller and machine control. There are currently three types of wind energy systems for large wind turbines [5]. Firstly, fixed speed WECS operating with a narrow speed range around the synchronous speed is directly tied to the grid. This type of squirrel-cage induction generator (SCIG) is used. Nowadays, SCIG is used at constant speed in many WECS productively and systematically, due to their rugged nature, low cost, low maintenance, and ductility. High stress and mechanical stress on the system, larger gearbox requirements, absence of voltage support to the grid, and absence of effective aerodynamic improvement are the drawbacks of the system [6, 7, 8]. The second type is a variable speed WECS that employs a full-scale power converter with a rating equal to the generator’s rating. The final category is a variable speed WECS, in which variable speed operation is carried out over a wide range of speeds. In this type of WECS, either a SCIG or asynchronous generator can be used. This type of WECS provides a smoother grid connection, increased controllability, reactive power compensation, and maximum power extraction by utilizing back-to-back power converters [6, 7, 8]. A Doubly fed induction generator (DFIG) is a wound rotor machine with stator windings connected to the three-phase constant-frequency grid and rotor windings connected to a reduced capacity back-to-back converter rated at 20–30% of the generator’s rating. In the case of PMSG-based WECS, the rating converters of the back-to-back connection are close to the generator’s maximum rating. Due to that, the power losses in the converter are lower compared with systems where the converters have to handle the full power resulting in total efficiency improvement. At low and variable wind speeds, DFIG outperforms PMSG in on-shore applications. PMSG is preferable to DFIG for off-shore applications due to its lower maintenance requirements and constant wind speed, because PMSG losses are reduced. Accordingly, DFIG is the most used in variable speed wind turbines [9]. Due to that, the power losses in the converter are lower compared with systems where the converters have to handle the full power resulting in total efficiency improvement. The DFIG-based WECS represents a conceptual control problem as the dynamic model in such systems is nonlinear and has a large number of variables. The control of the back-to-back converters has a significant impact on the dynamics of the DFIG wind turbine especially the rotor currents. As the rotor current increases to keep the terminal voltage of the generator and the rotating speed of the DFIG rotor, the current in the GSC also increases to preserve the dc-link voltage constant. Therefore, the overshoots of the currents flowing through the converter can stress the operation of the back-to-back converters [10]. The DFIG-based wind turbine controllers also face another important challenge in ensuring they have enormous parameters, which are necessary to be optimized for a good operation and interaction with the wind turbine. Therefore, for the stability of the closing-loop control system and sufficient transient response, good tuning of the controls must be guaranteed [11]. A lot of methodologies are proposed in the literature to solve the control problem of DFIG-based WECS. Many of these researches are worked on the decoupled control of the active and reactive power. Moreover, most DFIG control methodologies are based on the conventional proportional integral (PI) method. But, these methods do not consider the dynamics of wind energy systems based on DFIG since these systems are nonlinear and complex [12]. Currently, several research studies have been presented a system consisting of a wind turbine operating in response to wind speed changes, a doubly fed induction generator (DFIG) connected directly to the grid by the stator and fed by a power converter on the rotor side. Vector control is used to control active and reactive power between the stator of the (DFIG) and the grid independently, which is accomplished using traditional PI, fuzzy logic, and fuzzy self-tuning PI controllers [13]. These controllers generate the reference rotor voltages needed to ensure that active and reactive power meets their target values and MATLAB is used to model and simulate the system [14]. In [14], the author combines the conventional PI and fuzzy logic controllers to control the DFIG wind turbine. In [15], a classical PI mode vector control for a DFIG drive is used to control the output variables, which are the stator active and reactive power of the DFIG injected into the grid, and variable speed control of wind turbines is being investigated to maximize energy extraction from the wind. Simulation studies are carried out to validate the proposed PI controller’s performance in the presence of random wind fluctuations and reactive power variations. It should be noted that changes in wind speed at power control have a negative impact on the system’s performance. This controller lacks high-performance dynamic characteristics and is not completely resistant to wind variations. In this regard, intelligent control approaches such as artificial neural network control and fuzzy logic control are now being considered as a promising alternative to traditional control methods in the control of complex nonlinear plants with unstructured dynamical uncertainties. A model of fuzzy logic control for a doubly fed asynchronous machine is presented in [16], which compared classical PI controllers with fuzzy logic controllers. While [17] proposes a fuzzy logic controller for a variable speed DFIG wind turbine implemented using MATLAB software. It also showed that the fuzzy control is more robust and suitable replacement of the conventional PI controller to a higher performance DFIG system. In [18], a control method is used with DFIG based on fuzzy controller. It showed from results that fuzzy controller is more accurate control performance and more fast dynamic response with almost no steady-state error when compared with a system using conventional PI controller. In [19], an adaptive fuzzy controller is used to approximate the unknown system nonlinearities and cope with the model uncertainties that occur in the DFIG-base WECS model and the tracking error dynamics. In [20], a fuzzy controller is investigated to improve the dynamic performance of the delivered power. An intelligent fuzzy inference system is used to control the speed and the stator power of DFIG. It showed the superiority of the fuzzy controllers against the conventional PI controller in the stator power transient and steady-state responses. It also presented a fuzzy gain tuner of the PI controller in the vector control scheme of the GSC, while [21] proposed a methodology that uses particle swarm optimization (PSO) for optimizing the parameters of PI controllers of a wind turbine (WT) with DFIG. Optimal tuning of PI controller gains for a DFIG wind energy system is presented in [22]; the optimization is carried out using PSO and Gray wolf optimizer (GWO).

Previous researches showed that the PI controller is the most common type of automatic controller, but it is not the best one. These controller’s coefficients are difficult to be tuned for nonlinear plants with unpredictable parameter variations. This control technique necessitates automatically tuning the controller parameters based on the nature of the process. There are some constraints to tuning a PI controller. These constraints can be overcome by tuning the PI controller with intelligent techniques such as fuzzy logic, artificial neural networks, adaptive neuro-fuzzy inference systems, and genetic algorithms. Although fuzzy logic is used to adapt the PI controller to achieve better system performance, however, the conventional control technique does not provide the expected results [13]. Besides, fuzzy controllers cannot adapt to changes in their environment or operating conditions. Then, to improve and maintain control performance in a wide range of changing conditions, some form of adaptation that updates the controller parameters is required [19]. And depending on what was cleared, this study presents a new optimized fuzzy control method for variable speed grid-connected DFIG-based WT. Optimized fuzzy logic controller (OFLC) coefficients play an important role in the accuracy of the response and lower power errors; optimization algorithms can be used for the automatic adjustment of these coefficients. Among these intelligent techniques, PSO, GWO, MFO, and MVO can be applied to optimize the fuzzy controller parameters because of their advantages such as wide solution space, ease of discovering global optimum, resistance against becoming trapped in local optimum, and ease of implementation are highly attractive and available. PSO is previously used for the optimization of the parameters of the SISO fuzzy logic controller proposed for the DFIG controller [19]. GWO, MFO, and MVO are proposed in this paper as they are not adopted for fuzzy controller optimization in the case of DFIG control.

The main contribution of this study is that it proposes a new control methodology for a DFIG-based WECS. This strategy is to optimize FLC scaling factors by applying PSO, GWO, MFO, and MVO algorithms. Two FLC units are proposed; the first one is the FLC unit to control the dc-link voltage (Vdc) of the back-to-back converter. This controller has a single-input single-output (SISO) fuzzy membership function and is applied to adjust the Vdc according to the grid requirements and gives a good behavior under variable wind speed with smooth & stable transition from low to high. The other FLC is a multi-input multi-output (MIMO) controller to control the d-q component of rotor and stator currents to control the active and reactive power of the DFIG. The advantage of this MIMO-FLC used as the current controller is the using of one fuzzy controller for both GSC and RSC controllers instead of four fuzzy controllers as mentioned in previous literature which in consequence minimizes the time execution and gives better results with optimization techniques resulting in better overall performance. The operation of the proposed controller is tested under variable wind speed to investigate the DFIG behavior in case of transition from low to high gust and it is found that the optimized fuzzy logic controller (OFLC) has a better performance than the PI controller and a big improvement is achieved.

The rest of this paper is organized as follows: Sect. 2 introduces WECS basics. In Sect. 3, modeling and control of the DFIG are presented. The proposed fuzzy logic control design is presented in Sect. 4. Results and discussion are provided to validate the effectiveness of the proposed controller in Sect. 5. Finally, Sect. 6 contains the conclusion and future work.

2 Wind Energy Conversion System

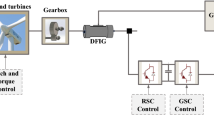
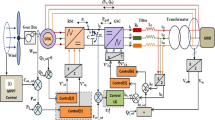
A simplified diagram of a DFIG-based WECS system connected to the electric grid is presented in Fig. 1. The aerodynamic system of the DFIG wind turbine is capable of operating over a wide range of wind speed profiles to achieve optimal efficiency. This variable speed technology allows the wind turbine to harvest the maximum energy; at low wind speeds, the turbine speed is optimized to extract the maximum power. Also, it reduces the mechanical stresses on the turbine during wind gusts. The wind turbine produces the maximum mechanical energy which is proportional to the wind speed using speed power tracking curves. Another advantage of DFIG technology is that the power electronic converter can be adjusted to deliver or absorb reactive power, hence eliminating the need for allocating capacitor banks. The DFIG-based WECS consists of a wind rotor (turbine blades), a wound rotor induction generator, and AC/DC/AC IGBT-based PWM power electronic converters [23, 21]. The AC/DC/AC back-to-back converters as stated before need only to manage a fraction of the full power, typically 30% of the nominal power. Therefore, the losses in the power electronic converters can be reduced, and also the cost is lowered due to the partial rating. The rotor is fed through the AC/DC/AC converter, while the stator is directly connected to the 50 Hz power grid. A back-to-back voltage source converter is used to generate sinusoidal AC output voltages with controllable magnitude and frequency. It consists of two converters: RSC and GSC. A dc-link capacitor is placed between these two converters, and in that case, the GSC objective is to maintain the voltage variation of this dc-link small. Via controlling the RSC, it is possible to control the speed of the DFIG wind turbine, the torque, and the active and reactive power at the stator terminals.

Fig. 1

Configuration of WECS

An expression is usually used to describe the mechanical power $({\text{P}}_{w})$ captured by a 3-blades horizontal axis wind turbine [24, 25, 26]:

$$ P_{w} = \frac{1}{2}C_{p} \left( {\lambda ,\theta } \right)\pi r^{2} \upsilon ^{3} \rho $$

(1)

where $r$ is the radius of rotor blades in m, $\upsilon$ is the wind speed in m/s, $\rho$ is the air density in kg/m³, ${\text{C}}_{\text{p}}$ is the wind turbine coefficient of performance, and it is dependent on $\lambda$ and the blade’s pitch angle $\theta$. $\lambda$ is the ratio of the turbine’s blade tip speed to the wind velocity. The power coefficient ${C}_{p}$ defines the aerodynamic efficiency of the wind turbine rotor.

3 Modeling and Control of the DFIG

The dynamic model of the stator and rotor voltages and fluxes for the DFIG in the d-q reference frame can be expressed by the following equations [21, 24,25,26]:

$$\left[\genfrac{}{}{0pt}{}{Vds}{Vqs}\right]=Rs\left[\genfrac{}{}{0pt}{}{Ids}{Iqs}\right]+\frac{d}{dt}\left[\genfrac{}{}{0pt}{}{\varphi ds}{{\varphi }_{qs}}\right]+{\omega }_{s}\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\genfrac{}{}{0pt}{}{\varphi ds}{{\varphi }_{qs}}\right]$$

(2)

$$\left[\genfrac{}{}{0pt}{}{Vdr}{Vqr}\right]=Rr\left[\genfrac{}{}{0pt}{}{Idr}{Iqr}\right]+\frac{d}{dt}\left[\genfrac{}{}{0pt}{}{\varphi dr}{{\varphi }_{qr}}\right]+s{\omega }_{s}\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\genfrac{}{}{0pt}{}{\varphi dr}{{\varphi }_{qr}}\right]$$

(3)

$$s(slip\,ratio)=\frac{{\omega }_{s}-{\omega }_{r}}{{\omega }_{s}}$$

(4)

$$\left[\begin{array}{c}\begin{array}{c}{\varphi }_{ds}\\ {\varphi }_{qs}\end{array}\\ \begin{array}{c}{\varphi }_{dr}\\ {\varphi }_{qr}\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{cc}{L}_{s}& 0\\ 0& {L}_{s}\end{array}& \begin{array}{cc}{L}_{m}& 0\\ 0& {L}_{m}\end{array}\\ \begin{array}{cc}{L}_{m}& 0\\ 0& {L}_{m}\end{array}& \begin{array}{cc}{L}_{r}& 0\\ 0& {L}_{r}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{I}_{ds}\\ {I}_{qs}\end{array}\\ \begin{array}{c}{I}_{dr}\\ {I}_{qr}\end{array}\end{array}\right]$$

(5)

$${L}_{s}={L}_{ls}+{L}_{m}$$

(6)

$${L}_{r}={L}_{lr}+{L}_{m}$$

(7)

where $Rs$, $Rr$, ${L}_{ls}$, and ${L}_{lr}$ are the stator and rotor windings resistances and the leakage inductances, respectively, ${L}_{m}$ is the mutual inductance, $V$, $I$, $\varphi$ are the voltage, current, and flux in coordinates d-q (subscripts s and r denote stator and rotor, respectively), ${\omega }_{s}$ and ${\omega }_{r}$ are the speeds of stator and rotor currents, and $\mathrm{s}$ is the machine slip ratio.

To simplify the control, for grid-connected DFIG system, considering negligible stator resistance $Rs$ while the stator flux is constant, therefore ${\varphi }_{ds}={\varphi }_{s}$ and ${\varphi }_{qs}=0$, then the stator voltage and flux equations can be simplified as [24][25][26]:

$$Vds=\frac{{d\varphi }_{ds}}{dt}=0$$

(8)

$${V}_{qs}={V}_{s}=\,{\omega }_{s}{\varphi }_{ds}$$

(9)

The stator active and reactive power can be expressed as follows [24,25,26]:

$${P}_{s}=-\,\frac{{L}_{m}}{{L}_{s}}{V}_{s}\,Iqr$$

(10)

$${Q}_{s}=\frac{{V}^{2}}{{{\omega }_{s}L}_{s}}-\frac{{L}_{m}}{{L}_{s}} {V}_{s}\,Idr$$

(11)

To keep the dc-link voltage constant irrespective of the grid-side voltage, the GSC is used to control the dc-link voltage of the back-to-back converters; a feed-forward decoupled control is used to control the active and reactive power exchange between the grid and the GRC [27]. The control is performed using a synchronous reference frame (d-axis) aligned to the grid voltage. Hence, the q-axis component of the grid voltage, ${V}_{q}$, will be zero. The objective is to maintain the dc-link voltage at a predetermined constant value by controlling ${I}_{d}$, while the other objective is to control the reactive power by adjusting ${I}_{q}$. This controller includes also an inner current loop that regulates the magnitude and phase of the GSC voltage signal (∆Vd, ∆Vq) as shown in Fig. 2.

Fig. 2

Block diagram of the GSC controller

The RSC controller, as shown in Fig. 3, is adjusted to regulate the generator speed and the reactive power at the point of interconnection with grid terminals. The d-axis of the rotating reference frame is aligned with the positive-sequence component of the stator voltage using a phase-locked loop (PLL) [27]. The three-phase phase-locked loop is an error feedback signal system and its main function is to transfer the signals from natural reference frame components (abc) to the direct and quadrature (d-q) reference synchronous frame components and vice versa to perform decoupled power control as shown in Fig. 4. The d-axis reference rotor current ${I}_{dr\_ref}$ is obtained by dividing the reference torque (Tem) by a scaled value of the flux. Then, the actual ${I}_{dr}$ current component is compared to ${I}_{dr\_ref}$ and the error is reduced to zero through a current regulator. The objective of the Volt-Var regulator shown in the figure is to control the voltage at the point of interconnection of the WECS with the grid by generating ${I}_{qr\_ref}$ that must be injected in the rotor through RSC to control the reactive power. Then, the same current regulator is used to regulate the actual ${I}_{qr}$ component to its reference value. The output of the current regulator is the voltage-controlled signals (∆Vdr, ∆Vqr) that will be generated by RSC. This controlled voltage signal is converted to the abc reference frame using the PLL to generate the switching pulses of the two back-to-back converters.

Fig. 3

Block diagram of the RSC controller

Fig. 4

Block diagram of DFIG based on OFLC

In this work, OFLC is used to evaluate system performance as presented in Fig. 4. OFLC is an intelligent control technique that controls complicated systems based on analogizing human way by fuzzy optimization thinking, so this applies fuzzy sets and fuzzy logic inference knowledge. Because OFLC control is marked by the benefits of good performance and robustness, it is not necessary to know the mathematical model of the system. OFLC is one of the best tools for formally describing, controlling, and applying a human’s heuristic knowledge about how to control systems [28]

4 Proposed Fuzzy Logic Controllers Design

FLC contains three functional blocks: fuzzification, fuzzy rule base, and defuzzification [29]. There are two input signals to the FLC, the error E(t), and the variation of the error which are translated by gain factors to obtain the output of the FLC (two input gains (Ke, Kde), one output gain (Ku)); the fuzzy controller structure is represented in Fig. 5. The triangular membership function is the most practically encountered FLC application. The triangular MF is formed by using straight lines. These straight lines of MFS have a simplicity advantage. And it is recommended to use triangular MF with 50% overlapping, followed by a tuning process in which the left and/or right spread and/or overlapping can be adjusted and keep doing this until getting a satisfying result [30]. Depending on that the number of MF has a bigger impact since it decides how long it takes to compute. As a result, in this study, the best model for achieving the best efficiency can be calculated by varying scaling factors of MFs [31]. There are two main fuzzy controllers. One of them is SISO-FLC with 7 triangular membership, and the other is MIMO-FLC with 5 triangular membership. The reason for choosing 7 MFs for the voltage controller is that it produces better results than the 5 MFs due to the formation of more accurate fuzzy rules (49 rule) for the single-input single-output controller. For the second current controller, the 5 MFs are chosen as the controller, in that case, deals with a large number of rules as it is a multi-input multi-output controller with 4 inputs and 4 outputs with a total number of rules 100 (25*4). Consequently, it affects the computation time; however, the 5 MFs give accurate results for the current controller. Also in this study, Mamdani fuzzy inference system is used as it has more intuitive and easier to understand rule bases.

Fig. 5

Fuzzy controller structurer

In this paper, FLC is used to control the behaviors of the DFIG wind turbine. There are two main fuzzy controllers; the first controller is used to replace the DC voltage regulator of the GSC controller. This controller is treated as a conventional FLC which has two inputs—error and change of error—summed as a single input and has a single output so this FLC is denoted as SISO-FLC. To control the dc-link voltage $(\mathrm{V}\mathrm{d}\mathrm{c})$ of the back to back, a reference value ${\mathrm{V}\mathrm{d}\mathrm{c}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ is compared to $\mathrm{V}\mathrm{d}\mathrm{c}$ to compute the error E(t) as indicated in Eq. 12, the variation of the error (∆E) which is translated by gain factors to obtain the output (∆U) of the FLC, and the 7 triangular membership used for the inputs and the output as shown in Fig. 6 are negative big (NG), negative medium (NM), negative small (NP), zero (EZ), positive small (PP), positive medium (PM), and positive big (PG). A 7 × 7 rule matrix was constructed to form 49 cells as represented in Table 1.

Fig. 6

Membership functions for the inputs E(t), ∆E(t), and the output ∆U(t)

Table 1 Fuzzy rule table of SISO-FLC

$$E\left(t\right)={V\mathrm{d}\mathrm{c}}_{\mathrm{r}\mathrm{e}\mathrm{f}}-V\mathrm{d}\mathrm{c}$$

(12)

The second controller is MIMO-FLC to control the d-q component of rotor and stator currents. This FLC is proposed to represent the two current regulators of GSC and RSC. The proposed FLC has 8 inputs; 4 to obtain the errors e₁(t), e₂(t), e₃(t), e₄(t), and 4 to measure the change of errors ∆e₁(t), ∆e₂(t), ∆e₃(t), ∆e₄(t), which are translated by gain factors to obtain the outputs ∆Vd, ∆Vq, ∆Vdr, ∆Vqr of the FLC. Figure 7 presents the functional block diagram of the proposed MIMO—FLC. The 5 triangular membership used for the inputs and the outputs is shown in Fig. 8. As mentioned earlier that the number of MFs affects the computation time and this MIMO-FLC contains 100 rules, so 5 MFs are used to reduce the computation time of the current controller. MFs are defined as big negative (BN), negative (N), zero (Z), positive (P), and big positive (BG). Table 2 indicates the fuzzy rule table of MIMO-FLC, every two inputs have 25 rules, and the total number of rules is 100.

Fig. 7

Block diagram of the proposed MIMO—FLC

Fig. 8

Membership functions for the inputs e(t), ∆e(t), and ∆u(t)

Table 2 Fuzzy rule table of MIMO-FLC

4.1 Multi-objective Optimization

A multi-objective optimization problem includes a set of parameters (decision variables), a set of objective functions, and a set of constraints. In this work, the main objectives are to minimize the steady-state errors (input to FLC) of dc-link voltage and d-q components of rotor and stator currents compared to reference values [32][33].

$$F\left(x\right)=min\left({f}_{1}\left(x\right),{f}_{2}\left(x\right),{f}_{3}\left(x\right),{f}_{4}\left(x\right),{f}_{5}\left(x\right)\right)$$

(13)

Subject to:

$$g\left(x\right)=\left({g}_{1}\left(x\right),{g}_{2}\left(x\right),{g}_{3}\left(x\right),{g}_{4}\left(x\right),{g}_{5}\left(x\right)\le 0\right)$$

(14)

where $x$ is the decision variables’ vector, and $F\left(x\right)$ is the vector of the objective functions. The constraints g(x) ≤ 0 determine the set of feasible solutions.

In this work, the set of objective functions to be minimized can be written as Eqs. 15–20; as shown in the following equations, the error objectives are calculated according to the integral time absolute error (ITAE) formula [21] [34]:

$${f}_{1}\left(x\right)=\int t\times \left|\left({Vdc}_{ref}-Vdc\right)\right|\mathrm{d}t$$

(15)

$${f}_{2}\left(x\right)=\int t\times \left|\left({Id}_{ref}-Id\right)\right|\mathrm{d}t$$

(16)

$${f}_{3}(x)=\int t\times \left|\left({Iq}_{ref}-Iq\right)\right|\mathrm{d}t$$

(17)

$${f}_{4}(x)=\int t\times \left|\left({Idr}_{ref}-Idr\right)\right|\mathrm{d}t$$

(19)

$${f}_{5}(x)=\int t\times \left|\left({Iqr}_{ref}-Iqr\right)\right|\mathrm{d}t$$

(20)

This problem is treated as multi-objective. All functions mentioned in equations from 15 to 20 are summed as follows:

$$ \begin{aligned} {\text{Min }}F\left( x \right)& = w1*f_{1} \left( x \right) + w2*f_{2} \left( x \right) + w3*f_{3} \left( x \right) \\ & \quad + ~w4*f_{4} \left( x \right) + ~w5*f_{5} \left( x \right) \end{aligned} $$

(21)

where $w1,w2,w3,w4, \mathrm{and}\,w5$ are weighting factors where their summation is equal to 1. These weighting factors are selected based on trial and error to get the best results, so the optimization is performed for many runs to get the best results. The optimal value for $w1$ is 0.4 and 0.15 for $w2$ to $w5$, respectively.

4.2 Fuzzy Optimal Control

Optimal tuning of fuzzy FLC using intelligent techniques as PSO, GWO, MFO, and MVO is presented in Fig. 9 which illustrates the flowchart of the control algorithm. The proposed strategy aims to optimize the scale factors by these algorithms to adjust v_dc according to grid requirements and achieve the best results with the best performance regarding the step response of controllers (minimum overshoot and better settling time with minimum s.s error).

Fig. 9

Fuzzy optimal control flowchart

In the following subsection, the PSO, GWO, MFO, and MVO optimization techniques are presented.

4.2.1 PSO Algorithm

The PSO was introduced by Kennedy and Eberhart [35]; it is a nature-based optimization algorithm inspired by the social behavior of birds. The main advantages of the PSO algorithm are that it is simple and has high robustness and can be used in a variety of applications with minor modifications and easy implementation. It has a strong computational efficiency when compared with other mathematical and heuristic optimization algorithms. It can quickly converge to the optimization value. It is simple to combine it with other algorithms to improve its performance.

The particle swarm depends on a set of operators, called particles, and each particle is considered as a solution to the optimization problem. In the solution space, the swarm particle $(i)$ is modeled during iteration k with position vector ${X}_{i}^{k}$ and velocity vector ${v}_{i}^{k}$. The quality of the particle swarm position at a specified point is determined by the value of the fitness function. This particle memorizes its better past position as $\boldsymbol{p}{\boldsymbol{b}\boldsymbol{e}\boldsymbol{s}\boldsymbol{t}}_{\boldsymbol{i}}$, while the global best position attained by all particles in the swarm is denoted as $\boldsymbol{g}\boldsymbol{b}\boldsymbol{e}\boldsymbol{s}\boldsymbol{t}$. The speed of each particle is then adjusted according to the particle’s flight experience and other experienced particles; position and velocity vectors, in that case, are updated according to the following equations [36][37]:

$${v}_{i}^{k+1}=w{v}_{i}^{k}+{c}_{1}{rand}_{1i}\left(p{best}_{i}-{X}_{i}^{k}\right)+{c}_{2}{rand}_{2i}\left(gbest-{X}_{i}^{k}\right)$$

(22)

$${X}_{i}^{k+1}={X}_{i}^{k}+{v}_{i}^{k+1}$$

(23)

where ${v}_{i}^{k}$ is the current velocity of particle $i$ at iteration$k$, while ${v}_{i}^{k+1}$ is the updated velocity of the particle$i$, $w$ is the inertia weight.${c}_{1}$, ${c}_{2}$ are two acceleration positive constants, ${X}_{i}^{k}$ is the current position of particle $i$ at iteration $k$, ${X}_{i}^{k+1}$ is the updated position of particle $i$ at iteration $k$, while ${rand}_{1i}$,${rand}_{2i}$ are random numbers [0 and 1]. The optimization is sustained until the stopping criterion is met, i.e., reaching the predefined maximum iteration number.

4.2.2 GWO Algorithm

GWO algorithm is first introduced by Mirjalili [38]. GWO theory is based on the hunting process of the gray wolf. Gray wolves usually prefer to live and hunt together in packs. (The average pack size consists of 5–12 wolves.) Search and hunting behavior can be discussed in the following steps:

• When gray wolves find a victim, they begin to follow, chase, and then approach him.

• When the prey ran away, the gray wolves chase after, circling, and harassing it until it stops moving. Finally, the gray wolves attack the prey.

Considering the social hierarchy of gray wolves, the mathematical model will be defined as follows: The fittest solution is called alpha ($\alpha$) as the leader in the gray wolves pack, the second-best solution is called beta ($\beta$) as the subordinate wolves in the gray wolves pack, and the third-best solution is named delta ($\delta$). All other nominee solutions are all considered omegas ($\omega$). All omegas will be led by these three gray wolves ($\alpha$, $\beta$, and $\delta$) during the searching and hunting optimization methodology.

The iterations start at ($t=1$) when the prey is found. After that, the wolves $\alpha$, $\beta$, and $\delta$ will lead, follow, and finally circle the prey. The encircling behavior will be described in the following equations using two coefficient vectors $\overrightarrow{A},\, \overrightarrow{C}$ [38]:

$$\overrightarrow{D}=\left|\overrightarrow{C}.\overrightarrow{{X}_{P}}(\mathrm{t})-\overrightarrow{X}(t)\right|$$

(24)

$$\overrightarrow{X}(t+1)=\overrightarrow{{X}_{P}}(t)+\overrightarrow{A}.\left(\overrightarrow{D}\right)$$

(25)

where $t$ is the current iteration, $\overrightarrow{X}(t)$ is the position vector of the gray wolf, while $\overrightarrow{{X}_{P}}(\mathrm{t})$ indicates the position vector of the prey.

The coefficient vectors $\overrightarrow{\mathrm{A}}$ and $\overrightarrow{\mathrm{C}}$ can be calculated as:

$$\overrightarrow{A}=2\overrightarrow{a}.\overrightarrow{{r}_{1}}-\overrightarrow{a}$$

(26)

$$\overrightarrow{C}=2.\overrightarrow{{r}_{2}}$$

(27)

where $\overrightarrow{a}$ components are linearly decreased from two to zero throughout iterations and $\overrightarrow{{r}_{1}}$, $\overrightarrow{{r}_{2}}$ are random vectors [0, 1].

The hunting process of gray wolves (for $\alpha$, $\beta$, and $\delta$ wolves) can be modeled mathematically as the following equations:

$$\overrightarrow{{D}_{\alpha }}=\left|\overrightarrow{{C}_{1}}.\overrightarrow{{X}_{\alpha }}-\overrightarrow{X}\right|$$

$$\overrightarrow{{D}_{\beta }}=\left|\overrightarrow{{C}_{2}}.\overrightarrow{{X}_{\beta }}-\overrightarrow{X}\right|$$

(28)

$$\overrightarrow{{D}_{\delta }}=\left|\overrightarrow{{C}_{3}}.\overrightarrow{{X}_{\delta }}-\overrightarrow{X}\right|$$

$$\overrightarrow{{X}_{1}}=\overrightarrow{{X}_{\alpha }}+\overrightarrow{{A}_{1}}.\left(\overrightarrow{{D}_{\alpha }}\right)$$

$$\overrightarrow{{X}_{2}}=\overrightarrow{{X}_{\beta }}+\overrightarrow{{A}_{2}}.\left(\overrightarrow{{D}_{\beta }}\right)$$

(29)

$$\overrightarrow{{X}_{3}}=\overrightarrow{{X}_{\delta }}+\overrightarrow{{A}_{3}}.\left(\overrightarrow{{D}_{\delta }}\right)$$

$$ \vec{X}\left( {t + 1} \right) = {\raise0.7ex\hbox{${\vec{X}_{1} + \vec{X}_{2} + \vec{X}_{3} }$} \!\mathord{\left/ {\vphantom {{\vec{X}_{1} + \vec{X}_{2} + \vec{X}_{3} } 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}} $$

(30)

where $\overrightarrow{{X}_{1}},\,\overrightarrow{{X}_{2}}$, and $\overrightarrow{{X}_{3}}$ are the position vectors of α, β, and δ wolves.

After obtaining the three best solutions, other search agents will be forced to update their positions according to the best leading solutions and calculate the fitness function value until the stopping criterion is met.

The proposed GWO has demonstrated superior characteristics such as high-quality solutions, stable convergence characteristics, high computational performance, and quick coverage to the optimal solution [39].

4.2.3 MFO Algorithm

The MFO is a nature-inspired algorithm that is originally proposed by S. Mirjalili [40]. Its advantages include simplicity, flexibility, robustness, speed in searching, and easy hybridization with other algorithms [41]. The moths are insects that look like a butterfly family and they have special ways of roaming at night called transverse orientation used for their navigation which depends mainly on moonlight. In this way, the moth flies in a mechanism to preserve a fixed angle relative to the moon which is considered a very effective way to travel long distances in a straight line. MFO steps can be summarized as[40]:

• The MFO algorithm is initialized by generating moths randomly within the search space.

• After that, it calculates the position of each moth (i.e., the fitness values), then adopting the best position by a flame.

• Then, the moths’ positions are updated using a spiral movement function to achieve the best positions labeled by a flame:

  $${M}_{i}=S\left({M}_{i},{F}_{j}\right)$$

  (31)
  $$S\left({M}_{i},{F}_{j}\right)={D}_{i}\mathrm{*}{e}^{bz}\mathrm{*}\mathrm{cos}\left(2\pi z\right)+{F}_{j}$$

  (32)
  $${D}_{i}=\left|{F}_{j}-{M}_{i}\right|$$

  (33)

where ${M}_{i},{F}_{j}$ are the j-th flame and the i-th moth, b is the variability of the model of the logarithmic maturation pattern, z is a random number within the range of [− 1, 1], and Di represents the i-th moth distance with j-th flame.

• Updating the number of flames according to the following formula:

  $$\mathrm{f}\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{e}\_\mathrm{n}\mathrm{o}=\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\left(N-l\mathrm{*}\frac{N-l}{T}\right)$$

  (34)

where $N$ stands for the maximum number of flames, $l$ indicates the current iteration, while $T$ denotes the maximum iterations. Finally, it updates the new best moths’ positions and repeats the previous steps until the stopping criterion is met.

4.2.4 MVO Algorithm

A multi-verse optimizer (MVO) is first introduced by Mirjalili; it produces very competitive results and outperforms the best algorithms in the literature. Mirjalili showed that the results of the real-world case studies also show MVO’s ability to solve real-world problems with unknown search spaces. [42]. Otherwise, for other biologically inspired optimization techniques, the MVO theory is based mainly on astrophysics. The multi-verse theory explains how the big bang creates an infinite number of universes and how these universes interact with each other through different types of holes known as a wormhole, black hole, and white hole. In MVO, each solution is equivalent to a universe and each variable in the solution is considered as an object in that universe. Each solution has an inflation rate, which is proportional to the corresponding fitness function value [42][43]. The inflation speed of a universe is very important to the suitability for life. The steps of the MVO algorithm can be summarized as follows:

• Initialize the positions of the universes

• Input minimum and maximum of wormhole existence probability and calculate according to:

  $$WEP={W}_{\mathrm{m}\mathrm{i}\mathrm{n}}+Iter\mathrm{*}\left(\frac{{W}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{W}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{Iter}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)$$

  (35)

• While iteration < max iteration

• Calculate the traveling distance rate for each universe

  $$ TDR = 1 - \frac{{Iter^{{\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 p}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$p$}}} \right)}} }}{{Iter_{{max}}^{{\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 p}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$p$}}} \right)}} }} $$

  (36)

• Update the position of universes and sort universes according to Roulette wheel selection

  $${x}_{i}^{j}=\left\{\begin{array}{cc}{x}_{k}^{j}& r1<NI(Ui)\\ {x}_{i}^{j}& ri\ge NI(Ui)\end{array}\right.$$

  (37)

• Check elitism and find the best universe

where ${W}_{min}$, ${W}_{max}$ are the minimum and maximum numbers taken as 0.2, 1 [42], $Iter$, ${Iter}_{max}$ are the current and maximum number of iterations, respectively, and $p$ is the precision of exploitation over iterations. ${x}_{i}^{j}$ indicates the j-th parameter of the universe, $Ui$ denotes the i-th universe, $NI(Ui$ is a normalized inflation rate of the i-th universe, $rl$ is a random number between [0, 1], and ${x}_{i}^{j}$ indicates the j-th parameter of the universe.

The pseudocodes of the PSO, GWO, MFO, and MVO optimization techniques are presented in Appendix 2. The algorithm’s parameters are also presented in Appendix 3.

5 Results and Discussion

Simulation is carried out for a grid-connected WECS based on 1.5 MW DFIG. (The parameters of the 1.5 MW DFIG-based WECS under stud are presented in Appendix 1 obtained from MATLAB environment.) For this purpose, the dynamic model of the proposed grid-connected WECS and its associated MIMO-FLC is presented. Furthermore, the simulation of the system is performed using MATLAB/SIMULINK and SIMPOWERSYSTEM toolbox to validate the performance of the optimized controllers. In this system, the stator is directly connected to the power grid, while the rotor’s terminals are connected to the grid through a back-to-back converter and the control procedure can be defined as follows:

• The control of dc-Link voltage and current regulators of the grid and rotor-side converter of the DFIG wind turbine is carried out using the fuzzy logic controller.

• The input and output scaling factors of the fuzzy controllers are optimized using different techniques (PSO, GWO, MFO, and MVO).

• A comparison between different optimization methods for optimal tuning of fuzzy controllers using PSO, GWO, MFO, and MVO is provided to choose the best methodology that gives the minimum error and more stable operation. Also, a comparison is provided between the proposed optimized controller and the PI-based controller.

The obtained results can be discussed as follows:

Table 3 illustrates the optimized input–output scaling factors of the FLC for the dc-link voltage and rotor–stator currents.

Table 3 Optimized FLC gains of voltage and current regulator

Figure 10 shows the convergence curves of the fitness function value for the PSO, GWO, MFO, and MVO optimization techniques, respectively. It can be noted from the figure that the MFO has the best mean objective function value and it has higher convergence speed and accuracy when compared with the other three optimization algorithms. Figures 11 and 12 represent the optimized surface area curve of the fuzzy controller for the dc-link voltage controller and grid-side and rotor-side current controllers, respectively.

Fig. 10

Convergence curves of different optimization techniques

Fig. 11

Optimized surface area curve of fuzzy controller for the dc-link voltage controller

Fig. 12

Optimized surface area curve of fuzzy controller for grid-side and rotor-side current controllers

Fig. 13

dc-link voltage of the back-to-back converter

Figure 13 shows the dc-Link voltage with PI and with optimized fuzzy-PSO, fuzzy-GWO, fuzzy-MFO, and fuzzy-MVO which illustrates that the GSC controller will strive to keep the dc-link voltage as constant as possible. Table 4 clarifies the step response for the different fuzzy optimized controllers

Table 4 Step response of voltage controller

It is clear from Fig. 13 and Table 4 that fuzzy-MFO has the minimum overshoot for dc-link voltage while preserving rising time and settling time at reasonable values. It is also obvious that PI has the worst step response with a 31.66% overshoot and a settling time of 0.1562 s. Although PSO gives better rising and settling times, the overshoot is higher than that of the MFO.

GWO and MVO give higher overshoot values than MFO and PSO while keeping the settling time and rising time at reasonable values.

Figures 14, 15, 16, and 17 represent the d-q components of rotor and stator currents in the case of PI and optimized fuzzy. It is clear from the figures that the optimized fuzzy controller gives a better response with minimum steady-state error and better settling time. It can be seen from the figures that the performance of different optimized controllers in the case of the current controller is slightly different, while MFO has the best performance. Although it has a high overshoot for some parameters, it has a very stable steady-state response compared to other algorithms.

Fig. 14

d-component of the stator current

Fig. 15

q-component of the stator current

Fig. 16

d-component of the rotor current

Fig. 17

q-component of the rotor current

Table 5 concludes the step response of the PI and fuzzy current controllers. It is clear from the table that MFO has the best step response for the grid-side current controller; it has better overshoot (49%), rise time, and settling time for the d-component of grid-side current; however, it brings higher overshoot for the q-component of grid-side current as shown in Fig. 15, but it has better rise time and settling time and also has a better steady-state response. So, most of the step response parameters for the GSC controller are better in the case of MFO-FLC. For the rotor-side controller, most controllers have very near results regarding the step response, the PI is the worst, and other techniques are almost the same; there is no priority of one of the optimized controllers than the other, but regarding Fig. 10 and the steady-state response of the MFO-FLC, it has the minimum settling time and steady error over all other controllers. So, regarding the step response results and also referring to Fig. 10 which presented the convergence curve of fitness function values, it can be concluded that MFO has the better performance.

Table 5 Step response of current controller

Figure 18 depicts the active and reactive power of DFIG wind turbines during an increase in wind speed (wind speed has a step change from 10 m/s to 15 m/s at time = 10 s). The power curve is determined according to the best-optimized controller which is MFO fuzzy. The reactive power control is adjusted to be zero as indicated in Fig. 18, i.e., the wind turbine generates only active power. Before the change in wind speed (at 10 m/s), it is observed that the active power output is below the rated power as the rated wind speed of that turbine is 12 m/s. During the transition in wind speed from low to high, the reactive output power is kept constant. However, the change in wind speed caused the real power controller to change the real power output to a slightly higher value than the rated value only for a few seconds, and then, the output is once again lowered to a rated real power (1.5 MW). The behavior of the model, in that case, is consistent with that of real DFIG-WECS as expected. From the obtained results, it is obvious that the optimized fuzzy controllers give a very good behavior under variable wind speed with a smooth and stable transition from low to high.

Fig. 18

Active and reactive power of the DFIG wind turbine

6 Conclusion

This paper presented an optimal tuning of fuzzy controllers for a 1.5-MW DFIG wind energy system connected to the grid using intelligent techniques as PSO, GWO, MFO, and MVO to optimize fuzzy controller parameters for both GSC and RSC. Control of active power was done by RSC through Idr and Iqr and keep dc-link voltage constant via GSC through Id and Iq, respectively. In this work, MIMO-FLC and multi-objective optimization algorithms are used to control the d-q component of rotor and stator currents. These techniques with the proposed MIMO-FLC improved the system performance; e.g., (less computation time, minimum overshoot, and better settling time with minimum steady-state error). The PI controller results are compared with fuzzy-PSO, fuzzy-GWO, fuzzy-MFO, and fuzzy-MVO to adopt the best-optimized FLC. In comparison with the PI controller, it is depicted that optimization techniques exhibit excellent steady-state and dynamic performances of controllers by using optimized fuzzy controllers. Also by comparing the optimized FLC using different optimization techniques, it is found that the fuzzy-MFO controller has the best performance regarding the step response of controller, convergence speed, and best fitness function value. As future work, the control of DFIG-based WECS will be extended to be a hybrid renewable energy system including photovoltaic (PV) solar arrays and energy storage to investigate the behavior of the hybrid PV–wind system and adopt an appropriate power management strategy.

Appendices

Appendix 1: Parameters of the 1.5 MW DFIG-based WECS

Appendix 2: The pseudocodes of the optimization techniques

Appendix 3: Parameters of the optimization algorithms