Enhancement of Sliding Mode Control Performance for Perturbed and Unperturbed Nonlinear Systems: Theory and Experimentation on Rehabilitation Robot

Abstract

This paper presents the design and validation of a new adaptive variable gain reaching law, integrated with sliding mode control (SMC), to control perturbed and unperturbed nonlinear systems. The novelty behind this law stems from its capability to overcome the main limitations involved with SMC. In contrast to existing reaching laws, system’s performance can be substantially enhanced via this law, with significant reduction in the chattering phenomenon, along ensuring rapid convergence time of system’s trajectories towards equilibrium. The designed law not only integrates the features of both the exponential reaching law (ERL) and the power rate reaching law (PRL), but also overcomes their limitations. Simulation and comparison studies against ERL and PRL were carried out to validate the effectiveness and advantages of the proposed reaching law scheme (Proposed-RL). Furthermore, controlled experimental investigations were conducted using an exoskeleton robot (ETS-MARSE) to validate the scheme in real-time.

1 Introduction

Robust control usually addresses the complex system analysis and control design for imperfectly known process models. It refers to the control of unknown systems with unknown dynamics subject to unknown perturbations. Major objectives of robust control are to ensure the overall stability and satisfactory system’s performance in the presence of dynamic disturbances. However, a critical issue that usually emerges when adopting robust control schemes is the involved uncertainties, raising the question of how to overcome those. Sliding mode control (SMC) is one of the widely common employed robust strategies in robotics systems [11, 14, 17, 20] due to its prominent features. One significant, perhaps the leading, feature of SMC is its complete insensitiveness to parametric uncertainties and external disturbances during sliding mode. To achieve this, in SMC, a switching surface is chosen so that system’s trajectories can begin from anywhere but are constrained to reach a neighborhood of the selected switching function in a reasonable finite time. Once on the surface, the dynamic behavior is reduced to a stable linear time-invariant system, which in turn is insensitive to parametric uncertainties and external disturbances [24]. Consequently, asymptotic convergence of the system’s state is then readily accomplished. Despite these various advantages of SMC, it still suffers from several shortcomings.

One of SMC’s limitations involves the control strategy’s gains. SMC’s gains play a dominant role in determining system’s trajectories asymptotic convergence time to the equilibrium point. Several control approaches have been proposed to solve this issue, with Terminal Sliding Mode Control (TSMC) [7] being one of those. TSMC uses a nonlinear fractional-order of switching function to guarantee finite-time convergence, permitting the state trajectories to converge to an equilibrium point faster. Lately, attempts were successful to enhance the performance of TSMC, via strategies such as the fast TSMC [21] and the non-singular TSMC [23].

Another limitation involved with SMC is that the control input holds the switching function signum [$\mathrm {sign(.)}$]. That is, in real-time, the switching function produces high frequencies, which induce undesirable chattering in the control input. As a result, system’s performance degrades and loses its precision, as well as the possibility of other problems appearing in the plant (motors). As a remedy, the switching function [$\mathrm {sign(.)}$] has been replaced by continuous approximations, such as a saturation function [17]. However, this solution comes with the cost of SMC losing its robustness, even under small disturbances and parametric uncertainties [17]. Still, many control approaches have been developed to reduce the chattering problem and enhance the time convergence of the system’s state trajectories. Such approaches included the second-order sliding mode control (SOSMC) [18, 22], along with its different types such as the super twisting control [5, 10] and the modified super twisting algorithm [4, 8]. Nonetheless, the second derivative of the system’s dynamics might result with plant instability, a risk that the parametric uncertainties and external disturbances further expand.

On the other hand, conventional reaching laws are numerous in literature [9]. Those include the constant reaching law, the constant plus proportional reaching law, and the power rate reaching law. Researchers often integrate the constant reaching law (CRL) in SMC due to the ability of CRL to force system’s trajectories to converge to the desired equilibrium state in a reasonable convergence time. However, one major concern is the emergence of high undesirable chattering as a result of choosing high control gain values, causing the time convergence to increase as well. In this case, the attenuation issue of the undesirable chattering becomes more attractive than the convergence speed option. In efforts of overcoming the aforementioned restriction, the constant plus proportional reaching law (CPPRL) was formulated as an improvement over CRL, which relatively succeeded in reducing the chattering problem [9]. Yet, the power rate reaching law (PRL) was one of the compelling suggestions to deal with convergence rate speed which, based on its surface, guarantees a chattering free process along with fast convergence speed. However, there is still the possibility of a reduction in its robustness nearby the selected surface. Lastly, the Exponential reaching law (ERL) [6] is considered one of the imperative solutions that were proposed to overcome the limitation involved with CRL. Essentially, the ERL was able to reduce the undesirable chattering, for the same CRL convergence speed, via using a simple exponential tuning. Thus, effectively achieving excellent performance with different robotics systems [12, 13, 15, 25]. Nonetheless, one of the shortcomings involved with ERL is its incapability to improve the convergence speed without inevitably stimulating the chattering phenomenon.

In response to the different limitations involved with the aforementioned reaching laws, the motivation behind this paper was to improve system trajectories’ convergence time without inducing any chattering reduction. Therefore, the aim of this research is to propose a new reaching law to address the mentioned problem; primarily, to improve the convergence speed of the system trajectories, along with enhancing the chattering attenuation process. The proposed law benefits from the properties of both ERL and PRL. That is, it employs a power rate term to reduce the chattering while utilizing ERL’s characteristic of providing a fast reaching time to the origin. In addition, in efforts of maintaining system’s robustness, a novel adaptive term was also integrated. Thereafter, simulation and comparison studies were conducted to investigate the robustness of the proposed reaching law (Proposed-RL) as well as potentially showing its faster convergence speed compared to PRL and ERL. Lastly, Experiments were performed by a real subject using an exoskeleton robot [2] to prove the feasibility and ease of implementation of the proposed law in real-time applications.

This paper is organized as follows: Problem formulation and motivation are described in Sect. 2. Section 3 presents the proposed reaching law in details. Simulation and comparison studies against ERL and PRL are presented in Sect. 4. An experimental study using the exoskeleton robot is given in Sect. 5. Section 6 concludes the research.

2 Problem Formulation and Motivation

Although the theory of SMC of non-linear systems is well-known in literature [19], a brief description highlighting its main advantages and shortcomings is still presented in this chapter. Fundamentally, such limitations were highly prompting to propose the novel, effective, reaching law approach detailed in the next section. To start, consider a general non-linear second-order dynamic system:

$$\begin{aligned} \ddot{x}=f (x,\dot{x} )+g ( x,\dot{x})u+w(x,\dot{x}) \end{aligned}$$

(1)

where $f\in \mathfrak {R}^{n}$ and $g\in \mathfrak {R}^{n\times n}$ are two non-linear functions, with g being an invertible matrix. $w\in \mathfrak {R}^{n}$ represents the unknown bounded uncertainty and disturbance forces. The tracking position error, which tends to zero, can be defined as: $e=x-x^{d}$ ,where $x^{d}\in \mathfrak {R}^{n}$ is the desired trajectory. Selecting a switching function S to track position and velocity errors is often one of the first steps in designing SMC controllers. Commonly, this sliding surface is chosen as follows:

$$\begin{aligned} S=\dot{e}+ \lambda e \end{aligned}$$

(2)

where $\lambda \in \mathfrak {R}^{n\times n}$ is a diagonal positive definite matrix. It is worth mentioning that the value of $\lambda$ plays a crucial role in the error tracking convergence rate to zero.

Consider the Lyapunov function: $V(S)=\dfrac{1}{2}S^{T}S$, with its time derivative given by:

$$\begin{aligned} \dot{V}=S^{T}\dot{S} \end{aligned}$$

(3)

The criterion for stability is therefore: $\dot{V}<0$. This requires $\dot{S}<0$ for $S>0$ and $\dot{S}>0$ for $S<0$, which gives rise to the commonly known control law switching phenomenon around $S=0$. Based on (2) and its derivative, the following control input is proposed:

$$\begin{aligned} u=g^{-1} [\ddot{x}^d-\lambda \dot{e}-f-w+\dot{S}] \end{aligned}$$

(4)

It is noteworthy, from (4), that the control input is highly dependant on $\dot{S}$, which in turn determines the rate of S. That is, if $\dot{S}\ll 0$ for $S>0$ (with the opposite being also true), the system’s forced trajectory converges to $S=0$. Hence, commonly referring to $\dot{S}$ as the ”reaching” law. When system’s trajectory is in the vicinity of $S=0$, with $\dot{V}<0$, $\dot{S}<0$ dictates how close is the system exactly from the sliding manifold $S=0$. Consequently, a ”switching” phenomenon emerges in order to maintain the condition: $S\dot{S}<0$.

That being said, numerous reaching laws that took into account the speed of the reaching time have been proposed in literature. These reaching laws can be summarized as follows [9]:

• Constant rate reaching law (CRL) [9]:

  $$\begin{aligned} \dot{S}_{i}=-K_{1i}sign(S_{i}) \end{aligned}$$

  (5)

  where $K_{1i}>0$ with $i=1 ldots n$ being a positive constant. The reaching law (5) forces the system’s trajectory ($e_{i},\dot{e}_{i}$) to converge to the switching surface $S_{i}$ in a reaching time given by: $Tr_{i}=\dfrac{\left| S_{i}\left( 0\right) \right| }{K_{1i}}$, where $S_{i}(0)$ is the initial condition of $S_{i}$. Thus, a higher $K_{1i}$ value is necessary for fast convergence. However, this comes with the cost of a worsened chattering when the system’s trajectory moves in the sliding manifold.

• Constant plus proportional rate reaching law (CPPRL)[9]:

  $$\begin{aligned} \dot{S}_{i}=-K_{1i}sign(S_{i})-K_{2i}S_{i} \end{aligned}$$

  (6)

  where $K_{1i},K_{2i}$ are positive constants. The CPPRL law ensures a convergence rate of: $Tr_{1i}=\dfrac{1}{K_{1i}} \mathrm {ln} \dfrac{K_{2i}\left| S_{i}(0) \right| +K_{1i}}{K_{1i}}$. Unlike the CRL, expression (6) improves the chattering phenomenon while maintaining a relatively fast convergence rate, which makes it one of the most powerful reaching law candidates.

• Power rate reaching law (PRL)[9]:

  $$\begin{aligned} \dot{S}_{i}=-K_{1i}\left| S_{i} \right| ^\sigma sign(S_{i}) \end{aligned}$$

  (7)

  where $0<\sigma <1$. The PRL law (7) is able to provide a reaching time of: $Tr_{2i}=\dfrac{\left| S_{i}(0) \right| ^{(1-\sigma )}}{(1-\sigma )K_{1i}}$. The primary advantage of this law is its capability to adjust the reaching time, a parameter that depends on the position of the state system relative to the sliding surface. In other words, when the system’s trajectory is distant from the surface, the PRL increases its reaching speed, with the opposite being true. The term $\left| S_{i}\right| ^\sigma$ guarantees a chattering-free process along fast convergence of the desired state. Depending on the choice of the power term $\sigma$, this might further lead to a loss in system’s robustness.

Remark 1

The control law defined by (4) is inputted to system (1) if it is unperturbed, i.e. for a given known $w(x,\dot{x})$. However, in real-time, system (1) will be subject to uncertainties and external disturbances. In such a case, an estimation of $w(x,\dot{x})$ will be integrated into control law (4) (see Sect. 3.2).

After closely assessing all three reaching laws, they have proven to be highly helpful and applicable in designing SMCs. Yet, adopting any of the aforementioned reaching laws seems to come with an inevitable trade-off between either the convergence rate and chattering reduction, or the chattering reduction and controller’s robustness. One common behavior between the three is that the choice of a large gain value $K_{1i}$ (coefficient of $sign(S_{i})$) is necessary to ensure a fast convergence rate to the desired surface. Though, this leads to chattering, the damaging effect that produces high-frequency dynamics. As a result, an adaptive reaching law has been proposed, namely the Exponential Reaching law (ERL) [6], as a remedy to the drawbacks of choosing a large gain value. The ERL is given by:

$$\begin{aligned} \dot{S}_{i}=-\dfrac{K_{1i}}{\mu _{i}+\left( 1- \mu _{i}\right) e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}}} } sign(S_{i}) \end{aligned}$$

(8)

where $\mu _{i}$, $\alpha _{i}$ and $p_{i}$ are strictly positive constants with $\mu _{i}<1$. As a consequence of (8), the limitation related to the gain value can be easily overcome with the controller dynamically self-adjusting to the variations resulting from the switching function $S_{i}$. This operation permits the gain $K_{1i}$ to smoothly vary between $K_{1i}$ and $K_{1i}/\mu _{i}$. Thus, the ERL method can ensure a reaching time of [6]:

$$\begin{aligned} Tr_{3i}\approx \mu _{i}\dfrac{\left| S_{i}(0) \right| }{K_{1i}} \end{aligned}$$

(9)

if $\alpha _{i}$ in (8) abides by the following condition [6]:

$$\begin{aligned} \alpha _{i}\gg \left( \dfrac{1-\mu _{i}}{\mu _{i}\left| S_{i}(0) \right| }\right) ^{1/{p_{i}}} \end{aligned}$$

(10)

Indeed, the ERL focuses primarily on reducing chattering using the innovative law defined by (8). However, completely eliminating this chattering effect remains questionable, especially when the term $K_{1i}sign(S_{i})$ is conserved, thus putting restrictions on improving the chattering. Besides, as can be inferred from (9), it is almost impossible to increase the convergence speed without causing chattering attenuation. That is, any decrease in the reaching time drives the term $K_{1i}$ higher, which again causes the chattering phenomenon. It was further noticed that the state of the control system does not perfectly overlap with the reference trajectory due to the continuous low chattering degree.

As a promising solution in this paper, integrating a power rate adjustment technique allowed for a significant enhancement in reducing the chattering, nearly eliminating such a phenomenon, with a remarkable improvement in the reaching speed without any direct effect on the chattering. The proposed reaching law was formulated such that it would be able to benefit from all reaching laws (6), (7) and (8) advantages. That is, the proposed law adopted the advantages of PRL and CPPRL, which outweigh the limitation of ERL, as well as integrating the feature of ERL, which in turn overcomes the restriction of both PRL and CPPRL.

3 Proposed Reaching law

The proposal of the adaptive reaching law, along comparing it against ERL, will be presented in Sect. 3.1. However, as mentioned in Remark 1, the uncertainties and external disturbances might cause some losses in the proposed reaching law robustness. In this case, reformulating some of the parameters is necessary as shown Sect. 3.2.

3.1 System Without Uncertainties and External Disturbances

This section presents the mathematical formulation of the proposed reaching law that would make use of ERL’s and PRL’s advantages, in addition to ensuring a convergence time less than that provided by ERL and PRL. The proposed reaching law is given by:

$$\begin{aligned} \dot{S}_{i}&=-\dfrac{K_{1i}}{\mu _{i}+\left( 1- \mu _{i}\right) e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}}}} \vert S_{i}\vert ^{\gamma } sign(S_{i}) \nonumber \\&\quad - \varrho _{i} \dfrac{ K_{1i}\left( 1-\gamma \right) }{ \mu _{i} }sign(S_{i}) \end{aligned}$$

(11)

where $\mu _{i}$, $\alpha _{i}$ and $p_{i}$ are strictly positive constants with $\mu _{i}<1$ and $0<\gamma <0.5$. $\varrho _{i}$ is determined by $\lim _{t\rightarrow \infty }(\varrho _{i})=0$ and $\int _{0}^{t}\varrho _{i}(w)dw=Q_{i}<\infty$, where $\varrho _{i}=1/(1+t^2_{i})$ and $t_{i}$ being the execution time of the exercise. In fact, the second term of the proposed law (11) is responsible for maintaining the robustness of the control input, especially around the starting point of the trajectory. It is worth mentioning that, as time elapses, this term would vanish according to the definition of $\varrho _{i}$.

In the preceding section, the advantages of each term, such as ERL and power rate, were briefly explained. It was noticed that the term $\gamma$ is usually assigned a high value in the conventional power rate law to ensure fast convergence to the equilibrium point, however resulting with undesirable chattering. In efforts of improving this, in the proposed law, a limit on $\gamma$ was enforced such that: $0<\gamma <0.5$. This would not only ensure fast convergence, but also minimize the chattering.

Proposition 1

For the same gain value $K_{1i},$ and in accordance with the choice of $\gamma$ defined earlier, the reaching law given by (11) always provides faster convergence to the equilibrium point than ERL [6].

Proof

The reaching time of the ERL is given by [6]:

$$\begin{aligned} Tr_{3i}=\dfrac{1}{K_{i}} \left( \mu _{i} | S_{i}(0) |+ (1- \mu _{i}) \int _{0}^{ | S_{i}(0) |}e^{{-\alpha _{i}} | S_{i} |^{p_{i}} }dS_{i} \right) \end{aligned}$$

(12)

To find the reaching time ($Tr_{4i}$) of the proposed reaching law (11), it is first rewritten as follows:

$$\begin{aligned} dt_{i}&=\dfrac{ ( \mu _{i}+ (1- \mu _{i})e^{{-\alpha _{i}} | S_{i} |^{p_{i}}})dS_{i}}{-K_{1i}\vert S_{i}\vert ^{\gamma } sign(S_{i})}\nonumber \\&\quad + \dfrac{\mu _{i} dS_{i}}{- \varrho _{i}K_{1i} (1-\gamma )sign(S_{i})}. \end{aligned}$$

(13)

Integrating (13) from zero to $Tr_{4i}$, with $S_{i}(Tr_{4i}=0)$, the following can be found:

$$\begin{aligned} Tr_{4i}&=\int _{S_{i}(0)}^{0}\dfrac{\left( \mu _{i}+\left( 1- \mu _{i}\right) e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}}}\right) dS_{i}}{-K_{1i}\vert S_{i}\vert ^{\gamma } sign(S_{i})}\nonumber \\&\quad + \int _{S_{i}(0)}^{0}\dfrac{\mu _{i} dS_{i}}{- \varrho _{i}K_{1i}\left( 1-\gamma \right) sign(S_{i})}. \nonumber \\&=\int _{0}^{S_{i}(0)}\dfrac{\left( \mu _{i}+\left( 1- \mu _{i}\right) e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}} }\right) dS_{i}}{K_{1i}\vert S_{i}\vert ^{\gamma } sign(S_{i})} \nonumber \\&\quad +\int _{0}^{S_{i}(0)}\dfrac{\mu _{i} dS_{i}}{\varrho _{i}K_{1i}\left( 1-\gamma \right) sign(S_{i})}. \end{aligned}$$

(14)

In the first case, if $S_{i}<0$ for all $ti<Tr_{4i}$, then:

$$\begin{aligned} Tr_{4i}&=\int _{0}^{-S_{i}(0)}\dfrac{\left( \mu _{i}+\left( 1- \mu _{i}\right) e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}}}\right) dS_{i}}{K_{1i}\vert S_{i}\vert ^{\gamma }}\nonumber \\&\quad +\int _{0}^{-S_{i}(0)}\dfrac{\mu _{i} dS_{i}}{\varrho _{i}K_{1i}\left( 1-\gamma \right) }. \end{aligned}$$

(15)

Otherwise, if $S_{i}>0$ for all $ti<Tr_{4i}$, this would result with:

$$\begin{aligned} Tr_{4i}&=\int _{0}^{S_{i}(0)}\dfrac{\left( \mu _{i}+\left( 1- \mu _{i}\right) e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}} }\right) dS_{i}}{K_{1i}\vert S_{i}\vert ^{\gamma }}\nonumber \\&\quad +\int _{0}^{S_{i}(0)}\dfrac{\mu _{i} dS_{i}}{\varrho _{i}K_{1i}\left( 1-\gamma \right) }. \end{aligned}$$

(16)

According to (15) and (16):

$$\begin{aligned} Tr_{4i}&=\int _{0}^{|S_{i}(0)|}\dfrac{ \mu _{i}dS_{i}}{K_{1i}\vert S_{i}\vert ^{\gamma }} +\int _{0}^{|S_{i}(0)|}\dfrac{\left( 1- \mu _{i}\right) e^{{-\alpha }\left| S_{i} \right| ^{p_{i}}}dS_{i}}{K_{1i}\vert S_{i}\vert ^{\gamma }}\nonumber \\&\quad +\int _{0}^{|S_{i}(0)|}\dfrac{\mu _{i} dS_{i}}{\varrho _{i}K_{1i}\left( 1-\gamma \right) }. \end{aligned}$$

(17)

Integrating (17), the reaching time is then given by:

$$\begin{aligned} Tr_{4i}&=\dfrac{1}{K_{1i}}(\mu _{i} \dfrac{|S_{i}(0)|^{(1-\gamma )}}{(1-\gamma )}+\dfrac{\mu _{i}|S_{i}(0)|}{\varrho _{i}\left( 1-\gamma \right) }\nonumber \\&\quad +(1-\mu _{i})\int _{0}^{|S_{i}(0)|}e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}}}|S_{i}|^{-\gamma }dS_{i}). \end{aligned}$$

(18)

In [6] the authors used the properties of Euler’s gamma function ($\Gamma$) to prove that the the reaching time $Tr_{3i}$ satisfies the following:

$$\begin{aligned} Tr_{3i} \le \dfrac{\mu _{i}}{K_{1i}}|S_{i}(0)|+\dfrac{(1-\mu _{i})}{K_{1i}\alpha _{i}^{1/p_{i}}}. \end{aligned}$$

(19)

Using a similar approach for the proposed reaching law, the last term of (18) can be rewritten in terms of the $\Gamma$ function such that:

$$\begin{aligned}&\int _{0}^{|S_{i}(0)|}e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}} }|S_{i}|^{-\gamma }dS_{i} \nonumber \\&= \alpha _{i}^{\gamma /{p_{i}}}\dfrac{\left[ \Gamma ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) -\Gamma \left( ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) ,\alpha _{i}|S_{i}(0)|^{p_{i}}\right) \right] }{p_{i}\alpha _{i}^{1/{p_{i}}}}. \end{aligned}$$

(20)

Based on the properties of the $\Gamma$ function:

$$\begin{aligned} \Gamma \left( ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) ,\alpha _{i}|S_{i}(0)|^{p_{i}}\right) \ll \Gamma ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) . \end{aligned}$$

(21)

Therefore, it is valid to assume that: $\Gamma \left( ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) ,\alpha _{i}|S_{i}(0)|^{p_{i}}\right) \approx 0$, and hence:

$$\begin{aligned} \int _{0}^{|S_{i}(0)|}e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}} }|S_{i}|^{-\gamma }dS_{i}= \alpha _{i}^{\gamma /{p_{i}}}\dfrac{\Gamma ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) }{p_{i}\alpha _{i}^{1/{p_{i}}}}. \end{aligned}$$

(22)

substituting (22) into (18), it is found that the reaching time fulfills the following condition:

$$\begin{aligned}&Tr_{4i}\le \dfrac{\mu _{i}}{K_{1i}}\left[ \dfrac{|S_{i}(0)|^{(1-\gamma )}+\varrho _{i}|S_{i}(0)|}{(1-\gamma )}\right] \nonumber \\&\quad +\left( \dfrac{1-\mu _{i}}{K_{1i}}\right) \dfrac{\Gamma ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) }{p_{i}\alpha _{i}^{\left( \dfrac{1-\gamma }{{p_{i}}}\right) }}. \end{aligned}$$

(23)

To prove that the proposed reaching law provides a reaching time less than that provided by ERL [6], it is essential to rewrite the reaching time of the proposed law as follows:

$$\begin{aligned} Tr_{4di}&= \dfrac{\mu _{i}}{K_{1i}}\left[ \dfrac{|S_{i}(0)|^{(1-\gamma )}+\varrho _{i}|S_{i}(0)|}{(1-\gamma )}\right] \nonumber \\&\quad +\left( \dfrac{1-\mu _{i}}{K_{1i}}\right) \dfrac{\Gamma ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) }{p_{i}\alpha _{i}^{\left( \dfrac{1-\gamma }{{p_{i}}}\right) }}. \end{aligned}$$

(24)

Therefore, the reaching time $Tr_{4i}$ should be less than the desired reaching time $Tr_{4di}$ for every value of $\alpha$ such that:

$$\begin{aligned} \alpha _{i}\gg \left[ \dfrac{(1-\mu _{i})\Gamma ^{-}\left( \dfrac{\gamma -1}{p_{i}}\right) (1-\gamma )}{\mu _{i}\left( |S_{i}(0)|^{(1-\gamma )}+\varrho _{i}|S_{i}(0)|\right) } \right] ^{\dfrac{p_{i}}{1-\gamma }}. \end{aligned}$$

(25)

Thus, the desired reaching law can be re-approximated as follows:

$$\begin{aligned} Tr_{4di} \approx \dfrac{\mu _{i}}{K_{1i}}\left[ \dfrac{|S_{i}(0)|^{(1-\gamma )}+\varrho _{i}|S_{i}(0)|}{(1-\gamma )}\right] . \end{aligned}$$

(26)

As a second condition, the gain $K_{1i}$ must satisfy:

$$\begin{aligned} K_{1i} \approx \dfrac{\mu _{i}}{ Tr_{4di}}\left[ \dfrac{|S_{i}(0)|^{(1-\gamma )}+\varrho _{i}|S_{i}(0)|}{(1-\gamma )}\right] . \end{aligned}$$

(27)

If both conditions (25) and (27) are satisfied, it can then be ensured that $Tr_{4i}<Tr_{4di}$. Since the proposed reaching law will be against the ERL [6], it would be helpful to mention the desired reaching law, along with the tuning gain, given by the ERL proposition:

$$\begin{aligned}&Tr_{3di}\approx \mu _{i}\dfrac{\left| S_{i}(0) \right| }{K_{1i}} \end{aligned}$$

(28)

$$\begin{aligned}&K_{1i}\approx \mu _{i}\dfrac{\left| S_{i}(0) \right| }{Tr_{3di}} \end{aligned}$$

(29)

Subtracting (26) from (28) yields:

$$\begin{aligned} Tr_{3di}-Tr_{4di}&\approx \mu _{i}\dfrac{\left| S_{i}(0) \right| }{K_{1i}}-\dfrac{\mu _{i}}{K_{1i}}\left[ \dfrac{|S_{i}(0)|^{(1-\gamma )}+\varrho _{i}|S_{i}(0)|}{(1-\gamma )}\right] \nonumber \\&\approx \dfrac{ \mu _{i}}{K_{1i}}\left| S_{i}(0) \right| \left[ 1-\left( \dfrac{|S_{i}(0)|^{-\gamma }+\varrho _{i}}{(1-\gamma )} \right) \right] \end{aligned}$$

(30)

Since $\mu _{i}$ and $K_{1i}$ are positive constants, it is then remarked that the term $\dfrac{\mu _{i}}{K_{1i}}\left| S_{i}(0) \right|$ is always positive.

In addition, it is essential to prove that the second term of (30) is always positive. Based on the definition of $\varrho _{i}$ in (11), as $t\longrightarrow \infty$, the term $\varrho _{i}\longrightarrow 0$. In this case, to ensure that the second term of (30) is always positive, the following must hold:

$$\begin{aligned} \dfrac{ 1}{|S_{i}(0)|^{\gamma }(1-\gamma )}<1 \end{aligned}$$

(31)

This means that it is indispensable for the following to hold:

$$\begin{aligned} |S_{i}(0)|> (1-\gamma )^{-1/\gamma } \end{aligned}$$

(32)

Hence,

$$\begin{aligned} \left( 1-\dfrac{ 1}{|S_{i}(0)|^{\gamma }(1-\gamma )}\right)>0, \forall |S_{i}(0)|> (1-\gamma )^{-1/\gamma } \end{aligned}$$

(33)

Alternatively, (30) can be rewritten as follows:

$$\begin{aligned}&Tr_{3di}-Tr_{4di}\approx \dfrac{ \mu _{i}}{K_{1i}}\left| S_{i}(0) \right| \left[ 1-\left( \dfrac{|S_{i}(0)|^{-\gamma }}{(1-\gamma )} \right) \right]>0, \nonumber \\&\quad \forall |S_{i}(0)|> (1-\gamma )^{-1/\gamma } \end{aligned}$$

(34)

It is noteworthy that, based on (23) and (24), $Tr_{4i}\le Tr_{4di}$. Furthermore, based on [6], $Tr_{3i}\le Tr_{3di}$. Thus, according to the condition given by (34), the following can be rewritten:

$$\begin{aligned} Tr_{3i}-Tr_{4i}>0, \forall |S_{i}(0)|> (1-\gamma )^{-1/\gamma } \end{aligned}$$

(35)

Consequently, depending on the value of $\gamma$, the reaching time provided by the proposed law is less than that provided by the ERL. Therefore, the proof is complete. $\square$

3.2 System with Bounded Uncertainties and External Disturbances

To consider the system with unknown bounded uncertainties and external disturbances, this would indeed impose multiple constraints on the proposed adaptive reaching law parameters. Firstly, recall that a non-linear second-order system can be described by:

$$\begin{aligned} \ddot{x}=f\left( x,\dot{x} \right) +g\left( x,\dot{x}\right) u +w\left( x,\dot{x} \right) \end{aligned}$$

(36)

Let $\hat{w}\left( x,\dot{x} \right)$ be the estimated value of $w\left( x,\dot{x} \right)$ and $B_{MAX}$ be the upper bound of the estimation error, defined as follows:

$$\begin{aligned} B_{MAX}=\sup _t\left| w(x,\dot{x})-\hat{w}(x,\dot{x}) \right| \end{aligned}$$

(37)

Using the same sliding surface described by (2), the conventional sliding mode control would be given by:

$$\begin{aligned} u=g^{-1}\left[ \ddot{x}^d-\lambda \dot{e}-f(x,\dot{x})-\hat{w}(x,\dot{x})-K_{1i}sign(S)\right] \end{aligned}$$

(38)

where $K>0$ and $sign(S)=[sign(S_{ii})\cdots sign(S_{nn})]$. This results with:

$$\begin{aligned} \dot{S}=(w_{i}(x,\dot{x})-\hat{w}_{i}(x,\dot{x}))-K_{1i} sign(S_{i}) \end{aligned}$$

(39)

From Equation (39), the convergence to zero can be achieved only if the following condition holds:

$$\begin{aligned} K_{1i}>(w_{i}(x,\dot{x})-\hat{w}_{i}(x,\dot{x}))\forall t \end{aligned}$$

(40)

As illustrated by (5), the value of $K_{1i}$ is constant in conventional sliding mode control. This implies that:

$$\begin{aligned} K_{1i}> B_{MAX} \end{aligned}$$

(41)

In fact, it is almost impossible to satisfy condition (41) without causing other problems such as the chattering phenomenon. This is mainly because the gain value $K_{1i}$ is usually large enough to guarantee the convergence of the sliding surface. With the proposed adaptive reaching law defined by (11), since $\lim _{t\rightarrow \infty }(\varrho _{i})=0$ and $\int _{0}^{t}\varrho _{i}(w)dw=Q_{i}<\infty$, the condition given by (41) can be rewritten as:

$$\begin{aligned} K_{1i}>\mu _{i} B_{MAX}+\left( 1- \mu _{i}\right) e^{{-\alpha _{i}}\left| S_{i} \right| ^{p_{i}}} B_{MAX} \end{aligned}$$

(42)

It is obvious from (42) that the gain $K_{1i}$ has to be at least superior to $B_{MAX}\mu _{i}$. Satisfying this minimum $K_{i}$ gain requirement, and subsequently solving for $S_{i}$ in (42), the following is obtained:

$$\begin{aligned} \left| S_{i} \right| = ^p\sqrt{\frac{\ln (\frac{B_{MAX} \left( 1- \mu _{i}\right) }{K_{1i}-B_{MAX}\mu _{i}})}{\alpha _{i}}}, K_{1i}>B_{MAX}\mu _{i} \end{aligned}$$

(43)

It can then be inferred from equation (43) that, to meet condition (42), the sliding surface $S_{i}$ can vary in a boundary of width Q defined by:

$$\begin{aligned} Q= ^p\sqrt{\frac{\ln (\frac{B_{MAX} \left( 1- \mu _{i}\right) }{K_{1i}-B_{MAX}\mu _{i}})}{\alpha _{i}}}, K_{1i}>B_{MAX}\mu _{i}, \end{aligned}$$

(44)

Thus, this boundary width Q is directly affected by the choice of $\alpha _{i}$.

To sum up, all aforementioned constraints, in subsections 3.1 and 3.2, provided insightful relations to be used in choosing the proposed adaptive reaching law parameters. These relations can be summarized as follows:

$$\begin{aligned} \frac{K_{i}}{\mu _{i}}>B_{MAX},\alpha _{i} \ge \frac{\ln (\frac{B_{MAX} \left( 1- \mu _{i}\right) }{K_{1i}-B_{MAX}\mu _{i}})}{Q^{p}} \end{aligned}$$

(45)

4 Simulation Study

In this section, three different numerical simulations were conducted, in Matlab(2018a)/Simulink software, to track the trajectory of a two degrees of freedom (2-DOFs) robot manipulator, as shown in Fig.1. The dynamics of 2-DOFs system is described by (1) with the applied control input given by (4). The simulation set consisted of substituting each of the reaching laws (7), (8) and the proposed one defined by (11). The primary goal was to create a comparison between all reaching laws, as well as to elaborate on the potential advantages of the suggested law.

Fig. 1

Two-link robot manipulator

The dynamic model of 2-DOfs robot manipulator is given by the following equation:

$$\begin{aligned} M(q)\ddot{q}+C(q,\dot{q})\dot{q}+G(q)+f_{dis}=\tau \end{aligned}$$

(46)

where $q\in R^{2}$ denotes the generalized coordinates vector. $M(q)\in R^{2\times 2}$, $C(q,\dot{q})\dot{q}\in R^{2}$, and $G(q)\in R^{2}$ are respectively the symmetric, bounded, inertia matrix, the Coriolis and centrifugal torques, and the gravitational torques. $\tau \in R^{2}$ is the torque input vector and $f_{dis} \in R^{2}$ represents the uncertainties and external disturbances. The earlier introduced matrices are defined as follows:

$$\begin{aligned} M(q)=\begin{pmatrix} M(1,1) &{} M(1,2) \\ M(2,1) &{} M(2,2) \end{pmatrix} \end{aligned}$$

with, $M(1,1)=l_{2}^{2}m_{2}+2l_{1}l_{2}m_{2}c_{2}+l_{2}^{2}(m_{1}+m_{2})+J_{1}$;

$M(1,2)=M(2,1)=l_{2}m_{2}(l_{1}+l_{2})$; $M(2,2)=l_{2}^{2}m_{2}+J_{2}$;

$$\begin{aligned} C(q,\dot{q})\dot{q}= & {} \left( {\begin{array}{c} -l_{1}l_{2}m_{2}s_{2}\dot{q}_{2}^{2}-2l_{1}l_{2}m_{2}s_{2}\dot{q}_{1}\dot{q}_{2} \\ l_{1}l_{2}m_{2}s_{2}\dot{q}_{2}^{2} \end{array}}\right) \\ G(q)= & {} \left( {\begin{array}{c} l_{2}m_{2}g c_{12}+(m_{1}+m_{2})l_{1}g c_{1} \\ l_{2}m_{2}g c_{12} \end{array}}\right) \end{aligned}$$

and,

$$\begin{aligned} f_{dis}=\left\{ \begin{array}{ll} \left[ \begin{array}{l} 4\sin (t)+\frac{1}{2}\sin (200\pi t)\\ \cos (3t)+\frac{1}{2}\sin (200\pi t) \end{array}\right] , \quad {If} \, \, t< 2.5s \\ \left[ \begin{array}{l} 15\sin (t)+6\sin (200\pi t)\\ 10\cos (3t)+6\sin (200\pi t) \end{array}\right] ,\qquad else \end{array}\right. \end{aligned}$$

where $s_{i}$, $c_{i}$ and $c_{ij}$ are defined such that: $s_{i}=\sin (q_{i})$, $c_{i}=\sin (q_{i})$, and $c_{ij}=\cos (q_{i}+q_{j})$. The parameters defining 2-DOFs manipulator are given in Table  1.

Table 1 Parameters of 2-DOFs robot manipulator [3]

Assuming that $q=x$ and $q_d=x^{d}$, the robot’s dynamics (46) can be rewritten in accordance with the general form of nonlinear systems given by (1):

$$\begin{aligned} \ddot{q}=f\left( q,\dot{q} \right) +g\left( q\right) u +w\left( q \right) \end{aligned}$$

(47)

where, $g\left( q\right) =M^{-1}(q)$, $u=\tau$, $f\left( q,\dot{q} \right) =-M^{-1}(q)\left( C(q,\dot{q})\dot{q}+G(q)\right)$, and $w\left( q\right) =M^{-1}(q)f_{dis}$.

Fig. 2

Joints position tracking

Fig. 3

Evolution of the surfaces

The controller objective is to track the reference trajectories given by:

$$\begin{aligned} q_{1d}&=cos(t) \nonumber \\ q_{2d}&=cos(t) \end{aligned}$$

(48)

All initial states (joint positions and velocities) were selected to be $q_{1}=q_{2}=0$ $\mathrm {rad}$ and $\dot{q}_{1}=\dot{q}_{2}=0$ $\mathrm {rad/s}$.

The parameters used in simulating the control input (4), coupled with the proposed reaching law (11), were chosen as follows: $K_{1i}=\mathrm {diag}(5,5)$, $\lambda =\mathrm {diag}(2,2)$, $\mu _{1}=\mu _{2}=0.6$, $\alpha _{1}=\alpha _{2}=20$, $p_{1}=p_{2}=1$, and $\gamma =0.5$. On the other hand, the parameter set for the case of the ERL (8) were: $K_{1}=\mathrm {diag}(5,5)$, $\lambda =\mathrm {diag}(2,2)$, $\mu _{1}=\mu _{2}=0.6$, $\alpha _{1}=\alpha _{2}=20$ and $p_{1}=p_{2}=1$. Lastly, for the case of PRL (7): $K_{1i}=\mathrm {diag}(5,5)$, $\lambda =\mathrm {diag}(2,2)$, and $\gamma =0.5$. In addition, the same gain values were utilized in all cases.

Fig. 4

Evolution of the torques

Fig. 5

Convergence of the states on phase plane

It is evident from Fig. 2, which tracks the joints position, that both the ERL and the proposed RL controllers closely matches the reference trajectory. On the other hand, the PRL seems to lose its accuracy in the first two seconds. Thereafter, it provides a similar performance compared to the ERL and the proposed RL. Figure 3 clearly shows that all controllers are able to drive the surface to the origin in a finite time, with the proposed RL being the fastest to do so among the other two controllers. Nevertheless, all controllers are able to reduce the chattering problem as shown by the torque inputs given by Fig. 4. Lastly, Fig. 5 shows the performance of each controller in the phase plane. All the state trajectories converge to the origin of the phase plane, with evidently the proposed RL again being the fastest among the other two. Such results support the high efficiency of the proposed RL.

5 Experimental Study

5.1 System Characterization

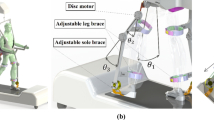
ETS-MARSE (Ecole de Technologie Supérieure—Motion Assistive Robotic-exoskeleton for Superior Extremity) is a 7 degrees of freedom (DOFs) exoskeleton robot (Fig. 6). This robot is fundamentally built to support in rehabilitation treatments provided to persons with an impaired upper-limb. Its mechanical design is inspired from the anatomy of the human upper-limb. The primary purpose is for it to be comfortably attached to the arm, permitting the subject’s arm to freely move. It consists of three joints shaping the shoulder member, one joint modelling the elbow member and three other joints shaping the wrist member. As described in Table 2, the motion each part of the exoskeleton manipulator is able to perform mimics human upper limb movements. All exceptional features of ETS-MARS, along with its comparison against other popular rehabilitation robots, can be found in [1, 16]. Table 2 presents the modified Denavit-Hartenberg (DH) parameters obtained from the coordinate frames attached to the robot as shown in Fig. 6. Those are later used to find the homogeneous transformation matrices.

5.2 Dynamic Model of ETS-MARSE Robot

The dynamic model of ETS-MARSE robot is expressed in joint space as follows:

$$\begin{aligned} M(\theta )\ddot{\theta }+C(\theta ,\dot{\theta })\dot{\theta }+G(\theta )+f_{dis}=\tau \end{aligned}$$

(49)

where $\theta \in \mathfrak {R}^{7}$ denotes a 7-vector of generalized coordinates. $M(\theta )\in \mathfrak {R}^{7\times 7}$, $C(\theta ,\dot{\theta })\dot{\theta }\in \mathfrak {R}^{7}$, and $G(\theta )\in \mathfrak {R}^{7}$ are respectively the symmetric, bounded, inertia matrix, the Coriolis and centrifugal torques, and the gravitational torques. $\tau \in \mathfrak {R}^{7}$ is the torque input vector and $f_{dis}\in \mathfrak {R}^{7}$ represents the external disturbances. Introducing $x=\theta$ and $\dot{x}=\dot{\theta }$, the dynamic model expressed in Eq. 49 can be rewritten in the form of Eq. 1 as follows:

$$\begin{aligned} \ddot{x}= f(x,\dot{x})+g(x)u+w(x,\dot{x}) \end{aligned}$$

(50)

with:

• $u=\tau$

• $g(x)=M^{-1}_0 (\theta )$

• $f(x,\dot{x})=M^{-1}_0 (\theta ) \left[ -C_0\left( \theta ,\dot{\theta }\right) \dot{\theta } - G_0 (\theta ) \right]$

• $w(x,\dot{x})=M^{-1}_0 (\theta ) \left[ -f_{ex}-\Delta M\left( \theta \right) \ddot{\theta } -\Delta C\left( \theta ,{\dot{\theta }} \right) \dot{\theta }-\Delta G (\theta ) \right]$

where $M_0(\theta )$, $C_0\left( \theta ,\dot{\theta }\right)$ and $G_0(\theta )$ are respectively the known inertia matrix, the Coriolis/centrifugal matrix, and the gravitational forces vector. $\Delta M\left( \theta \right)$, $\Delta C\left( \theta ,\dot{\theta }\right)$ and $\Delta G( \theta )$ are the associated uncertainties.

Coupling the control input (4) with the reaching law (11), the robot system should be able to follow the reference trajectory with the promising characteristics given by Proposition 1.

Fig. 6

a Human-exoskeleton robot. b Coordinate defining ETS-MARSE movements

Table 2 Modified Denavit–Hartenberg parameters

5.3 Real Time Setup

The rehabilitation robot system is composed of three processing units. The first is a PC unit where the top-level commands are transmitted to the exoskeleton robot using LabVIEW interface, i.e. to select the type of physiotherapy exercise and type of rehabilitation protocol to be specified. The performance of the exoskeleton robot is further evaluated at the level of this unit (PC). That is, it is also responsible for receiving all feedback data sent by the robot. The other two processing units are parts of a National Instruments PXI. One of those is a board (NI-PXI 8081 controller board), responsible for the management of the exoskeleton system, as well as executing the top-level command algorithms. In this case, the proposed control strategy was set to operate at a sampling time of 500 $\upmu \mathrm { s}$. Lastly, at the input/output level, a NI PXI-7813R remote input/output board with a Field Programmable Gate Array (FPGA) executes the low-level control; i.e., a PI current control loop (sampling rate of 50 $\upmu \mathrm { s}$) responsible for stabilizing the current of the motors as required by the main nonlinear controller. Furthermore, joints position is measured via Hall-sensors, where input/output tasks are executed at the level of this FPGA. The joints of ETS-MARSE are powered by Brushless DC motors (Maxon EC-45 and Maxon EC-90) coupled with harmonic drives (a gear ratio of 120:1 for motor-1 and motor-2, while a gear ratio of 100:1 for motors 3-7)[2].

5.4 Experimental Results

5.4.1 Joint Space

For the earlier mentioned purpose, a basic physiotherapy exercise was chosen (Elbow: Flexion/Extension; Shoulder Joint: Internal/External Rotation) in joint space. All experiments were performed by a real subject (age: 29 years; height: 176 cm; weight: 78 kg). The conducted exercise started from a $90^{\circ }$ Elbow joint initial position. For all controllers, the same gain values were manually chosen as follows: $K_{1}=150I_{7 \times 7}$, $\lambda =15I_{7 \times 7}$,$\mu _{i}=0.5$, $\alpha _{i}=0.03$, $p_{i}=5$, and $\gamma =0.5$.

Fig. 7

Performance of the proposed controller

Fig. 8

Performance of the Sliding Mode Control (SMC) coupled with the Power Rate Reaching Law (PRL)

5.4.2 Discussion of Joint Space Results

As shown by the first set of data of Figs. 7, 8 and 9, all controllers were able to provide a good tracking trajectory. Interestingly, looking at the second and third sets of data of Fig. 7 (surface and control input evolution respectively), the proposed controller (Proposed-RL) was uniquely able to both, track the trajectory to a very good extinct while significantly reducing the chattering. On the other hand, SMC with PRL (Fig. 8) was only efficient in reducing the chattering as compared to ERL (Fig. 9), as described by the second and third sets of data of both figures. Conversely, SMC with ERL was mainly efficient in providing high performance as compared to PRL, as illustrated by the second set of data of Figs. 8 and 9.

Fig. 9

Performance of the Sliding Mode Control (SMC) coupled with the Exponential Reaching Law (ERL) (Red color is the desired trajectory and blue one is the measured trajectory)

5.4.3 Cartesian Space

Fig. 10

Performance of the proposed controller on ETS-MARSE robot in 3D space

In this section, an exercise in 3D Cartesian space (Starting position $\rightarrow$ Target-A $\rightarrow$ Target-B) was performed using the proposed controller. This experiment was conducted by the same subject, starting from the same elbow joint initial position (Described in the previous Joint Space subsection). All controllers’ gains were also manually chosen as follows: $K_{1}=180I_{7 \times 7}$, $\lambda =20I_{7 \times 7}$,$\mu _{i}=0.7$, $\alpha _{i}=2$, $p_{i}=15$, and $\gamma =0.5$.

Fig. 11

Evolution of the Cartesian errors (positions and orientations of the end-effector) using the proposed approach

Fig. 12

Evolution of the torque inputs during the Cartesian described task using the proposed approach

5.4.4 Discussion of Cartesian Space Results

The performance of the proposed control approach on ETS-MARSE in 3D Cartesian space is summarized in Figs 10, 11 and 12. Concisely, collected results highly support the smooth and effective operation of the proposed controller. In details, Fig. 10 shows the high rate of convergence to the desired trajectory. Concurrently, Fig. 11 clearly shows that all errors eventually diminish to around zero. Evidently, Fig. 12 proves the satisfactory smooth control input. It is noteworthy that the control input is further smoother than that of SMCERL [15] which has been applied on the same robot (ETS-MARSE). Hence, the control scheme renders satisfactory outcomes.

6 Conclusion

In this paper, a sliding mode control (SMC) with a novel proposed reaching law were employed to control a perturbed and unperturbed nonlinear system. The proposed reaching law proved its capability to overcome and enhance the performance of SMC. It also assisted SMC in achieving high performance with a significant reduction in the chattering problem. It further proved to drive system’s trajectories towards the origin in a substantially fast convergence time as compared to existing reaching laws. Simulation and comparison results against existing successful approaches clearly supported the advantages of the proposed reaching law. Lastly, experimental results, with the aid of an exoskeleton robot, as performed by a real subject, proved the feasibility of the proposed reaching law for real-time implementation applications.