1 Introduction

Lower-limb rehabilitation plays a crucial role in improving mobility and autonomy for individuals affected by stroke and other conditions that cause lower-limb impairments [1,2,3]. Scientific studies have proven the efficacy of repetitive and intensive rehabilitation training in restoring ambulatory function. Traditionally, lower-limb rehabilitation relies on manual assistance from two or three therapists to facilitate leg mobilization and ensure postural stability. However, the increasing labor burden and healthcare costs have led to a demand for the development of robotized systems as an alternative to therapists for implementing rehabilitation interventions [4, 5].

Robotic rehabilitation has gained significant attention in recent years due to its effectiveness in treating motor impairments. Among the various robots used in rehabilitation, exoskeletons [6] have emerged as an important category since the 1960s in America, Japan, and Europe [7]. The Lokomat is a well-known example of such robotic systems [8, 9]. These wearable robots are designed with joints aligned coaxially with the patient's joints, allowing the patient’s body to replicate predetermined therapeutic movements [10]. Precise control of joint positions and effective management of interactive forces between the robot and the patient are essential factors in the control of exoskeleton robots [11]. The design of an appropriate controller directly influences the performance of the exoskeleton. The primary objective of this study is to develop an effective control methodology for lower-limb rehabilitation systems that interact with patients and the environment.

Sliding mode control (SMC) is an effective control approach known for its ability to reject uncertainties, eliminate external disturbances, and be less sensitive to variations in the robot’s parameters [12, 13]. However, it suffers from issues such as chattering and infinite-time convergence to the equilibrium point, which can be problematic for Euler–Lagrange systems [14]. To address these issues, several SMC-based methods have been proposed. Terminal sliding mode control (TSMC) guarantees finite-time convergence of the states to the equilibrium point [15,16,17,18]. High-order sliding mode control (HOSMC) promotes accuracy and eliminates chattering while retaining the robustness of conventional SMC [19]. Super-twisting-based second-order sliding mode control (SOSMC) has also shown promise in mitigating chattering and handling disturbances and uncertainties [20]. However, these control strategies rely on accurate model parameters or large amounts of data, which can be challenging to obtain in practical applications. To overcome this challenge, recent attention has been given to model-free adaptive and robust SMC strategies for uncertain and nonlinear robotic systems [21,22,23]. These strategies utilize an adaptation law to prevent the overestimation of control gain in the presence of uncertainty and ensure the sliding condition to mitigate the effects of unknown uncertainties.

In the case of joint injuries, it is essential for the robot to apply gentle force in the therapeutic direction to the affected joint [24,25,26]. Conversely, if the patient has joint mobility at other joints, the robot should enable the patient to exert their own force, promoting dynamic force interaction between the patient and the exoskeleton [27]. The Lokomat robot has used a combined control of force and position to enhance the patient’s active participation in walking. This control structure consists of a closed-loop PD position controller and a force controller, with the two loops being switched between the swing and stand phases of walking separately [28]. However, the switching process is not explicitly known and may result in a nonphysiological gait pattern in the patient’s walking.

The concept of impedance control is an effective approach used to uniformly reduce interaction forces of robots by incorporating a virtual mass, spring, and damper between the robot and a known environment [29]. Impedance and adaptive control approaches for lower-limb exoskeletons have been studied in various research projects, as seen in [30, 31]. Additionally, studies like [32,33,34,35] have proposed transparent or assist as-needed control methods for lower-limb exoskeletons, demonstrating advancements in able-bodied walking scenarios. These examples highlight the evolving landscape of control strategies in the field of rehabilitation robotics and emphasize the importance of exploring novel methodologies to enhance the transparency of lower-limb exoskeletons.

In the realm of lower-limb rehabilitation exoskeletons, where uncertainties in dynamics and the need for adaptable interaction between users and robots are paramount, variable impedance control plays a vital role. Recent advancements have demonstrated the effectiveness of variable impedance control in enhancing adaptability and performance in various robotic systems facing complex interactions and uncertain environments [36,37,38,39,40]. However, the integration of variable impedance control with model-free adaptive sliding mode control strategies remains largely unexplored in the context of lower-limb rehabilitation exoskeletons.

The synergy between variable impedance control and adaptive sliding mode control holds immense potential for optimizing the rehabilitation process by offering a tailored and responsive interaction between the exoskeleton and the user. This integration combines the adaptability of variable impedance control with the stability and robustness of adaptive sliding mode control, offering a comprehensive framework to address the challenges unique to lower-limb rehabilitation scenarios.

In this research, the authors introduce a novel approach to address the adverse effects of interaction forces in lower-limb rehabilitation exoskeletons. Their method combines a model-free adaptive sliding mode control (SMC) framework with a variable impedance strategy. The adaptive law effectively prevents the overestimation of control gain under uncertain conditions, ensuring the system maintains the sliding condition to counter unknown uncertainties. Moreover, the variable impedance strategy enables the system’s impedance to dynamically adjust throughout the gait cycle, enhancing the robot’s precision in tracking desired joint trajectories. By aiming to sustain interactive forces close to zero at the patient-robot connection points while allowing system-wide impedance adaptation during gait, the approach prioritizes patient comfort and usability by avoiding disruptive and erratic forces.

The study includes a comprehensive stability analysis utilizing Lyapunov theory, demonstrating the finite-time convergence of the defined sliding surface. The adaptive sliding mode controller, designed based on Lyapunov theory, is instrumental in achieving these stability goals. The proposed control methodology is rigorously evaluated through simulations on a dynamic model using MATLAB SimScape, offering a comparative analysis against traditional control strategies.

The structure of the paper is as follows: Sect. 2 provides a detailed description of the lower-limb rehabilitation exoskeleton model and introduces its dynamic equations. It also presents the design of the proposed primary control algorithm, namely the model-free adaptive sliding mode control. Additionally, the variable impedance strategy and the extended state observer are introduced in this section to enhance the primary controller. Section 3 presents the numerical simulation results and subsequent discussions. Finally, Sect. 4 concludes the paper and outline future research directions.

2 Materials and methods

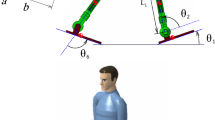
Figure 1 illustrates the schematic of the rehabilitation robot being investigated. It is evident that the robot possesses the capability to engage with each leg of the patient through three active joints (hip abduction–adduction, hip extension-flexion, knee extension-flexion) and one passive joint (ankle dorsiflexion). The robot introduced in this study, as previously mentioned, is specifically designed with an exoskeleton-like architecture. It is worth noting that while many rehabilitation robots are typically designed to operate solely in the sagittal plane with only one degree of freedom for the hip, a more realistic representation can be achieved by considering two degrees of freedom for the hip joint, as reported in [41]. This approach allows for a more natural range of motion and better mimics the movements required for various activities. Therefore, in our research, we evaluate the exoskeleton under the most challenging conditions, even though it has been validated for more simplified structures. Notably, the alignment of the robot’s joints with the patient's joints ensures congruity between their respective kinematics. The patient's ankle position relative to the pelvis is synchronized with the desired trajectory by the help of the robot. Moreover, the ankle joint of the robot is facilitated by a torsion spring, enabling passive movement and preventing foot drop in the patient during rehabilitation [42]. The presented robot utilizes body weight support (BWS) and is capable of neutralizing the entire weight of the patient [34]. In Fig. 1, \({\theta }_{\text{i}}\) and \({L}_{\text{i}}\) represent the angle and length of each link, respectively. Here, the angles \({\theta }_{\text{i}}\), where i ranges from 1 to 3, are considered as the generalized coordinates of the system. Specifically, \({\theta }_{1}\) corresponds to the hip abduction–adduction motion in the coronal plane, while \({\theta }_{2}\) and \({\theta }_{3}\) correspond to the hip and knee extension-flexion motions in the sagittal plane, respectively. In addition, \({m}_{\text{i}}\), \({C}_{{m}_{\text{i}}}\), and \({I}_{\text{i}}\) respectively denote the mass, the center of mass position, and the moment of inertia of each link of the robot integrated with the corresponding leg part of the subject. To extract the dynamic relations governing the robot, the Lagrange method has been used in the form of Eq. (1)

$$\tau_{{\text{i}}} = \frac{{\text{d}}}{{{\text{d}}t}} \left( {\frac{\partial K}{{\partial \dot{\theta }_{{\text{i}}} }}} \right) - \frac{\partial K}{{\partial \theta_{{\text{i}}} }} + \frac{\partial U}{{\partial \theta_{{\text{i}}} }}$$
(1)

Where \(K\) and \(U\) are the kinetic and potential energies of the robot and patient links, respectively. Also \({\tau }_{\text{i}}\) is the input torque applied to each joint of the robot. Briefly, the dynamic equations governing the robot are expressed in the form of Eq. (2).

$$\tau = M\left( \theta \right)\ddot{\theta } + C\left( {\theta .\dot{\theta }} \right) + G\left( \theta \right) + \tau_{{\text{d}}}$$
(2)

Where \(M(\theta )\) denotes the moment of inertia matrix, \(C\left(\theta .\dot{\theta }\right)\) is the matrix of centrifugal and Coriolis effects, and G(q) is the vector of gravitational forces as

$$M = \left[ {\begin{array}{*{20}c} {I_{2} + I_{3} + m_{2} C_{{m_{2} }}^{2} + m_{3} C_{{m_{3} }}^{2} } & {m_{3} L_{2} C_{{m_{3} }} C\left( {\theta_{2} } \right)} & {m_{3} L_{3} C_{{m_{3} }} C\left( {\theta_{2} + \theta_{3} } \right)} \\ {m_{3} L_{2} C_{{m_{3} }} C\left( {\theta_{2} } \right)} & {I_{3} + m_{3} C_{{m_{3} }}^{2} } & {m_{3} L_{3} C_{{m_{3} }} C\left( {\theta_{3} } \right)} \\ {m_{3} L_{3} C_{{m_{3} }} C\left( {\theta_{2} + \theta_{3} } \right)} & {m_{3} L_{3} C_{{m_{3} }} C\left( {\theta_{3} } \right)} & {I_{3} } \\ \end{array} } \right]$$
(2-1)
$$C = \left[ \begin{gathered} - m_{3} L_{2} C_{{m_{3} }} S\left( {\theta_{2} } \right)\dot{\theta }_{2} - m_{3} L_{3} C_{{m_{3} }} S\left( {\theta_{2} + \theta_{3} } \right)(\dot{\theta }_{2} + \dot{\theta }_{3} )\quad m_{3} L_{3} C_{{m_{3} }} S\left( {\theta_{2} + \theta_{3} } \right)\theta_{3} \quad - m_{3} L_{3} C_{{m_{3} }} S\left( {\theta_{2} + \theta_{3} } \right) \hfill \\ \quad \quad \quad \quad \quad \quad m_{3} L_{2} C_{{m_{3} }} S\left( {\theta_{2} } \right)\dot{\theta }_{1} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0\quad \quad \quad \quad \quad \quad \;m_{3} L_{3} C_{{m_{3} }} S(\theta_{3} )\theta_{3} \hfill \\ \quad \quad \quad \quad m_{3} L_{3} C_{{m_{3} }} S\left( {\theta_{2} + \theta_{3} } \right)(\dot{\theta }_{1} + \dot{\theta }_{2} )\quad \quad \quad \quad \quad \quad - m_{3} L_{3} C_{{m_{3} }} S\left( {\theta_{3} } \right)\dot{\theta }_{3} \quad \quad \quad \quad \quad 0 \hfill \\ \end{gathered} \right]$$
(2-2)
$$G = \left[ {\begin{array}{*{20}c} {\left( {m_{2} C_{{m_{2} }} + m_{3} C_{{m_{3} }} } \right)gS\left( {\theta_{1} } \right) + m_{3} L_{2} C_{{m_{3} }} gS\left( {\theta_{1} + \theta_{2} } \right)} \\ {m_{3} L_{2} C_{{m_{3} }} gS\left( {\theta_{1} + \theta_{2} } \right) + m_{3} L_{3} C_{{m_{3} }} gS\left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)} \\ {m_{3} L_{3} C_{{m_{3} }} gS\left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)} \\ \end{array} } \right]$$
(2-3)

in witch \(S(.)\) and \(C(.)\) denote sin(.) and cos(.). Also \({\tau }_{\text{d}}\) represents the disturbance torques applied to the system that can disrupt its desired behavior [35, 43]. The above model of the robot can be rewritten in the following form as.

$$\ddot{\theta } = M^{ - 1} \left( {\tau - C - G} \right) - M^{ - 1} \tau_{{\text{d}}} $$
(3)
Fig.1
figure 1

The schematic of a a typical lower body exoskeleton robot, b joint parameters definitions: \({\theta }_{1}\) indicates the hip abduction–adduction angle in coronal plane; \({\theta }_{2}\) and \({\theta }_{3}\) indicate the hip and knee extension-flexion angles in the sagittal plane, respectively, c physical parameters definitions

Full size image

Assumption 1 The exogenous disturbances \({\tau }_{\text{d}}\) are bounded and \(\left\| {\tau_{{\text{d}}} } \right\| \le \overline{\tau }_{{\text{d}}} < \infty\) in which \(\overline{\tau }_{{\text{d}}}\) is an unknown variable.

Assumption 2: The matrices presenting the dynamic model of the system M(\(\theta\)), C(\(\theta .\theta\)), and G(\(\theta\))are bounded such that:

$$M\left( \theta \right) \le \overline{m}I$$
(4)
$$C\left\| {C\left( {\theta .\dot{\theta }} \right) \le \overline{c}\dot{\theta }} \right\|$$
(5)
$$\left\| {G\left( \theta \right)} \right\| \le \overline{g}$$
(6)

Where \(\overline{m}\), \(\overline{c}\) and \(\overline{g}\) are upper bound positive constants and I denotes the identity matrix.

Property 1: For \(\frac{1}{2}\dot{M}(\theta )-C\left(\theta .\dot{\theta }\right)\), the equality \({x}^{T}\left(\frac{1}{2}\dot{M}(\theta )-C\left(\theta .\dot{\theta }\right)\right)x=0\) always holds for any \(x\).

Property 2: The norms of the inertia matrix \(M(\theta )\), \(C(\theta )\), and \(G(\theta )\) are bounded as considered in Assumption 2. This guarantees that the dynamic model of the system is bounded and can be effectively controlled.

2.1 Model-free adaptive sliding mode control

Consider the system dynamics, defined in Eq. (4), Eq. (5), and Eq. (6), with a combination of uncertainties and exogenous time-dependent bounded disturbances. Let us define the following error:

$$e = \theta - \theta_{{\text{d}}}$$
(7)
$$\dot{e} = \dot{\theta } - \dot{\theta }_{{\text{d}}}$$
(8)

where \({\theta }_{\text{d}}\) and \({\dot{\theta }}_{\text{d}}\) indicate the desired or reference joint angles and joint velocities, respectively. The basic sliding surface is defined as:

$$S = \dot{e} + \mathop \smallint \limits_{0}^{t} \left( {\lambda_{1} \left\| e \right\|^{p} \frac{e}{\left\| e \right\|} + \lambda_{2} \left\| {\dot{e}} \right\|^{q} \frac{{\dot{e}}}{{\left\| {\dot{e}} \right\|}}} \right)d\tau$$
(9)

Then, its time derivative can be expressed as:

$$\dot{S} = \ddot{\theta } - \ddot{\theta }_{{\text{d}}} + \lambda_{1} \left\| e \right\|^{p} \frac{e}{\left\| e \right\|} + \lambda_{2} \left\| {\dot{e}} \right\|^{q} \frac{{\dot{e}}}{{\left\| {\dot{e}} \right\|}}$$
(10)

\(p\) and \(q\) are unit power terms that impact control adaptation on errors and error velocities, respectively, while \(\lambda\) is an adjustable parameter affecting adaptation rate in the presence of errors and uncertainties. Accordingly, the following time-varying sliding surface and adaptive model-free control law can be defined to compensate the negative effects of disturbances and uncertainties.

$$\dot{S} = \ddot{\theta }_{{\text{d}}} - M^{ - 1} \left( {\tau_{{\text{d}}} + C\dot{\theta } + G - \tau } \right) + \lambda_{1} \left\| e \right\|^{p} \frac{e}{\left\| e \right\|} + \lambda_{2} \left\| {\dot{e}} \right\|^{q} \frac{{\dot{e}}}{{\left\| {\dot{e}} \right\|}}$$
(11)

Multiplying by \(M\) yields:

$$M\dot{S} = \tau - CS + \Xi$$
(12)
$$\Xi = - \left[ {C\dot{\theta } + G + \tau_{{\text{d}}} - CS - M\ddot{\theta }_{{\text{d}}} - M\left( {\lambda_{1} \left\| e \right\|^{p} \frac{e}{\left\| e \right\|} + \lambda_{2} \left\| {\dot{e}} \right\|^{q} \frac{{\dot{e}}}{{\left\| {\dot{e}} \right\|}}} \right)} \right]$$
(13)

According to property 1, \(\Vert M\Vert ,\Vert C\Vert ,\) and \(\Vert G\Vert\) satisfy property 2. By defining \(\Phi ={\left[\begin{array}{cc}e& \dot{e}\end{array}\right]}^{T},\Vert e\Vert \le \Vert \Phi \Vert \&\Vert \dot{e}\Vert \le \Vert \Phi \Vert\), then:

$$\left\| \Xi \right\| \le \Omega_{1} \left\| \Phi \right\|^{0} + \Omega_{2} \left\| \Phi \right\|^{1} + \Omega_{3} \left\| \Phi \right\|^{2}$$
(14)

In Eq. (14), \({\Omega }_{\text{i}}\) are unknown terms and it should be noted that Assumption 1 does not impose a priori bounds on the lumped term. Accordingly, the following adaptive model-free sliding mode control law is defined as:

$$\tau_{\eta } = - \left[ {\Gamma S + \Lambda {\text{sgn}} \left( S \right)} \right]$$
(15)
$$\Lambda = \hat{\Omega }_{1} \left\| \Phi \right\|^{0} + \hat{\Omega }_{2} \left\| \Phi \right\|^{1} + \hat{\Omega }_{3} \left\| \Phi \right\|^{2}$$
(16)
$$\dot{\hat{\Omega }}_{{\text{i}}} = \left\| S \right\| \cdot \left\| \Phi \right\|^{{\text{i - 1}}} - \gamma_{{\text{i}}} \hat{\Omega }_{{\text{i}}}$$
(17)

where \(\Gamma\) is a positive constant and \({\tau }_{\eta }\) represents the effecting control torque which can ensure the desired control performance. Note that \({\widehat{\Omega }}_{\text{i}}(0)>0\) and \({\gamma }_{\text{i}}\) is a positive constant as \({\gamma }_{\text{i}}>0\) for \(i=\text{1,2},3\).

Theorem 1 Considering the dynamic model, globally uniformly ultimately bounded (GUUB) of the closed-loop system will be analyzed under the effect of the proposed control law in Eq. (15) where an ultimate bound \(\omega\) on the sliding surface is \(\omega = \sqrt {\frac{{\mathop \sum \nolimits_{{\text{i = 0}}}^{2} \gamma_{{\text{i}}} \kappa_{{\text{i}}}^{ 2} }}{{\left( {\kappa - \eta } \right)}}{\text{with}} \triangleq 2\mathop {{\text{min}}}\limits_{i} \left\{ {\Gamma ,\frac{{\gamma_{{\text{i}}} }}{2}} \right\} > 0\;{\text{and}}\;} 0 < \eta < \kappa .\)

Proof: To show the stability of the closed-loop system, the following Lyapunov function can be defined. For the sake of compactness, the time dependency is omitted in the subsequent derivation.

$$V = \frac{1}{2}S^{T} MS + \mathop \sum \limits_{{\text{i = 1}}}^{3} \frac{1}{2}\tilde{\Omega }^{2}_{{\text{i}}}$$
(18)

By taking the time derivative of Eq. (16):

$$\begin{gathered}\dot{V}= S^{T} M\dot{S} + \frac{1}{2}S^{T} \dot{M}S + \mathop \sum \limits_{{\text{i = 1}}}^{3} \tilde{\Omega }_{{\text{i}}} \dot{\hat{\Omega }}_{{\text{i}}} = S^{T} \left( {\tau - CS + \Xi } \right) + \frac{1}{2}S^{T} \dot{M}S + \mathop \sum \limits_{{\text{i = 1}}}^{3} \tilde{\Omega }_{{\text{i}}} \dot{\hat{\Omega }}_{{\text{i}}} \hfill \\ \quad = S^{T} \left( { - \left[ {\Gamma S + \Lambda {\text{sgn}} \left( S \right)} \right] + \Xi } \right) + \frac{1}{2}S^{T} \left( {\dot{M} - 2C} \right)S + \mathop \sum \limits_{{\text{i = 1}}}^{3} \tilde{\Omega }_{{\text{i}}} \dot{\hat{\Omega }}_{{\text{i}}} \hfill \\ \quad \le - S^{T} \Lambda S - \mathop \sum \limits_{{\text{i = 1}}}^{3} \tilde{\Omega }_{{\text{i}}} \left[ {\left\| \vartheta \right\|.\left\| \Phi \right\|^{{\text{i - 1}}} - \gamma_{{\text{i}}} \hat{\Omega }_{{\text{i}}} } \right] \hfill \\ \end{gathered}$$
(19)

The following equality can be useful to simplify the above inequality.

$$\tilde{\Omega }_{{\text{i}}} \dot{\hat{\Omega }}_{{\text{i}}} = \left\| S \right\|\tilde{\Omega }_{{\text{i}}} \left\| {\Phi } \right\|^{{\text{i}}} + \gamma_{{\text{i}}} \hat{\Omega }_{{\text{i}}} \Omega_{{\text{i}}} - \gamma_{{\text{i}}} \hat{\Omega }_{{\text{i}}}^{2}$$
(20)

Substituting Eq. (17) into Eq. (18), then:

$$\dot{V} \le - \frac{{\lambda \left( \Lambda \right)_{{{\text{min}}}} }}{{n\left\| S \right\|^{2} \mathop \sum \nolimits_{{\text{i = 1}}}^{3} \left[ {\gamma_{{\text{i}}} \hat{\Omega }_{{\text{i}}} \Omega_{{\text{i}}} - \gamma_{{\text{i}}} \hat{\Omega }_{{\text{i}}}^{2} } \right]}} \le - \frac{{\lambda \left( \Lambda \right)_{{{\text{min}}}} }}{{n\left\| S \right\|^{2} \mathop \sum \nolimits_{{\text{i = 1}}}^{3} \left[ {\frac{{\gamma_{{\text{i}}} }}{2}\tilde{\Omega }^{2}_{{\text{i}}} - \frac{{\gamma_{{\text{i}}} }}{2}\Omega_{{\text{i}}}^{2} } \right]}}$$
(21)

With \({\lambda \left(\Lambda \right)}_{\text{min}}\) represents the minimum eigenvalue. Therefore, Eq. (19) can be rewritten as:

$$\dot{V} \le - \frac{{\lambda \left( \Lambda \right)_{\min } }}{{n\left\| S \right\|^{2} \mathop \sum \nolimits_{{\text{i = 1}}}^{3} \left[ {\gamma_{{\text{i}}} \hat{\Omega }_{{\text{i}}} \Omega_{{\text{i}}} - \gamma_{{\text{i}}} \hat{\Omega }_{{\text{i}}}^{2} } \right]}} \le - \frac{{\overline{m}}}{2}\left\| S \right\|^{2} + \mathop \sum \limits_{{\text{i = 1}}}^{3} \frac{1}{2}\tilde{\Omega }^{2}_{{\text{i}}}$$
(22)
$$\dot{V} \le - \psi V + \frac{1}{2}\mathop \sum \limits_{{\text{i = 1}}}^{3} \gamma_{{\text{i}}} \Omega_{{\text{i}}}$$
(23)

Where \(\psi = \mathop {{\mathrm{min}}}\limits_{{\text{i}}} \left\{ {\lambda \left( \Lambda \right)_{{{\text{i}}_{\min } }} ,\max \left\{ {\overline{m}/2,1/2} \right\}} \right\}\). By using \(0<\psi <\kappa\), yields:

$$\dot{V} \le - \kappa V - \left( {\psi - \kappa } \right)V + \frac{1}{2}\mathop \sum \limits_{{\text{i = 1}}}^{3} \gamma_{{\text{i}}} \Omega_{{\text{i}}}^{2}$$
(24)

By defining \({P}_{B}=\frac{{\sum }_{\text{i}=1}^{3}{\gamma }_{i}{\Omega }_{i}^{2}}{2\left(\psi -\kappa \right)}\), then \(V\le \text{max}\left\{V(0),P\right\},\forall t\ge 0\), it can be perceived that \(\dot{V}\le -\kappa V\), which ensures finite-time convergence of the Lyapunov function inside the ball defined by \({P}_{B}\).

Remark 1: The definition of the expressed Lyapunov function in Eq. (22) gives \(V=\frac{1}{2}{\left|S\right|}^{2}\). Consequently, we have the ultimate bound \(\omega\) which is global and uniform as it is free from initial condition. This completes the proof.

2.2 Finite-time convergence

In this section, finite-time stability of the sliding surface is investigated. When the closed-loop system reaches the sliding surface, \(S=0\), then

$$\dot{e} + \mathop \smallint \limits_{0}^{t} \left( {\lambda_{1} \left\| e \right\|^{p} \frac{e}{\left\| e \right\|} + \lambda_{2} \left\| {\dot{e}} \right\|^{q} \frac{{\dot{e}}}{{\left\| {\dot{e}} \right\|}}} \right)d\tau = 0$$
(25)

Taking time derivative of Eq. (23), yields:

$$\ddot{e} + \lambda_{1} \left\| e \right\|^{p} \frac{e}{\left\| e \right\|} + \lambda_{2} \left\| {\dot{e}} \right\|^{q} \frac{{\dot{e}}}{{\left\| {\dot{e}} \right\|}} = 0$$
(26)

By defining \({z}_{1}=e\) and \({z}_{2}=\dot{e}\), Eq. (24) is rewritten as:

$$\dot{z}_{1} = z_{2}$$
(27)
$$\dot{z}_{2} = - \lambda_{1} \frac{{z_{1} }}{{z_{1}^{1 - q} }} - \lambda_{2} \frac{{z_{2} }}{{z_{2}^{1 - p} }}$$
(28)

Now, the Lyapunov function is defined as:

$$V_{1} = \frac{{\lambda_{1} \left\| {z_{1} } \right\|^{q + 1} }}{q + 1} + \frac{{\left\| {z_{2} } \right\|^{2} }}{2}$$
(29)

By taking the time derivative of Eq. (27), we obtain:

$$\begin{gathered} \dot{V_{1}}= \lambda_{1} \left\| {z_{1} } \right\|^{q - 1} z_{1}^{T} .z_{1} - z_{2}^{T} \left( {\lambda_{1} \frac{{z_{1} }}{{\left\| {z_{1} } \right\|^{1 - q} }} + \lambda_{2} \frac{{z_{2} }}{{\left\| {z_{2} } \right\|^{1 - p} }}} \right) \hfill \\ \quad = \lambda_{1} \left\| {z_{1} } \right\|^{q - 1} z_{1}^{T} .z_{1} - \lambda_{1} \left\| {z_{1} } \right\|^{q - 1} z_{2}^{T} z_{1} - \lambda_{2} \left\| {z_{2} } \right\|^{p - 1} z_{2}^{T} z_{2} = - \lambda_{2} \left\| {z_{2} } \right\|^{p + 1} \hfill \\ \end{gathered}$$
(30)

By applying LaSalle’s invariance principle, the asymptotic convergence of \({z}_{1}\) and \({z}_{2}\) to zero is guaranteed. Thus, the tracking error can be driven to the origin along \(S=0\) in a finite time. This completes the proof.

2.3 Variable impedance strategy

Controlling the applied force of the robot to the human is the most important challenge of rehabilitation robots. Various strategies have been proposed for such force control [44,45,46]. The fundamental principle of impedance control is to provide assistance through rehabilitation robots only when necessary. In essence, the robot offers greater support to patients with significant disabilities, while providing lesser assistance to those with minor disabilities. The aim is to customize the level of support according to the individual needs of each patient, ensuring that the robot avoids unnecessary intervention when the patient is capable of independently performing the task. This personalized approach optimizes the effectiveness of the rehabilitation process by delivering the suitable amount of assistance at the appropriate time. The goal of the impedance in configuration space is to develop a dynamic relation between the external force and configuration error, as [40,41,42,43,44,45,46,47,48]:

$$M_{{\text{d}}} \left( {\ddot{\theta } - \ddot{\theta }_{{\text{d}}} } \right) + C_{{\text{d}}} \left( {\dot{\theta } - \dot{\theta }_{{\text{d}}} } \right) + K_{{\text{d}}} \left( {\theta - \theta_{{\text{d}}} } \right) = \tau_{{\text{e}}}$$
(31)

in which \({M}_{\text{d}}\),\({C}_{\text{d}}\),\({K}_{\text{d}}\) are the desired inertia, damping and stiffness, respectively; and \({\tau }_{\text{e}}\) represents the external force or torque applied to the system. These matrices are adjusted by the user in order to determine the behavior of the soft robot against external forces. In this research, the time-varying impedance control strategy is utilized. It means a virtual mass, spring and damper is applied such that they are variable with the time and can change the impedance of the whole system appropriately. It should be noted that asymptotic stability of the system can still be guaranteed if theses matrices are varying as follows.

Theorem 2: We consider \({M}_{\text{d}}\), \({C}_{\text{d}}\), \({K}_{\text{d}}\) as symmetric and positive definite matrices and also continuously differentiable varying profiles. It can be proved that the system of Eq. (29), when \({\tau }_{\text{e}}=0\), is uniformly globally and asymptotically stable (UGAS) if there exist a positive constant \(\alpha\) so that:

$$\dot{M}_{{\text{d}}} + \alpha M_{{\text{d}}} - C_{{\text{d}}} \le 0$$
(32)
$$\left( {\alpha^{2} + 2\alpha } \right)\dot{M}_{{\text{d}}} - \alpha \ddot{M}_{{\text{d}}} + \alpha \dot{C}_{{\text{d }}} + \dot{K}_{{\text{d}}} - 2\alpha K_{{\text{d}}} \le 0$$
(33)

Proof: In order to perform the stability analysis, we use a Lyapunov function:

$$V = \frac{1}{2}\left( {\Upsilon^{T} M_{d} \Upsilon + \Xi^{T} \mu \Xi } \right)$$
(34)

where \(\mu\) is a symmetric and positive definite matrix and \(\Upsilon =\dot{\Xi }+\alpha\Xi .\Xi =\Omega -{\Omega }_{\text{d}}\). By taking the time derivative of Eq. (32), we obtain:

$$\dot{V} = {\Upsilon }^{T} M_{{\text{d}}} \left( {{\ddot{\Xi }} + \alpha {\Xi }} \right) + \frac{1}{2}{\Upsilon }^{T} \dot{M}_{{\text{d}}} {\Upsilon } + {\Xi }^{T} \mu {\dot{\Xi }} + \frac{1}{2}{\Xi }^{T} \dot{\mu }{\Xi }$$
(35)

When \({\tau }_{e}=0\),

$$\begin{gathered} \dot{V} = \dot{\Xi }^{T} \left( {\dot{M}_{{\text{d}}} + \alpha M_{{\text{d}}} - C_{{\text{d}}} } \right)\dot{\Xi } + \dot{\Xi }^{T} \left( {\alpha^{2} M_{{\text{d}}} + \alpha \dot{M}_{{\text{d}}} - \alpha C_{{\text{d}}} - K_{{\text{d}}} + \mu } \right)\Xi \hfill \\ \quad \quad \quad \quad \quad + \Xi^{T} \left( {\alpha^{2} \dot{M}_{{\text{d}}} + \alpha^{2} M_{{\text{d}}} + \frac{1}{2}\dot{\mu } - \alpha K_{{\text{d}}} } \right)\Xi \hfill \\ \end{gathered}$$
(36)

By defining \(\mu =-{\alpha }^{2}{M}_{\text{d}}-\alpha \dot{{M}_{\text{d}}}+{K}_{\text{d}}+\alpha {C}_{\text{d}}\) and \(\dot{\mu }=-{\alpha }^{2}\dot{{M}_{\text{d}}}-\alpha \ddot{{M}_{\text{d}}}+\dot{{K}_{\text{d}}}+\alpha \dot{{C}_{\text{d}}}\), then:

$$\dot{V} = \dot{\Xi }^{T} \left( {\dot{M}_{{\text{d}}} + \alpha M_{{\text{d}}} - C_{{\text{d}}} } \right)\dot{\Xi } + \Xi^{T} \left[( {\frac{{\alpha^{2} }}{2} + \alpha } \right)\dot{M}_{{\text{d}}} - \frac{\alpha }{2}\ddot{M}_{{\text{d}}} + \frac{\alpha }{2}\dot{C}_{{\text{d}}} + \frac{{\dot{K}_{{\text{d}}} }}{2} - \alpha K_{{\text{d}}}]\Xi$$
(37)

In order to stabilize the system, the following inequality must be hold:

$$\dot{M}_{{\text{d}}} + \alpha M_{{\text{d}}} - C_{{\text{d}}} \le 0$$
(38)
$$\left( {\alpha^{2} + 2\alpha } \right)\dot{M}_{{\text{d}}} - \alpha \ddot{M}_{{\text{d}}} + \alpha \dot{C}_{{\text{d}}} + \dot{K}_{{\text{d}}} - 2\alpha K_{{\text{d}}} \le 0$$
(39)

Which completes the proof.

The conditions defined in Eq. (36) and Eq. (37) impose constraints on the impedance matrices that can be determined using an optimization procedure. In order to satisfy the necessary conditions for Theorem 2 and also least conservative constraints, \(\alpha\) should be determined using:

$$\alpha = \min \left( {\frac{{\lambda_{\min } \left( {C_{{\text{d}}} } \right) + \lambda_{\max } \left( {\dot{M}_{{\text{d}}} } \right)}}{{\lambda_{\max } \left( {M_{{\text{d}}} } \right)}}} \right)$$
(40)

To demonstrate the systematic procedure, let us define a symmetric and negative definite matrix as \(B= \dot{{M}_{\text{d}}}+\alpha {M}_{\text{d}}-{C}_{\text{d}}\) whose terms comprise symmetric matrices. For negativity of this matrix, its maximum eigenvalue \({\lambda }_{\text{max}}\) must be negative. Based on the triangle inequality for supremum norm, we have:

$$\begin{gathered} \lambda_{\max } \left( B \right) = \sup \nu^{T} B\nu \le \sup \nu^{T} \dot{M}_{{\text{d}}} \nu + \sup \nu^{T} \left( {\alpha M_{{\text{d}}} } \right)\nu + \sup \nu^{T} \left( { - C_{{\text{d}}} } \right)\nu . \lambda_{\max } \left( B \right) \hfill \\ \quad \quad \quad \quad \le \lambda_{\max } \left( {\dot{M}_{{\text{d}}} } \right) + \lambda_{\max } \left( {\alpha M_{{\text{d}}} } \right) - \lambda_{\min } \left( {C_{{\text{d}}} } \right) \hfill \\ \end{gathered}$$
(41)

and for satisfying the negative definiteness of B, \({\lambda }_{\text{max}}\left(\dot{{M}_{\text{d}}}\right) \le {\lambda }_{\text{min}}\left({C}_{\text{d}}\right)-{\lambda }_{\text{max}}\left(\alpha {M}_{\text{d}}\right)\). We move to the second constraint that imposes a limitation on the variation of stiffness matrix. Let us consider \(Q= \left({\alpha }^{2}+2\alpha \right)\dot{{M}_{\text{d}}}-\alpha \ddot{{M}_{\text{d}}}+ \alpha \dot{{C}_{\text{d}}}+\dot{{K}_{\text{d}}}-2\alpha {K}_{\text{d}}\) and similar to the first constraint using the triangle inequality, then:

$$\begin{gathered} \lambda_{\max } \left( {\dot{K}_{{\text{d}}} } \right) \le 2\alpha \lambda_{\min } \left( {k_{{\text{d}}} } \right) - \alpha \lambda_{\max } \left( {C_{{\text{d}}} } \right) - \left( {\alpha^{2} + 2\alpha } \right)\lambda_{\min } \left( {C_{{\text{d}}} } \right) + \alpha^{2} \left( {\alpha + 2} \right)\lambda_{\max } \left( {M_{{\text{d}}} } \right) + \alpha \lambda_{\min } \left( {\ddot{M}_{{\text{d}}} } \right) \hfill \\ \end{gathered}$$
(42)

Hence, the validity of the impedance profiles can be guaranteed through these conditions, which completes the proof of the stability of varying impedance control without dependency on state measurements.

2.4 Extended state observer

Since direct measuring of the forces and states are quiet challenging for a rehabilitation robot (specifically in view of practical application), an extended state observer is designed to measure the output signals (states variables). So, the dynamic model can be rewritten as:

$$\ddot{\theta } = \psi + M^{ - 1} \tau$$
(43)
$$\psi = - M^{ - 1} \left( {C\dot{\theta } + G + \tau_{{\text{d}}} } \right)$$
(44)

If \({z}_{1}=\theta\) and \({z}_{2}=\dot{\theta }\) and state variable \({z}_{3}=\psi\), the mathematical model of the high-order observer is expressed as follows:

$$\dot{z}_{1} = z_{2}$$
(45)
$$\dot{z}_{2} = z_{3} + b_{0} \tau$$
(46)
$$\dot{z}_{3} = \dot{\psi }$$
(47)

With the definition \(\tilde{z} = z_{1} - \hat{z}_{1}\), the nonlinear observer is introduced as follows:

$$\dot{\hat{z}}_{1} = \hat{z}_{2} + k_{01} \tilde{z}_{1}$$
(48)
$$\dot{\hat{z}}_{2} = \hat{z}_{3} + b_{0} \tau + k_{02} {\text{fal}}\left( {\tilde{z}_{1,0.5} ,h} \right)$$
(49)
$$\dot{\hat{z}}_{3} = k_{03} {\text{fal}}\left( {\tilde{z}_{1,0.25} ,h} \right)$$
(50)
$${\text{fal}}\left( {X,\sigma ,h} \right) = \left\{ {\begin{array}{*{20}c} {\frac{{\sigma^{2} }}{{h^{1 - \sigma } }}X} & {\left| X \right| \le h} \\ {\left| X \right|^{\sigma } {\text{sgn}} \left( X \right)\sigma^{2} } & {\left| X \right| > h} \\ \end{array} } \right.$$
(51)

Where \(\hat{z}_{{\text{i}}}\), \(k_{{{\text{0i}}}}\), X are the estimated values of \({z}_{i}\), observer gain and input error of the nonlinear function, respectively. Also \(0<\sigma <1\) is the accuracy index and \(h\) represents the width of the linear region of the nonlinear function.

The overall schematic of proposed control block diagram, called IMP-ASMC, can be seen in Fig. 2.

Fig. 2
figure 2

Schematic of proposed IMP-ASMC control block diagram

Full size image

3 Results and discussions

To demonstrate the effectiveness of the proposed controller in tracking the desired trajectories and providing appropriate interaction with the user, some sort of simulations is conducted. It is worth to note that the key physical parameters of a typical adult that used for all the simulations are shown in Table 1. Since the extracted dynamic model contains uncertainties, the developed approach is implemented on a virtual model derived with the assistance of MATLAB SimScape. Furthermore, in order to show the robustness of the proposed controller, parametric uncertainties and time-varying disturbances are applied in all simulations. The uncertainties were introduced by modifying each constant parameter of the model by approximately 20% to assess the response of the system. This adjustment accounts for variations in physical parameters such as mass or link lengths, simulating real-world conditions where exact values may not be known.

Table 1 Physical parameters used in simulations
Full size table

Figure 3 illustrates the tracking performance of the proposed controller, i.e., IMP-ASMC, for a natural walking trajectory from [30, 49]. Subfigures \(({a}_{1})\), (\({a}_{2}\)) and (\({a}_{3}\)) compare the actual (blue) and desired (red) trajectories for the joints \({\theta }_{1}\), \({\theta }_{2}\), and \({\theta }_{3}\), respectively. Further, subfigures (\({b}_{1}\)), (\({b}_{2}\)), and (\({b}_{3}\)) depict the corresponding joint tracking errors and provide a comparison with different well-known impedance-based controllers, i.e., the sliding mode controller, IMP-SMC, and the computed torque controller, IMP-CTC. Each control scheme was tuned to optimize its performance within the given uncertainties, allowing for a comprehensive comparison of their capabilities in handling uncertain dynamics. It can be clearly seen that the proposed controller maintains the tracking accuracy in an acceptable range under the detrimental effects of exogenous disturbance, uncertainty and interaction with the environment. The fluctuation of joint angles in the beginning period comes from the change in the desired trajectory imposed by the impedance control strategy. The remaining interval provides a general overview of the smooth tracked trajectory. Also, for the sake of comparison, it can be clearly seen that the proposed controller outperforms than IMP-SMC and IMP-CTC schemes. Besides, since IMP-ASMC and IMP-SMC strategies are robust against adversaries such as uncertainty and interaction with the environment, they provide more efficient performance than IMP-CTC. In general, the associated IMP-CTC controller caters poorest performance due to showing the largest tracking errors. This indicates the superiority of the proposed adaptive impedance controller rather than others.

Fig. 3
figure 3

Tracking performance of proposed IMP-ASMC controller. a Subfigures (a1), (a2), and (a3) compare the actual (blue) and desired (red) trajectories for joints θ1, θ2, and θ3, respectively. b Subfigures (b1), (b2), and (b3) present depict the corresponding joint tracking errors and provide a comparison with different controllers

Full size image

The estimated states by the proposed observer are also depicted in Fig. 4, illustrating the accuracy and robustness of the observer in estimating the required signals for instance. Indeed, the convergence time in the beginning of the interval shows the effectiveness and superiority of the observer while the estimated signal is started from a different point of the main signal.

Fig. 4
figure 4

The estimated states for θ1, θ2, and θ3 using the proposed IMP-ASMC controller

Full size image

Figure 5 illustrates the control efforts or joint torques exerted by the proposed controller on the three joints, namely \({\tau }_{1}\), \({\tau }_{2}\) and \({\tau }_{3}\). It is observed that the maximum torques remain within the saturation limit defined for the actuators. It is crucial to avoid excessive control effort as it can lead to discomfort for the patient and potentially disrupt their natural and physiological movements.

Fig. 5
figure 5

The control effort or joint torques exerted by the proposed controller on the three joint (τ1, τ2, τ3 indicate the torques related to θ1, θ2, and θ3, respectively)

Full size image

The reduction of interactive forces in rehabilitation robots is a crucial objective. Figure 6 (\({a}_{1}\)), (\({a}_{2}\)), and (\({a}_{3}\)) illustrates the interaction forces induced between the robot and the patient at joints \({\theta }_{1}\), \({\theta }_{2}\) and \({\theta }_{3}\), respectively, using the proposed IMP-ASMC controller. A comparison is made with the corresponding interaction forces generated by a pure ASMC controller, which does not employ an impedance strategy. The results clearly demonstrate that the developed control framework significantly reduces the interaction forces, whereas the pure ASMC controller generates high interaction forces that can adversely affect the performance of the control system and the comfort of the patient.

Fig. 6
figure 6

Interaction forces between the robot and the patient a Subfigures (a1), (a2), and (a3) compare the interaction forces at joints θ1, θ2 and θ3, respectively, for the proposed IMP-ASMC controller (blue) and the pure ASMC controller (red). b Subfigures (b1), (b2), and (b3) compare the interaction forces at joints θ1, θ2, and θ3; for the basic IMP-SMC (blue) and pure SMC (red) controllers

Full size image

For comparison purposes, the evaluation of interaction forces was also conducted within the framework of basic sliding mode controllers. Therefore, similarly, Fig. 6 (\({b}_{1}\)), (\({b}_{2}\)), and (\({b}_{3}\)) displays the interaction forces at joints \({\theta }_{1}\), \({\theta }_{2}\) and \({\theta }_{3}\), for both the conventional non-impedance-based and impedance-based schemes of the basic sliding mode controller, i.e., SMC and IMP-SMC, respectively. It is important to note that CTC-type controllers have been excluded from consideration due to their consistently poor performance in this context. Upon examination, it is evident that the pure SMC controller exhibits excessive chattering phenomena and fluctuations in the interaction forces, which can compromise the motion stability and patient comfort in the rehabilitation robot. IMP-SMC, on the other hand, eliminates the chattering phenomenon but exhibits large peaks in the interaction forces at the beginning.

Table 2 provides a summary of the comparison of tracking performance among three "variable impedance" controllers: the proposed one, IMP-ASMC, along with IMP-SMC and IMP-CTC, as well as a "fixed impedance" adaptive sliding mode controller known as ASTSM, recently discussed in [30, 31].

Table 2 A comparative analysis presents the average error of the obtained data relative to similar work
Full size table

To illustrate the capability of the proposed controller, an alternative trajectory tracking is also investigated and briefly shown in Fig. 7, following the same format of Fig. 3. It is still evident that the proposed controller outperforms the IMP-SMC and IMP-CTC schemes. Additionally, the IMP-ASMC and IMP-SMC strategies exhibit robustness against uncertainties and environmental interactions, resulting in more efficient performance compared to the IMP-CTC scheme.

Fig.7
figure 7

Tracking performance of IMP-ASMC controller for the second mentioned trajectory. a Comparison of actual versus desired joint trajectories θ1, θ2, and θ3 in subfigures (a1), (a2), and (a3). b The corresponding joint tracking errors and comparison with different controllers in subfigures (b1), (b2), and (b3)

Full size image

Overall, the findings indicate that the proposed controller excels in performance by consistently achieving the lowest average errors even in the presence of bounded uncertainties. Furthermore, it demonstrates superior capabilities in minimizing interaction forces and control effort, particularly when encountering variable impedance. These results confirm that the IMP-ASMC controller not only provides satisfactory performance but also effectively reduces chattering and undesirable forces, underscoring its effectiveness in the specific context under study.

Actually, in the field of robotic rehabilitation for physically disabled patients, the interface between the rehabilitation robot and the patient is crucial. Disabled patients may be hesitant to engage with a physiotherapist, let alone a rehabilitation robot. Indeed, in the realm of rehabilitation robotics, an advanced controller like the one proposed can equip robots with the following necessary capabilities to address rehabilitation issues effectively:

  • Tracking the optimal walking path determined by the physiotherapist, even in the presence of uncertainties, which significantly facilitate the proper rehabilitation process.

  • Ensuring the patient’s comfort within the device and avoiding the application of undesirable and chattering forces on the patient to enhance ease of use.

  • Providing tailored assistance to meet the patient's specific needs. Detecting the appropriate level of support directly impacts the reduction of contact forces between the patient and the robot, aligning with the core principle of the impedance control strategy, where minimizing contact forces during treatment is crucial. Additionally, the proposed impedance strategy is adaptable to accommodate communication with disabled patients exhibiting unknown and unpredictable movements.

  • Minimizing control effort is also critical. By reducing the control effort in the robot's joints, we can ensure the application of sufficient force to the patient in the safest possible positions

4 Conclusion

In this study, we have proposed a novel control strategy for a lower-limb gait rehabilitation exoskeleton, named IMP-ASMC. This approach integrates a model-free adaptive sliding mode control, which ensures the sliding condition to mitigate the effects of unknown uncertainties and prevents the overestimation of the control gain in the presence of uncertainty. Additionally, the strategy incorporates a variable impedance approach that enables the system's impedance to adapt dynamically over the gait, maintaining accurate tracking of desired joint trajectories. The stability of the proposed control strategy is rigorously proven using Lyapunov theory, providing confidence in its effectiveness. One important advantage of the proposed approach is its model-free nature, making it efficient for real-time applications.

The effectiveness of the proposed control strategy was thoroughly evaluated through simulations on a dynamic model, and comparative evaluations were conducted against two nonlinear controllers: conventional sliding mode control (SMC) and computed torque controller (CTC). The results confirm the assumptions of the proposed control approach, achieving a balance between force reduction and accurate gait trajectory tracking. It was shown that the incorporation of variable impedance in the control strategy significantly reduces the interaction forces experienced by both the robot and the user. Furthermore, the proposed controller demonstrates higher robustness compared to the other controllers when faced with increased uncertainties and external forces, outperforming them in challenging operating conditions.

Our findings contribute to the advancement of exoskeleton robotics by providing a foundation for reducing interaction forces between the patient and the robot, particularly in the field of rehabilitation where ensuring user comfort and safety is paramount. The presented control strategy has the potential to enhance the performance and usability of lower-limb exoskeleton robots, ultimately benefiting individuals undergoing rehabilitation. In the future work, we intend to investigate the findings of the variable impedance control along with the proposed controller, on an actual rehabilitation robot.