1 Introduction

Due to its firmer configuration, lower torque pulsation, wider speed range and higher power density, an interior permanent magnet synchronous motor (IPMSM) is extensively used in numerous traditional and emerging industrial fields, such as numerical control machine tools, wind power generation and electrical vehicles (EV), and especially becomes the first choice of EV tractions. For an IPMSM control system, to design an appropriate distribution theme for its stator current and make rational use of the resulting reluctance torque is greatly beneficial to improving the torque/speed output characteristics and the system’s operation efficiency [1, 2].

The maximum efficiency control is one of the most important design criteria in many industrial application fields. For example, the operation efficiency is a critical performance indicator in a motor drive and control system of EV powered by batteries. In an IPMSM’s operation area below the flux-weakening speed, its stator copper loss plays a major role compared with ignorantly slight iron loss and rotor copper loss. Thus, the maximum torque per ampere (MTPA) control can be considered as a kind of the maximum efficiency control, which is able to output the maximal torque with a certain stator current or to generate a certain torque with the minimal stator current and copper loss, aiming at increasing the system’s operation efficiency [3, 4].

An accurate mathematical model should be established with accurate pre-known parameters in order to obtain an optimal current vector complying with the MTPA definition. Nevertheless, an IPMSM’s electrical parameters, including the rotor flux linkage, the stator inductance and the stator resistance, may be time-varying with the actual inconstant operating speed and torque due to temperature rise, magnetic saturation, armature reaction, etc. And in general, the constant parameters were used in the traditional control methods, and an approximate and average MTPA trajectory was designed in the total working range, probably significantly inconsistent with the optimal one as a result of parameter variance.

The iterative method could not deduce an accurate function model and has not taken any effect of parameter change into consideration [5]. In the look-up table (LUT) method, the calculation complexity was simplified and the parameters were partially considered, but a huge amount of memory spaces were taken up and a heavy burden was placed on the off-line test [6]. The MTPA trajectory could be automatically approached under the condition of parameter variance with the auto-tracking method, which caused low convergence speed and low torque control accuracy [7]. The signal injection method was able to modify the present operating point according to the torque ripple generated by the injected signal so as for the real-time tracking of MTPA trajectory [8, 9]. However, the injected high-frequency current may result in additional torque ripple and power loss.

Consequently, the parameter identification method should be applied to enhance the system’s MTPA control properties. Nowadays, there are several practical and effective methods of parameter identification, including recursive least square method (RLS), extended Kalman filter method (EKF), model reference adaptive system method (MRAS) and neutral network method (NN).

In the RLS method, it is a must to store the necessary data from the former step during the current step of recursive calculation, which inevitably brings about data saturation [10,11,12]. In [10], a RLS method with a variable forgetting factor was used to estimate an IPMSM’s dq-axis inductances and resistance, which improved the identification accuracy and rate of convergence. A novel quasi-steady-state multi-parameter identification method for an SPMSM was proposed in [11], that is, the three parameters (flux linkage, inductance and resistance) were estimated in two steps using constant-current acceleration process and current injection. In [12], the influence of parameter variance on the MTPA control characteristics was analyzed, and a fast estimator was designed to estimate the d-q inductances while a slow one identified the rotor flux linkage and the stator resistance.

For a sensorless control system, its rotor position and speed can be well identified with the EKF method. However, the method has several obstacles to the identification of an IPMSM’s parameter. For instance, the flux linkage is identified in a 4th-order model causing a huge amount of real-time computing, and even in the low speed or light load, the smaller inputs or larger noises result in larger estimated errors [13]. Two estimators were separately designed with the MRAS method and the EKF method in [13], and it was shown that the latter method did not take on better estimation effect although its algorithm was more complex.

The design intentions of MRAS is that the adjustable model’s parameters are adjusted and identified with the predesigned adaptive laws, for the purpose of their progressive convergence to the real parameters in the reference model [14,15,16,17]. An estimator based on the Lyapunov Stability Theorem was designed and compared with the one using the Popov Hyper Stability Theorem in [14], and it was pointed out that the latter method had better tracking responses of parameter change with a integral item besides a proportional one. The three SPMSM electrical parameters were identified simultaneously in [15], but a rank-deficiency problem in the system model was ignored, which may give rise to multiple convergence results. In [16], firstly, the inductance was estimated in the q-axis current equation. Then, the resistance and flux linkage were identified with d-axis current injection. This method could overcome the rank-deficiency problem in the multi-parameter identification and ensure the uniqueness of estimated results.

The neutral network (NN) method can obtain excellent convergence characteristics, whereas the practical and extensive use was greatly confined due to its very complex algorithm [18, 19]. In [18], the three parameters of an SPMSM were estimated with a combination of on-line and off-line methods, which was unable to meet the high demand of real-time performance. A two-step method with injected current was presented for an SPMSM in [19]. In this method, considering the inverter’s nonlinearity, an identification model without voltage error was built up so as to enhance the identification accuracy.

Nevertheless, an IPMSM’s 3 parameters should be estimated and used for the MTPA trajectory tracking. At the same time, the estimator’s rank is 2, elaborated later in Sects. 2 and 3. As a result, the 2nd-order rank-deficiency model cannot guarantee that all the 3 parameters converge simultaneously with a certain degree of precision. In summary, the current solutions to the rank-deficiency problem now focus mainly on as follows:

  1. 1.

    Only 1 or 2 parameters were estimated on-line, while the rest ones were assumed to be constant or estimated off-line without consideration of the impact of parameter change on the MPTA control qualities [17, 18].

  2. 2.

    At least 2 parameters were identified simultaneously, but the rank-deficiency problem in the model was neglected. Hence, there are inadequate evidences in theory to support the uniqueness of convergent values [13,14,15].

  3. 3.

    A step-by-step method was adopted in which some parameters were identified on-line at the first step, and then the other ones were obtained with current injection in order to increase the system’s operation states and the model’s rank. However, the injected current had a bad influence on the torque control and identification accuracy, and the multi-step process worsened the system’s dynamic responses [10,11,12, 16, 19].

In conclusion, a modified MRAS-based method of parameter identification is introduced for the MTPA tracking control of an IPMSM. Initially, the variation tendency of MTPA trajectories is assessed under the condition of changeable parameters. After that, a full-rank estimator and its gain matrix on the flux linkage and the q-axis inductance are designed in accordance with the Popov Hyper Stability Theorem. Finally, the current operating point is recalculated and refreshed with the identified parameters in order for the on-line tracking of MTPA trajectory.

2 IPMSM Model and MTPA Control

The dq-axis equation of an IPMSM’s stator voltages can be described as

$$\left\{ \begin{aligned} u_{\text{d}} & = R_{\text{s}} i_{\text{d}} + L_{\text{d}} \frac{{{\text{d}}i_{\text{d}} }}{{{\text{d}}t}} - L_{\text{q}} \omega_{\text{e}} i_{\text{q}} \\ u_{\text{q}} & = R_{\text{s}} i_{\text{q}} + L_{\text{q}} \frac{{{\text{d}}i_{\text{q}} }}{{{\text{d}}t}} + L_{\text{d}} \omega_{\text{e}} i_{\text{d}} + \omega_{\text{e}} \psi_{\text{f}} \\ \end{aligned} \right.$$
(1)

where id and iq are the dq-axis currents, ud and uq are the dq-axis voltages, Ψf is the rotor permanent magnet flux linkage, Rs is the phase resistance, Ld and Lq are the dq-axis inductances, and ωe is the rotor electrical angular speed.

The corresponding electromagnetic torque is

$$T_{\text{e}} = 1.5p(\psi_{\text{f}} i_{\text{q}} + (L_{\text{d}} - L_{\text{q}} )i_{\text{d}} i_{\text{q}} )$$
(2)

where p is the number of pole pairs.

Using the toque angle β between q-axis and the stator current is, id and iq can be written as

$$\left\{ \begin{aligned} i_{\text{d}} & = - i_{\text{s}} \sin \beta \\ i_{\text{q}} & = i_{\text{s}} \cos \beta \\ \end{aligned} \right.$$
(3)

If a stator current control method is aiming at generating a certain torque with the least current amplitude or outputting the highest torque with a given current value, it is named as the maximum torque per ampere control (MTPA) [3]. For the purpose of a maximal ratio of Te to is, the torque angle β should be set as

$$\sin \beta = \frac{{\psi_{\text{f}} - \sqrt {\psi_{\text{f}}^{2} + 8(L_{\text{d}} - L_{\text{q}} )^{2} i_{\text{s}}^{ 2} } )}}{{4(L_{\text{d}} - L_{\text{q}} )i_{\text{s}} }}$$
(4)

Obviously, the expected values of the dq-axis currents can be calculated on-line according to Eqs. (3)–(4) in order to track the MTPA trajectory real-timely. However, in the actual operation of an IPMSM, its key electrical parameters, the rotor flux linkage and the dq-axis inductances included, must be variable with temperature rise, magnetic saturation, armature reaction, etc. As a result, the actual MTPA trajectory must be inconsistent with its optimal one due to the parameter change.

3 Influence of Parameter Variance on MTPA Trajectories

The stator resistance Rs becomes higher due to its temperature rise and appears to be an approximate linear-function of the temperature. Also, the rotor flux linkage Ψf will decrease if the temperature increases. Accordingly, the change in the flux density and magnetic permeability will influence on the stator inductance.

More importantly, the phenomenon of magnetic saturation will have effect on the stator inductance, i.e., the stator and rotor core exhibits a nonlinear current-flux feature and thus the inductance variance. Figure 1 reveals the variation tendency of dq-axis inductances with the stator current.

Fig. 1
figure 1

Inductance variances

Full size image

When id is tiny, the d-axis magnetic field Ψd is saturated to a certain extent, so Ld is almost unchangeable; otherwise, especially in the flux-weakening working area, Ψd will be greatly weakened, which reduces Ld slowly with the negative increase of id. On the other hand, the magnetic saturation influences on Lq more significantly. When iq is smaller and the q-axis magnetic field Ψq is linear with respect to iq, Lq approximates a constant; or in the saturated zone of Ψq, Lq goes down quickly with the positive increase of iq. In a word, for the whole operation range, Ld varies within a very small range and with a lower speed.

Additionally, Ψd affects its quadrature magnetic field Ψq, or vice versa, called armature reaction or cross coupling. As expressed in the stator voltages Eq. (1), there is a coupling item \(- L_{\text{q}} \omega_{\text{e}} i_{\text{q}}\) in the d-axis equation and a coupling item \(+ L_{\text{d}} \omega_{\text{e}} i_{\text{d}}\) in the q-axis equation, too.

As Fig. 2 shows, when Ld, Lq and Ψf change within ± 10% of their respective average values, the actual current working points deflect from the optimal MTPA trajectory under the condition of parameter change.

Fig. 2
figure 2

MTPA trajectory derivations with parameter variances. aLd. bLq. cΨf

Full size image

It is obvious that the variance of Lq or Ψf give rise to a significant derivation of the MTPA trajectory and operating point, while that of Ld brings about only a negligible trajectory derivation.

As mentioned above, weighing between the rank-deficiency phenomenon in the estimator’s model and the MTPA control performances, a new method of parameter identification is presented and designed for the MTPA tracking control of an IPMSM, in which Lq and Ψf are identified on-line with an assumption of a constant Ld.

4 Model Reference Adaptive System of IPMSM

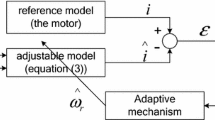
4.1 Structure of Model Reference Adaptive System

The structure diagram of a model reference adaptive system (MRAS) is depicted in Fig. 3. In this system, the predesigned adaptive laws force the output error e (between the reference model’s output y and the adjustable model’s output \(\hat{\varvec{y}}\)) to converge to zero, with which the parameters are adjusted and identified. That is to say that the adjustable model’s parameters to be identified will be approaching asymptotically the reference model’s real parameters.

Fig. 3
figure 3

Model reference adaptive system

Full size image

Mapping an IPMSM into the system as Fig. 3 depicts, the

system input is \(\varvec{u}\text{ = }\left[ {\begin{array}{*{20}l} {u_{\text{d}} } & {u_{\text{q}} } \\ \end{array} } \right]^{\text{T}}\), the reference model’s output is \(\varvec{y} = \varvec{i} = \left[ {\begin{array}{*{20}l} {i_{\text{d}} } & {i_{\text{q}} } \\ \end{array} } \right]^{\text{T}}\), the adjustable model’s output is \(\hat{\varvec{y}} = \hat{\varvec{i}} = \left[ {\begin{array}{*{20}l} {\hat{i}_{\text{d}} } & {\hat{i}_{\text{q}} } \\ \end{array} } \right]^{\text{T}}\), and the output error is \(\varvec{e} = \varvec{i} - \hat{\varvec{i}}\).

4.2 IPMSM’s Reference Model

For an IPMSM control system, the state space equation of dq-axis currents is derived from Eq. (1) as

$$\left[ \begin{array}{ll} \frac{{{{\rm d}}i_{{\rm d}} }}{{{{\rm d}}t}} \hfill \\ \frac{{{{\rm d}}i_{{\rm q}} }}{{{{\rm d}}t}} \hfill \\ \end{array} \right] = \left[ {\begin{array}{ll} { - \frac{{R_{{\rm s}} }}{{L_{{\rm d}} }}} & {\frac{{L_{{\rm q}} }}{{L_{{\rm d}} }}\omega_{{\rm e}} } \\ { - \frac{{L_{{\rm d}} }}{{L_{{\rm q}} }}\omega_{{\rm e}} } & { - \frac{{R_{{\rm s}} }}{{L_{{\rm q}} }}} \\ \end{array} } \right]\left[ \begin{array}{ll} i_{{\rm d}} \hfill \\ i_{{\rm q}} \hfill \\ \end{array} \right]{ + }\left[ {\begin{array}{ll} {\frac{1}{{L_{{\rm d}} }}} & 0 \\ 0 & {\frac{1}{{L_{{\rm q}} }}} \\ \end{array} } \right]\left[ \begin{array}{ll} u_{{\rm d}} \hfill \\ u_{{\rm q}} \hfill \\ \end{array} \right] + \left[ \begin{array}{ll} 0 \\ - \frac{{\psi_{{\rm f}} }}{{L_{{\rm q}} }}\omega_{{\rm e}} \\ \end{array} \right]$$
(5)

Regarding Eq. (5) as an IPMSM’s reference model follows that

$$\varvec{\dot{i} = Ai + Bu + C}$$
(6)

where,

$$\varvec{A} = \left[ {\begin{array}{*{20}l} { - \frac{{R_{\text{s}} }}{{L_{\text{d}} }}} & {\frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} } \\ { - \frac{{L_{\text{d}} }}{{L_{\text{q}} }}\omega_{\text{e}} } & { - \frac{{R_{\text{s}} }}{{L_{\text{q}} }}} \\ \end{array} } \right],\quad \varvec{B} = \left[ {\begin{array}{*{20}l} {\frac{1}{{L_{\text{d}} }}} & 0 \\ 0 & {\frac{1}{{L_{\text{q}} }}} \\ \end{array} } \right],\quad \varvec{C} = \left[ \begin{array}{ll} 0 \\ - \frac{{\psi_{\text{f}} }}{{L_{\text{q}} }}\omega_{\text{e}} \\ \end{array} \right]$$

4.3 Parameter Adjustable Model

Assuming that the rotor speed ωe is invariable during the process of parameter estimation, from the reference model Eq. (6), the adjustable model is established as

$$\varvec{\dot{\hat{i}} = \hat{A}\hat{i} + \hat{B}u + \hat{C}} - \varvec{Ge}$$
(7)

where,

$$\begin{aligned} \hat{\varvec{A}} & = \left[ {\begin{array}{*{20}l} { - \frac{{R_{\text{s}} }}{{L_{\text{d}} }}} & {\frac{{\hat{L}_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} } \\ { - \frac{{L_{\text{d}} }}{{\hat{L}_{\text{q}} }}\omega_{\text{e}} } & { - \frac{{R_{\text{s}} }}{{\hat{L}_{\text{q}} }}} \\ \end{array} } \right],\quad \hat{\varvec{B}} = \left[ {\begin{array}{*{20}l} {\frac{1}{{L_{\text{d}} }}} & 0 \\ 0 & {\frac{1}{{\hat{L}_{\text{q}} }}} \\ \end{array} } \right] \\ \hat{\varvec{C}} & = \left[ \begin{array}{ll} 0 \\ - \frac{{\hat{\psi }_{\text{f}} }}{{\hat{L}_{\text{q}} }}\omega_{\text{e}} \\ \end{array} \right],\quad \varvec{G} = \left[ {\begin{array}{*{20}l} { - g_{11} } & { - g_{12} } \\ {g_{21} } & { - g_{22} } \\ \end{array} } \right] \\ \end{aligned}$$

To select an appropriate gain matrix G, the parameter estimator can obtain desirable convergence properties and achieve anticipant asymptotic stability.

The system’s error equation can be deduced by Eq. (6) minus Eq. (7)

$$\varvec{\dot{e} = } (\varvec{A + G} )\varvec{e + }\Delta \varvec{A\hat{i} + }\Delta \varvec{Bu + }\Delta \varvec{C}$$
(8)

where \(\Delta \varvec{A} = \varvec{A} - \hat{\varvec{A}}\), \(\Delta \varvec{B} = \varvec{B} - \hat{\varvec{B}}\), and \(\Delta \varvec{C} = \varvec{C} - \hat{\varvec{C}}\).

5 Design of MRAS Parameter Estimator

This paper designs a MRAS parameter estimator in terms of the Popov Hyper Stability Theorem [20].

5.1 Equalization of Nonlinear Feedback System

With a definition of \(\varvec{w = } - (\Delta \varvec{A\hat{i} + }\Delta \varvec{Bu + }\Delta \varvec{C})\), the parameter identification model Eq. (8) can be reconstructed as

$$\varvec{\dot{e} = } (\varvec{A + G} )\varvec{e} - \varvec{w}$$
(9)

From the above equation, an equivalent nonlinear time-varying feedback system can be illustrated as in Fig. 4, where φ(e) stands for the parameters’ adaptive law.

Fig. 4
figure 4

Nonlinear feedback system

Full size image

5.2 Design of Adaptive Law

The Popov Integral Inequality is

$$\eta (0,t_{1} ) = \int_{0}^{{t_{1} }} {\varvec{e}^{\text{T}} \varvec{w}} {\text{d}}t \ge - \gamma^{2}$$
(10)

where a constant γ is positive and limited free of t ≥ 0.

Substituting e and w into Eq. (10), it follows two sub inequalities concerning the identified parameters Lq andΨf

$$\left\{ \begin{aligned} \eta_{1} (0,t_{1} ) & = \int_{0}^{{t_{1} }} {(\frac{1}{{\hat{L}_{\text{q}} }} - \frac{1}{{L_{\text{q}} }})[(u_{\text{q}} - R_{\text{s}} \hat{i}_{\text{q}} - \omega_{\text{e}} L_{\text{d}} \hat{i}_{\text{d}} )(i_{\text{q}} - \hat{i}_{\text{q}} )} \\ & \quad - \frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} L_{\text{q}} \hat{i}_{\text{q}} (i_{\text{d}} - \hat{i}_{\text{d}} )]{\text{d}}t \ge - \gamma_{1}^{2} \\ \eta_{2} (0,t_{1} ) & = \int_{0}^{{t_{1} }} { - (\frac{{\hat{\psi }_{\text{f}} }}{{\hat{L}_{\text{q}} }} - \frac{{\psi_{\text{f}} }}{{L_{\text{q}} }})\omega_{\text{e}} (i_{\text{q}} - \hat{i}_{\text{q}} ){\text{d}}t} \ge - \gamma_{2}^{2} \\ \end{aligned} \right.$$
(11)

In general, the adaptive law in reference to Lq is described as

$$\frac{1}{{\hat{L}_{\text{q}} }} = \frac{1}{{L_{\text{q}} }} + f_{ 1} (t )+ \int_{0}^{t} {f_{2} (\tau ) {\text{d}}\tau }$$
(12)

From Eq. (11) and Eq. (12), we get

$$\left\{ \begin{aligned} \eta_{11} (0,t_{1} ) & = \int_{0}^{{t_{1} }} {[(u_{\text{q}} - R_{\text{s}} \hat{i}_{\text{q}} - L_{\text{d}} \hat{i}_{\text{d}} \omega_{\text{e}} )(i_{\text{q}} - \hat{i}_{\text{q}} )} \\ & \quad - \frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} L_{\text{q}} \hat{i}_{\text{q}} (i_{\text{d}} - \hat{i}_{\text{d}} )]f_{1} (t ) {\text{d}}t \ge - \gamma_{11}^{2} \\ \eta_{12} (0,t_{1} ) & = \int_{0}^{{t_{1} }} {[(u_{\text{q}} - R_{\text{s}} \hat{i}_{\text{q}} - L_{\text{d}} \hat{i}_{\text{d}} \omega_{\text{e}} )(i_{\text{q}} - \hat{i}_{\text{q}} )} \\ & \quad - \frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} L_{\text{q}} \hat{i}_{\text{q}} (i_{\text{d}} - \hat{i}_{\text{d}} )]\int_{0}^{t} {f_{2} (\tau ) {\text{d}}\tau } {\text{d}}t \ge - \gamma_{12}^{2} \\ \end{aligned} \right.$$
(13)

Hence, the adaptive law regarding Lq can be deduced

$$\frac{1}{{\hat{L}_{\text{q}} }} = \frac{1}{{L_{\text{q}} }} + \left( {k_{1} + \frac{1}{{\tau_{1} s}}} \right)\left[ {\left( {u_{\text{q}} - R_{\text{s}} \hat{i}_{\text{q}} - \omega_{\text{e}} L_{\text{d}} \hat{i}_{\text{d}} } \right)\left( {i_{\text{q}} - \hat{i}_{\text{q}} } \right) - \frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} L_{\text{q}} \hat{i}_{\text{q}} \left( {i_{\text{d}} - \hat{i}_{\text{d}} } \right)} \right]$$
(14)

where k1 and τ1 represent the PI coefficients of Lq’s adaptive law.

Similarly, the adaptive law regarding the parameter Ψf can also be deduced

$$\frac{{\hat{\psi }_{\text{f}} }}{{\hat{L}_{\text{q}} }} = \frac{{\psi_{\text{f}} }}{{L_{\text{q}} }} - \left( {k_{ 2} + \frac{1}{{\tau_{2} s}}} \right)\omega_{\text{e}} \left( {i_{\text{q}} - \hat{i}_{\text{q}} } \right)$$
(15)

where k2 and τ2 represent the PI coefficients of Ψf’s adaptive law.

5.3 Design of Gain Matrix

For the system’s linear forward path in Fig. 4, its transfer function matrix is

$$\varvec{H}(s)\varvec{ = } [s\varvec{I} - (\varvec{A} + \varvec{G})]^{ - 1}$$
(16)

The Kalman-Yacubovich-Popov Positive Real Lemma states that “H(s) will be a severe positive real matrix, if the following equation is tenable

$$\varvec{A} + \varvec{G} + (\varvec{A} + \varvec{G})^{\text{T}} = - \varvec{Q}$$
(17)

where Q is a positive definite and real symmetric matrix, in a controllable and observable system Eq. (9)” [20].

After substitution of A and G into Eq. (17), we have

$$\left\{ \begin{aligned} \frac{{R_{\text{s}} }}{{L_{\text{d}} }} + {\text{g}}_{ 1 1} = \frac{{R_{\text{s}} }}{{L_{\text{q}} }} + {\text{g}}_{ 2 2} > 0 \hfill \\ \frac{{L_{\text{d}} }}{{L_{\text{q}} }}\omega_{\text{e}} + {\text{g}}_{ 1 2} = \frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} + {\text{g}}_{ 2 1} \hfill \\ \end{aligned} \right.$$
(18)

Based on the principle of the Popov Hyper Stability Theorem [20], the gain matrix G’s elements should be configured as Eq. (18) restricts.

The characteristic equation of the adjustable model Eq. (9) is

$${\text{det(}}s\varvec{I} - (\varvec{A} + \varvec{G})) = \left| {\begin{array}{*{20}l} {s + \frac{{R_{\text{s}} }}{{L_{\text{d}} }} + {\text{g}}_{ 1 1} } & { - \frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} + {\text{g}}_{12} } \\ {\frac{{L_{\text{d}} }}{{L_{\text{q}} }}\omega_{\text{e}} - g_{21} } & {s + \frac{{R_{\text{s}} }}{{L_{\text{q}} }} + {\text{g}}_{ 1 2} } \\ \end{array} } \right| = 0$$
(19)

Considering the designed estimator’s asymptotic stability and dynamic responses, the real parts of the closed-loop poles in the adjust model should be set m times as great as those in the reference model and be located at 135° and 225° in the complex plane (m = 2–4), separately [21]. And then combining with the limitation of Eq. (18) yields

$$\left\{ \begin{aligned} 2\left( {\frac{{R_{\text{s}} }}{{L_{\text{d}} }} + {\text{g}}_{ 1 1} } \right) & = m\left( {\frac{{R_{\text{s}} }}{{L_{\text{d}} }} + \frac{{R_{\text{s}} }}{{L_{\text{q}} }}} \right) \\ \left( {\frac{{R_{\text{s}} }}{{L_{\text{d}} }} + {\text{g}}_{ 1 1} } \right)^{2} & = \left( {\frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} - {\text{g}}_{21} } \right)^{2} \\ \end{aligned} \right.$$
(20)

Thus, from Eq. (18) and Eq. (20), the elements of the gain matrix G should be configured as follows

$$\varvec{G} = \left[ {\begin{array}{*{20}l} { - \left( {\frac{m - 2}{2}\frac{{R_{\text{s}} }}{{L_{\text{d}} }} + \frac{m}{2}\frac{{R_{\text{s}} }}{{L_{\text{q}} }}} \right)} & {\frac{m}{2}\left( {\frac{{R_{\text{s}} }}{{L_{\text{d}} }} + \frac{{R_{\text{s}} }}{{L_{\text{q}} }}} \right) - \frac{{L_{\text{q}} }}{{L_{\text{d}} }}\omega_{\text{e}} } \\ { - \frac{m}{2}\left( {\frac{{R_{\text{s}} }}{{L_{\text{d}} }} + \frac{{R_{\text{s}} }}{{L_{\text{q}} }}} \right){ + }\frac{{L_{\text{d}} }}{{L_{\text{q}} }}\omega_{\text{e}} } & { - \left( {\frac{m}{2}\frac{{R_{\text{s}} }}{{L_{\text{d}} }} + \frac{m - 2}{2}\frac{{R_{\text{s}} }}{{L_{\text{q}} }}} \right)} \\ \end{array} } \right]$$
(21)

To sum up, an overall structure of MTPA control system for an IPMSM is demonstrated in Fig. 5.

Fig. 5
figure 5

Structure diagram of IPMSM MTPA control system

Full size image

6 Simulation Results and Analysis

A simulation model of MTPA control system for an IPMSM system is established and tested in MATLAB. The prototype motor’s parameters are listed in Table 1, where the average values within the speed/torque operation area are used for the inductances and the flux linkage. The estimator’s key parameters are shown in Table 2.

Table 1 Parameters of IPMSM
Full size table
Table 2 Parameters of estimator
Full size table

In the simulation model, the space vector PWM inverter is considered to be an ideal amplifying element beneficial to prove the feasibility and validity of the used identification method avoiding disturbance from the inverter’s nonlinearity. Besides, the DC bus voltage is 320 V, and hence the maximal amplitude of the inverter’s output phase voltage can be calculated as follows

$$\frac{{V_{\text{DC}} }}{\sqrt 3 }{ = }\frac{{320{\text{V}}}}{\sqrt 3 } \approx 185{\text{V}}$$
(22)

Figures 6, 7 and 8 display the estimation effect of parameter, changing to 90%Lq, 110%Ψf and both of them, separately. When the parameters vary as mentioned above, the current errors ed and eq are convergent to zero quickly. Also, the estimated parameters approach rapidly the anticipant ones. In consequence, the proposed parameter estimator exhibits excellent tracking properties under the circumstance of parameter variance.

Fig. 6
figure 6

Estimation effect of q-axis inductance

Full size image
Fig. 7
figure 7

Estimation effect of flux linkage

Full size image
Fig. 8
figure 8

Estimation effect of inductance and flux linkage

Full size image

Comparisons of current tracking responses between the parameter invariance method and the parameter identification method are revealed in Figs. 9, 10 and 11. And Lq goes down by 10% in Fig. 9, Ψf goes up by 10% in Fig. 10, and both of them occur in Fig. 11.

Fig. 9
figure 9

Current responses with q-axis inductance variance

Full size image
Fig. 10
figure 10

Current responses with flux linkage variance

Full size image
Fig. 11
figure 11

Current responses with q-axis inductance and flux linkage variances

Full size image

Evidently, with the former method, the static dq-axis currents are so different from the expected ones that the resulting MTPA trajectory deflects greatly from the optimal one. Nevertheless, the latter method is able to force the current operating point into approaching the optimal MTPA trajectory immediately. Accordingly, the presented design method increases significantly the system’s robustness against parameter perturbations for MTPA control.

7 Experimental Results and Analysis

The experimental bench for the IPMSM drive and control system is exhibited in Fig. 12. In the experiment, the parameters of motor and estimator are identical with those in the simulation, as listed in Tables 1 and 2. And a three-phase full-bridge voltage source inverter are adopted with the space vector PWM method, where the DC bus voltage is 320 V, the switching frequency is 10 kHz and the dead time is 6.4 μs.

Fig. 12
figure 12

Experimental bench for IPMSM system

Full size image

Figure 13 manifests the MTPA current operation points with the presented parameter identification method compared with the optimal torque-current characteristics. To calculate the dq-axis currents according to Eq. (3) and Eq. (4) can plot a simulation waveform in Fig. 13, the parameter change not included. The optimal waveforms are gained by repeated modulation of torque angle β at each selected torque/speed operation point, where a torque point is chosen every 9 N m from light load (18 N m) to full load (72 N m). In the test, we recorded a group of the optimal data at each specified torque/speed point and stored the corresponding torque angle β in the look-up table (LUT). As stated above, the LUT method will cost a large amount of memory spaces and place a heavy burden on the off-line experiment. However, the resulting MTPA trajectories can be taken as the optimal torque-current characteristics, and thus be used to validate the performance and effect of the applied on-line parameter identification method. From Fig. 13, it is clear that the operation points with estimated parameters almost coincide with the optimal waveforms, so the designed MTPA control method has excellent static identification precision.

Fig. 13
figure 13

Torque-current characteristics and MTPA operation points

Full size image

It can be found out that there are significant differences between the simulation waveforms and the measured waveforms with on-line estimation, and the optimal waveform at 1000 r/min is also somewhat different from those at 2000 r/min and 3000 r/min, which diverges more greatly with the increase of torque. It is because the magnetic saturation has more remarkable influence on the motor’s parameter perturbation and the MTPA working points at a higher torque or speed. For further explanation, the rotor flux linkage and the stator q-axis inductance are reduced by the saturated magnetic field, and then a larger current is required to generate a certain torque, as described in the torque expression Eq. (2). Additionally, the inverter’s nonlinear output voltage will also lead to a difference between simulation and experiment, which can be improved by a dead-time compensation method [22].

Comparisons of load change responses between the LUT method and the identification method at the rated speed are shown in Figs. 14 and 15, where the torque is loaded from light load 18 N m to full load 72 N m suddenly at t = 15.0 s in Fig. 14, and the torque is unloaded from full load 72 N m to half load 36 N m abruptly at t = 5.5 s in Fig. 15. As explained above, the optimal torque angles in the off-line table are a set of reserved discontinuous data. And if the working condition (speed, torque, etc.) changes, the operation point may be reciprocating within a neighborhood of the target point, so the torque angle has to be switched frequently before the system arrives at a new balanced stability. Therefore, it must result in bad dynamic responses and even system oscillation. From Figs. 14 and 15, using the on-line identification based MTPA control method, the adjusting time becomes shorter, the overshoot decreases, and the static ripple is also weakened for the dq-axis current. Thus, the designed MTPA trajectory tracking control method owns better dynamic and static running qualities.

Fig. 14
figure 14

Loading responses of currents with rated speed. a LUT. b Identification

Full size image
Fig. 15
figure 15

Unloading responses of currents with rated speed. a LUT. b Identification

Full size image

Figures 16 and 17 illustrate current responses of loading and unloading between the LUT method and the identification method at the speed 1000 r/min, where the torque change is identical with that at the rated speed.

Fig. 16
figure 16

Loading responses of currents with 1000 r/min. a LUT. b Identification

Full size image
Fig. 17
figure 17

Unloading responses of currents with 1000 r/min. a LUT. b Identification

Full size image

It can be seen evidently that the static amplitudes of id and iq at the two different speeds are almost the same with the load torque 18 N m and 36 N m. Whereas, this is not the case with the full load torque 72 N m, in details, the static currents’ amplitudes are 62.7 Å and 149.5 Å at 1000 r/min, while they are 66.7A and 159.1A at 3000 r/min. To conclude, the stator currents at the two speeds are 114.7 Å and 122.0 Å, respectively, which complies with what is revealed and analyzed in Fig. 13.

Figures 18 and 19 are the system starting responses of the identification method compared with the LUT method. Obviously, during the starting process, the speed’s adjusting time is shorter, and its maximum overshoot is smaller with the identification method, so the designed MTPA control system can obtain good starting characteristics.

Fig. 18
figure 18

System starting responses with LUT

Full size image
Fig. 19
figure 19

System starting responses with identification

Full size image

8 Conclusion

Aiming at a solution to the problems of MTPA trajectory deviation due to parameter change and rank-deficiency identification model, a full-rank estimator was designed with reference to the rotor flux linkage and the q-axis inductance, and the estimated parameters were used to update the stator current and accordingly track the MTPA trajectory on-line. The designed estimator is easy to realize and practical in engineering, and has excellent parameter identification effect. Simulation and experimental results verify that the proposed method improves greatly the static and dynamic performances of the MTPA control under the conditions of parameter perturbation and load disturbance, which can especially meet the high demand of torque’s output capacity and dynamic response in application of EV motor drive. Furthermore, it needs further study and discussion on how the inverter nonlinearity will impact on the accuracy of parameter identification.