Keywords

41.1 Introduction

In recent years, the permanent magnet synchronous motor (PMSM) has received increasing interest in the field of industrial application [1]. Compared with other drive devices, the PMSM model can obtain higher power density, larger torque to inertia, and higher efficiency which makes the PMSM a prior choice in certain applications [2, 3]. It is noted that both the rotor position and the angular speed in PMSM system are the two main controlled objectives and have obtained widespread concerns (see [4–9]). However, the existence of nonlinearities, unknown disturbances, and load torque will influence the control performance of PMSM system [1, 2]. In order to solve these difficulties, some advanced control algorithms have been presented for the PMSM system, such as predictive control [2], adaptive control [3], backstepping method [8], sliding mode control [9], and so on.

It is well known that PI/PID control is widely applied in practical systems and some theoretical algorithms have also been discussed based on both the frequency-domain and time-domain approaches [10]. With the popularity of linear matrix inequality (LMI) techniques, the PI/PID controller-based LMI optimization algorithm has been designed to achieve satisfactory control performance in the scope of time domain [11]. For the control problem of PMSM system, the control gains in some traditional PI/PID algorithms can be obtained only by debugging repeatedly or depending on experience, which seriously affects the system performance of PMSM [3, 5]. Moreover, not enough sensors applied in PMSM system [7] will bring more difficulties in controlling the rotor position or the angular speed in PMSM system.

In this paper, a PI-type position controller based on LMIs is proposed for PMSM system. Instead of manual debugging repeatedly, the control gains can be computed by solving a series of convex LMIs and rigorous proof is given such that the closed-loop PMSM system can be guaranteed to be stable and the tracking error of rotor position can also converge to zero. At the same time, in order to deal with the in-measurable position problem when lacking position sensors, a linear Luenberger observer based on PMSM system is constructed to estimate the position variable. Furthermore, the peak-to-peak index is used to formulate the disturbance attenuation performance of PMSM system.

41.2 Mathematical Model of Surface-Mounted PMSM

After making some standard assumptions, the dynamical model of a surface-mounted PMSM can be written as follows: [1–3]

$$ \left( \begin{gathered} \dot{i}_{q} \hfill \\ \dot{i}_{d} \hfill \\ {\dot{\omega }} \hfill \\ {\dot{\theta }} \hfill \\ \end{gathered} \right) = \left( {\begin{array}{*{20}c} { - \frac{R}{L}} & { - p\omega } & { - \frac{{p\phi_{f} }}{L}} & 0 \\ {p\omega } & { - \frac{R}{L}} & 0 & 0 \\ {\frac{{K_{t} }}{J}} & 0 & { - \frac{B}{J}} & 0 \\ 0 & 0 & 1 & 0 \\ \end{array} } \right)\left( \begin{gathered} i_{q} \hfill \\ i_{d} \hfill \\ \omega \hfill \\ \theta \hfill \\ \end{gathered} \right) + \left( \begin{gathered} \;\frac{{u_{q} }}{L} \hfill \\ \;\frac{{u_{d} }}{L} \hfill \\ - \frac{{T_{L} }}{J} \hfill \\ \;\;0 \hfill \\ \end{gathered} \right) $$
(41.1)

where \( i_{d} \) and \( i_{q} \) are the \( d - q \) axis currents, \( u_{d} \) and \( u_{q} \) are the \( d - q \) axis voltages, \( \omega \) is the angular velocity, \( \theta \) is the rotor angle position, \( R \) is the stator resistance, \( L \) is the stator inductor, \( p \) is the pole pair, \( B \) is the viscous friction coefficient, \( J \) is the rotor moment of inertia, \( \phi_{f} \) is the rotor flux linkage, \( T_{L} \) is the load torque, \( K_{t} = 1.5\,p\phi_{f} \) is the torque constant.

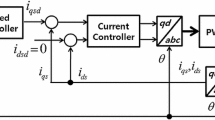
In order to eliminate the influence of the coupling terms between angular velocity and currents, the \( d \)-axis reference current is usually assumed as \( i_{d}^{ * } = 0 \). If the current controllers work well, the output term \( i_{d} = i_{d}^{ * } = 0 \). As a result, the PMSM system (41.1) can be simplified in the following form:

$$ \left( \begin{gathered} \dot{i}_{q} \hfill \\ {\dot{\theta }} \hfill \\ {\dot{\omega }} \hfill \\ \end{gathered} \right) = \left( {\begin{array}{*{20}c} { - \frac{R}{L}} & 0 & { - \frac{{p\phi_{f} }}{L}} \\ 0 & 0 & {\;\;1} \\ {\frac{{K_{t} }}{J}} & 0 & { - \frac{B}{J}} \\ \end{array} } \right)\left( \begin{gathered} i_{q} \hfill \\ \theta \hfill \\ \omega \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}c} {\frac{{u_{q} }}{L}} \\ 0 \\ { - \frac{{T_{L} }}{J}} \\ \end{array} } \right) $$
(41.2)

which makes the position controller design simpler.

With the desired angular position \( \theta^{ * } \), \( \zeta (t) \) is a designed auxiliary variable based on tracking error with the expression \( \dot{\zeta }(t) = \theta^{ * } - \theta (t) \). To achieve good control objective, the augmented state variable is defined as \( x(t) = \left[ {\begin{array}{*{20}c} {\theta (t),} & {i_{q} (t),} & {\zeta (t),} & {\omega (t)} \\ \end{array} } \right]^{T} \). Assuming \( u(t) = u_{q} (t) \) as the control input and \( d(t) = \left[ {\begin{array}{*{20}c} {\theta^{ * } ,} & {T_{L} } \\ \end{array} } \right]^{T} \) as the disturbance term, the state equation can be given in the following augmented form:

$$ \left\{ \begin{aligned} &\dot{x} = Ax(t) + Bu(t) + B_{1} d(t) \\ & z(t) = Cx(t) + Dd(t) \end{aligned} \right. $$
(41.3)

where \( z(t) \) is the reference output with known matrices \( C \) and \( D \), and

$$ A = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 \\ 0 & { - \frac{R}{L}} & 0 & { - \frac{{p\phi_{f} }}{L}} \\ { - 1} & 0 & 0 & 0 \\ 0 & {\frac{{3p\phi_{f} }}{2J}} & 0 & { - \frac{B}{J}} \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 0 \\ \frac{1}{L} \\ 0 \\ 0 \\ \end{array} } \right],\quad B_{1} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ 1 & 0 \\ 0 & { - \frac{1}{J}} \\ \end{array} } \right]\quad $$

41.3 PI-Type Controller Design

For the position tracking problem, a novel PI-type position controller is proposed as follows:

$$ u(t) = K_{P1} \theta (t) + K_{P2} i_{q} (t) + K_{I} \int\limits_{0}^{t} {(\theta^{ * } - \theta (\tau ))d\tau + K_{P3} \omega (t)} $$
(41.4)

where \( K_{P1} ,K_{P2} ,K_{P3} \) and \( K_{I} \) are controller gains to be determined later.

Substituting \( u(t) = Kx(t) \) into augmented system (41.3), the corresponding closed-loop PMSM system can be described as

$$ \left\{ \begin{aligned} & \dot{x}(t) = (A + BK)x(t) + B_{1} d(t) \\ & z(t) = Cx(t) + Dd(t) \\ \end{aligned} \right. $$
(41.5)

where \( K = \left[ {\begin{array}{*{20}c} {K_{P1} } & {K_{P2} } & {K_{I} } & {K_{P3} } \\ \end{array} } \right] \).

41.4 Stability Analysis with Disturbance Attenuation Performance

The following result provides a criterion for the performance analysis of the unforced PMSM system of (41.3).

Theorem 41.1

For the known parameters \( \lambda ,\mu_{i} (i = 1,2),\alpha > 0, \) suppose there exist matrices with appropriate dimensions \( P,T > 0, \) and parameter \( \gamma > 0 \) such that the following LMIs

$$ \left[ {\begin{array}{*{20}c} {{\text{sym}}(A^{T} P) + \mu_{1}^{2} T} & {PB_{1} } \\ {B_{1}^{T} P} & { - \mu_{2}^{2} I} \\ \end{array} } \right] < 0 $$
(41.6)
$$ \left[ {\begin{array}{*{20}c} {\mu_{1}^{2} T} & 0 & {C^{T} } \\ 0 & {(\gamma - \mu_{2}^{2} )I} & {D^{T} } \\ C & D & {\gamma I} \\ \end{array} } \right] > 0\quad \left[ {\begin{array}{*{20}c} {\alpha I} & T \\ T & T \\ \end{array} } \right] > 0\quad \left[ {\begin{array}{*{20}c} T & 0 & {C^{T} } \\ 0 & {(\gamma - \alpha x_{m}^{T} x_{m} )I} & {D^{T} } \\ C & D & {\gamma I} \\ \end{array} } \right] > 0 $$
(41.7)

are solvable, then the unforced system of (41.3) is stable, and the output satisfies the disturbance attenuation performance \( \sup_{{\left\| {d(t)} \right\|_{\infty } \le 1}} \left\| {z(t)} \right\|_{\infty } < \gamma^{2} \).

Proof

Defining a typical Lyapunov function as

$$ V(x(t),t) = x^{T} (t)Px(t) $$
(41.8)

Obviously it is noted that \( V(x(t),t) \ge 0 \). Furthermore, we can get

$$ \dot{V}(x(t),t) \le x^{T} (t)\Phi _{1} x(t) + \left\| {\mu_{2} d(t)} \right\|^{2} $$
(41.9)

where \( \Phi _{1} = {\text{sym}}(A^{T} P) + \mu_{2}^{ - 2} PB_{1} B_{1}^{T} P \).

Based on Schur complement formula, (41.6) implies that \( \Phi _{1} + \mu_{1}^{2} T < 0 \) holds. With (41.10), it can be seen that for any \( \left\| {d(t)} \right\|_{\infty } \le 1 \), we can get

$$ \dot{V}(x(t),t) \le - \mu_{1}^{2} x^{T} (t)Tx(t) + \mu_{2}^{2} $$
(41.10)

So for any \( x(t) \), it can be seen that

$$ x^{T} (t)Tx(t) < \hbox{max} \left\{ {\mu_{1}^{ - 2} \mu_{2}^{2} ,x_{m}^{T} Tx_{m} } \right\},\quad \left\| {x_{m} } \right\| = \sup_{ - d \le t \le 0} \left\| {x(t)} \right\| $$
(41.11)

which also implies that the unforced PMSM system of (41.3) is stable.

The proof of disturbance attenuation performance is omitted here to save space.

41.5 Position Tracking with Peak-to-Peak Performance

The following theorem provides an effective solution for the PI-type position tracking problem of closed-loop PMSM system (41.5).

Theorem 41.2

For the known parameters \( \mu_{i} (i = 1,2),\alpha > 0, \) suppose there exist matrices with appropriate dimensions \( Q = P^{ - 1} > 0,M = T^{ - 1} ,R > 0, \) and parameter \( \gamma > 0 \) such that the following LMIs

$$ \left[ {\begin{array}{*{20}c} {{\text{sym}}(AQ + BR)} & {B_{1} } & Q \\ {B_{1}^{T} } & { - \mu_{2}^{2} I} & 0 \\ Q & 0 & { - \mu_{1}^{ - 2} M} \\ \end{array} } \right] < 0 $$
(41.12)
$$ \left[ {\begin{array}{*{20}c} {\mu_{1}^{2} M} & 0 & {MC^{T} } \\ 0 & {(\gamma - \mu_{2}^{2} )I} & {D^{T} } \\ {CM} & D & {\gamma I} \\ \end{array} } \right] > 0\quad \left[ {\begin{array}{*{20}c} {\alpha I} & I \\ I & M \\ \end{array} } \right] > 0\quad \left[ {\begin{array}{*{20}c} M & 0 & {MC^{T} } \\ 0 & {(\gamma - \alpha x_{m}^{T} x_{m} )I} & {D^{T} } \\ {CM} & D & {\gamma I} \\ \end{array} } \right] > 0 $$
(41.13)

are solvable, then the closed-loop PMSM system (41.5) under the PI-type control law (41.4) is stable and satisfies both \( \lim_{t \to \infty } \theta (t) = \theta^{ * } \) and \( \sup_{{\left\| {d(t)} \right\|_{\infty } \le 1}} \left\| {z(t)} \right\|_{\infty } < \gamma^{2} \). In this case, the control gains \( K_{P1} ,K_{P2} ,K_{P3} \) and \( K_{I} \) can be solved via \( R = KQ \).

The proof of Theorem 41.2 is omitted here to save space.

41.6 Reduced Luenberger Observer Design

In this section, we focus on the motor model without position sensor. As a result, the position status of the rotor cannot be measured directly. So a typical reduced-order Luenberger observer needs to be constructed to observe the state variables of PMSM system and further to estimate the position values.

Based on the PMSM system (41.2), the reduced Luenberger observer is designed as follows:

$$ \left[ {\begin{array}{*{20}c} {\dot{\hat{i}}_{q} } \\ {\dot{\hat{\omega }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{R}{L}} & { - \frac{{p\phi_{f} }}{L}} \\ {\frac{{3p\phi_{f} }}{2J}} & { - \frac{B}{J}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{i}_{q} } \\ {\hat{\omega }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} \frac{1}{L} \\ 0 \\ \end{array} } \right]u + \left[ {\begin{array}{*{20}c} \varepsilon \\ 0 \\ \end{array} } \right](i_{q} - \hat{i}_{q} ) $$
(41.14)

where \( \hat{i}_{q} \) and \( \hat{\omega } \) represent the estimate values of \( i_{q} \) and \( \omega \), respectively.

Combining (41.2) with (41.14), we can get

$$ \left[ \begin{gathered} \frac{{{\text{d}}e_{q} }}{{{\text{d}}t}} \hfill \\ \frac{{{\text{d}}e_{\omega } }}{{{\text{d}}t}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} { - \frac{R}{L} - \varepsilon } & { - \frac{{p\phi_{f} }}{L}} \\ {\frac{{3p\phi_{f} }}{2J}} & { - \frac{B}{J}} \\ \end{array} } \right]\left[ \begin{gathered} e_{q} \hfill \\ e_{\omega } \hfill \\ \end{gathered} \right] $$
(41.15)

where \( e_{q} = i_{q} - \hat{i}_{q} ,e_{\omega } = \omega - \hat{\omega } \) represent the observation errors of \( i_{q} \) and \( \omega \). From (41.15), the observer gain \( \varepsilon \) can be designed to make the continuous error dynamics converge to zero asymptotically. It is shown that the proposed observer is of first order, so the computation burden is relatively light. Hence, the position of the rotor can be calculated by \( \theta = \int {\hat{\omega }dt} \).

41.7 Simulation Results

The specification of the PMSM system is shown in Table 41.1.

Table 41.1 Specification of the PMSM system
Full size table

From \( t = 0 \) to 20 s, the position command is designed as \( \pi \;{\text{rad}} \), and after t = 20 s, the position command is changed as \( 4\;{\text{rad}} \). Defining parameters \( \varepsilon = 5,T_{L} = 5\,{\rm N\,m} \). By using the LMI box, the PI-type controller can be computed as \( K_{P1} = - 1.5968,K_{P2} = 0.5192,K_{P3} = 0.1498,K_{I} = 1.1481 \).

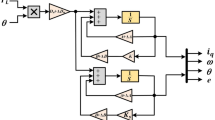
The above four figures show the dynamical responses of PMSM in combination with the PI-type controller and the Luenberger observer. From Fig. 41.1, the rotor position and the d-axis current are correct and rapidly converge to their reference values, respectively. The satisfactory position tracking and speed control are embodied in Fig. 41.2.

Fig. 41.1
figure 1

Position responses of with Luenberger observer and responses of the q-axis current

Full size image
Fig. 41.2
figure 2

Error between desired position and actual position and responses of angular speed

Full size image

41.8 Conclusion

This paper considers the tracking problem for the rotor position of PMSM system by combining a generalized PI-type controller with a reduced-order Luenberger observer. Based on convex optimization LMI techniques, some typical control objectives including stabilization, position tracking, and robustness for PMSM system can be guaranteed simultaneously.