Keywords

1 Introduction

The growing demand for transportation systems and the aging of their infrastructure have brought to light the need for cost-effective and efficient methods for the health monitoring of bridges, which are a crucial component of these systems. Traditional bridge health monitoring methods involve collecting data from sensors mounted on the bridge, but recent studies have shown that using accelerometers on vehicles crossing the bridge can be a more cost-effective and time-efficient alternative [1,2,3,4,5,6].

In recent years, researchers have turned to mobile sensor networks as an alternative method for bridge health monitoring. This approach utilizes data collected from the smartphones carried by passengers, instead of the costly installation of commercial-grade sensors on the vehicles. This method has the potential to significantly reduce costs while providing acceptable accuracy in understanding the dynamic behavior of bridges [7,8,9,10,11].

Crowdsensing-based techniques also show promise in detecting damage in bridges with increased efficiency. These techniques involve collecting and analyzing data from a large number of smartphones to form a comprehensive understanding of the dynamic characteristics of a bridge. However, the implementation of these techniques is still in the early stages of research and development, presenting challenges such as telecommunications limitations and the complexity of combining responses from multiple mobile sensors [12,13,14,15].

To accurately assess and detect damage in bridges, it is crucial to obtain a comprehensive understanding of their dynamic response. The authors' previous work proposed a novel method for mapping mobile data to some virtual fixed locations on the bridge and estimating bridge responses in order to identify the bridge mode shapes [16]. The main challenge in determining the dynamic response of a bridge at some assumed virtual fixed points using only the acceleration measured by the sensors mounted on the vehicles passing through them is the limitation in extracting the whole response signal of all the fixed points during total duration of loading, because the response estimated for a fixed point by interpolation of the mapped-response of the moving sensors to the adjacent fixed points, is usually valid only in the vicinity of the moving sensor locations. Herby, to complete or predict the invalid (missing) parts of the signals obtained for these fixed points, it is necessary to use statistical and mathematical techniques or machine learning approaches [16].

While the mode shapes of the bridge were successfully identified, the previously proposed technique, as proposed by the authors, relies heavily on subjective engineering judgment and lacks automation capabilities. This paper aims to address this challenge by proposing an algorithm to automate the procedure of soft-imputing in the signal completion step, eliminating the need for engineering judgment and streamlining the process of mode shape identification for the bridges through the vertical acceleration of the crossing vehicles and a novel modal FRF similarity measure. The proposed algorithm can potentially improve the efficiency and cost-effectiveness of bridge health monitoring and help ensure the safety and longevity of transportation infrastructure in smart cities.

2 Materials and Methods

2.1 Motivations and General Procedures

The previous study [16] found that by utilizing the soft-imputing method to complete the vertical response of passing vehicle axles, it is possible to estimate bridge responses at virtual fixed points and subsequently identify the bridge's mode shapes. However, a significant challenge in determining the optimal regularization parameter (λ) for accurate mode shape identification is that the exact mode shapes of the bridge are not known in real-world structural health monitoring (SHM) applications, requiring the use of engineering judgment [16].

The main objective of this paper is to develop a criterion for automatic determination of the optimal λ, in order to increase the accuracy of the identified mode shapes. Such increase in the accuracy will result in greater similarity between the extracted modal frequency response function (FRF) using the completed responses of the fixed points and the FRF of an ideal single-degree-of-freedom (SDOF) structure.

2.2 Bridge Response Estimation Through Soft-Imputing

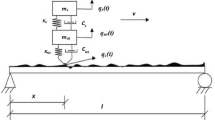
In order to estimate some parts of the bridge displacement response signals at some arbitrary virtual fixed points utilizing the vehicle acceleration response, inverse problem solution through linear interpolation first employed. The geometry of the bridge and parameters used in the following sections are shown in Fig. 1.

Fig. 1.
figure 1

Geometry and parameters of the one-span bridge.

Full size image

The continuous vertical displacement response of the bridge can be determined by considering a linear interpolating function and using the discrete responses of the bridge at the location of the virtual fixed points.

$$ y(x,t) = \left[ {\begin{array}{*{20}c} {N_1 (x)} & \cdots & {N_n (x)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {y_{s_1 } (t)} \\ \vdots \\ {y_{s_n } (t)} \\ \end{array} } \right\} = {{\bf{N}}}(x){{\bf{D}}}(t) $$
(1)

where D(t) is a vector containing vertical displacements of all the n fixed points (ysj(t)) and N(x) is linear interpolating function matrix.:.:

(2)

where sj is the location of the jth fixed points from the left support. j can be valued from 1 to (n-1).

By substituting the location history of the moving axles (x1(t) to xm(t)) in Eq. (1), the displacement responses of the moving axles can easily be extracted.

$$ {{\bf{Y}}}(t) = \left\{ {\begin{array}{*{20}c} {y_1^v (t)} \\ \vdots \\ {y_m^v (t)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{{\bf{N}}}(x_1 (t))} \\ \vdots \\ {{{\bf{N}}}(x_m (t))} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {y_{s_1 } (t)} \\ \vdots \\ {y_{s_n } (t)} \\ \end{array} } \right\} = {{\bf{N}}}_v (t){{\bf{D}}}(t) $$
(3)

where yiv (t) is vertical displacement of the ith axle and Nv(t) is an interpolating shape function matrix for estimating the response of the moving axles. The total number of the moving axles is m.

Multiplying Eq. (3) by the pseudoinverse of matrix Nv(t) produces the displacements of the fixed points as a function of moving axles displacements (m ≠ n).

$$ {{\bf{D}}}(t) = \left( {\left( {{{\bf{N}}}_v^{tr} (t){{\bf{N}}}_v^{\,} (t)} \right)^{ - 1} {{\bf{N}}}_v^{tr} (t)} \right){{\bf{Y}}}(t) $$
(4)

As previously discussed in [16], the response signals estimated using Eq. (4) are only accurate in the vicinity of the moving axles. The remaining parts of the signals should be considered missing due to high estimation error.

In order to complete the missing parts of the predicted signals, soft-imputing is applied on matrix D(t) with missing values based on the proposed technique in [16].

Soft-Imputing aims to make the valid regions (Ω) of the estimated matrix PΩ(Z) as similar as possible to the valid elements of the original matrix PΩ(D), while also keeping the rank of the estimated matrix as low as possible.

$$ {{\bf{P}}}_{{\bf{\Omega}}} ({{\bf{D}}})(i,j) = \left\{ {\begin{array}{*{20}c} {{{\bf{D}}}(i,j)} & {(i,j) \in \,{{\bf{\Omega}}}} \\ 0 & {(i,j) \notin \,{{\bf{\Omega}}}} \\ \end{array} } \right. $$
(5)
$$ {\text{Minimize}}\,J_{\lambda_k } ({{\bf{Z}}}) = \frac{1}{2}\left\| {{{\bf{P}}}_{{\bf{\varOmega}}} ({{\bf{D}}})(i,j)} \right\|_n^2 + \lambda_k \left\| {{\bf{Z}}} \right\|_* $$
(6)

where ||.||n and ||.||* represent the nuclear norm and the rank of a matrix respectively. λk is the regularization coefficient, which plays an important role in the algorithm. The solution for the optimization problem (Eq. (6)) is obtained through an iterative process.

$$ \begin{gathered} {{\bf{Z}}}_{new} = S_{\lambda_k } ({{\bf{P}}}_{{\bf{\varOmega}}} ({{\bf{D}}}) + {{\bf{P}}}_{{\bf{\varOmega}}}^\bot ({{\bf{Z}}}_{old} )) = {{\bf{U\varSigma}}}_{\lambda_k } {{\bf{V}}} \hfill \\ {{\bf{\varSigma}}}_{\lambda_k } = diag\left[ {\left( {d_1 - \lambda_k } \right)_+ , \cdots ,\left( {d_r - \lambda_k } \right)_+ } \right]\, \hfill \\ \end{gathered} $$
(7)

The method uses SVD on matrix [PΩ(D) + P⊥Ω(Zold)] to obtain matrices U, Σ and V, with Σ containing the singular values (=diag(d1, …, dr)). The soft-thresholded matrix of Σ, Σλi, is obtained by applying a thresholding technique to Σ.

In the present research, the optimal estimate of missing values (optimum point based on λk) is chosen using the objective function and a novel modal FRF similarity measure. The final estimate for a given λ is Zλ(t).

2.3 Modal Frequency Response Functions of the Bridge Under Moving Axles

According to the principle of modal analysis, the completed response signal matrix Zλ (t) can be represented by the matrix of mode shapes (Фsλ) and the modal coordinate response matrix (Qλ (t)):

$$ {{\bf{Z}}}_\lambda \left( t \right) = {{\bf{\varPhi}}}_\lambda^s {{\bf{Q}}}_\lambda \left( t \right) $$
(8)

SVD is utilized to identify mode shapes and modal coordinate responses as it can extract and ensure the orthogonality of matrices, a key characteristic of mode shapes [4].

$$ {{\bf{\varPhi}}}_\lambda^s = {{\bf{U\varSigma}}}^{^{\tfrac{1}{2}} } $$
(9)

And Qλ (t) can also be obtained using Eq. (1):

$$ {\bf{Q}}_\lambda (t) = \left[ {\left( {{\bf{\Phi }}_\lambda^{s^T } \times {\bf{\Phi }}_\lambda^s } \right)^{ - 1} \times {\bf{\Phi }}_\lambda^{s^T } } \right] \times {\bf{Z}}_\lambda (t) $$
(10)

The modal forces are also needed in order to extract the modal frequency response functions (FRFs) based on input and output data. Equation (4) can be used to model an m-axles moving load passing a bridge at a constant speed v, as depicted in Fig. 1.

$$ f(x,t) = \sum_{i = 1}^m {\delta \left( {x - x_i (t)} \right)f_{vi} \left( t \right)} $$
(11)

where the vertical dynamic forces applied by the vehicle to the bridge at the ith axle (fvi (t)) can be calculated using the absolute acceleration and the mass of that axle (\(\ddot{y}_{vi}\) and mvi) in the following equation:

$$ f_{vi} \left( t \right) = m_{vi} (g - \ddot{y}_{vi} ) $$
(12)

By considering n virtual points on the bridge as the fixed loading nodes and determining the vector of forces applied to these points using linear interpolation of intermediate loadings, the forces applied to the virtual fixed points (Fs (t)) can be calculated at any arbitrary time:

$$ {{\bf{F}}}_s (t) = {{\bf{N}}}(t){{\bf{F}}}_v (t) $$
(13)

where; Fv (t) is a vector containing the axles forces (fvi (t)).

The extracted force vector can be mapped to the modal space by multiplying Фsλ by Fs (t), which enables us to determine the vector of modal forces (Pλ(t)).

$$ {{\bf{P}}}_\lambda (t) = {{\bf{\varPhi}}}_\lambda^{s^T } {{\bf{N}}}(t){{\bf{F}}}_v (t) $$
(14)

Finally, having the input (prλ (t)) and output (qrλ (t)) for the rth mode, the FRF of that mode (Hr(ω)) can be determined by the following system identification techniques [17]:

$$ H_1 \left( \omega \right) = \frac{{S_{q_\lambda^r p_\lambda^r } (\omega )}}{{S_{p_\lambda^r p_\lambda^r } (\omega )}} $$
(15)
$$ H_2 \left( \omega \right) = \frac{{S_{q_\lambda^r q_\lambda^r } (\omega )}}{{S_{p_\lambda^r q_\lambda^r } (\omega )}} $$
(16)
$$ H^r \left( \omega \right) = \sqrt {H_1 (\omega ) \times H_2 (\omega )} $$
(17)

where \(S_{q_\lambda^r p_\lambda^r } (\omega )\) and \(S_{p_\lambda^r p_\lambda^r } (\omega )\) represent the cross and auto power spectral density spectrum, respectively.

2.4 Modal FRF Similarity Measure and Optimum λ

After the modal frequency response functions (FRFs) have been determined, an SDOF FRF model is fitted to each function using the least square technique. The proposed measure in Eq. (18) is then used to calculate the similarity between the modal FRFs and the fitted SDOF FRF model (MFRFSM (λ)). This measure enables us to quantify the accuracy of the identified mode shapes.

$$ MFRFSM(\lambda ) = \frac{1}{{N_{{\text{Modes}}} }}\sum_{r = 1}^{N_{{\text{Modes}}} } {corr(\left| {FRF_{SDOF}^r } \right|,\left| {FRF_{Estimated,\lambda }^r } \right|)} $$
(18)

The objective is to optimize the similarity measure in order to find the most appropriate value of the regularization coefficient (λ) and the corresponding optimal mode shapes. This automated approach allows for the identification of the most accurate mode shapes without the need for subjective engineering judgment.

3 Results and Discussion

3.1 Numerical Setup

To evaluate the effectiveness of the proposed framework, a single-span simply supported bridge under the loading of a two-axle moving vehicle is modeled and analyzed using ABAQUS. The first three natural frequencies of the model are 1.44, 5.76, and 12.95 Hz. The specifics of the numerical model can be found in previous research by the authors [16]. The model considers a bridge with a span length of 40 m and a distance between axles of 2.5 m. A constant speed of 60 km/h is assigned to all the axles, and the accelerometers are set to sample at a frequency of 200 Hz.

3.2 Results and Analysis

As shown in Fig. 2, the optimal value for the regularization parameter (λ) corresponding to the maximum average Modal Assurance Criterion (MAC) for all modes (compared to the exact ones) can be estimated using the proposed method without the need for engineering judgment. The optimal point of the modal FRF similarity measure (MFRFSM) is similar to that of the maximum MAC. This is of significant importance as it demonstrates a similar pattern between the two curves, enabling the proposed method to automatically identify more accurate mode shapes. Based on the optimal λ obtained using the proposed technique, the first four mode shapes of the bridge can be obtained using Eq. (9). The results of the comparison between the identified mode shapes and the corresponding exact mode shapes, as shown in Fig. 3, indicating that the proposed method is highly accurate in identifying the primary three mode shapes of the bridge.

Fig. 2.
figure 2

Comparison of the exact and identified mode shapes with varying regularization parameter using average (a) Modal Assurance Criterion (MAC) and (b) the Modal FRF Similarity Measure.

Full size image
Fig. 3.
figure 3

Selected Mode Shapes based on Optimal Regularization Parameter (λ).

Full size image

4 Conclusions

In this paper, we have presented a novel concept of utilizing modal frequency response functions (FRFs) to identify the optimal mode shapes through the application of soft-imputing and the vibration data from crossing vehicles. This approach enables the automatic system identification in drive-by bridge health monitoring applications, eliminating the need for subjective engineering judgment. The proposed algorithm was evaluated using data from numerical models, providing evidence of its effectiveness in identifying the optimal mode shapes. Additionally, the proposed method has the potential to reduce costs and improve the efficiency of bridge monitoring and maintenance. Overall, the results of this study demonstrate the potential for utilizing the proposed algorithm bridge health monitoring applications, thereby ensuring the safety and longevity of transportation infrastructure in smart cities.