Introduction

Exploration of clean and renewable energy has become important to reduce the dependency on fossil fuels and to address environmental crises. Moreover, technological advancement has introduced low-power, wireless and wearable electronic devices generating a demand for portable power supplies [1, 2]. This leads researchers to focus on capturing the energy from ambient sources such as thermal, vibration and radio frequency to minimize the use of batteries [3]. Human motion, vehicles, ocean waves, wind, etc. are possible vibration sources present in the ambient environment. These vibration sources can be converted into useful electrical energy through various transduction methods. To date, transduction methods such as triboelectric [4, 5], electrostatic [6], piezoelectric [7,8,9] and electromagnetic [10, 11] have been proposed. The electromagnetic transduction method to convert vibration into electrical energy is found to be more effective than piezoelectric methods with respect to power density, current output and internal resistance [11]. The major drawback of a conventional linear vibration energy harvester is its efficacy in a narrow range of frequencies. This makes them unsuitable for practical applications where the excitation sources have wideband vibration characteristics [12]. To address this issue, researchers have proposed nonlinear energy harvesters [13,14,15,16,17,18] and multiple/multi-frequency energy harvesters [7,8,9, 19] for broadband harvesting. The frequency bandwidth of multiple energy harvesters depends on variations in the geometry, mass, coupling, and nonlinearity.

Many researchers have proposed multiple energy harvesters to improve the bandwidth. Quing et al. [20] studied the cantilever energy harvester with additional mass and reported that it can harvest power at multiple frequencies. An energy harvester with folded geometry can also harvest power at multiple frequencies [21]. The distance between modes in the case of multimodal energy harvesters makes these harvesters ineffective for harvesting power over a continuous frequency band. A set of linear energy harvesters with different tip masses was analyzed theoretically and experimentally by Ferrari et al. [7] for broadband energy harvesting. Similar effects were reported with different energy harvester lengths and thicknesses [22,23,24]. A dual electromagnetic array consisting of rectilinear and rotary oscillators for broadband energy harvesting was proposed by Chen and Wang [25]. Zhang et al. and Wang et al.  [26, 27] presented a hybrid piezoelectric and electromagnetic energy harvester to overcome the limitations of the piezoelectric energy harvester. They reported enhancement in both the piezoelectric and the electromagnetic harvested powers. A set of non-similar energy harvesters that will have different natural frequencies can produce power over a wider bandwidth but requires more space and the magnitude of the power generated also reduced [24].

To take advantage of both multiple energy harvesters and multi-mode energy harvesters researchers analyzed harvesters coupled by springs (mechanical coupling) to enhance bandwidth. Yang and Yang [28] theoretically and numerically analyzed two bimorph beams connected by spring. They concluded that the resonances of these beams can be tuned using the spring as desired to get a broadband power output. Malaji and Ali [29] showed numerically and experimentally that multiple pendulum energy harvesters can increase the magnitude and bandwidth of power harvested using mechanical coupling. A linear multimodal energy harvester with weakly magnetic coupling was demonstrated by Zergoune et al. [30] to harvest energy by functionalizing the energy localization phenomenon. They reported that the energy localization phenomenon enhanced the harvester performance of the mistuned system compared to the tuned system. Metastructures for simultaneous vibration mitigation and energy harvesting were explored recently [31,32,33,34]. An internally coupled metastructure was proposed by Hu et al. [31]. They analyzed infinite and finite long models and reported a significant enhancement in vibration mitigation along with energy harvesting.

Multiple/multi-mode nonlinear energy harvesters have been a hot topic among researchers due to their capabilities to harvest power over wider bands [35, 36]. Litak et al. [35] examined numerically two mistuned magneto-piezoelastic oscillators with electric coupling and they found a typical resonance curve due to non-synchronization. Dual cantilever energy harvesters coupled with magnets were designed and analyzed numerically and experimentally by Su et al. [37]. They reported a huge bandwidth improvement over conventional energy harvesters. The existence of co-bistable responses with double magnetically coupled energy harvesters was reported by Zhou et al. [38]. They analyzed the system numerically and experimentally and reported that the optimum distance between the energy harvesters can enhance the bandwidth. Enhancement of the harvester performance with pendulum energy harvesters has been reported [39, 40]. A double pendulum has also been analyzed for broadband energy harvesting [41]. Malaji et al. [42] reported initial results on the effect of coupling and initial conditions on energy harvester performance. Leng et al. [43] demonstrated random excitations with variable intensity can produce maximum power output and sufficient electro-mechanical energy conversion with elastic support systems. A two-degree-of-freedom energy harvester with magnetic levitation exhibited experimentally and numerically improved power output and operating bandwidth [44]. Alevras et al. [45] investigated the dynamics of a nonlinear vibration energy harvester for rotating systems using harmonic balance and numerical analysis. They modeled the system as a Duffing oscillator. They reported a novel structure of multiple resonant zones having mono-stable and bi-stable dynamics with variations in stiffness and asymmetric forcing. Time-delayed feedback control was reported by Yang and Cao [46]. This technique stabilized unstable periodic orbits of the attractor under harmonic excitation to enhance the output power. They also reported that time delayed feedback control can enhance the stochastic resonance phenomenon. Iliuk et al. [47] proposed a pendulum controller for a nonideal portal frame energy harvester. This passive control method enhanced the energy harvested along with the elimination of chaotic motion.

An axially loaded beam energy harvester with an oscillator was considered to induce internal resonance by Jaing et al. [48]. The method of multiple scales was used to obtain solutions. They demonstrated that internal resonance is beneficial to improve the bandwidth of the energy harvester. Similarly, an internal resonance system comprising a two-degree-of-freedom airfoil with piezoelectric coupling was analyzed using the method of multiple scales by Liu et al. [49] to provide design insights. Rocha et al. [50, 51] considered a pendulum controller for a portal frame harvester with a two-to-one internal resonance to eliminate active control complexities [52, 53] and enhance the energy harvesting band. Fan et al. [54] presented a theoretical and experimental demonstration of a two-to-one internal resonance of a U-shaped harvester to harvest energy at low vibration levels.

The above research has demonstrated the ability of multiple/multi-mode harvesters to enhance the frequency bandwidth. However, only a few investigations on the effect of mechanical coupling on the energy harvested were carried out.

Therefore, this paper investigates the feasibility of harvesting from the pendulum energy harvesters with mechanical torsional coupling. The main contributions of this paper are as follows; first, the effect of mechanical torsional coupling and length mistuning on magnitude and bandwidth is analyzed. Identifying the range of torsional coupling where energy harvesting from only one or both harvesters can be considered to enhance performance and save material cost. Finally, dynamic analysis and cross-recurrence plots are presented to show the feasibility of high-energy orbit harvesting.

These kinds of energy harvesters have found applications in wave energy harvesting, control and energy harvesting of offshore structures, energy harvesting from human motions, etc. More details can be found in a review paper by Fu et al. [55]

This paper is organized as follows. Section 2 gives the mathematical model of the harvester and the harmonic balance solution. In Sect. 3, the effect of parameters on the harvester dynamics is presented. Analytical results are presented in sect. 4. Finally, conclusions are given.

Harvester Model

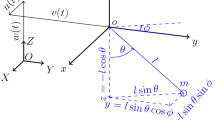
The mathematical model of the electro-mechanical system with torsionally coupled pendulums is reported in this section. Figure 1 shows the pendulums with lengths \(l_1\) and \(l_2\), masses \(m_1\) and \(m_2\) angular displacements \(\theta _1\), \(\theta _2\). The coupling between them is achieved by a torsional spring of stiffness \(k_c\) . These pendulums are connected to the shafts of the electromagnetic generators with a magnet attached to the pendulum as a rotor and coil as stator. Current i is generated due to electromagnetic induction whenever pendulum oscillates.

The physical realization of the coupled pendulums without harvesters can be found in the literature presented by Ikeda et al. [56] and Polczynski et al. [57]. A pendulum with stator rotar-based electromagnetic harvester was presented by Kecik and Mitura [58].

Fig. 1
figure 1

Schematic representation of the coupled harvester model

Full size image

The equations of motion of the pendulums are given as [42];

$$\begin{aligned} m_1l_1^2\ddot{\theta }_1 +c\dot{\theta }_1 +m_1 g l_1 \sin \theta _1+ k_c(\theta _1-\theta _2)-\phi i_1&=-m_1l_1 \ddot{x}_g \cos \theta _1, \nonumber \\ m_2l_2^2\ddot{\theta }_2 +c\dot{\theta }_2 +m_2 g l_2 \sin \theta _2+ k_c(\theta _2-\theta _1)-\phi i_2&=-m_2l_2 \ddot{x}_g \cos \theta _2, \end{aligned}$$
(1)

where c is the total damping constant, \(x_g\) is the excitation displacement, \(\phi\) is the magnetic field and overhead dot represents time derivative. In the next step, Kirchhoff’s voltage law is applied to the electrical circuits.

$$\begin{aligned}&\phi \dot{\theta }_1 -R_1i_1-L_1\dot{i}_1=0, \nonumber \\&\phi \dot{\theta }_2 -R_2i_2-L_2\dot{i}_2=0, \end{aligned}$$
(2)

where \(L_1,L_2\) are equivalent coil inductances, \(R_1=R_{c1}+R_{L1}\), \(R_2=R_{c2}+R_{L2}\) are total resistances. \(R_{c1},R_{c2}\) are coil resistances and \(R_{L1},R_{L2}\) are load resistances.

Assume that the coils are identical with \(L_1=L_2\), \(R_{c1}=R_{c2}=R_c\) and connected to identical load resistances of \(R_{L1}=R_{L2}=R_L\).

The power harvested across the resistances \(R_L\) is given as

$$\begin{aligned}&p_1=i_1^2R_L, \nonumber \\&p_2=i_2^2R_L. \end{aligned}$$
(3)

Multiple energy harvesters have been studied to enhance the power output and bandwidth [24, 59,60,61]. Liu et al. [59] compared the power obtained from energy harvester arrays when they are connected in series directly and connected in parallel with individual rectifier circuits. The directly connected configuration resulted in lower power compared to the rectified circuit due to phase lag. Similarly, Wang et al. [60] presented a method for energy harvesting from an array of piezoelectric harvesters with different circuits. They considered parallel connection through a single rectifier circuit, parallel connection through an individual rectifier circuit and a series circuit. Xiao et al. [61] considered a parallel circuit with individual rectifiers for an array of energy harvesters and concluded that the frequency range of total power, which is the sum of the product of individual voltage and current, was widened. Sari et al. [24] studied a micro-power generator for wideband power and showed that a better bandwidth can be harvested with an optimal number of energy harvesters and optimal length. When the power from different energy harvesters are combined the total power is always lower than the sum of the powers obtained from separate electrical circuits. Since this paper’s primarily contribution is to optimize the mechanical system, individual circuits are assumed, which gives an upper bound of the available harvested power. Hence, the bandwidth was calculated from overall power which is obtained by summing individual powers.

The total power is obtained by summing the individual powers.

$$\begin{aligned} p_t=p_1+p_2. \end{aligned}$$
(4)

For brevity, the dynamic model is nondimensionalized in the following simulation with the dimensionless parameters shown in Table 1

Table 1 Dimensionless parameters
Full size table

The corresponding non-dimensional electro-mechanical equations subjected to harmonic base excitation \(x_g=X_g cos (\omega t)\) are then

$$\begin{aligned}&\mu _1 \alpha _1^2 {\theta }''_1 + \gamma {\theta }'_1 + \alpha _1 \mu _1\sin \theta _1 + \beta (\theta _1 -\theta _2)-\psi I_1&= \mu _1 \alpha _1 f \omega ^2 \cos \omega \tau \cos \theta _1, \nonumber \\&\mu _2 \alpha _2^2 {\theta }''_2 + \gamma {\theta }'_2 + \mu _2 \alpha _2 \sin \theta _2 + \beta (\theta _2 -\theta _1) - \psi I_2&= \mu _2 \alpha _2 f \omega ^2 \cos \omega \tau \cos \theta _2 \end{aligned}$$
(5)

and

$$\begin{aligned} {\theta }'_1 -\zeta I_1- {I}'_1&=0, \nonumber \\ {\theta }'_2 -\zeta I_2-{I}'_2&=0. \end{aligned}$$
(6)

The mistuning in the system is introduced by varying length ratio \(\alpha _2\). The length of pendulum-1 is taken as a reference. Hence, \(\alpha _1=1\) always. The variation in mass ratio \(\mu _1\) or \(\mu _2\) does not introduce any mistuning as simple pendulum configuration is considered hence, \(\mu _1=\mu _2=1\) always. The mechanical coupling ratio \(\beta =0\) indicates an uncoupled pendulum system (absence of torsional spring).

Expressions in Eqs. (5) and (6) are nonlinear. To solve them numerically they are represented as

$$\begin{aligned} {X}'=f(X,t), \end{aligned}$$
(7)

where X is the state vector, given as \(X=\{\theta _1\quad {\theta _1}'\quad \theta _2\quad {\theta _2}'\quad I_1\quad I_2\}^T\) and f(X, t) is given as:

$$\begin{aligned} f(X,t)= \begin{bmatrix} x_2 \\ \frac{1}{\mu _1 \alpha _1^2} \{-\gamma x_2 - \alpha _1 \mu _1\sin x_1 - \beta (x_1 -x_3)-\psi x_5+\mu _1 \alpha _1 f \omega ^2 \cos \omega \tau \cos x_1\} \\ x_4 \\ \frac{1}{\mu _2 \alpha _2^2} \{-\gamma x_4 - \alpha _2 \mu _2\sin x_3 - \beta (x_3 -x_1)-\psi x_6+\mu _2 \alpha _2 f \omega ^2 \cos \omega \tau \cos x_3\}\\ x_2-\zeta x_5 \\ x_4-\zeta x_6 \end{bmatrix}. \end{aligned}$$

The non-dimensional power in terms of non-dimensional current I obtained from (7) can be expressed as

$$\begin{aligned} P_1&=I_1^2, \nonumber \\ P_2&=I_2^2, \nonumber \\ P_t&=P_1+P_2. \end{aligned}$$
(8)

Numerical Results and Discussion

This section presents the numerical results of the analytical formulation to study the effect of parameters on the harvested energy, bandwidth and dynamics of the pendulums. Nonlinear equations (5) and (6) of the harvesting system are solved numerically using Runge–Kutta integration as discussed in Eq. (7). The mass of each pendulum is assumed to be the same (\(\mu _1=\mu _2=1\)) as it does not affect the frequency. Other parameters \(\psi =0.1\), \(\gamma =0.025\), \(\alpha _1=1\) and \(f=0.04\) are kept constant throughout the simulation unless otherwise mentioned. Mechanical coupling ratio \(\beta\), length ratio \(\alpha _2\) and resistive coefficient \(\zeta\) are varied to study their effect on energy harvester performance.

Fig. 2
figure 2

Effect of mechanical coupling (\(\beta\)), \(\alpha _2=1.04\), \(\zeta =0.14\) and \(f=0.04\): a, b Current generated by pendulum-1 and pendulum-2, c, d Power generated by pendulum-1 and pendulum-2 , e Total Power. (The respective horizontal lines (bw) represent the bandwidth line at 10% of \(P_t\))

Full size image

Effect of Mechanical Coupling Ratio \(\beta\)

The effect of the mechanical coupling (torsional spring) on the current and power harvested is shown in Fig.2. The length ratio \(\alpha _2=1.04\) is considered to introduce mistuning in the system. \(\beta =0\) indicates uncoupled pendulums.

The mistuning in the length of the pendulums leads to two distinct natural frequencies for uncoupled case as shown in Figs. 2a, b. Response curves of both pendulums tend to bend towards a lower frequency, indicating a jump phenomenon due to spring softening. This spring softening is evident due to the presence of the \({\tt sin}\theta\) term in the restoring moment in Eq. (5). The reverse frequency sweep curves have higher current magnitude and covers more frequency range compared to forward sweep curves due to presence of hysteresis. The introduction of a coupling spring (\(\beta\)), converts the pendulums into a two degrees of freedom system, giving a bimodal response for each pendulum. This coupling will change the natural frequencies of the pendulums and hence a frequency shift of the response curves compared to the uncoupled pendulums can be observed. The increase in mechanical coupling tends to reduce the displacement of pendulums, and hence reduces hysteresis effect narrowing down the difference between forward and reverse sweep curves.

Figure 2c, d and e shows power generated by pendulum energy harvesters. Only forward sweep curves are considered to analyze minimum power harvested and frequency bandwidth with respect to mechanical coupling. With an increase in the coupling ratio \(\beta\), the second peak of the bimodal response of both pendulums moves away from the first peak. The maximum power harvested in pendulum-1 decreases, whereas it increases in pendulum-2 as shown in Fig. 2c and d. This increment in maximum power of pendulum-2 can be attributed to an energy transfer from pendulum-1 at the higher resonant frequency to pendulum-2 at the lower resonant frequency. The total power harvested from both pendulums is shown in Fig. 2e. The bandwidth (bw) of the energy harvesters is measured at 10% of the maximum of total power, \(P_t\) indicated by the respective horizontal lines. With increasing \(\beta\) the maximum power decreases whereas the frequency bandwidth enhances initially, and a further increase in \(\beta\) will increase the maximum power harvested with a reduction in the frequency band. To analyze the effect of length ratio \(\alpha _2\) and coupling ratio \(\beta\) on maximum power harvested and frequency band, contour plots are presented in Fig. 3.

Fig. 3
figure 3

Effect of length (\(\alpha _2\)) and coupling spring (\(\beta\)) on maximum power harvested and frequency bandwidth at \(P_t=10\%\) of peak, a \(P_{1max}\), b \(P_{2max}\), c \(P_{tmax}\), d,e,f) bandwidth of pendulum-1, pendulum-2 and total power at \(P_t=10\%\) of peak. (\(\zeta =0.14\) and \(f=0.04\))

Full size image

Figure 3a–c shows the maximum power harvested from pendulum-1, pendulum-2 and the maximum total power at different length ratios (\(\alpha _2\)) and mechanical coupling ratio (\(\beta\)). Maximum powers harvested are 0.7, 0.7 and 1.3 from pendulum-1, pendulum-2 and total power, respectively, with different parameter combinations (\(\alpha _2\) and \(\beta\)). The frequency band at 10% of the maximum of total power \(P_t\) is shown in Fig. 3d–f for pendulum-1, pendulum-2 and the total power, respectively. Maximum bandwidths of 0.18, 0.23 and 0.33 for pendulum-1, pendulum-2 and band of total power, respectively, are observed.

Figure 3a shows the variation of the maximum power with length ratio and coupling ratio of pendulum-1. A combination of lower coupling and length ratio gives more power compared to high coupling and high length ratio. An increase in length ratio or coupling ratio alone does not change the maximum power harvested at the lower coupling ratio or length ratio, respectively. But as the coupling ratio increases with increase in length ratio, energy transfers from pendulum-1 to pendulum-2, reducing the intensity of maximum power harvested of the former. Figure 3d shows the frequency bandwidth of pendulum-1. The maximum frequency band of 0.09 appears in the stripe \(\alpha _2\) [1.01–1.06] and \(\beta\) [0.01–0.02]. The region of maximum power and maximum frequency band do not coexist due to the conservation of energy.

Figure 3b shows the maximum power harvested by pendulum-2. Unlike pendulum-1, pendulum-2 has many zones of peak power. In these regions of peak power, pendulum-1 has the lowest performance as discussed above. The parameter region \(\alpha _2\) [1.02–1.09] and \(\beta\) [0.06–0.09] has highest bandwidth (0.12–0.14) as shown in Fig 3e. There exists a narrow region where one can harvest the peak power and the higher frequency bandwidth.

Figure 3c shows the variation in the maximum total power harvested with a change in length ratio and coupling ratio. An increase in coupling ratio increases the maximum total power at any length ratio. This is due to energy localization introduced by coupling. A lower length ratio gives a better magnitude of maximum power. Total bandwidth has its maximum when total power harvested is low as shown in Fig. 3f.

Harvesting maximum energy and higher frequency band simultaneously is not possible. One needs to find the trade-off between these objectives to optimize the harvester performance. Accordingly, the length ratio of 1.06 is selected to analyze the effect of the coupling ratio \(\beta\) on the maximum power and frequency band of pendulum-1, pendulum-2 and the total power as shown in Fig. 4.

Fig. 4
figure 4

Effect of coupling spring (\(\beta\)) on a power generated, b on frequency band at \(P=0.1\), \(\alpha _2=1.06\), \(\zeta =0.14\) and \(f=0.04\)

Full size image

The variation of maximum power and frequency band with coupling \(\beta\) can be categorized into 3 zones as shown in Fig. 4. The ranges for Zones I, II and III of maximum power are \(\beta\) [0–0.059], \(\beta\) [0.06–0.11] and \(\beta\) above 0.11, respectively (refer Fig. 4a, b). In Zone-I total power \(P_{tmax}\) and the total band are dominating over pendulum-1 and pendulum-2 as expected as shown in Fig. 4a, b. Undulations in the maximum total power with \(\beta\) can be observed as shown in Fig. 4a. This undulation in total power is due to variation in the peak power of pendulum-1 (Refer Fig.  2a) with a change in mechanical coupling.

In Zone-II, the performance of pendulum-2 is comparable with the total performance. In contrast, the performance of pendulum-1 is low. The difference in maximum total power \(P_{tmax}\) and \(P_{2max}\) varies between 10 and 15%. Whereas, the difference in bandwidth varies between 6 and 20%. In this zone, there is a drop of 10% in the total power and an increase of 25% in the total band compared to uncoupled pendulums. Pendulum-2 shows an increment of 39% in power and 75% in bandwidth. This enhancement in pendulum-2 counteracts the energy loss in pendulum-1. Saturation of maximum power and bandwidth can be observed in Zone-III. A slight increase in total power compared to uncoupled pendulums can be observed with the decrease in bandwidth.

From a designer’s point of view, Zone-II plays an important role for a given length ratio. In this zone, the performance of pendulum-2 is nearer to that of the total performance. One can choose to harvest power only from pendulum-2 and use pendulum-1 as an auxiliary oscillator. This will reduce the cost of the magnet and coil components and also reduces the electrical damping. This might further enhance the performance of pendulum-2. If one wants to harvest peak power irrespective of the frequency band, Zone-III can be selected with harvesting from both pendulums and adding them.

Dynamic Analysis of Pendulum Energy Harvesters

The dynamics of the two pendulum energy harvesters are presented in this section. Figure 5 shows the bifurcation diagrams of the current in pendulum-1 and pendulum-2 for the coupling ratio \(\beta\) at \(\omega =0.92\) and \(f=0.04\). Pendulum-1 exhibits low-magnitude periodic oscillations with smaller coupling ratios. High-magnitude quasi-periodic /chaotic oscillations can be observed for values of \(\beta\) [0.03–0.107] and beyond which again it enters low periodic oscilations as shown in Fig. 5a. Similar dynamics is observed for pendulum-2 as shown in Fig. 5b. This indicates that the mechanical coupling brings in rich dynamics into the energy harvesters.

Fig. 5
figure 5

Bifurcation diagrams of the current output as a function of coupling spring \(\beta\) at \(\omega =0.92\). \(\zeta =0.13\), \(\alpha _2=1.06\) and \(f=0.04\)

Full size image

The phase portraits and Poincare map corresponding to Fig. 5 at \(\beta =0\), 0.04 and 0.07 are shown in Fig. 6 which indicates quasiperiodic route to chaos. Figure 6a and d show phase portraits for angular velocity against angular displacement for pendulum-1 and pendulum-2 at \(\beta =0\). Pendulums 1 and 2 exhibit a periodic oscillation and a single Poincare point confirms this. A low-amplitude quasi-periodic response of pendulum-1 and high-amplitude quasi-periodic response of pendulum-2 can be observed for \(\beta =0.04\) as shown in Fig. 6b and e. Both pendulums exhibit high-amplitude chaotic response at \(\beta =0.07\) as shown in Fig. 6c and f.

The introduction of coupling induced nonlinearity in both pendulums. the amplitude and velocity also increased due to the quasi-periodicity and chaos induced in pendulums due to the coupling and better energy harvesting capabilities can be expected.

Fig. 6
figure 6

Phase portraits and Poincare maps (red and black dots) \(\alpha _2=1.06\), \(\zeta =0.13\) and \(f=0.04\): a, d \(\beta =0\), b, e \(\beta =0.04\), c, f \(\beta =0.07\)

Full size image
Fig. 7
figure 7

Bifurcation diagrams of the current output as a function of resistive coefficient \(\zeta\). \(\beta =0.07\), \(\alpha _2=1.06\) and \(f=0.04\)

Full size image
Fig. 8
figure 8

Phase portraits and Poincare maps \(\alpha _2=1.06\), \(\beta =0.07\) and \(f=0.04\): a, d \(\zeta =0.01\), b, e \(\zeta =0.07\), c, f \(\zeta =0.13\)

Full size image

Figure 7 shows the bifurcation diagrams of the current in pendulum-1 and pendulum-2 with respect to the resistive coefficient \(\zeta\) at \(\omega =0.92\) and \(\beta =0.07\). Both pendulum energy harvesters enter high-magnitude quasi-periodic/chaotic oscillations from low-magnitude periodic oscillations when \(\zeta >0.041\). The phase portraits for solutions on Fig. 7 at \(\zeta =0.01\), 0.07 and 0.13 are shown in Fig. 8. Figure 8 (a) and (d) shows phase portraits and Poincare maps for angular velocity against angular displacement for pendulum-1 and pendulum-2 at \(\zeta =0.01\). Low-magnitude periodic oscillations can be observed for pendulum-1 whereas, pendulum-2 exhibits high-amplitude periodic oscillations. A torus-shaped phase plot and closed orbit Poincare section on the phase plot indicates quasi-periodic oscillations of both pendulums at higher values of \(\zeta =0.07\) with high-amplitude current magnitude as shown in Fig. 8(b, e). A high-amplitude chaotic response is observed at higher value of \(\zeta =0.13\) as shown in Fig. 8(c, f). The higher resistive coefficient can induce the nonlinearity in both pendulums. The amplitude and velocity also increased due to the quasi-periodicity and chaos induced in both the pendulum energy harvesters when \(\zeta >0.041\).

Cross-Recurrence Plots

The cross-recurrence plots (CRP) [62, 63] method was used to analyze relations between two pendulum energy harvesters by comparing their states. If \(\textbf{x}_i\) and \(\textbf{y}_j\) are the two dynamical systems trajectories in the m-dimensional phase space, the cross recurrence is defined as:

$$\begin{aligned} CR_{ij}&=\Theta (\epsilon _i \Vert {\textbf{x}_i-\textbf{y}_j}\Vert ) \nonumber \\&\quad i,j=1....N. \end{aligned}$$
(9)

The recurrence rate describes density of the recurrence points and is defined as;

$$\begin{aligned} RR=\frac{1}{N^2}\sum _{i,j=1}^{N} CR_{ij}. \end{aligned}$$
(10)

Figure 9 shows orbits \(\theta _1\) versus \(\theta _2\) (\(\theta _1-\theta _2\)) and cross-recurrence plots for different coupling ratios. The threshold value of \(\epsilon =0.04\) is used to cover sufficient recurrences. Here, we used the original phase space coordinates (angular displacement and velocity) normalized to the size of attractors by the corresponding standard deviations. The enclosed symmetric \(\theta _1-\theta _2\) plot and long diagonal lines away from the main diagonal line in CRP in Fig. 9a of uncoupled pendulums (\(\beta =0\)) exhibits out of phase synchronization because of mistuned lengths. With the introduction of coupling (\(\beta =0.04\)) the two pendulums are asynchronous as indicated by Fig. 9b irregular \(\theta _1-\theta _2\) plot and short diagonal CRP. However, with an increase in the coupling (\(\beta =0.18\)), two pendulums will be in in-phase synchronous motion as shown in Fig. 9c with a diagonal line in \(\theta _1-\theta _2\) plot and long diagonal lines along with the main diagonal line in the CRP. The similar recurrence rate of 0.044 for \(\beta =0.04\) and 0.18 also confirms synchronization. Coupling of the pendulum energy harvesters changes the synchronization state and harvesting capabilities. Synchronized pendulums can harvest maximum power, whereas better bandwidth can be obtained from asynchronised pendulums (refer Fig 4). Generally, synchronization is stronger for nonlinear systems with respect to linear systems and influences the power output substantially.

Fig. 9
figure 9

\(\theta _1-\theta _2\) plots and cross-recurrence plots between pendulums corresponding to Fig. 6a \(\beta =0\), b \(\beta =0.04\), c \(\beta =0.18\). i, j enumerate the time series elements

Full size image

Analytical Results to Identify High-Energy Orbits

This section presents analytical results using the Harmonic Balance Method to identify high-energy orbits in different zones of Fig. 4.

The cos\(\theta\) and sin\(\theta\) terms in Eq. (5) are expanded up to cubic terms to obtain

$$\begin{aligned}&\mu _1 \alpha _1^2 {{\theta }_1}'' + \gamma _1 {{\theta }_1}' + \left( \mu _1 \alpha _1 + \beta \right) \theta _1 - \beta \theta _2 - \frac{1}{6} \mu _1 \alpha _1 \theta _1^3 \nonumber \\&\quad +\frac{1}{2} \mu _1 \alpha _1 f \omega ^2 \theta _1^2 \cos \omega \tau - \Psi I_1 = \mu _1 \alpha _1 f \omega ^2 \cos \omega \tau \nonumber \\&\mu _2 \alpha _2^2 {{\theta }_2}'' + \gamma _2 {{\theta }_2}' + \left( \mu _2 l_2 + \beta \right) \theta _2 - \beta \theta _1 - \frac{1}{6} \mu _2 l_2 \theta _2^3 \nonumber \\&\quad +\frac{1}{2} \mu _2 \alpha _2 f \omega ^2 \theta _2^2 \cos \omega \tau - \Psi I_2 = \mu _2 \alpha _2 f \omega ^2 \cos \omega \tau. \end{aligned}$$
(11)

The following solutions for the fundamental swinging harmonic motions are assumed for the angular displacement and current

$$\begin{aligned} \theta _1&= a_1 (\tau) \sin \omega \tau + b_1 (\tau) \cos \omega \tau, \nonumber \\ \theta _2&= a_2 (\tau) \sin \omega \tau + b_2 (\tau) \cos \omega \tau, \nonumber \\ I_1&= a_3 (\tau) \sin \omega \tau + b_3 (\tau) \cos \omega \tau, \nonumber \\ I_2&= a_4 (\tau) \sin \omega \tau + b_4 (\tau) \cos \omega \tau. \end{aligned}$$
(12)

From Eqs. (6) and (12), neglecting higher-order derivatives and balancing \(\cos \omega \tau\) and \(\sin \omega \tau\) terms one can obtain

$$\begin{aligned} a_3&= - \frac{ \omega \left( - \omega a_1 (\tau) + \zeta b_1 (\tau) \right) }{ \zeta ^2 + \omega ^2 }, \nonumber \\ b_3&= \frac{ \omega \left( \zeta a_1 (\tau) + \omega b_1 (\tau) \right) }{ \zeta ^2 + \omega ^2 }, \nonumber \\ a_4&= - \frac{ \omega \left( - \omega a_2 (\tau) + \zeta b_2 (\tau) \right) }{ \zeta ^2 + \omega ^2 }, \nonumber \\ b_4&= \frac{ \omega \left( \zeta a_2 (\tau) + \omega b_2 (\tau) \right) }{ \zeta ^2 + \omega ^2 }. \end{aligned}$$
(13)

Substituting Eqs. (12) and (13) into Eq. (5), neglecting higher order derivatives, setting time derivatives to zero and balancing \(\cos \omega \tau\) and \(\sin \omega \tau\) terms, one can obtain the nonlinear algebraic equations in terms of \(a_i\) and \(b_i\) as

$$\begin{aligned}&- \frac{1}{8} \mu _1 \alpha _1 \left( a_1^3 + b_1^2 a_1 \right) + \frac{1}{4} f \omega ^2 \mu _1 \alpha _1 b_1 a_1 \nonumber \\&\quad +\frac{\omega ^2 \left( - \mu _1 \alpha _1^2 \omega ^2 + \beta - \Psi - \zeta ^2 \alpha _1^2 \mu _1 + \mu _1 \alpha _1 \right) a_1}{ \omega ^2 + \zeta ^2} + \frac{ \zeta ^2 \left( \mu _1 \alpha _1 + \beta \right) a_1}{ \omega ^2 + \zeta ^2 } \nonumber \\&\quad + \frac{ \omega \left( - \gamma _1 \omega ^2 + \zeta \left( - \gamma _1 \zeta +\Psi \right) \right) b_1 }{ \omega ^2 + \zeta ^2} - a_2 \beta = 0 \nonumber \\&\quad - \frac{1}{8} \mu _1 \alpha _1 \left( b_1^3 + a_1^2 b_1 \right) + \frac{1}{8} f \mu _1 \alpha _1 \omega ^2 \left( 3 b_1^2 + a_1^2 \right) \nonumber \\&\quad +\frac{ \omega ^2 \left( 8 \beta - 8 \Psi - 8 \zeta ^2 \alpha _1^2 \mu _1 + 8 \mu _1 \alpha _1 + \zeta ^2 \left( \mu _1 \alpha _1 + \beta \right) ^2 \right) b_1}{ \omega ^2 + \zeta ^2 } \nonumber \\&\quad -\frac{ \omega \left( - \gamma _1 \omega ^2 + \zeta \left( - \gamma _1 \zeta + \Psi \right) \right) a_1}{ \omega ^2 + \zeta ^2 } - f \omega ^2 \mu _1 \alpha _1- b_2 \beta = 0 \nonumber \\&\quad - \frac{1}{8} \mu _2 \alpha _2 \left( a_2^3 + b_2^2 a_2 \right) + \frac{1}{4} f \omega ^2 \mu _2 \alpha _2 b_2 a_2 \nonumber \\&\quad +\frac{ \omega ^2 \left( - \mu _2 \alpha _2^2 \omega ^2 + \beta - \Psi - \zeta ^2 \alpha _2^2 \mu _2 + \mu _2 \alpha _2 \right) a_2 }{ \omega ^2 +\zeta ^2 } + \frac{ \zeta ^2 \left( \mu _2 \alpha _2 + \beta \right) a_2 }{ \omega ^2 + \zeta ^2 } \nonumber \\&\quad +\frac{ \omega \left( - \gamma _2 \omega ^2 + \zeta \left( - \zeta \gamma _2 + \Psi \right) \right) b_2}{\omega ^2 + \zeta ^2 } - a_1 \beta = 0 \nonumber \\&\quad - \frac{1}{8} \mu _2 \alpha _2 \left( b_2^3 + a_2^2 b_2 \right) + \frac{1}{8} f \mu _2 \alpha _2 \omega ^2 \left( 3 b_2^2 + a_2^2 \right) \nonumber \\&\quad +\frac{ \omega ^2 \left( 8 \beta - 8 \Psi - 8 \zeta ^2 \alpha _2^2 \mu _2 + 8 \mu _2 \alpha _2 + \zeta ^2 \left( \mu _2 \alpha _2 + \beta \right) ^2 \right) b_2 }{ \omega ^2 + \zeta ^2 } \nonumber \\&\quad -\frac{ \omega \left( - \gamma _2 \omega ^2 + \zeta \left( - \gamma _2 \zeta +\Psi \right) \right) a_2}{ \omega ^2 + \zeta ^2 } - f \omega ^2 \mu _2 \alpha _2 - b_1 \beta = 0. \end{aligned}$$
(14)

Equation (14) gives the simultaneous, nonlinear algebraic equations for \(a_i\) and \(b_i\). Solving these equations gives the steady-state solutions.

The steady-state amplitudes of the angular displacements and currents are

$$\begin{aligned} \Vert \theta _1 \Vert&= \sqrt{a_1^2+b_1^2}, \nonumber \\ \Vert \theta _2 \Vert&= \sqrt{a_2^2+b_2^2}, \nonumber \\ \Vert I_1 \Vert&= \sqrt{a_3^2+b_3^2}, \nonumber \\ \Vert I_2 \Vert&= \sqrt{a_4^2+b_4^2}. \end{aligned}$$
(15)

The stability of the steady-state solutions can be verified by considering small perturbations from the solution.

Fig. 10
figure 10

a, b Current output from uncoupled pendulums (\(\beta =0\)) (Forward, Reverse-Numerical results, Stable, Unstable-Harmonic Balance Method results), c Basins of attraction, d current time history \(\alpha _2=1.06\), \(\zeta =0.13\) and \(f=0.04\)

Full size image
Fig. 11
figure 11

a, b Current output from coupled pendulums (\(\beta =0.06\)), c Basins of attraction, d current time history \(\alpha _2=1.06\), \(\zeta =0.13\) and \(f=0.04\)

Full size image
Fig. 12
figure 12

a, b Current output from coupled pendulums (\(\beta =0.18\)), c Basins of attraction, d current time history \(\alpha _2=1.06\), \(\zeta =0.13\) and \(f=0.04\)

Full size image

Figure 10 presents the current–frequency response and basin of attraction for uncoupled pendulums \(\beta =0\) (from Zone-I of Fig. 4). Figures 10 (a) and (b) shows frequency response curves obtained by Harmonic Balance Method and numerical simulations (forward and reverse sweep curves). Blue dots represent the stable solution and unstable regions are represented by red dots. The numerical results with zero initial conditions are shown by black circles. The parameters used are; \(\alpha =1.06\), \(\zeta =0.13\) and \(f=0.04\). The numerical results are in good agreement with the Harmonic Balance results.The soft-spring characteristics in the frequency response curves can be observed with curves bending towards the low-frequency direction with 2 stable and 1 unstable steady-state solutions. A qualitative match between numerical and Harmonic balance Method results can be observed. The difference in these results is due to the effect of initial conditions considered during frequency sweeps. Beyond a certain frequency, the high-amplitude numerical solution does not exist in contrast to the Harmonic Balance analysis. The harmonic balance analysis indicates that there is a possibility of obtaining a high-amplitude current at lower frequencies provided proper initial conditions are chosen.

To check the possibilities of obtaining the high-amplitude solution at lower frequencies, a basin of attraction of the current amplitude is shown in Fig. 10c for \(\omega =0.85\) with the variation in initial conditions of pendulum-1 in a grid of 200\(\times\)200. The initial conditions of pendulum-2 are kept at zero. The solution pertaining to different branches for each set of initial conditions is color coded. A large set of initial conditions gives solution branch B indicating the possibility of obtaining high-energy orbit solutions. Figure 10d shows the effect of optimal initial conditions on the current magnitude. Pendulum-1 exhibits a significant enhancement with optimal initial conditions. No change in pendulum-2 performance is observed as its initial conditions are kept at zero and is unconnected from pendulum-1.

With the introduction of the coupling \(\beta =0.06\) (Zone-II), the system will be converted into a coupled two-degree-of-freedom system which can also be observed in the responses in the form of a second peak in both pendulum response curves as shown in Fig. 11 a and b. The variation of the current magnitude with \(\beta\) will take place as discussed in the previous section. There are 4 stable and 3 unstable steady-state solutions. An interesting phenomenon can be observed from the response curve of pendulum-1, where an isolated closed loop (with stable and unstable part) corresponding to high amplitudes coexists with low-amplitude responses at a lower frequency, similar to the frequency island phenomenon [64]. The existence of these frequency islands depends on the initial conditions. A basin of attraction of the current amplitude is shown in Fig. 11 c at \(\omega =0.85\). The basin of attraction is dominated by solution branch A and a narrow zone of initial conditions exists where one can obtain the solution branch B. The probability of obtaining a high-energy orbit solution is small compared to uncoupled pendulums (Fig. 10). Due to the coupling, enhancement in the performance of both energy harvesters at optimal initial conditions can be seen from Fig. 11d. The performance of pendulum-2 dominates compared to pendulum-1 with optimal initial conditions and hence harvesting from only pendulum-2 is preferable in this Zone-II as discussed earlier.

The isolated islands move away (towards low-frequency zone) from the main curve with an increase in mechanical coupling (\(\beta\)=0.18, Zone-III) as shown in Fig. 12a and b. The probability of obtaining a high-energy orbit solution reduces with the increase in coupling ratio as shown in Fig. 12c. At the optimal initial conditions, both the pendulums show enhancement in harvesting capability as shown in Fig. 12d. Hence in Zone-III, harvesting from both the pendulums is feasible with any set of initial conditions.

The performance of energy harvesters can be enhanced by choosing optimal initial conditions in the respective zones as reported in Malaji et al. [42]. Experimental realization of increase in pendulum amplitude was reported by Ikeda et al. [56]. This kind of setup can also be used to enhance energy harvesting.

Fig. 13
figure 13

Effect of resistance coefficient (\(\zeta\)) on the current generated, \(\alpha =1.06\), \(\beta =0.18\) and \(f=0.04\): a, d \(\zeta =0.05\), b, e \(\zeta =0.1\), c, f \(\zeta =0.13\)

Full size image

The variation of the current response with the resistance coefficient \(\zeta\) is shown in Fig. 13. Enhanced performance and frequency island formation can be observed when the resistance coefficient \(\beta\) is near to the coupling coefficient \(\psi\).

Fig. 14
figure 14

Effect of length ratio (\(\alpha _2\)) on the current generated, \(\beta =0.18\), \(\zeta =0.13\) and \(f=0.04\): a, d \(\alpha _2=1\), b, e \(\alpha _2=1.06\), c, f \(\alpha =1.08\)

Full size image

To study the effect of length ratio \(\alpha _2\) on the system behavior, \(\alpha _2\) is varied between 1 to 1.08. Figure 14 shows the effect of the length ratio on the system. When \(\alpha _1=\alpha _2=1\) both pendulums exhibit similar behavior with a single peak as the coupling spring does not twist and the pendulums are subjected to the same forcing as shown in Fig. 13a with d. The mistuning in the length introduces a second peak and isolated islands as shown in Fig. 13(b, e) with (c, f). The islands move away from the primary response curves with the increase in \(\alpha _2\)

Fig. 15
figure 15

Effect of coupling spring (\(\beta\)) on the current generated vs excitation amplitude at \(\omega =0.89\), \(\alpha =1.04\), \(\zeta =0.13\) and \(f=0.04\): a, d \(\beta =0\), b, e \(\beta =0.06\), c, f \(\beta =0.18\)

Full size image

The current–amplitude responses at different excitation amplitudes f are plotted in Fig. 15. For uncoupled pendulums \(\beta =0\) (Zone-I), as excitation amplitude increases, the current response is stable until f reaches f=0.02 for pendulum-1 and f=0.01 for pendulum-2. In the range 0.02<f<0.05 for pendulum-1 and 0.01<f<0.03 for pendulum-2, the system loses stability. Further increase in f results in stable responses as shown in Fig. 15 (a) and (d). When \(\beta\) is increased to 0.06 (Zone-II), both pendulums will have 2 stable and one unstable solution for f=0.01 and 0.2<f<0.25, 3 stable and 2 unstable solutions in the range 0.02<f<0.09 and 4 stable and 3 unstable solutions in the range 0.1<f<0.19 as shown in Fig. 15 (b) and (e). A similar trend for \(\beta =0.18\) (Zone-III) can be seen with a different range of f as shown in Fig. 15 (c) and (f).

Conclusion

A twin electromagnetic pendulum energy harvester with torsional coupling is analyzed to optimize the efficient energy harvesting and study the energy harvester dynamics. The paper categorized the three distinct zones based on the coupling ratio \(\beta\) and length ratio \(\alpha _2\). One can select parameters from these zones based on need. Zones II and III are the most promising zones. If one wants to harvest broader energy Zone-II is preferable with harvesting only from the energy harvester with a low resonant frequency which in turn saves material cost. To harvest peak power one can select Zone-III and harvest from both energy harvesters. The performance in the respective zones can be further enhanced using optimal initial conditions to obtain high-energy orbits at lower frequencies. The probability of obtaining high-energy orbits decreases with an increase in the coupling ratio. The effect synchronization with coupling on energy harvesting plays an important role form magnitude and bandwidth point of view. The analytical results obtained by the Harmonic Balance Method are in good agreement with numerical results.

The proposed concept can be useful for low-frequency sources to harvest power at wider frequency bandwidths. This idea can be further extended to metastructure energy harvesters with multiple pendulums to cover a wide frequency spectrum. The passive nature of pendulum metastructures in achieving the wider bandwidth is advantageous for practical implementation.