The Delayed van der Pol Oscillator and Energy Harvesting

Abstract

In the first part of the chapter, we present some results on quasi-periodic (QP) vibration-based energy harvesting (EH) in a delayed van der Pol oscillator with modulated delay amplitude. Two examples are considered which include a delayed van der Pol harvester coupled either to a delayed or undelayed electromagnetic sub- system. The influence of delay parameters on the performance of the harvester has been examined. It is shown that a maximum amplitude of the response does not induce necessarily a maximum output power. In the second part, we investigate QP vibration-based EH in the case where the van der Pol oscillator is subjected to external harmonic excitation and coupled to a delayed piezoelectric component. Perturbation method is applied near a resonance to obtain approximation of the periodic and QP responses as well as the amplitude of the harvested powers. To guarantee the robustness of the QP vibration during energy extraction operation, a stability anal- ysis is performed and the QP stability chart is determined. Results show that in the presence of time delay in the electrical circuit of the excited van der Pol oscillator, it is possible to harvest energy from QP vibrations with a good performance over a broadband of system parameters away from the resonance. Numerical simulations are conducted to support the analytical predictions.

4.1 Introduction

One of the major goals of using quasi-periodic (QP) vibrations to scavenge energy, usually made away from the resonance, is to improve the stability range and robustness of the energy harvester device which is not always secured when operating in the vicinity of the considered resonance. Indeed, when the harvester is operating in the linear regime, its best performance is achieved traditionally at the resonance peak with large-amplitude oscillations. However, such large-amplitude oscillations are obtained only in a narrow region located around the peak, thus limiting considerably the performance of the harvester device; see for instance [1,2,3,4]. In the nonlinear regime, on the other hand, energy harvesting (EH) capability can be improved by extending the bandwidth of the harvester over broadband of the excitation frequency. A major inconvenient is that the instability phenomenon induced in the nonlinear frequency response can reduce substantially the system performance when the response is attracted to the low-amplitude motions or when it suffers jump phenomena, as shown in [5]. Thus, the idea emerged from such a limitation is to use the possibility of harvesting energy from vibrations away from the resonance thereby circumventing instabilities. Under certain conditions, QP regime with large amplitude when present away from the resonance may constitute a good candidate.

A simple way to harvest energy in the QP regime away from the resonance is to consider self-induced vibrations represented by limit-cycle (LC) oscillations. Under certain conditions (for instance the presence of additional frequency in the system), the steady-state LC oscillations may lose stability via a secondary Hopf bifurcation producing QP vibrations. However, it is known that the amplitude of such QP vibrations occurring away from the resonance is smaller compared to that of the periodic ones; see for instance [6, 7]. In this case the harvester suffers a substantial reduction in the harvested power indicating that the QP regime should be avoided. For instance, in energy harvester systems subjected to combined aerodynamic and base excitations, it was observed that beyond the flutter speed, the QP response of the harvester leads to a substantial drop of the output power [8, 9]. However, in a recent work by Hamdi and Belhaq [10] it was reported analytically and using numerical simulations that in the delayed van der Pol oscillator with modulated delay amplitude, large-amplitude QP vibrations (larger than the periodic ones) performing in broader range of parameters can take place. This analytical finding has been first exploited by Belhaq and Hamdi [11] to demonstrate the possibility to scavenge energy directly from QP vibrations over a broadband of modulation frequency away from the resonance with a good performance. Later, Ghouli et al. [12] investigated QP vibration-based EH in a forced and delayed Duffing harvester device considering an electromagnetic coupling with time delay [13]. More recently, the problem of QP vibration-based EH in a Mathieu-van der Pol-Duffing MEMS device using time delay was studied in [14]. Other variants on the topic have been examined in [15, 16]. The conclusion emerged from these previous works was that for appropriate values of delay parameters, QP vibration-based EH can be used to extract energy over a broadband of excitation frequencies away from the resonance with good performance, thereby circumventing bistability and jump phenomena near the resonance.

The objective of this work is to provide, in a first part, a review on the main results obtained on the QP vibration-based EH in a van der Pol harvester and then investigate, in a second part, EH in a van der Pol oscillator subject to harmonic excitation and coupled to a delayed piezoelectric mechanism.

The chapter is organized as follows: In Sect. 4.2 we present a review on the recent results on QP vibration-based EH in a van der Pol oscillator with time-periodic delay amplitude coupled either to undelayed electromagnetic component or to delayed electromagnetic one. Section 4.3 investigates QP vibration-based EH in a forced van der Pol oscillator coupled to a delayed piezoelectric element. Approximations of the periodic response and the amplitude of the output power near the primary resonance are given using the multiple scales method. Section 4.4 provides approximation of the QP response and the corresponding harvested power applying the second-step multiple scales method. The influence of time delay parameters in the electrical circuit on the EH performance is analyzed. A summary of the results is given in the concluding section.

4.2 The van der Pol Oscillator and Energy Harvesting

The concept of harvesting energy from QP vibrations is demonstrated in this section through two examples. Namely, a delayed van der Pol oscillator coupled to undelayed or delayed electromagnetic component. First, consider a delayed pure van der Pol oscillator with time-periodic delay amplitude studied by Hamdi and Belhaq [10]. The authors analyzed the influence of the modulated time-delay amplitude on the response of the following van der Pol oscillator with time delay in the position and velocity

$$\begin{aligned} \ddot{x}+x-\varepsilon (\alpha -\beta x^2)\dot{x}-\varepsilon \lambda (t) x(t-\tau )-\varepsilon \lambda _3\dot{x}(t-\tau ) =0 \end{aligned}$$

(4.1)

where $\varepsilon$ is a small positive parameter, $\alpha$, $\beta$ are damping coefficients, $\lambda (t)$, $\lambda _3$ are delay amplitudes in the position and velocity, respectively, and $\tau$ is the time delay. An overdot denotes differentiation with respect to time t. Equation (4.1) can model ambient sustained self-excited vibrations under a delayed feedback control. Examples includes, for instance, controlled vibration produced by high speed rotating machines or regenerative effects in cutting processes [17,18,19]. To generate a resonant condition and guarantee the occurrence of QP vibrations, it was assumed that the delay amplitude in the position $\lambda (t)$ is time-periodic around a nominal value $\lambda _1$, such that

$$\begin{aligned} \lambda (t)=\lambda _1+\lambda _2\cos \,\omega t \end{aligned}$$

(4.2)

where $\lambda _2$ and $\omega$ are the amplitude and the frequency of the modulation. The nominal value $\lambda _1$ being the unmodulated delay amplitude. The case of delay parametric resonance for which the frequency $\omega$ of the modulation is near twice the natural frequency of the oscillator was considered. This resonance imposes the condition $1=(\frac{\omega }{2})^{2}+\varepsilon \sigma$ where $\sigma$ is the detuning parameter.

Fig. 4.1

a Stability chart of the QP response in the parameter plane $(\lambda _1, \tau )$; $\omega =2.1$ and $\lambda _2=0.8$, LC: Limit cycle, TS: trivial solution, b time histories corresponding to different regions [10]

The periodic response near this delay parametric resonance is approximated using the averaging method [20] and the amplitudes of the QP vibrations are obtained applying the second-step multiple scales method [22].

Figure 4.1a provides the stability chart of the QP vibrations in the parameter plane ($\lambda _{1}, \tau$) and Fig. 4.1b shows time histories corresponding to different regions of Fig. 4.1a. The transitions of solutions are shown by moving between the crosses 1, 2, 3 and 4 in Fig. 4.1a. For instance, between cross 2 and cross 1 the response of the system undergoes a transition between no oscillation and QP vibration which is a bifurcation of a trivial stable equilibrium point to a stable QP solution. From cross 2 to 3 Hopf bifurcation takes place leading to periodic response and from cross 3 to 4 the solution bifurcates from periodic to QP oscillation, and from cross 3 to 1 similar bifurcation occurs via a secondary Hopf bifurcation.

Fig. 4.2

Variation of periodic and QP responses versus $\lambda _1$ [10]

In Fig. 4.2 is shown the variation of periodic and QP repones versus $\lambda _1$ for $\lambda _3=\lambda _1$, $\lambda _2=0.8$ and $\tau =1.58$. The QP modulation envelope obtained by numerical simulation (circles) are compared to the analytical prediction (solid lines) for validation. Time series correspond to different regimes are also provided. The main result indicates that the modulation of the delay amplitude in the position gives birth to QP vibrations with large-amplitude performing away from the resonance in the region of negative $\lambda _1$.

Fig. 4.3

a Stability chart of QP solutions in the parameter plane $(\lambda _1, \tau )$, b time histories corresponding to different regions; $\lambda _2=0.2$, $\omega =2.1$ and $\gamma _2=1.33$. UQP: unstable QP, SQP: stable QP, LC: limit cycle [11]

Taking advantage of this previous finding, its first application to EH has been addressed in Belhaq and Hamdi [11]. They have considered a harvester device consisting in a delayed van der Pol oscillator coupled to an electromagnetic coupling in the form

$$\begin{aligned} \ddot{x}+x-\varepsilon (\alpha -\beta x^2)\dot{x}=\varepsilon \lambda (t) x(t-\tau )+\varepsilon \gamma _{1}i \end{aligned}$$

(4.3)

$$\begin{aligned} \frac{di}{dt}+\gamma _{2}i=-\dot{z} \end{aligned}$$

(4.4)

where $\varepsilon$ is a small positive parameter, $\alpha$, $\beta$ are damping coefficients, $\lambda (t)$ is the delay amplitude, $\tau$ is the time delay and $\gamma _{1}$ is the electromagnetic coupling coefficient. The delay amplitude $\lambda (t)$ is assumed to be modulated harmonically as $\lambda (t)=\lambda _1+\lambda _2\cos \,\omega t$, where $\lambda _1$ is the unmodulated delay amplitude and $\lambda _2$, $\omega$ are, respectively, the amplitude and the frequency of the modulation, while i and $\frac{di}{dt}$ have been substituted for electric charge coordinate q ($i=\dot{q}$). The coefficient $\gamma _{2}$ is the reciprocal of the time constant of the electrical circuit. It is worthy to point out that the delay in the mechanical part is not considered as an input power. It should be considered as inherently present in the harvester system as in milling and turning operations [17,18,19]. The system response was investigated near the delay parametric resonance assumig the resonance condition $1=(\frac{\omega }{2})^{2}+\varepsilon \sigma$ where $\sigma$ is a detuning parameter. Averaging method was used to approximate the amplitude and the output power of the periodic vibrations and the second-step perturbation method was applied to approximate the amplitude of the QP vibrations and the corresponding output power of the harvester device. For validation, the analytical prediction (solid lines) are compared to numerical simulation (circles) obtained using dde23 algorithm [21].

Fig. 4.4

Vibration (a) and power (b) amplitudes versus $\lambda _1$ for $\tau =1.58$, $\omega =2.1$ and $\gamma _2=1.33$; analytical (solid lines) and numerical (circles) approximations [11]

Fig. 4.5

a Stability chart of QP solutions in the plane $(\lambda _1, \tau )$, b time histories corresponding to different regions; $\lambda _2=0.2$, $\omega =2.1$ and $K=\gamma _2=1.33$. UQP: unstable QP, SQP: stable QP, LC: limit cycle [13]

Fig. 4.6

Vibration (a) and power (b) amplitudes versus $\lambda _1$ for $\tau =0.3$, $\lambda _2=0.2$, $\omega =2.1$ and $\gamma _2=1.33$; analytical (solid lines) and numerical (circles) approximations. Black line for delayed circuit $K=\gamma _2$, grey line for undelayed circuit $K=0$. Solid line for stable and doted line for unstable [13]

In Fig. 4.3a is presented the stability chart of the QP vibrations in the parameter plane ($\lambda _{1}, \tau$). Regions of stable and unstable QP vibrations are indicated, respectively, by UQP (aqua regions) and SQP (grey regions). Within the white region periodic oscillations indicated by LC occur. Time histories of responses and powers corresponding to different regions of Fig. 4.3a are shown in Fig. 4.3b. Bifurcation of solutions are obtained by moving between regions in Fig. 4.3a. For instance, from cross 2 to 3 Hopf bifurcation occurs giving rise to LC oscillations. The system behavior changes from LC to SQP oscillation with a slight modulation when moving from cross 3 to 4. It is worthy mentioning that cross 4 has been carefully chosen close to the bifurcation curve to demonstrate the accuracy of the analytical prediction of the stability chart. This is illustrated by comparison to time series corresponding to cross 4 in Fig. 4.3a (see Fig. 4.3b bottom).

Figure 4.4 depicts the variation of vibration and power amplitudes versus $\lambda _1$. One can clearly observe from Fig. 4.4a that for negative values of $\lambda _1$ the amplitude of the QP modulation is larger comparing to the amplitude of the periodic response. Accordingly, the corresponding power amplitudes shown in Fig. 4.4b demonstrate clearly that the performance of the extracted power in the QP region is better than the performance of the output power in the periodic region.

Another case has been considered by Ghouli et al. [13] for which the time delay is introduced in both mechanical and electrical components. In this case, the EH system consists of a delayed van der Pol oscillator coupled to a delayed electromagnetic element. The governing equations are written as

$$\begin{aligned} \ddot{x}+x-\varepsilon (\alpha -\beta x^2)\dot{x}=\varepsilon \lambda (t) x(t-\tau )+\varepsilon \gamma _{1}i \end{aligned}$$

(4.5)

$$\begin{aligned} \frac{di}{dt}+\gamma _{2}i=Ki(t-\tau )-\dot{z} \end{aligned}$$

(4.6)

where K is the delay amplitude in the electric circuit and $\tau$ is the time delay. The other parameters are defined as before.

As in the previous case (4.3), (4.4), the response of the system was investigated near the delay parametric resonance using a similar perturbation analysis.

Figure 4.5a presents the stability chart of the QP vibrations in the parameter plane ($\lambda _{1}, \tau$). The dashed lines delimit domains of unstable QP vibrations and the solid lines determine the domains where the QP vibrations are stable. Similarly, UQP (aqua regions) means unstable QP while SQP (grey regions) means stable QP. The periodic oscillations exist in the white regions and are indicated by LC. Time histories and the corresponding output power responses are shown in Fig. 4.5b. The transitions of solutions are obtained by moving between the crosses 1, 2 and 3 in Fig. 4.5a.

Figure 4.6 shows the variation of vibration and power amplitudes versus $\lambda _1$ for $K=0$ (undelayed circuit, grey lines) and $K=\gamma _2$ (delayed circuit, black lines). It can be seen that negative values of $\lambda _1$ decreases the amplitude of the QP modulation (Fig. 4.6a, black envelope), but on the contrary, increases the harvested power (Fig. 4.6b, black envelope). In other words, in the delayed van der Pol harvester in which the delay is also introduced in the electrical circuit the maximum output power extracted from QP vibration does not necessarily correspond to the maximum amplitude of QP oscillations.

4.3 The Excited van der Pol Oscillator and Energy Harvesting

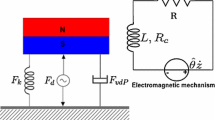
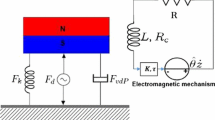
In this part we study QP vibration-based EH in an excited van der Pol oscillator coupled to a delayed piezoelectric device. The main purpose here is to examine the influence of the time delay in the electrical circuit on the energy extracted from QP vibrations. The corresponding schematic of the harvester is presented in Fig. 4.7 and the governing equations can be written in the dimensionless form as

$$\begin{aligned} \ddot{x}(t)+ x(t)-[\alpha -\beta x(t)^{2}]\dot{x}(t)-\chi v(t)=f \cos (\omega t) \end{aligned}$$

(4.7)

$$\begin{aligned} \dot{v}(t)+\lambda [v(t)-v(t-\tau )]+\kappa \dot{x}(t)=0\ \end{aligned}$$

(4.8)

where x(t) is the relative displacement of the rigid mass m, $\alpha$ and $\beta$ are the mechanical damping coefficients, f, $\omega$ are, respectively, the amplitude and the frequency of the harmonic excitation, v(t) is the voltage across the load resistance, $\chi$ is the piezoelectric coupling term in the mechanical attachment, $\kappa$ is the piezoelectric coupling term, $\lambda$ is the reciprocal of the time constant of the electrical circuit and $\tau$ is the time delay.

Fig. 4.7

Schematic description of the EH system

The objective is to investigate periodic and QP responses as well as the corresponding output powers of the harvester device (4.7), (4.8). We perform perturbation method near the principal resonance by introducing the resonance condition $1=\omega ^{2}+\sigma$ where $\sigma$ is a detuning parameter. The first-step multiple scales method is implemented by introducing a bookkeeping parameter $\varepsilon$ and scaling parameters such as (4.7) and (4.8) take the form

$$\begin{aligned} \ddot{x}(t)+\omega ^{2} x(t)=\varepsilon [(\alpha -\beta x(t)^{2})\dot{x}(t)+\chi v(t)+ f \cos (\omega t) -\sigma x(t)]\ \end{aligned}$$

(4.9)

$$\begin{aligned} \dot{v}(t)+\lambda [v(t)-v(t-\tau )]+\kappa \dot{x}(t)=0\ \end{aligned}$$

(4.10)

A solution to (4.9) and (4.10) can be sought in the form

$$\begin{aligned} x(t)=x_{0}(T_{0},T_{1})+\varepsilon x_{1}(T_{0},T_{1})+O(\varepsilon ^{2})\ \end{aligned}$$

(4.11)

$$\begin{aligned} v(t)=v_{0}(T_{0},T_{1})+\varepsilon v_{1}(T_{0},T_{1})+O(\varepsilon ^{2})\ \end{aligned}$$

(4.12)

where $T_{0}=t$ and $T_{1}=\varepsilon t$. The time derivatives become $\frac{d}{dt}=D_{0}+\varepsilon D_{1}+O(\varepsilon ^{2})$ and $\frac{d^{2}}{dt^{2}}=D_{0}^{2}+\varepsilon ^{2} D_{1}^{2}+2\varepsilon D_{0} D_{1}+O(\varepsilon ^{2})$ where $D_{i}^{j}=\frac{\partial ^{j}}{\partial ^{j} T_{i}}$. Substituting (4.11) and (4.12) into (4.9) and (4.10) and equating coefficient of like powers of $\varepsilon$, we obtain up to the second order the following hierarchy of problems:

At the first order:

$$\begin{aligned} D_{0}^{2}x_{0}+\omega ^{2}x_{0}=0\ \end{aligned}$$

(4.13)

$$\begin{aligned} D_{0}v_{0}+ \lambda [v_{0}- v_{0\tau }]+\kappa D_{0}x_{0}=0\ \end{aligned}$$

(4.14)

and at the second order:

$$\begin{aligned} D_{0}^{2}x_{1}+\omega ^{2}x_{1}=-2D_{0} D_{1}x_{0}+(\alpha -\beta x_{0}^{2})D_{0}x_{0} -\sigma x_{0}+\chi v_{0}+f\cos (\omega t)\ \end{aligned}$$

(4.15)

$$\begin{aligned} D_{0}v_{1}+\lambda [v_{1}-v_{1\tau }]=-D_{1}v_{0}-\kappa D_{0}x_{1}-\kappa D_{1}x_{0}\ \end{aligned}$$

(4.16)

Up to the first order the solution is given by

$$\begin{aligned} x_{0}(T_{0},T_{1})=A(T_{1})e^{i\omega T_{0}}+\bar{A}(T_{1})e^{-i\omega T_{0}}\ \end{aligned}$$

(4.17)

$$\begin{aligned} v_{0}(T_{0},T_{1})=\frac{-\kappa i\omega A(T_{1})}{\lambda +i\omega -\lambda e^{-i\omega \tau }} e^{i\omega T_{0}}+ \frac{\kappa i\omega \bar{A}(T_{1})}{\lambda -i\omega -\lambda e^{i\omega \tau }} e^{-i\omega T_{0}} \end{aligned}$$

(4.18)

where $A(T_{1})$ and $\bar{A}(T_{1})$ are unknown complex conjugate functions. Substituting (4.17) and (4.18) into (4.15) and (4.16) and eliminating the secular terms, one obtains

$$\begin{aligned} -2i\omega (D_{1}A)+i\alpha \omega A-i\beta \omega A^{2}\bar{A}-\sigma A-\frac{\kappa i\omega \chi A}{\lambda +i\omega -\lambda e^{-i\omega \tau }}+\frac{f}{2}=0\quad \end{aligned}$$

(4.19)

Expressing $A=\frac{1}{2}ae^{i\theta }$ where a and $\theta$ are the amplitude and the phase, we obtain up to the first order the modulation equations

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{da}{dt}=S_{1}a+S_{2}a^{3}+S_{3} \sin (\theta )\\ \displaystyle a\frac{d\theta }{dt}=S_{4}a+S_{3}\cos (\theta )\end{array} \right. \end{aligned}$$

(4.20)

where $S_{i} (i=1,...,4)$ are given by

$$\begin{aligned} S_{1}=\frac{\alpha }{2}-\frac{\kappa \chi (\lambda -\lambda \cos (\omega \tau ))}{2(\lambda -\lambda \cos (\omega \tau ))^{2}+2(\omega +\lambda \sin (\omega \tau ))^{2}}\ \end{aligned}$$

$$\begin{aligned} S_{2}=\frac{-\beta }{8}\,~~~~~S_{3}=-\frac{f}{2\omega }\ \end{aligned}$$

$$\begin{aligned} S_{4}=\frac{\sigma }{2\omega }+\frac{\kappa \chi (\omega +\lambda \sin (\omega \tau ))}{2(\lambda -\lambda \cos (\omega \tau ))^{2}+2(\omega +\lambda \sin (\omega \tau ))^{2}}\ \end{aligned}$$

The solution up to the first order given by (4.17) and (4.18) can be expressed as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle x_{0}(T_{0},T_{1})=a \cos (\omega t+\theta )\\ \\ \displaystyle v_{0}(T_{0},T_{1})=V \cos (\omega t+\theta +\arctan \frac{\lambda -\lambda \cos (\omega \tau )}{\omega +\lambda \sin (\omega \tau )})\end{array} \right. \end{aligned}$$

(4.21)

such that the condition $\omega +\lambda \sin (\omega \tau )\ne 0$ must be satisfied. Moreover, the voltage amplitude V is given by

$$\begin{aligned} V=\frac{\kappa \omega }{\sqrt{(\lambda -\lambda \cos (\omega \tau ))^{2}+(\omega +\lambda \sin (\omega \tau ))^{2}}}a\ \end{aligned}$$

(4.22)

The steady-state response of system (4.20), corresponding to periodic solutions of (4.9) and (4.10), are determined by setting $\frac{da}{dt}=\frac{d\theta }{dt}=0$. Eliminating the phase, we obtain the following algebraic equation in a

$$\begin{aligned} S_{2}^{2}a^{6}+2S_{1}S_{2}a^{4}+(S_{1}^{2}+S_{4}^{2})a^{2}-S_{3}^{2}=0 \end{aligned}$$

(4.23)

An expression for the average power is obtained by integrating the dimensionless form of the instantaneous power $P(t)= \lambda v(t)^{2}$ over a period T. This leads to

$$\begin{aligned} P_{av}=\frac{1}{T}\int _{0}^{T}\lambda v^{2}dt\ \end{aligned}$$

(4.24)

where $T=\frac{2\pi }{\omega }$. Then, the average power expressed by $P_{av}=\frac{\lambda V^{2}}{2}$ reads

$$\begin{aligned} P_{av}=\frac{1}{2}(\frac{\lambda \kappa ^{2}\omega ^{2}}{(\lambda -\lambda \cos (\omega \tau ))^{2}+(\omega +\lambda \sin (\omega \tau ))^{2}})a^{2}\ \end{aligned}$$

(4.25)

where the amplitude a is obtained from (4.23). Using the maximization procedure, the maximum power response is given by

$$\begin{aligned} P_{max}=\frac{\lambda \kappa ^{2}\omega ^{2}a^{2}}{(\lambda -\lambda \cos (\omega \tau ))^{2}+(\omega +\lambda \sin (\omega \tau ))^{2}}\ \end{aligned}$$

(4.26)

Equations (4.23) and (4.26) are used to examine the influence of different system parameters on the periodic response and on the corresponding maximum output power of the harvester.

To approximate the QP response of the original system, we apply the second-step perturbation method [22] on the modulation equations (4.20). To this end, it is convenient to transform the modulation equations (4.20) from the polar form to the following Cartesian system using the variable change $u=a \cos \theta$ and $w=-a \sin \theta$

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{du}{dt}=S_{4}w+\mu \{S_{1}u+S_{2}u(u^{2}+w^{2})\}\\ \\ \displaystyle \frac{dw}{dt}=-S_{4}u-S_{3}+\mu \{S_{1}w+S_{2}w(u^{2}+w^{2})\}\end{array} \right. \end{aligned}$$

(4.27)

where $\mu$ is a new bookkeeping parameter introduced to perform the second-step multiple scales method. A periodic solution of the slow flow (4.27) corresponding to the QP response of the original system (4.9), (4.10) can be expressed in the forme

$$\begin{aligned} u(t)=u_{0}(T_{0},T_{1})+\mu u_{1}(T_{0},T_{1})+O(\mu ^{2})\ \end{aligned}$$

(4.28)

$$\begin{aligned} w(t)=w_{0}(T_{0},T_{1})+\mu w_{1}(T_{0},T_{1})+O(\mu ^{2})\ \end{aligned}$$

(4.29)

where $T_{0}=t$ and $T_{1}=\mu t$. The time derivatives become $\frac{d}{dt}=D_{0}+\mu D_{1}+O(\mu ^{2})$ where $D_{i}^{j}=\frac{\partial ^{j}}{\partial ^{j} T_{i}}$. Substituting (4.28) and (4.29) into (4.27), and equating coefficient of like powers of $\mu$, we obtain at the first order

$$\begin{aligned} D_{0}^{2}u_{0}+S_{4}^{2}u_{0}=-S_{3}S_{4} \end{aligned}$$

(4.30)

$$\begin{aligned} S_{4}w_{0}=D_{0}u_{0} \end{aligned}$$

(4.31)

and at the second order we have

$$\begin{aligned}&\quad D_{0}^{2}u_{1}+S_{4}^{2}u_{1}=-D_{0}D_{1}u_{0}+S_{1}D_{0}u_{0}+S_{2}D_{0}u_{0}(u_{0}^{2}+w_{0}^{2})\nonumber \\&-S_{4}D_{1}w_{0}+S_{2}u_{0}D_{0}(u_{0}^{2}+w_{0}^{2})+S_{4}S_{1}w_{0}+S_{4}S_{2}w_{0}(u_{0}^{2}+w_{0}^{2}) \end{aligned}$$

(4.32)

$$\begin{aligned} S_{4}w_{1}=D_{0}u_{1}+D_{1}u_{0}-S_{1}u_{0}-S_{2}u_{0}(u_{0}^{2}+w_{0}^{2}) \end{aligned}$$

(4.33)

where $S_{4}$ is the frequency of the QP modulation. The solution up to the first order is written as

$$\begin{aligned} u_{0}(T_{0},T_{1})=R(T_{1})\cos (S_{4}T_{0}+\psi (T_{1}))-\alpha _{2} \end{aligned}$$

(4.34)

$$\begin{aligned} w_{0}(T_{0},T_{1})=-R\sin (S_{4}T_{0}+\psi (T_{1})) \end{aligned}$$

(4.35)

where R and $\psi$ are, respectively, the amplitude and the phase of the QP modulation and $\alpha _{2}=\frac{S_{3}}{S_{4}}$. Substituting (4.34) and (4.35) into (4.32) and removing secular terms gives the following slow-modulation equations

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{dR}{dt}=(S_{1}+2S_{2}\alpha _{2}^{2})R+S_{2}R^{3}\\ \\ \displaystyle R\frac{d\psi }{dt}=0\end{array} \right. \end{aligned}$$

(4.36)

The equilibria of this slow-modulation system determine the periodic solutions of the modulation equations (4.36), corresponding to the QP solutions of the original system (4.9), (4.10). The nontrivial equilibrium obtained by setting $\frac{dR}{dt}=0$ is given by

$$\begin{aligned} R=\sqrt{-\frac{S_{1}+2S_{2}\alpha _{2}^{2}}{S_{2}}}\ \end{aligned}$$

(4.37)

Consequently, the approximate periodic solution of the slow flow (4.27) is given by

$$\begin{aligned} u(t)=R cos(\theta t)-\alpha _{2} \end{aligned}$$

(4.38)

$$\begin{aligned} w(t)=-R sin(\theta t) \end{aligned}$$

(4.39)

The approximate amplitude a(t) of the QP response reads

$$\begin{aligned} a(t)=\sqrt{R^{2}+\alpha _{2}^{2}-2\alpha _{2}R \cos (\theta t)} \end{aligned}$$

(4.40)

and the QP modulation envelope is delimited by $a_{min}$ and $a_{max}$ given by

$$\begin{aligned} a_{min}=min\{\sqrt{R^{2}+\alpha _{2}^{2}\pm 2\alpha _{2}R}\} \end{aligned}$$

(4.41)

$$\begin{aligned} a_{max}=max\{\sqrt{R^{2}+\alpha _{2}^{2}\pm 2\alpha _{2}R}\} \end{aligned}$$

(4.42)

The explicit expression of the QP response of the original equation (4.9) is then written as

$$\begin{aligned} x(t)=u(t)\cos (\omega t)+w(t)\sin (\omega t) \end{aligned}$$

(4.43)

On the other hand, the QP solution of the voltage v(t), obtained by inserting (4.43) into (4.8), can be extracted via a convolution integral with the boundary condition $v (0) = v (T)$ where $T=\frac{2\pi }{\nu }$. This leads to

$$\begin{aligned} v(t)=-\kappa e^{(\lambda e^{\lambda \tau }-\lambda ) t}\int _{0}^{t}\dot{x}(t')e^{(\lambda -\lambda e^{\lambda \tau }) t'} dt'\end{aligned}$$

(4.44)

Consequently, the power, the average and the maximum output powers in the QP regime are given, respectively, by

$$\begin{aligned} P_{QP}(t)= \lambda (-\kappa e^{(\lambda e^{\lambda \tau }-\lambda ) t}\int _{0}^{t}\dot{x}(t')e^{(\lambda -\lambda e^{\lambda \tau }) t'} dt')^{2} \end{aligned}$$

(4.45)

$$\begin{aligned} P_{avQP}= \frac{\lambda \kappa ^{2}\nu ^{2}}{2[(\lambda -\lambda \cos (\omega \tau ))^{2}+(\nu +\lambda \sin (\omega \tau ))^{2}]}a^{2} \end{aligned}$$

(4.46)

$$\begin{aligned} P_{maxQP}= \frac{\lambda \kappa ^{2}\nu ^{2}}{[(\lambda -\lambda \cos (\omega \tau ))^{2}+(\nu +\lambda \sin (\omega \tau ))^{2}]}a^{2} \end{aligned}$$

(4.47)

where $\nu =S_4$ is the frequency of the QP modulation and a is now derived from (4.41) and (4.42).

Fig. 4.8

Vibration and power amplitudes versus $\omega$ for $\alpha =0.1$, $\beta =0.2$, $\chi =0.05$, $\lambda =0.05$, $\kappa =0.5$, $f=0.08$ and $\tau =0$. Analytical prediction (solid lines for stable and dashed line for unstable) and numerical simulation (circles)

Fig. 4.9

Vibration and power amplitudes versus $\omega$ for $\alpha =0.1$, $\beta =0.2$, $\chi =0.05$, $\lambda =0.05$, $\kappa =0.5$ and $f=0.08$. Analytical prediction (solid lines for stable and dashed line for unstable) and numerical simulation (circles). black lines for delayed electric circuit ($\tau =6.2$) and grey lines for undelayed circuit ($\tau =0$, Fig. 4.8)

Figure 4.8a, b show the frequency response of periodic and QP solutions and the corresponding output power amplitudes ($P_{max},P_{maxQP}$) versus the frequency $\omega$, respectively, in the case of the undelayed electrical circuit of the harvester ($\tau =0$). The periodic response is given by (4.23) and the boundaries of the QP modulation envelope are obtained from (4.41) and (4.42). Similarly, the maximum powers for periodic and QP vibrations are given, respectively, by (4.26) and (4.47). For validation, the analytical prediction (solid lines for stable and dashed line for unstable) are compared to numerical simulation (circles) obtained using Runge Kutta of order 4. The plots in Fig. 4.8b show that in the absence of time delay, periodic vibration-based EH can be achieved, but in a very narrow region located around the resonance peak. Instead, QP vibration-based EH can be obtained over a broadband of frequency away from the resonance with a performance comparable to that provided by periodic vibrations.

In Fig. 4.9 is shown the influence of time delay in the electrical component on the EH performance of the system. The curves given by the black lines correspond to the delayed case ($\tau =6.2$). For comparison, we plot in grey the case where the delay is absent ($\tau =0$). It can be observed that the presence of the delay in the electrical circuit increases the QP output power over a certain range of the frequency $\omega$ located away from the resonance (Fig. 4.9b). This QP output power can achieve a better performance comparing to the periodic output power, as illustrated in the vicinity of $\omega =0.8$ and $\omega =1.2$ (Fig. 4.9b).

To ensure the stability of the QP vibrations during energy extraction operation, it is important to determine the stability chart of the response. This can be done by considering the stability of the nontrivial solution of the slow-slow flow (4.36) obtained by calculating the eigenvalues of the corresponding Jacobian matrix $\mathbf J$. The curves delimiting the regions of existence of the QP oscillations and their domains of stability are given by the conditions ($Tr(\mathbf J )=-2S_{1}-4S_{2}\alpha _{2}^{2}<0$ and $Det(\mathbf J )=0$).

Fig. 4.10

a Stability chart in the plane $(f,\omega )$, b time and power histories corresponding to different regions picked from (a). SP: stable periodic, SQP: stable QP; $\alpha =0.1$, $\beta =0.2$, $\chi =0.05$, $\lambda =0.05$, $\alpha =0.1$, $\kappa =0.5$, and $\tau =6.2$

Figure 4.10a shows this stability chart in the parameter plane ($f,\omega$) for $\tau =6.2$ indicating the grey regions where stable QP (SQP) solutions take place and the white region corresponding to stable periodic (SP) solutions. In Fig. 4.10b are shown time histories and the corresponding output power responses related to crosses labelled 1, 2, 3 in Fig. 4.10a. From cross 1 to cross 2 or 3 the response bifurcates from SP to SQP oscillations via secondary Hopf bifurcation producing a slight modulation of the amplitude response and a significant performance of the output power at cross 3.

Finally, we show in Fig. 4.11 the variation of vibration and maximum power amplitudes $\chi$ versus the piezoelectric coupling coefficient $\chi$. It can be seen that a good performance of QP vibration-based EH can be achieved in certain range of negative $\chi$ located slightly at the right of the periodic region near $\chi =-0.5$ (Fig. 4.11b).

Fig. 4.11

Vibration and power amplitudes versus $\chi$ for $\alpha =0.1$, $\beta =0.2$, $\omega =0.8$, $\lambda =0.05$, $\alpha =0.1$, $\kappa =0.5$ and $f=0.08$. Analytical prediction (solid lines for stable and dashed line for unstable) and numerical simulation (circles). black lines for delayed circuit ($\tau =6.2$) and grey lines for undelayed circuit ($\tau =0$)

4.4 Conclusions

We have provided in a first part of the chapter recent results in QP vibration-based EH for some variants of delayed van der Pol harvesters for which the delay amplitude is modulated with certain amplitude and frequency around a nominal value. These variants include the delayed van der Pol harvester coupled either to delayed or undelayed electromagnetic subsystem. The influence of delay parameters on the performance of the harvester has been examined. In particular, it was shown that when the delay is introduced in both the mechanical oscillator and the electrical circuit the maximum output power extracted from QP vibrations does not necessarily correspond to the maximum amplitude of QP oscillations.

In a second part of the chapter we have investigated QP vibration-based EH in the case where the van der Pol oscillator is subjected to external harmonic excitation and coupled to a delayed piezoelectric component. The second-step multiple scales method was applied near the primary resonance to obtain approximation of the QP responses as well as the amplitude of the harvested power. Results showed that in the presence of time delay in the electrical circuit of the harvester, it is possible to harvest energy from the induced QP vibrations with a good performance over a broadband of system parameters away from the resonance. Such a performance is comparable to the one provided by the periodic vibrations, except that the energy extracted from periodic vibrations can be achieved only in a narrow region located around the resonance peak, while energy extracted from QP vibrations can be attained over a broadband of frequency away from the resonance. To guarantee the robustness of the QP vibration during energy extraction operation, a stability analysis was performed and the QP stability chart was determined. Numerical simulations have been conducted to confirm the analytical predictions. This study provides an interesting alternative to harvest energy in nonlinear harvesters away from the resonance, as instabilities and jump phenomena present often difficulty in maintaining energy harvesting operations in a stable and robust regime near the resonance.