Introduction

Vibrational energy harvesters (EH) have recently focused on extracting power for a variety of batteryless devices. As of today, most of the energy harvesting research has focused on using nonlinear systems that operate at resonance to produce the maximum of the power density in this area. The motivation for using vibration in power generation is to use the vibration energy available in the environment to power equipment placed in very hard-to-reach places. In general, they exist three different transduction mechanisms for vibration-based energy harvesting includes electrostatic [1], electromagnetic [2, 3], and piezoelectric [4]. Consequently, piezoelectricity is one of the physical effects allowing conversion of the mechanical energy to electrical energy with fairly high energy density enabling to miniaturize [5]. Traditionally, the piezoelectric harvester system is designed to work with mechanical resonator which for a linear characteristics has the best performance in the resonance region. To go beyond this limitation one has to adopt a resonator structure with multiple natural frequencies [6] or consider nonlinear design [7].

The recent research efforts have focused on introducing nonlinearities into formulation of the system, these can be introduced different types of generator depending on the potential energy function of the system [7, 8] either in the case of mono-stable harvester devices with softening [9] and hardening characteristic [10] or in the case of bistable ones [11,12,13]. This line of research was continued to more complex multi-sable system. Having intra-well and inter-well solutions of various characteristic frequencies [14,15,16,17,18] it was possible to model a frequency broadband response useful for ambient excitations of variable amplitudes and frequencies.

In the case of a mono-stable piezoelectric nonlinear energy harvester device consisting of a Duffing-type harvester with hardening stiffness [19] or system with impact [20] it is well known that, for appropriate choice of the nonlinearity, damping, and excitation amplitude, such a harvester may exhibit a broadband resonance interval in which the amplitude of the response and voltage are significantly large. In the bistable case where a number of separate large power or voltage outputs solutions are available, the compromise has been achieved between the system performance and complexity of the EH device [21].

However, the EH performance provided by nonlinear attachments can suffer from instabilities and jump phenomena near the boundaries of the stable branch of the frequency response. To circumvent such instabilities, the idea of using the effect of high-frequency excitation on vibration-based EH has been developed [22]. The authors studied the electrical response of a bistable system, by using a double-well Duffing oscillator, connected to a circuit through piezoceramic elements and driven by both a low and a high-frequency forcing and the demonstrate that by enhancing the oscillations with high-frequency we can harvest more electric energy. In this way, the effect of HF on nonlinear dynamics of a complex system has been largely studied in the literature [23, 24].

Motivated by such a performance of high-frequency in improving vibration-based energy harvesting, attention is paid here to examine the influence of high-frequency on EH in excited bistable Duffing-type harvester with nonlinear damping. Note that, the nonlinear form of damping assumed in this system will be modelled and realized in practice due to inherent nonlinearity within the piezoelectric laminate [25]. It has been shown that these nonlinear material effects are mainly due to higher-order elastic effects, with strong nonlinear damping also present.

In the next section we present the harvester system and we use the method of direct partition of motion (DMP) to analysis the influence of high-frequency on the slow dynamic of system. In “Periodic energy harvesting” we derive approximation of the periodic response and the expressions of the power extracted using the multiple scales method. The influence of different system parameters of the harvester device on the EH performance is analyzed in the presence of high-frequency in “Main results”. A summary of the results is given in the concluding section.

Model Description and Slow Vibration Energy Harvesting

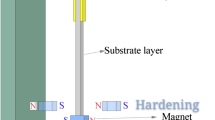
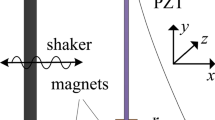
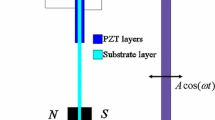
The energy harvester device considered here consists of a bistable-Duffing resonator coupled to an electrical circuit through a piezoelectric device as shown in the schematic presented in Fig. 1. Such that the dimensionless governing equations for the system can be written as

$$\begin{aligned}&\ddot{x}+(\mu _{a}+\mu _{b}x^{2})\dot{x}- x+\alpha x^{3}- \theta v=f \cos (\omega t) \nonumber \\&\quad +F \cos (\Omega t) \end{aligned}$$
(1)
$$\begin{aligned}&\dot{v}+\mu _{c} v+\kappa \dot{x}=0, \end{aligned}$$
(2)

where x is the relative displacement of the rigid mass m, v is the voltage across the load resistance, \(\mu _{a} \) and \(\mu _{b} \) are the mechanical damping ratio, \(\alpha \) is the stiffness parameter, \(\theta \) is the piezoelectric coupling term in the mechanical equation, \(\kappa \) is the piezoelectric coupling term in the electrical circuit equation, \(\mu _{c}\) is the reciprocal of the time constant of the electrical circuit, \(\omega \) and \(\Omega \) are the excitation frequency, and f and F are respectively the low and high-frequency inertial forces defined by \(f=A\omega ^{2}\), \(F=B\Omega ^{2}\). The intent of this paper is to applying analytical and numerical methods to enhance the output power by using a resonant phenomenon and study the effect of HF on our system that was investigated by Stanton et al. [25].

Fig. 1
figure 1

Schematic description of the bistable piezoelectric inertial generator with nonlinear damping and multiple excitation. v(t) denotes the output voltage on the resistor load R

Full size image

To analyze the influence of high-frequency \(\Omega \) excitation on the slow dynamic of system, we use the method of direct partition of motion (DPM) [26, 27]. By introducing two different time scales: a fast time \(T_{0}=\Omega t \) and slow time \(T_{1}=t\).

We split up x(t) into a slow part \(z(T_{1})\) and a fast part \(\epsilon \phi (T_{0},T_{1})\), we split up also v(t) into a slow part \(y(T_{1})\) and a fast part \(\epsilon g(T_{0},T_{1})\) as follows

$$\begin{aligned} x(t)&=z(T_{1})+\epsilon \phi (T_{0},T_{1}) \end{aligned}$$
(3)
$$\begin{aligned} v(t)&=y(T_{1})+\epsilon g(T_{0},T_{1}) , \end{aligned}$$
(4)

where z and y describes slow main motions at time-scale of oscillation, \(\epsilon \phi (T_{0}, T_{1})\) and \(\epsilon g(T_{0},T_{1})\) stands for an overly of the fast motion and \(\epsilon \) indicates that \(\epsilon \phi (T_{0},T_{1})\) and \(\epsilon g(T_{0},T_{1})\) are small compared to z and y. Since \(\Omega \) is considered as a large parameter we choose \(\epsilon =\Omega ^{-1}\), for convenience.

Introducing \(D_{i}^{j}=\frac{\partial ^{j}}{\partial ^{j} T_{i}}\) yields \(\frac{d}{dt}=\Omega D_{0}+D_{1}\), \(\frac{d^{2}}{dt^{2}}=\Omega ^{2} D_{0}^{2}+D_{1}^{2}+2\Omega D_{0} D_{1}\), and substituting (3) and (4) into (1) and (2) gives

$$\begin{aligned}&\epsilon ^{-1}D_{0}^{2}\phi +D_{1}^{2}z+\epsilon D_{1}^{2}\phi +2D_{0} D_{1}\phi \nonumber \\&\quad +(\mu _{a}+\mu _{b}z^{2}+\mu _{b}\epsilon ^{2}\phi ^{2}+2\mu _{b}\epsilon \phi z)(D_{0}\phi +D_{1}z+\epsilon D_{1}\phi ) \nonumber \\&\quad -\theta (y+\epsilon g)-(z+\epsilon \phi )+\alpha (z+\epsilon \phi )^{3} \nonumber \\& =A\omega ^{2}cos(\omega T_{1})+B\Omega ^{2}cos(T_{0}) \end{aligned}$$
(5)
$$\begin{aligned}&D_{0}g+D_{1}y+\epsilon D_{1}g+\mu _{c}(y+\epsilon g)+\kappa D_{0}\phi \nonumber \\&\quad +\kappa D_{1}z+\epsilon \kappa D_{1}\phi =0 . \end{aligned}$$
(6)

We suppose also that the fast part \(\epsilon \phi \) and \(\epsilon g\) its derivatives are \(2\pi \) periodic functions of fast time \(T_{0}\) with zero mean value with respect to this time, so that \(<x(t)>=z(T_{1})\) and \(<v(t)>=y(T_{1})\), where \(<>=\frac{1}{2\pi }\int ^{2\pi }_{0}()dT_{0}\) defines time averaging operator over one period of the fast excitation with the slow time \(T_{1}\) fixed. Averaging (5) and (6) leads to

$$\begin{aligned}&D_{1}^{2}z+[\mu _{a}+\mu _{b}z^{2}+\mu _{b}<\epsilon ^{2}\phi ^{2}>] \nonumber \\&D_{1}z-z+\alpha z^{3}+3\alpha z<\epsilon ^{2}\phi ^{2}>-\theta y=A\omega ^{2}cos(\omega t) \end{aligned}$$
(7)
$$\begin{aligned}&D_{1}y+\mu _{c} y +\kappa D_{1}z=0 . \end{aligned}$$
(8)

Subtracting (7) from (5) yields

$$\begin{aligned}&\epsilon ^{-1}D_{0}^{2}\phi +\epsilon D_{1}^{2}\phi +2D_{0} D_{1}\phi \nonumber \\&\quad +(\mu _{a}+\mu _{b}z^{2}+\mu _{b}\epsilon ^{2}\phi ^{2}+2\mu _{b}\epsilon \phi z)(D_{0}\phi +D_{1}z+\epsilon D_{1}\phi ) \nonumber \\&\quad -\theta \epsilon g-\epsilon \phi +\alpha (z+\epsilon \phi )^{3}-\alpha z^{3}=\epsilon ^{-1}(B\Omega )cos(T_{0}) . \end{aligned}$$
(9)

Subtracting (8) from (6) yields

$$\begin{aligned} D_{0}g+\epsilon D_{1}g+\mu _{c}\epsilon g+\kappa D_{0}\phi +\epsilon \kappa D_{1}\phi =0 .\ \end{aligned}$$
(10)

The approximate expression for \(\epsilon \phi \) is obtained from (9) by considering only the dominant terms of order \(\epsilon ^{-1}\) as

$$\begin{aligned} D_{0}^{2}\phi =(B\Omega )\cos (T_{0}) ,\ \end{aligned}$$
(11)

where it is assumed that \(B\Omega =O(1)\). The stationary solution to the first order for \(\phi \) is written as

$$\begin{aligned} \epsilon \phi =-B \cos (T_{0}) .\ \end{aligned}$$
(12)

The approximate expression for \(\epsilon g\) is obtained from (10) by considering only the dominant terms of order \(\epsilon ^{0}\) as

$$\begin{aligned} D_{0}g+\kappa D_{0}\phi =0 .\ \end{aligned}$$
(13)

The stationary solution to the first order for g is written as

$$\begin{aligned} \epsilon g= \kappa B\cos (T_{0}) .\ \end{aligned}$$
(14)

The equations governing the slow motion is derived from (7) and (8). Inserting \(\phi \) from (12) and using that \(<\epsilon ^{2}\phi ^{2}>=\frac{B^{2}}{2}\), we find the approximate equations for slow motions

$$\begin{aligned}&D_{1}^{2}z+[\mu _{a}+\mu _{b}z^{2}+\mu _{b}\frac{B^{2}}{2}]D_{1}z-z \nonumber \\&\quad +\alpha z^{3}+3\alpha \frac{B^{2}}{2} z-\theta y=A\omega ^{2}cos(\omega t) \end{aligned}$$
(15)
$$\begin{aligned}&D_{1}y+\mu _{c} y +\kappa D_{1}z=0 .\ \end{aligned}$$
(16)

In (15) and (16), the influence of the high-frequency \(\Omega \) is introduced in the natural frequency of the system as well as in the nonlinear damper. These equations can be written as

$$\begin{aligned}&\ddot{z}+[\mu _{a}+\mu _{b}z^{2}+\mu _{b}\frac{B^{2}}{2}]\dot{z}+\alpha z^{3}+\omega _{0}^{2}z-\theta y=f\cos (\omega t) \end{aligned}$$
(17)
$$\begin{aligned}&\dot{y}+\mu _{c}y +\kappa \dot{z}=0 ,\ \end{aligned}$$
(18)

where \(\omega _{0}^{2}=(\frac{3\alpha B^{2}}{2}-1)\) is the natural frequency for the slow dynamic system Eqs. (17, 18). A necessary condition for \(\omega _{0}^{2}>0\) is checked by the following condition if \(B>\sqrt{\frac{2}{3\alpha }}\) with \(\alpha >0\). The restoring force potential for the system of Eqs. (1, 2) may be expressed as \(V(x)=-\frac{x^{2}}{2}+\alpha \frac{x^{4}}{4}\) shown in figure (2,a) and for the system of Eqs. (17, 18) for the slow motion, the restoring force potential can be written as \(V(z)=\omega _{0}^{2}\frac{z^{2}}{2}+\alpha \frac{z^{4}}{4}\) shown in figure (2,b). Note that the high-frequency component of excitation is changing the property of the dynamical solution transforming it from double well (fig. 2,a) in original system Eqs. (1, 2) to single well (fig. 2,b) in slow variables dynamics Eqs. (17, 18).

Fig. 2
figure 2

Figures (a) and (b) show respectively the potential for the full motion Eqs. (1, 2) and the slow motion Eqs. (17, 18) for \(\alpha =1, F=81\) and \(\Omega =9\) (note that the vibration amplitude \(B=1\) for fast excitations)

Full size image

In figure (3,a), we show a comparison between the full motion x(t), and the slow motion z(t), and figure (3,b), show a comparison between the voltage from the full motion v(t), and the slow motion y(t). A good agreement between the full motion and slow motion is illustrated.

Fig. 3
figure 3

Figures (a) and (b) show respectively the displacement and the voltage histories from the full motion Eqs. (1, 2) and the slow motion Eqs. (17, 18) for \(f=0.2,\) \(F=81,\) \(\mu _{a}=0.08,\) \(\mu _{b}=0.01,\) \(\alpha =1,\) \(\theta =0.9, \) \(\kappa =0.9,\) \( \mu _{c}=0.01,\) \(\omega =1\) and \(\Omega =9\)

Full size image

Periodic Energy Harvesting

To study the response of the harvester in a slow variables dynamics near the principal primary resonance, after analyzing the influence of high-frequency excitation on a system of Eqs. (1, 2) using the method of direct partition of motion, we assume the resonance condition \(\omega _{0}^{2}=\omega ^{2}+\sigma \) where \(\sigma \) is a detuning parameter. Approximation of solutions are obtained using the method of multiple scales [28] by introducing a bookkeeping parameter \(\epsilon \) and scaling as \(\mu _{a}=\epsilon \tilde{\mu _{a}}, \mu _{b}=\epsilon \tilde{\mu _{b}}, \alpha =\epsilon \tilde{\alpha }, \theta =\epsilon \tilde{\theta }, f=\epsilon \tilde{f}\) and \(\sigma =\epsilon \tilde{\sigma }\). Equations (17) and (18) become

$$\begin{aligned} \ddot{z}+\omega ^{2}z & =\epsilon \left[-\left(\tilde{\mu _{a}}+\bar{\mu _{b}}z^{2}+\tilde{\mu _{b}} \frac{B^{2}}{2}\right)\dot{z}-\tilde{\alpha } z^{3} \right. \\ & \quad \left. -\tilde{\sigma } z+\tilde{\theta } y + \tilde{f} {\text{cos}} (\omega t)\right] \end{aligned}$$
(19)
$$\begin{aligned}&\dot{y}+\mu _{c} y +\kappa \dot{z}=0 . \end{aligned}$$
(20)

We seek a solution to equations (19) and (20) in the form

$$\begin{aligned} z(t)&=z_{0}(T_{1},T_{2})+\epsilon z_{1}(T_{1},T_{2})+O(\epsilon ^{2}) \end{aligned}$$
(21)
$$\begin{aligned} y(t)&=y_{0}(T_{1},T_{2})+\epsilon y_{1}(T_{1},T_{2})+O(\epsilon ^{2}) , \end{aligned}$$
(22)

where \(T_{1}=t\) and \(T_{2}=\epsilon t\). In terms of the variables \(T_{i}\), the time derivatives become \(\frac{d}{dt}=D_{1}+\epsilon D_{2}+O(\epsilon ^{2})\) and \(\frac{d^{2}}{dt^{2}}=D_{1}^{2}+\epsilon ^{2} D_{2}^{2}+2\epsilon D_{1} D_{2}+O(\epsilon ^{2})\) where \(D_{i}^{j}=\frac{\partial ^{j}}{\partial ^{j} T_{i}}\). Substituting (21) and (22) into (19) and (20) and equating coefficient of like powers of \(\epsilon \), we obtain

  • Order \(\epsilon ^{0}:\)

    $$\begin{aligned}&D_{1}^{2}z_{0}+\omega ^{2}z_{0}=0 \end{aligned}$$
    (23)
    $$\begin{aligned}&D_{1}y_{0}+ \mu _{c} y_{0}+\kappa D_{1}z_{0}=0 ,\ \end{aligned}$$
    (24)

  • Order \(\epsilon ^{1}:\)

    $$\begin{aligned}&D_{1}^{2}z_{1}+\omega ^{2}z_{1}=-2D_{1} D_{2}z_{0}-\tilde{\mu _{a}}D_{1} z_{0}-\tilde{\mu _{a}}z_{0}^{2}D_{1} z_{0} \nonumber \\&\quad -\frac{\tilde{\mu _{b}}B^{2}}{2}D_{1} z_{0}-\tilde{\alpha } z_{0}^{3}-\tilde{\sigma }z_{0}+\tilde{\theta } y_{0}+\tilde{f}\cos (\omega T_{1}) \end{aligned}$$
    (25)
    $$\begin{aligned}&D_{1}y_{1}+\mu _{c}y_{1}+\kappa D_{1}z_{1}=-D_{2}y_{0}-\kappa D_{2}z_{0} . \end{aligned}$$
    (26)

The solution to the first order are given by

$$\begin{aligned} z_{0}(T_{1},T_{2})&=C(T_{2})e^{i\omega T_{1}}+\bar{C}(T_{2})e^{-i\omega T_{1}} \end{aligned}$$
(27)
$$\begin{aligned} y_{0}(T_{1},T_{2})&=\frac{-ki\omega C(T_{2})}{\mu _{c}+i\omega }e^{i\omega T_{1}}+ \frac{ki\omega \bar{C}(T_{2})}{\mu _{c}-i\omega }e^{-i\omega T_{1} ,} \end{aligned}$$
(28)

where \(C(T_{2})\) and \(\bar{C}(T_{2}) \) are unknown complex conjugate functions. Substituting Eqs. (27), (28) into (25), (26) and eliminating the secular terms, gives

$$\begin{aligned}&-2i\omega (D_{2}C)-\tilde{\mu _{a}} i\omega C-\frac{\tilde{\mu _{b}}B^{2}}{2}i\omega C-\tilde{\theta }\frac{\kappa i\omega C}{\mu _{c}+i\omega } \nonumber \\&-3\tilde{\alpha } C^{2} \bar{C}-\tilde{\sigma } C-3i\omega \tilde{\mu _{b}}C^{2} \bar{C}+\frac{\tilde{f}}{2}=0 .\ \end{aligned}$$
(29)

Assuming \(C=\frac{1}{2}ae^{i\phi }\) where a and \(\phi \) are the amplitude and the phase we obtain the modulation equations

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{da}{dt}=S_{1}a+S_{2}a^{3}+S_{3}\sin (\phi )\\ \\ \displaystyle a\frac{d\phi }{dt}=S_{4}a+ S_{5}a^{3}+S_{3}\cos (\phi )\end{array} \right. , \end{aligned}$$
(30)

in which \(S_{i} (i=1,...,5)\) are given in Appendix. The solution given by (27), (28) reads

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle z_{0}(T_{1},T_{2})=a \cos (\omega t+\phi )\\ \\ \displaystyle y_{0}(T_{1},T_{2})=V \cos (\omega t+\phi +\arctan \frac{\mu _{c}}{\omega })\end{array} \right. \end{aligned}$$
(31)

with the voltage amplitude V is given by

$$\begin{aligned} V=\frac{\kappa \omega }{\sqrt{\mu _{c}^{2}+\omega ^{2}}}a .\ \end{aligned}$$
(32)

The steady-state response of system (30) obtained by setting \(\frac{da}{dt}=\frac{d\phi }{dt}=0\) corresponds to periodic solution of Eqs. (19) and (20). Eliminating the phase, the amplitude a is obtained by solving the following equation

$$\begin{aligned} (S_{2}^{2}+S_{5}^{2})a^{6}+(2S_{1}S_{2}+2S_{4}S_{5})a^{4} +(S_{1}^{2}+S_{4}^{2})a^{2}-S_{3}^{2}=0. \end{aligned}$$
(33)

The instantaneous power output can be estimated in the standard form \(P(t)=v^2(t)/R\), where R is an electrical resistance load. However, here for simplicity, in our dimensionless case (Eqs. 1 and 2) we express it in the related form of \(P(t)=\mu _c v^2\). Consequently, the average power, \(P_{av}\), is estimated by integrating the dimensionless form of the instantaneous power P(t) over a period T. This is given by

$$\begin{aligned} P_{av}=\frac{1}{T}\int _{0}^{T}\mu _{c}v^{2}dt,\ \end{aligned}$$
(34)

where \(T=\frac{2\pi }{\omega }\). Hence, the average power is decoupled into slow and fast components by

$$\begin{aligned} P_{av}= P^S_{av}+ P^F_{av}=\frac{\mu _{c} V^{2}}{2} + \frac{\mu _{c} F^2 \kappa ^2}{2\Omega ^4}. \end{aligned}$$
(35)

The slow component, dominating at the vicinity of excitation frequency \(\omega \), takes the form

$$\begin{aligned} P^S_{av}=\frac{1}{2}\left( \frac{\mu _{c} \kappa ^{2}\omega ^{2}}{\mu _{c}^{2}+\omega ^{2}}\right) a^{2},\ \end{aligned}$$
(36)

where the amplitude a is given by Eq. (33). Applying the maximization procedure, the maximum power reads

$$\begin{aligned} P^S_{max}=\frac{\mu _{c} \kappa ^{2}\omega ^{2}}{\mu _{c}^{2}+\omega ^{2}}a^{2} .\ \end{aligned}$$
(37)

Equations (33) and (37) will be used to study the effect of parameters on the steady-state response and on the output power of the harvester for slow variables dynamics.

Thus, the explicit expression of the original system (3) and (4) reads

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle x(t)=a \cos (\omega t+\phi )-\frac{F}{\Omega ^{2}}\cos (\Omega t)\\ \\ v(t)=\frac{\kappa \omega }{\sqrt{\mu _{c}^{2}+\omega ^{2}}}a \cos (\omega t+\phi +\arctan \frac{\mu _{c}}{\omega })+\frac{F}{\Omega ^{2}}\kappa \cos (\Omega t)\end{array} \right. . \end{aligned}$$
(38)

Main Results

Next, the influence of different parameters of the system on vibration amplitudes and maximal power outputs, \(P_{max}^S\), are examined. After studying the influence of high-frequency excitation on the system Eqs. (1, 2), by using the method of direct partition of motion we obtain the system of slow variables dynamics Eqs. (17, 18). The multiple scale method is applied to obtain approximations of periodic solutions for system of Eqs. (17, 18). Eq. (33) is used for periodic solutions for a slow variables dynamics and Eq. (37) is exploited to calculate the corresponding power response. The numerical simulation is obtained by the method of Runge–Kutta of order 4 applies to Eqs. (17) and (18). In what follows, we fix the parameters: \(\mu _{a}=0.08\), \(\mu _{b}=0.01\) and \(\alpha =1\).

Fig. 4
figure 4

Vibration amplitudes and maximal power outputs vs. \(\omega \) for \(f=0.2, F=81,\)\(\theta =0.9, \)\(\kappa =0.9,\)\(\mu _{c}=0.01\) and \(\Omega =9\). Analytical prediction (solid lines for stable and dashed line for unstable) and numerical simulation (circles)

Full size image

Figure 4 shows the variation of the amplitudes a of the periodic vibration as well as the corresponding output power amplitudes \(P_{max}^S\) versus the frequency \(\omega \). The periodic response is given by (33) and the maximum powers for periodic vibration is given by Eq. (37). For validation, the analytical prediction (solid lines for stable and dashed line for unstable) are compared to numerical simulation (circles) obtained by the method of Runge–Kutta of the 4th order. The plots in Fig. 4 present a typical response of an excited nonlinear Duffing harvester device (hardening characteristic) for the slow dynamic of the system under the influence of high-frequency, for that, the system change behavior from bistable to monostable one offering the possibility to harvest energy with performance near the nonlinear resonance.

Fig. 5
figure 5

Vibration amplitudes and maximal power outputs vs. \(\Omega \) for \(f=0.2, \) \(F=81,\) \(\theta =0.9, \) \(\kappa =0.9,\) \(\mu _{c}=0.01\) and \(\omega =1.4\)

Full size image

Figure 5 shows the variation of the amplitudes a of the periodic vibration as well as the corresponding output power amplitudes \(P_{max}^S\) versus the frequency \(\Omega \). Here, it can be observed that we can achieve enhanced energy extraction from high-level frequency excitations as a controller. Next, we show in Figs. 6, 7, respectively, the variation of the amplitudes a of the periodic vibration as well as the corresponding maximal power output \(P_{max}^S\) versus the low frequency inertial force f and the high-frequency inertial force F. It can be observed that, for the given values of parameters, In fig. 6 we can improve the energy extraction from low-level excitations under the influence of high-level excitations.

Fig. 6
figure 6

Vibration amplitudes and maximal power outputs vs. f for \(F=81, \) \(\theta =0.9, \) \(\kappa =0.9,\) \(\mu _{c}=0.01,\) \(\omega =1.4\) and \(\Omega =9\)

Full size image
Fig. 7
figure 7

Vibration amplitudes and maximal power outputs vs. F for \(f=0.2, \theta =0.9, \kappa =0.9, \mu _{c}=0.01, \omega =1.4\) \(f=0.2, \) \(\theta =0.9,\) \(\kappa =0.9, \) \(\mu _{c}=0.01, \) \(\omega =1.4\) and \(\Omega =9\)

Full size image

Similarly, we show in Figs. 8, 9, respectively, the influence of the piezoelectric coupling coefficients \(\theta \) and \(\kappa \) on the vibrations and powers. It can be observed that for the given values of parameters, the range values of \(\theta \) (Fig. 8b) and \(\kappa \) (Fig. 9b) where a good performance energy harvesting can be archived.

Fig. 8
figure 8

Vibration amplitudes and maximal power outputs vs. \(\theta \) for \(f=0.2, \) \(F=81,\) \(\kappa =0.9,\) \(\mu _{c}=0.01,\) \(\omega =1.4\) and \(\Omega =9\)

Full size image
Fig. 9
figure 9

Vibration amplitudes and maximal power outputs vs. \(\kappa \) for \(f=0.2,\) \(F=81, \) \(\theta =0.9,\) \(\kappa =0.9, \) \(\mu _{c}=0.01, \) \(\omega =1.4\) and \(\Omega =9\)

Full size image

Finally, Fig. 10 illustrates typical curves for \(\omega =1.4\) and \(f=0.2\) for the inter-well solutions. For each parameter set, there exist stable inter-well steady-state responses whose respective maximum power is shown in Fig. 10 indicates similar optimal values for \(\mu _{c}\) for the inter-well harmonic motions.

Fig. 10
figure 10

Maximal power outputs vs. \(\mu _{c}\) for \(f=0.2,\) \(F=81,\) \(\theta =0.9,\) \(\kappa =0.9,\) \(\omega =1\), and \(\Omega =9\)

Full size image

Conclusion

This work has focused on bistable energy harvesting dynamics with nonlinear damping in the presence of two components of inertial excitation forces with low and high excitation frequencies where the HF forcing is the environmental vibration, while the LF is controlled by us. Due to the high-frequency oscillations the set of equations was renormalized and the effective potential appeared to be mono-stable. This effect is in line with expectations in the presence of additional fast oscillation energy which enables the system to overcome the original potential barrier. In this system the resonance of the low frequency lead to the maximum power output. In this work, we investigate the phenomenon of vibrational resonance (VR) as a useful energy source mechanism. Low and high frequency power supply systems can vibration resonance phenomenon caused by two drive amplitudes oscillate and reach maximum amplitude. We apply this idea to Duffing-type bistable collector with nonlinear damping. Virtual Reality the phenomenon is usually based on the magnitude of the force or the frequency is not always easy to set and change. Here we check the VR that can be generated by adjusting another parameter manipulated when values are forced to depend on the environment situation. The analytical results obtained by multiple time scales approach were confirmed by numerical simulations.