Nonlinear Vibrations of FGM Circular Conical Panel Under In-Plane and Transverse Excitation

Abstract

Purpose

In this study, nonlinear forced vibrations of a functionally graded material circular conical panel under the transverse excitation and the in-plane excitation are discussed.

Method

The temperature field of the system is considered as a steady-state temperature. Material properties of temperature-dependence for the system vary along the thickness direction in the light of a power law. The nonlinear geometric partial differential equations expressed by general displacements are derived by the first-order shear deformation theory and Hamilton’s principle. Furthermore, the ordinary differential equations of the system are acquired by the Galerkin method. The nonlinear dynamic behaviors of the system are fully analyzed.

Results

Based on numerical simulations, time history records, Poincare maps, phase portraits and bifurcation diagrams are depicted to clarify the existence of complex nonlinear dynamic behaviors of the system.

Introduction

By changing the volume fraction of constituent materials smoothly and continuously, functionally graded material (FGM) structures can relieve the problems of stress concentration and interfacial debonding. Typically, FGM structures composited by metals and ceramics gradually are able to withstand high temperature environments more easily. They have been considered to be one of the most promising candidates in many engineering fields in the future, such as aerospace, rocketry, and many others in recent years [1, 2]. Compared with the homogeneous composite structures, FGM structures will have more complex dynamics under the effect of the thermal load and the mechanical load. It is well known that circular conical panels are usually used as fundamental and important load carrying components in more complicated structures in various engineering fields, such as turbo machinery blades or aircraft fuselages. By changing the initial curvatures or other geometric parameters of conical panels, the dynamic properties of them can be optimized. It is significant for us to predict and control dynamic behaviors of the FGM circular conical panel under various loads.

There are many results on the dynamics of isotropic homogeneous or laminated composite circular conical panels up to now. Teichmann [3] investigated free vibrations of clamped and free open conical shells using the Navier solution. Qiu and Zhou [4] explored nonlinear dynamic behaviors of circular plates under the effect of in-plane impact velocities. Based on Donnell’s theory and the fully clamped boundary condition, Srinivasan [5] studied natural frequencies of the isotropic circular conical shell by using an integral equation approach. Lim [6,7,8,9] developed global Ritz formulation to analyze the free vibration of circular conical panels, and vibration frequencies of laminated circular conical panels were given by employing the Ritz energy principle. Based on an improved generalized differential quadrature method, Lam [10] discussed natural frequencies of the conical panels by considering different boundary conditions. Correia [11] analyzed dynamic characteristics of the cylindrical/conical panel by comparing first-order displacement field and higher order displacement field. Based on the Mindlin’s theory and the finite element method, Dey [12] analyzed the effects of parameters on natural frequencies of pretwisted composite conical shells. According to the kp-Ritz method, taking into account arbitrary boundary conditions, Zhao [13] performed free vibrations of the conical panels.

For the past few years, the dynamic performances of the FGM conical shell or circular conical panel have been widely concerned. Sofiyev [14] investigated the stability problems of FGM conical shells under the effect of a uniform pulsive load. Naj [15] canvassed buckling behaviors of FGM conical shells. Taking into account the sinusoidal impulse and the step loads, Zhang [16] canvassed dynamic buckling behaviors of the clamped FGM conical shell. Using the Donnell shell theory and von-Karman type nonlinear kinematics, Sofiyev [17, 18] analyzed the nonlinear frequency and nonlinear stability of the FGM truncated conical shell. Deniz [19] developed a system with a homogeneous truncated conical shell and two FGM composite coatings, and performed the nonlinear stability of the system subjected to an axially compressed load. Considering the elastic foundations, Duc [20] studied stability behaviors of the FGM truncated conical shell.

When it comes to FGM circular conical panels, studies on dynamics of them were scarce in the open literature. According to the kp-Ritz method, Zhao [21] analyzed free vibration behaviors of FGM conical panels. Akbari [22] studied free vibrations of FGM conical panels, the curved edges of the structure are clamped, free or simply supported, and the straight edges of the structure are assumed as simply supported.

It should be remarked that the above-mentioned studies on the FGM circular conical panels have been focused on free vibration behaviors. Studies on nonlinear dynamical responses of FGM circular conical panels subjected to external excitations are rare. This paper aims to discuss nonlinear forced vibrations of the FGM circular conical panel under the transverse excitation and the in-plane excitation. Material properties of temperature-dependence for the system vary along the thickness direction in the light of a power law. The nonlinear geometric partial differential equations expressed by general displacements are derived by the first-order shear deformation theory and Hamilton’s principle. Furthermore, the ordinary differential equations of the system are acquired by the Galerkin method. Numerical simulations are carried out to illustrate that the FGM circular conical panel has very complex nonlinear dynamic behaviors.

Formulation

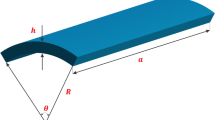
Consider an FGM circular conical panel with the length L, the subtended angle $\gamma$, the thickness $h$, the semi-vertex angle $\beta$ and radii at the two ends $R_{1}$ and $R_{2}$, respectively, as illustrated in Fig. 1. The radius at one point along the length direction is a parameter varying in x direction that can be obtained by $R = R_{1} + x\sin \beta$. We defined the coordinate system $\left( {x,\theta ,z} \right)$ on the mid-surface of the FGM circular conical panel, where x axis, θ axis are along the generatrix direction and the circumferential direction, and z axis is perpendicular to the mid-surface, positive outwards. The u, v and w are the displacements of a point with respect to x axis, θ axis and z axis, respectively. The transverse excitation $F(x,\,\theta )\cos \varOmega_{1} t$ and the in-plane excitation $p_{0} + p_{1} \cos \left( {\varOmega_{2} t} \right)$ at the two curved ends $x = 0$ and $x = L$ act on the FGM circular conical panel.

Fig. 1

Configuration of the FGM circular conical panel

Material Properties of the FGM

For purpose of getting the material properties, a power law is utilized. Thus, the volume fractions of the ceramic material and the metal material are expressed by

$$V_{\text{c}} (z) = \left( {\frac{ 1}{ 2} + \frac{z}{h}} \right)^{n} ,\;V_{\text{m}} (z) = 1 - V_{\text{c}} (z),$$

(1)

where V denotes the volume fraction, the subscript c represents the ceramic and the subscript m is the metal, the superscript n denotes the volume fraction index. Figure 2 shows the change of the ceramic volume fraction along the direction of the thickness for the structure.

Fig. 2

The ceramic volume fraction varies along the direction of the thickness

Based on the above material properties of FGM, the effective material properties, such as the mass density ρ, the thermal expansion coefficient α and Young’s modulus E, are determined by a homogenization scheme, which is a linear rule of mixture

$$P = P_{\text{c}} V_{\text{c}} + P_{\text{m}} V_{\text{m}} .$$

(2)

The typical temperature-dependent material properties is represented by

$$P_{i} = P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} } \right),\;i = {\text{c}},{\text{m,}}$$

(3)

where $P_{0}$, $P_{ - 1}$, $P_{1}$, $P_{2}$ and $P_{3}$ are the power law coefficients, and $T$ is the temperature expressed by Kelvin, which can be computed by

$$T(z) = T_{\text{m}} + \left( {T_{\text{c}} - T_{\text{m}} } \right)\eta (z),$$

(4)

where

$$\begin{aligned} \eta (z) = \frac{1}{C}\left[ {\left( {\frac{z}{h} + \frac{1}{2}} \right) - \frac{{k_{\text{cm}} }}{{k_{\text{m}} \left( {n + 1} \right)}}\left( {\frac{z}{h} + \frac{1}{2}} \right) + \frac{{k_{\text{cm}}^{2} }}{{k_{\text{m}}^{2} \left( {2n + 1} \right)}}\left( {\frac{z}{h} + \frac{1}{2}} \right)^{{\left( {2n + 1} \right)}} - \frac{{k_{\text{cm}}^{3} }}{{k_{\text{m}}^{3} \left( {3n + 1} \right)}}\left( {\frac{z}{h} + \frac{1}{2}} \right)^{{\left( {3n + 1} \right)}} } \right. \hfill \\ \left. { + \frac{{k_{\text{cm}}^{4} }}{{k_{\text{m}}^{4} \left( {4n + 1} \right)}}\left( {\frac{z}{h} + \frac{1}{2}} \right)^{{\left( {4n + 1} \right)}} - \frac{{k_{\text{cm}}^{5} }}{{k_{\text{m}}^{5} \left( {5n + 1} \right)}}\left( {\frac{z}{h} + \frac{1}{2}} \right)^{{\left( {5n + 1} \right)}} } \right], \hfill \\ \end{aligned}$$

$$C = 1 - \frac{{k_{{2{\text{m}}}} }}{{\left( {n + 1} \right)k_{\text{m}} }} + \frac{{k_{\text{cm}}^{2} }}{{\left( {2n + 1} \right)k_{\text{m}}^{2} }} - \frac{{k_{\text{cm}}^{3} }}{{\left( {2n + 1} \right)k_{\text{m}}^{3} }} + \frac{{k_{\text{cm}}^{4} }}{{\left( {2n + 1} \right)k_{\text{m}}^{4} }} - \frac{{k_{\text{cm}}^{5} }}{{\left( {2n + 1} \right)k_{\text{m}}^{5} }},$$

$$k_{\text{cm}} = k_{\text{c}} - k_{\text{m}} ,$$

(5)

where $k_{\text{c}}$ is the coefficient of heat conduction for the ceramic and $k_{\text{m}}$ is the coefficient of heat conduction for the metal.

Governing Equations

On the basis of the first-order shear deformation theory, relationships between the strains and the displacements are obtained by the von-Karman hypothesis, which can be given by

$$\left\{ \begin{gathered} \varepsilon _{{xx}} \hfill \\ \varepsilon _{{\theta \theta }} \hfill \\ \gamma _{{x\theta }} \hfill \\ \end{gathered} \right\} = \left\{ {\varepsilon ^{{(0)}} } \right\} + z\left\{ {\varepsilon ^{{(1)}} } \right\},\;\left\{ \begin{gathered} \gamma _{{\theta z}} \hfill \\ \gamma _{{xz}} \hfill \\ \end{gathered} \right\} = \left\{ {\begin{array}{*{20}l} {\phi _{\theta } + \frac{1}{R}\frac{{\partial w_{0} }}{{\partial \theta }} - \frac{1}{R}v_{0} \cos \beta } \\ {\frac{{\partial w_{0} }}{{\partial x}} + \phi _{x} } \\ \end{array} } \right\},$$

(6)

where

$$\left\{ {\varepsilon ^{{(0)}} } \right\} = \left\{ \begin{gathered} \varepsilon _{{xx}}^{{(0)}} \hfill \\ \varepsilon _{{\theta \theta }}^{{(0)}} \hfill \\ \gamma _{{x\theta }}^{{(0)}} \hfill \\ \end{gathered} \right\} = \left\{ {\begin{array}{*{20}l} {\frac{{\partial u_{0} }}{{\partial x}} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \\ {\frac{1}{R}\frac{{\partial v_{0} }}{{\partial \theta }} + \frac{1}{R}w_{0} \cos \beta + \frac{1}{R}u_{0} \sin \beta + \frac{1}{2}\frac{1}{{R^{2} }}\left( {\frac{{\partial w_{0} }}{{\partial \theta }}} \right)^{2} } \\ {\frac{1}{R}\frac{{\partial u_{0} }}{{\partial \theta }} - \frac{1}{R}v_{0} \sin \beta + \frac{{\partial v_{0} }}{{\partial x}} + \frac{1}{R}\frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial \theta }}} \\ \end{array} } \right\},\;\left\{ {\varepsilon ^{{(1)}} } \right\} = \left\{ \begin{gathered} \varepsilon _{{xx}}^{{(1)}} \hfill \\ \varepsilon _{{\theta \theta }}^{{(1)}} \hfill \\ \gamma _{{x\theta }}^{{(1)}} \hfill \\ \end{gathered} \right\} = \left\{ {\begin{array}{*{20}l} {\frac{{\partial \phi _{x} }}{{\partial x}}} \\ {\frac{1}{R}\frac{{\partial \phi _{\theta } }}{{\partial \theta }} + \frac{1}{R}\phi _{x} \sin \beta } \\ {\frac{1}{R}\frac{{\partial \phi _{x} }}{{\partial \theta }} - \frac{1}{R}\phi _{\theta } \sin \beta + \frac{{\partial \phi _{\theta } }}{{\partial x}}} \\ \end{array} } \right\},$$

(7)

where u₀, v₀ and w₀ represent displacement components on the middle surface, along x axis, θ axis and z axis, respectively. $\phi_{x}$ and $\phi_{\theta }$ are rotations of tangents about the middle surface.

The thermoelastic constitutive equation of the FGM circular conical panel is expressed as follows:

$$\left\{ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{x\theta } \hfill \\ \sigma_{\theta z} \hfill \\ \sigma_{xz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } \\ \end{array} } \right]\left\{ {\left\{ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \gamma_{x\theta } \hfill \\ \gamma_{\theta z} \hfill \\ \gamma_{xz} \hfill \\ \end{aligned} \right\} - \left\{ \begin{aligned} \alpha \\ \alpha \\ 0 \\ 0 \\ 0 \\ \end{aligned} \right\}\Delta T} \right\},$$

(8)

where $Q_{\text{ij}}$ are stress stiffnesses with

$$Q_{ 1 1} = Q_{ 2 2} = \frac{E}{{1 - \nu^{2} }},\;Q_{ 1 2} = \frac{\nu E}{{1 - \nu^{2} }},\;Q_{44} = Q_{55} = Q_{66} = \frac{E}{2(1 + \nu )},$$

(9)

where $\Delta T$ is the temperature increment relative to the reference temperature.

Based on Hamilton’s principle, which is a generalized virtual displacement principle, nonlinear partial differential equations of the FGM circular conical panel are derived by

$$N_{xx,x} + \frac{1}{R}N_{x\theta ,\theta } + \frac{1}{R}N_{xx} \sin \beta - \frac{1}{R}N_{\theta \theta } \sin \beta = I_{0} \ddot{u}_{0} + I_{1} \ddot{\phi }_{x} ,$$

(10a)

$$N_{x\theta ,x} + \frac{1}{R}N_{\theta \theta ,\theta } + \frac{2}{R}N_{x\theta } \sin \beta + \frac{1}{R}Q_{\theta } \cos \beta = I_{0} \ddot{v}_{0} + I_{1} \ddot{\phi }_{\theta } ,$$

(10b)

$$\begin{aligned} Q_{x,x} + \frac{1}{R}Q_{\theta ,\theta } + \frac{1}{R}Q_{x} \sin \beta - \frac{1}{R}N_{\theta \theta } \cos \beta + N_{xx,x} \frac{{\partial w_{0} }}{\partial x} + N_{xx} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{R}N_{xx} \frac{{\partial w_{0} }}{\partial x}\sin \beta \hfill \\ + \frac{1}{{R^{2} }}N_{\theta \theta ,\theta } \frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{{R^{2} }}N_{\theta \theta } \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}N_{x\theta ,\theta } \frac{{\partial w_{0} }}{\partial x} + \frac{2}{R}N_{x\theta ,\theta } \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta } + \frac{1}{R}N_{x\theta ,x} \frac{{\partial w_{0} }}{\partial \theta } \hfill \\ + F\cos (\varOmega_{1} t) - \gamma \dot{w}_{0} = I_{0} \ddot{w}_{0} , \hfill \\ \end{aligned}$$

(10c)

$$M_{xx,x} + \frac{1}{R}M_{x\theta ,\theta } - Q_{x} + \frac{1}{R}M_{xx} \sin \beta - \frac{1}{R}M_{\theta \theta } \sin \beta = I_{1} \ddot{u}_{0} + I_{2} \ddot{\phi }_{x} ,$$

(10d)

$$M_{x\theta ,x} + \frac{1}{R}M_{\theta \theta ,\theta } - \frac{1}{R}Q_{\theta } + \frac{2}{R}M_{x\theta } \sin \beta = I_{1} \ddot{v}_{0} + I_{2} \ddot{\phi }_{\theta } ,$$

(10e)

where γ denotes the structural damping coefficient, $(I_{0} ,I_{1} ,I_{2} )$ are the mass moments of inertia, which can be computed from

$$(I_{0} ,I_{1} ,I_{2} ) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {(1,z^{1} ,z^{2} )\rho } {\text{d}}z.$$

(11)

The components of stress and thermal stress resultants can be given by

$$\begin{aligned} \left\{ {\begin{array}{*{20}l} \varvec{N} \\ \varvec{M} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} \varvec{A} & \varvec{B} \\ \varvec{B} & \varvec{D} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\left\{ {\varepsilon_{0} } \right\}} \\ {\left\{ {\varepsilon_{1} } \right\}} \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\varvec{N}^{\text{T}} } \\ {\varvec{M}^{\text{T}} } \\ \end{array} } \right\},\;\left\{ \begin{aligned} Q_{x} \hfill \\ Q_{\theta } \hfill \\ \end{aligned} \right\} = K\left[ \varvec{A} \right]\left\{ \begin{aligned} \gamma_{xz} \hfill \\ \gamma_{\theta z} \hfill \\ \end{aligned} \right\} \hfill \\ \varvec{N} = \left\{ \begin{aligned} N_{xx} \hfill \\ N_{\theta \theta } \hfill \\ N_{x\theta } \hfill \\ \end{aligned} \right\},\;\varvec{M} = \left\{ \begin{aligned} M_{xx} \hfill \\ M_{\theta \theta } \hfill \\ M_{x\theta } \hfill \\ \end{aligned} \right\},\;(N^{\text{T}} ,M^{\text{T}} ) = \int {_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} } {\text{Q}}\alpha \Delta T(1,z){\text{d}}z, \hfill \\ \end{aligned}$$

(12)

where stiffness matrices $\varvec{A}$, $\varvec{B}$, $\varvec{D}$ and the variable $\varvec{Q}$ are expressed by

$$\begin{aligned} \varvec{A} = \left[ {\begin{array}{*{20}l} {A_{11} } & {A_{12} } & 0 \\ {A_{12} } & {A_{22} } & 0 \\ 0 & 0 & {A_{66} } \\ \end{array} } \right],\;\varvec{B} = \left[ {\begin{array}{*{20}l} {B_{11} } & {B_{12} } & 0 \\ {B_{12} } & {B_{22} } & 0 \\ 0 & 0 & {B_{66} } \\ \end{array} } \right] \hfill \\ \varvec{D} = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12}^{{}} } & 0 \\ {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {D_{66} } \\ \end{array} } \right],\;\varvec{Q} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right], \hfill \\ \end{aligned}$$

(13)

where $A_{ij}$, $B_{ij}$ and $D_{ij}$ denote the extension, bending-extension coupling and bending stiffness elements of, respectively, which can be calculated as follows:

$$(A_{ij} ,B_{ij} ,D_{ij} ) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {Q_{ij} (1,z,z^{2} )} {\text{d}}z.$$

(14)

In Eq. (12), $K$ denotes the shear correction factor. Here, the shear correction factor $K$ is selected as $5 / 6$.

Substituting Eqs. (11–14) to Eqs. (10a–10e), partial differential equations for the system expressed by the form of generalized displacements can be given by

$$L_{jL} (u_{0} ,v_{0} ,w_{0} ,\phi_{x} ,\phi_{\theta } ,\dot{w}_{0} ) = L_{jR} (\ddot{u}_{0} ,\ddot{v}_{0} ,\ddot{w}_{0} ,\ddot{\phi }_{x} ,\ddot{\phi }_{\theta } ),$$

(15)

where the detailed expressions of partial differential operators $L_{jL}$ and $L_{jR}$ are presented in Appendix 1.

All edges of the FGM circular conical panel are simply supported, which can be given by the following expressions:

$$\begin{aligned} v_{0} = w_{0} = \phi_{\theta } = M_{xx} = 0\;{\text{at}}\;x = 0,\;x = L \hfill \\ u_{0} = w_{0} = \phi_{x} = M_{\theta \theta } = 0\;{\text{at}}\;\theta = 0,\;\theta = \gamma . \hfill \\ \end{aligned}$$

(16)

Based on the above boundary conditions, the displacement components are expressed by the double Fourier series [23]

$$\begin{array}{*{20}l} {u_{0} = \sum\limits_{{m = 1}}^{M} {\sum\limits_{{n = 1}}^{N} {u_{{mn}} (t)} \cos \left( {\frac{{m\pi x}}{L}} \right)\sin \left( {\frac{{n\pi \theta }}{\gamma }} \right)} ,\;v_{0} = \sum\limits_{{m = 1}}^{M} {\sum\limits_{{n = 1}}^{N} {v_{{mn}} } (t)\sin \left( {\frac{{m\pi x}}{L}} \right)\cos \left( {\frac{{n\pi \theta }}{\gamma }} \right)} } \\ {w_{0} = \sum\limits_{{n = 1}}^{M} {\sum\limits_{{m = 1}}^{N} {w_{{mn}} (t)} \sin \left( {\frac{{m\pi x}}{L}} \right)\sin \left( {\frac{{n\pi \theta }}{\gamma }} \right)} ,\;\phi _{x} = \sum\limits_{{m = 1}}^{M} {\sum\limits_{{n = 1}}^{N} {\phi _{{xmn}} (t)} \cos \left( {\frac{{m\pi x}}{L}} \right)\sin \left( {\frac{{n\pi \theta }}{\gamma }} \right)} } \\ {\phi _{\theta } = \sum\limits_{{m = 1}}^{M} {\sum\limits_{{n = 1}}^{N} {\phi _{{\theta mn}} } (t)\sin \left( {\frac{{m\pi x}}{L}} \right)\cos \left( {\frac{{n\pi \theta }}{\gamma }} \right).} } \\ \end{array}$$

(17)

The transverse excitation is expanded by

$$F = \sum\limits_{n = 1}^{M} {\sum\limits_{m = 1}^{N} {F_{mn} } (t)\sin \left( {\frac{m\pi x}{L}} \right)\sin \left( {\frac{n\pi \theta }{\gamma }} \right)} ,$$

(18)

where n and m represent the number of circumferential waves and axial half waves number. u_mn, v_mn, w_mn, ϕ_xmn, $\phi_{\theta mn}$ and F_mn are time-dependent variables associated to every modes and external force, respectively. We focus on the first two order modes of the system.

The inertia terms of u, v, $\phi_{x}$ and $\phi_{\theta }$ in Eq. (15) can be ignored on the basis of the study given by Nosir and Bhimaraddi [24, 25]. Employing the Galerkin method, the displacements of in-plane and rotation can be replaced in terms of transverse displacement. Furthermore, ordinary differential equations for the FGM circular conical panel for transverse motion can be yielded

$$\varvec{\ddot{W}} + \varvec{\mu \dot{W}} + (\varvec{M} + \varvec{P})\varvec{W} + \varvec{NL} + \varvec{C} = \varvec{F}\cos \varOmega_{1} \varvec{t},$$

(19)

where coefficients are described in Appendix 2 in detail. It is notable that in Eq. (19), variable $\varvec{C}$ is a fixed value for a certain FGM circular conical panel in a certain thermal field described by Eq. (4). It can cause bending deformation for the FGM circular conical panel.

Numerical Results

The validation of the present model is verified by comparing with the Reddy’s results [26]. The dimensionless central moments of our works are compared with the study acquired by utilizing the method given by Ref [26], which can be seen in Table 1. Here, the FGM plate is composited of Ti–6Al–4V and Al₂O₃. The geometric properties of the FGM plate can be listed, which the length is a = 0.2 m, the width is b = 0.5 m and the thickness is h = 0.002 m. Good agreement is observed.

Table 1 Comparison of dimensionless central moments $\bar{M}_{xx}$ and $\bar{M}_{yy}$ for n = 0.5 and n = 1

The effect of the thickness–radius ratio and the volume fraction index on nonlinear dynamic behaviors of the FGM circular conical panel is analyzed by means of the fourth-order Runge–Kutta method with variable steps.

The material properties of the structure are the Si₃N₄ (silicon nitride) and the SUS304 (steel), which are temperature dependent and given in Table 2 [27]. Geometric parameters of the system are thickness h = 0.002 m, subtended angle γ = 60°, semi-vertex angle $\beta = 30{^\circ }$, length L = 0.8 m and the radius at the top end R₁ = 0.5 m, respectively. The temperature at the inner surface remained a constant at 300 K. The amplitudes of the in-plane pre-applied excitation and the transverse excitation are p₀ = 1.0 × 10⁶ N/m² and F = 6.0 × 10⁵ N/m², respectively. The frequencies of the external excitation are 318.5 Hz. The initial conditions are given, which are w₁ = − 0.001, $\dot{w}_{1} = - \;0.0001$, w₂ = − 0.00025 and $\dot{w}_{2} = - \;0.0001$. The damping coefficient is 0.09 kg/s in all calculations. We change the in-plane excitation when we investigate nonlinear dynamic responses of the system. The three-dimensional bifurcation diagrams for w₁, $\dot{w}_{1}$ and in-plane load, two-dimensional bifurcations, phase portraits, Poincare maps and time history diagrams are depicted to present the periodic and nonperiodic responses of the system.

Table 2 Coefficients of SUS304 and SI₃N₄ about temperature-dependence

Effect of Volume Fraction Index

Nonlinear dynamical analysis of the FGM circular conical panel is performed when we consider the volume fraction index to be n = 0.5, n = 5 and n = ∞, respectively. The thickness–radius ratio h/R₁ = 0.004 and the temperature T_c = 400 K are used in the calculations. Figure 3 depicts bifurcation diagrams for n = 0.5 when the change interval of the in-plane excitation is (1.0 × 10⁶ N/m², 3.5 × 10⁶ N/m²). Figure 3a, b describes bifurcation diagrams of the in-plane excitation versus w₁ and w₂. In Fig. 3a, b, it is difficult for us to see the chaotic motion and the quasi-periodic motion directly. But from three-dimensional bifurcation diagram of Fig. 3c, it is easily obvious that the process of the motions for the system exhibits the following law: the periodic-1 motion appears at first, then the quasi-periodic motion occurs, finally, the system exhibits the periodic-1 motion. The system has the quasi-periodic motion when the in-plane excitation is in the range from 2.59 × 10⁶ N/m² to 2.95 × 10⁶ N/m². Figures 4 and 5 are given to describe the responses of the system. It is shown that vibration of the first mode is outward while the second mode is inward.

Fig. 3

Bifurcation diagrams when the thickness–radius ratio is h/R₁ = 0.004, the temperature on the outer surface is T_c = 400 K and the volume fraction index is n = 0.5 for the system. a, b are bifurcation diagrams of the first mode and the second mode; c is the three-dimensional representation of the bifurcation diagram for the first mode

Fig. 4

The periodic-1 motion of the system appears when p₁ = 2.00 × 10⁶ N/m². a, c are phase portraits on the plane $(w_{1} \,,\;\dot{w}_{1} )$ and $(w_{2} \,,\;\dot{w}_{2} )$; b, d are time history records on the plane (t, w₁) and (t, w₂); e denotes the three-dimensional phase portrait in the space $(w_{1} \,,\;\dot{w}_{1} ,w_{2} )$; f is the Poincare map on the plane $(w_{1} \,,\;\dot{w}_{1} )$

Fig. 5

The quasi-periodic motion of the system appears when p₁ = 2.70 × 10⁶ N/m²

Figure 6 reveals the dynamic responses of the system for n = 5. It is obvious that the FGM circular conical panel has complex nonlinear dynamic responses. Three periodic motion ranges, one chaotic motion range and two quasi-periodic motion ranges are detected. The system exhibits chaotic motion when p₁ changes from 3.40 × 10⁶ N/m² to 3.50 × 10⁶ N/m². It is also evident that three jumps are detected in this figure. Bifurcation diagram in Fig. 7 has been obtained with n = ∞ when the change interval of the in-plane excitation is (1.0 × 10⁶ N/m², 3.5 × 10⁶ N/m²). In this case, it means that the FGM circular conical panel is fully metal. The periodic motion and the quasi-periodic motion appear at first. Then the system exhibits chaotic motion. The chaotic motion occurs when p₁ is larger than 2.56 × 10⁶ N/m². It is because that the higher value of n means less stiffness of the system.

Fig. 6

Bifurcation diagrams when the thickness–radius ratio is h/R₁ = 0.004, the temperature on the outer surface is T_c = 400 K and the volume fraction index is n = 5

Fig. 7

Bifurcation diagrams when the thickness–radius ratio is h/R₁ = 0.004, the temperature on the outer surface is T_c = 400 K and the volume fraction index is n = ∞

Effect of Thickness–Radius Ratio

Nonlinear dynamical responses of the FGM circular conical panel with different thickness–radius ratios h/R₁ = 0.002, h/R₁ = 0.004 and h/R₁ = 0.006 are studied in this subsection. The temperature T_c = 400 K and the volume fraction index n = 0.5 are used in the calculations. Figure 8 reveals bifurcation diagrams for h/R₁ = 0.002 when the change interval of the in-plane excitation is (1.0 × 10⁶ N/m², 3.0 × 10⁶ N/m²). The process of motions exhibits the following phenomenon: the periodic motion and the chaotic motion appear alternate three times. The first time, the system moves from periodic motion to chaotic motion. The second time, the system moves from periodic motion to quasi-periodic motion, and finally the motion becomes chaotic. The change law of the third time is the same as the second time. The corresponding motions are illustrated in Figs. 9, 10, 11 when the FGM circular conical panel at p₁ = 1.20 × 10⁶ N/m², p₁ = 2.30 × 10⁶ N/m² and p₁ = 2.60 × 10⁶ N/m², respectively. Figure 12 depicts bifurcation diagrams for h/R₁ = 0.006. When the in-plane excitation is in the range of $p_{1} \in (1.0 \times 10^{6} {\text{N}}/{\text{m}}^{2} ,\;3.0 \times 10^{6} {\text{N}}/{\text{m}}^{2} )$, it can be seen that there is only the periodic motion in the FGM circular conical panel.

Fig. 8

Bifurcation diagrams when the volume fraction index is n = 0.5, the temperature on the outer surface is T_c = 400 K and the thickness–radius ratio is h/R₁ = 0.002

Fig. 9

The periodic-1 motion of the system appears when p₁ = 1.20 × 10⁶ N/m²

Fig. 10

The quasi-periodic motion of the system appears when p₁ = 2.30 × 10⁶ N/m²

Fig. 11

The chaotic motion of the system appears when p₁ = 2.60 × 10⁶ N/m²

Fig. 12

Bifurcation diagrams when the volume fraction index is n = 0.5, the temperature on the outer surface is T_c = 400 K and the thickness–radius ratio is h/R₁ = 0.006

According to Figs. 3, 8 and 12, which have the same parameters except the thickness–radius ratio, it is observed that as the thickness–radius ratio increases, the in-plane excitation, which causes the system to change from the periodic motion to the chaotic motion, increases. This is reasonable because the Young’s modulus increases with the increase of h/R₁. It can increase the ability of the system to resist bending deformation. What’s more, we can calculate the change law of stress resultants from the dynamic response of displacements to meet the demand of design.

Conclusions

The dynamical response behaviors of the FGM circular conical panel under the transverse excitation and the in-plane excitation are studied. The temperature field of the system is considered as a steady-state temperature. Material properties of temperature-dependence for the system vary along the thickness direction in the light of a power law. The nonlinear geometric partial differential equations expressed by general displacements are derived by the first-order shear deformation theory and Hamilton’s principle. Furthermore, the ordinary differential equations of the system are acquired by the Galerkin method. The effects of the thickness–radius ratio and the volume fraction index are analyzed.

The nonlinear dynamic behaviors of the FGM circular conical panel are fully analyzed. Time history records, Poincare maps, phase portraits and bifurcation diagrams are depicted by means of numerical simulations to illustrate that the system has very complex nonlinear dynamical behaviors. One can observe that increasing the volume fraction index makes the FGM circular conical panel stiffer and the chaotic regions move forward gradually. Additionally, increasing the thickness–radius ratio may lead to higher bending stiffness. Therefore, the larger thickness–radius ratio leads to the higher in-plane excitation, which causes the FGM circular conical panel to move from the periodic motion to the chaotic motion.

Appendices

Appendix 1: The Partial Differential Operators $L_{jL}$ and $L_{jR}$ of Eq. (15)

$$\begin{aligned} L_{1L} = & \, A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}A_{66} \frac{{\partial^{2} u_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}A_{11} \frac{{\partial u_{0} }}{\partial x}\sin \beta - \frac{1}{{R^{2} }}A_{22} u_{0} \cos^{2} \beta + \frac{1}{R}(A_{12} + A_{66} )\frac{{\partial^{2} v_{0} }}{\partial x\partial \theta } \\ & \quad - \frac{1}{{R^{2} }}(A_{22} + A_{66} )\frac{{\partial v_{0} }}{\partial \theta }\sin \beta + \frac{1}{{R^{2} }}A_{66} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}(A_{12} + A_{66} )\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } + B_{11} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} \\ & \quad + A_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{1}{R}(B_{12} + B_{66} )\frac{{\partial^{2} \phi_{\theta } }}{\partial x\partial \theta } + \frac{1}{2R}(A_{11} - A_{12} )\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\sin \beta + \frac{1}{R}A_{12} \frac{{\partial w_{0} }}{\partial x}\cos \beta \\ & \quad - \frac{1}{{2R^{3} }}(A_{12} - A_{22} )\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\sin \beta - \frac{1}{{R^{2} }}(B_{22} + B_{66} )\frac{{\partial \phi_{\theta } }}{\partial \theta }\sin \beta - \frac{1}{{R^{2} }}A_{22} w_{0} \sin \beta \cos \beta \\ & \quad + \frac{1}{{R^{2} }}B_{66} \frac{{\partial^{2} \phi_{x} }}{{\partial \theta^{2} }} + \frac{1}{R}B_{11} \frac{{\partial \phi_{x} }}{\partial x}\sin \beta - \frac{1}{{R^{2} }}B_{22} \phi_{x} \sin^{2} \beta + \frac{1}{R}(N_{xx}^{T} - N_{\theta \theta }^{T} )\sin \beta , \\ \end{aligned}$$

(20)

$$L_{1R} = I_{0} \ddot{u}_{0} + I_{1} \ddot{\phi }_{x} ,$$

(21)

$$\begin{aligned} L_{2L} = & \frac{1}{R}(A_{12} + A_{66} )\frac{{\partial^{2} u_{0} }}{\partial x\partial \theta } + \frac{1}{{R^{2} }}(A_{22} + A_{66} )\frac{{\partial u_{0} }}{\partial \theta }\sin \beta + A_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}KA_{44} \frac{{\partial w_{0} }}{\partial \theta }\cos \beta \\ & \quad - \frac{1}{{R^{2} }}\left( {KA_{44} \cos^{2} \beta + A_{66} \sin^{2} \beta } \right)v_{0} + \frac{1}{R}A_{66} \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial \theta } \\ & \quad + \frac{1}{{R^{2} }}A_{22} \frac{{\partial^{2} v_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}A_{66} \frac{{\partial v_{0} }}{\partial x}\sin \beta + \frac{1}{{R^{2} }}A_{66} \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial x}\sin \beta + \frac{1}{{R^{2} }}A_{22} \frac{{\partial w_{0} }}{\partial \theta }\cos \beta \\ & \quad + \frac{1}{R}\left( {A_{12} + A_{66} } \right)\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial x} + \frac{1}{R}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} \phi_{x} }}{\partial x\partial \theta } + \frac{1}{{R^{2} }}\left( {B_{22} + B_{66} } \right)\frac{{\partial \phi_{x} }}{\partial \theta }\sin \beta \\ & \quad + \frac{1}{R}B_{66} \frac{{\partial \phi_{\theta } }}{\partial x}\sin \beta + \frac{1}{{R^{2} }}B_{22} \frac{{\partial^{2} \phi_{\theta } }}{{\partial \theta^{2} }} + \left( {\frac{1}{R}KA_{44} \cos \beta - \frac{1}{{R^{2} }}B_{66} \sin^{2} \beta } \right)\phi_{\theta } , \\ \end{aligned}$$

(22)

$$L_{2R} = I_{0} \ddot{v}_{0} + I_{1} \ddot{\phi }_{\theta },$$

(23)

$$\begin{aligned} L_{3L} = & \frac{2}{{R^{2} }}B_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial \phi_{x} }}{\partial \theta } + \frac{1}{2R}A_{11} \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{3} \sin \beta - \frac{1}{R}N_{\theta \theta }^{T} \cos \beta + \frac{1}{R}\left( {B_{11} + B_{22} } \right)\frac{{\partial \phi_{x} }}{\partial x}\frac{{\partial w_{0} }}{\partial x} \\ & \quad + A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} - \frac{1}{{R^{2} }}A_{66} \frac{{\partial v_{0} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial x}\sin \beta - \frac{1}{{R^{3} }}(A_{12} + A_{66} )\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} + B_{11} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} \\ & \quad + \frac{2}{{R^{2} }}(A_{12} + 2A_{66} )\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial x} + \frac{1}{R}(B_{12} + B_{66} )\frac{{\partial^{2} \phi_{\theta } }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}A_{66} \frac{{\partial^{2} u_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} \\ & \quad + \frac{1}{{2R^{2} }}(A_{12} + 2A_{66} )\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \frac{1}{R}\left( {KA_{55} + N_{xx}^{T} } \right)\frac{{\partial w_{0} }}{\partial x}\sin \beta + \frac{3}{2}A_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} \\ & \quad - \frac{1}{{R^{2} }}B_{66} \frac{{\partial \phi_{\theta } }}{\partial x}\frac{{\partial w_{0} }}{\partial x}\sin \beta + \frac{1}{2R}A_{12} \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} \cos \beta + \frac{1}{R}(A_{11} + A_{12} )\frac{{\partial w_{0} }}{\partial x}\frac{{\partial u_{0} }}{\partial x}\sin \beta \\ & \quad + \frac{1}{R}A_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}w_{0} \cos \beta + \frac{1}{{R^{2} }}A_{12} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial u_{0} }}{\partial x} + A_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial u_{0} }}{\partial x} + \frac{1}{R}B_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\phi_{x} \sin \beta \\ & \quad + \frac{2}{R}A_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial v_{0} }}{\partial x} - \frac{1}{{R^{2} }}A_{66} \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial v_{0} }}{\partial x} + \frac{1}{{R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}w_{0} \cos \beta - A_{12} \frac{{\partial u_{0} }}{\partial x}\cos \beta \\ & \quad - \frac{1}{{R^{2} }}A_{22} w_{0} \cos \beta + \frac{1}{{R^{3} }}B_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\phi_{x} \sin \beta + \frac{1}{R}(A_{12} + A_{66} )\frac{{\partial^{2} v_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial x} \\ & \quad + \left( {\frac{1}{R}KA_{55} - \frac{1}{{R^{2} }}B_{22} \cos \beta } \right)\varphi_{x} \sin \beta + \frac{1}{{R^{3} }}B_{66} \frac{{\partial w_{0} }}{\partial \theta }\varphi_{\theta } \sin^{2} \beta - \frac{2}{{R^{2} }}B_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\varphi_{\theta } \sin \beta \\ & \quad + \frac{1}{{R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}u_{0} \sin \beta - \frac{1}{{R^{2} }}A_{22} u_{0} \sin \beta \cos \beta + \frac{1}{{R^{3} }}\left( {B_{22} - B_{66} } \right)\frac{{\partial \phi_{x} }}{\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } - \gamma \dot{w}_{0} \\ & \quad - \frac{2}{{R^{2} }}A_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }v_{0} \sin \beta + \left( {KA_{55} + N_{xx}^{T} - (p_{0} + p_{1} \cos \varOmega_{2} t)} \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{R}A_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial \theta } \\ & \quad + \frac{1}{{R^{3} }}A_{66} \frac{{\partial^{2} v_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}A_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}u_{0} \sin \beta + \frac{1}{{R^{3} }}A_{66} \frac{{\partial w_{0} }}{\partial \theta }v_{0} \sin^{2} \beta + \frac{1}{R}B_{66} \frac{{\partial^{2} \phi_{\theta } }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial \theta } \\ & \quad + \frac{1}{{R^{2} }}\left( {KA_{44} + N_{\theta \theta }^{T} } \right)\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}A_{12} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial v_{0} }}{\partial \theta } + \frac{1}{{R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial v_{0} }}{\partial \theta } + KA_{55} \frac{{\partial \phi_{x} }}{\partial x}\frac{{\partial w_{0} }}{\partial \theta } \\ & \quad - \frac{1}{{R^{2} }}(KA_{44} + A_{22} )\frac{{\partial v_{0} }}{\partial \theta }\cos \beta + B_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial \varphi_{x} }}{\partial x} - \frac{1}{R}B_{12} \frac{{\partial \varphi_{x} }}{\partial x}\cos \beta + \frac{1}{{R^{2} }}B_{12} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial \varphi_{x} }}{\partial x} \\ & \quad + \frac{3}{{2R^{4} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\left( {\frac{{\partial w_{0} }}{\partial \theta }} \right)^{2} + \frac{2}{{R^{2} }}A_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial u_{0} }}{\partial \theta } + \frac{1}{{R^{2} }}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} \phi_{x} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } \\ & \quad + \frac{1}{{R^{2} }}B_{66} \frac{{\partial^{2} \phi_{x} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{1}{{2R^{3} }}A_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\cos \beta + \frac{2}{R}B_{66} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial \phi_{\theta } }}{\partial x} + \frac{1}{{R^{3} }}B_{22} \frac{{\partial^{2} \phi_{\theta } }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial \theta } \\ & \quad + \frac{1}{{R^{2} }}(A_{12} + A_{66} )\frac{{\partial^{2} u_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } - \frac{1}{{R^{2} }}B_{66} \frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial \varphi_{\theta } }}{\partial x}\sin \beta + \frac{1}{{R^{3} }}(A_{22} - A_{66} )\frac{{\partial w_{0} }}{\partial \theta }\frac{{\partial u_{0} }}{\partial \theta }\sin \beta \\ & \quad + \frac{1}{2R}(A_{12} + 2A_{66} )\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left( {\frac{{\partial w_{0} }}{\partial \theta }} \right)^{2} + F\cos \varOmega_{1} t, \\ \end{aligned}$$

(24)

$$L_{3R} = I_{0} \ddot{w}_{0} ,$$

(25)

$$\begin{aligned} L_{4L} = & \, B_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}B_{66} \frac{{\partial^{2} u_{0} }}{{\partial \theta^{2} }} + \frac{1}{R}B_{11} \frac{{\partial u_{0} }}{\partial x}\sin \beta - \frac{1}{{R^{2} }}B_{22} u_{0} \sin^{2} \beta + \frac{1}{R}(D_{12} + D_{66} )\frac{{\partial^{2} \phi_{x} }}{\partial x\partial \theta } \\ & \quad + \frac{1}{R}(B_{12} + B_{66} )\frac{{\partial^{2} v_{0} }}{\partial x\partial \theta } - \frac{1}{{R^{2} }}(B_{22} + B_{66} )\frac{{\partial v_{0} }}{\partial \theta }\sin \beta + \frac{1}{2R}(B_{11} - B_{12} )\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\sin \beta \\ & \quad + \frac{1}{R}B_{12} \frac{{\partial w_{0} }}{\partial x}\cos \beta + B_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}B_{66} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial x} - KA_{55} \frac{{\partial w_{0} }}{\partial x} + \frac{1}{{R^{2} }}D_{66} \frac{{\partial^{2} \phi_{x} }}{{\partial \theta^{2} }} \\ & \quad - \frac{1}{{R^{2} }}B_{22} w_{0} \sin \beta \cos \beta + \frac{1}{R}D_{11} \frac{{\partial \phi_{x} }}{\partial x}\sin \beta - \frac{1}{{2R^{2} }}(B_{12} + B_{22} )\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\sin \beta + D_{11} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} \\ & \quad + \frac{1}{{R^{2} }}(B_{12} + B_{66} )\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial \theta } - \left( {KA_{55} + \frac{1}{{R^{2} }}D_{22} } \right)\phi_{x} - \frac{1}{{R^{2} }}(D_{22} + D_{66} )\frac{{\partial \phi_{\theta } }}{\partial \theta }\sin \beta \\ & \quad + \frac{1}{R}M_{xx}^{T} \sin \beta - \frac{1}{R}M_{\theta \theta }^{T} \sin \beta , \\ \end{aligned}$$

(26)

$$L_{4R} = I_{1} \ddot{u}_{0} + I_{2} \ddot{\phi }_{x},$$

(27)

$$\begin{aligned} L_{5L} = & \frac{1}{R}(B_{12} + B_{66} )\frac{{\partial^{2} u_{0} }}{\partial x\partial \theta } + \frac{1}{{R^{2} }}(B_{22} + B_{66} )\frac{{\partial u_{0} }}{\partial \theta }\sin \beta + B_{66} \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}B_{22} \frac{{\partial^{2} v_{0} }}{{\partial \theta^{2} }} \\ & \quad + \left( {\frac{1}{R}KA_{44} \cos \beta - \frac{1}{{R^{2} }}B_{66} \sin^{2} \beta } \right)v_{0} + \frac{1}{{R^{2} }}\left( {D_{22} + D_{66} } \right)\frac{{\partial \phi_{\theta } }}{\partial \theta } + \frac{1}{{R^{2} }}B_{66} \frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial \theta }\sin \beta \\ & \quad + \left( {\frac{1}{{R^{2} }}B_{22} \cos \beta - \frac{1}{R}KA_{44} } \right)\frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{{R^{3} }}B_{22} \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{R}B_{66} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{{R^{2} }}D_{22} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }} \\ & \quad + \frac{1}{R}B_{66} \frac{{\partial v_{0} }}{\partial x}\sin \beta - \left( {KA_{44} + \frac{1}{{R^{2} }}D_{66} \sin^{2} \beta } \right)\phi_{\theta } + \frac{1}{R}\left( {B_{12} + B_{66} } \right)\frac{{\partial^{2} w_{0} }}{\partial x\partial \theta }\frac{{\partial w_{0} }}{\partial x} \\ & \quad + \frac{1}{R}(D_{12} + D_{66} )\frac{{\partial^{2} \phi_{x} }}{\partial x\partial \theta } + D_{66} \frac{{\partial^{2} \phi_{\theta } }}{{\partial x^{2} }} + \frac{1}{R}D_{66} \frac{{\partial \phi_{\theta } }}{\partial x}, \\ \end{aligned}$$

(28)

$$L_{5R} = I_{1} \ddot{v}_{0} + I_{2} \ddot{\phi }_{\theta }.$$

(29)

Appendix 2: Matrixes and Vectors of Eq. (19)

$$\varvec{W} = \left[ {\begin{array}{*{20}c} {w_{1} } & {w_{2} } \\ \end{array} } \right]^{T} ,\;\varvec{\mu}= \left[ {\begin{array}{*{20}c} {\mu_{1} } & 0 \\ 0 & {\mu_{2} } \\ \end{array} } \right],$$

(30)

$$\varvec{M} = \left[ {\begin{array}{*{20}c} {\xi_{10} } & 0 \\ 0 & {\xi_{20} } \\ \end{array} } \right],\,\varvec{P} = \left[ {\begin{array}{*{20}c} {\xi_{18} } & 0 \\ 0 & {\xi_{28} } \\ \end{array} } \right](p_{0} + p_{1} \cos \varOmega_{2} t),$$

(31)

$$\varvec{NL} = \xi \left[ {\begin{array}{*{20}c} {w_{1}^{3} } & {w_{1}^{2} w_{2} } & {w_{1}^{2} } & {w_{1} w_{2} } & {w_{2}^{2} } & {w_{1} w_{2}^{2} } & {w_{2}^{3} } \\ \end{array} } \right]^{\text{T}} ,$$

(32)

where

$$\xi = \left[ {\begin{array}{*{20}c} {\xi_{11} } & {\xi_{12} } & {\xi_{13} } & {\xi_{14} } & {\xi_{15} } & {\xi_{16} } & {\xi_{17} } \\ {\xi_{21} } & {\xi_{22} } & {\xi_{23} } & {\xi_{24} } & {\xi_{25} } & {\xi_{26} } & {\xi_{27} } \\ \end{array} } \right],$$

(33)

$$\varvec{C} = \left[ {\begin{array}{*{20}c} {\xi_{1} } & {\xi_{2} } \\ \end{array} } \right]^{\text{T}} ,\;\varvec{F} = \left[ {\begin{array}{*{20}c} {\xi_{19} F_{1} } & 0 \\ 0 & {\xi_{29} F_{2} } \\ \end{array} } \right].$$

(34)