1 Introduction

Most practical mechanical systems have nonlinear dynamic characteristics. When a general input is acted on a nonlinear dynamical system, the nonlinear dynamic behaviors can generate multiplication and intermodulation frequency components in the output spectra. Because the higher order frequency components are much richer than the input frequencies and multiple interferences may occur among all the frequency components, difficulties are often encountered when one wants to evaluate the nonlinear frequency responses of an unknown dynamical system or to quantify the real contribution of a special input to the output by using the measured data.

To address the problems of nonlinear systems, a verity of methods have been developed up to now. Usually, if the governing differential equation is available for an inspected nonlinear dynamic system, the solutions of differential equations can be achieved by using various analytical methods, including perturbation method [1,2,3,4,5], multiple scales method [6,7,8,9], KBM method [10, 11], and harmonic balance method [12,13,14,15] etc. However, in many practical cases, the governing equations of nonlinear systems are not available, and the analytical methods cannot be utilized. Then, in such cases, many mathematic models, such as Volterra series [16,17,18,19,20], NARMAX model [21,22,23], Taylor series [24,25,26], Wiener model [27,28,29], Hammerstein model [30,31,32], and Wiener-Hammerstein model [33,34,35] etc., can be used to identify the nonlinear systems. Among these mathematic models, Volterra series is a powerful tool for the analysis of nonlinear systems when the governing equation is not available. Because of the complexities of nonlinear systems and the well-known fact that the discrete time representation of a continuous time system is not unique, the NARMAX model representation for a nonlinear system may not be unique and, in most cases, also involve a large number of terms. In contrast, Volterra series gives a unified analytical expression for the input–output maps of nonlinear systems, and therefore has more reliability and robustness than NARMAX model. In addition, Volterra series has wider applications than Taylor series, Wiener model, Hammerstein model, and Wiener-Hammerstein model, because the Taylor series model does not take the past input of system into account, and both Wiener and Hammerstein models can be equalized to truncated Volterra series [36].

The multi-dimensional Fourier transforms of Volterra kernels is known as Generalised Frequency Response Functions (GFRFs), which provides a general framework to analyze nonlinear systems in frequency domain [37,38,39]. One of the methods for evaluating GFRFs was implemented by minimizing the mean square deviation of output under the condition that the input is a zero-mean stationary Gaussian process [40]. However, in many mechanical systems, the input does not satisfy Gaussian statistics, such as the vibration excitations generated by raceway geometrical errors in rolling bearings [41]. An extended approach was based on higher order spectra for estimating the linear and quadratic transfer functions of the quadratic time-invariant system with a general input [42] and two general inputs [43]. However, because the number of frequency interactions increases quickly with the order of GFRFs, explicit expressions of frequency interactions required in the extended approach become very complicated when the order is higher than two or three. Another way of GFRFs evaluation was to apply the parametric modeling techniques, typically involving orthonormal basis expansion [44], analytical derivation [45], and harmonic probing [46,47,48,49]. Although these parametric modeling methods can obtain the GFRFs theoretically, they require not only the output data available but also the knowledge of governing equations of nonlinear systems, and inherently have the problem of convergence in iteration processes [50]. Besides, many experiment-based nonlinear modal analysis approaches can be used to identify nonlinear systems [51,52,53,54,55]. For example, the nonlinear parameters can be estimated by the operation of subspace identification without the knowledge of system types [56, 57], or by oblique projection in the absence of input measurements [58]; the nonlinear normal modes of T-beams can be identified by response-controlled stepped-sine testing (RCT) [59, 60]. However, because the procedure of nonlinear modal analysis is very time-consuming, and may raise the risk of damage and fatigue, its effectiveness is affected in practice.

Recently, the concept of nonlinear output frequency response functions (NOFRFs) was proposed based on Volterra series [61], which allows the analyses of nonlinear systems to be carried out in a manner like linear systems. The effectiveness of NOFRFs has been extensively verified, involving energy transfer of bilinear oscillators [62], comparison between NOFRFs and harmonic balance of Duffing oscillators [63], parameter estimation of multi-degree-of-freedom (MDOF) nonlinear systems [64], and applications in structural damage detection of nonlinear systems [65, 66] etc. However, the determination method of NOFRFs in these studies generally requires experimental or simulation results for the nonlinear system under N different input signal excitations, which must have the same waveform but different magnitudes, and the number of different excitations should be equal or greater than the highest order of NOFRFs. Therefore, the existing determination method of NOFRFs is subject to the constraint that the input of system should be deterministic and adjustable exactly, which is infeasible in many practical analyses of mechanical systems.

In this paper, an alternative approach is introduced to evaluate the nonlinear frequency response components of nonlinear dynamical systems with respect to a general input. In Sect. 2, the approach was derived based on conditioned spectral analysis technique. In Sect. 3, two kinds of nonlinear systems were simulated to verify the accuracy of the method. In Sect. 4, an experiment analysis was set up to detect the nonlinear vibration transmissibility of loose bolt connection by applying the method. Section 5 concludes this study.

2 Method

For a stable time-invariant nonlinear system with a general input and a noise contaminated output, the input–output relationship about an equilibrium point can be expressed by Volterra series as

$$ \left\{ \begin{aligned} y\left( t \right) = \sum\limits_{n = 1}^{N} {y_{n} \left( t \right)} + n_{y} \left( t \right) \hfill \\ y_{n} \left( t \right) = \int_{ - \infty }^{\infty } { \cdots \int_{ - \infty }^{\infty } {h_{n} \left( {\tau_{1} , \cdots ,\tau_{n} } \right)\prod\limits_{i = 1}^{n} {\left[ {x\left( {t - \tau_{i} } \right){\text{d}}\tau_{i} } \right]} } } \hfill \\ \end{aligned} \right., $$
(1)

in which \(x(\bullet )\) and \(y(\bullet )\) represent the system input and output respectively, \({y}_{n}(t)\) the output components generated by the n-th order nonlinearity, \({h}_{n}({\tau }_{1},\cdots ,{\tau }_{n})\) is called ‘the n-th order Volterra kernel’ or ‘the n-th order impulse response function’ which can reduce to the well-known impulse response function of linear systems when \(n=1\), \({n}_{y}(t)\) the noise imposed on the output, \(N\) the maximum order of nonlinearities considered for the system. The output components of orders higher than \(N\) are omitted.

In frequency domain, the input–output maps of Eq. (1) can be formulated as

$$ \left\{ \begin{aligned} & Y\left( {{\text{j}}\omega } \right) = \sum\limits_{n = 1}^{N} {Y_{n} \left( {{\text{j}}\omega } \right)} { + }\;{\rm E}\left( {{\text{j}}\omega } \right)\quad \quad {\text{for}}\;\forall \omega \hfill \\& Y_{n} \left( {{\text{j}}\omega } \right) = \frac{1}{{n^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {2\pi } \right)^{n - 1} }}\int_{{\omega_{1} + \cdots + \omega_{n} = \omega }} {Y_{n} \left( {{\text{j}}\omega_{1} , \ldots ,{\text{j}}\omega_{n} } \right){\text{d}}\sigma_{n\omega } } \hfill \\& Y_{n} \left( {{\text{j}}\omega_{1} , \ldots ,{\text{j}}\omega_{n} } \right) = H_{n} \left( {{\text{j}}\omega_{1} , \ldots ,{\text{j}}\omega_{n} } \right)\prod\limits_{i = 1}^{n} {X\left( {{\text{j}}\omega_{i} } \right)} \hfill \\ \end{aligned} \right., $$
(2)

where \(\omega \) signifies the angular frequency, i.e., \(\omega =2\pi f\), \(X({\text{j}}\omega )\) the spectrum of input, \(Y({\text{j}}\omega )\) the spectrum of output, \({Y}_{n}({\text{j}}\omega )\) the n-th order output spectrum components, \({{\text{d}}\sigma }_{n\omega }\) refers to the area of a minute element on the n-dimensional hyperplane \(\omega ={\omega }_{1}+\cdots +{\omega }_{n}\), \({H}_{n}({\text{j}}{\omega }_{1},\dots ,{\text{j}}{\omega }_{n})\) is named GFRFs equaling to the multidimensional Fourier transform of the n-th order impulse response \({h}_{n}({\tau }_{1},\cdots ,{\tau }_{n})\). The integration operation in Eq. (2) means that \({Y}_{n}\left({\text{j}}\omega \right)\) can be achieved by integrating \({Y}_{n}({{\text{j}}\omega }_{1},\dots ,{{\text{j}}\omega }_{n})\) over a n-dimensional hyperplane \(\omega ={\omega }_{1}+\cdots +{\omega }_{n}\). The GFRFs are nature extensions of the linear frequency response function to nonlinear systems, as \({H}_{n}({{\text{j}}\omega }_{1},\dots ,{{\text{j}}\omega }_{n})\) is equal to the linear transfer function when \(n=1\).

Being different from linear systems, nonlinear systems have more complicated input–output relationship because of frequency multiplication and intermodulation, giving rise to the difficulties in identifying output frequency response components of different orders. To address this issue, the concept of NOFRFs was proposed by Lang and Billings [61], which is given by

$$ G_{n} \left( {{\text{j}}\omega } \right) = \frac{{\int_{{\omega_{1} + \cdots + \omega_{n} = \omega }} {H_{n} \left( {{\text{j}}\omega_{1} , \ldots ,{\text{j}}\omega_{n} } \right)\prod\limits_{i = 1}^{n} {X\left( {{\text{j}}\omega_{i} } \right)} {\text{d}}\sigma_{n\omega } } }}{{\int_{{\omega_{1} + \cdots + \omega_{n} = \omega }} {\prod\limits_{i = 1}^{n} {X\left( {{\text{j}}\omega_{i} } \right)} {\text{d}}\sigma_{n\omega } } }}, $$
(3)

under the condition that the denominator is not equal to zero. Then, the n-th order output frequency response of the system can be rewritten as

$$ Y_{n} \left( {{\text{j}}\omega } \right) = G_{n} \left( {{\text{j}}\omega } \right)X_{n} \left( {{\text{j}}\omega } \right), $$
(4)

where

$$ X_{n} \left( {{\text{j}}\omega } \right) = \frac{1}{{n^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {2\pi } \right)^{n - 1} }}\int_{{\omega_{1} + \cdots + \omega_{n} = \omega }} {\prod\limits_{i = 1}^{n} {X\left( {{\text{j}}\omega_{i} } \right)} {\text{d}}\sigma_{n\omega } } . $$
(5)

Equation (4) gives a compacted expression of \({Y}_{n}({\text{j}}\omega )\) in a manner like a linear system, where \({X}_{n}({\text{j}}\omega )\) is the spectrum of input and \({G}_{n}\left({\text{j}}\omega \right)\) is the linear transfer function. Because \({X}_{n}\left({\text{j}}\omega \right)\) is the Fourier transform of \(x\left(t\right)\) to the n-th power, that is,

$$ X_{n} \left( {{\text{j}}\omega } \right) = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^{\infty } {x^{n} \left( t \right){\text{e}}^{{ - {\text{j}}\omega t}} {\text{d}}t} , $$
(6)

the power function \({x}^{n}\left(t\right)\) can be regarded as the input of \({G}_{n}\left({\text{j}}\omega \right)\) in time domain. Substituting Eq. (4) into (2) gives

$$ Y\left( {{\text{j}}\omega } \right) = \sum\limits_{n = 1}^{N} {G_{n} \left( {{\text{j}}\omega } \right)X_{n} \left( {{\text{j}}\omega } \right)} { + }{\rm E}\left( {{\text{j}}\omega } \right), $$
(7)

which reflects that a nonlinear dynamical system can be decomposed into a MISO linear system. To identify the NOFRFs and evaluate the contributions of each order nonlinearity to the output, a digital approach is presented here based on CSA technique.

As for a MISO linear system, the input–output relationship can be quantified by ordinary coherence function

$$ \gamma_{iy}^{2} \left( {{\text{j}}\omega } \right) = \frac{{\left| {S_{iy} \left( {{\text{j}}\omega } \right)} \right|^{2} }}{{S_{ii} \left( {{\text{j}}\omega } \right)S_{yy} \left( {{\text{j}}\omega } \right)}} $$
(8)

under the condition that the inputs are uncorrelated, where \({S}_{ii}\left({\text{j}}\omega \right)\), \({S}_{yy}\left({\text{j}}\omega \right)\) and \({S}_{iy}\left({\text{j}}\omega \right)\) represent the auto-power and cross-power spectra and of the i-th input and the output respectively. In the study, however, the inputs of the equivalent MISO linear system may be correlated with each other, resulting in the difficulties in distinguishing the effects of different order nonlinearities on the output.

Conditioned spectral analysis provides a feasible way for solving the correlation problem of MISO linear systems, but it cannot be applied directly to nonlinear systems because the multiplication and intermodulation components of frequency are not considered in the present CSA process. Based on the model of NOFRFs, the CSA technique is extended to nonlinear systems in this study.

According to Eq. (7), a stable time-invariant nonlinear system with a general input is decomposed into a MISO linear system near an equilibrium point. The correlations between the inputs of different orders can be removed by taking conditioning operations, obtaining an equivalent MISO linear system with multiple uncorrelated inputs, as shown in Fig. 1, where \({X}_{i\bullet \left(i-1\right)!}\left({\text{j}}\omega \right), i=1,\cdots ,N+1\), represent the conditioned inputs. The i-th order input is conditioned by all the lower order inputs \({X}_{1}\left({\text{j}}\omega \right), {X}_{2}\left({\text{j}}\omega \right), \cdots , {X}_{i-1}\left({\text{j}}\omega \right)\) in sequence, meaning that the parts of \({X}_{i}\left({\text{j}}\omega \right)\) correlated with the lower order inputs are all removed. As a result, the conditioned inputs are uncorrelated with each other. The first order input \({X}_{1}\left({\text{j}}\omega \right)\) can be regarded as \({X}_{1\bullet 0!}\left({\text{j}}\omega \right)\), where \(0!\) denotes no conditioning operation. The last conditioned input \({X}_{\left(N+1\right)\bullet N!}\left({\text{j}}\omega \right)\) refers to the measured output conditioned by all the inputs \(\left\{{X}_{i}\left({\text{j}}\omega \right), i=1, 2, \cdots , N\right\}\), equaling to the spectrum of noise \({n}_{y}\left(t\right)\). It is worth noting that any order input is conditioned from the first order input to the higher order inputs. Obviously, conditioning in this sequence conforms to the physical meaning of Volterra series model, because the i-th input depends on the order of frequency intermodulation and the higher order intermodulation is based on the intermodulation of lower orders.

Fig. 1
figure 1

The CSA model of a nonlinear system linearized by NOFRFs

Full size image

In Fig. 1, \({L}_{iy}\left({\text{j}}\omega \right), i=1, 2, \cdots ,N+1\), denote the linear transfer functions between the i-th order conditioned input and the output, and \({L}_{\left(N+1\right)y}\left({\text{j}}\omega \right)\) equals to 1 according to the meaning of \({X}_{\left(N+1\right)\bullet N!}\left({\text{j}}\omega \right)\). Noted that although \(\left\{{L}_{iy}\left({\text{j}}\omega \right)\right\}\) are quite different from the NOFRFs \(\left\{{G}_{i}\left({\text{j}}\omega \right)\right\}\) except \({L}_{1y}\left({\text{j}}\omega \right)={G}_{1}\left({\text{j}}\omega \right)\), the contributions of the inputs to the output are not essentially influenced by the transforming. The relationship between the two models can be formulated as

$$ L_{iy} \left( {{\text{j}}\omega } \right) = \sum\limits_{j = i}^{N} {L_{ij} \left( {{\text{j}}\omega } \right)G_{j} \left( {{\text{j}}\omega } \right)} , $$
(9)

in which \(i=1, 2, \cdots , N\), and \({L}_{ij}\left({\text{j}}\omega \right)\) represents the linear transfer function between the conditioned inputs \({X}_{i\bullet \left(i-1\right)!}\left({\text{j}}\omega \right)\) and \({X}_{j\bullet \left(i-1\right)!}\left({\text{j}}\omega \right)\). It is supposed that \({L}_{ij}\left({\text{j}}\omega \right)=0\) when \(j<i\), and \({L}_{ij}\left({\text{j}}\omega \right)=1\) when \(j=i\).

The conditioned inputs \({X}_{i\bullet \left(i-1\right)!}\left({\text{j}}\omega \right), 2\le i\le N+1\), are formulated as

$$ X_{{i\left( {i - 1} \right)!}} \left( {j\omega } \right) = X_{i} \left( {j\omega } \right) - \sum\limits_{k = 1}^{i - 1} {L_{ki} \left( {j\omega } \right)X_{{k\left( {k - 1} \right)!}} \left( {j\omega } \right)} , $$
(10)

which can be implemented by the iteration

$$ X_{ik!} \left( {j\omega } \right) = X_{{i\left( {k - 1} \right)!}} \left( {j\omega } \right) - L_{ki} \left( {j\omega } \right)X_{{k\left( {k - 1} \right)!}} \left( {j\omega } \right), $$
(11)

where \(1\le k\le i-1\). The conditioned linear transfer functions \({L}_{ij}\left({\text{j}}\omega \right)\) are given by

$$ L_{ij} \left( {j\omega } \right) = \frac{{S_{{ij\left( {i - 1} \right)!}} \left( {j\omega } \right)}}{{S_{{ii\left( {i - 1} \right)!}} \left( {j\omega } \right)}}, $$
(12)

in which \(1\le i<j\le {\text{N}}+1\), \({L}_{i\left(N+1\right)}\left({\text{j}}\omega \right)\) refers to \({L}_{iy}\left({\text{j}}\omega \right)\), \({S}_{ii\bullet \left(i-1\right)!}\left({\text{j}}\omega \right)\) the auto-power spectral density of the conditioned input \({X}_{i\bullet \left(i-1\right)!}\left({\text{j}}\omega \right)\), and \({S}_{ij\bullet \left(i-1\right)!}\left({\text{j}}\omega \right)\) the cross-power spectral density of the conditioned inputs \({X}_{i\bullet \left(i-1\right)!}\left({\text{j}}\omega \right)\) and \({X}_{j\bullet \left(i-1\right)!}\left(\mathrm{j\omega }\right)\). The power spectral densities can be defined by

$$ S_{{ij\left( {i - 1} \right)!}} \left( {j\omega } \right) = E\left[ {X_{{i\left( {i - 1} \right)!}}^{*} \left( {j\omega } \right)X_{{j\left( {i - 1} \right)!}} \left( {j\omega } \right)} \right] $$
(13)

and

$$ S_{{ii\left( {i - 1} \right)!}} \left( {j\omega } \right) = E\left[ {X_{{i\left( {i - 1} \right)!}}^{*} \left( {j\omega } \right)X_{{i\left( {i - 1} \right)!}} \left( {j\omega } \right)} \right] $$
(14)

respectively, where \({\text{E}}\left[\bullet \right]\) denotes the value of expectation and the superscript * signifies complex conjugation.

The conditioned input power spectra can be obtained by

$$ S_{ijk!} \left( {j\omega } \right) = S_{{ij\left( {k - 1} \right)!}} \left( {j\omega } \right) - L_{kj} \left( {j\omega } \right)S_{{ik\left( {k - 1} \right)!}} \left( {j\omega } \right), $$
(15)

and

$$ S_{iik!} \left( {j\omega } \right) = S_{{ii\left( {k - 1} \right)!}} \left( {j\omega } \right) - \left| {L_{ki} \left( {j\omega } \right)} \right|^{2} S_{{kk\left( {k - 1} \right)!}} \left( {j\omega } \right). $$
(16)

in the case of \(i=j\).

By iterating Eqs. (12), (15) and (16) from the first order to the maximal order numerically, one can yield the optimum estimations of \(\left\{{L}_{ij}\left({\text{j}}\omega \right)\right\}\), \(\left\{{S}_{ij\bullet k!}\left(j\omega \right)\right\}\) and \(\left\{{S}_{ii\bullet k!}\left(j\omega \right)\right\}\).

Given the conditioned input–output transfer functions \(\left\{{L}_{iy}\left({\text{j}}\omega \right)\right\}\), the NOFRFs \(\left\{{G}_{i}\left({\text{j}}\omega \right)\right\}\) can be deduced from Eq. (9), that is,

$$ \left\{ \begin{aligned}& G_{N} \left( {{\text{j}}\omega } \right) = L_{Ny} \left( {{\text{j}}\omega } \right) \hfill \\& G_{i} \left( {{\text{j}}\omega } \right) = L_{iy} \left( {{\text{j}}\omega } \right) - \sum\limits_{j = i + 1}^{N} {L_{ij} \left( {{\text{j}}\omega } \right)G_{j} } \left( {{\text{j}}\omega } \right) \hfill \\ \end{aligned} \right., $$
(17)

in which \(i = N - 1,\;N - 2,\; \cdots ,\;1\). Equation (17) provides an alternative way for evaluating the NOFRFs of the nonlinear system.

To sum up, the presented digital method of evaluating NOFRFs of nonlinear systems with a general input is carried out by the algorithm as shown in Fig. 2.

Fig. 2
figure 2

The algorithm of evaluating NOFRFs by using CSA method

Full size image

As a result, the output spectra generated by each order unconditioned input can be yielded by Eq. (4), such that the contributions of each order nonlinearity to the output are distinguished by this way. In addition, the total output power spectrum responding to the original input \(x\left({\text{t}}\right)\) is given by

$$ S_{y:\;x} \left( {j\omega } \right) = \sum\limits_{i = 1}^{N} {\left| {L_{iy} \left( {j\omega } \right)} \right|^{2} S_{{ii\left( {i - 1} \right)!}} \left( {j\omega } \right)} $$
(18)

and the contribution ratio of the original input to the measured output can be quantified by

$$ \gamma_{xy}^{2} \left( {j\omega } \right) = \sum\limits_{i = 1}^{N} {\frac{{S_{{y:\;i\left( {i - 1} \right)!}} \left( {j\omega } \right)}}{{S_{yy} \left( {j\omega } \right)}}} . $$
(19)

3 Simulation studies

3.1 Duffing-Van der Pol oscillator

To verify the algorithm, two classic dynamic nonlinear systems are simulated here. The first nonlinear system is a Duffing-Van der Pol oscillator as shown in Fig. 3. Its motion equation is

$$ \left\{ \begin{aligned} & m\frac{{d^{2} y_{0} \left( t \right)}}{{dt^{2} }} + c\frac{{dy_{0} \left( t \right)}}{dt} + k_{1} y_{0} \left( t \right) + k_{2} y_{0}^{2} \left( t \right) + k_{3} y_{0}^{3} \left( t \right) = x\left( t \right) \hfill \\ & y\left( t \right) = y_{0} \left( t \right) + n\left( t \right) \hfill \\ \end{aligned} \right., $$
(20)

where \(x\left(t\right)\) denotes the force acted on the mass m, \({y}_{0}\left(t\right)\) the displacement of the mass, \(y\left(t\right)\) the measured displacement of the mass, \(n\left(t\right)\) a zero-mean Normally distributed random noise imposed on the measured data of \({y}_{0}\left(t\right)\). \(m=1 {\text{kg}}\), \(c=20 {\text{N}}\bullet {\text{s}}\cdot {{\text{m}}}^{-1}\), \({k}_{1}={10}^{4}\mathrm{ N}\cdot {{\text{m}}}^{-1}\), \({k}_{2}={10}^{7}\mathrm{ N}\cdot {{\text{m}}}^{-2}\) and \({k}_{3}=5\times {10}^{9}\mathrm{ N}\cdot {{\text{m}}}^{-3}\) are the characteristic parameters of the system.

Fig. 3
figure 3

Duffing-Van der Pol oscillator for simulation

Full size image

The general input of the system is given by

$$ x\left( t \right) = \frac{3}{2\pi }\frac{{\sin \left( {2 \times 55 \times \pi \times t} \right) - \sin \left( {2 \times 30 \times \pi \times t} \right)}}{t}, $$
(21)

in which \(-2.56\le t\le 2.56\) seconds as plotted in Fig. 4a. The output of the system is numerically simulated by using the fourth order Runge–Kutta method, as shown in Fig. 4b, and the input and output amplitude spectra obtained by FFT are as sketched in Fig. 5. The output spectrum distributes in the lower range of 0–20 Hz besides the input frequency range of 30–55 Hz, particularly near 15 Hz where a distinct peak appears, implying that a part of power is transferred to the lower frequency range.

Fig. 4
figure 4

The time sequences of the system input and output: a the input, b the output

Full size image
Fig. 5
figure 5

The amplitude spectra of the system input and output obtained by FFT: a the input, b the output

Full size image

To determine the correlations between the different order inputs, the ordinary coherence function \({\gamma }_{ij}^{2}\left(\omega \right)={\left|{S}_{ij}\left({\text{j}}\omega \right)\right|}^{2}{\left[{S}_{ii}\left({\text{j}}\omega \right){S}_{jj}\left({\text{j}}\omega \right)\right]}^{-1}\) is applied, in which \({S}_{ij}\left({\text{j}}\omega \right)\) represents the cross-spectral density functions of the i-th and j-th order inputs, \({S}_{ii}\left({\text{j}}\omega \right)\) and \({S}_{jj}\left({\text{j}}\omega \right)\) represent the auto-power spectral density functions. The coherence spectra between the first five order inputs are as plotted in Fig. 6. It is indicated that significant correlations exist between the inputs of different orders. Take \({\gamma }_{1j}^{2}, j=2, 3, 4, 5\), for example, as shown in Fig. 6a, \({x}_{1}\left(t\right)\) and \({x}_{2}\left(t\right)\) are highly correlated in the frequency bands of 24–30 Hz and 55–62 Hz, while \({x}_{1}\left(t\right)\) and \({x}_{3}\left(t\right)\) in the lower range of 0–13 Hz and the higher range of 70–100 Hz, \({x}_{1}\left(t\right)\) and \({x}_{4}\left(t\right)\) in the middle range of 30–55 Hz where the correlation between \({x}_{1}\left(t\right)\) and \({x}_{5}\left(t\right)\) is even higher. Similarly, distinct correlations also exist between the 2nd, 3rd, and 4th order inputs, which can be seen in Fig. 6b–d, respectively.

Fig. 6
figure 6

The coherence spectra of the input between the first five orders: a between the first and the higher orders, b between the second and the higher orders, c between the third and the higher orders, d between the fourth and the fifth orders

Full size image

The correlations between the inputs of different orders are removed by applying the CSA procedure, obtaining the first five order NOFRFs \(\left\{{G}_{i}\left({\text{j}}\omega \right), i=1, 2, \cdots , 5\right\}\) of the nonlinear system. Their amplitude spectra are as plotted in Fig. 7, which reflect the amplitude-frequency response characteristics of each order nonlinearity with respect to the input. For instance, in the frequency range of 30–55 Hz, the second to fifth order NOFRFs all have higher amplitudes, meaning that the nonlinear system has greater gains on the amplitudes of the second to fifth order unconditioned inputs in the frequency range. Besides, both \(\left|{G}_{3}\left({\text{j}}\omega \right)\right|\) and \(\left|{G}_{5}\left({\text{j}}\omega \right)\right|\) exhibit many distinct peaks in the lower range of 0–20 Hz, implying that the system has notable gains on the third and fifth order unconditioned inputs in the frequency range.

Fig. 7
figure 7

Amplitude spectra of the first five order NOFRFs: a \(\left|{G}_{1}\left(f\right)\right|\); b \(\left|{G}_{2}\left(f\right)\right|\); c \(\left|{G}_{3}\left(f\right)\right|\); d \(\left|{G}_{4}\left(f\right)\right|\); e \(\left|{G}_{5}\left(f\right)\right|\)

Full size image

The amplitude spectra of the first five order response components \(\left\{\left|{Y}_{i}\left({\text{j}}\omega \right)\right|, i=1,\cdots , 5\right\}\) are obtained as plotted in Fig. 8a–e, which reveal the contributions of each order nonlinearity to the system output without considering interferences. The first, third and fifth order inputs induce remarkable output responses in the frequency range of 30–55 Hz, which is identical with the first order input frequency range, while the second and fourth order inputs mainly give rise to the output components in the lower frequency range and the higher frequency range.

Fig. 8
figure 8

The amplitude spectra of the first five order unconditioned output components and the summing spectrum: a \(\left|{Y}_{1}\left(f\right)\right|\); b \(\left|{Y}_{2}\left(f\right)\right|\); c \(\left|{Y}_{3}\left(f\right)\right|\); d \(\left|{Y}_{4}\left(f\right)\right|\); e \(\left|{Y}_{5}\left(f\right)\right|\); f \(\left|Y\left(f\right)\right|\)

Full size image

The amplitude spectrum of total output yielded by summing the unconditioned output response components, i.e., \(\left|\sum_{i=1}^{5}{Y}_{i}\left({\text{j}}\omega \right)\right|\), is as shown in Fig. 8f, which matches the result of Runge–Kutta method in Fig. 5b very well, verifying numerically that the CSA approach is effective in distinguishing the contributions of each order nonlinearity to the output of the system quantitatively. For example, at the frequency of 15.44 Hz,30.30 Hz, 41.44 Hz and 54.73 Hz, the first five order responses and their summation are as listed in Table 1. The percentages of relative deviation between the total output amplitudes obtained by the two methods are 0.70%, 0.31%, 0.58% and 0.26% at these frequencies respectively. The relative deviations are mainly due to the noise \({n}_{y}(t)\) imposed on the output, which is common in practical mechanical systems. Besides, the interference between each order output components are revealed obviously. For example, at the frequency of 15.44 Hz, although the magnitudes of the second to fifth order output components are very high, mutual interference results in severe offset in the amplitude of total output.

Table 1 Contributions of the first five order nonlinearities to the output at some frequencies. (× 10−5 m)
Full size table

3.2 Quadratic system with time lags

The second case for simulation is a dimensionless quadratic system with time lags as shown in Fig. 9. Its governing equation is given by

$$ \left\{ \begin{aligned} & y_{0} \left( t \right) = k_{1} x\left( t \right) + k_{2} x\left( {t - \tau_{1} } \right) + k_{3} x^{2} \left( t \right) + k_{4} x^{2} \left( {t - \tau_{2} } \right) \hfill \\& y\left( t \right) = y_{0} \left( t \right) + n\left( t \right) \hfill \\ \end{aligned} \right., $$
(22)

where \(x\left(t\right)\) and \({y}_{0}\left(t\right)\) represent the input and output of the system in time domain respectively, \(y\left(t\right)\) the measured output of the system, \(n\left(t\right)\) a zero-mean Gaussian noise acted on the output, \({k}_{1}=-0.64\), \({k}_{2}=1.0\), \({k}_{3}=0.9\) and \({k}_{4}=1.0\) are characteristic parameters, \({\tau }_{1}=0.001{\text{s}}\) and \({\tau }_{2}=0.0005{\text{s}}\) refer to the time delays. Suppose that both input and output of the system are displacements and the input is formed by Eq. (21) as same as the first simulated system.

Fig. 9
figure 9

The quadratic nonlinear system with time lags for simulation

Full size image

The output time sequence obtained directly by the fourth order Runge–Kutta method is as shown in Fig. 10a, and the amplitude spectrum of output obtained by FFT is as sketched in Fig. 10b. Obviously, the output spectrum has prominent magnitude in the ranges of 0–25 Hz and 60–110 Hz, while in the frequency range of input, i.e., 30–55 Hz, the magnitude is approximately equal to zero, implying that almost all the power is transferred to the lower and higher frequency ranges.

Fig. 10
figure 10

The output time sequence and amplitude spectrum of the quadratic system with time lags: a the time sequence, b the amplitude spectrum

Full size image

By using the CSA method, the first five order NOFRFs \(\left\{{G}_{i}\left({\text{j}}\omega \right), i=1,\cdots , 5\right\}\) of the system are obtained and their amplitude spectra are as shown in Fig. 11, which reflect the amplitude-frequency response characteristics of each order nonlinearities with respect to the input. The amplitude spectra of the second to fifth order NOFRFs have higher magnitudes in the frequency range of 30–55 Hz which is equal to the original input frequency range. Besides, many distinct peaks exist in the lower and higher frequency ranges, e.g., \(\left|{G}_{3}\left({\text{j}}\omega \right)\right|\) in the ranges of 0–20 Hz and 70–100 Hz, indicating that the NOFRFs also have notable gains on the input at these frequencies.

Fig. 11
figure 11

The amplitude spectra of the first five order NOFRFs of the quadratic system with time lags: a \(\left|{G}_{1}\left(f\right)\right|\); b \(\left|{G}_{2}\left(f\right)\right|\); c \(\left|{G}_{3}\left(f\right)\right|\); d \(\left|{G}_{4}\left(f\right)\right|\); e \(\left|{G}_{5}\left(f\right)\right|\)

Full size image

The amplitude spectra of the first five order response components \(\left\{\left|{Y}_{i}\left({\text{j}}\omega \right)\right|, i=1,\cdots , 5\right\}\), and their summation \(\left|\sum_{i=1}^{5}{Y}_{i}\left({\text{j}}\omega \right)\right|\) are as plotted in Fig. 12. Obviously, the second and fourth order inputs give rise to prominent output responses in the frequency ranges of 0–25 Hz and 60–110 Hz. Although the first, third and fifth order inputs generate notable output responses in the frequency range of 30–55 Hz, the amplitude of their summation decreases nearly to zero due to interferences, as shown in Fig. 12f. Similarly, in the higher frequency range of 110–170 Hz, the output responses of the third to fifth orders also reduced nearly to zero due to interferences.

Fig. 12
figure 12

The amplitude spectra of the first five order unconditioned output components of the second nonlinear system and their summing spectrum: a \(\left|{Y}_{1}\left(f\right)\right|\); b \(\left|{Y}_{2}\left(f\right)\right|\); c \(\left|{Y}_{3}\left(f\right)\right|\); d \(\left|{Y}_{4}\left(f\right)\right|\); e \(\left|{Y}_{5}\left(f\right)\right|\); f \(\left| {\sum\nolimits_{i = 1}^{{5}} {Y_{i} \left( f \right)} } \right|\)

Full size image

The summation of the unconditioned output response components is very close to the result of Runge–Kutta method shown in Fig. 14b, verifying numerically that the approach is effective in quantifying the contributions of each order nonlinearity to the output of the system. For example, at the frequency of 15.05 Hz, 72.13 Hz, 85.23 Hz, 98.13 Hz, the first five order output responses and their summation are as listed in Table 2. The percentages of relative deviation between the total output amplitudes obtained by the two methods are 1.16%, 0.85%, 0.53% and 0.16% at these frequencies respectively, which are mainly due to the noise \({n}_{y}(t)\) imposed on the output. In addition, it is uncovered that mutual interference also happens between the output components of different orders. For example, at the frequency of 85.23 Hz, the amplitude of total output is smaller than \(\left|{Y}_{2}\right|\), \(\left|{Y}_{4}\right|\) and \(\left|{Y}_{5}\right|\) due to the interference between them.

Table 2 Contributions of the first five order nonlinearities to the output at some frequencies. (Dimensionless)
Full size table

4 Identification of bolt looseness

To verify the effectiveness of the method further, an experiment analysis was carried out, in which the method was utilized to test the vibration transferring characteristics of bolt connection when the bolt was tight and loose respectively. The experimental setup is as shown in Fig. 13. Two carbon fiber reinforced polymer (CFRP) plates were connected by a bolt and supported by cushions on both ends. The material properties of the plates are as listed in Table 3. A motor drives a grinding wheel at a speed of 10,200 rpm, generating a vibration excitation because of rotation unbalance. The vibration was transmitted by the plates from the right side of the bolt to the left side. With the purpose of measuring vibration, two acceleration sensors were fixed on each plate near the bolt, named Sensor 1 and Sensor 2 respectively, which were connected to a dynamic signal analysis system. The sampling frequency was 12.8 kHz and the sampling time length was 10 s every time.

Fig. 13
figure 13

The diagram and photograph of experiment apparatus

Full size image
Table 3 Material properties of carbon fiber reinforced epoxy resin composite
Full size table

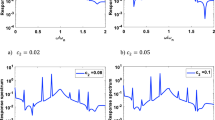
The bolt connection can be taken as a vibration transmission system, the input of which is the vibration generated by the motor and measured by Sensor 1, the output is the vibration measured by Sensor 2. In the light of embodying the influences of bolt tightness on its vibration transfer characteristics, two experiments were carried out in the study, that is, the bolt was fastened in experiment 1 and loose in experiment 2. When the bolt was fastened, the time sequences picked up by Sensor 1 and Sensor 2 are approximate in amplitude as shown in Fig. 14a. And their frequency spectra are almost the same as seen in Fig. 14b and c, in which the peak at 170 Hz is dominant in amplitude and the rest of components are very small, implying that the vibration transmission of the fastened bolt is close to linear. However, when the bolt was loose, the input and output signals were significantly different both in time and frequency domains, as depicted in Fig. 15. In time domain, the amplitude of the output was apparently lower than the input. And in frequency domain, the obvious differences between the multiple frequency components mean that the loose bolt connection has nonlinear vibration transferring properties. For example, at the frequencies of 1887 Hz and 2405 Hz, the amplitude ratios of input relative to 170 Hz were 0.30 and 0.095, while the amplitude ratios of output changed to 0.141 and 0.676, respectively.

Fig. 14
figure 14

The measured vibration of the two plates near the bolt connection when the bolt was fastened: a the time sequences; b the input spectrum; c the output spectrum

Full size image
Fig.15
figure 15

The measured vibration of the two plates near the bolt connection when the bolt was loose: a the time sequences; b the input spectrum; c the output spectrum

Full size image

The amplitude spectra of the first five order NOFRFs are as plotted in Fig. 16 when the bolt was loose and fastened, which are obviously different under the two conditions. The 1st order NORFR of the fastened bolt has signally greater amplitudes than the loose bolt at most frequencies, e.g., near 837 Hz, 2714 Hz and 2945 Hz, indicating that the fastened bolt has more linear vibration transferring characteristics. However, the differences change gradually with the increase of order. Conversely, the amplitudes of the 3rd, 4th and 5th order NOFRFs of loose bolt are more prominent than those of fastened bolt at a lot of frequencies, e.g., near 170 Hz, 1026 Hz and 2430 Hz. This is due to the fact that the loose bolt has obvious nonlinear vibration transferring characteristics. Therefore, the method can be used to detect bolt looseness by observing the changes in amplitude of NOFRFs.

Fig. 16
figure 16

The amplitude spectra of the first five order NOFRFs of the bolted connection system: a \(\left|{G}_{1}\left(f\right)\right|\); b \(\left|{G}_{2}\left(f\right)\right|\); c \(\left|{G}_{3}\left(f\right)\right|\); d \(\left|{G}_{4}\left(f\right)\right|\); e \(\left|{G}_{5}\left(f\right)\right|\)

Full size image

The amplitude spectra of the first five order output components \(\left\{\left|{Y}_{i}\left({\text{j}}\omega \right)\right|, i=1,\cdots , 5\right\}\), and their summation \(\left|\sum_{i=1}^{5}{Y}_{i}\left({\text{j}}\omega \right)\right|\) are as plotted in Fig. 17 when the bolt was fastened and Fig. 18 when the bolt was loose respectively, which reveal the contributions of each order nonlinearity of the system to the output before interference occurs with respect to the input. For example, when the bolt was loose, \(\left|{Y}_{1}\left(f\right)\right|\) had higher amplitudes at the frequencies of 170 Hz, 851 Hz and 2405 Hz, \(\left|{Y}_{2}\left(f\right)\right|\) at 170 Hz, 343 Hz, 1361 Hz, 1881 Hz and 2410 Hz, \(\left|{Y}_{3}\left(f\right)\right|\) at 170 Hz, 1874 Hz and 2396 Hz, \(\left|{Y}_{4}\left(f\right)\right|\) at 170 Hz, 343 Hz, 1361 Hz and 2396 Hz, \(\left|{Y}_{5}\left(f\right)\right|\) at 170 Hz, 1874 Hz and 2396 Hz, meaning that the output response components play an important role in the total output at these frequencies. Comparatively, the amplitudes of each order output were much smaller at the multiple frequencies when the bolt was fastened. Even though the 2nd and 4th order outputs had distinct amplitudes at some multiple frequencies as shown in Fig. 17b and d, they almost canceled each other out in the total output. The total output amplitude spectrum yielded by summing the first fourth order components when the bolt was fastened and loose are as plotted in Figs. 17f and 18f, both of which match the measured amplitude spectra of output very well.

Fig. 17
figure 17

The amplitude spectra of the first five order output response components when the bolt was fastened

Full size image
Fig. 18
figure 18

The amplitude spectra of the first five order output response components when the bolt was loose

Full size image

By comparing the summing output spectra Figs. 17f and 18f with the measured output spectra Figs. 14c and 15c, it is known that the approach is feasible in identifying the nonlinear output frequency response components of the bolt connected plate system. For instance, at the peak frequencies of 170 Hz, 508 Hz, 1169 Hz and 2202 Hz, the first five order output responses and their summations are as listed in Table 4. The percentages of relative deviation between the total output amplitudes obtained by the two methods are 0.002%, 1.61%, 0.25% and 0.03% at these frequencies respectively. A similar conclusion also can be reached when the bolt was loose. For example, at the peak frequencies of 170 Hz, 851 Hz, 1872 Hz, and 2406 Hz, the percentage of relative deviation are merely 0.23%, 0.87%, 0.004%, and 0.29%, as shown in Table 5.

Table 4 Contributions of the first five order nonlinearities to output at some frequencies when the bolt was fastened. (g)
Full size table
Table 5 Contributions of the first five order nonlinearities to the output at some frequencies when the bolt was loose. (g)
Full size table

In contrast, the existing NOFRFs evaluation method, which requires N different input signal excitations with the same waveform but different magnitudes, is infeasible in this case, because the waveform of the measured vibration excitation signals cannot remain unchanged exactly under different test conditions of magnitude. Therefore, the CSA based method has more feasibility in evaluating NOFRFs and nonlinear frequency response components when the input of system are stochastic or nonadjustable.

5 Conclusions

  1. (1)

    An alternative approach of quantifying the nonlinear frequency responses of dynamical systems with respect to a general input was presented based on Volterra and CSA theories in this study, as shown in Fig. 2, in which the correlations between different order inputs of the equivalent MISO system are removed by taking conditioning operations.

  2. (2)

    NOFRFs and nonlinear output response components of different orders were obtained efficiently, which reveal the characteristics of nonlineary frequency response and the contributions of each order nonlinearities to the output.

  3. (3)

    Two kinds of nonlinear dynamical systems were simulated to verify the accuracy of the method. One is a Duffing-Van der Pol oscillator, and the other is a quadratic system with time lags. The total output amplitude spectra reached by the proposed method are very close to the numerical results obtained by the fourth order Runge–Kutta method, verifying that the approach is promising in identifying the nonlinear output frequency responses of nonlinear dynamical systems with respect to a general input.

  4. (4)

    The effectiveness of the method was confirmed by vibration transmission experiments of bolt connected plates. Both when the bolt was fastened and loose, the outputted amplitude spectra of the presented approach match the measuring results very well, and the first five order frequency response components of the system were distinguished successfully.